 ,??, Xin-Yang Wang
,??, Xin-Yang Wang ,??, Wen-Biao Liu
,??, Wen-Biao Liu ,§Department of Physics, Beijing Normal University, Beijing 100875, China
,§Department of Physics, Beijing Normal University, Beijing 100875, ChinaCorresponding authors: ?? E-mail:shad.ali88@yahoo.com?? E-mail:xinyang_wang@foxmail.com§ E-mail:wbliu@bnu.edu.cn
Received:2018-12-12Online:2019-06-1
| Fund supported: |

Abstract
Keywords:
PDF (139KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Shad Ali, Xin-Yang Wang, Wen-Biao Liu. Entropy Evolution in the Interior Volume of a Charged $f(R)$ Black Hole *. [J], 2019, 71(6): 718-722 doi:10.1088/0253-6102/71/6/718
1 Introduction
The definition of the interior volume of a spherically symmetric black hole is proposed by Christodoulou and Rovelli.[1] This definition can be expressed as that the volume of the largest hypersurface inside the black hole bounded by two-sphere in the event horizon is the interior volume. Based on this definition, the interior volume of a Schwarzschild black hole has been calculated. It is shown that the contribution to the largest hypersurface mainly comes from the hypersurface at $r = {3}M/2$ at late time. Then the volume of the hypersurface at $r = {3}M/{2}$ can be regarded as the interior volume of a Schwarzschild black hole. In Eddington-Finkelstein coordinates, the interior volume of a Schwarzschild black hole can be expressed asas $v \gg M$, and $v$ is the advanced Eddington time which is given by $v = t + r_* = t + \int_r^{\infty} ({d r}/{N(r)})$, where $N(r)$ is the blackening factor in the metric. Since the interior volume has linear relation with $v$, it can be regarded as that the interior volume of a Schwarzschild black hole increases with the advanced time. Subsequently, the definition for the interior volume has been extended from a spherically symmetric black hole to an axially symmetric black hole, and then the interior volume of a Kerr black hole has been calculated.[2] In a Kerr black hole, the hypersurface at $r = r_v$ can also be regarded as the largest hypersurface approximately, where $r_v$ takes a special value which corresponds to the maximal value of the volume expression of the hypersurface at $r =$ constant. Therefore, the interior volume of a Kerr black hole is similar to the Schwarzschild case, and it also increases with the advanced time too.
The special property of the interior volume may be a candidate to resolve the information paradox problem.[3] Since the interior volume increases with advanced time, a black hole can have a large volume containing many modes of quantum field and the entropy of these modes may relate to the Bekenstein-Hawking entropy. It means that the lost information on the horizon claimed in Hawking radiation may be stored in the interior of the black hole as quantum states. Moreover, the information on the horizon is associated with Bekenstein-Hawking entropy.[4-6] So, if we obtain the entropy of the quantum field modes inside the black hole and construct the evolution relation between the entropy of the quantum field modes and Bekenstein-Hawking entropy under Hawking radiation, it may provide a way to solve the information paradox. Therefore, it is necessary to investigate the entropy of the quantum modes inside the black hole. The entropy of a scalar field in the interior volume of a Schwarzschild black hole has been investigated in Ref. [7]. Subsequently, the method has been extended from a Schwarzschild black hole to other kinds of black holes including a Kerr black hole.[8-11] It is shown that the entropy increases linearly with the advanced time too, because it is proportional to the interior volume. Moreover, for all kinds of black holes, the entropy of the scalar field in the interior volume is proportional to Bekenstein-Hawking entropy under Hawking radiation approximately except the late stage of Hawking radiation.
Besides, the modified gravity is focused on again in recent 20 years because our universe is experiencing an accelerated expansion. One kind of the modified approaches is adding higher powers of the scalar curvature $R$, the Riemann and Ricci tensors, or their derivatives in the Lagrangian formulation.[12] Among these attempts are Lovelock gravity, braneworld cosmology, scalar-tensor theory and $f(R)$ theory. In these modified gravity theories, $f(R)$ theory is proved to be able to mimic the whole cosmology history, from inflation to the actual accelerated expansion era.[13-14] So, it is interesting and meaningful to extend $f(R)$ gravity from cosmology to the black hole, which could provide us some features of black hole different from Einstein's gravity. Therefore, using the method proposed by Christodoulou and Rovelli, we calculate the interior volume of a charged $f(R)$ black hole. After that, based on the interior volume, we calculate the entropy of the quantum field modes in it, and attempt to construct the evolution relation between the entropy of the quantum field and Bekenstein-Hawking entropy under Hawking radiation. According to the result, we investigate how the modified coefficient in the $f(R)$ gravity theory affects the evolution relation of the two types of entropy.
The organization of the paper is as follows. In Sec. 2, we calculate the interior volume of a charged $f(R)$ black hole. In Sec. 3, we calculate the entropy of a scalar field in a $f(R)$ black hole, and construct the evolution relation between this entropy and Bekenstein-Hawking entropy under Hawking radiation. In Sec. 4, some discussions and conclusions are given.
2 The Interior Volume of a Charged $f(R)$ Black Hole
Christodoulou and Rovelli proposed the definition of the interior volume of a spherically symmetric black hole.[1] This definition can be expressed as that the volume of the largest hypersurface inside the black hole bounded by two-sphere in the event horizon is the interior volume. Based on the definition, the interior volume of a Schwarzschild black hole has been investigated. In a Schwarzschild black hole, the contribution to the largest hypersurface mainly comes from the hypersurface at $r = {3} M/2$ at the late advanced time. So, the interior volume of a Schwarzschild black hole can be regarded as the volume of the hypersurface at $r = {3} M/2$. In the meantime, the general expression for the interior volume of an arbitrary spherically symmetric black hole has been proposed aswhere $r_v$ corresponds to the particular hypersurface at constant $r$, which is the largest hypersurface in a spherically symmetric black hole.
The action of $R+f(R)$ gravity in 4-dimensional spacetime coupled to a nonlinear Maxwell field is
where $R$ is the Ricci scalar curvature, $f(R)$ is an arbitrary function of $R$, $F_{\mu \nu}$ is the electromagnetic field tensor which is related to the electromagnetic potential $A_\mu$ by $F_{\mu \nu} = \partial_\mu A_\nu -\partial_\nu A_\mu$. Considering the constant curvature scalar $R = R_0$, the metric for a 4-dimensional charged $f(R)$ black hole in the Eddington-Finkelstein coordinates is[12,15]
where
In this metric, the modified coefficient is $b = 1 + f' (R_0)$, and the parameter $m$ and $q$ are related to the ADM mass $M$ and the electric charge $Q$ of the black hole as
It illustrates that the modified coefficient $b$ in $f(R)$ gravity changes the mass $M$, the electric charge $Q$ of black hole and the corresponding thermodynamic potential. Treating the Ricci scalar curvature as $R_0 = -{12}/{l^2} = -4 \Lambda$, the metric is used to describe a asymptotical AdS spacetime. The Hawking temperature $T$ with the outer event horizon $r = r_+$ is
where
$ A = 8 -\frac{12 \sqrt{2} M} {b \sqrt{[{{2 \sqrt[3]{2} b (Q^2 R_0-1)}/{\sqrt[3]{C}}-{2^{2/3} \sqrt[3]{C}}/{b}+4}]/{R_0}}}-\frac{2 \sqrt[3]{2} b (Q^2 R_0 -1)}{\sqrt[3]{C}}+\frac{2^{2/3} \sqrt[3]{C}}{b}\,, \\ B = \frac{2 \sqrt[3]{2} b (Q^2 R_0-1)}{\sqrt[3]{C}}-\frac{2^{2/3} \sqrt[3]{C}}{b}+4\,, \\ C = \sqrt{b^2 R_0 (4 b^4 Q^2 (Q^2 R_0+3)^2-36 b^2 M^2 (3 Q^2 R_0+1)+81 M^4 R_0 )} +b^3 (6 Q^2 R_0+2) - 9 b M^2 R_0. $
Moreover, Bekenstein-Hawking entropy of a charged $f(R)$ black hole can be expressed as
where $r_+$ can be written as
$D = \frac{1}{R_0} \bigg[\frac{2 \sqrt[3]{2} b (Q^2 R_0-1)}{\sqrt[3]{C}}-\frac{2^{2/3} \sqrt[3]{C}}{b}+4 \bigg]\,, \quad E = -\frac{2 \sqrt[3]{2} b (Q^2 R_0-1)}{\sqrt[3]{C}}+\frac{2^{2/3} \sqrt[3]{C}}{b}+8\,, \\ C = \sqrt{b^2 R_0 (4 b^4 Q^2 (Q^2 R_0+3)^2-36 b^2 M^2 (3 Q^2 R_0 +1)+81 M^4 R_0)} + b^3 (6 Q^2 R_0+2) -9 b M^2 R_0. $
Since a charged $f(R)$ black hole is a spherically symmetric black hole, we can directly use the general expression Eq. (2) to calculate the interior volume. Analogous to the method in Ref. [1], the value of $r_v$ which is the position of the largest hypersurface in the black hole should satisfy
From Eq. (10), $r_v$ can be obtained as
where
$ F = -\frac{4 b (3 Q^2 R_0-4)}{\sqrt[3]{Z}}+\frac{\sqrt[3]{Z}}{b}+8\,, \quad G = \frac{4 b (3 Q^2 R_0-4)}{\sqrt[3]{Z}}-\frac{\sqrt[3]{Z}}{b}+16\,, \\ Z = 3 \sqrt{3} \sqrt{b^2 R_0 (64 b^4 Q^2 (Q^2 R+4)^2-288 b^2 M^2 (9 Q^2 R_0+4)+2187 M^4 R_0)} +243 b M^2 R_0 -16 b^3 (9 Q^2 R_0+4). $
Substituting the value of $r_v$ into Eq. (2), the interior volume of a charged $f(R)$ black hole can be obtained as
where
$ F = -\frac{4 b (3 Q^2 R_0-4)}{\sqrt[3]{Z}}+\frac{\sqrt[3]{Z}}{b}+8\,, \quad Y = -\frac{18 \sqrt{6} M}{b \sqrt{[{-{4 b (3 Q^2 R_0-4)}/{\sqrt[3]{Z}}+{\sqrt[3]{Z}}/{b}+8]}/{R_0}}}+\frac{4 b (3 Q^2 R-4)}{\sqrt[3]{Z}}-\frac{\sqrt[3]{Z}}{b}+16\,, \\ Z = 3 \sqrt{3} \sqrt{b^2 R_0 (64 b^4 Q^2 (Q^2 R_0+4)^2-288 b^2 M^2 (9 Q^2 R_0+4)+2187 M^4 R_0)} +243 b M^2 R_0 -16 b^3 (9 Q^2 R_0+4).$
3 Interior and Exterior Entropy Evolution under Hawking Radiation
Equation (12) indicates that the interior volume of a charged $f(R)$ black hole is proportional to the advanced time $v$. It means that the interior volume of a charged $f(R)$ black hole, like a Schwarzschild black hole, also increases with the advanced time. The particular character of the interior volume can influence the statistical properties of the quantum field modes in the volume. One quite important quantity for the distribution of the quantum field modes is entropy. So, the entropy of the quantum field can reflect the features of the interior volume and the quantum field modes. Moreover, the entropy of quantum field in the black hole may be a candidate to resolve the information paradox. The information paradox of the black hole arises because the radiation from a black hole is thermal and its detailed form is independent of the structure of matter that collapsed to form the black hole. From quantum perspective, this thermal radiation process makes a pure quantum state, which represents the state of the matter collapsed into a black hole, to transform into the mix state. This transformation would destroy the information of the original quantum state and violate the Liouville's theorem.[16-17] Therefore, the evaporation process of black hole presents the information paradox. However, the entropy is very closely related to the information. Considering Hawking radiation, Bekenstein-Hawking entropy decreases with the evaporation process. Actually, the interior volume of the black hole continues to increase under Hawking radiation, and the entropy of quantum field inside the black hole varies with the interior volume. It could mean that the entropy inside the black hole is very closely related to Bekenstein-Hawking entropy. So, if we can find the evolution relation between the two types of entropy under Hawking radiation, the entropy evolution of the interior (volume) and exterior (event horizon) of the black hole can be connected. From this perspective, it may provide a solution clue to the black hole information paradox. Therefore, it is significant to investigate the entropy of the quantum field in the interior volume and find the connection between this entropy and Bekenstein-Hawking entropy under Hawking radiation. In the following, we only consider the massless scalar field inside a charged $f(R)$ black hole, and Hawking radiation carrying only energy from the black hole, which means that the electric charge $Q$ of the black hole is regarded as a constant.According to Ref. [7], although the interior volume of a Schwarzschild black hole increases linearly with the advanced time, the equilibrium statistical method can also be used to calculate the statistical properties of the scalar field in the interior volume. It is mainly because the largest hypersurface which corresponds to the interior volume accumulates on the hypersurface at $r = {3}M/{2} $ at late advanced time. Therefore, near the hypersurface at $r = {3} M/2$, the proper time between two adjacent largest hypersurfaces tends to zero as the advanced time increases. It means that there is no evolution between these two adjacent largest hypersurfaces. In other words, calculating the statistical properties of the scalar field can be seen as on the approximate simultaneity hypersurface, and this simultaneity hypersurface just corresponds to the interior volume of a Schwarzschild black hole. Hence, the equilibrium statistical method can be used on the largest hypersurface to calculate the statistical properties of the scalar field. In Ref. [7], the entropy of the scalar field in the interior volume of a Schwarzschild black hole can be given as
where $\beta$ is the inverse temperature and $V_\Sigma$ is the interior volume of the black hole. Following this idea, we can also use the equilibrium statistical method to calculate the entropy of the scalar field in a charged $f(R)$ black hole. Since a charged $f(R)$ black hole is a spherically symmetric black hole, the largest hypersurface can also be regarded as accumulating on the hypersurface at $r = r_v$. Therefore, analogues to the Schwarzschild case, near the hypersurface at $r = r_v$, there is still no evolution between two adjacent largest hypersurfaces as the advanced time increases. It means that the equilibrium statistical method can also be used to calculate the statistical properties of the scalar field in a charged $f(R)$ black hole. In addition, according to Ref. [11], the entropy of the scalar field in the interior volume has been generally demonstrated that it can always be expressed as Eq. (13). Therefore, we can directly use Eq. (13) to investigate the evolution of the scalar field entropy under Hawking radiation.
Now, we want to find the connection between the evolution of the entropy of the scalar field in the interior volume and Bekenstein-Hawking entropy under Hawking radiation. According to Ref. [11], in order to construct the connection, two important assumptions as the black-body radiation and quasi-static process should be proposed. Based on these two assumptions, the temperature of the scalar field in the interior volume can be regarded as Hawking temperature in an infinitesimal evaporation process. Moreover, according to the above statement, the equilibrium statistical method can be used to calculate the statistical properties of the scalar field in the interior volume of the black hole in an infinitesimal process. Therefore, we should find the connection between the evolution of the two types of entropy in an infinitesimal evaporation process.
Substituting Hawking temperature Eq. (7) and the interior volume of a charged $f(R)$ black hole Eq. (12) into Eq. (13), the entropy of the scalar field in a charged $f(R)$ black hole can be expressed as
In an infinitesimal evaporation process, the evolution of the scalar field entropy can be expressed as the differential form as
Next, we want to construct the evolution relation between the entropy of the scalar field and Bekenstein-Hawking entropy under Hawking radiation. Taking the differentiation of Eq. (8), we have
According to the black body assumption, the radiation process should satisfy the Stefan-Boltzmann law as
where $\sigma$ is a positive constant related to the number of quantized matter fields coupling with gravity,[18] $A$ is the area of the event horizon, and $T$ is Hawking temperature. Substituting Hawking temperature $T$ and the area $A$ into Eq. (17), we have
Substituting Eq. (18) into Eq. (16), the differential relation between the Bekenstein-Hawking entropy and the advanced time can be given as
Finally, combining Eqs. (15) and (19), the proportional relation between the variation of the scalar field entropy and the variation of Bekenstein-Hawking entropy in an infinitesimal evaporation process can be expressed as
According to the quasi-static assumption, we have ${d M}/{d v} \ll 1$, and then the second term can be ignored. Therefore, writing the differential form as the derivative form, the evolution relation between the entropy of the scalar field in a charged $f(R)$ black hole and Bekenstein-Hawking entropy under Hawking radiation can be expressed as
where the dot indicates derivative by advanced time $v$ and $\gamma (M, Q; b) = {\alpha(M, Q; b)}/{\theta(M, Q; b)}$. Since the expansion of the function $\gamma(M, Q; b)$ is too long and very complicated, the concrete expression is not given here.
4 Discussions and Conclusions
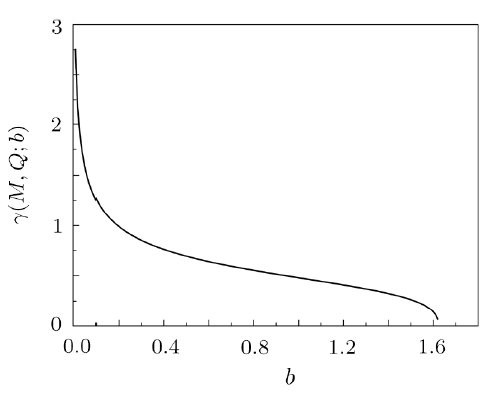
Based on the detailed numerical calculation, the relation between the proportionality coefficient $\gamma (M, Q; b)$ and the modified coefficient $b$ in the $f(R)$ gravity theory is shown in Fig. 1.Fig. 1
 New window|Download| PPT slide
New window|Download| PPT slideFig. 1The proportionality coefficient $\gamma (M, Q; b)$ as a function of $b$ while $M = 2$, $Q = 1$, and $R_0=-12$.
It is shown that $\gamma (M, Q; b )$ gradually decreases with increasing coefficient $b$. Since the solution will degenerate to standard Einstein charged AdS black holes as $b = 1$ and $R_0 = -{12}/{l^2} = -4 \Lambda$, the function $\gamma (M, Q; b )$ should be the evolution relation between the scalar field entropy and Bekenstein-Hawking entropy under Hawking radiation for usual charged AdS black holes. When $b < 1$, the value of the function $\gamma (M, Q; b )$ increases as $b$ decreases, and its value diverges at $b = 0$. It means that the variation of the scalar field entropy is greater than the variation of Bekenstein-Hawking entropy under an infinitesimal evaporation process. In other words, the growth rate of the scalar field entropy in the interior volume of the black hole is greater than the decreasing rate of Bekenstein-Hawking entropy under Hawking radiation. When $b > 1$, the value of the function $\gamma (M, Q; b )$ decreases, and its value will approach to zero at $b = 1.6$. It means that the variation of the scalar field entropy is much more less than the variation of Bekenstein-Hawking entropy. In other words, the growth rate of the scalar field entropy in the interior volume of the black hole is much more less than the decreasing rate of Bekenstein-Hawking entropy under Hawking radiation. Actually, the entropy of the scalar field in the interior volume always increases linearly with the advanced time. Therefore, we can conclude that as the modified coefficient $b$ increases, the decreasing rate of Bekenstein-Hawking entropy gradually increases, which means that the radiation rate of Hawking radiation can enhance with the increasing coefficient $b$.
Till now, the interior volume of a charged $f(R)$ black hole has been investigated. Considering the massless scalar field in the interior volume of the black hole, the entropy of the scalar field is calculated using the equilibrium statistical method. According to the two important assumptions, which are the black-body radiation and the quasi-static process, the evolution of the scalar field entropy in an infinitesimal Hawking radiation has been investigated. In an infinitesimal evaporation process, the evolution of Bekenstein-Hawking entropy can be obtained naturally. The proportional relation between the entropy of the scalar field and the Bekenstein-Hawking entropy under Hawking radiation is given. Finally, the relation between the proportionality coefficient of the two types of entropy and the modified coefficient $b$ in the $f(R)$ gravity theory is investigated. It is shown that the radiation rate for the Hawking radiation of a charged $f(R)$ black hole can enhance with the increasing modified coefficient $b$.
Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
PMID:28590252

Abstract We give a brief overview of the black hole information problem emphasizing fundamental issues and recent proposals for its resolution. The focus is on broad perspective and providing a guide to current literature rather than presenting full details. We concentrate on resolutions restoring naive unitarity.
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
