Chong-yao Chen¹, Muyang Chen^1,4, Yu-Xin Liu^,1,2,31Department of Physics and State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing 100871, China
²Collaborative Innovation Center of Quantum Matter, Beijing 100871, China
³Center for High Energy Physics, Peking University, Beijing 100871, China

First author contact: ⁴ Present address: Department of Physics, Hunan Normal University, Changsha 410081, China.
Received:2020-07-17Accepted:2020-07-22Online:2020-12-01


Abstract
We investigate the quantum numbers of the pentaquark states ${{\rm{P}}}_{{\rm{c}}}^{+}$, which are composed of 4 (three flavors) quarks and an antiquark, by analyzing their inherent nodal structure in this paper. Assuming that the four quarks form a tetrahedron or a square, and the antiquark is at the ground state, we determine the nodeless structure of the states with orbital angular moment L≤3, and in turn, the accessible low-lying states. Since the inherent nodal structure depends only on the inherent geometric symmetry, we propose the quantum numbers J^P of the low-lying pentaquark states ${{\rm{P}}}_{c}^{+}$ may be ${\tfrac{3}{2}}^{-}$, ${\tfrac{5}{2}}^{-}$, ${\tfrac{3}{2}}^{+}$and ${\tfrac{5}{2}}^{+}$, independent of dynamical models.
Keywords： pentaquark states;exotic hadrons;color confinement;symmetry analysis


PDF (261KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Chong-yao Chen, Muyang Chen, Yu-Xin Liu. Quantum numbers of the pentaquark states ${{\rm{P}}}_{{\rm{c}}}^{+}$ via symmetry analysis. Communications in Theoretical Physics, 2020, 72(12): 125202- doi:10.1088/1572-9494/abb7cd

1. Introduction

Searching for the multiquark states has attracted great attention for more than four decades [1-7]. Analyzing the J/ψp resonances in experiments at the LHCb indicates that there exist pentaquark states including heavy quarks (c and $\bar{c}$) [8]. One of the two resonances has a mass of 4380±8 ± 29MeV and a width of 205±18±86 MeV, and another has a mass of 4449.8± 1.7±2.5 MeV and a width of 39±5 ± 19 MeV. They are proposed to hold opposite parity, with one state having spin 3/2 and the other 5/2. Even though quite a lot of theoretical investigations have been accomplished consequently (see for example, [9-29], for reviews, see [3, 4]), the concrete spin and parity have not yet been well-assigned to the two states. Recently the pentaquark states have been updated as 4312 MeV with a width about 9.8 MeV, 4440 MeV with a width about 20.6 MeV and 4457 MeV with a width about 6.4 MeV [30], and the quantum numbers of the states have not yet been determined either [31], although many theoretical works have tried to shed light on this. For instance, by considering the states with molecular structure, the quantum numbers are proposed as ${J}^{P}={\tfrac{1}{2}}^{-},{\tfrac{1}{2}}^{-},{\tfrac{3}{2}}^{-}$ (or ${\tfrac{5}{2}}^{-}$) (see for example [32-39]), or ${\tfrac{1}{2}}^{-}$(or ${\tfrac{3}{2}}^{-}$) and excited states with ${J}^{P}={\tfrac{1}{2}}^{-}$ [40], which are not consistent with those proposed in reference [41]. Furthermore, stringently speaking, pentaquark states refer to the color singlets composed of 4 quarks and 1 antiquark. In such a compact pentaquark scenario, their quantum numbers are proposed as ${J}^{P}={\tfrac{3}{2}}^{-},{\tfrac{1}{2}}^{-},{\tfrac{3}{2}}^{-}$ via considering the uncertainty and the rearrangement decay properties (see, e.g., reference [42]). Since fundamental calculation for the pentaquark states via QCD is not available at the present stage, we investigate the quantum numbers by analyzing the symmetry, more explicitly the intrinsic nodal structure, of the color singlets including 4 three flavor quarks and 1 antiquark in this paper.

The remainder of this paper is organized as follows: in section 2, we give a classification of the wave functions of the pentaquark states according to the symmetries of the quarks. Then in section 3 we assume that the 4 quarks form a tetrahedron or a square and analyze the nodeless structure of the states with orbital angular momentum L≤3, in turn, proposing the quantum numbers of the pentaquark states. Finally, we give our conclusion and some remarks in the last section.

2. Structure of the wave functions

It has been known that the wave functions of few-body systems can usually be written as a coupling of the orbital part and an internal part, and the inherent nodal surface (INS) analysis approach is quite powerful to assign the quantum numbers to a system (see, e.g., references [43-46]). One can definitely take the INS analysis approach to investigate the pentaquark states (${q}^{4}\bar{q}$ systems) at the quark model level since they are typically few-body systems. Since quarks and antiquarks can never identified with each other, there does not exist antisymmetric restrictions on the wave function when interchanging a quark with the antiquark. However, if we consider only the 4 quarks, it should be antisymmetric, i.e. it has the symmetry [1⁴], if we ignore the current quark mass difference. Considering the system of the 4 quarks involve three flavors (e.g., uudc, uuds, uudb, and so on), one knows well that the system possesses the internal symmetry ${{SU}}_{{CFS}}(18)\supset {{SU}}_{C}(3)\otimes {{SU}}_{F}(3)\otimes {{SU}}_{S}(2)$. Meanwhile the orbital part holds the symmetry of the permutation group S₄. Let [f]_O, [f]_C and [f]_FS be the irreducible representation (IRREP) of the groups associated with the orbital, the color and the flavor-spin space, respectively, we should have(1)$\begin{eqnarray}{[{1}^{4}]\in {[f]}_{O}\otimes {[f]}_{C}\otimes [f]}_{{FS}}.\end{eqnarray}$The lack of experimental observation of free ‘color charge' indicates that all the hadronic states should be SU(3) color-singlets. For the ${qqqq}\bar{q}$ system, the IRREP of the SU(3) color space should be $[222]$. Consequently, we have the IRREP of the color part of the 4-quark system as ${[f]}_{C}=[211]$. Then [f]_O⨂[f]_FS should be [3 1], which is the conjugate of [211]. In turn, the configuration of [f]_O and [f]_FS can be fixed with the reduction principle of the direct product of the IRREPs of the unitary group.

The obtained possible [f]_FS and the corresponding [f]_O are listed in table 1. Corresponding to each IRREP ${[f]}_{{FS}}$, the flavor and spin decomposition of the three flavors q⁴ state and the ${q}^{4}\bar{q}$ state have been given in reference [47]. We recall them here in tables 2 and 3.


Table 1.
Table 1.IRREPs of the flavor-spin symmetry corresponding to each possible orbital symmetry.

[f]O	[f]FS
[4]	[31]
[31]	[4], [31], [22], [211]
[22]	[31], [211]
[211]	[31], [22], [211], [1111]
[1111]	[211]

New window|CSV


Table 2.
Table 2.Spin-flavor decomposition of the three flavor q⁴ states (taken from reference [47]. The subscripts stand for the dimensions of the IRREP).

[f]O	SUFS(6)		SUF(3)	⨂	SUS(2)
[4]	[4]126		[4]15	⨂	[4]5
			[31]15	⨂	[31]3
			[22]6	⨂	[22]1
[31]	[31]210		[4]15	⨂	[31]3
			[31]15	⨂	[4]5
			[31]15	⨂	[31]3
			[31]15	⨂	[22]1
			[22]6	⨂	[31]3
			[211]3	⨂	[22]1
			[211]3	⨂	[31]3
[22]	[22]105		[4]15	⨂	[22]1
			[31]15	⨂	[31]3
			[22]6	⨂	[4]5
			[22]6	⨂	[22]1
			[211]3	⨂	[31]3
[211]	[211]105		[31]15	⨂	[31]3
			[31]15	⨂	[22]1
			[22]6	⨂	[31]3
			[211]3	⨂	[4]5
			[211]3	⨂	[31]3
			[211]3	⨂	[22]1
[1111]	[1111]15		[22]6	⨂	[22]1
			[211]3	⨂	[31]3

New window|CSV


Table 3.
Table 3.Spin-flavor decomposition of the ${q}^{4}\bar{q}$ states (taken from reference [47]. The subscripts stand for the dimensions of the IRREP).

[f]O	SUsf(6)		SUf(3)	⨂	SUs(2)
[4]	[51111]700		[51]35	⨂	[5]6
			[51]35	⨂	[41]4
			[42]27	⨂	[41]4
			[42]27	⨂	[32]2
			[33]10	⨂	[32]2
			[411]10	⨂	[5]6
			[411]10	⨂	[41]4
			[411]10	⨂	[32]2
			[321]8	⨂	[41]4
			[321]8	⨂	[32]2
[4]+[31]	[411111]56		[411]10	⨂	[41]4
			[321]8	⨂	[32]2
[31]	[42111]1134		[51]35	⨂	[41]4
			[51]35	⨂	[32]2
			[42]27	⨂	[5]6
			2([42]27	⨂	[41]4)
			2([42]27	⨂	[32]2)
			[33]10	⨂	[41]4
			[33]10	⨂	[32]2
			[411]10	⨂	[5]6
			2([411]10	⨂	[41]4)
			2([411]10	⨂	[32]2)
			[321]8	⨂	[5]6
			2([321]8	⨂	[41]4)
			2([321]8	⨂	[32]2)
			[222]1	⨂	[41]4
			[222]1	⨂	[32]2
[f]O	SUsf(6)		SUf(3)	⨂	SUs(2)
[31]+[22]+[211]	[321111]70		[411]10	⨂	[32]2
			${[321]}_{8}$	⨂	[41]4
			[321]8	⨂	[32]2
			[222]1	⨂	[32]2
[22]	[33111]560		[51]35	⨂	[32]2
			[42]27	⨂	[41]4
			[42]27	⨂	[32]2
			[33]10	⨂	[5]6
			[33]10	⨂	[41]4
			[33]10	⨂	[32]2
			[411]10	⨂	[41]4
			[411]10	⨂	[32]2
			[321]8	⨂	[5]6
			2([321]8	⨂	[41]4)
			2([321]8	⨂	[32]2)
			[222]1	⨂	[41]4
[211]	[3211]540		[42]7	⨂	[41]4
			2([42]7	⨂	[32]2
			[33]10	⨂	[41]4
			[33]10	⨂	[32]2
			[411]10	⨂	[41]4
			[411]10	⨂	[32]2
			[321]8	⨂	[5]6
			2([321]8	⨂	[41]4)
			2([321]8	⨂	[32]2)
			[222]1	⨂	[5]6
			[222]1	⨂	[41]4
			[222]1	⨂	[32]2
[211]+[1111]	[222111]20		[321]8	⨂	[32]2
			[222]1	⨂	[41]4
[1111]	[22221]70		[33]10	⨂	[32]2
			[321]8	⨂	[41]4
			[321]8	⨂	[32]2
			[222]1	⨂	[32]2

New window|CSV

It is obvious that such an orbital and flavor-spin configuration space is very large. Therefore we should pick out the significant ones for the low-lying pentaquark states.

3. Inherent nodal structure analysis

From tables 1-3 we can notice that, given an IRREP of the orbital wave function, we can deduce the corresponding flavor and spin part of the wave function. Generally, the orbital wave function depends on the geometric configuration and the dynamics, or, in the present article, we should say models. In this section, we analyze the structure of the wave functions of the pentaquark states independent of dynamical models.

The zero points for the wave function are known as nodes. The locus for the nodes is a surface, i.e. the nodal surface, in configuration space. For usual bound states of a quantum system, the fewer nodes the configuration contains, the lower energy the state has. The dynamical nodal surface depends on the dynamics of the system, while the INS relies only on the inherent geometric configuration of the system.

Let ${ \mathcal A }$ be a geometric configuration in the coordinate space of a quantum system, and let $\hat{{O}_{i}}$ be an element of the operation on the wave function $F({ \mathcal A })$, we have(2)$\begin{eqnarray}\hat{{O}_{i}}F({ \mathcal A })=F(\hat{{O}_{i}}{ \mathcal A }).\end{eqnarray}$If the operation $\hat{{O}_{i}}$ leaves the configuration ${ \mathcal A }$ invariant, i.e. $\hat{{O}_{i}}{ \mathcal A }={ \mathcal A }$, the above equation becomes(3)$\begin{eqnarray}\hat{{O}_{i}}F({ \mathcal A })=F({ \mathcal A }).\end{eqnarray}$If there do not exist common non-zero solutions for the wave functions governed by equation (3), all the $F({ \mathcal A })$ must be zero at the configuration ${ \mathcal A }$, then a nodal surface appears.

The wave function of the 4 quarks with total angular momentum J and parity π can be written as(4)$\begin{eqnarray}{\rm{\Psi }}=\displaystyle \sum _{L,S,\lambda }{{\rm{\Psi }}}_{L\pi \lambda }^{S},\end{eqnarray}$with(5)$\begin{eqnarray}{{\rm{\Psi }}}_{L\pi \lambda }^{S}=\displaystyle \sum _{i,M,{M}_{S}^{}}{C}_{{LM},{{SM}}_{S}^{}}^{J,{M}_{J}^{}}{F}_{{LM}}^{\pi {\lambda }_{i}}{\chi }_{{{SM}}_{S}^{}}^{\tilde{{\lambda }_{i}}},\end{eqnarray}$where ${F}_{{LM}}^{\pi {\lambda }_{i}}$ is a function of the spatial coordinates, λ denotes an IRREP of the S₄ group, and i indexes the basis vectors of that IRREP. L and S are the total orbital angular momentum and the total spin of the 4 quarks, respectively. They couple to form J via the reduction principle of ${SU}(2)\otimes {SU}(2)\supset {SU}(2)$, i.e, ${C}_{{LM},{{SM}}_{S}^{}}^{J,{M}_{J}^{}}$ is the Clebsch-Gordan coefficient where M, M_S and M_J are the Z-components of L, S and J, respectively. The parity of the 4-quark cluster is given by $\pi ={\left(-1\right)}^{L}$, and the total parity of the pentaquark state $P=-\pi ={\left(-1\right)}^{L+1}$ since the antiquark holds an instinct negative parity. ${\chi }_{{{SM}}_{S}}^{\tilde{{\lambda }_{i}}}$ is the wave function of the inner space, belonging to the $\tilde{{\lambda }_{i}}$-representation, the conjugate of λ_i. ${F}_{{LM}}^{\pi {\lambda }_{i}}$ spans a representation of the direct product of the rotation group, the space inversion group and the permutation group S₄. Thus the transformation property of ${F}_{{LM}}^{\pi {\lambda }_{i}}$ with respect to the operations in terms of the above groups is prescribed, which will impose a very strong constraint on ${F}_{{LM}}^{\pi {\lambda }_{i}}$.

We assume that the 4 quarks form an equilateral tetrahedron (ETH) or a square, which is illustrated in figure 1. We determine all the accessible configurations with L≤3, extending the results of reference [48]. For the case of the ETH, we denote O as the center of the 4 quarks, $\hat{i},\hat{j},\hat{k}$ form the frame, and ${r}_{12}\perp \hat{k}$, ${r}_{34}\perp \hat{k}$. Referring to ${R}_{\delta }^{\vec{\nu }}$ as a rotation about the axis along the vector $\vec{\nu }$ by an angle δ, ${p}_{{ij}}^{}$ as an interchange of the particles i and j, ${p}_{{ijk}}^{}$ and ${p}_{{ijkl}}^{}$ as permutation among the 3 and 4 particles, and $\hat{P}$ as a space inversion, the ETH is evidently invariant to the operations:(6)$\begin{eqnarray}{\hat{O}}_{1}={p}_{12}{p}_{34}{R}_{\pi }^{\hat{k}},\end{eqnarray}$(7)$\begin{eqnarray}{\hat{O}}_{2}={p}_{34}{R}_{\pi }^{\hat{j}}\hat{P},\end{eqnarray}$(8)$\begin{eqnarray}{\hat{O}}_{3}={p}_{1423}{R}_{\pi /2}^{\hat{k}}\hat{P},\end{eqnarray}$(9)$\begin{eqnarray}{\hat{O}}_{4}={p}_{243}{R}_{2\pi /3}^{\hat{n}}.\end{eqnarray}$Inserting each of these operators into equation (3), we have a set of equations,(10)$\begin{eqnarray}({\hat{O}}_{i}-E){F}_{{LM}}^{\pi {\lambda }_{j}}({ \mathcal A })=0.\end{eqnarray}$${F}_{{LM}}^{\pi {\lambda }_{j}}({ \mathcal A })$ is the orbital wave function in the body frame, E is the identity matrix, j and M denote the constituent of λ and L. Equations (6)-(9) are the equations that ${F}_{{LM}}^{\pi {\lambda }_{j}}({ \mathcal A })$ has to fulfill. They are homogeneous linear algebraic equations. If they have common non-zero solutions, we have a nodeless structure. The representations of the permutation group S₄ and the rotation group are represented in tables 4 and 5 where we just show those for L=1 as an example. The equations can be solved easily. The obtained results are shown in table 6, where A denotes the accessible configuration (holds nodeless structure) and ‘−' stands for the inaccessible configuration.

Figure 1.

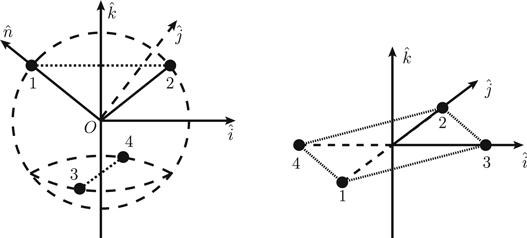New window|Download| PPT slide
Figure 1.Left panel: body frame illustration of the equilateral tetradedron (ETH) configuration. Right panel: body frame illustration of the square.



Table 4.
Table 4.IRREPs of the permutation group S₄ under the standard basis.

[4]	p12=p23=p34=p1423=p243=p1324=1,
[31]	${p}_{12}=\left(\begin{array}{ccc}-1 & 0 & 0\\ -1 & 1 & 0\\ -1 & 0 & 1\end{array}\right)$, ${p}_{23}=\left(\begin{array}{ccc}0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\end{array}\right)$, ${p}_{34}=\left(\begin{array}{ccc}1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0\end{array}\right)$,
	${p}_{1423}=\left(\begin{array}{ccc}0 & 1 & -1\\ 0 & 0 & -1\\ 1 & 0 & -1\end{array}\right)$, ${p}_{243}=\left(\begin{array}{ccc}0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{array}\right)$, ${p}_{1324}=\left(\begin{array}{ccc}0 & -1 & 1\\ 1 & -1 & 0\\ 0 & -1 & 0\end{array}\right)$,
[22]	${p}_{12}=\left(\begin{array}{cc}-1 & 0\\ -1 & 1\end{array}\right)$, ${p}_{23}=\left(\begin{array}{cc}0 & 1\\ 1 & 0\end{array}\right)$, ${p}_{34}=\left(\begin{array}{cc}-1 & 0\\ -1 & 1\end{array}\right)$,
	${p}_{1423}=\left(\begin{array}{cc}-1 & 0\\ -1 & 1\end{array}\right)$, ${p}_{243}=\left(\begin{array}{cc}-1 & 1\\ -1 & 0\end{array}\right)$, ${p}_{1324}=\left(\begin{array}{cc}-1 & 0\\ -1 & 1\end{array}\right)$,
[211]	${p}_{12}=\left(\begin{array}{ccc}1 & 0 & 0\\ 1 & -1 & 0\\ 1 & 0 & -1\end{array}\right)$, ${p}_{23}=\left(\begin{array}{ccc}0 & -1 & 0\\ -1 & 0 & 0\\ 0 & 0 & -1\end{array}\right)$, ${p}_{34}=\left(\begin{array}{ccc}-1 & 0 & 0\\ 0 & 0 & -1\\ 0 & -1 & 0\end{array}\right)$,
	${p}_{1423}=\left(\begin{array}{ccc}0 & -1 & 1\\ 0 & 0 & 1\\ -1 & 0 & 1\end{array}\right)$, ${p}_{243}=\left(\begin{array}{ccc}0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{array}\right)$, ${p}_{1324}=\left(\begin{array}{ccc}0 & 1 & -1\\ -1 & 1 & 0\\ 0 & -1 & 0\end{array}\right)$,
[1111]	p12=p23=p34=p1423=p1324=−1,p243=1.

New window|CSV


Table 5.
Table 5.IRREPs of the rotation group, j is the angular moment, m₁ and m₂ denote the rows and columns of the matrix, α, β, γ is the Eulerian angular.

	${D}_{{m}_{1},{m}_{2}}^{j}(\alpha ,\beta ,\gamma )$ $=\,{\sum }_{k}\tfrac{{\left(-1\right)}^{k}\sqrt{(j+{m}_{1})!(j-{m}_{1})!(j+{m}_{2})!(j-{m}_{2})!}\exp (-{\rm{i}}\alpha {m}_{1}-{\rm{i}}\gamma {m}_{2}){\sin }^{2k-{m}_{1}+{m}_{2}}\left(\tfrac{\beta }{2}\right){\cos }^{2j-2k+{m}_{1}-{m}_{2}}\left(\tfrac{\beta }{2}\right)}{k!(j-k+{m}_{1})!(j-k-{m}_{2})!(k-{m}_{1}+{m}_{2})!}$
L=1	${R}_{\pi }^{\hat{k}}=D(0,0,\pi )=\left(\begin{array}{ccc}-1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & -1\end{array}\right)$, ${R}_{\pi }^{\hat{j}}=D(0,\pi ,0)=\left(\begin{array}{ccc}0 & 0 & 1\\ 0 & -1 & 0\\ 1 & 0 & 0\end{array}\right)$, ${R}_{\pi /2}^{\hat{k}}=D(0,0,\pi /2)=\left(\begin{array}{ccc}-{\rm{i}} & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & {\rm{i}}\end{array}\right)$,
	${R}_{2\pi /3}^{\hat{n}}=D(0,-\theta ,0)\cdot D(2\pi /3,\theta ,0)\,=\,\left(\begin{array}{ccc}-{\rm{i}}/2 & 1/2+{\rm{i}}/2 & -1/2\\ 1/2+{\rm{i}}/2 & 0 & -1/2+{\rm{i}}/2\\ -1/2 & -1/2+{\rm{i}}/2 & {\rm{i}}/2\end{array}\right)$, $\quad \theta =\mathrm{Arccos}(\tfrac{1}{\sqrt{3}})$.

New window|CSV


Table 6.
Table 6.Obtained accessibility of the ETH configuration and the square configuration to the (Lπλ) and related configurations of the wave functions.

	Lπ	[4]	[31]	[22]	[211]	[1111]
ETH	0+	A	—	—	A	—
	1−	—	A	A	A	A
	2+	A	A	A	A	A
	3−	A	A	A	A	A
ETH3	0+	A	—	A	A	—
	1−	—	A	A	A	A
	2+	A	A	A	A	A
	3−	A	A	A	A	A
Square	0+	A	—	A	—	—
	1−	—	A	—	A	—
	2+	A	A	A	A	A
	3−	—	A	—	A	—
Square3	0+	A	A	A	A	—
	1−	—	A	—	A	—
	2+	A	A	A	A	A
	3−	—	A	—	A	-

New window|CSV

It is believed that the wave functions are strongly constrained at the ETH configuration, however they are less constrained in the neighborhood of the ETH, since it holds the highest symmetry. To check such an idea, we have performed calculations where the shape in the left panel of figure 1 is invariant under the operations ${\hat{O}}_{1}$, ${\hat{O}}_{2}$ and ${\hat{O}}_{3}$, but not ${\hat{O}}_{4}$. The obtained results are listed as those marked with ETH₃ in table 6. It shows apparently that all the configurations accessible to the ETH are definitely accessible to ETH₃, and more nodeless configurations are allowed for ETH₃.

For the case of the 4 quarks forming a square, the operations for the configuration to be invariant are(11)$\begin{eqnarray}{\hat{O}}_{1}={p}_{12}{p}_{34}\hat{P},\end{eqnarray}$(12)$\begin{eqnarray}{\hat{O}}_{2}={R}_{\pi }^{\hat{k}}\hat{P},\end{eqnarray}$(13)$\begin{eqnarray}{\hat{O}}_{3}={p}_{34}{R}_{\pi }^{\hat{j}},\end{eqnarray}$(14)$\begin{eqnarray}{\hat{O}}_{4}={p}_{1324}{R}_{\pi /2}^{\hat{k}}.\end{eqnarray}$Inserting them into equation (3), we get another set of equations as equation (10). The obtained accessible configuration of (Lπλ) and the IRREPs of the S₄ group of the wave functions are listed as those marked as ‘square' in table 6. In the neighborhood of the square, for example, prolonged along the $\hat{j}$-direction, it is still invariant under ${\hat{O}}_{1}$, ${\hat{O}}_{2}$ and ${\hat{O}}_{3}$, but not ${\hat{O}}_{4}$. The accessible configurations are also given in table 6 marked ‘square₃'. It is evident that the square-accessible component is inherently nodeless in the neighborhood of the square.

Combining tables 2 and 6 one can get the number of accessible (nodeless) states ${J}_{4}^{\pi }={L}^{\pi }\oplus S$ with orbital angular momentum L≤3. The obtained results are listed in table 7.


Table 7.
Table 7.Obtained number of the accessible (nodeless) states J^P with orbital angular momentum L≤3 of the ETH configuration and square configuration of the 4-quark system and the corresponding less restricted ones.

Configuration	0+	0−	1+	1−	2+	2−	3+	3−	4+	4−	5+	5−
ETH	7	10	19	22	25	28	15	26	4	15	0	4
square	7	7	18	15	25	19	15	17	4	10	0	2
ETH3	9	10	21	22	26	28	15	26	4	15	0	4
square3	11	7	25	15	27	19	15	17	4	10	0	2

New window|CSV

Considering the fact that, for usual bound states of the quantum system, the fewer nodes the configuration contains, the lower energy the state has, one can recognize that J^π of the lowest energy state involving 4 quarks with three flavors is ${J}_{4}^{\pi }={2}^{+}$ (the accessible number is 50). While that of the second and the third lowest states are 2⁻ and 3⁻ (the accessible numbers are 47 and 43, respectively). If the symmetry of the configurations are less constrained, such as those for ETH₃ and square₃, the result almost stays the same (the accessible numbers become 53, 47 and 46, respectively, but ${J}_{4}^{\pi }$ of the third lowest changes to 1⁺).

In our scheme regarding pentaquark states, we notice that the ${{\rm{P}}}_{c}^{+}$ states are composed of a 4-quark cluster involving a c-quark (uudc) and an antiquark $\bar{c}$ at the ground state. The total spin and the parity of the ${{\rm{P}}}_{c}^{+}$ states should be ${J}^{P}({{\rm{P}}}_{c}^{+})={{J}}_{4}^{\pi }({uudc})\oplus {\tfrac{1}{2}}^{-}(\bar{{\rm{c}}})\in \left\{{\tfrac{3}{2}}^{-},{\tfrac{5}{2}}^{-},{\tfrac{3}{2}}^{+},{\tfrac{5}{2}}^{+}\right\}$. Since the c-quark is much heavier than the u- and d-quarks, we can assume that the interaction between the cluster and the $\bar{c}$-quark is similar to that between the c- and $\bar{c}$-quarks. In view of heavy quark interaction, the energy sequence (from lower to higher) of the doublet with mainly ${J}_{4}^{\pi }={2}^{\pm }$, is $\left\{{\tfrac{3}{2}}^{-},{\tfrac{5}{2}}^{-}\right\}$, $\left\{{\tfrac{3}{2}}^{+},{\tfrac{5}{2}}^{+}\right\}$, respectively. Taking the fact that the spin-orbital splitting is proportional to the orbital angular momentum into consideration, one can assign the energy sequence of the J^P states to ${\tfrac{3}{2}}^{-}$, ${\tfrac{5}{2}}^{-}$, ${\tfrac{3}{2}}^{+}$, ${\tfrac{5}{2}}^{+}$.

It should also be mentioned that the pentaquark states do not appear as geometric tetrahedrons or squares. It is well known that a microscopic particle is in fact the quantization of a quantum field, or simply a quantum wave. The ETH configuration of the state will then appear as a spheroid, the deformed tetrahedron (for example that corresponding to the ETH₃) will appear as a pear, and the state with square configuration (Square₃) will display as an oblate ellipsoid (prolate ellipsoid). In this sense the pentaquark states may have finite quadruple moment or dipole moment. Then measuring the electromagnetic property of the pentaquark states could assign the configuration of the states.

4. Summary and remarks

In summary, by analyzing the symmetry, more concretely the inherent nodal structure, of the system including 4 quarks involving three flavors, we show dynamical model independently that the quantum numbers of the lowest-lying pentaquark states ${{\rm{P}}}_{c}^{+}$ could mainly be ${J}^{P}={\tfrac{3}{2}}^{-}$ with orbital angular momentum L=2. The quantum numbers of the other two low-lying pentaquark states ${{\rm{P}}}_{c}$ could be ${J}^{P}={\tfrac{3}{2}}^{+}$, ${\tfrac{5}{2}}^{+}$. And there may exist another ${{\rm{P}}}_{c}$ pentaquark state with ${J}^{P}={\tfrac{5}{2}}^{-}$, which may be observed by analyzing the structure of the peak around 4312 MeV. More experiments or analyzing the existing experiments with broader viewpoints (see, e.g., references [49, 50]) are then expected.

It is finally remarkable that our present results seem only valid for the pentaquark states without molecular structures, namely no color singlet 3-quark states and meson-like states. In fact we could not rule out the molecular structure, since we have not constrained the location of the antiquark in our analysis. If the antiquark locates at the center of the configurations that the 4 quarks formed or on the line perpendicular to the ‘plane' formed by the 4 quarks (the balance of the interactions between the antiquark and each of the quark may result in such features), a molecular structure really may not be involved. If the antiquark does not locate at the center or the 4 quarks' configuration is deformed, the antiquark may form a meson-like state with the quark closing to it, and the other 3 quarks may form a baryon. In this sense the molecular structure emerges. Anyway, our present result is a qualitative result based upon symmetry analysis. Taking the presently assigned configuration and the obtained results into dynamical model calculations can apparently help to reduce the load of numerical calculation tasks. In addition, the work analyzing the inherent nodal structure of the pentaquark states with molecular configurations will be given in a future article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Contracts No. 11435001, No. 11775041, and the National Key Basic Research Program of China under Contract No. 2015CB856900.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Jaffe R L 1977 Phys. Rev. Lett. 38 195
DOI:10.1103/PhysRevLett.38.195 [Cited within: 1]

[2]Jaffe R L 2005 Phys. Rept. 409 1
DOI:10.1016/j.physrep.2004.11.005

[3]Hicks K 2015 Phys. 8 77
DOI:10.1103/Physics.8.77 [Cited within: 1]

[4]Chen H X Chen W Liu X Zhu S L 2016 Phys. Rept. 639 1
DOI:10.1016/j.physrep.2016.05.004 [Cited within: 1]

Liu Y R Chen H X Chen W Liu X Zhu S L 2019 Prog. Part. Nucl. Phys. 107 237
DOI:10.1016/j.physrep.2016.05.004 [Cited within: 1]

[5]Esposito A Pilloni A Plosa A D 2017 Phys. Rept. 668 1
DOI:10.1016/j.physrep.2016.11.002

[6]Olsen S L Skwarnicki T Zieminska D 2018 Rev. Mod. Phys. 90 015003
DOI:10.1103/RevModPhys.90.015003

[7]Guo F K Hanhart C Meissner U-G Wang Q Zhao Q Zou B S 2018 Rev. Mod. Phys. 90 015004
DOI:10.1103/RevModPhys.90.015004 [Cited within: 1]

[8]Aaij R et al. (LHCb collaboration) 2015 Phys. Rev. Lett. 115 072001
DOI:10.1103/PhysRevLett.115.072001 [Cited within: 1]

[9]Chen R Liu X Li X Q Zhu S L 2015 Phys. Rev. Lett. 115 132002
DOI:10.1103/PhysRevLett.115.132002 [Cited within: 1]

[10]Chen H X Chen W Liu X Steele T G Zhu S L 2015 Phys. Rev. Lett. 115 172001
DOI:10.1103/PhysRevLett.115.172001

[11]Kubarovsky V Voloshin M B 2015 Phys. Rev. D 92 031502(R)
DOI:10.1103/PhysRevD.92.031502

[12]Wang Q Liu X H Zhao Q 2015 Phys. Rev. D 92 034022
DOI:10.1103/PhysRevD.92.034022

[13]Scoccola N N Riska D O Rho M 2015 Phys. Rev. D 92 051501(R)
DOI:10.1103/PhysRevD.92.051501

[14]Guo F K Meissner U-G Wang W Yang Z 2015 Phys. Rev. D 92 071502(R)
DOI:10.1103/PhysRevD.92.071502

[15]Roca L Nieves J Oset E 2015 Phys. Rev. D 92 094003
DOI:10.1103/PhysRevD.92.094003

[16]Mironov A Morozov A 2015 JETP Lett. 102 271
DOI:10.1134/S0021364015170099

[17]Maiani L Polosa A D Riquer V 2015 Phys. Lett. B 749 289
DOI:10.1016/j.physletb.2015.08.008

[18]Lebed R F 2015 Phys. Lett. B 749 454
DOI:10.1016/j.physletb.2015.08.032

[19]Meissner U-G Oller J A 2015 Phys. Lett. B 751 59
DOI:10.1016/j.physletb.2015.10.015

[20]Hsiao Y K Geng C Q 2015 Phys. Lett. B 751 572
DOI:10.1016/j.physletb.2015.11.016

[21]Li G N He X G He M 2015 J. High Energy Phys. JHEP12(2015)128
DOI:10.1007/JHEP12(2015)128

[22]Karliner M Rosner J L 2016 Phys. Lett. B 752 329
DOI:10.1016/j.physletb.2015.11.068

[23]He J 2016 Phys. Lett B 753 547
DOI:10.1016/j.physletb.2015.12.071

[24]Liu X H Wang Q Zhao Q 2016 Phys. Lett. B 757 231
DOI:10.1016/j.physletb.2016.03.089

[25]Mikhasenko M arXiv:1507.06552


[26]Anisovich V V Matveev M A Nyiri J Sarantsev A V Semenova A N arXiv:1507.07652


[27]Wang Z G 2016 Eur. Phys. J. C 76 70
DOI:10.1140/epjc/s10052-016-3920-4

[28]Wang Z G Huang T 2016 Eur. Phys. J. C 76 43
DOI:10.1140/epjc/s10052-016-3880-8

[29]Ghosh R Bhattacharya A Chakrabarti B 2017 Phys. Part. Nucl. Lett. 14 550
DOI:10.1134/S1547477117040100 [Cited within: 1]

[30]Aaij R et al. (LHCb collaboration) 2019 Phys. Rev. Lett. 122 222001
DOI:10.1103/PhysRevLett.122.222001 [Cited within: 1]

[31]Fernández-Ramírez C Pilloni A Albaladejo M Jackura A Mathieu V Mikhasenko M Silva-Castro J A Szczepaniak A P 2019 Phys. Rev. Lett. 123 092001
DOI:10.1103/PhysRevLett.123.092001 [Cited within: 1]

[32]Liu M Z Pan Y W Peng F Z Sánchez M S Geng L S Hosaka A Valderrama M P 2019 Phys. Rev. Lett. 122 242001
DOI:10.1103/PhysRevLett.122.242001 [Cited within: 1]

[33]Guo F K Jing H J Meissner U-G Sakai S 2019 Phys. Rev. D 99 091501(R)
DOI:10.1103/PhysRevD.99.091501

[34]Chen R Sun Z F Liu X Zhu S L 2019 Phys. Rev. D 100 011502(R)
DOI:10.1103/PhysRevD.100.011502

[35]Xiao C J Huang Y Dong Y B Geng L S Chen D Y 2019 Phys. Rev. D 100 014022
DOI:10.1103/PhysRevD.100.014022

[36]Meng L Wang B Wang G J Zhu S L 2019 Phys. Rev. D 100 014031
DOI:10.1103/PhysRevD.100.014031

[37]Chen H X Chen W Zhu S L 2019 Phys. Rev. D 100 051501(R)
DOI:10.1103/PhysRevD.100.051501

[38]Lin Y H Zou B S 2019 Phys. Rev. D 100 056005
DOI:10.1103/PhysRevD.100.056005

[39]Sakai S Jing H J Guo F K 2019 Phys. Rev. D 100 074007
DOI:10.1103/PhysRevD.100.074007 [Cited within: 1]

[40]Zhu R L Liu X J Huang H X Qiao C F 2019 Phys. Lett. B 797 134869
DOI:10.1016/j.physletb.2019.134869 [Cited within: 1]

[41]Winney D Fanelli C Pilloni A Hiller Blin A N Fernández-Ramírez C Albaladejo M Mathieu V Mokeev V I Szczepaniak A P 2019 Phys. Rev. D 100 034019
DOI:10.1103/PhysRevD.100.034019 [Cited within: 1]

[42]Cheng J B Liu Y R 2019 Phys. Rev. D 100 054002
DOI:10.1103/PhysRevD.100.054002 [Cited within: 1]

[43]Bao C G Lin C D 1995 Phys. Rev. A 52 3586
DOI:10.1103/PhysRevA.52.3586 [Cited within: 1]

Bao C G 1997 Phys. Rev. Lett. 79 3475
DOI:10.1103/PhysRevA.52.3586 [Cited within: 1]

[44]Bao C G Liu Y X 1999 Phys. Rev. Lett. 82 61
DOI:10.1103/PhysRevLett.82.61

[45]Liu Y X Li J S Bao C G 2002 Phys. Lett. B 544 280
DOI:10.1016/S0370-2693(02)02514-5

[46]Liu Y X Li J S Bao C G 2003 Phys. Rev. C 67 055207
DOI:10.1103/PhysRevC.67.055207 [Cited within: 1]

[47]Bijker R Giannini M M Santopinto E 2004 Eur. Phys. J. A 22 319
DOI:10.1140/epja/i2003-10232-x [Cited within: 3]

[48]Liu Y X Li J S Bao C G arXiv:hep-ph/0401197
[Cited within: 1]

[49]Voloshin M B 2019 Phys. Rev. D 100 034020
DOI:10.1103/PhysRevD.100.034020 [Cited within: 1]

[50]Wang X Y He J Chen X R Wang Q J Zhu X M 2019 Phys. Lett. B 797 134869
DOI:10.1016/j.physletb.2019.134862 [Cited within: 1]