Meng Ye¹, Jian-Hui Li¹, Yong Wang¹, Peng Gao¹, Xin-Xin Lu¹, Yong-Jun Qian^,21 Power Generation Company, GuangZhou 510700, China
² Anhui Qasky Quantum Technology Co., Ltd., Wuhu 241102, China

Received:2020-05-20Revised:2020-09-10Accepted:2020-09-10Online:2020-10-27


Abstract
In practical quantum key distribution (QKD) systems, a single photon-detector (SPD) is one of the most vulnerable components. Faint after-gate attack is a universal attack against the detector. However, the original faint after-gate attack can be discovered by monitoring the photocurrent. This paper presents a probabilistic generalization of the attack, which we refer to as probabilistic faint after-gate attack, by introducing probability control modules. Previous countermeasures for photocurrent monitoring may fail in detecting the eavesdropper under some specific probabilities. To mitigate this threat, we provide a method to determine the detectable boundary in the limitation of precision of photocurrent monitoring, and investigate the security of QKD systems under such boundaries using the weak randomness model.
Keywords： quantum key distribution;practical security;single photon-detector;weak randomness model


PDF (488KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Meng Ye, Jian-Hui Li, Yong Wang, Peng Gao, Xin-Xin Lu, Yong-Jun Qian. Quantum key distribution system against the probabilistic faint after-gate attack. Communications in Theoretical Physics[J], 2020, 72(11): 115102- doi:10.1088/1572-9494/abb7d8

1. Introduction

Quantum key distribution (QKD) enables two legitimate parties, Alice and Bob, to share a series of secure keys [1]. The unconditional security of QKD protocols, such as BB84, has been proven in theory [2 –5]. However, the components used for experimental realization of QKD system deviate from the models in the original security proofs. The imperfect components, such as the source, modulators or detectors, may leave loopholes that the eavesdroppers (Eve) can exploit to steal the secure keys [6 –24]. A single photon-detector (SPD) is a complex equipment at the measurement side, which is vulnerable to a serious of detector-related attacks [10 –23]. A typical example is detector blinding attack [12 –17]. Eve blinds the SPD by injecting bright illumination into the SPDs, and converts them into linear detectors which are not sensitive to single photon. Then Eve can use bright trigger pulses to remotely control the response of the SPDs, thereby stealing almost all key information without evidently increasing errors. Particularly, in a faint after-gate attack [19], Eve does not need to blind the SPD in advance, and the trigger pulses (≤120 photons/pulse) are weaker than the ones in detector blinding attack. Eve makes the trigger pulses arrive at the falling edge of the gate to control the response of the SPDs, thus stealing the key information.

To defense the faint after-gate attack, measurement device independent protocol is a promising approach that can close all loopholes from the measurement unit, however, the challenge is that the approach requires a two-photon interference [25]. Another approach is improving the practical QKD systems with security patches [26]. Since the faint after-gate attack leads to abnormally high photocurrent, monitoring the high current is a possible solution to reveal this attack [27 –29]. However, this solution depends on the precision of monitoring instrument, if the photocurrent increased by an attack is below the detectable bound, the countermeasure seems to fail to detect Eve’s presence. Based on the idea, we establish a model, called probabilistic faint after-gate attack model. If Eve partially implement the faint after-gate attack with a certain probability, she can still obtain information without being detected if the photocurrent increased by the attack is less than the detectable range.

Then we propose a countermeasure. As the open question is how to guarantee the practical security of QKD systems when the photocurrent is under the detectable boundary. The countermeasure gives a method of how to define the detectable bound with practical instrument. Furthermore, under the detectable bound we analyze the security of QKD system in view of the weak randomness model [30], and give a method of removing the information that Eve steals. Some quantum hacking can be described by the weak randomness model, which is proposed by Li et al [30 –33]. In the QKD system, Alice and Bob use true random number generators to prepare and measure the quantum states. The input random numbers which is entered into the quantum device control the classical bit encoding and the bases selection. If the random number is perfect, Eve has no prior knowledge about state preparation and measurement bases choice. However, if the random number is controlled or leaked to Eve, Eve can utilize the loophole to implement quantum hacking and steal the key. For example, in a wavelength attack [9], Eve can use different wavelengths to control the measurement bases selection, which can be treated as the process that the random number for selecting the measurement base is partly controlled by Eve. Similarly, in a time-shift attack [11], Eve can utilize different photon arrival times to control the time-dependent efficiency of two SPDs with different bit encoding. A part of random numbers for state preparation are thus known or controlled by Eve.

The paper is organized as follows. Section 2 describes the probabilistic blinding attack model. In section 3, we demonstrate a countermeasure against the probabilistic faint after-gate attack, and we give a security analysis in view of weak randomness. The secure key can be obtained by quantifying the maximal amount of information leaked to Eve when the increased photocurrent is under the detectable bound. Finally, conclusions are drawn in section 4 .

2. Probabilistic faint after-gate attack model

In this section, we firstly briefly review the original faint after-gate attack [19] The key device of SPD in most commercial QKD systems is avalanche photodiode (APD) [34]. Most of the SPDs operate in gated-mode. When the gate is on, the APD is reverse-biased above the breakdown voltage V_b, SPD is in Geiger mode and sensitive to the single photon. When the gate is off, the APD is reverse-biased below V_b, SPD is in linear mode and cannot detect the single photon. In normal operation, SPD can detect single photon, the quantum state arrives in the gate and generate a click with a detection probability. However, the gate signal is not perfect, the falling edge of the gate is not instantaneous, but has a certain width. In the region, SPD is not sensitive to the single photon pulse, but can detect bright trigger pulse. The detection probability is superlinear to the intensity of the bright trigger pulse: for a factor of two (3 dB) decrease in the intensity of trigger pulse, the detection probability drops steeply from high to low probability, the ratio of the detection probabilities is much larger than 2. The gaps between ideal models and imperfect devices would leave loopholes for Eve, she can exploit the loophole to implement the faint after-gate attack. Taking a polarization-encoding BB84 as an example, the attack process can be described as follows:(1) Alice randomly modulates quantum states from the chosen of four polarization $\{{\rm{H}},{\rm{V}},+,\,-\}$ and sends them to the quantum channel, Eve (Faked-Bob) owns a replica of Bob’s detection apparatus, with which she intercepts and measures the states sent by Alice.
(2) Based on the detection result, Eve (Faked-Alice) resends bright trigger pulses instead of single photon pulses, and makes them arrive at the falling edge of the gate. As the superlinearity of the SPD, Bob will detect the bright trigger pulses sent by Eve with a high probability if he uses the same basis as Eve, and otherwise, with incompatible bases, half of the power of the bright trigger pulses hits the conjugate basis detectors, and cause low probability to be detected.
(3) After Alice and Bob publicly announce basis choice and retain the identical choices, Eve can obtain the basis alignment information from the public channel and sift the measurement result. Therefore, the basis modulated by Eve will be either equal to or different with the basis modulated by Bob. If the modulated bases are equal, Eve can obtain almost all the information about the keys. If the modulated bases differ, the SPD clicks at Bob may introduce tiny error counts since the detection probability is low, thereby not increasing the quantum bit error rate (QBER) evidently. Some researchers find that the APD photocurrent is anomalously higher than the one in normal operation [27 –29]. Monitoring the photocurrent is the intuitive countermeasure against the faint after-gate.


Based on the principle of faint after-gate attack, the target components of probabilistic faint after-gate attack is APD single-photon detectors for gated-mode. Figure 1 shows the schematic of the probabilistic faint after-gate attack. The black lines depict the original quantum channel in normal QKD system. The red lines depict the eavesdropping channel established by Eve. The blue lines depict the composition of the public channel. Eve can obtain the basis alignment information from the public channel. Similarly, Eve (Faked-Bob) probabilistically intercepts the signal from Alice and randomly chooses one of two bases to measure. Compared with the original faint after-gate attack, the Probability Control module is added to control the number of times Eve intercepts the quantum states. Based on the detection result, Eve (Faked-Alice) modulates the corresponding polarization to the bright trigger pulse with specific optical power, and resends to Bob at the falling edge of the gate. The Probability Control module controls the number of times that Eve resends the bright trigger pulses. Therefore, the signals received at Bob’s side have two parts: the bright trigger pulses sent by Eve and the normal single-photon signals transmitted from Alice. After Alice and Bob publicly announce basis choice and retain the identical choices, Eve can eavesdrop part of the key information, which depends on the frequency of attack. If the probability is 100%, the attack is the original faint after-gate attack, and it leads to obviously high photocurrent [27 –29], we can use the countermeasure of monitoring photocurrent to detect Eve. However, if the probability of attack times is small enough, photocurrent monitoring may not reveal the eavesdropper due to limited precision of the monitoring instrument.

Figure 1.

New window|Download| PPT slide
Figure 1.Schematic of the probabilistic faint after-gate attack. Alice and Bob are legitimate communicate parties. For Alice, Eve is the role of Faked-Bob. For Bob, Eve plays the role of Faked-Alice. Probability control is the module that controls the Eve’s frequency of attack.

3. Countermeasure with weak randomness

To explore the security during the probabilistic faint after-gate attack, the countermeasure is as follows. First, the detectable bound of the photocurrent monitoring strategy is defined with a practical monitoring instrument. For the case that the photocurrent is above the detectable bound, this will trigger the alarm. Alice and Bob discard the keys of the time period. For the case that the photocurrent is below the detectable bound, the information that Eve steals can be estimated correctly; thus, Alice and Bob can still obtain the secure key after removing the information by the post-processing method.

For the photocurrent monitoring instrument, we define I₀ as the photocurrent in a normal QKD system and I₁ as the photocurrent during a probabilistic faint after-gate attack with 100% probability. The probability that Eve resends the bright trigger pulses in all received bits at Bob’s SPD is defined as B_a . The precision of the instrument to monitor the photocurrent is larger than p . The photocurrent monitoring instrument can detect the probabilistic blinding attack if their relationship satisfies(1)$ \begin{eqnarray}{B}_{{\rm{a}}}{I}_{1}+(1-{B}_{{\rm{a}}}){I}_{0}\geqslant p+{I}_{0}.\end{eqnarray}$

The minimum probability to resend the bright trigger pulses by Eve in all received bits at Bob’s SPD is defined as B_amin, which satisfies(2)$ \begin{eqnarray}{B}_{\mathrm{amin}}=\displaystyle \frac{p}{{I}_{1}-{I}_{0}}=\displaystyle \frac{p}{{\rm{\Delta }}I}=B,\end{eqnarray}$ where ΔI refers to subtraction of the photocurrent during normal operation and during a probabilistic faint after-gate attack with 100% probability. Thus the parameter B can depict the detectable bound with the practical monitoring instrument. It means monitoring approach will be invalid if the probability B_a is lower than B to detect Eve.

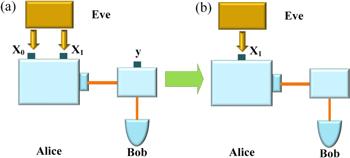
We analyze the security of a probabilistic faint after-gate attack using a weak randomness model. The weak randomness model is shown in figure 2 (a) [30], and there are two random input bits X₀ and X₁ in Alice’s side, which are used to select state preparation of encoding classical bits and bases, respectively. At Bob’s side, there is one random input bit y for the selection of state measurement basis. Alice and Bob publicly announce basis choice and retain the identical choice, which means the random input bits X₁ and y are equivalent after the sifting process. For convenience, we can only assume X₀ and X₁ to control the selection of encoding classical bit and bases. The weak randomness model can be viewed as the case that Eve plants hidden variable into quantum devices to control X₀ and X₁ .

Figure 2.

New window|Download| PPT slide
Figure 2.(a) Weak randomness model, there are two random input bits X₀ and X₁ at Alice’s side. At Bob’s side, there is one random input bit y, where X₀ refers the random input bits to the selection of classical encoding bit, X₁ refers the random input bits to the selection of preparation bases at Alice’s side, y refers to the random input bits to the selection of measurement bases at Bob’s side. (b) Weak randomness model of probabilistic faint after-gate attack, Eve plants hidden variable λ₁ into Alice’s side to control X₁, where X₁ refers the random input bits to the selection of preparation bases at Alice’s side.


For a probabilistic faint after-gate attack, in the intercept process, Eve randomly chooses bases to measure the quantum states from Alice, and then Eve resends the bright trigger pulses to Bob’s SPD, the pulse will be detected at a high probability if Eve chooses the right basis, otherwise it will be detected at a low probability if Eve chooses the wrong basis. In the weak randomness model, Eve plants hidden variable into Bob’s quantum device to control the measurement basis selection. According to the aforementioned simplification of the model, this is equivalent that Eve plants a hidden variable λ₁ into Alice’s quantum device to control the random input bits X₁, which is shown in figure 2 (b). This variable satisfies(3)$ \begin{eqnarray}p({X}_{1})={{\rm{\Sigma }}}_{j}{p}_{{\lambda }_{1}=j}p({X}_{1}| {\lambda }_{1}=j),\end{eqnarray}$ where λ₁ is controlled by Eve. p (X₁ =0∣λ₁ =j) is the probability that Eve modulates the quantum states in the rectilinear basis, and $p({X}_{1}=1| {\lambda }_{1}=j)=1-p({X}_{1}=0| {\lambda }_{1}=j)$ is the probability that Eve modulates the quantum states in the diagonal basis. Note that the hidden variable λ₁ should satisfy ${{\rm{\Sigma }}}_{j}{p}_{{\lambda }_{1}=j}=1$ . Then, the weak randomness model is given as(4)$ \begin{eqnarray}| p({X}_{1}| {\lambda }_{1}=j)-\displaystyle \frac{1}{2}| \,\leqslant \,{\varepsilon }_{1},\end{eqnarray}$ where $0\leqslant {\varepsilon }_{1}\leqslant \tfrac{1}{2}$, it reflects the range that Eve can partly control the selection of measurement bases. ϵ₁ =0 means that Eve cannot control the selection of measurement bases in the case without a probabilistic faint after-gate attack. ${\varepsilon }_{1}=\tfrac{1}{2}$ means that Eve can fully control the selection of measurement bases, and the QKD system cannot generate any secure key in this case.

The weak randomness model can describe the case that the QKD system is under a probabilistic faint after-gate attack using the countermeasure of monitoring photocurrent. For a prepare-and-measure QKD protocol, we apply entanglement distillation and purification technology [35] to analyze the security. Alice prepares maximally entangled state $| \varphi \rangle \,=\tfrac{1}{\sqrt{2}}(| 00\rangle +| 11\rangle )$ . In the probabilistic faint after-gate attack, the maximal amount of information Eve can obtain should be evaluated. According to the parameter of the detectable bound B, we consider the worst-case scenario, where B is actually the part with attack and the left $1-B$ is the part in normal operation. By considering Eve’s attacking behavior in the Pauli channel and the given hidden variable λ₁ =j, after the sifting process, the final quantum state preparation is given by(5)$ \begin{eqnarray}\begin{array}{rcl}{\rho }_{{{AB}}_{j}} & = & {{\rm{\Sigma }}}_{u,v}{q}_{u,v}\left((1-B)\displaystyle \frac{1}{2}I\otimes {X}^{u}{Z}^{v}| \varphi \rangle \langle \varphi | {Z}^{v}{X}^{u}\otimes I\right.\\ & & \left.+(1-B)\displaystyle \frac{1}{2}I\otimes {{HX}}^{u}{Z}^{v}H| \varphi \rangle \langle \varphi | {{HZ}}^{v}{X}^{u}H\otimes I\right.\\ & & \left.+{Bp}({X}_{1}=0| {\lambda }_{1}=j)I\otimes {X}^{u}{Z}^{v}| \varphi \rangle \langle \varphi | {Z}^{v}{X}^{u}\otimes I\right.\\ & & \left.+{Bp}({X}_{1}=1| {\lambda }_{1}=j)I\right.\\ & & \left.\otimes {{HX}}^{u}{Z}^{v}H| \varphi \rangle \langle \varphi | {{HZ}}^{v}{X}^{u}H\otimes I\Space{0ex}{2.8ex}{0ex}\right),\end{array}\end{eqnarray}$ where ${q}_{u,v}(u,v\in \{0,1\})$ is the probability which Eve introduces the ${X}^{u}{Z}^{v}$ operator. q₀₀ denotes the probability that Eve implements the operation $I=\left(\begin{array}{cc}1 & 0\\ 0 & 1\end{array}\right)$ . q₀₁ denotes the probability that Eve implements the operation $Z=\left(\begin{array}{cc}1 & 0\\ 0 & -1\end{array}\right)$, which introduces phase error rate. q₁₀ denotes the probability that Eve implements the operation $X=\left(\begin{array}{cc}0 & 1\\ 1 & 0\end{array}\right)$, which introduces bit error rate. q₁₁ denotes the probability that Eve implement the operation XZ, which introduces bit phase error rate. These parameters above meet the normalization condition of ${{\rm{\Sigma }}}_{u,v}{q}_{u,v}=1$ .

Since the behavior of Eve in the Pauli channel will increase the bit error rate e_b^j and phase error rate e_p^j, their expression can be given, respectively, as(6)$ \begin{eqnarray}{e}_{b}^{j}=\langle {\phi }_{2}| {\rho }_{{{AB}}_{j}}| {\phi }_{2}\rangle +\langle {\phi }_{4}| {\rho }_{{{AB}}_{j}}| {\phi }_{4}\rangle ,\end{eqnarray}$(7)$ \begin{eqnarray}{e}_{p}^{j}=\langle {\phi }_{3}| {\rho }_{{{AB}}_{j}}| {\phi }_{3}\rangle +\langle {\phi }_{4}| {\rho }_{{{AB}}_{j}}| {\phi }_{4}\rangle ,\end{eqnarray}$ where $| {\phi }_{1}\rangle $, $| {\phi }_{2}\rangle $, $| {\phi }_{3}\rangle $, $| {\phi }_{4}\rangle $ are the maximally entangled Bell states, which can be expressed by(8)$ \begin{eqnarray}| {\phi }_{1}\rangle =\displaystyle \frac{1}{\sqrt{2}}(| 00\rangle +| 11\rangle ),\end{eqnarray}$(9)$ \begin{eqnarray}| {\phi }_{2}\rangle =\displaystyle \frac{1}{\sqrt{2}}(| 01\rangle +| 10\rangle ),\end{eqnarray}$(10)$ \begin{eqnarray}| {\phi }_{3}\rangle =\displaystyle \frac{1}{\sqrt{2}}(| 00\rangle -| 11\rangle ),\end{eqnarray}$(11)$ \begin{eqnarray}| {\phi }_{4}\rangle =\displaystyle \frac{1}{\sqrt{2}}(| 01\rangle -| 10\rangle ).\end{eqnarray}$

For the hidden variable controlled by Eve ${\lambda }_{1}=j$, the upper bound of the phase error rate e^j_p can be deduced by the bit error rate e^j_b ,(12)$ \begin{eqnarray}\begin{array}{l}{e}_{p}^{j}-{e}_{b}^{j}\,=\,B(2p({X}_{1}=0| {\lambda }_{1}=j)-1)({q}_{01}-{q}_{10})\\ \quad \leqslant \,2B| p({X}_{1}=0| {\lambda }_{1}=j)-\displaystyle \frac{1}{2}| | {q}_{01}-{q}_{10}| \\ \quad \leqslant \,2B{\varepsilon }_{1}=\delta .\end{array}\end{eqnarray}$

Then, the secret key rate with ${\lambda }_{1}=j$ can be given as(13)$ \begin{eqnarray}{R}^{j}\geqslant 1-h({e}_{p}^{j})-h({e}_{b}^{j})\geqslant 1-h({e}_{b}^{j}+\delta )-h({e}_{b}^{j}).\end{eqnarray}$h (x) is the binary Shannon information function, with the form ${h}({x})=-{{x}{\rm{l}}{\rm{o}}{\rm{g}}}_{2}({x})-(1-{x}){\mathrm{log}}_{2}(1-{x})$ .

With ${e}_{b}={{\rm{\Sigma }}}_{j}{p}_{{\lambda }_{1}=j}{e}_{b}^{j}$, in which e_b is QBER in the practical QKD system, we can get the final secure key rate as(14)$ \begin{eqnarray}\begin{array}{l}R\geqslant {{\rm{\Sigma }}}_{j}{p}_{{\lambda }_{1}=j}{R}^{j}\geqslant {{\rm{\Sigma }}}_{j}{p}_{{\lambda }_{1}=j}(1-h({e}_{b}^{j}+\delta )-h({e}_{b}^{j}))\\ \quad \geqslant \,1-h({{\rm{\Sigma }}}_{j}{p}_{{\lambda }_{1}=j}{e}_{b}^{j}+\delta )-h({{\rm{\Sigma }}}_{j}{p}_{{\lambda }_{1}=j}{e}_{b}^{j})\\ \quad =\,1-h({e}_{b}+\delta )-h({e}_{b}).\end{array}\end{eqnarray}$

With equation (14 ), we investigate the performance of secure key rate with different control parameters of weak randomness ϵ₁ and the detectable bound B . Corresponding simulation results are shown in figure 3 . Compared with different ϵ₁ values (the red dot line and the blue solid line) with the same detectable bound B, if the value of ϵ₁ is larger, less secure keys are generated by the legitimate parties. Moreover, with the same control parameter ϵ₁, if the parameter of detectable bound B is larger (the blue solid line, the purple solid line and the green dot line), the probability that the trigger pulses resent by Eve in all bits received at Bob’s SPD is larger, therefore, more eavesdropped information should be removed to get the secure key rate.

Figure 3.

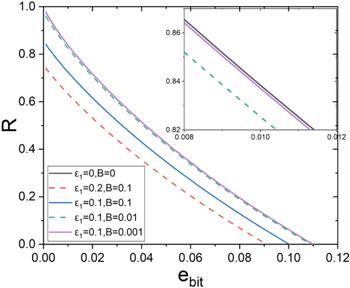
New window|Download| PPT slide
Figure 3.Secure key rate for different detectable bound B and randomness deviation parameters ϵ₁ . The black solid line(ϵ₁ =0, B =0) is described the case without faint after-gate attack.

4. Conclusion

In conclusion, we proposed a probabilistic faint after-gate attack, since the practical monitoring instrument in real-life have limited measurement precision. It is a general attack for APDs single-photon detectors and suitable for the operation mode of gated-mode. Moreover, we give a countermeasure which can define the detectable bound with the practical monitoring instrument. When the probability of a probabilistic faint after-gate attack is above the detectable bound, the monitoring approach is effective to detect Eve. If the probability is below the detectable bound, with the weak randomness model, we can estimate the maximal amount of the information that Eve obtain, then we can employ the post-processing method to remove it. This framework can be applied to analyze the practical security in QKD system with limited instrument precision.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Bennet C H Brassard G 1984 Proc. IEEE Int. Conf. on Computers, Systems and Signal Processing, Bangalore, India, 1984 New York Piscataway, NJ IEEE 175 179 pp 175–9
[Cited within: 1]

[2]Lo H-K Chau H F 1999 Science 283 2050
DOI:10.1126/science.283.5410.2050 [Cited within: 1]

[3]Gisin N Ribordy G Tittel W Zbinden H 2002 Rev. Mod. Phys. 74 145
DOI:10.1103/RevModPhys.74.145

[4]Gottesman D Lo H-K Lütkenhaus N Preskill J 2004 Quantum Inf. Comput. 4 325
DOI:10.5555/2011586.2011587

[5]Inamori H Lütkenhaus N Mayers D 2007 Eur. Phys. J. D 41 599
DOI:10.1140/epjd/e2007-00010-4 [Cited within: 1]

[6]Scarani V Bechmann-Pasquinucci H Cerf N J Dušek M Lütkenhaus N Peev M 2009 Rev. Mod. Phys. 81 1301
DOI:10.1103/RevModPhys.81.1301 [Cited within: 1]

[7]Lütkenhaus N Jahma M 2002 New J. Phys. 4 44
DOI:10.1088/1367-2630/4/1/344

[8]Xu F Qi B Lo H K 2010 New J. Phys. 12 113026
DOI:10.1088/1367-2630/12/11/113026

[9]Li H W et al. 2011 Phys. Rev. A 84 062308
DOI:10.1103/PhysRevA.84.062308 [Cited within: 1]

[10]Qi B Fung C H F Lo H K Ma X 2007 Quantum Inf. Comput. 7 73
[Cited within: 1]

[11]Zhao Y Fung C H F Qi B Chen C Lo H K 2008 Phys. Rev. A 78 042333
DOI:10.1103/PhysRevA.78.042333 [Cited within: 1]

[12]Lydersen L Wiechers C Wittmann C Elser D Skaar J Makarov V 2010 Nat. Photon. 4 686
DOI:10.1038/nphoton.2010.214 [Cited within: 1]

[13]Gerhardt I Liu Q Lamas-Linares A Skaar J Kurtsiefer C Makarov V 2011 Nat. Commun. 2 349
DOI:10.1038/ncomms1348

[14]Lydersen L Wiechers C Wittmann C Elser D Skaar J Makarov V 2010 Opt. Express 18 27938
DOI:10.1364/OE.18.027938

[15]Makarov V 2009 New J. Phys. 11 065003
DOI:10.1088/1367-2630/11/6/065003

[16]Sauge S Lydersen L Anisimov A Skaar J Makarov V 2011 Opt. Express 19 23590
DOI:10.1364/OE.19.023590

[17]Jiang M-S Sun S-H Tang G-Z Ma X-C Li C-Y Liang L-M 2013 Phys. Rev. A 88 062335
DOI:10.1103/PhysRevA.88.062335 [Cited within: 1]

[18]Wiechers C Lydersen L Wittmann C Elser D Skaar J Marquardt C Makarov V Leuchs G 2011 New J. Phys. 13 013043
DOI:10.1088/1367-2630/13/1/013043

[19]Lydersen L Jain N Wittmann C Marøy Ø Skaar J Marquardt C Makarov V Leuchs G 2011 Phys. Rev. A 84 032320
DOI:10.1103/PhysRevA.84.032320 [Cited within: 2]

[20]Lydersen L Akhlaghi M K Majedi A H Skaar J Makarov V 2011 New J. Phys. 13 113042
DOI:10.1088/1367-2630/13/11/113042

[21]Weier H Krauss H Rau M Fürst M Nauerth S Weinfurter H 2011 New J. Phys. 13 073024
DOI:10.1088/1367-2630/13/7/073024

[22]Bugge A N Sauge S Ghazali A M M Skaar J Lydersen L Makarov V 2014 Phys. Rev. Lett. 112 070503
DOI:10.1103/PhysRevLett.112.070503

[23]Qian Y-J He D-Y Wang S Chen W Yin Z-Q Guo G-C Han Z-F 2018 Phys. Rev. Appl. 10 064062
DOI:10.1103/PhysRevApplied.10.064062 [Cited within: 1]

[24]Xu F Ma X Zhang Q Lo H K Pan J W 2020 Rev. Mod. Phys. 92 025002
DOI:10.1103/RevModPhys.92.025002 [Cited within: 1]

[25]Lo H-K Curty M Qi B 2012 Phys. Rev. Lett. 108 130503
DOI:10.1103/PhysRevLett.108.130503 [Cited within: 1]

[26]Lo H-K Curty M Tamaki K 2014 Nat. Photon. 8 595
DOI:10.1038/nphoton.2014.149 [Cited within: 1]

[27]Yuan Z L Dynes J F Shields A J 2011 Appl. Phys. Lett. 98 231104
DOI:10.1063/1.3597221 [Cited within: 3]

[28]Lydersen L Makarov V Skaar J 2011 Appl. Phys. Lett. 99 196101
DOI:10.1063/1.3658806

[29]Yuan Z L Dynes J F Shields A J 2011 Appl. Phys. Lett. 99 196101
DOI:10.1063/1.3658806 [Cited within: 3]

[30]Li H W Yin Z Q Wang S Qian Y J Chen W Guo G C Han Z F 2015 Sci. Rep. 5 16200
DOI:10.1038/srep16200 [Cited within: 3]

[31]Zhao L Y Yin Z Q Li H W Chen W Fang X Han Z F Huang W 2018 Quantum Inf. Process. 17 55
DOI:10.1007/s11128-018-1830-0

[32]Zhang C M Wang W B Li H W Wang Q 2019 Opt. Lett. 44 1226
DOI:10.1364/OL.44.001226

[33]Li H W Xu Z M Cai Q Y 2018 Phys. Rev. A 98 062325
DOI:10.1103/PhysRevA.98.062325 [Cited within: 1]

[34]Eisaman M D Fan J Migdall A Polyakov S V 2011 Rev. Sci. Instrum. 82 071101
DOI:10.1063/1.3610677 [Cited within: 1]

[35]Shor P Preskill J 2000 Phys. Rev. Lett. 85 441
DOI:10.1103/PhysRevLett.85.441 [Cited within: 1]