Rong Huang¹, Yu Yan¹, Zhi-Xu Zhang¹, Lu Qi², Hong-Fu Wang^,1, Shou Zhang^,11Department of Physics, College of Science, Yanbian University, Yanji, Jilin 133002, China
²School of Physics, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China

Received:2020-04-20Revised:2020-06-3Accepted:2020-06-4Online:2020-09-23


Abstract
We explore some interesting phenomena in a simple non-Hermitian ladder system. Special modes with energy eigenvalues closely related to the inter-chain-coupling strength appear in the non-Hermitian ladder system. We show that a phase transition occurs whereby special modes with pure real eigenvalues can switch to special modes with pure imaginary eigenvalues, when the inter-chain-coupling strength changes from symmetric to asymmetric. We find that the density profiles of all the special modes are completely identical under certain conditions, even if the inter-chain-coupling strength is added into the non-Hermitian ladder system in different ways. Moreover, we also demonstrate that the different inter-chain couplings are fundamentally equivalent to adding different on-site potential energies into the non-Hermitian ladder system.
Keywords： non-Hermitian ladder system;special modes;inter-chain-coupling


PDF (3262KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Rong Huang, Yu Yan, Zhi-Xu Zhang, Lu Qi, Hong-Fu Wang, Shou Zhang. Special modes induced by inter-chain coupling in a non-Hermitian ladder system. Communications in Theoretical Physics, 2020, 72(10): 105101- doi:10.1088/1572-9494/aba252

1. Introduction

Non-Hermitian systems, as a current hot research subject of topological insulators, exhibit fascinating properties that are considerably different from those of Hermitian systems [1-24]. Robust edge states with real eigenvalues exist in Hermitian systems under a conventional bulk-boundary correspondence [25-27]. However, a great deal of theoretical study has found a breakdown of the conventional bulk-boundary correspondence in non-Hermitian systems [5-7, 28, 29]. Recently, however, studies have implied that the bulk-boundary correspondence is still valid in certain non-Hermitian systems [30]. Special spectral degeneracies and their associated novel topological properties greatly stimulate the studies of non-Hermitian systems, particularly the non-Hermitian systems induced by asymmetric hopping amplitudes. Biorthonormal eigenvectors [31, 32], new topological invariants [28, 33-36] and a new band theory [37-39] have been established to describe the non-Hermitian systems. With the further investigation of non-Hermitian systems, topological invariants of non-Hermitian systems in real space [40] and new topological classification of non-Hermitian systems have also been proposed [41]. Non-Hermitian systems have attracted a great deal of attention, not only theoretically but also experimentally [42-45].

For one-dimensional (1D) Hermitian systems, there exist extended bulk states in both the open boundary condition (OBC) and the periodic boundary condition (PBC). While the bulk states are exponentially localized at the edge of non-Hermitian systems under the OBC (known as the skin effect) [6], extended topological zero-energy states appear [7]. A size effect can significantly affect the anomalous topological phenomena in non-Hermitian systems under the OBC. The zero-energy edge states of a semi-infinite non-Hermitian system have been investigated in [46]. It has been found that even infinite non-Hermitian systems have differences compared to semi-infinite non-Hermitian systems [20]. Additionally, not only the size effect, but also the odd-even effect of lattice sites and the odd-even effect of cells can also affect the topological characteristics of non-Hermitian systems, which are worth exploring. So far, 1D non-Hermitian systems have been extensively studied. Non-Hermitian systems with higher dimensions are being theoretically investigated as well [33, 47-49]. Non-Hermitian systems with higher dimensions may exhibit richer topological characteristics, in contrast to 1D non-Hermitian systems.

In this paper, we study a non-Hermitian ladder system consisting of two identical Su-Schrieffer-Heeger (SSH) chains with asymmetric hopping amplitudes under the OBC. The inter-chain-coupling strength is added into the non-Hermitian ladder system in a symmetric or an asymmetric way. We find that the non-Hermitian ladder system grants special modes, the moduli of the eigenvalues of which are equal to the inter-chain-coupling strength leading to the appearance of the special modes, and that the eigenvalues are purely real or purely imaginary for the symmetric and asymmetric inter-chain-coupling strengths. Odd and even lattice sites (N) can affect the region of the special modes appearing in the gap. From the density profiles of the special modes, it is clear that the density profiles of all the special modes are completely identical at the same fixed parameter conditions even if the inter-chain-coupling strength is added into the non-Hermitian ladder system in different ways for odd lattice sites N. The density profiles of the special modes change for the other parameters due to the non-Hermitian skin effect [6], but the density profiles of all the special modes are still same as long as the other parameters are the same for the special modes appearing in all the symmetrical and asymmetrical inter-chain-coupling strengths. Finally, we illustrate that the ways of adding the inter-chain-coupling strength are fundamentally equivalent to adding on-site potential energies into the non-Hermitian ladder system in different ways. The special modes found in the non-Hermitian ladder system may provide a insight for quantum information processing in non-Hermitian systems such as the quantum state transfer between the left and the right edge states assisted by the topological zero mode in Hermitian systems [50-52]. Besides, just like the preparation of the topological laser of the Hermitian systems described in [45], the special modes may provide a new ideal for the preparation of topological lasers in non-Hermitian systems. Our work provides potential applications in quantum computation and quantum information processing.

The paper is organized as follows: in section 2, we give the Hamiltonian of the non-Hermitian ladder system and discuss the spectra and density profiles for symmetric and asymmetric inter-chain-coupling strengths under the OBC, respectively. In section 3, we theoretically explain the appearance of the special modes of the non-Hermitian ladder system. In section 4, we analyze the experimental feasibility of a non-Hermitian lattice with asymmetrical hopping amplitudes. A brief summary is given in section 5.

2. Special modes induced by inter-chain coupling in a non-Hermitian ladder system

2.1. The model and the Hamiltonian

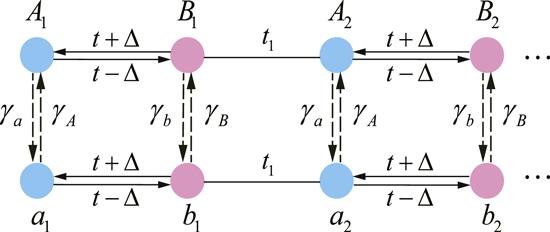
We consider a non-Hermitian ladder system consisting of two coupled identical SSH chains with asymmetrical intra-cell hopping amplitudes, as shown in figure 1. The corresponding Hamiltonian is H=H₁+H₂+H₃, with(1)$\begin{eqnarray}\begin{array}{c}\begin{array}{rcl}{H}_{1} & = & \displaystyle \sum _{n}\left[\left(t+{\rm{\Delta }}\right){A}_{n}^{\dagger }{B}_{n}+\left(t-{\rm{\Delta }}\right){B}_{n}^{\dagger }{A}_{n}\right.\\ & & \left.+{t}_{1}{B}_{n}^{\dagger }{A}_{n+1}+{t}_{1}{A}_{n+1}^{\dagger }{B}_{n}\right],\\ {H}_{2} & = & \displaystyle \sum _{n}\left[\left(t+{\rm{\Delta }}\right){a}_{n}^{\dagger }{b}_{n}+\left(t-{\rm{\Delta }}\right){b}_{n}^{\dagger }{a}_{n}\right.\\ & & \left.+{t}_{1}{b}_{n}^{\dagger }{a}_{n+1}+{t}_{1}{a}_{n+1}^{\dagger }{b}_{n}\right],\\ {H}_{3} & = & \displaystyle \sum _{n}\left({\gamma }_{a}{a}_{n}^{\dagger }{A}_{n}+{\gamma }_{A}{A}_{n}^{\dagger }{a}_{n}+{\gamma }_{b}{b}_{n}^{\dagger }{B}_{n}+{\gamma }_{B}{B}_{n}^{\dagger }{b}_{n}\right),\end{array}\end{array}\end{eqnarray}$where H₁ and H₂ are the Hamiltonian of two non-Hermitian chains. ${A}_{n}^{\dagger }$, ${B}_{n}^{\dagger }$, ${a}_{n}^{\dagger }$, and ${b}_{n}^{\dagger }$ (A_n, B_n, a_n, and b_n) are the creation (annihilation) operators at the nth $A\,(a)$ and $B\,(b)$ sites. The intra-cell forward and backward hopping amplitudes are t+Δ and t−Δ, respectively, and t₁ is the inter-cell hopping amplitude. H₃ is the interaction of the two non-Hermitian chains. γ_A, γ_a, γ_B, and γ_b are the inter-chain-coupling strength γ or −γ. The interaction is symmetric (asymmetric) when γ_A=γ_a (γ_A=−γ_a) and γ_B=γ_b (γ_B=−γ_b), and γ is a non-negative real value. The two coupled non-Hermitian SSH chains are decoupled into two general non-Hermitian SSH chains when γ=0. For the single decoupled non-Hermitian chain, the winding number established from H(k) [46] in view of the non-Hermitian skin effect is defined as a new non-Bloch topological invariant in a generalized Brillouin zone, $W=\tfrac{{\rm{i}}}{2\pi }{\int }_{{C}_{\beta }}{q}^{-1}{\rm{d}}{q}$, called a non-Bloch winding number [28]. It is shown in [28] that the numerical result of the non-Bloch winding number agrees well with the analytical spectra, and the edge modes can be predicted from the topological invariant in the non-Bloch bulk-boundary correspondence, and two zero modes appear in $-\sqrt{{t}_{2}^{2}+{\left(\gamma /2\right)}^{2}}\leqslant {t}_{1}\leqslant \sqrt{{t}_{2}^{2}+{\left(\gamma /2\right)}^{2}}$. Additionally, the H(k)-gap closing points $\pm ({t}_{2}-(\gamma /2))$ are where zero modes switch from the left (right) edge to the right (left) edge.

Figure 1.

New window|Download| PPT slide
Figure 1.A schematic diagram of two coupled identical non-Hermitian SSH chains. The number of lattice sites of one chain is N. The total number of lattice sites is L=2N.

2.2. Special modes induced by a symmetric inter-chain-coupling strength

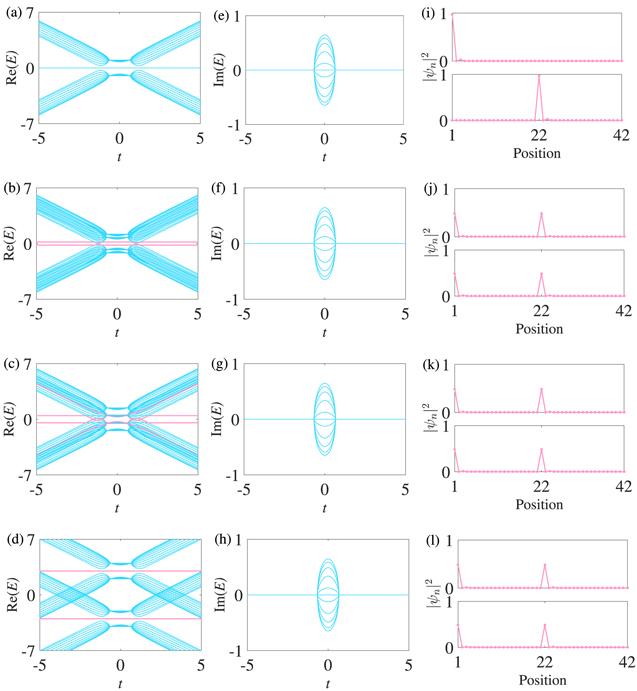
First, we consider the symmetric inter-chain-coupling strength with γ_A=γ_a=γ and γ_B=γ_b=γ. For N=21, we depict the real (imaginary) spectra as a function of t at fixed t₁=one (as an energy unit) and Δ=2/3 under the OBC, as shown in figure 2. Figures 2(a) and (e) show the spectra of two decoupled non-Hermitian chains, in which the spectra of the two decoupled non-Hermitian chains coalesce, as do the zero-energy modes. It is interesting that special modes with the moduli of their eigenvalues being γ ($| E| =\gamma $) appear in the gap and the eigenvalues are purely real as long as γ exists. There are always two special modes ($| E| =\gamma $) with pure real eigenvalues and the two special modes are continuous when γ≲0.4, as shown in figure 2(b). The two special modes partially integrate into bulk states and become discontinuous with increasing values of γ, as shown in figures 2(c) and (d). In figure 2(d), the two special modes still partially integrate into bulk states in region $| t| \gt 5$. From figures 2(b)-(d), moreover, the bands of one non-Hermitian chain move up and the bands of another non-Hermitian chain move down with increasing values of γ. Imaginary eigenvalues appear at −0.68 ≲ t ≲ 0.68 and there are no significant changes with varying γ in figures 2(f)-(h).

Figure 2.

New window|Download| PPT slide
Figure 2.Spectra under the OBC and the density profiles of the special modes. (i), (j), (k), and (l) are the density profiles of the special modes corresponding to (a), (b), (c), and (d) at a fixed t=0.5. In (a) and (e), γ=0; in (b) and (f), γ=0.2; in (c) and (g), γ=0.45; in (d) and (h), γ=3. The other parameters are Δ=2/3, t₁=1, and N=21. N is the number of lattice sites in one chain. The special modes with $| E| =\gamma $ are marked with solid pink.


In figures 2(i)-(l), we show the density profiles of the two special modes corresponding to figures 2(a)-(d) at a fixed t=0.5. For convenience here, positions 1-21 represent the lattice sites of the first non-Hermitian chain and positions 22-42 represent the lattice sites of the second non-Hermitian chain. Figure 2(i) shows the density profile of the two coalescent zero-energy modes of the decoupled non-Hermitian chains. In figure 2(j), the density profiles of the two special modes are completely identical and each mode simultaneously has maximum probability at positions 1 and 22, i.e., each mode is simultaneously localized at the left edge of the two non-Hermitian chains, which means each mode is localized at the left edge of the non-Hermitian ladder system. Notably, the density profiles of the two special modes do not change with γ and the moduli (not $| {\psi }_{n}{| }^{2}$) of the maximum probability amplitudes of each mode at positions 1 and 22 are always 0.6972, as shown in figures 2(j)-(l), that is, the density profiles of the two special modes are same for all parameters γ when t is fixed.

For N=22, figures 3(a) and (e) show the spectra of the two decoupled non-Hermitian chains. Four coalescent zero-energy modes appear in the center gap of the real spectra, in contrast with figure 2(a). There exist four special modes with $| E| =\gamma $ in the center gap of the real spectra due to an odd-even effect of the lattice site, the upper two and bottom two of which are respectively degenerate, as shown in figure 3(b). The four special modes integrate into bulk states and become discontinuous when 0.35≲γ≲0.5, as shown in figure 3(c). The four special modes then separate from the bulk states with increasing γ, as shown in figure 3(d). With increasing γ, the bands move in the same way as for N=21 in figure 2. Notably, in this case, the eigenvalues of the four special modes satisfy Re(E)=γ around t=0, in which the imaginary parts of the eigenvalues of the four special modes split due to the size effect of the non-Hermitian system [20], as shown in figures 3(f)-(h). However, the eigenvalues of the four special modes are still purely real for other parameters t of the center gap. The imaginary eigenvalues appear in $-0.68\lesssim t\lesssim 0.68$ and there are no significant changes with varying γ in the imaginary spectra.

Figure 3.

New window|Download| PPT slide
Figure 3.Spectra under the OBC. In (a) and (e), γ=0; in (b) and (f), γ=0.2; in (c) and (g), γ=0.45; in (d) and (h), γ=3. The other parameters are Δ=2/3, t₁=1, and N=22. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with solid pink.


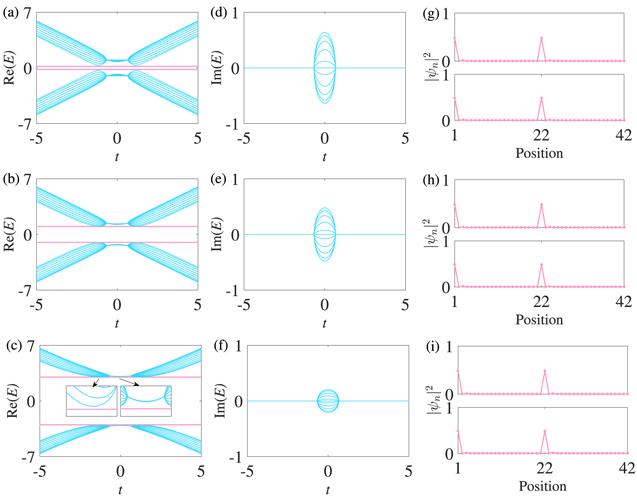
In figure 4, we show the real (imaginary) spectra with the inter-chain-coupling strengths γ_A=γ_a=γ and γ_B=γ_b=−γ when N=21. Two special modes ($| E| =\gamma $) with pure real eigenvalues appear in the gap of the real spectra, as shown in figures 4(a)-(c). For figures 4(a)-(c), one band of each non-Hermitian chain moves up and another band of each non-Hermitian chain moves down with increasing values of γ, which implies that the two bands of each non-Hermitian chain move in opposite directions with increasing values of γ when ${\gamma }_{B}={\gamma }_{b}=-\gamma $. So we only can see two bands in each real spectrum although there are two non-Hermitian chains, because the bands of the two chains of the non-Hermitian ladder system are degenerate. Imaginary eigenvalues appear in $-0.68\lesssim t\lesssim 0.68$ and all the imaginary eigenvalues gradually decrease with increasing values of γ, as shown in figures 4(d)-(f). In figures 4(g)-(i), the density profiles of all the special modes corresponding to figures 4(a)-(c) are completely identical, and each mode has maximum probability at positions 1 and 22 (each mode is localized at the left edge of the non-Hermitian ladder system) with the moduli of the maximum probability having an amplitude of 0.6972, which is the same as the density profiles of the special modes in figure 2.

Figure 4.

New window|Download| PPT slide
Figure 4.Spectra under the OBC and the density profiles of the special modes. (g), (h), and (i) are the density profiles of the special modes corresponding to (a), (b), and (c) at a fixed t=0.5. In (a) and (d), γ=0.2; in (b) and (e), γ=1; in (c) and (f), γ=3. The other parameters are Δ=2/3, t₁=1, and N=21. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with solid pink.


For N=22, there exist four special modes ($| E| =\gamma $) with pure real eigenvalues in the center gap of the real spectra, and the upper two special modes and the bottom two special modes are respectively degenerate, as shown in figures 5(a)-(c). The imaginary eigenvalues in figures 5(d)-(f) change in the same way as for N=21 in figure 4. But the pure real eigenvalues of the four special modes satisfy $| E| =\gamma $ approximately around t=0. For example, the eigenvalues of the four special modes are 0.9999, 0.9999, -0.9999, -0.9999 from the top to the bottom when t=0 in figure 5(b). This slight change is ignored here as well as in all the following discussions for N=22. With increasing values of γ, the bands move in the same way as for N=21 in figure 4.

Figure 5.

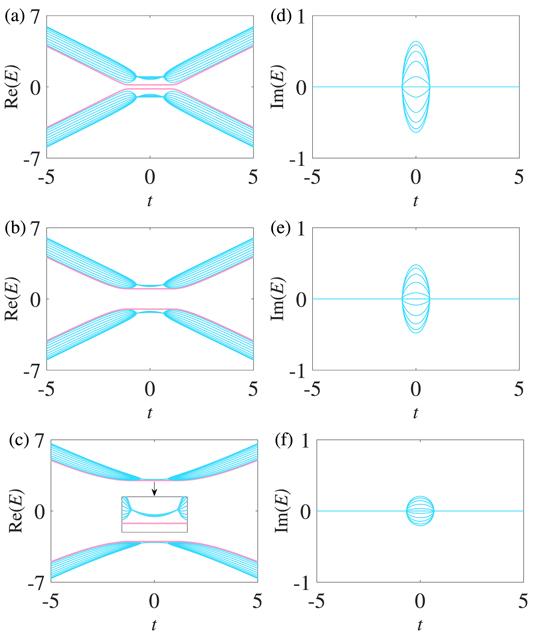New window|Download| PPT slide
Figure 5.Spectra under the OBC. In (a) and (d), γ=0.2; in (b) and (e), γ=1; in (c) and (f), γ=3. The other parameters are Δ= 2/3, t₁=1, and N=22. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with solid pink.


We now consider partial inter-chain coupling; the inter-chain-coupling strength is still symmetric. In figure 6, we show the real (imaginary) spectra with the inter-chain-coupling strength γ_A=γ_a=γ and γ_B=γ_b=0 when N=21. Two special modes ($| E| =\gamma $) with pure real eigenvalues appear in the gap of the real spectra, and the two special modes are continuous when $\gamma \lesssim 0.53$, as shown in figure 6(a). The two special modes partially integrate into bulk states and become discontinuous with increasing values of γ, as shown in figures 6(b) and (c). From figures 6(a)-(c), one band of each non-Hermitian chain additionally moves up or down and another band of each non-Hermitian chain does not move with increasing values of γ, which implies that only one band of each non-Hermitian chain moves only when γ_A and γ_a exist. The imaginary eigenvalues change in the same way as those shown in figures 4 and 5, as shown in figures 6(d)-(f). In figures 6(g)-(i), the density profiles of all the special modes corresponding to figures 6(a)-(c) are completely identical, and each special mode is localized at the left edge of the non-Hermitian ladder system with the moduli of the maximum probability having an amplitude of 0.6972, which is the same as the density profiles of the special modes in figures 2 and 4.

Figure 6.

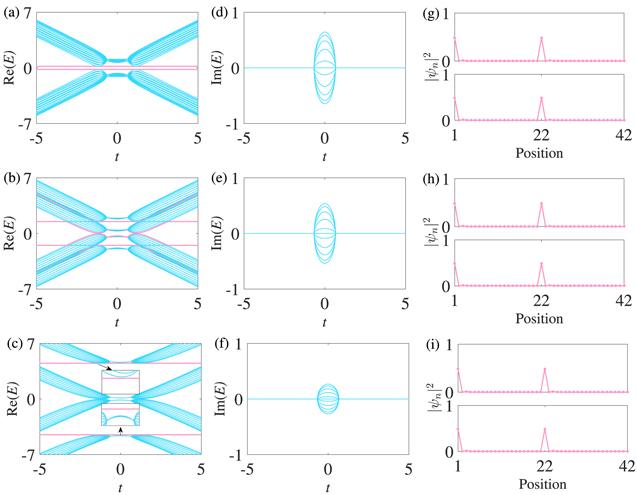New window|Download| PPT slide
Figure 6.Spectra under the OBC and the density profiles of the special modes. (g), (h), and (i) are the density profiles of the special modes corresponding to (a), (b), and (c) at a fixed t=0.5. In (a) and (d), γ=0.2; in (b) and (e), γ=1.5; in (c) and (f), γ=4.5. The other parameters are Δ=2/3, t₁=1, and N=21. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with solid pink.


For N=22, as opposed to the case for N=22 shown in figures 3 and 5, there exist two special modes ($| E| =\gamma $) with pure real eigenvalues and two degenerate zero-energy modes in the center gap of the real spectra, as shown in figure 7(a). The two degenerate zero-energy modes always exist, but the two special modes integrate into the bulk states and become discontinuous when $0.48\lesssim \gamma \lesssim 0.7$ in figure 7(b), in which γ=0.6. The two special modes appear again with increasing values of γ, as shown in figure 7(c). The imaginary eigenvalues in figures 7(d)-(f) change in the same way as those in figures 4-6.

Figure 7.

New window|Download| PPT slide
Figure 7.Spectra under the OBC. In (a) and (d), γ=0.2; in (b) and (e), γ=0.6; in (c) and (f), γ=4.5. The other parameters are Δ=2/3, t₁=1, and N=22. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with solid pink.


In figure 8, we show the real (imaginary) spectra with the inter-chain-coupling strength γ_A=γ_a=0 and γ_B=γ_b=γ when N=21. The special modes ($| E| =\gamma $) with pure real eigenvalues vanish and there are always two degenerate zero-energy modes in the gap of the real spectra for the parameters t and γ, as shown in figures 8(a)-(c). Similar to the case where only γ_A and γ_a exist in figure 6, one band of each non-Hermitian chain moves up or down and another band of each non-Hermitian chain does not move with increasing values of γ, only when γ_B and γ_b exist. The imaginary eigenvalues in figures 8(d)-(f) change in the same way as those shown in figures 4-7. The locality of the two degenerate zero-energy modes is sensitive to γ and t. In figures 8(g)-(i), we show the density profiles of the two degenerate zero-energy modes corresponding to figures 8(a)-(c) at a fixed t=3. The two zero-energy modes are respectively localized at positions 21 and 42 in figure 8(g), i.e., the two zero-energy modes are localized at the right edge of the first and second non-Hermitian chains, respectively. The two zero-energy modes are respectively localized at positions 42 and 21 in figure 8(h), i.e., the two zero-energy modes are localized at the right edge of the second and first non-Hermitian chains, respectively. While each zero-energy mode is simultaneously localized at positions 21 and 42 in figure 8(i), i.e., each zero-energy mode is simultaneously localized at the right edge of the two non-Hermitian chains. Therefore, the two zero-energy modes are localized at the right edge of the non-Hermitian ladder system when t=3.

Figure 8.

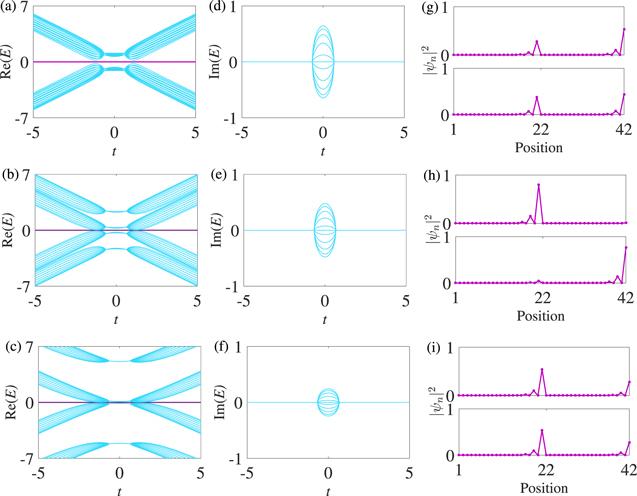New window|Download| PPT slide
Figure 8.Spectra under the OBC and the density profiles of the zero-energy modes. (g), (h), and (i) are the density profiles of the special modes corresponding to (a), (b), and (c) at a fixed t=3. In (a) and (d), γ=0.2; in (b) and (e), γ=2; in (c) and (f), γ=5. The other parameters are Δ=2/3, t₁=1, and N=21. N is the number of lattice sites of one chain. The zero-energy modes are marked with solid purple.


For N=22, there exist two special modes ($| E| =\gamma $) with pure real eigenvalues and two degenerate zero-energy modes in the center gap of the real spectra, as shown in figure 9(a). The two degenerate zero-energy modes always exist, but the two special modes integrate into the bulk states and become discontinuous when $0.48\lesssim \gamma \lesssim 0.7$ in figure 9(b). The two special modes appear again with increasing values of γ, as shown in figure 9(c). The imaginary eigenvalues in figures 9(d)-(f) change in the same way as those in figures 4-8.

Figure 9.

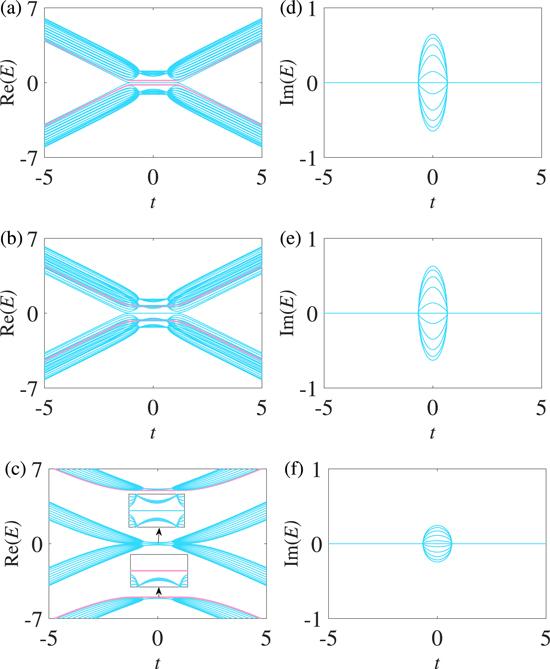New window|Download| PPT slide
Figure 9.Spectra under the OBC. In (a) and (d), γ=0.2; in (b) and (e), γ=0.6; in (c) and (f), γ=5. The other parameters are Δ=2/3, t₁=1, and N=22. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with solid pink.

2.3. Special modes induced by an asymmetric inter-chain-coupling strength

Next, we consider an asymmetric inter-chain-coupling strength. The real (imaginary) spectra with an inter-chain-coupling strength of γ_A=−γ_a=γ and γ_B=−γ_b=γ are shown in figure 10 when N=21. There are always two degenerate zero-energy modes in the real spectra and the real spectra of the two chains of the non-Hermitian ladder system are degenerate, as shown in figures 10(a)-(c).

Figure 10.

New window|Download| PPT slide
Figure 10.Spectra under the OBC and the density profiles of the special modes. (g), (h), and (i) are the density profiles of the special modes corresponding to (a), (b), and (c) at a fixed t=0.5. In (a) and (d), γ=0.2; in (b) and (e), γ=0.65; in (c) and (f), γ=3. The other parameters are Δ=2/3, t₁=1, and N=21. N is the number of lattice sites of one chain. The special modes modes are marked with prismatic pink.


However, this differs from all the cases above, in that the special modes ($| E| =\gamma $) with pure real eigenvalues switch to special modes ($| E| =\gamma $) with pure imaginary eigenvalues appearing in the imaginary spectra, and the two degenerate zero-energy modes in the real spectra correspond to the two special modes, as shown in figures 10(d)-(f). The two special modes are discontinuous when $\gamma \lesssim 0.32$ in figure 10(d). However, the two special modes become continuous and the imaginary bands of the two non-Hermitian chains move up and down with increasing values of γ, respectively, as shown in figures 10(e) and (f). In figures 10(g)-(i), the density profiles of the special modes corresponding to figures 10(d)-(f) are completely identical as well, and each mode is localized at the left edge of the non-Hermitian ladder system with the moduli of maximum probability having an amplitude of 0.6972, which is the same as the density profiles of the special modes in figures 2, 4, 6, and 8.

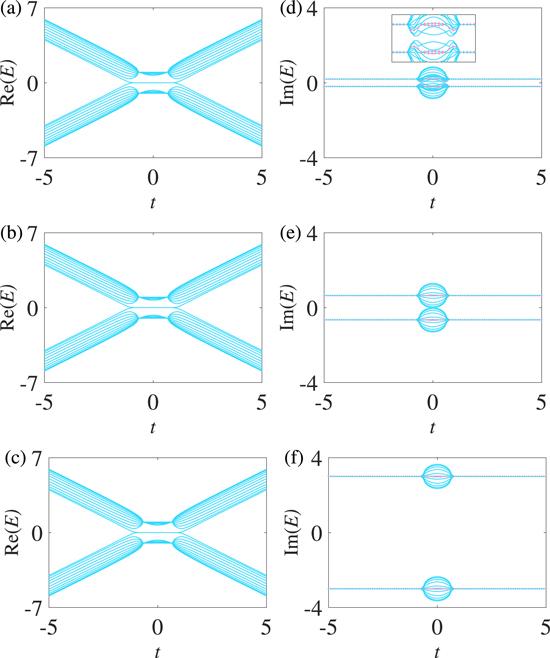
For N=22, four degenerate zero-energy modes always exist in the center gap of the real spectra and the real spectra of the two chains of the non-Hermitian ladder system are also degenerate, as shown in figures 11(a)-(c). Four special modes ($| E| =\gamma $) with pure imaginary eigenvalues appear in the imaginary spectra, the upper two and the bottom two of which are respectively degenerate, and the four degenerate zero-energy modes in the real spectra correspond to the four special modes, as shown in figures 11(d)-(f). The four special modes are discontinuous when $\gamma \lesssim 0.32$ in figure 11(d), while the four special modes become continuous and the imaginary bands of the two non-Hermitian chains respectively move up and down with increasing values of γ, as shown in figures 11(e) and (f). Note that the upper (bottom) two degenerate special modes split around t=0 [20].

Figure 11.

New window|Download| PPT slide
Figure 11.Spectra under the OBC. In (a) and (d), γ=0.2; in (b) and (e), γ=0.65; in (c) and (f), γ=3. The other parameters are Δ=2/3, t₁=1, and N=22. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with prismatic pink.


In figure 12, we plot the real (imaginary) spectra with an inter-chain-coupling strength γ_A=−γ_a=γ and −γ_B= γ_b=γ when N=21. This differs from the real spectra of N=21 in figure 10, in that there are two degenerate zero-energy modes in the real spectra for small values of γ, as shown in figure 12(a). The number of degenerate zero-energy modes increases with increasing values of γ, as shown in figures 12(a) and (b). The real spectra then partially move left and right with increasing values of γ, as shown in figures 12(b) and (c). Two special modes ($| E| =\gamma $ ) with pure imaginary eigenvalues appear in the imaginary spectra, which correspond to the two degenerate zero-energy modes that always exist in the real spectra, as shown in figures 12(d)-(f). The two special modes are partially in the bulk states and are discontinuous when $\gamma \lesssim 0.86$, as shown in figure 12(d). The two special modes separate from the bulk states and become continuous together with the imaginary bands of the two non-Hermitian chains extending as a whole with increasing values of γ, as shown in figures 12(e) and (f). In figures 12(g)-(i), the density profiles of all the special modes corresponding to figures 12(d)-(f) are the same as the density profiles of all the special modes described previously.

Figure 12.

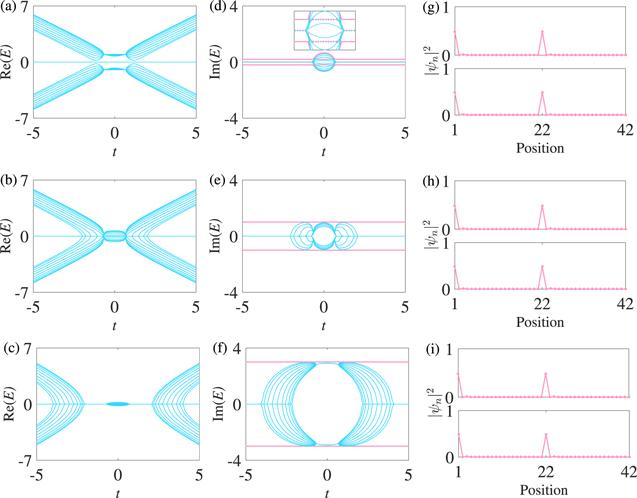New window|Download| PPT slide
Figure 12.Spectra under the OBC and the density profiles of the special modes. (g), (h), and (i) are the density profiles of the special modes corresponding to (a), (b), and (c) at fixed t=0.5. In (a) and (d), γ=0.2; in (b) and (e), γ=1; in (c) and (f), γ=3. The other parameters are Δ=2/3, t₁=1, and N=21. N is the number of lattice sites of one chain. The special modes modes are marked with solid pink.


For N=22, the changes in the real spectra are the same as the changes in figure 12 but with four degenerate zero-energy modes in the center gap for small values of γ, as shown in figures 13(a)-(c). Four special modes ($| E| =\gamma $) with pure imaginary eigenvalues appear in the imaginary spectra when $-1\lesssim t\lesssim 1$, which correspond to the four degenerate zero-energy modes the always exist in the real spectra, as shown in figures 13(d)-(f). The upper two special modes and the bottom two special modes are degenerate, respectively. The four special modes are partially in the bulk states and are discontinuous when $\gamma \lesssim 0.86$, as shown in figure 13(d). The four special modes separate from the bulk states and become continuous together with the imaginary bands of the two non-Hermitian chains extending as a whole with increasing values of γ, as shown in figures 13(e) and (f). For even lattices (N=22), different ways of inter-chain coupling and the inter-chain-coupling strength have different effects on the density profiles of the special modes, and the density profiles of the special modes are selectively sensitive to the ways of inter-chain coupling and the inter-chain-coupling strength due to the odd-even effect (see appendix).

Figure 13.

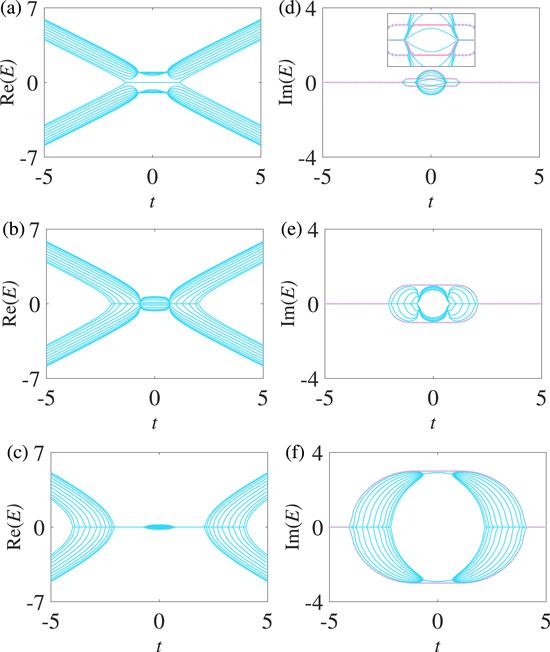New window|Download| PPT slide
Figure 13.Spectra under the OBC. In (a) and (d), γ=0.2; in (b) and (e), γ=1; in (c) and (f), γ=3. The other parameters are Δ=2/3, t₁=1, and N=22. N is the number of lattice sites of one chain. The special modes with $| E| =\gamma $ are marked with prismatic pink.

3. The interpretation of the special modes

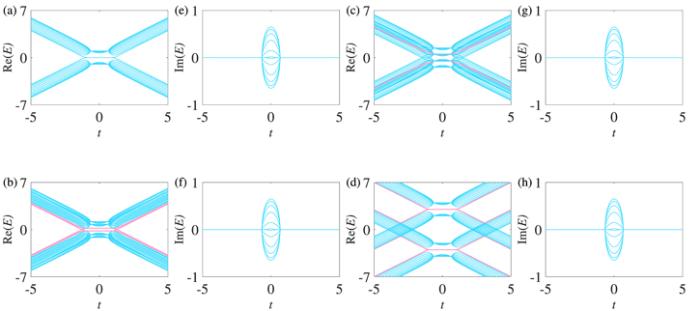
From figures 2-9, we find that the special modes ($| E| =\gamma $) with pure real eigenvalues appear for symmetrical inter-chain-coupling strengths. The bands of the two non-Hermitian chains move in opposite directions with varying values of γ, while the two bands of each non-Hermitian chain move in the same direction when γ_A=γ_a=γ_B=γ_b, and the two bands of each non-Hermitian chain move in opposite directions when γ_A=γ_a=−γ_B=−γ_b. Only one band of each non-Hermitian chain moves with varying values of γ when only γ_A (γ_a) or γ_B (γ_b) exists. In figures 10-13, the special modes ($| E| =\gamma $) with pure imaginary eigenvalues appear for asymmetrical inter-chain-coupling strengths, and the imaginary bands of the two non-Hermitian chains move in opposite directions or extend as a whole with varying values of γ. Indeed, the appearance of the special modes with $| E| =\gamma $ and the movements of the bands are closely related to the on-site potential energy. Consider a general non-Hermitian SSH chain with the on-site potential energy $\gamma \,(-\gamma )$ or ${\rm{i}}\gamma \,(-{\rm{i}}\gamma )$(2)$\begin{eqnarray}\begin{array}{rll}{H}_{1}^{{\rm{{\prime} }}} & = & {H}_{1}+\displaystyle \sum _{n}\left[\alpha {A}_{n}^{\dagger }{A}_{n}+\beta {B}_{n}^{\dagger }{B}_{n}\right],\\ {H}_{2}^{{\rm{{\prime} }}} & = & {H}_{2}+\displaystyle \sum _{n}\left[{\alpha }^{{\rm{{\prime} }}}{a}_{n}^{\dagger }{a}_{n}+{\beta }^{{\rm{{\prime} }}}{b}_{n}^{\dagger }{b}_{n}\right],\end{array}\end{eqnarray}$where H₁ and H₂ are given in equation (1). α $({\alpha }^{{\prime} })$ and β $({\beta }^{{\prime} })$ are the on-site potential energies γ, −γ, ${\rm{i}}\gamma $ or $-{\rm{i}}\gamma $. We first consider one non-Hermitian chain ${H}_{1}^{{\prime} }$ with N=21. We find that the on-site potential energies α and β cause the bands to move up and down. Real values of α and β correspond to the bands moving up and down in real spectra, and imaginary values of α and β correspond to the movement of the bands in imaginary spectra, while the on-site potential energy α on lattice site A additionally leads to the appearance of the special modes with $| E| =\gamma $, and the real (imaginary) values of α correspond to the special modes with pure real (imaginary) eigenvalues. For example, in figures 14(a) and (b), there is always a special mode with a pure real eigenvalue of 1.5 in the real spectra and the two bands both move up when α=γ=1.5 and β=γ=1.5. In figures 14(c) and (d), α=−γ=−1.5 and β=γ=1.5, and there is always a special mode with pure real eigenvalues of −1.5 in the real spectra, in which one of the bands moves down with α and another band moves up with β. In figures 14(e) and (f), $\alpha ={\rm{i}}\gamma =1.5{\rm{i}}$ and $\beta ={\rm{i}}\gamma =1.5{\rm{i}}$, a special mode with a pure imaginary eigenvalue of $1.5{\rm{i}}$ appears in the imaginary spectra, and the imaginary band moves up. In figures 14(g) and (h), $\alpha =-{\rm{i}}\gamma =-1.5{\rm{i}}$ and $\beta ={\rm{i}}\gamma =1.5{\rm{i}}$, a special mode with a pure imaginary eigenvalue of $-1.5{\rm{i}}$ appears in the imaginary spectra, and the imaginary band does not move up or down but extends as a whole. In the non-Hermitian ladder system, therefore, the inter-chain-coupling strength between lattice sites A (B) and a (b) can be equivalent to the on-site potential energy of each lattice site of one non-Hermitian chain ${H}_{1}^{{\prime} }$ and opposite to the on-site potential energy of each corresponding lattice site of another identical non-Hermitian chain ${H}_{2}^{{\prime} }$, where ${\alpha }^{{\prime} }=-\alpha $ and ${\beta }^{{\prime} }=-\beta $.

Figure 14.

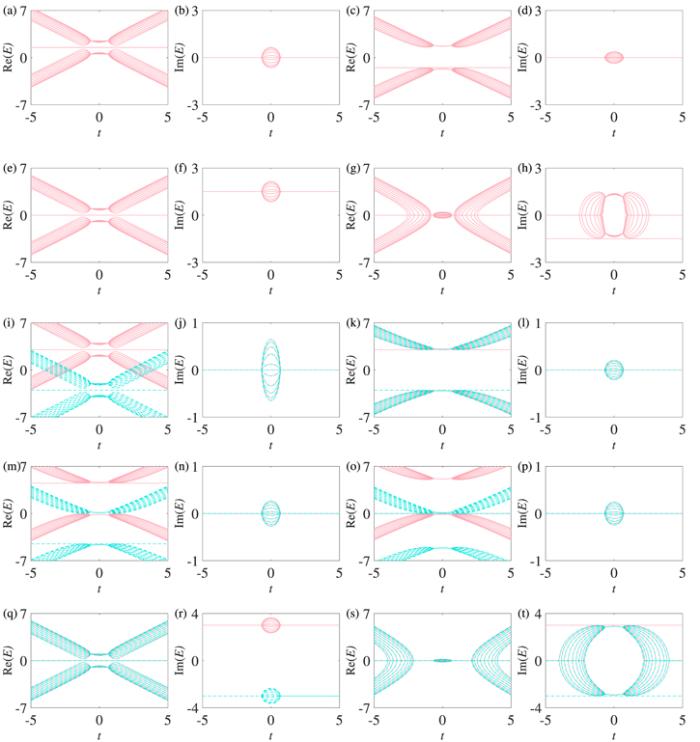New window|Download| PPT slide
Figure 14.The spectra of a general non-Hermitian SSH chain with on-site potential energy under the OBC. In (a) and (b), α=1.5, β=1.5; in (c) and (d), α=−1.5, β=1.5; in (e) and (f), $\alpha =1.5{\rm{i}},\,\beta =1.5{\rm{i}};$ in (g) and (h) $\alpha =-1.5{\rm{i}},\,\beta =1.5{\rm{i}};$ in (i) and (j), $\alpha =3,\,\beta =3,{\alpha }^{{\prime} }=-3,\,{\beta }^{{\prime} }=-3;$ in (k) and (l), $\alpha =3,\,\beta =-3,\,{\alpha }^{{\prime} }=-3,\,{\beta }^{{\prime} }=3;$ in (m) and (n) $\alpha =4.5,\,\beta =0,\,{\alpha }^{{\prime} }=-4.5,\,{\beta }^{{\prime} }=0;$ in (o) and (p), $\alpha =0,\,\beta =5,\,{\alpha }^{{\prime} }=0,\,{\beta }^{{\prime} }=-5;$ in (q) and (r), $\alpha =3{\rm{i}},\,\beta =3{\rm{i}},\,{\alpha }^{{\prime} }=-3{\rm{i}},\,{\beta }^{{\prime} }=-3{\rm{i}};$ in (s) and (t) $\alpha =3{\rm{i}},\,\beta =-3{\rm{i}},\,{\alpha }^{{\prime} }=-3{\rm{i}},{\beta }^{{\prime} }=3{\rm{i}}$. The other parameters are ${\rm{\Delta }}=2/3$, t₁=1, and N=21. N is the number of lattice sites of one chain. The bands of the two non-Hermitian chains are marked with solid red and dashed green lines, respectively.


For the symmetrical inter-chain-coupling strength, the inter-chain couplings ${\gamma }_{A}$, γ_a, γ_B, and γ_b all exist in figure 2, thus the equivalent on-site potentials of the inter-chain couplings of figure 2 are $\gamma {A}^{\dagger }A$ ($-\gamma {a}^{\dagger }a$) and $\gamma {B}^{\dagger }B$ ($-\gamma {b}^{\dagger }b$), and the on-site potential energies are real. The on-site potentials in parentheses are the on-site potentials of another identical non-Hermitian chain. Figures 14(i)-(t) show the spectra of each non-Hermitian chain with the equivalent on-site potential energies corresponding to figures 2, 4, 6, 8, 10, and 12. The bands of the two non-Hermitian chains are marked with solid red and dashed green lines, respectively. It is clear that the spectra of figures 2(d) and (h) are in good agreement with the spectra of figures 14(i) and (j). So the equivalent on-site potentials $\gamma {A}^{\dagger }A$ ($-\gamma {a}^{\dagger }a$) and $-\gamma {B}^{\dagger }B$ ($\gamma {b}^{\dagger }b$) correspond to figure 4, $\gamma {A}^{\dagger }A$ ($-\gamma {a}^{\dagger }a$) correspond to figure 6, and $\gamma {B}^{\dagger }B$ ($-\gamma {b}^{\dagger }b$) correspond to figure 8. The spectra of figures 4(c) and (f) (figures 6(c) and (f), figures 8(c) and (f)) agree well with the spectra of figures 14(k) and (l) [14(m) and 14(n), 14(o) and 14(p)], respectively. From figures 14(e) and (f) [14(g) and 14(h)], however, we find that the asymmetrical inter-chain-coupling strength is equivalent to the imaginary on-site potential energy. Hence, the equivalent on-site potential of the inter-chain couplings of figure 10 are ${\rm{i}}\gamma {{\rm{A}}}^{\dagger }{\rm{A}}$ ($-{\rm{i}}\gamma {{\rm{a}}}^{\dagger }{\rm{a}}$) and ${\rm{i}}\gamma {{\rm{B}}}^{\dagger }{\rm{B}}$ ($-{\rm{i}}\gamma {{\rm{b}}}^{\dagger }{\rm{b}}$), and the equivalent on-site potential of the inter-chain couplings of figure 12 are ${\rm{i}}\gamma {{\rm{A}}}^{\dagger }{\rm{A}}$ ($-{\rm{i}}\gamma {{\rm{a}}}^{\dagger }{\rm{a}}$) and $-{\rm{i}}\gamma {{\rm{B}}}^{\dagger }{\rm{B}}$ (${\rm{i}}\gamma {{\rm{b}}}^{\dagger }{\rm{b}}$). The spectra of figures 14(0) and (r) [14(s) and 14(t)] agree well with the spectra of figures 10(c) and (f) (figures 12(c) and (f)). Obviously, the symmetrical (asymmetrical) inter-chain-coupling strength is equivalent to the pure real (imaginary) on-site potential energies of the two chains of the non-Hermitian ladder system corresponding to the special modes with pure real (imaginary) eigenvalues, and the on-site potential energy α on lattice site A additionally leads to the appearance of the special modes. For N=22, the special modes can be induced by the on-site potential energy on both lattice sites A and B due to the odd-even effect. So there are four special modes when ${\gamma }_{A}={\gamma }_{a}\ne 0$ and ${\gamma }_{B}={\gamma }_{b}\ne 0$ in figures 3, 5, 11 and 13, while there are only two special modes when γ_A=γ_a=0 or γ_B=γ_b=0 in figures 7 and 9.

4. Experimental feasibility

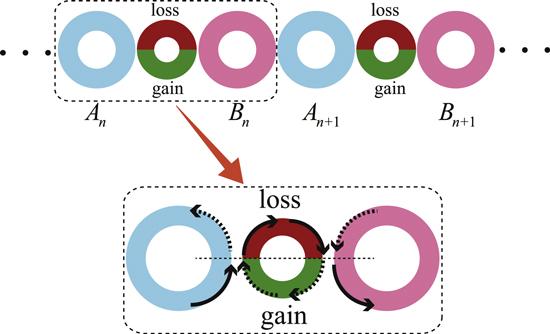
We now discuss the experimental feasibility of a non-Hermitian lattice with asymmetric hopping amplitudes. Intra-cell asymmetric hopping amplitudes can be realized based on a microresonator array with auxiliary hopping [53], as shown in figure 15. In the microresonator array, two intra-cell microresonators couple with each other via auxiliary microrings with gain in the upper half perimeter and loss in the bottom half perimeter, while the two inter-cell microresonators directly couple with each other. In this way, photons moving from microresonator A_n to B_n and photons moving from microresonator B_n to A_n pass through the microrings with a half perimeter loss (gain) accompanied by a decrease (amplification) of the hopping amplitude. Actually, the decrease and amplification of the hopping amplitudes is caused by a synthetic imaginary gauge field originating from the loss and gain of the auxiliary microrings.

Figure 15.

New window|Download| PPT slide
Figure 15.The experimental realization of a non-Hermitian lattice with asymmetrical hopping amplitudes based on coupled microresonators. Resonators A_n and B_n couple with each other via the microring with a half perimeter loss and gain. The photons in resonators A_n (B_n) hop into resonators B_n (A_n) through the paths marked with the black solid arrows and the black dashed arrows.


The existence of the synthetic imaginary gauge field causes the hopping amplitudes between the microresonators A_n and B_n to be(3)$\begin{eqnarray}{H}_{\mathrm{hopping}}=\displaystyle \sum _{n}{t}^{{\prime} }\left[{{\rm{e}}}^{-\lambda }{B}_{n}^{\dagger }{A}_{n}+{{\rm{e}}}^{\lambda }{A}_{n}^{\dagger }{B}_{n}\right],\end{eqnarray}$where ${t}^{{\prime} }$ is the intra-cell microresonators' hopping amplitudes in the absence of an imaginary gauge field and λ is the effect of the synthetic imaginary gauge field [53-55]. Thus, we can obtain the asymmetric hopping amplitudes between the microresonators A_n and B_n via an appropriate design of the synthetic imaginary gauge field, such as ${t}^{{\prime} }{{\rm{e}}}^{-\lambda }=t-{\rm{\Delta }}$ and ${t}^{{\prime} }{{\rm{e}}}^{\lambda }=t+{\rm{\Delta }}$.

5. Summary

In summary, we have explored the special modes in a non-Hermitian ladder system under the OBC. The moduli of the eigenvalues of the special modes are equal to the inter-chain-coupling strengths leading to the appearance of the special modes. For symmetrical and asymmetrical inter-chain-coupling strengths, a phase transition from the special modes with pure real eigenvalues to the special modes with pure imaginary eigenvalues occurs in the non-Hermitian ladder system. Furthermore, the special modes can appear in different gaps for odd and even lattice sites and the special modes can only be induced by the inter-chain-coupling strength between lattice sites A and a for odd lattice sites but can be induced by inter-chain-coupling strength between both lattice sites A (B) and a (b) for even lattice sites, which implies the influence of the odd-even effect of lattice sites on the non-Hermitian ladder system. For odd lattice sites, all the special modes which appear in the non-Hermitian ladder system for different inter-chain couplings have same density profiles as long as the hopping parameter is fixed and the same for all the inter-chain couplings. We have further demonstrated that the symmetric (asymmetric) inter-chain-coupling strength is essentially equivalent to the pure real (imaginary) on-site potential energy of one non-Hermitian chain and the opposite pure real (imaginary) on-site potential energy of another identical non-Hermitian chain, which correspond to the special modes with pure real (imaginary) eigenvalues.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant No. 61822114 and the Project of Jilin Science and Technology Development for Leading Talent of Science and Technology Innovation in Middle and Young and Team Project under Grant No. 20160519022JH.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Rotter I 2009 J Phys. A: Math. Theor. 42 153001
DOI:10.1088/1751-8113/42/15/153001 [Cited within: 1]

[2]Heiss W D 2012 J. Phys. A: Math. Theor. 45 444016
DOI:10.1088/1751-8113/45/44/444016

[3]Liang S D Huang G Y 2013 Phys. Rev. A 87 012118
DOI:10.1103/PhysRevA.87.012118

[4]Höckendorf B Alvermann A Fehske H 2019 Phys. Rev. Lett. 123 190403
DOI:10.1103/PhysRevLett.123.190403

[5]Lee T E 2016 Phys. Rev. Lett. 116 133903
DOI:10.1103/PhysRevLett.116.133903 [Cited within: 1]

[6]Song F Yao S Wang P Z 2019 phys. Rev. Lett. 123 170401
DOI:10.1103/PhysRevLett.123.170401 [Cited within: 2]

[7]Yuce C 2019 Phys. Lett. A 384 126094
DOI:10.1016/j.physleta.2019.126094 [Cited within: 2]

[8]Hassan A U Zhen B Soljačić M Khajavikhan M Christodoulides D N 2017 Phys. Rev. Lett. 118 093002
DOI:10.1103/PhysRevLett.118.093002

[9]Liertzer M Ge L Cerjan A Stone A D Türeci H E Rotter S 2012 Phys. Rev. Lett. 108 173901
DOI:10.1103/PhysRevLett.108.173901

[10]Lee C H Li L Gong J 2019 Phys. Rev. Lett. 123 016805
DOI:10.1103/PhysRevLett.123.016805

[11]Wang P Jin L Song Z 2019 Phys. Rev. A 99 062112
DOI:10.1103/PhysRevA.99.062112

[12]Wang B X Zhao C Y 2018 Phys. Rev. B 98 165435
DOI:10.1103/PhysRevB.98.165435

[13]Rufo S Lopes N Continentino M A Griffith M A R 2019 Phys. Rev. B 100 195432
DOI:10.1103/PhysRevB.100.195432

[14]Yuce C 2018 Phys. Rev. A 97 042118
DOI:10.1103/PhysRevA.97.042118

[15]Kunst F K Dwivedi V 2019 Phys. Rev. B 99 245116
DOI:10.1103/PhysRevB.99.245116

[16]Ke S Wang B Long H Wang K Lu P 2017 Opt. Express 25 11132
DOI:10.1364/OE.25.011132

[17]Wang H Ruan J Zhang H 2019 Phys. Rev. B 99 075130
DOI:10.1103/PhysRevB.99.075130

[18]Xing Y Qi L Cao J Wang D Y Bai C H Wang H F Zhu A D Zhang S 2017 Phys. Rev. A 96 043810
DOI:10.1103/PhysRevA.96.043810

[19]Gupta S K Zou Y Zhu X Y Lu M H Zhang L Liu X P Chen Y F 2018 Adv. Mater. 32 1903693
DOI:10.1002/adma.201903639

[20]Chen R Chen C Z Zhou B Xu D H 2019 Phys. Rev. B 99 155431
DOI:10.1103/PhysRevB.99.155431 [Cited within: 3]

[21]Yuce C 2015 Phys. Lett. A 379 1213
DOI:10.1016/j.physleta.2015.02.011

[22]Makris K G El-Ganainy R Christodoulides D N Musslimani Z H 2008 Phys. Rev Lett. 100 103904
DOI:10.1103/PhysRevLett.100.103904

[23]Jin L Wang P Song Z 2017 Sci. Rep. 7 5903
DOI:10.1038/s41598-017-06198-9

[24]Yuce C 2019 Phys. Lett. A 383 2567
DOI:10.1016/j.physleta.2019.05.031 [Cited within: 1]

[25]Qi L Xing Y Cao J Jiang X X An C S Zhu A D Zhang S Wang H F 2018 Sci. China: Phys. Mech. Astron. 61 080313
DOI:10.1007/s11433-018-9212-4 [Cited within: 1]

[26]Ganeshan S Sun K Sarma S D 2013 Phys. Rev. Lett. 110 180403
DOI:10.1103/PhysRevLett.110.180403

[27]Cao J Xing Y Qi L Wang D Y Bai C H Zhu A D Zhang S Wang H F 2017 Laser Phys. Lett. 15 015211
DOI:10.1088/1612-202X/aa9831 [Cited within: 1]

[28]Yao S Wang Z 2018 Phys. Rev. Lett. 121 086803
DOI:10.1103/PhysRevLett.121.086803 [Cited within: 4]

[29]Turker Z O Yuce C 2019 Phys. Rev. A 99 022127
DOI:10.1103/PhysRevA.99.022127 [Cited within: 1]

[30]Jin L Song Z 2019 Phys. Rev. B 99 081103
DOI:10.1103/PhysRevB.99.081103 [Cited within: 1]

[31]Kunst F K Edvardsson E Budich J C Bergholtz E J 2018 Phys. Rev. Lett. 121 026808
DOI:10.1103/PhysRevLett.121.026808 [Cited within: 1]

[32]Edvardsson E Kunst F K Bergholtz E J 2019 Phys. Rev. B 99 081302
DOI:10.1103/PhysRevB.99.081302 [Cited within: 1]

[33]Leykam D Bliokh K Y Huang C Chong Y D Nori F 2017 Phys. Rev. Lett. 118 040401
DOI:10.1103/PhysRevLett.118.040401 [Cited within: 2]

[34]Ghatak A Das T 2019 J. Phys.: Condens. Matter 31 263001
DOI:10.1088/1361-648X/ab11b3

[35]Yao S Song F Wang Z 2018 Phys. Rev. Lett. 121 136802
DOI:10.1103/PhysRevLett.121.136802

[36]Jiang H Lü R Chen S 2019 Eur. Phys. J. B 93 125
DOI:10.1140/epjb/e2020-10036-3 [Cited within: 1]

[37]Shen H Zhen B Fu L 2018 Phys. Rev. Lett. 120 146402
DOI:10.1103/PhysRevLett.120.146402 [Cited within: 1]

[38]Yokomizo K Murakami S 2019 Phys. Rev. Lett. 123 066404
DOI:10.1103/PhysRevLett.123.066404

[39]Lee J Y Ahn J Zhou H Vishwanath A 2019 Phys. Rev. Lett. 123 206404
DOI:10.1103/PhysRevLett.123.206404 [Cited within: 1]

[40]Song F Yao S Wang Z 2019 Phys. Rev. Lett. 123 246901
DOI:10.1103/PhysRevLett.123.246801 [Cited within: 1]

[41]Liu C H Chen S 2019 Phys. Rev. B 100 144106
DOI:10.1103/PhysRevB.100.144106 [Cited within: 1]

[42]Ashida Y Furukawa S Ueda M 2017 Nat. Commun. 8 15791
DOI:10.1038/ncomms15791 [Cited within: 1]

[43]Schomerus H 2013 Opt. Lett. 38 1912
DOI:10.1364/OL.38.001912

[44]Weimann S Kremer M Plotnik Y Lumer Y Nolte S Makris K G Segev M Rechtsman M Szameit A 2017 Nat. Mater. 16 433
DOI:10.1038/nmat4811

[45]Bandres M A Wittek S Harari G Parto M Ren J Segev M Christodoulides D N Khajavikhan M 2018 Science 359eaar4005
DOI:10.1126/science.aar4005 [Cited within: 2]

[46]Yin C Jiang H Li L Lü R Chen S 2018 Phys. Rev. A 97 052115
DOI:10.1103/PhysRevA.97.052115 [Cited within: 2]

[47]Yuce C Ramezani H 2019 Phys. Rev. A 100 032102
DOI:10.1103/PhysRevA.100.032102 [Cited within: 1]

[48]Yang Z Hu J 2019 Phys. Rev. B 99 081102
DOI:10.1103/PhysRevB.99.081102

[49]Yoshida T Peters R Kawakami N Hatsugai Y 2019 Phys. Rev. B 99 121101
DOI:10.1103/PhysRevB.99.121101 [Cited within: 1]

[50]Mei F Chen G Tian L Zhu S L Jia S 2018 Phys. Rev. A 98 012331
DOI:10.1103/PhysRevA.98.012331 [Cited within: 1]

[51]Qi L Liu S Zhang S Wang H F 2020 Opt. Lett. 45 2018
DOI:10.1364/OL.388835

[52]Dlaska C Vermersch B Zoller P 2017 Quant. Sci. Technol. 2 015001
DOI:10.1088/2058-9565/2/1/015001 [Cited within: 1]

[53]Longhi S Gatti D Valle G D 2015 Sci. Rep. 5 13376
DOI:10.1038/srep13376 [Cited within: 2]

[54]Brouwer P W Silvestrov P G Beenakker C W J 1997 Phys. Rev. B 56R4333
DOI:10.1103/PhysRevB.56.R4333

[55]Goldsheid I Y Khoruzhenko B A 1998 Phys. Rev. Lett. 80 2897
DOI:10.1103/PhysRevLett.80.2897 [Cited within: 1]