F Ungan^,1, M K Bahar², S Pal³, M E Mora-Ramos^4,51Faculty of Technology, Department of Optical Engineering, Sivas Cumhuriyet University, 58140 Sivas, Turkey
²Faculty of Science, Department of Physics, Sivas Cumhuriyet University, 58140 Sivas, Turkey
³Department of Quality Assurance, CQA(SA), DGQA Ichapur-Nawabganj, 24 Pgs(North), 743144, West Bengal, India
⁴Centro de Investigación en Ciencias, Instituto de Investigación en Ciencias Básicas y Aplicadas, Universidad Autónoma del Estado de Morelos, Av. Universidad 1001, CP 62209, Cuernavaca, Morelos, México
⁵Facultad de Ciencias Básicas, Universidad de Medellín, Medellín, Colombia

Received:2020-01-30Revised:2020-03-20Accepted:2020-03-30Online:2020-06-24


Abstract
We present a theoretical study on the effects of intense laser field (ILF) and static electric field on the linear and nonlinear optical properties of a cylindrical quantum dot with Rosen–Morse axial potential under the framework of effective mass and parabolic band approximations. This study also takes into account the effects of the structure parameters (η, V₁, and R). The analytical expressions of the linear, third-order nonlinear and total optical absorption coefficients (TOACs) and the relative refractive index changes (RRICs) are obtained by using the compact-density-matrix approach. The results of numerical calculations show that the resonant peak position of the TOACs and RRICs shifts towards lower energies and the magnitude of the peak increases with the effect of the static electric field and ILF. In addition, it is observed that while the resonant energies of the TOACs and RRICs of system shift towards the higher (lower) energies with the enhancement of η, V₁, they decrease with the augmentation of R. Thus, the findings of this study show that the optical properties of the structure can be adjusted by changing the magnitude of structure parameters and applied external fields.
Keywords： cylindrical quantum dot;nonlinear optical response;intense laser field;electric field


PDF (759KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
F Ungan, M K Bahar, S Pal, M E Mora-Ramos. Electron-related nonlinear optical properties of cylindrical quantum dot with the Rosen–Morse axial potential. Communications in Theoretical Physics, 2020, 72(7): 075505- doi:10.1088/1572-9494/ab8a1d

1. Introduction

Owing to rapid advancement in the field of nanotechnology during the past few decades, low-dimensional semiconductor structures have attracted a great deal of interest for applications in modulating optoelectronic devices. Among these nanosystems, quantum dots (QDs) are characterized by the three-dimensional spatial confinement of charge carriers. This feature causes a discrete atomic-like energy state, thus making QDs promising candidates in manufacturing new-generation optoelectronic devices. Among other advantages, these structures exhibit more pronounced nonlinear optical effects than the bulk materials [1, 2]. Such resemblance of carrier energy spectrum with that of an atom allows us to speak about a QD as an artificial atom. Because of the vast innovative physical properties of QDs, a large number of theoretical and experimental studies on the linear and nonlinear optical responses of these systems have been carried out. It is possible to mention, for example, the theoretical optical absorption coefficient (OAC) and refractive index change (RIC) coefficients; the nonlinear optical rectification (NOR), the second and third harmonic generation (SHG and THG), as well as the so-called electro optic effect (EOE), are investigated in several studies [3–14].

The description of electron states in QDs aligned with the direction of growth corresponds to the envelope function approximation, whose extension matches well with the width of the potential applied. Therefore, a number of researchers have taken interest in the nonlinear optical properties of QDs under the influence of several potentials with different potential shapes such as Coulomb, Rosen–Morse, Pöschl-Teller, Tietz-Hua, Woods-Saxon, Gaussian, Ellipsoidal and other potentials [15–31]. As the orbital wave functions of QDs are spatially extended they are susceptible to be influenced by external fields. Application of an external electromagnetic field in the direction of growth of the heterostructure modifies the quantized energy states of QDs by polarization of the carrier distribution [32]. The intensity output of the optoelectronic devices can be modulated considerably by monitoring the external fields. Therefore, several studies of external electromagnetic fields affecting linear and nonlinear optical properties of QDs have been conducted [11, 33–38]. As a summary, the presence of external perturbations in the form of static electric and magnetic fields, as well as that of the ILF, can play important roles in fabricating optical transition energy configurations, by tailoring confinement strength of the electron in QDs.

In this work, we have explored the detailed linear and third-order nonlinear optical responses in a cylindrical quantum dot (CQD) with Rosen–Morse axial potential, with the use of the numerical diagonalization of the associated Hamiltonian matrix. The calculations are done within the effective mass and parabolic band (EM+PB) theoretical frameworks. Based on this connection, additionally the influence of ILF and static electric field on the optical responses has also been investigated. The organization of the paper is as follows: the next section briefly presents the description of the theoretical modeling. In section 3, we analyze and discuss the results obtained. The corresponding conclusions are presented in section 4.

2. Theory

Here, we provide some details of the method for obtaining the electron subband energy levels and their related wave-functions of the CQD with Rosen–Morse axial potential, considering the influence of static electric field and ILF. The latter has polarization parallel to the growth (z) direction of the structure. Besides, the static electric field orients parallel to the z-direction. Under EM+PB, the Hamiltonian of a conduction band electron, confined within the CQD without ILF effects is using cylindrical coordinates given by [39](1)$ \begin{eqnarray}\begin{array}{rcl}H & = & -\displaystyle \frac{{{\hslash }}^{2}}{2{m}^{* }}\left(\displaystyle \frac{{{\rm{d}}}^{2}}{{\rm{d}}{\rho }^{2}}+\displaystyle \frac{1}{\rho }\displaystyle \frac{{\rm{d}}}{{\rm{d}}\rho }+\displaystyle \frac{1}{{\rho }^{2}}\displaystyle \frac{{{\rm{d}}}^{2}}{{\rm{d}}{\phi }^{2}}\right)\\ & & +V(\rho )-\displaystyle \frac{{{\hslash }}^{2}}{2{m}^{* }}\displaystyle \frac{{{\rm{d}}}^{2}}{{\rm{d}}{z}^{2}}+V(z)+{eFz},\end{array}\end{eqnarray}$where the quantity m^* is the electron effective mass. In addition, e is the electron charge, and F is the electric field strength, and $\rho (=\sqrt{{x}^{2}+{y}^{2}})$. The potential functions V(z) and V(ρ) correspond to the confinement along the z-direction and in the (x−y) plane, respectively. The functional form of V(ρ) is(2)$ \begin{eqnarray}V(\rho )=\left\{\begin{array}{ll}0, & \rho \leqslant R\\ {V}_{0}, & \rho \gt R\end{array}\right.\end{eqnarray}$where R is the QD radius and V₀=V₁+V₂. On the other hand, the functional form of the Rosen–Morse potential along the z-direction is given by(3)$ \begin{eqnarray}V(z)=-{V}_{1}{{\rm{{\rm{sech}} }}}^{2}(\eta z)+{V}_{2}{{\rm{\tanh }}}^{2}(\eta z),\end{eqnarray}$where V₁ and V₂ are the so-called depth energy parameters and η is the width parameter, with inverse length units. Under the additional influence of an ILF with angular frequency Ω, the Rosen–Morse confinement potential modifies according to the following transformation [40](4)$ \begin{eqnarray} \langle V(z,{\alpha }_{0}) \rangle =\displaystyle \frac{{\rm{\Omega }}}{2\pi }{\int }_{0}^{2\pi /{\rm{\Omega }}}V(z+{\alpha }_{0}\sin {\rm{\Omega }}t){\rm{d}}{\rm{t}},\end{eqnarray}$here, ${\alpha }_{0}={{eA}}_{0}/{m}^{* }{\rm{\Omega }}$ is the parameter of laser-dressing while A₀ represents the field strength. The electron wave function in the CQD can be written as(5)$ \begin{eqnarray}\psi ={Nf}(\rho )g(z),\end{eqnarray}$where N is the normalization constant, and f(ρ) and g(z) are the wave functions of the uncorrelated radial and axial electron states, respectively. The two-dimensional (lateral direction) effective-mass Schrödinger-like equation is(6)$ \begin{eqnarray}\left[-\displaystyle \frac{{{\hslash }}^{2}}{2{m}^{* }}\left(\displaystyle \frac{{{\rm{d}}}^{2}}{{\rm{d}}{\rho }^{2}}+\displaystyle \frac{1}{\rho }\displaystyle \frac{{\rm{d}}}{{\rm{d}}\rho }+\displaystyle \frac{1}{{\rho }^{2}}\displaystyle \frac{{{\rm{d}}}^{2}}{{\rm{d}}{\phi }^{2}}\right)+V(\rho )\right]f(\rho )={E}_{\rho }f(\rho ),\end{eqnarray}$which has a solution of the form [41, 42](7)$ \begin{eqnarray}f(\rho )=\left\{\begin{array}{ll}{N}_{1}{{\rm{J}}}_{0}({r}_{10}\rho ), & \rho \leqslant R\\ {N}_{1}\tfrac{{{\rm{J}}}_{0}({r}_{10}R)}{{{\rm{K}}}_{0}({b}_{10}R)}{{\rm{K}}}_{0}({b}_{10}\rho ), & \rho \gt R\end{array}\right..\end{eqnarray}$In this expression, N₁ labels the normalization constant, while J_m and K_m are the modified Bessel functions of mth order, ${r}_{10}=\sqrt{2{m}^{* }{E}_{\rho }/{{\hslash }}^{2}}$ and ${b}_{10}=\sqrt{2{m}^{* }{V}_{0}/{{\hslash }}^{2}-{r}_{10}^{2}}$. The energy eigenvalue E_ρ is determined by imposing the continuity of the wave function together with that of its first derivative at ρ=R. The bound energy levels in a Rosen–Morse confinement potential under the non-resonant ILF are determined by solving the following time-independent one-dimensional Schrödinger equation(8)$ \begin{eqnarray}\left[-\displaystyle \frac{{{\hslash }}^{2}}{2{m}^{* }}\displaystyle \frac{{{\rm{d}}}^{2}}{{\rm{d}}{z}^{2}}+\langle V(z,{\alpha }_{0})\rangle \right]g(z)={E}_{z}g(z).\end{eqnarray}$

The process that allows us to determine the energy levels, E_z, and the corresponding z-dependent wave functions, g(z), consists of the diagonalization of the Hamiltonian matrix obtained after the expansion of the electron states in a series of a complete orthogonal basis. We choose as the elements of this basis the set of eigenfunctions of the infinite potential well of width L_b. The suitable value of L_b ensures the convergence of the bound energy levels, which is significantly larger than the dimensions of the active system. Such a calculation scheme has been used in our previous study [43]. With the energy eigenvalues and corresponding envelope wave functions at hand, we evaluated the linear and nonlinear optical coefficients from [44, 45]:(9)$ \begin{eqnarray}{\beta }^{(1)}(\omega )=\omega \sqrt{\displaystyle \frac{\mu }{{\varepsilon }_{r}}}\displaystyle \frac{| {M}_{10}{| }^{2}{\sigma }_{v}{\hslash }{{\rm{\Gamma }}}_{10}}{{\left({E}_{10}-{\hslash }\omega \right)}^{2}+{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}},\end{eqnarray}$(10)$ \begin{eqnarray}\begin{array}{l}{\beta }^{(3)}(\omega ,I)=-2\omega \sqrt{\displaystyle \frac{\mu }{{\varepsilon }_{R}}}\left(\displaystyle \frac{I}{{\varepsilon }_{0}{n}_{r}c}\right)\\ \quad \times \,\displaystyle \frac{| {M}_{10}{| }^{4}{\sigma }_{v}{\hslash }{{\rm{\Gamma }}}_{10}}{{\left[{\left({E}_{10}-{\hslash }\omega \right)}^{2}+{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}\right]}^{2}}\left(1-\displaystyle \frac{| {M}_{11}-{M}_{00}{| }^{2}}{| 2{M}_{10}{| }^{2}}\right.\\ \quad \left.\times \,\displaystyle \frac{{\left({E}_{10}-{\hslash }\omega \right)}^{2}-{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}+2({E}_{10})({E}_{10}-{\hslash }\omega )}{{\left({E}_{10}\right)}^{2}+{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}}\right),\end{array}\end{eqnarray}$(11)$ \begin{eqnarray}\displaystyle \frac{{\rm{\Delta }}{n}^{(1)}(\omega )}{{n}_{r}}=\displaystyle \frac{{\sigma }_{v}| {M}_{10}{| }^{2}}{2{n}_{r}^{2}{\varepsilon }_{0}}\left[\displaystyle \frac{{E}_{10}-{\hslash }\omega }{{\left({E}_{10}-{\hslash }\omega \right)}^{2}+{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}}\right],\end{eqnarray}$(12)$ \begin{eqnarray}\begin{array}{l}\displaystyle \frac{{\rm{\Delta }}{n}^{(3)}(\omega ,I)}{{n}_{r}}=-\displaystyle \frac{\mu c| {M}_{10}{| }^{2}}{4{n}_{r}^{3}{\varepsilon }_{0}}\displaystyle \frac{{\sigma }_{v}I}{{\left[{\left({E}_{10}-{\hslash }\omega \right)}^{2}+{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}\right]}^{2}}\\ \times \,[4({E}_{10}-{\hslash }\omega )| {M}_{10}{| }^{2}-\displaystyle \frac{{\left({M}_{11}-{M}_{00}\right)}^{2}}{{\left({E}_{10}\right)}^{2}+{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}}\{({E}_{10}-{\hslash }\omega )\\ \times \,[({E}_{10})({E}_{10}-{\hslash }\omega )-{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}]-{\left({\hslash }{{\rm{\Gamma }}}_{10}\right)}^{2}(2({E}_{10})-{\hslash }\omega )\}].\end{array}\end{eqnarray}$

The total OAC, β(ω, I), and RRIC, $\tfrac{{\rm{\Delta }}n(\omega ,I)}{{n}_{r}}$, come from the addition of their corresponding linear and nonlinear contributions. In the equations above, n_r denotes the static refractive index of the structure. Furthermore, σ_v is the carrier volume density, and μ is the magnetic permeability. ϵ₀ is the dielectric constant of free space whilst ω and I are, respectively, the angular frequency and the intensity of the incident light causing the intraband optical transition of energy ${E}_{10}={E}_{1}-{E}_{0}$. The ${M}_{{ij}}=| \langle {\psi }_{i}| {ez}| {\psi }_{j}\rangle | $ (i, j=0,1) are the electric dipole moment matrix elements that also have the sense of geometric factor, whereas Γ₁₀=1/τ₁₀ is the relaxation rate associated with the process of transition between the final and initial states.

3. Results and discussion

In this study, we present the calculated results of the effect of static electric and non-resonant high-frequency intense THz laser fields on the TOAC and RRIC in a GaAs-based CQD with Rosen–Morse axial potential. In our calculations, the input parameters are: ${m}^{* }=0.067{m}_{0}$ (m₀ is the single electron bare mass), e=1.602×10⁻¹⁹ C, ${\hslash }=1.056\times {10}^{-34}\,$ Js, ϵ₀=8.854×10⁻¹² C²/Nm², μ=1.256×10⁻⁶ H/m, σ_v= 3.0×10²² m⁻³, V₀=300 meV, τ₁₀=0.14 ps.

The values of calculated energy difference E₁₀ and inter-state electric dipole moment matrix element M₁₀ for different structural and external field configurations are reported in table 1. Figures 1(a)–(c) exhibit the variation of TOACs in the cylindrical QD with the Rosen–Morse axial potential as a function of incident photon energy for three distinct values of η, V₁ and R respectively in the absence of ILF and static electric field. From figure 1(a), it is evident that as the width of the potential well (η) increases, the resonant energies of TOACs undergo a blue-shift which in turn signifies enhanced energy differences, related to transitions between the ground and first excited energy levels of the electron confined in the quantum well. The rise in the energy gap with the decrease of the confinement potential width is attributed by the greater repulsive interaction between the Rosen–Morse potential and the confined electron. On the contrary, the height of the TOACs peak diminishes with the increasing η value as a result of degradation of geometrical factor M₁₀. Consequently, the spatial overlap of the wave-functions of the two states is lowered. Figure 1(b) demonstrates the influence of the Rosen–Morse potential on TOACs, when keeping other parameters at a constant value as described in the figure. A clear blue-shift of absorption peak position is obtained with the increasing value of V₁. When potential strength increases, the electron suffers from greater confinement leading to an increase in the separation of energy levels of the electron. Additionally, with the increase in potential, the wave functions of individual energy states become more localized resulting in diminishing the values of the geometrical factor. As a result, the TOACs peak height gradually decreases with the increasing V₁. Figure 1(c) explicitly reveals the behavior of TOACs with QD radius. As the QD radius increases, the energy separation between the two lowest allowed levels also decreases, which is reflected as red-shift of peak position of TOACs. In this case the resonant peak height first increases with the increase of QD radius, although it is evident from table 1 that the geometrical factor M₁₀ evinces a sharp decrease from $29.9553\,\mathring{\rm{A}} $ to $11.5751\,\mathring{\rm{A}} $ when the QD radius increases from $60\,\mathring{\rm{A}} $ to $80\,\mathring{\rm{A}} $. Such an increase in peak amplitude can be assigned as a result of the higher extent of the overlapping of the wave-functions with the QD radius. When the QD radius increases, the confinement of electron weakens, which in turn makes the overlap easier to occur. However, as the QD radius increases more from $80\,\mathring{\rm{A}} $ to $100\,\mathring{\rm{A}} $, the peak height suddenly diminishes sharply, which is expected from the diminishing values of M₁₀ clearly shown in table 1.

Figure 1.

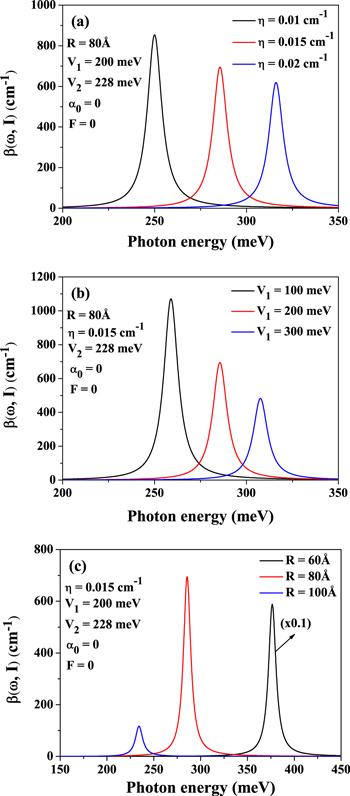New window|Download| PPT slide
Figure 1.The variations of TOACs in the cylindrical QD with the Rosen–Morse axial potential as a function of incident photon energy for three different structure parameters of (a) η, (b) V₁, and (c) R.



Table 1.
Table 1.The variation of electron subband energy differences and the dipole moment matrix elements associated to these subband energy differences for the cylindrical QD with the Rosen–Morse axial potential.

η (cm−1) (${V}_{1}=100\,\mathrm{meV},{V}_{2}=228\,\mathrm{meV},R=80$Å, α0=0, and F=0)	${E}_{1}-{E}_{0}(\mathrm{meV})$	M10 (Å)
0.01	249.938	13.7334
0.015	285.52	11.5751
0.02	315.988	10.3795
V1 ( meV) ($\eta =0.015\,{\mathrm{cm}}^{-1},{V}_{2}=228\,\mathrm{meV},R=80$Å, α0=0, and F=0)	${E}_{1}-{E}_{0}(\mathrm{meV})$	M10 (Å)
100	258.905	15.1299
200	285.52	11.5751
300	307.553	9.285 19
R (Å) ($\eta =0.015\,{\mathrm{cm}}^{-1},{V}_{1}=200\,\mathrm{meV},{V}_{2}=228\,\mathrm{meV},{\alpha }_{0}=0$, and F=0)	${E}_{1}-{E}_{0}(\mathrm{meV})$	M10 (Å)
60	376.469	29.9553
80	285.52	11.5751
100	234.154	5.227 33
F (kV/ cm) ($\eta =0.005\,{\mathrm{cm}}^{-1},{V}_{1}=200\,\mathrm{meV},{V}_{2}=228\,\mathrm{meV},R=80$Å, and α0=0)	${E}_{1}-{E}_{0}(\mathrm{meV})$	M10 (Å)
0	208.989	18.8477
75	204.51	19.675
100	199.82	20.5504
α0 (Å) ($\eta =0.015\,{\mathrm{cm}}^{-1},{V}_{1}=200\,\mathrm{meV},{V}_{2}=228\,\mathrm{meV},R=80$Å, and F=0)	${E}_{1}-{E}_{0}(\mathrm{meV})$	M10 (Å)
0	285.52	11.5751
25	272.596	12.2331
50	243.354	14.2881

New window|CSV

Figures 2(a)–(b) depict the variations of TOACs in the CQD with the Rosen–Morse axial potential as a function of incident photon energy for three different values of static electric field and ILF parameters, respectively. From figure 2(a), it is prominent that as electric field intensifies TOACs exhibit a red-shift with gradual increase in the peak height. From table 1, it can be explained that as the electric field increases, the energy separation between the ground state and first excited state decreases, whereas the geometrical factor M₁₀ enhances with increasing electric field. When the electric field is accelerated, the role of the Rosen–Morse potential starts to be faded out, which eventually makes the electron less confined. As a result, the wave functions of energy levels of the electron become more delocalized. Figure 2(b) also announces almost the same behavior as revealed in figure 2(a). Here, as ILF parameter (α₀) increases, TOACs exhibit a red-shift with rise in the peak height. The observation can be explained in light of diminishing impact of the Rosen–Morse potential on the electron in QD when ILF is switched on and enhanced gradually. As ILF increases, the overlap between the wave functions of the first two energy states is also increased due to the close proximity of the energy levels. This is the main cause of the red-shift of the TOACs, as well as of the increment in resonant peak amplitude with increasing ILF.

Figure 2.

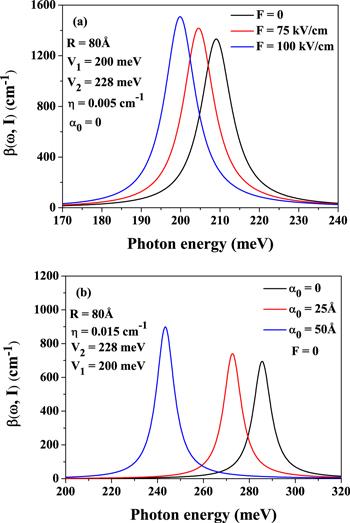New window|Download| PPT slide
Figure 2.The variations of TOACs in the cylindrical QD with the Rosen–Morse axial potential as a function of incident photon energy for three different values of (a) static electric field and (b) ILF parameters.


Figures 3(a)–(c) explicitly delineate the variation of RRICs in the CQD with the Rosen–Morse axial potential as a result of the increase of the incident photon energy. This appears for three different values of $\eta ,{V}_{1}$ and R respectively in the absence of ILF and static electric field. The RRICs undergo a sharp blue-shift with increasing η values as evident from figure 3(a). The maximum amplitude of the RRICs also decreases with increasing η. Table 1 clearly reveals that ${E}_{1}-{E}_{0}$ gradually enhances and M₁₀ sharply diminishes with the potential well width. The RRICs also experience a blue-shift with augmenting strength (V₁) of the Rosen–Morse potential as is evident from figure 3(b). Here also peak height gradually shrinks with increasing V₁. When the RRICs are plotted at three different values of QD radius (R), a red-shift is observed (figure 3(c)). The results are quite similar in nature as depicted in figures 1(a)–(c).

Figure 3.

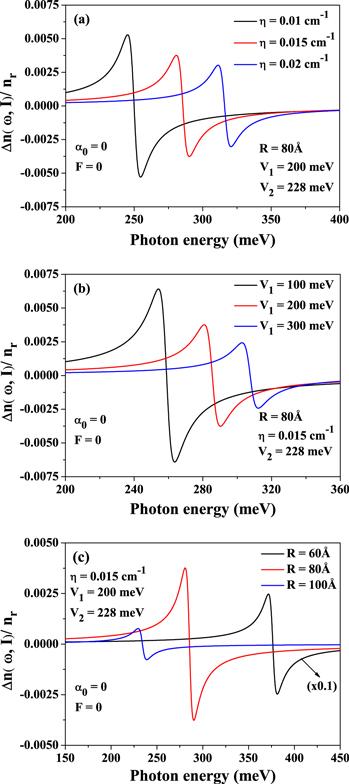New window|Download| PPT slide
Figure 3.The variations of RRICs in the cylindrical QD with the Rosen–Morse axial potential as a function of incident photon energy for three different structure parameters of (a) η, (b) V₁, and (c) R.


Figures 4(a)–(b) contain the dependence of RRICs in the CQD with the change of the Rosen–Morse axial potential, plotted as a function of energy of incoming light, for three different values of static electric field and ILF parameters, respectively. As the ILF increases, the RRICs go through a sharp red-shift due to the reduction of the difference of energy between the ground and first excited states. On the contrary, the geometrical factor enhances with increasing ILF, which is manifested as the increasing peak height of RRICs. Actually, when the system is perturbed with ILF it is fed with excess electrons, which in turn brings a repulsive interaction with the confined electron. Such repulsive interaction delocalizes the wave-functions of individual energy states. As a result, the superposition of energy states is accelerated enhancing the geometrical factor. Figure 4(a) promulgates the same behavior of RRICs when it is tailored at three increasing static electric fields. The static electric fields also enrich the QD system with excess electrons, which brings about a repulsive interaction with the electron confined in the Rosen–Morse potential. As a result the energy differences between the two states gradually diminishes resulting in a sharp enhancement in the geometrical factor M₁₀. Here, the RRICs undergo a red-shift with increasing electric field manifesting a rise in peak height.

Figure 4.

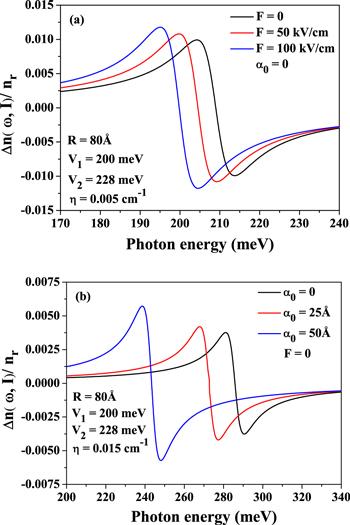New window|Download| PPT slide
Figure 4.The variations of RRICs in the cylindrical QD with the Rosen–Morse axial potential as a function of incident photon energy for three different values of (a) static electric field and (b) ILF parameters.

4. Conclusions

In conclusion, the total optical absorption and relative refractive index change coefficients of a CQD under the confinement of the Rosen–Morse axial potential, with the interplay of non-resonant intense laser and static electric field, are investigated. Both cases of optical response undergo a blue-shift with the increasing strength of the potential well due to an increase in energy separation between the ground state and first excited state, whereas the peak height gradually decreases with the increasing potential well width and strength, which can be attributed as a result of localization of wave-functions. The effect of the changes in the QD radius on total optical absorption and relative refractive index change coefficients is not straightforward. These coefficients delineate a red-shift with the increasing QD radius as a result of closeness of energy levels. The peak height first escalates with increase in radius, and then suddenly falls in a drastic manner with its further enhancement. Similarly, the influence of the intense laser and static electric fields on the studied optical coefficients is very prominent. Both properties exhibit a red-shift with increasing field intensities. The peak height, on the other hand, escalates with the increasing laser and static electric fields. Therefore, the present theoretical model sheds light on the qualitative and quantitative influences of the Rosen–Morse confining potential in conjunction with intense laser and static electric fields on the nonlinear optical properties of QDs.

Acknowledgments

MEMR is grateful to Universidad de Medellín for hospitality and support during their 2019–2020 sabbatical stay. He also acknowledges support from Mexican CONACYT through research Grant A1-S-8218.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Jacak L Hawrylak P Wojs A 1998 Quantum Dots Berlin Springer
[Cited within: 1]

[2]Masumoto Y Takagahara T 2002 Semiconductor Quantum Dots Berlin Springer
[Cited within: 1]

[3]Wang G H Guo K X 2002 Physica B 315 234
DOI:10.1016/S0921-4526(01)01562-9 [Cited within: 1]

[4]Çakir B Yakar Y Özmen A Özgür Sezer M Şhahin M 2010 Superlattices Microstruct. 47 556
DOI:10.1016/j.spmi.2009.12.002

[5]Datta N K Chatterjee K Ghosh M 2011 Solid State Sci. 13 1531
DOI:10.1016/j.solidstatesciences.2011.05.016

[6]Rezai G Kish S S 2013 Superlattices Microstruct 53 99
DOI:10.1016/j.spmi.2012.09.014

[7]Raigoza N Morales A L Duque C A 2006 Braz. J. Phys. 36 350
DOI:10.1590/S0103-97332006000300031

[8]Barseghyan M G Kirakosyan A A Duque C A 2009 Phys. Status Solidi b 246 626
DOI:10.1002/pssb.200880516

[9]Oubram O Navarro O Gaggero-Sager L M Martinez-Orozco J C Rodriguez-Vargas I 2012 Solid State Sci. 14 440
DOI:10.1016/j.solidstatesciences.2012.01.020

[10]Niculescu E C Eseanu E 2011 Eur. Phys. J. B 79 313
DOI:10.1140/epjb/e2010-10556-3

[11]Karabulut I Safak H Tomak M 2005 Solid State Commun. 135 735
DOI:10.1016/j.ssc.2005.06.001 [Cited within: 1]

[12]Karabulut I Mora-Ramos M E Duque C A 2011 J. Lumin. 131 1502
DOI:10.1016/j.jlumin.2011.03.044

[13]Pal S Ghosh M 2016 Opt. Quant. Electron 48 372
DOI:10.1007/s11082-016-0640-9

[14]Pal S Ganguly J Saha S Ghosh M 2016 J. Phys. Chem. Solids 88 85
DOI:10.1016/j.jpcs.2015.10.002 [Cited within: 1]

[15]Kazaryan E M Petrosyan L S Sarkisyan H A 2008 Phys. E 40 536
DOI:10.1016/j.physe.2007.08.013 [Cited within: 1]

[16]Sahin M 2009 J. Appl. Phys. 106 063710
DOI:10.1063/1.3225100

[17]Juharyan L A Kazaryanb E M Petrosyana L S 2006 Solid State Commun. 139 537 540
DOI:10.1016/j.ssc.2006.07.012

[18]Khordad R Mirhosseini B 2014 Opt. Spectrosc. 117 434
DOI:10.1134/S0030400X14090100

[19]Panda S Panda B K 2014 Superlattices Microstruct. 73 160
DOI:10.1016/j.spmi.2013.11.001

[20]Sakiroǵlu S Ungan F Yesilgul U Mora-Ramos M E Duque C A Kasapoglu E Sari H Sökmen I 2012 Phys. Lett. A 376 1875
DOI:10.1016/j.physleta.2012.04.028

[21]Aytekin O Turgut S Tomak M 2012 Phys. E 44 1612
DOI:10.1016/j.physe.2012.04.005

[22]Mora-Ramos M E Barseghyan M G Duque C A 2010 Phys. E 43 338
DOI:10.1016/j.physe.2010.08.007

[23]Unal U V Aksahin E Aytekin O 2013 Phys. 47 103E
DOI:10.1016/j.physe.2012.10.018

[24]Rezaei G Vahdani M R K Vaseghi B 2010 Current Appl. Phys. 11 176
DOI:10.1016/j.cap.2010.07.002

[25]Rezaei G Mousazadeh Z Vaseghi B 2010 Phys. E 42 1477
DOI:10.1016/j.physe.2009.11.122

[26]Khordad R Mirhosseini B 2015 Pramana J. Phys. 85 723
DOI:10.1007/s12043-014-0906-3

[27]Xie W 2014 Opt. Commun 284 4756
DOI:10.1016/j.optcom.2011.05.033

[28]Khordad R Bahramiyan H 2014 Superlattices Microstruct. 76 163
DOI:10.1016/j.spmi.2014.09.036

[29]Lu L Xie W Hassanabadi H 2001 J. Lumin. 131 2538
DOI:10.1016/j.jlumin.2011.06.051

[30]Xie W 2009 Superlattices Microstruct. 46 693
DOI:10.1016/j.spmi.2009.06.013

[31]Khaledi-Nasab A Sabaeian M Sahrai M Fallahi V Mohammad-Rezaee M 2014 Phys. E 60 42
DOI:10.1016/j.physe.2014.01.034 [Cited within: 1]

[32]John Peter A 2006 Phys. Lett. A 355 59
DOI:10.1016/j.physleta.2006.01.107 [Cited within: 1]

[33]Xie W 2010 Physica B 405 3436
DOI:10.1016/j.physb.2010.05.019 [Cited within: 1]

[34]Li B Guo K-X Liu Z-L Zheng Y-B 2008 Phys. Lett. A 372 1337
DOI:10.1016/j.physleta.2007.09.075

[35]Karabulut I Baskoutas S 2008 J. Appl. Phys. 103 073512
DOI:10.1063/1.2904860

[36]Karabulut I Baskoutas S 2009 J. Comput. Theor. Nanosci. 6 153
DOI:10.1166/jctn.2009.1020

[37]Duque C M Mora-Ramos M E Duque C A 2011 Superlattices Microstruct. 49 264
DOI:10.1016/j.spmi.2010.06.008

[38]Baskoutas S Paspalakis E Terzis A F 2007 J. Phys.: Condens. Matter 19 395024
DOI:10.1088/0953-8984/19/39/395024 [Cited within: 1]

[39]Wang R Q Xie H J Yu Y B 2004 Int. J. Mod. Phys. B 18 2887
DOI:10.1142/S0217979204026238 [Cited within: 1]

[40]Radu A Niculescu E Cristes M 2008 J. Optoelectron. Adv. Mater. 10 2555
[Cited within: 1]

[41]Emam T G 2009 Can. J. Phys. 87 1159
DOI:10.1139/P09-083 [Cited within: 1]

[42]Brown J W Spector H N 1986 J. Appl. Phys. 59 1179
DOI:10.1063/1.336555 [Cited within: 1]

[43]Kasapoglu E Ungan F Duque C A Yesilgul U Mora-Ramos M E Sari H Sökmen I 2014 Physica E 61 107
DOI:10.1016/j.physe.2014.03.024 [Cited within: 1]

[44]Boyd R W 2007 Nonlinear Optics3rd ednNew York Rochester
[Cited within: 1]

[45]Yildirim H Tomak M 2006 Phys. Status Solidi b 243 243
DOI:10.1002/pssb.200562461 [Cited within: 1]