Rashid Ahmad^,1, Uzma Sajjad, Muhammad SajidDepartment of Physics, Kohat University of Science and Technology, Kohat 26000, Khyber-Pakhtunkhwa, Pakistan

First author contact: ¹Author to whom any correspondence should be addressed.
Received:2019-10-2Revised:2020-02-14Accepted:2020-02-26Online:2020-05-13


Abstract
We investigate the evolution of a discrete-time one-dimensional quantum walk driven by a position-dependent coin. The rotation angle, which depends upon the position of a quantum particle, parameterizes the coin operator. For different values of the rotation angle, we observe that such a coin leads to a variety of probability distributions, e.g. localized, periodic, classical-like, semi-classical-like, and quantum-like. Further, we study the Shannon entropy associated with position and the coin space of a quantum particle, and compare them with the case of the position-independent coin. Our results show that the entropy is smaller for most values of the rotation angle as compared to the case of the position-independent coin. We also study the effect of entanglement on the behavior of probability distribution and Shannon entropy by considering a quantum walk with two identical position-dependent entangled coins. We observe that in general, a wave function becomes more localized as compared to the case of the position-independent coin and hence the corresponding Shannon entropy is lower. Our results show that a position-dependent coin can be used as a controlling tool of quantum walks.
Keywords： quantum walk;position-dependent coin;Shannon entropy


PDF (763KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Rashid Ahmad, Uzma Sajjad, Muhammad Sajid. One-dimensional quantum walks with a position-dependent coin. Communications in Theoretical Physics, 2020, 72(6): 065101- doi:10.1088/1572-9494/ab7ec5

1. Introduction

Classical random walks are widely used fundamental models of natural sciences in which the position of a classical particle is shifted depending upon the outcome of a classical coin. Such walks have found applications in different research areas including diffusion and mobility in materials [1], Brownian motion [2], polymer statistics [3], exchange rate forecast [4], solution of differential equations [5], quantum Monte Carlo techniques [6], and randomized algorithms [7]. Quantum random walks, motivated by classical random walks, were initiated by Aharonov et al in 1993 [8]. In quantum walks, a unitary process for a quantum particle (also known as a walker), i.e. electron, ion, atom, or photon, replaces the stochastic evolution of a classical particle. Thus quantum walks become fundamentally different from their classical counterpart due to quantum interference that arises when different trajectories of the walker intersect each other, hence leading to a very different probability distribution [9, 10].

There are basically two kinds of quantum walk which have already received a good deal of attention: continuous quantum walks [11–13] and discrete-time quantum walks (DTQWs) [14–16]. DTQWs have received much attention because of their applications in various disciplines. In physics, DTQWs are employed for the simulation of different physical phenomena, e.g. topological phenomena in condensed matter systems [17–20], quantum percolation [21], and the effect of disorder on quantum transport [22–24]. In quantum information sciences, due to the faster expansion of quantum walks compared to classical ones, DTQWs are used to develop fast algorithms for computations on a quantum computer [14, 25–33].

These applications have motivated the study of various properties of DTQWs [34–42] and have been realized in numerous experiments using different physical settings including neutral atoms [43–45], photons [46–50], trapped ions [51, 52], and superconducting qubits [53]. To control their behavior, different types of walks have been studied, e.g. DTQWs with decoherence [54, 55]. In a similar vein, recently coherent quantum walks with a step-dependent coin (SDC) operator have been studied [56]. Such a coin operator can be used to obtain the desired probability distribution by controlling the rotation angle. The authors considered different rotation angles and observed diverse probability distributions which are classified into different classes. This motivates us to consider whether quantum walks can also be controlled using a position-dependent coin (PDC) operator.

Moreover, quantum walks of a group of interacting particles in the realm of quantum computing [57] made it possible to link the phenomenon of quantum entanglement [58] with it. The entanglement of quantum bits will allow quantum computers to perform certain calculations much faster than common classical computers. In this context progress has been made, e.g. quantum walks on a line with two entangled particles [59], entanglement and interaction in a topological quantum walk [60], entanglement in quantum walks on a regular graph [61]. In addition, a mathematical model was formulated to understand unrestricted quantum walks using two entangled coins [62]. They demonstrated that the behavior of a walk with entangled coins is different as compared to the usual quantum walks using a single coin. Moreover, one-dimensional quantum walks with four internal degrees of freedom, i.e. two entangled coins, have been recently reported [63]. They have shown that entanglement between two coins could be used as a resource for obtaining different probability distributions in position space. We extend this study to one-dimensional quantum walks with two position-dependent entangled coins (PDEC).

This article is organized in the following way: in section 2, we outline the mathematical framework of the PDC and explain the classification of probability distributions. We discuss the Shannon entropy of the quantum walk with PDC and compare it to the case of the position-independent coin (PIC). We also show the standard deviation for the different classes of probability distributions. In section 3, we study quantum walks with PDEC in one dimension (1D). We compute the entropy in this case and compare it with position-independent entangled coins (PIEC). We conclude and give a brief outlook of our work in section 4.

2. Quantum walk with PDC

In DTQWs the evolution of a walker is controlled by a couple of unitary operators including a ‘coin operator’ and a ‘conditional shift operator’, applied repeatedly. A coin operator acts on the internal states of a walker, which for a walker with two internal degrees of freedom (similar to a spin-1/2 particle) are generally known as the spin-up state and the spin-down state. The conditional shift operator acts on the external degrees of freedom and moves a walker either to the left or right depending on its internal state. Here, we consider a single-qubit walker, i.e. a walker with two internal degrees of freedom, on a one-dimensional lattice. For a single-qubit walker, the Hilbert space ${{ \mathcal H }}_{c}$ associated with the internal states is spanned by state vectors $| 0\rangle ,| 1\rangle $. The Hilbert space ${{ \mathcal H }}_{p}$ associated with the position space is spanned by state vectors $| x\rangle :x$ $\epsilon \ {\mathbb{Z}}$. Thus the Hilbert space of the system is the tensor product of the two Hilbert spaces, i.e. ${{ \mathcal H }}_{c}\otimes {{ \mathcal H }}_{p}$. The PDC operator is defined as(1)$\begin{eqnarray}\begin{array}{rcl}\hat{C} & = & (\cos \hat{x}\theta \ | 0{\rangle }_{C}\langle 0| +\sin \hat{x}\theta \ | 0{\rangle }_{C}\langle 1| \\ & & +\sin \hat{x}\theta \ | 1{\rangle }_{C}\langle 0| -\cos \hat{x}\theta \ | 1{\rangle }_{C}\langle 1| )\otimes | x{\rangle }_{P}\langle x| ,\end{array}\end{eqnarray}$here θ is the rotation angle and $\hat{x}$ is the position operator which acts on the external degree of freedom. In contrast to previously studied inhomogeneous quantum walks [22, 30, 64, 65] we characterize the coin by a single rotation angle which depends on the position of the walker. Choosing different rotation angles results in diverse probability distributions. The conditional shift operator is defined as(2)$\begin{eqnarray}\begin{array}{rcl}\hat{S} & = & | 0{\rangle }_{C}\langle 0| \otimes \sum _{x}| x+1{\rangle }_{P}\langle x| \\ & & +| 1{\rangle }_{C}\langle 1| \otimes \sum _{x}| x-1{\rangle }_{P}\langle x| .\end{array}\end{eqnarray}$This shift operator shifts the walker in the spin-up state to the right and the one in spin-down state to the left by one lattice site. The evolution operator (or the walk operator) $\hat{U}=\hat{S}\hat{C}$ acts on the initial state (φ_int) of the walker. The repeated application of the walk operator to the initial state for a large number of steps results in the evolution of the walk, i.e.(3)$\begin{eqnarray}| \phi {\rangle }_{T}={\hat{U}}^{T}| \phi {\rangle }_{\mathrm{int}},\end{eqnarray}$here ${\phi }_{{T}}$ is the final state of the walker after T steps.

We consider the following initial states to study the evolution of the quantum walk with PDC operator(4)$\begin{eqnarray}| \phi {\rangle }_{\mathrm{int}1}=| 0{\rangle }_{C}\otimes | 0{\rangle }_{P},\end{eqnarray}$(5)$\begin{eqnarray}| \phi {\rangle }_{\mathrm{int}2}=| 1{\rangle }_{C}\otimes | 0{\rangle }_{P}.\end{eqnarray}$The states ${\phi }_{\mathrm{int}1}({\phi }_{\mathrm{int}2})$ describe a particle prepared in the spin-up (spin-down) internal state which is spatially localized around the origin of a 1D lattice. The stepwise evolution of the initial state φ_int1 of the walker can be mathematically written as(6)$\begin{eqnarray}\begin{array}{rcl}| 0{\rangle }_{C}\otimes | 0{\rangle }_{P} & \mathop{\Longrightarrow }\limits^{1\mathrm{st}} & | 0{\rangle }_{C}\otimes | 1{\rangle }_{P},\\ & \mathop{\Longrightarrow }\limits^{2\mathrm{nd}} & \cos \theta \ | 0{\rangle }_{C}\otimes | 2{\rangle }_{P}+\sin \theta \ | 1{\rangle }_{C}\otimes | 0{\rangle }_{P},\\ & \mathop{\Longrightarrow }\limits^{3\mathrm{rd}} & \cos 2\theta \cos \theta \ | 0{\rangle }_{C}\otimes | 3{\rangle }_{P}+\sin 2\theta \cos \theta \\ & & | 1{\rangle }_{C}\otimes | 1{\rangle }_{P}-\sin \theta \ | 1{\rangle }_{C}\otimes | -1{\rangle }_{P},\\ & \mathop{\Longrightarrow }\limits^{{T}{\rm{t}}{\rm{h}}} & \left(\prod _{n=0}^{T-1}\cos n\theta \right)\ | 0{\rangle }_{C}\otimes | T{\rangle }_{P}+.......,\end{array}\end{eqnarray}$and similarly for the second choice of the initial state, we have(7)$\begin{eqnarray}\begin{array}{rcl}| 1{\rangle }_{C}\otimes | 0{\rangle }_{P} & \mathop{\Longrightarrow }\limits^{1\mathrm{st}} & -| 1{\rangle }_{C}\otimes | -1{\rangle }_{P},\\ & \mathop{\Longrightarrow }\limits^{2\mathrm{nd}} & \sin \theta \ | 0{\rangle }_{C}\otimes | 0{\rangle }_{P}+\cos \theta \ | 1{\rangle }_{C}\otimes | -2{\rangle }_{P},\\ & \mathop{\Longrightarrow }\limits^{3\mathrm{rd}} & -\sin 2\theta \cos \theta \ | 0{\rangle }_{C}\otimes | -1{\rangle }_{P}+\sin \theta \\ & & | 0{\rangle }_{C}\otimes | 1{\rangle }_{P}-\cos 2\theta \cos \theta \ | 1{\rangle }_{C}\otimes | -3{\rangle }_{P},\\ & \mathop{\Longrightarrow }\limits^{{T}{\rm{t}}{\rm{h}}} & {\left(-1\right)}^{T}\left(\prod _{n=0}^{T-1}\cos n\theta \right)\ | 0{\rangle }_{C}\otimes | -T{\rangle }_{P}+......\end{array}\end{eqnarray}$After certain ‘T’ number of the steps of the walk, the final states show the walker can occupy at most T number of lattice sites. The final states also show that due to quantum interference a walker initially prepared in state ${\phi }_{\mathrm{int}1}({\phi }_{\mathrm{int}2})$ has zero probability at the x=−T (x=T) position. Also, for both initial states (φ_int1 and φ_int2), the occupied positions are always even for an even number of steps, and odd otherwise.

2.1. Classification of probability distributions

From equations (6) and (7) it is clear that the evolution of the quantum walk depends on the rotation angle (θ). In this section, we make use of this fact to feature the possible classes of the probability distributions of this walk by choosing different rotation angles. We carry out numerical simulations for the initial state ${\phi }_{\mathrm{int}1}$ and classify the resultant probability distributions according to their behavior. This classification is shown in table 1, which we are going to discuss in the following sections.

2.1.1. Free localized walk

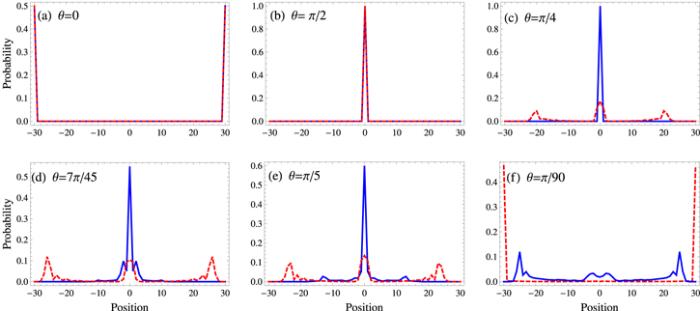
For rotation angle θ=0, the evolution of the walk shows that the walker is at position x=T with probability 1 after T steps as shown in figure 1(a). For this rotation angle the coin operator is an identity operator, and hence does not change the internal state of the walker. As a result the walker initially prepared in the spin-up state remains in the same internal state during the evolution of the walk and shifts to the right by a unit distance at each step of the walk.

Figure 1.

New window|Download| PPT slide
Figure 1.Probability distribution of the walk after T=30 for different rotation angles θ (indicated in the inset). The solid blue line represents the quantum walk with a position-dependent coin, and the dashed red line represents the quantum walk with a position-independent coin.

2.1.2. Bounded localized walk

For a rotation angle π/2, the walker is bounded to three positions ($x=0,\pm 1$) irrespective of the number of steps. The walker is localized because the probability is 1 at any of the three possible positions. The probability distribution of the walker after T=30 is shown in figure 1(b). This localization can be explained as follows. The coin operator is the identity operator at the initial position x=0, and acts as a spin-flip operator (changing spin-up to spin-down and vice versa) at x=±1. Hence, a walker initially prepared in the spin-up state will shift to the right during its evolution and will be reflected back from x=1. It will start moving to the left but will be reflected back again from the x=−1 position. This way the walker will oscillate between x=+1 and x=−1. For this rotation angle, the walk with PIC shows that the walker is localized and bounded to two positions (x=−1,0).

2.1.3. Bounded periodic walk

For a rotation angle π/4, the probability distribution shows the periodic behavior of a localized two-peak-zone and three-peak-zone for different numbers of steps. The probability is 1 at x=0 position (localized) for a certain number of steps, or equally distributed between positions x=±1 (two-peaks-zone), or distributed among positions 0,±2 with probabilities 0.5, 0.25 and 0.25, respectively (three-peak-zone). The probability distribution is shown in figure 1(c) for T=30, which shows the two-peak-zone. Moreover for this rotation angle, the coin operator becomes a spin-flip operator at x=±2, and hence the walker remains trapped between these positions. For this rotation angle, PIC is a simple Hadamard coin which shows an asymmetric probability distribution.

2.1.4. Classical-like walk

For a rotation angle 7π/45, the probability distribution shows Gaussian-like behavior, i.e. the maximum probability of finding the walker is at (or near) the x=0 position, and there is a comparatively smaller but non zero probability of finding the walker around the most probable position. For this rotation angle, a walk with PIC shows the maximum probability of finding the walker away from the initial position (figure 1(d)).

2.1.5. Bounded classical-like walk

For a rotation angle π/6, the probability distribution shows classical-like behavior but is bounded (see figure 1(e)). Here, the coin operator becomes a spin-flip operator at x=±3 and hence the walker gets reflected from these positions and becomes bounded to seven lattice sites. For this rotation angle, a walk with PIC is not bounded and the walker spreads away from its initial position.

2.1.6. Fast classical-like walk

For a rotation angle π/5, the probability distribution of the walk is Gaussian-like but for a given value of T the number of positions occupied by the walker is greater compared to the classical-like walk. Moreover, in the case of a fast classical-like walk the number of occupied positions increases more rapidly than the case of a classical-like walk. For this rotation angle, PIC shows the maximum probability away from the initial position (figure 1(f)).

2.1.7. Semi-classical-like walk

For a rotation angle 2π/5, the probability of finding the walker is maximum near the center of the occupied positions. There are other significant peaks towards the sides of the highest peak. We call this walk a semi-classical-like walk. For this rotation angle a walk with PIC shows the maximum probability towards the right (figure 1(g)).

2.1.8. Bounded semi-classical-like walk

For a rotation angle π/20, the probability distribution is semi-classical-like but is bounded to 31 lattice sites. The coin operator becomes a spin-flip operator at x=±15 and thus the walker cannot surpass these positions. We call the walk with this type of probability distribution a bounded semi-classical-like walk. The PIC for this rotation angle shows the maximum probability towards the right (figure 1(h)).

2.1.9. Fast semi-classical-like walk

For a rotation angle π/3, the probability distribution is semi-classical-like but the number of occupied positions is greater compared to the semi-classical-like walk. The PIC for this angle is semi-classical-like but not fast (figure 1(i)).

2.1.10. Bounded quantum-like walk

For a rotation angle π/90, the walk shows ballistic, asymmetric expansion. The walk is quantum-like but is bounded to finite positions. For this rotation angle the coin operator becomes a spin-flip operator at x=±45. We call this a bounded quantum-like walk. For this rotation angle, PIC shows the maximum probability at position x=T (figure 1(j)).

2.2. Shannon entropy

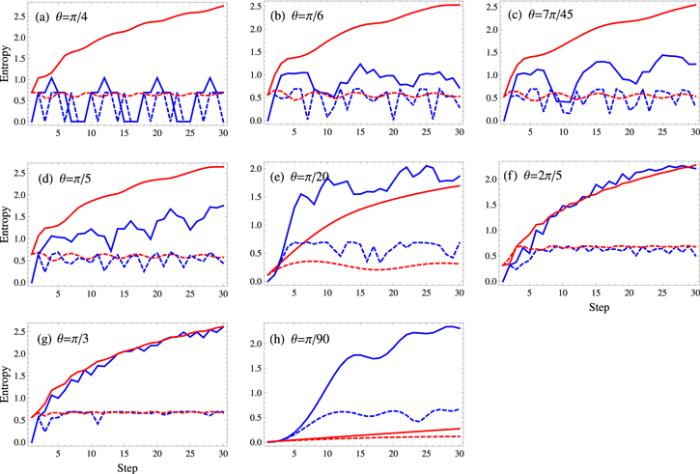
The idea of Shannon entropy was presented by Claude Shannon in 1948 [66]. In quantum walks, the Shannon entropy was introduced and numerically studied for a Hadamard coin [67, 68]. The Shannon entropy for each step of a walk is determined from the probabilities of positions and internal degrees of freedom occupied by a wave function. In quantum walks with PDC the Shannon entropy depends on the choice of rotation angle. We compute the Shannon entropy associated with position space (S_P) and coin space (S_C) for the PDC, and compare it with the case of PIC. The Shannon entropy is defined as(8)$\begin{eqnarray}{S}_{{\rm{P}}}=-\displaystyle \sum _{x}{P}_{x}{{\rm{log}}}_{e}{P}_{x},\end{eqnarray}$(9)$\begin{eqnarray}{S}_{{\rm{C}}}=-\displaystyle \sum _{i}{P}_{i}{{\rm{log}}}_{e}{P}_{i},\end{eqnarray}$here P_x is the probability of finding the walker at position x and _Pi is the probability of the walker in internal state i where i=0,1. The entropies for different rotation angles in the case of quantum walks with PDC and PIC are plotted in figure 2. For a walk with PIC, the entropy of position space always increases with the number of steps (T), and this behavior does not change with the rotation angle. For a walk with PDC, we observe the following regarding the entropy of position space (we will equally call it entropy):• Entropy is a measure of uncertainty in the state of the walker. Thus for a localized walk the entropy is always zero. This is the case for the two classes of walk, i.e. free localized walk (θ=0) and bounded localized walk (θ=π/2).
• For other rotation angles, the evolution of entropy shows three types of behavior, i.e. bounded periodic, bounded, and unbounded.
• For a bounded periodic walk (θ=π/4) the entropy is bounded periodic as the uncertainty in the position state of the system periodically changes. Whenever the walker is localized the entropy of the state is 0, for the two-peak-zone entropy is 0.7, and for the three-peak-zone the entropy is 1, as shown in figure 2(a).
• Entropies of the bounded walks are bounded but non-periodic. In this case the entropies of the walk do not increase after reaching their corresponding maximum limit, as shown in figures 2(b), (e), (h).
• For other classes of walk the behavior of the Shannon entropy is unbounded, i.e. it increases with the number of steps, as shown in figures 2(c), (d), (f), (g).
• The entropy for a quantum walk with PDC is lower as compared to PIC except for the bounded quantum-like walk. The exception is because this class of walk is observed for a small rotation angle (closer to 0). In this case, a quantum walk with PIC shows localized-like behavior and hence the corresponding entropy of the walk becomes lower. The same trend in the entropy is seen in the case of a bounded semi-classical-like walk. However, here this holds only for a smaller number of steps. For semi-classical-like and fast semi-classical-like walks the entropy has the same behavior for PDC and PIC. In both types of walk, the entropy increases with the number of steps.
The Shannon entropy (S_C) associated with the coin space of the walker in the case of PIC shows periodic behavior irrespective of the value of the rotation angle. For the walk with PDC, we observe the following:• For a periodic walk S_C shows periodic behavior. When the walk is localized then S_C is zero, similar to S_P. This takes place for specific values of T in a periodic walk.
• For all subclasses of the classical-like walks S_C is lower compared to their PIC counterparts. Generally, our results show that S_C of a walk with PDC is lower compared to PIC except for the bounded semi-classical-like and bounded quantum-like walks. For semi-classical-like and fast semi-classical-like walks, S_C is almost same and increases with the number of steps in both PDC and PIC cases.

Figure 2.

New window|Download| PPT slide
Figure 2.Shannon entropy versus the number of steps T. The blue line represents the quantum walk with PDC and the red line represents the quantum walk with PIC. The solid (dashed) line indicates the Shannon entropy associated with the position (coin) space.



Table 1.
Table 1.Classification of the probability distribution for quantum walks with a position-dependent coin.

Classes of walk	Rotation angle (θ)
Free localized walk	0
Bounded localized walk	π/2
Bounded periodic walk	π/4
Classical-like walk	7π/45
Bounded classical-like walk	π/6
Fast classical-like walk	π/5
Semi-classical-like walk	2π/5
Bounded semi-classical-like walk	π/20
Fast semi-classical-like walk	π/3
Bounded quantum-like walk	π/90

New window|CSV

2.3. Standard deviation

We compute the standard deviation (σ) for all classes of quantum walk with PDC. The results are shown in figure 3. For localized walks (both free and bounded) the standard deviation is 0, and for periodic walks it changes periodically. For other classes of walk we observe the following.

Figure 3.

New window|Download| PPT slide
Figure 3.Standard deviation (σ) versus the number of steps of the walk for T=30. (a) The dashed red line shows the standard deviation of a simple classical random walk ($\sigma =\sqrt{T}$). The dotted blue line represents a bounded classical-like walk, the solid blue line represents a normal classical-like walk, and the dashed blue line represents a fast classical-like walk. (b) The dotted red line shows the standard deviation of a simple Hadamard walk with position-independent coin ($\sigma \approx T$). The dotted blue line represents a bounded semi-classical-like walk, the solid blue line represents a normal semi-classical-like walk, and the dashed blue line represents a fast semi-classical-like walk. (c) The dotted red line shows the standard deviation of a simple Hadamard walk with a position-independent coin ($\sigma \approx T$). The dotted blue line represents a bounded quantum-like walk.

2.3.1. Classical-like walk

We compute the standard deviation of all three subclasses of the classical-like walk and compare it with the σ of the standard classical random walk (see figure 3(a)). The square root dependence of the σ on the number of steps (T) of the walk justifies their classification as a classical-like walk. Moreover, for a rotation angle π/5 the σ is greater than the other subclasses, which shows that for this rotation angle the classical-like walk spreads faster. In case of a bounded classical-like walk, σ does not increase from a certain maximum limit.

2.3.2. Semi-classical-like walk

For all the subclasses of semi-classical-like walk we compare the standard deviations of a quantum walk with a position-independent Hadamard coin. The walker’s initial state is chosen as in equation (4). In the case of normal and fast semi-classical-like walks, the standard deviations increase linearly with T similar to the case of a simple Hadamard walk, albeit rather slowly. This justifies the name of this class. In the case of a bounded semi-classical-like walk, initially the standard deviation increases linearly with T, but this is not the case for higher T as the walker is bounded. This behavior is shown in figure 3(b).

2.3.3. Quantum-like walk

For the quantum-like walk we have only one subclass, i.e. a bounded quantum-like walk. We compare the standard deviation of this walk to the standard deviation of a Hadamard walk. Our results show that the standard deviation of this walk increases linearly for initial steps; however, because of the fact that the walker is bounded, the standard deviation does not increase further as shown in figure 3(c).

3. Quantum walk with PDEC

We consider a walker with four internal degrees freedom to study a quantum walk with PDEC. The Hilbert space ${{ \mathcal H }}_{{EC}}$ associated with the internal states of the entangled two-qubit walker is spanned by the state vectors $| 00\rangle ,| 01\rangle ,| 10\rangle ,\mathrm{and}\,| 11\rangle $. The entangled coin operator is given by the tensor product of the two identical PDCs given in equation (1), i.e. ${\hat{{C}}}_{{EC}}=\hat{{C}}\otimes \hat{{C}}$(10)$\begin{eqnarray}\begin{array}{rcl}{\hat{{C}}}_{{EC}} & = & ({\cos }^{2}\hat{x}\theta \ | 00{\rangle }_{{CC}}\langle 00| +\sin x\theta \cos \hat{x}\theta \ | 01{\rangle }_{{CC}}\langle 00| \\ & & +\sin \hat{x}\theta \cos \hat{x}\theta \ | 10{\rangle }_{{CC}}\langle 00| +{\sin }^{2}\hat{x}\theta \ | 11{\rangle }_{{CC}}\langle 00| \\ & & +\sin \hat{x}\theta \cos \hat{x}\theta \ | 00{\rangle }_{{CC}}\langle 01| -{\cos }^{2}\hat{x}\theta \ | 01{\rangle }_{{CC}}\langle 01| \\ & & +{\sin }^{2}\hat{x}\theta \ | 10{\rangle }_{{CC}}\langle 01| -\sin \hat{x}\theta \cos \hat{x}\theta \ | 11{\rangle }_{{CC}}\langle 01| \\ & & +\sin \hat{x}\theta \cos \hat{x}\theta \ | 00{\rangle }_{{CC}}\langle 10| +{\sin }^{2}\hat{x}\theta \ | 01{\rangle }_{{CC}}\langle 10| \\ & & +{\cos }^{2}\hat{x}\theta \ | 10{\rangle }_{{CC}}\langle 10| -\sin \hat{x}\theta \cos \hat{x}\theta \ | 11{\rangle }_{{CC}}\langle 10| \\ & & +{\sin }^{2}\hat{x}\theta \ | 00{\rangle }_{{CC}}\langle 11| -\sin \hat{x}\theta \cos x\theta \ | 01{\rangle }_{{CC}}\langle 11| \\ & & +\sin \hat{x}\theta \cos x\theta \ | 10{\rangle }_{{CC}}\langle 11| +{\cos }^{2}\hat{x}\theta \ | 11{\rangle }_{{CC}}\langle 11| )\\ & & \otimes | x{\rangle }_{P}\langle x| .\end{array}\end{eqnarray}$The conditional shift operator in the case of PDEC is defined as(11)$\begin{eqnarray}\begin{array}{rcl}{\hat{{S}}}_{{EC}} & = & | 00{\rangle }_{{CC}}\langle 00| \otimes \sum | x+1{\rangle }_{P}\langle x| \\ & & | 01{\rangle }_{{CC}}\langle 01| \otimes \sum | x{\rangle }_{P}\langle x| \\ & & | 10{\rangle }_{{CC}}\langle 10| \otimes \sum | x{\rangle }_{P}\langle x| \\ & & +| 11{\rangle }_{{CC}}\langle 11| \otimes \sum | x-1{\rangle }_{P}\langle x| .\end{array}\end{eqnarray}$In the case of PDEC the shift operator (${\hat{S}}_{{EC}}$), depending on a internal state of a walker, also acts as an identity operator. This is important difference as compared to the PDC where the shift operator merely shifts the walker to the right and left. We consider a walker with the initial state defined by(12)$\begin{eqnarray}\begin{array}{rcl}| {\rm{\Phi }}{\rangle }_{\mathrm{int}} & = & ({\alpha }_{1}| 00{\rangle }_{{CC}}+{\alpha }_{2}| 01{\rangle }_{{CC}}+{\alpha }_{3}| 10{\rangle }_{{CC}}\\ & & +{\alpha }_{4}| 11{\rangle }_{{CC}})\otimes | 0{\rangle }_{P},\end{array}\end{eqnarray}$where ${\sum }_{i}{\alpha }_{i}^{2}=1$ and the quantity α_i specifies the amount of entanglement. We consider two maximally entangled Bell states: (i) when α₂=α₃=0 and ${\alpha }_{1}=\cos \eta ,{\alpha }_{4}=\sin \eta $ where $\eta =\pi /4$; (ii) when α₁=α₄=0 and ${\alpha }_{2}=\cos \eta ,{\alpha }_{3}=\sin \eta $ with η=π/4. Therefore the two maximally entangled initial states of the walker are(13)$\begin{eqnarray}| {\rm{\Phi }}{\rangle }_{\mathrm{int}1}=\displaystyle \frac{1}{\sqrt{2}}(| 00{\rangle }_{{CC}}+| 11{\rangle }_{{CC}})\otimes | 0{\rangle }_{P},\end{eqnarray}$(14)$\begin{eqnarray}| {\rm{\Phi }}{\rangle }_{\mathrm{int}2}=\displaystyle \frac{1}{\sqrt{2}}(| 01{\rangle }_{{CC}}+| 10{\rangle }_{{CC}})\otimes | 0{\rangle }_{P}.\end{eqnarray}$For the initial state Φ_int1 the stepwise evolution of the walker, by applying the walk operator ($\hat{U}={\hat{S}}_{{EC}}{\hat{C}}_{{EC}}$), can be mathematically written as(15)$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{1}{\sqrt{2}}(| 00{\rangle }_{{CC}}+| 11{\rangle }_{{CC}})\otimes | 0{\rangle }_{P}\\ \mathop{\Longrightarrow }\limits^{1\mathrm{st}}\,\displaystyle \frac{1}{\sqrt{2}}(| 00{\rangle }_{{CC}}\otimes | 1{\rangle }_{P}+| 11{\rangle }_{{CC}}\otimes | -1{\rangle }_{P}),\\ \mathop{\Longrightarrow }\limits^{2\mathrm{nd}}\,\displaystyle \frac{1}{\sqrt{2}}({\sin }^{2}\theta | 00{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}+{\cos }^{2}\theta | 00{\rangle }_{{CC}}\otimes | 2{\rangle }_{P}\\ +\,\cos \theta \sin \theta | 01{\rangle }_{{CC}}\otimes | -1{\rangle }_{P}+\cos \theta \sin \theta | 01{\rangle }_{{CC}}\otimes | 1{\rangle }_{P}\\ +\,\cos \theta \sin \theta | 10{\rangle }_{{CC}}\otimes | -1{\rangle }_{P}+\cos \theta \sin \theta | 10{\rangle }_{{CC}}\otimes | 1{\rangle }_{P}\\ +\,{\sin }^{2}\theta | 11{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}+{\cos }^{2}\theta | 11{\rangle }_{{CC}}\otimes | -2{\rangle }_{P}),\\ \mathop{\Longrightarrow }\limits^{{T}{\rm{t}}{\rm{h}}}\,\prod _{n=0}^{T-1}\displaystyle \frac{{\cos }^{2}n\theta }{\sqrt{2}}\ \left(| 00{\rangle }_{{CC}}\otimes | T{\rangle }_{P}\right)+.........\\ +\,\prod _{n=0}^{T-1}\displaystyle \frac{{\cos }^{2}n\theta }{\sqrt{2}}\ \left(| 11{\rangle }_{{CC}}\otimes | -T{\rangle }_{P}\right).\end{array}\end{eqnarray}$Similarly by applying the walk operator on the initial state Φ_int2 we get(16)$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{1}{\sqrt{2}}(| 01{\rangle }_{{CC}}+| 10{\rangle }_{{CC}})\otimes | 0{\rangle }_{P}\\ \mathop{\Longrightarrow }\limits^{1\mathrm{st}}\,-\displaystyle \frac{1}{\sqrt{2}}(| 01{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}+| 10{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}),\\ \mathop{\Longrightarrow }\limits^{2\mathrm{nd}}\,\displaystyle \frac{1}{\sqrt{2}}(| 01{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}+| 10{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}),\\ \mathop{\Longrightarrow }\limits^{{T}{\rm{t}}{\rm{h}}}\,{\left(-1\right)}^{T}\displaystyle \frac{1}{\sqrt{2}}\left(| 01{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}+| 10{\rangle }_{{CC}}\otimes | 0{\rangle }_{P}\right).\end{array}\end{eqnarray}$

3.1. Probability distribution

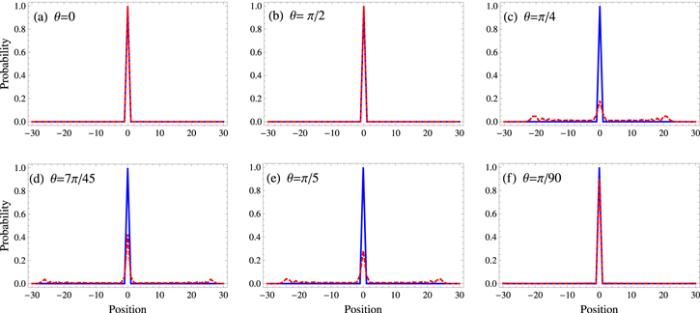
We study the evolution of the walk driven by PDEC, and compare it with the case of PIEC in order to demonstrate the effect of position dependence. We carry out numerical simulations for the two initial states given in equations (13) and (14). For the initial state Φ_int1, the probability distribution for different rotation angles is shown in figure 4. We observe the following properties:1. For θ=0, in figure 4(a) the probability distribution of both types of walk, i.e. a quantum walk with PDEC and one with PIEC, show similar behavior. After T steps of both types of walk, the walker occupies positions x=±T each with probability 0.5.
2. For θ=π/2, in figure 4(b) the probability distribution of the quantum walk with PDEC shows similar behavior to the one with PIEC. The walker is localized at position x=0 for an even number of steps. For odd values of T the probability of the walker splits equally on two lattice sites x=±1.
3. For θ=π/4, in figure 4(c) the probability distribution of the quantum walk with PDEC is periodic and bounded to the range of lattice sites x=±2. For any value of T there are three possible configurations of the probability distribution: (a) the walker has probability 1 at position x=0 (localized), (b) the walker occupies positions x=±1 each with probability 1/2, (c) the walker occupies positions x=0,±1 each with 1/4 probability, and x=±2 both with 1/8 probability. For this rotation angle, the probability distribution of the walk with PIEC shows a three-peak-zone. By increasing the number of steps the probability increases at the initial position. The behavior of the probability distribution does not depend on the choice of the initial state in contrast to the case of PDEC.
4. For θ=7π/45, in figure 4(d) the probability distribution of the walk with PDEC shows bounded behavior. Moreover, the walker has a higher probability at the initial position as compared to the other accessible lattice sites. In the case of PIEC, the number of occupied positions increases with the number of steps and the maximum probability is at positions x=±T.
5. For θ=π/5, in figure 4(e) the probability distribution of the walk with PDEC increases with T at the initial position, i.e. the walker becomes more localized as compared to the walk with PIEC.
6. For θ=π/90, in figure 4(f) the quantum walk with PDEC shows maximum probability towards the sides. Although there is a small probability near the initial position of the walker, it increases with the number of steps of the walk. For a quantum walk with PIEC the probability is maximum at positions x=±T, which resembles the case of θ=0.

Figure 4.

New window|Download| PPT slide
Figure 4.Probability versus position for T=30 and initial state Φ_int1. The solid blue line represents position-dependent entangled coins (PDEC), and the dashed red line represents position-independent entangled coins (PIEC).


Generally, for the quantum walk with PDEC we observe that the walker is more localized at the initial position as compared to the quantum walk with PIEC (except for rotation angles closer to 0).

For the second choice of the initial state (Φ_int2) the probability distribution is plotted in figure 5 where our observations are as follows.

Figure 5.

New window|Download| PPT slide
Figure 5.Probability versus position for T=30 and initial state Φ_int2. The solid blue line represents position-dependent entangled coins, and the dashed red line represents position-independent entangled coins.


The stepwise evolution of the quantum walk with PDEC shows that the probability distribution does not depend on the choice of rotation angle. The walker is completely localized at the initial position for any choice of rotation angle and for any number of steps of the walk. This is because the shift operator ${\hat{S}}_{{EC}}$ does not change the position of a walker prepared in this particular internal state. The localization here is different from the well known Anderson localization [69] which arises due to spatial disorder in a system. In our case the localization is due to the shift operator ${\hat{S}}_{{EC}}$ which does not shift the walker in a particular internal state and thus remains trapped at the initial position.

The probability distribution in the case of PIEC changes with rotation angle. Although the most probable position is x=0 for different rotation angles, still the probability distribution does not show complete localization as in the case of PDEC (for example, see figures 4(c), (d), and (e)).

3.2. Shannon entropy

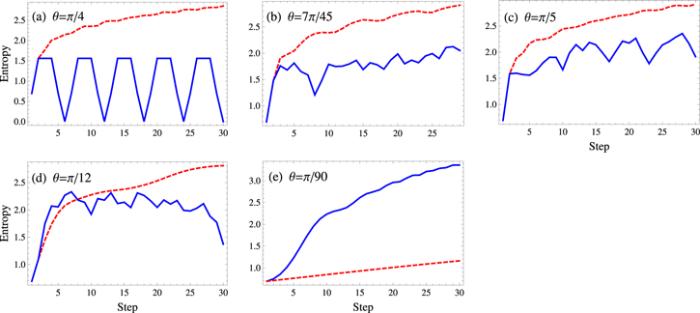
The Shannon entropy associated to the position space of the quantum walk with PDEC is plotted as a function of T for the initial state Φ_int1 (figure 6). For a pure maximally entangled state the entropy associated to coin space is zero. For position space we observe that the entropy is generally smaller for a walk with PDEC as compared to the walk with PIEC (except θ=π/90). This confirms the fact that PDEC localizes a walker as we have demonstrated on the basis of probability distribution (see figure 4). Additionally, for the initial state Φ_int2 the Shannon entropy is zero for any choice of rotation angle because of the localization of the walker.

Figure 6.

New window|Download| PPT slide
Figure 6.Entropy versus the number of steps of the walk up to T=30 and initial state Φ_int1. The solid blue line represents the Shannon entropy of the quantum walk with position-dependent entangled coins (PDEC) and the dashed red line represents the case of position-independent entangled coins (PIEC). Entropy is lower for PDEC as compared to PIEC for different rotation angles except for θ=π/90.

4. Conclusion

We studied quantum walks in one dimension where the coin operator is characterized by a position-dependent rotation angle. We demonstrated that the probability distribution shows diverse behavior for different rotation angles. Based on the probability distribution we classified the walk in different classes. This classification shows that PDC serves as a controlling tool to obtain different probability distributions where the controlling parameter is the rotation angle.

Moreover, we studied the effect of position dependence of the rotation angle on the Shannon entropy of the quantum walk by comparing with the position-independent case. We observed that the entropy in the case of PDC is smaller compared to the walk with PIC, except for the bounded semi-classical-like and bounded quantum-like walk. This exception occurs because of the relatively more localized behavior of the probability distribution in the case of PIC. Generally, the entropy of the quantum walk with PIC increases with the number of steps irrespective of the rotation angle. In the case of PDC the behavior of entropy depends on the rotation angle.

We further investigated 1D quantum walks with two identical PDEC. We considered two pure maximally entangled Bell states as the initial states of the quantum walks. We compared the probability distribution for the walk with PDEC to the case of PIEC. For the case of PDEC we observed that the probability distribution of the walker becomes bounded to limited positions. The walker becomes more localized as compared to PIEC, except for the rotation angles 0 and π/90. In the case of a specific initial state, the probability distribution showed that the walker becomes completely localized irrespective of the considered rotation angle. We also found that the Shannon entropy in the case of PDEC is smaller as compared to PIEC.

This study of PDC in 1D quantum walks can be generalized to study quantum walks with PDC in higher dimensions and with multi-particles. Moreover, the study of quantum walks with two PDEC can be generalized to more than two entangled qubits. The case of non-identical sub coins will be interesting to study, as will quantum walks using coins with different values of entanglement. We will leave these matters for future works.

Acknowledgments

US acknowledges S Panahiyan for his valuable suggestions.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Metzler R Klafter J 2000 The random walk’s guide to anomalous diffusion: a fractional dynamics approach
Phys. Rep. 339 1
DOI:10.1016/S0370-1573(00)00070-3 [Cited within: 1]

[2]Knight F B 1962 On the random walk and Brownian motion
Trans. Am. Math. Soc. 103 218228
DOI:10.1090/S0002-9947-1962-0139211-2 [Cited within: 1]

[3]Michael S 2005 Protein-DNA interaction, random walks and polymer statistics
PhD ThesisMassachusetts Institute of Technology
[Cited within: 1]

[4]Rogoff K 1992 Traded goods consumption smoothing and the random walk behavior of the real exchange rate, monetary and economic studies, institute for monetary and economic studies
Bank of Japan 10 2
DOI:10.3386/w4119 [Cited within: 1]

[5]Hoshino S Ichida K 1971 Solution of partial differential equations by a modified random walk
Numer. Math. 18 1
DOI:10.1007/BF01398459 [Cited within: 1]

[6]Ceperley D Alder B 1986 Quantum Monte Carlo
Science 231 4738
DOI:10.1126/science.231.4738.555 [Cited within: 1]

[7]Motwani R Raghavan P 1995 Randomized AlgorithmsNew YorkCambridge University Press
[Cited within: 1]

[8]Aharonov Y Davidovich L Zagury N 1993 Quantum random walks
Phys. Rev. A 48 1687
DOI:10.1103/PhysRevA.48.1687 [Cited within: 1]

[9]Kempe J 2003 Quantum random walks: an introductory overview
Contemp. Phys. 44 307
DOI:10.1080/00107151031000110776 [Cited within: 1]

[10]Venegas-Andraca S E 2012 Quantum walks: a comprehensive review
Quantum Inf. Proc. 11 1015
DOI:10.1007/s11128-012-0432-5 [Cited within: 1]

[11]Farhi E Gutmann S 1998 Quantum computation and decision trees
Phys. Rev. A 58 915
DOI:10.1103/PhysRevA.58.915 [Cited within: 1]

[12]Rossi M A C Benedetti C Borrelli M Maniscalco S Paris M G A 2017 Continuous-time quantum walks on spatially correlated noisy lattices
Phys. Rev. A 96040301
DOI:10.1103/PhysRevA.96.040301

[13]Mülken O Blumen A 2011 Continuous-time quantum walks: models for coherent transport on complex networks
Phys. Rep. 502 23
DOI:10.1016/j.physrep.2011.01.002 [Cited within: 1]

[14]Lovett N B Cooper S Everitt M Trevers M Kendon V 2010 Universal quantum computation using the discrete-time quantum walk
Phys. Rev. A81042330
DOI:10.1103/PhysRevA.81.042330 [Cited within: 2]

[15]Hamilton C S Barkhofen S Sansoni L Jex I Silberhorn C 2016 Driven discrete time quantum walks
New J. Phys. 8073008
DOI:10.1088/1367-2630/18/7/073008

[16]Kurzyński P Wójcik A 2016 Discrete-time quantum walk approach to state transfer
Phys. Rev. A 18062315
DOI:10.1103/PhysRevA.83.062315 [Cited within: 1]

[17]Kitagawa T Rudner M S Berg E Demler E 2010 Exploring topological phases with quantum walks
Phys. Rev. A 82033429
DOI:10.1103/PhysRevA.82.033429 [Cited within: 1]

[18]Obuse H Asbóth J K Nishimura Y Kawakami N 2015 Unveiling hidden topological phases of a one-dimensional Hadamard quantum walk
Phys. Rev. B 92045424
DOI:10.1103/PhysRevB.92.045424

[19]Obuse H Kawakami N 2011 Topological phases and delocalization of quantum walks in random environments
Phys. Rev. B 84195139
DOI:10.1103/PhysRevB.84.195139

[20]Asbóth J K Obuse H 2013 Bulk-boundary correspondence for chiral symmetric quantum walks
Phys. Rev. B 88121406
DOI:10.1103/PhysRevB.88.121406 [Cited within: 1]

[21]Chandrashekar C M Busch T 2014 Quantum percolation and the transition point of a directed discrete-time quantum walk
Sci. Rep 4 6583
DOI:10.1038/srep06583 [Cited within: 1]

[22]Shikano Y Katsura H 2010 Localization and fractality in inhomogeneous quantum walks with self-duality
Phys. Rev. E 82031122
DOI:10.1103/PhysRevE.82.031122 [Cited within: 2]

[23]Rakovszky T Asboth J K 2015 Localization, delocalization, and topological phase transitions in the one-dimensional split-step quantum walk
Phys. Rev. A 92052311
DOI:10.1103/PhysRevA.92.052311

[24]Chattaraj T Krems R V 2016 Effects of long-range hopping and interactions on quantum walks in ordered and disordered lattices
Phys. Rev. A 94023601
DOI:10.1103/PhysRevA.94.023601 [Cited within: 1]

[25]Childs A M Cleve R Deotto E Farhi E Gutmann S Spielman D A 2003 Exponential algorithmic speedup by a quantum walk
Proc. 35th Annual ACM Symp. on Theory of ComputingSan Diego, CA, USA9−11 June
DOI:10.1145/780542.780552 [Cited within: 1]

[26]Childs A M Goldstone J 2004 Spatial search by quantum walk
Phys. Rev. A 70022314
DOI:10.1103/PhysRevA.70.022314

[27]Poulin D Blume-Kohout R Laflamme R Ollivier H 2004 Exponential speedup with a single bit of quantum information: measuring the average fidelity decay
Phys. Rev. Lett. 92177906
DOI:10.1103/PhysRevLett.92.177906

[28]Ambainis A 2007 Quantum walk algorithm for element distinctness
SIAM J. Comput 37 1
DOI:10.1137/S0097539705447311

[29]Magniez F Santha M Szegedy M 2007 Quantum algorithms for the triangle problem
SIAM J. Comput. 37 2
DOI:10.1137/050643684

[30]Ambainis A 2003 Quantum walks and their algorithmic applications
Int. J. Quantum Inf. 1 507
DOI:10.1142/S0219749903000383 [Cited within: 1]

[31]Shenvi N Kempe J Whaley K B 2003 Quantum random-walk search algorithm
Phys. Rev. A 67052307
DOI:10.1103/PhysRevA.67.052307

[32]Childs A M 2009 Universal computation by quantum walk
Phys. Rev. Lett. 102180501
DOI:10.1103/PhysRevLett.102.180501

[33]Childs A M Gosset D Webb Z 2013 Universal computation by multiparticle quantum walk
Science 339 6121
DOI:10.1126/science.1229957 [Cited within: 1]

[34]Mackay T D Bartlett S D Stephenson L T Sanders B C 2002 Quantum walks in higher dimensions
J. Phys. A: Math. Gen 32352745
DOI:10.1088/0305-4470/35/12/304 [Cited within: 1]

[35]Kendon V 2006 Quantum walks on general graphs
Int. J. Quantum Inf. 04 5
DOI:10.1142/S0219749906002195

[36]Brun T A Carteret H A Ambainis A 2003 Quantum walks driven by many coins
Phys. Rev. A 67052317
DOI:10.1103/PhysRevA.67.052317

[37]Pathak P K Agarwal G S 2007 Quantum random walk of two photons in separable and entangled states
Phys. Rev. A 75032351
DOI:10.1103/PhysRevA.75.032351

[38]Ribeiro P Milman P Mosseri R 2004 Aperiodic quantum random walks
Phys. Rev. A 93190503
DOI:10.1103/PhysRevLett.93.190503

[39]Brun T A Carteret H A Ambainis A 2003 Quantum random walks with decoherent coins
Phys. Rev. A 67032304
DOI:10.1103/PhysRevA.67.032304

[40]Flitney A P Abbott D Johnson N F 2004 Quantum walks with history dependence
J. Phys. A: Math. Gen. 37 30
DOI:10.1088/0305-4470/37/30/013

[41]Du J Li H Xu X Shi M Wu J Zhou X Han R 2003 Experimental implementation of the quantum random-walk algorithm
Phys. Rev. A 67042316
DOI:10.1103/PhysRevA.67.042316

[42]Ryan C A Laforest M Boileau J C Laflamme R 2005 Experimental implementation of a discrete-time quantum random walk on an NMR quantum-information processor
Phys. Rev. A 72062317
DOI:10.1103/PhysRevA.72.062317 [Cited within: 1]

[43]Karski M Förster L Choi J M Steffen A Alt W Meschede D Widera A 2009 Quantum walk in position space with single optically trapped atoms
Science 325 174
DOI:10.1126/science.1174436 [Cited within: 1]

[44]Genske M Alt W Steffen A Werner A H Werner R F Meschede D Alberti A 2013 Electric quantum walks with individual atoms
Phys. Rev. Lett. 110190601
DOI:10.1103/PhysRevLett.110.190601

[45]Robens C Alt W Meschede D Emary C Alberti A 2015 Ideal negative measurements in quantum walks disprove theories based on classical trajectories
Phys. Rev. X 5011003
DOI:10.1103/PhysRevX.5.011003 [Cited within: 1]

[46]Broome M A Fedrizzi A Lanyon B P Kassal I Aspuru-Guzik A White A G 2010 Discrete single-photon quantum walks with tunable decoherence
Phys. Rev. Lett. 104153602
DOI:10.1103/PhysRevLett.104.153602 [Cited within: 1]

[47]Schreiber A Cassemiro K N Potoček V Gábris A Mosley P J Andersson E Jex I Silberhorn C 2010 Photons walking the line: a quantum walk with adjustable coin operations
Phys. Rev. Lett. 104050502
DOI:10.1103/PhysRevLett.104.050502

[48]Sansoni L Sciarrino F Vallone G Mataloni P Crespi A Ramponi R Osellame R 2012 Two-particle bosonic-fermionic quantum walk via integrated photonics
Phys. Rev. Lett. 108010502
DOI:10.1103/PhysRevLett.108.010502

[49]Kitagawa T Broome M A Fedrizzi A Rudner M S Berg E Kassal I Aspuru-Guzik A Demler E White A G 2012 Observation of topologically protected bound states in photonic quantum walks
Nat. Commun 3 882
DOI:10.1038/ncomms1872

[50]Peruzzo A et al. 2010 Quantum walks of correlated photons
Science 329 1500
DOI:10.1126/science.1193515 [Cited within: 1]

[51]Zähringer F Kirchmair G Gerritsma R Solano E Blatt R Roos C F 2010 Realization of a quantum walk with one and two trapped ions
Phys. Rev. Lett. 104100503
DOI:10.1103/PhysRevLett.104.100503 [Cited within: 1]

[52]Schmitz H Matjeschk R Schneider Ch Glueckert J Enderlein M Huber T Schaetz T 2009 Quantum walk of a trapped ion in phase space
Phys. Rev. Lett. 103090504
DOI:10.1103/PhysRevLett.103.090504 [Cited within: 1]

[53]Flurin E Ramasesh V V Hacohen-Gourgy S Martin L S Yao N Y Siddiqi I 2017 Observing topological invariants using quantum walks in superconducting circuits
Phys. Rev. X 7031023
DOI:10.1103/PhysRevX.7.031023 [Cited within: 1]

[54]Kendon V 2006 Decoherence in quantum walks—a review
Math. Struct. Comput. Sci. 17 1169
DOI:10.1017/S0960129507006354 [Cited within: 1]

[55]Alberti A Alt W Werner R Meschede D 2014 Decoherence models for discrete-time quantum walks and their application to neutral atom experiments
New J. Phys. 16123052
DOI:10.1088/1367-2630/16/12/123052 [Cited within: 1]

[56]Panahiyan S Fritzsche S 2018 Controlling quantum random walk with step dependent coin
New J. Phys 20083028
DOI:10.1088/1367-2630/aad899 [Cited within: 1]

[57]DiVincenzo D P 1995 Quantum computation
Science 270 5234
DOI:10.1126/science.270.5234.255 [Cited within: 1]

[58]Horodecki R Horodecki P Horodecki M Horodecki K 2009 Quantum entanglement
Rev. Mod. Phys. 81 865
DOI:10.1103/RevModPhys.81.865 [Cited within: 1]

[59]Omar Y Paunković N Sheridan L Bose S 2006 Quantum walk on a line with two entangled particles
Phys. Rev. A 74042304
DOI:10.1103/PhysRevA.74.042304 [Cited within: 1]

[60]Verga A D Elias R G 2018 Entanglement and interaction in a topological quantum walk
SciPost Phys. 5 019
DOI:10.21468/SciPostPhys.5.2.019 [Cited within: 1]

[61]Carneiro I Loo M Xu X Girerd M Kendon V Knight P L 2005 Entanglement in coined quantum walks on regular graphs
New J. Phys 7 156
DOI:10.1088/1367-2630/7/1/156 [Cited within: 1]

[62]Venegas-Andraca S E Ball J L Burnett K Bose S 2005 Quantum walks with entangled coins
New J. Phys 7 221
DOI:10.1088/1367-2630/7/1/221 [Cited within: 1]

[63]Panahiyan S Fritsch F 2018 One-dimensional quantum walks driven by two entangled coins
arXiv:1810.11020 [quant-ph]
[Cited within: 1]

[64]Ambainis A Kempe J Rivosh A 2005 Coins make quantum walks faster
Proc. 16th Annual ACM-SIAM Symp. on Discrete AlgorithmsVancouver, British Columbia23–25 January10991108
[Cited within: 1]

[65]Linden N Sharam J 2009 Inhomogeneous quantum walks
Phys. Rev. A 80052327
DOI:10.1103/PhysRevA.80.052327 [Cited within: 1]

[66]Shannon C E 1948 A mathematical theory of communication
Bell Syst. Tech. 27 3
DOI:10.1002/j.1538-7305.1948.tb01338.x [Cited within: 1]

[67]Bracken A J Ellinas D Tsohantjis I 2004 Pseudo memory effects, majorization and entropy in quantum random walks
J. Phys. A: Math. Gen. 37 91
DOI:10.1088/0305-4470/37/8/L02 [Cited within: 1]

[68]Chandrashekar C M Srikanth R Laflamme R 2010 Optimizing the discrete time quantum walk using a SU(2) coin
Phys. Rev. A 77032326
DOI:10.1103/PhysRevA.77.032326 [Cited within: 1]

[69]Anderson P W 1958 Absence of diffusion in certain random lattices
Phys. Rev. 109 1492
DOI:10.1103/PhysRev.109.1492 [Cited within: 1]