Single-photon quantum router based on asymmetric intercavity couplings
本站小编 Free考研考试/2022-01-02
Ji-Yang Li1, Xin-Lei Li1, Guo-An Yan,College of Physics and Engineering, Qufu Normal University, Qufu 273165, China
First author contact:1 Both authors contributed equally to this work. Received:2020-01-8Revised:2020-02-13Accepted:2020-02-26Online:2020-04-22
Abstract As a special quantum node in a quantum network, the quantum router plays an important role in storing and transferring quantum information. In this paper, we propose a quantum router scheme based on asymmetric intercavity couplings and a three-level Λ-type atomic system. This scheme implements the quantum routing capability very well. It can perfectly transfer quantum information from one quantum channel to another. Compared with the previous quantum routing scheme, our proposed scheme can achieve the transfer rate of single photons from one quantum channel to another quantum channel reaching 100%, the high transfer rate is located in the almost quadrant regions with negative values of the two variables λa and λb, and their maximum values ${T}_{u}^{b}+{T}_{d}^{b}=1$ emerge in the center point λa=λb=−1. Therefore, it is possibly feasible to efficiently enhance the routing capability of the single photons between two channels by adjusting the inter-resonator couplings, and the asymmetric intercavity coupling provides a new method for achieving high-fidelity quantum routers. Keywords：quantum router;asymmetric intercavity;quantum information processing
PDF (863KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite Cite this article Ji-Yang Li, Xin-Lei Li, Guo-An Yan. Single-photon quantum router based on asymmetric intercavity couplings. Communications in Theoretical Physics, 2020, 72(5): 055101- doi:10.1088/1572-9494/ab7ed5
1. Introduction
The scalable quantum information processing [1–9] in the fields of quantum communication and quantum computation is achieved based on quantum networks [10]. A quantum network is composed of the quantum nodes and quantum channels. Quantum nodes coherently connect different channels, in which the routers control the transport of signals in the different channels. In an efficient optical quantum network, photons are used as ideal information carriers due to their fast propagation speeds, stable coherence, and low dissipations. Recently, the rapid development of photon transport technology in coupled-resonator waveguide (CRW) systems [11–15] provides an ideal platform for single-photon quantum routing, in which the CRW is utilized as a quantum channel for optical signal transmission, and the quantum emitter coupled to the CRW is used to route photons to each channel. Currently, considerable attention has been paid to photon quantum routing that has been implemented in many systems including a whispering-gallery-mode resonator [16], quantum dot [17], cavity quantum electrodynamics [18–22], and optomechanical system [23].
However, in the current routing system, the routing rate of the routers from the main channel to other channels is not more than 50% [18–20], which may limit its more potential applications. A high routing rate can achieve an efficient expected allocation of information between channels. Therefore, it is vital to design a quantum router with a high routing rate for a multi-channel quantum network. To address the problem, many proposals based on the chiral photon-emitter couplings in waveguide-emitter routers have been put forward recently [24–29]. However, in this work, we propose a single-photon routing scheme using the two one-dimensional CRWs with tunable asymmetric intercavity couplings and a three-level Λ-type atomic system. Compared with previous work, our proposed scheme can improve the transfer rate of a single photon from one quantum channel to another, and the maximum transfer rate can reach 100%. We also find that the present setup can be directly realized by the four resonators coupled by a coupler qutrit.
2. Model and Hamiltonian
The system under consideration is composed of two one-dimensional CRWs whose cavity modes are described by the creation operators ${a}_{x}^{\dagger }$ and ${b}_{x}^{\dagger }$(and subscript $j=-\infty ,\,\ldots ,\,+\infty $), and a three-level system characterized by a ground state $| g\rangle $, an intermediate state $| s\rangle $ and an excited state $| e\rangle $. The transition $| g\rangle \leftrightarrow | e\rangle $ is dipole-coupled to the cavity modes a0 and b0 with a coupling strengths of ga and gb. A classical field drives the transition $| s\rangle \leftrightarrow | e\rangle $ with the Rabi frequency Ω. For the two one-dimensional CRWs, we will focus on the case of asymmetric intercavity couplings. Here, we assume that all resonators in CRW−a(CRW−b) have the same frequency ωa(ωb), and the hopping energies ζa (ζb) between any two nearest-neighbor cavities in CRW−a(CRW−b) are the same, except two couplings(${\zeta }_{a}^{{\prime} }$ and ${\zeta }_{b}^{{\prime} }$)between the 0th and 1st resonates in the two one-dimensional CRWs. ${\lambda }_{a}(b)=({\zeta }_{a}^{{\prime} }(b)-{\zeta }_{a}(b))/{\zeta }_{a}(b)$ is introduced to denote the relation between ${\zeta }_{a}(b)$ and ${\zeta }_{a}^{{\prime} }(b)$ [30]. The model is schematically depicted in figure 1.
Figure 1.
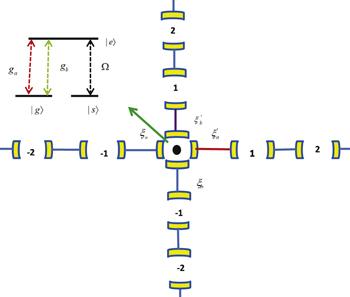New window|Download| PPT slide Figure 1.Schematic of the single-photon quantum router in two channels made of two CRWs.
The Hamiltonian of the whole system is (setting ℏ=1)$\begin{eqnarray}H={H}_{a}+{H}_{c}+{H}_{{\rm{int}}},\end{eqnarray}$where$\begin{eqnarray*}\begin{array}{rcl}{H}_{a} & = & {\omega }_{s}| s\rangle \langle s| +{\omega }_{e}| e\rangle \langle e| ,\\ {H}_{c} & = & \sum _{j}[{\omega }_{a}{a}_{j}^{\dagger }{a}_{j}-{\zeta }_{a}({a}_{j}^{\dagger }{a}_{j+1}+{\rm{h}}{\rm{.}}{\rm{c}}.)]\\ & & -{\lambda }_{a}{\zeta }_{a}({a}_{0}^{\dagger }{a}_{1}+{a}_{1}^{\dagger }{a}_{0})\\ & & +\sum _{j}[{\omega }_{b}{b}_{j}^{\dagger }{b}_{j}-{\zeta }_{b}({b}_{j}^{\dagger }{b}_{j+1}+{\rm{h}}{\rm{.}}{\rm{c}}.]\\ & & -{\lambda }_{b}{\zeta }_{b}({b}_{0}^{\dagger }{b}_{1}+{b}_{1}^{\dagger }{b}_{0}),\\ {H}_{{\rm{int}}} & = & {g}_{a}| e\rangle \langle g| {a}_{0}+{\rm{\Omega }}| e\rangle \langle s| +{g}_{b}| e\rangle \langle g| {b}_{0}+{\rm{h}}{\rm{.}}{\rm{c}}.,\end{array}\end{eqnarray*}$where the Hamiltonian Hc describes the free energy of two one-dimensional ${\rm{CRWs}},{H}_{a}$ is the free Hamiltonian of the three-level atom, and Hint describes the interactions among the cavity mode, the classical field and the atom. The frequencies ωs and ωe are the energy of the intermediate state and excited state, respectively. Using the Fourier transform $D={D}_{x}{{\rm{e}}}^{{{\rm{i}}{k}}_{D}x}/\sqrt{2\pi }$, (D=a, b), we can find that each bare CRW supports plane waves with a nonlinear dispersion relation ${E}_{k}^{D}={\omega }_{D}-2{\zeta }_{D}\cos {{lk}}_{D}$ (setting l=1), and each CRW owns an energy band with the bandwidth 4ζD [22]. Here, l is the distance between two neighboring cavities, and k is the photon wave vectors.
For the photonic band inside the CRWs, the single photon incident with energy E is scattered elastically. Therefore, the particle either is propagated inside the cavity or is absorbed by the three-level atom system. This means that the stationary eigenstate of the full system is$\begin{eqnarray}\begin{array}{rcl}| {\rm{\Psi }}\rangle & = & \sum _{j}\alpha (j){a}_{x}^{\dagger }| g{0}_{p}\rangle +\sum _{j}\beta (j){b}_{x}^{\dagger }| g{0}_{p}\rangle \\ & & +{u}_{s}| s{0}_{p}\rangle +{u}_{e}| e{0}_{p}\rangle ,\end{array}\end{eqnarray}$where $| {0}_{p}\rangle $ denotes the joint state in which the field is the vacuum state of the two CRWs, and α(j) and β(j) are the probability amplitudes of the single photon in the jth cavity of the two CRWs. us and ue are the probability amplitudes of the atomic state $| s\rangle $ and $| e\rangle $.
Using the eigenequation $H| {\rm{\Psi }}\rangle =E| {\rm{\Psi }}\rangle $, we can obtain the discrete scattering equation$\begin{eqnarray*}\begin{array}{rcl}(E-{\omega }_{a})\alpha (j) & = & -{\zeta }_{a}[\alpha (j-1)+\alpha (j+1)]+{\delta }_{j0}[\alpha (0){V}_{a}\\ & & +\beta (0)G]-{\delta }_{j1}{\lambda }_{a}{\zeta }_{a}\alpha (0)-{\delta }_{j0}{\lambda }_{a}{\zeta }_{a}\alpha (1)\\ (E-{\omega }_{b})\beta (j) & = & -{\zeta }_{b}[\beta (j-1)+\beta (j+1)]+{\delta }_{j0}[\beta (0){V}_{b}\\ & & +\alpha (0)G]-{\delta }_{j1}{\lambda }_{b}{\zeta }_{b}\beta (0)-{\delta }_{j0}{\lambda }_{b}{\zeta }_{b}\beta (1),\end{array}\end{eqnarray*}$where ${V}_{a}={g}_{a}^{2}(E-{\omega }_{s})/[(E-{\omega }_{e})(E-{\omega }_{s})-{{\rm{\Omega }}}^{2}]$ and ${V}_{b}\,={g}_{b}^{2}(E-{\omega }_{s})/[(E-{\omega }_{e})(E-{\omega }_{s})-{{\rm{\Omega }}}^{2}]$ are defined as energy-dependent delta-like potential, and $G\,={g}_{a}{g}_{b}(E-{\omega }_{s})/[(E-{\omega }_{e})(E-{\omega }_{s})-{{\rm{\Omega }}}^{2}]$ is the effective dispersive coupling strength, which leads to the channel-switching.
The wave functions in the asymptotic regions are given, respectively, by$\begin{eqnarray*}\alpha (j)=\left\{\begin{array}{ll}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}j}+{r}^{a}{{\rm{e}}}^{-{{\rm{i}}{k}}_{a}j} & j\lt 0,\\ {t}^{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}j} & j\gt 0,\end{array}\right.\end{eqnarray*}$and$\begin{eqnarray*}\beta (j)=\left\{\begin{array}{ll}{t}_{d}^{b}{{\rm{e}}}^{-{{\rm{i}}{k}}_{b}j} & j\lt 0,\\ {t}_{u}^{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}j} & j\gt 0,\end{array}\right.\end{eqnarray*}$where ${r}^{a},{t}^{a},{t}_{d}^{b}$ and tbu and denote the left, right, down, and up transmission amplitude of the router, respectively. By solving the above equation, we can obtain the scattering amplitudes$\begin{eqnarray}{r}^{a}=\displaystyle \frac{2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}(2{\rm{i}}{\zeta }_{b}{\rm{\sin }}{k}_{b}-{V}_{b}+2{\lambda }_{b}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}}+{\lambda }_{b}^{2}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}})}{(2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}-{V}_{a}+2{\lambda }_{a}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}}+{\lambda }_{a}^{2}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}})(2{\rm{i}}{\zeta }_{b}{\rm{\sin }}{k}_{b}-{V}_{b}+2{\lambda }_{b}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}}+{\lambda }_{b}^{2}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}})-{G}^{2}}-1,\end{eqnarray}$$\begin{eqnarray}{t}^{a}=\displaystyle \frac{2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}(2{\rm{i}}{\zeta }_{b}{\rm{\sin }}{k}_{b}-{V}_{b}+2{\lambda }_{b}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}}+{\lambda }_{b}^{2}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}})(1+{\lambda }_{a})}{(2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}-{V}_{a}+2{\lambda }_{a}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}}+{\lambda }_{a}^{2}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}})(2{\rm{i}}{\zeta }_{b}{\rm{\sin }}{k}_{b}-{V}_{b}+2{\lambda }_{b}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}}+{\lambda }_{b}^{2}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}})-{G}^{2}},\end{eqnarray}$$\begin{eqnarray}{t}_{u}^{b}=\displaystyle \frac{2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}G(1+{\lambda }_{b})}{(2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}-{V}_{a}+2{\lambda }_{a}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}}+{\lambda }_{a}^{2}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}})(2{\rm{i}}{\zeta }_{b}{\rm{\sin }}{k}_{b}-{V}_{b}+2{\lambda }_{b}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}}+{\lambda }_{b}^{2}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}})-{G}^{2}},\end{eqnarray}$$\begin{eqnarray}{t}_{d}^{b}=\displaystyle \frac{2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}G}{(2{\rm{i}}{\zeta }_{a}{\rm{\sin }}{k}_{a}-{V}_{a}+2{\lambda }_{a}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}}+{\lambda }_{a}^{2}{\zeta }_{a}{{\rm{e}}}^{{{\rm{i}}{k}}_{a}})(2{\rm{i}}{\zeta }_{b}{\rm{\sin }}{k}_{b}-{V}_{b}+2{\lambda }_{b}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}}+{\lambda }_{b}^{2}{\zeta }_{b}{{\rm{e}}}^{{{\rm{i}}{k}}_{b}})-{G}^{2}}.\end{eqnarray}$ It can be observed that ${t}_{u}^{b}={t}_{d}^{b}=0$ at E=ωs, which means that the incident photon with energy E=ωs will be totally transmitted in its original CRW due to the vanishing the effective dispersive coupling strength. It also means that a single photon cannot enter from one quantum channel to another.
3. Single-photon quantum router
To compare with previous research work, we first discuss the routing capability when ${\lambda }_{a}={\lambda }_{b}=0$, this case is the same as the single-photon quantum router scheme proposed by Zhou et al [18]. The quantum router can implement the routing capability regardless of turned on or turned off of the classical field, but the maximum conversion rate of the information carried by a single photon is only 50%. To visually express the conversion rate of a single photon in this case, in figure 2, we plotted the transmittance Ta, transfer rate ${T}_{u}^{b}+{T}_{d}^{b}$ and reflectance Ra as function of the incident energy E. Three different band configurations are presented.
Figure 2.
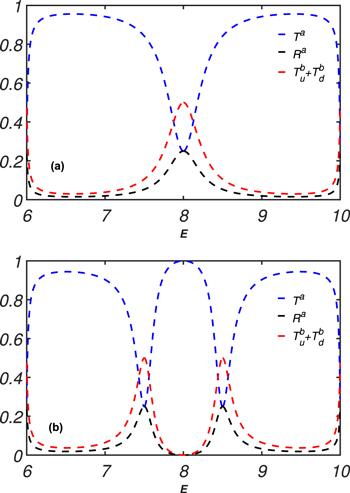New window|Download| PPT slide Figure 2.(a)Ra, Ta and ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ωs=Ω=0; (b) Ra, Ta and ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when Ω=0.5 and ωs=8. The remaining parameters are set as follows: ωa=ωb=ωe=8, ζa= ζb=1, λa=λb=0, and ga=gb=0.5.
For ${\lambda }_{a}\ne 0,{\lambda }_{b}=0$ and Ω=0, to study this mechanism, we plot the current flow of the photon in CRW−b in figure 3(a), which are described by the coefficients ${T}_{u}^{b}+{T}_{d}^{b}$. We find that when ${\lambda }_{a}\geqslant 0$, the transfer ${T}_{u}^{b}+{T}_{d}^{b}$ into CRW−b is limited to be no more than 50%, which has been examined in the previous schemes. But when λa<0, the transfer rate far more than 50%, and the peak transfer rate are centered at E=ωs. The width of the peak for the transfer rate ${T}_{u}^{b}+{T}_{d}^{b}$ is determined by the λa. The smaller the product λa is, the wider the peak is. When a classical field is turned on, we plot ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave in figure 3(b), except the classical field makes one dip be split into two dips, the conservation relation and the related scattering properties are the same as those in figure 3(a). In figure 4, we plot the transfer rate ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ${\lambda }_{a}=0,{\lambda }_{b}\ne 0$ and ${\rm{\Omega }}=0({\rm{\Omega }}\ne 0)$. We find that no matter what λb≥0 or λb<0, the transfer ${T}_{u}^{b}+{T}_{d}^{b}$ into CRW−b is limited to be no more than 50%, and other physical phenomena are the same as in figure 3.
Figure 3.
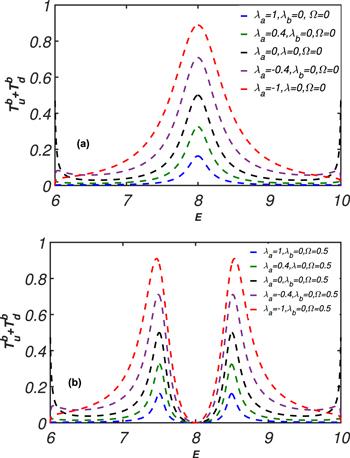New window|Download| PPT slide Figure 3.(a) ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ωs=Ω=0; (b) ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ωs=8 and Ω=0.5. Other parameters are taken as ωa=ωb=ωe=8, ζa=ζb=1, ωs=8, and ga=gb=0.5.
Figure 4.
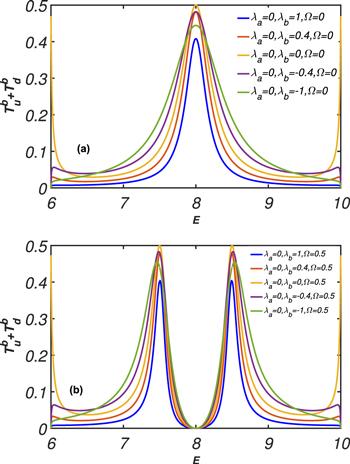New window|Download| PPT slide Figure 4.${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ωs=Ω=0; (b) ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ωs=8 and Ω=0.5. Other parameters are taken as ωa=ωb=ωe=8, ζa=ζb=1, and ga=gb=0.5.
We know from figures 3 and 4 that whether or not the classical field exists, only when λa<0, the transfer rate ${T}_{u}^{b}+{T}_{d}^{b}$ will far exceed 50%. To gain a deeper insight into the dependence of the photon routing capability on the two variables λa and λb, figure 5 displays the transfer rate ${T}_{u}^{b}+{T}_{d}^{b}$. As seen, the high transfer rate is located in the almost quadrant regions with negative values of the two variables, and their maximum values ${T}_{u}^{b}+{T}_{d}^{b}=1$ emerge in the center point ${\lambda }_{a}={\lambda }_{b}=-1$. So, it is possibly feasible to efficiently enhance the routing capability of the single photons between two channels by adjusting the inter-resonator couplings.
Figure 5.
New window|Download| PPT slide Figure 5.(a)–(c) ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ωs=Ω=0; (d), (e) and (f) ${T}_{u}^{b}+{T}_{d}^{b}$ as a function of the energy of the incident wave when ωs= and Ω=0.5. Here, the chosen parameters ωa=ωb=ωe=8, ζa=ζb=1, and ga=gb=0.5.
4. Discuss and conclusion
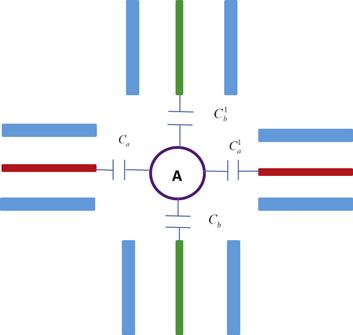
The tunable coupling between two neighboring resonators can be realized by coupled single-mode superconducting transmission line resonators and a gap-tunable qubit. Consider a system composed of four resonators and a superconducting qutrit A with states $| 0\rangle ,| 1\rangle ,| 2\rangle $, for the four resonators each of which consists of N identical superconducting transmission line resonators, linked with each other through capacitors. The model is schematically depicted in figure 6. The four resonators coupled by a coupler superconducting qutrit may be used as a basic circuit block to build a two-dimensional quantum network for quantum information processing. This is exactly similar to the function of quantum routers in quantum networks. In other words, the quantum routers we propose can be implemented in superconducting circuits. For the model in figure 6, Yang et al [31] and Li et al [32] have verified its practicability, and the model has high fidelity for information transmission.
Figure 6.
New window|Download| PPT slide Figure 6.Diagram of a superconducting qutrit A coupled capacitively to four one-dimensional coplanar waveguide resonators through ${C}_{a},{C}_{a}^{1},{C}_{b},{C}_{b}^{1}$, respectively.
In conclusion, we considered a system composed of two one-dimensional CRWs with two inter-resonator hopping coefficients that are designed to be tunable and a Λ-type atom which behaves as a quantum multichannel router. Whether the classical field exists or not, the quantum router we propose can implement the routing function. Compared with previous work, our proposed scheme can improve the transfer rate of a single photon from one quantum channel to another, and the maximum transfer rate can reach 100%. We also find that the present setup can be directly realized by the four resonators coupled by a coupler qutrit. Thus, we believe that the present investigation may open an approach for the realization of a large-scale quantum network.
Acknowledgments
This work is supported by the Project of Introduction and Cultivation for Young Innovative Talents in Colleges and Universities of Shandong Province.
ChenG-YLambertNChouC-HChenY-NNorF2011 Surface plasmons in a metal nanowire coupled to colloidal quantum dots: scattering properties and quantum entanglement Phys. Rev. B 84 045310 DOI:10.1103/PhysRevB.84.045310 [Cited within: 1]
ZhengHBarangerH U2013 Persistent quantum beats and long-distance entanglement from waveguide-mediated interactions Phys. Rev. Lett. 110 113601 DOI:10.1103/PhysRevLett.110.113601
ZhengHGauthierD JBarangerH U2013 Waveguide-QED based photonic quantum computation Phys. Rev. Lett. 111 090502 DOI:10.1103/PhysRevLett.111.090502
Gonzalez-BallesteroCMorenoEGarcia-VidalF J2014 Generation, manipulation, and detection of two-qubit entanglement in waveguide QED Phys. Rev. A 89 042328 DOI:10.1103/PhysRevA.89.042328
FacchiPKimM SPascazioSPepeF VPomaricoDTufarelliT2016 Bound states and entanglement generation in waveguide quantum electrodynamics Phys. Rev. A 94 043839 DOI:10.1103/PhysRevA.94.043839
VermerschBGuimondP OPichlerHZollerP2017 Quantum state transfer via noisy photonic and phononic waveguides Phys. Rev. Lett. 118 133601 DOI:10.1103/PhysRevLett.118.133601
MahmoodianSLodahlPSorensenA S2016 Quantum networks with chiral-light–matter interaction in waveguides Phys. Rev. Lett. 117 240501 DOI:10.1103/PhysRevLett.117.240501
ShenJ TFanS H2005 Coherent single photon transport in a one-dimensional waveguide coupledwith superconducting quantum bits Phys. Rev. Lett. 95 213001 DOI:10.1103/PhysRevLett.95.213001
ChengM-TMaX-SDingM-TLuoY-QZhaoG-X2012 Single-photon transport in one-dimensional coupled-resonator waveguide with local and nonlocal coupling to a nanocavity containing a two-level system Phys. Rev. A 85 053840 DOI:10.1103/PhysRevA.85.053840 [Cited within: 1]
ShiTFanSSunC P2011 Two-photon transport in a waveguide coupled to a cavity in a two-level system Phys. Rev. A 84 063803 DOI:10.1103/PhysRevA.84.063803
ZhouLGongZ RLiuY-XSunC PNoriF2008 Controllable scattering of a single photon inside a one-dimensional resonator waveguide Phys. Rev. Lett. 101 100501 DOI:10.1103/PhysRevLett.101.100501
WerraJ F MLongoPBuschK2013 Spectra of coherent resonant light pulses interacting with a two-level atom in a waveguide Phys. Rev. A 87 063821 DOI:10.1103/PhysRevA.87.063821
ZhengHGauthierD JBarangerH U2012 Strongly correlated photons generated by coupling a three-or four-level system to a waveguide Phys. Rev. A 85 043832 DOI:10.1103/PhysRevA.85.043832 [Cited within: 1]
CaoCDuanW YChenXZhangRWangT JWangC2017 Implementation of single-photon quantum routing and decoupling using a nitrogen-vacancy center and a whispering-gallery-mode resonator-waveguide system Opt. Express 25 16931 DOI:10.1364/OE.25.016931 [Cited within: 1]
BenthamCItskevichI EColesR JRoyallBClarkeEOHaraJPrtljagaNFoxA MSkolnickM SWilsonL R2015 On-chip electrically controlled routing of photons from a single quantum dot Appl. Phys. Lett. 106 221101 DOI:10.1063/1.4922041 [Cited within: 1]
LuJZhouLKuangL MNoriF2014 Single-photon router: coherent control of multichannel scattering for single photons with quantum interferences Phys. Rev. A 89 013805 DOI:10.1103/PhysRevA.89.013805
YanG AQiaoH XLuHChenA X2017 Quantum information-holding single-photon router based on spontaneous emission Sci. China Phys., Mech. Astron. 60 090311 DOI:10.1007/s11433-017-9059-3 [Cited within: 1]
ZhengH XGauthierD JBarangerH U2011 Cavity-free photon blockade induced by many-body bound states Phys. Rev. Lett. 107 223601 DOI:10.1103/PhysRevLett.107.223601
LiTMiranowiczAHuX DXiaK YNoriF2018 Quantum memory and gates using a Λ-type quantum emitter coupled to a chiral waveguide Phys. Rev. A 97 062318 DOI:10.1103/PhysRevA.97.062318
ChengM TMaX RFanJ WXuJ PZhuC J2017 Controllable single-photon nonreciprocal propagation between two waveguides chirally coupled to a quantum emitter Opt. Lett. 15 42 DOI:10.1364/OL.42.002914
ChengM TMaX SZhangJ YWangB2016 Single photon transport in two waveguides chirally coupled by a quantum emitter Opt. Express 17 24 DOI:10.1364/OE.24.019988
Gonzalez-BallesteroCMorenoEGarcia-VidalF JGonzalez-TudelaA2016 Nonreciprocal few-photon routing schemes based on chiral waveguide-emitter couplings Phys. Rev. A 94 063817 DOI:10.1103/PhysRevA.94.063817
YangC PSuQ PZhengS BHanS Y2013 Generating entanglement between microwave photons and qubits in multiple cavities coupled by a superconducting qutrit Phys. Rev. A 87 022320 DOI:10.1103/PhysRevA.87.022320 [Cited within: 1]
,College of Physics and Engineering, 
New window|Download| PPT slide
New window|Download| PPT slide
New window|Download| PPT slide
New window|Download| PPT slide
New window|Download| PPT slide
New window|Download| PPT slide
