Macroscopic-microscopic calculations of fission potential surface of uranium isotopes in the three q

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-02

Xin Zhu¹, Zhi-Ming Wang¹, Wen-Jie Zhu, Chun-Lai Zhong, Yi-Mo Zhang, Long-Yong Liao, Tie-Shuan Fan^,State Key Laboratory of Nuclear Physics and Technology, Institute for Heavy Ion Physics, School of Physics, Peking University, Beijing, 100871, China

First author contact: ¹ These authors contributed equally to this work.
Received:2020-06-01Revised:2020-06-10Accepted:2020-06-11Online:2020-09-23

Abstract
Five-dimensional (5D) fission potential energy surfaces (PES) for uranium nuclei are investigated based on the macroscopic-microscopic Lublin-Strasbourg drop model in the three-quadratic-surface parametrization, and the heights of static fission barriers are obtained. Asymmetric and symmetric fission paths are presented on the 5D PES of ²³⁶U for different nuclear shapes. The calculated barrier heights, E_A and E_B, are quite consistent with the experimental data for all even-even nuclei of uranium isotopes, from ²³⁰U to ²⁴⁴U.
Keywords： potential energy surface;uranium nuclei;three quadratic surfaces

PDF (815KB)Metadata Metrics Related articlesExportEndNote|Ris|Bibtex Favorite
Cite this article
Xin Zhu, Zhi-Ming Wang, Wen-Jie Zhu, Chun-Lai Zhong, Yi-Mo Zhang, Long-Yong Liao, Tie-Shuan Fan. Macroscopic-microscopic calculations of fission potential surface of uranium isotopes in the three quadratic surfaces parametrization. Communications in Theoretical Physics, 2020, 72(10): 105301- doi:10.1088/1572-9494/aba257

1. Introduction

The main theoretical methods of fission research can be roughly divided into macroscopic-microscopic (MM) models and microscopic theory. The representative ones of the microscopic theories [1-6] are based on the self-consistent mean field theory, such as energy density functional method [7]. In terms of the MM theory, in the 1980s-90s Brosa et al [8, 9] proposed the random neck scission model and obtained the fission potential energy surface (PES) in a five-dimensional (5D) deformation space. In addition, multi-fission channels, such as standard, superlong and supershort-short, were given theoretically and confirmed by many later published works [10-12]. From the 1960s onwards, Möller et al [13-16] developed another set of deformation parameters describing the nuclear shape, and established a finite-range liquid-drop model for the calculation of fission macroscopic energy. The folded Yukawa potential model of finite range [17] was applied for calculating the single-particle potential energy. The calculated fission barriers for 1585 nuclei from Z=78 to Z=125 were presented [13]. It also confirmed that there are two fission modes of symmetric and asymmetric fission in most heavy nuclei [18].

We have established a MM model using Lublin-Strasbourg drop (LSD) formula in calculation of macroscopic energy, and folded-Yukawa potential and Strutinsky's shell-correction method in single-particle potential energy, and the generalized Lawrence shape to calculate the potential energy [19]. And then a fission barrier search technique [19], a watershed algorithm [20], was developed on a 5D PES to obtain the fission barriers for U and Pu isotopes. Next, in order to get a more accurate PES in large deformation, we use two-center oscillator basis to calculate the microscopic energy [20, 21]. In the same work, we also developed a new multi-modal fission paths search algorithm, which can automatically find at least two different fission paths on a 5D PES.

One important issue for a MM model is how to choose an appropriate shape parameterization, which should accurately describe the nuclear shape evolution all the way from the ground state to the scission configuration. The complexity of a parameterization involves a trade-off between accuracy of the model and computational feasibility. The increased computational cost brought by considering excessive degrees of freedom would effectively inhibit the accessibility of that parameterization. Therefore a realistic parameterization should be both accurate and simple so as to reduce the computation to a reasonable size. Several popular parameterizations are available such as the Cassinian ovals [22], the funny-Hills parameterization [23], the matched quadratic surfaces [24], and the generalized Lawrence shapes [9].

In this paper, we use the MM-LSD model with three quadratic surface (3QS) parameterization to calculate the potential energy surface in a 5D deformation space with 5906 250 grid points for heavy elements. In section 2, We systematically calculate the PES for even-even uranium nuclei in mass range 230≤A≤244, and then search for fission barriers and fission paths. In section 3, we show the results, which are compared with the experimental data. Finally, conclusions are presented in section 4.

2. Calculation of PES

2.1. MM model

In the MM-LSD model, the total potential energy E as a function of deformation parameters consists of a macroscopic part and a microscopic part representing the quantum effect correction as(1)$\begin{eqnarray}E={E}_{{\rm{m}}{\rm{a}}{\rm{c}}}+{E}_{{\rm{m}}{\rm{i}}{\rm{c}}}.\end{eqnarray}$

As mentioned above, the LSD formula [25] is used for the macroscopic model. For the microscopic term E_mic, the folded-Yukawa potential [26-28] is used for the independent particle potential, whereas the shell correction method of Strutinsky [29, 30] and the smooth BCS pairing model [29, 31] are used to calculate the deformation energy of the compound nucleus.

2.2. Shape description and numerical details

The fission potential energy is calculated as a function of deformation parameters in the MM model. Generally speaking, we focus on the shape description of large deformation, which can be divided into the generalized ellipsoid, the Cassini ovals and the matched quadratic surfaces. The idea of connecting multiple surfaces to describe the shape of an atomic nucleus was originally proposed by Grammaticos et al [32]. Later, Swiatecki [33] realized that the elongated deformed nucleus probably has a neck. He added a cylindrical neck in the middle of the connecting surface and got a connecting surface similar to the dumbbell shape. After that, based on the dumbbell shaped connection, Nix proposed the three quadric surfaces [24, 34, 35], which was called the most versatile shape description by Hasse and Myers [36].

In the 3QS parameterization [34], the shape of nuclear surface consists of three smoothly joining portions of quadratic surfaces of rotation and is defined by(2)$\begin{eqnarray}{\rho }_{s}^{2}=\left\{\begin{array}{l}{a}_{1}^{2}-\displaystyle \frac{{a}_{1}^{2}}{{c}_{1}^{2}}{(z-{l}_{1})}^{2},{l}_{1}-{c}_{1}\leqslant z\leqslant {z}_{1},\\ {a}_{2}^{2}-\displaystyle \frac{{a}_{2}^{2}}{{c}_{2}^{2}}{(z-{l}_{2})}^{2},{z}_{2}\leqslant z\leqslant {l}_{2}+{c}_{2}\\ {a}_{3}^{2}-\displaystyle \frac{{a}_{3}^{2}}{{c}_{3}^{2}}{(z-{l}_{3})}^{2},{z}_{1}\leqslant z\leqslant {z}_{2}.\end{array}\right.,\end{eqnarray}$Here the index 1 and 2 denotes the left-hand surface and the right-hand one, both spheroids, for which a, c, l are the semi major axis length, the semi minor axis length and the location of the center of the spheroid, respectively. The middle body, denoted by the subscript 3, may be a spheroid with c₃ being a real number or a hyperboloid with c₃ being an imaginary number. Finally, z₁ and z₂ are the left and right connecting points of the middle surface with the two end spheroids, respectively. However, those parameters are not independent. With smoothly connecting constrains, only five independent parameters are left. To make it more realistic, we use the electric quadrupole moment Q₂, the neck radius d, the asymmetry parameter α_g, the left fragment deformation parameter ϵ_f1 and the right fragment deformation parameter ϵ_f2 as a set of deformation parameters to describe the evolution of the nuclear shape [13].

The expression of electric quadrupole moment for a homogeneously charged volume is given in a cylindrical coordinate system by(3)$\begin{eqnarray}{Q}_{2}=\displaystyle \int \left({\rho }^{2}{z}^{2}-\displaystyle \frac{1}{4}{\rho }^{4}\right){\rm{d}}z,\end{eqnarray}$where the charge dimension and other coefficients are ignored.

The neck radius of the nuclear shape d is equal to a₃:(4)$\begin{eqnarray}d={a}_{3}.\end{eqnarray}$

The other three parameters, σ₃, α₃ and α_g, are defined from Moller et al [10] with the following expressions, respectively:(5)$\begin{eqnarray}{\sigma }_{3}=\displaystyle \frac{1}{2}\left[{\left(\displaystyle \frac{3-2{\varepsilon }_{f1}}{3+{\varepsilon }_{f1}}\right)}^{2}+{\left(\displaystyle \frac{3-2{\varepsilon }_{f2}}{3+{\varepsilon }_{f2}}\right)}^{2}\right],\end{eqnarray}$(6)$\begin{eqnarray}{\alpha }_{3}=\left[{\left(\displaystyle \frac{3-2{\varepsilon }_{f1}}{3+{\varepsilon }_{f1}}\right)}^{2}-{\left(\displaystyle \frac{3-2{\varepsilon }_{f2}}{3+{\varepsilon }_{f2}}\right)}^{2}\right],\end{eqnarray}$and(7)$\begin{eqnarray}{\alpha }_{g}=\displaystyle \frac{{M}_{1}-{M}_{2}}{{M}_{1}+{M}_{2}}=\displaystyle \frac{{a}_{1}^{2}{c}_{1}-{a}_{2}^{2}{c}_{2}}{{a}_{1}^{2}{c}_{1}+{a}_{2}^{2}{c}_{2}},\end{eqnarray}$where ${M}_{1}$ and ${M}_{2}$ are the volume inside the end quadratic surfaces, respectively.

The density of the gird points on the PES should be selected and moderate in the 3QS parametrization. Because there are some fluctuations in the binding energy of the nuclei calculated by the shell correction method, when the mesh is sufficiently fine, further reducing the step size will not make the result more accurate, and will waste a lot of computing time. If the grid is spaced too sparsely, the key points (the ground state, the saddle point and the scission point) and the path information extracted from it are not accurate enough. In this work we select the grid points corresponding to(8)$\begin{eqnarray}{Q}_{2}=\displaystyle \frac{{\rm{Z}}}{A}{R}_{cn}^{3}\times 3.766i,\,{\rm{where}}\,i=1,2,\mathrm{3...50},\end{eqnarray}$

(9)$\begin{eqnarray}{\alpha }_{g}=0.02(i-2),\,{\rm{where}}\,i=1,2,\mathrm{3...35},\end{eqnarray}$

(10)$\begin{eqnarray}d={R}_{cn}\times 0.08\times (16-i),\,{\rm{where}}\,i=1,2,\mathrm{3...15},\end{eqnarray}$and concurrently the left fragment deformation parameter ϵ_f1 and the right fragment deformation parameter ϵ_f2 are selected as$\begin{eqnarray*}\begin{array}{l}\left(-0.2,-0.15,-0.1,0.00,0.1,0.15,0.175,0.2,\right.\\ \,\left.0.225,0.25,0.275,0.3,0.35,0.4,0.5\right).\end{array}\end{eqnarray*}$

As mentioned above, 5906 250 grid points are produced in the five-dimensional space of the 3QS parametrization.

2.3. Search for multi-mode fission paths

The watershed algorithm [20] was used to search the fission path on the 5D PES. For the multi-mode fission path, we project the 5D PES to the two most important dimensions to find the approximate fission path. The ²³⁶U nucleus, which is important and representative, is selected in this work. The 5D PES calculated for ²³⁶U is projected in the two directions of the electric quadrupole moment Q₂ and the asymmetry parameter α_g, and then the three-dimensional plot shown in figure 1 and the two-dimensional (2D) contour in figure 2 are obtained, respectively.

Figure 1.

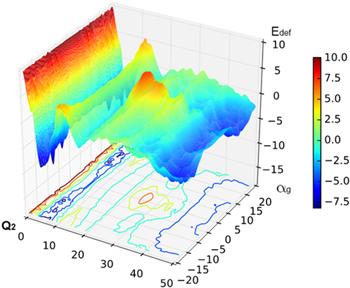New window|Download| PPT slide
Figure 1.The 3D plot of 5D potential energy surface in the directions of Q₂ and α_g for ²³⁶U, in which the abscissa is Q₂, the ordinate is α_g, and the size of E_def (Q₂, α_g) is scaled by color.

Figure 2.

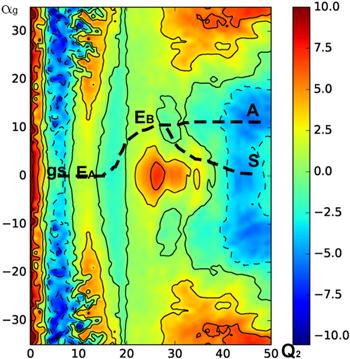New window|Download| PPT slide
Figure 2.The 2D projection of the PES for ²³⁶U, in which the abscissa is Q₂, the ordinate is α_g, and the size of E_def (Q₂, α_g) is scaled by color.

In 2D projection contour, as shown figure 2, we can see two fission paths intuitively and clearly, which have beam marked with black-dotted lines to guide the eye on the figure 2.

3. Results and discussion

3.1. Shape evolution in the PES

Taking figure 2 as an example, there are two well separated fission channels for ²³⁶U, both share the same inner barrier and deviate at the point of second minimum, and finally the asymmetric path ends at the point A and the symmetric path ends at the point S. From this figure, we can find that the value of the asymmetric parameter α_g is about 11.3, which means the mass of heavy fragment should be close to 140, according to equation (7), while the value of α_g is about 0 for the symmetric channel. The notation g_s in the figure presents the location of the approximate ground state. The shape of a heavy nucleus in the ground state should be an ellipsoid, so the value of α_g should be approximately 0. The first barrier along the fission path at E_A is the inner barrier. Then, the second barrier is crossed at E_B, which is the outer barrier, and its energy value is the height of the outer barrier. After that, the two fission paths are clearly separated. During reaching scission points, the asymmetric fission path will cross a new barrier with lower height than the outer barrier E_B. But the height of the barrier that the symmetric fission path needs to cross is higher than E_B, so the height of the outer barrier of the symmetric fission channel should be the height of the barrier that needs to cross again.

Once the energy of the inner and outer saddle points are determined, and the deformation parameters can be obtained for these saddle points in the PES. However, it is a tough task to search millions of lattice points in the 5D PES, so we attempt to use the saddle point position on the 2D PES to draw the shape sketch. We output the other three coordinates of each E_def (Q₂, α_g) to get E_def (Q₂, d, α_g, ϵ_f1, ϵ_f2). For ²³⁶U, we can draw the shapes corresponding to all positions, four of which, i.e. the inner saddle point, the outer saddle point, the second potential well and the scission point, are shown in figure 3.

Figure 3.

New window|Download| PPT slide
Figure 3.The nuclear shapes at the inner saddle point (a), the outer saddle point (b), the second potential well (c), and the scission point (d).

3.2. Barrier heights

The main weakness [13] of the 3QS parametrization is that it is not very good for the description of the ground state and the small deformation region, so different shape descriptions are used to calculate the PES in different regions from ground state to the saddle point and then to the scission point, and the shape of each position and the height of fission potential barrier are obtained feasible. For the the ground state and the small deformation regions, the potential energy was calculated in the generalized Lawrence shape parametrization, and then the barrier height is obtained.

In this work, for all even-even nuclei of U isotopes, from ²³⁰U to ²⁴⁴U, the 5D PESs are calculated systematically. Then the inner barrier height E_A and the outer barrier height E_B are obtained and compared with the experimental data and theoretical results of other authors, as shown in table 1 and figure 4.

Table 1.
Table 1.Calculated barrier heights for the even-even nuclei of U isotopes.

	²³⁰U	²³²U	²³⁴U	²³⁶U	²³⁸U	²⁴⁰U	²⁴²U	²⁴⁴U
E_A/MeV	3.152	3.842	4.360	5.241	6.162	7.182	7.429	7.660
E_B/MeV	3.539	4.305	4.320	5.035	5.537	6.430	7.017	7.390

New window|CSV

Figure 4.

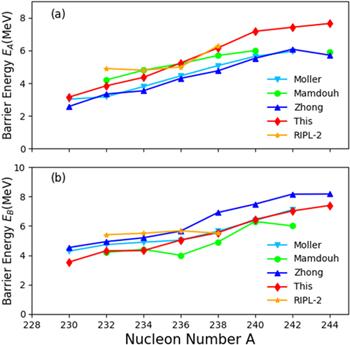New window|Download| PPT slide
Figure 4.The comparison of the calculated barrier heights, E_A (a) and E_B (b), for the even-even nuclei of U isotopes. Moller's data are taken from [13]. Mamdouh's ETFSI results are taken from [37]. Zhong's data are taken from [19]. The experimental data are taken from the Reference Input Parameter Library (RIPL-2) [38].

It can be seen that the calculated results of this work, especially the outer barrier in the large deformation area, are in good agreement with the experimental data of RIPL library [38], which shows that the calculation of PES in this work is quite successful and reliable. Compared with the results of Zhong's [19] generalized Lawrence shape calculation, our results in the large deformation region are improved and in better agreement with the experimental data, which shows that three quadric surfaces in the large deformation region is closer to the real nuclear shape than the generalized Lawrence shape. Our results of the outer barrier are very close to Moller's results [12], both are almost coincident especially for those nuclei from ²³⁶U to ²⁴²U.

4. Conclusions

Calculations of fission PES in a 5D deformation space for actinide nuclei have been performed based on a MM-LSD model in the 3QS parametrization. The dependence of the PES on the description of the shape for heavy nuclei and reliability of the description of different shape parameterizations are investigated. Compared with the generalized Lawrence shape calculation, our results of fission barrier heights in the large deformation region are improved and in better agreement with the experimental data. We confirm that the shape of 3QSs is well described in addition to a certain inherent defect in the ground state, especially in the large deformation region, which is much closer to the real nucleus shape than the generalized Lawrence shapes.

Acknowledgments

This work is supported by the Major Program of the National Natural Science Foundation of China under Grant No. 11790324. The National Magnetic Confinement Fusion Science Program of China under Grant Nos. 2013GB106004 and 2012GB-101003. The National Key Research and Development Program of China under Grant Nos. 2016YY0200804 and 2017YFF0206205.