Ying-Bo Zhao¹, Wei Zhang², Qing-Yang Fan^,2,?1 School of Mechanical and Electrical Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China
2 School of Microelectronics, Xidian University, Xi'an 710071, China
3 School of Information and Control Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China

Corresponding authors: ?E-mail:qyfan_xidian@163.com

Received:2019-03-18Online:2019-08-1

Fund supported:

*Supported by the National Natural Science Foundation of China under Grant.61804120 the Talent Science and Technology Foundation of Xi'an University of Architecture and Technology under Grant.RC1612

Abstract
Two new Group IV element allotropes Si$_{3}$ and Ge$_{3}$ in P6$_{2}$22 phase are predicted in this work and their physical properties are investigated using the density functional theory. Each of the newly predicted allotropes has a super dense structure, which is mechanically, dynamically, and thermodynamically stable, as verified by elastic constants, phonon dispersion spectra and relative enthalpies, respectively. The mechanical anisotropy propertiesare studied in detail by illustrating the directional dependence of Young's modulus, discussing the universal anisotropic index, and calculating shear anisotropy factors together with bulk moduli. It shows that P6$_{2}$22-Si$_{3}$ exhibits the greater anisotropy than P6$_{2}$22-Ge$_{3}$,and interestingly both of the newly predicted crystals appear to be isotropic in the (001) plane. Additionally, the Debye temperature, sound velocities, and the minimum thermal conductivity are examined to evaluate the thermodynamic properties of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase, and the electronic band structures are achieved by HSE06 hybrid functional, which indicate that P6$_{2}$22-C$_{3}$ and -Si$_{3}$ are indirect band gap semiconductors and P6$_{2}$22-Ge$_{3}$ exhibits the metallic feature.
Keywords： group 14 element allotropes;mechanical properties;electronic properties;elastic anisotropy properties


PDF (6201KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Ying-Bo Zhao, Wei Zhang, Qing-Yang Fan. Physical Properties of Group 14 in $P6_{2}$22 Phase: First-Principles Calculations ^*. [J], 2019, 71(8): 1036-1046 doi:10.1088/0253-6102/71/8/1036

1 Introduction

Due to increasing concerns about the limited supply of current and future fossil fuels, a lot of work has been undertaken to find clean and sustainable energy sources over the past several decades. The effort to search new element allotropes has been continuously made to solve the fossil energy crisis and reduce the pollution from fossil fuel consumption. Among which, the search for new Group IV element (C, Si, and Ge) allotropes has been extensively studied,^[1-10] owing to their importance in fundamental science and various possible applications in virtue of their special physical and chemical properties exhibited.

Carbon is known as the most plentiful element on earth, and pure carbon is mainly in graphite and diamond forms, which owns some of the strongest bonds naturally as ever known. The carbon allotropes have been investigated previously and show an extremely wide range of structures from super-hard semiconductors to ultra-soft semimetals with advanced mechanical and electronic properties, due to their special abilities to form sp, sp$^{2}$, and sp$^{3}$ hybridized bonds.^[11-16] The bct C$_{4}$ was investigated by Umemoto, et al.^[14] based on first-principle calculations .It was reported that C$_{4}$ appears to be transparent and dynamically stable at zero pressure, and beyond 18.6 GPaexhibiting more stability than graphite. Wei, et al.^[15] studied the mechanical and electronic properties ofImma-carbon, which is a super-hard sp$^{3}$ carbon allotrope, and it was found that Imma-carbon isa direct semiconductor with a band gap of 4.17 eV and a high bulk modulus of 440 GPa. Recently,Fan et al.^[16] investigated Lonsdaleite C, Si, and Ge and Lonsdaleite C-Si and Si-Ge alloys,and found that Lonsdaleite C$_{0.25}$Si$_{0.75}$ exhibits metallic properties and Lonsdaleite Si$_{0.25}$Ge$_{0.75}$ isa narrow direct semiconductor with a band gap of 0.76 eV. For the minimum thermal conductivity, Lonsdaleite C$_{0.75}$Si$_{0.25}$and Lonsdaleite C$_{0.5}$ Si$_{0.5}$ are greater than that of diamond-C.

Silicon is the second most plentiful element on earth and considered the cornerstone of the semiconductor industry. It is known that silicon exists in a great deal of allotropes, including the most stable cubic diamond-Si and several metastable silicon allotropes.^[17-25] For example, four novel silicon allotropes were proposed by us,^[23] including three indirect gap phases: C2/m-16, C2/m-20, I-4, and one quasi-direct gap phase: Amm2 phases. Six metastable silicon allotropes were predicted by Wang, et al.,^[24] utilizing ab initio calculations at ambient pressure, and these structures appear attractive features as being capable of absorbing sunlight with different frequencies. Fan, et al.^[25] a while ago proposed a new silicon allotrope t-Si$_{64}$, which is a metastable structure in I4$_{1}$/amd phase. Since the minimum thermal conductivity of t-Si$_{64}$ was found to be much smaller than that of diamond-Si, it was reported that the Si-Ge alloys in I4$_{1}$/amd phase are potential thermoelectric materials.

For germanium allotropes, many works have been done to investigate their properties.^[26-32] Nguyen, et al.^[30] found a new dynamically stable germanium in a distorted sp$^{3}$-hybridized framework structure with P4$_{2}$/mnm symmetry. Saleev, et al.^[31] predicted six new allotropes of silicon and germanium, and examined their structural, elastic, electronic and optical properties using ab initio quantum mechanical methods. The results showed that some allotropes of Ge might be metallic and these phases might be high-temperature variants. Bautista-Hernandez, et al.^[32] proposed elastically and vibrationally stable silicon and germanium in the monoclinic and orthorhombic phases, with energies slightly larger than that of diamond-Si and -Ge.

All the previous works have laid solid foundations for us to a broader search for new allotropes of Group IVelement that possibly exhibit novel properties. In this work, two new Group IV element allotropes Si$_{3}$ and Ge$_{3}$in P6$_{2}$22 phase with superdense structures are predicted.The crystal structures of P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ are composed of a lattice similar tothat of carbon,^[33] with silicon and germanium atoms substituting carbon atoms. Densities of P6$_{2}$22-Si$_{3}$and -Ge$_{3}$ are 2.574 g/cm$^{3}$ and 5.647 g/cm$^{3}$, which are 10.1% and 8.1% higher than those in diamond phase,respectively, thus making them superdense crystals. The mechanical, dynamic and thermodynamic stabilities of these newly predicted crystals are verified, and other important physical properties are systematically investigated.

2 Calculation Method

This work was carried out in the framework of density functional theory (DFT)^[34-35] based onCambridge Serial Total Energy Package (CASTEP) plane-wave code.^[36] All of the theoretical calculations were performed withthe generalized gradient approximation (GGA) in the form of the Perdew-Burke-Ernzerhof (PBE)^[37] functional andthe Perdew-Burke-Ernzerhof functional for solids (PBEsol), and the local density approximation (LDA) in the form of Ceperly and Alder,as parameterized by Perdew and Zunger (CA-PZ)^[38-39] exchange correlation potential.The structural parameters were obtained using the Broyden-Fletcher-Goldfarb-Shenno (BFGS)^[40] minimization technique.The interactions of core electrons were represented with ultrasoft pseudopotentials. Besides, the Voigt-Reuss-Hillapproximation was employed to estimate elastic moduli including the bulk modulus, shear modulus, and Young's modulus.The phonon frequency was achieved based on liner response theory.^[41] Additionally, the Heyd-Scuseria-Ernzerhof (HSE06)hybrid functional^[42] was utilized to calculate the electronic band structures of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase. The k points over the Brillouin zone were selected using the Monkhorst-Pack scheme,^[43] with a grid spacing less than 0.025 $\mathring{A}$. Energy cutoffs of 400 eV, 340 eV, and 240 eV were used for the wave function expansion and the high-density k-point sampling for C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase, respectively, in order to ensure good convergences of computed phases and energies of these three Group IV element allotropes.

3 Results and Discussion

3.1 Structural Properties

The crystal structure of C$_{3}$ with the space group of P6$_{2}$22 (No. 180) phase is shown in Fig. 1,and the structure observed is comprised of several zigzag six-membered carbon rings. For P6$_{2}$22-Si$_{3}$and -Ge$_{3}$, their crystal structures are similar to the one of P6$_{2}$22-C$_{3}$,^[33]which were obtained by replacing carbon atoms with silicon and germanium atoms, respectively.There are three atoms per conventional cell of P6$_{2}$22-X$_{3}$ (X=C, Si, Ge)in hexagonal symmetry, and the atoms occupy the crystallographic 3c sites with the atomic positionof (0.500, 0.000, 0.000). When viewed along the [110] and [001] direction, the crystalstructures are shown in Figs. 1(b) and 1(c), respectively. Densities of these three GroupIV element allotropes are 3.647 g/cm$^{3}$ (C$_{3}$), 2.574 g/cm$^{3}$ (Si$_{3}$),and 5.647 g/cm$^{3}$ (Ge$_{3}$), which are 3.6%, 10.1%, and 8.1% higher than thosein diamond (Fd-3m, No. 227) phase, respectively, thus making them superdense crystals.At ambient pressure, the lattice parameters of C$_{3}$, Si$_{3}$, and Ge$_{3}$ inP6$_{2}$22 phase and in diamond phase are listed in Table 1. As can be seen, the lattice constantsof P6$_{2}$22-C$_{3}$ calculated from the PBE are $a=b=2.602$ $\mathring{A}$ and $c=2.797$ $\mathring{A}$,which indeed show a good correlation with the reference data ($a=b=2.605$ $\mathring{A}$ and $c=2.801$ $\mathring{A}$).^[33]And for the lattice parameters of diamond-C ($a=3.566$ $\mathring{A}$), -Si ($a=5.465$ $\mathring{A}$),and -Ge ($a=5.694$ $\mathring{A}$), the theoretical values are in excellent agreement with the experimentaldata (C: $a=3.567$ $\mathring{A}$,^[44] Si: $a=5.430$ $\mathring{A}$,^[45] and Ge: $a=5.660$ $\mathring{A}$ ^[45]). Apparently, the values obtained from the PBE are closer to the reported data, and thus the PBE method will be primarily utilized for the following discussions.

Fig. 1

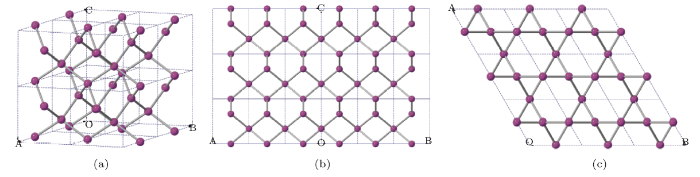New window|Download| PPT slide
Fig. 1(Color online) (a) The crystal structure of P6$_{2}$22-X$_{3}$ (X=C, Si, Ge), (b) the structural view along the [110] direction, and (c) the structural view along the [001] direction.




Table 1
Table 1The density ($\rho$ in g/cm$^{3}$) and lattice parameters (in $\mathring{A}$) of C$_{3}$, Si$_{3}$, and Ge$_{3}$$^{ }$ in P6$_{2}$22 phase.
^aRef. [33]; ^bRef. [44]; ^cRef. [45].

New window|CSV

It is worth to note that in dense covalent systems the bulk modulus (B in GPa) isstrongly correlating with the average interatomic distance, and the larger the value of B is,the shorter the average distance between adjacent atoms gets.^[46-47] The bond length of P6$_{2}$22-C$_{3}$appears to be uniform of 1.601 $\mathring{A}$, and the bulk modulus is 426 GPa. For the silicon and germanium allotropes inP6$_{2}$22 phase, the uniform bond lengths are 2.386 $\mathring{A}$ and 2.520 $\mathring{A}$, and the corresponding bulk moduli are94 GPa and 64 GPa, respectively. These three bond lengths in $P6_222$ phase mentioned above are all longer than those indiamond phase correspondingly (C-C: 1.535 $\mathring{A}$,^[2] Si-Si: 2.373 $\mathring{A}$,^[23] and Ge-Ge: 2.484 $\mathring{A}$^[27]), therefore resulting in a relatively smaller B than that in diamond phase (C: 431 GPa, Si: 98 GPa, and Ge: 73 GPa) as can be seen in Table 2.


Table 2
Table 2The elastic constants (in GPa) and elastic moduli (in GPa) of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase.
^aRef. [48]; ^bRef. [49].

New window|CSV

3.2 Stability

As the stability plays an inevitable role in deciding whether or not newmaterials can exist under certainconditions, some important values are analyzedin detail to examine the mechanical, dynamic, and thermodynamic stability of the new crystals. The calculated elastic constants, the elastic moduli of C$_{3}$, Si$_{3}$, and Ge$_{3}$$^{ }$ in P6$_{2}$22 phase and in diamond phase arelisted in Table 2. The structure in this work consists of five independentelastic constants ($C_{11}$, $C_{33}$, $C_{44}$,$C_{12}$, and $C_{13}$), and these elastic constants obey thefollowing generalized Born's mechanical stability criteria for hexagonal crystalsas shown:^[50] $C_{11}$>0, $C_{44}$>0,$C_{11}$>$\vert{}$C_{12}$\vert{}$,($C_{11}$+$C_{22}$)$C_{33}$-$2C_{13}^2>$0, which indicates these new crystals are mechanically stable.

As for the elastic moduli, which refer to the bulk modulus B, shear modulus G,Young's modulus E, and Poisson's ratio v, they are obtained by different methods.Bulk modulus B and shear modulus G are achieved using the Voigt-Reuss-Hill approximation,where B is the arithmetic mean of B$_{R}$ and B$_{V}$, $G$ the arithmetic mean ofG$_{R}$ and G$_{V}$. For Young's modulus E, and Poisson's ratio v,these two values are calculated based on E=9BG/(3B+G),v=(3B-2G)/(6B+2G),^[51-52] respectively.For the P6$_{2}$22 phase, the elastic constants and the elastic moduliincluding B, G, and E are decreased basically in the sequence ofC$_{3}$, Si$_{3}$, and Ge$_{3}$. By comparing the elastic constants C$_{11}$,C$_{44}$, and C$_{12}$ with those of diamond phase,it is found that $C_{11}$ of P6$_{2}$22 phase (C$_{3}$: 1161 GPa, Si$_{3}$:185 GPa, and Ge$_{3}$: 123 GPa) is slightly larger than that of diamond phase(C: 1053 GPa, Si: 165 GPa, and Ge: 121 GPa), where as C$_{44}$ andC$_{12}$ of P6$_{2}$22 phase are all smaller than those ofdiamond phase, respectively. In addition, the elastic moduli of diamond-C, -Si,and -Ge are compared with Refs. [48] and [49], and the values are clearly inexcellent agreement with reported experimental data. Moreover, Pugh^[53]proposed that the ratio of bulk to shear modulus (B/G) is an indicator distinguishing between the ductility and brittleness of crystal materials, that materials usually show obvious ductileproperty with a B/G value greater than 1.75, other wise the brittle property exhibited.Also, it should be noted that Poisson's ratio v is basically related to theB/G value, and thus v can be used to quantify the malleability.The ductile property will be displayed with v greater than 0.26, and incontrast the brittleness will behave with v less than 0.26.^[54]

From Table 2, it can be seen that all of v are less than 0.26, and hence all materials demonstrate the brittle feature.This is consistent with the discussion above about the implication of B/G value, since diamond-Ge has themaximum B/G value equaling 1.46 among all materials (and the maximum v of 0.22 as well). Therefore, it is easily found that diamond-Ge has the most brittle feature, while P6$_{2}$22-C$_{3}$ has the least brittle feature.

Dynamic stabilities of P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ are verified by their phonon dispersion spectracalculations at ambient pressure as illustrated in Fig. 2, and can be seen there are no imaginary frequenciesat any wave vectors, indicating P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ are dynamically stable.Then, the relative enthalpies of P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ are calculated to investigatetheir thermodynamic stabilities. The relative enthalpies are obtained by the formula of$\Delta$H=H$_{\rm{new phase}}$/n$_{1}$-H$_{\rm{diamond-Si(Ge)}}$/n$_{2}$,where n$_{1}$ and n$_{2}$ are the number of Si (Ge) atoms in the new phase and diamond phase,respectively.

Fig. 2

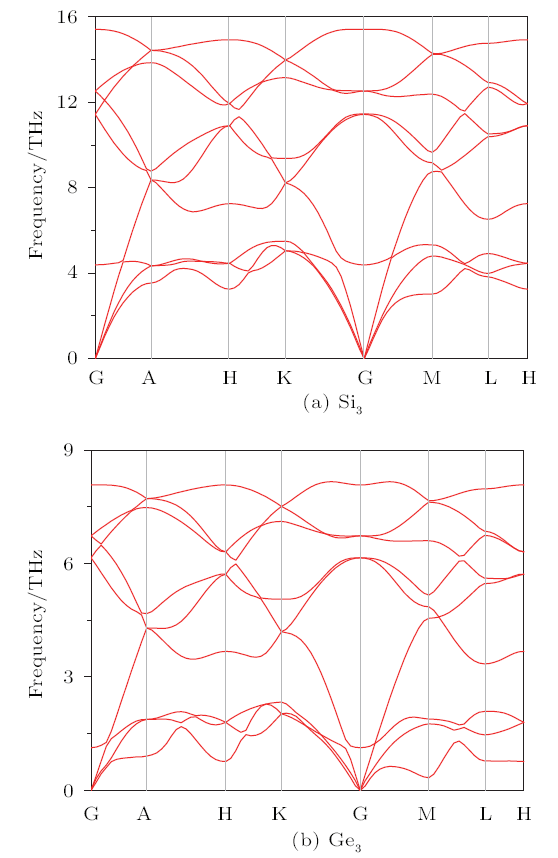New window|Download| PPT slide
Fig. 2(Color online) The phonon spectra of Si$_{3}$ and Ge$_{3}$ in P6$_{2}$22 phase at ambient pressure.



Figure 3 shows the calculated relative enthalpies of reported silicon structuresincluding C2/m-16 Si,^[23]hP12-Si, oF16-Si,^[24]lonsdaleite-Si,^[29]M-Si, Z-Si,^[32] and experimentally known $\beta{}$-Sn phase Si, compared to diamond-Si and P6$_{2}$22-Si$_{3}$at ambient pressure. It is found that diamond-Si remains the most stable than other phases atambient pressure. The metastable lonsdaleite-Si is second to diamond phase in terms ofthermodynamic stability, with the energy of 0.017 eV/atom.

Fig. 3

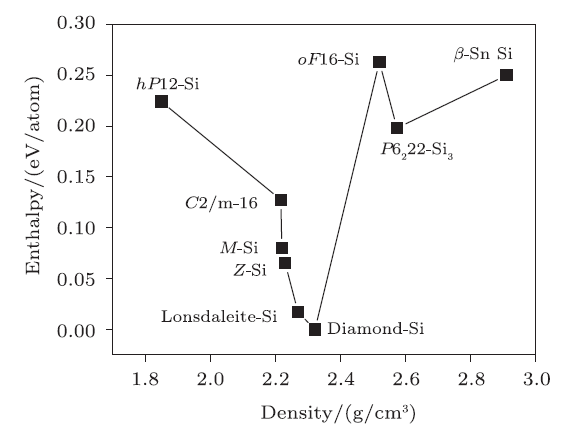New window|Download| PPT slide
Fig. 3(Color online) Calculated enthalpies of different Si structures compared to diamond-Si at ambient pressure.



The newly predictedcrystal P6$_{2}$22-Si$_{3}$ is higher in energy than diamond-Si by 0.198 eV/atom.By comparison with tP16-Si,^[24] it is seen that tP16-Si is higherin energy than diamond-Si by 0.269 eV/atom, which is 35.9\% energetically higher thanour P6$_{2}$22-Si$_{3}$. And P2$_{1}$3-Si^[17] is higher in energythan our P6$_{2}$22-Si$_{3}$ by 0.102 eV/atom, which is due to the reasonthat a more severe distortion of the tetrahedron in the metastable structure leadsto higher energies. For P6$_{2}$22-Ge$_{3}$, it is higher in energy than diamond-Geby a smaller value of 0.168 eV/atom. Generally, it can be concluded that the new crystals are thermodynamically stable.

3.3 Mechanical Anisotropy Properties

The mechanical anisotropy is one of the most important properties in crystal materials. The anisotropy of crystal lattice along different directions, which is due to the arrangement of atoms with periodic and different stacking spares degrees, leads to a variety of crystal properties along different axes, for instance the hardness, fracture resistance, thermal expansion coefficient, thermal conductivity, mobility, effective mass, and elastic modulus. Also, it is well known that the mechanical anisotropy is an important implication in engineering science and crystal physics, and detailed analysis about this issue is especially helpful to understand the mechanisms of crystal materials' micro-cracks and durability.

Firstly, we focus on the three-dimensional (3D) surface construction of Young's modulus E for C$_{3}$, Si$_{3}$,and Ge$_{3}$ in P6$_{2}$22 phase as shown in Fig. 4, and it can be used as an effective tool to directly describe themechanical anisotropy of these three Group IV element allotropes. For an isotropic structure, the 3D image should exhibita spherical shape, which indicates the physical, chemical and other natural aspects of the material will not change todifferent directions. When the deviation from the spherical shape occurs, the anisotropic property will show,^[55] and it isself-evident that the amount of deviation from the spherical shape reflects the level of anisotropy. Clearly,P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ exhibit the greater anisotropy than P6$_{2}$22-C$_{3}$,as the 3D surface construction of Young's modulus for P6$_{2}$22-C$_{3}$ appears almost in a perfect spherical shape shownin Fig. 4(a). However, it is difficult to compare P6$_{2}$22-Si$_{3}$ with -Ge$_{3}$ regarding the anisotropy, as the deviations from the spherical shape shown in Figs. 4(b) and 4(c) are very similar. Therefore, the two-dimensional (2D) representation of Young's modulus is used to make a more detailed analysis in different planes, which can give us a quantitative assessment of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase in terms of anisotropic properties.

Fig. 4

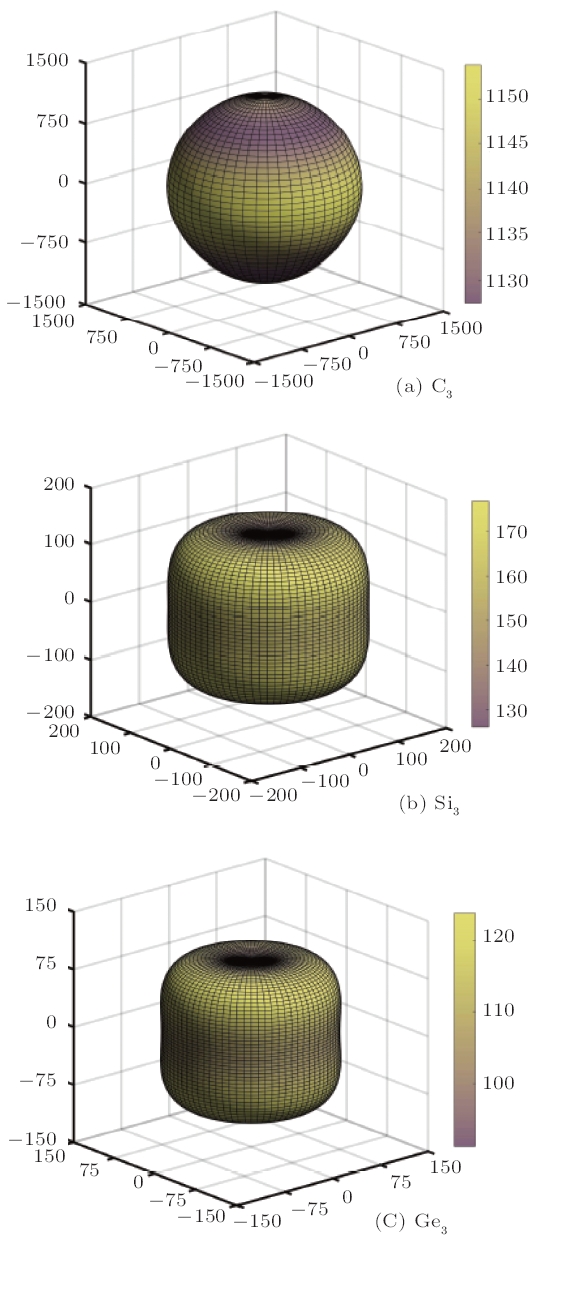New window|Download| PPT slide
Fig. 4(Color online) The directional dependence of Young's modulus for C$_{3}$ (a), Si$_{3}$ (b), and Ge$_{3}$ (c) in P6$_{2}$22 phase.



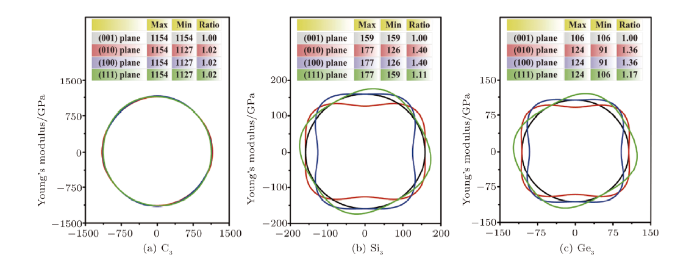
In Fig. 5, the black-, red-, blue-, and green- lines depict the value of Young's modulus in the (001),(010), (100), and (111) planes, respectively. It can be obviously seen in Fig. 5(a) that the 2Drepresentations of Young's modulus for P6$_{2}$22-C$_{3}$ in the four planes are almostthe same in a circular shape, indicating the greatest isotropy than that of P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$. Interestingly, both of P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$also show the isotropic property in the (001) plane with only one value of Young's modulusexisted (Si$_{3}$: 159 GPa and Ge$_{3}$: 106 GPa), as we can clearly see from Figs. 5(b) and 5(c) that theblack line indeed forms a perfect circle.

Fig. 5

New window|Download| PPT slide
Fig. 5(Color online) 2D representation of Young's modulus for C$_{3}$ (a), Si$_{3}$ (b), and Ge$_{3}$ (c) in P6$_{2}$22 phase. The black-, red-, blue-, and green-lines depict the value of Young's modulus in the (001), (010), (100), and (111) planes, respectively.



At the same time, it is found that the (010) and (100) planes are similar in Young's modulus for both of P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ as the red and blue lines are symmetrically displayed. By comparing the ratios of the maximum Young's modulus (E$_{\rm max}$) to the minimum Young's modules (E$_{\rm min}$) among the four planes, it is also found that both P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ have the greatest anisotropy appearing in the (010) and (100) planes with the largest E$_{\rm max}$/E$_{\rm min}$ value of 1.40 (Si$_{3}$: 177/126) and 1.36 (Ge$_{3}$: 124/91), respectively. Finally, we can draw the conclusion related to the anisotropic properties in different planes that all of the three crystals exhibit the isotropy in the (001) plane, and P6$_{2}$22-Si$_{3}$ shows the greatest anisotropy appearing in the (010) and (100) planes.

Then, the universal anisotropic index $A^{U}$ is used to further analyze the anisotropy of these three crystals. In this work, the parameters ($A^{U}$) of the three crystals including C$_{3}$, Si$_{3}$, and Ge$_{3}$ in $P6_{2}$22 phase are calculated. The equation of $A^{U}$ combines the shear and bulk modulus based on the Voigt and Reuss averages, expressed as $A^{U}$=5$G_{V}$/$G_{R}$+$B_{V}$/$B_{R}$-6,^[56] where the subscript V denotes the Voigt approximation and the subscript R represents the Reuss approximation. For an isotropic structure, A$^{U}$ must be 0; and any fluctuation the value of A$^{U}$ varies from 0, the anisotropic property shows. The bulk modulus B of P6$_{2}$22-Si$_{3}$ is B$_{V}$=94.411 GPa when using the Voigt approximation and B$_{R}$=94.231 GPa when using the Reuss approximation. For P6$_{2}$22-Ge$_{3}$, B$_{V}$=63.927 GPa, and B$_{R}$=63.917 GPa, it can be seen that the difference in bulk modulus between B$_{V}$ and B$_{R}$ is significantly small for both P6$_{2}$22-Si$_{3}$, and -Ge$_{3}$. While for P6$_{2}$22-Si$_{3}$, the difference (1.696 GPa) in shear modulus between the G$_{V}$ (69.087 GPa) and G$_{R}$ (67.391 GPa) is greater compared to that in bulk modulus. And for P6$_{2}$22-Ge$_{3}$, the difference between the G$_{V}$ (48.130 GPa) and G$_{R}$ (46.985 GPa) is 1.145 GPa. Through calculation, it is found that the A$^{U}$ values of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 are 0.001, 0.128, and 0.122, respectively. Thus, P6$_{2}$22-Si$_{3}$ has the greatest anisotropy as the A$^{U}$ is the largest, and P6$_{2}$22-C$_{3}$ has the least anisotropy as the A$^{U}$ is nearly equal to 0. Obviously, what the results show is consistent with the description in terms of Young's modulus above.

Lastly, the shear anisotropy factors A$_{1}$, A$_{2}$, and A$_{3}$ are utilized, which provide a measurement of mechanical anisotropy degree in the bonding between atoms in different planes, to better characterize the anisotropy of the newly predicted crystals. The equations of A$_{1}$, A$_{2}$ and A$_{3}$ are expressed as:^[57]A$_{1}$=4C$_{44}$/(C$_{11}$+C$_{33}$-2C$_{13}$), A$_{2}$=4C$_{55}$/(C$_{22}$+C$_{33}$-2C$_{23}$), and A$_{3}$=4C$_{66}$/(C$_{11}$+C$_{22}$-2C$_{12}$), where A$_{1}$ represents the [011] to [010] direction in the (100) shear plane, A$_{2}$ represents the [101] to [001] direction in the (010) shear plane, and A$_{3}$ represents the [110] to [010] in the (001) shear plane. In hexagonal symmetry, A$_{1}$ is equal to A$_{2}$. For an isotropic structure, these three factors of A$_{1}$, A$_{2}$, and A$_{3}$ must be 1.00, and any fluctuation of these values indicates the content of anisotropy. Furthermore, another five bulk moduli ($A_{Ba}$, $A_{Bc}$, $B_{a}$, B$_{b}$, and B$_{c}$) are considered together with $A_{1}$, A$_{2}$, and A$_{3}$ to describe the anisotropy of crystals. The equations of $A_{Ba}$ and A$_{Bc}$, expressed as below,^[58] are the bulk moduli along the a-axis and c-axis with respect to b-axis, respectively, when with the value of 1.00, indicating the isotropic property exhibited. $B_{a}$, $B_{b}$, and $B_{c}$ are the bulk moduli along a, b, and c axes, which are also listed below.^[58] From Table 3, it is seen that C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase exhibit the anisotropy symmetrically along a-axis and b-axis, and P6$_{2}$22-Si$_{3}$ has the greatest anisotropy in the (100) and (010) shear planes, while P6$_{2}$22-C$_{3}$, -Si$_{3}$, and -Ge$_{3}$ exhibit almost the isotropy in the (001) shear plane. And the anisotropy in the (100) and (010) shear planes increases in the sequence of C$_{3}$, Si$_{3}$ and Ge$_{3}$. Again, what the data show in Table 3 is obviously consistent with the mechanical anisotropy discussion as mentioned before.

(1) $A_{B_{a}} = \frac{B_{a}}{B_{b}},$
(2) $A_{B_{c}} = \frac{B_{c}}{B_{b}},$
(3) $B_{a} = a\frac{\rm{dP}}{\rm{da}} = \frac{ \wedge }{\rm{1 + \alpha+ \beta }},$
(4) $B_{b} = b\frac{\rm{dP}}{\rm{db}} = \frac{B_{a}} {\alpha},$
(5) $B_{c} = c\frac{\rm{dP}}{\rm{dc}} = \frac{B_{a}}{\beta},$
(6) $\wedge {\rm{}} = {C_{{\rm{11}}}}\! +\! {\rm{2}}{C_{{\rm{12}}}}\alpha \! +\! {C_{{\rm{22}}}}{\alpha ^2}\! +\! 2{C_{{\rm{13}}}}\beta \! +\! {C_{{\rm{33}}}}{\beta ^2}\! +\! 2{C_{{\rm{23}}}}\alpha \beta,$
(7) $\alpha = \frac{{\left( {{C_{{\rm{11}}}}\! -\! {C_{{\rm{12}}}}} \right)\left( {{C_{{\rm{33}}}}\! -\! {C_{{\rm{13}}}}} \right)\! -\! \left( {{C_{{\rm{11}}}}\! -\! {C_{{\rm{12}}}}} \right)\left( {{C_{{\rm{33}}}}\! -\! {C_{{\rm{13}}}}} \right)}}{{\left( {{C_{{\rm{33}}}}\! -\! {C_{{\rm{13}}}}} \right)\left( {{C_{{\rm{22}}}}\! -\! {C_{{\rm{12}}}}} \right)\! -\! \left( {{C_{{\rm{11}}}}\! -\! {C_{{\rm{12}}}}} \right)\left( {{C_{{\rm{33}}}}\! -\! {C_{{\rm{13}}}}} \right)}},$
(8) $\beta = {\rm{}}\frac{{\left( {{C_{{\rm{22}}}}\! -\! {C_{{\rm{12}}}}} \right)\left( {{C_{{\rm{11}}}}\! -\! {C_{{\rm{13}}}}} \right)\! -\! \left( {{C_{{\rm{11}}}}\! -\! {C_{{\rm{12}}}}} \right)\left( {{C_{{\rm{23}}}}\! -\! {C_{{\rm{12}}}}} \right)}}{{\left( {{C_{{\rm{22}}}}\! -\! {C_{{\rm{12}}}}} \right)\left( {{C_{{\rm{33}}}}\! -\! {C_{{\rm{13}}}}} \right)\! -\! \left( {{C_{{\rm{12}}}}\! -\! {C_{{\rm{23}}}}} \right)\left( {{C_{{\rm{13}}}}\! -\! {C_{{\rm{23}}}}} \right)}}.$

Table 3
Table 3The shear anisotropic factors A$_{1}$, A$_{2}$, and A$_{3}$, and the bulk moduli A$_{Ba}$, A$_{Bc}$, B$_{a}$, B$_{b}$, and B$_{c}$ of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase.

New window|CSV

3.4 Electronic Properties

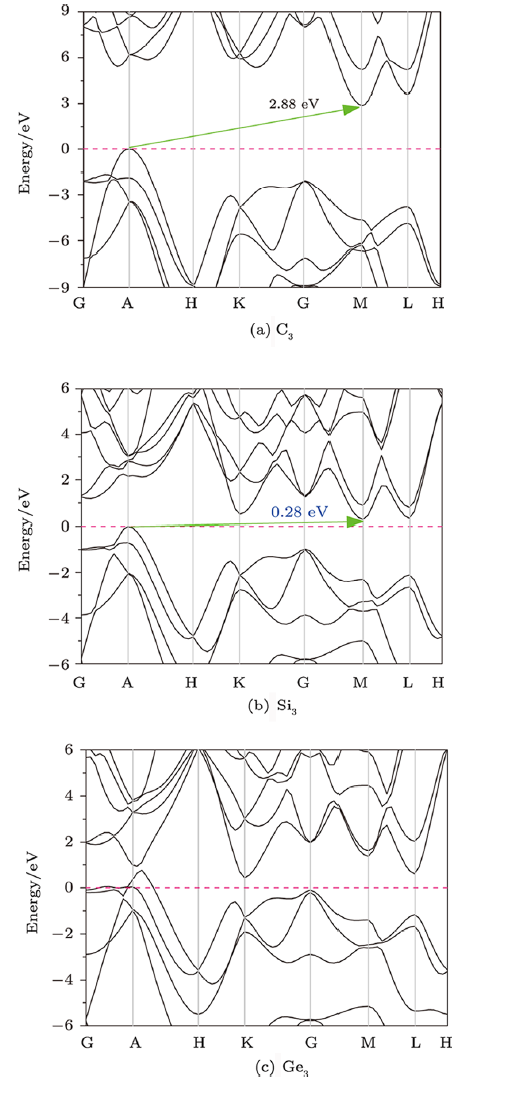
As the electronic band structure describes the forbidden or allowed energy of electronscaused by the quantum dynamics of electron diffraction in periodic lattices, many fundamentalproperties of materials in solid-state physics can be further investigated by analyzing theelectronic band structure. Therefore, the electronic band structures of C$_{3}$, Si$_{3}$, andGe$_{3}$ in P6$_{2}$22 phase are examined shown in Fig. 6. As can be seen,the dashed line represents the Fermi level (0 eV), and the minimal-energy state in theconduction band and the maximum-energy state in the valence band are each characterized bya certain crystal momentum (k-vector) in the Brillouin zone. It can be found thatthe valence band maximums (VBMs) of both P6$_{2}$22-C$_{3}$ and -Si$_{3}$ are locatedat the A point, and the conduction band minimums (CBMs) are located at the M point.Therefore, both P6$_{2}$22-C$_{3}$ and -Si$_{3}$ are indirect band gap semiconductors,and with the band gap of 2.88 eV and 0.28 eV, respectively.As shown in Fig. 6(c),the CBM of P6$_{2}$22-Ge$_{3}$ is located at the K point; however itsvalence bands along A-H direction show the metallic feature as the top dispersive bandcrossing the Fermi level to the upper region with positive energies.

Fig. 6

New window|Download| PPT slide
Fig. 6(Color online) The electronic band structures of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase.

3.5 Thermodynamic Properties

The Debye temperature $\mathit\Theta_{D}$, sound velocities, and the thermal conductivity $\kappa$$_{{\rm min}}$ are primarily discussed in this work to evaluate the thermodynamic properties of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase. Debye temperature $\mathit\Theta_{D}$ can be obtained by formula (9) as below:^[60]

(9) $\Theta_{D} = \frac{h}{k_{B}}\Bigl[ {\frac{\rm{3n}}{\rm{4\pi }} \Bigl( {\frac{N_{A \rho }}{M}} \Bigr)} \Bigr]^{1/3}{v_m},,$
where h is Planck's constant, $k_{B}$ is Boltzmann's constant,n is the number of atoms in the molecule, $N_{A}$ is Avogadro's number,$\rho$ is the density, and M is the molecular weight. In this formula,$v_{m}$ represents the mean sound velocity, which is expressed by formula (10):^[60]

(10) $v_m = \frac{1}{3}\mathop \sum \limits_{i{\rm{ = 1}}}^3 \mathop \int \nolimits\frac{1}{{v_i^3\left( {\theta ,\varphi } \right)}}\frac{{{\rm{d}}\Omega }}{{4\pi }} ={\Bigl[ {\frac{1}{3}\Bigl( {\frac{1}{{v_l^3}} + \frac{2}{{v_t^3}}} \Bigr)} \Bigr]^{ - {1}/{3}}},$
where $\theta$ and $\varphi$ are angular coordinates (d$\mathit\Omega$ =sin$\theta$d$\theta$d$\varphi$). v$_{l}$ and v$_{t}$ are the longitudinaland transverse sound velocities, respectively. If the bulk modulus B, shear modulusG, and the density $\rho$ of crystals are known, these two parameters can be simplycalculated by Navier's equation, expressed as v$_{l}$ = [(3B+4G)/3$\rho$]$^{1/2}$ andv$_{t}$ = (G/$\rho$)$^{1/2}$.^[61]


Table 4
Table 4The Debye temperature ($\mathit\Theta_{D}$ in K), and the longitudinal, transverse, mean sound velocity ($v_{l}$, $v_{t}$, and $v_{m}$ in m/s) of $C_{3}$, $Si_{3}$, and $Ge_{3}$ in $P6_{2}$22 phase.
^aRef. [59].

New window|CSV

The calculated Debye temperature and sound velocities of these three Group IV element allotropes in P6$_{2}$22 phase and in diamond phase are listed in Table 4. Since densities of $C_{3}$, $Si_{3}$, and $Ge_{3}$ in P6$_{2}$22 phase are correspondingly higher than those in diamond phase, while the bulk modulus and shear modulus of $C_{3}$, $Si_{3}$, and $Ge_{3}$ in P6$_{2}$22 phase are slightly smaller than those in diamond phase (see Table 2), and consequently sound velocities ($v_{l}$, $v_{t}$, and $v_{m}$) of $C_{3}$, $Si_{3}$, and $Ge_{3}$ in P6$_{2}$22 phase are all lower than those in diamond phase. Meanwhile, it is seen that the values of $\mathit\Theta_{D}$ in P6$_{2}$22 phase are decreased from $C_{3}$ to $Ge_{3}$, and this is due to the fact that mean sound velocities acted as dominant factors are correspondingly reduced from $C_{3}$ to $Ge_{3}$. Moreover, it is found that the values of $\mathit\Theta_{D}$ in P6$_{2}$22 phase are slightly smaller than those in diamond phase, and the values of $\mathit\Theta_{D}$ in diamond phase are in excellent agreement with the reported work.^[59]

Since sound waves travel at different speeds in different directions for crystal materials, anisotropic sound velocities need to be further discussed. According to Brugger,^[62] the single-crystal elastic constants can be used to calculate the phase velocity in pure longitudinal and transverse modes. The directions associated with sound traveling in crystals are basically classified into two categories, as the propagation direction and the polarizing direction. For hexagonal symmetry, sound velocities along the [001] and [100] propagation direction can be obtained by formula (11) and (12), respectively, as listed:^[63]

(11) $\left[ {{\rm{001}}} \right]{\rm{:}}\left[ {{\rm{001}}} \right]{v_l} =\sqrt {\frac{{{C_{{\rm{33}}}}}}{\rho }} {\rm{,}}\nonumber\\ \left[ {{\rm{100}}} \right]{v_{t1}} =\left[ {{\rm{010}}} \right]{v_{t2}} = \sqrt {\frac{{{C_{{\rm{44}}}}}}{\rho }},$
(12) $\left[ {{\rm{100}}} \right]{\rm{:}}\left[ {{\rm{100}}} \right]{v_{l}} =\sqrt {\frac{{{C_{{\rm{11}}}} - {C_{{\rm{12}}}}}}{{2\rho }}} {\rm{,}}\nonumber\\ \left[ {{\rm{010}}} \right]{v_{t1}} = \sqrt {\frac{{{C_{{\rm{11}}}}}}{\rho }} {\rm{,}}\quad\left[ {{\rm{001}}} \right]{v_{t2}} = \sqrt {\frac{{{C_{{\rm{44}}}}}}{\rho }},$
where v$_{l}$ is the longitudinal sound velocity, and v$_{tl}$ and v$_{t2}$ are the transverse sound velocities in the first and second mode, respectively. As seen in these two formulas above, C$_{33}$ and C$_{44}$ determine the longitudinal and transverse sound velocities along the [001] propagation direction, respectively, and C$_{11}$ and C$_{44}$ dominate sound velocities along the [100] propagation direction. The calculated anisotropic sound velocities of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase are listed in Table 5. It can be seen that the highest sound velocity among these three Group IV element allotropes is 17843 m/s appeared in P6$_{2}$22-C$_{3}$, and the lowest sound velocity is 2900 m/s appeared in P6$_{2}$22-Ge$_{3}$, both of which are exhibited in the [100] propagation direction. In the [001] propagation direction, each of these three crystals demonstrates the symmetrical transverse sound velocity in the first and second mode. Meanwhile, it is obvious that the highest sound velocity along different directions is the longitudinal sound velocity in the [001] propagation direction, and the transverse sound velocity in the first mode in the [100] propagation direction. In addition, since the density of P6$_{2}$22-C$_{3}$ (5.647 g/cm$^{3}$) is the highest while its elastic constants (see Table 2) are the smallest among these three crystals, its sound velocities along different directions are certainly lower than those of P6$_{2}$22-C$_{3}$ and Si$_{3}$ as shown in Table 5. The sound velocities along different directions of P6$_{2}$22-C$_{3}$ are all largely higher than those of P6$_{2}$22-Si$_{3}$, which is due to the fact that the dominant elastic constants (C$_{11}$, C$_{33}$, and C$_{44}$) of P6$_{2}$22-C$_{3}$ largely outweigh those of P6$_{2}$22-Si$_{3}$, even though the density of P6$_{2}$22-Si$_{3}$ (2.574 g/cm$^{3}$) smaller than that of P6$_{2}$22-C$_{3}$ (3.647 g/cm$^{3}$).

The minimum thermal conductivity $\kappa$$_{{\rm min}}$, which is another important physical parameter to evaluate the thermodynamic properties of materials, can be calculated based on Cahill's model by formula (13) as below:^[64]

(13) $k_{min} = (\frac{\pi}{6})^{1/3}k_{B}N^{2/3}\sum_{i}{v_i}(\frac{T}{\Theta_{i}})^{2}\\ \times \int_{0}^{\Theta_{i}/T}\frac{x^{3}e^{x}}{(e^{x}-1)^{2}}dx$

Table 5
Table 5The calculated anisotropic sound velocities (in m/s) of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase.

New window|CSV

where N is the number density of atoms, v$_{i}$ represents three sound wave velocities (includingone longitudinal and two transverse sound wave velocities), and $\mathit\Theta_{i}$ expressed asv$_{i}$[h/(2$\pi$k$_{B}$)](6$\pi$$^{2}$N)$^{1/3}$ is the cut-offfrequency for each polarization. Figure 7 shows the variations of the minimum thermal conductivities$\kappa$$_{\rm min}$ affected by the temperature (from 0 K to 2000 K) of C$_{3}$, Si$_{3}$, andGe$_{3}$ in P6$_{2}$22 phase. It is seen that $\kappa$$_{\rm min}$ is increased in thesequence of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in low temperature region (0 K < T< 110 K), while $\kappa$$_{\rm min}$ of P6$_{2}$22-C$_{3}$ beginsto be far larger than those of P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ above 230 K.In high temperature region (T > 800 K), the minimum thermal conductivitiesof P6$_{2}$22-Si$_{3}$ and -Ge$_{3}$ are almost constant, and $\kappa$$_{\rm min}$of P6$_{2}$22-Si$_{3}$ is steadily larger than that of P6$_{2}$22-Ge$_{3}$.Among these three Group IV element allotropes, P6$_{2}$22-C$_{3}$ owns the largestvalue of $\kappa$$_{\rm min}$ (1.70 W/cmK), while P6$_{2}$22-Ge$_{3}$ ownsthe smallest value of $\kappa$$_{\rm min}$ (0.71 W/cmK) at 300 K.

Fig. 7

New window|Download| PPT slide
Fig. 7(Color online) The minimum thermal conductivities $\kappa$$_{\rm min}$ of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase.



Furthermore, the minimum thermal conductivities are studied in detail by analyzing them indifferent primary directions. The values of $\kappa$$_{\rm min}$ in different directions at 300 K are all listed in Table 6. As can be seen, the values of$\kappa$$_{\rm min}$ in primary directions are all slightly larger than those inall directions, and the values of $\kappa$$_{\rm min}$ in the [001] directionare generally equal to those in the [100] direction. Moreover, the minimumthermal conductivities of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22phase are compared with those in diamond phase. It is obviously shown that$\kappa$$_{\rm min}$ of P6$_{2}$22-C$_{3}$ and -Ge$_{3}$ are very close tothose of diamond-C and -Ge, while $\kappa$$_{\rm min}$ of P6$_{2}$22-Si$_{3}$is slightly larger than that of diamond-Si. In addition, by comparing $\kappa$$_{\rm min}$ of P6$_{2}$22-Si$_{3}$ with other related silicon allotropes including C2/m-16 Si, C2/m-20 Si, P2$_{1}$/m Siand I4$_{1}$/amdt-Si$_{64}$, it is found that for most ofsilicon allotropes, their minimum thermal conductivities are approximately equalto 1 W/cmK.^[25] Since the minimum thermal conductivities of C$_{3}$, Si$_{3}$,and Ge$_{3}$ in P6$_{2}$22 phase are all close to those of diamond-C, -Si,and -Ge, it is known that these three Group IV element allotropes have great thermalconductivity and can be used as materials of microelectronic devices due to their goodheat radiation characteristics.


Table 6
Table 6The minimum thermal conductivities ($\kappa$$_{\rm min}$ in W/cmK) in all directions and in different primary directions of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase at 300 K.

New window|CSV

4 Conclusion

Two new Group IV element allotropes Si$_{3}$ and Ge$_{3}$ in P6$_{2}$22 phase were reported in this work. First-principles computations were utilized to investigate the physical properties, including the structural properties, stability, mechanical anisotropy properties, electronic properties, and thermodynamic properties. There are three atoms per conventional cell of the crystal structure in hexagonal symmetry, and densities of the newly predicted crystals are correspondingly higher than those in diamond phase. The mechanical, dynamic, and thermodynamic stabilities of the newly predicted crystals were verified. By plotting the 3D and 2D directional dependence of Young's modulus, discussing the universal anisotropic index, and calculating shear anisotropy factors together with bulk moduli, we found that P6$_{2}$22-Si$_{3}$ exhibits the greatest anisotropy while P6$_{2}$22-C$_{3}$ exhibits the isotropy, and interestingly all these three Group IV element allotropes in P6$_{2}$22 phase appear to be isotropic in the (001) plane. Furthermore, the electronic band structures were calculated by HSE06 hybrid functional, indicating that P6$_{2}$22-C$_{3}$ and -Si$_{3}$ are indirect band gap semiconductors with the band gap of 2.88 eV and 0.28 eV, respectively, and P6$_{2}$22-Ge$_{3}$ exhibiting the metallic feature. Lastly, the thermodynamic properties of C$_{3}$, Si$_{3}$, and Ge$_{3}$ in P6$_{2}$22 phase were discussed, and it was found that these three Group IV element allotropes have possible applications in microelectronic industry due to their great thermal conductivity.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] Q. Wei, Q. Zhang, H. Y. Yan, M. G. Zhang, J. Mater. Sci. 52 (2017) 2385.
[Cited within: 1]

[2] M. J. Xing, B. H. Li, Z. T. Yu, Q. Chen, J. Mater. Sci. 50 (2015) 7104.
[Cited within: 1]

[3] M. J. Xing, B. H. Li, Z. T. Yu, Q. Chen, Commun. Theor. Phys. 64 (2015) 237.


[4] M. G. Zhang, Q. Wei, H. Y. Yan, et al., Phys. Chem. C 118 (2014) 3202.


[5] Y. G. Guo, Q. Wang, Y. Kawazoe, P. Jena, Sci. Rep. 5 (2016) 14342.


[6] Q. Y. Fan, C. C. Chai, Q. Wei, Y. T. Yang , Phys. Chem. Chem. Phys. 18 ( 2016) 12905.


[7] D. Y. Kim, S. Stefanoski, O. O. Kurakevych, T. A. Strobel, Nat. Mater. 14 (2015) 169.


[8] Q. Y. Fan, C. C. Chai, Q. Wei , et al., J. Solid. State. Chem. 233 (2016) 471.


[9] S. Q. Wang and H. Q. Ye , J. Phys. Condens. Matter 15(2003) L197.


[10] S. Q. Wang and H. Q. Ye , J. Phys. Condens. Matter 15 ( 2003) 5307.
[Cited within: 1]

[11] Q. Wei, Q. Zhang, M. G. Zhang, et al., Front. Phys. 13 (2018) 136105.
[Cited within: 1]

[12] J. T. Wang, C. F. Chen, E. Wang, Y. Kawazoe, Sci. Rep. 4 (2014) 4339.


[13] M. J. Xing, B. H. Li, Z. T. Yu, Q. Chen, Materials 9 (2016) 484.


[14] K. Umemoto, R. M. Wentzcovitch, S. Saito, T. Miyake, Phys. Rev. Lett. 104 (2010) 125504.
[Cited within: 1]

[15] Q. Wei, M. G. Zhang, H. Y. Yan, et al., Europhys. Lett. 107 (2014) 27007.
[Cited within: 1]

[16] Q. Y. Fan, C. C. Chai, Q. Wei, et al., J. Mater. Sci. 53 (2018) 2785.
[Cited within: 2]

[17] H. J. Xiang, B. Huang, E. J. Kan, et al., Phys. Rev. Lett. 110 (2013) 118702.
[Cited within: 2]

[18] C. P. Tang, J. Cao, S. J. Xiong , Physica B Condens. Matter 466-467 ( 2015) 59.


[19] C. Y. He, C. X. Zhang, J. Li , et al., Phys. Chem. Chem. Phys. 18 ( 2016) 9682.


[20] I. H. Lee, Y. J. Oh, S. Kim, et al., Comput. Phys. Commun. 203 (2016) 110.


[21] M. Amsler, S. Botti, M. A. L. Marques, et al., Phys. Rev. B 92 (2015) 014101.


[22] L. A. Jantke, S. Stegmaier, A. J. Karttunen, T. F. Fassler, Chem. Eur. J. 23 (2017) 2734.


[23] Q. Y. Fan, C. C. Chai, Q. Wei, et al., J. Appl. Phys. 118 (2015) 185704.
[Cited within: 3]

[24] Q. Q. Wang, B. Xu, J. Sun , et al., J. Am. Chem. Soc. 136 ( 2014) 9826.
[Cited within: 3]

[25] Q. Y. Fan, R. Niu, W. Z. Zhang, et al., Chem. Phys. Chem. 20 (2019) 128.
[Cited within: 3]

[26] Q. Y. Fan, C. C. Chai, Q. Wei, et al., Mater. Des. 132 (2017) 539.
[Cited within: 1]

[27] Q. Y. Fan, C. C. Chai, Q. Wei , et al., Mater. Sci. Semicond. Process. 43 ( 2016) 187.
[Cited within: 1]

[28] A. Mujica, C. J. Pickard, R. J. Needs, Phys. Rev. B 91 (2015) 21410.


[29] A. De and C. Y. Pryor , J. Phys. Condens. Matter 26 (2014) 045801.
[Cited within: 1]

[30] M. C. Nguyen, X. Zhao, C. Z. Wang, K. M. Ho, Phys. Rev. B 89 (2014) 184112.
[Cited within: 1]

[31] V. A. Saleev, A. V. Shipilova, D. M. Proserpio, G. Fadda , Eur. Phys. J. B 90 ( 2017) 150.
[Cited within: 1]

[32] A. Bautista-Hernandez, T. Range, A. H. Romero, et al., J. Appl. Phys. 113 (2013) 193504.
[Cited within: 3]

[33] Q. Zhu, A. R. Oganov, M. A. Salvado, et al., Phys. Rev. B 83 (2011) 193410.
[Cited within: 4]

[34] P. Hohenberg and W. Kohn, Phys. Rev. 136 (1964) B864.
[Cited within: 1]

[35] W. Kohn and L. J. Sham, Phys. Rev. 140 (1965) A1133.
[Cited within: 1]

[36] S. J. Clark, M. D. Segall, C. J. Pickard, et al., Z. Kristallogr. 220 (2005) 567.
[Cited within: 1]

[37] J. P. Perdew, K. Burk, M. Ernzerhof, Phys. Rev. Lett. 77 (1996) 3865.
[Cited within: 1]

[38] D. M. Ceperley and B. J. Alder, Phys. Rev. Lett. 45 (1980) 566.
[Cited within: 1]

[39] P. Perdew and A. Zunger, Phys. Rev. B 23 (1981) 5048.
[Cited within: 1]

[40] B. G. Pfrommer, M. Cote, S. G. Louie, M. L. Cohen, J. Comput. Phys. 131 (1997) 233.
[Cited within: 1]

[41] S. Baroni, S. De Gironcoli, A. Dal Corso, P. Giannozzi, Rev. Mod. Phys. 73 (2001) 515.
[Cited within: 1]

[42] J. Heyd, G. E. Scuseria, M. J. Ernzerhof, J. Chem. Phys. 118 (2003) 8207.
[Cited within: 1]

[43] H. J. Monkhorst and J. D. Pack, Phys. Rev. B 13 (1976) 5188.
[Cited within: 1]

[44] M. L. Petrescu, Diam. Relat. Mater. 13 (2004) 1848.
[Cited within: 2]

[45] D. R. Lide, Handbook of Chemistry and Physics, 73rd ed, Chemical Rubber, Florida (1994).
[Cited within: 3]

[46] M. L. Cohen, Phys. Rev. B 32 (1985) 7988.
[Cited within: 1]

[47] Z. Z. Li, J. T. Wang, L. F. Xu, C. F. Chen, Phys. Rev. B 94 (2016) 174102.
[Cited within: 1]

[48] M. Grimsditch, E. S. Zouboulis, A. Polian, J. Appl. Phys. 76 (1994) 832.
[Cited within: 2]

[49] R. Gomez-Abal, X. Li, M. Scheffler, C. Ambrosch-Draxl, Phys. Rev. Lett. 101 (2008) 106404.
[Cited within: 2]

[50] B. B. Karki, G. J. Ackland, J. Crain , J. Phys. Condens. Matter 9 (1997) 8579.
[Cited within: 1]

[51] R. Hill , Proc. Phys. Soc. Lond. Sect. A 65 (1952) 349.
[Cited within: 1]

[52] Q. Y. Fan, W. Z. Zhang, S. N. Yun, et al., Chem. Eur. J. 24 (2018) 17280.
[Cited within: 1]

[53] S. F. Pugh, Philos. Mag. 45 (1954) 823.
[Cited within: 1]

[54] Q. Y. Fan, Q. Wei, H. Y. Yan , et al., Acta Phys. Pol. A 126 (2014) 740.
[Cited within: 1]

[55] W. C. Hu, Y. Liu, D. J. Li, et al., Comput. Mater. Sci. 83 (2014) 27.
[Cited within: 1]

[56] S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett. 101 (2008) 055504.
[Cited within: 1]

[57] Q. Y. Fan, Q. Wei, H. Y. Yan, et al., Comput. Mater. Sci. 85 (2014) 80.
[Cited within: 1]

[58] P. Ravindran, L. Fast, P. A. Korzhavyi, et al., J. Appl. Phys. 84 (1998) 4891.
[Cited within: 2]

[59] H. Siethoff and K. Ahiborn , Phys. Status. Solidi. B 190 (1995) 179.
[Cited within: 2]

[60] O. L. Anderson , J. Phys. Chem. Solids. 24 (1963) 909.
[Cited within: 2]

[61] K. B. Panda and K. S. Ravi, Comput. Mater. Sci. 35 (2006) 134.
[Cited within: 1]

[62] K. Brugger, J. Appl. Phys. 36 (1965) 768.
[Cited within: 1]

[63] Y. H. Duan, Y. Sun, M. J. Peng, S. G. Zhou, J. Alloys. Compd. 595 (2014) 14.
[Cited within: 1]

[64] D. G. Cahill, K. S. Wastson, R. O. Pohl, Phys. Rev. B 46 (1992) 6131.
[Cited within: 1]