Gurjit Kaur^,1, Manoj K Sharma^,School of Physics and Materials Science, Thapar Institute of Engineering and Technology, Patiala—147004, Punjab, India

First author contact: ¹ Author to whom any correspondence should be addressed.
Received:2019-09-9Revised:2019-11-7Accepted:2019-11-22Online:2020-02-03


Abstract
The capture and fission analysis of heavy ion induced fusion reactions leading to the formation of Z=107–111 superheavy nuclei has been carried out. Attempts have been made to analyze the synthesis traits, such as excitation functions, formation probabilities, barrier characteristics etc. The ℓ-summed Wong model provides a decent description of available data on capture (σ_Cap) and fusion-fission (σ_ff) cross-sections and hence is exploited to make relevant predictions for future experiments. The capture and fusion-fission excitation functions are predicted for the least explored region of superheavy nuclei (SHN) i.e. Z=107–111. The role of mass-asymmetry (η), Coulomb factor (Z_PZ_T), deformation and orientations, Businari-Gallone mass-asymmetry (α_BG), fission barrier (B_f) etc is duly explored. The present study concludes that the mass-asymmetric reactions involving ²⁴Mg, ³⁰Si, and ³⁶S projectiles are preferred for the synthesis of unknown isotopes of Z=107–111. Alternatively, the doubly magic ⁴⁸Ca-projectile also provides a competing alternative to produce neutron-rich isotopes of the above-mentioned SHN.
Keywords： Capture and fission cross-section;compound nucleus formation probability;quasi-fission


PDF (1465KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Gurjit Kaur, Manoj K Sharma. Capture and fission analysis of various superheavy isotopes with A_CN=258–280. Communications in Theoretical Physics, 2020, 72(2): 025302- doi:10.1088/1572-9494/ab617d

1. Introduction

The fusion of two colliding nuclei is a fundamental phenomenon, though there are various dynamical aspects that are not fully explored. The development of intensive beam currents and sensitive detection methods have enabled us to synthesize and study the nuclei in the unexplored region of the nuclear chart. Numerous reactions and recognition techniques have been applied in the past to scrutinize transuranic elements. The most successful methods have been the fusion evaporation reactions of already known elements, recoil-separation techniques, identification through detectors etc. Such techniques are constantly further refined and employed for the exploration of nuclear properties of new elements. The cold fusion reactions (²⁰⁸Pb, ²⁰⁹Bi + massive projectile (A_P > 50)) have been used since 1974 for the synthesis of elements with Z=107–112 [1–3]. Unfortunately, the forecasts for cold fusion reactions are not optimistic because of increased fusion hindrance and small neutron excess. Within the last two decades, researchers successfully synthesized six new superheavy elements with Z=113–118 by following a different approach in which the high intensity beam of ⁴⁸Ca projectile is aimed at actinide targets [4–6]. Instead of this, the mass-asymmetric reactions of actinide nuclei with lighter projectiles like magnesium (Mg) to potassium (K) are also of great interest to fill the gap between hot and cold fusion reactions.

Several experiments were performed for the cold synthesis of Z=107–112 superheavy nuclei. The Z=107 superheavy system was produced in ²⁰⁹Bi(⁵⁴Cr,1n-2n)^261–262Bh and ²⁰⁸Pb(⁵⁵Mn,1n-2n)^261−262Bh [7] reactions pairs and ²⁰⁸Pb(⁵⁸Fe,1n)²⁶⁵Hs [8] report the synthesis of Z=108. Additionally, the pair reactions ²⁰⁹Bi(⁵⁸Fe,1n)²⁶⁶Mt and ²⁰⁸Pb(⁵⁹Co,1n)²⁶⁶Mt [9] were investigated for the production of Z=109. The experiments involving the synthesis of elements Z=110, 111, and 112 use respectively, ²⁰⁸Pb(⁶⁴Ni,1n)²⁷¹Ds, ²⁰⁹Bi(⁶⁴Ni,1n)²⁷²Rg; ²⁰⁸Pb(⁶⁵Cu,1n)²⁷²Rg, and ²⁰⁸Pb(⁷⁰Zn,1n)²⁷⁷Cn [10–12]. The long lived isotopes of superheavy elements (SHE) produced in the experiments are still neutron deficient. The short lifetime and low production cross-sections have posed difficulties in studying the various properties of superheavy elements. Therefore, the quest for suitable target-projectile combinations for the synthesis of stable superheavy elements is still going on. For the purpose, one can use the actinide targets with stable projectile lighter than ⁴⁸Ca to produce some unknown neutron deficient isotopes with high efficiency. Some of the aforementioned elements were also synthesized using the types of reaction choices like ²⁴⁸Cm(²⁶Mg,5n-3n)^269–271Hs [13], ²³⁸U(³⁶S,5n-3n)^269–271Hs [14], ²²⁶Ra(⁴⁸Ca,4n)²⁷⁰Hs [15], and ²³⁸U(⁴⁸Ca,4n-3n)^282–283Cn [5]. The idea of using a more asymmetric reaction pair reduces the suppression of fusion and hence results in higher compound nuclear formation cross-sections. Hence it will be of interest to explore the peculiarities of different target-projectile (t-p) combinations for the synthesis of elements like Z=107, 109, 110, and 111 already synthesized in cold fusion reactions.

The sensibility of colliding partners of a reaction leading to the formation of superheavy nuclei play significant role even at energies close to the barrier. The synthesis cross-sections of these nuclei are very small. Hence, the precise calculations and predictions of cross-sections are very important so that experimentalists are able to select the best target-projectile (t-p) combinations as well as required energy for the feasibility of superheavy nuclei. In this article, the main concern is on the coalescence of unknown superheavy isotopes with charge number Z=107–111. For this purpose, different actinide-based hot fusion reactions with light, medium, and heavy t-p combinations are considered. Firstly, the available experimental data is addressed for reliable predictions of capture (σ_capture) and fusion (σ_fusion) excitation functions. For light and medium nuclei, the fission barrier (B_f) is high and compound nucleus formation probability (P_CN) is close to unity i.e. P_CN≈1 and hence σ_capture≈σ_fusion≈σ_ER [16–18]. But for heavy/superheavy systems, the scenario is different and non-compound nucleus (nCN) (or quasi-fission (QF)) processes and fusion-fission channels substantially determine the whole dynamics. The P_CN < 1, which leads to σ_capture=σ_fusion+σ_QF. Further, the contribution of evaporation residues (ERs) to fusion is very small (nb or pb order) and fusion-fission (ff) processes dominate, so σ_fusion≈σ_ff [19–21].

As the evaporation residue study of some isotopes of Z=107–111 is already done in [22], the main interest of the present work is to study the following: (i) to predict the capture and fusion-fission excitation functions for unknown superheavy nuclei with Z=107–111 in hot fusion reactions; (ii) the competition between quasi-fission and fusion-fission events is explored in terms of mass-asymmetry (η), Coulomb factor (Z₁Z₂), Businaro-Gallone mass-asymmetry point (α_BG) etc; (iii) the determination of compound nucleus formation probability (P_CN); (iv) the effect of deformations and orientations on the fusion mechanism.

In view of the above, the paper is organized as follows: section 2 gives a brief overview of the methodology (ℓ-summed Wong model). Subsequent to this, the details of calculations and the results are discussed in section 3. Finally, the summary and conclusions are presented in section 4.

2. Methdology

2.1. The potential

The total interaction potential for two colliding nuclei is calculated by adding the repulsive Coulomb term (V_C), centrifugal potential (V_ℓ), and nuclear potential (V_N). Numerous efforts have been straggled to determine the exact behavior of inter nuclear potential [23–28] and the proximity potentials have been employed with resealable success [27, 28]. The total interaction potential is the function of radial distance (R) between two nuclei, collision angle (θ), deformation parameter (β_i), temperature (T) and is given by(1)$\begin{eqnarray}\begin{array}{rcl}{V}_{T}^{{\ell }}(R,{\theta }_{i}) & = & {V}_{C}(R,{Z}_{i},{\beta }_{\lambda i},{\theta }_{i},T)+{V}_{P}(R,{A}_{i},{\beta }_{\lambda i},{\theta }_{i},T)\\ & & +{V}_{{\ell }}(R,{A}_{i},{\beta }_{\lambda i},{\theta }_{i},T).\end{array}\end{eqnarray}$

The nuclear proximity potential [27, 28] for deformed, orientated nuclei is given by(2)$\begin{eqnarray}{V}_{N}({s}_{0}(T))=4\pi \bar{R}\gamma b(T){\rm{\Phi }}({s}_{0}(T))\end{eqnarray}$where $b(T)=0.99(1+0.009{T}^{2})$ is the nuclear surface thickness, γ is the surface energy constant and $\bar{R}(T)$ is the mean curvature radius. Φ is a universal function which is independent of the shapes of nuclei or the geometry of the nuclear system but depends on minimum separation distance s₀(T) [27].

The Coulomb potential for a multipole-multipole interactions and two non-overlapping charge distributions [29, 30] is defined as(3)$\begin{eqnarray}\begin{array}{rcl}{V}_{C}(R,{Z}_{i},{\beta }_{\lambda i},{\theta }_{i},T) & = & \displaystyle \frac{{Z}_{1}{Z}_{2}{e}^{2}}{R}+3{Z}_{1}{Z}_{2}{e}^{2}\\ & & \times \sum _{\lambda ,i=1,2}\displaystyle \frac{{R}_{i}^{\lambda }({\alpha }_{i})}{(2\lambda +1){R}^{\lambda +1}}\\ & & \times {Y}_{\lambda }^{(0)}({\theta }_{i})\left[{\beta }_{\lambda i}+\displaystyle \frac{4}{7}{\beta }_{\lambda i}^{2}{Y}_{\lambda }^{(0)}({\theta }_{i})\right].\end{array}\end{eqnarray}$The centrifugal potential of the nuclei is given by(4)$\begin{eqnarray}{V}_{{\ell }}(R,{A}_{i},{\beta }_{\lambda i},{\theta }_{i},T)=\displaystyle \frac{{{\hslash }}^{2}{\ell }({\ell }+1)}{2I}\end{eqnarray}$where ℓ is angular momentum and I=I_S = $\mu {R}^{2}\,+\tfrac{2}{5}{A}_{1}{{mR}}_{1}^{2}({\alpha }_{1},T)+\tfrac{2}{5}{A}_{2}{{mR}}_{2}^{2}({\alpha }_{2},T)$ is the moment of inertia.

2.2. Capture or total cross-sections

The capture cross-section, in terms of angular-momentum (ℓ) partial waves, for two deformed and oriented nuclei (with orientation angles θ_i), lying in the same planes and colliding with center-of-mass energy ${E}_{{\rm{c}}.{\rm{m}}.}$, is(5)$\begin{eqnarray}{\sigma }_{{\rm{cap}}}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})=\sum _{{\ell }=0}^{\infty }{\sigma }_{{\ell }}=\displaystyle \frac{\pi }{{k}^{2}}\sum _{{\ell }=0}^{\infty }(2{\ell }+1){P}_{{\ell }}\end{eqnarray}$with k=$\sqrt{\tfrac{2\mu {E}_{{\rm{c}}.{\rm{m}}.}}{{{\hslash }}^{2}}}$ and μ is the reduced mass, ${P}_{{\ell }}$ is the transmission coefficient for each ℓ, which describes the penetrability across the barrier.

The penetrability P_ℓ, used in equation (5), is defined as(6)$\begin{eqnarray}{P}_{{\ell }}={\left[1+\exp \left(\displaystyle \frac{2\pi ({V}_{B}^{{\ell }}-{E}_{{\rm{c}}.{\rm{m}}.})}{{\hslash }{\omega }_{{\ell }}}\right)\right]}^{-1}.\end{eqnarray}$

In equation (6), Hill Wheeler approximation [31] is applied to calculate the penetrability. In such an approximation, the dependance of transmission probability is worked out in terms of fusion barrier height ${V}_{B}^{{\ell }}$ and curvature ${\hslash }{\omega }_{{\ell }}$(${E}_{{\rm{c}}.{\rm{m}}.}$,θ_i). There are alternative methods such as the Wentzel-Kramers-Brillouin (WKB) method [32] where the integration over the whole barrier is taken. In the recent past, one of us and collaborators have made a comparison of both the approximations, i.e. Hill Wheeler and WKB in [33] and found that either of the two methods may be applied for the addressal of fusion cross-sections. In penetrability expression, ${\hslash }{\omega }_{{\ell }}$ is evaluated at the barrier position $R={R}_{B}^{{\ell }}$ corresponding to barrier height ${V}_{B}^{{\ell }}$ and is given as(7)$\begin{eqnarray}{\hslash }{\omega }_{{\ell }}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})={\hslash }{\left[| {{\rm{d}}}^{2}{V}_{T}^{{\ell }}(R)/{{\rm{d}}{R}}^{2}{| }_{R={R}_{B}^{{\ell }}}/\mu \right]}^{1/2}\end{eqnarray}$with ${R}_{B}^{{\ell }}$ obtained from the condition $| {{\rm{d}}{V}}_{T}^{{\ell }}(R)/{\rm{d}}{R}{| }_{R={R}_{B}^{{\ell }}}=0$. Instead of solving equation (5) explicitly, which requires the complete ℓ-dependent potentials ${V}_{T}^{{\ell }}$(R, ${E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i}$), Wong [29] carried out the ℓ-summation approximately under specific conditions:(i) ℏω_ℓ ≈ℏω₀ and (ii)${V}_{B}^{{\ell }}$ ≈${V}_{B}^{0}+\tfrac{{{\hslash }}^{2}{\ell }({\ell }+1)}{2\mu {R}_{B}^{0}2}$, which means to assume ${R}_{B}^{{\ell }}$≈R⁰_B also. Using these approximations and replacing the ℓ summation in equation (5) by an integral gives the ℓ=0 barrier-based Wong formula(8)$\begin{eqnarray}{\sigma }_{{\rm{Cap}}}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})=\displaystyle \frac{{R}_{B}^{02}{\hslash }{\omega }_{0}}{2{E}_{{\rm{c}}.{\rm{m}}.}}\mathrm{ln}\left\{1+\exp \left[\displaystyle \frac{2\pi }{{\hslash }{\omega }_{0}}({E}_{{\rm{c}}.{\rm{m}}.}-{V}_{B}^{0})\right]\right\}.\end{eqnarray}$

The barrier radius (R_B) for ℓ=0 is obtained from condition(9)$\begin{eqnarray}{\left|\displaystyle \frac{{{\rm{d}}{V}}_{T}(R)}{{\rm{d}}{R}}\right|}_{R={R}_{B}}=0.\end{eqnarray}$The curvature ${\hslash }{\omega }_{0}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})$, calculated at the barrier position $R={R}_{B}^{0}$ corresponding to the maximum barrier height ${V}_{B}^{0}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})$, is given as(10)$\begin{eqnarray}{\hslash }{\omega }_{0}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})={\hslash }{\left[| {{\rm{d}}}^{2}{V}^{0}(R)/{{\rm{d}}{R}}^{2}{| }_{R={R}_{B}^{0}}/\mu \right]}^{1/2}.\end{eqnarray}$

In equation (5), ${\sigma }_{{\rm{Cap}}}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})$ is calculated for each orientation and then integrated over angle θ_i (i=1, 2) to give the final capture cross-section as(11)$\begin{eqnarray}{\sigma }_{{\rm{Cap}}}({E}_{{\rm{c}}.{\rm{m}}.})={\int }_{{\theta }_{i}=0}^{\pi /2}\sigma ({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})\sin {\theta }_{1}{\rm{d}}{\theta }_{1}\sin {\theta }_{2}{\rm{d}}{\theta }_{2}.\end{eqnarray}$

Recently, Kumar and collaborators [34] carried out the extension of the Wong formula known as the ℓ-summed extended Wong formula. The extended version includes ℓ summation up to ℓ_max, given as(12)$\begin{eqnarray}{\sigma }_{{\rm{cap}}}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})=\displaystyle \frac{\pi }{{k}^{2}}\sum _{{\ell }=0}^{{{\ell }}_{\max }}(2{\ell }+1){P}_{{\ell }}.\end{eqnarray}$

The maximum possible angular momentum (ℓ_max) of a system at a given energy is calculated using relation [35](13)$\begin{eqnarray}{{\ell }}_{\max }=\displaystyle \frac{{R}_{a}\sqrt{2\mu [{E}_{{\rm{c}}.{\rm{m}}.}-V({R}_{a},{\ell }=0)]}}{{\hslash }}\end{eqnarray}$

2.3. Fusion cross-sections

The fusion for superheavy nuclei constitute only a part to the capture events, so the fusion cross-section is always equal to or less than the capture cross-section and is expressed as(14)$\begin{eqnarray}{\sigma }_{{\rm{fusion}}}({E}_{{\rm{c}}.{\rm{m}}.},{\theta }_{i})=\displaystyle \frac{\pi }{{k}^{2}}\sum _{{\ell }=0}^{\infty }(2{\ell }+1){P}_{{\ell }}{P}_{{\rm{CN}}}.\end{eqnarray}$

2.4. Compound nucleus formation probability (P_CN)

In above equation, P_CN is the compound nucleus formation probability. The mean fissility parameter (x_m) dependent formation probability (P_CN) is defined as the linear combination of the effective fissility parameter x_eff and compound nucleus fissility parameter x_CN. The mean fissility parameter is defined as [36](15)$\begin{eqnarray}{\text{}}{x}_{{\rm{m}}}=0.75{\text{}}{x}_{\mathrm{eff}}+0.25{\text{}}{x}_{{\rm{CN}}}.\end{eqnarray}$

The compound nucleus fissility parameter x_CN is the ratio of competing Coulomb and nuclear forces for compact shapes and is given by [37](16)$\begin{eqnarray}{\text{}}{x}_{\mathrm{CN}}=\displaystyle \frac{({Z}^{2}/A)}{{\left({Z}^{2}/A\right)}_{\mathrm{crit}}}=\displaystyle \frac{({Z}^{2}/A)}{50.883[1-1.782\,6{I}^{2}]}\end{eqnarray}$where I=(A-2Z)/A is the relative neutron excess of compound nucleus. The effective fissility parameter x_eff, which includes the effect of mass and charge asymmetry, is as [37](17)$\begin{eqnarray}{\text{}}{x}_{\mathrm{eff}}=\displaystyle \frac{4{Z}_{1}{Z}_{2}/[{A}_{1}^{1/3}{A}_{2}^{1/3}({A}_{1}^{1/3}+{A}_{2}^{1/3})]}{50.883[1-1.782\,6{I}^{2}]}.\end{eqnarray}$

The value of ${P}_{\mathrm{CN}}^{0}$, which is the ‘asymptotic’ fusion probability, was proposed by Zagrebaev and Greiner [38]. It depends on the above parameters of the colliding nuclei by the relation(18)$\begin{eqnarray}{P}_{\mathrm{CN}}^{0}=\displaystyle \frac{1}{1+\exp ({\text{}}{x}_{{\rm{m}}}-\xi )/\tau }.\end{eqnarray}$

The parameters of equation (18), giving better agreement with the estimated values of ${P}_{\mathrm{CN}}^{0}$ for reactions with actinide targets, are defined as τ=0.022 6 and ξ=0.721 [36]. The energy dependence of fusion probability can be approximated by simple relation as [38](19)$\begin{eqnarray}{P}_{\mathrm{CN}}({E}^{* },{\ell })=\displaystyle \frac{{P}_{\mathrm{CN}}^{0}}{1+\exp [({E}_{B}^{* }-{E}_{\mathrm{CN}}^{* })/\bigtriangleup ]}.\end{eqnarray}$Here ${E}_{B}^{* }$ is the excitation energy of compound nucleus equal to bass barrier, ${E}_{\mathrm{CN}}^{* }$ is the excitation energy, and △ is the adjustable parameter of about 4 MeV. Also, the Businaro-Gallone mass asymmetry (α_BG) is calculated using empirical relation [39](20)$\begin{eqnarray}{\alpha }_{{BG}}=\left\{\begin{array}{l}0;{x}_{\mathrm{CN}}\lt 0.396\\ 1.12\sqrt{\tfrac{{x}_{\mathrm{CN}}-0.396}{{x}_{\mathrm{CN}}-0.156}};{x}_{\mathrm{CN}}\gt 0.396\end{array}\right..\end{eqnarray}$

3. Results and discussions

This section is divided into two subsections: section 3.1 and section 3.2. In section 3.1, the stratagem described above is applied to the analysis of experimental findings [18, 36, 40–43] over a wide range of superheavy nuclei. A comparison of formation cross-sections for Z=104–120 superheavy elements and barrier characteristics is made at energies near and above the Coulomb barrier. Afterwards in section 3.2, the same methodology is used to evaluate the capture and fusion (or fusion-fission) excitation functions for ^{258,267,269,271}Bh, ^{267,271,273,275}Mt, ^{274,275,278,280}Ds, and ^275,277,279Rg nuclei. The projectile and target combinations are chosen in such a way that their half lives are significantly large. As mentioned in the introduction, the contribution of evaporation residue cross-sections, σ_ER (of the order of nb and pb) toward fusion is very small as compared to the fusion-fission cross-sections (of the order of mb), which means that σ_fusion∼σ_ff and hence the fusion cross-sections (σ_fusion) estimated using Wong criteria are termed as fusion-fission cross-sections (σ_ff). Beside this, an attempt is made to analyze the different factors effecting the quasi-fission and fusion-fission contributions.

3.1. Comparison of barrier characteristics and cross-sections with available data

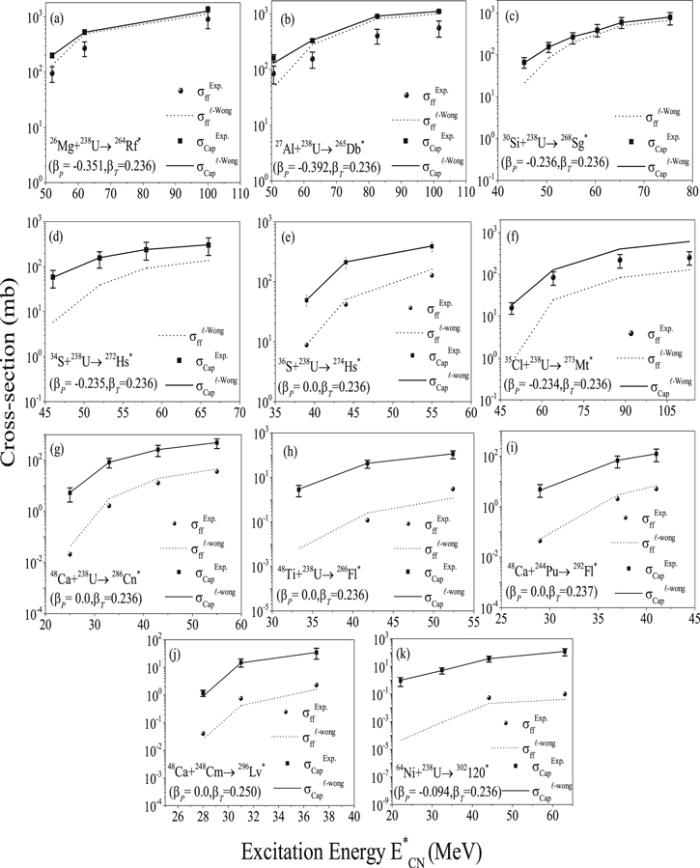
Figure 1 shows the capture and fusion (equivalently fusion-fission) excitation functions of superheavy nuclei with Z=104–120 at energies near and above the Coulomb barrier. The experimentally available capture (σ_Cap) and fusion-fission (σ_ff) cross-sections are compared with the theoretical estimates of the ℓ-sum Wong model. For the purpose, ²⁶Mg+²³⁸U→²⁶⁴Rf* [18], ²⁷Al+²³⁸U→²⁶⁵Db* [18], ³⁰Si+²³⁸U→²⁶⁸Sg* [40], ³⁴S+²³⁸U→²⁷²Hs* [41], ³⁶S+²³⁸U→²⁷⁴Hs* [42], ³⁵Cl+²³⁸U→²⁷³Mt* [18], ⁴⁸Ca+²³⁸U→²⁸⁶Cn* [43], ⁴⁸Ti+²³⁸U→²⁸⁶Fl* [36], ⁴⁸Ca+²⁴⁴Pu→²⁹²Fl* [43], ⁴⁸Ca+²⁴⁸Cm→²⁹⁶Lv* [43], and ⁶⁴Ni+²³⁸U→³⁰²120* [36] reactions are taken into account and variation of cross-sections with excitation energy (E${}_{\mathrm{CN}}^{* }$) is plotted in figure 1. This figure clearly illustrates that theoretically calculated cross-sections (denoted by lines) are in reasonable agrement with the available experimental data (denoted by filled symbols) for most of the cases. An important result that can be depicted from this figure is that the capture cross-sections (σ_Cap) for all the aforesaid reactions are in good agrement with the experimental data but there is some discrepancy in the fusion-fission cross-sections (σ_ff) for some reactions.

Figure 1.

New window|Download| PPT slide
Figure 1.Comparison of experimental (symbols) and theoretically calculated (lines) capture (σ_Cap) as well as fusion-fission (σ_ff) cross-sections for Z=104 to Z=120 superheavy nuclei formed in different hot fusion reactions.


The σ_Cap as well as σ_ff data of ²⁶⁸Sg${}^{* }{,}^{272}$Hs${}^{* }{,}^{274}$Hs${}^{* }{,}^{286}$Cn*, ²⁸⁶Fl${}^{* }{,}^{292}$Fl${}^{* }{,}^{296}$Lv*, and ³⁰²120* superheavy nuclei is reproduced well (see figures 1(c)–(e), (g)–(k)). On the other hand, for ²⁶⁴Rf*, ²⁶⁵Db*, and ²⁷³Mt${}^{* },{\sigma }_{{\rm{Cap}}}$ is fitted but σ_ff show deviation from experimental data. The σ_ff are overestimated for ²⁶⁴Rf* and ²⁶⁵Db* superheavy nuclei and underestimated for the ²⁷³Mt* system as shown in figures 1(a)–(b), and (f) respectively. It is relevant to mention here that, the experimental data available for these three systems is rather old [18] in comparison to other cases [36, 40–43]. The inconsistency in theoretically estimated fission cross-sections might be due to the anomaly in compound nuclear formation probability (P_CN) values calculated using equation (19).

The extensive comparative study of fusion barrier characteristics for colliding nuclei mentioned in figure 1 is also carried out. The barrier characteristics are estimated by taking β₂-deformations of nuclei with optimum orientations [44]. It may be noted that the position and height of the Coulomb barrier could not be measured directly in an experiment and the barrier characteristics mentioned in experimental work of [18, 36, 40–43] are close to the one calculated using the NRV code (link is provided in [21]). The percentage deviation of theoretical (ℓ-summed Wong model) and experimental Coulomb barrier height (V_B) and Coulomb barrier radius (R_B) are plotted in figure 2 as a function of charge product of incoming nuclei. The percentage deviation of Coulomb barrier height, ΔV_B (%) and Coulomb barrier radius, ${\rm{\Delta }}{R}_{B}$ (%) is defined as(21)$\begin{eqnarray}{\rm{\Delta }}{V}_{B}( \% )=\displaystyle \frac{{V}_{B}^{{\rm{Exp}}.}-{V}_{B}^{{\ell }}}{{V}_{B}^{{\rm{Exp}}.}};{\rm{\Delta }}{R}_{B}( \% )=\displaystyle \frac{{R}_{B}^{{\rm{Exp}}.}-{R}_{B}^{{\ell }}}{{R}_{B}^{{\rm{Exp}}.}}\end{eqnarray}$

Figure 2.

New window|Download| PPT slide
Figure 2.The percentage deviation of (a) barrier height (V_B) and barrier radius (R_B) from experimental numbers as a function of the charge product (Z₁Z₂) by taking deformations up to β₂ at ‘optimum’ orientations.


The theoretically calculated barrier heights (V_B) and radius (R_B) are in good agrement with the experimental one. The calculated barrier parameters have an accuracy of ∼98% and can be reproduced in an approximate deviation range of±2%. Conclusively, one can say that the ℓ-summed Wong model reproduces the barrier characteristics and hence the cross-sections nicely and hence could be used to make some relevant predictions.

3.2. Production of Z=107 (Bh), 109 (Mt), 110 (Ds), and 111 (Rg) superheavy isotopes

After comparing the barrier characteristics and cross-sections with available experimental data, the ℓ-summed Wong model is applied to study the least explored superheavy nuclei i.e. Z=107, 109, 110, and 111. The main aim of the present work is to predict the capture and fusion-fission cross-sections for different isotopes of superheavy nuclei. For the purpose, various t-p combinations are taken into account as shown in table 1. The fusion barrier parameters (R_B, V_B) for the chosen reaction partners are tabulated in table 1 along with deformations (${\beta }_{\lambda i}$), Coulomb factor (Z_PZ_T), critical Businaro-Gallone mass asymmetry (α_BG), entrance channel mass-asymmetry (η), and $| Q| $-value. In the case of superheavy nuclei, the chances of fusion are relatively less as compared to the lighter mass systems and it is hindered by quasi-fission (QF) events. Hence, all the above mentioned factors impart considerable significance in the estimation of fusion-fission cross-sections of superheavy nuclei.


Table 1.
Table 1.ℓ-summed Wong calculated Coulomb barrier height (V_B), barrier position (R_B), along with deformations (${\beta }_{2i}$), Coulomb factor (Z_PZ_T), Businaro-Gallone mass asymmetry (α_BG), entrance channel mass-asymmetry (η), $| Q| $-value of entrance channel for the synthesis of Z=107, 109, 110, and 111 superheavy nuclei.

Reaction	β2i	ZPZT	αBG	η	RB	VB	$| Q| $
Z=107
48Ti+210At→258Bh*	(0.00,0.00)	1870	0.927	0.628	12.60	202.56	172.60
48Ca+223Fr→271Bh*	(0.00,0.132)	1740	0.922	0.646	13.00	181.60	151.83
36S+231Pa→267Bh*	(0.00,0.195)	1456	0.924	0.730	12.60	155.30	116.00
31P+238U→269Bh*	(−0.218,0.236)	1380	0.923	0.769	12.20	152.30	98.61
30Si+237Np→267Bh*	(−0.236,0.226)	1302	0.924	0.775	12.20	143.50	98.30
24Mg+243Am→267Bh*	(0.393,0.237)	1140	0.924	0.820	11.70	128.70	75.52
Z=109
48Ti+223Fr→271Mt*	(0.00,0.132)	1914	0.929	0.645	12.90	199.90	161.20
48Ca+227Ac→275Mt*	(0.00,0.164)	1780	0.927	0.651	13.00	186.12	157.00
36S+237Np→273Mt*	(0.00,0.226)	1488	0.928	0.736	12.60	158.40	120.22
35Cl+238U→273Mt*	(−0.234,0.236)	1380	0.928	0.743	12.30	171.10	116.20
30Si+243Am→273Mt*	(−0.236,0.237)	1330	0.928	0.780	12.20	146.30	101.70
24Mg+247Bk→271Mt*	(0.393,0.249)	1140	0.930	0.823	11.90	130.80	79.50
Z=110
48Ti+226Ra→274Ds*	(0.00,0.164)	1936	0.931	0.649	12.90	202.20	163.90
48Ca+232Th→280Ds*	(0.00,0.205)	1800	0.929	0.662	12.90	187.34	159.03
40Ar+238U→278Ds*	(−0.031,0.236)	1656	0.930	0.712	11.90	179.10	134.07
36S+242Pu→278Ds*	(0.00,0.237)	1504	0.930	0.741	12.60	159.50	122.20
30Si+248Cm→278Ds*	(0.0,0.235)	1344	0.930	0.784	12.20	147.50	103.30
24Mg+251Cf→275Ds*	(0.393,0.250)	1140	0.931	0.825	11.80	132.20	81.40
Z=111
48Ti+227Ac→275Rg*	(0.00,0.164)	1958	0.934	0.651	12.80	204.80	167.90
48Ca+231Pa→279Rg*	(0.00,0.195)	1820	0.932	0.656	12.90	190.00	162.30
39K+238U→277Rg*	(−0.032,0.236)	1748	0.933	0.718	12.20	191.50	134.70
36S+243Am→279Rg*	(0.00,0.237)	1520	0.932	0.742	12.60	161.80	125.00
30Si+247Bk→277Rg*	(−0.236,0.249)	1358	0.933	0.783	12.20	149.20	107.10

New window|CSV

The following observations can be withdrawn from table 1: (i) the Coulomb barrier height (V_B) decreases with the decrease in Coulomb factor (Z_PZ_T) and increase in mass-asymmetry (η). This ultimately effects the fusion (hence fission) cross-sections and these are expected to increase with an increase in η. (ii) The Coulomb factor (Z_PZ_T) is related to the Coulomb repulsive energy in entrance channel and higher magnitude of Coulomb factor indicates the possible occurrence of quasi-fission (QF). According to the macroscopic-microscopic model [45], if Z_PZ_T > 1600, QF events are more prominent. In table 1, reactions are chosen in such a way that Z_PZ_T of entrance channel lies across the aforesaid limit. The Z_PZ_T for ⁴⁸Ti- and ⁴⁸Ca-induced reactions is above 1600 and the same for ²⁴Mg, ³⁰Si, and ³⁶S induced reactions is below this limit. This indicates that for more asymmetric reactions, there are higher chances of fusion. Also, with the increase in charge number (Z), the Coulomb factor (Z_PZ_T) for most of the reactions start approaching this threshold value. Conclusively, the symmetric interacting pairs generally lead to significant contribution of QF components. (iii) In asymmetric combinations of colliding nuclei, fusion suppression can also be observed by an effect of the conditional barrier. So, for the case, Businaro-Gallone mass asymmetry point (α_BG) define the fusion process. Systems having η∼α_BG, there are higher chances of fusion. In contrast, for η < α_BG, it is expected that fusion is not complete and there are chances of QF. For the reaction pairs mentioned in table 1, η < α_BG and it is expected that QF appears in the company of fusion-fission processes. The contribution of QF may be different for different channels depending on the deviation of η from α_BG and some other related factors.

Figure 3.

New window|Download| PPT slide
Figure 3.Theoretically predicted capture (σ_Cap) and fusion-fission (σ_ff) excitation functions for the synthesis of (a), (b) Z=107, (c), (d) Z=109, (e), (f) Z=110, and (g), (h) Z=111 superheavy nuclei. The respective ℓ-values are also shown in the inset of figures.


The theoretically calculated capture (σ_Cap) and fusion-fission (σ_ff) excitation functions for the reaction partners mentioned in table 1 are plotted in figure 3 for near and above barrier energies. Figures 3(a), (c), (e), (g) represent the capture and figures 3(b), (d), (f), (h) show the fusion-fission cross-sections as a function of excitation energy (E${}_{\mathrm{CN}}^{* }$). The respective angular momentum values (ℓ_max) are plotted in the inset as a function of excitation energy (E${}_{\mathrm{CN}}^{* }$). It is evident from this figure that the variation of cross-sections is smooth with excitation energy. The cross-section increases with increase in energy and then start saturating. An important observation that can be noticed from this figure is that the magnitude of capture cross-sections (σ_Cap) for the chosen reactions are quite close to each other. The comparison of σ_Cap at energies close to the Coulomb barrier shows that the ratio of cross-section values for reactions with lowest mass-asymmetry to highest mass asymmetry (i.e. ${\sigma }_{{Cap}}^{{\eta }_{{\rm{lowest}}}}$/${\sigma }_{{Cap}}^{{\eta }_{{\rm{highest}}}}$) is ≈1–2. In contrast to above, the fusion-fission cross-sections are evidently different for the reactions under consideration. Higher fusion-fission cross-sections are observed for superheavy nuclei formed in ²⁴Mg-induced reactions followed by ³⁰Si and ³⁶S. The observed fission cross-sections are nearly identical for ³⁰Si and ³⁶S projectiles for most of the cases. Although the cross-sections are obtained higher with ²⁴Mg, ³⁶S can still be a preferable choice due to relatively lower excitation energies. Also, the reactions with a doubly magic ⁴⁸Ca projectile have sufficiently values with lower excitation energies, which can be a good alternative for the synthesis of such nuclei. It can be used for the synthesis of neutron rich isotopes of respective nuclei. The least cross-sections are observed for the use of ⁴⁸Ti-induced reactions.

Figure 4.

New window|Download| PPT slide
Figure 4.Variation of capture and fusion-fission cross-sections for Z=107 as a function of excitation energy (E${}_{{\rm{CN}}}^{* }$) for (a) ²⁴Mg+²⁴³Am (b) ⁴⁸Ti+²¹⁰At reactions.


Figure 4 is plotted to analyze the contribution of quasi-fission process towards capture cross-sections. The variation of σ_Cap and σ_ff is plotted as a function of excitation energy (E${}_{\mathrm{CN}}^{* }$) for two extreme mass-asymmetric reaction pairs leading to the formation of Z=107 (Bh) superheavy isotopes. Larger capture and fusion-fission cross-sections are observed for ²⁴Mg+²⁴³Am→²⁶⁷Bh* reaction as compared to ⁴⁸Ti+²¹⁰At→²⁵⁸Bh*. The difference between capture and fusion-fission cross-sections is significantly large for ⁴⁸Ti-induced reaction and is observed least for the use of ²⁴Mg-projectile. For energies near the Coulomb barrier, the difference is larger as compared to the above barrier region. This deviation between cross-sections indicate the contribution of QF processes. Hence one can say that the quasi-fission events are more pronounced for ⁴⁸Ti-projectiles compared to others, which in turn further justify the above points. Similar types of results are observed for Z=109, 110, and 111 superheavy nuclei, which are not shown here to avoid repetition. This difference in σ_Cap and σ_ff is evidently caused by the corresponding change in the compound nucleus formation probability (P_CN) value.

As mentioned in section 2, equation (19) determines the compound nucleus formation probability (P_CN) for the reactions leading to the formation of heavy/superheavy nuclei. The calculated P_CN for different incoming channels are plotted in figure 5. P_CN is the measure of fusion suppression effects correlated with the entrance channel mass-asymmetry (η). Variation of P_CN is smooth and increases exponentially with the increase in excitation energy (E${}_{\mathrm{CN}}^{* }$). It becomes nearly constant at higher energies. Figure 5(a) shows that, out of all the reactions under consideration for the synthesis of Z=107, the P_CN values are observed higher and comparable for ²⁴Mg+²⁴³Am and ³⁰Si+²³⁷Np reactions followed by ³⁶S+²³¹Pa. In contrast, the least values are observed for ⁴⁸Ti+²¹⁰At. For Z=109 (see figure 5(b)), Z=110 (see figure 5(c)), and Z=111 (see figure 5(d)), the formation probability of ³⁶S and ³⁰Si induced reactions are comparable. A drastic difference in the formation probability is observed for the interaction with ⁴⁸Ca and ⁴⁸Ti projectiles. The Coulomb barrier is larger and mass-asymmetry is lesser for the latter case. Hence lower P_CN values are observed for ⁴⁸Ti, which in turn result in stronger fusion hindrance as compared to the ⁴⁸Ca projectile.

Figure 5.

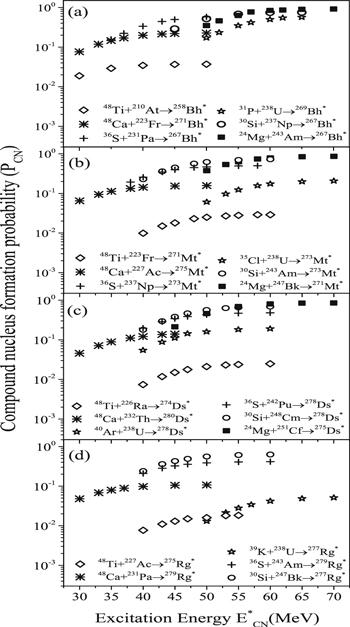New window|Download| PPT slide
Figure 5.Compound nucleus formation probabilities (P_CN) plotted as a function of excitation energy (E${}_{{\rm{CN}}}^{* }$) for Z=107, 109, 110, and 111 superheavy nuclei formed via different entrance channels.

Figure 6.

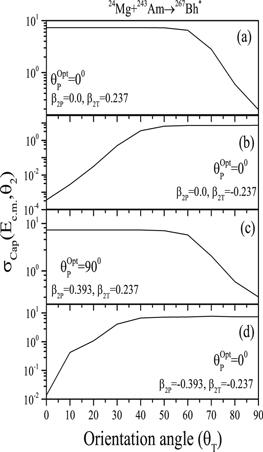New window|Download| PPT slide
Figure 6.Variation of capture cross-section at each target angle (θ_T) for ²⁴Mg+²⁴³Am reaction at energy near the Coulomb barrier (E${}_{{\rm{CN}}}^{* }$=52 MeV).


The respective orientations of the interacting nuclei also play an important role and effect the cross-section contribution significantly. The same is explored via figure 6 which shows the variation of capture cross-sections (σ_Cap) at different orientation angles for ²⁴Mg+²⁴³Am→²⁶⁷Bh* reaction. Figures 6(a)–(d) are plotted respectively for spherical+prolate, spherical+oblate, prolate+prolate, and oblate+oblate choices of interacting nuclei. The projectile angle (θ_P) is kept fixed at optimum orientation [44] and target angle (θ_T) is varied. It is observed that the capture cross-section is maximum at θ_T=0⁰ for prolate and θ_T=90⁰ for oblate nuclei. Also, the observed σ_Cap are slightly higher for the deformed choice of nuclei relative to spherical+spherical (not shown here) and spherical+deformed pairs. This is possibly due to the fact that the deformation and orientation of nuclei change the balance between repulsive and attractive forces, which ultimately effect the Coulomb barrier and hence the cross-sections.

Figure 7 shows the variation of fission barrier heights (B_f) and neutron separation energy (B_n) with a compound nucleus fissility parameter (x_CN). Experimental nuclear masses [46] are used for the determination of neutron separation energies (B_n). The Möller and Nix masses of [47] are used where the experimental data is not available. It is relevant to mention that the theoretical estimations of fission barrier for superheavy nuclei are not yet very reliable and differ significantly for different choices of methodologies, therefore systematic study of such quantities is highly desirable. It is evident from this figure that, with the increase in proton number Z of nuclei, the compound nucleus fissility parameter (x_CN) increases. Higher values of x_CN suggest the higher chances of separation of a compound nucleus. Also, with the increment in the mass of the superheavy isotopes, the fission barrier (B_f) decreases for most of the cases under consideration (see figure 7(a)). However, some uncertainty is observed for ²⁶⁹Bh*, which is possibly due to the appearance of deformed neutron magic (N=162). The neutron separation energy (B_n) is plotted as a function of x_CN in figure 7(b). The magnitude of B_n is relatively higher as compared to B_f for most of the cases, which in turn suggests that fission is more prominent than the neutron evaporation process. The evaporation residue study of ³⁶S-induced reactions for Z=109–111 was performed in [22] so using the evaporation residue data from [22] and fusion-fission cross-sections from present calculations, the survival probabilities (W_Surv) are calculated and mentioned in table 2. The W_Surv is calculated using relation W_Surv=$\tfrac{{\sigma }_{{\rm{ER}}}}{{\sigma }_{{\rm{ER}}}+{\sigma }_{{\rm{ff}}}}$ [43]. This table shows that for a given compound system, the survival probability decreases with the increase in excitation energy (E${}_{\mathrm{CN}}^{* }$). Also, for given energies, the survival probability of 4n channel is higher as compared to that of 3n.

Figure 7.

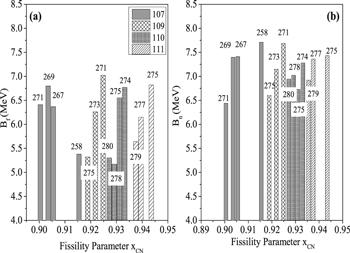New window|Download| PPT slide
Figure 7.Variation of fission barrier heights (B_f) and neutron separation energy (B_n) as a function of compound nucleus fissility parameter (x_CN) for Z=107, 109, 110, and 111 superheavy nuclei.



Table 2.
Table 2.Survival probability of 3n and 4n evaporation channel (W${}_{{\rm{Surv}}}^{3n}$ and W${}_{{\rm{Surv}}}^{4n}$) calculated using relation W_Surv=$\tfrac{{\sigma }_{{\rm{ER}}}}{{\sigma }_{{\rm{ER}}}+{\sigma }_{{\rm{ff}}}}$ by considering present calculations and evaporation data of [22].

${E}_{{CN}}^{* }$	σ3n	σ4n	σff	${{\rm{W}}}_{{Surv}}^{3n}$	${{\rm{W}}}_{{Surv}}^{4n}$
(MeV)	(pb)	(pb)	(mb)
		36S+237Np→273Mt*
38		0.78	0.399		1.95×10−9
40		3.12	2.13		1.45×10−9
43		6.29	32.2		1.95×10−10
45		5.38	60.8		8.84×10−11
50		1.05	137.2		7.65×10−12
		36S+242Pu→278Ds*
40	0.144	0.66	2.52	5.70×10−11	2.60×10−10
43	0.089	0.96	16.07	4.97×10−12	5.90×10−11
45	0.046	0.79	41.25	1.15×10−12	1.90×10−11
47	0.019	0.47	69.31	2.70×10−13	6.78×10−12
50	—	0.16	111.62	—	1.43×10−12
		36S+243Am→279Rg*
40	0.813	2.36	0.95	8.53×10−10	8.70×10−10
43	0.266	2.24	27.70	9.60×10−12	8.8×10−11
45	0.109	1.31	49.04	2.20×10−12	2.6×10−11
47	—	0.65	72.83	—	8.9×10−12
50	—	0.20	111.18	—	1.8×10−12

New window|CSV

4. Summary

A systematic analysis of barrier characteristics, capture and fusion-fission cross-sections is carried out at near and above the Coulomb barrier energies using the ℓ-summed Wong methodology and the experimental data is adequately addressed for 104≤Z≤120 nuclei. Further, this approach is implemented to the estimations of capture and fission excitation functions for the isotopes of ^{258,267,269,271}Bh, ^{267,271,273,275}Mt, ^{274,275,278,280}Ds, and ^275,277,279Rg nuclei. It has been observed that the mass-asymmetric reactions involving ²⁴Mg, ³⁰Si, and ³⁶S projectiles seem more suitable to synthesize the above-mentioned superheavy isotopes. But due to lower excitation energy and higher cross-sections, ³⁶S can gain much attention. Beside this, the doubly magic ⁴⁸Ca provides an alternativee option for the synthesis of neutron rich isotopes which result in enhanced cross-sections in comparison to the ⁴⁸Ti projectile. Finally, an effort is made to analyze the relative contribution of fusion-fission and quasi-fission components. With the increase in Z-number and hence Coulomb factor (Z_PZ_T), the deviation of η from α_BG increases, which indicates the enhanced contribution of QF events. For a given Z, the magnitude of capture cross-section is nearly the same, whereas the σ_ff varies, significantly suggesting different involvement of the QF component. The deformations and orientations also play an important role in the determination of cross-sections. The cross-section values enhance with the addition of deformations as compared to the spherical case.

Acknowledgments

The financial support from the UGC-DAE Consortium for Scientific Research, F.No. UGC-DAE-CSR-KC/CRS/19/NP09/0920, is gratefully acknowledged. G.K. is thankful to DST, New Delhi, for the INSPIRE-fellowship (grant no. DST/INSPIRE/03/ 2015/000199).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Hofmann S 1997 Nucl. Instrum. Methods. Phys. Res. B 126 310 315
DOI:10.1016/S0168-583X(96)01000-2 [Cited within: 1]

[2]Hofmann S 1999 Nucl. Phys. A 654 252c 269c
DOI:10.1016/S0375-9474(99)00257-2

[3]Oganessian Y T 1975 Nucl. Phys. A 239 353 364
DOI:10.1016/0375-9474(75)90456-X [Cited within: 4]

[4]Oganessian Y T 2007 J. Phys. G: Nucl. Part. Phys. 34 R165 R242
DOI:10.1088/0954-3899/34/4/R01 [Cited within: 1]

[5]Oganessian Y T et al. 2004 Phys. Rev. C 70 064609
DOI:10.1103/PhysRevC.70.064609 [Cited within: 1]

[6]Oganessian Y T et al. 2013 Phys. Rev. C 87 014302
DOI:10.1103/PhysRevC.87.014302 [Cited within: 1]

[7]Nelson S L et al. 2008 Phys. Rev. C 78 024606
DOI:10.1103/PhysRevC.78.024606 [Cited within: 1]

[8]Hofmann S et al. 1997 Z. Phys. A 358 377 378
DOI:10.1007/s002180050343 [Cited within: 1]

[9]Nelson S L et al. 2009 Phys. Rev. C 79 027605
DOI:10.1103/PhysRevC.79.027605 [Cited within: 1]

[10]Folden C M et al. 2004 Phys. Rev. Lett. 93 212702
DOI:10.1103/PhysRevLett.93.212702 [Cited within: 1]

[11]Morita K et al. 2004 J. Phys. Soc. Jpn. 73 1738 1744
DOI:10.1143/JPSJ.73.1738

[12]Morita K et al. 2007 J. Phys. Soc. Jpn. 76 043201
DOI:10.1143/JPSJ.76.043201 [Cited within: 1]

[13]Dvorak J et al. 2006 Phys. Rev. Lett. 97 242501
DOI:10.1103/PhysRevLett.97.242501 [Cited within: 1]

Dvorak J et al. 2008 Phys. Rev. Lett. 100 132503
DOI:10.1103/PhysRevLett.97.242501 [Cited within: 1]

[14]Graeger R et al. 2010 Phys. Rev. C 81 061601(R)
DOI:10.1103/PhysRevC.81.061601 [Cited within: 1]

[15]Oganessian Y T et al. 2013 Phys. Rev. C 87 034605
DOI:10.1103/PhysRevC.87.034605 [Cited within: 1]

[16]Toke J et al. 1985 Nucl. Phys. A 440 327
DOI:10.1016/0375-9474(85)90344-6 [Cited within: 1]

[17]Back B B et al. 1981 Phys. Rev. Lett. 46 1068 1071
DOI:10.1103/PhysRevLett.46.1068

[18]Shen W Q et al. 1987 Phys. Rev. C 36 115 142
DOI:10.1103/PhysRevC.36.115 [Cited within: 7]

[19]Adamian G G et al. 1998 Nucl. Phys. A 633 409 420
DOI:10.1016/S0375-9474(98)00124-9 [Cited within: 1]

[20]Cherepanov E A 2004 Nucl. Phys. A 734 E13 E16
DOI:10.1016/j.nuclphysa.2004.03.008

[21]Itkis M G et al. 2015 Nucl. Phys. A 944 204 237
DOI:10.1016/j.nuclphysa.2015.09.007 [Cited within: 2]

[22]Hong J Adamian G G Antonenko N V 2016 Eur. Phys. J. A 52 305
DOI:10.1140/epja/i2016-16305-9 [Cited within: 4]

[23]Mayers W D et al. 2000 Phys. Rev. C 62 044610
DOI:10.1103/PhysRevC.62.044610 [Cited within: 1]

[24]Zagrebaev V I 2004 Nucl. Phys. A 734 164
DOI:10.1016/j.nuclphysa.2004.01.025

[25]Dutt I Puri R K 2010 Phys. Rev. C 81 044615
DOI:10.1103/PhysRevC.81.044615

[26]Denisov V Y 2002 Phys. Lett. B 526 315 321
DOI:10.1016/S0370-2693(01)01513-1

[27]Blocki J et al. 1977 Ann. Phys. (N. Y.) 105 427 462
DOI:10.1016/0003-4916(77)90249-4 [Cited within: 3]

[28]Gupta R K Singh N Manhas M 2004 Phys. Rev. C 70 034608
DOI:10.1103/PhysRevC.70.034608 [Cited within: 3]

[29]Wong C Y et al. 1973 Phys. Rev. Lett. 31 766 769
DOI:10.1103/PhysRevLett.31.766 [Cited within: 2]

[30]Alder K Winther A 1969 Nucl. Phys. A 132 1 4
DOI:10.1016/0375-9474(69)90607-1 [Cited within: 1]

[31]Hill D L Wheeler J A 1953 Phys. Rev. 89 1102
DOI:10.1103/PhysRev.89.1102 [Cited within: 1]

Thomas T D 1959 Phys. Rev. 116 703
DOI:10.1103/PhysRev.89.1102 [Cited within: 1]

[32]Miller S C Good R H 1953 Phys. Rev. 91 174 179
DOI:10.1103/PhysRev.91.174 [Cited within: 1]

[33]Jain D et al. 2014 Eur. Phys. J. A 50 155
DOI:10.1140/epja/i2014-14155-1 [Cited within: 1]

[34]Kumar R et al. 2009 Phys. Rev. C 80 034618
DOI:10.1103/PhysRevC.80.034618 [Cited within: 1]

[35]Gull M et al. 2018 Phys. Rev. C 98 034603
DOI:10.1103/PhysRevC.98.034603 [Cited within: 1]

[36]Kozulin E M et al. 2016 Phys. Rev. C 94 054613
DOI:10.1103/PhysRevC.94.054613 [Cited within: 7]

[37]du Rietz R et al. 2013 Phys. Rev. C 88 054618
DOI:10.1103/PhysRevC.88.054618 [Cited within: 2]

[38]Zagrebaev V I Greiner W 2015 Nucl. Phys. A 944 257
DOI:10.1016/j.nuclphysa.2015.02.010 [Cited within: 2]

Zagrebaev V I Greiner W 2008 Phys. Rev. C 78 034610
DOI:10.1016/j.nuclphysa.2015.02.010 [Cited within: 2]

[39]Saxena A et al. 1994 Phys. Rev. C 49 932 940
DOI:10.1103/PhysRevC.49.932 [Cited within: 1]

[40]Nisho K et al. 2010 Phys. Rev. C 82 044604
DOI:10.1103/PhysRevC.82.044604 [Cited within: 4]

[41]Nisho K et al. 2010 Phys. Rev. C 82 024611
DOI:10.1103/PhysRevC.82.024611 [Cited within: 1]

[42]Itkis M G et al. 2010 Nucl. Phys. A 834 374 377
DOI:10.1016/j.nuclphysa.2010.01.043 [Cited within: 1]

[43]Kozulin E M et al. 2014 Phys. Rev. C 90 054608
DOI:10.1103/PhysRevC.90.054608 [Cited within: 7]

[44]Gupta R K et al. 2005 J. Phys. G: Nucl. Part. Phys. 31 631 644
DOI:10.1088/0954-3899/31/7/009 [Cited within: 2]

[45]Swiatecki W J 1981 Phys. Scr. 24 113
DOI:10.1088/0031-8949/24/1B/007 [Cited within: 1]

[46]Wang M 2012 Chin. Phys. C 36 1603 2014
DOI:10.1088/1674-1137/36/12/003 [Cited within: 1]

[47]Moller P 2016 At. Data Nucl. Data tables 109–110 1 204
DOI:10.1016/j.adt.2015.10.002 [Cited within: 1]