全文HTML
--> --> -->电离之后电子的运动主要受激光场的影响. 如果能够控制激光电场的波形, 那么就能够控制电离电子的运动及其返回和再碰撞过程[20,21]. 近年来, 人们提出利用两个频率不同的圆偏振激光脉冲组成复合光场来控制电离电子的运动轨迹. 通过改变两个圆偏振脉冲的参数, 可以实现复合激光电场波形的灵活控制. 基于simple-man模型, 假设电子电离时刻的初始速度为零, 电离后忽略掉母离子对电子的库仑作用力. 那么, 两个圆偏脉冲的旋转方向相反时, 电离电子有较大的概率返回发生再碰撞, 两个圆偏脉冲的旋转方向相同时, 电离电子几乎不可能返回母离子[1]. 因此在过去的几年里人们的精力主要集中在反向旋转的双色圆偏振脉冲. 人们已经利用反旋双色圆偏场驱动电子返回再碰撞获得了圆偏振的高次谐波[22], 同时在反旋双色圆偏场阈上电离的电子谱上发现了有趣的干涉条纹[23-25]. 2016年Chaloupka和Hickstein[26]在理论上研究了反旋双色圆偏场驱动原子的NSDI, 他们观察了两电子的运动轨迹, 证实了反旋双色圆偏场中原子NSDI的产生机制仍然是再碰撞. 紧接着人们在实验上观测到了反旋双色圆偏场中双电离信号的增强[27-29]. 随后的研究发现, 反旋双色圆偏场中NSDI的产量、电子动量分布和再碰撞轨道依赖于两圆偏脉冲的幅值比和相对相位[30-36]. 与反向旋转的情况相比, 同向旋转双色圆偏场中电子再碰撞的概率非常低[37-41]. 先前的数值计算表明, 同旋双色圆偏场中原子NSDI的概率要比反旋的情况低一到两个量级[39,40]. 近期人们发现, 同旋双色圆偏场中Ar (1600 nm + 800 nm), He (800 nm + 400 nm)和H2 (780 nm + 390 nm)的NSDI产量依赖于两脉冲的幅值比[39-41]. 在这些关于同向旋转双色圆偏场中NSDI的研究中, 两脉冲的频率比都被固定为2. 对于同向旋转圆偏场中原子的NSDI对频率比依赖的研究尚未开展, 相关的动力学过程仍不清楚.
本文利用三维经典系综模型研究同向旋转双色圆偏场中Ar原子NSDI电子超快动力学. 这里固定两圆偏脉冲的幅值比为2. 同时固定一脉冲的角频率为0.0285 a.u. (对应波长为1600 nm). 改变另一脉冲的频率, 使两脉冲的频率比在2—5之间变化, 以此来研究NSDI中电子超快动力学对两脉冲频率比的依赖. 数值结果表明, 同旋双色圆偏场中NSDI的概率随两脉冲频率比的增加而增加. 主要的再碰撞轨道是一个环形的短轨道. 轨道分析表明, 随频率比的增加电子的返回能量减小, 碰撞时两电子的距离增大. 这导致随两脉冲频率比的增加, 碰撞激发电离机制对NSDI的贡献逐渐增大.
为获得系综的初始状态, 首先将两电子随机地放在核子附近. 然后给两电子一个确定的动能, 使得系统的总能量, 即两电子的势能和动能之和, 等于原子的第一、第二电离能之和. 本文设置总能量为–1.59 a.u. (对应Ar的第一、二电离能之和). 将动能随机地分配给两个电子, 并且这两电子的速度方向随机给定. 然后两电子系统在没有激光场的情况下, 按照牛顿运动方程自由演化. 经过一段时间后(300 a.u.). 可以得到一个稳定的初始系综分布. 初始系综确定后, 原子在激光场的作用下演化, 直到激光脉冲结束, 即可得到系综中各个原子的最终状态, 包括位置和动量. 分析两个电子的能量, 如果两个电子的末态能量都大于零, 则认为该原子发生了双电离.
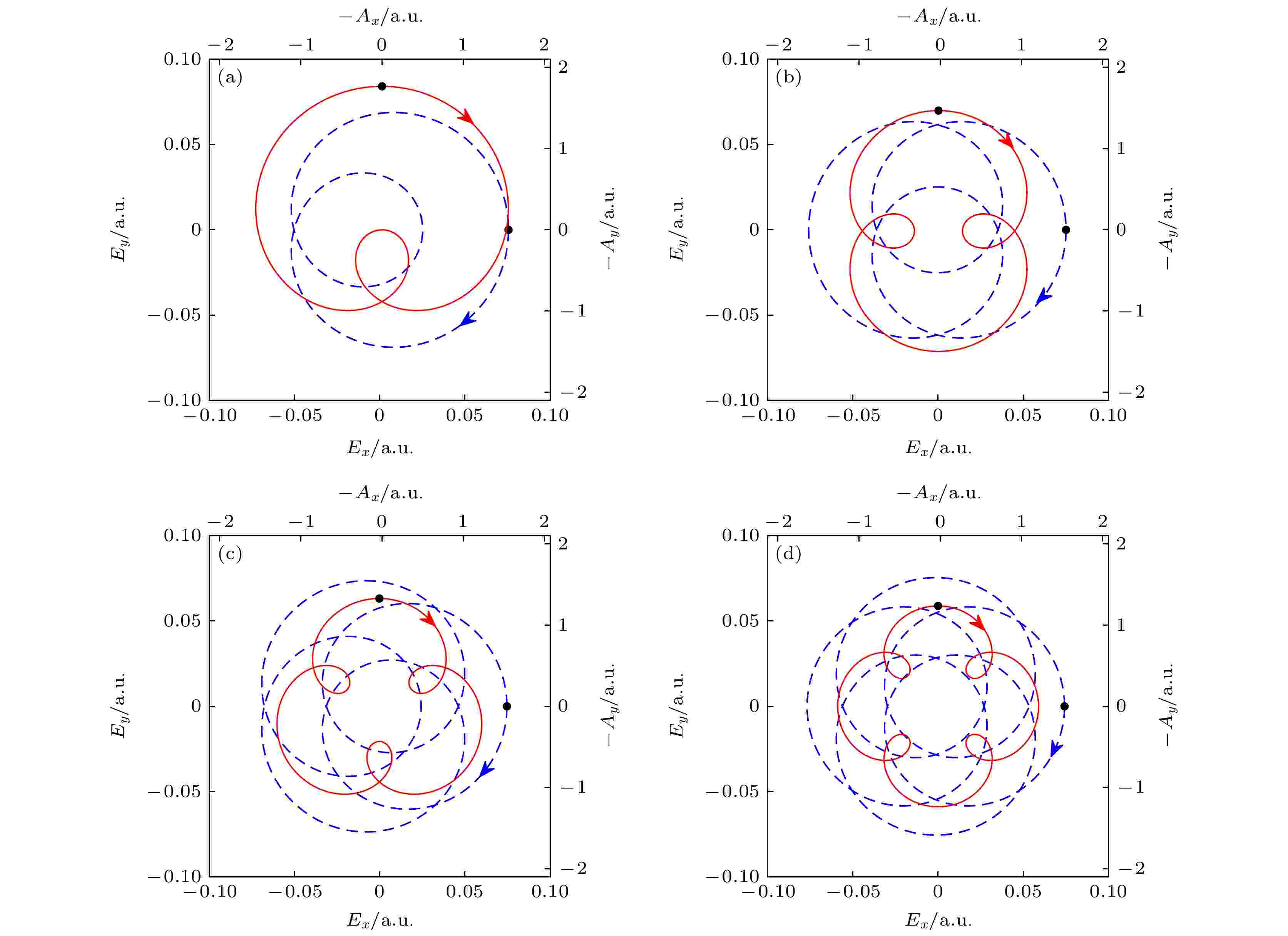图 1 不同频率比时同向旋转双色场的电场矢量(蓝虚线)和负矢势(红实线) (a) 频率比为2; (b) 频率比为3; (c) 频率比为4; (d) 频率比为5. 箭头标出了时间演化的方向, 黑点标出了一个电场极大值及其对应的负矢势Figure1. Combined laser electric field E(t) (dashed curves) and the corresponding negative vector potential A(t) (solid curves) for co-rotating two-color circularly polarized laser fields at different frequency ratios of (a) 2, (b) 3, (c) 4, (d) 5. The arrows indicate the time evolution direction. The black dots mark a field maximum and its negative vector potential.
实验上最容易测量的是双电离的产量. 图2给出了不同频率比时双电离与单电离的概率比. 可以看出, 随着频率比的增加, NSDI概率逐渐增加. 在频率比为2时NSDI概率约为1 × 10–4. 而当频率比增加到5时, NSDI概率达到了1 × 10–3, 增加了一个数量级. 不同频率比的复合电场的峰值强度是相同的. 随着频率比的增加, 每个周期内电场极大值的数目相应地增加, 这就加大了电子电离的概率.
图 2 双电离与单电离的概率比对频率比的依赖Figure2. Dependence of the ratio of double ionization probability to single ionization probability on frequency ratio.
图3给出了不同频率比时NSDI中电离电子的动量分布, 在图中叠加了相应的负矢势曲线. 可以看出, 电子主要沿着负矢势曲线成弧形分布. 这是因为电离之后电子的动量主要来源于随后激光电场的加速. 随着两脉冲频率比的增加, 电场和负矢势曲线的旁瓣数目增多, 电子分布的圆弧数目也随之逐渐增多. 最终电子动量分布也呈现出(n – 1)重对称性. 值得一提的是, 电子动量分布相对于负矢势的极大值存在一定的偏移, 这已经被先前的研究归因于母核的库仑势对电离电子的影响[40].
图 3 不同频率比时的电子动量分布 (a) 频率比为2; (b) 频率比为3; (c) 频率比为4; (d) 频率比为5Figure3. Electron momentum distributions in the field plane at different frequency ratios of (a) 2, (b) 3, (c) 4, (d) 5.
为了深入理解同向旋转双色圆偏场中原子NSDI的超快动力学及其对两脉冲频率比的依赖, 向后跟踪了NSDI轨道并作了统计分析. 通过跟踪双电离轨迹, 能够确定单电离时间(tSI)、再碰撞时间(tR)和双电离时间(tDI). 将一个电子的能量首次为正的时刻定义为单电离时间, 其中电子的能量由电子的动能、电子与原子核相互作用的势能和电子间的排斥势能的一半所组成. 把第一个电子电离之后, 它跟另一个电子最靠近的时刻定义为再碰撞时间. 在再碰撞时刻两电子之间的距离定义为碰撞距离. 把碰撞之后第二个电子能量为正的时刻定义为双电离时间.
原子中第一个电子电离之后, 首先被激光电场驱动远离母离子, 待激光电场改变方向后, 电离电子再被拉回母核发生再碰撞. 通常把该电子电离到返回再碰撞之间的时间间隔称为返回电子的旅行时间. 图4给出了不同频率比时电子旅行时间的概率分布. 可以看出, 电子的旅行时间主要分布在一个非常狭窄的时间窗内. 当频率比为2时, 旅行时间的峰值处在0.5T （T 为1600 nm激光脉冲的周期）附近. 随着频率比的增加电子的旅行时间逐渐减小. 对于绝大多数的NSDI, 电子的旅行时间都小于一个周期. 把这样的轨道称为短的再碰撞轨道(short recollision trajectory, SRT). 图5给出了4个典型的SRT轨道, 分别对应了4个不同的频率比. 可以看出, 这些轨道都呈环形, 他们的空间范围随频率比的增加而减小, 这是因为随频率比的增加电子的旅行时间减小了.
图 4 不同频率比时电子旅行时间的概率分布Figure4. Distributions of electron traveling time at frequency ratios of 2, 3, 4 and 5.
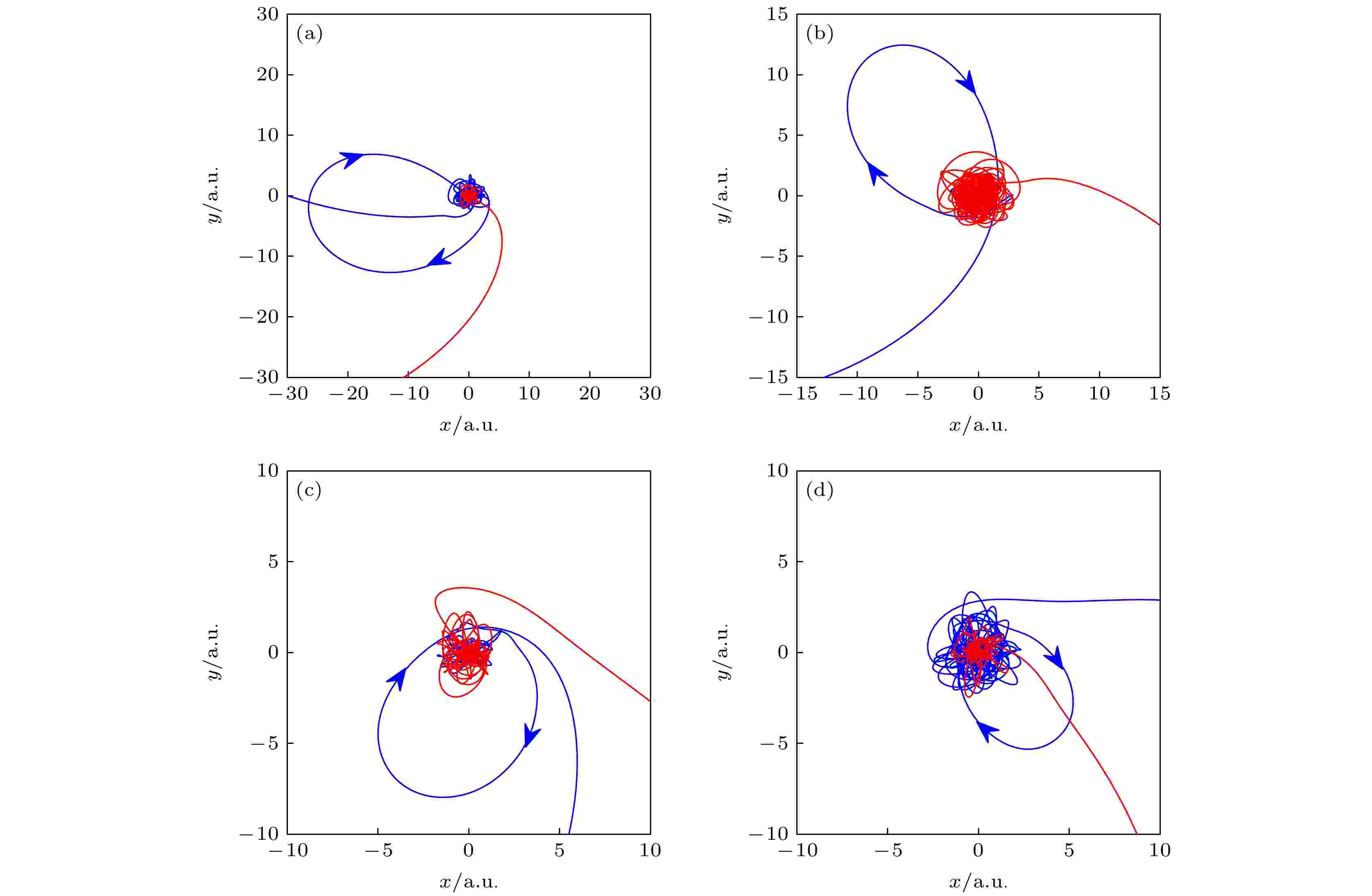图 5 不同频率比时的再碰撞轨道 (a) 频率比为2; (b) 频率比为3; (c) 频率比为4; (d) 频率比为5Figure5. Sample recollision trajectories at different frequency ratios of (a) 2, (b) 3, (c) 4, (d) 5.
从图4可以发现, 当频率比为2和3时, 有少量的旅行时间大于一个周期的轨道, 称之为长的再碰撞轨道(long recllision trajectory, LRT). 且频率比为2时的LRT轨道数目明显多于频率比为3时的LRT轨道. 图6给出了两个典型的LRT轨道. 左列为两电子能量的时间演化, 右列为两电子空间坐标的时间演化. 第一行对应频率比为2, 第二行对应频率比为3. 对比图6和图5可以发现, 对于LRT轨道, 电子电离后将在空间中绕行数圈才会返回与母离子发生再碰撞, 如图6(b)和图6(d)所示. 碰撞过程中两电子之间发生了显著的能量转移, 如图6(a)和图6(c)所示.
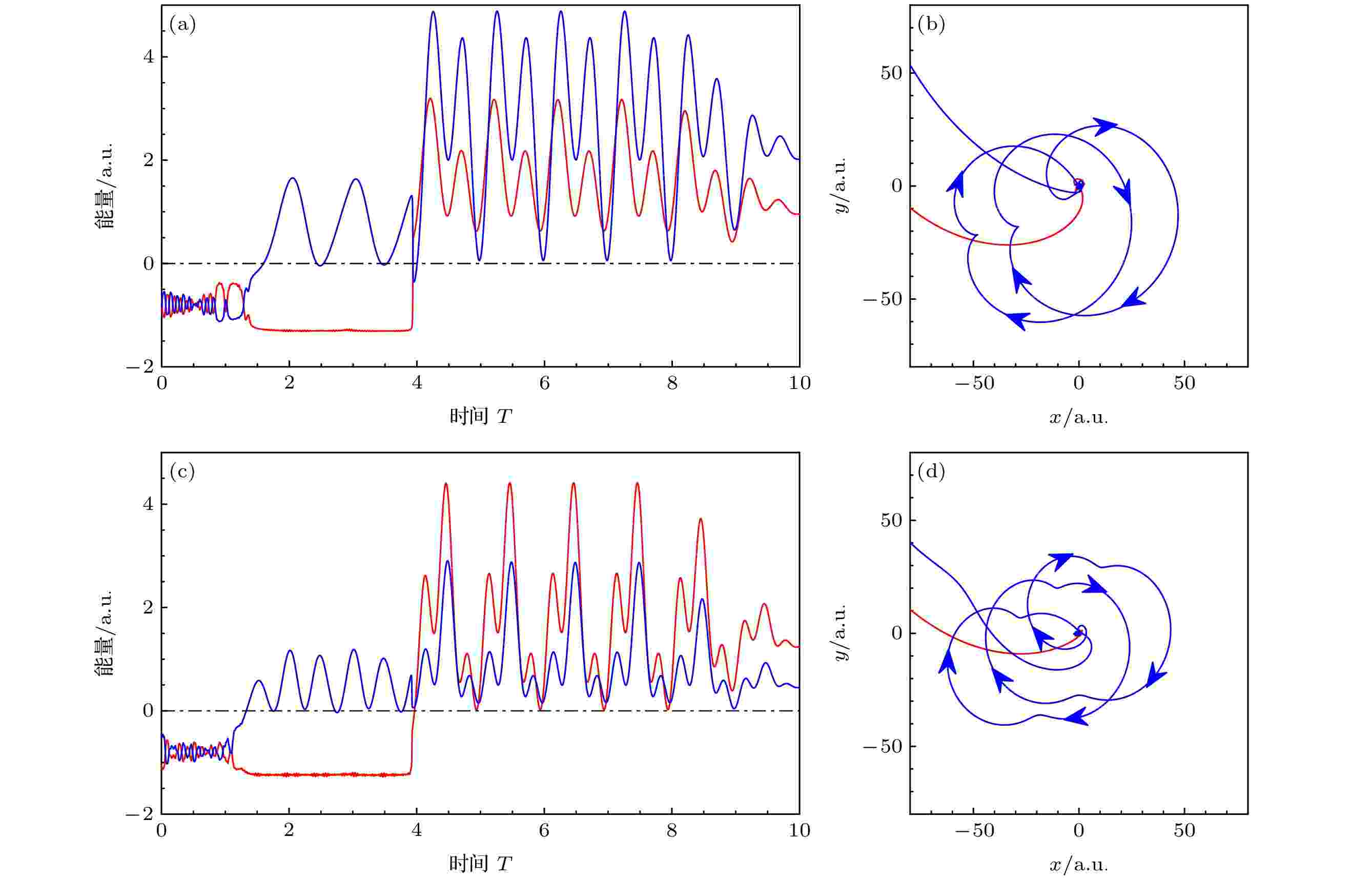图 6 频率比分别为2 ((a), (b))和3 ((c), (d))时的两个长轨道 (a), (c)两电子能量的时间演化; (b), (d)两电子空间坐标演化Figure6. Electron energies ((a), (c)) and positions in the field plane ((b), (d)) versus time for two sample long trajectories. Frequency ratios are 2 ((a), (b)) and 3 ((c), (d)), respectively.
图7给出了双电离与再碰撞之间延迟时间的概率分布. 当频率比为2时, 碰撞后第二个电子迅速电离, 具有很短的时间延迟. 当频率比为3时, 可以看出有相当一部分的电子具有长的时间延迟, 整个分布呈现出一个多峰的分布. 当频率比增加至4和5时, 可以看出大多数电子具有较长的时间延迟. 这里定义延迟时间大于0.18T为RESI事件, 延迟时间小于0.18T为RII事件. 图8给出了不同频率比时RESI和RII机制在NSDI中所占的比例. 除了频率比为2, 其他频率比时, NSDI的主要机制都是RESI. 随着频率比的增加, RESI机制对NSDI的相对贡献从频率比为2时的39%增加至频率比为5时的95%. 图9给出了频率比为2 (左列)和3 (右列)时RII机制(图9(a)和图9(b))和RESI机制(图9(c)和图9(d))对应的电子动量分布. 可以看出, RESI机制产生的光电子几乎都沿着负矢势曲线分布, 而对于RII机制, 有大量的电子偏离负矢势曲线, 电子的分布范围更广. 这是因为RESI机制中通过场致电离的电子初始动量几乎为0, 它的最终动量主要来源于电场的加速, 所以电子动量沿负矢势曲线分布. 而通过RII机制立即电离的电子存在较大的残余动量, 该动量叠加到激光场的加速, 导致电子的末态动量偏离负矢势.
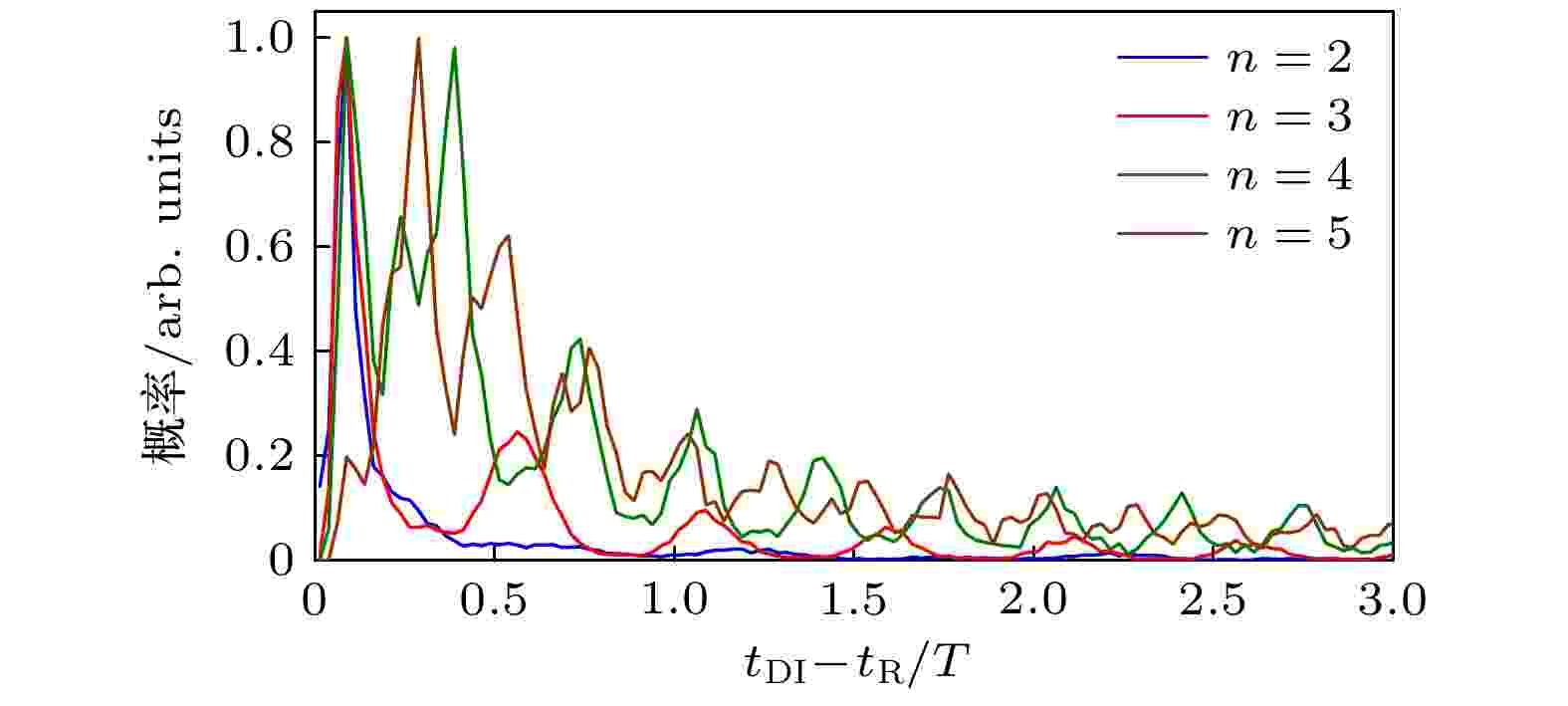图 7 不同频率比时双电离延迟时间的概率分布Figure7. Distributions of the delay time between double ionization and the recollision at frequency rations of 2, 3, 4 and 5.
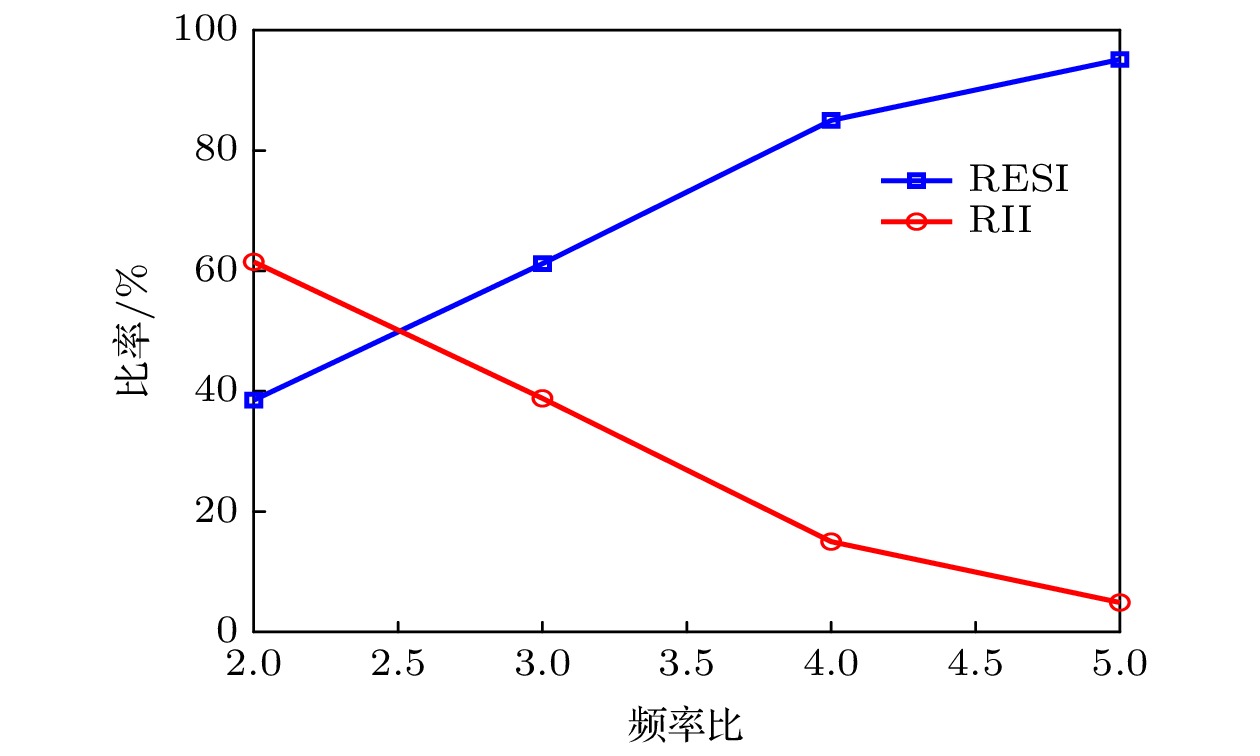图 8 RESI和RII机制在NSDI中所占的比率对频率比的依赖Figure8. Dependence of proportions of RESI and RII mechanism in NSDI on frequency ratio.
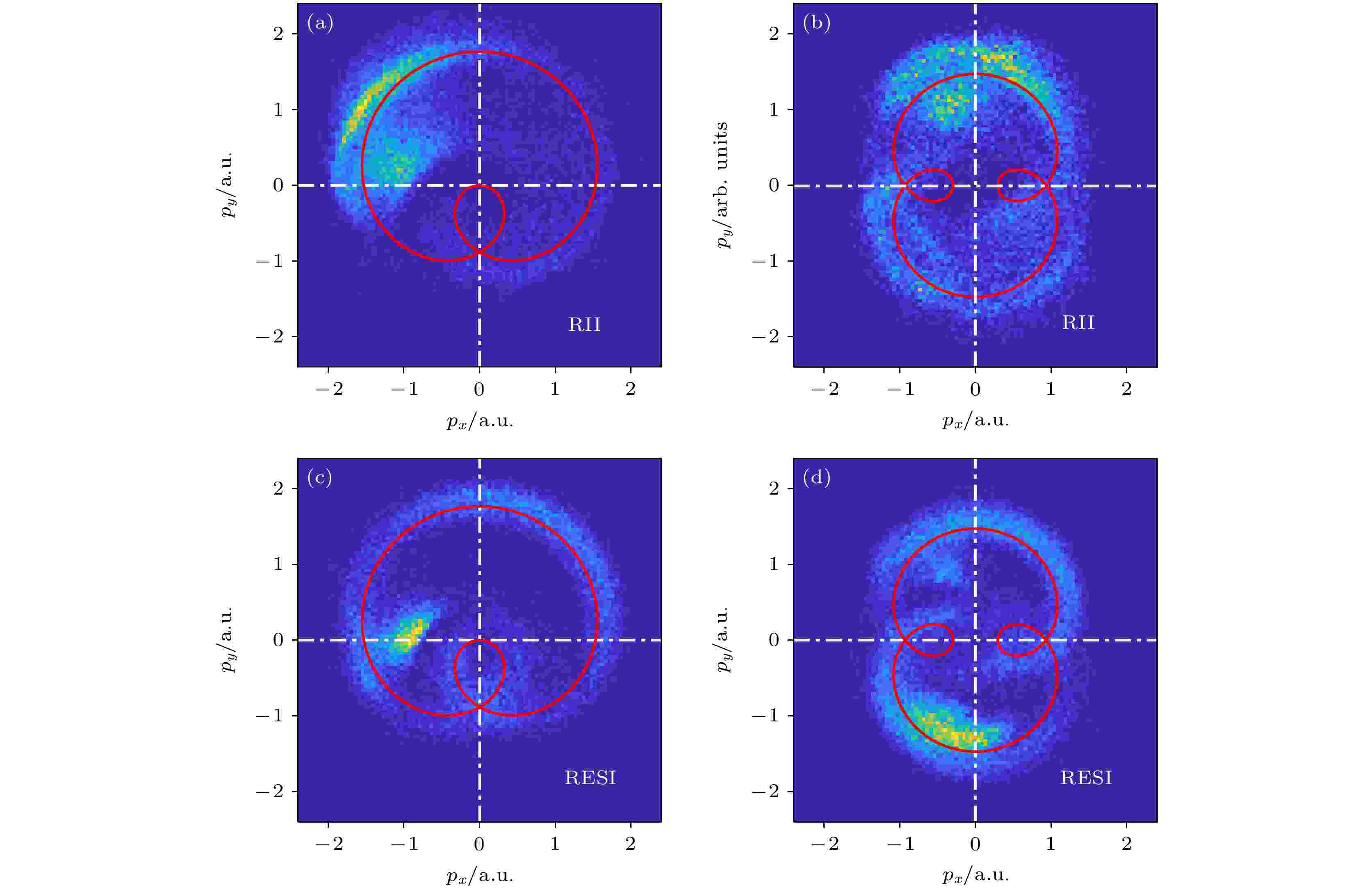图 9 频率比分别为2 ((a), (c)); 3 ((b), (d))时, RII机制((a), (b))和RESI机制((c), (d))对应的电子动量分布Figure9. Electron momentum distributions in the field plane for RII ((a), (b)) and RESI ((c), (d)) mechanisms. Frequency ratios are 2 ((a), (c)) and 3 ((b), (d)), respectively.
为了理解为什么RESI机制的贡献随着频率比的增加而逐渐增大, 分析了返回电子的能量和两电子的碰撞距离. 图10和图11分别给出了不同频率比情况下碰撞能量和碰撞距离的概率分布. 可以看出, 随着频率比的增加返回电子的能量减小, 碰撞距离增大. 对于较大的频率比, 返回电子的能量较低, 很难直接碰撞敲出第二个电子. 同时, 更大的碰撞距离也减弱了两电子之间的能量交换. 这两个因素都不利于RII机制的发生. 所以随着频率比的增加, RESI机制的贡献逐渐增大.
图 10 NSDI事件关于碰撞能量的概率分布Figure10. Distributions of recollision energy at different frequency ratios of 2, 3, 4 and 5.
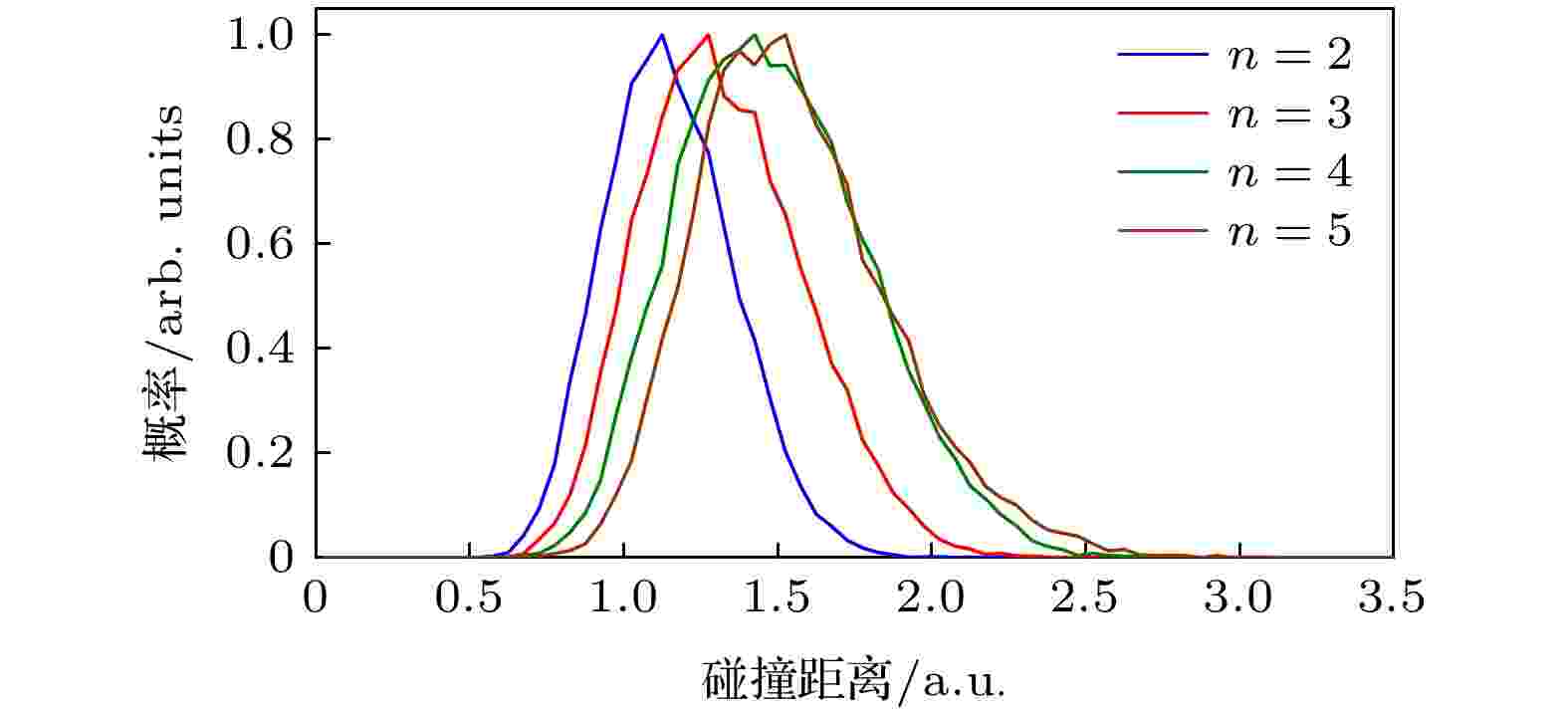图 11 NSDI事件关于碰撞距离的概率分布Figure11. Recollison distance in NSDI at different frequency ratios.
以上的分析显示, 随着频率比的增加, 碰撞能量降低和碰撞距离增加. 这两个因素在一定程度上会降低双电离的概率. 但同时随频率比的增加, 再散射轨道电子的旅行时间和旅行距离显著缩短(见图4和图5), 这极大地减弱了电子的扩散效应, 使得电子返回母离子发生碰撞的概率显著增加, 从而使得双电离概率随频率比的增大而增加.
