摘要: 利用密度矩阵重整化群计算了光学腔中一维无自旋玻色-哈伯德模型的基态. 通过研究超流序、局域密度分布、二阶和三阶关联函数, 发现该系统出现了超越平均场理论的两个奇异超固相. 这两个超固相同时具备对角和非对角长程序, 其中一个展现出包络形式的密度调制振荡, 另一个展现出均匀的密度分布. 另外, 结合光场的超辐射序参量和腔内的平均光子数, 发现奇异超固相与腔光场的涨落存在密切关系. 该工作给出了光学腔内玻色哈伯德模型的超越平均场理论的新物理, 并提供了探索光学腔内光与物质集体物态的完整计算方法.
关键词: 量子相变 /
密度矩阵重整化群 /
光学腔 English Abstract Exotic supersolid phase of one-dimensional Bose-Hubbard model inside an optical cavity Zhou Xiao-Fan 1,2 ,Fan Jing-Tao 1,2 ,Chen Gang 1,2,3 ,Jia Suo-Tang 1,2 1.State Key Laboratory of Quantum Optics, Quantum Optics Devices, Institute of Laser Spectroscopy, Shanxi University, Taiyuan 030006, China Fund Project: Project supported by the National Basic Research Program of China (Grant No. 2017YFA0304203), the National Natural Science Foundation of China (Grant Nos. 11674200, 12074232, 12004230, 11804204), the Fund for Shanxi “1331 Project” Key Subjects Construction, and the Research Project Supported by Shanxi Scholarship Council of China (Grant No. HGKY2019003)Received Date: 22 April 2021Accepted Date: 17 May 2021Available Online: 07 June 2021Published Online: 05 October 2021Abstract: Using a state-of-the-art numerical method density-matrix renormalization-group, we study the ground states of one-dimensional spinless Bose-Hubbard model inside a red-detuned cavity. By calculating the superfluid order, density distribution, second and third-order correlation functions, we find that there exist two novel supersolid phases with diagonal, off-diagonal orders beyond mean-field theory. One has package type density modulation along the lattice axis, another exhibits uniform density distribution. Moreover, by calculating the superradiant order parameter and the number of photon inside the cavity, we find that the novel supersolid phases are highly related to cavity-field fluctuation. Our work gives the physics beyond the mean-field theory of the Bose-Hubbard model inside an optical cavity, and provides the complete approach to fully explore the collective state of light and matter inside an optical cavity.Keywords: quantum phase transition /density-matrix renormalization-group /optical cavity 全文HTML --> --> --> 1.引 言 超冷量子气体为多体相互作用系统的量子模拟提供了独特的环境[1 ] . 将超冷量子气体俘获在光学晶格中可以模拟强关联晶格模型, 其中最典型的模型是玻色-哈伯德模型. 这一模型中存在超流相和莫特绝缘体之间的量子相变[2 -4 ] . 在超冷原子实验中, 原子间具有天然的有限长程相互作用, 它可以通过Feshbach共振技术进行调节[3 ,4 ] . 而凝聚态系统中还存在大量由无限长程相互作用驱动的多体现象, 这为基于超冷原子的量子模拟提出了新的挑战. 幸运的是, 光学腔中的光子可以充当原子间沟通的中继站, 进而诱导出有效的无限长程相互作用[5 -8 ] . 在晶格系统中, 该无限长程相互作用会与原子动能和在位相互作用能竞争, 进而衍生出周期是晶格周期两倍的密度关联, 并驱动奇偶格点分布差异的原子密度波[9 ] . 以上特征使得光学腔内的玻色-哈伯德模型具备更加丰富的基态属性[10 -20 ] .[21 ] . 它也是一个对角序和非对角序(相位相干和空间序)共存的热力学稳态[22 -27 ] . 在平均场理论下, 光学腔中玻色原子的超固相通常出现在光场的超辐射区间, 且晶格的密度分布呈现奇偶振荡[12 -18 ] . 然而, 由于该理论在原理上忽略了物理量的高阶涨落, 故不足以完整描述量子场的密度关联. 特别是当腔光场未发生超辐射时, 腔场涨落可能剧烈增强, 此时平均场理论变得更加不可靠[19 ,20 ] . 因此, 为了更加精确地理解光学腔中玻色原子的超固相, 有必要超越传统的平均场理论, 系统计算原子的局域密度分布、二阶和三阶关联函数.[28 ,29 ] (DMRG)数值计算系统基态的单体超流序、局域密度分布、二阶和三阶关联函数, 探究系统的非对角和对角序. 发现了超越平均场理论的两个奇异超固相, 其中一个展现出包络形式的密度调制振荡, 另一个展现出均匀的密度分布. 另外, 结合光场的超辐射序参量和腔内的平均光子数, 发现奇异超固相与腔光场的涨落存在密切关系.2.模型和序参量 基于最近实现的光学腔实验平台[10 ] , 本文考虑的系统是装载在准一维(1D)背景光晶格中的超冷玻色气与光学腔的耦合, 如图1 所示. 其中光晶格的晶格深度为${V_0}$ , 腔的频率为${\omega _{\rm{c}}}$ . 所有共振频率为ω 的二能级原子不仅与$\hat x$ 方向的腔场耦合, 还被$\hat z$ 方向的泵浦光所驱动. 泵浦光驱动频率和振幅分别为${\omega _{\rm{p}}}$ 和Ω . 为了有效地降低原子发热, 这里只考虑红失谐腔, 即${\varDelta _{\rm{c}}} = {\omega _{\rm{c}}} - {\omega _{\rm{p}}} < 0$ . 在大失谐极限时, 激发态可以被绝热消除. 考虑紧束缚近似后的有效哈密顿量为[30 ] 图 1 左图: 玻色原子沿着腔轴方向$\hat x$ 被俘获在准一维(1D)背景光学晶格中, 费米气被两束圆偏振的横向(沿着$\hat z$ 方向) 抽运激光驱动. 右图: 隧穿系数t , 接触型相互作用${U_{\rm{s}}}$ 和无限长程相互作用${U_{\rm{l}}}$ Figure1. Left: Proposed experimental setup that the bosonic atoms trapped in a quasi-1D optical lattice interact with an optical cavity. Right: Illustration of the competing terms among the hopping t , the contact interaction ${U_{\rm{s}}}$ and the global-range interaction ${U_{\rm{l}}}$ .$\hat b_i^{\dagger} $ 和${\hat b_i}$ 为基态能级的玻色子产生和湮灭算符, 粒子数算符${\hat n_i} = \hat b_i^{\dagger} \hat b_i^{}$ . ${\hat a^{\dagger} }$ 和$\hat a$ 是量子化腔场的产生和湮灭算符. o和e分别是奇偶格点指标. t 为跃迁系数, ${U_{\rm{s}}}$ 是玻色子排斥相互作用强度. $\delta = {M_1}N$ 是腔的色散偏移, 其中${M_0} = \displaystyle \int {\rm{d}}xW_i^*\left( x \right) \cos \left( {{k_0}x} \right) $ $ {W_i}\left( x \right)$ , ${M_1} = \left( {{g^2}/\varDelta } \right)\displaystyle \int {{\rm{d}}xW_i^*\left( x \right){{\cos }^2}\left( {{k_0}x} \right){W_i}\left( x \right)}$ , N 是原子总数, ${W_i}\left( x \right)$ 是局域在格点的瓦尼儿函数, ${k_0}$ 为腔场波矢, g 为腔内单光子耦合常数, $\eta = $ $ g\varOmega /\varDelta$ 是有效的光与原子耦合强度.1 )可以写出光场消灭算符所满足的量子郎之万方程:κ 远大于原子反冲能, 此时可作绝热近似, 即忽略噪声项, 认为光场始终驰豫在稳态[30 ] . 从方程(2 )出发得到光场的稳态形式为[10 ] 3 )引入(1 )式的哈密顿量, 可以得到有效哈密顿量为${U_{\rm{l}}} = - L\hbar {\left| {\eta {M_0}} \right|^2}( {{\varDelta _{\rm{c}}} - \delta } )/\left[ {{{\left( {{\varDelta _{\rm{c}}} - \delta } \right)}^2} + {\kappa ^2}} \right]$ [10 ] , L 是晶格的尺寸. 哈密顿量(4 )中的${U_{\rm{l}}}$ 项清楚地展示了光学腔中以光子为媒介诱导的原子原子之间无限长程相互作用, 它可以通过改变泵浦激光的大小来独立调整. 至此就得到了一个隧穿、在位相互作用和无限长程相互作用共存且竞争的有趣模型, 如图1 所示.$n(k) = \dfrac1L\displaystyle\sum\nolimits_r $ $ {{{\rm{e}}^{{\rm{i}}kr}}G(r)}$ . $n(k = 0)$ 是凝聚系数, 表示占据超流态的玻色子的密度. 如果$G(r)$ 具有长程序, 则$n( k = $ $ 0 ) > 0$ , 此时系统表现出相位相干. 局域密度分布为$\nu \left( k \right) = \dfrac1L\displaystyle\sum\nolimits_j {{{\rm{e}}^{{\rm{i}}kj}}\left\langle {{{\hat n}_j}} \right\rangle }$ . $\nu \left( k \right)$ 的尖峰位置所对应的动量值${\nu _{{\rm{peak}}}}$ 描述的是密度分布的振荡周期. 如果密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ 呈现的是奇偶晶格振荡, 则${\nu _{{\rm{peak}}}} = {\text{π}}$ ; 如果密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ 呈现的是均匀分布, 则${\nu _{{\rm{peak}}}} = 0$ ; 如果密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ 呈现的是包络型的非公度振荡分布, 则$\nu \left( k \right)$ 会出现两个尖峰, 且每个尖峰都满足$0 < {\nu _{{\rm{peak}}}} < {\text{π}}$ . 二阶关联函数(对角序)必须去除掉局域密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ 的贡献, 即$S(k) = \dfrac1L\displaystyle\sum\nolimits_{l, j} {{{\rm{e}}^{{\rm{i}}k\left( {l - j} \right)}}\left\langle {{{\hat n}_l}{{\hat n}_j}} \right\rangle }$ . 当$\left\langle {{{\hat n}_l}{{\hat n}_j}} \right\rangle $ 表现为奇偶振荡, 则$S(k = {\text{π}}) > 0$ , 此时系统存在对角序. 三阶关联函数必须减去来自二阶关联${D^2}\left( {l, j} \right)$ 和局域密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ 的贡献, 它的定义为[31 -35 ] [19 ,20 ] . 事实上, 光学腔中的光子是原子之间的耦合媒介, 它在系统的集体动力学中往往发挥着重要作用. 这里重点考察两个与光子相关的物理量, 第一个是基于平均场理论的超辐射序参量:${\left| {\left\langle {\hat a} \right\rangle } \right|^2} = \left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle $ [36 ] . 在超辐射区间, ${\left| {\left\langle {\hat a} \right\rangle } \right|^2} > 0$ , 腔场涨落较小, 平均场理论一般能较好描述系统的动力学性质. 而对于非超辐射区间, 超辐射序参量为零, 即${\left| {\left\langle {\hat a} \right\rangle } \right|^2} = 0$ , 此时腔场涨落可能会对系统状态有较大影响[36 ] .L 最大为96, DMRG最大态数为200, 扫描次数为30, 此时的截断误差最大为${10^{ - 8}}$ . 令$t = 1$ 作为能量单位.3.量子多体相 首先, 将一个较大的无限长程相互作用(例如${U_{\rm{l}}} = 6$ )引入到${U_{\rm{s}}} = 10$ 的玻色-哈伯德模型中. DMRG数值结果显示, 超流序$G(r)$ 随着格点间隔r 的增大呈现幂次衰减(幂率值为0.7)且奇偶振荡, 此时$n(k = 0) > 0$ , 如图2(a1) 所示. 这说明此时体系存在相位相干, 即存在非对角长程序. 密度分布$\left\langle {{{\hat n}_i}} \right\rangle $ 呈现奇偶振荡, 此时${\nu _{{\rm{peak}}}} = {\text{π}}$ , 如图2(a2) 所示. 消除了密度分布$\left\langle {{{\hat n}_i}} \right\rangle $ 的贡献, 二阶关联${D^2}(l, j)$ 接近0, 如图2(a3) 所示. 二阶关联的贡献全部来自奇偶振荡的密度分布$\left\langle {{{\hat n}_i}} \right\rangle $ . 这一参数下系统对应的基态与平均场近似理论的结果一致. 我们又计算了这一参数下的三阶关联函数${D^3}(i, l, j)$ . 消除了密度分布$\left\langle {{{\hat n}_i}} \right\rangle $ 和二阶关联${D^2}(l, j)$ 的贡献, 三阶关联${D^3}(i, l, j)$ 接近0, 如图2(a4) 所示. 本文将这一传统的超固相称为超固0相.图 2 (a1), (b1), (c1)超流序$G(r)$ 和插图$n(k)$ ; (a2), (b2), (c2)密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ ; (a3), (b3), (c3)二阶关联${D^2}(l, j)$ ; (a4), (b4), (c4)三阶关联${D^3}\left( {i, l, j} \right)$ . (a1)—(a3) 超固0相, 相互作用参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 6$ ; (b1)—(b3) 超固1相, 相互作用参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 4.4$ ; (c1)—(c3) 超固2相, 相互作用参数${U_{\rm{s}}} = 2$ 和${U_{\rm{l}}} = 4.4$ . 所有图中, 共有参数$L = 96$ , $\rho = 0.4375$ Figure2. (a1), (b1), (c1) Superfluid order $G(r)$ and $n(k)$ ; (a2), (b2), (c2) density profile $\left\langle {{{\hat n}_j}} \right\rangle $ ; (a3), (b3), (c3) two order correlation ${D^2}\left( {l, j} \right)$ ; (a4), (b4), (c4) three order correlation ${D^3}\left( {i, l, j} \right)$ for $i = j$ of (a1)–(a3) supersolid 0 phase with ${U_{\rm{s}}} = 10$ and ${U_{\rm{l}}} = 6$ , (b1)–(b3) supersolid 1 phase with ${U_{\rm{s}}} = 10$ and ${U_{\rm{l}}} = 4.4$ , and (c1)–(c3) supersolid 2 phase with ${U_{\rm{s}}} = 2$ and ${U_{\rm{l}}} = 4.4$ . In all subfigure, we have $L = 96$ and $\rho = 0.4375$ .${U_{\rm{s}}} = 10$ 的玻色-哈伯德模型中引入一个大小适中的无限长程相互作用(以${U_{\rm{l}}} = 4.4$ 为例). DMRG数值结果显示, 超流序$G(r)$ 随着格点间隔r 的增大幂率衰减(幂率值为0.56), 且此时$n(k = 0) > 0$ , 如图2(b1) 所示. 密度分布$\left\langle {{{\hat n}_i}} \right\rangle $ 呈现包络型振荡, 此时$0{{ < }}{\nu _{{\rm{peak}}}} < {\text{π}}$ , 如图2(b2) 所示. 二阶关联${D^2}(l, j)$ 呈现奇偶振荡且不随格点间距增大而衰减, 如图2(b3) 所示. 二阶关联的贡献全部来自关联效应, 这一数值结果完全超越了平均场理论. 三阶关联函数${D^3}(i, l, j)$ 呈现奇偶振荡且不随格点间距增大而衰减, 如图2(b4) 所示. 这一包络型分布的奇偶格点原子总数相等, 即$\left\langle { \displaystyle\sum\nolimits_{\rm{e}} {{{\hat n}_{\rm{e}}}} - \sum\nolimits_{\rm{o}} {{{\hat n}_{\rm{o}}}} } \right\rangle = 0$ . 然而, 无限长程相互作用能$\left\langle {{{\Big(\displaystyle\sum\nolimits_{\rm{e}} {{{\hat n}_{\rm{e}}}} - \sum\nolimits_{\rm{o}} {{{\hat n}_{\rm{o}}}} \Big)}^2}} \right\rangle > 0$ . 这两个值之间的差异主要源自于量子涨落. 本文中, 具有$0{{ < }}{\nu _{{\rm{peak}}}} < {\text{π}}$ 特征的超固相被称为超固1相.${U_{\rm{s}}} = 2$ 为例), 但无限长程相互作用不变, 仍为${U_{\rm{l}}}{{ = }}4.4$ . $G(r)$ 随着格点间隔r 的增大幂率衰减(幂率值为0.24), 且此时$n(k = 0) > 0$ , 如图2(c1) 所示. 此时体系存在相位相干, 即存在非对角长程序. 这一参数对应的基态同样为超固相, 但是这一超固相不同于超固0相和超固1相. 密度分布$\left\langle {{{\hat n}_i}} \right\rangle $ 是均匀的, 此时${\nu _{{\rm{peak}}}} = 0$ , 如图2(c2) 所示. 二阶关联${D^2}(l, j)$ 和三阶关联${D^3}(i, l, j)$ 呈现奇偶振荡且不随格点间距增大而衰减, 如图2(b3) 和图2(b4) 所示. 本文中, 特征为${\nu _{{\rm{peak}}}} = 0$ 的超固相被称超固2相.$G(r)$ 的存在, 计算了多个尺寸的数据, 并做了有限尺寸分析, 如图3 所示. 在有限尺寸下, 超固1相和超固2相的超流序$G(r)$ 随着距离呈幂率衰减, 将幂率做有限尺寸分析发现, 在热力学极限下($L \to \infty $ )幂率在$\left( {0, 1} \right)$ 区间, 如图3(a1) 和图3(b1) 所示. 对$n(k = 0){{/}}L$ 做有限尺寸分析可以发现, 在热力学极限下($L \to \infty $ )超固1相和超固2相的$n(k = 0){{/}}L > 0$ , 如图3(a2) 和图3(b2) 所示. 综上可得, 超固1相和超固2相的超流序是固然存在的, 不因尺寸变化而消失.图 3 (a1), (b1)不同尺寸下的超流序$G(r)$ , 插图为冥率的有限尺寸分析; (a2), (b2) $n(k = 0){{/}}L$ 的有限尺寸分析. (a1), (a2)超固1相, 参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 4.4$ ; (b1), (b2) 超固2相, 参数${U_{\rm{s}}} = 2$ 和${U_{\rm{l}}} = 4.4$ . 所有图中, 共有参数$\rho = 0.4375$ Figure3. (a1), (b1) Superfluid order $G(r)$ of several lattice length. The inset is the finite-size scaling of the decay rate. (a2), (b2) Finite-size scaling of $n(k = 0){{/}}L$ . (a1), (a2) Supersolid 1 phase with ${U_{\rm{s}}} = 10$ and ${U_{\rm{l}}} = 4.4$ . (b1), (b2) Supersolid 2 phase with ${U_{\rm{s}}} = 2$ and ${U_{\rm{l}}} = 4.4$ . In all subfigure, we have $\rho = 0.4375$ .图4(a1) —(a3) 所示. 且不同尺寸的${\nu _{{\rm{peak}}}}$ 相同, 通过有限尺寸分析可以发现, 热力学极限下($L \to $ $ \infty$ )的${\nu _{{\rm{peak}}}}$ 与有限尺寸的${\nu _{{\rm{peak}}}}$ 相等, 如图4(a4) 所示. 超固2相在不同尺寸时的密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ 都是均匀的, 如图4(b1) —(b3) 所示. 不同尺寸包括热力学极限下($L \to \infty $ )的${\nu _{{\rm{peak}}}} \equiv 0$ , 如图4(b4) 所示.图 4 (a1)—(a3)和(b1)—(b3)密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ ; (a4), (b4) ${\nu _{{\rm{peak}}}}$ 的有限尺寸分析. (a1)—(a4) 超固1相, 参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 4.4$ ; (b) 超固2相, 参数${U_{\rm{s}}} = 2$ 和${U_{\rm{l}}} = 4.4$ . (a1), (b1) $L = 80$ ; (a2), (b2) $L = 64$ ; (a3), (b3) $L = 48$ . 所有图中, 共有参数$\rho = 0.4375$ Figure4. (a1) –(a3) and (b1) –(b3) the density profile $\left\langle {{{\hat n}_j}} \right\rangle $ ; (a4), (b4) the finite-size scaling of the ${\nu _{{\rm{peak}}}}$ . (a1)–(a4) Supersolid 1 phase with ${U_{\rm{s}}} = 10$ and ${U_{\rm{l}}} = 4.4$ ; (b1)–(b4) supersolid 2 phase with ${U_{\rm{s}}} = 2$ and ${U_{\rm{l}}} = 4.4$ . (a1), (b1) $L = 80$ ; (a2), (b2) $L = 64$ ; (a3), (b3) $L = 48$ . In all subfigure, we have $\rho = 0.4375$ .$n(k = 0)$ 和$S(k = {\text{π}})$ 的值, 即可辨别超流、莫特绝缘体、电荷密度波和超固相. 但是, 需要使用${\nu _{{\rm{peak}}}}$ 来区分超固0相、超固1相和超固2相, 如表1 所列.序/相简写 超流SF 莫特绝缘体MI 电荷密度波CDW 超固0相SS0 超固1相SS1 超固2相SS2 $n~(k = 0)$ > 0 0 0 > 0 > 0 > 0 $S~(k = {\text{π} })$ 0 0 > 0 > 0 > 0 > 0 ${\nu _{{\rm{peak}}}}$ 0 0 π π $(0, {\text{π}})$ 0
表1 量子相对应的序参量Table1. Corresponding orders of the phases.${U_{\rm{s}}} = 10$ 和填充因子$\rho = 0.4375$ , 将无限长程相互作用强度${U_{\rm{l}}}$ 从0不断增大. 这一过程中$n(k = 0) > 0$ . 当$0 < {U_{\rm{l}}} < 3.3$ 时, $S(k = {\text{π}}) = 0$ 和${\nu _{{\rm{peak}}}} = 0$ , 对应的量子相为超流; 当$3.3 < {U_{\rm{l}}} < $ $ 4.6$ 时, $S(k = {\text{π}}) > 0$ 和${\nu _{{\rm{peak}}}} \in (0, {\text{π}})$ , 对应的量子相为超固1相; 当${U_{\rm{l}}} > 4.6$ 时, $S(k = {\text{π}}) > 0$ 和${\nu _{{\rm{peak}}}} = {\text{π}}$ 对应的量子相为超固0相, 如图5(a) 所示. 基态从超流相变为超固1相, 最终又相变为超固0相, 临界点为$U_{\rm{l}}^{\rm{c}} = 3.3$ 和4.6. 超辐射相变同样发生在无限长程相互作用${U_{\rm{l}}}$ 较大时, 如图5(b) 所示. 超固0相是超辐射驱动的, 在此区域中DMRG的结果显示${\left| {\left\langle {\hat a} \right\rangle } \right|^2} = \left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle > 0$ . 然而, 超固1相不是超辐射驱动, 是腔光场涨落驱动的. 此时${\left| {\left\langle {\hat a} \right\rangle } \right|^2} = 0$ 且${\left| {\left\langle {\hat a} \right\rangle } \right|^2} \ne \left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle $ , 如图5(b) 所示.图 5 $S(k = {\text{π}})$ (黑色实线)和 ${\nu _{{\rm{peak}}}}$ (蓝色方块) (a) 关于${U_{\rm{l}}}$ 的变化, 固定${U_{\rm{s}}} = 10$ ; (c) 关于${U_{\rm{s}}}$ 的变化, 固定${U_{\rm{l}}} = 4.4$ . 平均光子数${\left| {\left\langle {\hat a} \right\rangle } \right|^2}$ 和腔中的光子数$\left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle $ 关于 (b) 关于${U_{\rm{l}}}$ 的变化, 固定${U_{\rm{s}}} = 10$ ; (d) 关于${U_{\rm{s}}}$ 的变化, 固定${U_{\rm{l}}} = 4.4$ . 所有图中, 共有参数$L = 96$ 和$\rho = 0.4375$ . SF表示超流, MI表示莫特绝缘体, CDW表示电荷密度波, SS0 表示超固0相, SS1 表示超固1相, SS2 表示超固2相Figure5. The $S(k = {\text{π}})$ (black solid line) and ${\nu _{{\rm{peak}}}}$ (blue square) as function of (a) ${U_{\rm{l}}}$ with ${U_{\rm{s}}} = 10$ , and (c) ${U_{\rm{s}}}$ with ${U_{\rm{l}}} = 4.4$ . The number of cavity photons $\left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle $ and mean cavity-field ${\left| {\left\langle {\hat a} \right\rangle } \right|^2}$ as a function of (b) ${U_{\rm{l}}}$ with ${U_{\rm{s}}} = 10$ , (d) ${U_{\rm{s}}}$ with ${U_{\rm{l}}} = 4.4$ . In all subfigure, we have $L = 96$ and $\rho = 0.4375$ . SF denotes superfluid, MI denotes Mott insulator, CDW denotes charge density wave, SS0 denotes supersolid 0, SS1 denotes supersolid 1, SS2 denotes supersolid 2.${U_{\rm{l}}} = 4.4$ 和填充因子$\rho = 0.4375$ , 将在位相互作用强度${U_{\rm{s}}}$ 从0不断增大. 这一过程中$n(k = 0) > 0$ 和$S(k = {\text{π}}) > 0$ . 当$0 < {U_{\rm{s}}} < 5.5$ 时${\nu _{{\rm{peak}}}} = 0$ , 对应的量子相为超固2相; 当$5.5 < {U_{\rm{s}}} < 11.5$ 时${\nu _{{\rm{peak}}}} \in (0, {\text{π}})$ , 对应的量子相为超固1相; 当${U_{\rm{s}}} > 11.5$ 时${\nu _{{\rm{peak}}}} = {\text{π}}$ , 对应的量子相为超固0相, 如图5(c) 所示. 我们同样计算了这一过程的超辐射序参量和光子数, 发现超固1相和超固2相这两个相的${\left| {\left\langle {\hat a} \right\rangle } \right|^2} = 0$ 且${\left| {\left\langle {\hat a} \right\rangle } \right|^2} \ne \left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle $ , 如图5(d) 所示. 综上, 可以得出结论, 超固1相和超固2相是腔光场涨落驱动的.图6 所示. 图6(a) —(c) 给出了${U_{\rm{l}}}$ -ρ 平面的相图, 其中(a) ${U_{\rm{s}}} = 0$ , (b) ${U_{\rm{s}}} = 5$ 和(c) ${U_{\rm{s}}} = 10$ . 当无在位相互作用和无限长程相互作用时, 体系基态在任何填充率ρ 下都是超流. 当引入无限长程相互作用${U_{\rm{l}}}$ 后体系变为超固2相, 继续增强${U_{\rm{l}}}$ 体系变为超固0相, 如图6(a) 所示. 当${U_{\rm{s}}} = 5$ 时, 无限长程相互作用${U_{\rm{l}}}$ 驱动体系产生超固0相、超固1相和超固2相. 只有$\rho = 0.5$ 和1时, 体系会出现莫特绝缘体和电荷密度波, 如图6(b) 所示. 当${U_{\rm{s}}} = 10$ 时, 超固2相被压缩而消失, 相图中仍然有超流、莫特绝缘体、电荷密度波、超固0相和超固1相, 如图6(c) 所示. 为了更直观地展示在位相互作用和无限长程相互作用的竞争, 给出了${U_{\rm{l}}}$ -${U_{\rm{s}}}$ 平面的相图, 如图6(d) 所示. 无限长程相互作用${U_{\rm{l}}}$ 驱动产生超固相, ${U_{\rm{l}}}$ 很大时体系为超固0相. 当无限长程相互作用${U_{\rm{l}}} = 4$ 左右时, 在位相互作用${U_{\rm{s}}}$ 驱动超固2相变为超固1相.图 6 (a)—(c) ${U_{\rm{l}}}$ -ρ 平面的相图 (a) ${U_{\rm{s}}} = 0$ ; (b) ${U_{\rm{s}}} = 5$ ; (c) ${U_{\rm{s}}} = 10$ . (d) ${U_{\rm{l}}}$ -${U_{\rm{s}}}$ 平面的相图, 参数$\rho = 0.4375$ . 所有图中, 共有参数$L = 96$ . SF表示超流, MI表示莫特绝缘体, CDW表示电荷密度波, SS0 表示超固0相, SS1 表示超固1相, SS2 表示超固2相Figure6. (a)–(c) Phase-diagram between ${U_{\rm{l}}}$ and ρ with (a) ${U_{\rm{s}}} = 0$ , (b) ${U_{\rm{s}}} = 5$ and (c) ${U_{\rm{s}}} = 10$ . (d) Phase-diagram between ${U_{\rm{l}}}$ and ${U_{\rm{s}}}$ , with filling $\rho = 0.4375$ . In all subfigure, we have $L = 96$ . SF denotes superfluid, MI denotes Mott insulator, CDW denotes charge density wave, SS0 denotes supersolid 0, SS1 denotes supersolid 1, SS2 denotes supersolid 2.4.总 结 上述量子相在目前的实验平台上都是可以观测的, 动量分布可以通过时间飞行探测, 结构因子可以通过布拉格散射探测[37 ,38 ] , 密度分布可以通过单格点分辨进行探测[39 ] . 





 图 1 左图: 玻色原子沿着腔轴方向
图 1 左图: 玻色原子沿着腔轴方向



























































































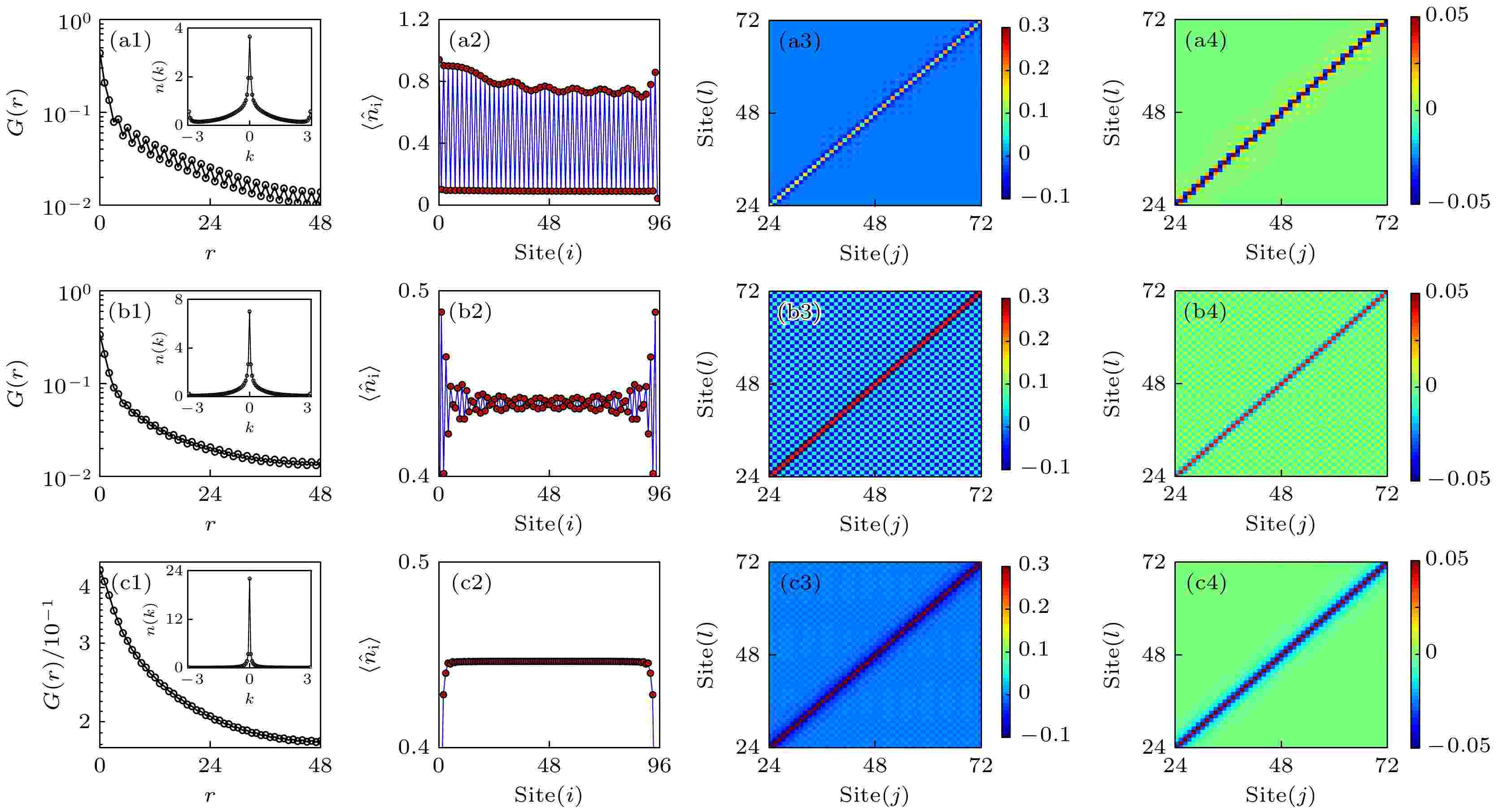 图 2 (a1), (b1), (c1)超流序
图 2 (a1), (b1), (c1)超流序





































































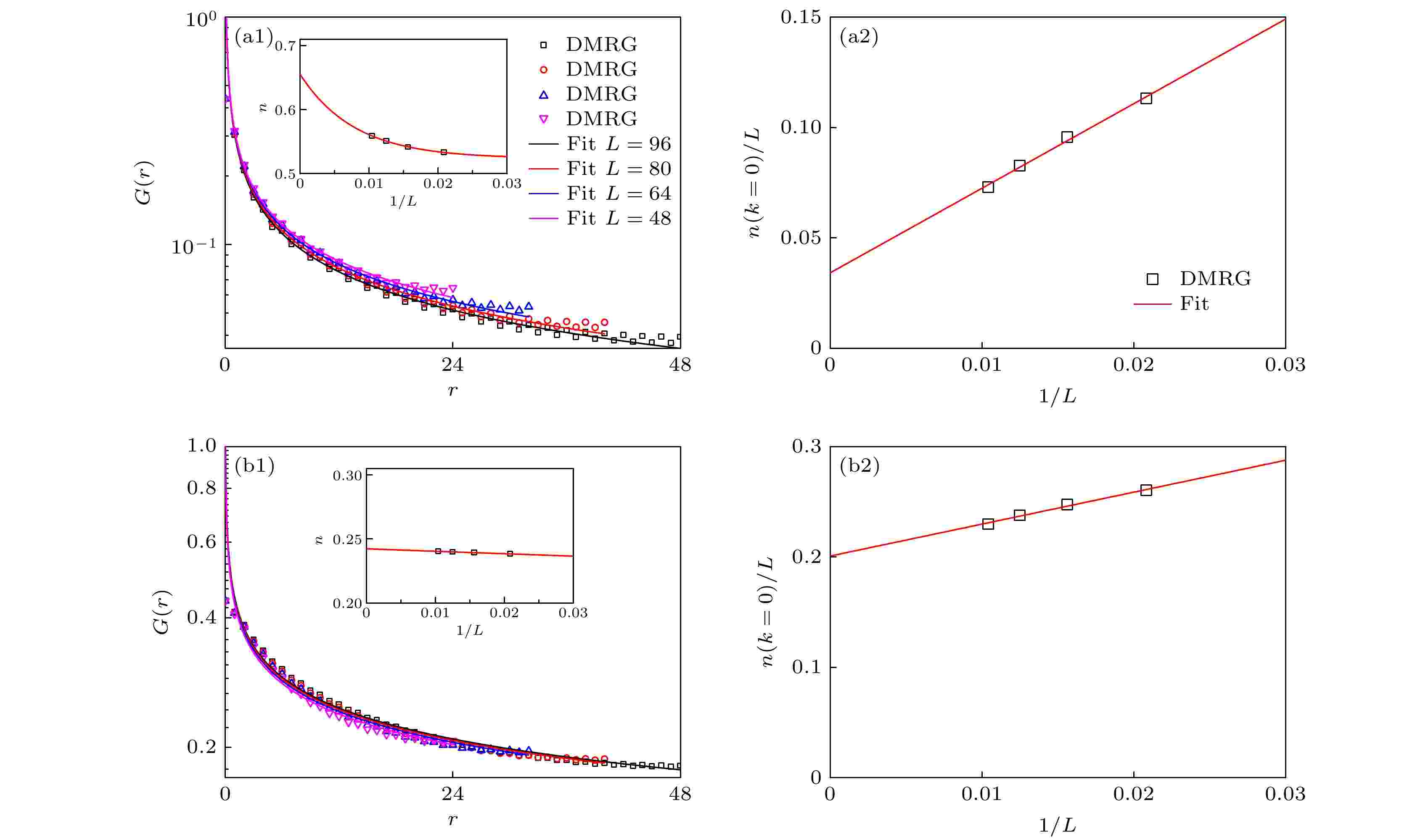 图 3 (a1), (b1)不同尺寸下的超流序
图 3 (a1), (b1)不同尺寸下的超流序































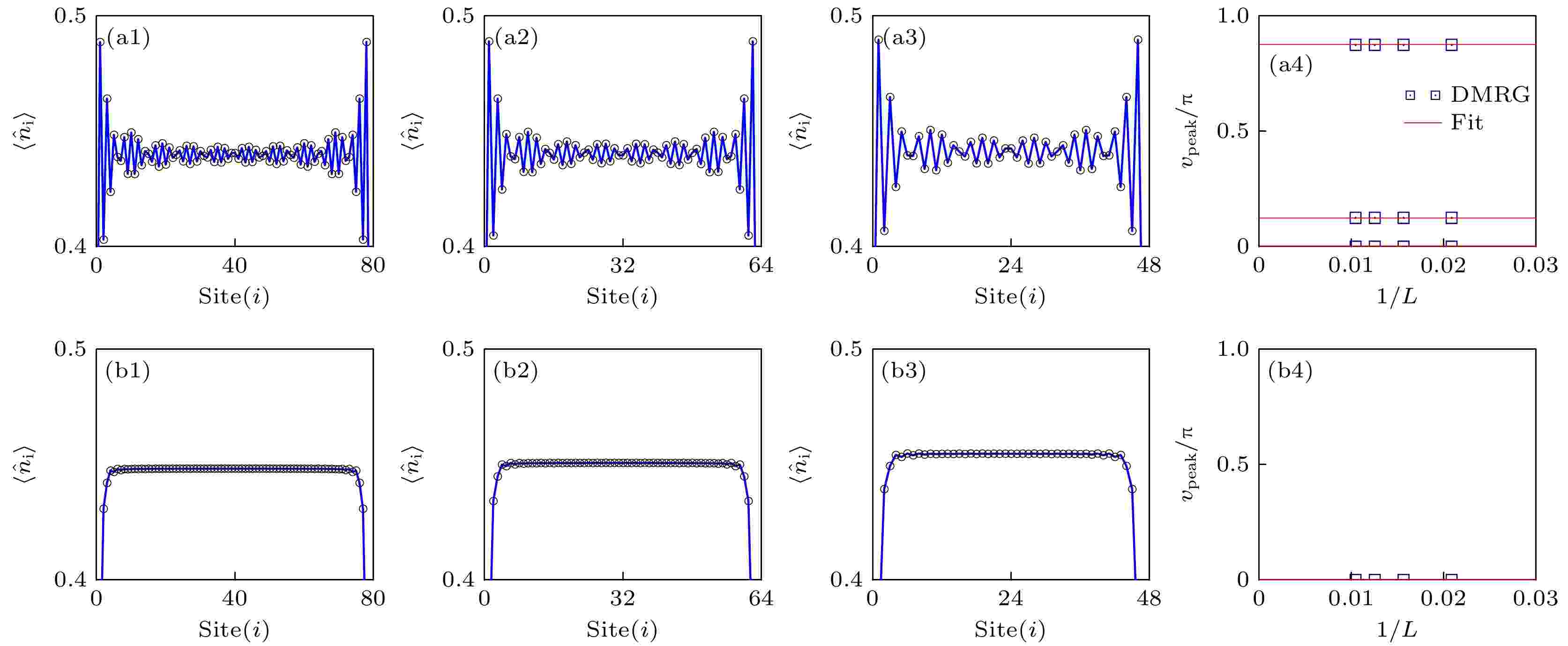 图 4 (a1)—(a3)和(b1)—(b3)密度分布
图 4 (a1)—(a3)和(b1)—(b3)密度分布

















































 图 5
图 5 
























































































































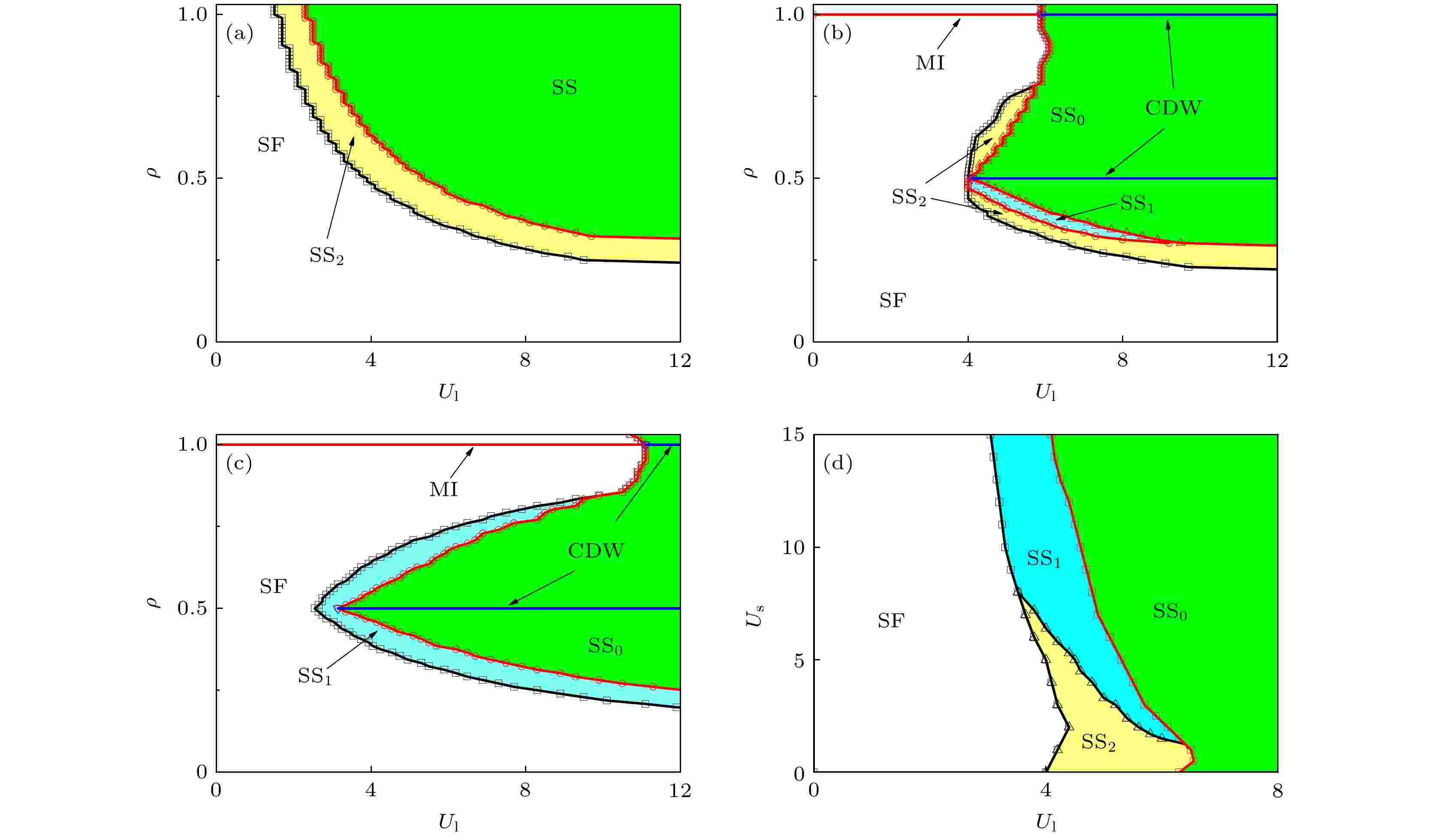 图 6 (a)—(c)
图 6 (a)—(c) 



















