摘要:钙钛矿锰氧化物具备磁热效应高、性能稳定可控、成本低廉等显著优点, 是适用于室温磁制冷领域的优质候选工质材料之一. 但该体系内部电磁学性质复杂, 特别是关于铁磁相互作用机制和磁相变性质等关键科学问题仍然有待深入探索. 分析磁相变临界行为有利于揭示磁性材料内部的铁磁相互作用距离和机制等重要信息. 本文简要介绍了钙钛矿锰氧化物相关理论背景以及各种磁相变临界行为分析方法, 随后归纳了近年来多种钙钛矿锰氧化物的磁相变临界行为研究, 系统对比了不同带宽典型锰氧化物在单晶和多晶形态下的磁相变临界行为, 讨论了A/B位掺杂不同元素以及不同制备工艺条件对其临界参数的影响, 对其中渡越于一级和二级相变的La-Ca-Mn-O体系在不同磁场范围下的临界参数演化进行了讨论. 最后对处于磁相变三重临界点附近的部分锰氧化物材料的磁热效应研究进行了总结和展望.
关键词: 钙钛矿锰氧化物/
磁相变临界行为/
磁热效应

English Abstract

全文HTML

--> --> -->

基于磁热效应的室温磁制冷技术因具备高效率、低能耗、零排放等显著优势, 已成为最有望取代传统气体压缩制冷方式的新型绿色制冷技术之一. 随着近几十年来该领域的快速发展, 目前已探索出许多适用于室温磁制冷领域的工质材料, 其中部分优质候选材料已用于室温磁制冷样机并进入商品化试验阶段. 为了进一步加快室温磁制冷技术的商品化进程, 关于核心材料的磁热性能和磁相变物理特性的研究仍是目前最为关键的环节. 目前除了基于传统二级磁相变的稀土Gd及其合金以外, 最引人关注的仍是具备巨磁热效应的一级磁相变材料, 如Gd-Si-Ge^[1], La(Fe, Si)₁₃^[2], Mn-Fe-P-As^[3], Ni-Mn基哈斯勒合金^[4,5], 以及空穴掺杂型稀土钙钛矿锰氧化物等^[6,7]. 其中稀土锰氧化物凭借其低场下具有较大的磁熵变、化学稳定性好、居里温度可调控、成本低等优点成为最近十几年来备受关注的热点材料之一. 由于该体系内部自旋、晶格、轨道和电荷自由度之间强烈的耦合关联作用而显示出十分丰富的电磁学性质, 在比如巨磁阻和室温磁制冷等关键领域具备较大的应用前景.
在磁制冷研究领域中, 普遍认为一级磁相变是产生巨磁热效应的关键, 但一级磁相变往往伴随着磁滞热滞较大、制冷温区较窄、相对制冷能力较小等问题, 而二级磁相变所对应的最大磁熵变仍然过低而难以实用化. Law等^[8]指出, 理想的磁制冷材料可能介于一级和二级磁相变之间的临界状态. 关于一级相变磁热效应材料的相变调控研究一直以来都是磁制冷领域的研究重点, 如La(Fe, Si)₁₃体系、Ni-Mn基哈斯勒合金等具备一级磁晶耦合相变的磁热效应材料, 通过间隙原子掺杂^[9]或引入应力场^[10,11]等方式能够调控其相变性质, 抑制热磁滞现象, 优化制冷温区和相对制冷能力等重要指标. 而典型的空穴掺杂型钙钛矿锰氧化物材料(如La-Ca-Mn-O体系等)本身同时存在一级和二级两种磁相变模式, 涉及到双交换、超交换相互作用模型、Jahn-Teller极化子局域化、电荷轨道有序以及磁性相分离等物理模型综合作用, 其内部铁磁相互作用以及磁相变机制仍然比较模糊. 因此锰氧化物体系化合物无论是在磁相变理论研究领域还是室温磁制冷应用研究领域都有深入挖掘的空间.
磁相变临界行为分析是探索复杂体系磁性材料内部铁磁相互作用机制的关键技术手段之一. 近年来已发表了许多针对钙钛矿锰氧化物磁相变临界行为的研究工作, 特别是关于从一级相变到二级相变渡越过程(crossover)及三重临界点(tricritical point)附近的磁热效应和磁熵变标度律等问题十分引人关注^[8,12-14]. 该方向的研究工作对于深入理解磁制冷材料的相变性质以及磁性相互作用机制具备一定的科学意义, 有助于进一步提高室温磁制冷及相关领域的实用化前景.

理想的钙钛矿锰氧化物为如图1所示ABO₃型立方结构, 其中三价稀土离子(La³⁺, Pr³⁺等)或掺杂二价碱土金属离子(Ca²⁺, Sr²⁺, Ba²⁺等)占据A位于立方顶角, 而锰离子(Mn³⁺, Mn⁴⁺)或掺杂的其他过渡族金属(Fe, Co, Ni, Cr等)离子则占据B位于立方体心. 临近的6个氧离子O^2–占据立方面心, 且与B位构成配位八面体. A位二价碱土金属离子的掺杂量等于B位四价离子的含量, 可根据碱土金属离子的掺杂量分为空穴掺杂型、电子掺杂型和半掺杂型等. 对于锰离子(Mn³⁺或Mn⁴⁺)而言, 在晶体场中其3d轨道分裂的二重简并轨道e_g中将有一个巡游电子(Mn³⁺)或空穴(Mn⁴⁺), 而其余的3个电子占据较低能量的三重简并轨道t_2g且自旋一致. 相邻的Mn离子形成Mn—O—Mn键并通过双交换或超交换相互作用呈现铁磁或反铁磁性. 由于晶格中A位或B位离子半径的差异, 理想的立方晶格通常畸变为正交对称型或菱面体对称型.
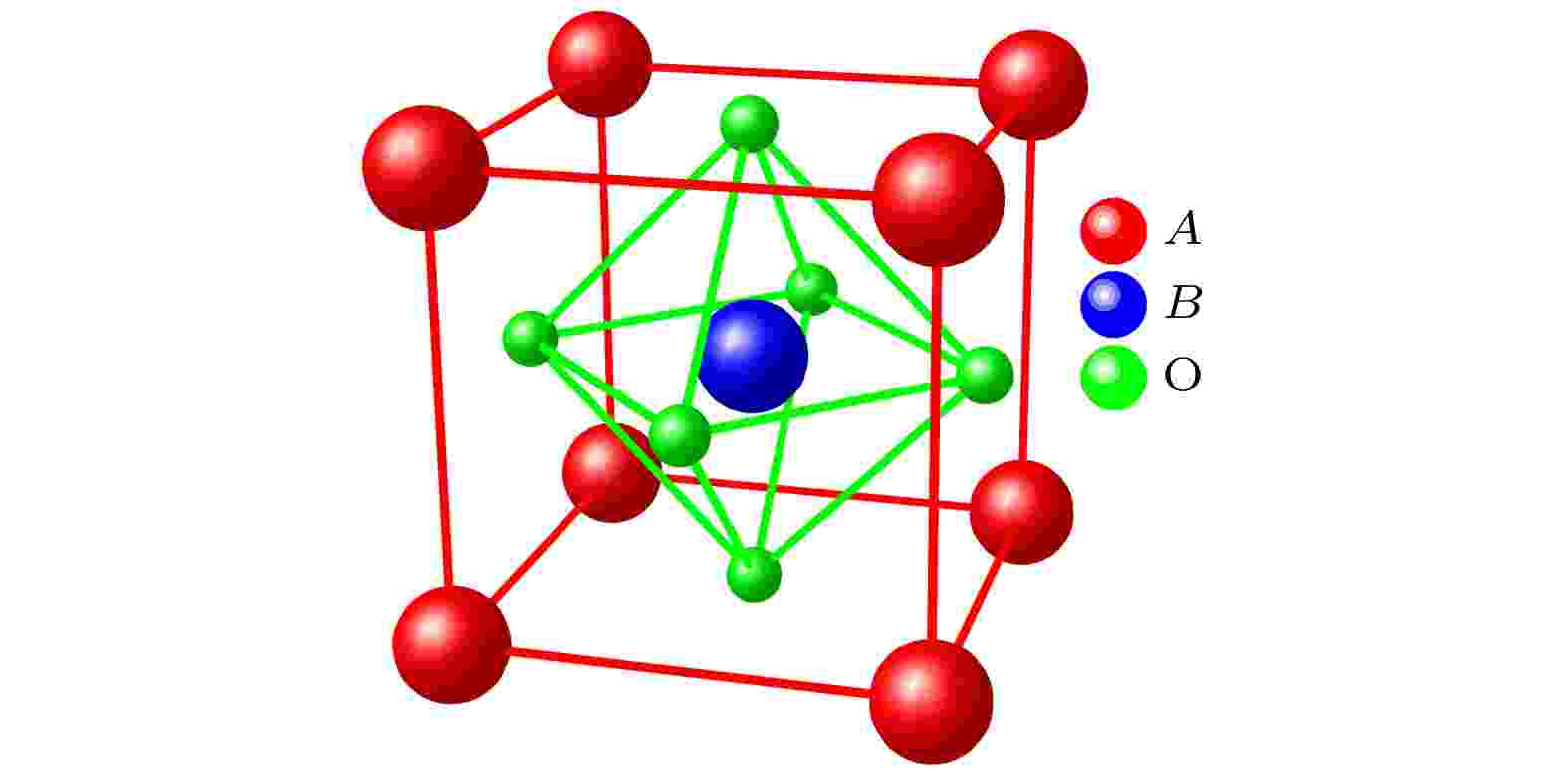图 1 理想钙钛矿ABO₃立方结构示意图
Figure1. Ideal perovskite ABO₃ cubic structure.

由双交换作用理论可知, Mn—O—Mn的键长和键角将直接影响到e_g轨道中的巡游电子传输带宽和双交换作用的强度. 传输带宽越大, 则双交换作用倾向越明显. Dagotto等^[15]根据双交换作用带宽将钙钛矿锰氧化物分为大带宽型(如La-Sr-Mn-O系)、中等带宽型(如La-Ca-Mn-O系)、小带宽型(如Pr-Ca-Mn-O系)等. 虽然双交换作用是其铁磁性和导电性的主要来源, 但双交换作用理论并不能完全解释该体系复杂的磁学和电学输运性质. 由于Mn³⁺离子3d轨道上e_g电子在简并轨道中的不对称占据, 氧八面体也会发生Jahn-Teller畸变, 形成晶格极化子伴随巡游电子局域化^[16], 影响体系的磁电输运性质和磁相变机制. 而在中等和小带宽半掺杂锰氧化物中常常还会发现电荷轨道有序态现象, 这些都使得体系的相图变得异常复杂. 不同带宽锰氧化物的典型磁相图如图2所示, 图中各相符号含义分别为: PM, 顺磁金属; PI, 顺磁绝缘; FM, 铁磁金属; AFM, 反铁磁金属; FI, 铁磁绝缘; CO, 电荷有序; CI, 自旋倾斜绝缘; CAF, 自旋倾斜反铁磁; CAFI, 自选倾斜反铁磁绝缘等^[15]. 另外, 通过实验和理论研究发现, 锰氧化物具有本征的电子和磁性相分离^[17]倾向—由于电子密度的不均匀形成纳米级电子铁磁性团簇. 这种磁性相分离机制已被认为是解释锰氧化物巨磁阻效应和特殊输运行为的关键.
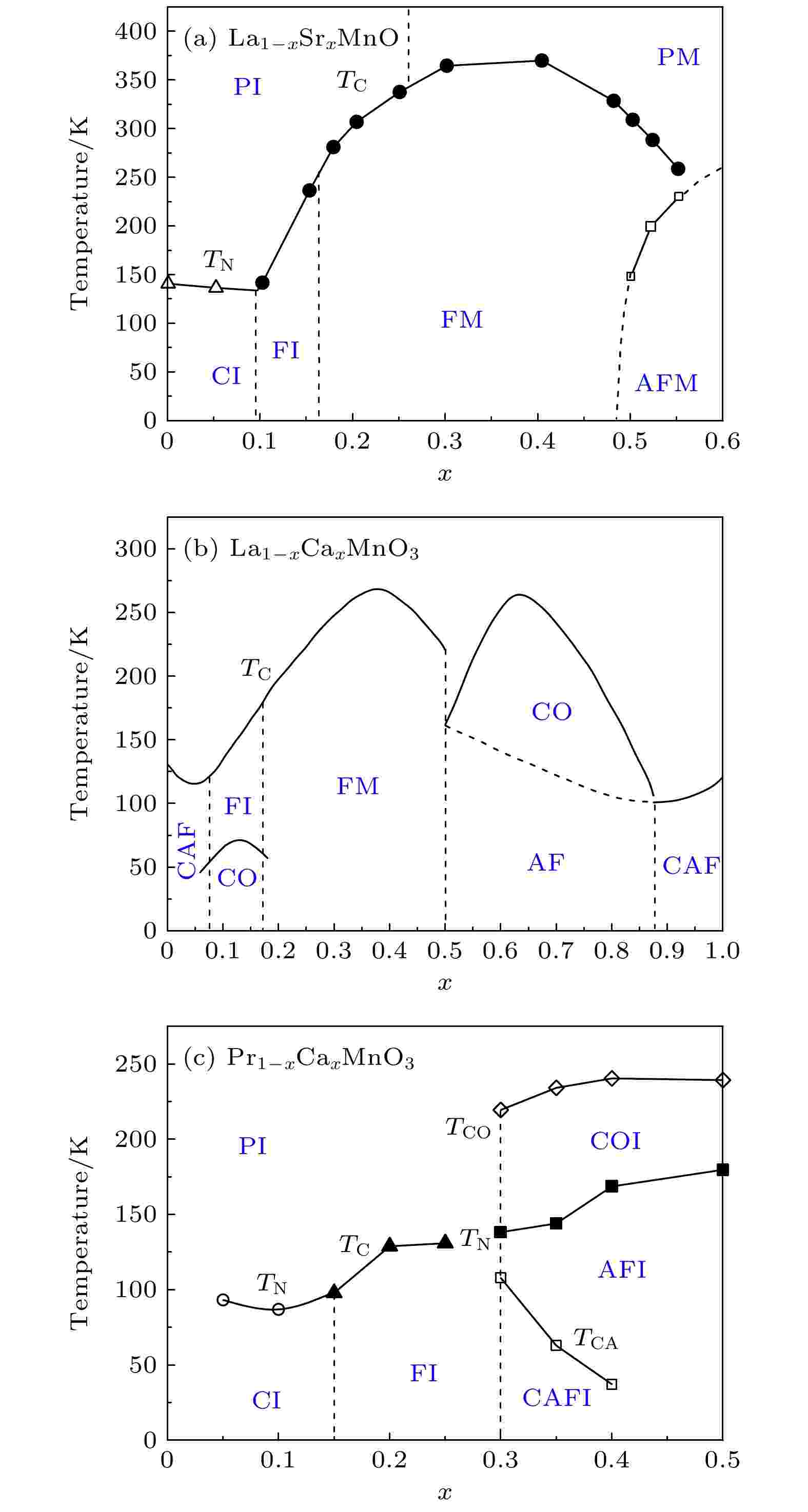图 2 不同带宽钙钛矿锰氧化物的典型磁相图　(a)大带宽型La_1–xSr_xMnO₃; (b)中等带宽型La_1–xCa_xMnO₃; (c)小带宽型Pr_1–xCa_xMnO₃^[15]
Figure2. Typical magnetic phase diagrams of different bandwidth manganites: (a) Large bandwidth La_1–xSr_xMnO₃; (b) intermediate bandwidth La_1–xCa_xMnO₃; (c) small bandwidth Pr_1–xCa_xMnO₃^[15].

磁热效应是磁性材料在外加磁场变化下表现出来的吸热和放热效应, 一般在居里温度附近达到最大值, 其表征参数主要为基于Maxwell关系式的等温磁熵变. 对于二级相变磁性材料而言, 其相变临界居里点附近还表现出各种奇特的临界行为, 例如比热、热膨胀系数以及铁磁序参量发生突变或异常现象, 因此对于磁性材料的相变临界行为分析能够为揭示体系内部的铁磁相互作用机制提供重要线索.
为了分析磁性体系的相变临界行为, 首先需要判断其相变属性. 对于一般磁性材料而言, 二级磁相变往往表现为仅有磁结构的变化, 而一级磁相变通常伴随着晶体结构或晶格参数的不连续变化. 根据Landau相变理论, 相变过程中自由能一阶偏导不连续为一级相变, 而自由能一阶偏导连续则为二级相变. Landau-Lifshitz 近似状态方程可表示为

$H = a(T)M + b(T){M^3} + c(T){M^5} + \cdots,$

其中a(T )与初始磁化率的倒数相关, 根据居里-外斯定律可以得出其在T_C处接近于0; 根据b(T )的符号可以判断相变是否为连续: 若为正数则表明相变为连续二级相变, 而若为负数则表明相变为不连续, 即一级相变. 可通过测试分析Arrott图, 通过斜率来初步判断b(T )的正负(即Banerjee准则)^[18]. 但当体系渡越于一级和二级相变之间的三重临界点时, Banerjee准则不再适用, 这是由于此时b(T )接近于0, 状态方程中的高次项不能被忽略, 而当b(T )为很小的负数(实际为一级相变)时Arrott图仍表现为正斜率, 由Banerjee准则易误判为二级相变. 此时可采取多项式拟合获取a(T )及b(T )参数, 根据a(T )最小值即T_C附近对应b(T )值的正负性来判断磁相变的性质, 而若b(T )值接近于0, 则该样品的磁相变或处于三重临界点附近.
磁相变临界参数包括β, γ和δ, 分别描述铁磁有序相(T < T_C), 顺磁无序相(T > T_C)和相变临界点(T = T_C)处的行为. 通过分析磁相变临界行为和获取临界参数有助于理解相变过程中的铁磁相互作用机制. 在磁性系统中磁相变的临界参数定义为

${M_{\rm{s}}}(T) = {M_0}{( - \varepsilon )^\beta },\;\;~~\varepsilon < {\rm{ }}0,$

$H = D{M^\delta },~~~~\varepsilon = {\rm{ }}0,$

$\chi _0^{ - 1} = \left( {{{{H_0}} / {{M_0}}}} \right){\varepsilon ^\gamma },~~~~\varepsilon > {\rm{ }}0,$

其中$\varepsilon = {{\left( {T - {T_C}} \right)} / {{T_C}}}$为对比温度. 3个临界参数符合Widom标度关系

$\delta = 1 + {\gamma / \beta }.$

基于Arrott-Noakes状态方程

${\left( {{H / M}} \right)^{{1 / \gamma }}} = {{\left( {T - {T_{\rm{C}}}} \right)} / {{T_1}}} + {\left( {{M / {{M_1}}}} \right)^{{1 / \beta }}},$

能够由T_C附近的等温磁化曲线M(H )图获取磁相变相应的临界参数. 利用绘制修正的Arrott图(modified Arrott plot, MAP), 选择合适的初始临界参数值β和γ对高场数据进行线性拟合, 通过外推得到的数轴截距得到自发磁化强度M_S(T )和初始磁化率倒数χ₀^–1(T ), 然后利用指数函数拟合来得到新的临界参数, 经过反复迭代法直到临界指数收敛不再变化为止, 即可得到最终的合适临界参数. 利用得到的临界参数绘制的MAP应为一系列平行线.
另外, 为了得到更为精确的临界参数, 往往用到Kouvel-Fisher (KF)线性拟合方法来取代指数函数拟合方法.

${M_{\rm{S}}}(T){\left[ {{{{\rm{d}}{M_{\rm{S}}}(T)} / {{\rm{d}}T}}} \right]^{ - 1}} = {{\left( {T - {T_{\rm{C}}}} \right)} / \beta },$

$\chi _0^{ - 1}(T){\left[ {{{{\rm{d}}\chi _0^{ - 1}(T)} / {{\rm{d}}T}}} \right]^{ - 1}} = {{\left( {T - {T_{\rm{C}}}} \right)} / \gamma }.$

Franco等^[19]依据上述标度方程(6)和磁熵变Maxwell公式推导得出了关于磁熵变的标度律公式, 即在T_C附近最大磁熵变ΔS_{M max}随磁场H变化的关系式:

$\left| {\Delta {S_{{\rm{M\,max}}}}} \right| \propto {H^n},$

$n = 1 + {{\left( {\beta - 1} \right)} / {\left( {\beta + \gamma } \right)}}.$

对于二级相变材料而言, 不同磁场下的磁熵变曲线ΔS_M (T, H)能被标度为一条普适曲线^[20], 标度磁熵变ΔS ′和对应标度温度θ分别为

$\Delta S' = {{\Delta {S_{\rm{M}}}(T,H)} / {\Delta {S_{{\rm{M}}\max }}}},$

$\theta = \left\{ {\begin{aligned} &{ - {{\left( {T - {T_{\rm{C}}}} \right)} / {\left( {{T_{{\rm{r1}}}} - {T_{\rm{C}}}} \right)}},~~~T \leqslant {T_{\rm{C}}}}, \\ &{{{\left( {T - {T_{\rm{C}}}} \right)} / {\left( {{T_{{\rm{r2}}}} - {T_{\rm{C}}}} \right)}},~~~~~~T > {T_{\rm{C}}}} ,\end{aligned}} \right.$

其中${T_{{\rm{r1}}}}$和${T_{{\rm{r2}}}}$分别为磁熵变曲线半高处的两个参考温度.
由于标度磁熵变和磁相变临界参数存在(9)式和(10)式表达的关系, 可通过MAP或KF方法获取临界参数后对磁熵变进行标度, 检验其自洽性. 另外也可通过拟合磁熵变标度幂函数获取指数n, 并结合Widom标度关系(5)式, 通过计算获得磁相变临界参数, 可称为磁熵变法(MCE方法)^[21,22].
由于计算拟合过程受测试数据的精度以及拟合数据的选择范围影响较大, 要求等温磁化曲线测试精确且温度间隙较小. 在得到最终临界参数后, 可利用假定状态的标度方程对临界参数β和γ进行验证:

$M{\left| \varepsilon \right|^{ - \beta }} = {f_ \pm }\left( {H{{\left| \varepsilon \right|}^{ - \left( {\beta + \gamma } \right)}}} \right),$

式中f₊和f_–分别代表 T > T_C 和 T < T_C 时的正则解析函数. 若临界参数β和γ取值正确则将会标度为两条普适曲线.
通过对比各理论模型的理想参数可分析磁性材料内部铁磁相互作用机制. 描述长程相互作用的Mean-field模型以及描述短程相互作用的3D-Heisenberg模型和3D-Ising模型, 对应的理论临界参数如表1^[23,24]所列.

Model	β	γ	δ	Ref.
Mean-field	0.5	1.0	3.0	[23]
Tricritical-Mean-field	0.25	1.0	5.0	[23]
3D-Heisenberg	0.365	1.386	4.80	[24]
3D-Ising	0.325	1.241	4.82	[24]

表1典型理论模型的临界参数
Table1.Critical parameters of theoretical models.

按照重整化群理论, 对于均匀的三维磁性体系而言, 磁相变的普适性取决于自旋相互作用的衰减距离^[25] J(r)∝r^–3–σ. 这里σ与相互作用距离相关, 当σ < 3/2时适用于Mean-field模型, 磁相互作用随距离的衰减程度J(r)小于r^–4.5, 即长程相互作用; 当σ > 2时适用于3D-Heisenberg模型, 磁相互作用随距离的衰减程度J(r)大于r^–5, 即短程相互作用; 而当σ处于中间值时(3/2 ≤ σ ≤ 2), 其临界参数为其他不同模型. 显然, 通过对各类磁性材料铁磁相变的临界行为分析以及理论模型参考, 能够为理解其磁性相互作用模式提供线索.

2

-->

4.1.典型锰氧化物材料的磁相变临界行为

磁性材料的临界行为表现往往受到诸多因素的影响, 特别是对于复杂体系的临界行为分析很难完全体现其本征特性. 即使是结构和成分均匀的单相材料也会由于晶粒大小、晶体形态等因素影响其宏观磁学特性表象, 当材料处于单晶、多晶等形态时由于无序态晶界密度不同可能使得磁相变临界行为存在较大差异. 对于存在本征磁性相分离的钙钛矿锰氧化物材料体系而言, 其磁相变临界参数往往偏离典型理论模型, 因此有必要首先对典型锰氧化物材料处于单晶和多晶形态下的磁相变临界行为进行对比分析. 表2^[26-42]列出了部分关于优化空穴掺杂型(掺杂浓度约为0.1—0.4)大带宽La-Ba-Mn-O, La-Sr-Mn-O体系, 中带宽La-Ca-Mn-O, Nd-Sr-Mn-O, Pr-Sr-Mn-O体系, 以及小带宽Pr-Ca-Mn-O体系在单晶和多晶形态下的临界参数对比. 其中涵盖了MAP, KF等基于磁性测试数据的计算分析方法, 考虑到数据拟合和实验误差, 不同方法计算所得临界参数基本相符.

Material	Technique	β	γ	δ	Model	Ref.
La0.7Ba0.3MnO3SC	MAP	0.35	1.41	5.5	3D-Heisenberg	[26]
La0.7Ba0.3MnO3PC	MAP	0.493	1.059	3.15	Mean-field	[27]
La0.67Ba0.33MnO3PC	MAP	0.464	1.29	3.78	Mean-field/3D-Heisenberg	[28]
La0.7Sr0.3MnO3SC	MAP	0.37	1.22	4.25	close to 3D-Heisenberg	[29]
La0.75Sr0.25MnO3SC	MAP	0.4	1.27	4.12	Mean-field/3D-Ising	[30]
La0.8Sr0.2MnO3PC	MAP	0.5	1.08	3.13	Mean-field	[31]
La0.875Sr0.125MnO3SC	MAP	0.37	1.38	4.72	3D-Heisenberg	[32]
La0.6Ca0.4MnO3PC	MAP	0.25	1.03	5	Tricritical-Mean-field	[33]
La0.79Ca0.21MnO3SC	MAP	0.09	1.71	20	nonuniversal	[34]
La0.8Ca0.2MnO3SC	MAP	0.374	1.382	4.779	3D-Heisenberg	[35]
La0.82Ca0.18MnO3SC	MAP	0.374	1.379	4.783	3D-Heisenberg	[35]
Nd0.6Sr0.4MnO3SC	KF	0.308	1.172	4.75	3D-Ising	[36]
Nd0.6Sr0.4MnO3PC	MAP	0.51	1.01	3.13	Mean-field	[37]
Nd0.67Sr0.33MnO3PC	MAP	0.23	1.05	5.13	Tricritical-Mean-field	[37]
Nd0.7Sr0.3MnO3PC	MAP	0.271	0.922	4.4	Tricritical-Mean-field	[38]
Pr0.6Sr0.4MnO3SC	KF	0.312	1.106	4.545	3D-Ising	[36]
Pr0.6Sr0.4MnO3SC	MAP	0.365	1.309	4.648	3D-Heisenberg	[39]
Pr0.6Sr0.4MnO3PC	MAP	0.276	0.918	4.325	Tricritical-Mean-field	[40]
	KF	0.273	1.001	4.325
Pr0.71Ca0.29MnO3SC	MAP	0.37	1.38	4.62	3D-Heisenberg	[41]
Pr0.71Ca0.29MnO3PC	MAP	0.521	0.912	2.71	Mean-field	[42]
Pr0.73Ca0.27MnO3SC	MAP	0.36	1.36	4.81	3D-Heisenberg	[41]
Pr0.73Ca0.27MnO3PC	MAP	0.362	1.132	4.09	3D-Heisenberg	[42]
注: SC表示单晶; PC表示多晶.

表2典型锰氧化物材料在各种形态下的临界行为分析
Table2.Critical behavior analysis of manganites in different morphologies (SC, single crystal; PC, polycrystalline).

对于大带宽型La-Ba-Mn-O和La-Sr-Mn-O体系而言, 由于双交换作用占据主导地位, 其电磁学性质应基本反映双交换作用的行为特点. 而基于双交换作用理论以及基于单晶材料的相关实验结果均表明, 大带宽型La-Ba-Mn-O和La-Sr-Mn-O体系的铁磁相互作用基本符合基于短程相互作用模式的3D-Heisenberg模型^[26,29,32]. 但从表2可看出, 对于多晶材料却往往反映出长程相互作用的平均场模型^[27,31]或介于平均场和3D-Heisenberg(或3D-Ising)模型之间的临界参数^[28,30]. 根据Kim等^[30]的研究, 这是由于对于多晶材料而言, 在接近居里点时其相干长度可能会超出晶粒尺度范围, 此时涨落效应可能被平均场理论所取代, 或出现渡越于多重模型之间的现象. 从表2中各体系下相同成分单晶和多晶的临界参数对比中可以看出此现象具备一定普遍性.
在中等带宽型锰氧化物中最为著名的体系是La-Ca-Mn-O体系. 当空穴掺杂量在0.3附近时, 由于强烈的电子晶格耦合、Jahn-Teller效应、极化子巡游电子局域化及磁性相分离等因素综合作用, 该化合物呈现出明显的晶格参数突变和一级磁相变特性, 且伴随着巨磁热效应和巨磁阻效应等极其优异的性质, 因而被广泛关注. 由于居里温度接近室温, 目前是室温磁制冷领域中最具应用前景的材料之一. Kim等^[33]首次在空穴掺杂浓度为0.4附近的多晶体系中发现了介于一级和二级相变之间的三重临界点现象. 图3所示为三重临界点示意图, 三重临界点渡越于可由掺杂空穴浓度、磁场强度等因素调控的一级和二级磁相变之间, 处于一级/二级相变分界线和铁磁/顺磁相变分界线的交点. Jiang等^[35]对于该体系在磁性金属性和绝缘性临界点附近(空穴浓度接近0.2)的磁相变临界参数进行了深入分析, 结果表明金属性(空穴浓度0.2)和绝缘性(空穴浓度0.18)成分的临界参数均符合3D-Heisenberg模型, 这是由于主导绝缘性的轨道有序超交换模型和主导金属性的轨道无序双交换模型共同作用且强度接近, 两者均能够用3D-Heisenberg模型来描述磁性相互作用模式. 另外, Jiang等^[34]还对锰氧化物中体现无序性的Griffith相进行了探讨, 重点分析了存在Griffith相的La-Ca-Mn-O (空穴浓度0.21)化合物的磁相变临界行为, 得到了不符合任何已知物理模型的反常临界参数. Griffith相存在于接近相变临界点的顺磁区域, 可通过获取低场下磁化率倒数曲线对其进行分析. Griffith相体现锰氧化物体系的本征相分离特性, 由于接近临界点的顺磁区域往往存在局域铁磁团簇, 因此会在很大程度上影响其临界行为, 导致非普适临界参数.
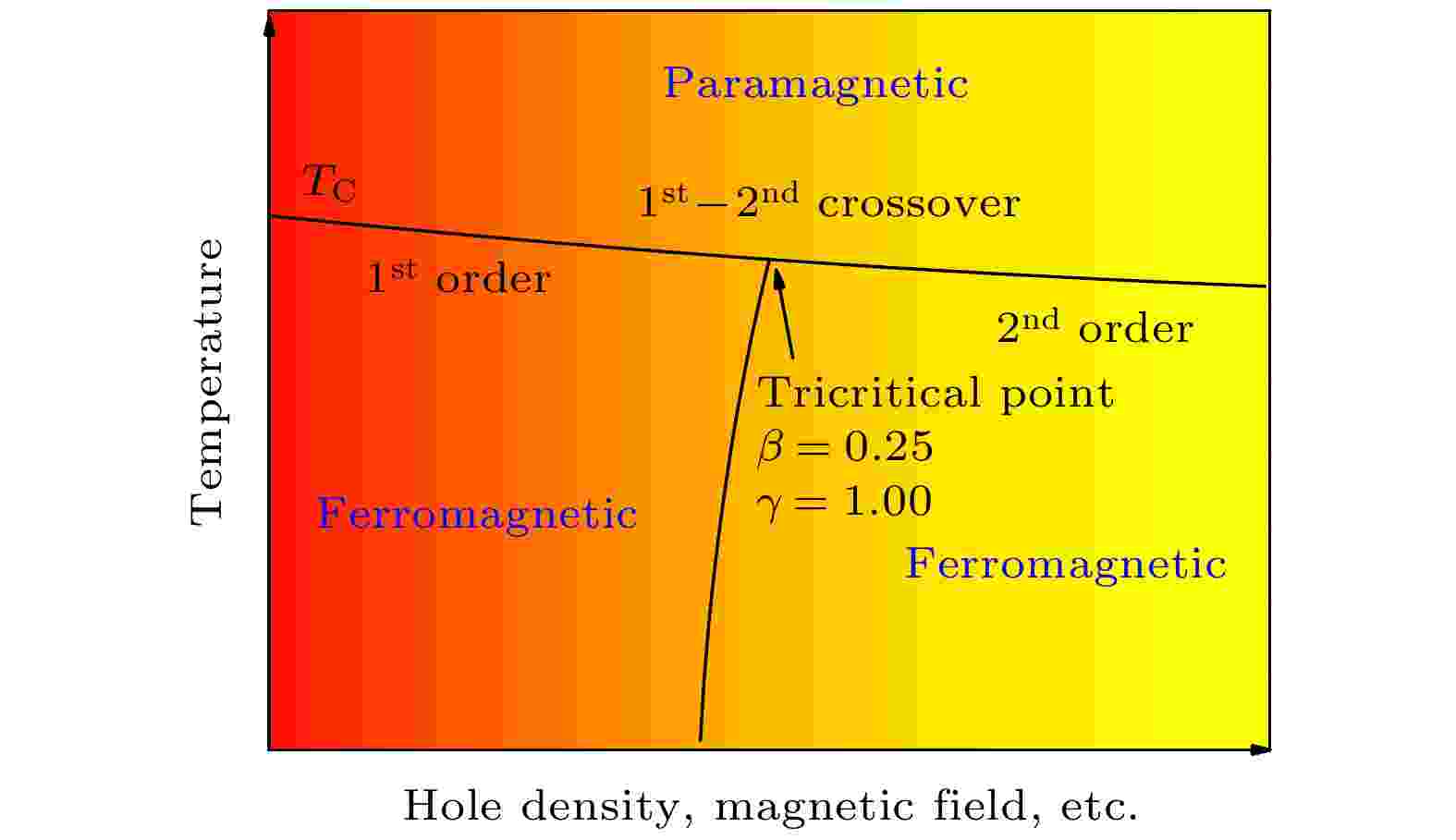图 3 三重临界点的示意图
Figure3. Schematic diagram of Tricritical point.

而同样为中等带宽的Nd-Sr-Mn-O和Pr-Sr-Mn-O体系则存在一定的相似性, 在空穴浓度在0.3—0.4之间的Nd-Sr-Mn-O和Pr-Sr-Mn-O多晶材料中均发现了渡越于一级和二级相变的三重临界点^[37,38,40]. 另外, Oleaga等^[36]精细分析了处于双交换作用主导(空穴浓度0.4)的此两种锰氧化物单晶材料的临界行为, 讨论了对于单晶材料中的磁晶各向异性能够影响其临界行为, 单一的双交换作用并不能完全体现其铁磁相互作用机制, 且所得的临界参数更加接近具有各向异性特点的3D-Ising模型. 这也解释了上述典型双交换作用单晶锰氧化物的临界参数中存在偏离3D-Heisenberg模型的现象.
对于小带宽Pr-Ca-Mn-O系, A位离子的错配和较小的容差因子使其相图中存在典型一级相变区域, 且因其更加趋向于电荷有序相, 只在很窄的空穴浓度(0.15—0.3)区间具备铁磁绝缘相. 其铁磁相基本认为是以相分离型双交换作用为主导. 通过对接近电荷有序相的两个单晶材料(0.27和0.29)的磁相变临界行为进行分析^[41]可知, 其临界行为均体现了典型双交换作用性质的3D-Heisenberg模型, 但接近电荷有序相区域(0.29)可能受到部分电荷有序相中反铁磁相互作用的影响. 而Ho等^[42]对相同成分的多晶材料的研究发现, 空穴浓度为0.29的样品呈现出长程相互作用的平均场模型. 这可能是由于其更加接近电荷有序相, 而超交换作用程略长于双交换作用^[35], 相干长度更易达到晶粒尺度范围从而转变为平均场模型.
2 -->

4.2.A/B位掺杂锰氧化物的磁相变临界行为

虽然从单晶和多晶材料临界参数对比可以看出, 同成分的锰氧化物在不同晶体形态下的临界行为存在一定差异, 但仍能够通过对比反映丰富的内部磁性物理性质. 若在制备工艺条件相同的情况下对母相成分进行掺杂或微调, 通过对比磁相变临界行为, 能够有效分析内部磁性相互作用模式演化等信息. 对于ABO₃钙钛矿结构锰氧化物而言, 其成分的掺杂微调一般可根据掺杂位置不同分为A位掺杂和B位掺杂等方式.
A位掺杂元素一般为离子半径接近的二价碱土金属离子或三价稀土离子等, 通过价态比例可调节空穴浓度. 但A位离子平均半径的变化将导致容差因子t的不同从而改变双交换作用带宽, 进而导致磁性和相变特性的显著变化. 另一方面, 由于部分稀土离子自身磁矩较大, 对体系整体磁性的贡献往往不可忽略. 因此通过分析A位掺杂锰氧化物的磁相变临界行为能够帮助深入理解磁性相互作用模式影响等重要信息. 目前已有大量关于A位掺杂对临界行为影响的研究工作, 表3^{[27,28,40,43-50]}列出了部分A位掺杂锰氧化物临界参数分析结果, 下面对部分代表性工作进行简单介绍.

Material	Technique	β	γ	δ	Model	Ref.
La0.67(Ca0.5Ba0.5)0.33MnO3	MAP	0.402	1.110	3.761	Mean-field/3D-Heisenberg	[28]
La0.7Ca0.15Ba0.15MnO3	MAP	0.438	1.032	3.360	Mean-field	[27]
La0.7Ca0.2Ba0.1MnO3	MAP	0.284	0.909	4.200	Tricritical-Mean-field/3D-Ising	[43]
	KF	0.297	0.925	4.110
La0.7Ca0.15Sr0.15MnO3	MAP	0.491	1.054	3.150	Mean-field	[27]
La0.7Ca0.1Sr0.2MnO3	KF	0.360	1.220	4.400	3D-Heisenberg	[44]
La0.7Ca0.2Sr0.1MnO3	KF	0.260	1.060	5.100	Tricritical-Mean-field	[44]
La0.69Dy0.01Ca0.3MnO3	MAP	0.230	0.920	5.000	Tricritical-Mean-field	[45]
	KF	0.250	0.870	4.480
La0.7Ca0.28Sn0.02MnO3	KF	0.218	0.858	4.936	Tricritical-Mean-field	[46]
La0.7Ca0.26Sn0.04MnO3	KF	0.467	1.095	3.345	Mean-field	[46]
La0.75Dy0.05Sr0.2MnO3	MAP	0.266	0.920	4.460	Tricritical-Mean-field	[47]
	KF	0.272	0.931	4.420
La0.1Nd0.6Sr0.3MnO3	MAP	0.248	1.066	5.170	Tricritical-Mean-field	[48]
	KF	0.257	1.120	5.170
Pr0.4Sm0.15Sr0.45MnO3	KF	0.324	1.212	4.812	3D-Ising	[49]
Pr0.3Sm0.25Sr0.45MnO3	KF	0.255	0.957	5.105	Tricritical-Mean-field	[49]
La0.57Nd0.1Sr0.33MnO3	MAP	0.356	1.152	4.235	3D-Heisenberg	[50]
	KF	0.368	1.191	4.236
La0.57Nd0.1Sr0.28□0.05MnO3	MAP	0.312	1.173	4.760	3D-Ising	[50]
	KF	0.326	1.183	4.619
Pr0.6Sr0.4MnO3	MAP	0.276	0.918	4.325	Tricritical-Mean-field	[40]
	KF	0.273	1.001	4.325
Pr0.6Sr0.3□0.1MnO3	MAP	0.253	0.987	4.890	Tricritical-Mean-field	[40]
	KF	0.242	0.945	4.890
Pr0.5□0.1Sr0.4MnO3	MAP	0.323	1.113	4.446	3D-Ising	[40]
	KF	0.325	1.092	4.446
注: □表示离子空位.

表3A位掺杂不同元素或空位的锰氧化物临界行为分析
Table3.Critical behavior analysis of manganites doped with different elements (vacancy) at A site (□, Ion vacancy).

对于最引人关注的中带宽La-Ca-Mn-O体系, 在空穴掺杂量为0.3左右时其磁相变类型为一级相变, 而通过如Ba, Sr等大离子半径碱土金属元素掺杂后, 其磁相变可转变为二级, 并呈现出长程平均场模型或介于平均场和短程3D-Heisenberg模型之间的临界行为^[27,28]. 值得注意的是, 当掺杂量达到某特定程度时, 可能获得由一级向二级相变渡越的三重临界点^[43,44]. 对于磁制冷材料而言, 渡越于一级和二级相变之间的材料可能兼具两者的优点, 实现制冷能力最优化, 可见处于三重临界点的材料具备一定的理论和应用研究价值. 与碱土金属元素不同, 研究发现在A位掺杂微量的稀土元素Dy(1%)^[45]和Sn(2%)^[46]后便已出现类似三重临界行为, 可能是由于离子半径或价态等错配度明显高于碱土金属元素, 微量掺杂便足以削弱其晶格极化子局域化所导致的一级磁晶相变特征.
而典型大带宽La-Sr-Mn-O系受双交换作用主导作用, 其母相主要表现为二级磁相变特征. Elghoul等^[47]对La-Sr-Mn-O系A(La)位掺杂5%的Sm, Eu, Gd, Ho和Dy等稀土离子后发现, 除Dy以外其余成分均表现为短程3D-Ising模型, 但掺Dy样品表现出三重临界平均场模型. 普遍认为, 部分稀土元素自身的较大磁矩会对整体铁磁相互作用和相变行为造成一定影响, 但与Dy磁矩接近的Ho掺杂样品并未呈现相似特性. Elghoul等^[47]根据前期研究结果发现Dy离子在单位晶胞中所占体积高于其他稀土元素, 使得锰氧八面体具有更大的Mn—O键长和Mn—O—Mn键角, 这可能是造成掺Dy样品磁相变临界行为特异性的主要原因.
而在其他存在一级磁相变的中带宽体系中, 如Nd-Sr-Mn-O和Pr-Sr-Mn-O等, 关于A位稀土元素掺杂获得三重临界点的研究报道已有许多. 如Fan等^[48]在La_0.1Nd_0.6Sr_0.3MnO₃多晶材料中发现了三重临界行为, 且所得临界参数相比于Nd_0.7Sr_0.3MnO₃多晶^[38]而言更为接近理论值. Mleiki等^[49]在Pr(Sm)-Sr-Mn-O体系展开研究, 通过调节Pr/Sm比例, 在成分为Pr_0.3Sm_0.25Sr_0.45MnO₃中同样获得了磁相变三重临界参数.
除了碱土或稀土等元素掺杂, 关于掺杂离子空位的影响也十分值得关注. Mnefgui等^[50]在La_0.57Nd_0.1Sr_0.33MnO₃多晶材料中在Sr位引入少量(5%)空位, 结果表明其铁磁临界参数β有所降低, 且使描述模型由适合3D-Heisenberg转向更为接近3D-Ising模型. 而顺磁临界参数γ均接近于平均场, 可由长程偶极相互作用来解释. Elleuch等^[40]以Pr_0.6Sr_0.4MnO₃多晶材料为基础, 分别在Pr和Sr位引入10%空位, 在Pr_0.6Sr_0.3□_0.1MnO₃ (□表示离子空位)中得到非常接近理论值的三重临界点, 而Pr_0.5□_0.1Sr_0.4MnO₃的磁相变临界参数接近于短程3D-Ising模型. 上述研究表明, 离子空位的引入会加剧系统无序度, 进而影响磁相变临界行为.
虽然部分A位稀土元素自身磁矩较大, 对体系存在一定的磁性贡献或影响, 但体系铁磁性主要仍来自B位Mn离子之间通过O离子形成的双交换或超交换作用. 与各类A位掺杂的锰氧化物相关研究不同, 通过B位掺杂各种3d过渡族金属离子取代Mn离子可从本质上改变或调节铁磁相互作用. 因此, 近年来已有针对B位掺杂的大量研究工作, 表4^[51-68]列出了各体系B位掺杂锰氧化物磁相变临界行为的部分代表性研究结果.

Material	Technique	β	γ	δ	Model	Ref.
La0.67Ba0.33Mn0.98Ti0.02O3	MAP	0.537	1.015	2.890	Mean-field	[51]
	KF	0.551	1.020	2.851
La0.67Ba0.33Mn0.95Fe0.05O3	KF	0.504	1.013	3.040	Mean-field	[52]
La0.7Ba0.3Mn0.95Ti0.05O3	MAP	0.374	1.228	4.260	3D-Heisenberg	[53]
La0.7Ba0.3Mn0.9Ti0.1O3	MAP	0.339	1.307	4.780	3D-Ising	[53]
La0.8Ba0.2Mn0.8Fe0.2O3	MAP	0.365	1.227	4.362	3D-Heisenberg	[54]
	KF	0.318	1.159	4.645
La0.67Sr0.33Mn0.9Fe0.1O3	MAP	0.450	1.240	3.740	Mean-field/3D-Heisenberg	[55]
	KF	0.538	1.330	3.470
La0.7Sr0.3Mn0.95Al0.05O3	KF	0.458	1.001	3.185	Mean-field	[56]
La0.7Sr0.3Mn0.95Ti0.05O3	KF	0.344	1.149	4.340	Mean-field/3D-Heisenberg	[56]
La0.7Sr0.3Mn0.9Co0.1O3	KF	0.457	1.114	3.440	Mean-field/3D-Heisenberg	[57]
La0.7Sr0.3Mn0.99Ni0.01O3	MAP	0.394	1.092	3.990	Mean-field/3D-Heisenberg	[58]
La0.7Sr0.3Mn0.98Ni0.02O3	MAP	0.400	1.082	3.790	Mean-field/3D-Heisenberg	[58]
La0.7Sr0.3Mn0.97Ni0.03O3	MAP	0.468	1.010	2.670	Mean-field	[58]
La0.7Sr0.3Mn0.98Cu0.02O3	KF	0.464	1.162	3.546	close to Mean-field	[59]
La0.7Sr0.3Mn0.96Cu0.04O3	KF	0.449	1.202	3.681	close to Mean-field	[59]
La0.67Ca0.33Mn0.9Cr0.1O3	MAP	0.555	1.170	2.710	Mean-field	[60]
La0.67Ca0.33Mn0.75Cr0.25O3	MAP	0.680	1.090	2.936	close to Mean-field	[60]
La0.67Ca0.33Mn0.9Ga0.1O3	MAP	0.380	1.365	4.590	3D-Heisenberg	[61]
	KF	0.387	1.362	4.520
La0.7Ca0.3Mn0.95Ti0.05O3	KF	0.601	1.171	2.950	Mean-field	[62]
La0.7Ca0.3Mn0.9Ti0.1O3	KF	0.389	1.403	4.400	3D-Heisenberg	[62]
La0.7Ca0.3Mn0.91Ni0.09O3	MAP	0.171	0.976	6.700	Tricritical-Mean-field	[63]
La0.7Ca0.3Mn0.88Ni0.12O3	MAP	0.262	0.978	4.700	Tricritical-Mean-field	[63]
La0.7Ca0.3Mn0.85Ni0.15O3	MAP	0.320	0.990	4.100	3D-Ising	[63]
La0.7Ca0.3Mn0.95Cu0.05O3	MAP	0.490	1.040	3.120	Mean-field	[64]
La0.7Ca0.3Mn0.9Zn0.1O3	MAP	0.474	1.152	3.430	Mean-field	[65]
La0.8Ca0.2Mn0.9Co0.1O3	MAP	0.204	1.969	11.983	nonuniversal	[66]
	KF	0.123	1.351	11.983
La0.8Ca0.2Mn0.8Co0.2O3	MAP	0.401	1.332	4.321	3D-Heisenberg	[66]
	KF	0.418	1.303	4.321
Nd0.67Sr0.33Mn0.9Cr0.1O3	MAP	0.337	0.784	3.326	nonuniversal	[67]
Nd0.67Sr0.33Mn0.9Fe0.1O3	MAP	0.436	0.94	3.156	Mean-field	[67]
Nd0.67Sr0.33Mn0.9Co0.1O3	MAP	0.431	0.929	3.155	Mean-field	[67]
Pr0.67Sr0.33Mn0.95Al0.05O3	MAP	0.381	1.323	4.635	3D-Heisenberg	[68]
	KF	0.381	1.320	4.635
Pr0.67Sr0.33Mn0.9Al0.1O3	MAP	0.374	1.333	4.667	3D-Heisenberg	[68]
	KF	0.377	1.331	4.667

表4B位掺杂不同元素的锰氧化物临界行为分析
Table4.Critical behavior analysis of manganites doped with different elements at B site.

目前大量的研究工作均表明, B位元素的微量掺杂即可显著调节甚至改变其内部铁磁相互作用模式. 这是由于以双交换作用为主导的磁性相互作用机制受到了直接影响. 随着Mn离子被各价态不同的其他3d过渡金属元素(Tm)所取代, 铁磁性双交换耦合Mn³⁺-O-Mn⁴⁺将逐渐替换为以反铁磁超交换相互作用为主的Mn³⁺-O-Tm³⁺或Tm³⁺-O-Tm³⁺等, 显然由于其他元素3d轨道电子结构与Mn离子的差异性, 使得部分铁磁双交换作用可转变为反铁磁超交换作用. 而部分如Al³⁺等非磁性元素离子可稀释体系内部铁磁相互作用, 并能够体现在磁相变临界参数的变化中. 一般来说, B位掺杂能够显著增加磁性体系无序度, 当无序性达到较高程度时, 可能会出现偏离标准理论模型^[59,60]甚至非普适性临界行为的现象^[66,67].
与A位掺杂获得三重临界点现象类似, 许多研究发现对La-Ca-Mn-O一级相变区域通过适量B位掺杂, 能够将一级相变渡越为二级相变, 并随掺杂量的改变而从长程平均场模型^[60,64,65]逐渐转变为短程3D-Heisenberg模型^[61,62]等. Phan等^[63]研究B位掺杂Ni的La_0.7Ca_0.3Mn_1–xNi_xO₃化合物发现, 当掺杂量x约为0.12时接近三重临界点模型.
除此之外, 还有关于A位和B位同时掺杂和分析氧空位影响的大量研究工作, 受篇幅限制本文无法逐一列举. 总的来说, 通过不同元素的掺杂和成分的微调能够明显调控内部磁性相互作用模式以及相变特性, 其中关于一级和二级相变渡越现象和三重临界行为十分值得进一步深入探索.
2 -->

4.3.不同制备方法对磁相变临界行为的影响

除了通过掺杂其他元素以外, 许多研究表明即使是相同成分的锰氧化物若采用不同方法制备, 所得样品的各项性质也存在明显区别. 可见锰氧化物的晶粒大小和成分均匀性等因素的影响也不可忽视, 表5^{[43,55,69-82]}列出了关于各种制备方法所得典型锰氧化物材料的临界行为对比的部分代表性研究.

Material	Technique	β	γ	δ	Model	Ref.
La0.6Sr0.4MnO3SG/800 oC	KF	0.560	1.140	3.035	close to Mean-field	[69]
La0.6Sr0.4MnO3SG/1100 oC	KF	0.480	1.052	3.190	Mean-field	[69]
La0.6Sr0.4MnO3SS	KF	0.530	1.110	3.094	Mean-field	[69]
La0.67Sr0.33MnO3SS	MAP	0.333	1.325	4.978	3D-Heisenberg	[70]
La0.67Sr0.33MnO3SG	MAP	0.500	1.150	3.290	Mean-field	[55]
	KF	0.479	1.260	3.630
La0.7Ba0.1Ca0.1Sr0.1MnO3WM	MAP	0.448	1.148	3.563	Mean-field	[71]
	KF	0.476	1.029	3.096
La0.7Ba0.1Ca0.1Sr0.1MnO3SG	MAP	0.235	1.153	5.906	Tricritical-Mean-field	[71]
	KF	0.262	1.165	5.447
La0.7Ca0.2Ba0.1MnO3BM	MAP	0.265	0.867	4.271	Tricritical-Mean-field	[72]
	KF	0.261	0.988	4.386
La0.7Ca0.2Ba0.1MnO3SS	MAP	0.284	0.909	4.200	Tricritical-Mean-field/3D-Ising	[43]
	KF	0.297	0.925	4.110
La0.7Ca0.2Sr0.1MnO3BM	MAP	0.397	0.966	3.430	3D-Heisenberg	[73]
La0.7Ca0.2Sr0.1MnO3SS	MAP	0.276	0.966	4.500	Tricritical-Mean-field	[74]
	KF	0.315	0.954	4.028
La0.7Ca0.2Sr0.1MnO3SG	MAP	0.484	1.037	3.143	Mean-field	[74]
	KF	0.469	1.013	3.160
La0.7Ca0.3MnO3BM/40 nm	MAP	0.485	1.051	3.100	Mean-field	[75]
La0.7Ca0.3MnO3BM/16 nm	MAP	0.621	0.825	2.200	nonuniversal
La0.7Ca0.3MnO3SG	MAP	0.240	1.010	3.090	Tricritical-Mean-field	[76]
La0.75Ca0.25MnO3SG	MAP	0.521	0.94	2.804	Mean-field	[77]
	KF	0.529	0.939	2.775
La0.8Ca0.2MnO3SG	MAP	0.505	1.004	3.060	Mean-field	[78]
	KF	0.499	1.007	3.060
Nd0.7Ca0.15Sr0.15MnO3BM/4 h	KF	0.243	0.907	4.540	Tricritical-Mean-field	[79]
Nd0.7Ca0.15Sr0.15MnO3BM/24 h	KF	0.311	1.100	4.130	3D-Ising	[79]
Pr0.6Ca0.1Sr0.3Mn0.975Fe0.025O3SS	MAP	0.644	1.075	2.763	Mean-field	[80]
	KF	0.622	1.097	2.763
Pr0.6Ca0.1Sr0.3Mn0.975Fe0.025O3SG	MAP	0.357	1.292	4.290	3D-Heisenberg	[80]
	KF	0.370	1.220	4.290
Pr0.8Sr0.2MnO3SG	MAP	0.260	0.978	4.760	Tricritical-Mean-field	[81]
	KF	0.260	0.993	4.810
Pr0.8Sr0.2MnO3SS	MAP	0.318	1.260	4.960	3D-Ising	[82]
	KF	0.326	1.246	4.960
注: SS表示固相反应法; SG表示溶胶凝胶法(附烧结温度工艺条件); WM表示湿混法; BM表示球磨法(附平均粒径尺寸或球磨时间等工艺条件).

表5不同制备方法锰氧化物的临界行为对比分析
Table5.Critical behavior analysis of manganites from different preparation methods (SS, solid state reaction; SG, sol-gel; WM, wet mixing; BM, ball milling).

4.1节已讨论过关于锰氧化物单晶和多晶的磁相变临界行为分析对比, 总的来说均匀单晶和大颗粒单晶所得磁相变临界行为在很大程度上能够体现该体系本征磁性相互作用性质. 而当晶粒尺度下降到纳米级时, 晶界附近的离子错配所引起的系统无序度问题则会显著影响材料的整体磁性和相变性质. 锰氧化物多晶材料的制备工艺多种多样, 其中传统且工艺成熟的方法包括典型的固相反应法、湿混法和溶胶凝胶法等. 一般认为固相反应法在合适工艺下通常能够获得微米级多晶材料, 而溶胶凝胶法等化学方法由于工艺可调控性强, 十分适合于制备晶粒大小和成分均匀的纳米晶材料. 此外, 机械球磨法也常常用来降低和调控样品的颗粒尺度, 达到微米至纳米级.
从表5可知, 对于不同方法制备的相同成分的锰氧化物, 磁相变临界行为存在明显差异. Raoufi等^[69]对比了通过溶胶凝胶法两种不同烧结温度(800和1100 oC)和固相反应法制备的La_0.6Sr_0.4MnO₃典型大带宽锰氧化物, 结果表明以1100 oC 工艺条件溶胶凝胶法和烧结温度为1400 oC的固相反应法制备的两个样品的磁相变临界行为均接近长程平均场模型, 两者颗粒尺度分别在120 nm以上和2 μm左右. 而以800 oC 工艺条件溶胶凝胶法制备所得样品则明显偏离平均场模型, 颗粒平均尺度约为70 nm. 这与晶粒大小造成的Mn—O键长和Mn—O—Mn平均键角的改变有关, 而晶界密度增大所造成的体系无序程度对磁性相互作用和磁相变临界行为表现产生了重要影响. 相同成分材料通过这两种不同方法所得的磁相变临界行为也可能分别归属于完全不同的模型^[55,70], 这与单晶和多晶材料对比的部分情况是类似的, 均可能与3D-Heisenberg模型相互作用相干长度与晶粒尺度接近密切相关.
Munazat等^[71]则对比了湿混法和溶胶凝胶法制备的纳米晶La_0.7Ba_0.1Ca_0.1Sr_0.1MnO₃的磁相变临界行为, 结果表明湿混法所得平均晶粒大小为40 nm且磁相变表现出长程平均场模型, 而在平均晶粒大小为62 nm的溶胶凝胶法样品中发现了类似三重临界行为. 对于如La-Ca-Mn-O等典型具备一级相变的中带宽锰氧化物而言, 采用球磨^[72,75,79]和溶胶凝胶法^[76,81]等制备方法, 并通过制定合适的烧结温度或球磨时间等工艺条件能够实现晶粒大小的精细调控, 可能将一级相变转变为二级并在特定条件下获得三重临界点.
2 -->

4.4.不同磁场强度范围所得磁相变临界参数对比分析

在关于La-Ca-Mn-O体系临界行为的研究工作中^[83], 我们注意到若选取的计算拟合磁场范围不同, 所得磁相变临界行为也可能发生明显变化, 这体现出体系内部磁性相互作用模式对磁场强度也十分敏感. 对比分析不同磁场范围下的磁相变临界行为能有效帮助分析磁性相互作用模式随场强变化的动态演化规律. 表6^[83-85]列出了部分La-Ca-Mn-O材料体系随拟合场强变化的磁相变临界参数对比结果.

Material	Field range	Technique	β	γ	δ	Model	Ref.
La0.6Ca0.4MnO3	1—2 T	KF	0.249	1.008	5.043	Tricritical-Mean-field	[83]
	2—3 T	KF	0.255	0.857	4.359	crossover
	3—4 T	KF	0.262	0.833	4.18	crossover
	4—5 T	KF	0.267	0.797	3.983	crossover
	5—6 T	KF	0.263	0.776	3.954	close to Tricritical-Mean-field
La0.8Ca0.2MnO3	1—2 T	KF	0.349	1.231	4.524	3D-Heisenberg/Ising	[83]
	2—3 T	KF	0.316	1.081	4.421	crossover
	3—4 T	KF	0.281	0.992	4.534	crossover
	4—5 T	KF	0.272	0.91	4.341	crossover
	5—6 T	KF	0.259	0.918	4.552	Tricritical-Mean-field
La0.7Ca0.275Ba0.025MnO3	2—3 T	MAP	0.209	—	—	Tricritical-Mean-field	[84]
	3—4 T	MAP	0.218	1.098	6.04
	4—5 T	MAP	0.227	1.06	5.67
La0.7Ca0.25Ba0.05MnO3	1—2 T	MAP	0.221	—	—	Tricritical-Mean-field	[84]
	2—3 T	MAP	0.225	1.052	5.68
	3—4 T	MAP	0.235	1.012	5.31
	4—5 T	MAP	0.249	1.022	5.1
La0.7Ca0.225Ba0.075MnO3	1—2 T	MAP	0.216	0.973	5.5	Tricritical-Mean-field	[84]
	2—3 T	MAP	0.224	0.982	5.38
	3—4 T	MAP	0.238	1.016	5.27
	4—5 T	MAP	0.253	0.992	4.92
La0.7Ca0.2Ba0.1MnO3	1—2 T	MAP	0.301	1.382	5.59	Tricritical-Mean-field/3D-Ising	[84]
	2—3 T	MAP	0.312	1.38	5.42	3D-Ising
	3—4 T	MAP	0.322	1.381	5.29	3D-Ising
	4—5 T	MAP	0.326	1.342	5.12	3D-Ising
La0.7Ca0.3MnO3	10—14 T	MAP	0.252	1.005	—	Tricritical-Mean-field	[85]

表6关于不同磁场强度范围所得磁相变临界参数的对比分析
Table6.Comparative analysis of critical parameters in different magnetic field ranges.

对于La-Ca-Mn-O体系而言, 当空穴浓度约为0.2时其磁相变为二级, 在低场下获取的磁相变临界参数表明其内部铁磁相互作用接近短程3D-Heisenberg模型^[35]. 而空穴浓度约为 0.4时体现为三重临界行为^[33]. 经过研究发现, 在临近一级磁相变空穴浓度区间(0.2—0.4)由于存在几乎简并的多重态相互竞争, 使得磁场对其磁性相互作用模式十分敏感^[83]. 当空穴浓度约为 0.2时在高场下其临界参数由低场下接近3D-Heisenberg模型逐渐渡越为接近三重临界平均场模型, 这表明极化子局域化模式被高磁场压制, 使得巡游电子去局域化, 并将系统由短程的超交换相互作用主导转变为相对长程的双交换相互作用模式, 并接近类似于0.4空穴浓度的三重临界点. 而对于空穴浓度0.4的多晶样品而言, 由于在顺磁区域存在铁磁团簇而表现出Griffith相, 因此顺磁临界参数γ随着磁场的增大而逐渐低于理论值.
Phan等^[84]在接近三重临界点的La_0.7Ca_0.3–xBa_xMnO₃多晶材料中也研究了关于磁场变化对其临界行为和Griffith相等相关特性的影响. 另外, 在对典型具备一级相变的La_0.7Ca_0.3MnO₃多晶材料施加超高场的磁性研究中发现, 当磁场强度达到10—14 T范围时, 其一级相变特性被明显抑制, 且磁相变临界参数与三重临界点十分符合^[85]. 而Ghorai等^[86]近期在关于La_0.4Pr_0.3Ca_0.1Sr_0.2MnO₃多晶材料在不同磁场下的临界行为研究中发现了二级向一级相变渡越的现象, 并在高场下获得了三重临界参数. 显然, 该体系材料受磁场强度的影响也极为敏感, 其内部晶格极化子、巡游电子去局域化和Griffith相等各种磁性相互作用模式随磁场变化的动态演化特征值得进一步深入探索.

关于磁相变临界行为的研究以及对内部磁性物理机理的深入理解有助于挖掘其在诸多领域的应用前景. 对于钙钛矿锰氧化物而言, 最为引人关注的应用领域包括巨磁阻效应和近室温巨磁热效应等. 经过近十几年的快速发展, 关于钙钛矿锰氧化物材料的磁热效应研究工作已大量开展. 如前所述, 在室温磁制冷领域, 理想的工质材料应兼具一级相变和二级相变各自的优点, 因此对于钙钛矿锰氧化物而言, 当其磁相变渡越于一级和二级相变之间(三重临界点)时, 其磁热效应尤为引人关注. 本文针对三重临界点附近的室温磁热效应相关研究, 总结了接近三重临界点的部分钙钛矿锰氧化物材料的最大等温磁熵变和相对制冷能力(RCP)等重要参数, 列于表7^{[45,46,71,73,86-94]}中.

Material	TC/K	ΔH/ T	–ΔSM/(J·kg–1·K–1)	RCP/(J·kg–1)	Ref.
La0.7Ba0.2Ca0.1MnO3SG	350	2	2.35	70	[87]
		5	5.80	167
La0.7Ba0.2Ca0.1Mn0.95Al0.05O3SG	321	2	2.12	85	[87]
		5	5.30	180
La0.7Ba0.2Ca0.1Mn0.9Al0.1O3SG	300	2	1.86	96	[87]
		5	4.60	193
La0.7Ca0.3MnO3SS	255	1	4.52	45.2	[46]
La0.7Ca0.28Sn0.02MnO3SS	200	1	2.79	55.8	[46]
La0.7Ca0.26Sn0.04MnO3SS	167	1	1.58	69.5	[46]
La0.69Dy0.01Ca0.3MnO3SS	246	5	14.94	100.24	[45]
La0.6Ca0.3Ag0.1MnO3SS	256	2	3.89	55.51	[88]
		5	6.95	179.78
La0.6Ca0.3Ag0.1MnO3SG	270	2	5.55	84.46	[88]
		5	8.67	230.35
La0.6Ca0.3Sr0.1MnO3SG	304	2	2.89	98.17	[89]
		5	5.26	262.53
La0.7Ca0.2Sr0.1MnO3SS	284	3	4.30	150	[90]
La0.7Ca0.2Sr0.1MnO3BM	297	1	1.47	54.4	[73]
La0.7Ca0.19Sr0.11MnO3BM	301	1	1.42	52.5	[73]
La0.7Ca0.18Sr0.12MnO3BM	309	1	1.38	44.2	[73]
La0.7Ca0.27Na0.03MnO3SS	260	4	8.10	232	[91]
La0.7Ca0.24Na0.06MnO3SS	263	4	7.00	234	[91]
La0.7Ca0.21Na0.09MnO3SS	271	4	6.90	236	[91]
La0.7Ba0.1Ca0.1Sr0.1MnO3WM	315	2	1.34	102.51	[71]
		5	3.16	284.53
La0.7Ba0.1Ca0.1Sr0.1MnO3SG	330	2	2.58	74.92	[71]
		5	4.89	229.29
La0.8Na0.2Mn0.97Bi0.03O3SS	320	5	4.77	218	[92]
La0.8Na0.2Mn0.97Bi0.03O3SG	257	5	5.88	252	[92]
La0.4Pr0.3Ca0.1Sr0.2MnO3SS	289	2	3.08	83.3	[86]
La0.6Gd0.1Sr0.3Mn0.8Si0.2O3SG	271	5	5.35	180	[93]
La0.7Bi0.05Sr0.15Ca0.1Mn0.95In0.05O3SG	310	5	6.00	258	[94]
注: 1) 表中符号含义如下: TC为居里温度; ΔH为磁场变化范围; –ΔSM为最大磁熵变值; RCP为相对制冷能力, 由磁熵变曲线的峰值与半峰宽数值相乘而得; 2) SS表示固相反应法; SG表示溶胶凝胶法; WM表示湿混法; BM表示球磨法.

表7接近三重临界点的部分近室温钙钛矿锰氧化物的最大磁熵变和相对制冷能力
Table7.Maximum magnetic entropy change and RCP values of perovskite manganites near tricritical point.

从表7可知, 对于钙钛矿锰氧化物体系而言, 无论是通过掺杂等成分调控还是通过制备工艺的调整, 相比于对应的一级相变和远离一级相变的二级相变成分区间, 当材料处于三重临界点附近时均表现出了综合制冷能力优异的特点. 如微量Dy掺杂La_0.69Dy_0.01Ca_0.3MnO₃多晶材料^[45]在5 T磁场变化下, 最大等温磁熵变仍达到了14.94 J·kg^–1·K^–1. 而微量Sn掺杂的La_0.7Ca_0.28Sn_0.02MnO₃化合物^[46]在仅为1 T磁场变化下的最大磁熵变仍保持了2.79 J·kg^–1·K^–1, 且相对制冷能力达到55.8 J·kg^–1. 微量Na掺杂的La_0.7Ca_0.27Na_0.03MnO₃化合物^[91]在4 T磁场变化下最大磁熵变为8.1 J·kg^–1·K^–1, 相对制冷能力则达到了232 J·kg^–1. 另外, 在通过溶胶凝胶法制备的锰氧化物La_0.8Na_0.2Mn_0.97Bi_0.03O₃^[92], La_0.6Gd_0.1Sr_0.3Mn_0.8Si_0.2O₃^[93]以及La_0.7Bi_0.05Sr_0.15Ca_0.1Mn_0.95In_0.05O₃^[94]中, 综合磁热效应均表现优异, 而这些材料都被发现处于三重临界点附近. 可以看出, 对于接近三重临界点的钙钛矿锰氧化物体系而言, 其磁热效应十分值得进一步深入挖掘.

钙钛矿锰氧化物因复杂的电磁学和相变特性, 在室温磁制冷及相关领域的应用前景十分光明, 一直以来都是磁学和材料学研究领域关注的重点. 正是由于内部复杂的电磁学及相互作用性质, 无论是在理论研究还是在应用领域都存在极大的挖潜空间, 这正是对其磁相变临界行为深入研究的意义所在. 本文详细介绍了钙钛矿锰氧化物的相关电磁学和相变理论, 介绍了分析磁相变临界行为和磁热效应的分析方法, 重点着眼于综述以几种典型钙钛矿锰氧化物体系为基础, 分析对比通过不同成分不同位置的掺杂、以及不同制备工艺所得材料的磁熵变和磁相变临界行为, 在一定程度上归纳了部分普遍性结论, 对进一步深入研究该体系以及其他磁热效应材料的磁学特性提供了一定的借鉴. 对于目前各种具备一级相变的磁制冷材料而言, 关于三重临界点的相关研究工作可有助于获得可逆的大磁热效应, 并有望进一步扩大室温磁制冷领域的应用前景.