摘要:超冷长程Rydberg-基态分子由一个Rydberg原子与一个或多个基态原子通过Rydberg电子与基态原子的低能散射形成. 这类分子具有尺寸大和永久电偶极矩大等优良特性, 是近年来人们研究的热点课题. 本文综述了超冷Rydberg-基态分子的最新理论和实验进展, 包括Rydberg电子与基态原子低能散射的理论模型和势能曲线, 光缔合Rydberg分子的实验制备和光谱特性, Rydberg-基态分子永久电偶极矩的测量等. 最新的研究发现Cs nD_J -型Rydberg-基态分子的永久电偶极矩为负值, 这与以往的此类分子(电偶极矩为正)不同. 负电偶极矩反映了Rydberg电子的概率密度在基态(微扰)原子附近是减少的, 由微扰原子附近Rydberg电子波函数的相消干涉产生.
关键词: 超冷长程Rydberg-基态分子/
Fermi赝势/
绝热势能曲线/
永久电偶极矩

English Abstract

全文HTML

--> --> -->

长程Rydberg-基态分子是由一个Rydberg原子与一个或多个基态原子形成的一类奇异的分子, 具有尺寸大(～μm)和永久电偶极矩大(～kilo-Debye)等性质. 这种奇异分子的束缚机制是Rydberg电子与中性原子之间的低能散射相互作用, 是不同于共价键、离子键及范德瓦耳斯相互作用的一种新型束缚机制.
低能散射相互作用的研究可追溯到20世纪30年代. 1934年, Amaldi和Segré^[1]在Rydberg原子碰撞实验中发现了与预期不同的结果, 即: 在钠或钾的蒸汽中充入H₂和N₂等气体的实验中, 并没有观察到预期的Rydberg原子吸收谱线由于碰撞导致的展宽, 而是谱线的频移. 这一现象无法用已知的理论进行解释, 他们在与Fermi的讨论中发现, 这些能级的频移是由碱金属原子的价电子与外部气体原子散射引起的. 随后Fermi发展了量子散射理论并在该理论中引入了散射长度的概念, 导致Fermi赝势(Fermi pseudopotential)^[2]的产生. 在Fermi的理论中只考虑了s-波散射相互作用, 1977年, Omont^[3]发展了这一理论并考虑了任意高阶波散射, 完善了中性原子的散射理论. 2000年, Greene等^[4]首次在理论上预言了超冷长程Rydberg-基态分子的存在, 理论上计算了铷Rydberg-基态分子的绝热势能曲线, 并获得了巨大的分子永久电偶极矩. 计算的电子波函数概率密度呈三叶虫型, 因此这类分子被称为三叶虫型分子^[4]. 不久, 理论学家又预测出形如蝴蝶状的电子波函数概率密度的分子, 被称为蝴蝶型分子^[5,6].
2009年, Bendkowsky等^[7]首次在实验中成功观测到s-波散射形成的超冷Rb nS态Rydberg-基态分子. 之后, 其他研究小组分别观测到了Rb原子nP_{1/2, 3/2}^[8]和nD_3/2,5/2^[9-11]态以及Cs原子nS_1/2^[12,13], nP_3/2^[14]和nD_3/2,5/2^[15-17]的Rydberg-基态分子. 近年来, 人们在实验中观测到了p-波共振形成的内层势阱分子^[18,19]. 2020年, Peper和Deiglmayr^[20]提出一种超冷原子离子对态的激发方式, 提出了一种形成heavy-Rydberg态^[21]的新方法. 由于Rydberg-基态分子的尺寸大且具有巨大的永久电偶极矩, 使得这类分子成为研究量子模拟^[22]和量子信息过程^[23-25]的理想介质.
本文主要介绍Rydberg-基态分子的束缚机制和实验研究成果, 包括Rydberg电子与基态原子低能电子散射的理论模型、Fermi赝势和Rydberg-基态分子的绝热势能曲线、光缔合光谱及永久电偶极矩的测量等.

在Rydberg电子与基态原子相互碰撞散射过程中, 基态原子被视为微扰, 其散射相互作用势能由Fermi赝势描述^[2,3]. 图1为散射相互作用的示意图, 在以Cs⁺离子为参考的坐标系中, 散射相互作用能表示为^[3]
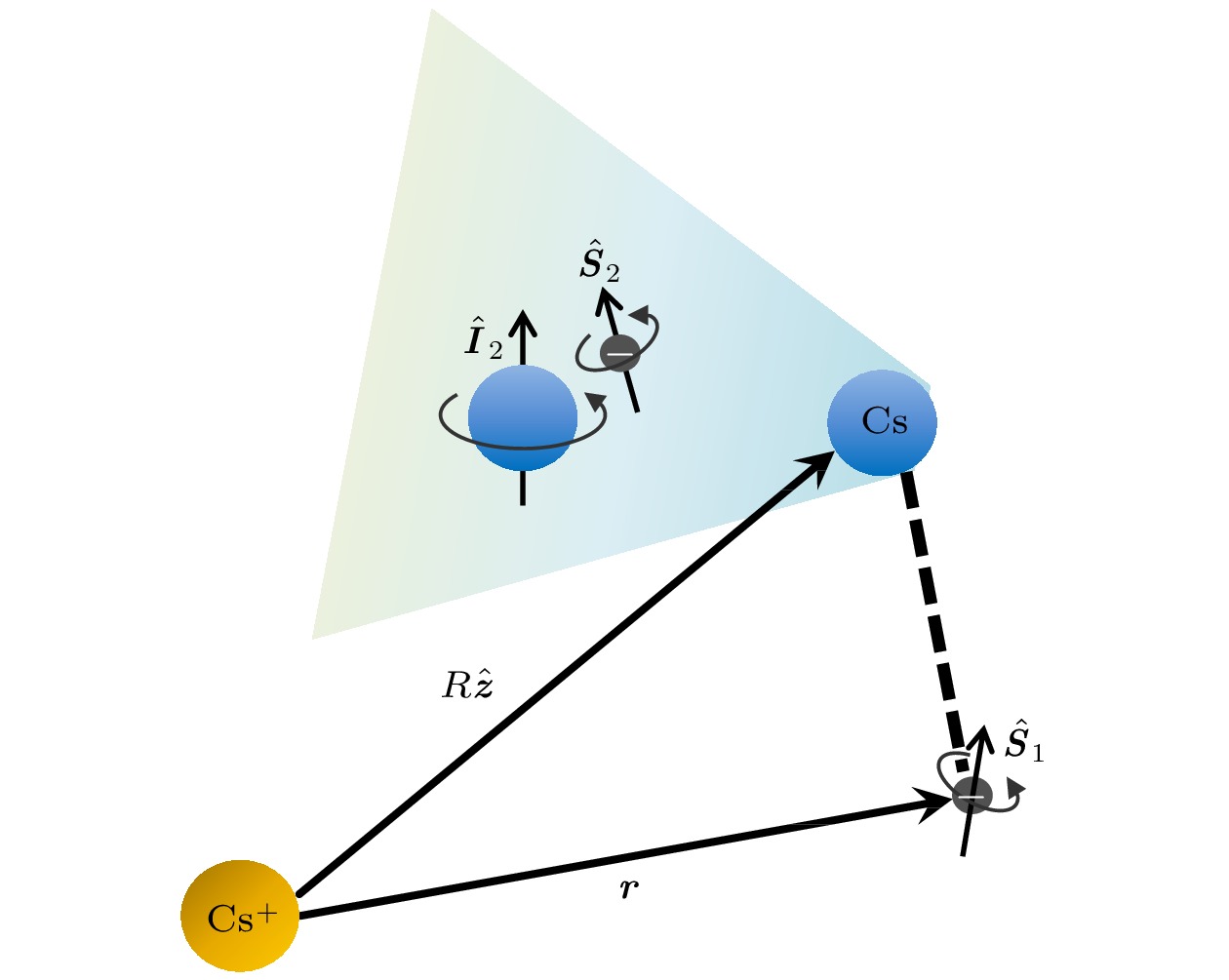图 1 Rydberg-基态分子示意图. 自旋为$ { \widehat{{S}}}_{1} $的Rydberg电子和基态原子分别位于以Cs⁺离子为参考系的位置r和$R\hat{{z}}$处. $ {\widehat{{S}}}_{2} $和$ {\widehat{{I}}}_{2} $分别是基态原子的电子自旋和核自旋
Figure1. Schematic of the molecular system. The Rydberg electron with spin $ {\widehat{{S}}}_{1} $ sits at position r relative to the ionic core. A cesium ground state atom is located at position $R\hat{{z}}$ relative to the ionic core of the Rydberg atom. $ {\widehat{{S}}}_{2} $ and $\hat{ I}_2$ are electronic and nuclear spin of the ground state atom, respectively.

$\begin{split}\widehat{V}\left({{r}};R\right)=\;&2{\rm{\pi }}{a}_{\rm{s}}\left(k\right){\delta }^{3}\left({{r}}-R\widehat{ {z}}\right)\\&+6{\rm{\pi }}{\left[{a}_{\rm{p}}\left(k\right)\right]}^{3}{\delta }^{3}\left({{r}}-R\widehat{ {z}}\right)\overleftarrow{\nabla } \cdot \overrightarrow{\nabla },\end{split}$

其中, r和$ R\widehat{{z}} $分别是Rydberg电子和基态原子相对Cs⁺离子的位置, $ {a}_{\rm{s}}\left(k\right) $为s-波散射长度, $ {a}_{\rm{p}}\left(k\right) $为p-波散射长度, δ为δ函数, $\nabla $表示梯度算符, k是Rydberg电子的动量. 散射长度$ {a}_{l}\left(k\right) $与能量有关, 表示为$ {{a}_{l}\left(k\right)}^{2 l+1}=-{\rm{tan}}{\eta }_{l}\left(k\right)/{k}^{2 l+1} $, 其中, l为散射波阶数, l = 0或1表示s-波或p-波散射, $ {\eta }_{l} $是散射相移.
Rydberg原子与基态原子相互作用的总哈密顿量表示为^[26]

$ \widehat{H}\left({{r}};R\right)={\widehat{H}}_{0}+\sum _{i={\rm{S}},{\rm{T}}}\widehat{V}\left({{r}};R\right)\widehat{{P}}\left(i\right)+{A}_{{\rm{H}}{\rm{F}}{\rm{S}}}{\widehat{{S}}}_{2} \cdot {\widehat{{I}}}_{2}{. } $

(2)式等号右侧第一项$ {\widehat{H}}_{0} $是Rydberg原子的哈密顿量, 包含Rydberg态的量子亏损和精细结构. 第二项描述的是散射相互作用, 对于碱金属原子来说, Rydberg电子自旋S₁和基态原子电子自旋S₂耦合形成自旋单态S (S₁ + S₂ = 0)和自旋三重态T (S₁ + S₂ = 1), 用投影算符$\widehat{{P}}\left({\rm T}\right)\!=\! {\widehat{{S}}}_{1} \cdot {\widehat{{S}}}_{2} \!+\! 3/4$, $\widehat{{P}}\left({\rm S}\right)= 1-\widehat{{P}}\left({\rm T}\right)$表示. 最后一项表示基态原子的电子自旋$ {\widehat{{S}}}_{2} $与核自旋$ {\widehat{{I}}}_{2} $耦合的超精细相互作用F, $ {A}_{{\rm{H}}{\rm{F}}{\rm{S}}} $为超精细结构常数.
将(2)式在核间距R上进行对角化可得到分子绝热势能曲线^[4,7]. 分子的振动态和转动态可通过分子哈密顿理论^[27-29]计算获得. 对于双原子Rydberg-基态分子来说, 可以通过相应的绝热势能曲线准确地获得振动态和振动波函数. 多原子分子^[30-33]却很难获得准确的振转能级.
图2所示为理论计算的n = 19附近的Cs Rydberg-基态分子的势能曲线. 处于700a₀附近(标注I)的外层势阱主要由三重态³s-波散射形成, 对应的电子波函数概率密度形如三叶虫, 见插图I, 这类Rydberg-基态分子称为“三叶虫型”分子^[4]. 处于200a₀—400a₀附近(标注II)的内层势阱, 主要由三重态³p-波散射形成, 对应的电子波函数概率密度形如蝴蝶状, 见插图II, 这类Rydberg-基态分子称为 “蝴蝶型”分子^[5,6]. “蝴蝶型”分子的势阱深度比“三叶虫型”分子深, 而平衡核间距小. 图2中的电子波函数中(插图)黑色点表示Cs离子, 蓝色点表示基态原子.
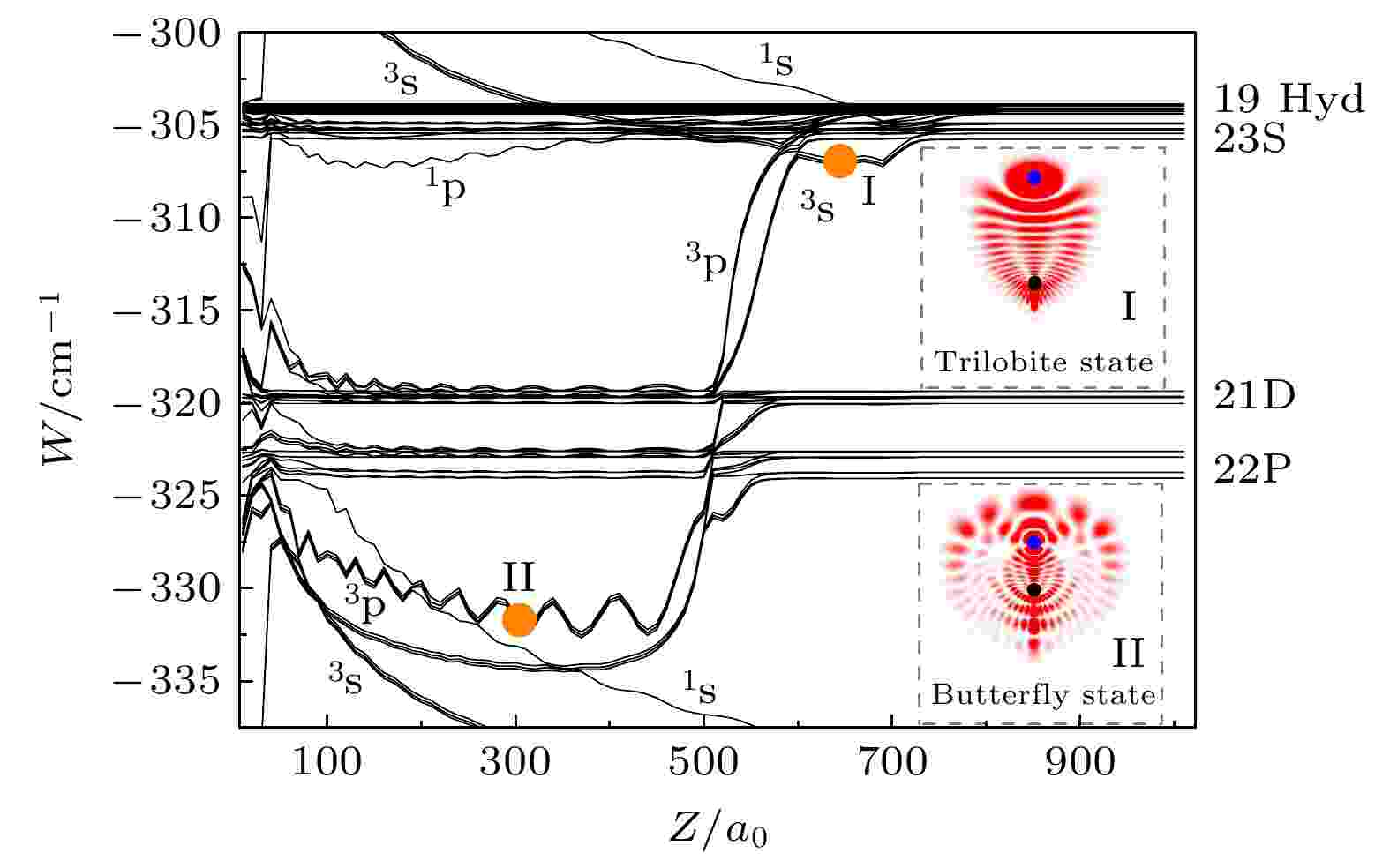图 2 理论计算的n =19附近的Cs分子势能曲线, 其中插图是橙色原点标记I (II)处势阱对应的“三叶虫型”(“蝴蝶型”)分子的电子概率密度
Figure2. Calculations of potential energy curves of the Cs Rydberg-ground molecule near n = 19. Inset I (II) displays the electronic wave function densities of “Trilobite” (“Butterfly”) molecules at the orange points marked I (II) in the figure.

这里主要考虑最外层势阱形成的三叶虫型分子. 以铯原子37D_5/2 + 6S_1/2形成的分子为例进行说明, 对应的势能曲线如图3所示^[17]. 图3中虚线所示的势能曲线是只考虑s-波散射的结果, 包含两个势阱, 深势阱(^TΣ)主要由s-波自旋三重态T(³s)散射形成, 浅势阱(^STΣ)由s-波自旋单态S和自旋三重态T的超精细结构混合形成. 图3的实线表示同时考虑s-波和p-波散射时的绝热势能曲线. 从图3可以看出, p-波散射对势能曲线的最外层势阱几乎没有影响, 因此s-波散射可以很好地描述分子势能曲线最外层势阱的性质. 然而, p-波散射对内层势阱有较大的影响, 使内层势阱的阱深显著增加, 如图3中核间距R < 1800a₀处的势阱. 以p-波散射为主形成的分子的电子波函数概率密度形如蝴蝶状, 如图2所示, 形成的Rydberg-基态分子叫作“蝴蝶型”分子^[5,6].
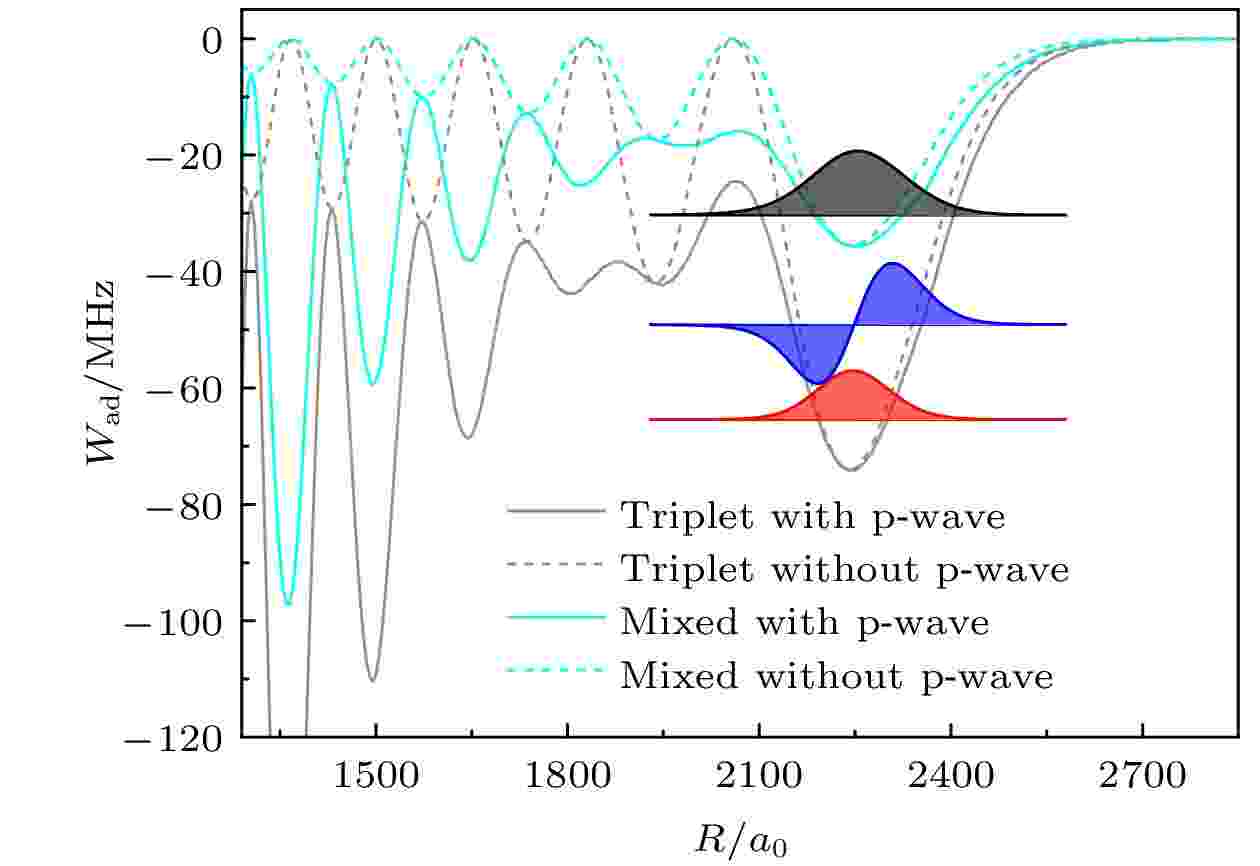图 3 数值计算的37D_5/2 + 6S_1/2 (F = 4) Rydberg-基态分子的绝热势能曲线. 深势阱(灰色线)主要由自旋三重态T形成, 浅势阱(蓝色线)主要由自旋单态S和自旋三重态T超精细结构混合而形成. 实线和虚线分别是考虑和不考虑p-波散射相互作用时的分子绝热势能曲线. 彩色填充线分别是最外层深势阱^TΣ (v = 0)和^TΣ (v = 1)的振动波函数, 黑色填充线是最外层浅势阱^STΣ (v = 0)的振动波函数^[17]
Figure3. Calculations of potential energy curves of the Rydberg-ground molecule that is asymptotically related to the 37D_5/2 Rydberg atomic line with (solid lines) and without (dashed lines) taking the p-wave scattering interaction into account. The deep potential (gray) for the triplet state and shallow wells (blue) for hyperfine-mixed singlet-triplet potential state. The vibrational wave functions in the outmost wells are indicated in filled curves for ^TΣ (v = 0) and ^TΣ (v = 1) of deep potential and ^STΣ (v = 0) of shallow potential^[17].

基态原子的超精细结构F对Rydberg分子的最外层深势阱^TΣ态几乎没有影响, 但是浅势阱^STΣ态的阱深则与基态原子所处的超精细结构有关. 以Cs原子为例, 如图4所示^[16]. 图4(a)为理论计算的36D_5/2 + 6S_1/2 (F = 4) (黑色虚线) 和36D_5/2 + 6S_1/2 (F = 3) (青色实线) 的分子势能曲线. 深势阱对应的势能曲线主要由自旋三重态³s-波散射形成, 对于基态原子处于F = 4和F = 3的超精细能级, 深势阱^TΣ态的势阱深度相同, 不随基态原子的超精细能级的变化而变化; 浅势阱对应的势能曲线由单重态¹s和三重态³s-波散射混合形成, 浅势阱^STΣ态的势阱深度依赖于基态原子所处的超精细能级, 即基态原子处于超精细能级F = 3的势阱深度大于F = 4的势阱深度.
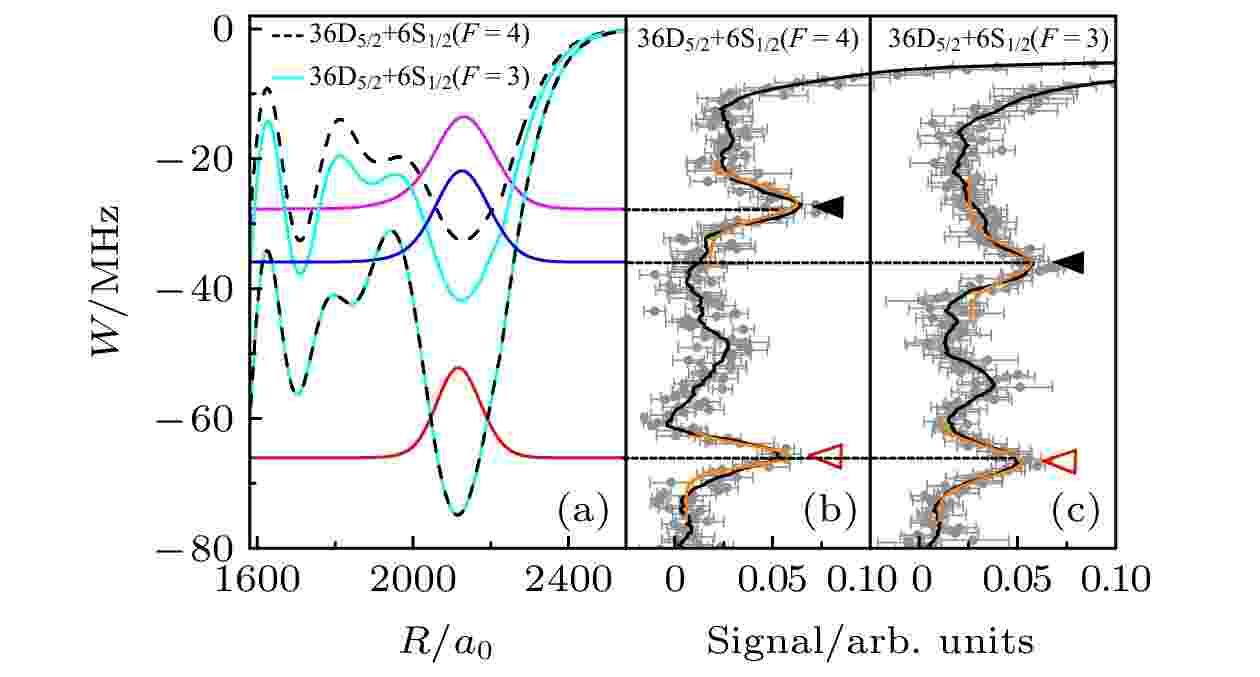图 4 (a) 数值计算的Cs原子36D_5/2 + 6S_1/2 (F = 4)(黑色虚线)和36D_5/2 + 6S_1/2 (F = 3)(青色实线) Rydberg-基态分子的绝热势能曲线. 深势阱(^TΣ)主要由自旋三重态T的s-波散射形成, 势阱深度不随基态原子的超精细能级F的变化而变化. 浅势阱(^STΣ)主要由自旋单态S和自旋三重态T超精细结构混合而形成, 其势阱深度与基态原子所处的超精细能级F有关, 基态原子处于超精细能级F = 3的势阱深度大于F = 4的势阱深度. 彩色的实线表示v = 0的振动波函数. (b), (c)为实验测得的36D_5/2 + 6S_1/2 (F = 4)和36D_5/2 + 6S_1/2 (F = 3)的光缔合光谱. 实心(空心)三角表示由浅势阱(深势阱)形成的分子信号. 黄色线是高斯拟合曲线^[16]
Figure4. (a) Calculations of potential energy curves (PECs) for 36D_5/2 + 6S_1/2 (F = 4) (black dashed lines) and PECs for 36D_5/2 + 6S_1/2 (F = 3) (cyan solid lines) molecules, respectively. The deep potentials (^TΣ) mostly arise from triplet s-wave scattering and do not depend on F. The shallow potentials (^STΣ) mostly arise from mixed singlet-triplet s-wave scattering and depend on F; The potential energy curves for F = 3 is deeper than that for F = 4. The colored lines show the v = 0 vibrational wave functions of the potential energy curves. (b), (c) Experimental photo-association spectra for 36D_5/2 + 6S_1/2 (F = 4) and 36D_5/2 + 6S_1/2 (F = 3) molecules. Filled (open) triangles mark the molecular signals formed by mixed (triplet) potentials. The yellow lines display Gaussian fittings^[16].

实验上对浅势阱和深势阱形成的分子的束缚能的精确测量, 可以提供对s-波单态和三重态散射相移及散射长度的精确萃取. 因此, 长程Rydberg-基态分子可以作为高精度的散射实验材料制备, 以及用于探测超慢电子-原子碰撞(电子能量低于10 meV)实验, 这是通过电子传输^[34]等方法难以实现的. 通过长程Rydberg-基态分子已经实现了s-波相移^[14,35,36]和p-波相移^{[11,18,35,37]}的测量.

2

-->

3.1.双原子Rydberg-基态分子

Bendkowsky等^[7]于2009年首次在实验上观测到了铷原子主量子数取值为n = 34—40的长程Rydberg-基态分子, 并对分子寿命以及分子在外电场作用下的Stark频移进行了测量. 图5是实验测量的铷原子n = 35—37 S态Rydberg-基态分子的光缔合光谱^[7], 在相对于原子共振负失谐处获得了非常明显的分子信号, 他们用s-波散射理论解释了实验结果. 之后, 人们又实现了不同原子种类和同位素(¹³³Cs, ⁸⁴Sr, ⁸⁷Sr, ⁸⁵Rb)以及不同电子态(P态和D态)的长程Rydberg-基态分子的实验观察^{[9-11,13,16,17,38-42]}. 实验上, 人们用光缔合的方法对双原子(一个Rydberg原子和一个基态原子)Rydberg-基态分子进行制备, 所要求的冷原子密度在10¹⁰—10¹³ cm^–3量级.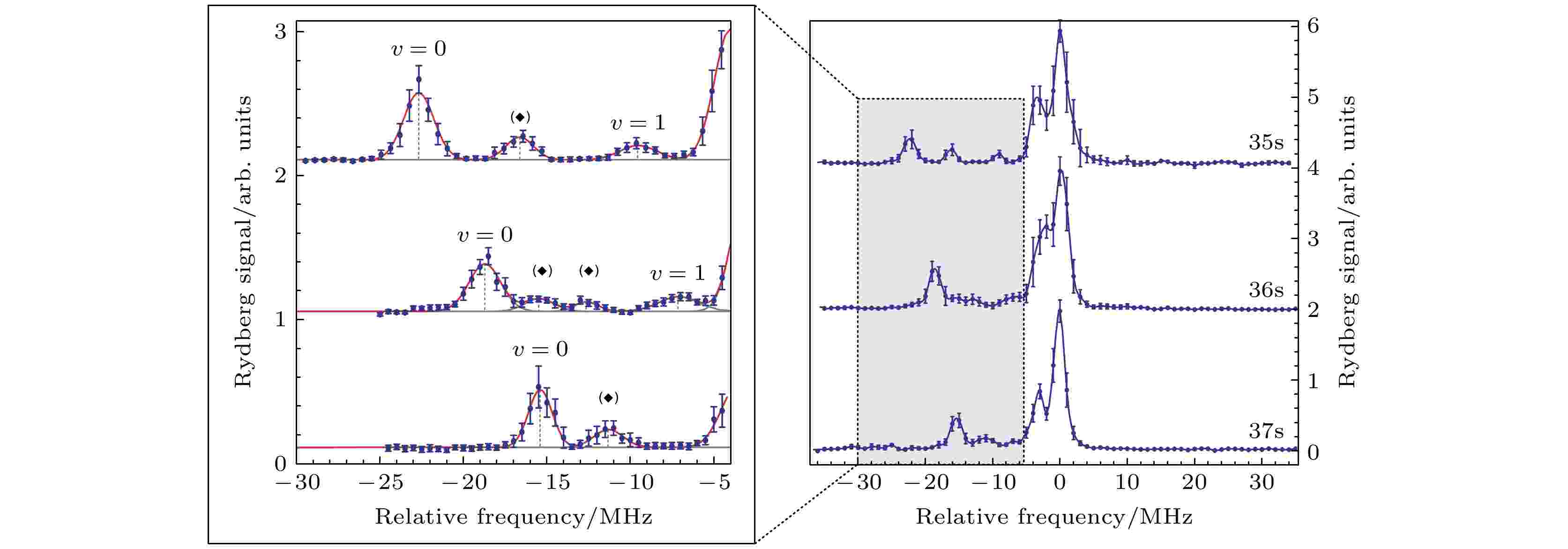
图 5 实验测量的Rb nS + 5S (n = 35—37) Rydberg-基态分子的光缔合光谱. 左图是右图灰色部分的放大^[7]
Figure5. Measured spectra of nS + 5S (n = 35–37) of Rb atoms. The left panel shows the enlarged view of the gray area on the right^[7].

图4为实验测量的Cs原子36D_5/2 + 6S_1/2的光缔合光谱线与理论计算的势能曲线的对比. 图4(b)和图4(c)是实验测量的双光子光缔合光谱, 对应基态原子分别处于超精细结构F = 4和F = 3. 图中灰色的点是原始实验数据, 黑色线是实验数据的15次平均值, 黄色线是对分子信号进行高斯拟合的结果. 图4(a)是理论计算的绝热势能曲线. 黑色虚线和青色实线分别是基态原子处于F = 4和F = 3的势能曲线, 红色、蓝色和粉色实线分别表示势能曲线的振动基态(v = 0)波函数. 实验测量与第二部分所述的低能电子散射理论的计算结果相符合, 基态原子的超精细结构使基态原子为F = 3的浅势阱(^STΣ)比基态原子为F = 4时的势阱深, 而深势阱(^TΣ)的势阱深度不随基态原子的超精细结构变化.
2 -->

3.2.多原子Rydberg-基态分子

长程Rydberg-基态分子是在高密度的冷原子样品中通过光缔合的方法制备的. 当密度足够大时, Rydberg电子可与多个基态原子散射形成多原子Rydberg-基态分子^[43]. 关于多原子Rydberg-基态分子^[43]的文献介绍了包含2个、3个和4个基态原子的Rydberg-基态多聚体. 在这种情况下得出的一个重要结论是三原子的Rydberg-基态三聚体形成稳定的环状结构, 但相应的二聚体(双原子分子)却相互排斥^[44]. 由于选择定则的限制, 通过光缔合的实验方案很难实现高-? Rydberg态的激发, 因此随后的大多数实验和理论工作都集中在低-? (? ≤ 2)的Rydberg-基态分子.
在实验上观测到二聚体Rydberg-基态分子后不久, 人们就观测到了三聚体的光缔合光谱^[35], 以及四聚体、五聚体和六聚体的Rydberg-基态分子^[45]. 研究表明, 这些多原子聚合物的结合能与基态原子数成线性比例关系, 即结合能是二聚体结合能的整数倍. 图6是Rb (nS) 态的多原子Rydberg-基态分子光缔合光谱, 其中多原子分子线由彩色菱形标记^[45]. 如图6所示, 三聚体(紫色菱形)是二聚体(红色菱形)结合能的两倍, 因为两个基态原子都以能量最低的二聚体模式被Rydberg电子束缚. 这种构造原理后来被推广到壳结构模型^[46].
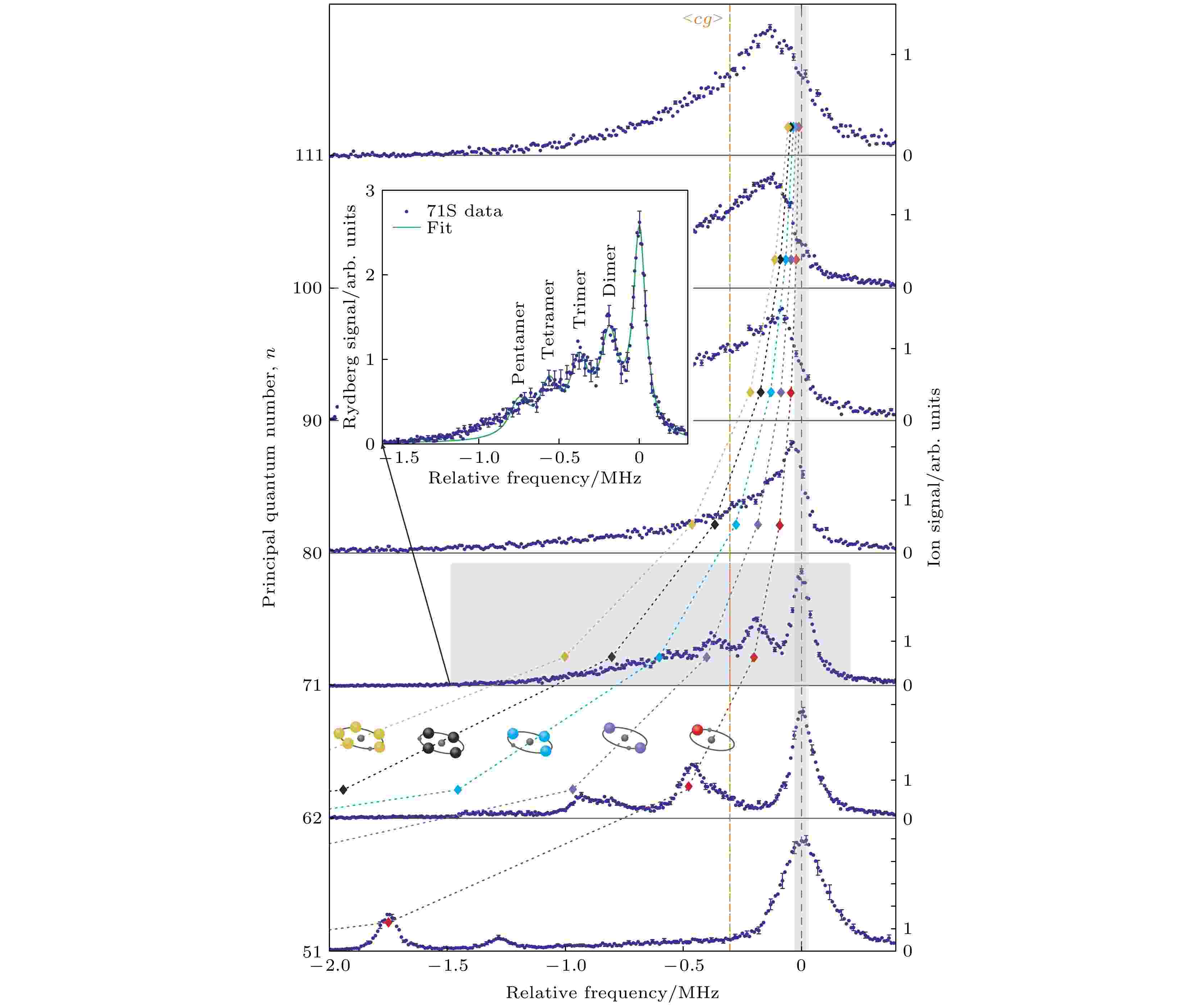图 6 不同主量子数n 的Rb (nS)多原子Rydberg-基态分子的光缔合光谱, 其中多原子分子的谱线由彩色菱形标记^[45]
Figure6. Photoassociation spectra of polyatomic Rb (nS) ultra-long Rydberg-ground molecules for different principal quantum numbers n. Polyatomic lines are marked by colored diamonds^[45].

图6所示为原子密度等于10¹² cm^–3且在不同主量子数n下测得的多原子Rydberg-基态分子的光缔合光谱. 当主量子数n ≤ 71时, 可以很好地区分多原子Rydberg-基态分子的信号, 但对于更大的主量子数n的多聚体, Rydberg电子轨道内基态原子数目以n⁶增加, 而束缚能却以n^–6减小. 在这种情况下, 实验光谱显示了一个碰撞加宽的Rydberg谱线而不是分离的分子共振线, 如图6中n = 111的情况. 在平均场极限下, 碰撞加宽的谱线呈现出与原子Rydberg态有一定失谐的高斯峰^[1,47,48], 这一现象可由Fermi^[2]理论进行解释, 对应的失谐量由所有基态原子的平均相互作用能给出:

$ \varDelta=\int {\rm{d}}{R}^{3}{\rm{d}}{r}^{3}V\left({{r}};R\right){\left|{\varphi }_{n{\rm{s}}}\left({{r}}\right)\right|}^{2}\rho \left(R\widehat{{z}}\right){,} $

$ \varDelta\approx 2{\rm{\pi }}{a}_{\rm{s}}\left[0\right]{\rho }_{0}{,} $

其中, $ {\varphi }_{n{\rm{s}}}\left({{r}}\right) $是Rydberg电子波函数, $\rho \left(R\hat{{z}}\right)$是原子密度. 假设$\rho \left(R\hat{{z}}\right)={\rho }_{0}$, 且将电子-原子相互作用$ V({{r}};R) $用s-波散射相互作用在零能极限下的s-波散射长度$ {a}_{\rm{s}}\left[0\right] $代替, 即可得到(4)式. (4)式的广义形式包括与能量有关的散射长度、p-波的贡献以及不均匀的原子密度.
无论实验还是理论, S-态Rydberg系统都具有一定的优势: 1) S-态的各向同性可以使理论模型得以简化; 2)较大的Franck-Condon因子在实验上产生较大的激发概率. 相反, ? > 0的态Franck-Condon因子相对减小, 由于原子的各向异性和基矢所需的更大的希尔伯特空间, 使高?态的Rydberg-基态分子难以实现精确的理论描述. 但高?态的复杂性可以导致更丰富的物理特性. 特别是? > 0的多原子Rydberg-基态分子的Born Oppenheimer势能曲面与角度相关, 即这些势能曲面不仅取决于基态原子的径向距离, 还取决于基态原子间的相对角度^[15,49-51], 使高?态的Rydberg-基态分子具有丰富的光谱特性.

分子的电偶极矩对化学反应精确控制^[52,53]、精密光谱测量、实现量子模拟^[22]、量子信息处理^[23]及基本对称性测试^[53]等方面具有重要意义. 分子的永久电偶极矩是对称性破缺的体现, 因此, 同核分子一般不具有永久电偶极矩, 但Rydberg-基态分子是例外, 这类分子具有永久电偶极矩, 且达到约kilo-Debye量级^[4,12].
2011年, Li等^[54]首次测量了Rb原子nS态长程Rydberg-基态分子的永久电偶极矩, 测量结果为1 Debye, 与理论计算符合得很好; 测量的Rb原子25P态势能曲线附近的蝴蝶型分子的永久电偶极矩约为500 Debye^[55]. 2015年, Booth等^[12]测量了Cs原子nS态的Rydberg-基态分子的永久电偶极矩, 其值高达~2000 Debye, 图7所示为对应的实验结果. 由于Cs原子nS态的量子亏损为4.05, 接近于整数, 因此nS Rydberg态具有非常接近类氢原子的势能曲线, 使高-?的三叶虫型分子的势能曲线与nS态交叉. 三叶虫分子态是高角动量量子态, 根据角动量守恒一般不能由单光子或者双光子激发获得三叶虫分子态, 但由于铯原子三叶虫型分子的势能曲线与nS态之间的这种交叉, 使得在Cs原子中三叶虫型分子混合了S-态特性, 导致nS态Rydberg-基态分子具有巨大的永久电偶极矩.
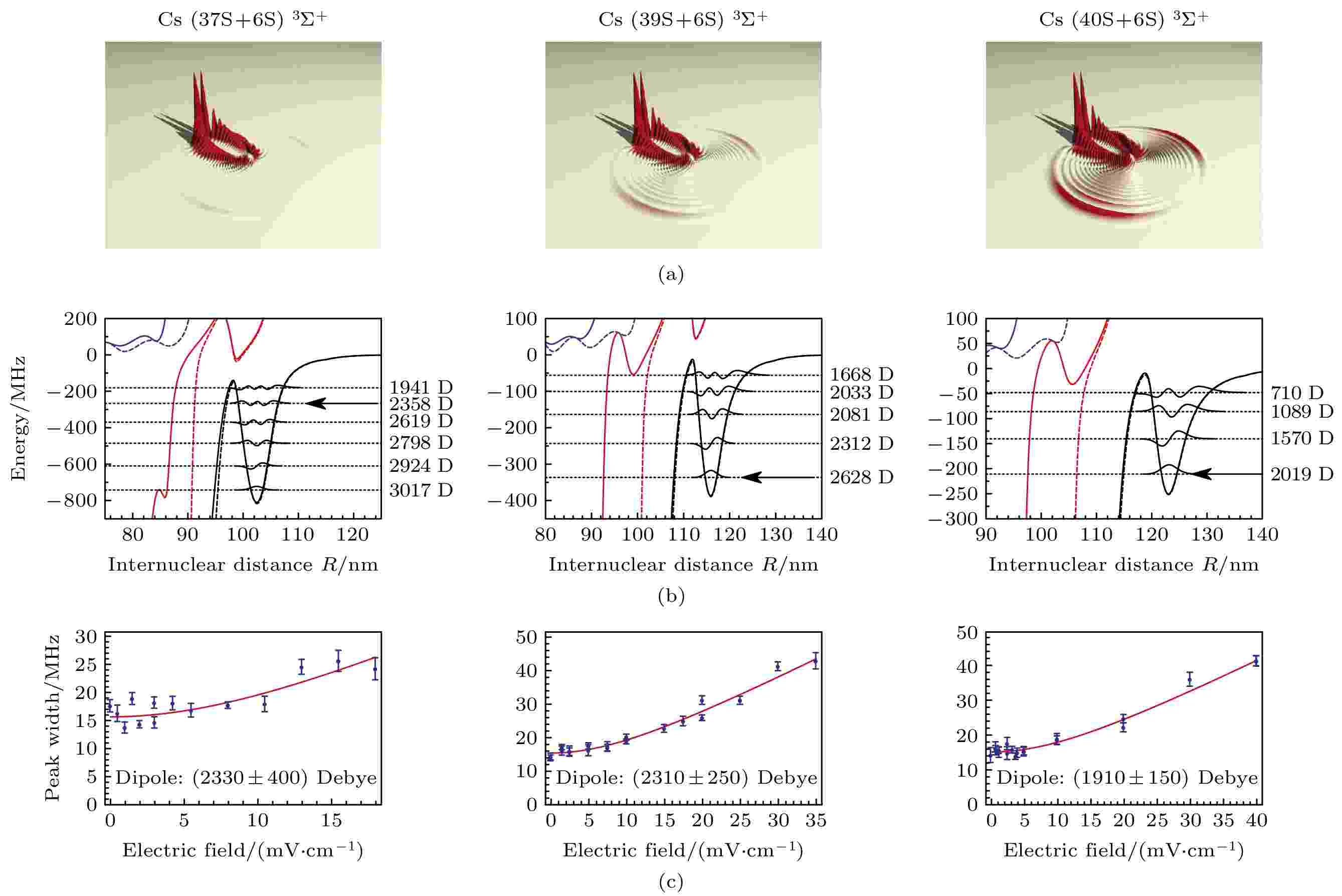图 7 (a) 理论计算的Cs nS + 6S (n = 37, 39, 40) ^TΣ⁺态电子波函数密度^[12]; (b) 相应于(a)图的势能曲线和振动能级^[12]; (c)为(b)图中箭头标注的振动能级在外电场中分子谱线的展宽^[12]
Figure7. (a) Calculated densities of electron wave functions for the ^TΣ⁺ states of Cs nS + 6S (n = 37, 39, 40)^[12]; (b) the corresponding potential energy curves for the states shown in panel (a) with calculated vibrational levels^[12]; (c) the broadening of the vibrational levels indicated by an arrow in panel (b) as a function of applied electric field^[12].

研究表明这些分子的永久电偶极矩都是正的^[12-14,56], 这说明Rydberg电子波函数在微扰原子附近是干涉相长的. 2020年, Bai等^[16]在实验上制备了Cs nD_J + 6S_1/2 Rydberg-基态分子并测量了其永久电偶极矩. 理论模拟结果显示, Cs nD态Rydberg-基态分子的永久电偶极矩是负值, 这与文献报道的研究结果不同. 偶极矩的负值反映了在基态(微扰)原子附近的Rydberg电子密度的减少, 这是由电子结构混合引起的.
实验上可通过测量分子信号在弱电场作用下的分子谱展宽实现对电偶极矩d的测量. Rydberg分子在弱电场中的能量表示为($ -{{d}} \cdot {{E}} $)(E为电场强度), 远小于分子束缚能. 这时分子信号在弱电场中将沿分子信号中心产生非均匀展宽, 对应的展宽由矩形函数$ 2 dE/h $表示. 考虑到激发光线宽和原子云处的电磁场的非均匀性等因素, 实际测量的分子信号并不是理想的矩形线型. 为了获得分子信号的展宽信息, 我们将无外场时信号的高斯线型函数与矩形函数$ 2 dE/h $进行卷积运算获得实际光谱的线型函数, 进而获得Rydberg-基态分子的电偶极矩. 弱电场中Rydberg-基态分子的线型 $ S(\Delta f) $是激发光失谐量$ \Delta f $的函数, 表示为

$\frac{h}{{2dE}}\left[ {{\rm{erf}}\left( {\frac{{\Delta f + dE/h}}{{\sqrt 2 {\sigma _{\rm{f}}}}}} \right) - {\rm{erf}}\left( {\frac{{\Delta f - dE/h}}{{\sqrt 2 {\sigma _{\rm{f}}}}}} \right)} \right],$

其中, h为普朗克常数; $ {\sigma }_{\rm{f}} $为高斯线型的标准差, 由高斯拟合无外电场时的分子信号获得. (5)式中电场E可以通过Rydberg原子Stark光谱准确测得, 只有一个待定参数, 即偶极矩d. 由(5)式拟合实验测量的外场中的Rydberg分子谱即可获得偶极矩d的值, 进而实现Rydberg-基态分子永久电偶极矩的测量. 图8左侧为不同电场下的光缔合谱线, 分子谱的线宽随着电场的增加而增加. 图8右侧给出了电场为E = 0.37 V/cm时深势阱(^TΣ)和浅势阱(^STΣ)分子振动基态v = 0的谱线、(5)式的拟合结果以及测得的电偶极矩|d|值. 对于图8所示的n = 37的^TΣ (v = 0)分子态的振动基态, 实验测量的平均偶极矩为d = (4.79 ± 0.78)ea₀, 与理论计算的结果d_Theor. = –4.64ea₀符合得很好.
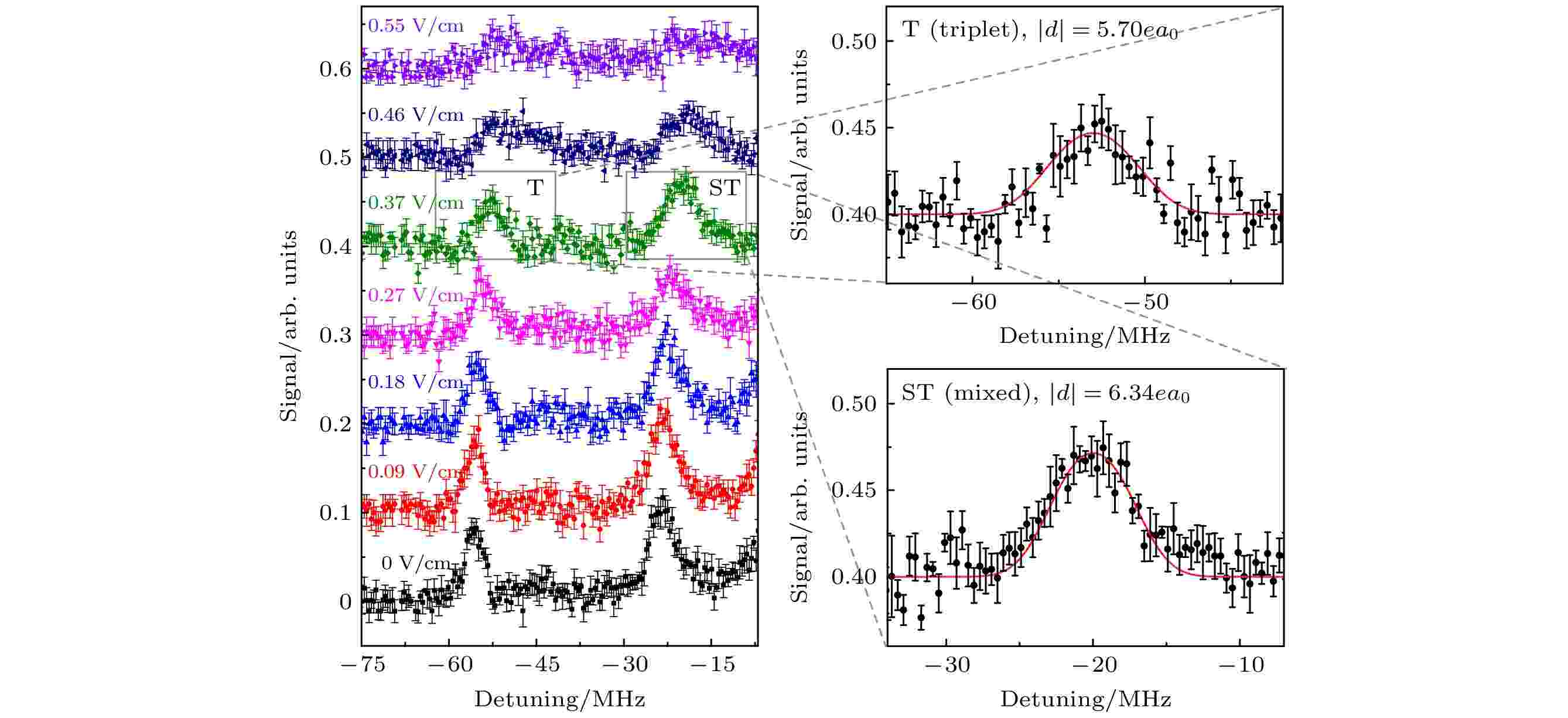图 8 不同电场E下的37D_5/2 + 6S_1/2 (F = 4) Rydberg-基态分子的光缔合光谱. 分子信号在外电场的作用下向蓝失谐处平移, 且在电场E ≥ 0.27 V/cm时开始展宽. 右图是放大的E = 0.37 V/cm下的分子信号, 红色实线是理论拟合线^[16]
Figure8. Spectra of 36D_5/2 + 6S_1/2 (F = 4) Rydberg-ground molecules with indicated electric fields E. The molecular peaks are blue shifted by E and substantially broadened in fields E ≥ 0.27 V/cm. The right panel shows zoom-ins of molecules peaks with E = 0.37 V/cm. The red solid lines show model spectra^[16].

我们注意到, 理论计算的铯原子nD_5/2 + 6S_1/2 Rydberg-基态分子的永久电偶极矩为负值, 这与文献报道的Rydberg-基态分子类型不同(偶极矩为正)^[12-14,56]. 在物理上, 偶极矩的符号反映了相对于基态原子的位置, 电子电荷沿分子轴移动的方向. 负偶极矩对应于微扰基态原子(Cs 6S_1/2)附近电子电荷的减少, 这种情况通常可以描述为Rydberg电子波函数在微扰原子附近的相消干涉, 或者等效地描述为微扰原子附近的Rydberg电子轨道的线性组合(linear combination of atomic orbitals picture).
图9给出了Cs原子D-型(偶极矩为负)和P-型(偶极矩为正) Rydberg-基态分子最外层势阱相应的基态原子位于1500a₀附近时的电子波函数概率密度. 图9上部为理论计算的31D_5/2 + 6S_1/2和32P_3/2 + 6S_1/2 Rydberg分子的电子波函数概率密度, 由于Rydberg电子结构混合较弱不易区分两者的差别, 图9下部给出了分子波函数减去Rydberg原子波函数之后的结果. 可以清晰地看出, P-型分子微扰原子附近的波函数主要表现为相长干涉, 产生正偶极矩; 而D-型分子微扰原子附近的波函数的干涉模式比较复杂, 在微扰原子周围有相长干涉部分, 但是在距微扰原子一定距离处也有相消干涉部分. 总体而言, 相消干涉占主导地位, 导致了负偶极矩的产生.
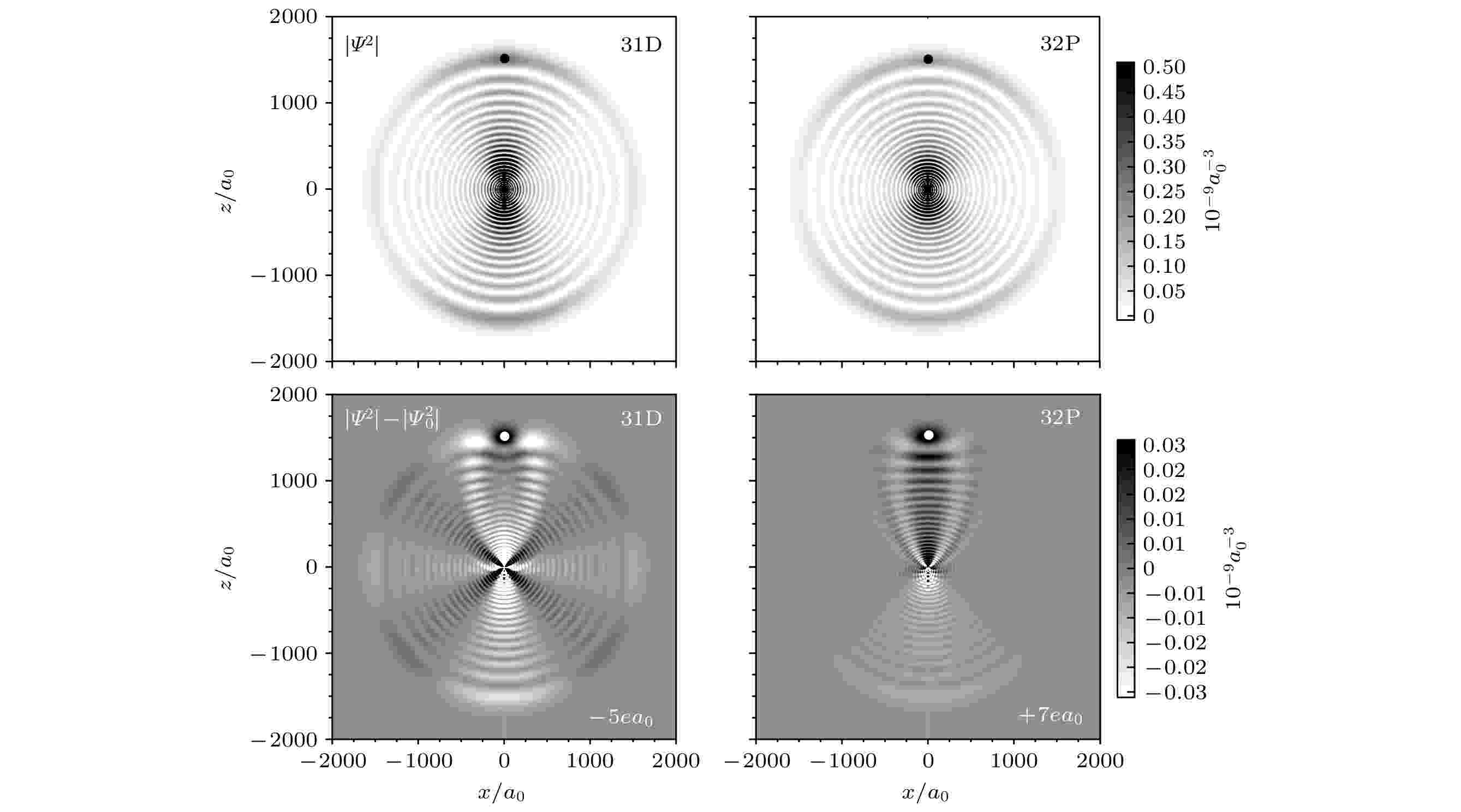图 9 Cs 31D_5/2 + 6S_1/2 (左) 和32P_3/2 + 6S_1/2 (右) Rydberg分子的绝热电子波函数密度, 对应的基态原子位于1500a₀附近(图中点的位置). 上图为波函数密度, 下图为分子减去原子的电子波函数密度, 白色和黑色表示密度的减少和增加^[16]
Figure9. Densities of adiabatic wave functions for Cs 31D_5/2 + 6S_1/2 (F = 4) triplet (left) and 32P_5/2 + 6S_1/2 (F = 4) triplet (right), with the perturber located at ≈1500$ {a}_{0} $(dot). Top panel shows the wave function densities. Bottom panels shows the difference between electronic wave function densities of molecules and atoms on a linear grayscale, with white and black indicating reductions and increases by amounts shown on the gray-scale bar^[16].

本文介绍了由Rydberg电子和基态原子低能电子散射机制形成的超冷长程Rydberg-基态分子, 综述了Rydberg电子与基态原子的散射相互作用的理论模型、数值计算的绝热势能曲线的特性; Rydberg-基态分子按照波函数的形状可以分成“三叶虫型”分子和“蝴蝶型”分子. 当冷原子密度足够大时, Rydberg电子可与多个基态原子散射形成多原子Rydberg-基态分子; 长程Rydberg-基态分子具有巨大的永久电偶极矩, 目前已知的最大电偶极矩可达到kilo-Debye. 最近的文献报道Cs nD_J -型Rydberg-基态分子具有负偶极矩^[16]. 偶极矩的负值反映了在基态(微扰)原子附近的Rydberg电子密度的减少, 这种情况通常可以描述为基态(微扰)原子附近Rydberg电子波函数的相消干涉. 随着对Rydberg-基态分子的研究, 人们将进一步加深对此类分子的认识.
除了对Rydberg-基态分子的束缚能、寿命和永久电偶极矩等固有属性的研究之外, 研究波包在振荡势能曲线中的传播是研究长程Rydberg-基态分子动力学过程的全新思路, 这为研究Rydberg-基态分子的化学反应过程奠定了基础. 对此类分子的研究不局限于碱金属原子, 这种独特的束缚机制适用于所有具有单通道和多通道散射的Rydberg系统.