摘要:Cu₃SbSe₄是一种具有黄铜矿结构的三元p-型半导体材料, 在热电领域颇受重视. 本次工作采用在Cu₃SbSe₄中先掺杂Sn与S, 然后再掺杂Ga₂Te₃这一多组元掺杂方式, 通过能带及晶体结构计算, 了解多组元掺杂后热电性能提升的结构因素. 能带计算表明, 共掺杂Sn与S后, 禁带区域萌生出杂质带, 导致材料的载流子浓度(n_H)和电学性能大幅提高. 在691 K时, 功率因子(PF)从本征的5.2 μW·cm^–1·K^–2增大到13.0 μW·cm^–1·K^–2. 虽然Ga占位在Sb或Te占位在Se位置对能带结构作用甚少, 但四面体[SbSe₄]和[SeCu₃Sb]的键长和键角发生了改变, 从而产生了明显的局部点阵畸变. 因此, 在691 K时, 晶格热导率(κ_L)从1.23 W·K^–1·m^–1降低到0.81 W·K^–1·m^–1, 有效地抑制了总热导率(κ)的提高. 最终, 材料的最大热电优值(ZT)为0.64, 而本征Cu₃SbSe₄的ZT值为0.26.
关键词: 热电性能/
能带结构/
Cu₃SbSe₄/
热导率/
晶体结构

English Abstract

全文HTML

--> --> -->

热电材料是一种通过载流子运动实现热能与电能相互转换的功能材料, 在制冷和发电领域具有巨大的应用价值. 但商用材料的热电转换效率不是很高, 因此了解其声电协调机制继续改善现有热电材料性能仍然十分必要.
Cu₃SbSe₄是一种具有黄铜矿结构的三元p-型半导体材料, 因其具有较大的载流子有效质量(1.1 m_e)和较窄的带隙宽度(0.13—0.29 eV)^[1-3], 在热电领域颇受重视. 但本征Cu₃SbSe₄的热电性能并不高, 需要进行结构或成分调控加以提高. 典型的研究策略为单元素掺杂调控载流子浓度, 同时可以增加点缺陷降低热导率. 例, 采用Ib族Ag, IIIb族 (Al, Ga, In) 或IVb族(Ge, Sn)等单元素掺杂^[1,2,4-13], 可将热电优值(ZT)从原来的~0.30提升到0.50—0.9. 多元素掺杂效果似乎更好^[14,15]. 通过Ti, Hf 或Zr结合Sn替换Sb可将热电优值提升到0.82^[16,17]; 采用Sn和S共掺杂可将ZT值提升到1.11—1.32^[18,19]. 在共掺杂Ag和Sn的同时, 在材料中自萌生Cu₂Se纳米相后可将材料的ZT值提升到1.18^[20]. 上述热电性能的改善一方面依赖于能带结构的调控; 另一方面则依赖于点缺陷的增加. 研究表明^[21], 掺杂Ga和Sn后, 带隙宽度变窄, 费米能级进入到价带. 当S替换Se后, 费米能级会向导带方向移动进入到禁带区域^[22]. 这些结构变化可在不同程度上调整材料的载流子浓度, 从而对电学性能产生影响. 另外, 从热学角度, 在300(660) K时本征Cu₃SbSe₄的晶格热导率(κ_L)大约为 2.4 (1.1) W·K^–1·m^–1[12,23], 远高于Slack and Morelli 建模计算得出的最小值κ_{L, min} (κ_{L, min} = 0.47 W·K^–1·m^–1)^[24], 因此仍有进一步降低的潜力和空间.
我们在之前的研究中采用了多组元掺杂方法. 即让Cu₃SnS₄与Cu₃SbSe₄形成固溶体后再掺杂ZnSe^[25]. 虽然这种多组元掺杂方式在一定程度上提升了热电性能, 但对电学和热学性能的改善机理研究不足. 进一步解析多组元掺杂的作用机理, 对继续开展这一领域的研究有参考价值.
基于以上考虑, 本次工作将继续采用多组元掺杂方法, 即先在Cu₃SbSe₄中添加S和Sn两元素与其形成固溶体, 然后再掺杂Ga₂Te₃. 因为Ga₂Te₃是一种具有1/3阳离子结构空位的闪锌矿结构化合物(space group: F-43m)^[26], 掺杂Ga₂Te₃后可增强黄铜矿结构阳离子空位处的声子散射、调控Cu₃SbSe₄固溶体的载流子浓度^[27]. 同时, 通过研究多组元掺杂后的能带和晶体结构, 进一步阐明改变电学和热学性能的根本原因.

2

-->

2.1.材料与样品制备

第一步, 按照化学式Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4制备Sn和S分别替换Sb和Se的固溶体; 第二步在固溶体Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4中再添加Ga₂Te₃, 制成(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0.01, 0.0125, 0.015, 0.0175)材料. 具体实验步骤为: 先根据分子式Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4称取Cu, Sb, Sn, Se, S五种高纯度元素(纯度: 5 N), 封装在真空石英管内. 然后在高温炉中缓慢升温到1173 K, 升温时间为10 h. 升温结束后在该温度保温12 h; 后缓慢冷却到773 K, 再放到水中急冷. (Cu₃Sb_0.9 Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0.01, 0.0125, 0.015, 0.0175)材料的制备工艺大体与上相同, 所不同的是, 该材料合成后需在390 K退火72 h, 目的是防止Ga₂Te₅相的析出^[28]. 获得的(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4) (Ga₂Te₃)_x铸锭在放有石油醚的球磨罐里球磨5 h, 球磨机转速为350 r/min. 干燥后的粉末在放电等离子烧结系统(SPS-1030)中烧结成块体. 烧结温度控制在850 K, 烧结压力为55 MPa. 采用Archimedes排水法测量块体材料密度. 实测密度大约是理论密度的95%.
样品尺寸有2.5 mm×3 mm×12 mm, ?10 mm×1.5 mm和2 mm×2 mm×7 mm³三种, 分别供电学、热学性能和Hall系数(R_H)测量.
2 -->

2.2.性能测试

材料的Seebeck系数(α)和电导率(σ)由ZEM-3(ULVAC-RIKO, Japan)热电性能测试仪在He环境中测试, 测试温度为室温~725 K. 热扩散系数(λ)由TC-1200 RH (ULVAC-RIKO, Japan) 测试仪测试. 前者不可控测试误差率 < 5%, 后者 < 10%. 材料的热容(C_p)由Dulong–Petit公式估算. 载流子热导率κ_e 由Wiedemann–Franz (W–F)定律计算, κ_e = LσT, 其中L为Lorenz常数, 由公式L = 1.5 + exp(–|α|/116)计算获得^[29]. L的单位为10^–8 W·Ω·K^–2, |α|的单位为μV·K^–1.
Hall系数(R_H)在PPMS(Model–9)中测试, Hall迁移率(μ)和载流子浓度(n_H)根据μ = |R_H|σ和n_H = 1/(eR_H)计算获得, e为电子电荷.
2 -->

2.3.成分和结构分析

样品(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0.015)的元素分布和化学成分由扫描电镜(S-4800, Hitachi, Japan)结合电子探针 (EPMA) 观察分析. 成分分析精度高于97%.
粉末材料的相结构由X射线衍射仪(XRD)(D8 Advance)在50 kV和40 mA的条件下分析测试. 衍射角2θ范围为10°—110°, 扫描步长为0.01°. 晶体结构常数a和c (误差大约为0.5%)、原子空间坐标位置以及其他晶体学等数据直接由XRD精修获得.
掺杂前后四种材料(Cu₂₄Sb₈Se₃₂, Cu₂₄Sb₇Sn₁Se₂₈S₄, Cu₂₄Sb₇Ga₁Se₃₂, Cu₂₄Sb₈Se₃₁Te)的能带结构和态密度(DOS)以及元素的形成能采用密度函数理论(DFT)计算^[30,31]. 交换关联泛函采用广义梯度近似(GGA)中的Perdew-Burke-Ernzerh(PBE). 价电子波函数按平面波展开(PAW), 其他电子用冻结芯近似; 平面波截断能为500 eV^[32]. 计算模型使用2 × 2 × 1超胞, 布里渊区采样选用以Γ为中心的2 × 2 × 2格点. 计算时采用共轭梯度最小化算法^[33], 将原子坐标和晶格矢量同时进行结构优化. 作用在每个原子上的力不超过0.02 eV/?. 电子结构计算采用4 × 4 × 4k点网格.

2

-->

3.1.结构计算与研究

图1(a)为材料(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0.015)的背散射扫描电镜图像, 表面有少量气孔, 材料致密度不高(实测密度只有Cu₃SbSe₄理论密度的95%左右). 图1(b)为块体样品断口形貌. 图1(c)—(i)为面扫描元素(依次为: Cu, S, Se, Te, Sb, Sn, Ga)分布图像. 经仔细观察, Ga元素的分布形貌与Sb的比较接近, 而Te的与Se接近. 因此, 部分Ga可能占位在Sb的晶格位置, 但也不能排除占位在Cu位置的可能性. 而Te应该占位在Se位置或间隙位置. 具体占位情况需根据形成能的计算结果进一步确定.
图 1 (a) (Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)_1–x(Ga₂Te₃)_x (x = 0~0.0175)的粉末XRD图谱; (b) 晶格结构常数a和c; (c) 四方相晶体结构变形参数η; (d) 内部点阵结构扭曲参数ψ
Figure1. (a) X-ray diffraction patterns of the powders (Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)_1–x(Ga₂Te₃)_x (x = 0~0.0175); (b) lattice constants a and c; (c) tetragonal deformation parameters η; (d) internal lattice distortion parameter ψ.

图2为室温时(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0~0.0175)的粉末XRD精修图谱. 精修后, 并未发现杂相, 所有衍射峰角度均与PDF25-063标准卡片相对应, 见图1(a). 说明添加元素Ga和Te均已固溶到Cu₃SbSe₄晶体结构中. 晶体结构常数a和c与Ga₂Te₃含量的关系总结于图1(b). 根据精修结果, Sn占位在Sb(2a)位置, S在Se(8i)位置. 但目前还不能通过精修精确确定Ga和Te元素的占位位置. 另外, 由图1(b)可知, 常数a和c值并未随着x值而发生线性下降. 当x > 0.01时, 常数c反而呈增大趋势. 常数a的变化颇为复杂, 但总体看来, 随x值增大而变小. 这些变化与原子Ga和Te的原子半径及占位位置有关, 同时也与不同原子占位后发生的键反应有关^[34,35]. Ga的共价键半径为1.26 ?, 介于Cu (1.17 ?)和Sb (1.31 ?)之间, Ga占据Sb和Cu位置的可能性并存; 而多余的Te可占位在间隙位置. 不同原子的占位可导致不同的键反应, 因而改变了局部的键长和键角, 最终导致晶胞常数的复杂变化. 这些占位问题还可以通过形成能的计算而更加明确, 具体见下节讨论. 图1(c)总结了四方相晶体结构形变参数η与x值的关系. 同样地, η随x值增大并非线性增大. 但总体看来, 随着x值增大, 参数η接近于1, 说明晶胞的变形程度在减弱. 这也是一个比较有意思的结果, 可能是由于不同元素同时占位后, 晶体结构畸变互相抵消之故. 根据掺杂Ga₂Te₃后精修分析的Se原子空间坐标(X, Y, Z), 计算出内部点阵结构扭曲参数ψ^[36]与Ga₂Te₃含量的关系, 见图1(d), 其中Cu₃Sb_0.9Sn_0.1 Se_3.6S_0.4 (x = 0)中Se原子的空间坐标(X = 0.2451, Y = 0.2451, Z = 0.3700)作为比较对象. 根据图1(d), 当x = 0.015时, ψ取得最大值, 说明该材料的点阵扭曲程度最大.
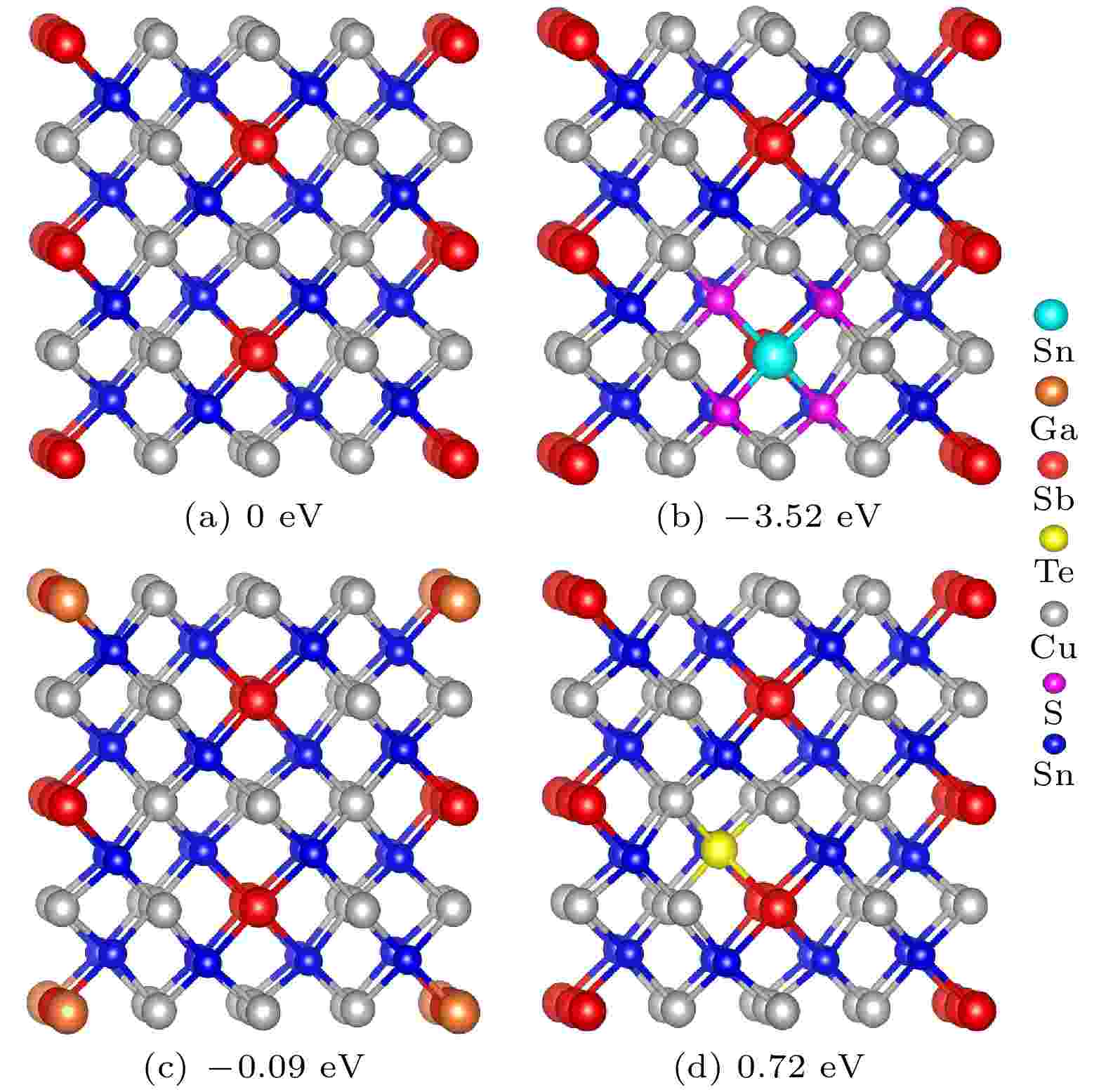图 2 三种不同占位材料的计算形成能(E_f)　(a) 本征Cu₂₄Sb₈Se₃₂ (E_f = 0), 作为比较对象; (b) Sn和S共掺杂的Cu₂₄Sb₇Sn₁Se₂₈S₄; (c) Ga占位在Sb位置(Cu₂₄Sb₇Ga₁Se₃₂); (d) Te 占位在Se位置(Cu₂₄Sb₈Se₃₁Te₁). E_f值均是相对于本征Cu₂₄Sb₈Se₃₂的形成能
Figure2. Formation energies (E_f) of three solid solutions with different element occupations. (a) Pristine Cu₂₄Sb₈Se₃₂ (E_f = 0) for comparidon; (b) Sn and S co-doped Cu₂₄Sb₇Sn₁Se₂₈S₄; (c) Ga residing at Sb site (Cu₂₄Sb₇Ga₁Se₃₂); (d) Te residing at Se site (Cu₂₄Sb₈Se₃₁Te₁). The E_f values are their corresponding formation energies in comparison to that of the pristine structure.

为了进一步了解各元素在Cu₃SbSe₄中的占位情况, 先计算Sn和S在各种占位情况下的形成能(E_f), 具体占位与形成能的关系见图3. 计算结果表明, 在第一种占位情况下(用虚线方框表示)的晶体结构形成能最小, 其值为0; 其他占位的形成能(E_f)均大于0. 接下来, 以本征Cu₂₄Sb₈Se₃₂作为比较对象(E_f = 0), 计算以下三种情况下的形成能, 分别为: 1) Sn和S 共掺杂Cu₂₄Sb₇Sn₁Se₂₈S₄ (即图3中的第一种占位情况); 2) Ga 占位在Sb位置(Cu₂₄Sb₇Ga₁Se₃₂); 3) Te占位在Se位置(Cu₂₄Sb₈Se₃₁Te₁). 具体占位情况见图2, 其形成能的计算公式如下所示:
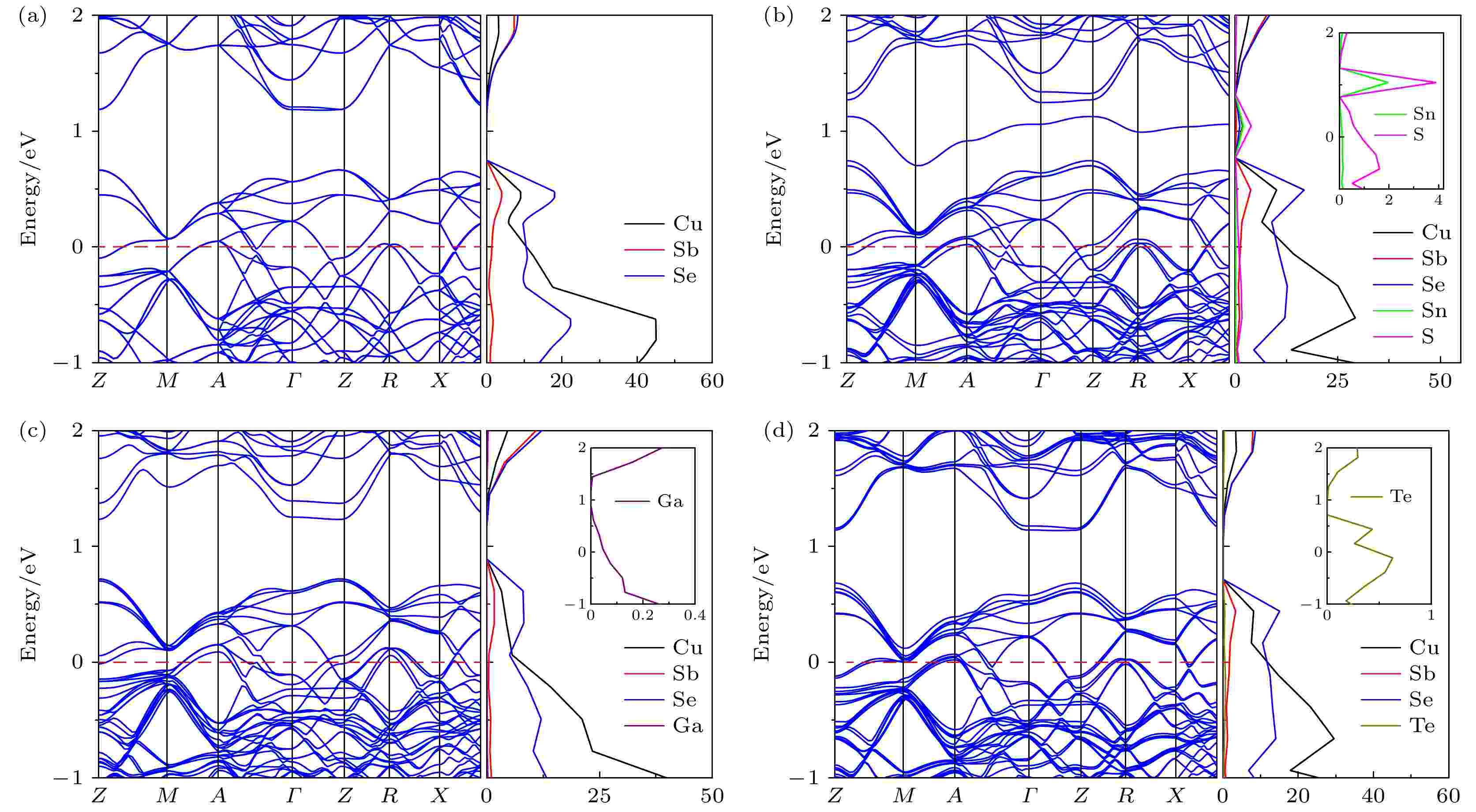图 3 各种材料的能带结构与态密度(DOS)　(a) Cu₂₄Sb₈Se₃₂; (b) Sn and S co-doped Cu₂₄Sb₇Sn₁Se₂₈S₄; (c) Ga doped Cu₂₄Sb₇Ga₁Se₃₂; (d) Te doped Cu₂₄Sb₈Se₃₁Te₁ compounds
Figure3. Band structures and the density of the states (DOS) of different materials: (a) Pristine Cu₂₄Sb₈Se₃₂; (b) Sn and S co-doped Cu₂₄Sb₇Sn₁Se₂₈S₄; (c) Ga doped Cu₂₄Sb₇Ga₁Se₃₂; (d) Te doped Cu₂₄Sb₈Se₃₁Te₁ compounds.

$\begin{split}&E_{{\rm{formation}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{7}}}{\rm{S}}{{\rm{n}}_{\rm{1}}}{\rm{S}}{{\rm{e}}_{{\rm{28}}}}{{\rm{S}}_{\rm{4}}}} = E_{{\rm{compound}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{7}}}{\rm{S}}{{\rm{n}}_{\rm{1}}}{\rm{S}}{{\rm{e}}_{{\rm{28}}}}{{\rm{S}}_{\rm{4}}}} - E_{{\rm{pristine}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{8}}}{\rm{S}}{{\rm{e}}_{{\rm{32}}}}} \\&\qquad\qquad\qquad\quad+ {E_{{\rm{Sb}}}} + 4{E_{{\rm{Se}}}} - {E_{{\rm{Sn}}}} - {4_{{\rm{Es}}}}{\rm{ ,}}\\&E_{{\rm{formation}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{7}}}{\rm{G}}{{\rm{a}}_{\rm{1}}}{\rm{S}}{{\rm{e}}_{{\rm{32}}}}} = E_{{\rm{compound}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{7}}}{\rm{G}}{{\rm{a}}_{\rm{1}}}{\rm{S}}{{\rm{e}}_{{\rm{32}}}}} - E_{{\rm{pristine}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{8}}}{\rm{S}}{{\rm{e}}_{{\rm{32}}}}} \\&\qquad\qquad\qquad\quad+ {E_{{\rm{Sb}}}} - {E_{{\rm{Ga}}}}{\rm{ ,}}\\&E_{{\rm{formation}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{8}}}{\rm{S}}{{\rm{e}}_{{\rm{31}}}}{\rm{T}}{{\rm{e}}_{\rm{1}}}} = E_{{\rm{compound}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{8}}}{\rm{S}}{{\rm{e}}_{{\rm{31}}}}{\rm{T}}{{\rm{e}}_{\rm{1}}}} - E_{{\rm{pristine}}}^{{\rm{C}}{{\rm{u}}_{{\rm{24}}}}{\rm{S}}{{\rm{b}}_{\rm{8}}}{\rm{S}}{{\rm{e}}_{{\rm{32}}}}}\\&\qquad\qquad\qquad\quad+ {E_{{\rm{Se}}}} - {E_{{\rm{Te}}}}{\rm{ }}.\end{split}$

计算结果表明, 若以本征Cu₂₄Sb₈Se₃₂作为比较对象, Sn和S 共掺杂Cu₂₄Sb₇Sn₁Se₂₈S₄的形成能最小(E_f = –3.52 eV), 因此可以确定Sn和S分别占位在Sb和Se位置; Ga占位在Sb位置后(Cu₂₄Sb₇Ga₁Se₃₂)其E_f = –0.09 eV. 因此, Ga占位在Sb晶格位置的可能性很大. 当Te占位在Se位置后(Cu₂₄Sb₈Se₃₁Te₁)其E_f = 0.72 eV. 这一占位从热力学角度稍有些不稳定, 但不能排除其可能性. 有研究表明, 若有元素占位在Se位置, 其形成能一般均为正值^[22]. 因此结合能量计算, 基本了解了Ga和Te的占位情况.
外加元素占位后, 对材料的能带结构会发生变化^[37]. 为此, 我们计算了不同掺杂后的能带结构及态密度, 本征Cu₂₄Sb₈Se₃₂的能带结构作为比较, 见图3(a). 本征材料的带隙宽度约为0.5 eV, 大于报道的带隙值(0.13—0.35 eV) ^[1-3,21,22]. 同时, 价带顶(VBM)和导带底(CBM)也不在高对称点Γ^[21,38], 这与Garcia等^[21]和Do与Mahanti ^[38]计算的略有不同. 严格地说, Do和Mahanti^[38]计算的VBM和CBM也不在高对称点Γ, 但在Γ点有三重简并带, 而我们计算的只有两重带(图3(a)), 共掺杂Sn和S后才出现三重带, 见图3(b). 此外, 在禁带区域还引进了一条杂质带. 在态密度中还可以看出, 杂质带主要来自于Sn和S的贡献. 这条杂质带在Li等^[19]计算的Cu₃SbSe₄态密度中没有出现. 这些结构差异是否与建模计算时外加原子的不同占位有关, 值得进一步研究. 一般, 由于计算时采用了广义梯度近似(GGA), 通常计算带隙总是小于实测值^[39]. 另外, 掺杂前后费米能级均已进入到价带, 价带顶的态密度主要来自于Cu-Se的轨道杂化贡献, 这与报道的一致^[21]. 在本征Cu₂₄Sb₈Se₃₂中掺杂Ga后, 在禁带附近的导带发生了分裂现象, 价带数量增多, 但均已简并(见图3(c)). 当Te占位在Se位置时, 价带数量增多, 带隙也有缩小趋势, 见图3(d). 但与Sn、S的贡献相比, 来自于Ga和Te的态密度贡献很小. 因此, 掺杂Ga₂Te₃对能带结构的改变作用不大. 通过上述分析, 可以得出结论, Sn和S对能带结构有重大贡献. 掺杂Sn和S后出现的杂质带“缩小了禁带宽度”, 减小了载流子的热输运阻力, 因此大大提高了材料的载流子浓度. 杂质带的这种作用在许多材料中均有报道, 例Tl-PbTe^[40], Sn-β-As₂Se₃^[41]及Cu_1.15In_2.29Te₄^[42]等. 但也有报道^[43], 在TiO₂中出现的杂质能带可以起作电子-空穴湮灭中心的作用, 从而降低了载流子浓度. 对于带隙宽度的作用也存在着不同的说法. 例, 在 p-型PbTe/CdTe材料中增大带隙宽度可以抑制少子的热输运, 改善热电性能^[44].
Te和Ga两元素对能带结构影响不大, 但对晶体结构的影响值得研究. 为此, 计算了Te和Ga分别占位在Se和Sb后的多面体结构参数, 包括键长和键角, 具体数据见图4. 当Te占位在Se位置后, 四面体[SeCu₃Sb]键长明显变长. 在同一方位, Sb—Se (Cu—Se)键长分别从2.63 ? (2.42 ?)增长到2.79 ? (2.54 ?). 同时, 也因Te占位在Se位置, 两个Cu—Se—Sb的键角变小, 而两个Cu—Se—Cu的键角变大. 当Ga占位在Sb后, 四面体[SbSe₄]的键长Se—Sb从2.63 ?缩短到同方位的2.46 ?; 但键角变化不大. 以上变化说明, 掺杂Ga和Te后, 虽然对能带结构影响不大, 但对局部的点阵畸变非常明显, 因此对高温下的声子散射影响较大.
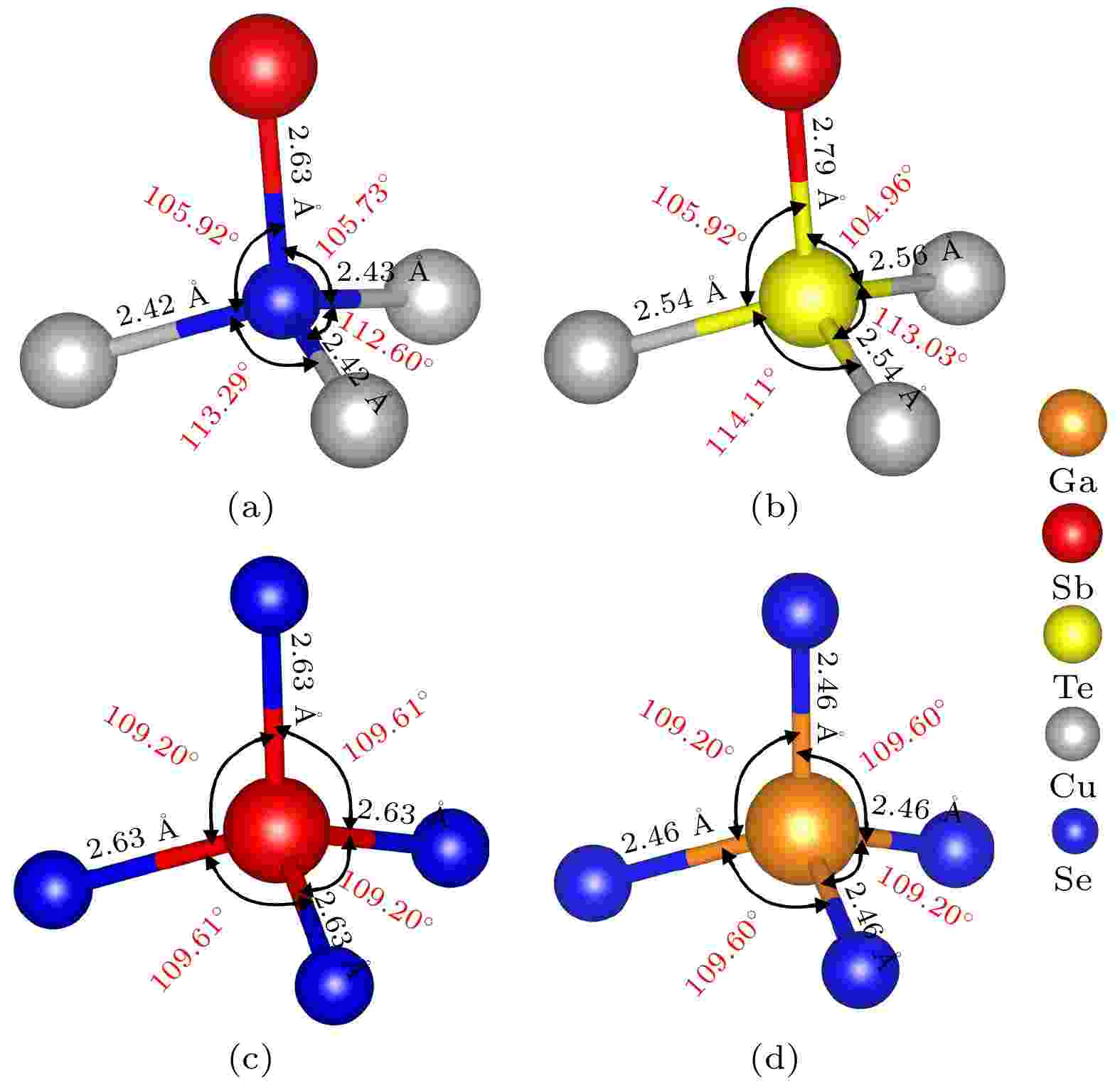图 4 Te和Ga分别占位在Se和Sb前后的多面体[SeCu₃Sb]和[SbSe₄]结构参数(键长和键角)
Figure4. Structural parameters (bond lengths and angles) of the polyhedrons [SeCu₃Sb] and [SbSe₄] before and after residing of Te and Ga at Se and Sb sites respectively.

2 -->

3.2.载流子输运及热电性能

为证实多组元掺杂对材料载流子浓度的贡献, 多次测试了室温下(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0~0.0175)材料的Hall系数. 计算获得的载流子浓度(n_H)和迁移率(μ)见图5. 其中图5(a)是载流子浓度(n_H), 平均n_H值大约为10²⁷—10²⁸ m^–3, 而本征Cu₃SbSe₄的n_H值为~10²⁴ m^–3[25]. 虽然载流子浓度随Ga₂Te₃含量(即x值)增大呈下降趋势, 但均比本征Cu₃SbSe₄的n_H大3—4个数量级. 说明共掺杂Sn和S后引进的杂质能级对载流子输运起到了重要作用. 而掺杂Ga和Te则对载流子的浓度作用很小, 这与能带结构的变化相吻合. 材料的迁移率(μ)随x值增大呈增大趋势, 见图5(b). 其原因是载流子浓度降低导致载流子之间的散射下降. 另外, 同一种材料的n_H和μ值比较分散, 可能与截取材料的致密度有关.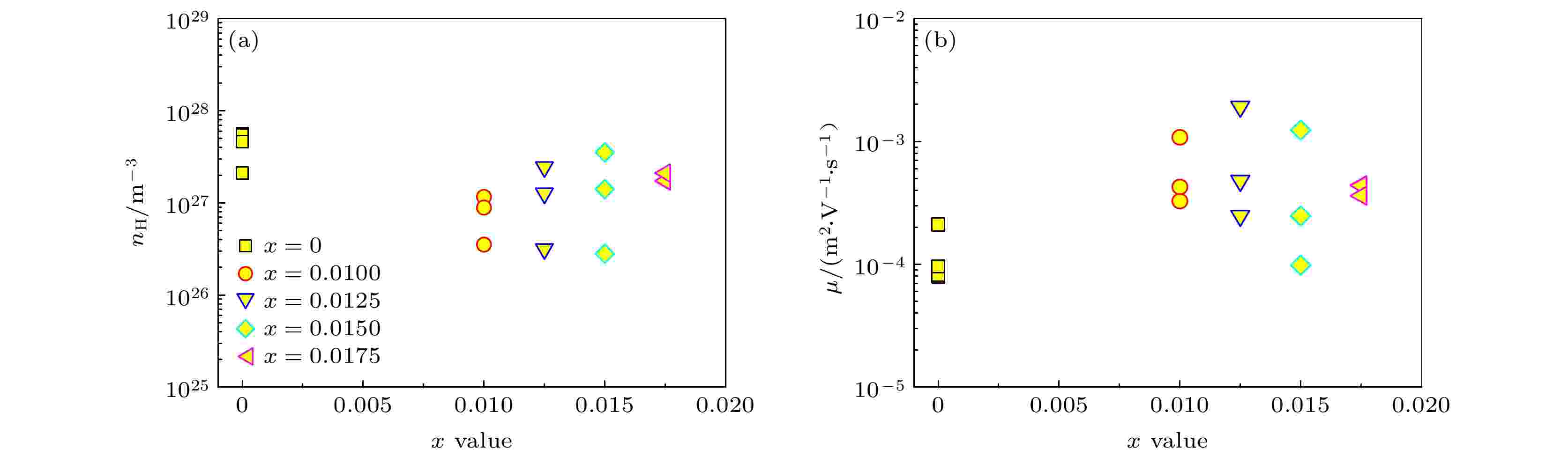
图 5 (a) 在室温下(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0~0.0175)材料的霍尔载流子浓度(n_H)与Ga₂Te₃含量(x值)的关系; (b) 在室温下迁移率(μ)与Ga₂Te₃含量(x值)的关系
Figure5. (a) Hall carrier concentration (n_H) as a function of Ga₂Te₃ content (x value) at room temperature (RT) for (Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0~0.0175); (b) mobility (μ) as a function of Ga₂Te₃ content (x value) at RT.

图6是(Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0~0.015)材料的热电性能与温度的关系, 本征Cu₃SbSe₄的热电性能作为比较^[25]. Seebeck系数(α)与温度的关系见图6(a). α值均为正值, 说明材料是p-型半导体. 多组元掺杂后, 材料的α值明显低于本征Cu₃SbSe₄的值. 但随Ga₂Te₃含量(即x值)变化, α值变化不明显, 这与掺杂Ga或Te对能带结构不敏感相吻合. 但多元素掺杂后α值均随温度升高而增大, 这与本征材料的变化趋势相反, 说明掺杂后材料的导电机制发生了根本性的改变. 电导率(σ)的变化正好相反, 多组元掺杂后电导率大幅增大, 且随温度升高而下降, 见图6(b), 呈现出金属特征行为. 这是由于引进了杂质带, 载流子浓度获得了大幅度的提高之故. 图6(c)是功率因子(PF) 与温度的关系. 材料的PF值随温度升高而增大. 当温度达到691 K时材料x = 0.015 的PF值为13.0 μW·cm^–1·K^–2, 大约是本征Cu₃SbSe₄的2.5倍.
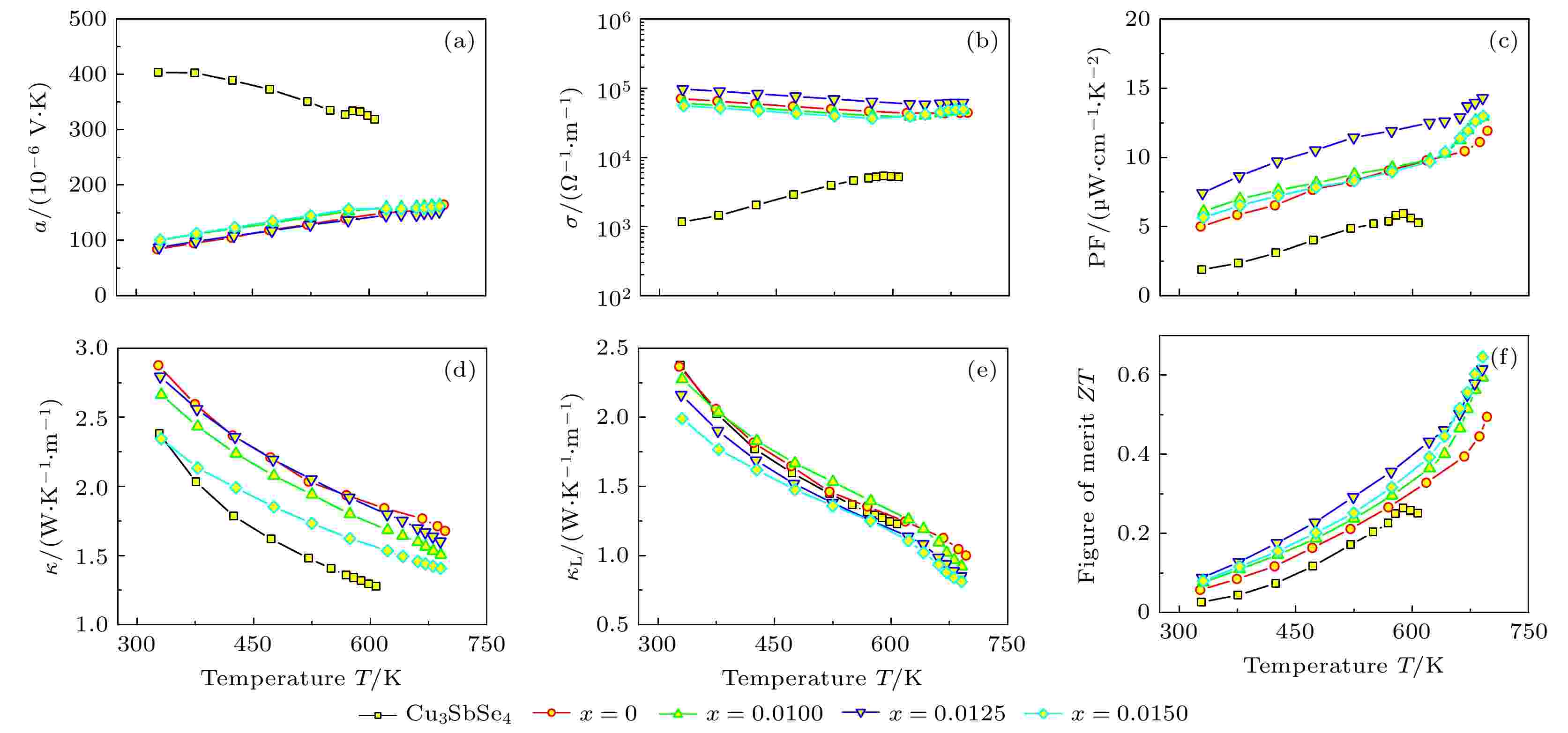图 6 (Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0.01—0.015)材料的热电性能与温度的关系, 本征Cu₃SbSe₄的性能作为比较　(a) Seebeck 系数(α)与温度的关系; (b) 电导率(σ)与温度的关系; (c) 功率因子(PF) 与温度的关系; (d) 总热导率(κ)与温度的关系; (e) 晶格热导率(κ_L)与温度的关系; (f) 热电优值(ZT)与温度的关系
Figure6. TE performance of (Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0.01–0.015) as a function of temperature, and the TE performance of pristine Cu₃SbSe₄ is provided for comparison: (a) Seebeck coefficients as a function of temperature; (b) electrical conductivities as a function of temperature; (c) power factor (PF) as a function of temperature; (d) total thermal conductivities (κ) as a function of temperature; (e) lattice part (κ_L) as a function of temperature; (f) TE figure of merit (ZT) as a function of temperature.

虽然多组元掺杂后材料的电学性能获得了巨大的改善, 但总热导率(κ)比本征材料有所提高, 见图6(d). 在691 K时, x = 0.015的材料 其κ值为1.41 W·K^–1·m^–1, 而本征材料的κ值为1.28 W·K^–1·m^–1 (607 K). 晶格热导率(κ_L)与总热导率的成份依赖关系明显不同, 见图6(e). 随Ga₂Te₃含量的增大, κ_L值降低. 本征材料的最低κ_L值可达1.23 W·K^–1·m^–1 (691 K), 而x = 0.015的材料其κ_L值只有0.81 W·K^–1·m^–1. 由于晶格热导率(κ_L)的降低, 所以抑制了总热导率的大幅度上升.
结合上述三参数(α, σ, κ)值, 我得到了热电优值(ZT), 见图6(f). 随Ga₂Te₃含量的增大, ZT值呈上升趋势. x = 0.015的材料在691 K时达到最大值0.64, 大约是本征Cu₃SbSe₄的2.6倍.
虽然这一材料的性能与目前报道的同类材料相比并不是太高^[2,13,19], 但材料性能的提升原因已经基本阐明. 热电性能提升主要由于能带结构的改变, 使得功率因子提升了2.5倍. 但添加Ga₂Te₃的作用与原先的设想有些差异. 通过Ga和Te的固溶并没有大幅改变能带结构和态密度, 但改变了晶胞结构参数(包括四方相晶体形变参数η和点阵扭曲系数(ψ)). 前者随x值成增大趋势(见图1(c)), 因此对声子散射程度减弱^[45-47]; 后者在x = 0.015时达到最大值(见图1(d)), 因而对高频声子散射最大. 综合两方面的晶体结构因素, 可以解释为何在高温下x = 0.015的材料晶格热导率最低的原因. 同时也说明, 添加Ga₂Te₃后, 材料晶格热导率获得了较大幅度的降低, 从而有效地抑制了总热导率的提高. 因此, 本次工作还是比较清晰地阐明了热电性能提升的结构因素.

在Cu₃SbSe₄中分别掺杂Sn和S, 然后再掺杂Ga₂Te₃制备出多组元掺杂的 (Cu₃Sb_0.9Sn_0.1Se_3.6S_0.4)(Ga₂Te₃)_x (x = 0—0.0175)固溶体, 并研究了其能带和晶体结构对电学和热学性能的影响. 研究得出, 掺杂Sn和S后, 禁带区域萌生出杂质带, 极大地提高了载流子浓度和电学性能. 而掺杂Te和Ga后, 对能带结构影响不大, 但对局部的点阵结构参数影响严重, 具体表现为键长和键角的明显改变, 因此极大地增大了高温下的声子散射、有效地抑制了总热导率的升高. 最终在691 K时, 最高热电优值从本征Cu₃SbSe₄的0.26提升到0.64. 本次工作比较清晰地阐明了热电性能提升的结构因素.