全文HTML
--> --> -->有关电子密度的研究主要包括对电子密度诊断方法的研究、对电子密度时空演化和随实验参数演变的研究. 其中, 对电子密度诊断方法的研究旨在探索全新的诊断技术或者对一些较成熟的诊断技术进行改进. 例如, Torres等[10]根据Hγ谱线和Hβ谱线各自的Stark展宽与电子温度和电子密度的函数关系式, 在测量两种谱线的Stark展宽后, 分别绘制每条谱线的Te-ne曲线, 则曲线的交叉点位置就是等离子体的电子温度和电子密度. 潘成刚等[11]用傅里叶变换的方式提取高密度(1016— 1017 cm–3)焊接电弧光谱的Stark展宽, 该方法有效地分离了谱线的高斯线宽和洛伦兹线宽, 而且无需测量气体温度和仪器展宽, 使Stark展宽技术应用更为便利. 针对低密度等离子体(低于1014 cm–3)发射谱线所涉及到的精细结构的问题, Palomares等[12]改进算法在谱线精细结构中成功提取Stark展宽, 使Hβ谱线测量的电子密度低至5 × 1012 cm–3. 此外, Akatsuk[13]在综述文献中总结了碰撞辐射模型, 将基于这种模型的电子密度诊断技术归纳为三种方法, 并对每种方法的优势和局限性作出评价. 2019年, 我们课题组提出一种基于等离子体图像测量开放环境下等离子体密度的方法, 该方法不仅可以估算开放环境下的等离子体边界, 而且能够反映开放环境对等离子体密度的影响[14]. 此外, 人们还针对等离子体电子密度时空演化和随实验参数演变的问题, 进行了广泛和深入的研究, 如纳秒脉冲放电等离子体电子密度时间演化的实验研究[15,16], 外加电压与介质阻挡放电微放电通道中的电子密度、斑图形态三者之间关系的研究[17], 电子密度的时空分布规律研究[18,19], 脉冲形状对等离子体密度影响的模拟研究[20]等.
为了进一步探究常压等离子体电子密度随放电参数的变化规律, 本文开展了两方面的工作, 一方面对等离子体发射光谱的原子谱线作插值处理, 以减小谱线的Stark展宽读取误差; 另一方面, 使用Stark展宽法和图像法对比研究针-板放电等离子体密度的变化规律, 并采用全局模型分析影响电子密度变化的主要因素. 实验和模型分析的结果表明, 等离子体放电体积变化是影响针-板放电等离子体密度的主要因素.
2.1.Stark展宽法
Stark展宽法作为直接且有效的电子密度诊断方法, 一直被视为大气压等离子体电子密度诊断的首要途径. 其基本原理是原子发射光谱的Stark展宽和电子密度之间存在一定范围内的线性响应[21]. 原子发射光谱的展宽机制主要包含Stark展宽Δλs, van der Waals展宽Δλw, Doppler展宽ΔλD和仪器展宽Δλi. 其中, Doppler展宽和仪器展宽都属于Gauss线型, 对应展宽为ΔλG, 而van der Waals展宽和Stark展宽则同属于Lorentz线型, 对应展宽为ΔλL. 对这两种线型的谱线进行卷积运算, 可以得到Voigt线型函数的原子发射光谱, 设该光谱的线宽为ΔλV, 则上述多种展宽机制满足如下的关系式[22,23]:采用Stark展宽法计算等离子体密度首先要确定谱线的半高全宽(full width of half maximum, FWHM). 对于实际测量得到的谱线, 其波长采样间隔直接影响谱线FWHM的计算误差. 以本文所用的光谱仪为例, 其2400线/毫米光栅的波长采样间隔为0.0076 nm, 根据(2)式和(3)式中所需满足的电子密度测量范围, 即使对于Hα和Hβ谱线可以计算的最低电子密度(5 × 1014和1 × 1014 cm–3)而言, 这一波长采样间隔可能引起的电子密度最大计算误差分别可以达到38.8%和26.6%. 因此, 需要对实验中获得的光谱数据点进行插值处理, 降低数据的波长间隔带给电子密度的诊断误差. 如图1(a)所示, 如果使用原始实验采样数据, 会造成对FWHM边界波长的判断出现误差. 而当对实验光谱采用三次样条插值处理后, 波长数据点之间的间隔可以缩短至0.0001 nm, 此时FWHM边界的判断相对更准确, 即获得更准确的FWHM. 采用插值方法处理后, Hα和Hβ谱线在实际电子密度为5 × 1014和1 × 1014 cm–3时对应的电子密度最大计算误差则分别下降到1%和0.34%.
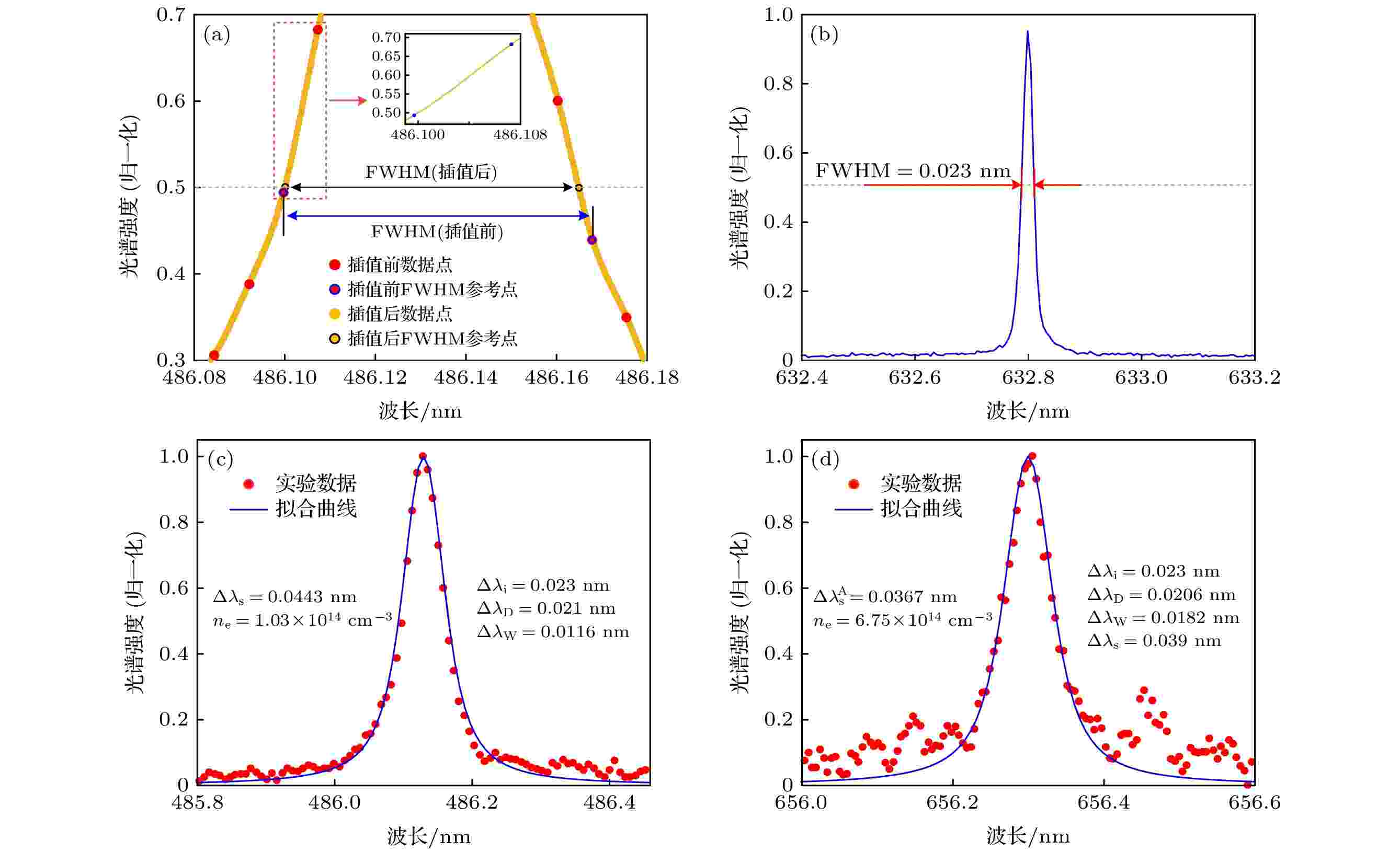图 1 Stark展宽法测量电子密度的相关步骤 (a) Hβ谱线的插值处理; (b) 光谱仪测得的氦氖激光器发射光谱; (c) Hβ谱线的Stark展宽拟合实例(实验条件: 粗径电极脉冲放电, 频率为5 kHz, 占空比为50%, 电压幅值为2 kV, 气体流量为25 sccm (1 sccm = 1 mL/min)); (d) Hα谱线的半面积Stark展宽拟合实例(实验条件: 细径电极直流放电, 电流幅值为20 mA, 气体流量为25 sccm)Figure1. Measurement steps of the electron density by using the Stark broadening method: (a) Interpolation of the Hβ line; (b) emission line of the He-Ne laser; (c) fitting of the Hβ line (Experimental conditions: pulsed discharge by the larger inner electrode with 5 kHz pulse frequency, 50% duty cycle, 2 kV voltage and 25 sccm gas flow rate); (d) fitting of the Hα line (Experimental conditions: DC discharge by the thinner inner electrode with 20 mA discharge current and 25 sccm gas flow rate).
在一定波段范围内, 光谱仪的仪器展宽应该是基本一致的, 采用波长相近的激光谱线可以直接得到光谱仪的仪器展宽[24]. 如图1(b)所示, 使用型号为DH-HN250P的氦氖激光器(线宽2 pm)测得波长632.8 nm处光谱仪的仪器展宽为0.023 nm, 该展宽即可视为实验中的仪器展宽Δλi.
常压等离子体的电子密度取值一般在1013—1014 cm–3, 这一密度范围与氢巴尔末线的测量范围基本符合. 特别是Hα谱线(656.3 nm)和Hβ谱线(486.1 nm), 其电子密度的测量下限分别为6 × 1014和4 × 1013 cm–3[21,25]. 因此, 通常采用这两种谱线作为电子密度的诊断工具. 对于氩气或氦气放电, 理论上还可以用Ar I谱线(430或696.5 nm)或He I谱线(471.3, 501.6, 667.7, 728.1 nm)[21]测量电子密度, 但是因为测量下限高达1016 cm–3, 使其应用范围受到了一定的限制.
对于低密度的等离子体(ne < 1 × 1015 cm–3), 可通过直接测量Hβ的Stark展宽Δλs获得电子密度. 在这一密度范围内, Δλs只是电子密度ne的函数[26], 表达式为[27]
对于高密度的等离子体(ne > 1 × 1015 cm–3), Hβ谱线的Stark展宽不仅取决于电子密度, 同时也受电子温度的影响. 此外, 由于Hβ谱线具有较低的信噪比, 且在氩气放电时易受临近的Ar+谱线(488和484.8 nm)干扰[28], 因此当待测电子密度较大时, 则应该采用不受电子温度干扰的Hα谱线的半面积Stark展宽(full width at half area, FWHA, 定义详见参考文献[27])计算电子密度, 表达式为[21]
由(1a)式和(1b)式可知, 谱线的Δλw和ΔλD可以通过测量气体温度直接计算得到. 通过拟合双原子分子的辐射谱线计算气体的转动温度Trot是诊断气体温度Tg的主要手段[29]. 这种诊断方法的优点在于这是一种非接触的测量方法, 相对于一些接触性的测量技术, 如热耦合器件或探针诊断, 这种方法可以避免电磁场对测量结果的影响, 同时也不会对等离子体本身的性质造成影响[30]. 对于常压氩气放电等离子体, 由于环境中水蒸气的存在, 可以通过拟合OH (A-X)谱带(305.5—309.75 nm)估算转动温度Trot[31]. 实验中使用的拟合软件为LIFBASE[32], 拟合实例如图2所示.
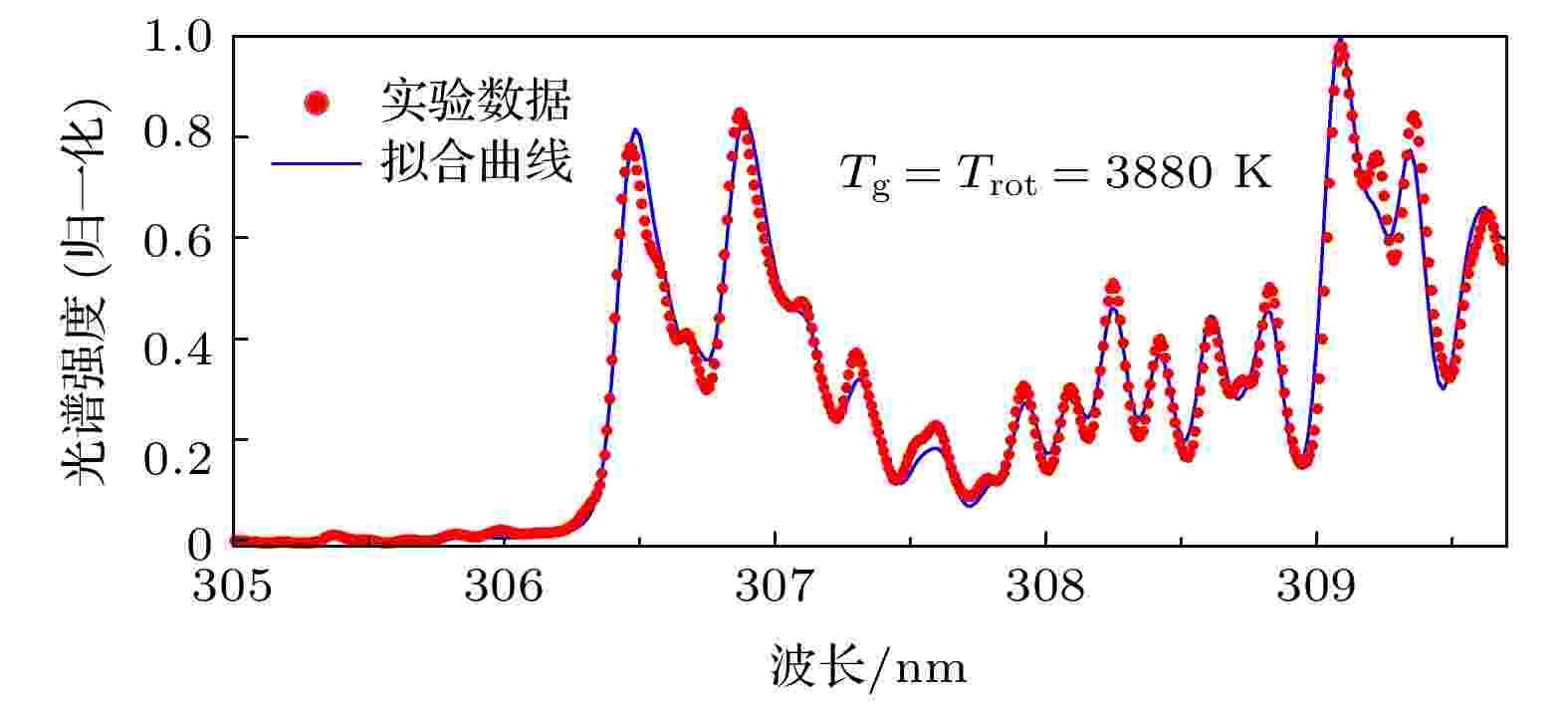图 2 拟合OH (A-X)谱带估算气体的转动温度(实验条件: 粗径电极脉冲放电, 频率为8 kHz, 占空比为80%, 电压幅值为2 kV, 气体流量为25 sccm)Figure2. Fitting of the OH (A-X) bands to estimate the gas temperature (Experimental conditions: pulsed discharge by the larger inner electrode with 8 kHz pulse frequency, 80% duty cycle, 2 kV voltage and 25 sccm gas flow rate)
2
2.2.图像法
除了常用的Stark展宽法外, 本课题组提出了一种可以通过等离子体图像计算电子密度的方法[14]. 该方法基于等离子体的等效电路模型[33], 根据主等离子体区的等效电感与电子密度之间的函数关系2
2.3.全局模型
全局模型(global model)是一种忽略了等离子体空间差异以便提高计算效率的数值模拟方法. 这种模型通过建立流体方程来描述等离子体的空间平均化参数, 包括电子温度、电子密度以及其他重粒子的密度[35]. 全局模型主要基于两种方程: 粒子平衡方程和功率平衡方程. 当研究对象为电子时, 所建立的方程即为电子平衡方程. 电子产生的主要方式共有两种: 其一是电子碰撞中性粒子发生电离产生的新电子; 其二是被电场加速的离子轰击阴极而产生的二次电子, 电子在电场中定向运动至阳极则是电子损失的主要方式. 考虑到电子密度ne随时间t的变化率, 设阴极的二次电子发射系数为γse, 粒子平衡方程可以表示为[36]等离子体在电场中吸收的功率则通过如下两种途径消耗: 其一是电子与中性粒子发生碰撞造成的能量损失, 包括电离、激发和弹性碰撞三种过程; 此外, 电子和离子在电场中分别定向运动至阳极和阴极的过程中, 也会损失各自所拥有的动能. 因此, 设等离子体吸收的功率为P, 考虑到电子温度Te随时间t的变化率, 则功率平衡方程满足[36]:
3.1.实验系统
实验中采用的常压等离子体放电系统的示意图可以参考文献[14]. 电源系统包括高压直流电源(SL2000, SPELLMAN)和高压脉冲开关(PVX-4110), 在实验过程中根据需要可随时组合或拆分, 以便产生需要的高压直流或高压脉冲信号. 钨钢管(内径1 mm)或不锈钢毛细管(内径175 μm)直接接地, 作为放电阴极, 中间通入纯净的氩气, 其端面距离液面的高度可以调节. 将铂电极插入饱和碳酸氢钠溶液, 并连接电源高压端, 使溶液成为放电阳极, 该系统即为针-板放电系统. 产生在钨钢管端面与液面之间的等离子体的发射光谱和图像则通过光谱仪(SP-2500, Princeton Instruments)和ICCD (PI-MAX4, Princeton Instruments)分别探测. 实验中ICCD和光谱仪被组合为一台仪器, 二者通过移动收集透镜后面的狭缝进行切换. 在脉冲放电时, 触发信号为不同频率和占空比的脉冲信号, 由任意函数发生器(AFG3052C, Tektronix)产生, 用于对ICCD和高压脉冲开关的调节和同步测量. 测量过程中, 需保证ICCD的曝光时间以及光谱仪的积分时间与脉冲工作时间完全匹配. 此外, 在测量光谱时, 根据等离子体的成像位置, 选取等离子体轴向正中心轴线处作为狭缝正对的位置. 因此, 实验中光谱法诊断的等离子体参数(电子密度、气体温度), 既属于谱线积分时间内的时间平均参数, 也属于等离子体轴向位置处的空间上平均参数. 而图像法诊断的电子密度, 则既属于图像曝光时间内的时间平均电子密度, 也属于等离子体放电空间内的平均电子密度. 电路中的电流和等离子体分压则分别用电流探头(TCP0030A, Tektronix)和电压探头(P6015, Tektronix)探测并显示在示波器(Tektronix MDO3024)上.2
3.2.脉冲频率对电子密度的影响
占空比是影响脉冲放电等离子体特性的主要方式. 改变占空比有两种方式: 其一是固定脉冲频率, 改变脉冲宽度; 其二是固定脉冲宽度, 改变脉冲频率. 我们在文献[36]中对前一种方案已经进行了深入研究, 相对于固定脉冲频率改变脉冲宽度的方案, 固定脉冲工作的时间, 只改变间歇时间, 则更能体现脉冲间歇时间对放电特性的影响. 实验中脉冲频率从2 kHz调节到9 kHz, 同时脉冲的占空比由20%增加到90%, 从而保证脉冲宽度在实验过程中始终保持在100 μs, 该时间也是ICCD的曝光时间和光谱仪的积分时间. 脉冲电源的电压幅值保持在2 kV, 实验中使用内径为1 mm的钨钢管电极, 钨钢管端面与液面的间距为2 mm, 氩气流量为25 sccm.图3(a)为使用ICCD采集的不同脉冲频率下的等离子体辐射强度分布图. 根据这些等离子体图像, 使用图像法计算的等离子体尺寸和电子密度如图3(c)和图3(d)所示. 图3(c)中的平均半径为等离子体在轴向各个位置对应的半径平均值. 图3(b)为采用拟合OH (A-X)谱线得到的气体温度变化曲线, 使用Stark展宽法得到的电子密度诊断结果如图3(d)所示.
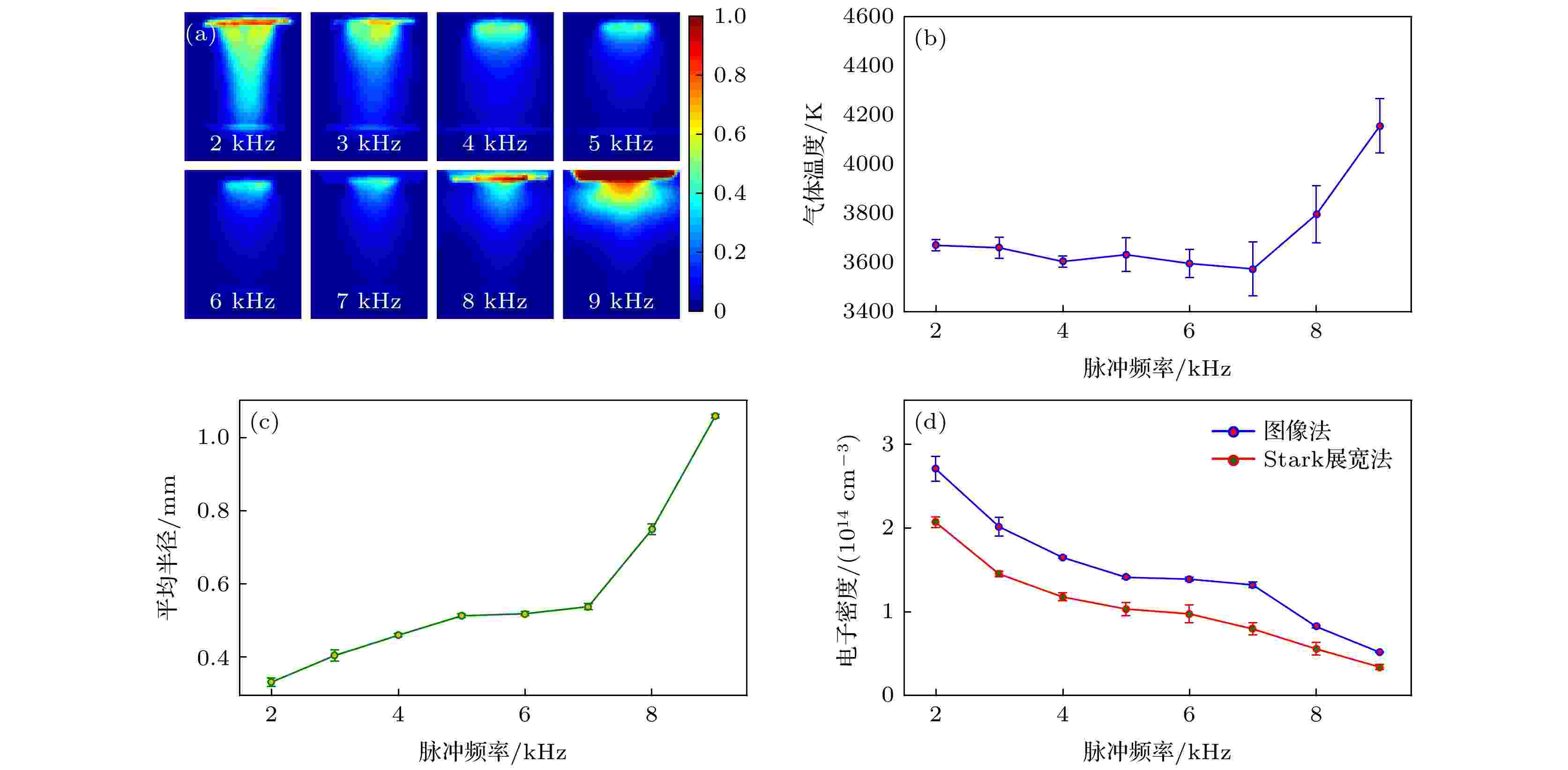图 3 不同脉冲频率下的等离子体参数测量结果 (a) 等离子体辐射强度分布图; (b) 气体温度; (c) 平均半径; (d) 电子密度Figure3. Measurement results of the plasma parameters at different pulse frequencies: (a) Normalized spatially resolved emission intensity; (b) gas temperature; (c) average radius; (d) electron density.
图3(d)中两种方法的电子密度诊断曲线演化趋势都显示, 随着脉冲频率的增加, 等离子体的电子密度逐渐下降. 图3及后文中的所有实验数据的误差线均为5次测量的标准差. 因为实验中测得的电子密度为脉冲工作期间的时间平均值, 所以为了使用全局模型分析这一过程, 需要关注在脉冲工作期间, 包括脉冲开启瞬间与稳态放电两个时间段内吸收功率的变化情况. 因此有必要测得等离子体在脉冲工作期间的波形图, 如图4(a)和图4(b)所示.
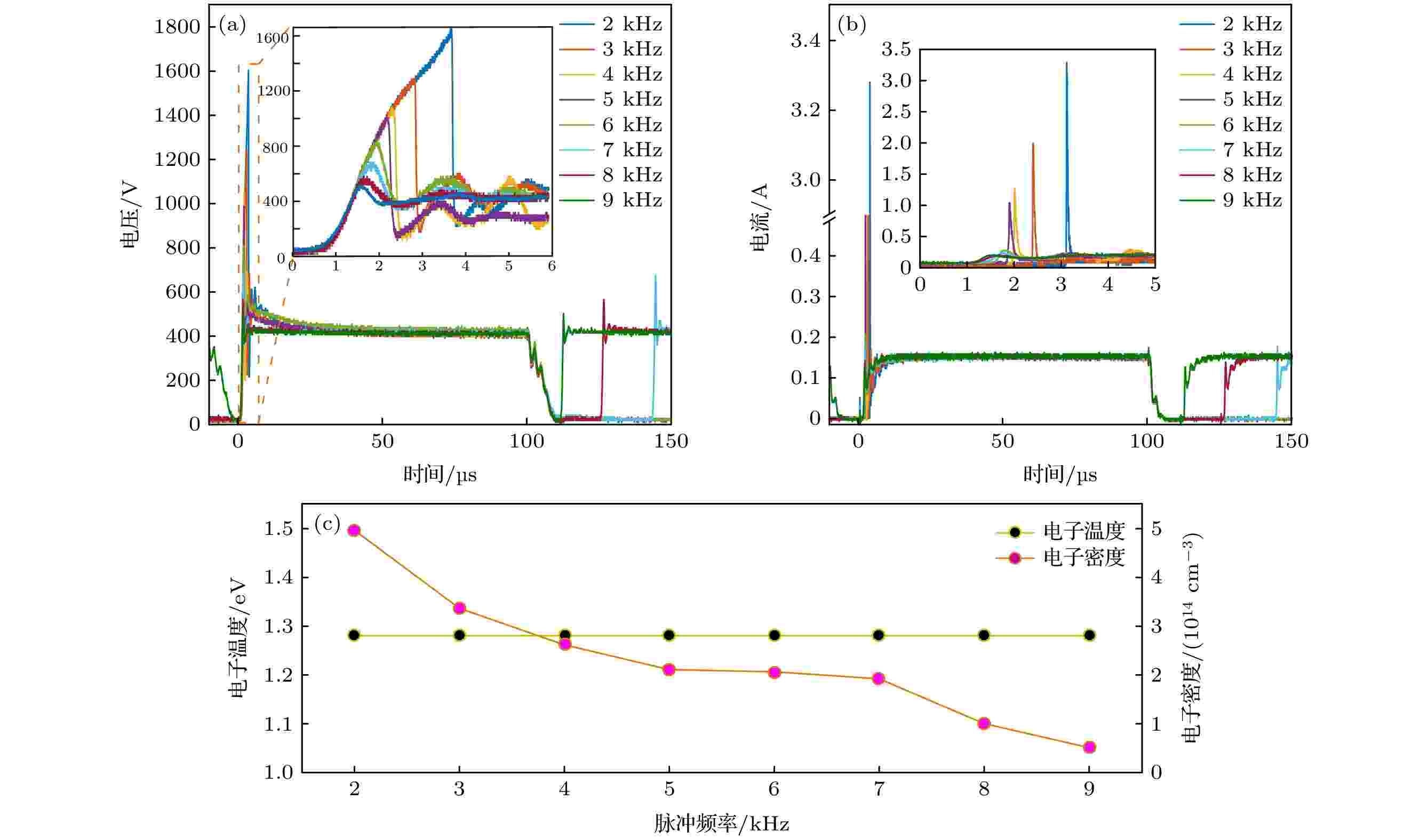图 4 不同脉冲频率时等离子体的波形图和基于全局模型的数值模拟结果 (a) 极间电压; (b) 回路电流; (c) 稳态下的电子温度和电子密度数值模拟结果Figure4. Waveform and simulated results based on global model at different pulse frequencies: (a) Voltage drop; (b) discharge current; (c) simulated results of the electron temperature and electron density at the steady state.
在图4(a)和图4(b)中可以发现, 当改变脉冲频率时, 稳定放电状态下的极间电压和回路电流没有变化, 分别为400 V和150 mA, 但是降低脉冲频率则会大幅度提高等离子体的击穿电压和击穿电流[39], 并且延长击穿所需的时间. 这主要是由于低脉冲频率的情况下, 脉冲处于间歇期的时间较长. 前一次放电结束残留的电荷随脉冲间歇时间的延长呈指数形式衰减[36], 使下一次放电的种子电荷数减少, 导致发生气体击穿所需时间延长, 因此对应的击穿电压升高, 击穿电流增大. 结合图3(c)中的等离子体尺寸数据, 基于全局模型可以计算出如图4(c)所示的稳态等离子体的电子温度和电子密度.
由图4(a)和图4(b)可知, 随着脉冲电源频率的增加, 等离子体在稳态放电时的吸收功率保持不变, 同时图4(c)的数值模拟结果显示等离子体的稳态电子温度也没有变化. 此时由于前一次脉冲结束后残留的种子电荷数在增加, 使下一次脉冲的放电通道数增加[40], 导致等离子体的放电体积在逐渐扩大, 引起等离子体稳态电子密度的下降. 另外, 图4(a)和图4(b)还显示, 在脉冲频率增加时, 峰值吸收功率也在下降. 根据文献[36]的报道, 脉冲间歇时间直接影响气体击穿瞬间的电子密度, 间歇时间越短, 击穿瞬间的电子密度越低. 在上述因素共同作用下, 随着脉冲频率的上升, 时间平均电子密度是逐渐下降的.
在图3(b)中, 等离子体的气体温度在脉冲频率从2 kHz调节到7 kHz时没有明显变化; 而在7 kHz以上则呈现快速升高的趋势. 这是因为一方面在脉冲频率增加的过程中, 等离子体的放电体积逐渐增大, 导致具有较高气体温度的等离子体与环境空气之间发生传导散热的接触面积不断扩大, 即散热效果更为明显. 另一方面, 在脉冲频率由2 kHz增加到9 kHz的过程中, 脉冲占空比由20%增加到90%, 如图4(a)和图4(b)所示, 稳态时的等离子体吸收功率不随脉冲频率发生变化, 因此脉冲占空比的增加意味着在一定时间内等离子体在电场中获得了更多的能量, 从而导致气体温度上升到更高的数值. 两种效果相反的因素使得图3(b)中脉冲频率在7 kHz以下时气体温度变化不是很明显. 此外, 根据文献[41]的结论, 对于脉冲放电等离子体, 前一个脉冲周期结束后气体的“剩余温度”越高, 下一次脉冲开启后气体温度将会以更快的速度上升至更高的数值. 由于前后两次脉冲间隔的时间直接影响到气体热量的弛豫时间, 这也是导致气体温度在7 kHz以上时上升较快的原因. 但是如果弛豫时间足够长, 放电气体温度则会直接下降至室温, 此时“剩余温度”对下一次脉冲放电时的气体温度的影响则可以忽略不计.
2
3.3.电极间距对等离子体电子密度的影响
在常压等离子体放电系统中, 改变放电系统的电极间距, 也是一种直接而有效的改变等离子体特性的方式. 实验中, 粗径钨钢管端面(内径1 mm)距液面的高度依次调整为1, 1.5, 2, 2.5和3 mm, 同时氩气流量控制在25 sccm, 此时不再使用高压脉冲开关, 而是采用高压电源进行直流放电. 在改变电极间距的过程中, 通过改变电压保持回路中的电流为50 mA. 与前文类似, 不同电极间距情况下的等离子体辐射强度分布图、气体温度、平均半径和电子密度的变化如图5所示.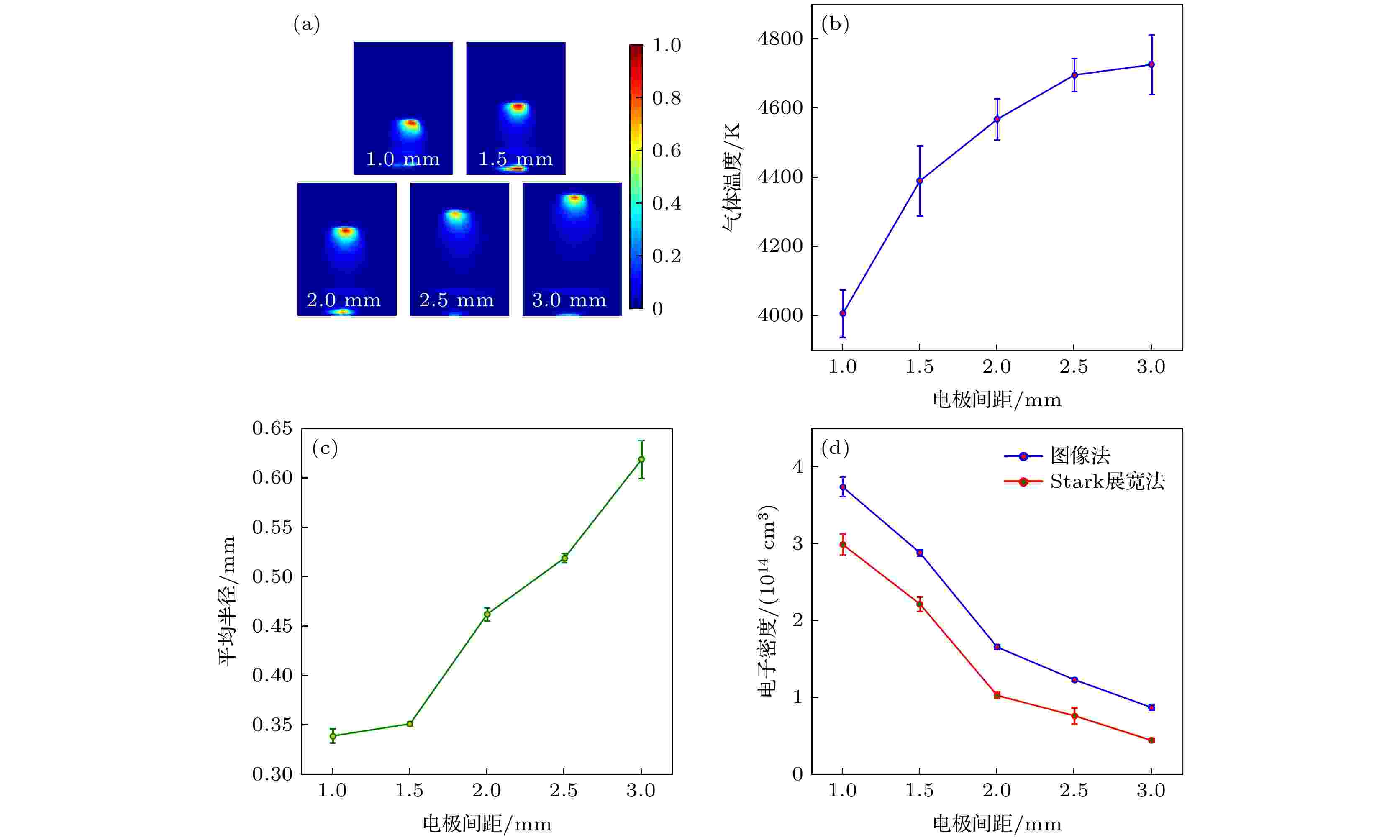
图 5 不同电极间距时的等离子体参数测量结果 (a) 等离子体辐射强度分布图; (b) 气体温度; (c) 平均半径; (d) 电子密度Figure5. Measurement results of the plasma parameters at different gap distances: (a) Normalized spatially resolved emission intensities; (b) gas temperature; (c) average radius; (d) electron density.
由图5(c)可知, 随着电极间距的增加, 等离子体的平均半径逐渐增大, 导致电子密度下降, 如图5(d)所示. 联系图3(d)中的实验结果可以发现, 尽管两种诊断方法得到的电子密度演化趋势是一致的, 但是Stark展宽法与图像法的测量结果的绝对数值存在一定的差异. 这是因为在图像法诊断的过程中, 将主等离子体区视为标准圆柱状是一种简化近似, 这种近似必然会对图像法的诊断结果造成影响. 同时在Stark展宽法中, 即使采用插值的方法降低了测量误差, 但是气体温度诊断误差以及不可避免的环境扰动也会对Stark展宽法的诊断结果造成影响. 换句话说, 在使用这两种方法诊断电子密度时, 多种诊断误差都会对两种方法的绝对数值造成影响.
在电极间距增加、等离子体密度下降的过程中, 等离子体的吸收功率和放电体积都发生了变化, 因此, 采用全局模型作数值模拟时须同时兼顾这几种因素的影响. 通过测量得到图6(a)所示的等离子体在不同电极间距时的极间电压后, 可以计算得到等离子体的吸收功率. 将这一数据代入(8)式和(9)式, 基于全局模型就可以计算得到如图6(b)所示的稳态电子密度和稳态电子温度.
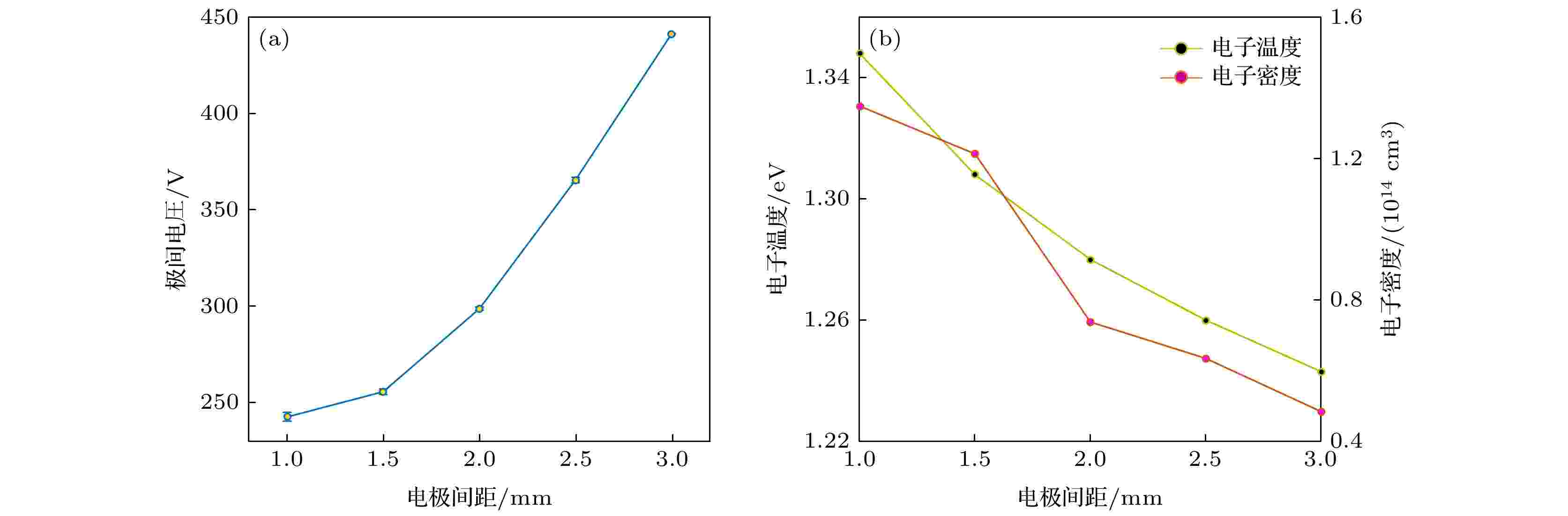图 6 不同电极间距时等离子体极间电压和基于全局模型的数值模拟结果 (a) 极间电压; (b) 稳态下的电子温度和电子密度数值模拟结果Figure6. Voltage drop and simulated results based on global model at different gap distances: (a) Voltage drop; (b) simulated results of the electron temperature and electron density at the steady state.
在图6(b)中可以发现, 与固定电极间距的情况不同, 随着电极间距的增加, 等离子体的电子温度逐渐下降. 这是因为电极间距的增加导致电子从阴极到阳极的过程中与中性粒子发生碰撞的概率增大, 使自身损失了更多的能量. 而文献[42]中的理论则进一步证明了吸收功率的增加对稳态电子温度几乎没有影响, 这就意味着电子将更多自身的能量传递给了中性气体, 一方面使其发生电离和激发, 另一方面也使气体的温度上升, 如图5(b)所示. 当气体温度上升到一定程度后, 不断增大的等离子体与空气接触面积使气体温度的上升速度逐渐放缓.
由于此时的放电环境为直流放电, 因此只需要考虑稳态放电情况下的电子密度变化情况. 根据稳定放电状态下的功率平衡方程(9), 等离子体的体积(图5(c))、极间电压(图6(a))以及稳态电子密度和电子温度的数值模拟结果(图6(b))可知, 改变电极间距会同时对等离子体放电体积和极间电压造成影响, 而电子密度的变化则是等离子体放电体积和吸收功率共同作用的结果. 其中, 放电体积增大会降低电子密度, 而等离子体吸收功率上升则会提高电子密度. 图5(d)的实验结果和图6(b)中的模拟结果则说明相比于吸收功率的增加, 放电体积的增大是增加电极间距的过程中电子密度降低的主导性因素.
2
3.4.电极内径对电子密度的影响
等离子体的放电体积对电子密度起到了决定性的作用. 当改变电极的内径时, 等离子体的放电体积会随之发生变化. 如图7(a)所示, 使用内径为1 mm的粗径电极和内径为175 μm的细径电极, 在表1所列的相同的放电条件下, 进行直流放电, 放电图像如图7(b)所示. 其中, 表1不仅列出放电实验参数, 也给出了对等离子体气体温度、尺寸、电子密度的诊断结果.表1的数据显示, 在相同的放电条件下, 细径电极所产生的等离子体放电体积更小, 因而也更容易产生较高的电子密度. 同时, 虽然细径电极产生的等离子体与环境空气接触面积更小, 造成的传导散热更少, 但作为气体流体, 气体在两种电极中的流速差异很大(0.53 m/s, 17.31 m/s), 对流传热差异使得细径电极中的气体带走了更多的热量, 因此它所产生的等离子体气体温度更低一些.
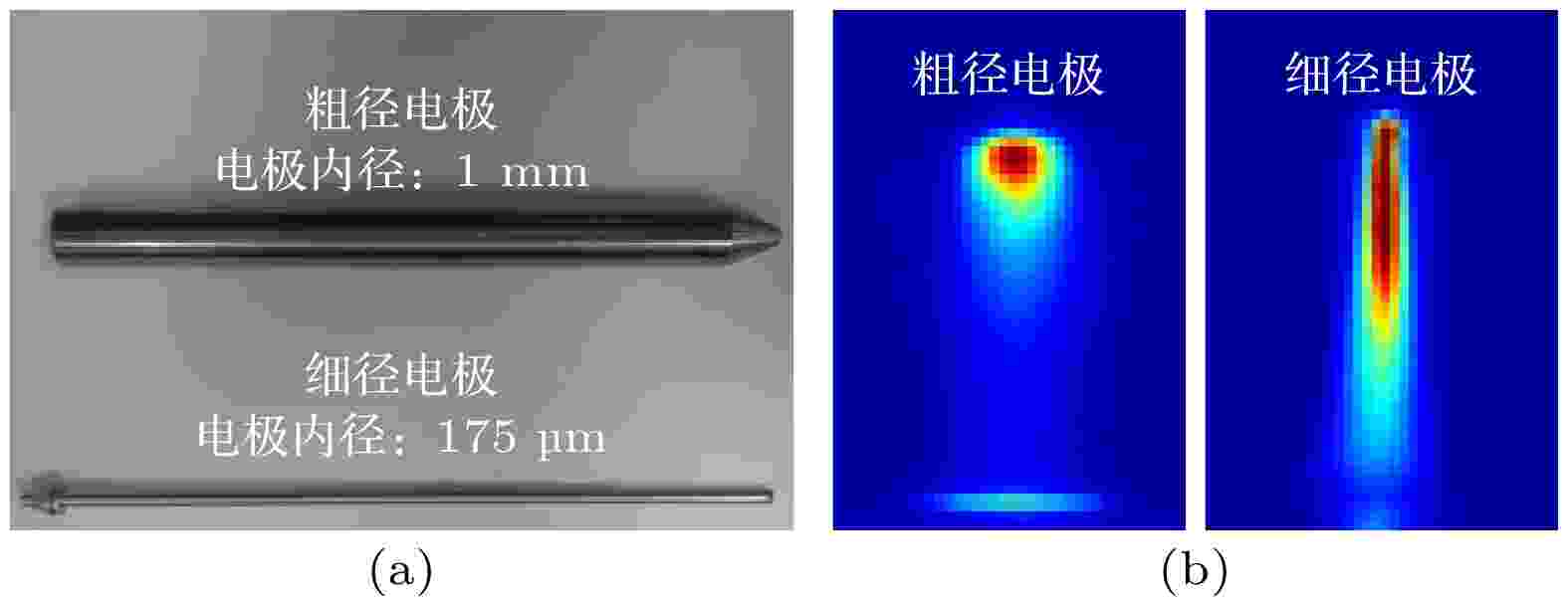图 7 两种不同内径电极放电图片 (a) 电极实物图; (b) 辐射强度分布图Figure7. Photographs of the electrodes for two different inner diameters and their plasma images: (a) Photographs of the electrodes; (b) normalized spatially resolved emission intensities.
| 放电参数 | 粗径电极 | 细径电极 |
| 电极内径/mm | 1 | 0.175 |
| 气体流量/sccm | 25 | 25 |
| 放电电流/mA | 20 | 20 |
| 气体温度/K | 2736 ± 21 | 1914 ± 13 |
| 等离子体平 均半径/μm | 238 ± 4.6 | 170 ± 1.5 |
| 电子密度 (图像法)/cm–3 | (4.61 ± 0.13)×1014 | (7.91 ± 0.12)×1014 |
| 电子密度 (Stark展宽法)/cm-3 | (3.73 ± 0.45)×1014 | (6.46 ± 0.68)×1014 |
表1两种不同内径电极的放电参数
Table1.Discharge parameters of two kinds of electrodes with different inner diameters.
