摘要:金刚石氮-空位色心结构因在量子精密测量领域的高灵敏度优势而备受关注. 本文引入耦合声子场对氮-空位色心原子自旋进行共振调控, 以提高氮-空位色心的自旋跃迁效率. 首先, 基于波函数和晶格的点阵位移矢量关系, 分析了声子与晶格能量交互作用, 研究了基于声子共振调控的氮-空位色心的自旋跃迁机理, 建立了基于应变诱导的能量转移声子-自旋交互耦合激发模型. 其次, 基于氮-空位色心晶格振动理论, 引入满足布洛赫定理的系数矩阵, 建立了不同轴向氮-空位色心第一布里渊区特征区域的声子谱模型. 同时, 基于德拜模型, 考虑热膨胀效应, 解析该声子共振系统的声子热平衡性质, 并对其比热模型进行研究. 最后, 基于分子动力学仿真软件CASTEP和密度泛函理论进行第一性原理研究, 构建了声子模式下不同轴向氮-空位色心的结构优化模型, 并分析了其结构特性、声子特性和热力学特性. 研究结果表明, 系统声子模式的演化依赖于氮-空位的占位, 声子模式强化伴随着热力学熵的降低. 含氮-空位色心金刚石的共价键较纯净无缺陷金刚石更弱, 热力学性质更不稳定. 含氮-空位色心金刚石的声子主共振频段处于THz量级, 次共振频率约为[800,1200] MHz. 根据次共振频段设计叉指宽度为1.5 μm的声表面波共振机构, 其中心频率约为930 MHz. 在该声子共振调控参数条件下, 声子共振调控方法可有效增大氮-空位色心的自旋跃迁概率, 实现氮-空位色心原子自旋操控效率的提高.
关键词: 氮-空位色心/
声子耦合/
原子自旋/
共振调控

English Abstract

全文HTML

--> --> -->

氮-空位(Nitrogen-Vacancy, NV)色心是金刚石中的一种原子点缺陷. 自从实现NV色心的光探测磁共振以来, NV色心受到了人们的广泛关注^[1]. 室温下, NV色心这一固态单自旋体系具有毫秒量级的相干时间, 可用光学共聚焦系统进行初始化和读出, 并且利用交变磁场实现单个自旋量子态的调控. 这些优良性质使之被用于量子计算^[2]、量子模拟^[3]及量子物理基本问题^[4-7]等研究. 近年来, 基于体系设计的纳米分辨率量子探测器, 在物理学、化学、生物学等领域具有广泛而重要的应用前景^[8].
将声子场耦合到量子位引起了量子声学的研究热潮. 声子是晶体中离子或原子振动的量子化表现^[9]. 声子特征与晶体材料的输运性质及多体相互作用下的元激发性质、元激发寿命、谱线宽度、磁化率、热性质等都密切相关^[10,11]. 因声子波长小、无辐射等优点已经应用到量子计算^[12-16]和超导量子位计算^[17-20]中. 通过将声子机械或电磁耦合到人造含掺物(如NV色心), 研究者已开展自旋纠缠、自旋压缩和声子换能的研究^[12,21-24]. ****通过研究发现NV色心的自旋态与金刚石的声子模式相关^[25-40]. NV色心声子-自旋耦合强度的形变势与能隙相关^[41], 其自旋相干性导致基态自旋的声子耦合非常弱^[42,43], 激发态下NV色心自旋比基态自旋的声子耦合程度大6个量级^[44,45]. 因此可通过声子辅助多物理场对NV色心进行耦合控制^[46].
目前, ****工作主要集中在研究声子作用下NV色心的自旋跃迁性质, 即“声子耦合作用于NV色心, 其自旋跃迁性质会发生什么变化? ”这一命题. 目前对金刚石NV色心的原子自旋声子耦合机理研究很少, 特别是缺乏NV色心自旋跃迁的声子耦合介导机理和声子模式下含NV色心金刚石热力学性质的文献报道. 本文重点研究金刚石氮-空位色心的原子自旋声子耦合机理, 即“声子如何耦合作用于NV色心? ”这一关键命题. 本文引入了耦合声子场对NV色心自旋进行共振调控, 重点研究声子模式下NV色心的结构特性、声子特性和热力学特性, 为后续研究声子辅助操控NV色心原子自旋, 实现自旋跃迁效率的提高具有一定的指导意义. 本文各部分研究内容阐述如下.
第一部分: 介绍了NV色心量子传感的应用背景, 具体阐述了目前声子耦合操控NV色心自旋跃迁的研究现状.
第二部分: 阐述了含NV色心金刚石的晶体结构、自旋跃迁性质和量子敏感机理.
第三部分: 首先, 基于波函数和晶格的点阵位移矢量关系, 分析了声子与晶格能量交互作用, 研究了基于声子共振调控的NV色心的自旋跃迁机理, 建立了基于应变诱导的能量转移声子-自旋交互耦合激发模型. 其次, 基于NV色心晶格振动理论, 引入满足布洛赫定理的系数矩阵, 建立了不同轴向NV色心第一布里渊区特征区域的声子谱特征. 同时, 基于德拜(Debye)模型, 考虑热膨胀效应, 解析该声子共振系统的声子热平衡性质, 并对其比热性质进行研究.
第四部分: 基于分子动力学仿真软件CASTEP和密度泛函理论进行第一性原理研究, 构建了声子模式下不同轴向NV色心的结构优化模型, 并分析了其结构特性、声子特性和热力学特性.
第五部分: 对本文工作进行总结.

2

-->

2.1.NV色心的结构和自旋跃迁性质

金刚石NV色心的几何结构如图1(a)所示, 当金刚石晶格中有一个N原子取代了C原子, 而相邻位置又缺少一个C原子而留下空位时, 就形成了NV色心. 大多数NV色心带有一个负电荷或处于电中性状态, 分别记为NV^–和NV⁰. 本文中提到的NV色心均指NV^–, 它有6个价电子, 占据4个分子轨道. NV色心的能级结构及自旋跃迁性质如图1(b)所示. 第一激发态与基态的能级差为1.945 eV, 对应的波长是637 nm, 采用532 nm波长的激光可激发这一跃迁. 处于激发态的NV色心有两条主要的退激发途径, 其中之一是发射荧光回到基态, 另一条途径是发生系间窜越, 经由单态¹A₁和¹E回到基态, 这一过程不辐射荧光^[8].
图 1 NV色心几何结构和自旋跃迁性质　(a)几何结构; (b)能级结构及自旋跃迁性质
Figure1. Structures and spin transition properties of a negatively charged NV center: (a) Geometric structure; (b) energy level structure and spin transition properties.

由于金刚石具有$ {{C}}_{{3}{V}} $对称性, 在金刚石样品中NV色心存在4个不同的量子化轴, 分别为[1, 1, 1]轴向、[1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向. NV色心量子化轴如图2所示. 金刚石中4个不同轴向NV色心分布及NV坐标系如图3所示.
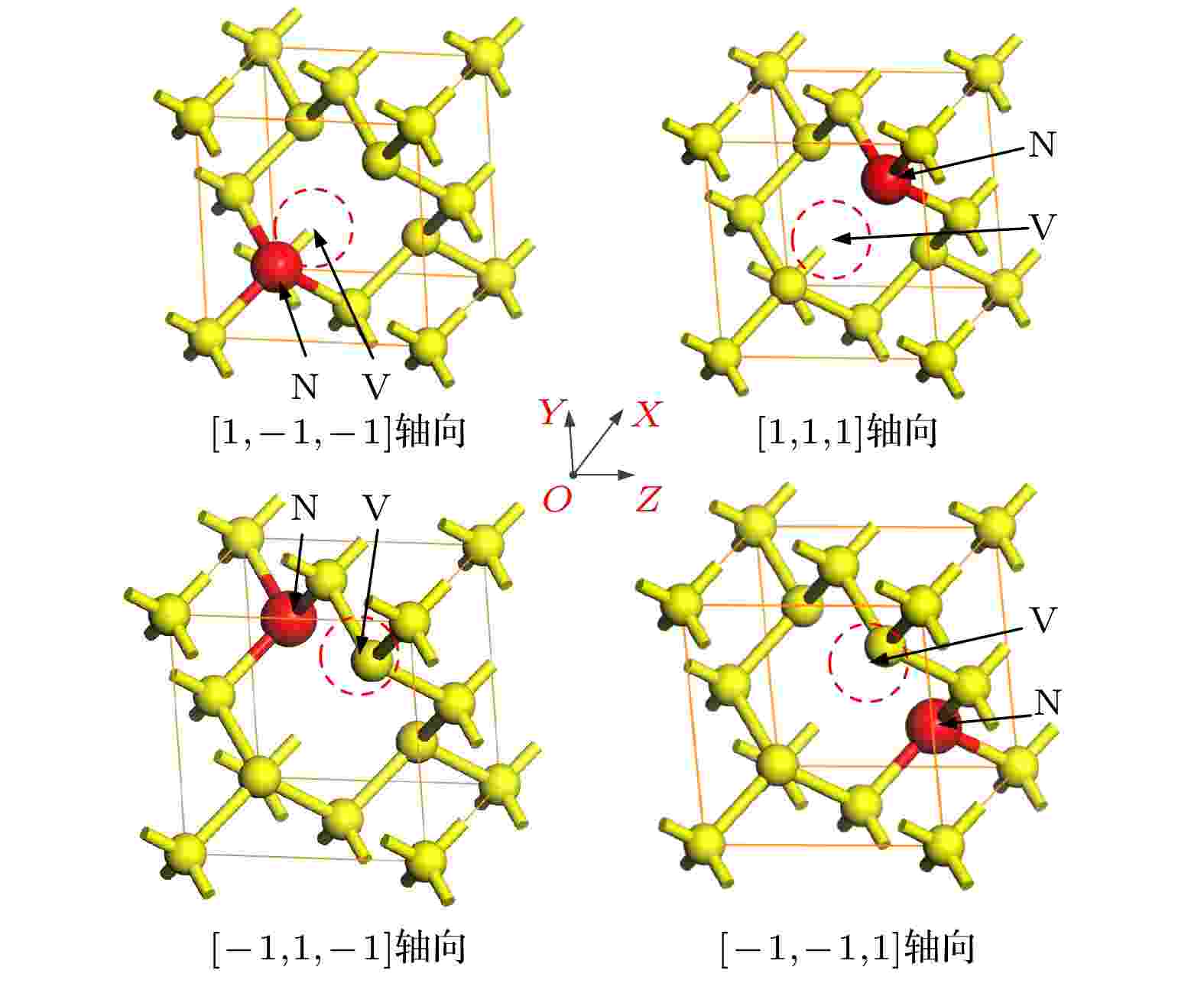图 2 NV色心量子化轴示意图
Figure2. Schematic diagram of quantization axis for NV center

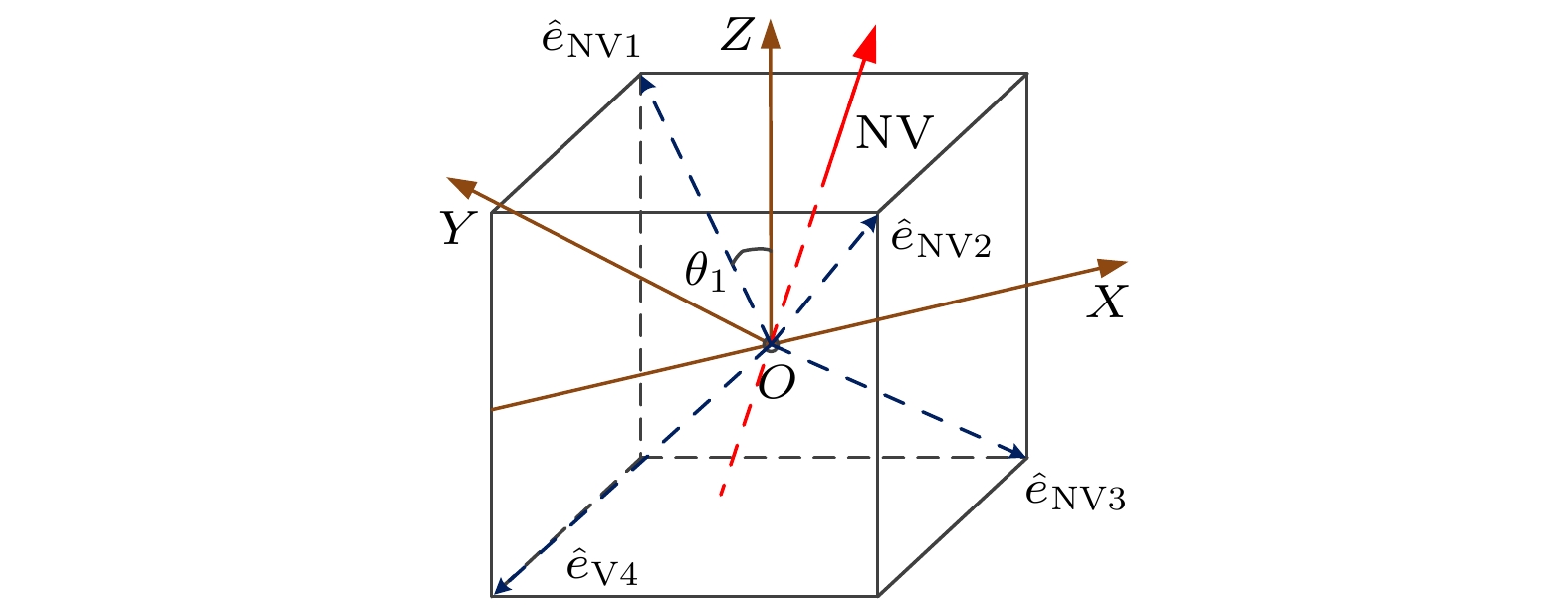图 3 金刚石中4个轴向NV色心分布及NV坐标系
Figure3. Four axial NV center distributions and their NV coordinate systems in diamond.

2 -->

2.2.NV色心的量子敏感原理

NV色心基态自旋能量的哈密顿方程为

$H = \frac{1}{\hbar }DS_Z^2 + \frac{{g{\mu _{\rm{B}}}}}{\hbar }{{B}} \cdot S,$

式中D为NV色心的零场分裂参量, $ D= $2.87 GHz; B为外部磁场矢量; g为波谱分裂因子, $ g= 2 $; $ {{\mu }}_{\rm{B}} $为玻尔磁子, ${{\mu }}_{\rm{B}}= 1.4$ MHz/G; $ \hbar ={h}{/(2{\text{π}})} $是约化普朗克常数; S为不确定度, 其表达式为

$S = \sin \theta \cos \varphi {S_X} + \sin \theta \sin \varphi {S_Y} + \cos \theta {S_Z},$

其中, S_X, S_Y和S_Z分别为量子化轴X, Y和Z方向的不确定度.
(1)式等号右侧第一项为NV色心零场分裂哈密顿量; 第二项为加外部磁场后NV色心自旋作用哈密顿量.
由于塞曼效应, 其中沿着$ {{B}}_{{Z}} $方向的静磁场使得原本简并的$ \left| {{m_{\rm{s}}} = \pm 1} \right\rangle $态发生能级分裂. 两个能级$\left| {{m_{\rm{s}}} = 0} \right\rangle \to \left| {{m_{\rm{s}}} = + 1} \right\rangle $和$\left| {{m_{\rm{s}}} = 0} \right\rangle \to \left| {{m_{\rm{s}}} = - 1} \right\rangle $产生不同的退激发频率$ {{\nu }}_{1} $和$ {{\nu }}_{2} $, 并释放出荧光. $\left| {{m_{\rm{s}}} = 0} \right\rangle $态和$\left| {{m_{\rm{s}}} = \pm 1} \right\rangle $态分别对应本征值$ {E}_{0} $, $ {E}_{-1} $和$ {E}_{+1} $可以给出:

$\left\{ {\begin{aligned}&{{E_0} = \frac{1}{3}\left[ {2D - 2\sqrt N \times \sin \left( {\frac{\varOmega }{3} + \frac{{\rm{\pi }}}{6}} \right)} \right],}\\&{{E_{ - 1}} = \frac{1}{3}\left[ {2D + 2\sqrt N \times \sin \left( {\frac{\varOmega }{3} - \frac{{\rm{\pi }}}{6}} \right)} \right],}\\&{{E_{ + 1}} = \frac{1}{3}\left[ {2D + 2\sqrt N \times \sin \left( {\frac{\varOmega }{3}} \right)} \right],}\end{aligned}} \right.$

其中, $\cos \varOmega=M/\sqrt {{M^2}+{K^2}}=M/(2\sqrt {{N^3}} )$; $\sin \varOmega = $$ K/\sqrt {{M^2}+{K^2}}=K/(2\sqrt {{N^3}} )$; $M=- 9\big(\| B\|^2- 3 B_Z^2 \big) \gamma _e^2 $$ - 2{D^3}$; $K = - {\rm{i}}\sqrt { - 4{N^3} + {M^2}} $, $K \geqslant 0$; ${\left\| B \right\|^2} = $$ B_X^2 + B_Y^2 + B_Z^2$; $\varOmega $为自旋跃迁频率, 相应退激发频率$ {{{\nu }}}_{{1}} $和$ {{{\nu }}}_{2} $分别表达如下:

$\left\{ {\begin{aligned}&{{\nu _1} = \frac{{2\sqrt N }}{{\sqrt 3 }}\sin \left( {\frac{\varOmega }{3}} \right),}\\&{{\nu _2} = \sqrt N \cos \left( {\frac{\varOmega }{3}} \right) + \frac{{\sqrt N }}{{\sqrt 3 }}\sin \left( {\frac{\varOmega }{3}} \right).}\end{aligned}} \right.$

因此, 由两个退激发频率(通过荧光检测)就可获得磁场强度B和相对于该NV轴的极化角$ \theta $:

${{B}} =\sqrt {\frac{{\left( {2{\nu _1}-{\nu _2}-D} \right)\left( {{\nu _1}-2{\nu _2}+D} \right)\left( {{\nu _1} + {\nu _2} + D} \right)}}{{9D\left( {\nu _1^2 - {\nu _1}{\nu _2} + \nu _2^2 - {D^2}} \right)}}},$

$\begin{split} & \theta = \\& \arccos \left[ {\sqrt {\frac{{( {2{\nu _1}-{\nu _2}-D} )( {{\nu _1}-2{\nu _2}+D} )( {{\nu _1}+{\nu _2}+D} )}}{{9D( {\nu _1^2-{\nu _1}{\nu _2}+\nu _2^2-{D^2}} )}}} } \right].\end{split}$

2

-->

3.1.NV色心自旋跃迁的声子共振调控机理

声子本质是声子场在金刚石内部传输时, 介质的晶格振动能量的量子. 在基于声子共振调控的NV色心原子自旋量子态操控系统中, 声子与自旋的交互作用实为晶格振动与自旋的相互作用. 自旋在晶格的周期性势场中, 由于晶格原子不停地在其平衡位置附近发生小振动, 从而破坏了晶格的周期性势场, 产生了附加形变势. 自旋因受到附加势场的作用, 激发势能发生改变^[47].
绝热近似下, 金刚石晶格的运动简化为两个相对较小的子系统(电子系统和原子实系统)的运动. 对给定的电子系统状态n, 原子实系统受到有效势场${V_{\rm{N}}}\left( {{R}} \right)$为原子实间的库仑相互作用${V_{{\rm{LL}}}}\left( {{R}} \right)$与电子能${E_n}\left( {{R}} \right)$之和, 即:

${V_{\rm{N}}}\left( {{R}} \right) = {V_{{\rm{LL}}}}\left( {{R}} \right) + {E_n}\left( {{R}} \right).$

则原子实系统运动的哈密顿方程表达如下:

$\begin{split}{E_n}X\left( {{R}} \right) =\;& - \frac{\hbar }{2}\mathop \sum \nolimits_{\rm{I}} \frac{1}{M}\nabla _{\rm{I}}^2X\left( {{R}} \right)\\&+ \left[ {{V_{{\rm{LL}}}}\left( {{R}} \right) + {E_n}\left( {{R}} \right)} \right]X\left( {{R}} \right).\end{split}$

其中, $ X\left( {{R}} \right) $是原子实系统运动轨迹向量.
采用周期性边界条件, 在金刚石第n个原胞中, 第l个原子的平衡位置为${{{R}}_{n\alpha }} = {{{R}}_n} + {{{R}}_l}$, $ {{{R}}_n}$和$ {{{R}}_l} $分别为原胞位置和原子l在$ {{l}}^{'} $原胞中的相对位置, 则金刚石面心立方晶体的原子振动方程转化为如下形式:

$M_l^\alpha = - \sum\nolimits_{{l^\prime },\beta } {{\phi _{\alpha \beta }}} \left( {l - {l^\prime }} \right)u_{{l^{'}}}^\beta,$

其中, $\sum\nolimits_{{l^\prime }, \beta } {{\phi _{\alpha \beta }}} \left( {l - {l^\prime }} \right)$表示$ {{l}}^{'} $原胞中原子沿$ \beta $方向位移单位距离时原子作用力沿$ \alpha $方向的分量, 称力常数; $ {{M}}_{{l}}^\alpha $表示原子l在$ \alpha $分量方向的振动矢量; $ u_{{l^{'}}}^\beta $表示原胞$ {{l}}^{'} $在$ \beta $方向的振动矢量.
由于金刚石是对周期排布的原子晶体, 在正则坐标系下对(9)式进行简谐近似, 转化为如下形式的格波$s_{na\beta }^{\left( {{{q}}, \sigma } \right)}\left( t \right)$:

$s_{na\beta }^{( {{{q}},\sigma } )}( t )=-\frac{1}{{\sqrt {NM_l^\alpha } }}e_{\alpha \beta }^{(\sigma )}( {{q}} )\exp \{ {\beta [ {{{q}} \cdot {{{R}}_n}-{\omega _\sigma }( {{q}} )t} ]} \}.$

其中, $e_{\alpha \beta }^{(\sigma )}\left( {{q}} \right)$为极化基矢, 是以波矢为$ {{q}} $, 频率为$ {\omega }_{\sigma } $传播的格波; $ {\omega }_{\sigma }\left({{q}}\right) $是频率为$ {\omega }_{\sigma } $, 波矢为$ {{q}} $的声子谱; $ {\sigma } $表示本征态, ${\sigma }= 1, 2, 3$; N表示金刚石中原胞数目; $ {{R}}_{{n}} $和$ {{R}}_{{l}} $分别为金刚石第n个原胞的原胞位置和原子l在原胞中相对代表点的位置; $ {{M}}_{{l}}^\alpha $表示原子l在$ \alpha $分量方向的振动矢量. (10)式阐释了金刚石晶格原子振动的基本模式.
由上述分析可知, 在声子场作用下, 可实现NV色心晶格原子的定向振动, 声子场共振结构及调控机理示意图分别如图4(a)和图4(b)^[48]所示.
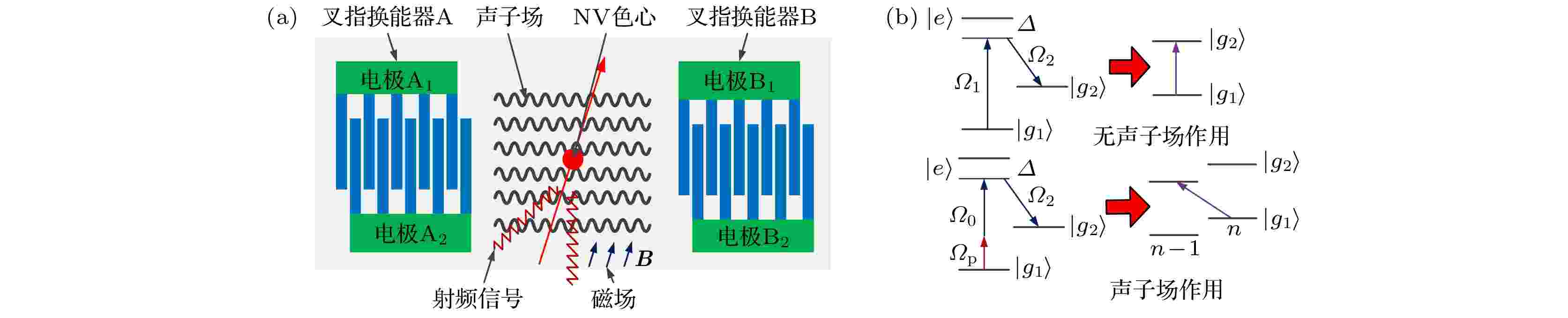图 4 (a)声子场共振结构示意图; (b)声子场共振调控机理示意图^[48]
Figure4. (a) Schematic diagram of phonon field resonance structure; (b) mechanism diagram of phonon field resonance control.

在无声子场作用时, 由拉比频率$ {\varOmega }_{1} $光场驱动的NV色心自旋跃迁系统在大偶极子$ \varDelta $失谐极限内, 等效于的两个较低状态的光驱动之间的自旋跃迁. 在含声子场作用时, 由声子场驱动系统从$|{g} \rangle$到$|{e} \rangle$的声子共振调控自旋跃迁, 其有效拉莫尔频率为$ {\varOmega }_{\rm{P}} $. 在大偶极子$ \varDelta $失谐极限下, 该系统等效于2个较低状态的声子阶梯之间的自旋跃迁, 其中n表示声子数.
NV色心的激发态与波长晶格应变强烈耦合. 这种电子-声子耦合可以导致应变诱导的能量转移, 也可以导致相关激发态的状态混合. 对于$ {E}_{y} $态, 描述应变诱导的能量转移的电子-声子相互作用哈密顿量模型为

${H_{{\rm{e \text{-} phonon}}}} = \hbar {g_2}\left( {b + {b^ + }} \right)\left| {{E_y} \rangle\langle {E_y}} \right|$

其中, b是声子的湮灭算符; $ {{b}}^{+} $是声子的产生算符; ${g_2} = {\text{δ}}{\varepsilon _{\rm{c}}}{k_{\rm{m}}}\sqrt {\hbar /2 m{\omega _{\rm{m}}}} $是电子-声子有效耦合率; $ {\varepsilon }_{\rm{c}} $表示晶格振动时的带边能量; $ {\text{δ}}{\varepsilon }_{\rm{c}} $是形变势, 且${\text{δ}}{\varepsilon }_{\rm{c}}=\left(\dfrac{\partial {\varepsilon }_{\rm{c}}}{\partial {V}}\right){\text{δ}}{V}$, $ {\text{δ}}{V} $是晶格振动的纵向声学模引起的晶格体积V的局域变化; $ {k}_{\rm{m}} $是声子模的波数; m是有效的力学质量振荡器; $ {\omega }_{\rm{m}} $是声子振荡频率.
对于从$ {m}_{\rm{s}}= 0 $到$ {E}_{y} $态的声子共振调控的自旋跃迁, 与位移成线性关系的有效哈密顿量$ {H}_{\rm{R}} $为^[29]

$\begin{split}{H_{\rm{R}}} = \;&\hbar \cdot \frac{{{\varOmega _0}}}{2} \cdot \frac{{{g_2}}}{{{\omega _{\rm{m}}}}}( b\left| {{E_y} \rangle\langle{m_{\rm{s}}} = 0} \right| + {b^ + }\left| {{m_{\rm{s}}} = 0\rangle\langle {E_y}} \right| ),\end{split}$

其中, $ {\varOmega }_{0} $是耦合到$ {m}_{\rm{s}}= 0 $到$ {E}_{y} $态跃迁的激光场的拉莫尔频率. 因此, 声子共振调控的自旋跃迁(红色带边跃迁)的有效拉比频率$ {\varOmega }_{\rm{P}} $由下式给出:

${\varOmega _{\rm{P}}} = {g_2}\sqrt {\left\langle n \right\rangle } \cdot {\varOmega _0}/{\omega _{\rm{m}}},$

其中, $ \left\langle {{n}} \right\rangle $是平均声子数. 当激光从红色带边过渡到蓝色带边时, 其哈密顿量类似.
将声子共振调控的自旋跃迁结合到三能级系统中, 并使用激发态电子-声子耦合来介导NV色心自旋和机械自由度之间的相互作用. 电子被困在两个较低的态中, 形成由两个较低能级的相干叠加导致的暗态, 该暗态可以介导和控制NV色心自旋状态与相关声子模式之间的相互作用, 由下式给出:

$|{\psi _{\rm{d}}} \rangle =\frac{1}{{\sqrt {\varOmega _{\rm{P}}^2+\varOmega _ \pm ^2} }}({\varOmega _{\rm{P}}}|{m_{\rm{s}}}= \pm 1 \rangle -{\varOmega _ \pm }|{m_{\rm{s}}}=0 \rangle ),$

其中, $ {\varOmega }_{\rm{P}} $和$ {\varOmega }_ \pm $是分别耦合到$ {m}_{\rm{s}}= 0 $和$ {m}_{\rm{s}}{= \pm 1} $状态的两个跃迁的拉比频率. 结合(1)式, 对于声子共振调控下NV色心的量子测量模型, 其哈密顿方程为

$H = \frac{1}{\hbar }DS_{{{{Z}}^{\prime}}}^2 + \frac{{g{\mu _{\rm{B}}}}}{\hbar } \cdot B \cdot S + {H_{{\text{e-phonon}}}} + {H_{\rm{R}}}.$

从(15)式可以看出, 以声子场辅助射频场和磁场共振耦合调控, 可实现NV色心原子自旋的共振耦合调控.
2 -->

3.2.NV色心的声子谱解析

根据(11)式和(12)式, 声子场辅助射频场和磁场共振耦合调控取决于电子-声子相互作用$ {H}_{\rm{e\text{-}phonon}} $和声子共振调控的自旋跃迁作用$ {H}_{\rm{R}} $. $ {H}_{\rm{e\text{-}phonon}} $和$ {H}_{\rm{R}} $与声子模式下晶格的形变势$ {\text{δ}}{\varepsilon }_{\rm{c}} $密切相关, 关系方程如下:

${\text{δ}}{\varepsilon _{\rm{c}}} = {f_{{\rm{NV}}}}\left(\sqrt {\omega _\sigma ^2\left( {{q}} \right)/V_{{\rm{LA}}}^2 - q_{\rm{z}}^2} \right)$

其中, $ {f}_{\rm{NV}} $为NV色心晶格结构特征函数; $ {\omega }_{\sigma }\left({{q}}\right) $为频率为$ {\omega }_{\sigma } $, 波矢为$ {{q}}$的声子谱; $ {{V}}_{\rm{LA}} $为晶格的纵向声学模; $ {{q}}_{{z}} $为波矢为$ {{q}}$的z向分量. 因此对NV色心声子谱$ {\omega }_{\sigma }\left({{q}}\right) $的解析至关重要.
由于(10)式所示的格波色散关系在波矢空间是周期为${\text{π}}/a$的周期性函数($E\left( k \right) = E\left( {k + \pi /a} \right)$), 因此只需用第一布里渊区中的波矢来描述能带电子、点阵振动和自旋波的状态. 纯净无缺陷的金刚石为面心立方晶体, 其第一布里渊区模型如图5(a)所示. 该模型为十四面体结构, 包含$ {\varGamma } $点、L点、U点、X点、W点和K点6个布里渊区特征点, 还包括$ {\varLambda } $线、$ {\varSigma } $线和$ \varDelta $线3个布里渊区特征线. 对于含NV色心的金刚石, 根据晶格动力学理论^[49], 本文通过在单个NV色心晶格的交界面上对称扩展方式建立第一布里渊区模型, 如图5(b)所示, 该模型为六面体结构, 包含$ {\varGamma } $点、Z点、Q点、K点、B点和F点6个布里渊区特征点, 还包括$ {\varLambda } $线、$ {\varSigma } $线、$ \varDelta $线和M线4个布里渊区特征线.
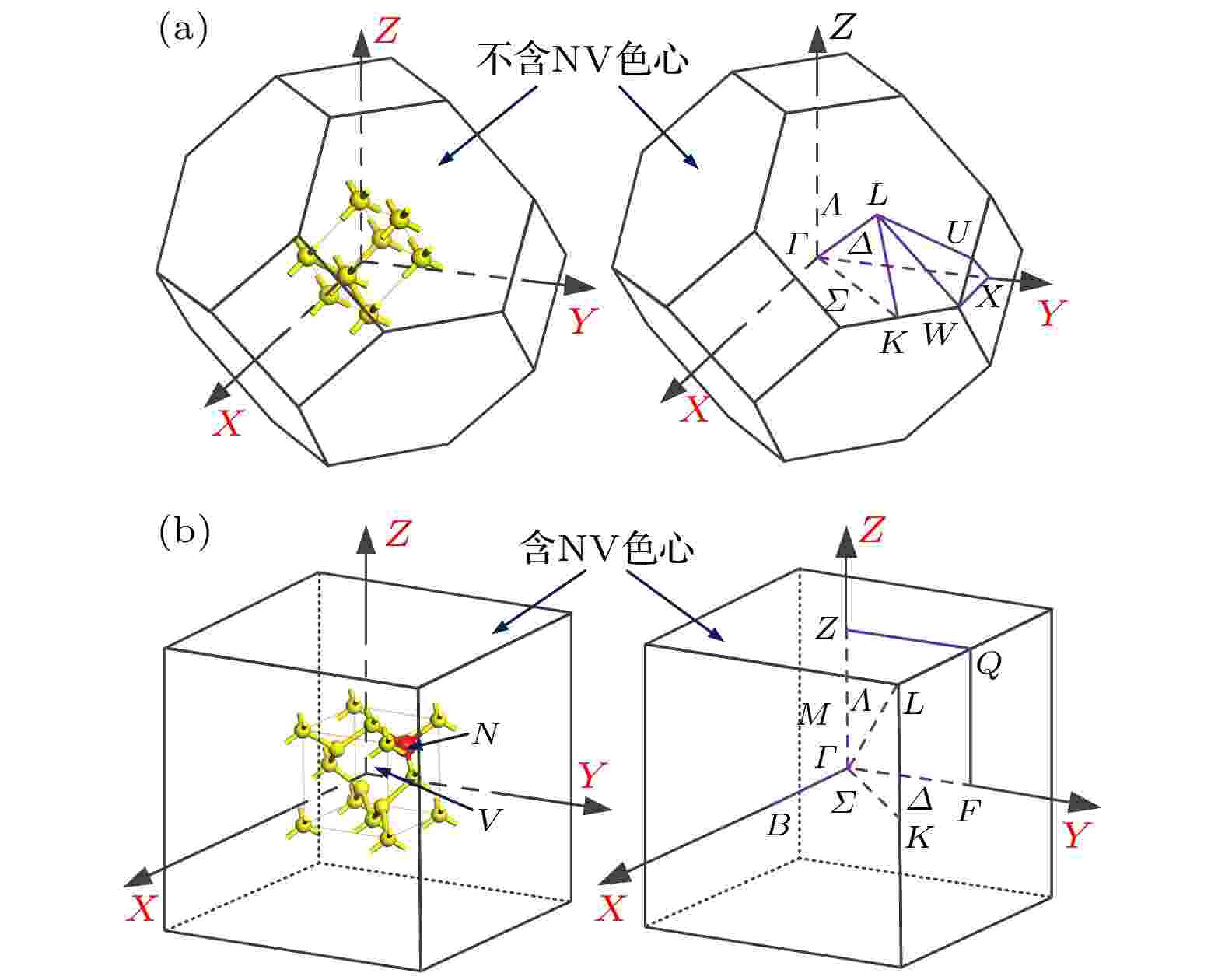图 5 金刚石第一布里渊区特征　(a)不含NV色心; (b)含NV色心
Figure5. Characteristics of first Brillouin zone of diamond: (a) Without NV center; (b) contain NV center.

本文基于晶体原子振动方程((9)式)对金刚石NV色心的声子谱进行解析, 由于(9)式是3N_m(N_m为第一布里渊区内的原子数)个二阶微分方程联立耦合的方程组, 为了对其进行声子谱解析, 引入满足布洛赫(Bloch)定理的系数矩阵^[49], 结合(10)式, 得到晶格动力学矩阵元$ {D}_{\alpha \beta} $, 表达如下:

${D_{\alpha \beta }} = \frac{1}{{M_l^\alpha }}\mathop \sum \nolimits_l {\phi _{\alpha \beta }}(l){{\rm{e}}^{ - {\rm{i}}{{qR}}}}.$

晶格动力学矩阵元$ {D}_{\alpha \beta} $的非零解的条件是

$\det \left\| {{D_{\alpha \beta }}\left( {{q}} \right) - {\omega _\sigma }^2\left( {{q}} \right){\delta _{\alpha \beta }}} \right\| = 0,$

其中, $ {\omega }_{\sigma }\left({{q}}\right) $为频率为$ {\omega }_{\sigma } $, 波矢$ {{q}}=\left({{q}}_{{x}}, {{q}}_{y}, {{q}}_{{z}}\right) $的声子谱; $ {{\rm{\delta }}}_{\alpha \beta} $表示原子沿$ \beta $方向位移单位距离时原子作用力沿$ \alpha $方向分量的声子谱系数.
将(18)式展开, 忽略三次及以上近邻力高阶项, 可得到3个声子谱$ {\omega }_{\sigma }\left({{q}}\right)\left({\sigma }{= 1, 2, 3}\right) $及对应的3个极化向量${{{e}}_{q\sigma }} = \left( {{e_{qx\sigma }}, \;{e_{qy\sigma }}, \;{e_{qz\sigma }}} \right)$(表示金刚石原子的振动方向), 其动力学矩阵元分解式为

$\left\{ \begin{aligned}&{D_{xx}}\left( {{q}} \right) = \left( {2{f_1}/M_l^\alpha } \right)\left[ {1 + 2\eta - \cos {q_x}a - \eta \cos {q_x}a\left( {\eta \cos {q_y}a + \cos {q_z}a} \right)} \right],\\&{D_{yy}}\left( {{q}} \right) = \left( {2{f_1}/M_l^\alpha } \right)\left[ {1 + 2\eta - \cos {q_y}a - \eta \cos {q_y}a\left( {\eta \cos {q_x}a + \cos {q_z}a} \right)} \right],\\&{D_{zz}}\left( {{q}} \right) = \left( {2{f_1}/M_l^\alpha } \right)\left[ {1 + 2\eta - \cos {q_z}a - \eta \cos {q_z}a(\eta \cos {q_x}a + \cos {q_y}a)} \right],\end{aligned} \right.\tag{19a}$

$\left\{ {\begin{aligned}&{{D_{xy}}\left( {{q}} \right) = \left( {2{f_1}/M_l^\alpha } \right)\eta \sin {q_x}a\sin {q_y}a,}\\&{{D_{xz}}\left( {{q}} \right) = \left( {2{f_1}/M_l^\alpha } \right)\eta \sin {q_x}a\sin {q_z}a,}\\&{{D_{yz}}\left( {{q}} \right) = \left( {2{f_1}/M_l^\alpha } \right)\eta \sin {q_y}a\sin {q_z}a,}\end{aligned}} \right.\tag{19b}$

其中, $ {f}_{1} $是最近邻力常数, $ {f}_{2} $是次近邻力常数, $ {\eta}={f}_{2}/{f}_{1} $是次近邻力常数与最近邻力常数之比, $ \alpha $是金刚石近邻原子间平衡间距, $ {a}{= 1.544}$ ?, 波矢$ {{q}}=\left({{q}}_{{x}}, {{q}}_{y}, {{q}}_{{z}}\right) $.
对于四种轴向的NV色心金刚石晶体, 晶格动力学矩阵元的不对称关系如表1所列. 其中, $ {k}_{{[1, 1, 1]}} $, $ {k}_{[1, -1, -1]} $, $ {k}_{{[-1, 1, -1]}} $和$ {k}_{{[-1, -1, 1]}} $分别是[1, 1, 1]轴向、[1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向NV色心金刚石晶体的氮-空位不对称系数.

NV色心轴向	晶格动力学矩阵元不对称关系		NV色心轴向	晶格动力学矩阵元不对称关系
无NV色心	$\left\{ \begin{aligned}&{ {D_{xy} }\left( {{q} } \right) = {D_{yx} }\left( {{q} } \right)}\\&{ {D_{yz} }\left( {{q} } \right) = {D_{zy} }\left( {{q} } \right)}\\&{ {D_{xz} }\left( {{q} } \right) = {D_{zx} }\left( {{q} } \right)}\end{aligned} \right.$		[–1, 1, –1]轴向	$\left\{ {\begin{aligned}&{{D_{xy}}\left( {{q}} \right) = - {k_{[ - 1, 1, - 1]}}{D_{yx}}\left( {{q}} \right)}\\&{{D_{yz}}\left( {{q}} \right) = - {k_{[ - 1, 1, - 1]}}{D_{zy}}\left( {{q}} \right)}\\&{{D_{xz}}\left( {{q}} \right) = {k_{[ - 1, 1, - 1]}}{D_{zx}}\left( {{q}} \right)}\end{aligned}} \right.$
[1, 1, 1]轴向	$\left\{ {\begin{aligned}&{{D_{xy}}\left( {{q}} \right) = {k_{[1, 1, 1]}}{D_{yx}}\left( {{q}} \right)}\\&{{D_{yz}}\left( {{q}} \right) = {k_{[1, 1, 1]}}{D_{zy}}\left( {{q}} \right)}\\&{{D_{xz}}\left( {{q}} \right) = {k_{[1, 1, 1]}}{D_{zx}}\left( {{q}} \right)}\end{aligned}} \right.$		[–1, –1, 1]轴向	$\left\{ {\begin{aligned}&{{D_{xy}}\left( {{q}} \right) = {k_{[ - 1, - 1, 1]}}{D_{yx}}\left( {{q}} \right)}\\&{{D_{yz}}\left( {{q}} \right) = - {k_{[ - 1, - 1, 1]}}{D_{zy}}\left( {{q}} \right)}\\&{{D_{xz}}\left( {{q}} \right) = - {k_{[ - 1, - 1, 1]}}{D_{zx}}\left( {{q}} \right)}\end{aligned}} \right.$
[1, –1, –1]轴向	$\left\{ {\begin{aligned}&{{D_{xy}}\left( {{q}} \right) = - {k_{[1, - 1, - 1]}}{D_{yx}}\left( {{q}} \right)}\\&{{D_{yz}}\left( {{q}} \right) = {k_{[1, - 1, - 1]}}{D_{zy}}\left( {{q}} \right)}\\&{{D_{xz}}\left( {{q}} \right) = - {k_{[1, - 1, - 1]}}{D_{zx}}\left( {{q}} \right)}\end{aligned}} \right.$

表1不同轴向NV色心的晶格动力学矩阵元的不对称关系
Table1.Asymmetrical relations of lattice dynamics matrix elements for NV centers of different axes.

由于四种轴向NV色心的金刚石晶体具有相似性, 在进行声子谱解析时仅晶格动力学矩阵元不对称关系不同, 所以本节仅以[1, 1, 1]轴向NV色心的金刚石晶体进行详细解析. 在[1, 1, 1]轴向NV色心金刚石晶体中, 令:

$ \left\{\begin{aligned}&{b}=-{D}_{{xx}}\left({{q}}\right)-{D}_{{yy}}\left({{q}}\right){-{D}}_{{zz}}\left({{q}}\right), \\&{c} ={D}_{{xx}}\left({{q}}\right){D}_{{yy}}\left({{q}}\right)+{D}_{{xx}}\left({{q}}\right){D}_{{zz}}\left({{q}}\right)\\ & \qquad +{D}_{{yy}}\left({{q}}\right){D}_{{zz}}\left({{q}}\right) -{{k}_{{[1,1,1]}}{D}_{{xy}}\left({{q}}\right)}^{2} \\ & \qquad -{{k}_{{[1,1,1]}}{D}_{{yz}}\left({{q}}\right)}^{2} {{-{k}}_{{[1,1,1]}}{D}_{{xz}}\left({{q}}\right)}^{2}, \\ &{d} ={{k}_{{[1,1,1]}}{D}_{{xy}}\left({{q}}\right)}^{2}{D}_{{zz}}\left({{q}}\right) \\ & \qquad +{{k}_{{[1,1,1]}}{D}_{{yz}}\left({{q}}\right)}^{2}{D}_{{xx}}\left({{q}}\right) \\ & \qquad +{{k}_{{[1,1,1]}}{D}_{{xz}}\left({{q}}\right)}^{2}{D}_{{yy}}\left({{q}}\right) \\&\qquad -{{2}{D}}_{{xy}}\left({{q}}\right){D}_{{yz}}\left({{q}}\right){D}_{{xz}}\left({{q}}\right) \\ & \qquad {-{D}}_{{xx}}\left({{q}}\right){D}_{{yy}}\left({{q}}\right){D}_{{zz}}\left({{q}}\right). \end{aligned}\right. $

金刚石NV色心的第一布里渊区一般点(非简并点)上的声子能量为

${\omega _\sigma }\left( {{q}} \right) = \sqrt {n\cos \left[ {u + 2{\rm{\pi }}(\sigma - 1)/3} \right] - b/3},$

其中, $u = \arccos \left[ {\left( { - \tau /2} \right){{\left( { - p/3} \right)}^{ - 3/2}}} \right]/3$; ${\tau }={d}- $$ {bc}/3 +2{{b}}^{{3}}{/27}$; $ {p}={c-}{{b}}^{2}{/3} $; $ n=\sqrt{-{4}{p}{/3}} $; $ {\sigma } $表示不同本征态, ${\sigma }= 1, 2, 3$. 对应的极化向量${{{e}}_{q\sigma }} = $$ \left( {{e_{qx\sigma }}, \;{e_{qy\sigma }}, \;{e_{qz\sigma }}} \right)$的波矢空间的笛卡尔表示为

$\left\{ {\begin{aligned}&{{e_{qx\sigma }} = {X_{1\sigma }}\Big/\sqrt {X_{1\sigma }^2 + X_{2\sigma }^2 + 1,} }\\&{{e_{qy\sigma }} = {X_{2\sigma }}\Big/\sqrt {X_{1\sigma }^2 + X_{2\sigma }^2 + 1},}\\&{{e_{qz\sigma }} = 1\Big/\sqrt {X_{1\sigma }^2 + X_{2\sigma }^2 + 1},}\end{aligned}} \right.$

式中, $ {{X}}_{{1}{\sigma }} $和$ {{X}}_{{2}{\sigma }} $分别为原子实系统的一阶本征态振动量和二阶本征态振动量, 表达式如下:

$\left\{ {\begin{aligned}&{X_{1\sigma }} = \frac{{{D_{xy}}}}{{{D_{xx}} - {\lambda _\sigma }}} \cdot \frac{{{D_{yz}}\left( {{D_{xx}} - {\lambda _\sigma }} \right) - {D_{xy}}{D_{xz}}}}{{\left( {{D_{yy}} - {\lambda _\sigma }} \right)\left( {{D_{xx}} - {\lambda _\sigma }} \right) - D_{xy}^2}}\\&\qquad\;\;\;\;- \frac{{{D_{xz}}}}{{{D_{xx}} - {\lambda _\sigma }}},\\&{{X_{2\sigma }} = - \frac{{{D_{yz}}\left( {{D_{xx}} - {\lambda _\sigma }} \right) - {D_{xy}}{D_{xz}}}}{{\left( {{D_{yy}} - {\lambda _\sigma }} \right)\left( {{D_{xx}} - {\lambda _\sigma }} \right) - D_{xy}^2}},}\\[-10pt]\end{aligned}} \right.$

其中, $ {\lambda}_{\sigma } $为第$ {\sigma } $本征态($ {\sigma }{= 1, 2, 3} $)的本征值.
由(19)—(23)式可以解析出[1, 1, 1]轴向NV色心金刚石晶体特征线及特征面的声子谱, 其中, $ {\varLambda } $特征线及$ {{q}}_{{z}}= 0 $特征面的解析结果如下.
1)第一布里渊区$ {\varLambda } $特征线上(${{q}}_{{x}}={{q}}_{y}= {{q}}_{{z}}={q}$)的声子谱:

$\left. {\begin{aligned}&{{\omega _1} = \sqrt {n\cos u - b/3},}~~~~{{\omega _2} = \sqrt {n\cos \left[ {u + 2\pi /3} \right] - b/3} },~~ {{\omega _3} = \sqrt {n\cos \left[ {u + 4\pi /3} \right] - b/3.} }\end{aligned}} \right. $

当$ {{q}}_{{x}}={{q}}_{y}={{q}}_{{z}}={q} $时, 令

$\left\{ {\begin{aligned}&A_{[1,1,1]}^\varLambda = \left( {2{f_1}/3{k_{[1,1,1]}}M_l^\alpha } \right)[ 2 - 2\cos \left( {qa/2} \right) + \eta - \eta \cos \left( {qa} \right) ],\\&B_{[1,1,1]}^\varLambda = \left( {2{f_1}/3{k_{[1,1,1]}}M_l^\alpha } \right)[ \sin \left( {qa/2} \right) + 2\cos \left( {qa/2} \right)\sin \left( {qa/2} \right)\sin \left( {qa} \right) ],\end{aligned}} \right.$

(24)式化简为

$\left. {\begin{aligned}&{{\omega _1} = \sqrt {A_{[1,1,1]}^\varLambda + 2B_{[1,1,1]}^\varLambda },}~~~~{{\omega _2} = {\omega _3} = \sqrt {A_{[1,1,1]}^\varLambda - B_{[1,1,1]}^\varLambda } .}\end{aligned}} \right.$

根据(22)式, $ {\omega }_{1} $, $ {\omega }_{2} $, $ {\omega }_{3} $分别对应的极化向量为

$\left\{ \begin{aligned}&{{{e}}_{q1}} = \left( {\frac{{{X_{11}}}}{{\sqrt {X_{11}^2 + X_{21}^2 + 1} }},\frac{{{X_{21}}}}{{\sqrt {X_{11}^2 + X_{21}^2 + 1} }},\frac{1}{{\sqrt {X_{11}^2 + X_{21}^2 + 1} }}} \right) = \left( {\frac{1}{{\sqrt 3 }},\frac{1}{{\sqrt 3 }},\frac{1}{{\sqrt 3 }}} \right),\\&{{{e}}_{q2}} = \left( {\frac{{{X_{12}}}}{{\sqrt {X_{12}^2 + X_{22}^2 + 1} }},\frac{{{X_{22}}}}{{\sqrt {X_{12}^2 + X_{22}^2 + 1} }},\frac{1}{{\sqrt {X_{12}^2 + X_{22}^2 + 1} }}} \right) = \left( { - \frac{1}{{\sqrt 2 }},\frac{1}{{\sqrt 2 }},0} \right),\\&{{{e}}_{q3}} = \left( {\frac{{{X_{13}}}}{{\sqrt {X_{13}^2 + X_{23}^2 + 1} }},\frac{{{X_{23}}}}{{\sqrt {X_{13}^2 + X_{23}^2 + 1} }},\frac{1}{{\sqrt {X_{13}^2 + X_{23}^2 + 1} }}} \right) = \left( { - \frac{1}{{\sqrt 6 }}, - \frac{1}{{\sqrt 6 }},\frac{{\sqrt 6 }}{3}} \right).\end{aligned} \right.$

因此, $ {\omega }_{1} $是纵向声子, $ {\omega }_{2} $与$ {\omega }_{3} $是横向声子, 而且横向声子在第一布里渊区$ {\varLambda } $特征线上有二重简并.
2)第一布里渊区$ {{q}}_{{z}}= 0 $平面的声子谱.
第一布里渊区$ {{q}}_{{z}}= 0 $特征面的声子谱同(21)式, 但其条件满足$ {{q}}_{{z}}= 0 $, 令:

$\left\{ \begin{aligned}&A_{[1,1,1]}^{{q_z} = 0} = \left( {{f_1}/{k_{[1,1,1]}}M_l^\alpha } \right)\left\{ {2 + 4\eta - \left( {1 + \eta } \right)\left[ {\cos \left( {{q_x}a} \right) + \cos \left( {{q_y}a} \right)} \right]} \right\},\\&B_{[1,1,1]}^{{q_z} = 0} = \left( {{f_1}/{k_{[1,1,1]}}M_l^\alpha } \right)\left[ {2\eta \cos \left( {{q_x}a} \right)\cos \left( {{q_y}a} \right)} \right],\\&C_{[1,1,1]}^{{q_z} = 0} = \left( {{f_1}/{k_{[1,1,1]}}M_l^\alpha } \right){\left\{ {{{\left( {1 + \eta } \right)}^2}{{\left[ {\cos \left( {{q_x}a} \right) - \cos \left( {{q_y}a} \right)} \right]}^2} + 4{\eta ^2}{{\sin }^2}\left( {{q_x}a} \right){{\sin }^2}\left( {{q_y}a} \right)} \right\}^{1/2}},\\&D_{[1,1,1]}^{{q_z} = 0} = \left( {2\eta {f_1}/{k_{[1,1,1]}}M_l^\alpha } \right)\left[ {2 - \cos \left( {{q_x}a} \right) + \cos \left( {{q_y}a} \right)} \right].\end{aligned} \right.$

可得

$\left\{ {\begin{aligned} {\omega _1} = \;&{\omega _3} \\=\;& \sqrt {A_{[1,1,1]}^{{q_z} = 0} - B_{\left[ {1,1,1} \right]}^{{q_z} = 0} + C_{[1,1,1]}^{{q_z} = 0}},\\{\omega _2} =\; &\sqrt {D_{[1,1,1]}^{{q_z} = 0}} .\end{aligned}} \right.$

根据(22)式, $ {\omega }_{1} $, $ {\omega }_{2} $, $ {\omega }_{3} $分别对应的极化向量为

$\left\{ {\begin{aligned}&{{{{e}}_{q1}} = \left( {\frac{e}{{\sqrt {{e^2} + 1} }},\frac{1}{{\sqrt {{e^2} + 1} }},0} \right),}\\&{{{{e}}_{q2}} = \left( {0,0,1} \right),}\\&{{{{e}}_{q3}} = \left( {\frac{e}{{\sqrt {{e^2} + 1} }},\frac{1}{{\sqrt {{e^2} + 1} }},0} \right),}\end{aligned}} \right.$

其中,

$\begin{split} e =\;& \dfrac{1}{{2\eta \sin ( {{q_x}a} )\sin ( {{q_y}a} )}}\\ &\times \big\{ t( {1 + \eta } )[\cos( {{q_y}a} )- \cos ( {{q_x}a})] + \sqrt f \big\},\\ f =\;& {( {1 + \eta })^2}{[ {\cos ( {{q_x}a} ) - \cos( {{q_y}a} )} ]^2} \\ &+ 4{\eta ^2}{\sin ^2}( {{q_y}a} ){\sin ^2}( {{q_y}a} ). \end{split}$

因此, $ {\omega }_{2} $是纵向声子, $ {\omega }_{1} $与$ {\omega }_{3} $是横向声子, 而且横向声子在第一布里渊区$ {{q}}_{{z}}= 0 $平面上有二重简并.
[1, 1, 1]轴向NV色心金刚石第一布里渊区内的其余特征线或特征面的声子谱解析过程与$ {\varLambda } $特征线和$ {{q}}_{{z}}= 0 $特征面类似, 均基于(19)—(23)式仅变换波矢q的声子谱条件, 详细解析过程不再赘述. 相关特征线的声子谱分析结果如表2所列.

特征线	声子谱波矢条件	声子谱函数	极化向量
Λ 线	$ {{q}}_{{x}}={{q}}_{y}={{q}}_{{z}}={q} $	$\left\{\begin{aligned}&{\omega }_{1}=\sqrt {{ {A} }_ {[1, 1, 1]} ^ {\varLambda } + {2}{B} _ {[1, 1, 1]} ^ {\varLambda }} \\ &{\omega }_{2}=\sqrt {{ {A} }_ {[1, 1, 1]} ^ {\varLambda } {-}{ {B} }_ {[1, 1, 1]} ^ {\varLambda } } \\ &{\omega }_{3}=\sqrt{ { {A} }_ {[1, 1, 1]} ^ {\varLambda } {-}{ {B} }_ {[1, 1, 1]} ^ {\varLambda } }\end{aligned}\right.$	$ \left\{\begin{aligned}&{{e}}_{{q}{1}}=\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)\\ &{{e}}_{{q}{2}}=\left({-}\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}{, 0}\right)\\ &{{e}}_{{q}{3}}=\left({-}\frac{1}{\sqrt{{6}}}{, -}\frac{1}{\sqrt{{6}}}, \frac{\sqrt{{6}}}{3}\right)\end{aligned}\right. $
$ \varDelta $线 (ΓF 线) (ZQ 线)	$ {{q}}_{{x}}={{q}}_{{z}}{=0} $	$\left\{\begin{aligned}&{\omega }_{1}=\sqrt{ { {A} }_{[1, 1, 1]}^{\varDelta }+{ {B} }_{[1, 1, 1]}^{\varDelta} }\\ &{\omega }_{2}=\sqrt{ { {B} }_{[1, 1, 1]}^{\varDelta } }\\ &{\omega }_{3}=\sqrt{ { {B} }_{[1, 1, 1]}^{\varDelta} }\end{aligned}\right.$	$ \left\{\begin{aligned}&{{e}}_{{q}{1}}=\left({0, 1, 0}\right)\\ &{{e}}_{{q}{2}}=\left({1, 0, 0}\right)\\ &{{e}}_{{q}{3}}=\left({0, 0, 1}\right)\end{aligned}\right. $
Σ 线	${ {q} }_{ {x} }={ {q} }_{y}={q},$ $ {{q}}_{{z}}= 0 $	$\left\{\begin{aligned}&{\omega }_{1}=\sqrt{ { {A} }_{ [1, 1, 1] }^{\varSigma }+{ {B} }_ {[1, 1, 1]} ^ {\varSigma } }\\ &{\omega }_{2}=\sqrt{ { {A} }_{[1, 1, 1]} ^ {\varSigma } {-}{ {B} }_{[1, 1, 1]} ^ {\varSigma } } \\ &{\omega }_{3}=\sqrt{ { {C} }_ {[1, 1, 1]} ^{\varSigma } } \end{aligned}\right.$	$ \left\{\begin{aligned}&{{e}}_{{q}{1}}=\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}{, 0}\right)\\ &{{e}}_{{q}{2}}=\left({-}\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}{, 0}\right)\\ &{{e}}_{{q}{3}}=\left({0, 0, 1}\right)\end{aligned}\right. $
M 线 (ΓZ 线) (FQ 线)	$ {{q}}_{{x}}={{q}}_{y}={0} $	$\left\{\begin{aligned}&{\omega }_{1}=\sqrt{ { {A} }_ {[1, 1, 1]} ^{ {M} }+{ {B} }_ {[1, 1, 1]} ^{ {M} } }\\ &{\omega }_{2}=\sqrt{ { {B} }_ {[1, 1, 1]} ^{ {M} } }\\ &{\omega }_{3}=\sqrt{ { {B} }_ {[1, 1, 1]} ^{ {M} } }\end{aligned}\right.$	$ \left\{\begin{aligned}&{{e}}_{{q}{1}}=\left({0, 0, 1}\right)\\ &{{e}}_{{q}{2}}=\left({1, 0, 0}\right)\\ &{{e}}_{{q}{3}}=\left({0, 1, 0}\right)\end{aligned}\right. $
注: $A_{[1, 1, 1]}^\varDelta = \left( {2{f_1}/3{k_{[1, 1, 1]}}M_l^\alpha } \right)\left[ {2 - 2\cos \left( {{q_y}a/2} \right)} \right]$, $B_{[1, 1, 1]}^\varDelta = \left( {2{f_1}/3{k_{[1, 1, 1]} }M_l^\alpha } \right)\left[ {\eta - \eta \cos \left( { {q_y}a} \right)} \right]$, $A_{[1, 1, 1]}^\varSigma = \left( { {f_1}/3{k_{[1, 1, 1]} }M_l^\alpha } \right)\{ 3 - 2\cos \left( {qa/2} \right) - \cos \left( {qa} \right) + \left[ {2\eta - 2\eta \cos \left( {qa} \right)} \right]\}$, $B_{[1, 1, 1]}^\varSigma = \left( { {f_1}/3{k_{[1, 1, 1]} }M_l^\alpha } \right)\left[ {1 - \cos \left( {qa} \right)} \right]$, $C_{[1, 1, 1]}^\varSigma = \left( {2{f_1}/3{k_{[1, 1, 1]} }M_l^\alpha } \right)\left[ {2 - 2\cos \left( {qa/2} \right)} \right]$, $A_{[1, 1, 1]}^M = \left( {2{f_1}/3{k_{[1, 1, 1]}}M_l^\alpha } \right)\left[ {2 - 2\cos \left( {{q_z}a/2} \right)} \right]$, $B_{[1, 1, 1]}^M = \left( {2{f_1}/3{k_{[1, 1, 1]}}M_l^\alpha } \right)\left[ {\eta - \eta \cos \left( {{q_z}a} \right)} \right]$.

表2[1, 1, 1]轴向NV色心金刚石布里渊区特征线的声子谱解析结果
Table2.Phonon spectrum analysis results at the characteristic line of the Brillouin zone in the diamond with the NV center of [1, 1, 1] axis.

2 -->

3.3.NV色心的声子热力学解析

3 -->

3.3.1.声子热平衡解析

在NV色心自旋跃迁过程是在振动态声子热平衡条件下进行的, 且达到热平衡的过程比自旋跃迁的速率快得多, 所以需要对NV色心声子共振系统的热力学性质进行解析.
在热平衡条件下, 一个频率为$ {\omega }_{\sigma } $的振动模$ {\omega }_{\sigma }\left({{q}}\right) $, 处于本征态$ {\sigma } $, 模中有n个声子的概率$ {P}_{{n}} $, 正比于玻尔兹曼(Boltzmann)因子: $\exp \left[ { - n\hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)} \right]$, $ {k}_{\rm{B}} $是Boltzmann常数, T为声子热平衡温度.
因总概率$\sum\nolimits_n {{P_n}} = 1$, $ {P}_{{n}} $可以表示为

$\begin{split}\;& {P_n} = \frac{{\exp \left[ { - n\hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)} \right]}}{{\displaystyle\sum\nolimits_{n = 0}^\infty \exp \left[ { - n\hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)} \right]}}\\=\;& \big[ {1 - {{\rm{e}}^{ - \hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)}}} \big]{{\rm{e}}^{ - n\hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)}}.\end{split}$

令$\gamma = {{\rm{e}}^{ - n\hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)}}$, (31)式变换为

${P_n} = \left( {1 - \gamma } \right){\gamma ^n}.$

频率为$ {\omega }_{\sigma }\left({{q}}\right) $的振动模中的热平均声子数$ \left\langle {{n}} \right\rangle $可以表示为

$\begin{split}\left\langle n \right\rangle =\;&\mathop \sum\limits_{n = 0}^\infty n{P_n} = \frac{{\mathop \sum \limits_{n = 0}^\infty n\exp \left[ { - n\hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)} \right]}}{{\mathop \sum \limits_{n = 0}^\infty \exp \left[ { - n\hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)} \right]}} \\=\;& \frac{{{{\rm{e}}^{ - \hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)}}}}{{1 - {{\rm{e}}^{ - \hbar {\omega _\sigma }\left( {{q}} \right)/({k_{\rm{B}}}T)}}}} = \frac{\gamma }{{1 - \gamma }}.\\[-15pt]\end{split}$

化简(33)式得到

$ \gamma =\frac{\left\langle {{n}} \right\rangle}{{1+}\left\langle {{n}} \right\rangle} .$

代入$ \gamma $, 可得到声子热平衡温度函数, 即:

$T = \frac{{ - \hbar {\omega _\sigma }\left( {{q}} \right)}}{{{k_{\rm{B}}}\ln \left( {\frac{{\left\langle n \right\rangle }}{{1 + \left\langle n \right\rangle }}} \right)}}.$

为了定量计算不同轴向结构参数金刚石NV色心的声子热力学性质, 结合(21)式和(35)式NV色心金刚石晶体的不同轴向结构参数声子热平衡温度为

$T = \frac{{ - \hbar \sqrt {n\cos \left[ {u + 2{\rm{\pi }}(\sigma - 1)/3} \right] - b/3} }}{{{k_{\rm{B}}}\ln \left( {\dfrac{n}{{1 + n}}} \right)}}.$

其中, $ \left\langle {{n}} \right\rangle $表示平均声子数. (36)式中, 参数u, b, n均与NV色心金刚石晶体轴向结构有关. 特别地, 取$ {\sigma }{= 1} $时的声子热平衡温度, 所以(36)式可转化为

$T = \frac{{ - \hbar \sqrt {n\cos u - b/3} }}{{{k_{\rm{B}}}\ln \left( {\dfrac{{\left\langle n \right\rangle }}{{1 + \left\langle n \right\rangle }}} \right)}}.$

对于[1, 1, 1]轴向NV色心金刚石, 声子热平衡温度解析结果如表3所列, 其中, $ {T}_{{\varLambda }} $, $ {T}_{\varDelta } $, $ {T}_{{\varSigma }} $和$ {T}_{\rm{M}} $分别为声子极化方向为$ {\varLambda } $线、$ \varDelta $线、$ {\varSigma } $线和M线方向的声子热平衡温度.

声子极化方向	声子热平衡温度		声子极化方向	声子热平衡温度
$ {\varLambda } $线方向	${T}_{ {\varLambda } }=\dfrac{ {-}{\hbar }\sqrt{ { {A} }_{ {[1, 1, 1]} }^{ {\varLambda } }+{ {2}{B} }_{ {[1, 1, 1]} }^{ {\varLambda } } } }{ {k}_{\rm{B} }{\ln}\left(\frac{\left\langle { {n} } \right\rangle}{ {1+}\left\langle { {n} } \right\rangle}\right)}$		$ {\varSigma } $线方向	${T}_{ {\varSigma } }=\dfrac{ {-}{\hbar }\sqrt{ { {A} }_{ {[1, 1, 1]} }^{ {\varSigma } }+{ {B} }_{ {[1, 1, 1]} }^{ {\varSigma } } } }{ {k}_{\rm{B} }{\ln}\left(\frac{\left\langle { {n} } \right\rangle}{ {1+}\left\langle { {n} } \right\rangle}\right)}$
$ \varDelta $线方向	${T}_{\varDelta }=\dfrac{ {-}{\hbar }\sqrt{ { {A} }_{ {[1, 1, 1]} }^{\varDelta }+{ {B} }_{ {[1, 1, 1]} }^{\varDelta } } }{ {k}_{\rm{B} }{\ln}\left(\frac{\left\langle { {n} } \right\rangle}{ {1+}\left\langle { {n} } \right\rangle}\right)}$		M 线方向	${T}_{ {M} }=\dfrac{ {-}{\hbar }\sqrt{ { {A} }_{ {[1, 1, 1]} }^{ {M} }+{ {B} }_{ {[1, 1, 1]} }^{ {M} } } }{ {k}_{\rm{B} }{\ln}\left(\frac{\left\langle { {n} } \right\rangle}{ {1+}\left\langle { {n} } \right\rangle}\right)}$
注: 参数$ {{A}}_{{[1, 1, 1]}}^{{\varLambda }}, {{B}}_{{[1, 1, 1]}}^{{\varLambda }}, {{A}}_{{[1, 1, 1]}}^{\varDelta }, {{B}}_{{[1, 1, 1]}}^{\varDelta } $, $ {{A}}_{{[1, 1, 1]}}^{{\varSigma }}, {{B}}_{{[1, 1, 1]}}^{{\varSigma }}, {{A}}_{{[1, 1, 1]}}^{{M}} $和$ {{B}}_{{[1, 1, 1]}}^{{M}} $同表2.

表3[1, 1, 1]轴向NV色心金刚石的声子热平衡温度解析结果
Table3.Phonon thermal equilibrium temperature analysis results of the diamond with the NV center of [1, 1, 1] axis.

3 -->

3.3.2.比热解析

比热是反应晶体的重要物理量之一, 本节基于$ {\rm{Debye}} $模型对声子模式下NV色心金刚石晶格三维模型进行比热解析, 探究声子作用对NV色心金刚石晶格的比热影响机理.
在金刚石NV色心三维波矢空间内, 格波的等频面为球面, 在${{q}} \to {{q}} + {\rm{d}}{{q}}$方向上波速为$ {{v}}_{{{q}}} $的格波数目$ {\rm{d}}{{z}}_{{{q}}} $为

${\rm{d}}{{z}}_{{{q}}}=\frac{\rm{V}}{{\left({2{\rm{\pi }}}\right)}^{3}}{4{\rm{\pi }}}{\left({{q}}\right)}^{2}{\rm{d}}\left({{q}}\right)=\frac{{\omega }_{\sigma }\left({{q}}\right)}{{{2{\rm{\pi }}}}^{2}{\left({{v}}_{{{q}}}\right)}^{3}}{\rm{d}}{\omega }_{\sigma }, $

其中, V是含NV色心金刚石的晶格体积, 且${3}/{{\left({{v}}_{{{q}}}\right)}^{3}}= {1}/{{\left({{v}}_{\rm{H}}\right)}^{3}}+ {2}/{{\left({{v}}_{\rm{T}}\right)}^{3}}$; $ {{v}}_{\rm{H}} $是横向声子波速; $ {{v}}_{\rm{T}} $是纵向声子波速.
由(38)式可得到声子模式下的NV色心金刚石的晶格振动密度$ \rho \left[{\omega }_{\sigma }\left({{q}}\right)\right] $:

$\begin{split} \rho \left[{\omega }_{\sigma }\left({{q}}\right)\right]= \frac{{3}{V}{{\omega }_{\sigma }}^{2}\left({{q}}\right)}{{2}{{{\rm{\pi }}}}^{2}{\left({{v}}_{{{q}}}\right)}^{3}} = \frac{{V}{{\omega }_{\sigma }}^{2}\left({{q}}\right)\big[{\left({v}_{\mathrm{T}}\right)}^{3}+{2\left({v}_{\rm{H}}\right)}^{3}\big]}{{2}{{{\rm{\pi }}}}^{2}{\left({{v}}_{\rm{H}}\right)}^{3}{\left({{v}}_{\rm{T}}\right)}^{3}} . \end{split}$

根据(39)式可得到声子模式下的NV色心金刚石的晶格自由能:

$\begin{split}{E}_{\rm{V}}=\;&\frac{{V}{{\omega }_{\sigma }}^{2}\left({{q}}\right)\big[{\left({v}_{\mathrm{T}}\right)}^{3}+{2\left({v}_{\rm{H}}\right)}^{3}\big]}{{2}{{{\rm{\pi }}}}^{2}{\left({v}_{\rm{H}}\right)}^{3}{\left({v}_{\rm{T}}\right)}^{3}}\\&\times{\int }_{0}^{{\omega }_{{m}}}\frac{{{\hbar }\left({\omega }_{\sigma }\right)}^{3}\left({{q}}\right)}{{\left[{\rm e}^{\hbar {\omega }_{\sigma }\left({{q}}\right)/\left({k}_{\mathrm{B}}T\right)}-1\right]}^{2}}{\rm{d}}{\omega }_{\sigma }, \end{split}$

其中, ${\omega }_{m}=\dfrac{{3}{\left({v}_{\rm{T}}\right)}^{3}+{{6}\left({v}_{\rm{H}}\right)}^{3}}{{\left({v}_{\rm{H}}\right)}^{3}{\left({v}_{\rm{T}}\right)}^{3}}\sqrt[{3}]{{6}{{{\text{π}}}}^{2}{N}/{V}}$, N为NV色心金刚石的晶格原子数目.
根据(40)式可以得到声子模式下的NV色心金刚石的晶格热容量:

$\begin{split}{C}_{\rm{V}}=\;&\frac{{V}{{\omega }_{\sigma }}^{2}\left({{q}}\right)\left[{\left({v}_{\mathrm{T}}\right)}^{3}+{2\left({v}_{\rm{H}}\right)}^{3}\right]}{{2}{{{\rm{\pi }}}}^{2}{\left({v}_{\rm{H}}\right)}^{3}{\left({v}_{\rm{T}}\right)}^{3}}{\int }_{0}^{{\omega }_{m}}{\left(\frac{{\hbar }{\omega }_{\sigma }\left({{q}}\right)}{{k}_{\rm{B}}{T}}\right)}^{2}\\&\times\frac{{{\hbar }\left({\omega }_{\sigma }\right)}^{3}\left({{q}}\right)}{{\left[{\rm e}^{\hbar {\omega }_{\sigma }\left({{q}}\right)/\left({k}_{\mathrm{B}}T\right)}-1\right]}^{2}}{\rm{d}}{\omega }_{\sigma }{.}\\[-15pt]\end{split}$

为了定量计算不同轴向结构参数金刚石NV色心的声子热力学性质, 根据(21)式, 令${\omega _\sigma }\left( {{q}} \right) = $$ \sqrt {n\cos \left[ {u + 2{\text{π}}(\sigma - 1)/3} \right] - b/3}$, 参数u, b, n均与NV色心金刚石晶体轴向结构有关, 将(21)式代入(40)式和(41)式可分别解析出NV色心金刚石晶体的不同轴向结构晶格自由能和晶格热容量.

2

-->

4.1.计算方法

本文基于应变诱导能量转移的电子-声子相互作用哈密顿量模型和密度泛函理论^[50], 采用分子动力学仿真软件CASTEP构建不同轴向的NV色心金刚石晶体的结构模型, 在声子共振调控条件下的氮-空位色心的结构优化模型, 分析该优化模型不同NV色心占位时的结构特性、声子特性和热力学特性.
本文的第一性原理计算是基于密度泛函理论, 采用分子动力学软件CASTEP通过平面波赝势方法实现. 为了准确描述氮-空位原子域电子间的关联作用, 计算基于广义密度近似的Ceperley Alder-Perdew Zunger模型, 晶胞中价电子与离子核的相互作用通过超软赝势Ultrasoft描述. 第一布里渊区内采用8 × 8 × 8的Monkhorst-Pack网格. 自洽计算的收敛精度为总能量的变化低于${10^{ - 8}}$ eV. 晶胞内各原子的受力不超过0.01 eV/?.
声子谱的计算是基于密度泛函微扰理论的局域密度近似下的Perdew-Burke-Ernzerh模型实现. 计算过程中, 布里渊区内格波的波矢q采用6 × 6 × 6的无偏移网格. 考虑材料泊松系数随体积的变化, 声子热力学性质的计算采用晶格振动谐振近似下的Debye模型. 在采用有限粒子数来模拟实际体系中粒子的运动时, 通过施加三维周期性边界条件使处于模拟体系中的粒子的运动空间成为赝无限来减少界面对体系中粒子振动的影响. 在模拟体系设定的温度、压力和粒子的初始速度下, 基于等温等压系综, 根据埃瓦尔德(Ewald)求和技术^[51]进行解析, 每个平衡态计算10000步, 步长为1 fs.
2 -->

4.2.计算结果

3 -->

4.2.1.结构特性

基于分子动力学软件CASTEP对不同轴向NV色心的晶格结构进行优化, 使晶格能最低. 不同轴向NV色心金刚石的晶格能优化特征如图6所示. 从图6可以看出, 经过结构优化迭代后, 晶格能降到平衡状态. 结构优化后纯净无缺陷的金刚石晶格总能量为–309.802 eV, [1, 1, 1]轴向的NV色心金刚石晶格能为–1198.548 eV, 其余三种轴向的NV色心金刚石晶格能相差不大, 约为–1197.3 eV. 所以, 含NV色心缺陷的金刚石晶格能小于纯净无缺陷的金刚石.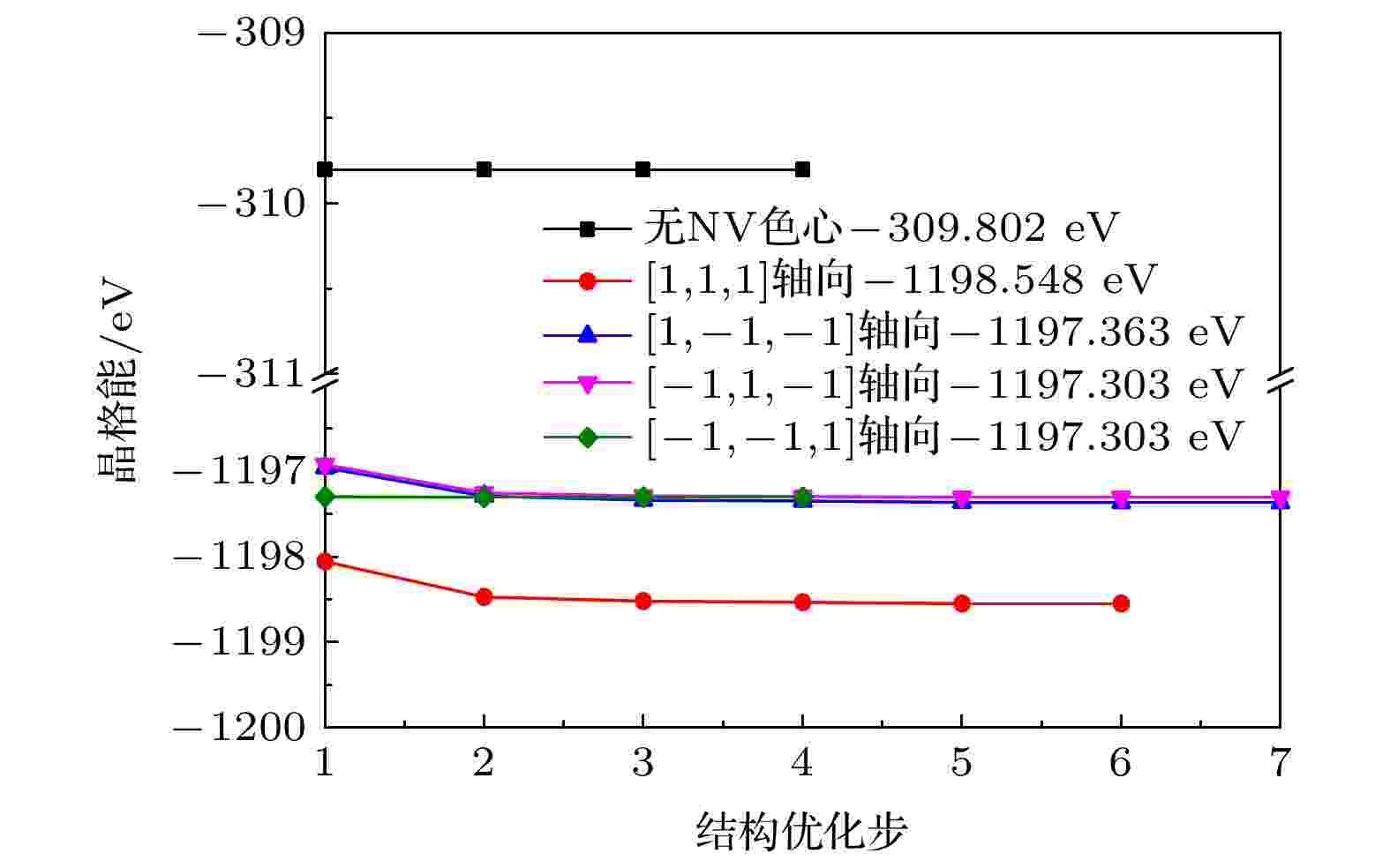
图 6 不同轴向NV色心金刚石的晶格能优化特征
Figure6. Lattice energy optimization characteristics for the diamond with NV centers of different axes.

晶格能优化后的不同轴向NV色心金刚石的带隙特征如图7所示. 从图7可以看出, 无NV色心金刚石的带隙特征是沿着第一布里渊区特征点W点、L点、$ \varGamma $点、X点、W点和K点连线展开的. 四种轴向NV色心金刚石的带隙特征是沿着第一布里渊区特征点$ \varGamma $点、F点、Q点、Z点和$ \varGamma $点连线展开的. 无NV色心金刚石的带隙为4.325 eV. [1, 1, 1]轴向、[1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向的NV色心金刚石的带隙分别为0.6257, 1.6012, 1.2295, 1.2864 eV. 因此, 相比于纯净无缺陷金刚石, 含有NV色心的金刚石减小了导带的最低点和价带的最高点的能量之差. 电子由价带被激发到导带更容易, 本征载流子浓度更高, 电导率更高. 对比四种不同轴向NV色心金刚石的带隙特征可知, [1, 1, 1]轴向NV色心金刚石的带隙最低, 具有最高的本征载流子浓度和电导率. 反之, [1, –1, –1]轴向NV色心金刚石的带隙最高, 其本征载流子浓度和电导率最低.
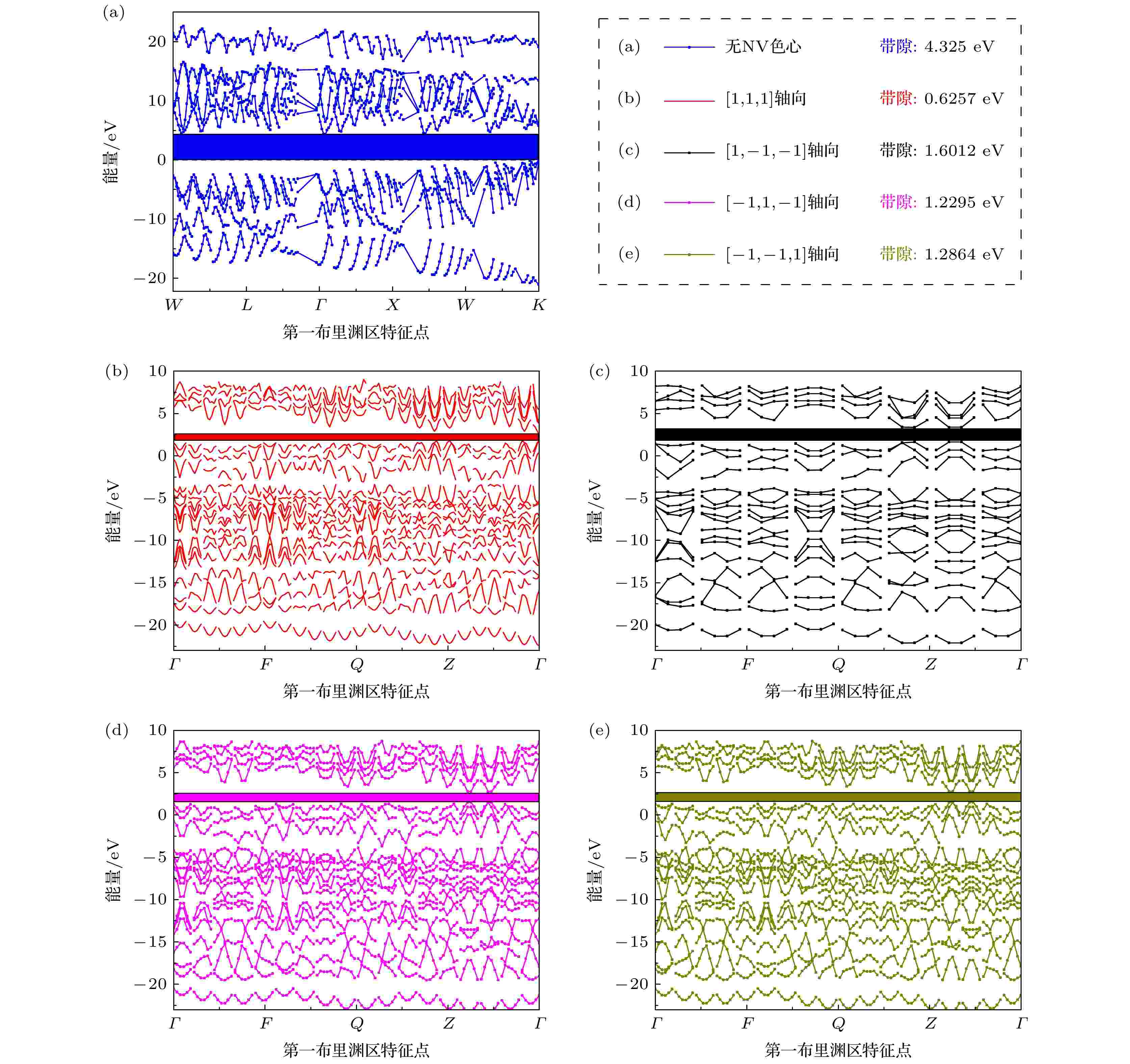图 7 不同轴向NV色心金刚石的带隙特征　(a)无NV色心; (b) [1, 1, 1]轴向; (c) [1, –1, –1]轴向; (d) [–1, 1, –1]轴向; (e) [–1, –1, 1]轴向
Figure7. Band gap characteristics for the diamond with NV centers of different axes: (a) Without NV center; (b) axis direction of [1, 1, 1]; (c) axis direction of [1, –1, –1]; (d) axis direction of [–1, 1, –1]; (e) axis direction of [–1, –1, 1].

不同轴向NV色心金刚石的态密度曲线如图8所示, 可以看出, 含NV色心的金刚石态密度(density of states, DOS)分布较纯净无缺陷金刚石的局域尖峰更加明显. [1, 1, 1]轴向、[1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向的NV色心金刚石的最大DOS分别为3.3149, 3.7512, 3.5727, 3.5695 electrons/eV, 对应的晶格能位分别为–5.78, –5.96, –5.83, –5.82 eV. 纯净无缺陷的金刚石的最大DOS仅为1.2516 electrons/eV, 对应的晶格能位为8.29 eV. 因此, 含有NV色心的金刚石相比于纯净无缺陷金刚石具有更强的电子局域化性质. 从图8还能看出不同轴向NV色心金刚石的能带特性. 由于赝能隙直接反映了该体系成键的共价性的强弱. 赝能隙越宽, 共价性越强. 含NV色心的金刚石的赝能隙较纯净无缺陷金刚石的赝能隙更窄. 因此, 其共价键较纯净无缺陷金刚石更弱. 从DOS曲线还可以看出不同轴向NV色心金刚石在一定的晶格能区间均具有零带隙, 与图7结果相吻合.
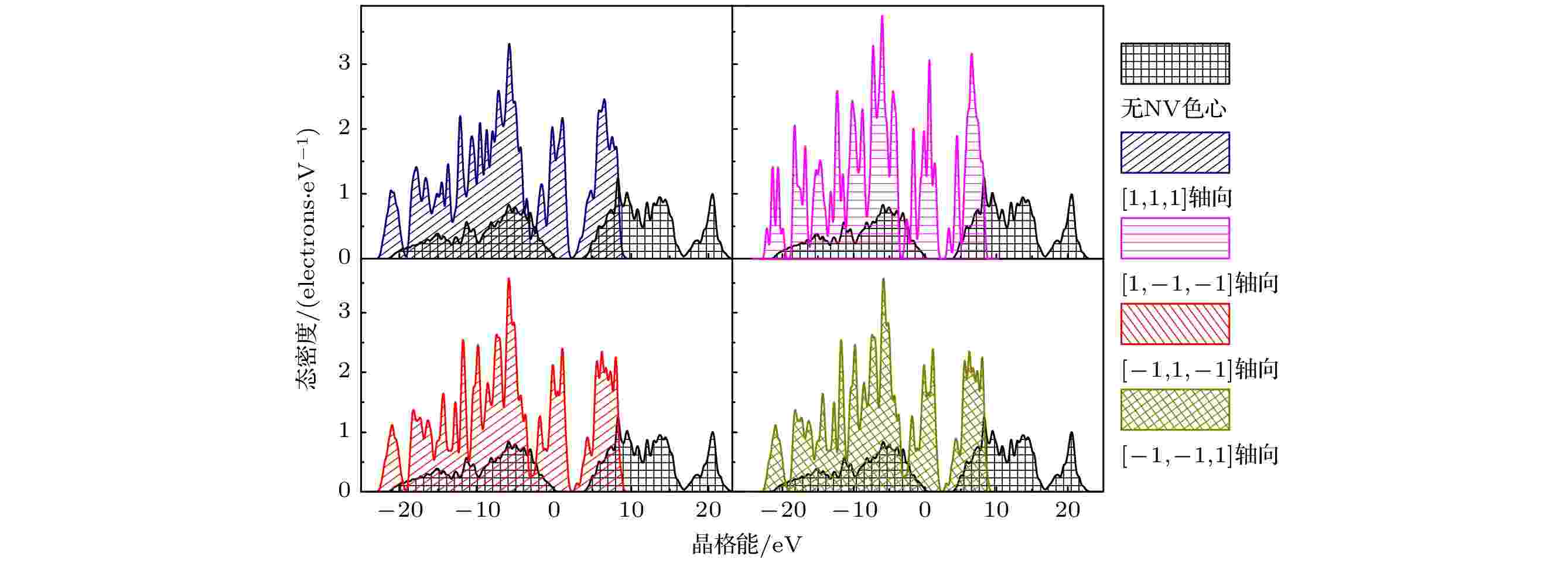图 8 不同轴向NV色心金刚石的态密度曲线
Figure8. State density curves of the diamond with NV centers of different axes.

3 -->

4.2.2.声子特性

图9为不同轴向NV色心金刚石沿着第一布里渊区特征线的声子谱. 从图9可以看出, 纯净无缺陷金刚石的原胞具有2个原子, 产生6个色散关系(3个声分支和3个光学分支). 含NV色心金刚石的第一布里渊区模型是通过对称扩展交界面的方式形成的, 其原胞具有7个原子, 产生21个色散关系(6个声分支和15个光学分支). 纯净无缺陷金刚石和四种不同轴向NV色心的金刚石的禁带宽度最窄的地方均出现在$ {\varGamma } $点处, 且价带的最高点与导带最低点在同一点, 故属于直接带隙. 四种不同轴向NV色心的金刚石声子谱略有差异, 这是不同轴向NV色心金刚石晶体的晶格动力学矩阵元不对称关系导致的.
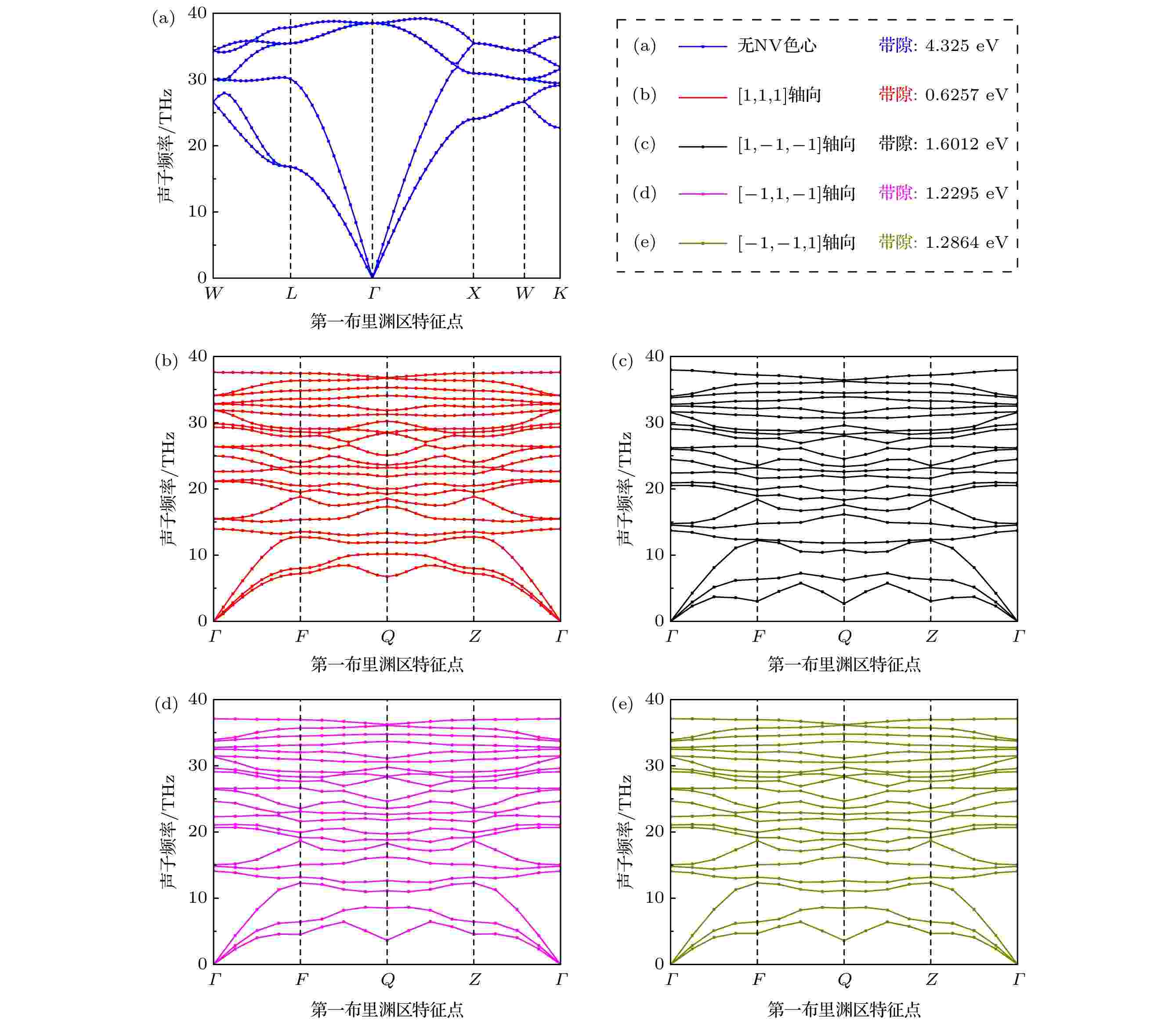图 9 不同轴向NV色心金刚石的声子谱　(a)无NV色心; (b) [1, 1, 1]轴向; (c) [1, –1, –1]轴向; (d) [–1, 1, –1]轴向; (e) [–1, –1, 1]轴向
Figure9. Phonon spectrum curves of the diamond with NV centers of different axes: (a) Without NV center; (b) axis direction of [1, 1, 1]; (c) axis direction of [1, –1, –1]; (d) axis direction of [–1, 1, –1]; (e) axis direction of [–1, –1, 1].

分析不同轴向NV色心金刚石声子态密度(图10)可发现, 纯净无缺陷金刚石晶体中声子振动模式主要出现在10—38 THz频段, 特别在35—37 THz频段最大声子态密度为0.13395 (unit cell)/THz, 在此频段下出现声子振动模式的概率较高. 四种不同轴向的声子态密度曲线略有差异, [1, 1, 1]轴向NV色心金刚石具有较多的大概率声子振动模式频段, 其最大声子态密度为0.10904 (unit cell)/THz. [1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向的NV色心金刚石的大概率声子振动模式频段基本一致. [1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向的NV色心金刚石的最大声子态密度分别为0.12681, 0.1308, 0.13211 (unit cell)/THz. 由图10可知, 四种不同轴向NV色心金刚石的声子主共振频段均处于THz量级, 声子耦合激励至主共振频率技术较难实现. NV色心金刚石的次共振频率约为[800, 1200] MHz. 根据该频段设计等效的声表面波共振机构, 其叉指的宽度w为1.5 μm. 由于声表面波在金刚石中传播速度v_s约为5600 m/s, 且声表面波中心频率ω_m = v_s/4w. 推算设计的声表面波叉指电极中心频率约为930 MHz, 处于次共振频率范围. 在该声子共振调控参数条件下, 声子共振调控方法可有效增大氮-空位色心的自旋跃迁概率.
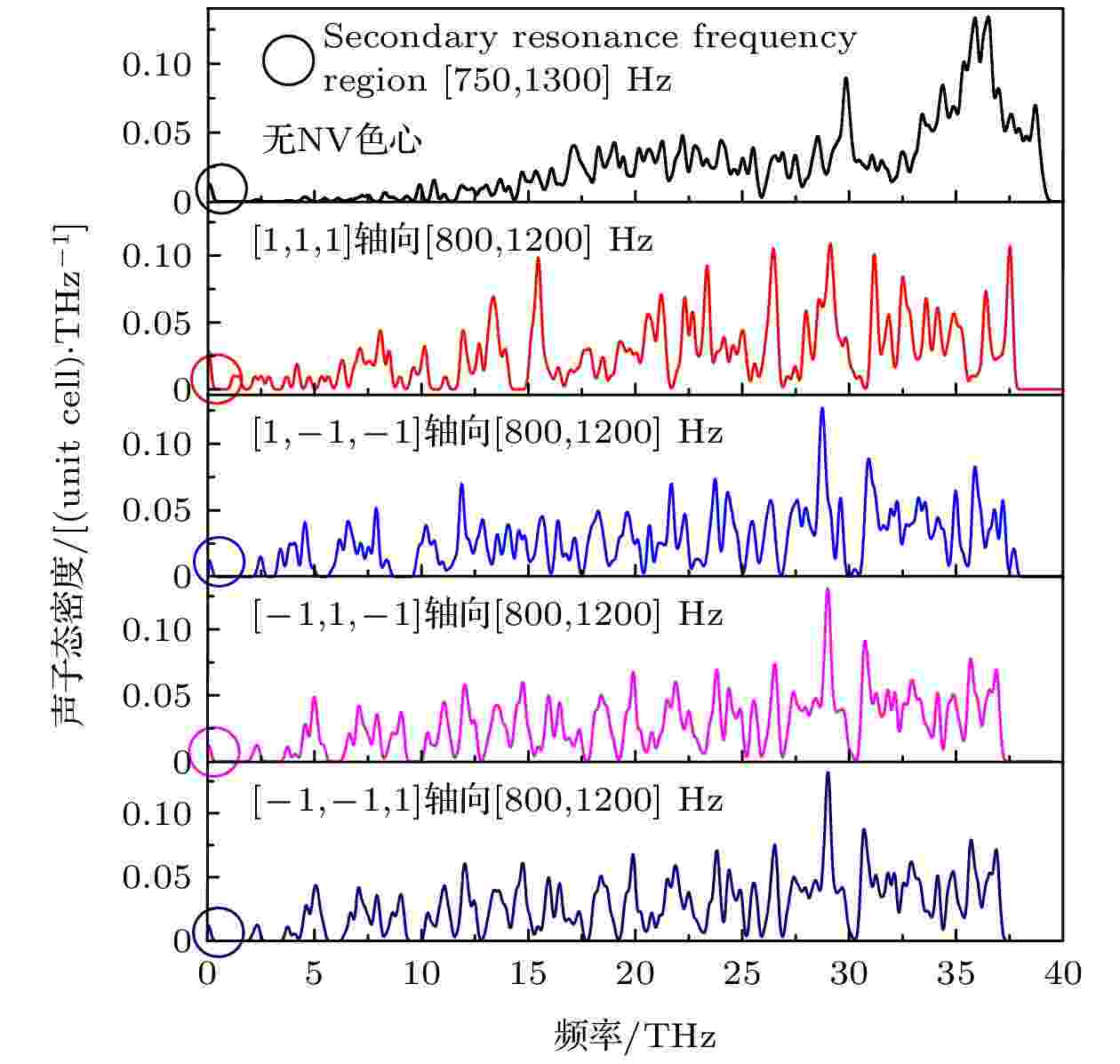图 10 不同轴向NV色心金刚石的声子态密度曲线
Figure10. Phonon state density curves of the diamond with NV centers of different axes.

3 -->

4.2.3.热力学特性

Debye温度不仅反映晶体点阵的动畸变程度, 还是物质原子间结合力的表征, 物质的弹性、硬度、熔点和比热等物理量均与它有关. 根据不同轴向NV色心金刚石的Debye温度曲线(图11)可知, 当温度为25 K时, Debye温度均达到C点, 纯净无缺陷金刚石、[1, 1, 1]轴向、[1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向的NV色心金刚石的C点Debye温度值分别为2614.50934, 3379.62378, 1233.70678, 1145.47014, 1165.59051 K. 当温度为500 K以上时, 不同轴向NV色心金刚石的Debye温度均达到稳定, 纯净无缺陷金刚石、[1, 1, 1]轴向、[1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向的NV色心金刚石的稳定Debye温度值分别为1489.99201, 1575.97472, 1542.95619, 1547.77852, 1547.94141 K. 从稳定Debye温度可知, 纯净无缺陷金刚石的稳定Debye温度高于含NV色心的金刚石, 因此, 纯净无缺陷金刚石的原子健结合力更强, 熔点更高. 同理, 对于四种不同轴向NV色心的金刚石来说, [1, 1, 1]轴向NV色心金刚石的原子健结合力和熔点略大于其余三种轴向.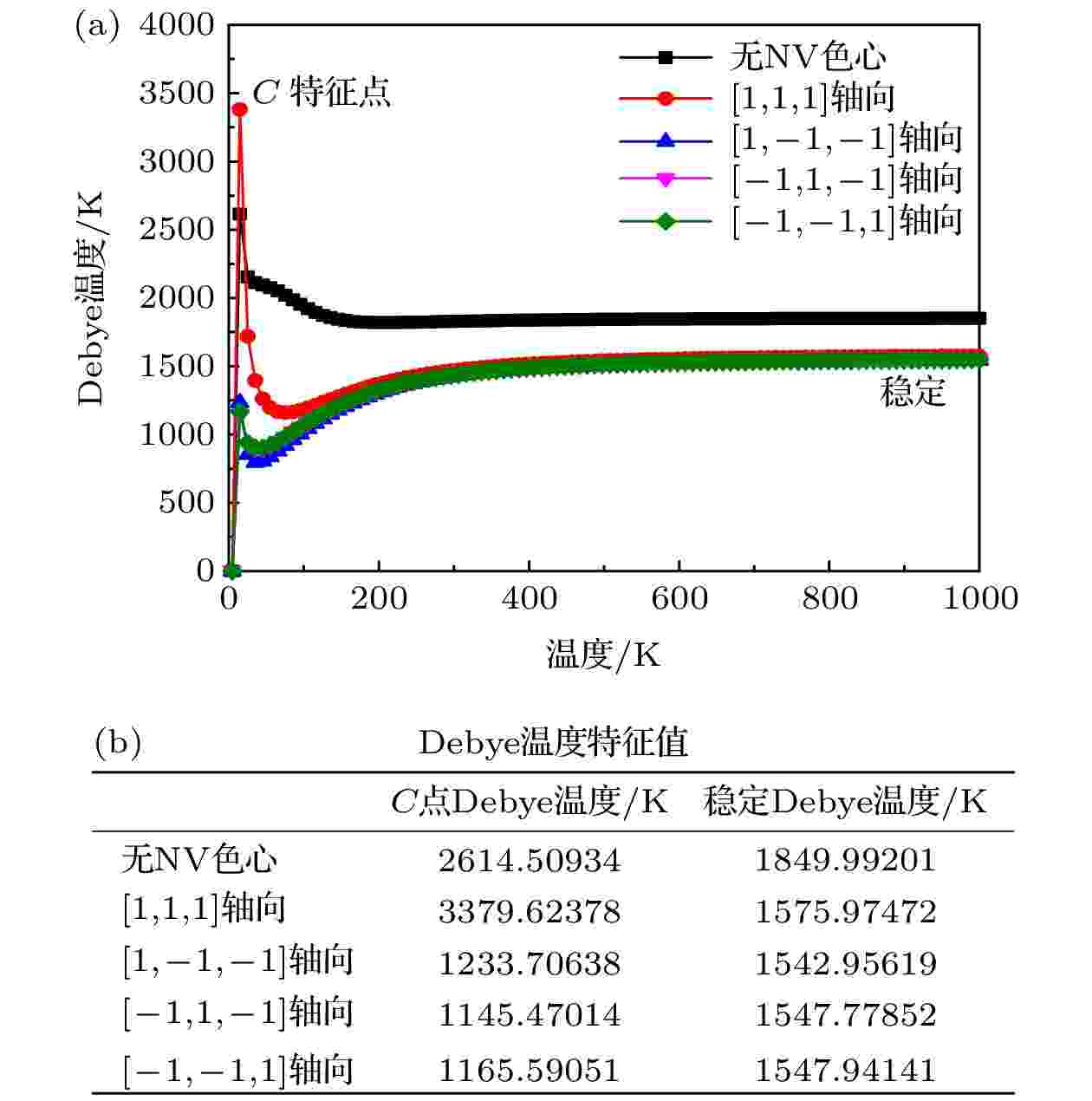
图 11 不同轴向NV色心金刚石的Debye温度特征　(a)特征曲线; (b)特征值
Figure11. Debye temperture characteristics of the diamond with NV centers of different axes: (a) Characteristic curves; (b) characteristic values.

不同轴向NV色心金刚石的声子热力学曲线(图12)表明, 热焓、热熵随着温度的升高而增加, 且纯净无缺陷金刚石的热焓随着温度升高, 其增长幅度远小于含NV色心的金刚石(图12(a)). 同时, 热熵的增长幅度也远小于含NV色心的金刚石(图12(b)). 另外, 自由能随着温度的升高而下降, 且纯净无缺陷金刚石自由能的下降幅度不及含NV色心的金刚石(图12(c)). 四种不同轴向NV色心的金刚石的声子热力学性质差异不明显. 纯净无缺陷金刚石与含NV色心的金刚石相比, 具有更加稳定的热力学性质. 图12(a)、图12(b)和图12(c)还分别基于三次多项式方程($ {y}={A}+{B}{{x}}^{2}+{C}{{x}}^{3} $)对不同轴向NV色心金刚石的热焓、热熵和自由能曲线进行拟合, 其拟合方程分别列入图12中. 基于上述拟合方程可描述和预测不同轴向NV色心金刚石的热焓、热熵和自由能等声子热力学性质. 研究结果还表明, 系统声子模式的演化依赖于NV色心的占位, 声子模式强化伴随着热力学熵的降低.
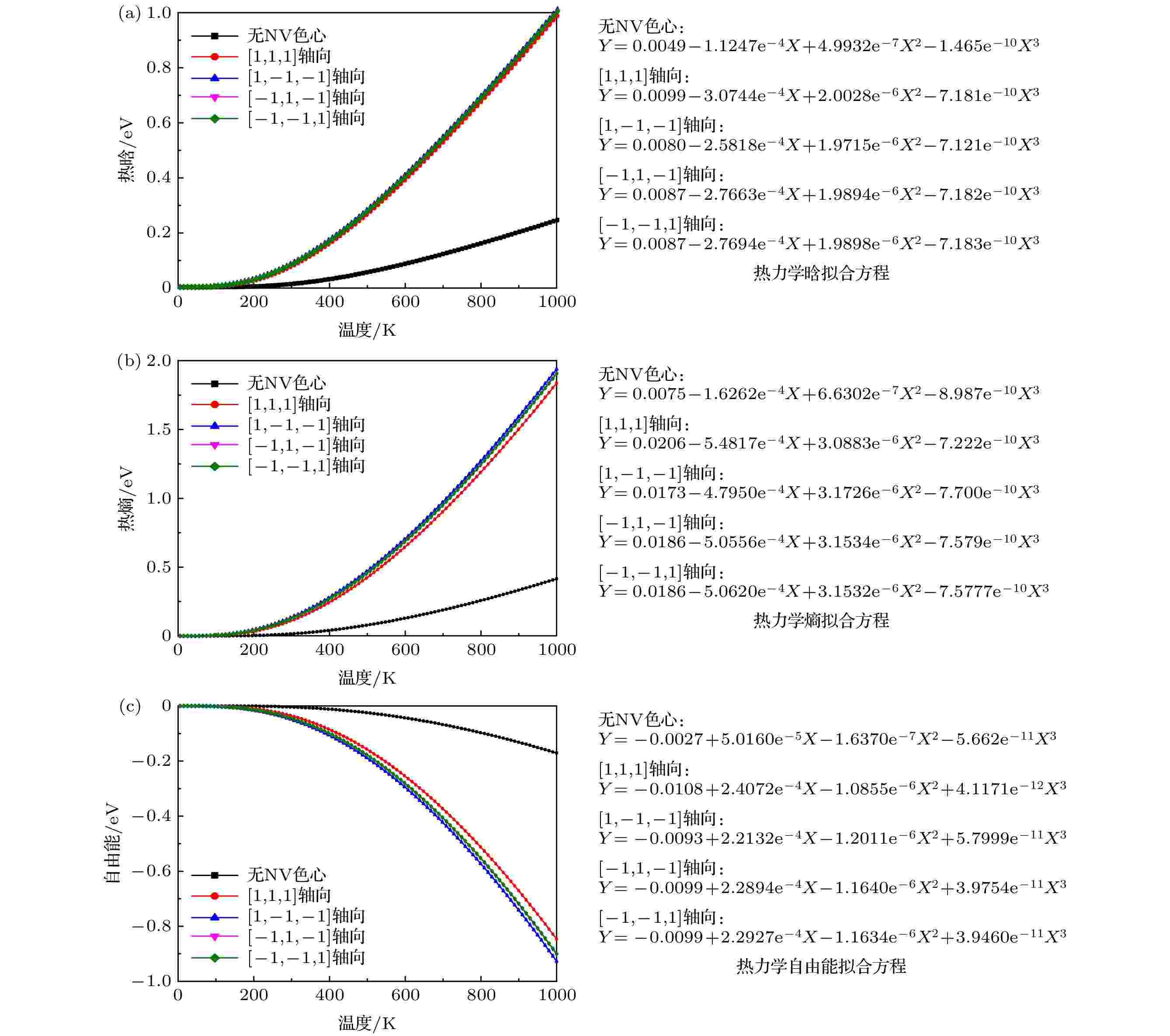图 12 不同轴向NV色心金刚石的声子热力学曲线　(a)热力学晗; (b)热力学熵; (c)热力学自由能
Figure12. Debye temperture curves of the diamond with NV centers of different axes: (a) Enthalpy; (b) entropy; (c) free Energy.

不同轴向NV色心金刚石的热容曲线(图13)表明, 热容随着温度的升高而增加, 且逐渐趋向于平衡. 高温下纯净无缺陷金刚石的热容远小于含NV色心的金刚石. 四种不同轴向NV色心的金刚石的热容性质差异不明显. 特别的, 当温度为250 K时, 纯净无缺陷金刚石、[1, 1, 1]轴向、[1, –1, –1]轴向、[–1, 1, –1]轴向和[–1, –1, 1]轴向的热容分别为1.999, 11.874, 12.751, 12.473, 12.469 cal/(cell·K). 当温度为1000 K时, 对应的热容分别为10.108, 36.975, 37.157, 37.131, 37.130 cal/(cell·K).
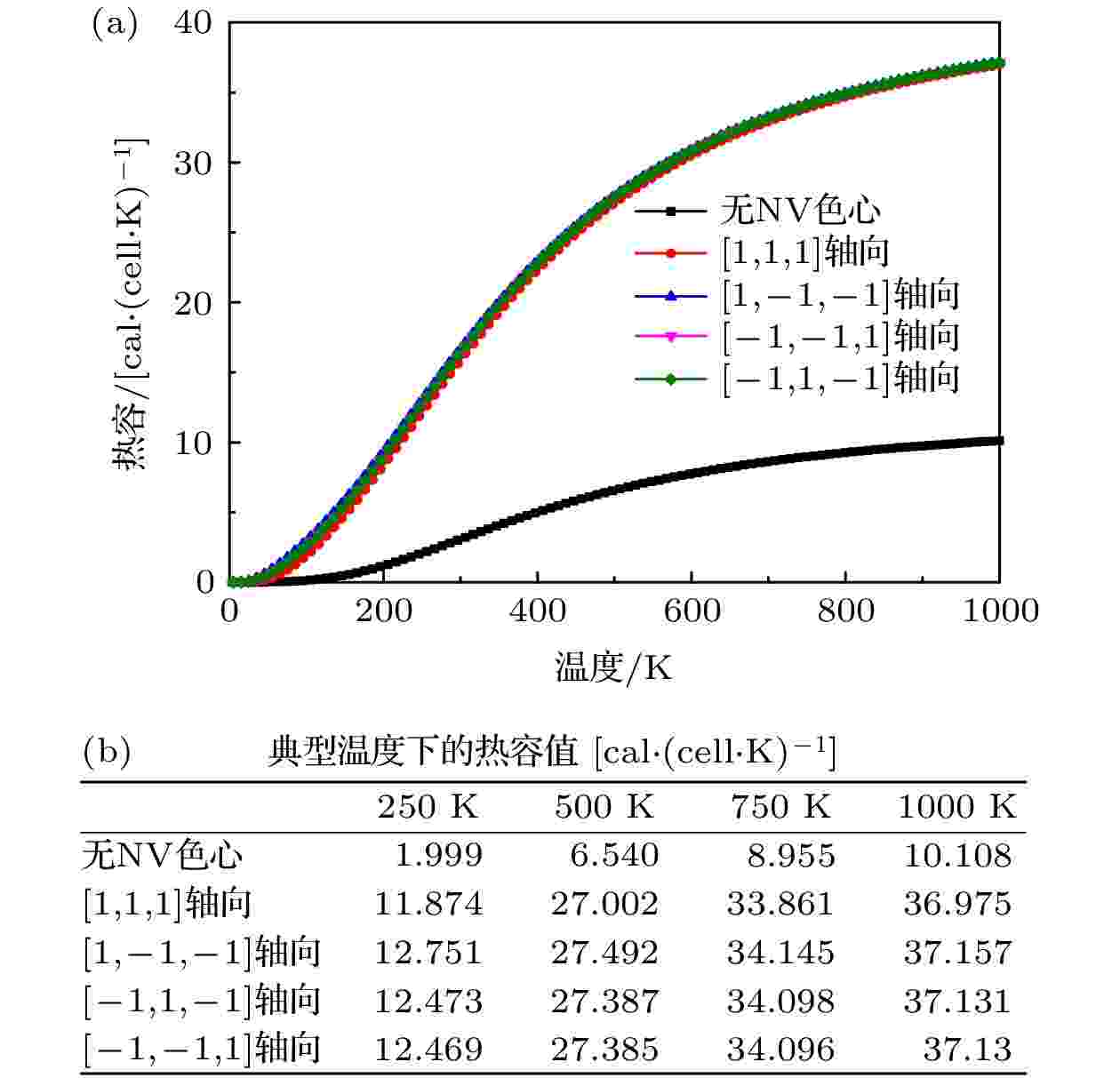图 13 不同轴向NV色心金刚石的热容特性　(a)热容曲线; (b)热容值
Figure13. Heat capacity characteristics of the diamond with NV centers of different axes: (a) Heat capacity curves; (b) heat capacity values.

本文引入耦合声子场对NV色心自旋进行共振调控, 重点研究声子模式下NV色心的自旋操控机理和热力学性质, 研究内容及相关结论如下:
1)基于波函数和晶格的点阵位移矢量关系, 分析了声子与晶格能量交互作用, 研究了基于声子共振调控的NV色心的自旋跃迁机理, 建立了基于应变诱导的能量转移声子-自旋交互耦合激发模型.
2)基于NV色心晶格振动理论, 引入满足布洛赫定理的系数矩阵, 建立了[1, 1, 1]轴向NV色心第一布里渊区特征区域的声子谱特征函数, 并对相应的极化向量进行了解析. 解析结果表明: 横向声子$ {\omega }_{2} $与$ {\omega }_{3} $在NV色心金刚石晶格的第一布里渊区$ {\varLambda } $特征线产生二重简并; 横向声子$ {\omega }_{1} $与$ {\omega }_{3} $在其第一布里渊区$ {{q}}_{{z}}= 0 $平面上产生二重简并.
3)基于Debye模型, 考虑热膨胀效应, 对声子共振系统的声子热平衡性质进行解析, 建立[1, 1, 1]轴向NV色心沿着声子极化方向的声子热平衡温度模型. 同时, 对声子模式下不同轴向NV色心结构的晶格自由能和晶格热容量进行了解析. 解析结果表明: NV色心金刚石晶体的声子热平衡温度, 晶格自由能和晶格热容量均与其晶体结构参数密切相关.
4)基于分子动力学仿真软件CASTEP和密度泛函理论进行第一性原理研究, 构建了声子模式下不同轴向NV色心的结构优化模型, 并分析了其结构特性、声子特性和热力学特性. 研究结果表明, 系统声子模式的演化依赖于氮-空位的占位, 声子模式强化伴随着热力学熵的降低. 含NV色心的金刚石共价键较纯净无缺陷金刚石更弱, 热力学性质更不稳定. 含NV色心金刚石的声子主共振频段均处于THz量级, 次共振频率约为[800, 1200] MHz. 声子耦合激励至主共振频率技术较难实现. 根据次共振频段设计叉指宽度为1.5 μm的声表面波共振机构, 其中心频率约为930 MHz. 在该声子共振调控参数条件下, 声子共振调控方法可有效增大氮-空位色心的自旋跃迁概率, 实现氮-空位色心原子自旋操控效率的提高.
本文工作为后续研究声子辅助操控NV色心原子自旋, 实现自旋跃迁效率的提高具有一定的指导意义.