全文HTML
--> --> -->1974年, Nye和Berry[1]通过类比晶体位错, 在波动理论中引入了相位位错的概念, 并对其进行了三种分类: 刃型位错、螺型位错和刃型螺型混合位错. 自20世纪90年代以来, 这些相位奇异性引起了人们广泛的兴趣, 在光学[2-17]、电磁学[18-24]和声学等领域得到了广泛的研究. 其中, 螺型位错在光学通信和微粒操控领域凭借其独特的优势更是占据了重要地位. 涡旋光束就是一种具有螺旋型位错, 并携带轨道角动量的光束. 当高斯光束带有螺旋型的相位时, 光束便携带了轨道角动量, 其中心的相位不确定性导致了相位奇点的产生, 在光强上表现为中心位置出现一个圆形暗核.
由于声波和光波在波动传输方面具有类似的特性, 在OAM光束提出来不久, OAM声束也开始进入了人们的研究范围. 1979年, Broadbent和Moore[25]首次提出OAM声束的概念, 并对OAM声束进行了理论分析. 和OAM光束类似, OAM声束也具有同样的相位奇异性, 可通过数学形式exp(imθ)来表述, 其中θ被称为方位角, m被称为涡旋波的拓扑荷(阶数), 定义为在一个波长传播距离内波阵面扭转的次数, 其符号与扭转方向有关, 且在理论上可以任意取值.
OAM声束具有许多吸引人的特性, 首先就是携带不同拓扑荷的OAM声束之间相互正交. 假设两束OAM声束的拓扑荷分别为m1和m2, 通过内积计算可以看出其正交性:
OAM声束除了在声通信系统中具有重要作用外, 其在相位奇点处相干相消呈现出的“甜甜圈”状的场强分布, 还可以在声波定位仪器中作为校准工具. 除此之外, 人们还发现了OAM声束在粒子操控等领域的巨大潜力. 声涡旋可以对液体或空气中的物体施加力[26-33]和力矩[34-39]. 相比于OAM光束, OAM声束不仅具有连续的螺旋相位分布, 同时还具有良好的物体穿透性和较小的生物损耗[40,41], 有助于实现相对较大尺寸、非磁性且不导电微粒的捕获、悬浮和操纵[42-54]; 而且, 由于声波的无损穿透性, 声涡旋可以操控物体内部微粒, 因此在医学超声领域上关于细胞或者微流的精准操控方面有着巨大的优越性.
本文全面综述了声涡旋信息及应用系统方面的研究进展. 对近些年在OAM声束的产生及复用方法、检测与解调方法、传输特性, 及其在通信领域的应用等方面的研究成果进行了阐述分析. 最后, 对目前研究工作中仍存在的不足进行了总结, 并对OAM声通信技术的未来发展趋势及其前景进行了展望.
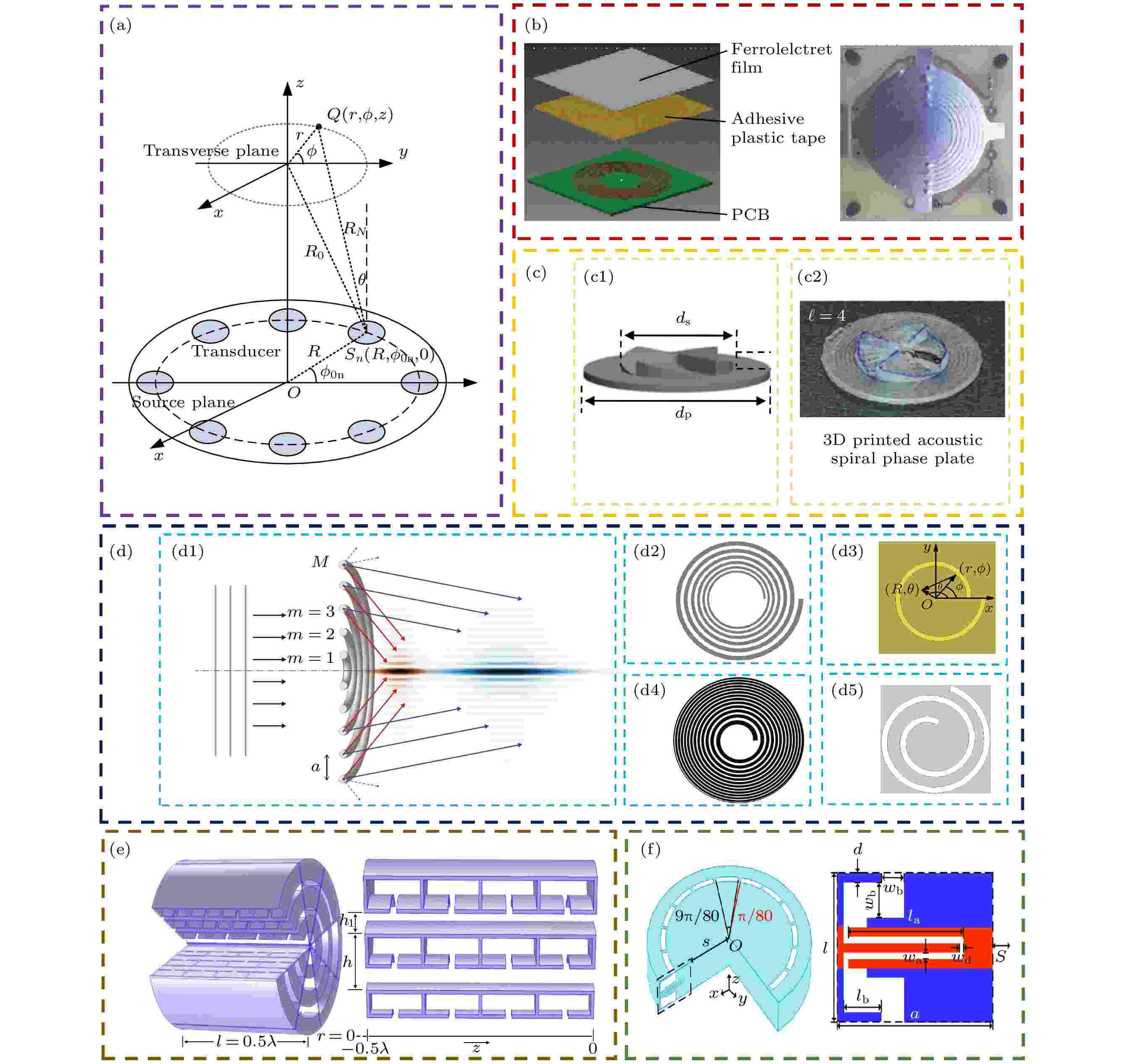图 1 (a) 利用换能器阵列产生OAM声束示意图[56]; (b) 利用螺旋型有源衍射声栅产生OAM声束示意图[57]; (c) 利用声学SPP产生m = 4的OAM声束示意图(c1)和3D打印实物图(c2)[62]; (d) 用于产生OAM声束的(d1)轴对称声栅[63]、(d2)对数螺旋声栅[64]、(d3)阿基米德螺旋声栅[66]、(d4)菲涅耳半波片声栅[67,68]、(d5)费马螺旋声栅[69]; (e) 共振型环形超表面产生OAM声束示意图[72]; (f) 复合迷宫型环形超表面产生OAM声束示意图[73]Figure1. (a) Schematics of generating acoustic OAM beams using transducers array[56]; (b) schematics of generating acoustic OAM beams by spiral active diffraction grating[57]; (c) schematics of a SPP with topological charge m = 4 (c1), picture of the 3D printed thermoplastic acoustic SPP (c2)[62]; (d) using the axisymmetric sound grating[63] (d1), logarithmic spiral sound grating[64] (d2), Archimedes spiral sound grating[66] (d3), Fresnel zone plate sound grating[67,68] (d4), Fermat spiral sound grating[69] (d5) to generate acoustic OAM beams; (e) acoustic OAM beams generated by resonant ring metasurface[72]; (f) acoustic OAM beams generated by the complex labyrinth type ring metasurface[73].
2018年, Muelas-Hurtado等[57]提出了一种利用螺旋型有源衍射声栅产生涡旋声束的高效方法. 如图1(b)所示, 螺旋源粘在印刷电路板上, 由柔性铁电极构成, 螺旋路径的宽度和它们之间的间距是恒定的. 当接入超声频率的交流电压后, 螺旋源发生共振, 从而产生具有螺旋波前相位的涡旋声束. 该方法的工作频率为30—300 kHz, 且利用声栅不同的衍射阶次, 该装置可以同时产生具有不同拓扑荷的OAM声束, 它们沿着传播轴彼此分离.
与有源方法相比, 使用无源方法产生涡旋声束更具方便性和可靠性, 对资源的消耗较小. 2004年, Gspan等[61]提出了利用光声效应产生涡旋声束的方法, 当脉冲激光照射到水箱中的用来产生OAM声束的螺旋相位板(sprial phase plate, SPP)后, 受热弹效应影响相位板会向另一侧传播压力波. 其中, 特殊设计的相位板厚度h是方位角θ的一个连续函数: h = λθ/[2πf (c0–1 – c–1)], 其中, c0是周围介质中的声速, c是相位板中的声速, f是入射波的频率. 2015年, Wunenburger等[62]设计了一个SPP用于产生高阶声涡旋. 该螺旋相位板的示意图如图1(c1)所示, 这个螺旋相位板由圆柱形底座和4个梯度随方位角变化的螺旋梯度表面组成. 当声波入射该结构时, 每个螺旋表面可以产生从0到
针对上述工作存在的困境, 2014年, Jimenez等[63]提出了一种具有亚波长厚度的轴对称声栅, 可以用来产生近似贝塞尔涡旋的声束. 如图1(d1)所示, 平面声波通过声栅后发生衍射, 在近轴区域能产生OAM声束. 此后, 研究人员将螺旋声栅的臂替换为对数螺旋线[64] (图1(d2))、阿基米德螺旋线[65,66] (图1(d3))、菲涅耳半波带[67,68] (图1(d4))、费马螺旋线[69] (图1(d5))等形状, 均能很好地产生OAM声束. 此外, 进一步的研究证明了通过调整螺旋声栅的臂数可以控制产生OAM声束的拓扑荷. 值得一提的是, 利用螺旋声栅不仅能产生整数阶OAM声束, 也能产生分数阶OAM声波[70]和聚焦OAM声束[71], 这对于涡旋声束的应用提供了更多切实有效的途径.
为进一步减小装置的尺寸, 近年来, 被广泛用于声波波前调控的超材料和超表面为产生涡旋声波提供了一个新的途径[72-82]. 超表面通常由亚波长结构单元组成, 通过引入共振或改变有效路径长度来控制波束的相位和振幅. 2016年, Jiang等[72]设计了一款基于声学共振的超表面, 使得入射平面波透射该结构后会携带螺旋波前相位. 如图1(e)所示, 该结构由八个相同的扇形共振腔组成, 每个扇形都由三层沿径向分布的共振腔组成, 每行共振腔均由四个亥姆霍兹共振腔和一个长直管组合而成, 通过改变长直管的高度, 可调节透过超表面的传输相移. 因此, 只需将每个扇形对应的相位分布满足离散螺旋波前相位分布, 就能产生目标OAM声束. 2018年, Jia等[73]设计了一种由复合迷宫结构(compound labyrinth structure, CLS)子单元组成的环形声超表面, 用于在空气中产生分数阶OAM声束. 如图1(f)所示, 通过改变CLS子单元的一个结构参数来改变声波通过的有效路径的长度, 可灵活而有效地控制声波通过CLS子单元的传输相移.
2019年, 合肥工业大学郭忠义团队[74]对声学共振结构进行了进一步研究, 实现了高阶及复合涡旋产生. 首先, 该工作研究了采用该种共振结构产生OAM声波的频率适用范围. 随后, 采用该种结构产生了高阶OAM声波, 并分析了结构半径、扇区数目和产生拓扑荷之间的关系, 如图2(a1)所示, 分别展示了产生拓扑荷为5的OAM声波的结构示意图以及在不同传输平面上声压和相位的分布情况. 最后, 使用改进的Lin算法获得了多路复用的相位分布, 从而产生了复合涡旋声束. 图2(a2)为通过改进的Lin算法计算得到的拓扑荷为–1和2复合涡旋的相位分布全息图, 对其进行离散化(图2(a3))并加载到超表面上, 便可实现复合涡旋声束的产生. 为了证实该方法的可行性, 工作中通过将该复合相位结构与产生拓扑荷为1和–3的结构相级联(图2(a4)), 在每个区域的轴线上对声压进行检测来判断是否有所需拓扑荷的存在. 该工作为OAM声波的高效复用提供了新的思路.
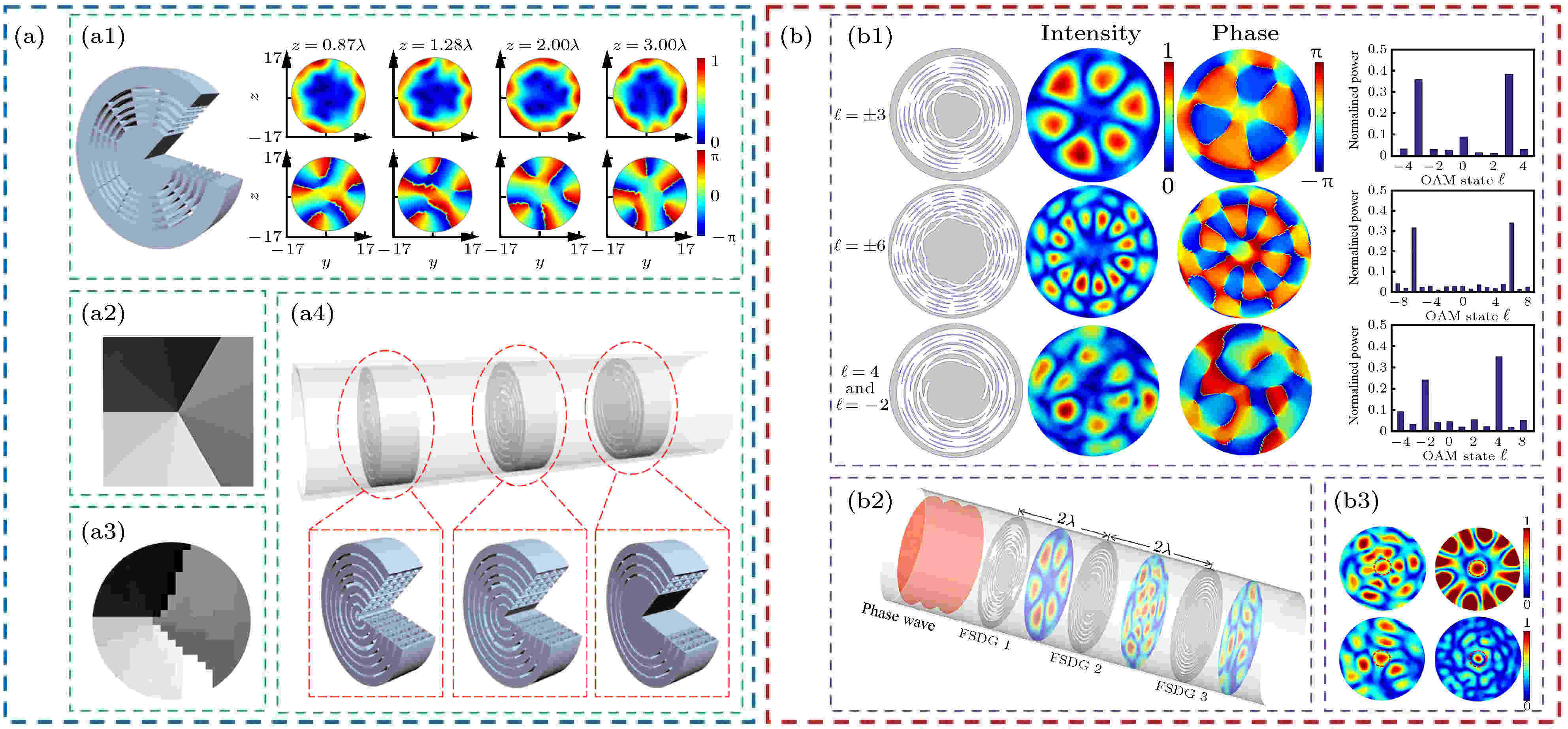图 2 (a)采用声学共振结构实现高阶和复合OAM声束的产生[74], (a1)结构示意图及不同检测平面上的声压与相位分布, (a2)产生复合OAM声束的相位全息图, (a3)加载到超表面上的离散化相位全息图, (a4)检测产生声场组成的结构示意图; (b)采用费马螺旋实现高阶和复合OAM声束的产生[69], (b1)结构示意图、声压和相位分布以及模式检测结果, (b2)进行模式分离的原理图及(b3)结果Figure2. (a) Generation of high-order and multiplexed acoustic OAM beams by acoustic resonance structure[74], (a1) structure and the distributions of pressure and phase of different planes, (a2) multiplexed phase hologram of OAM sound beams, (a3) discretization phase hologram, (a4) structure to detect vortex field; (b) generation OAM sound beams by Fermat’s spiral diffraction grating[69], (b1) structural diagram, sound pressure, phase distribution, and power density spectrum, (b2) schematic diagram for detection, and (b3) results.
同年, 该团队又提出采用费马螺旋产生高阶和复用的涡旋[69]. 图2(b1)为产生高阶和复合OAM声波的结构示意图、声压和相位分布以及对拓扑荷纯度进行检测后的结果. 此外, 该工作中还通过级联不同的螺旋结构(图2(b2))实现了对复合OAM态的解调, 图2(b3)为每个区域的声压分布, 可以看出在声场中心有亮斑的出现, 进一步说明了采用该方法产生复合涡旋的可行性. 该工作中还对拓扑荷的纯度进行了分析, 证明了该方法产生复合OAM声束的高效性. 此外, 考虑到该结构在实际操作中的缺点, 还提出用不同声阻抗的材料对镂空部分进行填充的方法. 这种方法不仅可以解决结构的缺陷, 还可以改变OAM声束强度的大小, 提高所设计的费马螺旋衍射声栅的实用性, 也为其他声栅更好的应用提出了一种普适性方法.
相较而言, 由于没有共振器件, 使用螺旋相控源和螺旋型源等有源方法产生OAM声束具有更宽的工作带宽, 并且可以灵活的改变工作状态, 但其结构尺寸过大, 实现过程复杂, 而使用相位板、螺旋声栅和超表面等无源器件则更为简单和廉价. 常用的不同涡旋声束产生方案在多个方面的性能比较如表1所列.
| 有源方法 | 无源方法 | |||||
| 螺旋相控源 | 螺旋型源 | 相位板 | 螺旋声栅 | 超表面 | ||
| 成本 | 高 | 高 | 低 | 低 | 低 | |
| 速度 | 正常 | 正常 | 正常 | 正常 | 正常 | |
| 可靠性 | 高 | 高 | 高 | 高 | 高 | |
| 复杂性 | 高 | 高 | 低 | 低 | 低 | |
| OAM模式 | 复合 | 复合 | 单一 | 复合 | 复合 | |
| 工作频段 | 宽 | 宽 | 窄 | 宽 | 窄 | |
表1不同涡旋声束产生方案性能比较
Table1.Performance comparison of different schemes of generating acoustic vortex beams.
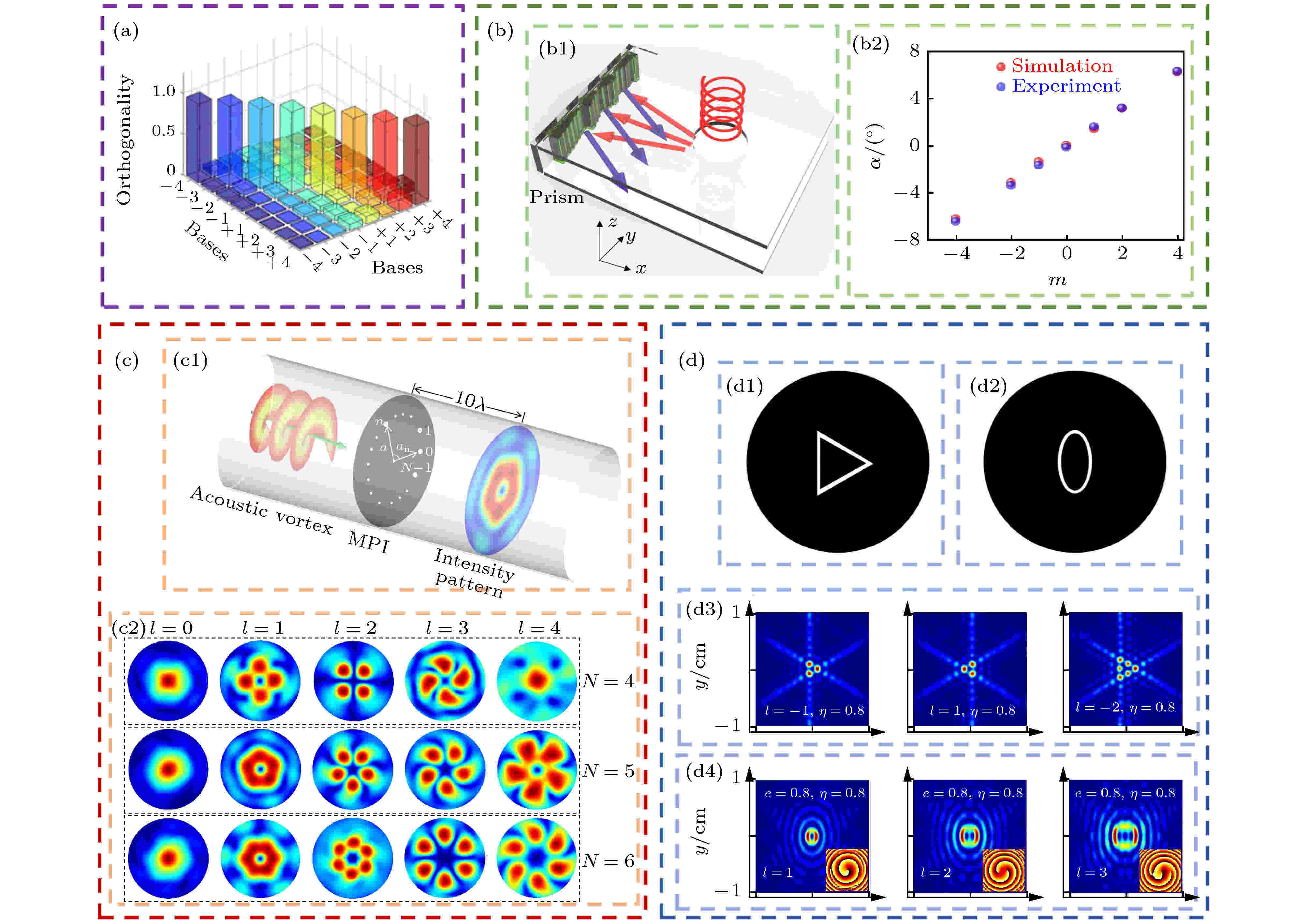图 3 (a)利用内积算法检测OAM声束示意[83]; (b)利用抛物线型解码超表面检测OAM声束示意图(b1)和拓扑荷值m和反射角α的函数关系(b2)[87]; (c)利用圆孔阵列干涉屏检测OAM声束的(c1)示意图和(c2)远场强度分布图[89]; (d)利用(d1)环形三角孔径与(d2)环形椭圆孔径实现OAM声束检测示意图(d1), (d2)及远场强度分布(d3), (d4)[90]Figure3. (a) Inner product algorithm is used to detect OAM sound beams[83]; (b) detection of OAM sound beams by using parabolic decoding metasurface (b1), relationship between the reflection angle, α, and OAM charge, m[87] (b2); (c) detection principle of multipoints interferometer (c1), far-field intensity distributions (c2)[89]; (d) sketch map (d1), (d2) and far-field intensity distributions (d3), (d4) for (d1) annular triangle aperture and (d2) annular ellipse aperture[90].
针对上述工作存在的困境, 2018年, Jiang等[84]利用拓扑荷为零的OAM声束中心声强不为零的特点, 通过不断的降低拓扑荷的值来对OAM声束解调. 该方案使OAM声束不断的经过能产生拓扑荷为–1的OAM声束的超材料结构, 若在第m层结构处观察到中心处的非零声强, 则代表该OAM声束中包含有拓扑荷为m的信息. 该方法中的超材料结构可广泛地被其他能产生OAM声束的结构所替代, 且不需要声传感器阵列, 为提高检测效率和减小成本提供了一种新的思路.
近些年, 机器学习凭借其优秀的数据分析和信息处理能力在各种领域都展示了它的作用. 2019年, Stankevich[85]采用一个双层卷积神经网络, 实现了对OAM声束的解复用. 输入层包含有R个输入的10个卷积神经元, 通过减少与输出层的连接数, 提高了学习速度, 并将神经元滤波器输出的序列分成互不相交的5点区间, 在每个区间选取最大值. 该方法能在一定的噪音干扰和传播距离下, 仅使用10个接收器, 仍保持较高的检测准确率.
除此之外, 利用特殊设计的结构将携带不同拓扑荷的OAM声束进行分离, 进而解调出对应的拓扑荷值的方法也得到了研究. 2019年, Liu等[86]利用相反OAM模式涡旋声波的布拉格散射带隙不同, 用一种带有周期性支管阵列的螺旋波导实现了旋转方向相反的涡旋声束的分离, 为声波束通信的解复用提供了一条新的途径. 该复合波导由一个与分流管周期性连接的右手螺旋形波导组成, 通过合理选择分流管的几何参数影响能带结构中的阻带开启, 进而将不同旋向的OAM声束分离. 该方法对于拓扑荷符号的检测简单且有效, 在一些特定场合有着重要作用.
2020年, Jiang等[87]将自由空间传播的多路涡旋声波通过波导壁顶部的一个孔耦合到波导中, 再使用抛物线型解码超表面将OAM声束携带的OAM转换为横向线性动量, 如图3(b1)所示, 使得携带不同拓扑荷的涡旋声束经过解码超表面后反射的平面波会沿不同步方向传播, 进而只需通过检测特定空间角的反射波就可以检测出对应的拓扑荷值. 图3(b2)为反射角度α与拓扑荷值m的关系, 从仿真和实验结果均可看出, 二者具有近似线性的关系. 该方法能够在一个较宽的频带快速并行地读出携带的OAM模式信息, 同时还可以通过修改解码超表面的几何参数, 优化携带不同拓扑荷的OAM声束对应的空间分离角的分辨率.
在光涡旋中, 基于干涉或者衍射原理, 利用涡旋波的特性来检测拓扑荷是一种普遍的检测方法[88]. 2020年, 合肥工业大学郭忠义课题组提出, 利用涡旋声波的干涉或者衍射原理来测量拓扑荷也是可行的, 并分别采用圆孔阵列干涉屏[89]、环形三角孔径与环形椭圆孔径[90]实现了对声涡旋的检测. 对于圆孔阵列干涉屏而言, 如图3(c)所示, 假设携带拓扑荷为m的声涡旋在带有N个圆孔的圆孔阵列干涉屏的检测范围内, 则携带拓扑荷为
关于OAM声束解调现在仍处于起步阶段, 但在水下通信中, 利用OAM声束传输数据具有其他方法不可比拟的优势, 因此寻找并完善简单高效的OAM声束解调方法仍是未来研究的重中之重. 目前提出的不同涡旋声束解调方案在多个方面的性能比较如表2所列.
| 内积算法 | 降低OAM模式的阶数 | 机器学习 | 螺旋波导 | 抛物线型解码超表面 | 圆孔阵列/环形孔径 | |
| 成本 | 高 | 低 | 低 | 低 | 低 | 低 |
| 速度 | 正常 | 正常 | 正常 | 正常 | 正常 | 正常 |
| 可靠性 | 高 | 高 | 高 | 高 | 高 | 高 |
| 复杂型 | 复杂 | 复杂 | 简单 | 简单 | 简单 | 简单 |
| OAM模式 | 复合 | 复合 | 复合 | 仅能分辨符号 | 复合 | 单一 |
| 工作频段 | 宽 | 窄 | 宽 | 窄 | 窄 | 宽 |
表2不同涡旋声束解调方案性能比较
Table2.Performances comparison of different demodulation schemes of acoustic vortex beams.
2003年, Thomas 和Marchiano[92]提出一个仅用线性场来定义的伪动量的概念, OAM声束和OAM光束也具有相同的性质. 虽然伪动量只涉及线性场, 但声波的传播始终是一个非线性现象, 而非线性将引起高次谐波的产生. 该工作指出, 在均匀无损介质中, 拓扑荷随谐波的阶数线性增加, 所有谐波的伪角动量与伪能量之和守恒. 此外, 在假定波的角动量等于其伪角动量的前提下, 可以计算施加于吸声物体或各向异性介质上的力矩. 2005年, 他们[93]又指出拓扑荷为m的高阶声涡旋具有不稳定性, 任何微弱的扰动都可能会使其变成|m|个拓扑荷为1(或–1)的涡旋. 此外, 该工作还研究了具有相同或相反拓扑荷的两个OAM声束间的相互作用, 证实了两个携带相同拓扑荷的OAM声束在传播过程中不会相互影响, 而当携带的拓扑荷符号相反时, 两束OAM声束会逐渐靠近直至融合, 并且融合后的波束将不再具有螺型位错的特征.
在考虑实际情况或应用时, 介质通常在不同的空间区域对应的参数也不同. 例如, 在生物医学超声研究中, 声速在各组织间存在较大差异[94,95]; 在深海环境中, 声速是深度的函数, 是由温度、盐度分层和压力变化造成的[96]. 2008年, Marchiano等[97]对在均匀或非均匀介质中OAM声束的三维非线性传播进行了数值研究. 对非线性系统的动力学特性及均匀介质中OAM声束非线性特性的研究表明, OAM声束在传播过程中产生激波, 形成一个带有方位激波的波场. 此外, 该课题组还利用不同的聚焦透镜对非线性区域内的拓扑荷动力学(即OAM声束的本征性质)进行了研究, 结果表明, 如果OAM声束通过一维聚焦介质(圆柱形透镜)传播, 拓扑荷会出现反转(图4(a)), 而如果传播介质是二维聚焦介质(球形透镜), 拓扑荷会保持不变(图4(b)). 通过对线性光学中已经观察到的结果进行推广, 并结合对谐波的研究, 证实OAM声束的三维非线性行为也基本相同.
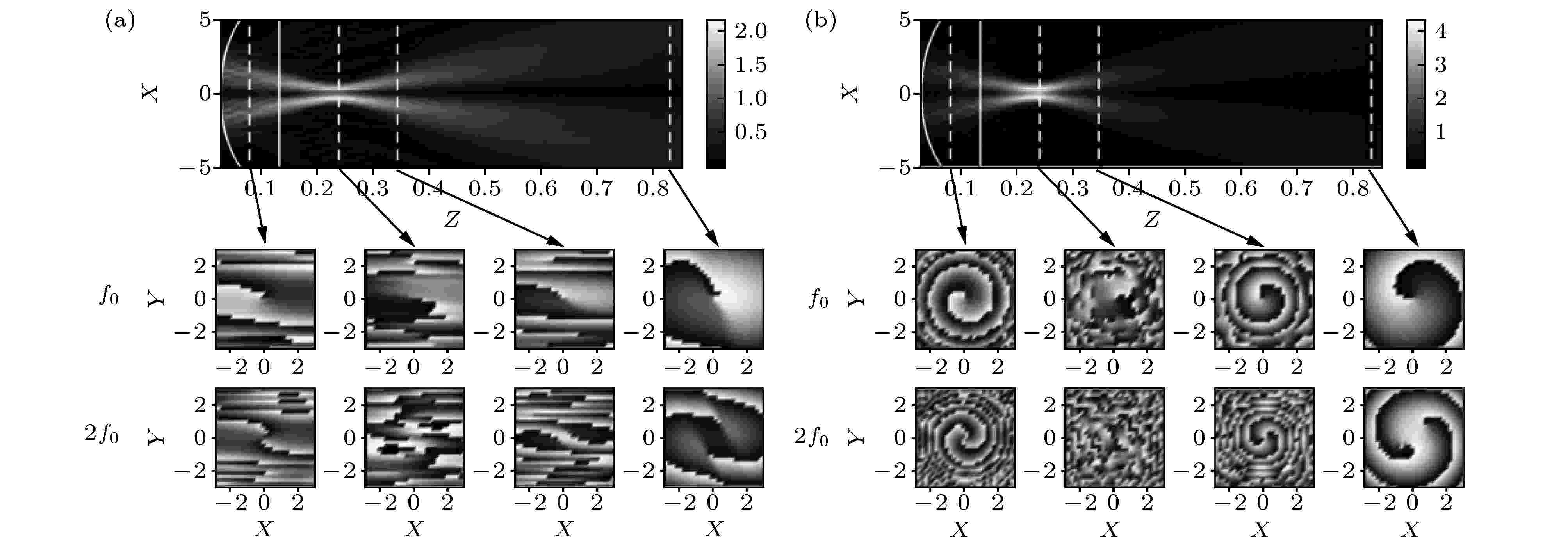图 4 OAM声束通过(a)一维声透镜和(b)二维声透镜的非线性传播[97], 其中上图显示XOZ平面的均方根振幅. 下图是基波和二次谐波在虚线表示的不同距离(Z = 0.07, 0.23, 0.32和0.85)的XY平面上的相位Figure4. Nonlinear propagation of a single OAM sound beams through (a) a 1D acoustical lens and (b) a 2D acoustical lens[97]. Top view presents the RMS (root mean square) amplitude in the XOZ plane. Bottom views are representations of the phase for the fundamental frequency and the second harmonic across plane X, Y at different distances: Z = 0.07, 0.23, 0.32, and 0.85 the positions of these planes are indicated by dashed lines on the top view.
2009年, Brunet等[98]通过实验观察到携带不同拓扑荷的非线性声涡旋在传播时会产生激波, 进一步推动了对OAM声束传播特性的研究. 由于有限振幅波的传播速度取决于压力的瞬时值, 因此波的高振幅部分比低振幅部分传播得更快, 而且由于水是声波的准非色散介质, 会导致时间剖面上的畸变, 这些因素最终导致了激波的形成. 针对这些具有三维螺旋形状的激波, 该课题组对其纵向分量和方位角分量都进行了研究. 图5(a)显示了拓扑荷分别为m = 1 (左)和m = 3 (右)的OAM声束在同一平面上以时间间隔T/3 (T为周期)测得的瞬时声压情况. 值得注意的是, 激波的波前仍显示为螺旋状. 实验结果表明, 在激波形成的距离之外, 频率与拓扑荷守恒定律仍然有效. 激波的形成不会破坏OAM声束结构的稳定性, 而且强化了OAM声束在非线性扰动下的结构稳定.
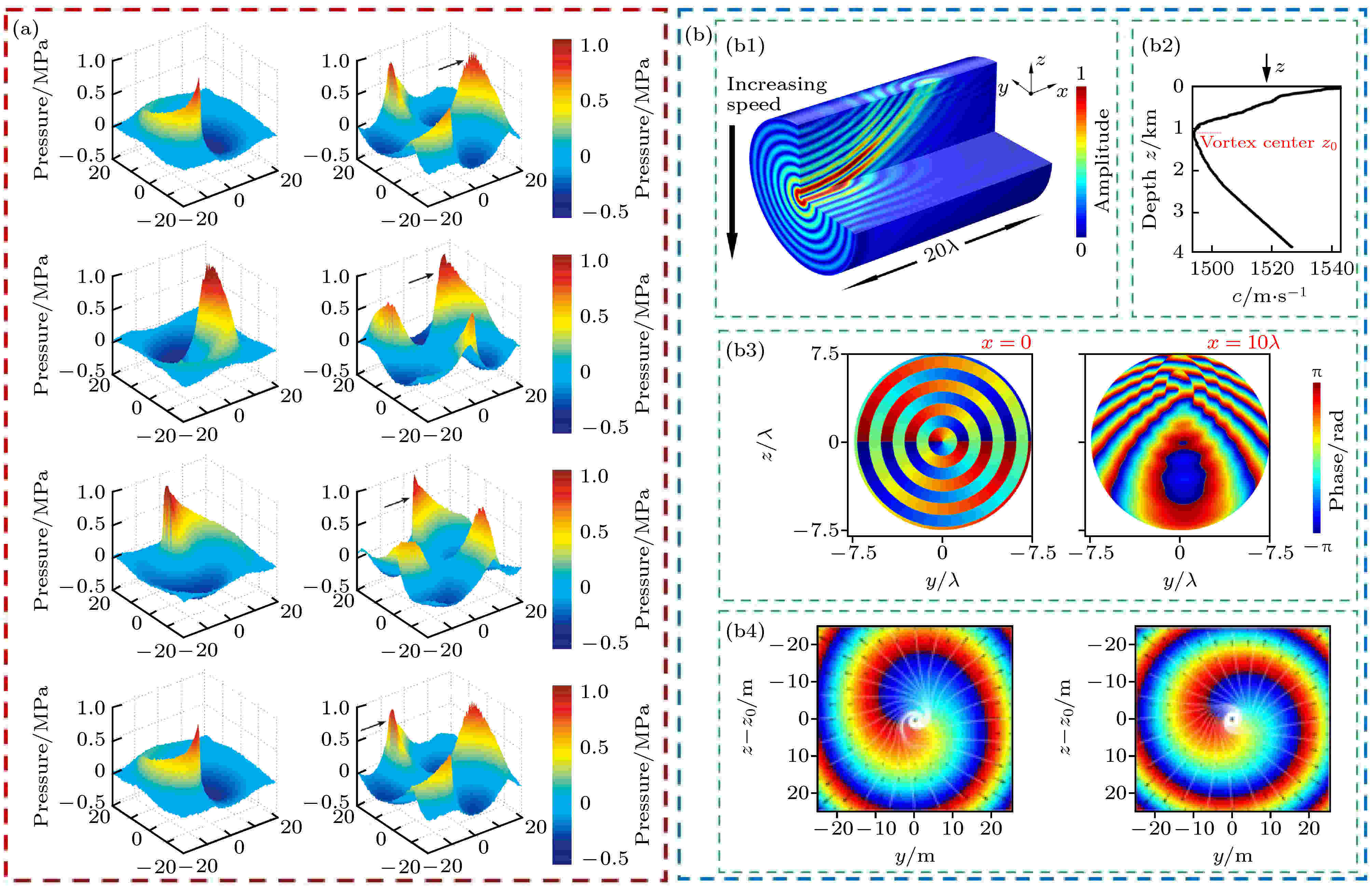图 5 (a) 携带拓扑荷m = 1 (左)和m = 3 (右)的非线性OAM声束在不同时刻的瞬时声压(黑色箭头表示其中一个激波的位置)[98]; (b) (b1)分层介质中OAM声束弯曲的模拟, (b2)深度与声速的关系, (b3)在不同的传播距离x下, 相位在y-z截面上的拉伸和变形, (b4)在分层海洋中(左)的相位(彩色图)和能量通量(黑色箭头和白色流线)(顶部)以及与在非分层海洋中(右)的传播的比较[99]Figure5. (a) Instantaneous sound pressure of a nonlinear OAM beam carrying topological charge m = 1 (left) and m = 3 (right) at different moments[98]. The black arrows indicate the position of one of the three shocks. (b) (b1) Simulation of OAM sound beams bending in a stratified medium, (b2) the sound speed profile, (b3) stretching and distorting of the phase on y-z cross sections at different propagating distances x, (b4) vortex phases (color plots) and energy flux (black arrows and white streamlines) in the stratified ocean (left) and a comparison with propagation in an unstratified ocean (right)[99].
2019年, Fan等[99]对OAM声束在非均匀介质中的传播进行了研究. 首先, 该课题组对线性分层流体(声速为c = c0–Gz, G为梯度)中OAM声束的传播进行了模拟(图5(b1)). 通过仿真发现, OAM声束向上弯曲并向分层方向拉伸, 图5(b3)为在不同传播距离处的相位分布情况. 此外, 该课题组还模拟了OAM声束在深海环境中的传播. 通过温度、盐度和声压的变化计算出了声速的分布(图5(b2)), 结果表明, 海洋分层同样会使OAM声束变形(垂直拉伸), 也同样出现了不对称特征, 但由于分层相对较弱, 不对称现象不像之前那样强烈(图5(b4)分别为分层(左)与非分层(右)海洋模型中相位和能流的分布情况), 即非线性梯度使OAM声束向声速最小方向聚焦, 而线性梯度则使OAM声束向一个方向弯曲. 该工作为复杂介质中OAM声束的传播研究开辟了一条新的途径, 其研究结果将有助于OAM声束在非均匀介质(如海洋和生物医学组织)中的应用.
2017年, Shi等[83]提出一种基于OAM的高速声通信技术, 使用–4到+4的八种拓扑荷实现了(8.0 ± 0.4) (bit/s)/Hz的数据传输. 其原理是通过计算机控制的数模转换电路产生信号来控制换能器阵列(图6(a1): 共四圈, 每一圈包括16个等间距放置的换能器)将编码成多路OAM声束的信息发射到自由空间, 并在接收端采用声学相控阵进行接收和解调. 该工作中展示了英文单词“Berkly”的传送, 每个字母用8 bit长度的ASCII码编码. 如图6(a2)所示, 当对应的拓扑荷阶数上有信号输出时, 编码为“1”; 信号关闭时, 编码为“0”, 信号能量平均分配在每个字节对应的所有编码为“1”的态上. 图6(a3)为携带不同字母信息的复用OAM声束的声压和相位分布. 在接收端处进行声场扫描, 并利用计算机对扫描得到的声场幅度与相位进行内积运算. 经过这种信号后处理, 将相互重叠的八种拓扑荷分离开来, 并从中解调出了所包含的信息. 该工作还通过理论计算与实验测量分析了这种OAM传输技术的误比特率(bit error rate, BER)与接收端换能器数目之间的关系, 发现只有当换能器数目较大时方可获得较低BER, 但继续增加换能器数目并不会进一步降低BER.
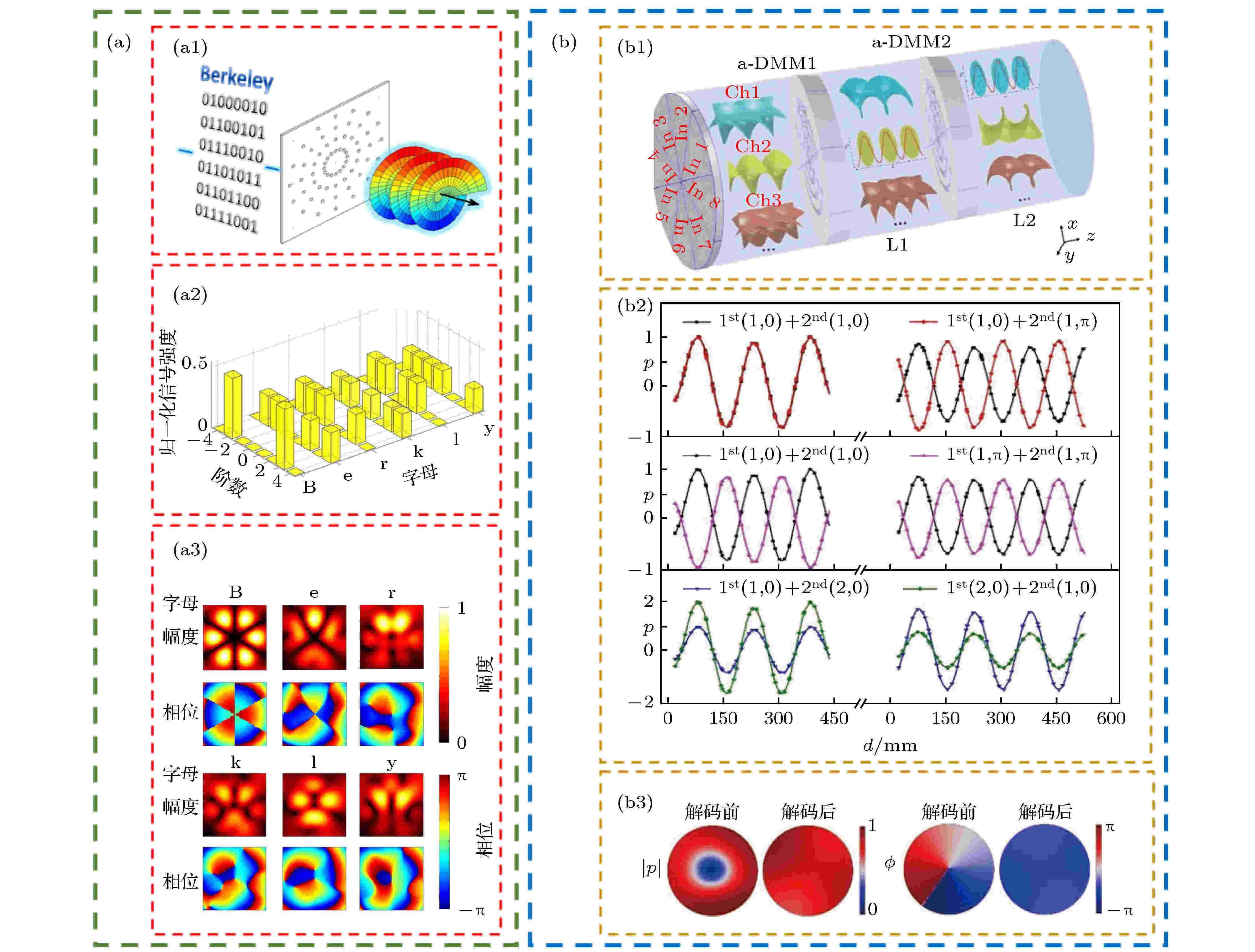图 6 (a) (a1)实验原理示意图, (a2)单词“Berkly”对应的ASCII编码方式, (a3)实验测量得到的单词“Berkly”对应的调制信号包含的八种拓扑荷的声压幅度与相位[83]; (b) (b1)基于OAM声束的调制-解调原理示意图, (b2)不同复合信号在解码端两个区域中的分布情况, (b3)用超表面解码前后的信号幅度(左侧)及相位(右侧)分布图[84,102]Figure6. (a) (a1) Schematic diagram of the experiment, (a2) the ASCII code corresponding to the word “Berkly”, (a3) the amplitude and phase of the eight topological charges contained in the modulation signal corresponding to the word “Berkly” as measured by the experiment[83]; (b) (b1) schematic diagram of the modulation-demodulation principle based on the OAM sound beams, (b2) distribution of different composite signals in two regions of the decoding terminal, (b3) distribution diagram of signal amplitude (left) and phase (right) before and after the decoding with the hypersurface[84,102].
与该方案中将信息加载在OAM的开关态上不同, Cheng课题组[84,102]直接将携带不同拓扑荷的OAM声波作为信息载体. 如图6(b1)所示, 该工作使用8个换能器单元组成的相控阵来实现复合OAM声波的产生, 其中每个单元信号的幅度和相位均可独立调控. 以单频声波为例, 利用拓扑荷m = 1和m = 2两种OAM声束进行编码可以传输2 bits的信息; 但如果将信息编码在相位, 可利用现有的1/4, 1/8及1/16相位键控技术等已有编码手段来实现编码, 分别传输4, 8, 及16 bits的信息, 若同时再采用幅值进行编码, 同样可根据不同的幅值编码技术实现多bit的信息传输. 图6(b2)展示了不同复合信号在解码端两个区域中的分布情况, 其中m-th (A, ?)表示拓扑荷为m, 幅度和相位分别为A和?的OAM声束的声压. 从图6可以看出, 利用OAM声束来编码信息时, 携带不同拓扑荷的OAM声束不仅相互之间完全正交, 而且与复合信号的幅度与相位也独立. 因此, 这种编码方式可以直接与现有的多路复用技术兼容, 在不增加额外信道负担的情况下开辟一种新的通信自由度. 在接收端, 则采用了基于超表面的实时解调原理. 对于共使用N阶OAM声束进行编码的系统, 通过在接收端依次放置N个相同的解调超表面(de-multiplexing metasurface, DMM)(每个表面设计为将拓扑荷数m降低1阶), 可将OAM声束转化为阶数变化的OAM声束或平面波. 以m = 1阶的OAM声束为例, 经过第一个DMM后, 波束将转化为平面波, 其中心处的声压将不再为零(图6(b3)). 由于当且仅当m降至0时解调端对称中心处的场强方不为零, 因此, 通过依次在每一个DMM之后的区域中直接检测中心处声强大小, 即可简便而高效地测量出发射端处具有相应阶数的OAM声束的幅值和相位信息.
2019年, Zhang和Yang[103]利用声涡旋传输的形式实现了一幅大小为256 × 256像素的标准灰度图像的传输. 在该工作中, 发射端的原理图如图7(a)所示, 每个像素被编码为8位二进制数据, 并将图像的像素独立编码为开-关键控(on-off keying, OOK)形式的OAM声载波, 每个比特占据指定的独立OAM通道. 该团队采用20个换能器组成的半径为λ的环形阵列, 以10 kHz的频率发射拓扑荷为+1到+8的多路涡旋声束, 图像数据通过多路复用的OAM声束并行传输, 并在距离发射面20个波长处的接收端, 通过方形接收阵列在一个1.5λ × 1.5λ的扫描区域进行声压场数据采集. 将所记录的幅值和相位数据与8个具有与发射OAM拓扑荷反向的OAM态进行内积, 以恢复原始信号. 他们在该工作中指出, 这种方案使频谱效率达到8 (bit/s)/Hz, 与直接的OOK调制相比, 信息传输速率提高了8倍. 若结合更多的OAM模式与先进的调制格式, 可以实现频谱效率的进一步提高. 此外, 在该工作中, 还对可用OAM信道的数目和系统的接收性能进行了系统研究, 结果发现, 可用的OAM通道的数量与发射端换能器的数量有关, 而接收性能与接收器的数量和扫描面积有关, 与布置方式无关, 分辨率越高, 覆盖范围越广, 接收性能越好.
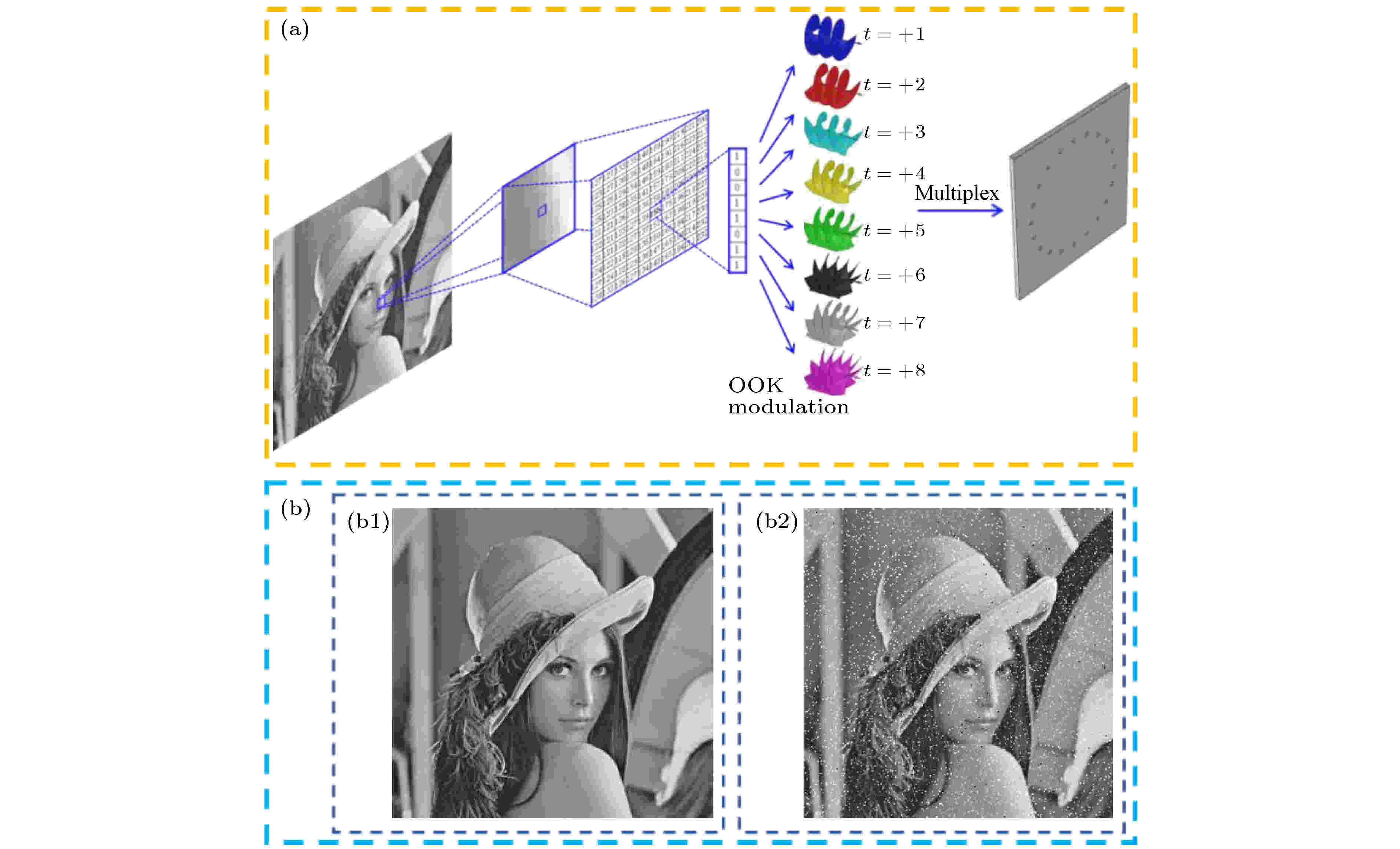图 7 (a) 水声通信系统多路复用8 OAM模式的概念示意图; (b) (b1) 通信系统传输的256 × 256像素的灰度图像lena (lena.jpg); (b2) 在20 dB信噪比下, 仅考虑加性高斯白噪声得到的接收图像[103]Figure7. (a) Notion of underwater acoustic communication system multiplexing 8 OAM topological charges; (b) (b1) the gray scale image with 256 × 256 pixels of lena (lena.jpg) to be transmitted through the communication system, (b2) the receiving image obtained at 20 dB SNR where additive white gaussian noise (AWGN) was only concerned[103].
为了实现设计结构简单、控制方便的收发信机阵列, 2020年, Li等[104]采用简化的单点收发器阵列构建了OAM声束通信的理论模型, 通过建立的环形16声源阵列实验系统, 研究了OAM声束通信原理和性能. 该方案基于相位编码技术形成拓扑荷可控的OAM声束, 通过拓扑荷调控和多OAM声束的合成, 构建同轴传输的OAM复用声束. 在接收端, 通过单环接收阵列进行声场信号的检测和OAM声束的正交解码, 成功实现了基于单环收发阵列的OAM声束通信(单环收发阵列由M个接收单元和N个发射单元组成). 然后, 该工作又模拟了对于m = 7的单OAM声束, 采用16 × 16和32 × 32的收发器阵列时的信道容量和信噪比(signal-to-noise ratio, SNR)的关系, 并将其与相应的多入多出(multiple input-multiple output, MIMO)系统进行了比较. 研究表明, OAM通信系统的信道容量随着信噪比的增大而增大. 对于相同信噪比的情况, 信道容量随收发器阵列单元数的增加而增大. 对于不同OAM态的情况, 该工作也对信道容量及SNR的关系进行了研究. 此外, 该工作还研究了单OAM, 8-OAM和14-OAM波束信道容量与SNR的关系. 在SNR为30 dB时, 8-OAM的信道容量为31.072 bit/s/Hz, 比相同情况时采用单OAM的信道容量高了15.703 bit/s/Hz, 比采用14-OAM时的信道容量低了4.01 bit/s/Hz. 结果表明, 单OAM声束的信道容量远小于多OAM声束, 且随多路声涡旋的OAM态的增加而增大. 因此, 基于OAM的声波通信可以有效增加信道容量, 同时避免了不同模式之间的串扰, 具有良好的解码稳定性. 该工作为OAM声束在通信中的阵列设计、数据传输、解码和校准提供了理论基础和技术支持, 在水声通信领域具有广阔的应用前景.
值得注意的是, 对于声学OAM通信系统的研究仍处于初级阶段, 声学OAM通信的可行性, 特别是水下声学OAM通信, 还需要进一步的实验验证. 除了固有的OAM声束发散和偏移问题外, 水下环境(水生生物, 湍流效应等)对OAM链路的影响也需要进一步研究. 目前, 大多数OAM声束相关的实验都是在实验室可控环境下进行的. 实验室之外的测试和OAM系统的实际部署应该是未来研究活动的重点.
当前研究中尽管已经初步证明了涡旋声束所蕴含的潜力, 但还远远无法满足实际应用的需求. 涡旋声束未来的成功很大程度上将依赖于OAM声束发射机、多路复用器、解复用器和接收机等系统组件的研究与开发. 然而, 当前许多与声OAM相关的实验仍然使用体积庞大且价格昂贵的组件, 这些组件不适合实际实现和大规模使用. 如何有效降低组件的成本和尺寸, 并保证其与现有技术相兼容仍旧需要深入的研究. 此外, 传播信道的状态对基于OAM的链路有很大的影响, 在一些复杂信道条件下出现的问题也需要得到解决. 总之, 目前对OAM声束的研究仍处于起步阶段, 存在着许多问题与挑战, 值得进一步深入研究和解决. 但可以预见的是, 随着研究的深入, OAM这一全新维度的引入将有助于在医学诊疗、水下通信和海洋探测等方面取得重大突破.
