摘要:对钙钛矿锰氧化物的磁性进行调控在科学上具有重要意义, 在自旋电子学领域更是有紧迫需求. 利用外延应变和铁电极化双重调控超晶格材料的磁性不但更加接近体系的真实状态, 而且能诱导出丰富的物理性质. 本文采用第一性原理计算, 系统地研究了外延应变和铁电极化对LaMnO₃/BaTiO₃超晶格磁性的鲁棒控制. 通过精确调控Mn原子磁矩的大小和方向, 实现了铁磁$\leftrightarrow$反铁磁$\leftrightarrow$亚铁磁之间的可逆转变, 同时产生了强烈的磁电耦合效应. 除此之外, 本文在超晶格中实现了铁电极化和金属性共存. 通过分析Jahn-Teller效应, 氧八面体旋转、倾斜以及体系内部电子转移对磁性的影响, 揭示了磁性调控的物理机制. 研究结果不但对系统地了解LaMnO₃体系的磁性变化具有重要意义, 而且可以为设计基于钙钛矿锰氧化物的自旋电子器件提供理论指导.
关键词: 第一性原理/
钙钛矿超晶格/
电控磁性/
界面效应

English Abstract

全文HTML

--> --> -->

传统磁存储材料是由非磁性和磁性薄层交替排列在基底材料上形成的, 不仅读写速度慢、能耗高, 而且耐热冲击性差. 不断涌现的多铁材料因为能实现较强的磁电耦合, 所以为磁存储和自旋电子器件的研发提供了一条新的道路^[1]. 令人遗憾的是, 铁磁性和铁电性在本质上是互斥的, 两者很难在单相材料中共存. 截至目前, 在单相多铁材料中实现磁性调控仍然十分困难. 人工制备的超晶格材料可以解决这一难题. 超晶格是由两种材料交替堆叠形成的^[2-4], 研究者希望组成超晶格的两种材料分别提供磁性和铁电性, 从而产生强烈的磁电耦合效应^[5,6]. 近年来, 大量的研究集中在钙钛矿氧化物材料上^[7-9], 这是因为它们可以容纳不同种类的元素, 因而具备丰富多彩的物理性质.
利用外场条件(应变、电场、压力、化学掺杂等)驱动材料产生结构变化和电子重排, 从而对材料的物理性质进行调控, 是发现新物性的有效途径^[10]. 应变可以改变二维钙钛矿氧化物的界面结构, 从而调控其物理性质. 然而, 衬底的种类有限使得很难获得任意晶格参数的外延衬底, 实验上通过外延应力调控体系的性质更是需要高质量的薄膜. 采用第一性原理计算可以让我们在原子尺度上精确的控制超晶格的结构、应力和极化, 从而克服了上述缺点. 2013年, Zhou等^[11]发现在SrMnO₃/LaMnO₃超晶格中, 当外延应变从压应变拓展到拉应变时, 体系遵循C型反铁磁→铁磁→A型反铁磁的相变规律. Zhong等^[12]发现可以通过应变驱动的氧八面体扭转来控制二维LaMnO₃(LMO)薄膜的铁磁性. Wang等^[13]在SrTiO₃表面生长了LaMnO₃薄膜. 当薄膜的厚度增大到5层时, 体系突然从非磁性结构变成磁性材料, 磁性起源于自掺杂效应.
电控磁性通常包括两种手段: 一是施加外电场, 二是利用铁电材料的自发极化. 文献[14]发现通过外加电场调控La_1–xD_xMnO₃/BaTiO₃ (D = Ca, Sr, Ba)薄膜的磁性和导电性是完全可行的. 然而, 外电场穿透材料表面后会由于静电屏蔽效应而被屏蔽掉. 事实上, 采用铁电材料的自发极化控制磁性的技术近年来得到了快速发展. 2013年, Dong和Dagotto^[15]研究了利用BaTiO₃(BTO)的铁电极化调控La_0.75Sr_0.25MnO₃薄膜的磁性, 随后被Cui等^[16]的实验证实, 磁性改变的原因是Ti原子的位移诱发了界面处的轨道重构^[17]. 截至目前, 利用铁电极化调控LaMnO₃多种性质的研究也有很多^[18-22].
找到合适的铁电体与LaMnO₃搭建超晶格十分重要, 因为本研究的目标不是单纯调控磁性, 还要实现较强的磁电耦合. BTO具备两大优点: (1)生长过程中可以承担较大的应力, 有利于其他材料在BTO上的生长^[23,24]; (2)与PbTiO₃相比, BTO的自发极化高达27 μC/cm^2[25], 无毒性而且极化强度可以通过Sr/Ca部分替换Ba等手段进一步增强^[26]. 在实验制备的“铁磁/铁电”超晶格中, 外延应变造成的晶格失配、对称性失配引起的氧八面体耦合、铁电极化诱导的反演对称性破缺以及衬底引入的氧缺陷往往同时存在^[27-29]. 将铁电极化和外延应变结合起来, 不但更接近体系的真实情况, 而且更可能诱导出新物理现象.
目前关于LMO薄膜磁性的实验和理论结果并不统一, 特别是对LaMnO₃/BaTiO₃超晶格磁性的调控、磁电耦合以及背后的物理机制仍不清楚. 再考虑到实验制备的LMO/BTO超晶格中往往同时存在应变、极化、氧空位等影响磁性的因素. 同时考虑双轴应变和铁电极化对体系的影响, 可以更好地模拟超晶格的真实状态, 也更容易诱导出丰富的物理性质. 因此, 本文采用第一性原理方法, 通过双轴方向微调晶格参数的方法引入外延应变(包括拉应变和压应变), 从LMO/BTO超晶格的结构入手考查铁电极化和外延应变对LMO薄层的界面重构和电子重组的影响, 系统地研究电控磁性和磁电耦合效应的微观物理机制.

本文的研究是在密度泛函理论框架下用第一性原理计算完成的, 结合了投影缀加波(PAW)方法和广义梯度近似下的Perdew-Burke-Ernzerhof (PBE)交换关联泛函^[30]. 采用在位(on-site)库仑相互作用下的Liechtenstein方案^[31]处理Mn的3d轨道, 合适的U和J值分别是2.7和1.0 eV^[32]. La元素的4f轨道本身就离费米能级较远, 因此不需要在4f轨道上加U. 平面波截断能量是500 eV, 各原子的价电子设置为La-5s²5p⁶5d¹6s², Mn-3p⁶3d⁵4s², Ba-5s²5p⁶6s², Ti-3p⁶3d²4s²和O-2s²sp⁴. 结构优化和电子结构计算需要的Monkhorst-Pack k点分别是5 × 5 × 1和11 × 11 × 1, 采用BFGS方法对所有原子的内坐标进行弛豫^[33]. 能量收敛精度设定为10^–5 eV, 施加在各个原子上的Hellmann-Feynman力小于0.1 eV/nm. 由于没有找到LaMnO₃/BaTiO₃超晶格的实验值, 文献[21]中对LaMnO₃块材的晶胞常数、磁序、Mn原子的磁矩和带隙进行了计算, 结果与实验值符合的很好.
如图1所示, 超晶格是由LaMnO₃和BaTiO₃沿着z轴交替堆叠而成的. 因为足够厚的BTO才具有较强的铁电极化, 所以选择四层BTO晶胞. 又因为铁磁层(图1中9—12层)的厚度应当较薄才能使铁电极化P有效穿透铁磁层, 所以构建了单层的LMO薄层. 本文考虑了两种极性界面: 由TiO₂-LaO-MnO₂层构成的n型界面和TiO₂-BaO-MnO₂层构成p型界面^[15], 极化的方向(±P)在图1中给出. 在xy平面内对超晶格进行$\sqrt 2 \times \sqrt 2 $扩胞是为了使LMO层包含4个Mn离子, 这样可以更好的描述反铁磁序. 外延应变(–3%—3%)是指对面内晶格常数的应变. 保持对称性并固定晶胞参数a和b不变, 对晶胞参数c和原子内坐标进行优化. 通过对超晶格进行这样的约束性结构优化可以引入应变.
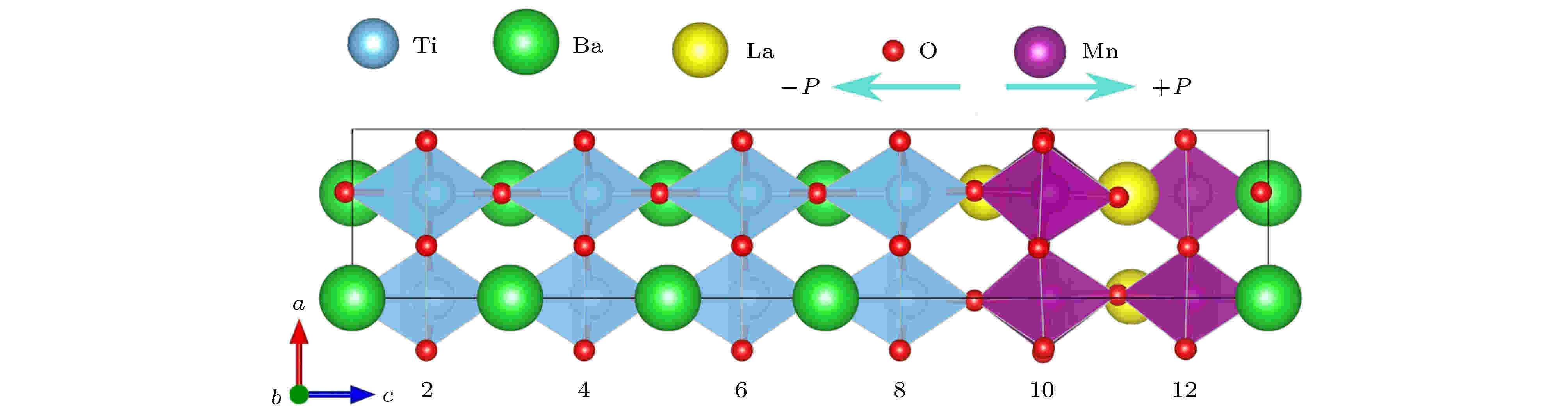图 1 LaMnO₃/BaTiO₃超晶格的结构示意图(± P铁电极化的方向如箭头所示)
Figure1. Schematic structure of the LaMnO₃/BaTiO₃ superlattice. (The arrows denote the directions of ferroelectric polarization).

图2给出了LMO/BTO超晶格的磁序和能量随着外延应变和铁电极化的变化示意图. 图中蓝色(红色)原子代表自旋向上(向下)的Mn原子. 极化和应变的双重调控使得体系实现了铁磁$ \leftrightarrow $反铁磁$ \leftrightarrow $亚铁磁之间的可逆转变, 同时伴随着超晶格导电性的改变(见表1), 进而丰富了LaMnO₃材料的相图. 从图2(o)中可以看到, 较小的外延应变对应的能量较低, 体系更稳定. 值得关注的是, 当极化翻转时, –3%[图2(a)和2(h)]和3%应变[图2(g)和2(n)]对应的超晶格分别出现了FiM2型亚铁磁→FM以及FM→A-AFM之间的转变. 下面将以这两种情况为例分析引起磁性变化的原因.

应变	极化	磁序	m1	m2	M	导电性	θ1	θ2	φ1	φ2	Q2	Q3
—	+	FM	3.56	3.56	14.65	金属	5.7	6.6	4.4	5.3	0.0015	0.0259
—	–	FiM2	3.38	–3.76	6.41	金属	6.5	7.8	5.1	7.1	0.0017	0.0172
—	+	FiM2	3.41	–3.86	6.34	金属	7.2	8.2	4.5	6.9	0.0016	0.0198
—	–	FM	3.59	3.59	14.76	金属	7.5	8.7	5.3	7.8	0.0026	0.0199
—	+	FiM1	3.60	–3.72	6.78	金属	8.8	10.0	3.9	6.9	0.0019	0.0229
—	–	FiM3	3.55	–3.59	7.20	半金属	9.3	10.4	4.1	5.8	–0.0007	0.0347
0	+	A-AFM	3.24	–3.55	—	金属	1.7	1.2	11.7	1.2	0.0010	0.0139
0	–	FM	3.67	3.67	15.28	半金属	7.1	9.1	9.3	0.8	0.0047	0.0042
1%	+	A-AFM	3.66	–3.68	—	金属	9.3	9.9	7.5	6.4	0.0449	0.0272
1%	–	A-AFM	3.46	–3.92	—	半金属	11.5	12.4	4.4	8.0	0.0071	0.0286
2%	+	G-AFM	3.31	–3.95	—	绝缘体	11.9	11.1	6.1	7.0	0.0507	0.0165
2%	–	FiM4	-3.78	3.66	7.24	半金属	12.5	11.1	3.3	8.8	0.0013	0.0114
3%	+	A-AFM	3.71	–3.72	—	绝缘体	12.2	12.2	6.3	7.4	–1.0308	0.0967
3%	–	FM	3.75	3.75	15.17	半金属	13.7	13.3	5.0	8.9	0.0208	0.0324

表1计算得到的LaMnO₃/BaTiO₃超晶格的基态性质: m₁和m₂ (μ_B)是Mn原子的平均磁矩, M (μ_B)是超晶格的净磁化强度, 导电性, LaMnO₃层的Jahn-Teller畸变Q₂, Q₃(nm), 氧八面体倾斜角θ和旋转角φ
Table1.The calculated ground-state properties of the LaMnO₃/BaTiO₃ superlattice at different strains: m₁ and m₂ (μ_B) are the local magnetic moment for the Mn atoms, M (μ_B) is the net magnetization, the conductivity, the Jahn-Teller distortions Q₂, Q₃ (nm), the octahedral tilt angle θ and rotation angle φ (degree) of the LaMnO₃ layers.

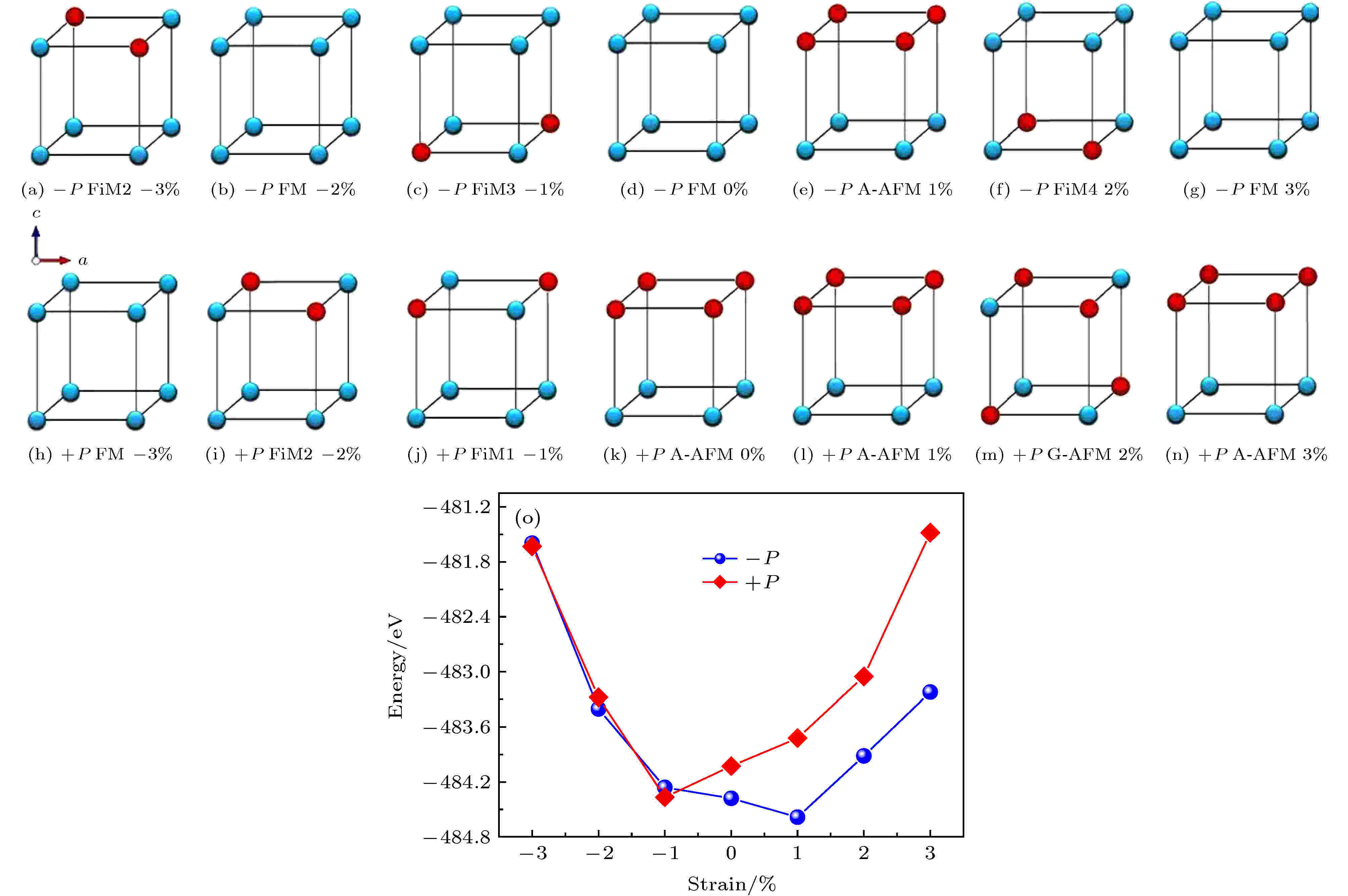图 2 (a)?(n) LaMnO₃/BaTiO₃超晶格的磁序随着外延应变(–3%?3%)和极化方向的变化示意图 (蓝色代表自旋向上的Mn原子, 红色代表自旋向下的Mn原子); (o) 不同应变对应的最稳定结构的能量
Figure2. (a)?(n) Schematic diagram of the magnetic configuration variation with the epitaxial strain (–3%?3%) and the direction of ferroelectric polarization in the LaMnO₃/BaTiO₃ superlattices (The blue and red balls represent the spin-up and spin-down Mn atoms, respectively); (o) the total energies of the ground-state superlattices under different strains.

构建了11种铁磁、反铁磁和亚铁磁结构的LMO/BTO超晶格, 通过优化得到最低能量的磁结构. 表1中给出了不同外延应变(–3%—3%)和 ±P极化下超晶格的性质. m₁和m₂是4个Mn的平均磁矩(铁磁), 或者分别代表两个自旋向上和两个自旋向下的Mn原子的平均磁矩(反铁磁), 或者分别表示3个自旋向上Mn的平均磁矩和1个自旋向下Mn的磁矩(亚铁磁). 2008年, Ciucivara等^[34]采用第一性原理方法研究了(LaMnO₃)_4.5/(BaTiO₃)_4.5超晶格的磁性, 但没有考虑应变的影响. 本文计算得到的无应变时超晶格的晶胞常数a = b ＝ 0.5641 nm和Mn原子的平均磁矩m = 3.64 μ_B与他们的结果(a = b ＝ 0.5650 nm, m = 3.82 μ_B)符合得很好.
在不同的外延应变条件下, 极化对体系磁序的影响截然不同. 压应变时体系出现亚铁磁和铁磁态, 拉应变则主要呈现出A型和G型反铁磁态. 从压应变到拉应变过程中, 体系从金属逐渐转变成绝缘体(或半金属), 但Mn原子的磁矩变化不大. A-和G-AFM的净磁化强度M不为零, 一是因为极化破坏了体系的反演对称性, 二是与计算时选取的Wigner-Seitz半径的大小有关. 当外延应变为1%时, 体系始终保持A-AFM不变, 此时的超晶格可以当作磁性存储器的衬底材料使用. 当外延应变固定为0和3%时, 极化从+P翻转到－P导致体系净磁化强度的变化量都是100.1%. 我们精确控制了Mn原子的磁矩大小和方向, 从而调控了净磁化强度.
Jahn-Teller畸变可以这样描述^[35]: ${Q_2} \!=\! \left( {1/\sqrt 2 } \right) \left( {{X_1} - {X_4} - {Y_2} + {Y_5}} \right)$, ${Q_3} = \left( {1/\sqrt 6 } \right)( 2{Z_3} \!-\! 2{Z_6} \!-\! {X_1} \!+ {X_4} - {Y_2} + {Y_5} )$, 其中X, Y和Z分别代表周边6个氧原子的坐标. LaMnO₃块材的Q₂和Q₃畸变值分别是0.0074和0.0413 nm^[35]. 与块材相比, LMO/BTO超晶格的Jahn-Teller畸变显著减小. 从表1中可以看到, 3%外延应变产生的畸变是最显著的. 除了Jahn-Teller效应之外, 还有两个重要物理量必须予以考虑, 即MnO₆八面体的旋转角φ和倾斜角θ. 它们是这样定义的: θ ＝ (180°－Θ)/2, 其中Θ代表Mn—O—Mn键沿着z轴方向的键角^[36]. xy平面内的旋转角φ ＝ (90°－Ω)/2, 其中Ω代表两个相连的氧八面体在xy平面内的3个氧原子构成的夹角^[37]. φ₁和θ₁(φ₂和θ₂)分别是图1中9—11层(11—13层)的MnO₆八面体的旋转角和倾斜角. 可以看到, 压应变对应的旋转角和倾斜角差别不大. 当压应变过渡到拉应变时, 倾斜成了氧八面体的主要运动方式, 旋转角仍然变化不大. θ逐渐增大表明Mn-O-Mn键角逐渐偏离180°, 有利于反铁磁态的形成. 需要说明的是, 无论是氧八面体旋转和倾斜, 还是Jahn-Teller畸变都不是超晶格磁性改变的主要原因.
图3给出了LMO/BTO超晶格在–3%外延应变和 ± P极化时的总态密度, 分层态密度和La/Mn/O原子的分波态密度. 从图3(a)和(b)中可以看到, 总态密度都呈现出金属性. BTO层和LMO层都是导电的. 四层BTO的态密度体现出明显的对称特性, 表明BTO中的Ti原子是无磁性的. 自旋向上和自旋向下的态密度不对称说明超晶格中存在自旋极化现象, 自旋极化的大小可以用自旋极化率P_S描述. 自旋极化率的定义是${P_{\rm{S}}} = \big| [{N_{\rm{up}}}({E_{\rm{F}}}) - {N_{\rm{dn}}}({E_{\rm{F}}})]/[{N_{\rm{up} }}({E_{\rm{F}}}) \!\!+\!\! {N_{\rm{dn}}}({E_{\rm{F}}})] \big|$, 其中${N_{\rm{up}}}({E_{\rm{F}}})$和${N_{\rm{dn}}}({E_{\rm{F}}})$分别是自旋向上和向下时费米能级处的态密度^[38]. –P和+P极化对应的P_S分别是58.7%和0.5%, 这表明铁电极化对自旋极化率的调控相当明显.
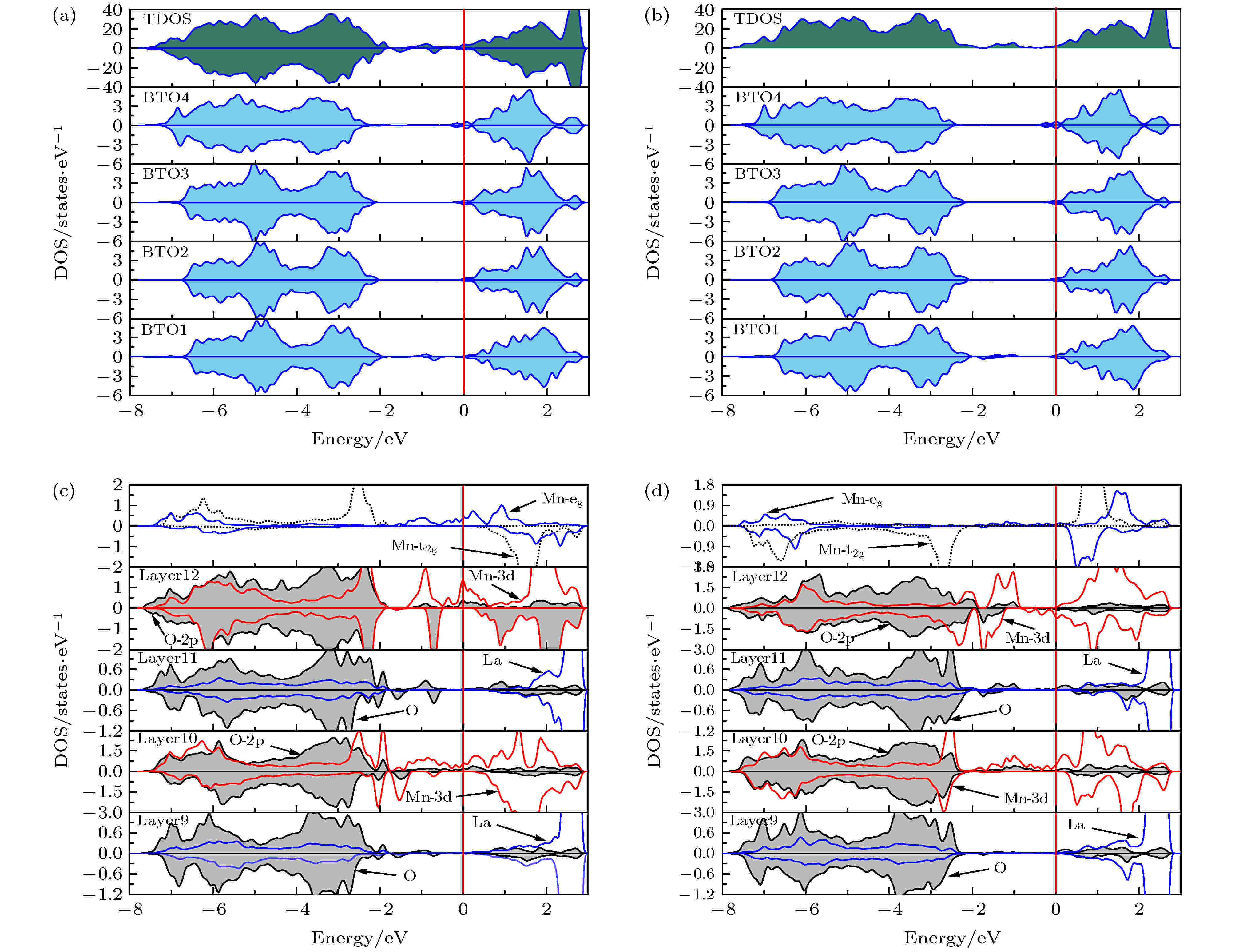图 3 LaMnO₃/BaTiO₃超晶格的态密度:　(a)–P极化和–3%外延应变时的总态密度和BaTiO₃层的分层态密度; (b) +P极化和–3%外延应变时的总态密度和BaTiO₃层的分层态密度; (c)–P极化和–3%外延应变以及(d) +P极化和–3%外延应变时的LaMnO₃层的分层态密度和Mn原子的e_g/t_2g轨道的态密度
Figure3. The total density of states (TDOS) and layer-resolved DOS of the BaTiO₃ part of the LaMnO₃/BaTiO₃ superlattice: (a) for the –P case with –3% epitaxial strain; (b) for the +P case with –3% strain. The Mn-e_g/t_2g DOS and the layer-resolved DOS of the LaMnO₃ part (c) for the –P case with –3% epitaxial strain; (d) for the +P case with –3% strain.

由图3(c)和3(d)可知, 费米能级处的态密度主要是由Mn-3d轨道贡献的. LMO层的价带态密度集中在–7到–2 eV区间内, 主要是Mn和O原子的贡献. 导带则主要是La和Mn的贡献. Mn-3d轨道在八面体晶体场中会劈裂成非局域化的e_g和t_2g两部分, e_g和t_2g轨道与O-2p轨道之间都存在强烈的轨道杂化. 它们都是部分占据的, 表明体系中同时存在双交换和超交换作用. 当铁电极化从–P翻转到＋P时, 第10层(12层)的Mn-3d的自旋向上和向下通道的态密度之差减小(增大), 导致该层Mn原子的磁矩减小(增大), 与表1的结论一致.
图4给出的3%应变下超晶格的态密度(DOS)与图3给出的–3%应变下的态密度很相似, 但也有区别. 从图4(a)中可以看到, 费米能级处的总态密度呈现出明显的半金属特性. 当极化变为+P时(图4(b), 带隙出现表示超晶格是绝缘体. 由图4(a)和4(c)可知, 当极化为–P时BTO层和LaO层都是不导电的, 只有MnO₂层的自旋向上通道出现了显著的半金属特性. 超晶格中存在金属性的LMO层, 电子无法沿着z轴方向穿透不导电的BTO区域. 图4(c)是铁磁序对应的态密度, 两个MnO₂层的DOS比较相似, 图4(d)代表的反铁磁序的第10层和第12层的DOS却明显不同. –P极化时价带的Mn-O相互作用主要集中在–3到–1 eV区间内, +P时则拓展到–7到–1 eV区间. 当极化从–P翻转到+P时, 价带态密度的范围变大, 表明Mn-O轨道杂化更强烈. 超晶格的半金属性主要是由Mn原子贡献的. 归其本质半金属性是由界面处的电荷不平衡造成的, 由于TiO₂层不再提供电子导致MnO₂层的电子数减少. 当铁电极化从–P翻转到+P时[图4(b)和4(d)], LMO和BTO层都不导电, 费米能级向高能量区移动, 破坏了半金属性. 体系的自旋极化率从100%变为0%, 还伴随着金属-绝缘体相变. 值得注意的是, BTO具有较强的铁电极化, 仅仅两层的MnO₂导电层不足以屏蔽铁电极化, BTO的面外极化仍然可以有效穿透整个LMO区域. 当极化由–P翻转为+P时, 体系从A-AFM变为FM, 净磁化强度的改变量为100.1%, 证实本文能实现对LMO/BTO超晶格磁性的有效调控.
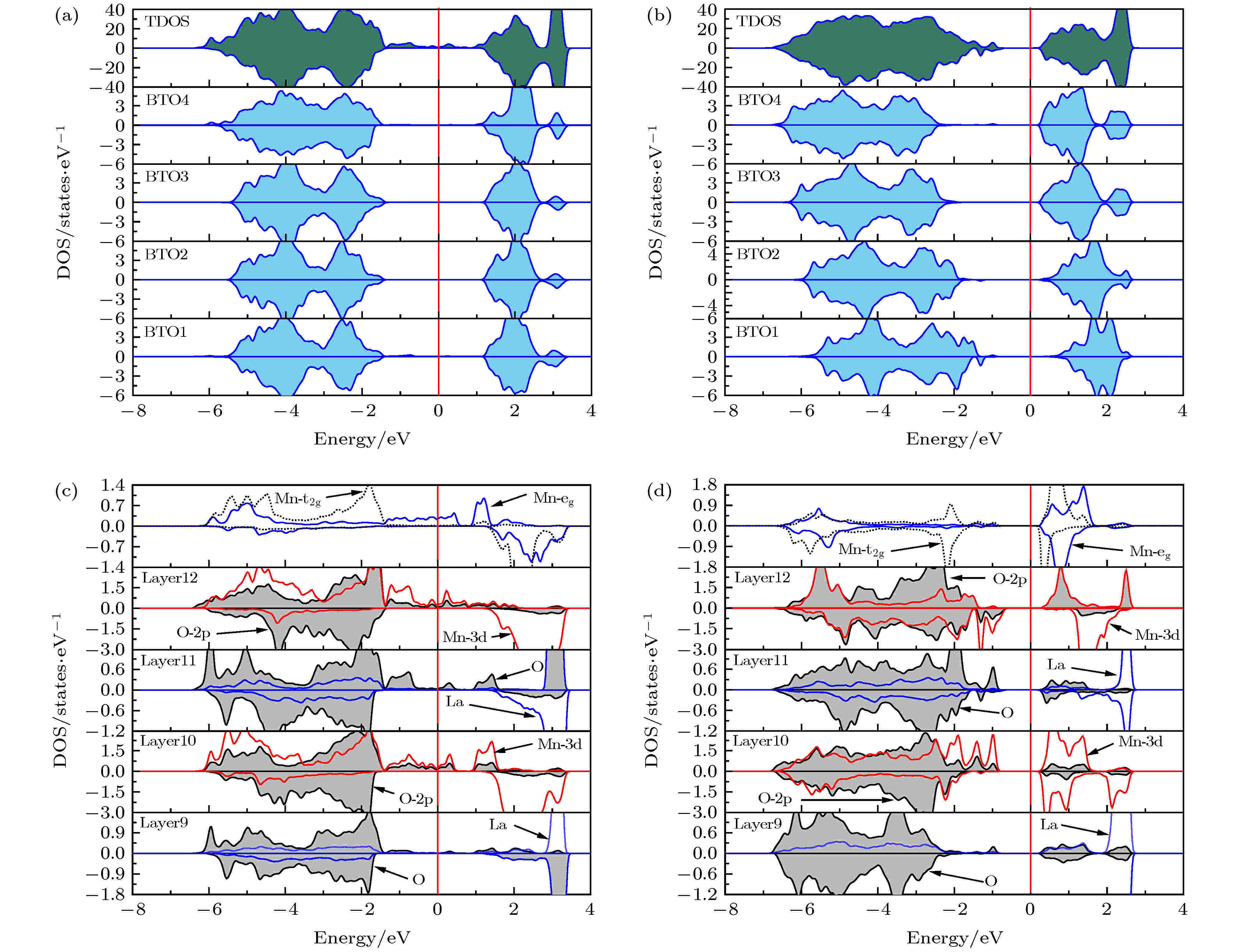图 4 LaMnO₃/BaTiO₃超晶格的态密度:　(a) –P极化和3%外延应变时的总态密度和BaTiO₃层的分层态密度; (b) +P极化和3%外延应变时的总态密度和BaTiO₃层的分层态密度; (c) –P极化和3%外延应变以及(d) +P极化和3%外延应变时的LaMnO₃层的分层态密度和Mn原子的e_g/t_2g轨道的态密度
Figure4. The total density of states (TDOS) and layer-resolved DOS of the BaTiO₃ part of the LaMnO₃/BaTiO₃ superlattice: (a) for the –P case with 3% epitaxial strain; (b) for the +P case with 3% strain. The Mn-e_g/t_{2 g} DOS and the layer-resolved DOS of the LaMnO₃ part (c) for the –P case with 3% strain; (d) for the +P case with 3% strain.

图5给出了LMO/BTO超晶格的差分电荷密度, 图中黄色区域代表电荷的聚集, 蓝色区域代表电荷的耗散. 电荷主要聚集在TiO₂/LaO界面处的O原子附近, 转移的电荷是由界面处的Ti原子和4个Mn原子贡献的. La/Ba原子与其他原子之间的电荷转移不明显. 铁电极化从–P变为+P或者外延应变从–3%变成3%都会使体系的原子间距增大, 从而导致电荷转移减少. 很明显Mn-Mn和Mn-Ti之间的相互作用都是通过O离子实现的. 同层的Mn原子和O原子之间的电子云出现少量重叠, 而且Mn原子周围的电子云具有明显的方向性, 故两者之间形成了包含离子键成分的共价键. 从图5中可以看到两个明显特征: (1)第10层和第12层的Mn原子的差分电荷密度不相同, 因为它们的周边原子环境不同; (2)当外延应变固定而极化从–P变为+P时, z轴方向的蓝色区域增大表明Mn-${\rm{d}}_{z^2}$轨道失去更多的电子, Mn-t_2g轨道得到电子.
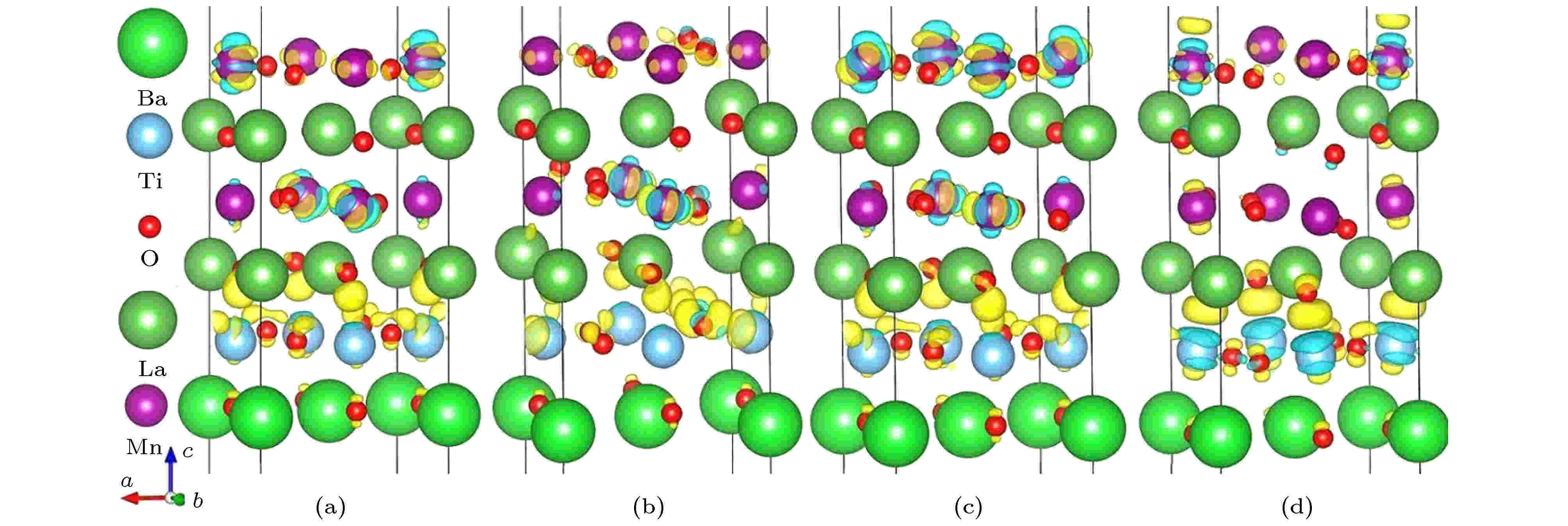图 5 LaMnO₃/BaTiO₃超晶格在　(a) –P极化和–3%外延应变; (b) –P极化和3%外延应变; (c) +P极化和–3%外延应变和(d) +P极化和3%外延应变条件下的差分电荷密度图(等值面的数值为0.01 e/bohr³)
Figure5. Charge density difference of the LaMnO₃/BaTiO₃ superlattices for the (a) –P polarization and –3% epitaxial strain; (b) –P polarization and 3% strain; (c) +P polarization and –3% strain; and (d) +P polarization and 3% strain. The isosurface value is set to be 0.01 e/bohr³.

在氧八面体晶体场中, Mn原子的3d轨道会劈裂为能量较高的e_g轨道(${\rm{d}}_{z^2} $, ${\rm{d}}_{x^2-y^2}$)和能量较低的t_2g轨道(d_xy, d_yz, d_xz) ^[39]. 铁电极化又造成了e_g轨道和t_2g轨道的进一步退简并. 研究发现极化和外延应变会影响BTO层和LMO层之间的电子转移, 但Mn-3d轨道的电子数基本不变, 说明BTO和LMO之间的电子转移不是影响体系磁性的主要原因. 在表1呈现研究了超晶格的氧八面体旋转、倾斜和Jahn-Teller效应, 发现这些都不是体系磁性变化的主要原因. 影响体系磁性的主要原因是极化翻转造成的e_g轨道和t_2g轨道之间的电子转移.
当极化为+P时, 外延应变由负到正的过程使得体系从FM磁序变成A-AFM磁序. 当外延应变固定为–3%(0/3%)时, 极化从–P变为+P导致e_g轨道向t_2g轨道转移了0.1(0.15/0.22)个电子(表2). 我们发现电子转移较少(≤ 0.1 e)会导致体系的FM/FiM磁序趋于稳定, 而电子转移较多(> 0.1 e)时, 体系的AFM磁序更加稳定. 但是, 这一结论仍需实验验证. 2009年, Aruta等^[40]采用磁圆二色性技术观察到(SrMnO₃)_n/(LaMnO₃)_2n超晶格的AFM→FM相变, 磁性变化的原因是Mn-e_g轨道(${\rm{d}}_{z^2}$, ${\rm{d}}_{x^2-y^2} $)内部的电子转移.

应变	极化	磁序	eg轨道	t2g轨道	3d轨道
–3%	–P	FiM2	1.77	3.15	4.92
	+P	FM	1.68	3.26	4.94
0	–P	FM	1.91	3.03	4.94
	+P	A-AFM	1.75	3.16	4.91
3%	–P	FM	1.80	3.02	4.81
	+P	A-AFM	1.60	3.26	4.87

表2不同外延应变和极化条件下LaMnO₃/BaTiO₃超晶格的Mn-3d轨道(含e_g和t_2g)的电子数
Table2.Number of electrons for the Mn-3d orbitals (both e_g and t_2g) in the LaMnO₃/BaTiO₃ superlattice at different conditions.

另外, 本文还计算了体系的磁电耦合系数α_S. 磁电耦合系数的计算公式是μ₀ΔM = α_SE^[41], μ₀是真空中的磁导率, ΔM是极化从–P变成+P时体系净磁化强度的变化量, E是BaTiO₃的矫顽电场, 数值为100 kV/cm^[42]. 由此计算得到的–3%(+3%)应变对应的LMO/BTO超晶格的磁电耦合系数α_S ≈ 3.21 × 10^–9(5.23 × 10^–9) Gcm²/V. +3%应变下体系的α_S增大是因为出现了反铁磁到铁磁的相变, ΔM的变化较大. 与Sr₂CoMoO₆/BaTiO₃^[42]和Fe/PbTiO₃^[43]体系相比, 本文计算的α_S明显高于文献[42-43]证实超晶格中存在相对较强的磁电耦合效应.

调控铁磁材料的磁性并产生强的磁电耦合仍是具有挑战性的课题. 本文构建了LaMnO₃/BaTiO₃超晶格, 并实现了铁电极化和外延应变对磁性的双重调控. 研究发现, 极化和应变可以单独或共同控制超晶格的磁序和净磁化强度, 并实现较强的磁电耦合. 双重调控使体系实现了铁磁$ \leftrightarrow $反铁磁$ \leftrightarrow $亚铁磁之间的可逆转变, 同时伴随着导电性的变化. 通过精确控制Mn原子磁矩的大小和方向, 超晶格净磁化强度的变化达到100.1%, 超过了前人报道的最大值93.9%. 3%外延应变诱导出金属性的LMO层, –3%应变时出现了铁电极化与金属性共存的“铁电金属”现象. Mn-O和La-O共价键不构成铁电极化穿透LMO层的障碍. 本文全面分析了Jahn-Teller畸变, 氧八面体倾斜、旋转和超晶格内部的电子转移对磁性的影响. 电控磁性的物理机制是: 在不同应变条件下, 铁电极化的翻转导致e_g轨道和t_2g轨道之间出现电子转移, 从而决定了体系的磁性. 本文的研究结果有利于拓展钙钛矿锰氧化物在自旋电子学和低功耗磁存储领域的应用.