摘要:铁电材料因其具有可被外场调控的电极化状态, 以及在传感器、光电器件和信息存储器件中具有潜在应用前景, 所以一直以来都是凝聚态物理领域的研究热点. 随着微电子集成技术的飞速发展, 电子器件日益趋于微型化、集成化和多功能化. 传统块体铁电材料因受尺寸效应、界面效应等因素影响, 难以满足此发展需求, 因而低维铁电材料引起了学术界的广泛关注. 近年来, 实验上已成功制备出稳定的室温二维铁电材料, 第一性原理计算等理论方法对新材料的预测和设计也促进了二维铁电材料的发展. 同时, 利用二维铁电性与铁谷性、磁性的多铁耦合效应, 可以实现电控谷极化、电控磁性等调控机制. 多重自由度的相互耦合, 会产生如能谷间圆(线)偏振光学选择性、量子自旋霍尔效应等奇异物理特性, 对于自旋电子学、谷电子学及光学的发展具有重大的意义. 本文首先介绍近年来新型二维铁电材料在理论和实验方面的研究进展, 以及二维铁电材料在铁电隧道结、铁电二极管等二维铁电器件中的应用. 其次阐述了二维电控铁谷性和电控磁性的多铁耦合效应及其衍生出的新物理现象和机制. 最后对二维铁电材料和其他物理性质耦合所具有的丰富物理内涵和广阔应用前景, 进行了分析与探讨.
关键词: 二维铁电材料/
二维铁电器件/
多铁耦合/
第一性原理计算

English Abstract

全文HTML

--> --> -->

铁电材料是一类在居里温度以下具有非易失性铁电畴的功能材料. 铁电材料中存在能量简并、结构对称性等价的不同极化态, 利用外加电场的手段可实现不同极化态之间的相互切换. 基于此特性, 其可被设计成逻辑单元, 从而实现信息存储. 此外, 铁电材料因空间反演对称性破缺和内建电场的存在, 兼具光电效应、压电效应及热释电效应等物理特性, 被广泛应用在铁电场效应晶体管、铁电隧道结(ferroelectric tunnel junction, FTJ)、传感器、光电器件等功能器件中^[1-6]. 铁电元件一直以来都具有小型化、高度集成化的发展趋势, 因此低维纳米尺度的铁电材料是新型功能材料领域的研究热点^[7-9]. 在过去的十几年里, 由于薄膜制备工艺的日渐成熟, 大量探究低维铁电性的工作陆续展开. 在PbTiO₃^[10,11], BaTiO₃^[12,13], BiFeO₃^[14,15]等薄膜材料中低维铁电性均被证明存在, 这些研究结果突破了传统理论上的临界尺寸效应^[16,17]对于低维铁电性的限制, 具有重大意义. 然而, 一些有害的界面效应^[18]会对纳米尺度薄膜中低维铁电性的稳定存在产生严重影响, 这在一定程度上限制了传统铁电材料在高速微型化铁电元器件中的应用.
自从石墨烯被成功制备以来^[19,20], 石墨烯因蕴含量子霍尔效应、超高载流子迁移率、超高透光率等优异电学及光学性质而备受瞩目, 同时二维材料的研究热潮也开始兴起. 近年来, 理论方面和实验方面对二维铁电性的研究都取得了诸多进展^[21-23], 原子厚度的二维铁电材料有望被用于微型化铁电元器件的制造中. 此外, 二维铁电性与铁谷性、磁性之间的多铁耦合效应, 使得电控谷极化和电控磁性成为可能的同时, 也产生了很多奇异的物理现象. 这不仅拓宽了二维铁电材料在纳米器件中的应用, 也为自旋电子学、谷电子学及光学等研究领域的发展提供了一个优质的平台. 本文将介绍二维铁电材料研究的最新进展: 首先对具有不同电偶极矩表现形式的新型本征二维铁电材料及相关的铁电功能器件作简要介绍, 随后介绍基于二维铁电材料的电控铁谷性和电控磁性的多铁耦合效应, 最后充分挖掘二维铁电材料和其他物理性质之间的耦合, 并简要展望其未来的发展趋势.

2

-->

2.1.本征型二维铁电材料

依据铁电性来源不同, 二维铁电材料可分为诱导型与本征型. 诱导型二维铁电材料主要是通过化学基团的表面吸附、层间原子插入等特殊手段来产生铁电性^[24-27]. 本征型二维铁电材料中的自发铁电极化则来源于材料自身的结构对称性. 实验上获取本征型二维铁电材料的方法主要有: 通过机械剥离法、液相剥离法等方法从层状块体材料中剥离出二维铁电材料; 利用分子束外延法或化学气相沉积法制备理论上已预测的二维铁电材料. 与诱导型二维铁电材料相比, 本征型二维铁电材料的制备更为简易. 根据电偶极矩的不同表现形式, 本征型二维铁电材料可分为三种类型: 面外极化型二维铁电材料、面内极化型二维铁电材料及同时具有面内、面外极化型二维铁电材料.
具有面外极化的二维铁电材料, 可施加垂直方向的电场来实现铁电极化的反转, 因此极具研究价值. 2014年, Shirodkar和Waghmare^[28]从理论上预测1T-MoS₂具有垂直方向的铁电极化, 1T-MoS₂单层中Mo原子三聚化畸变的产生是由不稳定的K₃光学模导致的. 随着从c1T相转变为d1T相时, 即由中心对称的结构转变成空间反演对称性破缺的结构时, 1T-MoS₂产生了垂直于平面方向的极化, 因此极化模和结构畸变间的非线性耦合作用是该材料产生垂直极化的原因. 近年来, 通过理论和实验研究的结合, d1T-MoTe₂在室温下的垂直铁电性已经得到证实^[29]. 2015年, Belianinov等^[30]报道了层状CuInP₂S₆ (CIPS)材料的室温铁电性, 他们在厚度大于100 nm的CIPS薄片中观测到了清晰的铁电畴和较为明显的电滞回线, 并发现通过外加电场的手段能实现铁电极化的反转. 然而当CIPS薄片厚度降到50 nm时, 受退极化场等因素影响, 铁电极化会消失. 这项工作证实了铁电极化在层状CIPS中存在, 对于进一步深入探索极限原子厚度铁电材料具有启发作用. 2016年, Liu等^[31]在室温下探测到4 nm CIPS薄片的面外铁电极化, 该二维薄片的铁电相变温度约为320 K. CIPS结构侧视图如图1(a)所示, Cu离子和In离子分别在垂直于平面的方向上发生反向位移, 打破了空间反演对称性, 导致自发极化的产生. 该室温面外极化型二维本征铁电材料的发现, 丰富了二维铁电材料的种类, 为新型二维铁电器件的制备开辟了新机会. 2017年, Xu等^[32]利用第一性原理预测了与CIPS同属过渡金属磷酸盐家族的单层AgBiP₂Se₆具有面外铁电极化. 2018年, 双层或三层的拓扑半金属WTe₂被证明存在可被栅极电压调控的自发面外极化^[33]. 如图1(b)所示, 单层的WTe₂具有中心反演对称, 因此是非极性结构. 然而双层和三层的WTe₂结构中由于存在垂直方向的电偶极矩, 从而具有自发的面外铁电极化. 电极化强度可由石墨烯作为电场传感器进行直接测量. 此外, 铁电相WTe₂的居里温度高于350 K, 这使得其铁电极化态能在室温下稳定存在.
图 1 (a) CIPS晶体结构侧视图^[31]; (b) 三维层状1 T′WTe₂的结构示意图^[33]
Figure1. (a) The side view of CuInP₂S₆ (CIPS)^[31]; (b) structure of three-dimensional 1 T′WTe₂^[33].

除了上述具有面外极化的二维铁电材料, 面内极化型的二维铁电材料同样也引起了研究人员的极大兴趣. 在2016年, 多项理论研究工作预言了第Ⅳ主族单硫属化合物MX (M = Ge, Sn; X = S, Se)单层具有稳定的面内极化^[34-36]. 如图2(a)所示, MX具有类似黑磷的正交型结构. 图2(b)表明该体系铁电性的产生是由于阴阳离子具有相对的平面内位移, 从而打破了空间反演对称性. 与此同时, Chang等^[37]利用分子束外延技术成功制备出性能稳定的高质量SnTe薄膜, 并通过研究畴结构、晶格畸变、能带弯曲、电场调控铁电畴反转等现象证明了铁电性在SnTe薄膜中的存在. 单原子厚度SnTe的居里温度高达270 K, 相比于体材料的居里温度98 K有极大提高. 薄膜SnTe作为一种具有较高居里温度的二维铁电材料, 在实现非易失性高密度存储器、纳米级传感器等器件应用方面极具潜力. 2018年, Liu等^[38]利用第一性原理预测了SbN和BiP这两种室温二维新铁电材料. 其中, SbN的面内铁电极化强度高达7.81 × 10^–10 C/m, 是目前发现的具有最大面内自发极化强度的二维铁电材料.
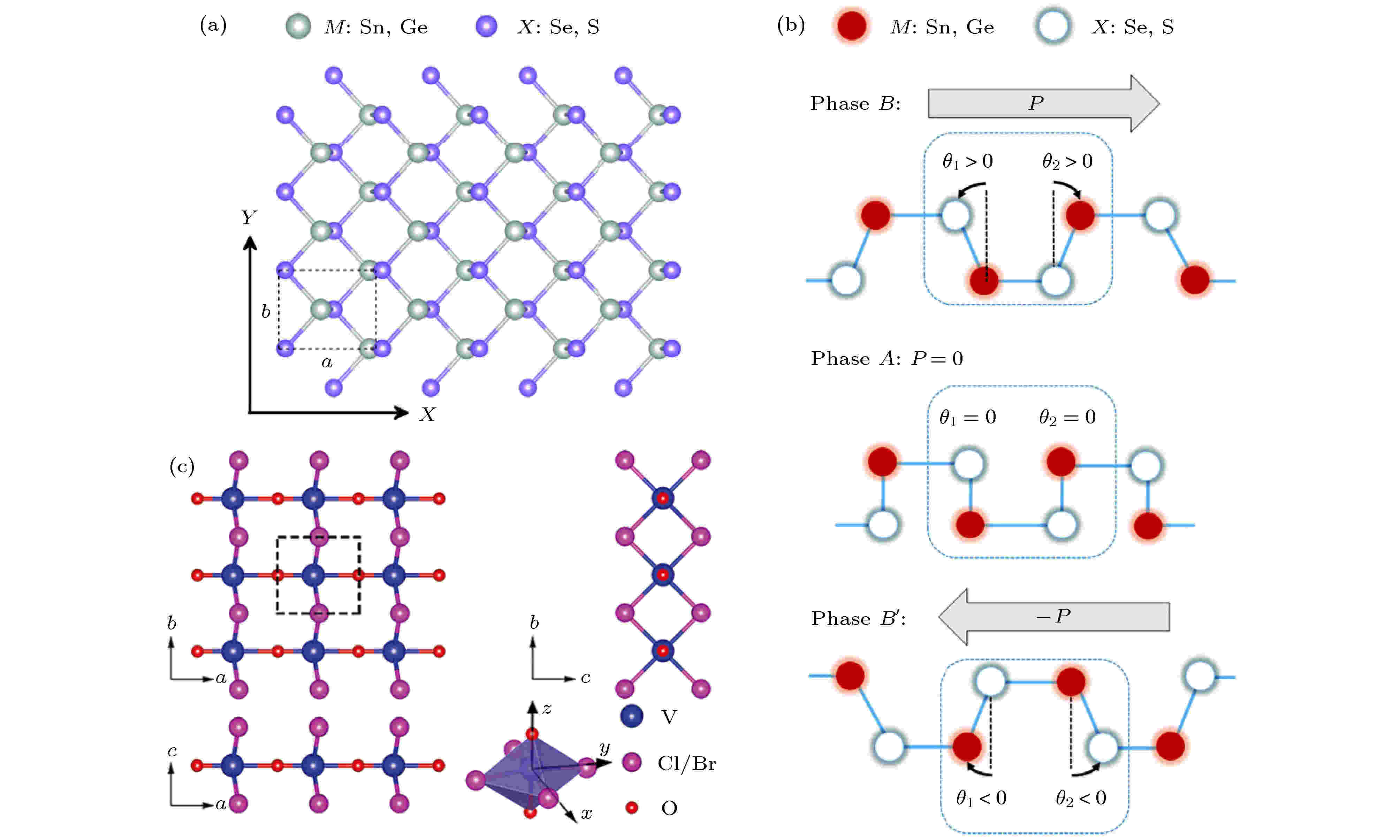图 2 (a) 单层第Ⅳ主族单硫属化合物MX铁电相结构俯视图; (b) 两个等价的极性相B和B′及高对称性非极性相A的侧视图^[34]; (c) VOCl₂单层结构的俯视图及侧视图^[40]
Figure2. (a) Top view of the structure of monolayer group-IV monochalcogenides; (b) the schematic side views of the two distorted degenerate polar structures (B and B′) and the high symmetry nonpolar phase (A)^[34]; (c) the top view along the vertical direction and side views of the VOCl₂ monolayer^[40].

区别于由不同种类元素组成的复合型铁电材料. 2018年, 在第V主族元素(As, Sb, Bi)单层^[39]中也发现了二维面内铁电性. 该体系的原子层在垂直于平面的方向上会产生上下起伏的褶皱现象, 结构的扭曲打破了空间反演对称性, 同时电荷在每个原子周围实现重新分布, 使正负电荷中心得以产生, 从而引起面内自发铁电极化. 2019年, Ai等^[40]和Tan等^[41]分别用第一性原理计算证明了可从层状体材料中剥离出来的单层VOX₂ (X = Cl, Br, I)是铁电性和铁磁性(反铁磁性)共存的本征二维多铁材料. VOX₂体系的铁电性和铁磁性(反铁磁性)都起源于V离子, 单层的VOCl₂和VOBr₂同时具备铁电性和反铁磁性, 单层的VOI₂同时具备铁电性和铁磁性. 图2(c)是VOCl₂单层的结构图, V离子因受到二阶Jahn-Teller效应影响, 自发地沿a轴靠近其中一个氧原子并远离另一个氧原子, 产生了偏离八面体中心的位移, 导致单层VOCl₂空间反演对称性的破缺, 从而产生自发的面内极化. 此材料体系中铁电和铁磁的共存, 为探索二维本征多铁材料中的磁电耦合提供了一个新途径.
区别于仅具有面内极化或仅具有面外极化的二维铁电材料, Ding等^[42]在2017年通过理论计算预测了一类二维室温铁电材料: In₂Se₃及其他III₂-VI₃族范德瓦耳斯材料. 这类材料是同时具备面内极化与垂直极化特性的铁电材料. In₂Se₃结构的侧视图和俯视图如图3(a)和图3(b)所示, 图3(a)中黑色虚线框内5层原子之间以共价键结合, 按照Se-In-Se-In-Se的原子顺序交替排列, 堆叠形成1个二维单元(quintuple layer, QL). QL之间通过较弱的范德瓦耳斯力在垂直于平面的方向结合, 堆叠形成In₂Se₃体材料. 他们利用密度泛函理论对多种QL构型进行研究, 最终预测图3(c)—(h)中的FE-ZB′和FE-WZ′是能量简并的两种基态结构. 从图3(f)和图3(g)可知, 中间位置的Se原子层与位于其上下的In原子层的水平距离及垂直距离均有明显的差异, 导致该体系空间反演对称性破缺, 从而同时具有面内与面外两个方向的铁电极化. 随后, In₂Se₃的二维铁电性陆续被一系列实验工作证实. Zhou等^[43]通过对结构、光学和电学特性的表征, 探讨了多层α-In₂Se₃面外的压电性和铁电性. 通过压电力显微镜, 他们观测到α-In₂Se₃薄膜中具有清晰的偶极矩方向相反的铁电畴, 并发现在厚度约为10 nm的α-In₂Se₃样品中可实现面外铁电极化的反转. 2018年, Cui等^[44]通过实验证明了In₂Se₃面外极化与面内极化的相互耦合特性, 即面外极化被垂直电场反转的同时也会引起面内极化的反转. 在这种面外、面内极化相互耦合的奇异材料中, 有望实现对铁电极化更为灵活的调控. 此外, In₂Se₃作为具有六角晶格的二维铁电材料, 便于与石墨烯、WSe₂等性能优异的二维材料复合形成异质结构, 从而实现可电控的非易失性调控机制.
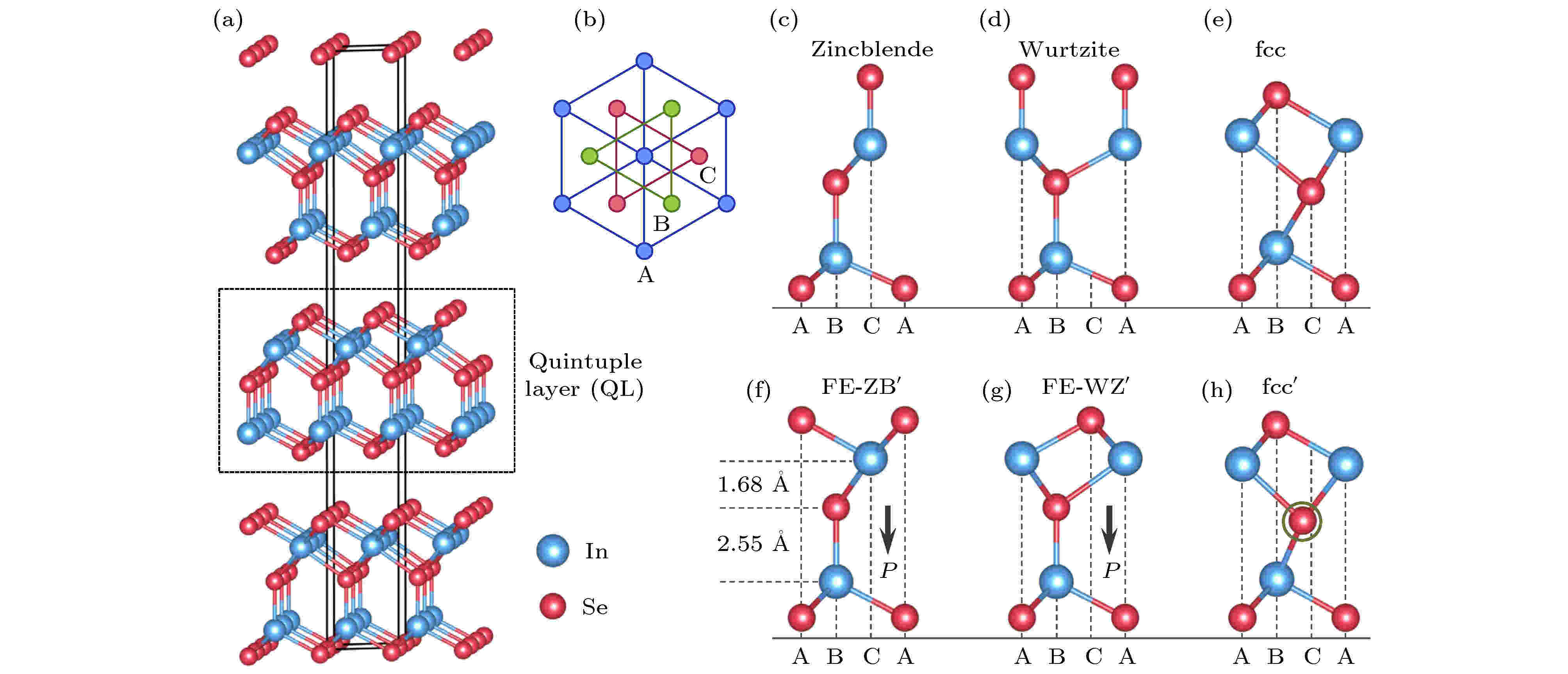图 3 (a) 层状In₂Se₃的三维晶体结构示意图; (b) 沿垂直方向的俯视图; (c)—(h) quintuple layer (QL) In₂Se₃的几种典型结构的侧视图^[42]
Figure3. (a) Three-dimensional crystal structure of layered In₂Se₃; (b) top view of the system along the vertical direction; (c)–(h) side views of several representative structures of one quintuple layer (QL) In₂Se₃^[42].

2 -->

2.2.二维铁电材料的器件应用

铁电材料由于具有可被外场调控的自发极化状态和非易失性铁电畴, 而被广泛应用在如铁电场效应晶体管、FTJ等铁电元件中. 随着二维铁电材料的涌现, 基于二维铁电材料的电子学器件, 可以满足微电子集成技术不断微型化的发展趋势, 进而实现纳米级器件的应用.
单向导电性作为二极管重要的特性, 一般会在p-n结或肖特基金属/半导体等非对称界面位置处发生^[45]. 铁电材料由于受到内建电场的作用, 偶极矩取向相反的铁电极化畴表面或边界区域的能带弯曲具有一定的差异性, 基于此特性, Wan等^[46]构建了石墨烯/α-In₂Se₃薄膜异质结, 并以此来实现极性可控的二维铁电整流二极管. 图4(a)和图4(b)给出了该铁电二极管器件的结构及光学图像, 其中约5 nm厚度的超薄α-In₂Se₃作为铁电层, 顶电极和底电极分别是金属铝和石墨烯. 图4(c)和图4(d)的I-V特性曲线表明该器件具有较明显的整流功能, 并且随着α-In₂Se₃面外极化方向的反转, 整流方向也随之发生反转. 此外, 该铁电二极管的开关比高达10⁴, 可作为一个极性可控的良好开关器件.
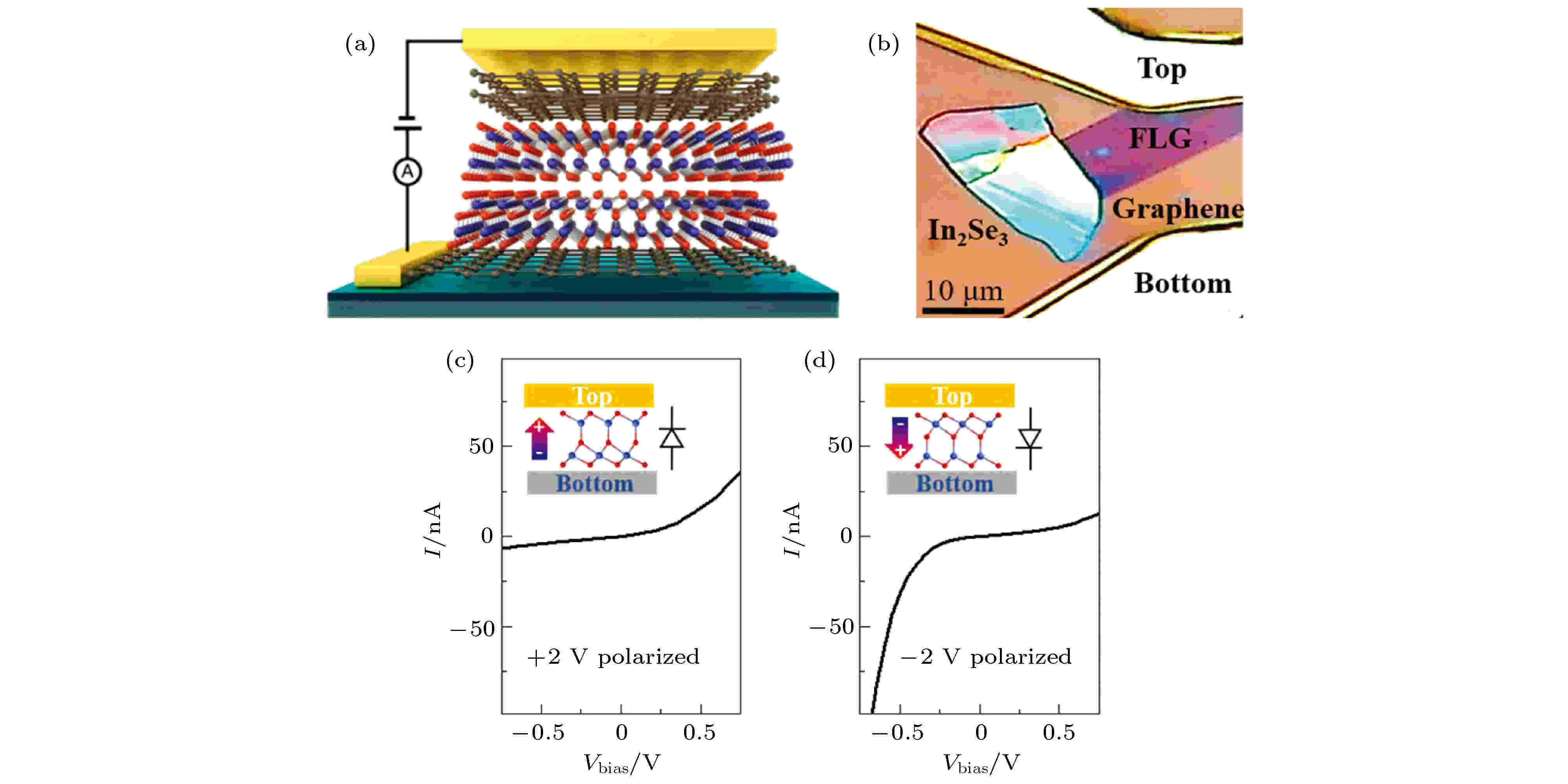图 4 (a) 基于α-In₂Se₃薄层铁电二极管示意图; (b) 器件的光学图像; (c), (d) 可切换的有整流特性的铁电二极管的I-V曲线^[46]
Figure4. (a) Schematic and (b) optical image of the device; (c), (d) I-V curves of the ferroelectric diode with switchable rectifying behavior^[46].

在2005年, FTJ的概念由Kohlstedt等^[47]正式提出. FTJ是以铁电超薄膜材料作为中间势垒层, 并在铁电薄膜两侧夹以金属电极的类似三明治的双端器件. 对中间的铁电薄膜进行极化切换会导致隧穿电阻的剧烈变化, 即隧穿电致电阻(tunneling electroresistance, TER)效应^[48]. 最近, Shen等^[49]从理论上设计了一种具有同质结构的新型二维面内In∶SnSe/SnSe/Sb∶SnSe FTJ. 他们通过对TER机制的唯象模型分析, 以及对电极中的屏蔽极化电荷、铁电薄膜势垒层的金属化效应及电荷在铁电势垒/半导体电极界面处的积累与排斥现象进行充分研究, 证明了在该二维FTJ中可并行地调控铁电势垒层宽度及高度. 图5(a)和图5(b)分别为该二维FTJ的模型和原子结构的示意图. 中间的铁电势垒层是由18个单胞的二维铁电SnSe沿[100]方向堆叠形成的, 左右电极分别是在本征的SnSe中掺杂施主杂质In和受主杂质Sb形成的p-型半导体(In∶SnSe)与n-型半导体(Sb∶SnSe). 通过在左右电极间施加沿面内方向的电场, 可以在该器件中实现两种不同铁电极化态间的反转, 从而实现信息存储. 图5(c)是该同质FTJ中系统总能随归一化的铁电极化位移λ的变化关系, 表明在掺杂半导体界面的影响下, 单层SnSe的铁电极化依旧可以稳定存在. 此外, 由于左右电极的掺杂类型差异导致掺杂界面不等价, 对应着系统势能曲线在相反铁电极化态处的不对称特性, 因此该FTJ中具有非对称的铁电性^[50], 这意味着势垒高度会在外加电场使铁电极化反转的过程里发生变化. 最后通过计算发现, 由于在该二维FTJ中可以并行地调控铁电势垒层的宽度及高度, 因此开关电阻比高达1460%. 该工作通过理论预测设计了具有显著TER效应的二维同质FTJ, 为实现低功耗的新型纳米存储设备提供了新思路.
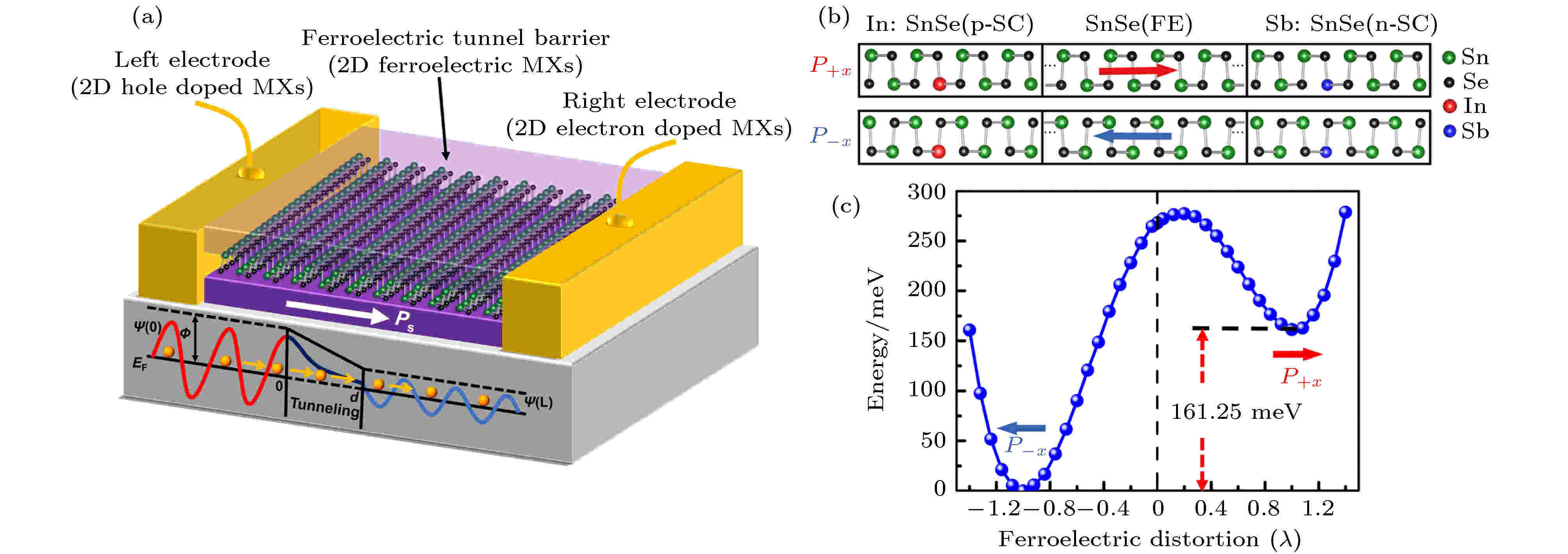图 5 (a) 二维铁电同质FTJ器件模型示意图; (b) 二维FTJ In∶SnSe/SnSe/Sb∶SnSe结构示意图; (c) 二维同质FTJ In∶SnSe/SnSe/Sb∶SnSe中, 系统总能随铁电位移λ变化的关系图^[49]
Figure5. (a) Schematic diagram of a two-dimensional ferroelectric tunnel junction (2D-FTJ) device based on homostructure; (b) the schematic diagram (shaded regions) of 2D-FTJ In∶SnSe/SnSe/Sb∶SnSe; (c) asymmetric potential energy profile as a function of ferroelectric distortions in the 2D-FTJ In∶SnSe/SnSe/Sb∶SnSe^[49].

2

-->

3.1.铁谷性

谷(valley)自由度是电子除内禀的电荷自由度和自旋自由度外的一种赝自由度, 它是指晶体动量空间中的布洛赫电子能带色散的极值点. 以石墨烯为例, 图6(a)是其六角蜂窝晶格结构和布里渊区示意图, 图6(b)是其能带色散分布图^[51]. 对于破坏了PT联合对称的2H相单层过渡金属二硫族化合物(transition-metal dichalcogenides, TMDs)等蜂窝状晶格体系而言, 其分布于第一布里渊区狄拉克点处的价带和导带打开了能隙, 形成K₊或K_–处光学带隙相同的两个能谷. 两个狄拉克点彼此间虽无法通过平移对称性来实现相互切换, 但可通过时间反演对称性产生联系. 同时, K₊和K_–能谷间较大的动量空间距离可避免电子在能谷间发生散射, 因而具有相对稳定的能态. 这样, 能谷K₊和K_–可用来构造彼此相互独立的二元状态, 形成一种新型电子自由度—谷自由度. 如果材料中具备两种或多种非简并谷自由度, 那么利用非等价谷对外场响应的不同, 便可以构成可探测的二元逻辑的非简并谷极化, 这在基于谷电子材料的信息存储器件设计及制备方面具有很大的潜力^[52,53]. 2016年, Tong等^[54]通过研究单层2H-VSe₂, 提出了铁谷材料(ferrovalley materials)这一新概念. 区别于传统谷电子材料依赖于外加磁场诱导形成的谷极化, 图6(c)—(e)所示的单层TMDs能谷K₊和K_–附近的能带结构示意图表明, TMDs体系中谷极化来源于内禀的铁磁交换关联作用和自旋轨道耦合(spin-orbit coupling, SOC)效应. 同时, 2H-VSe₂由于空间反演对称的破缺, 具有反常谷霍尔效应和谷手征依赖的旋光选择性, 因而这种本征的非易失性自发谷极化对于谷电子学应用意义重大. 由于该体系中内禀的铁磁性交换关联作用是自发谷极化的来源, 因此可通过施加磁场诱导谷极化的反转.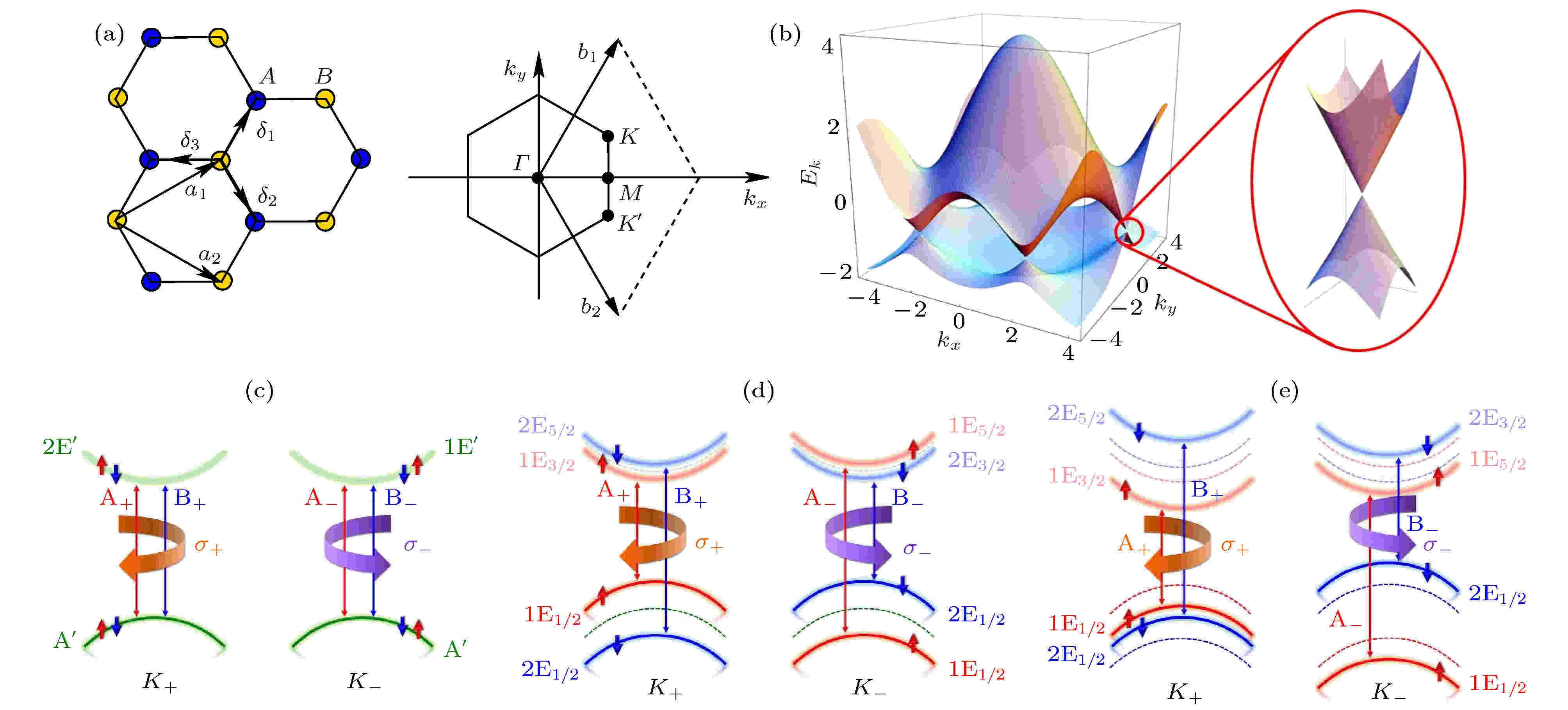
图 6 (a) 石墨烯的晶格结构及布里渊区; (b) 蜂窝晶格中的电子能带色散图^[51]; (c)—(e) 2H相TMDS单层能谷K₊与K_–附近的能带结构示意图: (c)不含SOC效应, (d)含SOC效应, (e)同时存在SOC效应与为正的交换场作用, 即对应谷极化情况^[54]
Figure6. (a) Honeycomb lattice and its Brillouin zone; (b) electronic dispersion in the honeycomb lattice^[51]; (c)–(e) the schematic band structures at valleys K₊ and $ K_- $ of representative 2H-phase TMD monolayers: (c) without SOC effect, (d) with SOC effect and (e) with SOC effect and a positive exchange field, that is, the valley-polarized case^[54].

2 -->

3.2.铁电与铁谷的耦合

实现铁谷性与铁电性这两种优异铁性的耦合, 可以形成一种高速、低能耗的电控铁谷态的新机制. 与通过外加磁场等调控方法相比, 电控方法能耗更低, 有望成为理想的谷自由度调控方式. 具有正交结构的单层第Ⅳ主族单硫属化合物MX已被理论预测出是一种铁谷性和铁电性结合的新型本征铁谷体^[55]. 其自发谷极化是由面内的铁电性诱导形成的. 不同于六角蜂窝格子, 正交晶格的两个不等价的谷是由于二重旋转对称和镜面对称的有无而形成的, 其波矢群分别是C_2v和C_s, 因此各自导带和价带的成分由$ \left\langle {i|{{k}} \cdot {{p}}|j} \right\rangle \ne 0 $所允许的态组成. 在单层GeSe正交晶格结构中, 出现在高对称线的两个谷V_x和V_y的导带和价带则分别由宇称相同的p_x或p_y态占据, 并随面内x和y方向的铁电极化形成V_x和V_y两种谷极化状态. 能谷相关的光学选择定则, 可以在角动量守恒定理的基础上, 通过群论里的大正交定理进行分析. 假设跃迁的初态与末态的不可约表示分别为$ {A}_{i} $和$ {A}_{j} $, $ {A}_{k} $为入射光微扰的不可约表示, 倘若初态与微扰不可约表示两者间的约化直积形式$ {A}_{i}\otimes {A}_{k} $中包含有跃迁末态的不可约表示$ {A}_{j} $, 那么当电偶极跃迁动量矩阵元不等于零时, 电子在该微扰下初态和末态间的辐射跃迁才被允许发生. 由于铁谷态GeSe的导带和价带只有p_x和p_y轨道成分, 对于x和y方向面内极化, 对应于全局带隙的V_x和V_y能谷只和单一线偏振态的入射光锁定. 因此, 在此正交晶系里, 本征铁电性的引入使得空间反演对称性被打破, 并导致能谷间的能级产生退简并现象, 产生可利用铁电极化来调控的自发谷极化态, 实现电控铁谷极化的新机制. 如图7(a)和图7(b)所示, 能谷V_x和V_y具有不相等的带隙, 标志着自发谷极化的产生. 铁电极化由沿x方向转变到沿y方向时, 铁谷的状态也会发生改变. 通过光学性质的计算, 如图7(c)和图7(d)所示, 复介电函数虚部的曲线xx和yy不等价的光学带隙说明了能谷间的退简并化, 并且铁电极化的反转会引起铁谷性状态的反转. 他们基于能谷的退简并及线偏振光依赖的光学带隙的特性, 设计了一种新颖的二维铁谷器件. 如图7(e)所示, 在此电控起偏器中, 通过外加电场的调控手段可以得到不同状态的谷极化, 进而能够选择性地获得不同方向的动态起偏激光束. 与传统的机械驱动起偏器相比, 这种新型的电控起偏器不仅能准确获得特定方向的线偏振光, 而且也能选择性地获得左旋及右旋圆偏振光, 进一步拓宽了铁谷材料在谷电子学及光电子学的应用.
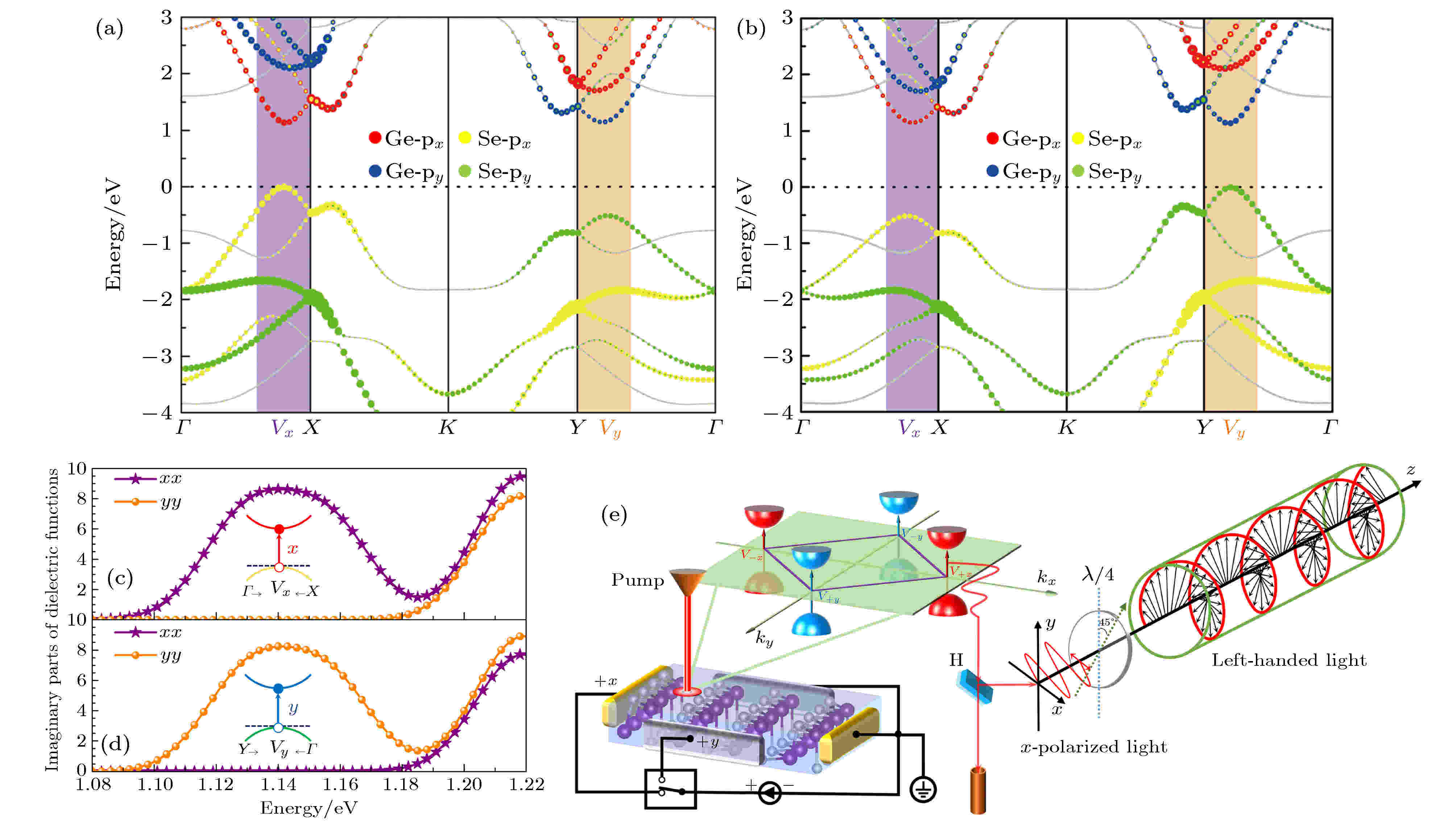图 7 铁电GeSe单层(a) p_x相和(b) p_y相的能带结构; (c) p_x相和(d) p_y相GeSe单层中, 在$ \widehat{x} $和$ \widehat{y} $线偏振光激发下的复介电函数虚部ε₂; (e) 基于铁谷GeSe单层提出的电控起偏器工作原理示意图^[55]
Figure7. The band structure of ferroelectric phase GeSe monolayer in (a) p_x and (b) p_y state; the imaginary parts of complex dielectric function ε₂ excited by linearly x-polarized light and y-polarized light of ferrovalley GeSe monolayer of (c) p_x and (d) p_y state; (e) proposed electrically tunable polarizer based on the ferrovalley GeSe monolayer^[55].

Haldane模型是一种无需依赖外加强磁场产生朗道能级而实现量子反常霍尔效应的途径, 其中时间反转不变性可被该模型中交错的磁通量打破, 但整个系统中的总磁通量始终保持为零. 类似地, 铁磁序也是铁谷性产生的充分非必要条件, 反铁磁性也可以诱导自发铁谷性的产生. Hu等^[56]利用理论计算等手段, 通过构造CIPS/MnPS₃范德瓦耳斯异质结构, 实现了由磁近邻效应诱导的、铁电场可调控的谷极化. 属于P3空间群的CIPS具有类六角的布里渊区, 在较小的晶格失配产生的应力下, 由于时间反演对称性的存在, 同样可在K₊和K_–处产生自旋劈裂的能谷简并状态, 即顺谷态. 构造异质结后, 极化垂直向下和向上的异质结构侧视图分别如图8(a)和图8(b)所示, 具有反铁磁性的MnPS₃层的磁近邻效应会导致铁电CIPS层中产生感应磁场. 具体而言, 当CIPS层具有向下的铁电极化时, Cu原子与具有正磁矩的Mn1原子距离更近, 会因磁邻近效应而产生正向磁场. 当CIPS层具有向上的铁电极化时, In原子与具有负磁矩的Mn2原子距离更近, 因而会感应磁近邻效应导致的负磁场. 这一现象使得局部时间反演对称性被打破的同时, 还导致能谷处产生较大的能带劈裂. 由于相反的铁电极化态对应的感应磁场方向是相反的, 所以在CIPS层铁电极化方向反转时会对应着谷极化的反转. 图8(c)—(e)是不同铁磁序与铁电序相互组合的能带图, 图8(c)和图8(d)中铁电极化方向均向下且Mn原子的磁序相反, 图8(e)中的铁电极化方向向上且Mn原子的磁序与图8(c)中相同. 能带图结果表明, 利用铁电场实现了谷极化反转. 此外, 他们还计算了该异质结不同铁电序的谷手征的圆偏振光吸收特性. 图8(f)和图8(g)分别对应的是铁电极化向下和向上的异质结的圆偏振光吸收, 可看出铁电极化方向相反时对应的旋光吸收也不相同, 进一步证实在该异质结的谷极化随铁电极化反转而反转的特性. 图8(h)和图8(i)是基于此特性设计的电控谷极化器件, S和D分别表示该器件的源极与漏极, 反铁磁半导体MnPS₃层在该器件中作为衬底, 并通过磁近邻效应诱导与之相邻的CIPS单层产生谷极化. 基于反常谷霍尔效应, 利用外加电场的手段调控不同的谷极化状态可以实现二进制信息存储. 这种将铁电极化与磁近邻效应结合的异质结构使电控铁谷机制成为可能, 在实现具有信息存储功能的谷电子器件中具有广阔的应用前景.
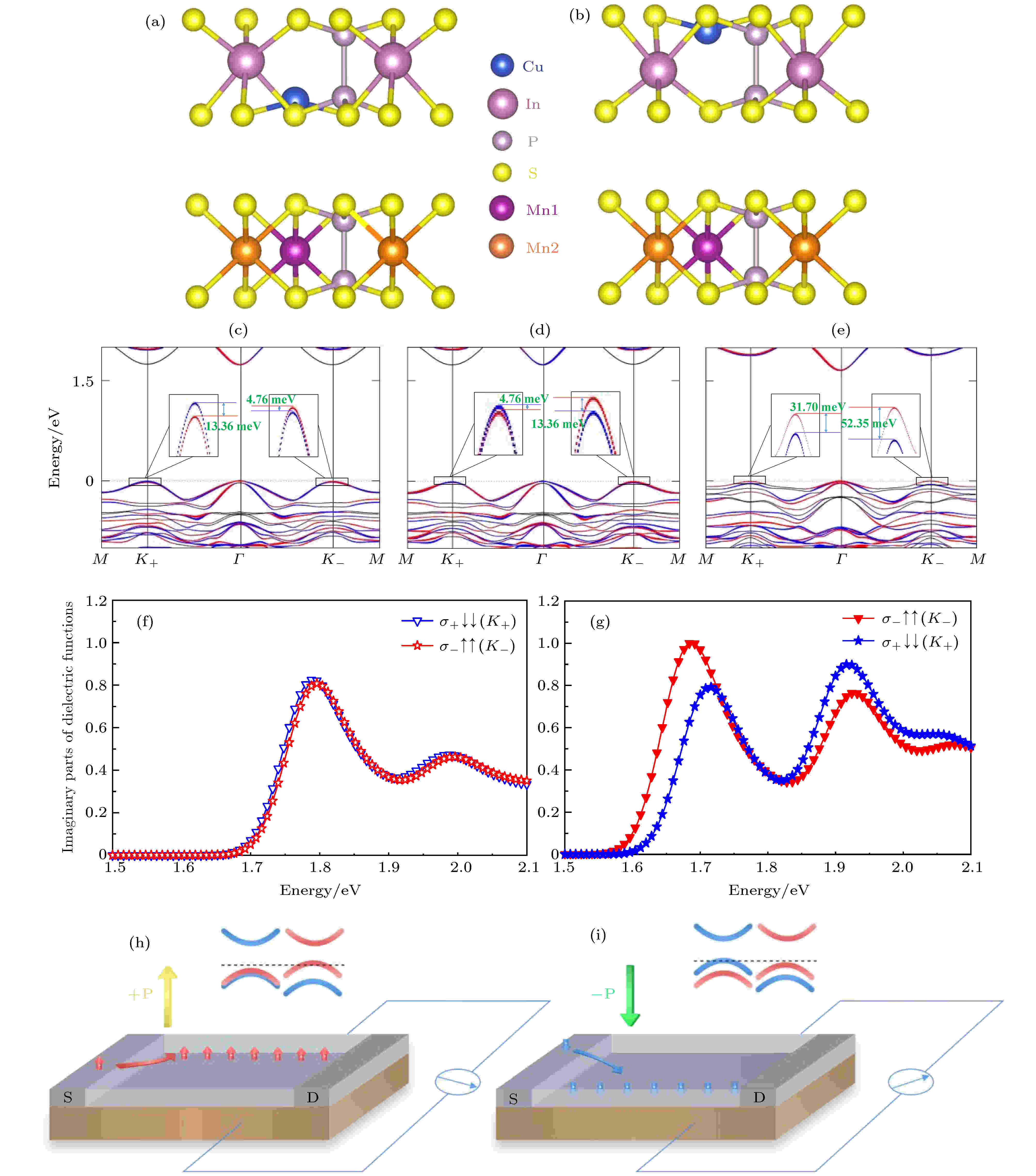图 8 (a), (b) CuInP₂S₆/MnPS₃异质结构图; (c)—(e) 不同铁磁序和铁电序异质结的能带图; (f), (g) 异质结中左旋圆偏振光σ₊和右旋圆偏振光σ_–激发下的复介电函数虚部ε₂; (h), (i) CuInP₂S₆/MnPS₃异质结构的电控谷自由度器件^[56]
Figure8. (a), (b) Structure configurations of CuInP₂S₆/MnPS₃ heterostructures; (c)–(e) band structures of CuInP₂S₆/MnPS₃ heterostructures; the imaginary parts of complex dielectric function ε₂ for CuInP₂S₆/MnPS₃ heterostructure with (f) downward and (g) upward ferroelectric polarization; electrical switch of valley degree in CuInP₂S₆/MnPS₃ heterostructures in (h) upward ferroelectricity and (i) downward ferroelectricity^[56].

2

-->

4.1.磁性的调控方法

对自旋的调控和实现磁性的反转是自旋电子学器件得以应用的关键. 在基于巨磁阻效应的磁存储技术广泛应用以后, 一系列诸如自旋阀、自旋转移力矩、自旋抽运、自旋塞贝克效应和基于SOC的自旋霍尔效应等新概念的衍生, 使得自旋自由度达到了与电荷自由度同等重要的地位. 但是在由Datta和Das^[57]提出自旋场效应晶体管概念之后的很多年, 在实际应用中存在的性能问题仍然阻碍着以自旋为主的有效晶体管的发展. 其中最突出的问题是由于界面处电导率的不匹配导致的自旋注入和铁磁体探测效率低. 所以在不使用辅助铁磁材料和磁场的情况下, 利用半导体器件内部的自旋属性来充分挖掘材料中电子控制潜力的目标尚未实现. 目前对磁性的控制包括但不限于: 外加磁场控磁、自旋极化电流控磁、热辅助控磁等多种手段. 以磁电耦合为物理基础的电控磁性, 作为一种低能耗的控磁技术可以很好地满足当今信息技术发展的需求. 实现电控磁性的方法有很多种, 广义上来讲, 任何利用外加电场的手段实现对材料磁学性质的调控都可以称为电控磁. 电控磁效应涉及晶格畸变与电荷、轨道、自旋和外场的耦合, 同时这些序参量又和晶格结构的对称性交织在一起, 形成一派洋洋大观. 载流子调控机制、轨道调控、应力机制等都在电控磁效应中具有重要地位. 近年来, 二维铁电材料的蓬勃发展, 使得基于二维铁电的电控磁成为一种新型的磁性调控方法. 该方法有望实现多种形式的磁电耦合效应, 因而具有丰富的物理内涵和潜在的应用价值.
2 -->

4.2.二维铁电与自旋织构的磁电耦合

在空间反演对称破缺的体系里, 晶体势场里的电子运动会受到一个由相对论效应产生的额外磁场的影响^[58], 导致电子动量$ {{p}} $和自旋$ {{\sigma }} $之间耦合, 这一现象称为SOC效应, 可由$ {{{H}}=-{\mu }_{\rm{B}}{{\sigma }} \cdot {{B}}}_{\rm{eff}} $刻画, 其中有效磁场$ {{{B}}}_{\rm{eff}}=\left({{p}}\times {{E}}/\left(2 m{c}^{2}\right)\right) $, $ {{\sigma }} $, $ {\mu }_{\rm{B}} $, m, c则分别是泡利矩阵、玻尔磁子、载流子有效质量和光速. 可见, 有效磁场的强度及其产生的自旋极化是严重依赖于$ {{p}} $和$ {{E}} $及其向量叉乘方向的. 因此, 电子的手性自旋极化状态可以通过铁电极化来调控, 这使得在非磁性材料中实现全电学控制自旋器件的方法成为可能. 其中研究广泛的为Rashba型的SOC效应^[59]和铁电Rashba半导体^[60]. 形如$ \sim ({{z}}\times {{p}}) \cdot {{\sigma }} $的Rashba效应出现在具有中心反演对称破缺的系统中, 面外偶极子产生的电场造成动量相关的面内自旋极化. 二维有机-无机杂化铁电材料因其独特的光学、电学特性和简易的制备工艺而备受关注, 是理想的Rashba材料^[61-63]. 这类材料主要由原子序数较大的金属和卤素原子组成, 且其结构不具备空间反演对称中心, 因此往往具有较强的SOC效应和Rashba效应. 利用铁电极化可对这类材料中的Rashba效应进行反转调控, 从而实现磁电耦合, 对自旋电子学的发展具有深远的意义.
一般而言, 在含奇数次方自旋轨道耦合的有效哈密顿量中, 自旋的方向可以随铁电的反转而反转, 而与具体的哈密顿量形式无关^[64]. 这一点可以这样看出. 由于铁电极化的布洛赫态$ \left| {+{{P}}, {{{p}}}^{2{{n}}+1}} \right\rangle $在时间反演T和空间反演I联合操作下极化发生反转, 即$ {{T}}{{I}}\left| {+{{P}}, {{{p}}}^{2{{n}}+1}} \right\rangle =\left| {-{{P}}, {{{p}}}^{2{{n}}+1}} \right\rangle $, 则自旋角动量的平均值

$\begin{split}&\left\langle {{S}} \right\rangle \left[ { - {{P}},{{{p}}^{2{{n}} + 1}}} \right] = \left\langle { - {{P}},{{{p}}^{2{{n}} + 1}}|{{S}}| - {{P}},{{{p}}^{2{{n}} + 1}}} \right\rangle \\= &\left\langle { + {{P}},{{{p}}^{2{{n}} + 1}}|{{{I}}^{ - 1}}{{{T}}^{ - 1}}{{STI}}| + {{P}},{{{p}}^{2{{n}} + 1}}} \right\rangle \\=&\left\langle { + {{P}},{{{p}}^{2{{n}} + 1}}| - {{S}}| + {{P}},{{{p}}^{2{{n}} + 1}}} \right\rangle \\=&\left\langle { - {{S}}} \right\rangle \left[ { + {{P}},{{{p}}^{2{{n}} + 1}}} \right].\end{split}$

2019年, Ai等^[65]利用对称性不变量构造了形如$ {{{\sigma }}}_{{{z}}}\times {{{k}}}_{{y}} $的$ {{k}}\cdot {{p}} $模型, 不仅说明了具有面内铁电性的WO₂Cl₂单层中的[110] Dresselhaus型自旋轨道耦合作用, 其面外等效磁场$ \propto $[0, 0, k_y], 而且在该体系中发现了可随极化反转而反转的自旋织构. 图9(a)是考虑SOC作用的能带图, 可以看出单层WO₂Cl₂导带底(CBM) Γ点处产生了较大的Dresselhaus型能带劈裂, 图9(b)是该体系在导带底附近的二维能带图, 位于上方和下方的图分别与导带底能带劈裂的“外”分支和“内”分支相对应. 图9(c)是具有相反面内极化WO₂Cl₂单层位于CBM + 0.2 eV能量截面位置的自旋织构图, 表明自旋极化主要是由面外分量S_z贡献的, 面内分量S_x和S_y对自旋极化几乎没有贡献, WO₂Cl₂的有效磁场具有单一化的面外分量表明在该体系中可以实现持续螺旋态. 此外, 图9(c)也表明反转铁电极化方向时, 自旋织构也随之发生反转. 该理论研究不仅实现了电控自旋螺旋态, 而且扩宽了二维铁电的应用范畴, 为自旋电子学研究领域提供了一类多功能的新型二维材料.
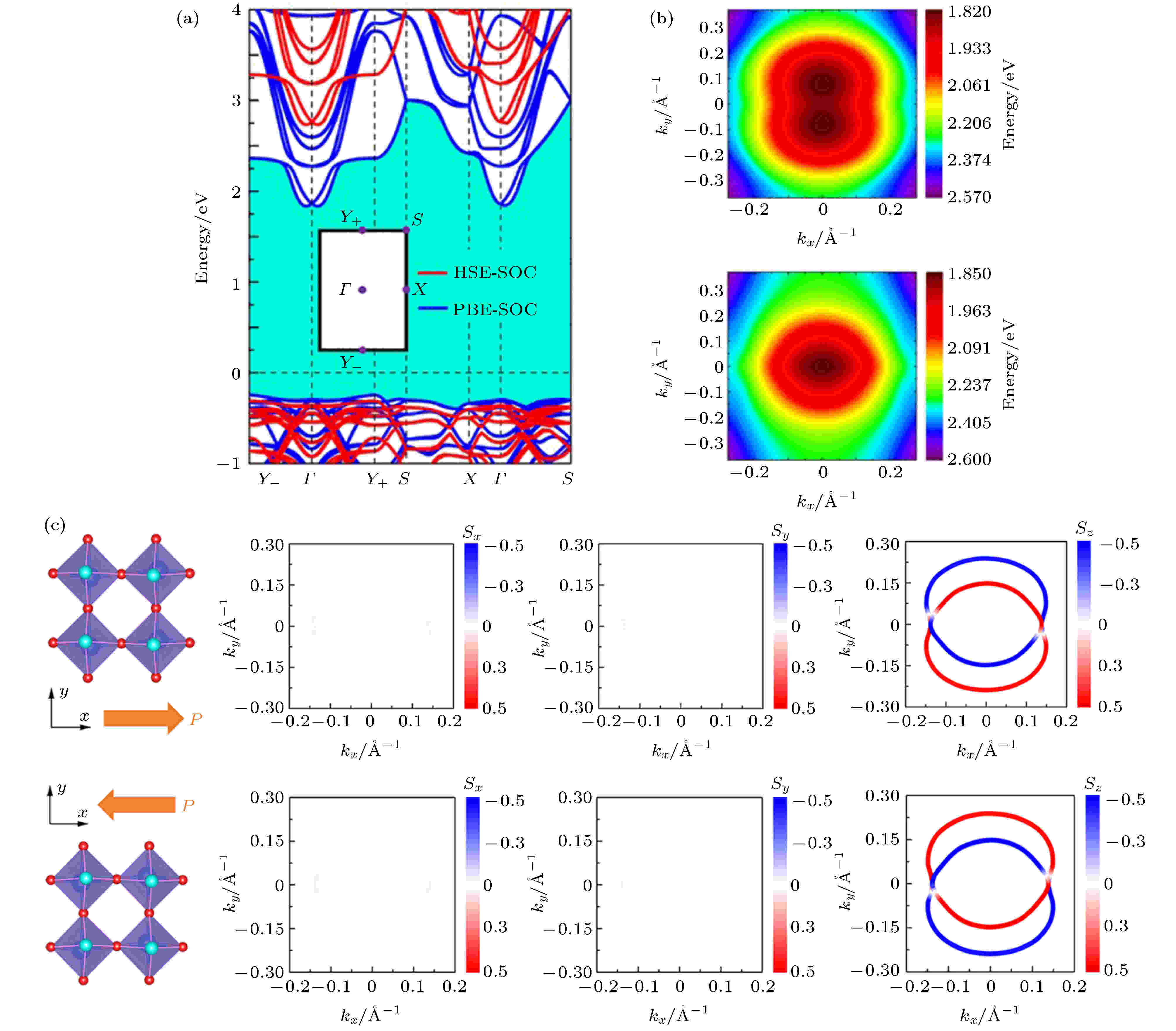图 9 (a) 考虑SOC作用时, 使用PBE泛函和HSE06泛函计算的单层弱铁电WO₂Cl₂的能带图; (b) [110] Dresselhaus型自旋分裂能带CBM处的能量分布图, 其中上方图对应“外”分支, 下方图对应“内”分支; (c)不同极化方向的单层WO₂Cl₂的三种自旋分量S_x, S_y和S_z在kx, ky平面内的自旋织构分布图, 能量截面位于CBM+0.2 eV处^[65]
Figure9. (a) Electronic band structures of the WFE WO₂Cl₂ monolayer in the PBE and HSE06 approximations with SOC; (b) DFT energy profiles for the CBM outer (top) and inner (bottom) branches of the [110] Dresselhaus-type spin split bands; (c) out-of-plane and in-plane spin component distributions with different ferroelectric polarizationon the constant energy contours corresponding to a cut at 0.2 eV above the CBM^[65].

此外, 铁电还可以与自旋涡旋和磁斯格明子等拓扑非平庸的自旋织构相互耦合. 磁性材料的线性响应对应了磁振子(magnon)激发, 当计入磁振子相互作用时, 将存在一个比磁振子激发能量更低的非线性拓扑激发—孤子激发(soliton). 孤子最先是Skyrme在核物理领域研究非线性sigma模型时引入的一个拓扑非平庸的一个局域解, 它代表了一个具有局域构型的、稳定的准粒子, 自旋涡旋和磁斯格明子都属于磁性材料里的孤子激发, 可以通过拓扑荷(topological charge)加以区别. 在实际材料中, 这些非共线的磁结构往往意味着多种相互作用间的竞争. 考虑Heisenberg交换作用和SOC效应的Dzyaloshinskii-Moriya (DM)相互作用. 自旋对称的Heisenberg交换作用倾向于自旋平行排列, 而自旋反对称的DM相互作用倾向于自旋垂直排布, 当两者共存而相互竞争时, 则可以形成非共线的自旋结构, 甚至是拓扑非平庸的孤子磁态. 而DM相互作用只能在空间反演对称破缺的体系中存在, 这就为铁电调控孤子磁态创造了可能. 当铁电极化的反转通过逆DM相互作用^[66,67], 改变了螺旋自旋的手性, 则可望实现对孤子磁态拓扑荷的调控. Xu等^[68]通过Monte Carlo模拟结合第一性原理计算, 在单层多铁VOI₂中实现了电控磁拓扑荷的反转. VOI₂具有较强的DM相互作用和面内磁各向异性, 这有助于稳定由磁涡旋和反涡旋对构成的拓扑非平庸的双半子(bimeron)态. 通过外加电场反转铁电极化和DM相互作用矢量的符号, 进而导致双半子态中磁涡旋和反涡旋的切换, 从而反转了双半子态拓扑荷.
2 -->

4.3.二维铁电和二维磁性的磁电耦合

铁电性和铁磁性的共存和相互耦合导致了多铁性^[69,70]. 部分同时含有铁电性和铁磁性的多铁材料中存在磁电耦合效应, 从而允许通过磁场控制电荷或通过电场控制自旋. 随着二维铁电材料的发展, 对二维多铁材料的研究也开始出现萌芽. 目前主要是通过理论手段设计二维多铁材料. 例如: 单层CrN被预测同时具有铁磁性和铁电性, 是一种具有金属性质的多铁材料, 单层CrB₂则具有铁磁/垂直方向铁电的亚稳态结构^[71]; 单层Hf₂VC₂F₂被理论预测是奈尔温度为313 K的多铁材料, Hf₂VC₂F₂中铁电极化是由Y型反铁磁序诱导产生的. 此外, 通过外加磁场的手段, 较强的本征磁电耦合在该体系中被证明^[72]; 单层的CuMP₂X₆ (M = Cr, V; X = S, Se)也被预测是铁电性和铁磁性共存的多铁材料^[73]. 更加振奋人心的是, Lai等^[74]不仅从理论上证明了二维CuCrP₂S₆材料中自旋、电偶极子和铁谷的相互耦合, 而且在实验中观察到了室温下CuCrP₂S₆纳米片(约13 nm)的面外铁电性, 并且在温度为10 K时, 他们观察到了大量堆积的CuCrP₂S₆纳米片的磁滞回线. 这些研究都表明铁电性和铁磁性可以在同一材料中共存, 这为实现多铁材料中磁电耦合的实际应用带来了希望.
通过构建二维异质结, 利用铁电场效应和磁近邻效应, 可以间接地实现磁电耦合. Gong等^[75]通过将原子厚度的具有铁磁性的Cr₂Ge₂Te₆和具有铁电性的In₂Se₃堆叠在一起, 形成了二维Cr₂Ge₂Te₆/In₂Se₃范德瓦耳斯异质结. 图10(a)所示是分别具有向上极化和向下极化的Cr₂Ge₂Te₆/In₂Se₃二维异质结构. 图10(b)给出了Cr₂Ge₂Te₆的磁晶各向异性与范德瓦耳斯层间距离的关系, 表明Cr₂Ge₂Te₆和In₂Se₃之间增强的界面杂化倾向于将Cr₂Ge₂Te₆的磁晶各向异性从易平面方向切换到易轴方向. 因此, 在这种异质结构中, 强烈的磁电耦合效应为逻辑器件的铁磁性切换提供了潜在的途径. 图10(c)和图10(d)分别是异质结构中最接近Cr₂Ge₂Te₆的表面的Se1原子层和次接近Cr₂Ge₂Te₆表面的In1原子层的自旋能态密度图, 以及由磁邻近效应引起的Se1原子和In1原子中自旋磁矩随范德瓦耳斯层间距离变化的关系图, 表明In₂Se₃中的非零磁矩是由Cr₂Ge₂Te₆的磁近邻效应诱导的. 在有限温度下, 二维In₂Se₃的易平面磁化易受热扰动影响, 且不存在长程磁序, 而二维In₂Se₃的易轴磁化可打破自旋旋转不变的戈德斯通模式, 打开自旋波声学带隙, 可在有限温度下维持自旋极化. 因此, 在二维Cr₂Ge₂Te₆/In₂Se₃范德瓦耳斯异质结中, 不仅可实现电控Cr₂Ge₂Te₆的磁晶各向异性, 还可在二维In₂Se₃中实现可调控的铁磁性和铁电性, 极大地拓宽了多铁材料的范围, 并为大量涌现的界面现象提供新的材料平台.
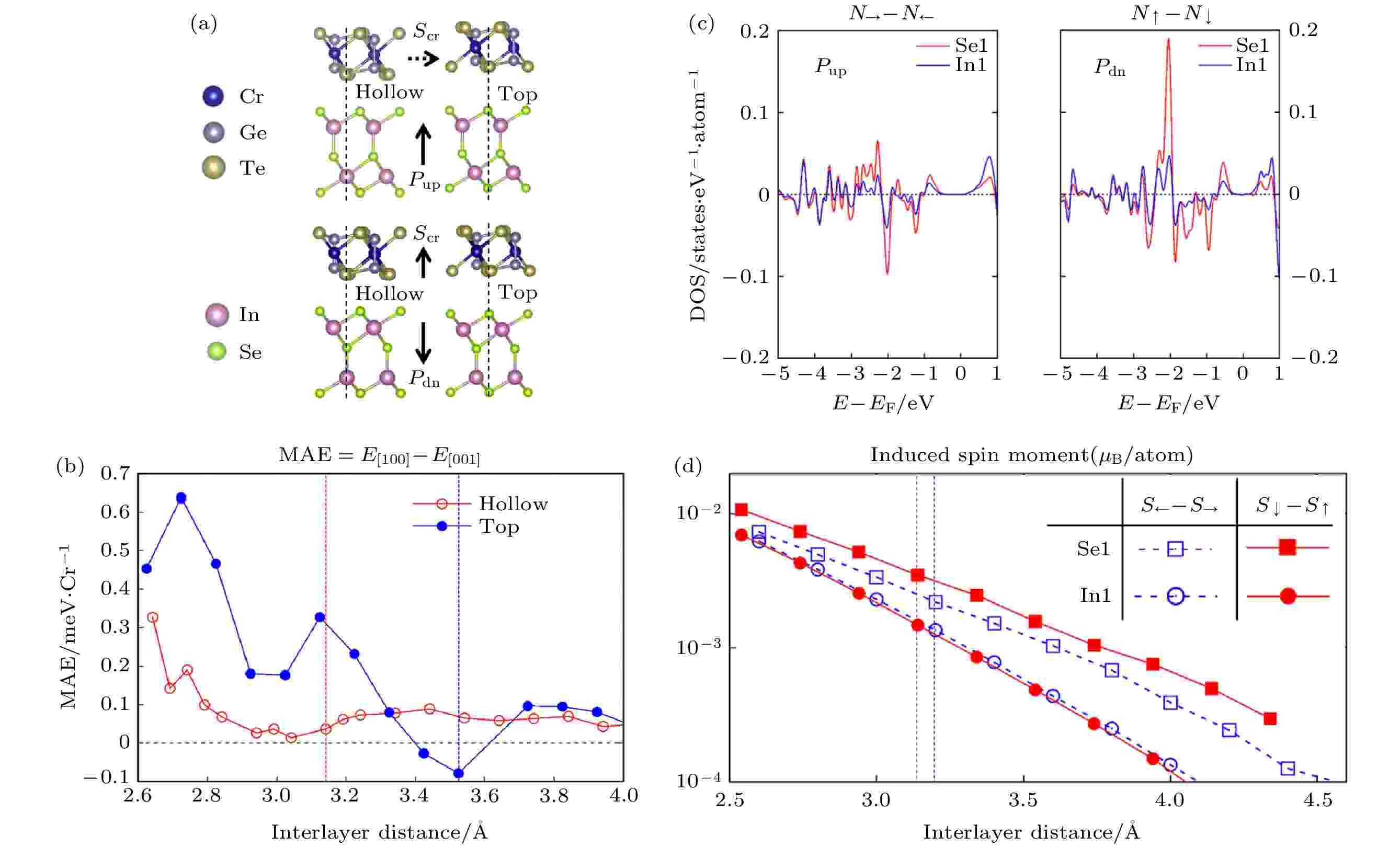图 10 (a) 分别有向上和向下的垂直电偶极矩的In₂Se₃单层的Cr₂Ge₂Te₆/ In₂Se₃二维异质结构图; (b) Cr₂Ge₂Te₆/ In₂Se₃二维异质结构中Cr₂Ge₂Te₆的磁晶各向异性与范德瓦耳斯层间距离的关系图; (c) 接近Cr₂Ge₂Te₆的表面(Se1)和次表面(In1)原子层的自旋状态密度; (d) 由磁邻近效应引起的原子Se1和原子In1自旋磁矩随层间距的变化图^[75]
Figure10. (a) Heterostructure side views with the In₂Se₃ ferroelectric dipole moment directed upward and downward (P_up and P_dn), respectively; (b) calculated magnetocrystalline anisotropy of Cr₂Ge₂Te₆ in the heterostructure versus the van der Waals interlayer distance; (c) projected spin density of states for the surface (Se1) and subsurface (In1) atomic layers close to Cr₂Ge₂Te₆; (d) interlayer distance dependence of the proximity-induced Se1 and In1 spin moments^[75].

二维铁电材料与当今电子器件的高密度存储、低维化、多功能化的发展需求相契合, 从而备受基础科学研究和应用研究者的关注. 虽然利用外场调控和新颖器件结构设计等手段使二维铁电材料的理论和实验研究取得了诸多进展, 但是目前实验上已经成功制备的铁电材料数量仍是比较有限的. 因此, 对具有较高居里温度和合适反转势垒的二维铁电的理论及实验的探索仍要继续进行. 本文根据电偶极矩的表现形式, 对本征铁电体进行了分类, 展现了二维铁电性丰富的物理内涵. 二维铁电材料在铁电元器件的应用方面具有独特的优势, 充分借鉴传统铁电材料的技术和概念, 是实现诸如铁电二极管、FTJ的优异原材料. 二维铁电材料也为各种衍生现象的出现提供了平台. 二维铁电材料中实现的铁电与多种铁性之间的相互耦合, 如铁电与铁谷耦合、铁电与铁磁耦合甚至铁磁、铁电与铁谷多场耦合等, 对谷电子学、光电子学乃至自旋电子学的发展而言意义匪浅. 此外, 铁电与SOC效应、磁斯明格子、自旋涡旋之间耦合产生的奇异物理特性, 为实现非共轭物理量之间的调控, 尤其是电场调控, 打开了新思路. 对二维铁电材料的关注虽源于对低维铁电性存在的研究, 但对其物理内涵的探索已大大超出这一初衷, 这为发展新型微纳器件的理论和实验研究注入了活力.
本文撰写得到华东师范大学多功能创新平台的支持.