摘要:压电陶瓷作为一种能够实现机械能和电能相互转换的功能材料, 在民用和军事方面都有着广泛应用. 随着人们环保及健康意识的提高, 高性能兼具环境协调性的无铅压电陶瓷的研究成为了一项紧迫任务. 在众多无铅材料中, (K, Na)NbO₃ (KNN)基陶瓷因其优异的综合性能而受到关注, 但是利用相界同时调控高压电和电卡性能的研究偏少. 本文采用传统固相方法制备了0.944K_0.48Na_0.52Nb_0.95Sb_0.05O₃-0.04Bi_0.5(Na_0.82K_0.18)_0.5ZrO₃-1.6%(Ag_xNa_1–x)SbO₃-0.4%Fe₂O₃ (x = 0—1.0)无铅压电陶瓷, 重点研究了AgSbO₃/NaSbO₃对陶瓷相结构、压电和电卡性能的影响. 研究结果表明: 陶瓷在研究组分范围内均为“三方-正交-四方”三相共存; 随着AgSbO₃含量的增加, 该陶瓷的压电及铁电性能均有所波动(d₃₃ = 518—563 pC/N, k_p = 0.45—0.56, P_max = 21—23 μC/cm²和P_r = 14—17 μC/cm²). 同时, 利用间接法表征了该陶瓷的电卡效应, 在居里温度附近得到了较高的电卡温变值(>0.6 K). 因此, 在KNN基陶瓷中通过相界构建能够同时实现高压电和良好的电卡性能.
关键词: 铌酸钾钠/
相界/
压电效应/
电卡效应

English Abstract

全文HTML

--> --> -->

近年来, 铌酸钾钠((K, Na)NbO₃, KNN)由于相对较好的电学性能受到研究者的广泛关注. 研究者通常通过组分改性实现相界构建, 最终获得具有高压电性能的KNN基陶瓷^[1-7]. 例如, 2004年, 日本丰田研究所Saito等^[2]采用织构方法和正交-四方相界设计制备出了高压电性能KNN基无铅织构陶瓷($ d_{33}\sim 416 $ pC/N), 这一研究成果让KNN基无铅压电陶瓷成为了研究的热点. 但是后续的研究结果也表明, 利用传统固相法所制备的正交-四方相界的陶瓷压电性能很难达到织构陶瓷的效果. 因此, 如何进一步提升KNN基陶瓷的压电性能成为研究焦点和难点. 2014年以来, 本课题组在一系列KNN陶瓷中构建出了三方-四方或者三方-正交-四方新型相界, 并获得了增强的压电性能(490—570 pC/N)^[3,4]. 2019年, 通过新型相界并辅以弛豫特性调控, 在KNN基陶瓷中实现了更高的压电性能($ d_{33}\sim 650 $ pC/N)^[5]. 由此可见, 利用组分调控构建新型相界已成为当前获得高性能KNN基陶瓷的重要手段^[6-8].
众所周知, 铁电材料的相界对于电卡效应的研究同样具有重要意义. 电卡效应是指极性材料在施加或去除电场时, 极性偶极子的有序度发生改变, 引起系统熵变化, 最终导致材料温度发生变化的一种物理现象^[9-16]. 铁电材料在施加或去除电场时会产生较大的极化变化, 在绝热条件下材料本身会发生温度的升高和下降, 因此被认为是制备下一代固态制冷器件的理想材料之一. 过去, 研究者为了获得高的电卡温变值(ΔT), 主要将目光集中在PbZr_0.95Ti_0.05O₃, PbMg_1/3Nb_2/3O₃-PbTiO₃等含铅铁电材料^[9-11]上. 随着人们环保意识的增强以及欧盟、中国、日本等国家一系列“铅禁”法律法规的相继出台, 越来越多的研究者将目光转向了环境友好型的无铅压电材料, 如钛酸钡、钛酸铋钠、铌酸钾钠等^[12-16].
作为具有一级相变的正常铁电体, 钛酸钡(BaTiO₃, BT)具有非常高的电卡效应峰值和电卡强度(ΔT/ΔE), 但是过于狭窄的相变温区(≤10 K)以及较高的居里温度(～400 K)限制了其实际应用. 钛酸铋钠((Bi, Na)TiO₃, BNT)的铁电-顺电相变温度在620 K左右, 不利于制冷器件的实际应用. 为了降低居里温度、优化铁电特性, 往往在BNT陶瓷中固溶其他铁电材料, 使材料可以在室温附近具有较高的电卡性能. 但是该类陶瓷高电导率产生的较大漏电流使得利用间接法表征其电卡性能的准确性仍存在争议^[17]; 同时, 较高的矫顽场也使其难以充分极化. 众所周知, KNN基陶瓷压电性能的大幅提升得益于相界的构建, 而多相共存同样有利于电卡效应的提升: 当电卡材料处于多相共存时, 各相之间的热力学能垒很小, 有利于不同相之间的极化矢量进行偏转, 在电场作用下材料内部的偶极子就更容易翻转至与电场方向一致^[18,19]. 然而, 远离室温的居里温度以及狭窄的相变温区使得目前对KNN基陶瓷电卡效应的研究偏少^[20], 特别是对于具有高压电性能材料体系的电卡性能研究更少. 因此, 本文以0.944 K_0.48Na_0.52Nb_0.95Sb_0.05O₃-0.04 Bi_0.5(Na_0.82K_0.18)_0.5ZrO₃-1.6% (Ag_xNa_1–x)SbO₃-0.4%Fe₂O₃ (KNNS-BNKZ-A_xN_1–xS-Fe, x = 0 —1.0)陶瓷为对象, 重点研究其在相界处的压电及电卡效应, 分析相界对于陶瓷压电及电卡效应的影响.

2

-->

2.1.制备工艺

本文采用传统固相法制备了KNNS-BNKZ-A_xN_1–xS-Fe (x = 0—1.0)无铅陶瓷. 所用原料均为国药集团化学试剂有限公司生产, 具体为K₂CO₃ (99%), Na₂CO₃ (99.8%), Nb₂O₅ (99.95%), Sb₂O₃ (99.99%), Bi₂O₃ (99.999%), Ag₂O (99.7%), ZrO₂ (99%), Fe₂O₃ (99%). 首先, 按照体系的化学计量比进行称量, 将原料放入装有氧化锆球的尼龙罐中, 以酒精为介质球磨(20—24 h); 将干燥的粉体在850 ℃下预烧(6 h); 加入适量聚乙烯醇水溶液(PVA)作为黏合剂, 研磨得到具有良好流动性的细小颗粒; 将造好粒的粉体压制成直径为10 mm的圆片, 在550 ℃下进行排胶处理; 最后将这些圆片在1080—1090 ℃下烧结(3 h). 烧结后的陶瓷直接用作相结构和微观形貌的表征. 为测试电学性能, 需在陶瓷片两个表面镀上电极. 本文中采用烧渗银电极法: 在烧结好的陶瓷片的两个表面均匀涂上银浆, 烘干后在600 ℃下烧结(10 min). 对被好银的样品作极化处理以测试其电学性能. 极化前须保证样品的两个表面互不导通, 然后将样品置于室温(20 ℃)硅油浴中利用极化仪施加1.6—1.8 kV的直流电压进行极化(10 min).
2 -->

2.2.结构及性能表征

采用X射线衍射仪(Bruker D8, 德国Bruker公司)和拉曼光谱仪(LabRAM HR Nano, 日本Horiba公司) 对样品进行相结构表征; 使用哈尔滨工业大学生产的低温介电性能测试系统测试陶瓷样品介电常数随温度的变化情况并确定相变温度; 使用扫描电子显微镜(JSM-7500LV, 日本电子公司)表征样品的表面形貌; 使用LCR测试仪(4980A, 美国Agilent公司) 测量样品的室温介电性能; 利用铁电压电综合测试系统(TF2000 Analyzer, 德国aixACCT公司)测试样品的电滞回线和场致应变曲线; 采用准静态d₃₃测量仪(ZJ-3A, 中国科学院声学研究所)测量室温下压电系数d₃₃; 使用阻抗分析仪(4294A, 美国Agilent公司) 测试平面机电耦合系数k_p.

2

-->

3.1.相结构

图1(a)为KNNS-BNKZ-A_xN_1–xS-Fe系列陶瓷样品在衍射角2θ区间为20°—70°时的X射线衍射(XRD)图谱. 由图1(a)可见, 所有样品均呈单一钙钛矿结构, 无杂相生成, 说明ANS已进入KNNS-BNKZ晶格并形成固溶体. 从衍射峰形状上判断, 组分变化并没有导致KNNS-BNKZ-A_xN_1–xS-Fe陶瓷发生明显的结构相变, 在x = 0—1的范围陶瓷具有相同的相结构. 图1(b)是该陶瓷样品在衍射角2θ区间为45°—46°时的放大图谱. 衍射峰位置无明显变化, 说明少量ANS固溶相的引入对晶胞的尺寸影响不大.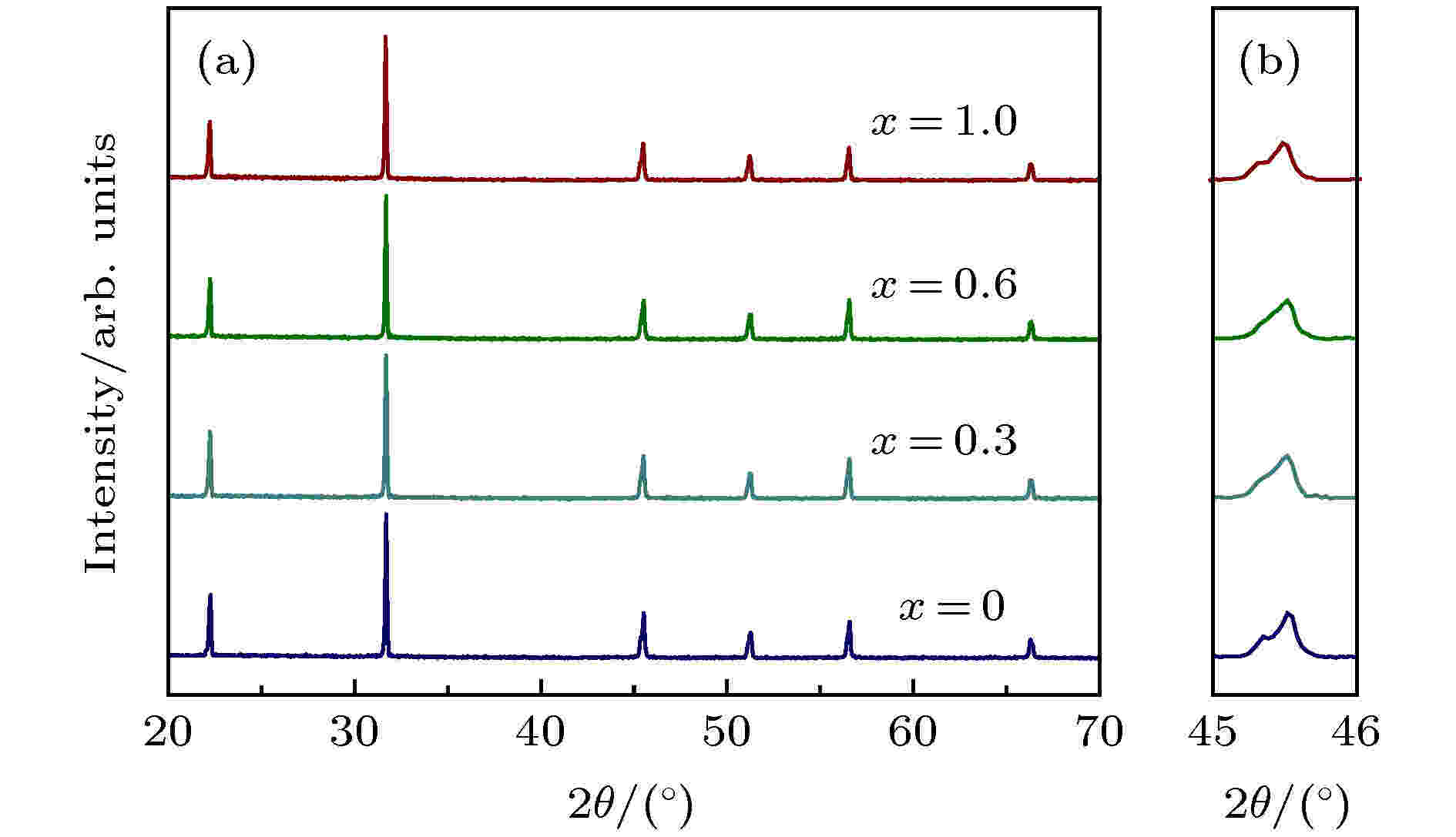
图 1 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的XRD图谱　(a) 2θ = 20°—70°; (b) 2θ = 45°—46°
Figure1. XRD patterns of KNNS-BNKZ-A_xN_1–xS-Fe ceramics: (a) 2θ = 20°? 70°; (b) 2θ = 45°? 46°.

为了进一步表征 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的相结构, 图2(a)给出了系列陶瓷样品介电常数随温度的变化曲线(ε_r-T), 测试温度为–150—200 ℃, 频率为10 kHz. 对于各组分, 可观察到3个介电异常峰, 分别对应材料的T (tetragonal phase, 四方相)-C (cubic phase, 立方相), O (orthorhombic phase, 正交相)-T以及微弱的R (rhombohedral phase, 三方相)-O相转变. 同时, O相被严重压缩, R-O与O-T相变相互靠近, 形成了弥散的“R-O-T”介电峰. 对于这种“弥散”现象, 一种合理的解释是, 由于晶体学的等效位置被不同的阳离子随机占据, 使得材料的成分出现了统计学波动^[21]. 图2(b)为根据介温曲线绘制得到的KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的相图. 系列陶瓷样品的相变温度(T_C～175 ℃, T_O-T～50 ℃, T_R-O～–10 ℃)在x = 0—1的范围内基本保持不变. 结合XRD图谱, 判断KNNS-BNKZ-A_xN_1–xS-Fe陶瓷在室温下一个较宽的温度范围内为三方-正交-四方(R-O-T)相共存结构.
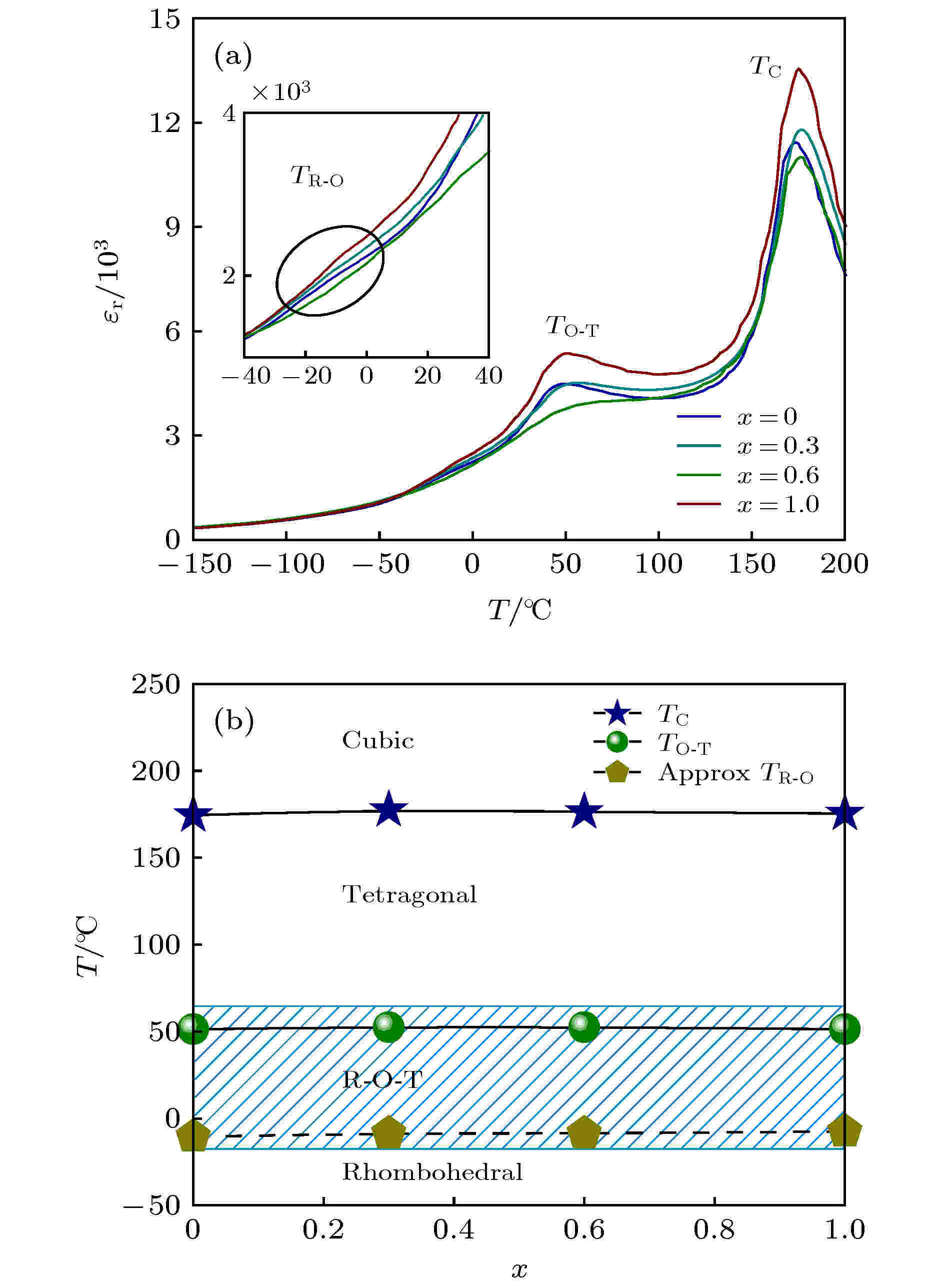图 2 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的(a) ε_r-T曲线(测试温度范围为–150—200 ℃, 频率为10 kHz)和(b)相图
Figure2. (a) ε_r-T curves measured at –150–200 ℃ and 10 kHz and (b) the phase diagram of KNNS-BNKZ-A_xN_1–xS-Fe ceramics.

为了进一步讨论KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的物相结构, 对样品进行了拉曼光谱分析(图3). 图3(a)给出了KNNS-BNKZ-A_xN_1–xS-Fe陶瓷各组分的拉曼光谱. 所有组分的陶瓷都呈现相似的拉曼光谱, 这也说明组分变化并未对材料结构产生明显影响. 对KNN基压电材料而言, 500—700 cm^–1的高频特征峰与NbO₆的拉伸振动有关^[22,23]. 通过对特征峰进行高斯拟合(图3(b)), 可以提取出ν₁振动模式(～600 cm^–1)的具体信息. 如图3(c)所示, ν₁振动模式的拉曼位移发生了微小的变化. 由于拉曼特征峰所对应的拉曼位移表征的是相互作用的原子之间的结合能, 因此, ν₁振动模式下拉曼位移的减小表示随着AS含量的增大, B⁵⁺与其配位O的结合强度有所减弱. 同时, 拉曼位移的连续变化说明, 在研究的组分范围内材料并未发生相转变^[22]. 图3(d)为ν₁振动模式的半高宽随组分的变化. 对KNNS-BNKZ-NS晶格A位的取代, 导致多种氧八面体振动模式动态耦合, 使得拉曼峰的半高宽增大.
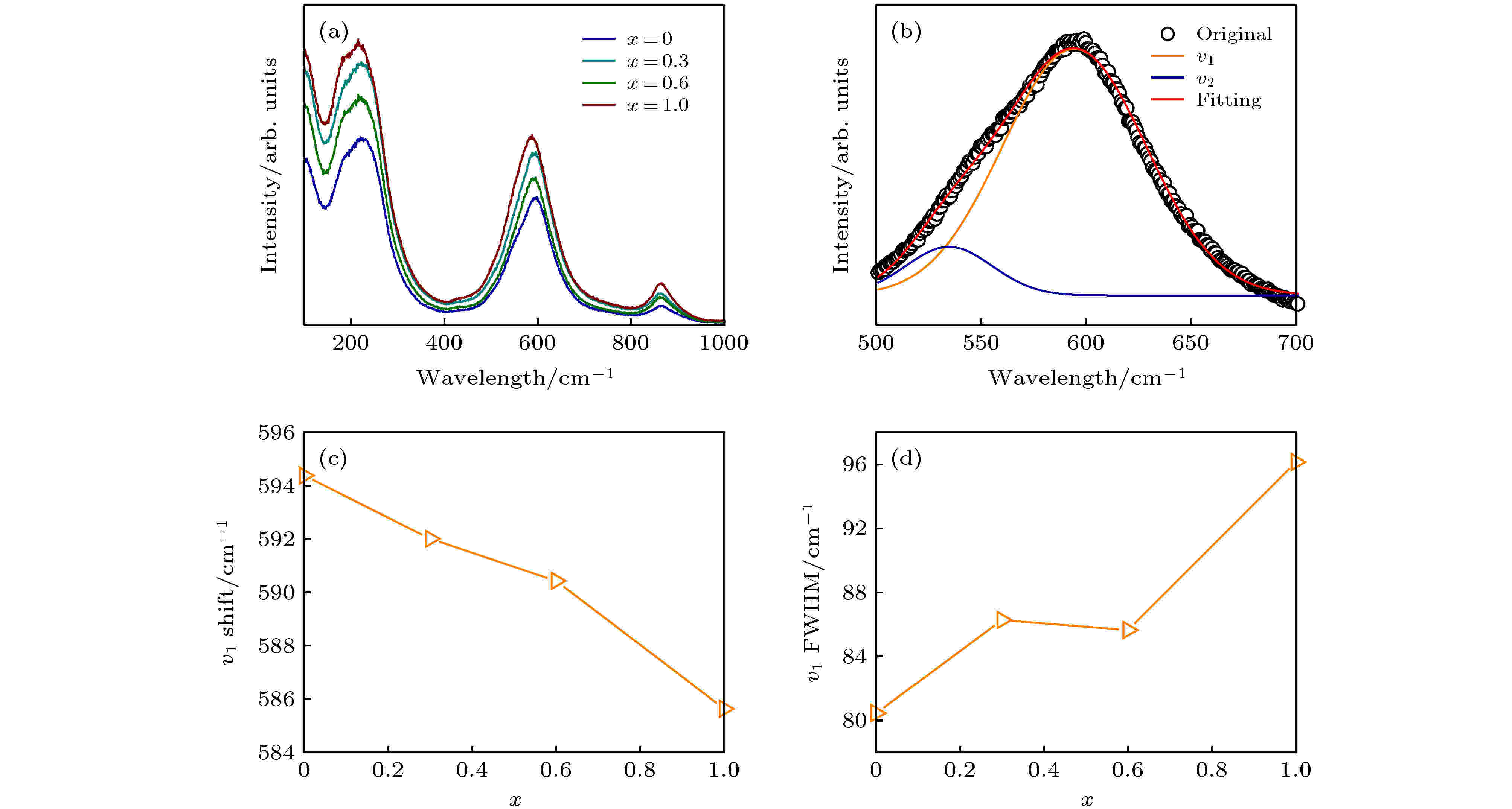图 3 (a) KNNS-BNKZ-A_xN_1–xS-Fe陶瓷各组分的拉曼光谱; (b) x = 0组分的ν₁和ν₂特征峰拟合图; (c) ν₁振动模式的拉曼位移; (d) ν₁振动模式的半高宽随组分的变化
Figure3. (a) Raman spectra of KNNS-BNKZ-A_xN_1–xS-Fe; (b) Gaussian fitting of Raman spectra for x = 0; (c) Raman shift of v₁ mode; (d) full width at half maximum (FWHM) as a function of composition at v₁ mode.

2 -->

3.2.微观形貌

图4给出了KNNS-BNKZ-A_xN_1–xS-Fe陶瓷样品表面形貌随AS含量的变化图. 如图4所示, 所有样品均呈现出明显的大小晶粒夹杂, 大晶粒可以达到15—20 μm, 但多数为2—3 μm的小晶粒. 总体上晶粒尺寸对x的含量无明显的依赖关系, 但当掺杂的固溶相全部为AS时(x = 1), 较大尺寸的晶粒数量有所增多. 就晶粒生长过程而言, 高的粉体颗粒表面自由能和顺利的晶界迁移过程都有利于晶粒长大.
图 4 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的SEM图谱
Figure4. SEM surface images of KNNS-BNKZ-A_xN_1–xS-Fe ceramics.

2 -->

3.3.压电、介电及铁电性能

图5(a)给出了KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的压电系数d₃₃和机电耦合系数k_p对组分的依赖关系. 随x的增大, d₃₃和k_p有所波动(d₃₃～518—563 pC/N, k_p～0.45—0.56). 高的压电性能主要归结于三方-正交-四方相界的形成. 图5(b)为陶瓷的介电常数ε_r和介电损耗tanδ随组分的变化情况, 测试频率为100 kHz. 结果表明, 介电常数随AS含量变化轻微波动, 介电损耗基本维持在0.07—0.08. 图5(c)为KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的室温电滞回线随组分的变化, 测试频率为1 Hz. 所 有样品均呈现饱和的电滞回线, 说明陶瓷是良好的铁电体. 该体系较低的矫顽场(E_c) (～4.8 kV/cm)主要来自于室温下多相共存时较小的能量势垒, 有利于铁电畴在外场下的翻转. 为了更清楚地反映该材料体系铁电性能随组分的变化趋势, 图5(d)总结了各组分的最大极化强度(P_max)和剩余极化强度(P_r). 随着AS的增加, 二者均呈现轻微变化(P_max～21—23 μC/cm²和P_r～14—17 μC/cm²).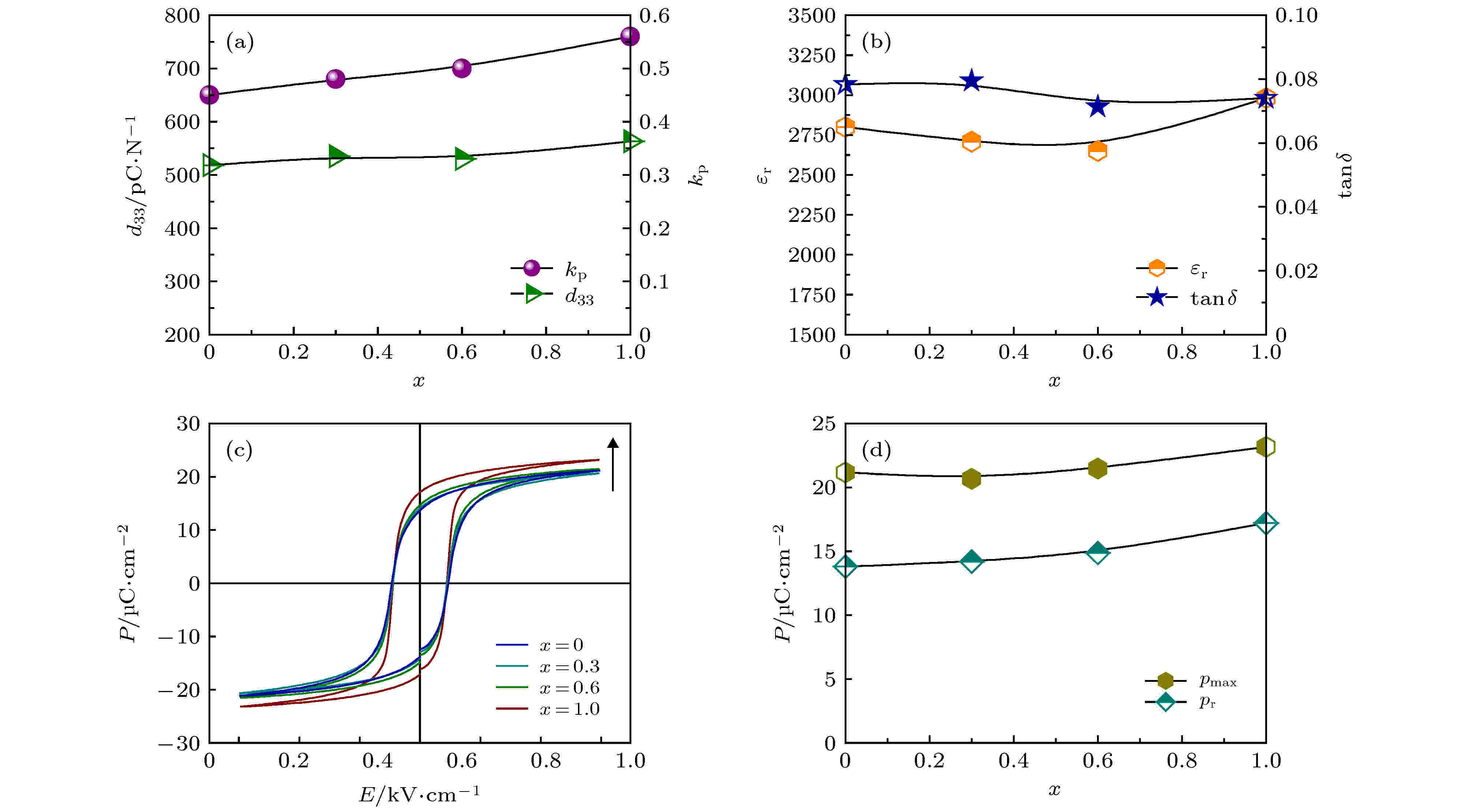
图 5 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的室温(a)压电, (b)介电和(c), (d)铁电性能
Figure5. (a) Piezoelectric, (b) dielectric and (c), (d) ferroelectric properties of KNNS-BNKZ-A_xN_1–xS-Fe ceramics at room temperature

2 -->

3.4.电卡效应

图6测试了KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的变温电滞回线, 测试温度范围为30—180 ℃, 测试频率为1 Hz. 从图6可以看出, 所有组分样品的电滞回线随着温度升高逐渐变得细长, P_max和E_C随着温度的升高逐渐降低. 此外, 由低温介温图谱(图2)可知, 所有组分样品在室温～200 ℃温度范围内均存在两个相变点, 分别是～50 ℃的正交-四方(O-T)相变和～175 ℃的四方-立方(T-C)相变, 对应于图6中各组分的${\left( {{{\partial P}/{\partial T}}} \right)_E} \text{-} T$曲线在T_O-T和T_C附近出现的拐点, 高于居里温度所产生的退极化作用使得P_max值的降低速率显然增大.
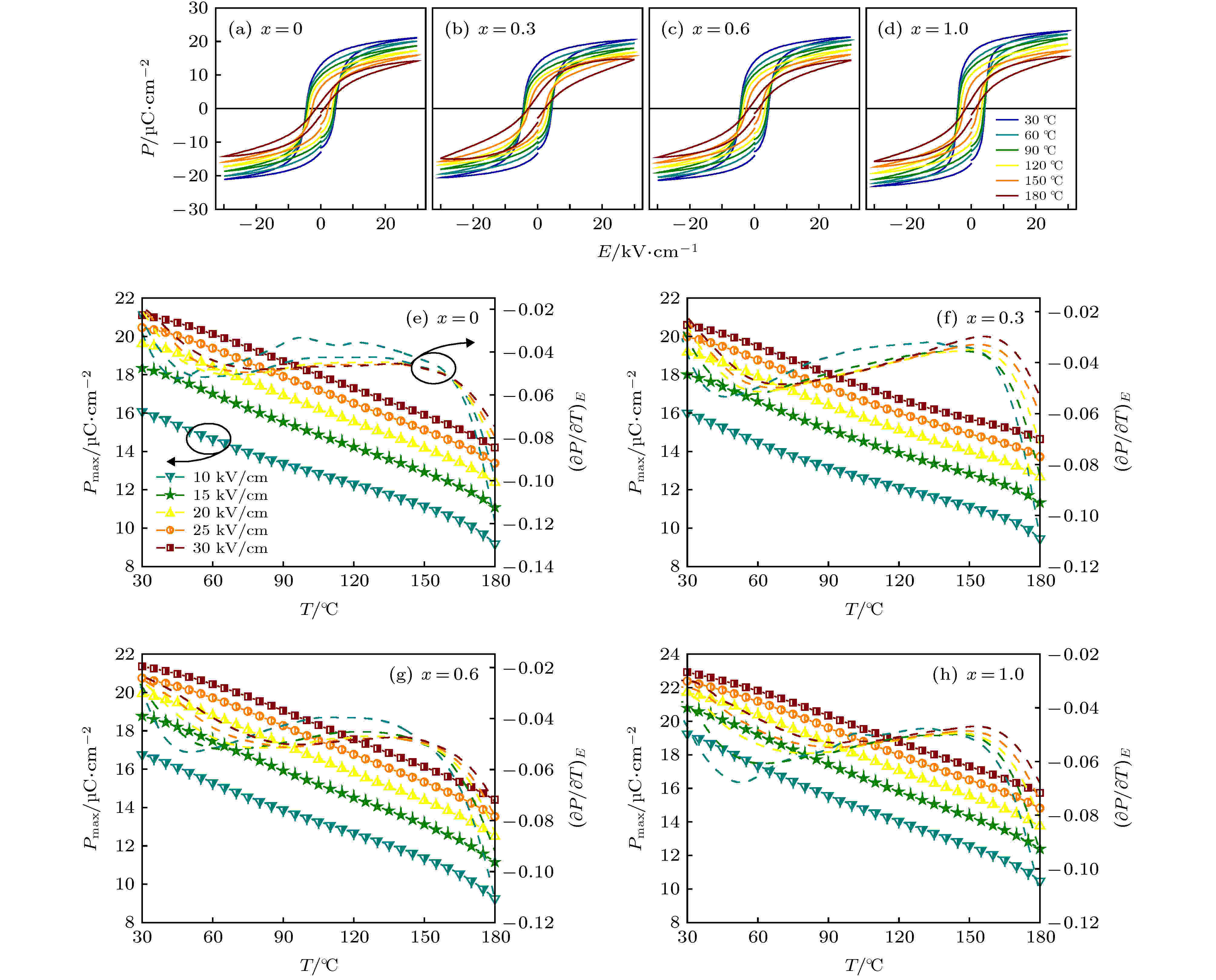图 6 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的(a)—(d)变温电滞回线, 以及(e)—(h)最大极化强度P_max和${\left( {{{\partial P}/{\partial T}}} \right)_E}$随温度的变化
Figure6. (a)?(d) P-E loops, (e)?(h) maximal polarization and ${\left( {{{\partial P}/{\partial T}}} \right)_E}$ as a function of temperature for KNNS-BNKZ-A_xN_1–xS-Fe ceramics.

根据上述实验, 采用间接法^[24]对KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的电卡效应进行计算:

$\Delta T = - \frac{T}{\rho }\int_{{E_1}}^{{E_2}} {\frac{1}{{{C_P}}}} {\left( {\frac{{\partial P}}{{\partial T}}} \right)_E}{\rm{d}}E,$

其中, ${\left( {{{\partial P}/{\partial T}}} \right)_E}$ 为某一固定电场下极化强度随温度的变化速率, 这一值是通过将最大极化强度P_max对温度T进行四项式拟合再求一阶微分得到的; E₁, E₂为初始电场与施加电场, 本文的初始电场为零, 即E₁ = 0; C_P为比热容^[25]; ρ为密度^[26]. 计算得到的电卡温变ΔT如图7(a)—(d)所示, 可以看出, ΔT随着电场强度的增加而增加, 所有组分陶瓷的ΔT在铁电-顺电相变附近产生最大值, 且最大值随电场强度的增加有向高温方向漂移的趋势. 进一步分析发现, 各组分陶瓷在O-T相变附近都获得了展宽的温度区间(～90 K), 但相应ΔT值较低; 反之, 在居里点附近虽然可以获得较大的电卡温变(ΔT_max > 0.6 K, x = 0.1), 但与之相伴的是狭窄的温度区间. 如图8所示, 随着AS含量的增加, T_C处的ΔT先降后升, 说明AS和NS对T_C处的电卡贡献相同; T_O-T处的ΔT随AS增加有轻微变化, 与室温下的铁电变化趋势一致.
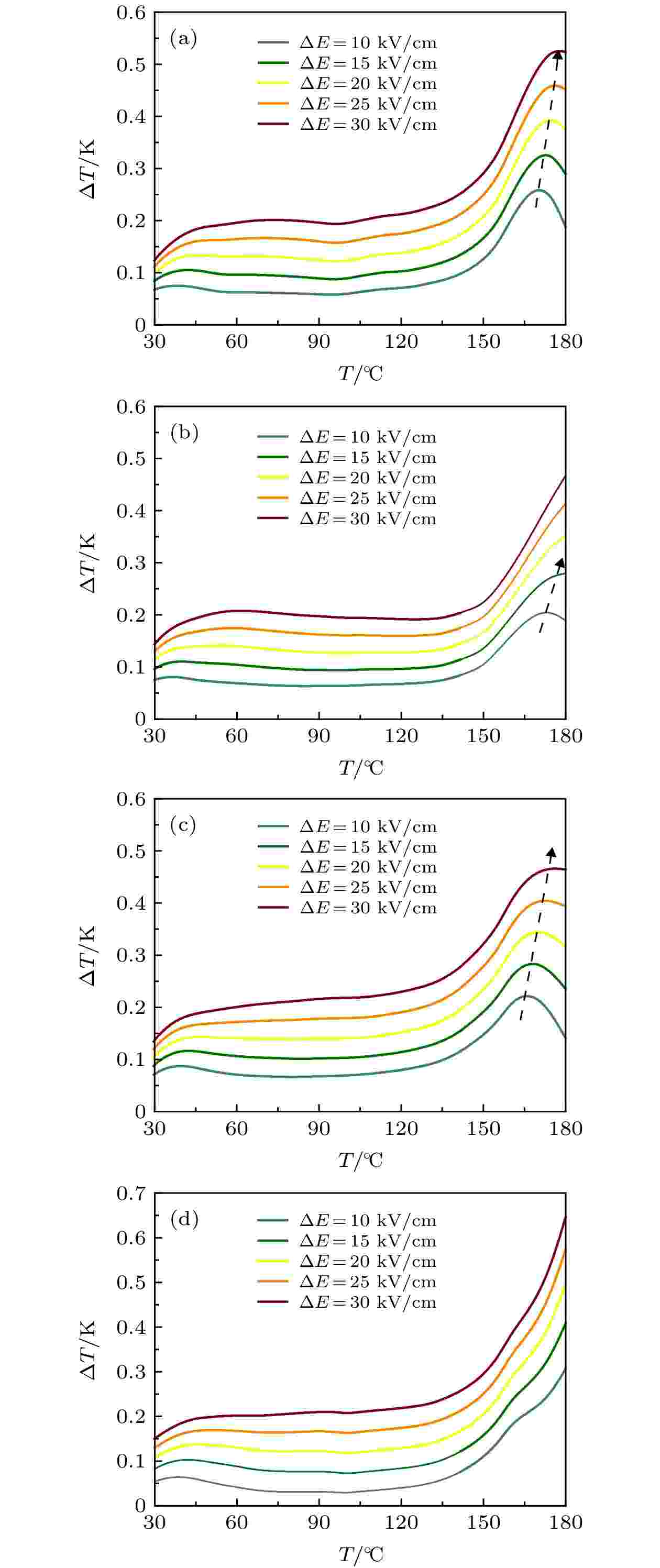图 7 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的电卡温变ΔT随温度和电场的变化规律　(a) x = 0; (b) x = 0.3; (c) x = 0.6; (d) x = 1.0
Figure7. Electrocaloric temperature change ΔT of KNNS-BNKZ-A_xN_1–xS-Fe ceramics as functions of temperature and electric field: (a) x = 0; (b) x = 0.3; (c) x = 0.6; (d) x = 1.0.

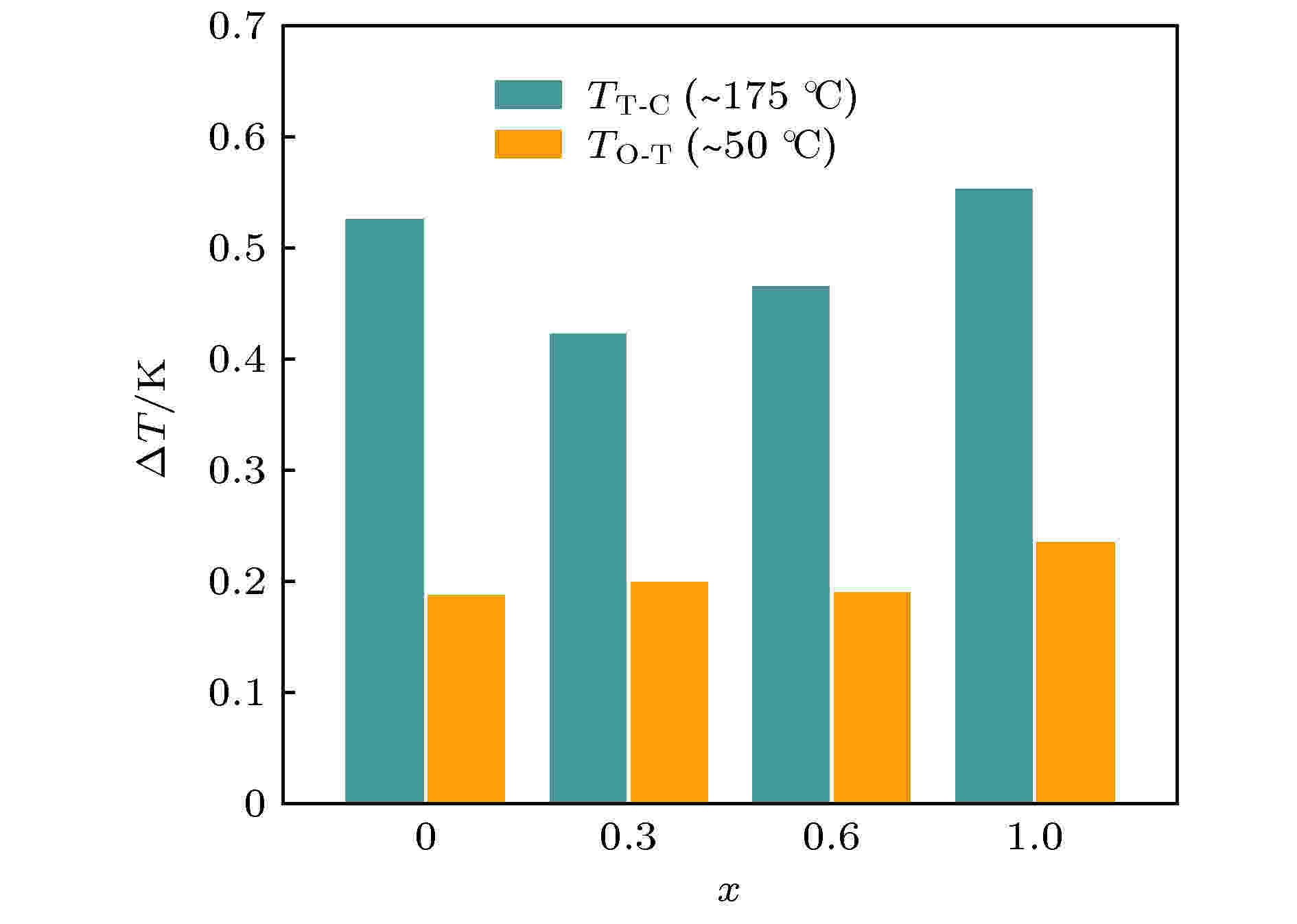图 8 KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的电卡温变ΔT随组分的变化
Figure8. Electrocaloric temperature change ΔT of KNNS-BNKZ-A_xN_1–xS-Fe ceramics as a function of composition.

鉴于在不同相变处获得的电卡效应的巨大差异, 考虑相变对于电卡效应的影响. 由间接法公式可以看出, 电卡材料的绝热温变与极化强度随温度的变化$\left( {{{\partial P}/{\partial T}}} \right)$有关, 极化强度随温度的变化越剧烈, 电卡温变值越大. 对铁电材料来说, 晶体发生结构相变时, 其物理性质往往会出现强烈改变^[27]. 铁电材料的结构相变主要由铁电-顺电相变和铁电-铁电相变组成. 铁电材料在居里温度以下表现出铁电相, 遍布自发极化矢量, 在电场作用下极化矢量极易取向一致, 表现出极化有序状态; 超过居里温度转变为顺电相, 是无极化状态. 这种由极化有序向极化无序状态的改变导致极化强度的大幅度下降, 从而在居里温度附近铁电材料的电卡温变一般会产生最大值. 在铁电-铁电相变时, 自发极化虽然不是从无到有(或相反), 但其大小和方向仍会发生较大的变化. 在本文中, 弥散的R-O-T相变虽然拓宽了相变温区, 代价则是$\left( {{{\partial P}/{\partial T}}} \right)$的相对减小; 铁电-顺电相变附近能获得较大的$\left( {{{\partial P}/{\partial T}}} \right)$, 但其也存在问题, 相变温区太窄且不在室温附近. 因此, 根据不同需求选择合适的相变, 是提高电卡材料实际应用价值的重要方法.
为了深入研究KNNS-BNKZ-A_xN_1–xS-Fe陶瓷的电卡性能随温度和电场的变化规律, 选择x = 0.6组分进行分析, 如图9(a)和图9(b)所示. 从图9(a)可以看出, ΔT和电场强度基本呈现线性关系, 但是在不同的温度下其线性斜率不同, 在铁电-顺电相变温度(～175 ℃)附近的温度区间, 斜率随温度的升高而持续增大. 图9(b)给出了x = 0.6组分的电卡系数(ΔT/ΔE)随温度和电场的变化. 同一电场下的电卡系数随温度上升经历了先增大后减小再到不变的过程, 在铁电-顺电相变温度附近达到极大值. 与ΔT的变化规律相似, ΔT/ΔE的最大值随电场强度的增加向高温移动; 不同的是, 电卡系数随着电场强度的变化会在一些温度点出现交点. 为了解释这一现象, 对x = 0.6组分160—180 ℃温度段的电卡强度进行分析. 由图9(b)内插图可以看出, 材料的电卡系数随着电场的增加趋于一定值, 即达到饱和. 这可能是由于在不同电场下, 铁电材料内的极化机制有所差异, 如畴翻转、宏畴-微畴转变、场致铁电相变和介电极化等, 导致对电卡效应的贡献不同造成的^[28]. 图10对比了x = 1.0时, 本工作与现有报道的KNN基电卡材料在小于等于40 kV/cm电场下的电卡性能^{[14,25,29-33]}. 从图10可以看出, 本文在铁电-顺电相变附近, 能够在较低的电场(30 kV/cm)下得到较高的ΔT (～0.65 K)和ΔT/ΔE (～2.17 × 10^–7 K·m·V^–1).
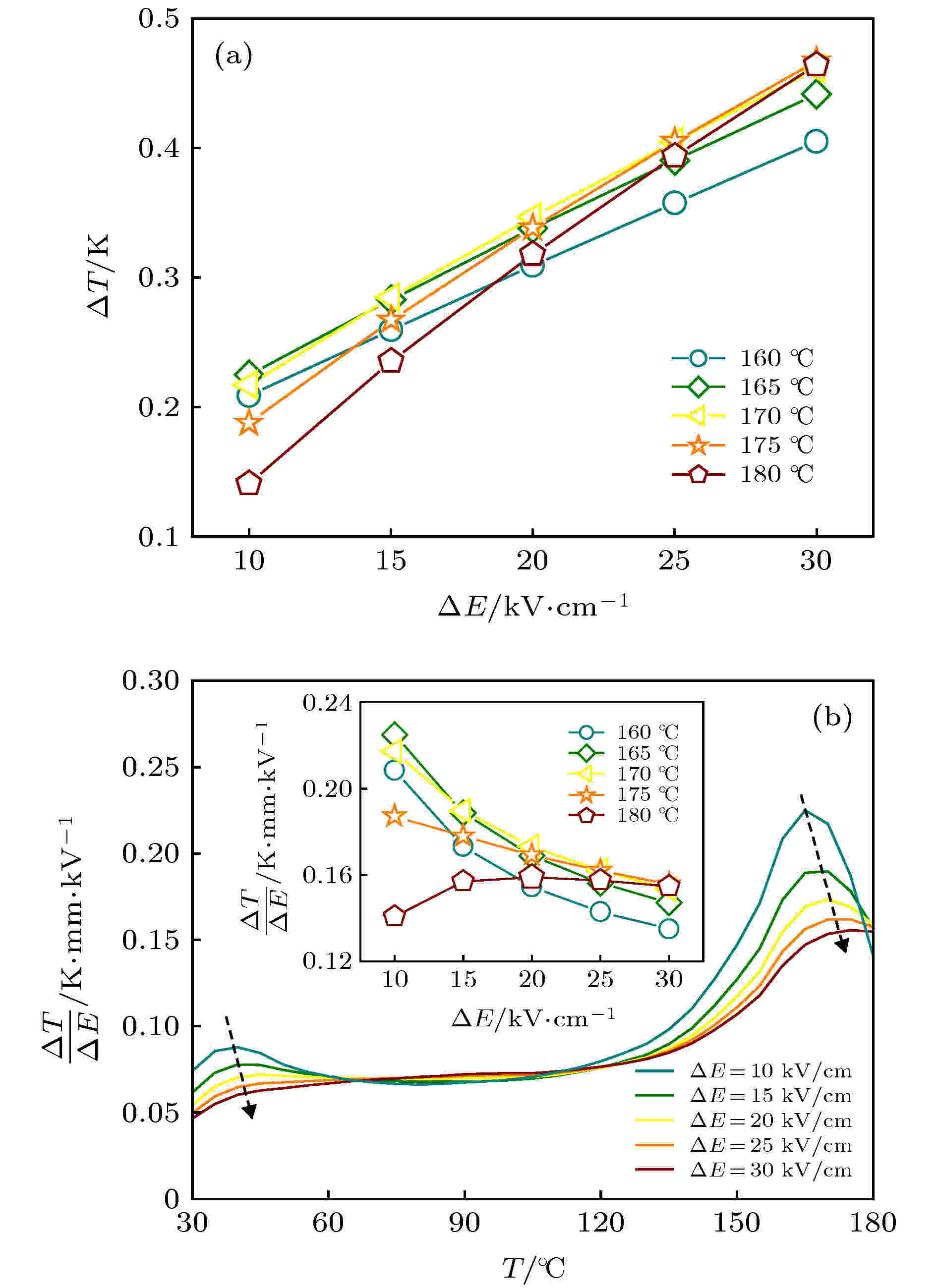图 9 KNNS-BNKZ-A_0.6N_0.4S-Fe陶瓷的电卡性能　(a)电卡温变ΔT; (b)电卡系数ΔT/ΔE随温度和电场的变化规律
Figure9. Electrocaloric property of KNNS-BNKZ-A_0.6N_0.4S-Fe ceramic: (a) Electrocaloric temperature change ΔT; (b) electrocaloric coefficient ΔT/ΔE as functions of temperature and electric field.

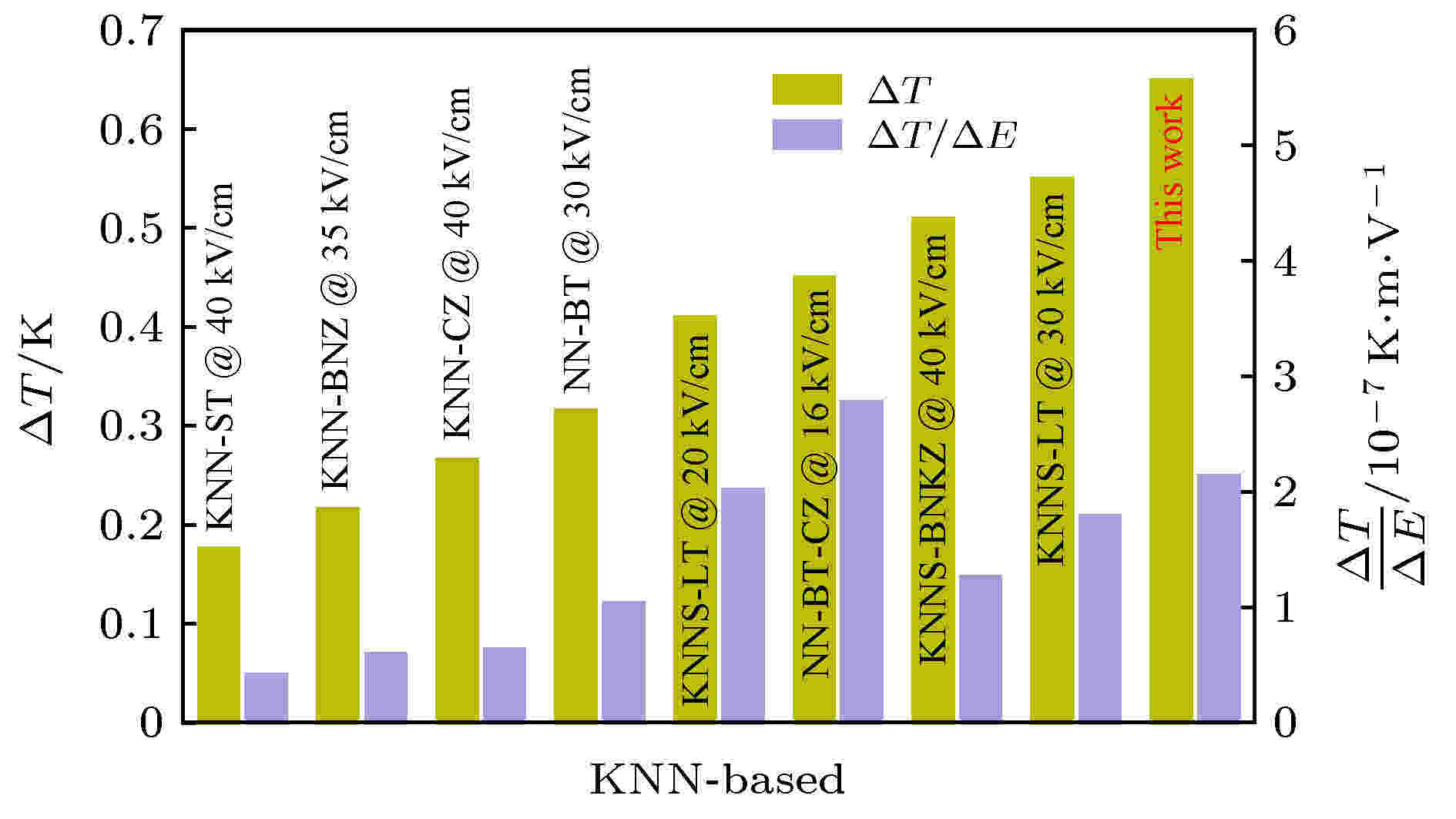图 10 本文获得的ΔT和ΔT/ΔE与已报道KNN基陶瓷相应结果的对比
Figure10. Comparison of ΔT and ΔT/ΔE achieved in this work with other previously reported KNN-based ceramics.

采用传统固相法制备了0.944 K_0.48Na_0.52Nb_0.95Sb_0.05O₃-0.04 Bi_0.5(Na_0.82K_0.18)_0.5ZrO₃-1.6%(Ag_xNa_1–x)SbO₃-0.4%Fe₂O₃陶瓷, 讨论了AS/NS比例的变化对陶瓷样品结构和电学性能的影响. 对相结构的研究表明, 所有样品均为R-O-T三相共存. AS的掺入还使得BO₆氧八面体中B—O键的强度有所减弱, 同时B位的复杂取代也导致了多种氧八面体振动模式的动态耦合. 随着x含量的增加, 样品的压电、介电和铁电性能有所波动, 但是所有组分均呈现高的压电常数. 电卡效应的研究显示, 不同相变对于电卡效应的影响有所不同. 弥散的相变虽然拓宽了材料的工作温区, 但是以牺牲$\left( {{{\partial P}/{\partial T}}} \right)$为代价的; 铁电-顺电相变附近能获得较大的电卡温变, 但其问题在于相变温区太窄且不在室温附近. 而且, 在不同电场下, 铁电材料内的极化机制有所不同, 从而导致对电卡效应的贡献不同. 本文将为KNN基陶瓷压电和电卡性能的进一步研究提供思路.