摘要: 基于现有实验, 本文构建一束弱线性偏振光在平行于传播方向的磁场作用下分裂为两正交偏振光, 当其与三角形三量子点相互作用后形成五能级M型三量子点电磁感应透明介质模型. 随后, 利用多重尺度结合傅里叶积分方法研究体系中的光孤子传播及两孤子间的碰撞特性, 结果发现孤子间的碰撞方式是由其初始相位差所决定. 当孤子间初相位差为0时, 孤子间的碰撞为周期性弹性碰撞; 当初相位差为
$\text{π} /4$ ,
$ \text{π} /2$ 和
$ \text{π} $ 时, 孤子间会产生排斥作用力而使两孤子分离. 有趣的是, 孤子间的碰撞特征受量子点间的隧穿强度的调控. 当点间隧穿强度的增加, 初相位差为0的孤子间的碰撞周期减小; 而初相位差为
$ \text{π} /4$ ,
$ \text{π} /2$ 和
$ \text{π} $ 时孤子间的排斥力增大. 这为实验上如何操控半导体量子点器件中的孤子动力学提供了一定的理论依据.
关键词: 点间隧穿 /
孤子碰撞 /
相位差 /
电磁诱导透明介质 English Abstract Controlling collision properties of solitons in five-level M-type triple quantum dot electromagnetically induced transparency medium by inter-dot tunneling coupling Yang Xuan Wang Yin Wang Deng-Long Ding Jian-Wen School of Physics and Optoelectronics, Xiangtan University, Xiangtan 411105, China Received Date: 20 January 2020Accepted Date: 22 May 2020Available Online: 05 June 2020Published Online: 05 September 2020Abstract: Experimentally, the triple-quantum-dots system can be produced on a GaAs $ \left[ {001} \right]$ substrate by molecular beam epitaxy or in-situ atomic layer precise etching, thus enabling a triangle triple quantum dot (QD) aligned along the $ \left[ {1\bar 10} \right]$ direction. According to this, we first propose a five-level M-type triple QD electromagnetically induced transparency (EIT) model which consists of a triple QD molecule interacting with a weakly linearly polarized probe field with two orthogonal polarization components under the action of a magnetic field parallel to the light propagation direction. Subsequently, by using the multiple-scale method combined with the Fourier integration method, the propagation characteristics of the optical solitons and the collision characteristics of two solitons in the system are studied. It is shown that the optical solitons can form and propagate stably in this system under the action of quantum inter-dot tunneling coupling whose formation mechanism is different from the soliton-forming mechanism in ultra-cold atomic, single QD, and double QD EIT system. This is because the necessary condition for forming a soliton is to use a strong light beam to modulate a weak light beam, whether it is in an ultra-cold atom system, or a single quantum dot EIT medium or a double quantum dot EIT medium. In a word, the formation of soliton in previous EIT systems needs an additional strong controlling field, while the five-level M-type triple QD EIT system is dependent on the inter-dot tunneling. Since the solitons can propagate stably, the collision properties of the solitons may be studied in this system. Finally, by applying Fourier integration method, it is found that the collision behaviors of two solitons are determined by their initial phase difference. When their initial phase difference is 0, the collision behavior between the solitons is periodic elastic collision. While their initial phase difference is separately $ {\rm{\pi }}/4$ , $ \text{π}/2$ , and $ \text{π}$ , the collision behaviors exhibit separation phenomenon due to repulsive effect. Interestingly, the collision characteristics of two solitons are controlled by the inter-dot tunneling strength. With the increase of inter-dot tunneling strength, the collision period of two solitons with the initial phase difference of 0 decreases, and the repulsive force of two solitons with the initial phase difference being separately π/4, π/2 and π increases. This provides some theoretical basis for experimentally controlling the soliton dynamical properties in semiconductor quantum dot devices. Keywords: inter-dot tunneling coupling /solition collision behaviors /phase difference /electromagnetically induced transparency medium 全文HTML --> --> --> 1.引 言 孤子是由色散效应(或衍射效应)与非线性效应相平衡所形成的载体[1 ] , 由于孤子在传播中具有保持波形不变、保真度高和抗干扰能力强等优势[2 -8 ] , 在量子通信和量子调控等领域具有良好的应用. 当孤子作为量子信息通信过程的传播载体时会同时出现多个, 则这些孤子间可能会出现碰撞从而产生畸变, 导致信息失真[9 ,10 ] . 因此探讨孤子间的碰撞特性成为当今量子通信领域的研究热点问题之一[11 -15 ] . 能产生孤子的媒质一般需要具备较强的非线性效应, 电磁感应透明(EIT)介质正是通过弱光激发出强的非线性效应[16 -21 ] . 最早的EIT介质是超冷原子体系. 在超冷原子体系中, Wu和Deng[22 ,23 ] 发现当探测光通过该体系时受控制光的调制后, 系统可产生光孤子; Huang等[24 ] 也证实了光孤子能够存在于超冷原子体系中且孤子间会产生弹性碰撞. 随后Kumar等[25 ] 证实超冷原子体系的孤子间不仅能发生弹性碰撞类型也能发生非弹性碰撞类型, 且碰撞类型可通过控制光去调节. Chen等[26 ] 证实超冷原子体系中超慢光孤子间可发生弹性碰撞外, 还可通过耦合光去操控探测光的光存储和读取. 然而, 由于超冷原子EIT介质温度过低、材料性能难以精确控制, 很难形成大规模化的器件, 因而在实际应用中具有很大的局限性.[27 -31 ] 等优势, 因而被认为是最有希望实现EIT应用的介质. Yang等[32 ] 在单个量子点中通过双激子相干成匹配慢光孤子对, 发现孤子间碰撞的作用力是吸引还是排斥是由孤子间的相位差来控制的. 尽管使用的是单量子点模型, 研究的却是光通过一系列量子点阵列. 当量子点之间的距离比较大时, 量子点与点之间的相互作用比较弱几乎可以忽略不计. 当量子点与点之间的距离较小时, 量子点间就会出现隧穿等耦合作用, 且实验上通过外加门电压能使量子点间的隧穿作用大大加强[33 ,34 ] . 从而研究者开始使用由双量子点所组成的量子点分子模型去研究其中的物理性质. 现有研究表明, 双量子点模型由于隧穿耦合所引起的非线性效应比单量子点中的非线性效应强得多[35 ,36 ] . 我们课题组曾在双量子点间外加垂直方向电场, 通过控制隧穿和电场强度实现了亮暗孤子之间的转换[37 ] . 相对于单量子点和双量子点模型, 三量子点模型通过两个隧穿效应不仅能产生双诱导透明窗口而且还能获得巨大的克尔非线性效应[38 ] , 因而三量子点模型的非线性性质将更加丰富、新颖和有趣[39 -41 ] . 由于三量子点EIT介质的物理性质研究还刚刚起步, 因此有关三量子点EIT介质中的光孤子, 尤其是其中的孤子碰撞特性的研究尚未涉及.2.五能级M型三量子点EIT介质模型 根据目前实验[42 ,43 ] , 以半导体GaAs$\left[ {001} \right]$ 为衬底, 采用分子束外延和原位原子层精密蚀刻(in-situ atomic layer precise etching)技术组合而成, 沿$\left[ {1\bar 10} \right]$ 方向可生长出三角形排列的三量子点. 当一束弱线偏振探测光与此三量子点分子相互作用后就可形成五能级M型三量子点模型[41 -44 ] , 如图1 所示. 根据文献[44 -47 ], 整个模型的具体构成如下: 当一束弱线偏振探测光在与其平行的磁场作用下会分裂成左旋偏振光(${\sigma ^{{ - }}}$ )和右旋偏振光(${\sigma ^{{ + }}}$ )两偏振分量, 然后, 在外加电场(即给量子点之间提供门电压)后, 可将中间量子点的电子从价带激发到导带形成空穴, 由于导带电子和价带的空穴存在相互作用, 便会形成电子-空穴对, 即图1 中的激子态$\left| 1 \right\rangle $ 和$\left| 2 \right\rangle $ . 而隔开量子点的势垒高度可通过量子点之间的门电压来控制. 当中间量子点与左、右量子点之间同时附加偏压后, 则会导致中间量子点导带的电子隧穿到左、右量子点的导带中, 由于量子点间间距较小(一般仅为几个nm), 电子和空穴间的作用仍然比较强, 从而仍然会形成激子态, 如图1 中的间接激子态$\left| 3 \right\rangle $ 和$\left| 4 \right\rangle $ . 此时, 能级$\left| 0 \right\rangle $ , $\left| 1 \right\rangle $ , $\left| 3 \right\rangle $ 与能级$\left| 0 \right\rangle $ , $\left| 2 \right\rangle $ , $\left| 4 \right\rangle $ 分别组成不对称的$\Lambda $ 型三能级量子点分子模型. 两个$\Lambda $ 型三能级量子点共用一个基态$\left| 0 \right\rangle $ , 组合以后就形成了图1 中所描绘的五能级M型三量子点模型. 根据旋波近似和电偶极近似, 在相互作用绘景下体系的哈密顿量可写为图 1 五能级M型三量子点电磁感应透明介质能级结构图. $ \left| 0 \right\rangle $ 表示基态, $ \left| 1 \right\rangle $ 和$ \left| 2 \right\rangle $ 表示直接激子态, $ \left| 3 \right\rangle $ 和$ \left| 4 \right\rangle $ 是间接激子态, $ T{e_1}$ 和$ T{e_2}$ 分别表示中间量子点与左、右量子点间的点间隧穿耦合强度Figure1. Energy level structure diagram of a five-level M-type three-quantum-dot electromagnetically induced transparent medium. Here $ \left| 0 \right\rangle $ is the ground state, $ \left| 1 \right\rangle $ and $ \left| 2 \right\rangle $ are the direct exciton state, $ \left| 3 \right\rangle $ and $ \left| 4 \right\rangle $ represent the indirect exciton state, and $ T{e_1}$ and $ T{e_2}$ represent the strength of tunneling coupling between the intermediate quantum dot and the left and right quantum dot, respectively.B 作用下所引起的能级间隔. 因此, 能级$\left| 1 \right\rangle $ 和$\left| 2 \right\rangle $ 之间由塞曼分裂所引起的能级间隔为$\varDelta {{ = }}{\mu _{\rm{B}}}{M_{\rm{F}}}{g_{\rm{F}}}B/\hbar $ , ${\mu _{\rm{B}}}$ 表示玻尔磁子, ${g_{\rm{F}}}$ 表示朗德因子, ${M_{\rm{F}}} = \pm 1$ 表示相应的磁量子数. (1 )式中${\varDelta _1} \!=\! {\omega _{10}} \!-\! {\omega _{\rm{p}}}$ , ${\varDelta _2} \!=\! \varDelta \!+\! {\omega _{10}} \!-\! {\omega _{\rm{p}}}$ 是单光子失谐, ${\varDelta _3} = {\omega _{10}} - {\omega _{\rm{p}}} + {\omega _{13}}$ , ${\varDelta _4} = \varDelta + {\omega _{10}} - {\omega _{\rm{p}}} + {\omega _{24}}$ 为双光子失谐. 探测光的左旋、右旋两偏振分量的半拉比频率可分别表示为${\varOmega _{{\rm{p}}1}} = {{{{{e}}_{{\rm{p}}1}} \cdot {{{p}}_{10}}{\varepsilon _{{\rm{p}}1}}} / \hbar }$ , ${\varOmega _{{\rm{p}}2}} = {{{{{e}}_{{\rm{p}}2}} \cdot {{{p}}_{20}}{\varepsilon _{{\rm{p}}2}}} / \hbar }$ , 其中${{{e}}_{{\rm{p}}1}}$ (${{{e}}_{{\rm{p}}2}}$ )为振幅包络为${\varepsilon _{{\rm{p}}1}}$ (${\varepsilon _{{\rm{p}}2}}$ )探测光的左旋(右旋)偏振分量的单位矢量, ${{{p}}_{ij}}$ (i = 1, 2; j = 0)表示从$\left| i \right\rangle $ 跃迁到$\left| j \right\rangle $ 的电偶极矩阵元. $T{e_1}$ 和$T{e_2}$ 分别表示中间量子点与左、右量子点间的点间隧穿耦合强度, H.c.表示体系哈密顿量的复共轭项.${{{E}}_{{\rm{p}}1}} = {{{e}}_{{\rm{p}}1}}{\varepsilon _{{\rm{p}}1}}\exp \left[{\rm{i}}\left({{{k}}_{{\rm{p}}1}}\cdot {{r}} - {\omega _{\rm{p}}}t \right) \right] + {\rm c.c.}$ , ${{{E}}_{{\rm{P}}2}} = {{{e}}_{{\rm{p}}2}}{\varepsilon _{{\rm{p}}2}}\exp \left[ {{\rm{i}}\left( {{{{k}}_{{\rm{p}}2}}\cdot {{r}} - {\omega _{\rm{p}}}t} \right)} \right] + {\rm c.c.}$ , ${{{k}}_{{\rm{p}}1}}$ 表示左旋偏振分量波矢, ${{{k}}_{{\rm{p}}2}}$ 表示右旋偏振分量波矢, $\rm c.c.$ 表示复共轭函数. ${\varepsilon _0}$ 是真空中的介电常数, c 为真空中的光速. 左旋偏振分量的电极化强度表示为${{{P}}_{{\rm{p}}1}} = {N_{{\rm{a1}}}}{{{p}}_{10}}{A_1}A_0^ * \exp \left[ {{\rm{i}}({{{k}}_{{\rm{p}}1}}\cdot {{r}} - {\omega _{\rm{p}}}t)} \right] + \rm c.c.$ , 右旋偏振分量的电极化强度表示为${{{P}}_{{\rm{p}}2}} = {N_{{\rm{a2}}}}{{{p}}_{20}}{A_2}A_0^ * \times \exp \left[ {{\rm{i}}({{{k}}_{{\rm{p}}2}}\cdot {{r}} - {\omega _{\rm{p}}}t)} \right] + \rm c.c.$ , ${N_{{\rm{a}}i}}\;\left( {i = 1, 2} \right)$ 表示原子数密度, ${A_l}$ (l = 0, 1, 2, 3, 4)表示$\left| l \right\rangle $ 能级的概率幅, 满足守恒关系${\left| {{A_0}} \right|^2} + {\left| {{A_1}} \right|^2} + {\left| {{A_2}} \right|^2} + {\left| {{A_3}} \right|^2} + {\left| {{A_4}} \right|^2} = 1$ . 根据薛定谔方程${\rm{i}}\hbar \dfrac{\partial }{{\partial t}}\left| \varPsi \right\rangle = H\left| \varPsi \right\rangle $ , 并对麦克斯韦方程(2 )式做慢变包络近似, 整理可得到探测光左旋、右旋两偏振分量与量子点相互作用下的麦克斯韦-薛定谔方程组为${d_j} = {\varDelta _j} + {\rm{i}}{\gamma _j}$ (j = 1, 2, 3, 4), 其中${\gamma _j}$ 表示能级$\left| j \right\rangle $ 上总衰减率, 故有${\gamma _j} = {\gamma _{j{\rm{l}}}} + {\gamma _{j{\rm{d}}}}$ , 其中${\gamma _{j{\rm{l}}}}$ 为$\left| j \right\rangle $ 上的辐射衰减, 主要是由于低温下纵波光学声子发射产生, 且随着系统中温度的增加其变化范围可从${\text{μ}}{\rm{eV}} $ 变化到meV; ${\gamma _{j{\rm{d}}}}$ 表示解相(dephasing)率, 主要由于电子与电子、电子与声子散射以及表面粗糙所引起. (3 )式中的${\kappa _{01}} = {N_{{\rm{a}}1}}{\left| {{{{p}}_{01}}\cdot {{{e}}_{{\rm{p}}1}}} \right|^2}{\omega _{\rm{p}}}/(2\hbar {\varepsilon _0}c)$ , ${\kappa _{02}} = {N_{{\rm{a}}2}}{\left| {{{{p}}_{02}}\cdot {{{e}}_{{\rm{p}}2}}} \right|^2}{\omega _{\rm{p}}}/(2\hbar {\varepsilon _0}c)$ 为传播系数.3.孤子的稳定性分析 一般情况下麦克斯韦-薛定谔方程组(3 )式难以直接解析求解, 从而使用多重尺度法且基于目前实验条件对其近似求解. 故引入渐近展开式${t_l} = {\varepsilon ^l}t$ , ${z_l} = {\varepsilon ^l}z \; (l = 0, 1, 2, \cdots )$ , 各式中的$\varepsilon $ 是描述各能态布居衰减相关的特征小参量. 将上述各式代入方程(3 )中有$j = 1$ 时, 令$\varOmega _{{\rm{p}}1}^{(1)} = {F_1}\exp \left[ {{\rm{i}}({K_1}{z_0} - \omega {t_0})} \right]$ , $\varOmega _{{\rm{p}}2}^{(1)} = {F_2}\exp \left[ {{\rm{i}}({K_2}{z_0} - \omega {t_0})} \right]$ , 其中${F_{1(2)}}$ 是关于慢变量${t_{1(2)}}$ 和${z_{1(2)}}$ 的包络函数, 代入方程(4 )中得到一阶情况下线性偏振光的两正交偏振分量的线性色散关系:${D_1} \!=\! {| {T{e_1}} |^2} - (\omega + {d_1})(\omega + {d_3})$ , ${D_2} \!=\! {| {T{e_2}}|^2} - (\omega + {d_2})(\omega + {d_4})$ . 对探测光的两偏振分量进行泰勒展开有${K_1}\left( \omega \right) = K_1^{\left( 0 \right)} + K_1^{\left( 1 \right)}\omega + \dfrac{1}{2}K_1^{\left( 2 \right)}{\omega ^2} + \cdots $ , ${K_2}\left( \omega \right) = K_2^{\left( 0 \right)} + K_2^{\left( 1 \right)}\omega + \dfrac{1}{2}K_2^{\left( 2 \right)}{\omega ^2} + \cdots $ , 其中$(j = 0, 1, 2, \cdots ), {\rm{Re}} ( {K_1^{( 0 )}} )$ , ${\rm{Re}} ( {K_2^{( 0)}})$ 分别表示左旋、右旋两偏振分量的线性色散, ${\rm{Im}} ( {K_1^{( 0)}})$ , ${\rm{Im}} ( {K_2^{( 0)}} )$ 表示左旋、右旋两偏振分量的线性吸收, 且有 $K_1^{(1)} = \dfrac{{\rm d} K_1(\omega)} {{\rm d}\omega} \Big|_{\omega = 0} = \dfrac{1}{Vg_1}$ , $K_2^{\left( 1 \right)} = \dfrac{{\rm d}K_2(\omega)}{{\rm d}\omega}\Big| _{\omega = 0} = \dfrac{1}{V g_2}$ 表示群速度的倒数, $K_1^{\left( 2 \right)} = \dfrac{{\rm d} ^2 {K_1}(\omega)} {{\rm d} \omega ^2} \Big|_{\omega = 0}$ , $K_2^{\left( 2 \right)} = \dfrac{{\rm d} ^2 K_2 (\omega)}{{\rm d}{\omega ^2}}\Big|_{\omega = 0}$ 表示群速度色散.$j = 2$ 时消除久期项得到$j = 3$ 时类似地消除久期项得到7 )中的色散系数与非线性系数均为复数, 因而难以求得其解析解. 在此, 我们对色散系数和非线性系数的实部和虚部进行比较. 基于目前实验文献[24 ], 可选择量子点的各参数分别为: ${\gamma _1} \!=\! {\gamma _2} \!=\! 0.054\;{\rm{meV}}$ , ${\gamma _3} = {\gamma _4}\! =\! 5.4 \!\times \!{10^{ - 5}}\;{\rm{meV}}$ , 探测光传播系数${\kappa _{01}} = {\kappa _{02}} = 340\;{\rm{meV}}/\text{μ}{\rm m},$ 失谐量$\varDelta \!= \!0.0054\;{\rm{meV}}, $ ${\varDelta _1}\! =\! 0.1674\;{\rm{meV}},$ ${\varDelta _3}\! =\! 0.6480\;{\rm{meV}},$ ${\varDelta _2} = 0.1728\;{\rm{meV}} $ , ${\varDelta _4} \!= \!0.6534\;{\rm{meV}} $ , ${\tau _0} \!= \!3 \!\times \!{10^{ - 8}}\;{\rm{s}}$ . 图2(a) 给出了色散系数的虚部与实部的比值, 可看出$K_1^{\left( 2 \right)}$ 和$K_2^{\left( 2 \right)}$ 的虚部($K_{1{\rm{i}}}^{\left( 2 \right)}$ 和$K_{2{\rm{i}}}^{\left( 2 \right)}$ )远小于相对应的实部($K_{1{\rm{r}}}^{\left( 2 \right)}$ 和$K_{2{\rm{r}}}^{\left( 2 \right)}$ ).图 2 (a) 色散系数和 (b) 非线性系数的虚部与实部的比值随量子点间隧穿强度的变化关系. 图中所选参数已在正文中给出Figure2. The ratio of the imaginary part to the real part of (a) dispersion coefficient and (b) nonlinear coefficient as a function of tunneling strength of the quantum inter-dot. The parameters used are given in the text.图2(b) 示出了非线性系数(${w_{11}}$ , ${w_{12}}$ , ${w_{21}}$ 和${w_{22}}$ )的虚部与实部的比值, 可以看出它们的虚部(${w_{11 i}}$ , ${w_{12 i}}$ , ${w_{21 i}}$ 和${w_{22 i}}$ )也远远小于实部(${w_{11{{r}}}}$ , ${w_{12{{r}}}}$ , ${w_{21{{r}}}}$ 和${w_{22{{r}}}}$ ). 而且, 随着量子点间隧穿强度的增加, 虚部相对于实部的比值越来越小. 因此, 以下的研究过程中忽略虚部的影响, 仅仅考虑实部的影响. 所以, 方程(7 )转化为${t_l} = {\varepsilon ^l}t$ $\left( {l = 1, 2} \right)$ 与${z_2} = {\varepsilon ^2}z$ 将${t_{1\left( 2 \right)}}$ 与${z_2}$ 返回为t 和z . 且定义新的物理参数${U_1} = \varepsilon {F_1}$ , ${U_2} = \varepsilon {F_2}$ , $\tau = t - {z / {Vg}}$ , 其中${1 / {Vg}} = {1 / {2 V{g_1}}} + {1 / {2 V{g_2}}}$ . 同时引入无量纲参数$\sigma = {\tau / {{\tau _0}}}$ , $s = {z / {{L_{\rm{D}}}}}$ , ${u_1} = {{{U_1}} / {{U_0}}}$ , ${u_2} = {{{U_2}} / {{U_0}}}$ , 方程(8 )可以写成如下无量纲形式:${g_{\delta} } = \left( {{{{L_{\rm{D}}}} / {{L_{\delta} }}}} \right){\rm{sgn}} \left( \delta \right)$ , $\delta = 1/2V{g_1} - 1/2V{g_2}$ , ${g_{{\rm{D}}1}} = \dfrac{{K_{1{\rm{r}}}^{\left( 2 \right)}}} {{| {K_{2{\rm{r}}}^{\left( 2 \right)}} |}}$ , ${g_{{\rm{D}}2}} = \dfrac{{K_{2{\rm{r}}}^{\left( 2 \right)}} }{ {| {K_{2{\rm{r}}}^{\left( 2 \right)}} |}}$ , ${g_{nm}} = \dfrac{{w_{nm{\rm{r}}}}} {\left| {{w_{22{\rm{r}}}}} \right|}$ (m = 1, 2; n = 1, 2), 其中${L_{\delta} } = {{{\tau _0}} / {\left| \delta \right|}}$ 表示群速度失配长度, ${L_{\rm{D}}} = \dfrac{{2\tau _0^2}}{{| {K_{2{\rm{r}}}^{\left( 2 \right)}} |}}$ 为色散长度, ${L_{{\rm{NL}}}} = \dfrac{1}{{ {U_0^2\left| {{w_{22{\rm{r}}}}} \right|} }}$ 为非线性长度. 由于孤子的形成条件是系统的非线性效应与色散效应相平衡, 因而可令${L_{{\rm{NL}}}} = {L_{\rm{D}}}$ . 根据目前实验实现量子点的条件[19 ] 可估算方程(9 )中的几个主要物理参数. 当$T{e_1} = T{e_2} = 2.16\;{\rm{meV}} $ 时, ${g_{{\rm{D}}1}} \approx 0.9856$ , ${g_{{\rm{D}}2}} = 1$ , ${g_{11}} \approx 0.9875$ , ${g_{12}} \approx 0.9908$ , ${g_{21}} \approx 0.9967$ , ${g_{22}} = 1$ , ${g_{\delta} } \approx - 1.6056 \times {10^{ - 10}}$ ; 而当$T{e_1} = T{e_2} = 4.32\;{\rm{meV}} $ 时, ${g_{{\rm{D}}1}}\! \approx\! 0.9882$ , ${g_{{\rm{D}}2}} \!=\! 1$ , ${g_{11}}\! \approx\! 0.9907$ , ${g_{12}} \!\approx\! 0.9915$ , ${g_{21}} \approx 0.9992$ , ${g_{22}} = 1$ , ${g_{\delta} } \approx - 1.6090 \times {10^{ - 10}}$ . 因此, 可归纳出${g_{\delta} }$ 始终远小于其他系数, 从而可忽略${g_{\delta} }$ 对体系的贡献. 此时方程(9 )可简化为${g_{{\rm{D}}1}}{g_{22}} = {g_{{\rm{D}}2}}{g_{12}}$ 时, 方程(10 )有如下亮-亮矢量孤子解:${C_1}$ 是自由参数, 定义${C_2} = \left[\left( 2{g_{{\rm{D}}1}} - {g_{11}}C_1^2 \right)/{g_{12}} \right]^{1/2}$ . 相应地, 线性偏振光的两偏振分量${\varOmega _{{\rm{p}}1}}$ 和${\varOmega _{{\rm{p}}2}}$ 可描述为图3 示出了方程(12 )所描述的线性探测光的左旋和右旋两偏振分量的波形${\left| {{\varOmega _{{\rm{p}}1}}/{U_0}} \right|^2}$ 和${\left| {{\varOmega _{{\rm{p}}2}}/{U_0}} \right|^2}$ 分别增加5%的微扰后在EIT介质中随时间的演化情况, 所选量子点参数为:图 3 不同时刻线性探测光的两偏振分量(a) $ {\left| {{\varOmega _{{\rm{p}}1}}/{U_0}} \right|^2}$ 和(b)$ {\left| {{\varOmega _{{\rm{p}}2}}/{U_0}} \right|^2}$ 的传播情况, 图中所用参数为$ {C_1} = 1$ , $ T{e_1} = T{e_2} = 2.16\;{\rm{meV}}$ , 其他的参数已在文中给出Figure3. The propagation behaviors of two polarized components (a) $ {\left| {{\varOmega _{{\rm{p}}1}}/{U_0}} \right|^2}$ and (b) $ {\left| {{\varOmega _{{\rm{p}}2}}/{U_0}} \right|^2}$ of the linear probe field under the different time. The parameters used are $ {C_1} = 1$ , $ T{e_1} = T{e_2} = 2.16\;{\rm{meV}}$ . Other parameters used are given in the text.图3(a) 中可以看出在初始时刻($t/{\tau _0} \!=\! 0$ ), 左旋偏振分量${\left| {{\varOmega _{{\rm{p}}1}}/{U_0}} \right|^2}$ 在$z/{L_{\rm{D}}} \!=\! 0$ 处形成一亮光孤子; 随着时间的推移(如$t/{\tau _0} = 6.0, 12.0$ )该亮孤子向右传播, 并且保持幅度和宽度稳恒不变. 同时图3(b) 中也给出了右旋偏振分量${\left| {{\varOmega _{{\rm{p}}2}}/{U_0}} \right|^2}$ 随时间的演化情况, 发现初始时刻右旋分量与左旋分量同在($z/{L_{\rm{D}}} = 0$ )处形成一亮光孤子, 且随着时间的推移孤子也能在介质中保持幅度和宽度不变地稳定地向右传播. 由此可归纳出线性探测光的左旋、右旋两偏振分量所形成的亮孤子能在五能级M型三量子点体系中稳定地传播. 并且体系所形成孤子的机制是由量子点间的双隧穿耦合调制来实现, 这完全不同于超冷原子和单、双量子点模型中形成孤子的机制. 这是因为无论是超冷原子体系还是单、双量子点EIT介质中, 形成孤子必要条件是一束强控制光去调制一束弱探测光才能形成孤子.4.孤子的碰撞特征 既然体系通过双点间隧穿诱导探测光的两偏振分量所形成的孤子能稳定地传播, 从而就可以探讨孤子间的碰撞行为. 在此, 通过分步傅里叶积分法分析不同初始相位差在不同点间隧穿强度下孤子间碰撞特性. 可选左旋和右旋偏振分量的初始条件分别为${\theta _1}$ 和${\theta _2}$ 分别表示${u_1}$ 和${u_2}$ 两偏振分量的初始相位差. 随后, 将上述左旋和右旋偏振分量的初始条件均代入方程(10a )中, 并对该方程进行分步傅里叶积分就可以获得孤子间的碰撞行为.图4 给出的是隧穿强度$T{e_1} = T{e_2} = 2.16\;{\rm{meV}} $ 探测光的左旋偏振分量在不同初始相位差下的碰撞行为. 从图4(a) 可以看出, 当初相位差为0时, 两孤子相互吸引融合在一起从而产生碰撞, 且在碰撞位置孤子的振幅增加; 碰撞以后两孤子彼此分离, 其振幅又恢复到碰撞前的幅度; 分开一段距离后又再次出现吸引作用而融合, 且各自能量(幅度)保持不变; 所以在此情况下, 孤子间的碰撞行为表现为周期性的弹性碰撞. 当初相位差选为${\text{π}} /4$ 时(图4(b) ), 可看出两孤子先是相互靠近然后因排斥作用相互分离, 相位落后(右边)的孤子传播方向稍微向右偏离, 相位领先(左边)的孤子传播方向向左偏离且远离的速度大于相位落后的孤子. 当初相位差为${\text{π}} /2$ 时(图4(c) ), 与图4(b) 相比, 孤子间碰撞方式类似, 但相互分离的速度明显增加, 相位领先的孤子的传播方向极大地向左偏离, 相位落后的孤子向右偏离的角度也增加了. 当初相位差为${\text{π}} $ 时, 从图4(d) 中可以明显观察到孤子之间的相互排斥作用, 两孤子均偏离原来的方向, 偏离方向相反, 不同于图4(b) 与图4(c) 的是, 两孤子以相同的角度偏离且其偏离的角度明显大于图4(b) 与图4(c) . 由此可归纳出, 孤子间的碰撞方式是由其初相位差所确定. 当初相位差为0(同相)时, 孤子间的碰撞行为表现为周期性的弹性碰撞. 当初相位差为${\text{π}} /4$ , ${\text{π}} /2$ 和${\text{π}} $ 时, 孤子间会产生排斥作用力而使两孤子分离, 而且相位越超前孤子偏离中心位置越远.图 4 当两点间隧穿强度均为2.16 meV时, 孤子对在不同初相位差时的碰撞行为 (a) $ {\theta _1} = 0$ ; (b) $ {\theta _1} = {{\text{π}} / 4}$ ; (c) $ {\theta _1} = {{\text{π}} / 2}$ ; (d) $ {\theta _1} = {{\text{π}} }$ Figure4. The collision behaviors of two solitons with the different initial phase differences under the condition that both tunneling strengths are 2.16 meV: (a) $ {\theta _1} = 0$ ; (b) $ {\theta _1} = {{\text{π}} / 4}$ ; (c) $ {\theta _1} = {{\text{π}} / 2}$ ; (d) $ {\theta _1} = {{\text{π}} }$ .图5 描绘了线性偏振光的左旋偏振分量振幅随点间隧穿强度变化的关系, 发现当点间隧穿强度比较小时, 孤子的振幅会随着隧穿强度的增加而缓慢增加; 而当点间隧穿强度增加至大约$4\;{\rm{meV}} $ 后, 孤子的振幅不再随点间隧穿强度的增加而增加而是趋于一稳定值. 因而随后选取点间隧穿强度为$T{e_1} = T{e_2} = 4.32\;{\rm{meV}} $ 时, 探寻点间隧穿强度对孤子间碰撞特征的影响.图 5 左旋偏振光的振幅随着点间隧穿强度变化关系. 图中所用各参数已在文中给出Figure5. The amplitude of the left-handed polarized light as a function of the tunneling strength of the inter-dot. The parameters used are given in the text.图6 描绘出了点间的隧穿强度$T{e_1} = T{e_2} = 4.32{\kern 1 pt} \;{\rm{meV}} $ (即振幅稳定后)时左旋偏振分量的碰撞行为. 通过将图6(a) 和图4(a) 进行比较, 可发现当初相位差为0时, 随着隧穿强度增加, 孤子对的碰撞距离间隔缩短了, 这说明随着点间隧穿强度的增加, 孤子的弹性碰撞周期减小了. 随后, 对图6(b) 和图4(b) 进行比较, 显然孤子的偏离角度增大, 从而说明初相位差为${\text{π}} /4$ 时的孤子间排斥力会随着点间隧穿强度的增加而增大, 类似地, 对图6(c) 与图4(c) (当初相位差为${\text{π}} /2$ 时), 以及图6(d) 与图4(d) (初相位差为${\text{π}} $ 的情况)进行一系列比较, 可看出孤子间碰撞方式保持一致, 但随着点间隧穿强度的增加孤子的偏离角度增大, 这说明孤子间的排斥力会随着点间隧穿强度的增加而增大.图 6 当隧穿强度为4.32 meV时, 孤子对在不同初相位差时的碰撞行为 (a) $ {\theta _1} = 0$ ; (b) $ {\theta _1} = {{\text{π}} / 4}$ ; (c) $ {\theta _1} = {{\text{π}} / 2}$ ; (d) $ {\theta _1} = {{\text{π}} }$ Figure6. When the tunneling strength is 4.32 meV, the collision behaviors of two solitons with the different initial phase: (a) $ {\theta _1} = 0$ ; (b) $ {\theta _1} = {{\text{π}} / 4}$ ; (c) $ {\theta _1} = {{\text{π}} / 2}$ ; (d) $ {\theta _1} = {{\text{π}} }$ .图1 中, 线性偏振光在与其平行的磁场作用下会分裂成左旋偏振光(${\sigma ^{{ - }}}$ )和右旋偏振光(${\sigma ^{{ + }}}$ )两偏振分量, 可看出左旋偏振光是由基态$\left| 0 \right\rangle$ 和直接激子态$\left| 1 \right\rangle$ 及间接激子态$\left| 3 \right\rangle $ 构成一个$\Lambda $ 型三能级系统, 而右旋偏振光是由基态$\left| 0 \right\rangle $ 和激子态$\left| 2 \right\rangle $ 以及间接激子态$\left| 4 \right\rangle $ 构成另一个$\Lambda $ 型三能级系统. 前面已经探讨了左旋光受点间隧穿调制下的孤子碰撞特征; 类似地, 点间隧穿对右旋偏振光所形成的孤子之间的碰撞性质影响也具备类似的特征. 在此这里就不再叙述.5.结 论 本文构建了一弱线偏振光在平行于传播方向的磁场的作用下, 弱线偏振光分裂为左旋、右旋两正交偏振分量, 并与三角形三量子点相互作用, 中间量子点中的电子从价带被激发到导带, 导带的电子与价带的空穴的相互作用形成激子态, 在外加门电压的作用下, 导带的电子通过隧穿作用隧穿至左、右量子点的导带上, 由于量子点间的间距较小, 电子与空穴仍旧具有较强的相互作用形成间接激子态, 这就形成了五能级M型三量子点模型. 通过多重尺度法, 分析了孤子在介质中的传播性质, 确定了在点间隧穿的作用下左旋、右旋两偏振分量能在隧穿的调制下形成稳定传播的孤子. 体系所形成孤子的机制是由量子点间的双隧穿耦合调制来实现, 这完全不同于超冷原子和单、双量子点模型中形成孤子的机制. 这是因为无论是超冷原子体系还是单、双量子点EIT介质中, 形成孤子必要条件是一束强控制光去调制一束弱探测光才能形成孤子.$T{e_1} = T{e_2} = 2.16\;{\rm{meV}} $ 时孤子间的碰撞特性. 结果表明孤子间的碰撞方式由初始相位差决定. 当初相位差为0时, 孤子间发生周期性弹性碰撞; 当初相位差为${\text{π}} /4$ , ${\text{π}} /2$ 和${\text{π}} $ 时, 孤子间会产生排斥作用力而使两孤子分离, 而且相位越超前孤子偏离中心位置越远. 随后发现左旋偏振分量所形成的孤子的振幅随着点间隧穿强度的增加而增加, 当隧穿强度增加到$4\;{\rm{meV}} $ 后, 孤子振幅趋于一稳定值. 因此, 选取了隧穿强度为$T{e_1} = T{e_2} = 4.32\;{\rm{meV}} $ 时, 探究点间隧穿强度对孤子碰撞特性的影响. 发现当初相位差为0(同相)时, 碰撞周期随着点间隧穿强度的增大而减小; 当初相位差为${\text{π}} /4$ , ${\text{π}} /2$ 和${\text{π}} $ 时, 孤子间的偏转角度(排斥力)随着点间隧穿强度的增大而增大. 这一结果为以后研制量子点光学器件和光孤子通讯的能提供一定的理论依据. 
































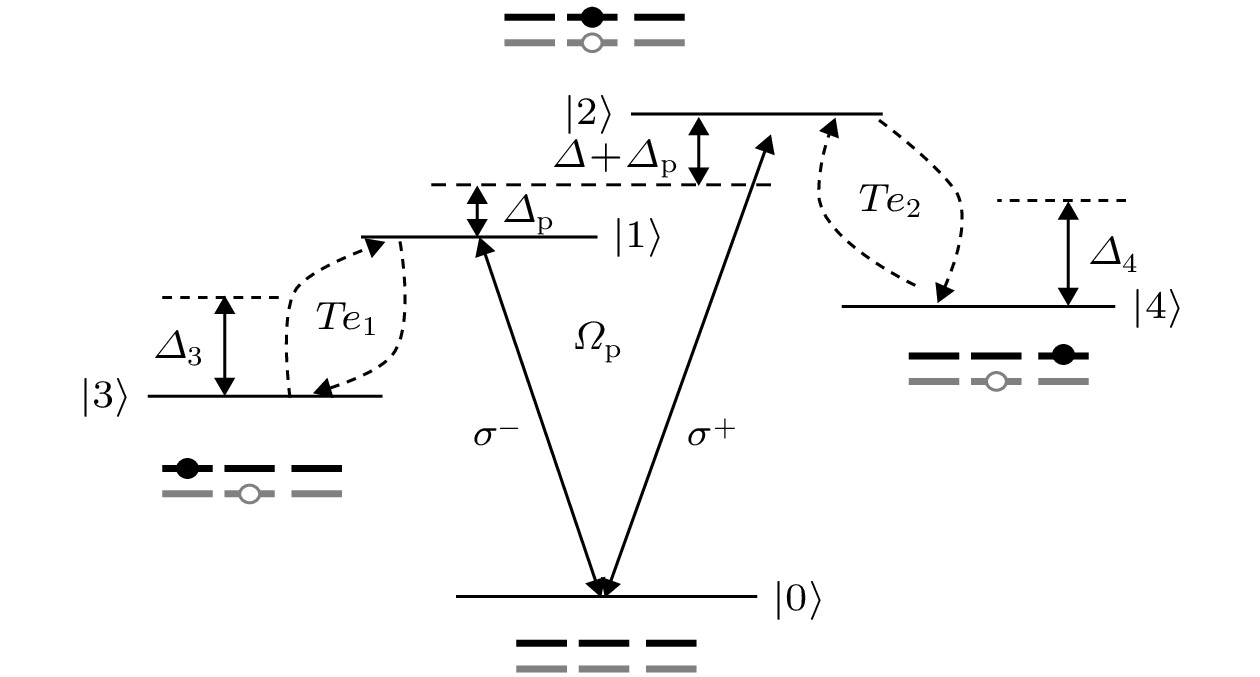 图 1 五能级M型三量子点电磁感应透明介质能级结构图.
图 1 五能级M型三量子点电磁感应透明介质能级结构图. 

































































































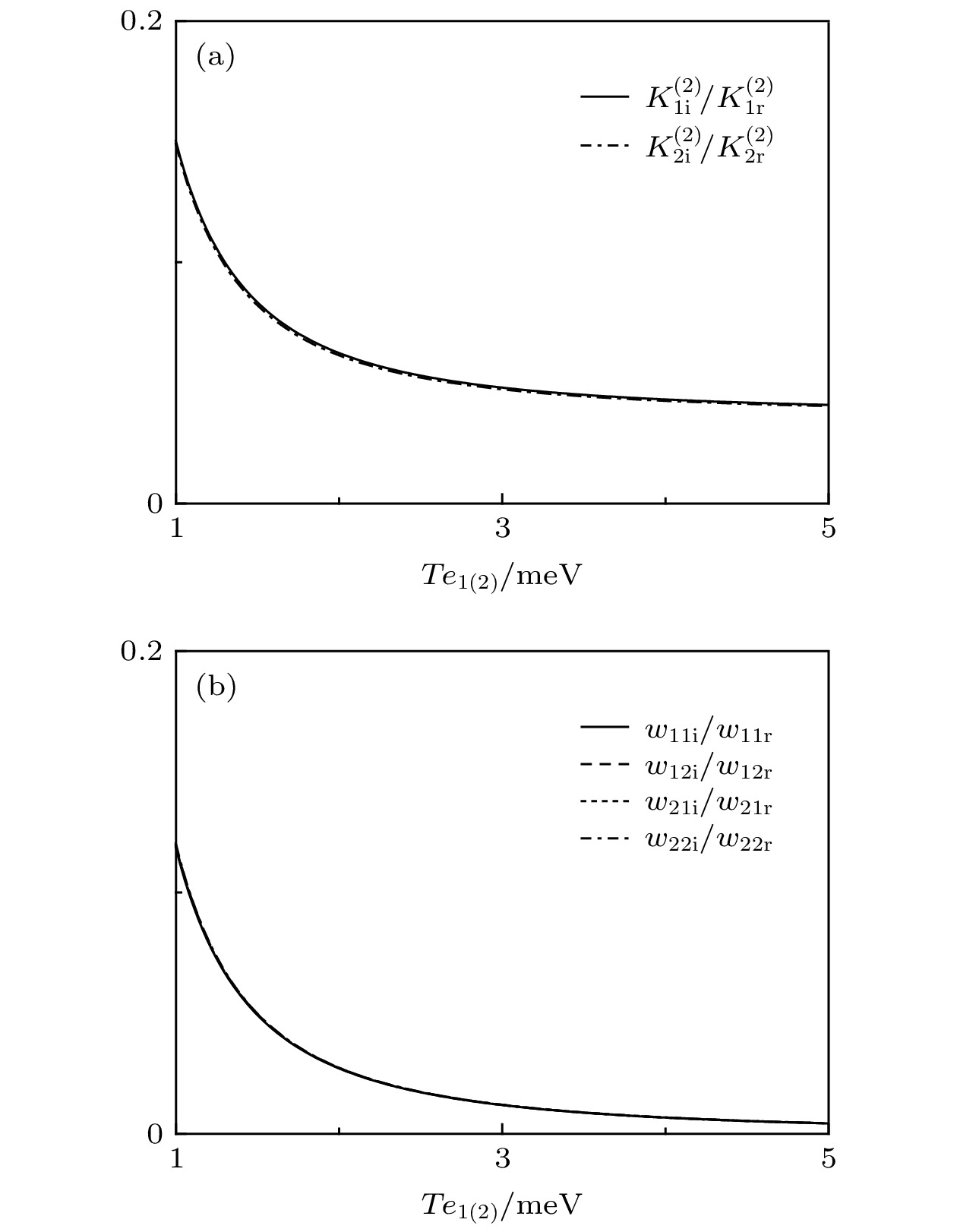 图 2 (a) 色散系数和 (b) 非线性系数的虚部与实部的比值随量子点间隧穿强度的变化关系. 图中所选参数已在正文中给出
图 2 (a) 色散系数和 (b) 非线性系数的虚部与实部的比值随量子点间隧穿强度的变化关系. 图中所选参数已在正文中给出






























































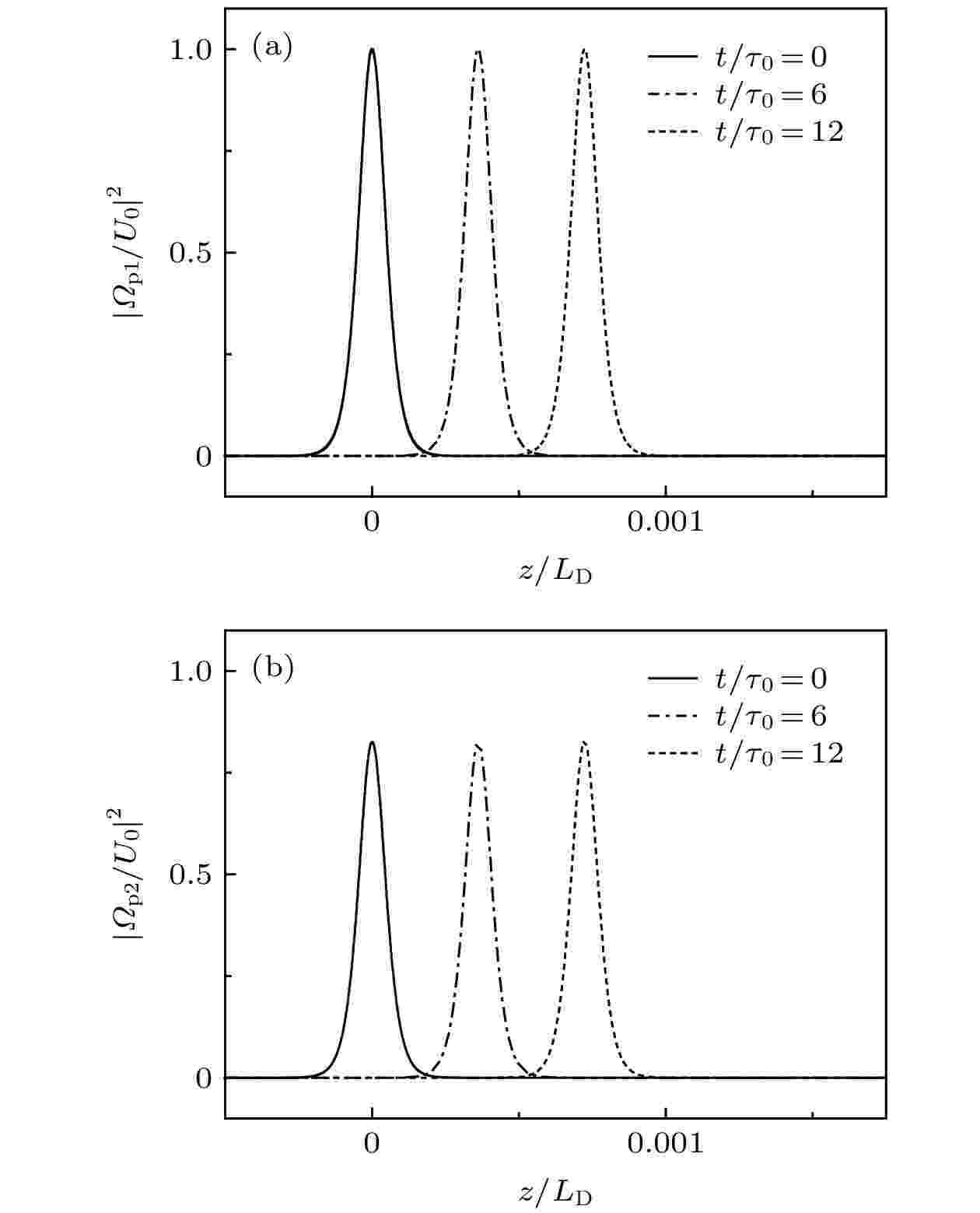 图 3 不同时刻线性探测光的两偏振分量(a)
图 3 不同时刻线性探测光的两偏振分量(a) 






























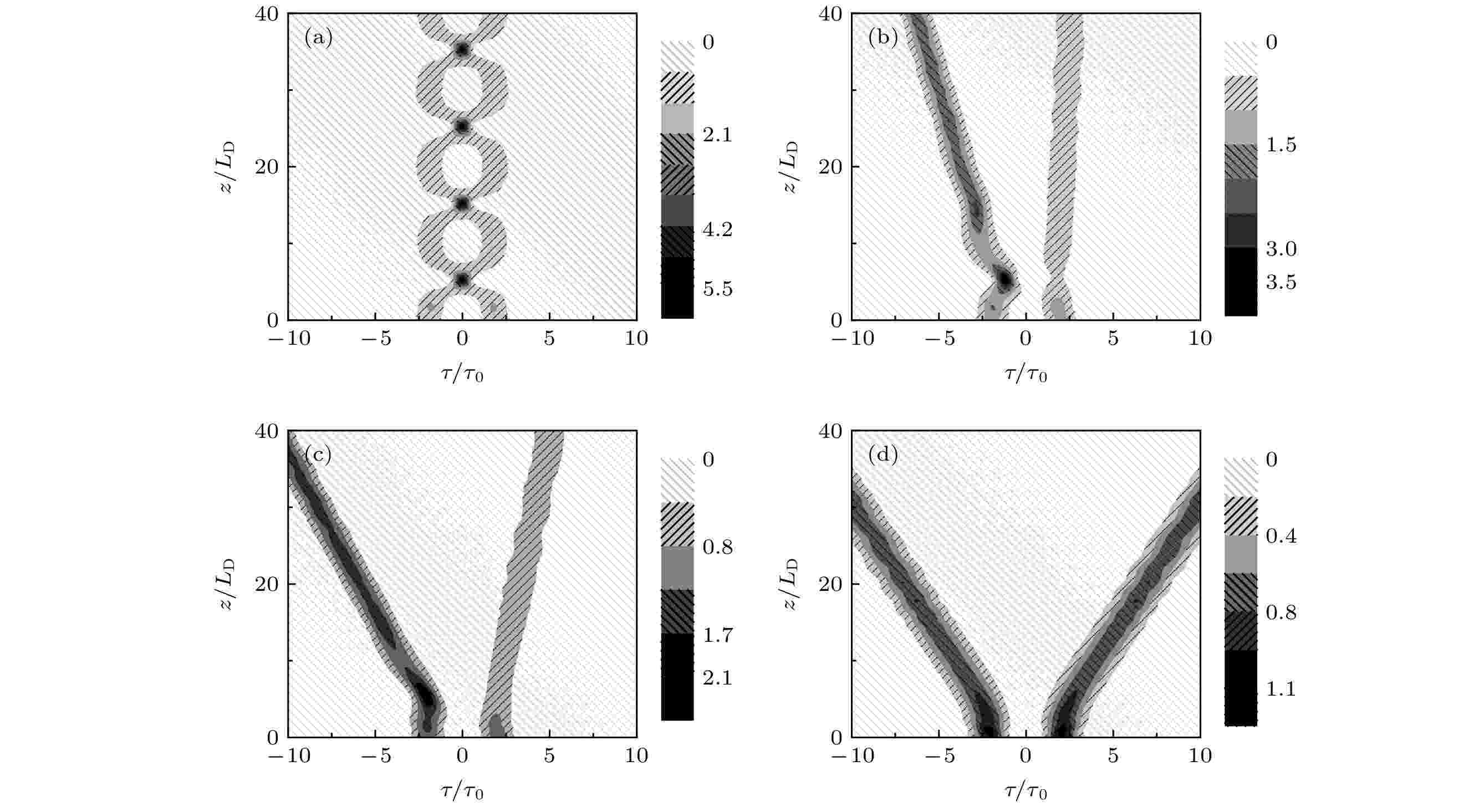 图 4 当两点间隧穿强度均为2.16 meV时, 孤子对在不同初相位差时的碰撞行为 (a)
图 4 当两点间隧穿强度均为2.16 meV时, 孤子对在不同初相位差时的碰撞行为 (a) 









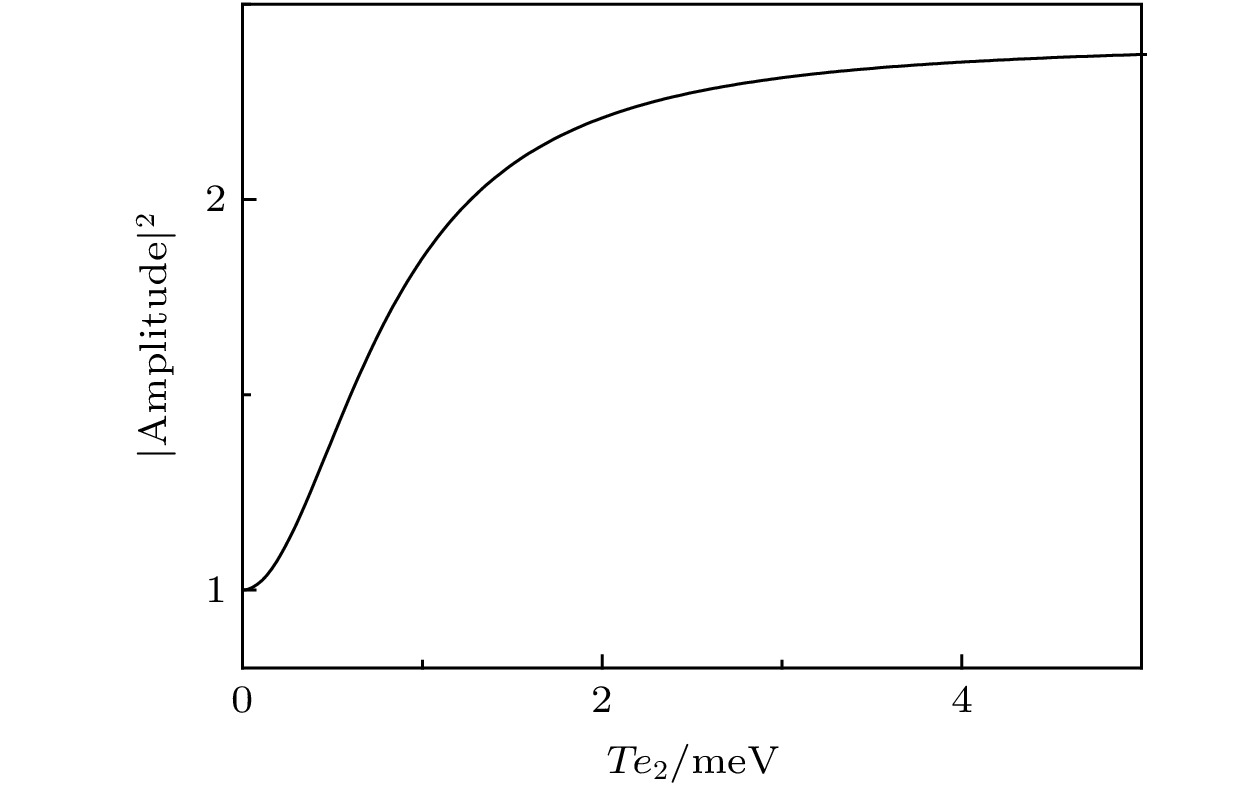 图 5 左旋偏振光的振幅随着点间隧穿强度变化关系. 图中所用各参数已在文中给出
图 5 左旋偏振光的振幅随着点间隧穿强度变化关系. 图中所用各参数已在文中给出



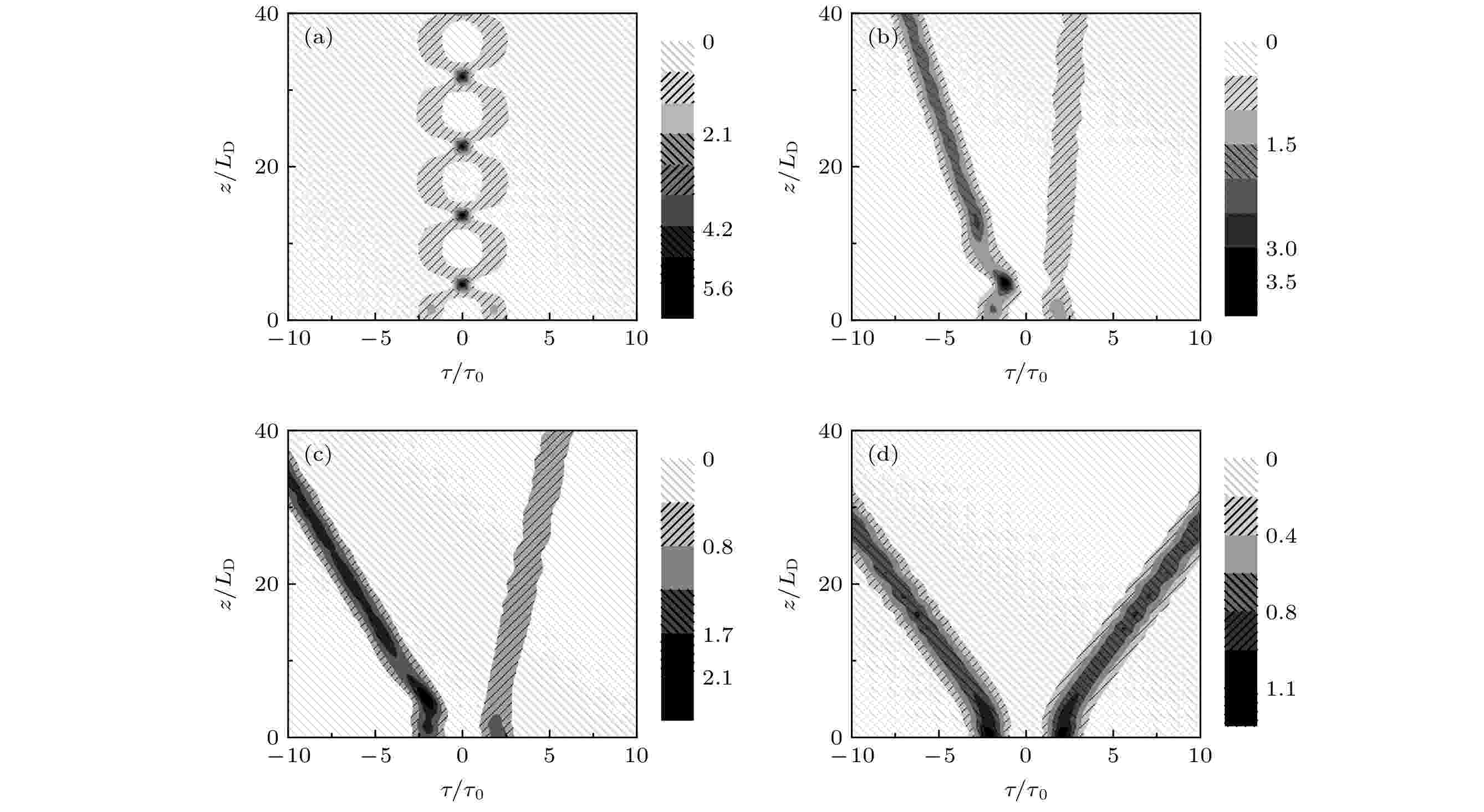 图 6 当隧穿强度为4.32 meV时, 孤子对在不同初相位差时的碰撞行为 (a)
图 6 当隧穿强度为4.32 meV时, 孤子对在不同初相位差时的碰撞行为 (a) 











































