摘要: 表面等离极化激元在片上信号传输、增强非线性/拉曼效应、生物/化学传感、超分辨成像等方面具有重要应用. 在这些应用中, 表面等离极化激元的近场传输及远场散射起着重要作用. 然而, 长期以来人们对相关物理效应缺乏简单有效的理论理解, 这也限制了人们对表面等离极化激元的自由调控. 本文首先简单回顾了表面等离极化激元的发展历史及现状, 接着着重介绍了表面等离极化激元的近场传输效应和远场散射效应, 包括其理论进展及其相关应用; 最后还介绍了表面等离极化激元的近场波前调控的相关方法. 基于这些进展, 人们对表面等离极化激元的散射特性有了更为深刻的理解和更加强大的调控能力, 这将对未来表面等离极化激元相关研究和应用带来启发.
关键词: 表面等离极化激元 /
传输及散射 /
超构表面 English Abstract Scatterings and wavefront manipulations of surface plasmon polaritons Guan Fu-Xin 1 ,Dong Shao-Hua 2 ,He Qiong 1 ,Xiao Shi-Yi 3 ,Sun Shu-Lin 2 ,Zhou Lei 1 1.Department of Physics, Fudan University, Shanghai 200433, China Received Date: 26 April 2020Accepted Date: 28 May 2020Available Online: 15 June 2020Published Online: 05 August 2020Abstract: Surface plasmon polaritons (SPPs) have found many important applications in on-chip signal transportation, enhanced nonlinear/Raman effect, biological/chemical sensing, super resolution imaging, etc. In these applications, the near-field propagation and far-field scattering of SPPs play a vital role. However, there has been strong desire to understand these physical effects. In this paper, we first briefly review the history and progress of SPPs. Next, we mainly focus on the near-field propagation and far-field scattering of SPPs, including their fundamental theories and practical applications. Finally, we review several different approaches to manipulating the near-field wavefronts of SPPs. These researches offer us a more in-depth understanding and the ability to more strongly control the scattering characteristics of SPPs, which may promote the scientific researches and practical applications of SPPs in the future.Keywords: surface plasmons /transmission and scattering /metasurfaces 全文HTML --> --> --> 1.引 言 表面等离极化激元(surface plasmon polaritons, SPPs)是一种束缚在金属和介质交界面传输的电磁本征模式[1 ,2 ] , 其所携带沿传播方向的水平波矢分量大于真空中的电磁总波矢, 这使得SPPs具有亚波长分辨和近场增强等奇异性质. 近年来, 随着理论研究的深入和纳米科技的进步, SPPs逐渐成为纳米光学领域的研究热点, 在增强光学透射[3 ] 、超分辨成像[4 ] 、纳米通信器件[5 ,6 ] 、太阳能电池[7 ] 和生物传感[8 ] 等多方面具有重要的应用前景.[9 ,10 ] . 1950年, Beeck和Ritchie[11 ] 报道了高速电子束经过金属薄膜时损失的能量可以激发金属上的一种表面电磁模式, 这使得人们对SPPs有了初步的认识. 近年来, 伴随着纳米科技的发展, SPPs相关研究逐步成为国际学术研究前沿. 1998年, Ebbesen等[3 ] 在实验上发现, 光经过刻有周期性亚波长空气孔洞阵列的金属薄膜时, 透射率远远超过经典理论的预测值, 并进一步将这种异常光学透射(extraordinary optical transmission, EOT)的根源归为金属膜上的SPPs的激发. 2005年, 张翔课题组[4 ] 设计制备出超分辨棱镜, 借助纳米银薄膜上的SPPs, 将物体发出的承载高分辨信息的倏逝波模式传递到超棱镜的像平面, 实现了突破光学衍射极限的高分辨成像.[12 ] 在理论上证明, 尽管低频段金属不支持可有效束缚光的等离激元模式, 但是在其表面制作周期性亚波长微结构之后(如填入高折射率材料的孔洞), 则该体系可以支持人工SPPs模式, 它的等效共振频率由微结构阵列的几何参数决定, 性质非常类似光波段SPPs模式. 2005年, Hibbins等[13 ] 设计出一种金属网栅结构, 并利用微波实验证明了它可以支持人工SPPs模式, 测量的色散关系与理论计算完美符合. 随后Maier等[14 ] 提出在具有不同表面形貌的金属上刻蚀空气槽结构, 可在不同波段灵活调控人工SPPs的传输行为, 例如用尖锥型结构实现SPPs聚焦效应. 然而, 尽管SPPs有诸多应用, 但是它与传播模式的波矢失配, 导致如何高效激发SPPs一直是个难题. 2012年, 周磊课题组[15 ] 首次提出超构表面可以作为连接远场传输波和近场表面波的桥梁, 实现SPPs模式的高效激发. 相较传统SPPs耦合器件, 超构表面耦合器具有尺寸小、效率高、易于集成等优势.图1(a) ). 例如, 当SPPs遇到金属表面的几何变形或者缺陷时(如图1(b) ), SPPs模式会发生非常复杂的散射效应, 包括SPPs的透射、反射、以及向自由空间的远场辐射. 另外, 当SPPs斜入射到两种不同的媒质的交界面时(如图1(c) , 包括两种不同金属/介质的交界面), SPPs会发生类似于自由空间波的反射和折射效应, 可以通过调控两边的参数来灵活调控SPPs的传输行为[16 ] . 在这些物理过程中, 远场散射不仅会造成能量的损耗, 甚至会影响和改变SPPs传输器件的功能. 人们也在思考如何主动调控这个物理过程从而产生一些重要的实际应用. 例如, 利用SPPs在纳米线结构中的法布里-珀罗(Fabry-Perot, FP)共振效应[17 ] , 可以产生特定波长的等离激元体激光效应, 这些近场能量会在纳米线波导的界面辐射到远场空间, 如图1(d) 所示, 相对而言等离激元激光器具有尺寸小、光束缚性极强等优势, 更重要的是可以直接在纳米尺度上产生远超衍射极限的相干光场. 另外, 通过在金属界面上精妙设计的一些规则的纳米散射结构, SPPs所携带的近场能量还可以被散射到远场, 从而实现聚焦等效应(如图1(e) 所示)[18 ] .图 1 (a) SPPs的复杂散射效应; (b) SPPs遇到金属表面缺陷时的散射效应; (c) SPPs的反射和折射效应[16 ] ; (d) 亚波长等离激元纳米激光器[17 ] ; (e) SPPs的三维远场聚焦效应[18 ] Figure1. (a) Complex scattering effects of SPPs; (b) scattering effect of SPPs striking a defect on the plasmonic metal; (c) reflection and refraction effects of SPPs[16 ] ; (d) subwavelength plasmonic nano-laser[17 ] ; (e) three-dimensional far-field focusing effect of SPPs[18 ] .2.表面等离极化激元传输行为 寻找能够替代传统大尺寸光学器件的小型化、高局域、易集成的新型光学系统是未来光学应用的发展趋势, 基于SPPs的人工亚波长纳米光学器件有望实现该目标, 其中SPPs在这类系统中的近场传输行为具有重要的理论研究价值和应用意义. 我们知道, SPPs在平整金属表面上可以沿平面上任何方向自由传输而不受约束, 为此需要引入各种SPPs波导体系. 例如, 人们曾提出利用纳米金属球链来引导SPPs的传播, 每个金属球颗粒的尺寸均远小于波长, 而且球链的排布方向可以在某个位置偏折一定角度, 从而改变SPPs的传输方向[19 –21 ] . 2004年, Law等[22 ] 利用纳米条带状波导实现了亚波长的集成光路, 如图2(a) 所示, 在金属平面上放置一个弯曲的条带状SnO2 波导, 利用连续谱激光照射在波导一端可激发SPPs模式并在波导内传播, 在波导另一端可探测到强烈的远场光散射信号. 基于此人们可以拼接其他的纳米元件来组成光学器件网路. 除了利用介质材料来制作纳米波导之外, 2005年, Ditlbacher等[23 ] 利用银纳米线制备出了SPPs的法布里-珀罗谐振腔体, 其直径只有120 nm左右. 同年, Yin等[24 ] 报道了一种可实现SPPs的聚焦和导引的集成纳米光学系统, 其工作原理如图2(b) 所示: 当外界光照射在金属上的圆弧形空气孔洞阵列结构时, 会在金属平面上激发SPPs并且传播汇聚到焦点处, 在焦点处放置一个银的条状纳米波导可以将SPPs束缚到50 nm宽的区域中进行近场传播. 2011年, Wei等[25 ] 利用等离激元纳米线网络实现了一个等离激元体二进制或非门的光学应用, 这为未来光学计算技术的发展提供了一个新方案. 在近二十年间, SPPs在集成纳米光学中的应用迎来了飞速发展[26 –32 ] , 其中SPPs遇到各种各样的非连续界面时的传输行为, 会对这些应用产生重要的影响.图 2 (a) SPPs在介质波导中的传输及辐射[22 ] ; (b) SPPs聚焦装置[24 ] Figure2. (a) Propagation and radiation of SPPs inside a dielectric waveguide[22 ] ; (b) anano-device for SPPs focusing[24 ] .[33 ] 针对SPPs在对接等离激元波导体系中的传输行为进行了理论研究. 如图3(a) 所示, 体系由一层真空层和两种不同的金属${\varepsilon _{\rm{1}}}(\omega )$ 和${\varepsilon _{\rm{2}}}(\omega )$ 组成, 体系的上下边界设为完美电导体边界条件, 因此该系统可视为一种空气/金属组成的一维周期性结构. 一支SPPs模式从左边入射到${x_1} = 0$ 的界面处会产生SPPs透反射和散射波, 这些散射波可以解析描述为一系列离散化波导模式, 利用模式展开方法可计算SPPs反射率随金属与空气厚度d 变化的谱线(如图3(b) , d 的单位为真空中的波长). 随着d 的增加, 新的传播模式会逐渐释放出来, 因而SPPs反射率会出现一些振荡行为[33 ,34 ] . 2008年, 范汕洄课题组[35 ] 研究了一个孤立的亚波长等离激元波导体系(如图3(c) 所示), 计算了SPPs在两个不同开口大小($b = 0.9\lambda $ 和$b'$ )金属波导体系交界面处的透反射行为. 改变右边波导的空气层厚度$b'$ , 他们利用散射矩阵的方法计算体系中SPPs的传输行为, 将计算得到的${S_{11}}$ (蓝色)与${S_{22}}$ (绿色)用史密斯图展示出来, 随着$b'$ 从初值($b' = b$ )逐渐变小, 体系的反射系数大小均逐渐增大(如图3(d) 所示).图 3 (a), (b)等离激元金属/真空对接系统(上下为完美电导体边界)中的表面等离极化激元反射谱[33 ] ; (c), (d) 等离激元波导对接系统中的SPPs反射系数[35 ] ; (e), (f) 金属/介质开放体系中的SPPs的散射系数(R , T , S )[36 ] Figure3. (a), (b) SPPs reflectance spectrum of a plasmonic metal/vacuum junction system surrounded by perfect electric conductors[33 ] ; (c), (d) SPPs reflection coefficients of a plasmonic waveguide junction[35 ] ; (e), (f) scattering coefficients $ (R, T, S) $ of SPPs inside a jointed metal/dielectric open system[36 ] .[36 ] 研究了如图3(e) 所示的系统, 它由两种不同的半无限大金属(${\varepsilon _{{\rm{m}}, i}}, {\varepsilon _{{\rm{m}}, j}}$ )/介质(${\varepsilon _{{\rm{d}}, i}}, {\varepsilon _{{\rm{d}}, j}}$ )系统在x = 0位置对接组成. 我们知道具有有限横截面尺寸的等离激元波导体系中的散射模式是离散化并可解析求解的(如图3(a) 和图3(c) ), 然而开放式等离激元体系的远场散射模式是连续分布的, 在理论上很难精确处理. 为了绕过这一难题, 张翔课题组[36 ] 大胆地对解析模型采取了一定近似, 即在体系满足弱散射条件时忽略掉远场散射波的贡献, 从而近似推导出一套类似菲涅耳公式的SPPs反射方程:${n_i} = \sqrt {{{{\varepsilon _{{\rm d}, i}}{\varepsilon _{{\rm m}, i}}} / {({\varepsilon _{{\rm d}, i}} + {\varepsilon _{m, i}})}}}$ 是第i 个区域中的SPPs的等效折射率. 他们利用(1 )式计算了SPPs在由相同的金属与不同介质组成的非连续界面(见图3(f) 中的插图)处的透反射率(T , R )和散射强度(S ), 计算结果如图3(f) 所示(黑色点是解析结果, 实线是全波模拟结果). 显然, (1 )式可以较好地描述弱散射区域(两边介质参数较为匹配) SPPs的透反射行为, 而在强散射区域(${\varepsilon _{\rm{d}}} \gg 1$ )则明显失效. 之后, 人们又将SPPs的界面散射行为的研究拓展到了对接的二维石墨烯材料上[37 ] , 给出了一种近似的解析方法来求解SPPs透反射系数以及远场辐射性质, 还研究了这些物理量随着石墨烯电导率或环境材料参数改变时的变换关系.[38 ] .2.1.基于周期性体系的模展开求解方法 2.1.基于周期性体系的模展开求解方法 为了建立一个完善的理论以便于深入理解SPPs遇到非连续性界面时远场散射的物理机理, 本课题组基于图4(a) 所示的系统进行了研究[38 ] , 即将两种不同的金属($\varepsilon _{\rm m}^{\rm I}, \varepsilon _{\rm m}^{\rm II}$ )/介质($\varepsilon _{\rm d}^{\rm I}, \varepsilon _{\rm d}^{\rm II}$ )周期性体系在x = 0处对接. 当左边入射的SPPs模式遇到x = 0处的界面时, 由于体系光学参数的非连续性会产生近场透反射模式和远场散射模式, 它们均为周期性体系的布洛赫模式. 考虑体系中所有的本征模式并匹配x = 0处的边界条件, 就可以基于模展开方法求解两边体系所有模式的强度和相位. 图4(a) 所示的周期性系统的好处在于: 1)可将开放体系(如图3(e) )中难以处理的连续化散射模式转换成可解析求解的离散化布洛赫模式, 从而进一步求解. 2)该体系可在不同极限下自动回到两类之前人们广泛研究的体系, 当金属层与介质层厚度都足够大时, 该体系等效为图3(e) 所示的金属/介质单界面开放系统; 而当介质层厚度${d_{\rm d}}$ 远小于波长时, 体系近似等效于常见的等离激元波导. 总的来说, 基于图4(a) 的体系可以定量化求解等离激元单界面体系和波导体系两大常见系统中的SPPs传输行为, 可谓一举两得.图 4 (a) 周期性等离激元体对接结构; 特定等离激元周期结构中的(b) SPPs和散射模式以及(c)倏逝波模式的色散关系[38 ] Figure4. (a) Periodic plasmonic junction system; dispersion relations of (b) SPPs and scattering modes, and (c) evanescent modes inside a typical plasmonic superlattice[38 ] .图4(a) 体系中SPPs的透反射系数, 首先需要利用转移矩阵方法计算周期性体系中的本征布洛赫模式[39 ] , 考虑到SPPs为TM偏振, 其对应的色散方程为[40 ,41 ] K P 为晶格常数; k 0 是真空中的波矢, ${k_0} = {\omega / c}$ , 其中c 是真空中的光速; ${k_{z, l}} = \sqrt {{\varepsilon _l}k_0^2 - k_x^2} $ 为z 方向电磁波的波矢, l = m, d代表金属或介质材料区域; ${Z_{\rm{d}}} = {{{k_{z, {\rm{d}}}}} / {{\varepsilon _{\rm{d}}}}}, {Z_{\rm{m}}} = {{{k_{z, {\rm{m}}}}} / {{\varepsilon _{\rm{m}}}}}$ 分别是介质和金属中电磁波的阻抗. 在图4(a) 的系统中, 由于所考虑的SPPs是沿x 轴正向入射到界面的, 因此只需考虑(2 )式中$K \equiv 0$ 情况下的本征模式并选择其中的磁场对称模式. 图4(b) 和图4(c) 分别展示了一个特定的周期性等离激元体系统中存在的所有${k_x}$ 为实数和虚数的本征模式色散关系, 以$\omega = 0.4{\omega _{\rm{p}}}$ 处为例, 体系存在一支SPPs模式(标记为n = 0, ${k_x} > {k_0}$ ), 一个散射波模式 (n = 1, ${k_x} < {k_0}$ ), 以及许多倏逝波模式 (n > 1, ${k_x}$ 是纯虚数).图4(a) 中x = 0界面左侧的场分布包括入射SPPs模式、反射SPPs模式和左向传输的散射波模式; 右边的场分布包括透射SPPs模式和右向传输的散射波模式. 两边的场分布需要在x = 0处匹配边界条件, 并利用模式之间的正交条件[40 ] 就可以求出不同模式的系数, 例如可以解析得到SPPs的反射系数${r_0}$ 为[38 ] ${Z_{{\rm{eff}}}}$ 为体系的等效阻抗, 交叠积分S A I ${Z_{{\rm{eff}}}}$ 描述了体系左边和右边两个等离激元体系的阻抗“失配程度”. 由于高阶倏逝波只能局域在x = 0界面附近而不带走能量, 它与SPPs之间的耦合又几乎为0, 因此在选取布洛赫模式时可以选择一个合理的截断整数M , 此时只需考虑0—M 阶以内的所有模式来计算体系的等效阻抗${Z_{{\rm{eff}}}}$ . 采用模展开方法除了可以得到${r_0}$ 以外, 还可以利用相同的办法得到${t_0}$ 和其他系数${r_n}, {t_n}(n \geqslant 1)$ .${d_{\rm{m}}} \!\to\! \infty$ , ${d_{\rm{d}}} \ll {\lambda _0}$ 时, 图4(a) 中的周期性系统自动回归到金属-介质-金属等离激元波导体系(如图5(a) )[38 ] . 则x = 0两边区域只存在SPPs模式和高阶倏逝波模式(不带走能量), 且两者耦合很弱, 因此就可以采用单模近似(single mode approximation, SMA)的方法来化简等效阻抗的形式, 即只需考虑SPPs模式对体系等效阻抗的贡献, SPPs反射系数((3 )式和(4 )式)可简化为如下的单模近似菲涅耳公式形式(SMA):图 5 (a) 等离激元波导对接体系; (b), (c) 不同金属和不同介质对接的波导体系中SPPs的反射率谱线; (d) 开放式等离激元对接体系; (e) 反射率的变化谱线; (f) 体系中存在一阶波导模式时的场分布[38 ] Figure5. (a) Plasmonic waveguide junction system; (b), (c) SPPs reflectance spectra in a waveguide junction system with different metals or dielectrics; (d) an open plasmonic junction system; (e) SPPs reflection amplitude as function of periodicity P in such system; (f) field distributions inside such plasmonic system with the first-order scattering modes appearing[38 ] .2.2.波导体系和开放体系中的应用 -->2.2.波导体系和开放体系中的应用 利用模展开方法还可以解析计算图5(a) 所示的亚波长波导体系中的SPPs反射率. 假设将区域I中的介质层取为空气, 固定金属的$\omega _{\rm{p}}^{\rm{I}} = 2\omega _0^{}$ ($\omega _0^{}$ 是工作频率), 可以连续地改变II区域金属的$\omega _{\rm{p}}^{{\rm{II}}}$ (图5(b) )或者介质的介电常数$\varepsilon _{\rm{d}}^{{\rm{II}}}$ (图5(c) ). 图5(b) 和图5(c) 比较了SPPs在两种体系中的反射率$R_0^{}$ 谱线, 包括严格的模展开公式((3 )式和(4 )式)、单模近似公式((5 )式)和全波模拟的计算结果. 显然, 单模近似结果与严格解和全波模拟的结果都完美符合, 证明了单模近似在该类系统中的合理性. 另外, 我们还比较了前人提出的SPPs反射率经验公式[35 ] :图5(b) 和图5(c) 所示, (6 )式(图5(b) 中空心点)虽然近似可以描述体系中SPPs的反射率, 但是在强散射区域还存在一定误差. 对比(5 )式与(6 )式可以看出, 波导体系中SPPs的等效阻抗不能简单用传播波矢的比值描述, 还需要包含不同模式波函数之间的交叠积分. 相较来说, (6 )式的形式较为简单但需工作在弱散射区域, 而(5 )式的形式稍微复杂但是适用范围要更广.3 )式和(4 )式), 还可以研究两个不同的金属/介质单界面体系. 将图4(a) 所示的周期性体系, 当${d_{\rm{d}}}, {d_{\rm{m}}} \to \infty $ 时, 在介质中会支持越来越多的离散化远场散射模式, 如果模式数足够多则可以近似认为散射波是连续模式, 该系统将等效于如图5(d) 的开放式系统. 首先设定金属厚度均远大于SPPs的衰减长度, 接着逐渐增大介质厚度${d_{\rm{d}}}$ 并计算体系的SPPs反射率${R_0}$ , 会发现SPPs的反射谱会产生一系列振荡(如图5(e) ), 并且在${d_{\rm{d}}}$ 足够大的情况下振荡行为会变得越来越弱, 因为体系中的散射模式已经趋近于稳定状态, 最终会收敛于模拟计算的开放体系结果. 通过深入研究发现每个振荡位置都伴随着在体系的某一侧产生了一只新的布洛赫散射波模式(图5(f) ), 这是熟知的Wood anomaly现象[42 ] ; 更重要的是, 随着P 的增大${R_0}$ 的振荡行为会逐步减弱并且收敛, 该收敛值与全波模拟计算的开放单界面体系的反射率(蓝色虚线)几乎相等, 因此证明了模展开方法在体系周期取得足够大时, 给出的${R_0}$ 是完全可以描述半无限大体系中SPPs的反射行为. 在弱散射近似下, SPPs的反射系数的严格解还可以进一步化简, 从而更清楚地揭示方程背后的物理, 在这里就不过多展开了.3.表面等离极化激元的远场辐射 第2 节主要关注了SPPs的近场传输特性, 此外远场散射效应也是SPPs的一种重要性质. 对于等离激元的众多应用来说, 远场散射会造成近场能量的损失, 因此需要对其进行压制. 2006年, Bozhevolnyi等提出了V型SPPs波导, 所支持的通道等离激元(channel plasmon polariton, CPP)模式具有高度局域和长程传输等特性[43 ] . 首先, V型SPPs波导的开口角和深度都经过优化, 其支持的SPPs模式非常局域, 不易受外界环境影响. 另外V型波导经过设计优化在拐弯处非常平滑, 从而抑制了SPPs的远场辐射行为, 即使是遇到大角度弯折和分路区域时SPPs的远场散射损耗仍然较低, 从而能够实现SPPs Y型分流器、Mach-Zehnder干涉仪(如图6(a) )和波导环形谐振腔等功能. 同年, Stockman[44 ] 提出了一种可实现SPPs全反射的纳米光学器件. 如图6(b) 所示, 在金属上放置一个厚度远小于波长的介质层, 通过优化其厚度和介电参数使得覆盖该介质薄膜的金属区域不支持SPPs的传输(即SPPs “禁带”), 因而从旁边金属区域上入射的SPPs将被完全反射, 几乎不伴随远场的散射损耗, 可作为SPPs的全反射镜. 2010年, 张翔课题组[45 ] 利用转换光学的概念, 在一个具有半圆型端面的银/介质交界面体系中, 使得SPPs完美“转弯”而几乎没有任何散射损耗(如图6(c) 所示).图 6 (a) 等离激元体Y型分流器和Mach-Zehnder干涉仪[43 ] ; (b) 基于纳米薄膜的SPPs全反射[44 ] ; (c) SPPs的180°转向效应[45 ] Figure6. (a) Plasmonic Y-splitter and Mach-Zehnder interferometer[43 ] ; (b) total reflection of SPPs based on a nano-layer system[44 ] ; (c) 180° bending effect of SPPs[45 ] .[46 ] 报道了一种基于SPPs的远场散射来重建3D彩色图像的全息成像技术. 如图7(a) 所示, 首先三束白光光束从不同方向以不同的角度经过棱镜入射到银薄膜上, 基于全反射效应可以分别激发红、绿、蓝三个波长的SPPs模式; 接着再通过银表面附近的光栅式全息板将SPPs解耦合到远场, 最终呈现三色的苹果远场全息图像, 如图7(b) 所示. 此外, 人们还报道了很多SPPs远场散射聚焦的相关工作[47 –49 ] , 如图7(c) 所示, 通过在金属表面加工出周期渐变的光栅结构, 从而让SPPs从左向右传输至光栅不同位置时获得不同的横向倒格矢, 实现散射远场的光汇聚到焦点位置上(如图7(c) 和图7(d) 所示)[49 ] . 2014年, Zhang等[50 ] 基于全波模拟研究了在金属纳米线的端面处加工不同尺寸和间距的亚波长纳米天线结构, 用它来增强或抑制外界远场光与金属纳米线SPPs之间的正向或逆向耦合效应. 2018年, 方哲宇团队[51 ] 报道了一种可对近场和远场光进行集成调控的超表面器件, 它可以同时激发定向传输的SPPs模式, 以及将入射场散射到透射区域实现远场聚焦, 当改变入射圆偏振光的自旋态时, SPPs的传输方向以及聚焦效应的虚实均可切换.图 7 (a) SPPs彩色全息术; (b) 重建的三色苹果全息图像[46 ] ; (c), (d) SPPs远场聚焦[49 ] Figure7. (a) Colorful holography of SPPs; (b) reconstructed image of 3D colorful apple[46 ] ; (c), (d) far-field focusing of SPPs[49 ] .[52 –54 ] . 比如, Shchegrov等[53 ] 利用简化的瑞利散射公式, 计算了SPPs在圆形对称的金属散射体上的远场微分散射截面, 可以发现SPPs散射波的远场辐射行为具有明显的方向性, 这一研究结果与实验现象相符合. 2015年, Evlyukhin和Bozhevolnyi[55 ] 研究了SPPs撞击到高折射率硅纳米颗粒上的散射行为, 他们利用离散偶极近似法对散射特性进行了数值计算, 讨论了球形硅纳米颗粒在光频波段的消光和散射截面谱, 揭示了电和磁偶极子的面内分量和面外分量在散射过程中所扮演的作用. 此外, 人们还对SPPs在不同形状散射体上的辐射行为进行了研究[56 -58 ] . 2007年, Al-Bader和Jamid[58 ] 解析计算了不同的SPPs模式在金属纳米线截断边界处的反射及远场辐射行为, 系统探讨了不同的SPPs模式的散射特性与纳米线直径的依赖关系.[59 ] .3.1.等效电流源模型研究三维等离激元体系 3.1.等效电流源模型研究三维等离激元体系 考虑一种最基本的非连续等离激元系统: 两个半无限大的具有不同负介电常数金属(${\varepsilon _1}$ 和${\varepsilon _2}$ )的对接体系(如图8(a) 所示)[59 ] . 假设一束单位强度的SPPs从左边沿着+x 方向传播, 在x = 0处的交界面发生近场透反射及远场散射效应, 其透反射系数和界面两侧SPPs的本征波矢分别是${r_{{\rm{SPP}}}}$ 和${t_{{\rm{SPP}}}}$ 与$k_{{\rm{SPP}}}^{\rm{I}}$ 和$k_{{\rm{SPP}}}^{{\rm{II}}}$ . 为了清楚呈现SPPs的散射特性, 首先利用全波模拟计算了对接体系中磁场分布, 例如当${\varepsilon _1} = - 1.12$ , ${\varepsilon _2} = - 16$ 时体系中表SPPs在界面处远场散射的主辐射角度为${\varphi _{\rm{p}}} = {25.1^{\rm{\circ}}}$ , 半峰宽为$\Delta \varphi = {71.1^{\rm{\circ}}}$ (见图8(b) 插图). 为了更加清楚理解SPPs的散射规律, 又进一步计算了散射场强度随着$\varphi $ 和${\varepsilon _2}$ 变化的相图(如图8(b) 所示), 显然${\varepsilon _2}$ 从–16变化到–1时, 由于两边金属的介电常数更为接近, 体系的等效阻抗差异变小, 因而散射远场的强度明显变弱; 更重要的是, 可以发现散射远场的主辐射角度和半峰宽也随之增大.图 8 (a) 半无限大等离激元体金属对接系统; (b) 远场散射强度随着散射角度$\varphi $ 和$\sqrt {\left| {{\varepsilon _2}} \right|} $ 的变化; (c) 特定等离激元对接体系中的远场散射角分布[59 ] Figure8. (a) Semi-infinite plasmonic metal junction system; (b) scattering far-field intensity as function of $\varphi $ and $\sqrt {\left| {{\varepsilon _2}} \right|} $ ; (c) scattering far-field angular distribution of SPPs in a typical plasmonic junction system[59 ] .[59 ] . 考虑到远场辐射是由金属中的振荡电流源产生的, 这个辐射次波源可以被表示成${{j}}({{r}}) = - {\rm{i}}\omega [\varepsilon ({{r}}) - {\varepsilon _0}]{{{E}}_{{\rm{local}}}}({{r}})$ . 然而这个局域电场${{{E}}_{{\rm{local}}}}({{r}})$ 不但包含了入射SPPs的电场, 而且还包含了透反射SPPs、辐射远场和高阶倏逝波共同贡献的场. 在将整个体系自洽地求解清楚之前, 很难得到任何一种模式对应的场分布信息. 为了抓住复杂的远场散射过程中的主要物理, 先对整个局域场做最低阶近似, 也就是忽略传输波和倏逝波对局域场的贡献, 认为局域场${{{E}}_{{\rm{local}}}}({{r}})$ 主要由SPPs对应的场组成. 因此, 在金属I中的电流源只是由入射和反射SPPs对应的电流源${{j}} = {{{j}}_{{\rm{in}}}} + {{{j}}_{\rm{r}}}$ 组成, 在金属II中的电流源只是由透射SPPs对应的电流源(${{j}} = {{{j}}_{\rm{t}}}$ )决定. 考虑到SPPs的局域场在金属中会迅速衰减到0, 因而可以通过数学积分将SPPs的体电流源简化成为面电流的形式${{J}}(r, t) = {{J}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{SPP}}}}x}}{{\rm{e}}^{ - {\rm{i}}\omega t}}\delta (z)$ [60 ] , 其中${{J}} = ({J^x}{{x}} + {J^z}{{z}})$ 包含x 和z 方向的两个分量,${\alpha _{\rm{m}}} = \sqrt {{{\left( {{k_{{\rm{SPP}}}}} \right)}^2} - {\varepsilon _{\rm{m}}}{{\left( {{k_0}} \right)}^2}} $ 为SPPs在金属中的衰减速率), 最后体系中总电流源的表达式为$\theta (x) = \left\{\!\! {\begin{array}{*{20}{c}}{1, \;\;\;x \geqslant 0} \\{0, \;\;\;x < 0}\end{array}} \right.$ 是阶梯函数, ${{{J}}_{{\rm{in}}}}, {{{J}}_{\rm{r}}}$ 和${{{J}}_{\rm{t}}}$ 分别是由入射、反射和透射SPPs波产生的电流源强度. 现在开始解析求解(7 )式的电流源辐射行为, 首先考虑入射的半无限大表面电流源:8 )式)所产生的辐射场[61 ] :x 偏振和z 偏振的表面电流所贡献. 首先, 对x 方向偏振的电流辐射做简单的数学推导, 发现${k_{{\rm{SPP}}}}$ 越大时其边界辐射的角度越倾向于$\varphi = {90^{\rm{\circ}}}$ 方向, 并且半峰宽越大. 对于x 偏振的半无限大电流源, 在边界处会展现出沿x 方向的偶极子辐射特性, 其主辐射方向为90°, 另外不同位置处的电流源也会展现出干涉特性, 其辐射场倾向于沿0°方向, 最终的辐射远场由这两项的竞争决定. 当${k_{{\rm{SPP}}}}$ 越大, SPPs的场分布高度局域, 其与沿0°方向辐射场的耦合效应越来越弱(由于波矢越来越失配), 使得边界处的偶极子辐射占据主导效应, 这导致了辐射远场倾向于沿90°方向. 并且, 当${k_{{\rm{SPP}}}}$ 越大时, 由于SPPs在空间上高度局域, 这就决定了其在动量空间的变化范围很大, 这也解释了辐射半峰宽变大的原因. 利用相同的方法可以很容易地分析和解析计算出, z 方面偏振的SPPs电流源边界辐射的主极大固定在$\varphi = {0^{\rm{\circ}}}$ , 且其半峰宽随${k_{{\rm{SPP}}}}$ 也呈现单调递增的趋势.7 )式)辐射的解析方程如下[59 ] :${{{E}}_0}(r) = - \dfrac{{{\mu _0}\omega }}{{{\rm{i}}\sqrt {8{\text{π}}{k_0}r} }}{{\rm{e}}^{{\rm{i}}({k_0}r - {{\text{π}} / 4})}}{{{e}}_\varphi }$ . 再利用第2 节介绍的单模近似方法[38 ] 得到${{J}}_{\rm{t}}^{}$ , ${{J}}_{\rm{r}}^{}$ 与${{J}}_{{\rm{in}}}^{}$ 的关系式, 将${{{J}}_{\rm{t}}}$ 和${{{J}}_{\rm{r}}}$ 代入到(10 )式中来计算远场辐射能流的角谱分布, 其中利用总能流按照入射SPPs的能流做归一化. 利用(10 )式计算图8(a) 所示的体系, 两侧金属的介电常数满足Drude模型形式${\varepsilon _1} = 1 - {\left( {{{{\omega _{\rm{p}}}} / \omega }} \right)^2}$ , ${\varepsilon _2} = 1 - {\left( {{{{{\tilde \omega }_{\rm{p}}}} / \omega }} \right)^2}$ , 其中的${\tilde \omega _{\rm{p}}} = {\omega _{\rm{p}}}/\sqrt 3 $ . 发现利用电流源模型与全波模拟计算的SPPs远场散射分布具有一定差距(如图8(c) 所示), 这些差异主要来源于纵向(z )偏振电流源在横波条件的限制下会受到金属“屏蔽”效应的影响. 因而, 该电流源模型尤其适合于研究那些只有切向(x )偏振电流源的体系. 显然, 二维材料 (如石墨烯等)和极端各向异性的体系(如双曲材料)等正好满足这个条件, 接着将利用电流源模型研究这些二维体系中的SPPs的远场辐射特性.3.2.二维等离激元体系的远场辐射性质 -->3.2.二维等离激元体系的远场辐射性质 首先, 研究一个理想的半无限大二维等离激元体系统, 如图9(a) 所示, 显然其透射SPPs电流源系数${\rm{ }}J_{\rm{t}}^x$ 等于0, 于是可以利用(10 )式(其中z 偏振的电流源强度均为0)来研究SPPs的远场辐射行为. 图9(b) 展示了SPPs在该理想二维体系中的色散关系$k_{{\rm{SPP}}} \!= {k_0} \cdot \sqrt {1 - {{4{\varepsilon _0}} / {({\mu _0}{\sigma ^2})}}} $ , 其中$\sigma (\omega ) = \dfrac{{{\rm{i}}{{\rm{e}}^2}{v_{\rm{f}}}\sqrt n }}{{\hbar \sqrt {\text{π}} (\omega + {\rm{i}}\varGamma )}}$ 是其表面电导率, ${v_{\rm{f}}} = 9 \times {10^5}~{{\rm{m}} / {\rm{s}}}$ 是费米速率, $n = 5 \times {10^{11}}~{\rm{c}}{{\rm{m}}^{{\rm{ - 2}}}}$ 是载流子浓度, $\varGamma = 0$ 表示阻尼率(首先忽略损耗). 选择两个不同的工作频率0.14和0.74 THz, 通过全波模拟和解析理论得到SPPs在该体系中的远场辐射行为, 如图9(c) 所示, 理论预测与模拟结果完美符合. 另外, 在0.12 THz时, 体系散射的峰值和展宽都很小(26.3°和59.3°), 但在0.74 THz时峰辐射的角度和展宽明显地增大(78.5°和92.2°), 考虑到$k_{{\rm{SPP}}}^{}$ 从$1.1 k_{\rm{0}}^{}$ 变大到$3{k_0}$ , 以上行为完全符合(9 )式分析的预测. 并且(10 )式完全可以用来计算石墨烯[62 –65 ] 的边界辐射行为, 这里就不展开讨论了.图 9 (a) 理想的半无限大二维等离激元体系统; (d) 半无限大人工金属网栅结构; (b), (e)相应体系中的SPPs的色散关系; (c), (f) 相应体系中的SPPs散射远场角谱分布[59 ] Figure9. (a) An ideal semi-infinite 2D plasmonic system; (d) a semi-infinite artificial metallic mesh structure; (b), (e) dispersion relations and (c), (f) scattering far-field angular distributions of SPPs in two plasmonic systems[59 ] .图9(d) 所示的亚波长半无限大的金属网栅(晶格常数为a )可以被看作为二维等离激元体材料, 并且支持微波段的人工SPPs模式, 显然该体系没有垂直方向的电响应. 图9(e) 中展示了这个体系中的人工SPPs的色散关系, 任意选择两个频率(8.5和19.1 GHz)来研究SPPs在这个体系中的远场辐射行为, 图9(f) 表明解析公式和模拟计算得到的远场散射结果可以很好地符合在一起, 再次证明电流源理论模型确实抓住了SPPs辐射的主要物理性质.4.表面等离极化激元的近场波前操控 前面两节介绍了SPPs遇到一些非连续界面时的散射特性的相关研究, 通过一些方法可以得到或者调控SPPs在界面处的透射、反射以及远场辐射分布. 为了能更为灵活有效地利用SPPs, 就需要找到有效的方法来调控SPPs的波前分布, 例如实现SPPs反射/折射、SPPs聚焦、甚至SPPs全息成像等, 这些研究具有重要的科学意义和应用价值.[66 ] , 类似的方法也在2010年被Devaux等[67 ] 进一步验证, 如图10(a) 和图10(b) . 这种调控思想非常类似于传统光学器件利用传播相位的积累来对远场光的调控, 然而这些器件存在尺寸大、功能有限等问题. 借助于纳米加工技术, Radko等[68 ] 提出设计制备周期性亚波长纳米颗粒结构来调控SPPs波前, 这种方法可以自由改变阵列的形状, 比如可以制备三角形的纳米颗粒阵列实现SPPs折射效应(如图10(c) ).图 10 (a), (b) 利用不同形状的介质光学器件来调控SPPs的波前[66 ,67 ] ; (c) 利用纳米颗粒阵列实现SPPs折射[68 ] Figure10. (a), (b) SPPs wavefront manipulations with dielectric optical elements of different shapes[66 ,67 ] ; (c) refraction of SPPs with nanoparticle array[68 ] .[69 ] 设计制备了周期性银纳米凸起(Nano-bump)结构, 可以作为SPPs的高效布拉格反射镜, 反射系数达到90%左右 (图11(a) ); 基于类似原理, Drezet等[70 ] 制备了一个由银纳米凸起结构的周期排列形成的椭圆型“围栏”结构, 在这个椭圆结构的一个焦点处激励起SPPs, 它们可以借助布拉格散射效应汇聚在另一个焦点上; 除了利用金属纳米颗粒结构外, Randhawa等[71 ] 利用多层介质板制备成了布拉格反射镜, 可通过增添介质板的层数来调控SPPs的反射率, 理论上介质板的层数达到20层, 反射率可达到76% (图11(b) ); 2014年, Chen等[72 ] 在金属板上精确设计复杂的沟槽图样实现了SPPs的全息成像效应, 可以实现例如SPPs的点聚焦等复杂的波前操控功能(图11(c) ); 2011年, 南京大学李涛课题组[73 ] 提出了一种可实现SPPs艾里光束(Airy beam)激发的体系, 如图11(d) 所示, 在平整金属表面上加工制作渐变周期的纳米孔洞阵列结构, SPPs传播经过这些阵列时, 会获得额外的面内倒格矢从而被散射到结构两侧的区域发生干涉产生艾里光束, 通过优化纳米孔洞的尺寸可减弱体系的远场散射损耗; 2013年, 该团队[74 ] 借助类似的理念和制备工艺, 实现了SPPs的线聚焦效应, 在一定距离范围内线焦斑上的SPPs强度几乎恒定. 利用纳米结构调控SPPs的方法, 充分发挥其排列方式灵活多变这一重要自由度, 可以实现更为复杂的SPPs波前操控, 然而由于需要依赖多重散射效应, 使得这种器件的尺寸至少需要数个波长以上的量级.图 11 基于(a)纳米颗粒阵列[69 ] 和(b)介质光栅[71 ] 的SPPs布拉格反射; (c) SPPs全息[72 ] ; (d) SPPs的艾里光束激发[73 ] Figure11. Bragg reflections based on (a) nanoparticle array[69 ] and (b) dielectric grating[71 ] ; (c) SPP holography[72 ] ; (d) SPPs Airy beam generation[73 ] .[15 ,75 -77 ] , 它是一种由不同人工原子按照特定排列方式组成的平面式超构材料, 通过精心调控每个位置处人工原子的电磁响应(主要是透射/反射相位)[78 ,79 ] , 基于惠更斯原理干涉形成各式各样的电磁波前分布, 实现了奇异偏折[80 ] 、超棱镜[81 ] 、光束聚焦[82 ] 、表面波激发[83 ,84 ] 、光子自旋霍尔效应[85 ] 、特殊光束激发等[86 -88 ] 物理效应, 然而这些工作大多数是针对远场传输波进行调控的. 最近, 我们课题组将超构表面的概念从远场传输波调控拓展至近场SPPs调控, 接下来将介绍该方法的物理原理和调控功能[89 ,90 ] .4.1.超构表面对表面等离极化激元波前调控的物理思想 4.1.超构表面对表面等离极化激元波前调控的物理思想 如果要利用超构表面实现对近场SPPs波前的自由调控, 根据惠更斯原理, 首先就需要能够对SPPs的相位进行全幅度调控, 研究发现, 将一个折射率可调的介质薄膜附着在平面金属镜上组成的双层体系可以实现这个目标. 其中, 金属镜可以确保将入射的SPPs完全反射, 当介质层的介电常数改变时, SPPs在介质层中传播时的水平波矢得以改变, 从而调控SPPs在结构中积累的相位$\phi $ . 原则上讲, 如果可以通过调控介质层的折射率来实现$\phi $ 的360°全覆盖, 就能设计出超构表面呈现出合适的$\phi (y)$ 相位分布, 进而可以有效地塑造出任意形式的SPPs波前分布. 例如, 如果超构表面的相位分布$\phi (y)$ 满足:${\theta _{\rm{i}}}$ 和${\theta _{\rm{r}}}$ 分别是SPPs的入射角和反射角, ${{ k}_{{\rm{SPP}}}}$ 是SPPs的波矢, 而$\xi $ 是超构表面的反射相位梯度. 同理, 可以设计一个超构表面实现SPPs的聚焦效应, 其反射相位分布$\phi (y)$ 满足抛物线分布:F 是SPPs聚焦的焦距.4.2.超构表面的单元结构设计 -->4.2.超构表面的单元结构设计 首先基于有效媒质模型来验证超构表面调控SPPs的构想是可行的. 为了方便实验的验证, 选择在微波段开展研究. 由于天然的SPPs只存在于可见光频段, 可以将一个2 mm厚的介质层(${\varepsilon _{\rm{d}}}$ = 2.65)放在一个完美电导体上, 该结构支持一种人工SPPs模式[12 ,89 ,91 ,92 ] ; 我们设计的超构表面是由一层5 mm厚的介质层(介电常数为${\varepsilon _{\rm{g}}}$ )和一个金属反射镜组成. 接着, 将这种超构表面垂直放置在已设计的人工等离激元体金属上, 通过计算发现人工SPPs被均匀超构表面反射后的相位会随着${\varepsilon _{\rm{g}}}$ 的变换而覆盖整个360°的范围; 另外, SPPs的反射幅度也始终稳定在0.9附近, 这表明在SPPs的散射损耗很小.[80 ,93 ,94 ] 上加工一些亚波长空气孔阵列(直径为D 、周期为P , 如图12(a) ), 该系统可等效模拟一个具有确定介电常数的“均匀”介质板, 并可以通过改变空气孔直径D 来调控超构表面的等效介电常数[89 ] . 如图12(b) , 在工作频率12 GHz处, 如果空气孔直径D 从0变到2.88 mm, SPPs的反射相位可以覆盖360°, 其反射幅值也一直保持在较高数值(大于0.9)[89 ] . 由于几何结构的各向异性, 决定了超构表面也具有各向异性的等效介电常数张量[95 –97 ] :图 12 (a) 真实的超构表面结构及(b)其对SPPs的反射系数[89 ] Figure12. (a) Practical metasurface and (b) corresponding SPPs reflection coefficients[89 ] .y-z 面)时, 入射电磁波将只会感受到等效介电常数的平行分量(即${\varepsilon _{/\!/}}$ ). 在这种偏振下, 电磁波看到的是高折射率介质材料中包覆了圆柱形空气孔, 对这种构型可以利用Bruggeman理论[95 ] 来获得${\varepsilon _{/\!/}}$ :${\varepsilon _1}$ 和${\varepsilon _2}$ 分别是空气孔和高折射率材料的介电常数, 而f 1 和f 2 分别为这两个材料所占的体积分数. 当电场垂直于超构表面时(即x 方向), 电磁波将会感受到等效介电常数的另一个分量${\varepsilon _ \bot }$ , 由于电场平行于空气孔和高折射率介质的交界面, 此时${\varepsilon _ \bot }$ 可以利用体平均的方法求得[96 ,97 ] :15 )式和(16 )式, 可以计算出${\varepsilon _{/\!/}}$ 和${\varepsilon _ \bot }$ 随着空气孔直径D 的变化规律. 基于有效媒质理论得到的参数, 模拟计算了SPPs的反射幅度和反射相位; 与基于真实结构的全波模拟计算结果对比, 发现两者完美符合(如图12(b) ), 此时已经为设计真实超构表面打好了基础.4.3.表面等离极化激元的波前调控效应 -->4.3.表面等离极化激元的波前调控效应 接下来介绍梯度超构表面对SPPs的波前调控. 图13(a) 展示了一种具有线性相位分布的超构表面的样品照片, 其相位梯度为$\xi = 0.79{k_{{\rm{spp}}}}$ , 其超原胞由直径在0—2.77 mm范围内变化的空气孔阵列组成, 其中心工作频率为12 GHz. 根据(12 )式, 可以预测正入射SPPs的奇异反射角为52.2°, 全波模拟验证了这种奇异反射效应(如图13(b) ), 计算得到的反射角为${\theta _{\rm{r}}} \approx {52.3^ \circ }$ , 与理论预测符合得很好. 而且, 从模拟的场分布图中可以直观地看到镜像反射模式和–1阶衍射模式(${\theta _{\rm{r}}} = - {52.3^ \circ }$ )都被深度压制, 表明SPPs奇异反射的效率很高(模拟结果约为70%).图 13 (a) 超构表面样品; (b), (c) 模拟和(d) 实验验证SPPs异常反射[89 ] Figure13. (a) Metasurface sample and (b), (c) numerical / (d) experimental verifications of SPPs anomalous reflection[89 ] .[15 ] 激发SPPs, 另外采用单极子天线测量等离金属表面的Ez 场(实部)分布, 测试结果如图13(d) 所示. 图13(c) 展示的是全波模拟得到的与实验测试相同区域的近场Ez 分布, 显然实验和模拟结果很好地符合, 实验测试的奇异反射角${\theta _{\rm{r}}} \approx {\rm{5}}{{\rm{1}}^ \circ }$ , 也和理论预测的${\theta _{\rm{r}}} = {52.2^ \circ }$ 符合得很好. 此外, 实验和模拟还验证了超构表面对SPPs的奇异反射效应存在一定频率带宽.图14(a) 所示的具有对称式线性相位梯度分布的梯度超构表面, 使得入射SPPs光束反射后形成两束沿对称的斜方向传播的SPPs光束, 它们会干涉形成一个SPPs贝塞尔光束. 另外, 基于超构表面的概念, 我们也在通信波段基于硅这种高折射率材料, 设计出相应的超构表面结构验证了SPPs的聚焦效应, 如图14(b) . 之后, 还在微波段实现了SPPs聚焦效应[90 ] .图 14 超构表面实现(a) SPPs贝塞尔光束激发和(b)SPPs聚焦效应[89 ] Figure14. Metasurfaces for (a) SPPs Bessel beam generation and (b) SPPs focusing[89 ] .5.总 结 近二十余年间, SPPs相关研究取得了突飞猛进的发展, 在增强光与物质相互作用、超分辨成像、纳米集成光路、数据存储、生物/化学传感等领域具有重要的应用价值. 其中, SPPs的一些基础理论问题一直吸引着人们的目光, 包括SPPs在非连续性界面的近远场散射、SPPs的波前调控等. 本文首先简单回顾了SPPs的发展历程及现状; 接着, 着重介绍了包括模展开计算、电流源模型等理论方法, 来解析求解SPPs的透射、反射及远场散射特性, 这些研究帮助人们理解SPPs散射规律; 最后, 回顾了利用超构表面来自由调控SPPs波前分布的工作, 它为SPPs的相关应用提供了理想的平台. 回顾这些研究成果, 将帮助人们深入理解SPPs的基本物理性质, 并为SPPs的应用带来新的启示. 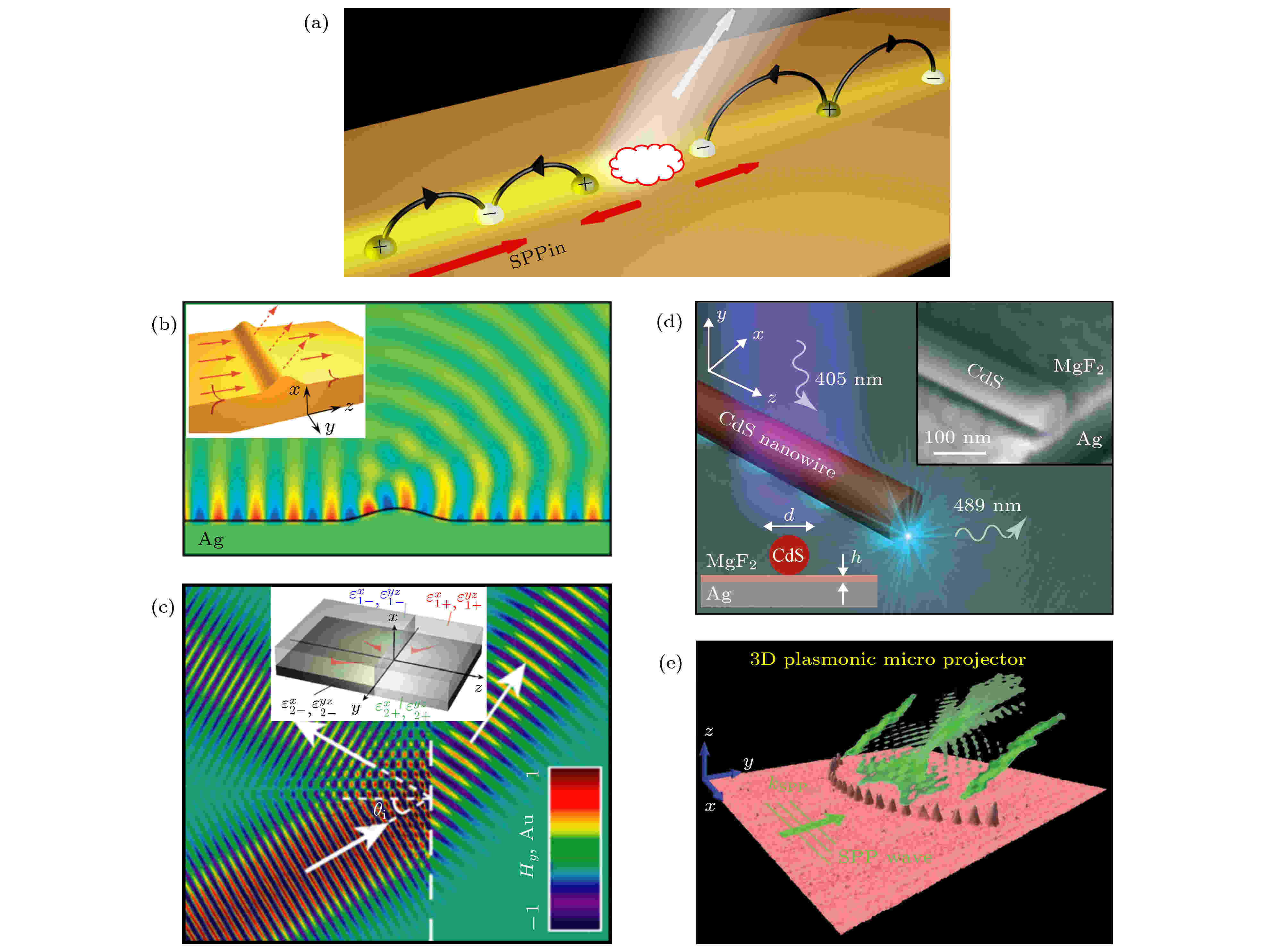 图 1 (a) SPPs的复杂散射效应; (b) SPPs遇到金属表面缺陷时的散射效应; (c) SPPs的反射和折射效应[16]; (d) 亚波长等离激元纳米激光器[17]; (e) SPPs的三维远场聚焦效应[18]
图 1 (a) SPPs的复杂散射效应; (b) SPPs遇到金属表面缺陷时的散射效应; (c) SPPs的反射和折射效应[16]; (d) 亚波长等离激元纳米激光器[17]; (e) SPPs的三维远场聚焦效应[18]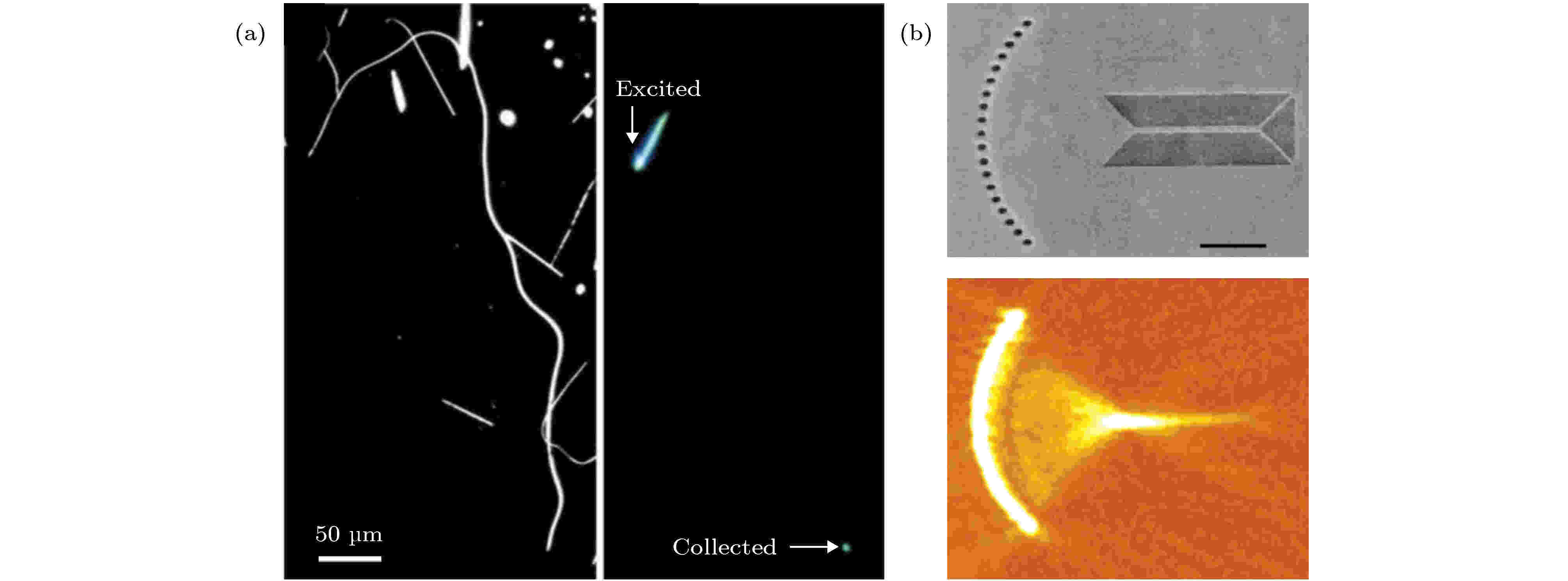 图 2 (a) SPPs在介质波导中的传输及辐射[22]; (b) SPPs聚焦装置[24]
图 2 (a) SPPs在介质波导中的传输及辐射[22]; (b) SPPs聚焦装置[24]















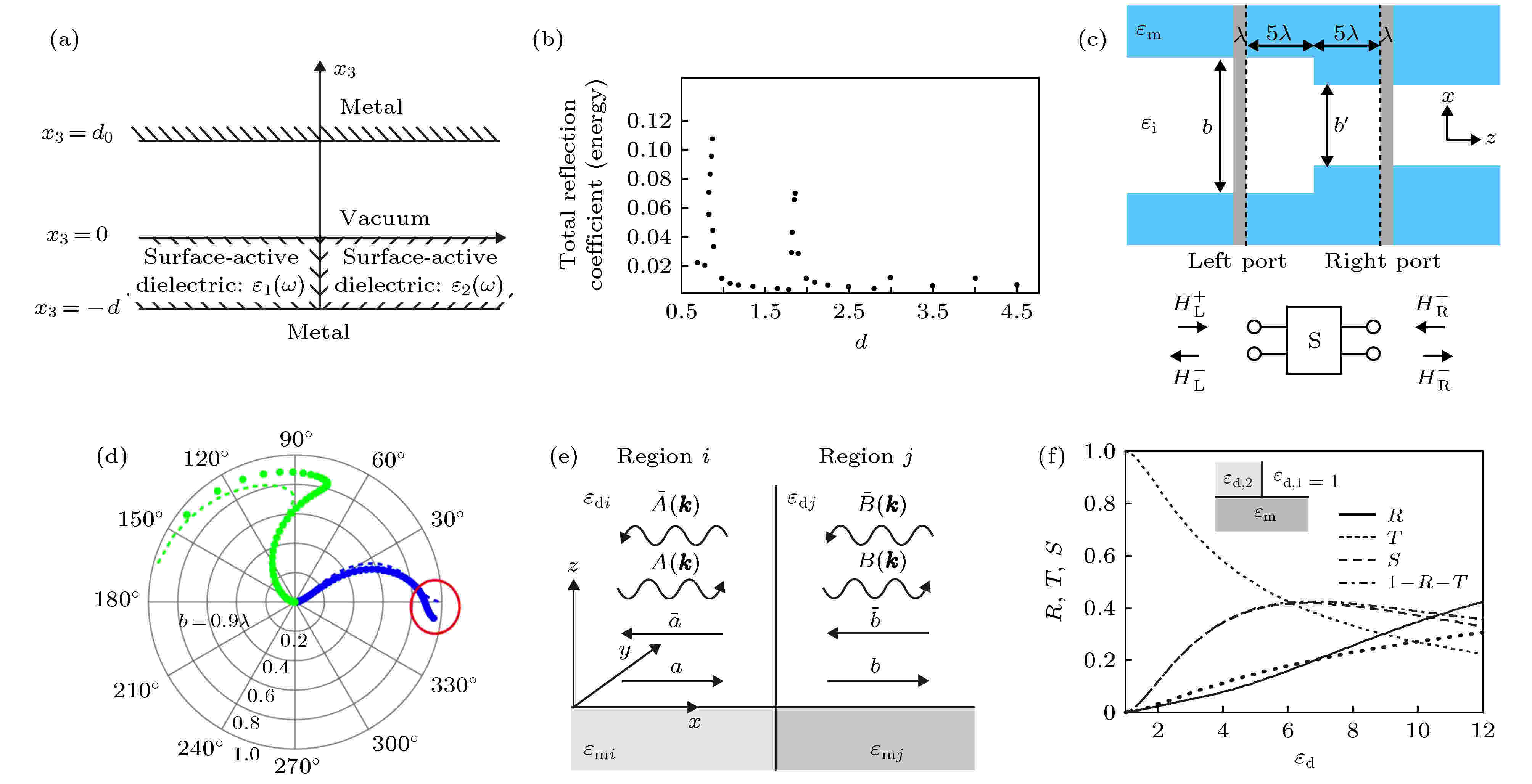 图 3 (a), (b)等离激元金属/真空对接系统(上下为完美电导体边界)中的表面等离极化激元反射谱[33]; (c), (d) 等离激元波导对接系统中的SPPs反射系数[35]; (e), (f) 金属/介质开放体系中的SPPs的散射系数(R, T, S)[36]
图 3 (a), (b)等离激元金属/真空对接系统(上下为完美电导体边界)中的表面等离极化激元反射谱[33]; (c), (d) 等离激元波导对接系统中的SPPs反射系数[35]; (e), (f) 金属/介质开放体系中的SPPs的散射系数(R, T, S)[36]







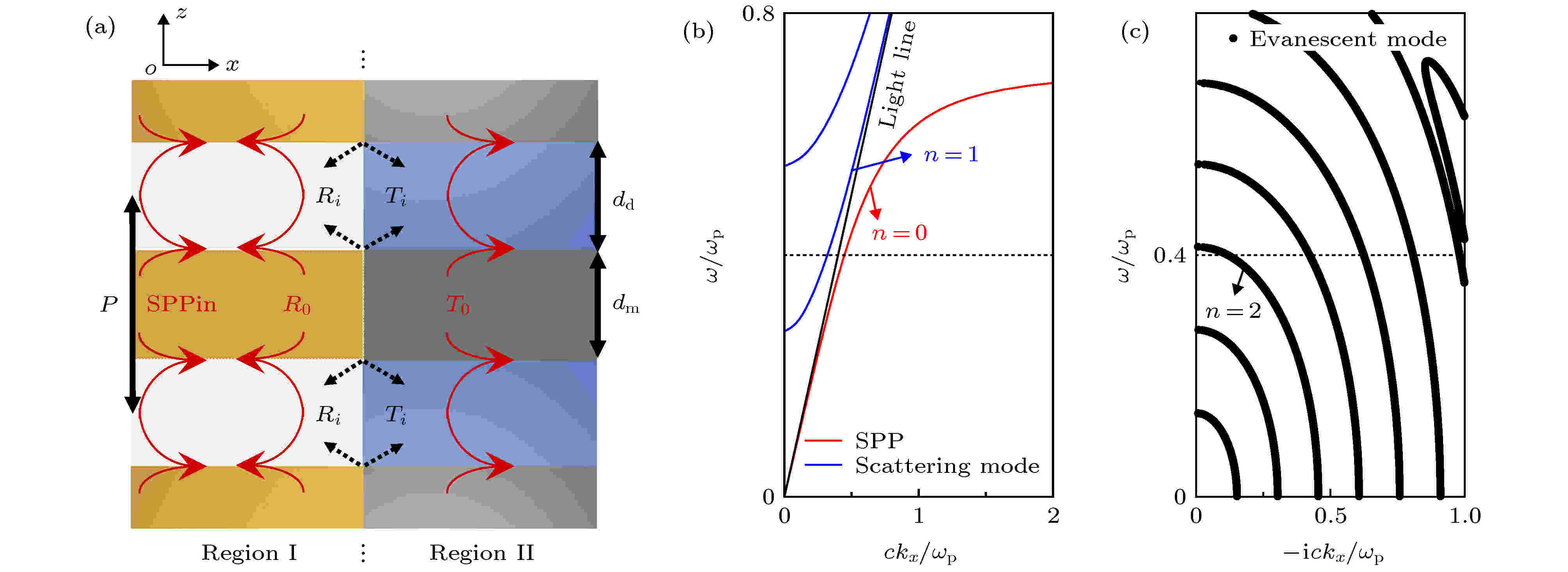 图 4 (a) 周期性等离激元体对接结构; 特定等离激元周期结构中的(b) SPPs和散射模式以及(c)倏逝波模式的色散关系[38]
图 4 (a) 周期性等离激元体对接结构; 特定等离激元周期结构中的(b) SPPs和散射模式以及(c)倏逝波模式的色散关系[38]





















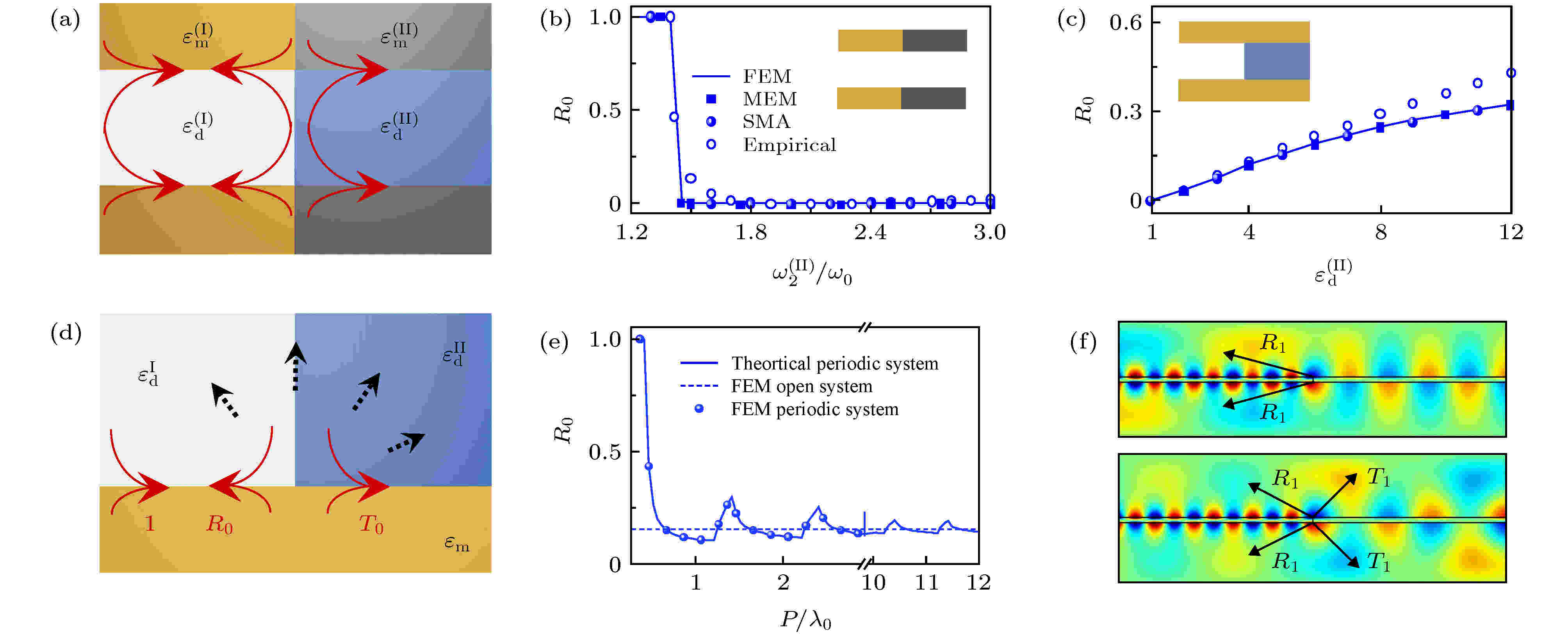 图 5 (a) 等离激元波导对接体系; (b), (c) 不同金属和不同介质对接的波导体系中SPPs的反射率谱线; (d) 开放式等离激元对接体系; (e) 反射率的变化谱线; (f) 体系中存在一阶波导模式时的场分布[38]
图 5 (a) 等离激元波导对接体系; (b), (c) 不同金属和不同介质对接的波导体系中SPPs的反射率谱线; (d) 开放式等离激元对接体系; (e) 反射率的变化谱线; (f) 体系中存在一阶波导模式时的场分布[38]


















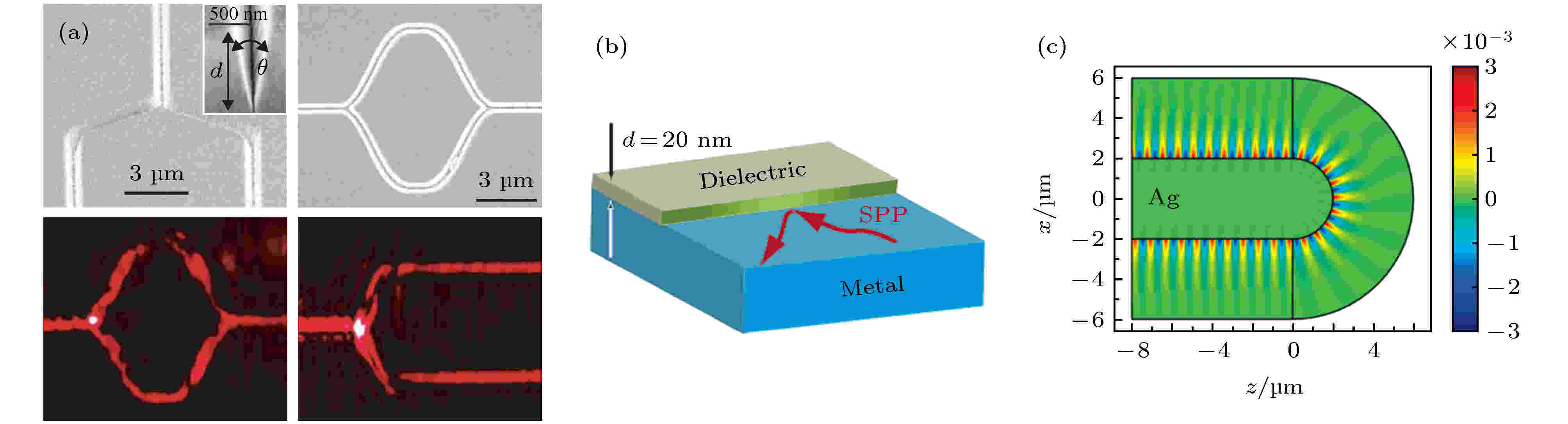 图 6 (a) 等离激元体Y型分流器和Mach-Zehnder干涉仪[43]; (b) 基于纳米薄膜的SPPs全反射[44]; (c) SPPs的180°转向效应[45]
图 6 (a) 等离激元体Y型分流器和Mach-Zehnder干涉仪[43]; (b) 基于纳米薄膜的SPPs全反射[44]; (c) SPPs的180°转向效应[45]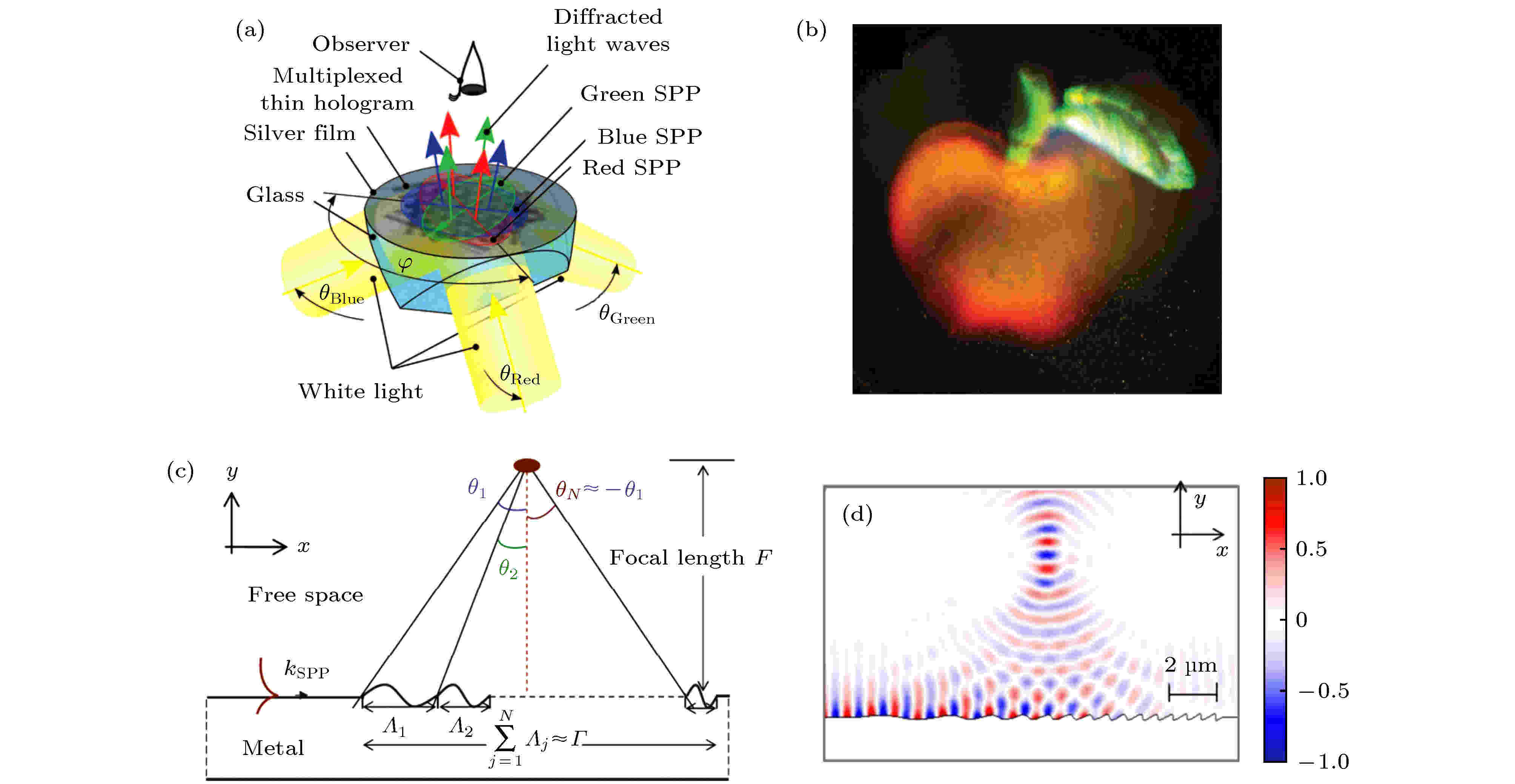 图 7 (a) SPPs彩色全息术; (b) 重建的三色苹果全息图像[46]; (c), (d) SPPs远场聚焦[49]
图 7 (a) SPPs彩色全息术; (b) 重建的三色苹果全息图像[46]; (c), (d) SPPs远场聚焦[49]


















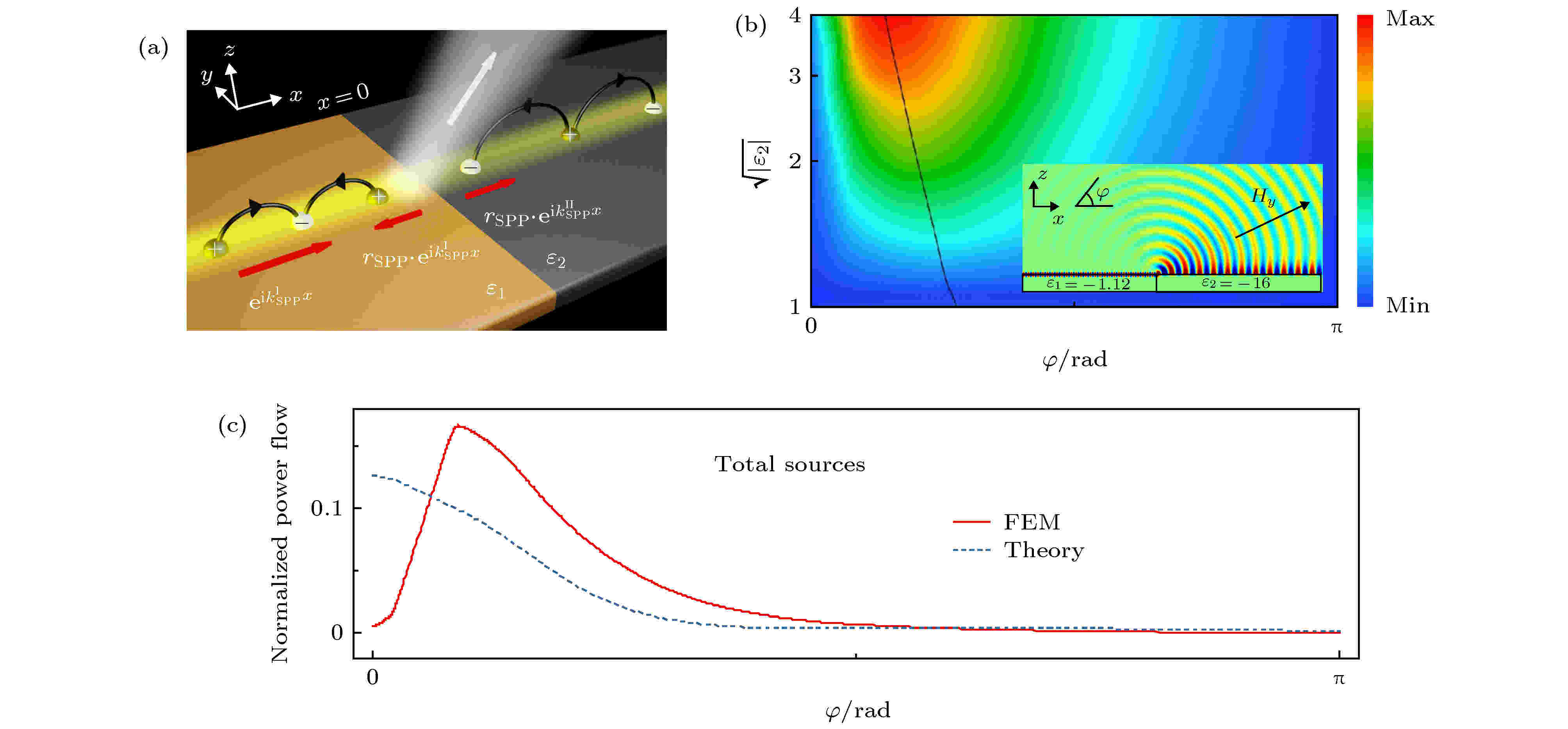 图 8 (a) 半无限大等离激元体金属对接系统; (b) 远场散射强度随着散射角度
图 8 (a) 半无限大等离激元体金属对接系统; (b) 远场散射强度随着散射角度




















































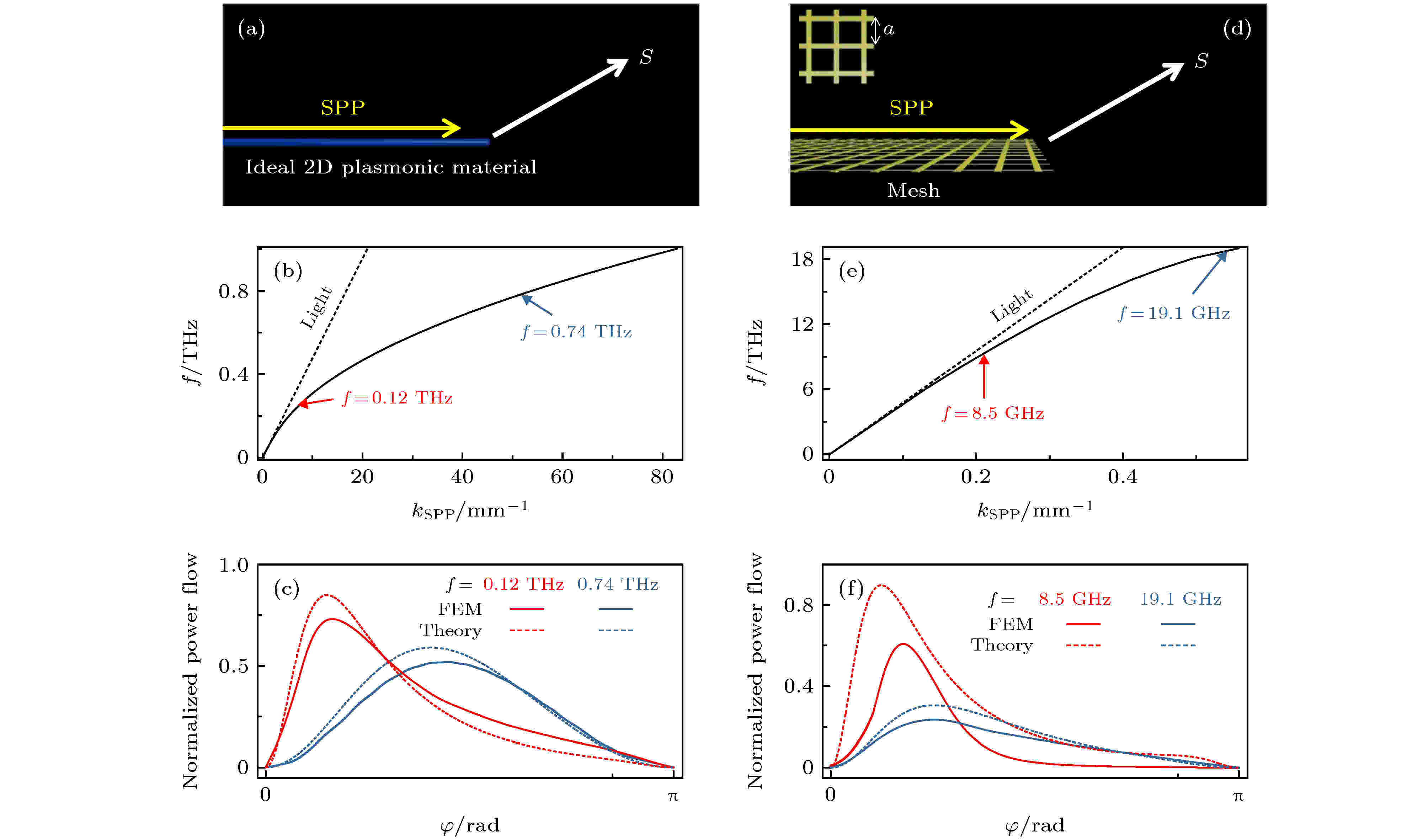 图 9 (a) 理想的半无限大二维等离激元体系统; (d) 半无限大人工金属网栅结构; (b), (e)相应体系中的SPPs的色散关系; (c), (f) 相应体系中的SPPs散射远场角谱分布[59]
图 9 (a) 理想的半无限大二维等离激元体系统; (d) 半无限大人工金属网栅结构; (b), (e)相应体系中的SPPs的色散关系; (c), (f) 相应体系中的SPPs散射远场角谱分布[59] 图 10 (a), (b) 利用不同形状的介质光学器件来调控SPPs的波前[66,67]; (c) 利用纳米颗粒阵列实现SPPs折射[68]
图 10 (a), (b) 利用不同形状的介质光学器件来调控SPPs的波前[66,67]; (c) 利用纳米颗粒阵列实现SPPs折射[68]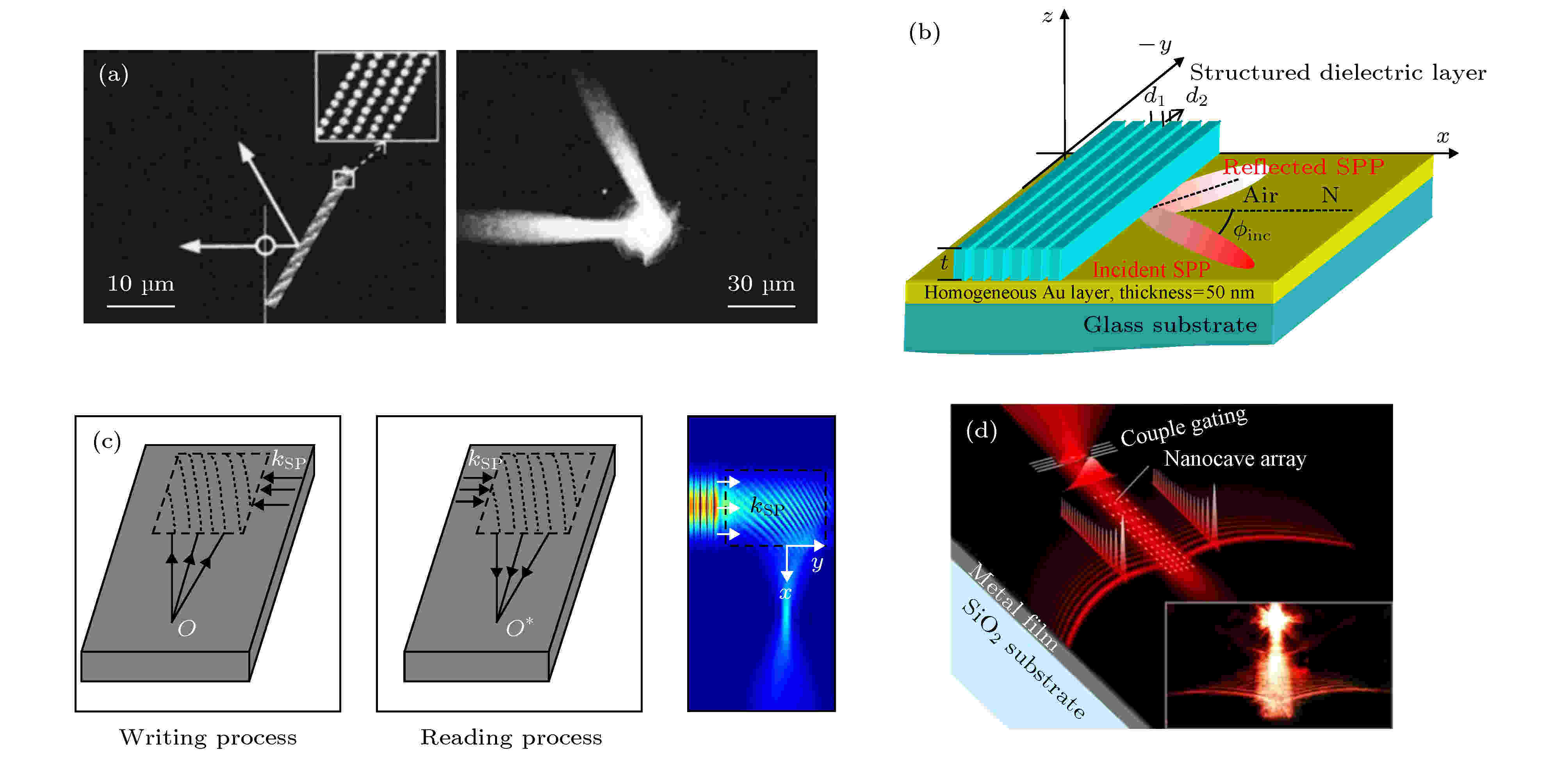 图 11 基于(a)纳米颗粒阵列[69]和(b)介质光栅[71]的SPPs布拉格反射; (c) SPPs全息[72]; (d) SPPs的艾里光束激发[73]
图 11 基于(a)纳米颗粒阵列[69]和(b)介质光栅[71]的SPPs布拉格反射; (c) SPPs全息[72]; (d) SPPs的艾里光束激发[73]

















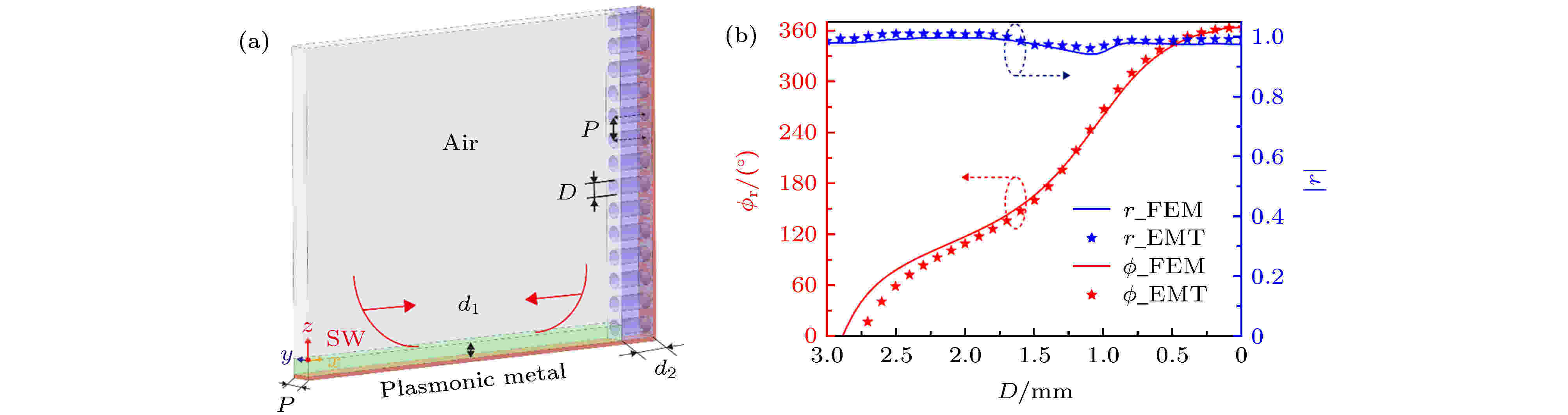 图 12 (a) 真实的超构表面结构及(b)其对SPPs的反射系数[89]
图 12 (a) 真实的超构表面结构及(b)其对SPPs的反射系数[89]














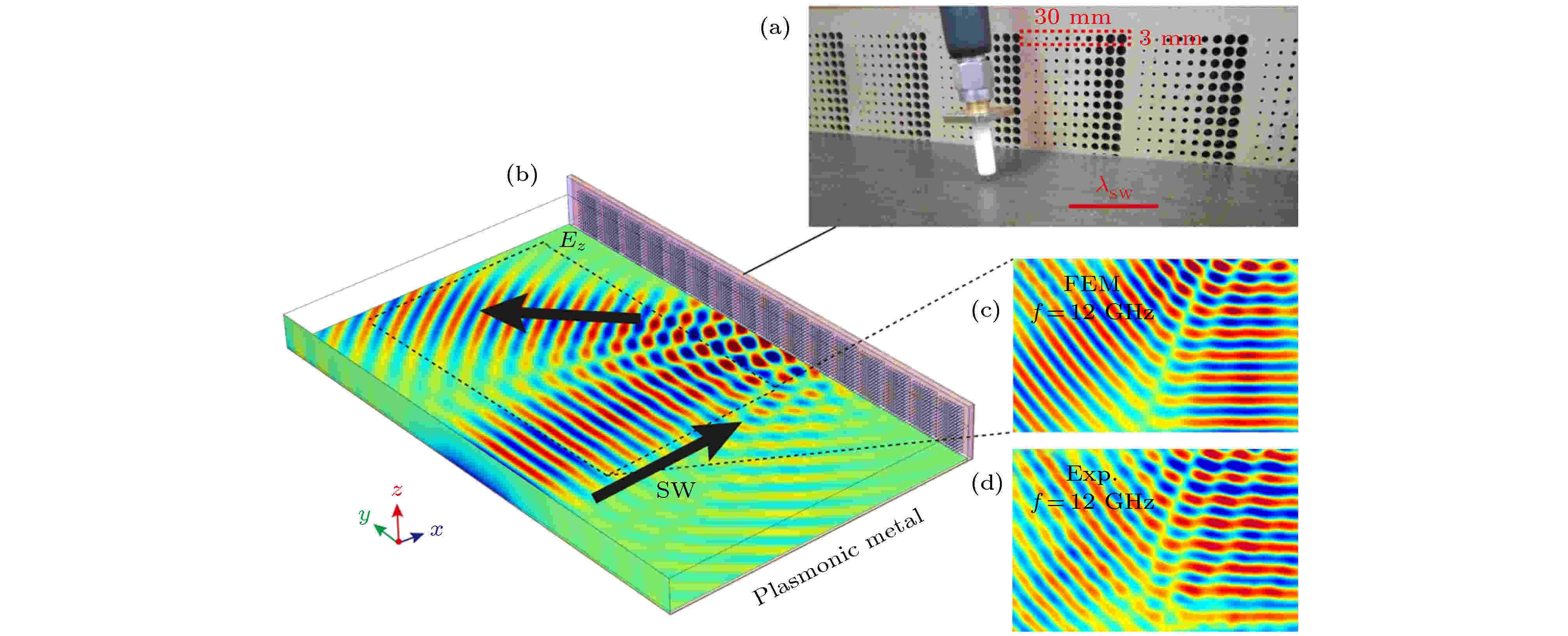 图 13 (a) 超构表面样品; (b), (c) 模拟和(d) 实验验证SPPs异常反射[89]
图 13 (a) 超构表面样品; (b), (c) 模拟和(d) 实验验证SPPs异常反射[89]

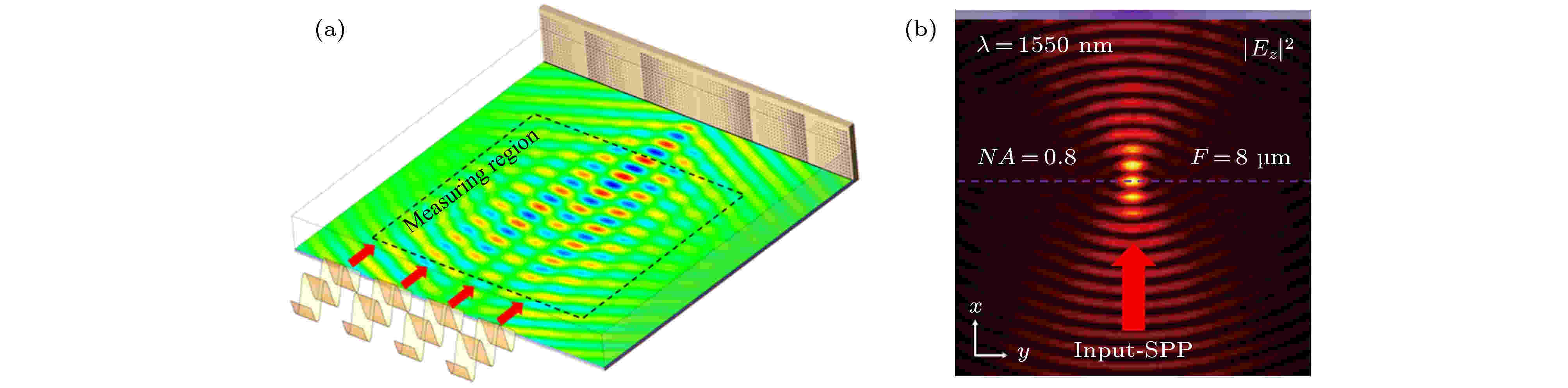 图 14 超构表面实现(a) SPPs贝塞尔光束激发和(b)SPPs聚焦效应[89]
图 14 超构表面实现(a) SPPs贝塞尔光束激发和(b)SPPs聚焦效应[89]