摘要: 本文介绍了转角双层石墨烯和多层石墨烯中的电子结构、拓扑性质以及轨道磁性. 在转角双层石墨烯中, 由于两层石墨烯之间的相对旋转会形成具有长周期的摩尔条纹. 由转角产生的摩尔势场会在摩尔超元胞中产生方向相反的赝磁场, 与两层的石墨烯中的狄拉克电子耦合, 从而产生赝朗道能级. 而魔角石墨烯中的每个谷和自旋自由度的两条平带就等价于两个具有相反陈数的零赝朗道能级. 这样的赝朗道能级表示可以很自然地解释一系列“魔角”的来源, 也对理解魔角双层石墨烯中观测到的关联绝缘态和量子反常霍尔效应具有重要意义. 本文进一步讨论了转角多层石墨烯, 并发现转角多层石墨烯体系中普遍存在具有非平庸拓扑性质的平带. 这些拓扑平带通常具有非零的谷陈数, 并且在一定近似下可以由一个普适的规律描述. 本文还讨论了转角石墨烯体系中的拓扑平带所具有的轨道磁性. 如果时间反演对称性自发破缺, 转角石墨烯体系会处于一个谷极化的基态. 这样的谷极化基态是一个在摩尔尺度上的轨道磁性态, 在摩尔超胞中具有纳米尺度的环状电流分布. 之前的理论提出在转角双层石墨烯体系中观测到的关联绝缘态的本质就是一种净磁矩为零的“摩尔轨道反铁磁态”. 当体系的
$C_{2z}$ 对称性被氮化硼衬底破坏时, 转角石墨烯中的谷极化基态则变成了一种“摩尔轨道铁磁态”, 它不仅具有(量子)反常霍尔效应, 也具有新奇的磁光效应和非线性光学响应.
关键词: 转角石墨烯 /
能带拓扑 /
轨道磁性 English Abstract Topological properties and orbital magnetism in twisted graphene systems Liu Jian-Peng 1,2 ,Dai Xi 2 1.School of Physical Science and Technology, Shanghai Tech University, Shanghai 201210, China Fund Project: Project supported by the Hong Kong Research Grants Council Project, China (Grant No. GRF16300918Received Date: 07 April 2020Accepted Date: 19 June 2020Available Online: 10 July 2020Published Online: 20 July 2020Abstract: We review and discuss the electronic structures, topological properties and orbital magnetism in twisted bilayer (TBG) and multilayer graphene systems. Moiré pattern is formed in twisted bilayer graphene due to the mutual twist of the two graphene layers. The moiré potential induced by the twist can generate opposite pseudo magnetic fields in the Moiré supercell, which are coupled with the Dirac fermions and generate two sets of pseudo Landau levels with opposite Chern numbers $\pm1$ . The two flat bands for each valley each spin of TBG are equivalent to the two zeroth pseudo Landau levels with opposite Chern numbers and opposite sublattice polarizations. Such a pseudo-Landau-level representation has significant implications on the quantum anomalous Hall states observed at integer fillings of the flat bands in TBG at the magic angle. The origin of the magic angle can also be naturally explained by using the pseudo-Landau-level picture. We further discuss twisted multilayer graphene systems, and show that topological flat bands generally exist in the twisted multilayer graphene systems. These topological flat bands have nonzero valley Chern numbers, which can be described by a succinct formula under certain approxmations. These topological flat bands in twisted bilayer and multilayer graphene systems are associated with orbital magnetism. A valley polarized state in the twist graphene system is an orbital magnetic state with nontrivial current-loop pattern in the moiré supercell. The experimentally observed correlated insulating states at $\pm 1/2$ fillings and at charge neutrality point of magic-angle TBG can be valley polarized states, which are associated with compensating current loops and induce staggered orbital magnetizations on the moiré length scale. If $C_{2z}$ symmetry is broken due to the alignment of hexagonal boron nitride substrate, then a valley-polarized ground state would be a moiré orbital ferromagnetic state, which exhibits not only (quantum) anomalous Hall effect, but also novel magneto-optical and nonlinear optical responses.Keywords: twisted graphene systems /band topology /orbital magnetism 全文HTML --> --> --> 1.引 言 转角双层石墨烯是通过将两层石墨烯堆叠并相互旋转之后形成的一个人工合成体系. 在转角双层石墨烯中, 由于两层石墨烯之间的相对旋转, 在某些匹配的角度下会形成具有长程周期性的摩尔条纹. 这些摩尔超胞的晶格尺度反比于转角$ \theta $ , 因此在小转角下, 摩尔尺度上的低能物理是由原子尺度上的石墨烯中狄拉克费米子衍生出的全新的物理. 之前的理论表明, 转角双层石墨烯中的低能态中包含4条带宽很小的自旋简并的平带, 分别来自于两个彼此几乎不耦合的K 和K' 谷[1 -6 ] . 在所谓的第一“魔角”$ \theta\approx1.05^{\circ} $ , 4条低能能带的费米速度消失为零, 能带带宽也变得非常小($ \lessapprox10\, {\rm{meV}}$ ), 这意味着在魔角附近低能态电子的动能被强烈抑制, 而电子的库仑关联作用会起到重要的作用[4 ] . 在2018年3月, 来自麻省理工学院Jarillo-Herrero组[7 ] 的实验学家成功将转角双层石墨烯调节到了魔角附近, 并且在$ \pm1/2 $ 填充, 即每个摩尔超元胞有2个电子/空穴的时候, 观测到了由库仑关联效应导致的绝缘相. 在$ \pm 1/2 $ 填充下的关联绝缘态附近进一步调节载流子浓度, Jarillo-Herrero组[8 ] 又观测到了超导相的出现. 紧接着Dean的研究组[9 ] 进一步表明, 在魔角出现的关联绝缘态和超导态可以通过层间压强来调节. 当两层石墨烯被压缩, 层间距变小的时候, 相应的关联绝缘态和超导态可以在更大的角度出现. 这表明魔角不一定总是固定在$ 1.05^{\circ} $ , 而是随着层间距离和层间耦合强度的变化而变化的. 更有趣的是, 2019年1月, 斯坦福大学的Goldhaber-Gordon组[10 ] 将六角氮化硼(hBN)衬底跟处于魔角的转角双层石墨烯对齐, 发现当平带在3/4填充, 即每个摩尔超元胞填充3个电子的时候, 体系出现了非常显著的反常霍尔效应, 其反常霍尔电导最高达到了$ 2.4\, e^2/h $ . 2019年7月, Young研究组[11 ] 在同样的hBN对齐的魔角双层石墨烯3/4填充的时候观测到了陈数为1的量子反常霍尔效应. 2019年11月, Efetov研究组[12 ] 同样在hBN对齐的魔角双层石墨烯体系–1/2填充的时候观测到了陈数为2的量子反常霍尔绝缘态. 在转角双层石墨烯中展现出的一些列关联绝缘态、超导态以及量子反常霍尔效应, 让这个体系引起了广泛的关注. 理论学家们分别从不同的角度和观点[13 -35 ] 来解释实验上观测到的超导、关联绝缘态以及量子反常霍尔效应.[13 -15 ,36 -39 ] . 三个理论研究组分别发现转角双层石墨烯中的平带具有受$ C_ {2 z}{\cal{T}} $ ($ {\cal{T}} $ 表示时间反演)对称性保护的“脆弱拓扑性”, 并且其威尔逊圈具有类似于二维拓扑绝缘体的非平庸的缠绕特征. Liu等[40 ] 进一步证明, 转角双层石墨烯中由于彼此旋转产生的摩尔势能会在摩尔条纹中的AA 区域产生方向相反的赝磁场. 赝磁场跟两层石墨烯中的狄拉克电子耦合产生赝朗道能级. 而转角双层石墨烯中在魔角附近每个谷和每个自旋自由度的两条平带正是两个具有相反陈数的零赝朗道能级. 这为转角石墨烯中平带非平庸“脆弱拓扑性”的来源提供了解释. 这种赝朗道能级表示可以很自然地解释转角双层石墨烯中为什么会有一系列“魔角”的存在. 与此同时, 转角石墨烯平带的赝朗道能级表示将该体系平带的库仑关联问题等效成一个多重简并的赝朗道能级在库仑作用下自发对称性破缺的问题, 这对理解实验中不同填充下观测到的关联绝缘态和量子反常霍尔效应的本质有重要意义[40 ] .[41 -55 ] . 如果双层石墨烯堆叠在双层石墨烯上并彼此旋转一个角度$ \theta $ 之后, 又有新的物理现象出现. 来自中国科学院物理研究所、哈佛大学和麻省理工学院的实验学家们发现在一定垂直偏压下, 这样的“转角双层-双层石墨烯 (twisted double bilayer graphene)”体系会在$ \theta\!\approx\!1.24^{\circ} $ 以及$ \theta\!\approx\!1.33^{\circ} $ 时出现可能具有自旋铁磁性的关联绝缘态, 并在关联绝缘态附近出现了超导态[41 -43 ] . 来自加州大学伯克利分校的实验学家又在hBN-ABC 三层石墨烯中1/4空穴填充(即–1/4填充)下观测到了陈数为2的量子反常霍尔效应[44 ] . 这一些列的实验现象表明具有非平庸拓扑性质的平带在转角石墨烯以及摩尔石墨烯异质结体系中广泛存在. 本文作者考虑了一种普适的转角多层石墨烯体系, 即M 层石墨烯堆叠在N 层石墨烯上并彼此旋转$ \theta $ . 并提出拓扑平带在这样的转角多层石墨烯体系中普遍存在. 这些平带普遍具有非零的谷陈数, 而这些平带的谷陈数在“手性近似”下满足一个普适的规律[48 ] . 非零的谷陈数也意味着每个谷的拓扑平带都具有轨道磁性. 如果谷对称性, 即轨道时间反演对称性自发破缺, 那么这样的转角多层石墨烯体系的基态就是一个由谷极化导致的轨道铁磁态[48 ] . 这种轨道铁磁态通过自发时间反演对称性破缺而产生, 不需要任何自旋铁磁性和自旋轨道耦合. 这种全新的摩尔轨道铁磁态在摩尔超元胞中具有纳米尺度上的自发的电流回路[48 ] , 不仅具有显著的、甚至量子化的反常霍尔效应, 也可能导致新奇的磁光响应和非线性光学响应[56 ] .2.转角石墨烯体系的晶格结构 下面首先介绍转角石墨烯体系的晶格结构. 当两层彼此“稍微不同”的二维材料放到一起时, 在特定条件下会形成长周期的摩尔条纹. 两层之间的差异可以是晶格常数之间的少许不同或是彼此之间形成一个转角$ \theta $ . 假设第一层某个晶格矢量为$ {{R}}_1 $ , 如果第二层的晶格矢量$ {{R}}_2 $ 被拉伸或压缩了$ \eta $ , 并相对第一层旋转了$ \theta $ , 那么数学上$ {{R}}_2 $ 可以写成: ${{R}}_2\! = \!\eta{ {\cal{R}}}(\theta){{R}}_1 $ , 这里$ {{\cal{R}}}(\theta) $ 是笛卡尔坐标系下的旋转矩阵. 当第二层的晶格矢量$ {{R}}_2 $ 跟第一层的矢量$ {{R}}_1 $ 的差$ {{R}}_2 \!-\! {{R}}_1 $ , 恰巧跟底层二维材料的原子晶格矢量$ {{a}} $ 匹配, 即$ \eta{ {\cal{R}}}(\theta){{R}}_1 -{{R}}_1\! = \!{{a}} $ 时, 该双层体系即会形成一个具有长程周期性的摩尔超元胞. 该摩尔超胞的超晶格常数即是: $ L_{\rm{s}}\! = \!a/\sqrt{\eta^2 \!+\! 1 \!-\! 2\eta\cos{\theta}} $ . 很显然当$ \eta\!\approx\!1 $ 且$ \theta $ 比较小的时候$ L_{\rm{s}} $ 会远大于原子晶格常数a . 对于转角石墨烯体系, $ \eta\! = \!1 $ , 因此$ L_{\rm{s}}\! = \!a/[2\sin(\theta/2)] $ , $ a\! = \!2.46\, $ 是单层石墨烯的晶格常数.图1(a) 展示了转角双层石墨烯的摩尔超元胞示意图. 可以看到在转角石墨烯的摩尔条纹中有AA , AB , 以及BA 区域的周期性调制. 在AA 或AB/BA 区域内, 系统局域上类似于$ AA $ 或$ AB/BA $ 堆叠的双层石墨烯. 当转角$ \theta $ 比较小时, $ L_{\rm{s}}\!\approx\!a/ \theta \!\gg\!a $ , 相对应的摩尔布里渊区(图1(c) )则比单层石墨烯的原子布里渊区小很多. 实际上摩尔布里渊区仅仅覆盖石墨烯K 和K' 谷附近的一小部分. 如图1(c) 所示, 当两层发生旋转之后, 第一层的K 点($ K_1 $ )和第二层的K' 点($ K_2' $ )投影到摩尔布里渊区的$ K_{\rm{s}} $ 点, 而$ K_1' $ 和$ K_2 $ 点则投射到摩尔布里渊区的$ K_{\rm{s}}' $ 点. 两层之间的旋转和层间耦合会产生一个以摩尔超晶格矢量$ {{R}} $ 为周期的摩尔势能$ U({{r}})\! = U({{r}}+{{R}}) $ , 可以用摩尔超晶胞的倒易格矢$ {{G}} $ 展开:图 1 (a)转角双层石墨烯的摩尔条纹示意图, 插图展示两层石墨烯在不同区域层间距离的褶皱起伏; (b) 转角双层-双层石墨烯体系的示意图; (c)转角石墨烯体系的摩尔布里渊区示意图Figure1. (a) Schematic illustration of the moiré pattern in twisted bilayer graphene, the inserted shows the wrinkles of the graphene for different layer distances; (b) schematic illustration of twisted double bilayer graphene system; (c) moiré Brillouin zone of twisted graphene systems.$ U({{r}}) $ 在摩尔尺度上是个平滑函数, 其傅里叶分量$ U({{G}}) $ 会随着$ \vert{{G}}\vert $ 的增大而迅速衰减[5 ] . 因此, 由于K 点和K' 点在倒易空间中的距离$|{{K}}-{{K}}' | = 4{\text{π}}/(3a)$ 远远大于摩尔倒易格矢$\vert{{G}} _1\vert = 4{\text{π}}/{\sqrt{3}L_{\rm{s}}}$ , 其对应的傅里叶分量$ U(4{\text{π}}/(3 a)) $ 在转角$ \theta $ 较小的时候是完全可以忽略的. 因此在转角$ \theta $ 较小的时候, 转角双层石墨烯中来自K 和K' 的低能态可以近似认为是彼此独立没有耦合的[4 ,57 ] . 值得注意的是, 在转角双层石墨烯中两层石墨烯的层间距离会在不同的区域发生变化[58 ] . 如图1(a) 中的插图所示, 在AB 区域中层间距离$ d_{AB}\!\approx\!3.35^{\, }$ 要小于AA 区域的层间距离$ d_{AA}\!\approx\!3.6\, $ . 这种层间距离在摩尔尺度上的褶皱起伏对低能电子结构有重要影响[14 ,59 ] .$ (M+N) $ 层石墨烯的情况, 即考虑N 层石墨烯堆叠在M 层石墨烯上面, 并彼此旋转一个角度$ \theta $ . 一个典型的例子就是图1(b) 中所示的转角双层-双层石墨烯体系, 对应于$ M = 2, $ $ N = 2 $ 的情况. 最近(可能的)自旋铁磁关联绝缘态以及在此关联绝缘态附近的超导态也在转角双层-双层石墨烯中被观测到[41 -43 ] . 当转角较小时, 这样的转角多层石墨烯体系也会形成摩尔条纹, 其对应的摩尔布里渊区跟转角双层石墨烯是一样的 (见图1(c) ).3.转角双层石墨烯的连续模型、电子结构及拓扑性质 23.1.连续模型及能带结构 3.1.连续模型及能带结构 转角双层石墨烯的低能电子结构可以用连续模型来很好地描述[1 ,4 ,5 ] . 转角双层石墨烯的能带结构可以从如下角度来理解. 首先, 由于摩尔超晶格的形成, 来自底层和顶层石墨烯的狄拉克锥被折叠到小的摩尔布里渊区里, 导致一些列线性色散、彼此交叉的能带. 这些折叠的狄拉克锥在摩尔布里渊区里有一个有效的能带带宽$ w_{\rm{s}}\approx 2{\text{π}}\hbar v_{\rm{F}}/L_{\rm{s}}\approx 2{\text{π}}\hbar v_{\rm{F}}\theta/a $ . 第二, 折叠到摩尔布里渊区的狄拉克电子进一步跟由摩尔条纹产生的摩尔势能($ U({{r}}) $ )耦合在一起. 在转角$ \theta $ 比较大时, 摩尔势能$ U({{r}})\approx 0.1\, {\rm{eV}}$ [4 ,5 ] 比有效带宽$ w_{\rm{s}} $ 小. 这样$ U({{r}}) $ 可以被看作是对折叠的狄拉克锥的一种微扰, 会让原本彼此交叉的狄拉克线性能带打开带隙, 让一些低能能带跟其他能带在能量上由带隙区分开. 然而, 当转角$ \theta $ 足够小, 以至于有效带宽$ w_{\rm{s}}\lessapprox U({{r}}) $ 时, 摩尔势能$ U({{r}}) $ 的效果不能再当作微扰来处理. 这时转角石墨烯在一系列“魔角”上会出现带宽非常小且费米速度消失的平带[4 ] .K 和 K' . 当转角较小时它们彼此之间在倒易空间中的距离$ \vert{{K}}-{{K}}'\vert = 4{\text{π}}/(3 a) $ , 远大于摩尔倒易晶格矢量的模$\vert{{G}} _1\vert = 4{\text{π}}/(\sqrt{3}L_{\rm{s}})\approx 4{\text{π}}\theta/({\sqrt{3}a})$ . 另一方面, 鉴于摩尔势能$ U({{r}}) $ 在摩尔尺度上的平滑性, 其傅里叶分量$ U({{G}}) $ ((1 )式) 随$ \vert{{G}}\vert $ 的增大而迅速衰减以至于在小转角时$ U(\vert{{K}}-{{K}}'\vert) $ 是完全可忽略的. 在小转角时, 来自于K 和K' 的两组低能态可以近似认为是彼此不耦合的. 因此来自每个谷的电荷分别守恒, 该体系有一个与谷相对电荷守恒相对应的谷$ U(1) $ 对称性, 标记为$ U_v(1) $ 对称性. 另一方面, 由于在石墨烯中自旋轨道耦合极其微弱、可以忽略, 转角石墨烯体系的每个谷分别有自旋旋转对称性 (自旋$ SU(2) $ 对称性), 这样该体系的连续对称性可以表示为$ U(1)\times U_v(1)\times SU(2)\times SU(2) $ , 这里$ U(1) $ 表示跟体系总电荷守恒相对应的对称性.K 和K' 点的布洛赫函数为基底具体写出来:$ {\sigma}^{\mu}\! = \![\mu\sigma_x, \sigma_y] $ 是定义在石墨烯$ A/B $ 子晶格空间内的泡利矩阵, $ \mu\! = \!\pm $ 是谷自由度指标, $ K^{-} = K $ , $ K^{+} = K' $ . $ v_{\rm{F}} $ 是单层石墨烯平面内的费米速度, 而$ U_{\mu}({{r}}) $ 表示投射到$ K^{\mu} $ 谷的摩尔势能:${{r}}_{AB} = (\sqrt{3}L_{\rm{s}}/3, 0)$ , $u_0 \approx 0.08\, {\rm{eV}}$ 和$u_0' \approx 0.098\, {\rm{eV}}$ [14 ] 表示不同子晶格之间和相同子晶格之间的层间耦合参数. 层间距离在摩尔尺度上的褶皱起伏效应导致$ u_0 < u_0' $ [14 ] . (3 )式中的相位因子$ g_{\mu}({{r}}) $ 定义为$g_{\mu}({{r}}) = \displaystyle\sum\nolimits_{j = 1}^{3}{\rm{e}}^{-{\rm{i}}\mu{{q}}_j\cdot{{r}}}$ , 其中三个波矢$ {{q}}_1 = (0, -4{\text{π}}/ (3 L_{\rm{s}})) $ , $ {{q}}_2 = (-2{\text{π}}/(\sqrt{3}L_{\rm{s}}), -2{\text{π}}/(3 L_{\rm{s}})) $ , $ {{q}}_3 = (2{\text{π}}/(\sqrt{3}L_{\rm{s}}), -2{\text{π}}/(3 L_{\rm{s}})) $ . (3 )式中$ \Delta{{K}}\! = \!{{K}}_2-{{K}}_1 = [0, 4{\text{π}}/(3 L_{\rm{s}})] $ . 除了$ U_v(1)\times SU(2)\times SU(2) $ 对称性, 该体系每个谷的连续模型还具有$ C_{3 z} $ , $ C_{2 x} $ 以及$ C_{2 z}{\cal{T}} $ 对称性, 这里$ {\cal{T}} $ 是指轨道时间反演对称性. K 和K' 两个谷可以通过$ {\cal{T}} $ , $ C_{2 z} $ 以及$ C_{2 y} $ 对称性操作联系起来.AA 区域内底层石墨烯的A 子晶格下面正对着氮原子, 而B 子晶格下面正对着硼原子, 这会在AA 区域产生一个符号交错的子晶格在位能(用$ \varDelta_{\rm M} $ 表示), 会在摩尔布里渊区里的$ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ (见图1(c) )点打开能隙, 给狄拉克电子带来一个“质量项”. 另一方面, 由于hBN跟石墨烯的晶格常数有少许的失配, 这也会产生一个由于晶格失配导致的摩尔势能. 但是这种hBN-石墨烯晶格失配导致的摩尔势能要比由于两层石墨烯旋转导致的摩尔势能弱一个数量级[60 ,61 ] , 因此可以忽略掉. 在这样的近似下, hBN衬底与转角石墨烯对齐之后相当于给该体系加了一个交错的子晶格在位能, 破坏了体系的$ C_{2 z} $ 对称性, 因此也破坏了每个谷原本具有的$ C_{2 z}{\cal{T}} $ 对称性. 这使得每个谷的平带具有了非零的陈数, 进而在谷对称性 (即时间反演对称性) 破缺之后才可能产生反常霍尔效应甚至量子反常霍尔效应[10 ,11 ] .2 )式中的连续哈密顿量, 在魔角$ \theta\! = \!1.05^{\circ} $ 时得到图2(a) 中的能带. 实线和虚线分别代表来自K 和K' 谷的能带, 并且每条能带都是自旋简并的. 蓝色的能带表示狄拉克质量项$ \varDelta_{\rm M}\! = \!0 $ 时的情况, 这时每个谷具有$ C_ {2 z}{\cal{T}} $ 对称性, 它和$ C_{3 z} $ , $ C_{2 x} $ 对称性一起保证了能带在$ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ 点简并的稳定性. 可以注意到, 在魔角时$ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ 点附近的费米速度完全消失, 而两条平带整体的带宽也不超过10 meV. 红色的能带则表示由于体系跟hBN衬底对齐, 导致一个非零的狄拉克质量项$ \varDelta_{\rm M} = 15\, {\rm{meV}}$ 的情形. 这时由于$ C_{2 z}{\cal{T}} $ 对称性的破坏, 在$ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ 的狄拉克点打开了带隙. 更有趣的是, 这个带隙是拓扑非平庸的, 具有非零谷陈数$ \pm 1 $ [25 ,59 ,62 ] , 稍后会解释拓扑非平庸性的起源及其对理解实验上观测到的量子反常霍尔效应的重要性.图 2 (a)转角双层石墨烯在魔角时的能带; (b)转角双层石墨烯中K 谷两条平带的威尔逊圈 (以$2{\text{π}}$ 为单位)Figure2. (a) Band structures of twisted bilayer graphene at the magic angle; (b)Wilson loops of the two flat bands from the K valley of twisted bilayer graphene (in $2{\text{π}}$ ).3.2.能带拓扑性及赝朗道能级表示 -->3.2.能带拓扑性及赝朗道能级表示 有趣的是, 在$ \varDelta_{\rm M}\! = \!0 $ , 体系具有$ C_{2 z}{\cal{T}} $ 时, 转角双层石墨烯中每个谷每个自旋自由度的两条平带具有受$ C_{2 z}{\cal{T}} $ 保护的非平庸的“脆弱拓扑性”[36 ,37 ,63 ] . 这种非平庸拓扑性体现在图2(b) 所示的奇数次缠绕的威尔逊圈上. 在拓扑能带论里, “威尔逊圈”[64 ] , 又称“杂化瓦尼尔中心演化图”[65 ] , 是理解能带拓扑性的一个核心物理量. 假定有一组能带跟其他能带在能量上由非零的带隙分开, 那么这组能带的威尔逊圈即是这组能带沿着$ k_1 $ 方向积分得到的非阿贝尔贝里相矩阵在每个$ k_2 $ 点的本征值$ w(k_2) $ 随$ k_2 $ 由0增长到1的演化图样, 这里$ 0\leqslant k_1\, , \, k_2\leqslant 1 $ 是布里渊区里波矢的简化坐标(见图2(b) ). 对于一条陈数为C 的能带, 其在$ k_2 $ 点的贝里相$ w(k_2) $ 会随着$ k_2 $ 从0增大到1而改变$ 2{\text{π}} C $ . 而在Kane-Mele模型里[66 ,67 ] , 一个二维的拓扑绝缘体或量子自旋霍尔绝缘体可以被理解为体系的两个自旋自由度具有相反的陈数$ \pm 1 $ , 彼此通过带自旋的时间反演操作$ {\rm{i}}{ {\sigma}}_y{\cal{K}} $ ($\cal{K}$ 表示复共轭) 联系起来. 因此, 对于一个有两个占据能带的二维拓扑绝缘体, 其占据态的威尔逊圈就由两条线组成: 一条随着$ k_2 $ 增长变化了$ +2{\text{π}} $ , 另外一条随着$ k_2 $ 增长变化了$ -2{\text{π}} $ . 这两条贝里相位的曲线彼此缠绕奇数次, 在$ k_2\! = \!0 $ 和$ 0.5 $ 这样的时间反演不变点保持以$ 2{\text{π}} $ 为模的二重简并, 并且这种简并受到自旋体系时间对称性的保护[68 ] . 而转角双层石墨烯每个谷每个自旋的两条也具有与二维拓扑绝缘体类似的拓扑性质. 如图2(b) 所示, 两条平带的威尔逊圈也具有奇数次缠绕的特征, 并且在$ k_2 = 0 $ 和$ k_2 = 0.5 $ 时保持简并 (以$ 2{\text{π}} $ 为模). 但是转角石墨烯里自旋轨道耦合可忽略, 我们考虑的能带是无自旋的能带, 所以这里威尔逊圈在高对称点的二重简并不是受自旋时间反演对称性保护, 而是受$ C_{2 z}{\cal{T}} $ 保护[37 ,59 ] , 这里$ {\cal{T}} $ 是指轨道时间反演操作. 更详细的对称性分析表明, 这种受$ C_{2 z}{\cal{T}} $ 保护的威尔逊圈的简并只对两能带体系成立[37 ,59 ] . 如果有更多的能带跟这两条能带纠缠在一起, 没有一个有限的能隙分开, 那么威尔逊圈在时间反演不变点的简并就不再受$ C_ {2 z}{\cal{T}} $ 的保护, 因此这种非平庸拓扑性成为脆弱拓扑.2 )式和(3 )式中的连续哈密顿量. 选取AA 区域的中心为原点, 对(3 )式中的摩尔势能对$ r/L_{\rm{s}} $ 做一个线性展开, 然后对连续哈密顿量的基底函数$ \{\psi_{ls}({{r}})\} $ 做如下的幺正变换:K 谷的连续模型展开到$ r/L_{\rm{s}} $ 的线性项变成:$ {{A}} $ 表示由摩尔条纹产生的有效矢量势, $ {{A}}\! = \!(2{\text{π}} u_0')/(L_{\rm{s}} ev_{F})\, [y\, , -x\, ] $ . 如果没有非对角项$ \pm3{\rm{i}}u_0 $ , (5 )式中哈密顿量的对角块就是两个狄拉克费米子跟方向相反的赝磁场耦合的哈密顿量. 这里赝磁场$ \pm{{B}}_{\rm{s}} = \pm\nabla\times{{A}} $ , 其强度$ \vert{{B}}_{\rm{s}}\vert = 4{\text{π}} u_0'/(ev_{\rm{F}} L_{\rm{s}}) $ . 没有非对角项$ \pm3{\rm{i}}u_0 $ , (5 )式中哈密顿量的本征能量($ E_{\pm N, k} $ )就是狄拉克费米子的朗道能级, 即$ E_{\pm N, k} = \pm\hbar\omega_{\rm c}\sqrt{N} $ ($ N\geqslant 0 $ ). 这些赝朗道能级所对应的回旋频率$ \omega_{\rm c} $ 以及特征磁长度$ l_{\rm B} $ 为:[69 ] . 由于(2 )式中的对角块是狄拉克费米子跟方向相反的赝磁场耦合的哈密顿量, 它们的两个零赝朗道能级会具有完全相反的子晶格极化, 并且具有相反的陈数$ \pm 1 $ . 如果加入非对角项$ \pm 3{\rm{i}} u_0 $ , 会把两套赝朗道能级耦合起来. 然而注意到非对角耦合项$ \pm3{\rm{i}}u_0 $ 在子晶格空间中是对角的, 这意味着它只会把子晶格相同的态耦合在一起. 而两个零朗道能级具有完全相反的子晶格极化, 因此在零朗道能级的子空间里, 这一个非对角耦合项是完全消失的!但是更高的朗道能级由于不再具有100%的子晶格极化, 它们会被这个非对角耦合项耦合到一起, 从而使得原本严格平的朗道能级有了展宽, 形成了纠缠在一起的高能能带. 由于非对角项把陈数$ \pm1 $ 的高朗道能级耦合在一起, 这让高朗道能级失去了拓扑性质, 而零朗道能级由于具有完全相反的子晶格极化, 在其子空间里(2 )式非对角耦合项消失, 因此零朗道能级保持其平带以及拓扑的特征. 这就是转角双层石墨烯体系非平庸拓扑性的起源. 如果看不同的摩尔$ {{k}} $ 点的波函数在实空间中的分布, 会发现$ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ 点的波函数绝大部分都是局域在AA 区域[3 ] , 而上述赝朗道能级的论证也在AA 区域更好地成立, 这意味着在魔角附近每个谷$ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ 点附近的平带正是等价于两个陈数相反、子晶格极化相反且简并的零赝朗道能级. 如果一个交错的子晶格将位能狄拉克质量项加在体系上, 就会让两个零朗道能级的简并度劈裂开, 打开能隙. 同时由于填充的能带是赝朗道能级, 有狄拉克质量项打开的这个带隙因此具有非零的谷陈数$ \pm 1 $ .$ C_{2 z}{\cal{T}} $ 算符恰巧可以由$ {\rm{i}}{ {\sigma}}_y{\cal{K}} $ 来表示, 这里$ { {\sigma}}_y $ 是定义在子晶格空间中的泡利矩阵, $ {\cal{K}} $ 表示复共轭. 因此, $ C_{2 z}{\cal{T}} $ 对称性操作在每个谷的两个零朗道能级子空间中就像是带自旋的时间反演操作一样, 即$ (C_{2 z}{\cal{T}})^2 = -1 $ , 因此可以保护两个零朗道能级的二重克莱姆简并. 如果每个谷的$ C_{2 z}{\cal{T}} $ 对称性被破坏, 那么两个零朗道能级的克拉姆简并就不再存在, 两个零朗道能级会劈裂开. 这就是为什么转角双层石墨烯与hBN衬底是否对齐会导致截然不同的实验结果[7 ,10 -12 ] . 如果hBN衬底没与转角石墨烯对齐, 在摩尔尺度上转角石墨烯中每个谷的狄拉克费米子还具有$ C_ {2 z}{\cal{T}} $ 对称性; 而如果hBN衬底与转角石墨烯对齐之后, 对齐的hBN衬底在摩尔尺度上破坏了每个谷的$ C_{2 z}{\cal{T}} $ 对称性, 导致两个原本克莱姆简并的零朗道能级劈裂开, 产生了非零的谷陈数. 如果带有非零谷陈数的拓扑平带被部分填充, 那么体系很有可能处于一个谷极化的、自发破缺反演对称性的基态, 这就是实验上在转角石墨烯体系中观测到量子反常霍尔效应[10 -12 ] 的微观物理机理.$ C_{2 z}{\cal{T}} $ 操作只有在零朗道能级的子空间才会被表示成$ {\rm{i}}{ {\sigma}}_y{\cal{K}} $ . 这是由于$ C_{2 z} $ 操作需要交换两个子晶格, 而每个谷的两个零朗道能级恰好具有完全相反的子晶格极化. 对于更高的赝朗道能级, $ C_{2 z}{\cal{T}} $ 就没法再用$ {\rm{i}} { {\sigma}}_y{\cal{K}} $ 表示, 因此每个谷的两套更高的赝朗道能级不再具有克莱姆简并度. 在这种意义上, 只有零朗道能级所对应的两条平带再具有受$ C_{2 z}{\cal{T}} $ 保护的克莱姆简并, 因此具有跟二维拓扑绝缘体类似的非平庸拓扑性质. 如果其他高能带跟平带纠缠在一起, 那么它们就不再具有被$ C_ {2 z}{\cal{T}} $ 保护的非平庸拓扑, 这就是该体系的平带拓扑性质称为“脆弱拓扑”的根本原因.AA 区域的赝磁场为这个体系引进了一个新的特征长度, 即(6 )式中的磁长度$ l_{\rm B} $ . 每包含一个赝量子磁通所需要的面积则是$ S_0\! = \!{\text{π}} l_{\rm B}^2\! = \!L_{\rm{s}}\hbar v_{\rm{F}}/(4 u_0')\!\approx\! a\hbar v_{\rm{F}}/(4 u_0' \theta) $ . 另一方面, 摩尔超胞中AA 区域的面积$ \varOmega_{AA}\approx L_{\rm{s}}^2\approx a^2/\theta^2 $ . 因此, 当$ \theta $ 较大时, $ S_0 > \varOmega_{AA} $ . 随着$ \theta $ 减小, $ \varOmega_{AA} $ 增大的速度比$ S_0 $ 更快. 在某个临界角度, AA 区域恰巧可以包含一个赝量子磁通, 即$ \varOmega_{AA} = S_0 $ . 这时由赝磁场引进的磁周期性跟摩尔超胞本身的周期性完全匹配, 在AA 区域中的电子可以在赝磁场的驱动下做完整的回旋运动, 不需要为了满足摩尔超胞的周期性而改变自身的状态. 因此, 这时AA 区域的零赝朗道能级即是该体系严格本征态很好的近似. 由于摩尔布里渊区里$ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ 附近的本征波函数局域在AA 区域, 这意味着$ \varOmega_ {AA} = S_0 $ 的条件满足时, $ K_{\rm{s}} $ 和$ K_{\rm{s}}' $ 附近的本征态可近似成两个零赝朗道能级, 并且它们由于$ C_ {2 z}{\cal{T}} $ 对称性保持二重简并, 费米速度完全消失. $ \varOmega_{AA} = S_0 $ 的条件即是第一魔角出现的条件. 如果$ \theta $ 进一步缩小, $ \varOmega_{AA} $ 可以继续扩大包含整数个量子磁通, 即n 个魔角的条件. 令$ \varOmega_{AA}\! = \!\lambda\varOmega_{\rm M} $ , 其中$ \varOmega_{\rm M} $ 为摩尔超元胞的面积, 而经验参数$ \lambda $ 通过强制第一魔角为$ 1.05^{\circ} $ 来确定. 这样根据(7 )式进一步计算了转角双层石墨烯中的前5个魔角, 结果列在表1 中. 可以发现, 由(7 )式计算的魔角跟文献[4 ]中通过直接计算能带费米速得到的结果几乎完全一致.n 1 2 3 4 5 文献[4 ] 1.05° 0.50° 0.35° 0.24° 0.20° (7 )式 1.05° 0.52° 0.35° 0.26° 0.21°
表1 由赝朗道能级图像推算出的魔角Table1. Magic angles derived from the pseudo Landau-level picture.4.转角多层石墨烯的能带拓扑性 具有非平庸拓扑性的平带不仅在转角双层石墨烯中存在, 在其他摩尔石墨烯体系, 如转角多层石墨烯[47 -55 ] 、以及hBN-多层石墨烯异质结体系[44 ,70 ,71 ] 中也广泛存在. 本文主要讨论转角多层石墨烯的情况.N 层手性堆垛的多层石墨烯体系放在M 层手性堆垛的多层石墨烯上面, 并彼此之间有一个转角$ \theta $ . 这里多层石墨烯的堆垛手性有两种选择: 如果每两层之间是AB 堆垛, 即第二层的A 子晶格在第一次的B 子晶格上面, 那么手性定义为$ + $ ; 如果每两层之间是BA 堆垛, 即第二层的B 子晶格在第一层的A 子晶格上面, 那么其堆垛手性定义为 –. 一个典型的例子即是如图1(b) 所示的转角双层-双层石墨烯, 对应于$ M = 2, N = 2 $ 的情形. 这样的$ M+N $ 层转角多层石墨烯对于K 谷的连续模型可以通过将(2 )式进一步推广而得到:$ { H}^{K}_{\alpha}(M) $ 和 $ { H}^{+}_{\alpha'}(N) $ 是M 层和N 层石墨烯的有效哈密顿量, 其堆垛手性分别为$ \alpha $ 和$ \alpha' $ . $ { H}^{K}_{\alpha}(M) $ 具有如下表达形式:$ h_{0}({{k}})\! = \!-\hbar v_{\rm F}({{k}}-{{K}}_{\rm M})\cdot{\sigma}^{-} $ 是单层石墨烯在狄拉克点$ {{K}} _{\rm M} $ 附近的低能有效哈密顿量, $ {\sigma}^{-} = [-\sigma_x, \sigma_y] $ . 而$ { h}_{\alpha} $ ($ \alpha = \pm $ )则代表M 层石墨烯体系中的层间跃迁项,${ h}_{-} = { h}_{+}^{\dagger}$ . 相位因子$ {{k}} $ 是多层石墨烯原子布里渊区里的波矢. $ t_{\perp} $ , $ t_3 $ , $ t_4 $ 是不同的层间跃迁参数, 其中$ t_{\perp} $ 是最近邻的不同子晶格之间的跃迁参数. 层间跃迁参数的具体数值在不同的文献中有不同的选择[48 ,52 ,72 ] , 这里采取文献[48 ]里的参数取值: $ t_{\perp}\! = \!0.33\, {\rm{eV}}$ , $t_{2} = t_4 = 0.21\, {\rm{eV}}$ . 需要强调的是, 对于层间跃迁参数的不同选择只会改变转角多层石墨烯体系的少许能带细节[48 ,52 ] , 而不会改变其拓扑性质.图3(a) 展示了转角双层-双层石墨烯体系的能带结构. 其中蓝色和红色的线分别表示AB -AB 堆叠和AB -BA 堆叠的转角双层-双层石墨烯体系在转角$ \theta = 1.24^{\circ} $ 时的能带, 而实线和虚线分别表示来自K 谷和K' 谷的能带. 可以发现, 在转角双层-双层石墨烯体系中每个谷自由度仍然有两条带宽在10 meV左右的平带. 另外, 尽管AB -AB 堆叠和AB -BA 堆叠的能带结构非常相似, 然而它们的拓扑性质却截然不同. 对于AB -AB 堆叠的情况, 每个谷自由度两条平带的总陈数$C_{\rm v} = 0$ ; 对于AB -BA 堆叠, 两条平带总的谷陈数$C_{\rm v} = \pm 2$ (即对K 谷为2, 对K' 谷为–2)[48 ,52 ] . 该体系在不同堆垛下不同的拓扑性质可以从对称性的角度来理解. AB -AB 堆垛的转角双层-双层石墨烯具有$ C_{2 x} $ 对称性, 而每一个谷在$ C_{2 x} $ 操作下保持不变, 因此$ C_{2 x} $ 对称性每一个谷在摩尔布里渊区里贝里曲率的积分为零, 因此谷陈数为零. AB -BA 堆垛的转角双层-双层石墨烯有$ C_{2 y} $ 对称性, 而$ C_{2 y} $ 会将K 和$ K' $ 两个谷相互交换, 这意味着K 谷和K' 谷的陈数加起来是零 (与时间反演对称性符合), 但是每个谷允许有非零的谷陈数. 因此, 如果通过外加垂直偏压来破坏AB -AB 堆垛转角双层-双层石墨烯体系的$ C_{2 x} $ 对称性, 那么该体系就允许有非零的谷陈数. 图3(b) 展示了AB -AB 堆垛转角双层-双层石墨烯体系中K 谷的导带平带的陈数随垂直偏压$ U_{\rm d} $ (以eV为单位) 和转角$ \theta $ 的依赖关系. 随着$ U_{\rm d} $ 和$ \theta $ 的变化, 导带平带的陈数可以是$ 0 $ , $ -3 $ , $ -2 $ 和$ 1 $ . 这意味着该体系平带的拓扑性质可以被转角和外加偏压来充分地调节.图 3 (a) 转角双层-双层石墨烯在$1.24 ^{\circ}$ 时的能带; (b) AB -AB 堆垛的转角双层-双层石墨烯在$1.24 ^{\circ}$ 时K 谷第一个导带陈数随转角$\theta$ 和垂直偏压$U_{\rm{d}}$ 的变化Figure3. (a) Band structures of twisted double bilayer graphene at $\theta=1.24^{\circ}$ ; (b) the Chern number of the first conduction band for the K valley of AB -AB stacked twist-ed double bilayer graphene vs . the twist angle $\theta$ and vertical potential drop $U_{\rm{d}}$ .$ M+N $ 层手性石墨烯体系, 可以证明在小转角时每个谷会普遍存在两条带宽较小的低能能带[48 ] . 如果只保留(10 )式中最近邻层间跃迁项$ t_{\perp} $ , 该体系的连续哈密顿量由于只存在不同子晶格之间的矩阵元, 具有手性对称性. 可以证明当转角$\theta = 1.05 ^{\circ}$ , 即转角双层石墨烯的魔角时, 这种手性对称性保证了对于任意$ M+N $ 层转角石墨烯体系的每个谷自由度总是存在两条平带[48 ] . 换句话说, 在这种手性近似下, 转角双层石墨烯的魔角也是$ M+N $ 层转角多层石墨烯体系的魔角. 在这种手性近似下, 可以进一步证明$ M+N $ 层转角石墨烯体每个谷的两条平带普遍具有非零的谷陈数, 并且两条平带的陈数之和($ C^{K^{\mu}}_{\alpha, \alpha'} $ ) 满足以下规律[48 ] :$ \alpha $ , $ \alpha' = \pm $ 表示M 层和N 层石墨烯的堆垛手性, M 和N 为层数, $ \mu $ 为谷指标, $ \mu = -1(+1) $ 表示K ($ K' $ )谷. (11 )式的严格证明可以参考文献[48 ]的附录B.5.转角石墨烯体系中的轨道磁性及关联绝缘态 能带的拓扑性质通常由布里渊区里的贝里曲率来决定, 而贝里曲率也与体系的轨道磁性密切相关[73 -75 ] . 由于在转角石墨烯体系中每个谷普遍存在拓扑非平庸的平带, 而两个谷又通过时间反演对称性联系起来, 进而可以推测如果时间反演对称性(谷对称性)自发破缺, 那么在转角石墨烯中就可能实现一个非平庸的轨道磁性态. 上文提到转角双层石墨烯中在魔角附近每个谷的两个平带等价于两个陈数相反的零赝朗道能级, 而处于朗道能级中的电子会自发地做回旋运动而形成电流回路. 因此, 在转角双层石墨烯中每个谷的两个陈数相反的零赝朗道能级可能会贡献两套沿着相反方向流通的电流回路. 为了验证此猜想, 假设每个谷的化学势都在电中性点上, 分别对转角双层石墨烯的K 谷和$ K' $ 谷计算在摩尔超胞中实空间的电流密度分布. K 谷和$ K' $ 谷电流密度分布的结果分别展示在图4(a) 和图4(b) 中. 可以很清楚地看到K 谷和$ K' $ 谷的基态在摩尔尺度上都具有新奇的电流分布: 由于每个谷的$ C_{3 z} $ 和$ C_{2 z}{\cal{T}} $ 对称性, 每个谷的基态在摩尔超胞中有6个围绕$ AA $ 点的电流回路, 3个逆时针旋转, 3个顺时针旋转, 在摩尔尺度上形成了交错的轨道磁通量. 因此, 在转角双层石墨烯中每一个谷的基态都具有一种非平庸的、摩尔尺度上的电流回路序参量. 这种序参量会产生摩尔尺度上的交错的轨道磁矩, 形成一种摩尔轨道反铁磁序. 然而两个谷通过时间反演或$ C_{2 z} $ 联系起来, 以致于两个谷电流密度在实空间的每一点都彼此相反, 从而叠加起来会彼此抵消. 因此, 如果两个谷保持简并, 体系保持时间反演和$ C_{2 z} $ 对称性, 那么转角石墨烯体系的基态则不会具有这样的电流回路序参量或摩尔轨道反铁磁序参量. 另一方面, 在魔角附近, 由于摩尔势产生的赝磁通跟摩尔超胞彼此匹配, 这时由赝磁场束缚的零赝朗道能级近似为该体系的本征态. 如上所述, 这时体系的低能电子态由8条自旋和谷简并的拓扑平带组成. 如果这8条拓扑平带中的整数个被填充, 那么电子的库仑作用会倾向于将填充的能带和未填充的能带劈裂开, 产生带隙, 以降低系统总能量. 这样库仑作用就会让体系从一个自旋和谷简并的金属态变成一个对称性自发破缺的、有带隙的绝缘态, 形成一个关联绝缘体. 而之前的平均场计算表明, 几乎对于所有的整数填充, 即8条平带中填充整数n 条 ($ 1\!\leqslant\!n\!\leqslant\!8 $ ), 库仑作用都倾向于让这8条平带产生一个谷劈裂, 从而产生一个具有谷极化的基态[40 ] . 在文献[40 ]中, 基于非束缚的Hartree-Fock变分方法, 作者进一步预测实验上在$ \pm 1/2 $ 填充和电中性点观测到的关联绝缘态[7 ,76 ,77 ] 就是一种谷极化的绝缘态. 这种谷极化的基态自发地破坏了$ {\cal{T}} $ 对称性和$ C_{2 z} $ 对称性, 但是却具有$ C_{2 z}{\cal{T}} $ 这种组合对称性. 由于这种摩尔轨道反铁磁序破坏了$ C_{2 z} $ 对称性, 我们推测在转角双层石墨烯中一个谷极化基态会具有由摩尔轨道反铁磁序引起的非线性光学响应[40 ] .图 4 魔角双层石墨烯平带对应的实空间电流密度分布 (a) K 谷, $\varDelta_{\rm M}=0$ ; (b) $K'$ 谷, $\varDelta_{\rm M}=0$ ; (c) K 谷, $\varDelta_{\rm M}=15\, {\rm{meV}}$ ; (d) $K'$ 谷, $\varDelta_{\rm M}=15\, {\rm{meV}}$ , 图中黑色箭头代表电流方向, 颜色编码表示电流诱导的磁场强度, 单位为TFigure4. Real-space current-density distribution contributed by the flat bands of magic-angle twisted bilayer graphene: (a) K valley, $\varDelta_{\rm M}=0$ ; (b) $K'$ valley, $\varDelta_{\rm M}=0$ ; (c) K valley, $\varDelta_{\rm M}=15\, {\rm{meV}}$ ; (d) $K'$ valley, $\varDelta_{\rm M}=15\, {\rm{meV}}$ . The black arrows indicate the dire-ctions of the current density, and the color coding indicates the magnetic field induced by the current in unites of Tesla.$ AA $ 区域引入一个交错的子晶格在位能$ \varDelta_{\rm M}\approx 15\, {\rm{meV}}$ , 那么体系的$ C_{2 z} $ 对称性会被hBN衬底破坏, 因此每个谷也不再具有$ C_ {2 z}{\cal{T}} $ 对称性. $ C_{2 z}{\cal{T}} $ 对称性会强制每个谷的贝里曲率在摩尔布里渊区里处处为零, 因此与贝里曲率相关的物理量如轨道磁矩和反常霍尔电导都是零. 如果$ C_{2 z}{\cal{T}} $ 被hBN衬底破坏, 每个谷的贝里曲率不再是零, 因此每个谷的平带会具有非零的轨道磁矩、反常霍尔电导和非零的陈数$ \pm 1 $ . 两个谷的轨道磁矩则由于时间反演对称性的要求彼此反号. 在魔角的时候, 转角石墨烯的带宽非常小, 因此在8条具有自旋和谷简并度的平带被部分填充时, 谷简并度会通过交换库仑作用劈裂开, 让填充的平带就有谷极化, 形成自发破缺时间反演对称性的基态. 这样的谷极化态会是一个由时间反演对称性自发破缺导致的轨道铁磁态, 会导致显著的、甚至量子化的反常霍尔效应. 实验上在$ -1/2 $ 和$ 3/4 $ 填充下观测到的陈数为2和1的量子反常霍尔效应就可以通过这样的机制来解释[10 -12 ,23 ,25 ,26 ,28 ,40 ] . 除了量子反常霍尔效应, 这种谷极化的摩尔轨道铁磁态最近也在转角$ \theta = 1.68^{\circ} $ 、以多层石墨烯为衬底的转角石墨烯体系中通过磁场下的扫描隧道显微镜测量得到了验证[55 ] . 这种摩尔轨道铁磁态伴随着手性的、绕着$ AA $ 区域中心旋转的电流回路. 图4(c) 和图4(d) 展示了hBN对齐的转角双层石墨烯由K 谷和$ K' $ 谷平带贡献的实空间电流密度分布图. 这些电流回路的特征半径大概是摩尔晶格常数$ L_{\rm{s}} $ 的数量级, 而电子的绝对动量$ p\approx \hbar v_{\rm{F}} K $ 与单层石墨烯中的电子动量相当. 因此可以期待处于这样摩尔轨道铁磁态的电子会带有非常大的z 方向轨道角动量$ L_z\approx {{r}}\times {{p}} \approx \hbar v_{\rm{F}} L_{\rm{s}}/a $ , 从而会带有巨大的轨道磁矩. 对于其他转角多层石墨烯体系, 如转角双层-双层石墨烯体系, 体系本身就没有$ C_{2 z} $ 对称性, 因此绝大多数情况每个谷的低能能带会有非零的贝利曲率, 从而带有非零轨道磁矩. 基于同样的论证, 可以推测在转角多层石墨烯体系中每个谷的低能平带也会带有巨大的轨道磁矩.[73 -75 ] , 分别计算了hBN对齐的转角双层石墨烯、AB -AB 堆垛和 AB -BA 堆垛的转角双层-双层石墨烯体系来自K 谷平带的轨道磁矩$ M_{ \rm{orb}} $ 随化学势$\varepsilon_{\rm{F}}$ 的变化. 图5(a) 展示了hBN对齐的转角双层石墨烯在魔角$ \theta = 1.05^{\circ} $ 时, K 谷的两个平带所贡献的轨道磁矩$ M_{ \rm{orb}} $ 随化学势$\varepsilon_{\rm{F}}$ 的变化, 蓝色虚线标注导带平带的能量最高点. 可以看到两个平带所贡献的轨道磁矩能达到$1\mu_ {\rm{B}}$ (每个摩尔超胞), 远远大于传统的自旋铁磁体中由自旋轨道耦合所产生的轨道磁矩的大小. 另外, 对齐的hBN衬底会在摩尔布里渊区的狄拉克点 (电中性点) 打开一个大小为$ 4\, {\rm{meV}}$ 左右、谷陈数为$ \pm 1 $ 的带隙. 注意到当化学势在这个带隙里面时, 由于手性拓扑边界态的存在, $ M_{ \rm{orb}} $ 随$\varepsilon_{\rm{F}}$ 线性变化[74 ] . 图5(b) 展示了转角双层-双层石墨烯在$ \theta\! = \!1.24^{\circ} $ 时, K 谷的两条平带所贡献的轨道磁矩随化学势的变化. 蓝色和红色的垂直虚线分别表示AB -BA 堆垛和AB -AB 堆垛情况下导带平带的能量最高点. 可以看到两种情况下平带都会贡献巨大的轨道磁矩, 每个摩尔超胞的轨道磁矩能达到$5\mu_{\rm B}$ —$ 10\mu_{\rm B} $ . 有趣的是, 在AB -BA 堆垛时, K 谷的两条平带的总陈数为$ 2 $ (见(11 )式). 因此当两条平带被完全填充时 ($\varepsilon_{\rm{F}} > 0.023\, {\rm{eV}}$ ), 化学势处于体带隙, 这时候由于手性拓扑边界态的存在, $ M_ { \rm{orb}} $ 会随着$\varepsilon_{\rm{F}}$ 的增长而线性增长[74 ] .图 5 (a)转角双层石墨烯在魔角时K 谷平带贡献的轨道磁矩($M_ {\rm {orb}}$ )随化学势 ($\varepsilon_{\rm{F}}$ )的变化; (b)转角双层-双层石墨烯在$\theta=1.24^ {\circ}$ 时K 谷平带贡献的轨道磁矩随化学势的变化Figure5. (a) The orbital magnetization contributed by the flat bands of the K valley of twisted bilayer graphene at the magic angle; (b) the orbital magnetization contributed by the flat bands of K valley for twisted double bilayer graphene at $\theta=1.24^{\circ}$ .[78 ,79 ] . 在转角石墨烯的轨道铁磁体中, 轨道时间反演对称性是通过电子库仑作用自发破缺的, 不需要任何自旋磁序和自旋轨道耦合, 因此其展现出的反常霍尔效应更加显著. 例如, 在文献[10 ]中, 当平带hBN对齐的魔角双层石墨烯被3/4填充时, 观测到的反常霍尔电导峰值达到了$ 2.4\, e^2/h $ . 我们知道光直接与电子的轨道耦合, 因此可以预料在自发破缺时间反演对称性的轨道铁磁体里会有显著的磁光效应. 计算表明在太赫兹和远红外波段hBN对齐的转角双层石墨烯在摩尔轨道铁磁态时具有巨大的法拉第和科尔转角[56 ] . 另一方面, 当转角石墨烯体系的基态破坏$ C_ {2 z} $ 对称性时, 体系允许有非线性光学效应. 进一步的微观计算表明, 由于转角石墨烯中广泛存在的平带以及较小的带隙, 在hBN对齐的转角双层石墨烯和转角双层-双层石墨烯中会存在巨大的非线性光学响应, 如位移电流和二次谐波的产生[56 ] . 而且转角石墨烯体系中的轨道磁性会对非线性光学响应有巨大的贡献, 会导致新奇的磁性非线性光学效应[56 ] .6.总结与展望 本文回顾并讨论了转角双层石墨烯和转角多层石墨烯体系的电子结构、能带拓扑性及轨道磁性. 在转角双层石墨烯中由于旋转产生的摩尔势能会在AA 区域产生相反的赝磁场. 这些赝磁场与狄拉克电子耦合从而产生两套具有相反陈数的赝朗道能级, 而在转角双层石墨烯低能态存在的两条平带正是来自于两个陈数相反的、具有相反子晶格极化的零朗道能级. 用这样的赝朗道能级图像, 可以清晰地解释转角双层石墨烯中一些列魔角的来源. 这样的赝朗道能级表示把转角双层石墨烯中的库仑关联问题等效成了多重简并的赝朗道能级在部分填充下简并度劈裂的问题, 也就是“量子霍尔铁磁性”的问题[80 ] . 这对理解实验上观测到的量子反常霍尔效应具有重要意义. 我们提出转角双层石墨烯的谷极化的基态具有摩尔尺度上的电流回路, 会产生一个摩尔轨道反铁磁序. 这样的一个谷极化的摩尔轨道反铁磁态很可能就是实验上在$ \pm 1/2 $ 填充和电中性电观测到的关联绝缘态. 当hBN衬底与转角双层石墨烯体系对齐时, 由于每个谷$ C_ {2 z}{\cal{T}} $ 对称性的破缺, 一个谷极化的基态就变成了一个具有手性电流回路的摩尔轨道铁磁态. 这种摩尔轨道铁磁不仅具有显著的、甚至量子化的反常霍尔效应, 也有新奇的磁光效应和非线性光学效应.[8 ,41 -43 ,45 ] , 目前还缺乏一个被普遍认可的理论. 本文中讨论的电流环路序参量也许可以给该体系中的超导现象提供一个新的视角. 摩尔轨道磁性态是一个新的量子态, 它对外界电磁场的响应、集体激发行为[28 ] 以及量子相变行为等, 都是全新的物理问题, 亟需更深入和广泛的研究. 从材料学角度来讲, 摩尔二维范德瓦耳斯材料这个领域方兴未艾. 对于其他摩尔二维材料的研究, 如转角过渡金属二硫族化物[81 -86 ] , 转角磁性体系[87 ,88 ] 等等, 目前还处于非常初期的阶段. 期待会有更多新奇的物理在这个领域里出现. 





























































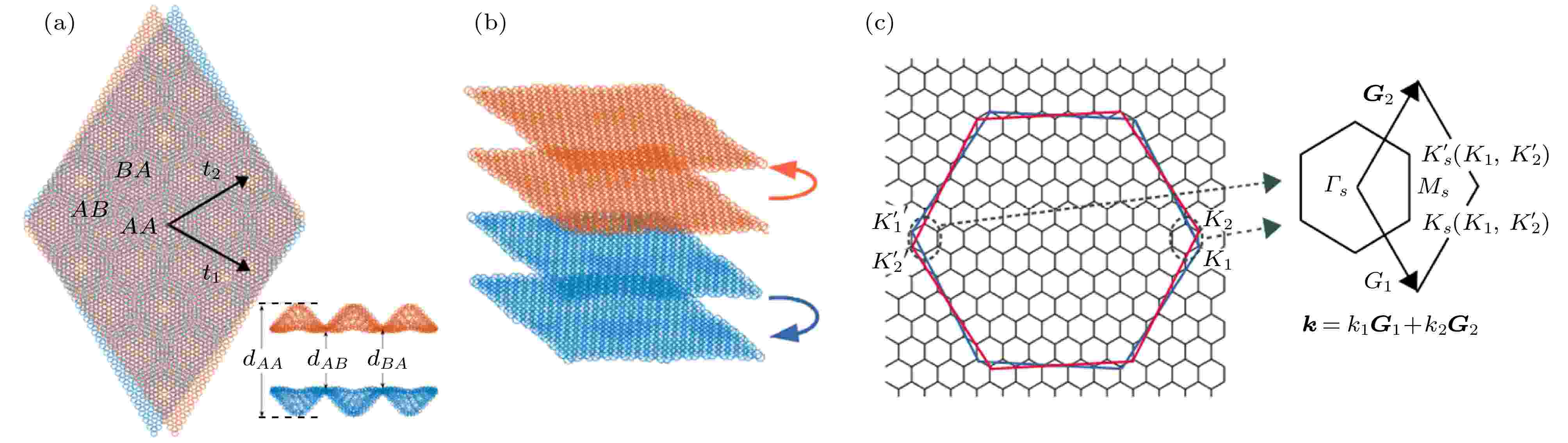 图 1 (a)转角双层石墨烯的摩尔条纹示意图, 插图展示两层石墨烯在不同区域层间距离的褶皱起伏; (b) 转角双层-双层石墨烯体系的示意图; (c)转角石墨烯体系的摩尔布里渊区示意图
图 1 (a)转角双层石墨烯的摩尔条纹示意图, 插图展示两层石墨烯在不同区域层间距离的褶皱起伏; (b) 转角双层-双层石墨烯体系的示意图; (c)转角石墨烯体系的摩尔布里渊区示意图








































































































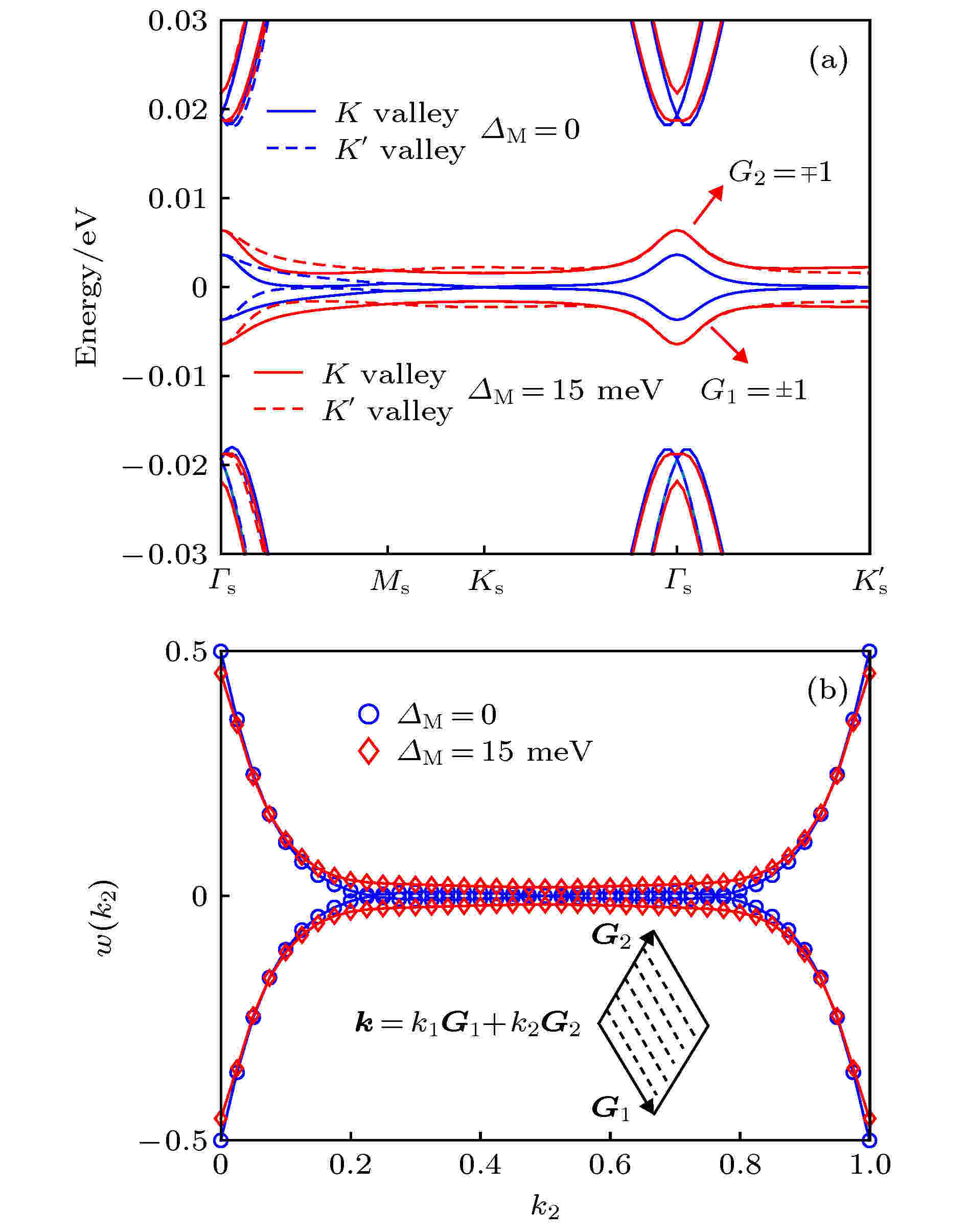 图 2 (a)转角双层石墨烯在魔角时的能带; (b)转角双层石墨烯中K谷两条平带的威尔逊圈 (以
图 2 (a)转角双层石墨烯在魔角时的能带; (b)转角双层石墨烯中K谷两条平带的威尔逊圈 (以
















































































































































































































































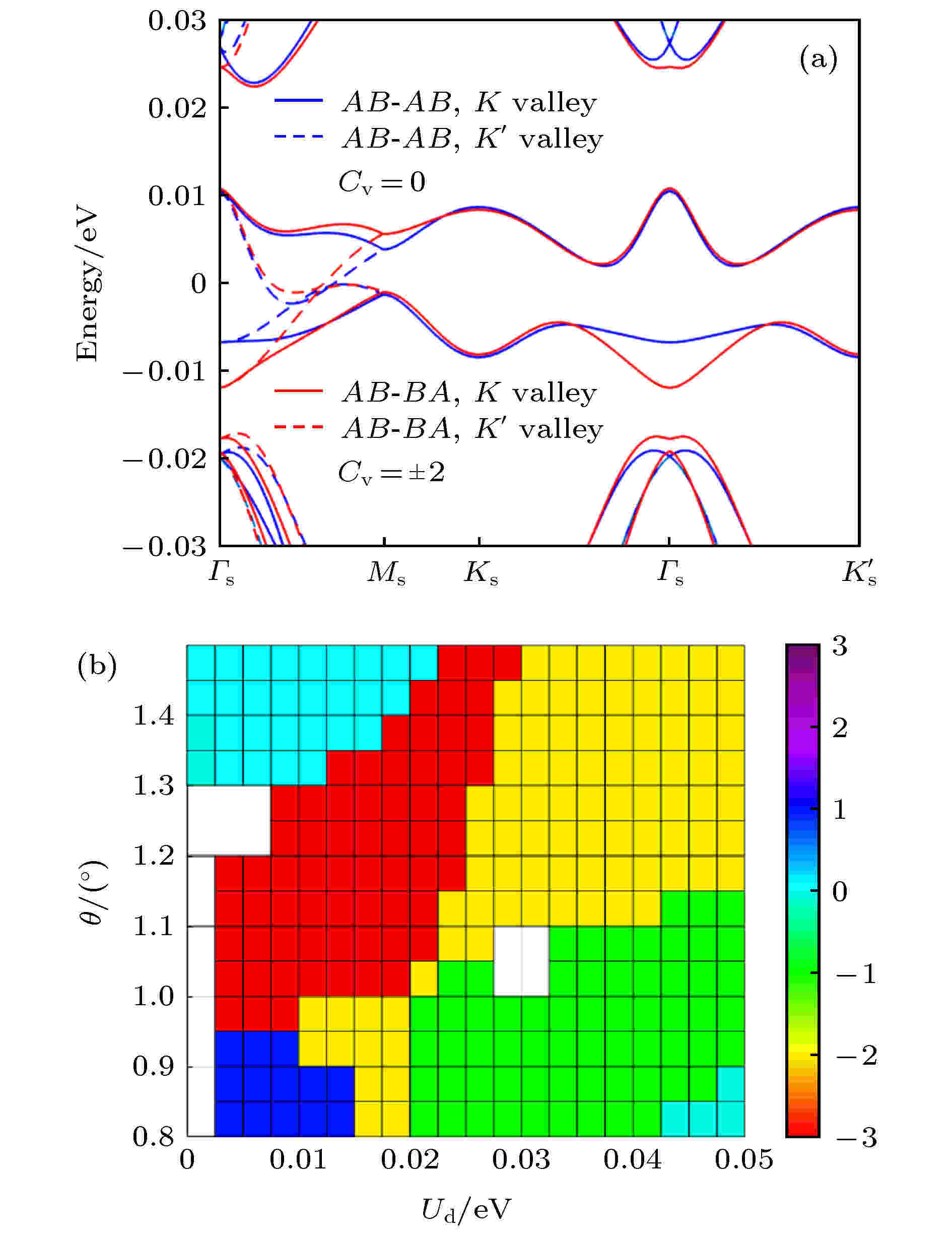 图 3 (a) 转角双层-双层石墨烯在
图 3 (a) 转角双层-双层石墨烯在


































































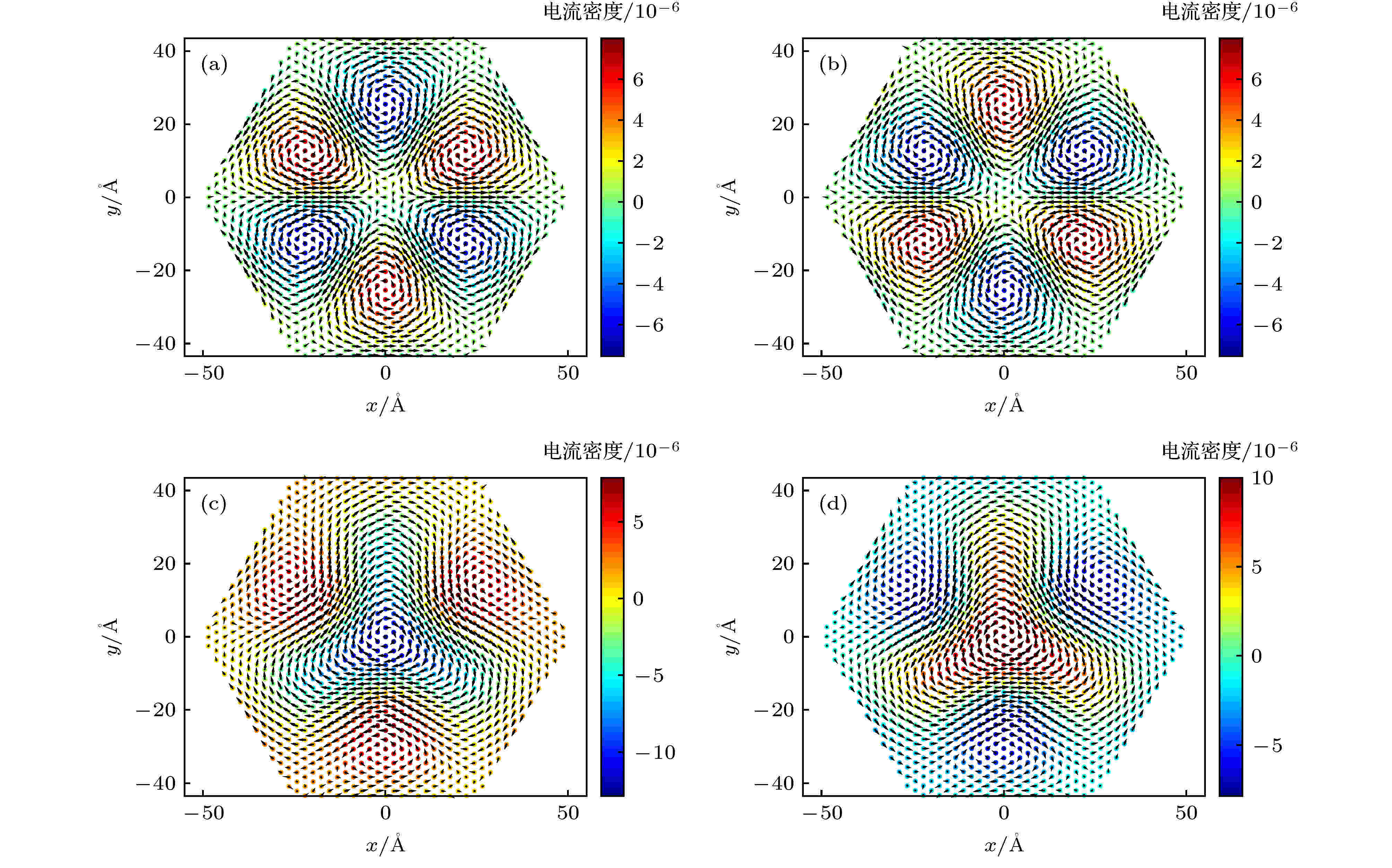 图 4 魔角双层石墨烯平带对应的实空间电流密度分布 (a) K谷,
图 4 魔角双层石墨烯平带对应的实空间电流密度分布 (a) K谷, 
















































































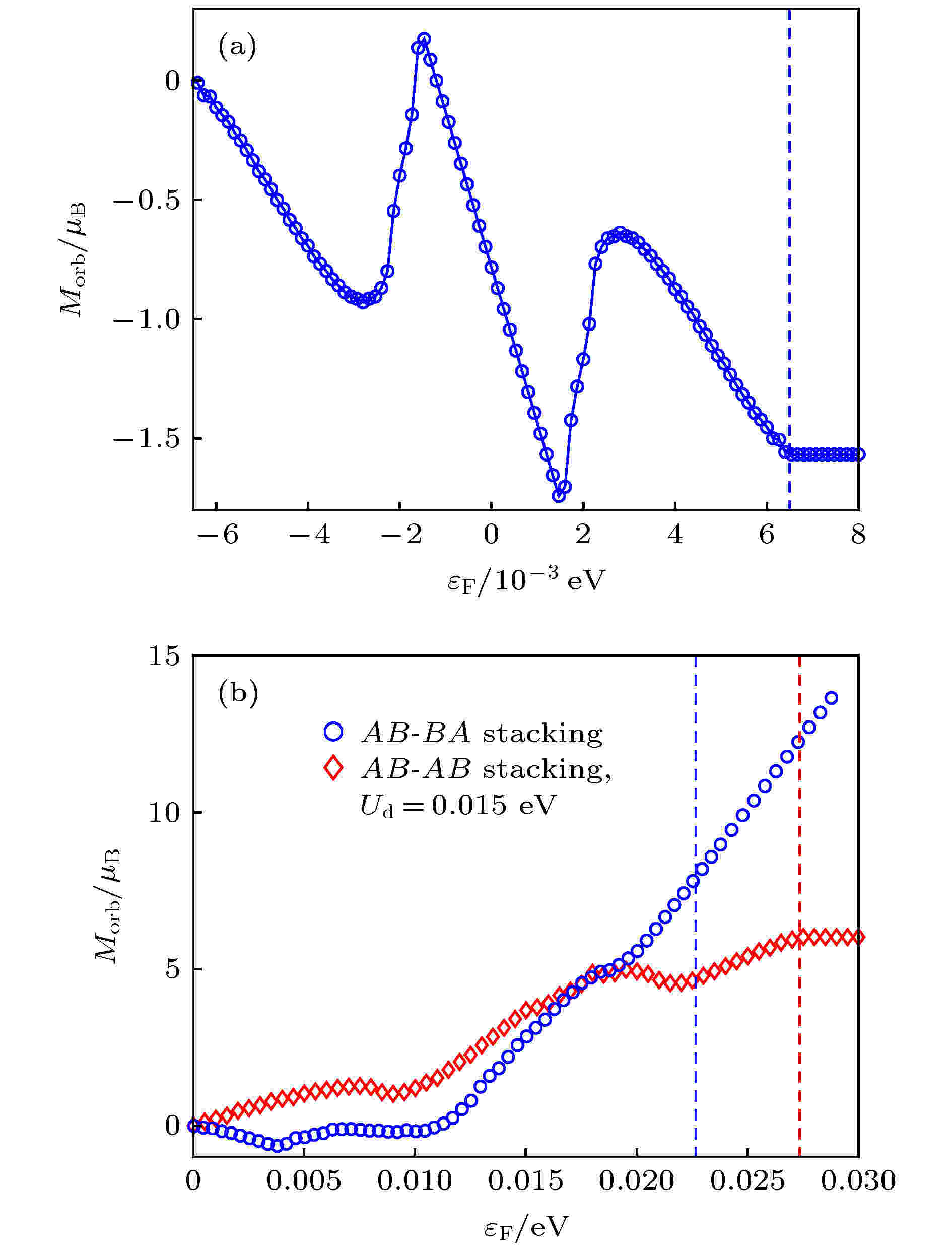 图 5 (a)转角双层石墨烯在魔角时K谷平带贡献的轨道磁矩(
图 5 (a)转角双层石墨烯在魔角时K谷平带贡献的轨道磁矩(











