摘要: 分离流动是一种复杂湍流现象, 其中微小尺度结构的发展演化有着重要的影响, 但是湍流数值模拟中数值方法的固有耗散会抑制小尺度流动结构的发展. 因此, 本文结合延迟分离涡模拟方法, 基于五阶耗散紧致格式, 通过引入流场相关的调节因子, 构造自适应耗散调节方法, 使其在大涡模拟区域降低耗散影响以提高对小尺度流动结构的辨识能力, 在雷诺平均区域恢复正常耗散水平以保持稳定求解. 本文首先通过近似色散关系和涡输运算例说明该方法可有效降低数值耗散影响, 同时具有更高分辨率的涡保持能力; 随后通过各向同性衰减湍流和平板槽道流动展示了该方法可有效提高对微小流动结构的辨识能力, 同时在存在大梯度的流场中可保持求解稳定性; 最后求解
Re = 3900 亚临界状态下的圆柱绕流, 通过对比流场云图、时均速度和雷诺应力分布曲线, 说明了该方法通过减小分离区耗散影响, 可有效提高对典型分离流动求解的准确性.
关键词: 分离流动 /
延迟分离涡模拟 /
自适应耗散方法 /
耗散紧致格式 English Abstract A method of adaptively adjusting dissipation for the simulation of separated flow Li Hao Liu Wei Wang Sheng-Ye College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China Received Date: 15 January 2020Accepted Date: 12 April 2020Available Online: 09 May 2020Published Online: 20 July 2020Abstract: Separate flow is a typical complex turbulent phenomenon. The full development of small-scaled structures is of great importance for accurate numerical simulation. However, these small-scaled structures can be easily damped by the inherent dissipation of numerical method. Therefore, based on the 5th-order dissipative compact scheme (DCS), we propose an adaptive dissipative compact scheme (ADCS), which can adjust the numerical dissipation with self-adaptive capability by incorporating a flow related adjusting parameter. Combining with the delay detached eddy simulation (DDES), the ADCS can reduce the influence of numerical dissipation in LES region to enhance the ability to discern small-scaled structures, and restore the normal dissipation level in the RANS region to keep numerical stability. In the process of numerical simulation, firstly, the approximate dispersion relation (ADR) is obtained, it shows that the ADCS method can effectively reduce the influence of dissipation in the high wave number region, without contaminating the dispersive performance, which is conducive to enhancing the resolution of turbulent structures. Secondly, the advection of vortical structure is simulated. Compared with DCS, the ADCS can reach the theoretical accuracy in an efficient way and acquire more advanced resolution of vortical structure even on a relatively coarse mesh scale, which proves that the ADCS reduces the negative influence of dissipation on vortical structure. The third case is the decay of isotropic turbulence. The energy spectral curves stay close to the reference before cut-off number, showing that more small-scaled structures can be distinguished by the ADCS method, and most of the vortical dominated regions are solved at a near-minimum level. The forth case is the plate channel turbulent flow. Both of DCS method and ADCS method give acceptable results. The ADCS method is performed with optimal dissipation in the near-wall region and reduces the dissipative level in the vortex dominated region, and it is also exhibited that the ADCS method can maintain the stability for flow with high gradient and avoid divergence. Finally, the sub-critical Re = 3900circular cylinder is simulated, and the fully separate flow is developed in the wake. The turbulent fluctuation near the wall is sensitive to the effect of numerical dissipation. The contour of flow field shows that the ADCS method obtains more small-scale structures. As for the pressure coefficient and mean velocity, the ADCS method shows an acceptable accuracy. Considering the Reynolds stress profile, which can be easily affected by the dissipation, the ADCS exhibits more accurate results than the traditional DCS method. Generally, the ADCS method can reduce the influence of dissipation and is beneficial to acquiring more accurate results in separate flow.Keywords: separated flow /delayed-detached eddy simulation /adaptive dissipative method /dissipative compact scheme 全文HTML --> --> --> 1.引 言 分离流动是流体力学中一类复杂的流动现象, 分离现象对物体的绕流和流体动力学特性有着十分重要的影响. 随着飞行器性能的不断提高和对分离流动研究的深入, 人们已经从传统的尽量避免分离的气动设计理念发展到控制和利用分离流动的新阶段[1 ] . 战斗机的边条翼/鸭翼, 地球再入返回舱以及火星着陆舱的稳定耳片都属于控制和利用分离流及其有利干扰的气动设计, 分离流动对于气动力、气动声学和气动光学等现象都有着重要的影响, 目前已经成为流体力学的重要研究分支[2 ] . 典型分离流动通常先在壁面处产生细小的涡结构, 随后脱离壁面逐渐发展为大尺度漩涡. 目前工程中常用的方法会引入过多的耗散, 抑制微小流动结构的发展, 进而影响对分离流场求解的准确性, 而采用加密网格的方式又会给工程实际问题增加难以接受的计算量. 高精度数值格式通常具有较高的流场分辨率, 适用于求解分离流动[3 ,4 ] , 但为了保证迭代求解的稳定性, 需要引入一定的耗散, 也不可避免地会影响到对微小湍流结构的辨识能力. 最理想的方式就是在涡结构占主导的分离流动区域适当降低耗散以精确求解, 同时在其他区域恢复正常的耗散水平以维持计算稳定性[5 ] . 因此, 有必要针对分离流动构造一种流场相关的可自适应调节耗散的高精度方法.[6 -10 ] 通过改进间断处的耗散引入方式, 使其在可压缩湍流数值模拟中, 可同时高效准确地处理激波和湍流问题. 通过构造混合格式一定程度也可以解决上述问题, Wong和 Lele[11 ] 将带有耗散的迎风差值同中心差值混合, 减少了间断和高波数流场区域数值震荡的影响. Adams和Shariff[12 ] 将迎风格式和激波捕捉本质无振荡(essentially non-oscillatory, ENO)格式耦合, Priozzoli[13 ] 将守恒型格式同WENO格式耦合, 以及其他多种类似思路的混合格式[6 ,14 ] 都可以有效提高对激波和湍流结构的捕捉能力. 而另一类紧致格式能够在相同的模板下具有更高的精度, 为求解小尺度流动提供更高的分辨率, 适用于求解高波数湍流流动[15 ] . Lele[16 ] 提出一类中心紧致格式, 但其无耗散特性在求解分离流动时会在高波数范围引起非物理振荡, 需要结合滤波使用. 但滤波技术的引入可能会导致模板增加, 失去紧致格式的优势. Deng和Shen[17 ] 提出了一类耗散紧致格式(dissipative compact scheme, DCS), 通过选择适当的控制参数, 能够调节高波数范围的耗散水平, 进一步提高对小尺度流动的求解能力. 上述方法都是通过人工引入固有耗散, 需要一定的经验性, 难以应用到更为复杂的分离流动中.[18 ] . 通过结合RANS方法和LES 方法各自的优势, 可有效提高对分离流动求解的准确性, 但是过多的数值耗散有时甚至会掩盖物理黏性耗散的作用, 导致小尺度湍流结构不能被准确求解[19 ] . Mary和Sagaut[20 ] 在2阶MUSCL格式的基础上, 通过引入感受因子来调节方法耗散. Anderson等[21 ] 在3阶迎风格式的基础上, 为了提高求解准确性, 将耗散水平降低为原1/8. Bui[22 ] 通过在MUSCL格式中引入控制系数, 根据不同流动问题, 人工调整其耗散水平. 采用类似的思路, Qin和Xia[23 ] 及Yoon等[24 ] 分别基于Roe格式和Steger-Warming格式提出了相应的低耗散方法. 尽管这些方法对于精确求解湍流流动有一定的改进作用并且易于实现, 但是经验性较强, 而且引入不合理的参数也会导致非物理现象的出现. Travin[5 ] 通过在中心/迎风混合格式中引入调和函数, 结合RANS/LES混合方法, 在LES区域和RANS区域分别提高中心格式和迎风格式的权重, 在保证计算稳定的前提下提高对小尺度结构的求解能力, Mockett[25 ] 改进调和函数的构造形式以实现自适应调节耗散. Tajallipour等[26 ] 通过自适应调节对流通量中迎风项的权重, 可有效提高非结构网格上大涡模拟求解的准确性. Xiao等[27 ] 基于SST-DDES模型比较了固定耗散和自适应耗散的结果, 证明了自适应耗散方法可有效提高求解准确性.2.计算方法 22.1.耗散紧致格式 2.1.耗散紧致格式 耗散紧致格式是在中心紧致格式无耗散特性的基础上, 通过人工引入耗散项, 使其在保持紧致格式优点的同时具有一定的耗散水平, 提高计算稳定性[17 ] . 通过调整模板数量, 可得到5阶, 7阶, 9阶等一系列耗散紧致格式. 在格式中, 半节点处的数值通量可通过如下公式得到:$ \tilde{U}^{\rm L}_{j\pm1/2} $ , $ \tilde{U}^{\rm R}_{j\pm1/2} $ 是半节点处的流动变量, 在中心紧致格式中有$ \alpha $ 是控制参数, 用以调节耗散项的权重, 这里仅给出本文涉及的5 阶耗散紧致格式的形式:2.2.SST-DDES模型 -->2.2.SST-DDES模型 分离涡模拟方法最初是在SA模型的基础上提出的, 通过当地网格尺度与壁面距离之间的大小关系进行判断, 实现在以大涡输运为主要特征的区域采用LES方法求解, 其他区域采用RANS方法求解[28 ] . 2001年, Strelets [29 ] 将分离涡模拟的思路推广到SST模型上, 守恒型SST模型方程形式如下:29 ], 为了避免出现网格诱导分离现象, 通过引入延迟函数, 提出DDES模型[30 ] , 将原湍动能$ k $ 方程中的耗散项通过下式替代:$r_{\rm d}$ , 在边界层对数率层内为1, 在边界层边缘过渡到0, 并构造转换函数$f_{\rm d}$ :$\varDelta_{\rm {max}}$ 为当地最大网格尺度, ${\sqrt k}/{(C_{\mu} \omega)}$ 为SST模型中定义的湍流长度尺度, 其他参数的详细介绍可参阅文献[30 ].2.3.自适应耗散方法 -->2.3.自适应耗散方法 在耗散紧致格式中, 通过调节$ \alpha $ 值的大小可以调节计算方法的耗散水平, 当$ \alpha = 0 $ 时, 格式恢复到无耗散形式. 因此可构造流场相关的调节参数$ \alpha $ , 使其可根据流场中不同流域的求解需求, 自适应地调整计算方法耗散水平. 结合SST-DDES模型, 为了提高对分离流动求解的准确性, 希望计算方法在分离流动占主导区域, 即LES求解区域表现为低耗散求解形式, 在其他区域恢复到正常耗散水平. 保证计算稳定的前提下, 尽可能地降低耗散的影响. 因此, 借鉴SST-DDES模型的思路, 基于5阶DCS格式, 构造自适应耗散调节因子:$ \alpha_{\rm {max}} $ 为通过色散保持关系得到的理论值, 这里取$ \alpha_{\rm {max}} = 0.31 $ , (11 )式中函数$ A $ 定义为$ C_{\rm {DDES}} $ 为SST-DDES模型的模型系数, Δ 为网格特征长度, $ l_{\rm {turb}} $ 为湍流长度尺度, 这里定义为:$ l_{\rm {turb}} $ 由层流黏性$ \nu $ , 湍流黏性$ \nu_{\rm t} $ , 正应变率张量$ S $ 和涡量Ω 共同决定, 其中$ \tau $ 为特征对流时间, 这里起到限制器的作用. 在函数$ A $ 中的参数$ g $ 定义如下:$ g $ 的作用是在流场中的无旋区, 即RANS求解区域, 使方法恢复的正常耗散水平. 函数中的其他参数定义为:$ \alpha $ 的最小值, 即$ \alpha = {\rm {max}}(\alpha_{\rm {max}}{\rm {tanh}}(A^{C_{\rm {H1}}}), \alpha_{\rm {min}}) $ .2.4.自适应耗散方法分析 -->2.4.自适应耗散方法分析 32.4.1.近似色散关系 -->2.4.1.近似色散关系 近似色散关系( approximate dispersion relation, ADR) 常用于在谱空间上分析非线性格式的耗散色散特性[31 ] . 这里借助近似色散关系, 分析自适应耗散方法在非线性情况下的耗散色散特性, 同时引入了传统的DCS格式和常用的MUSCL格式的结果用于比较. 因为本算例中控制方程为一维对流方程, 涡量为零, ADCS方法中的自适应耗散调节因子无法启动, 因此这里将其强制设置为最小值, 用以分析自适应耗散方法在极限情况下的耗散色散特性.图1 分别给出了修正波数的虚部和实部曲线, 其中虚部$ \omega^*_{\rm i}h $ 对应格式的耗散特性, 实部$ \omega^*_{\rm r}h $ 对应格式的色散特性. 图1(a) 中给出了理想无耗散曲线$ \omega^*_{\rm i}h = 0 $ 作为参考, 与之差异越小表示格式具有越好的耗散保持特性. 可以看出, 随着波数$ \omega h $ 增加, MUSCL率先出现了明显的差异, 随后是DCS, 而ADCS 几乎与理想无耗散曲线保持一致, 即耗散作用对ADCS 在高波数区求解的影响更小. 图1(b) 对应色散保持特性, 同样给出了参考曲线用于对比. 在理论上, ADCS方法中引入的自适应耗散调节因子仅用于调节迎风偏置模板的权重, 因此仅影响其耗散特性, 对色散特性几乎无影响. 图1(b) 中随着波数$ \omega h $ 增加, MUSCL较早出现偏差, 而DCS和ADCS保持相似的色散特性, 符合理论结果. 总的来说, ADCS方法在保持原有色散特性的基础上, 具有更好的耗散保持特性, 因此更加适用于求解含有微小流动结构的分离流动.图 1 耗散色散特性分析 (a) 耗散特性; (b) 色散特性Figure1. Analysis of dissipation and dispersion: (a) Dissipation; (b) dispersion2.4.2.非定常涡输运 -->2.4.2.非定常涡输运 本算例计算二维均匀流中非定常涡输运情况, 可用于分析计算方法中耗散对涡保持特性的影响[32 ] . 在xy 方向, 计算域的范围分别取为$ 0\leqslant x \leqslant 0.1 $ , $ 0\leqslant y \leqslant 0.1 $ , 各个方向均采用周期性边界条件. 通过不同密度的均匀网格($ 32^2, 48^2, 64^2, 96^2, 128^2 $ ) 分析方法的求解精度和涡保持能力. 控制方程为二维欧拉方程, 时间推进方法采用三阶龙格库塔方法, 计算50个对流周期T 得到瞬态结果.$ u_0, v_0 $ 分别为速度分量, $ R = 0.005 $ 为涡核半径, 其他参数分别为$ P_{\infty} = 10^5 $ Pa, $ T_{\infty} = 300 $ K, $ Ma_{\infty} = 0.05 $ , $ \beta = 1/50 $ .$ L_2 $ 误差, 对计算方法准确性进行定量分析, 其定义如下:表1 给出了不同方法熵$ L_2 $ 误差及计算精度的比较, 图2 给出了熵$ L_2 $ 误差随网格尺度和CPU时间的变化, 其中引入网格自由度(degree of freedoms, DoFs), 即网格单元总数[33 ] , 来计算网格尺度$ h = 1/({\rm {DoFs}})^{1/{\rm {dim}}} $ , $ {\rm {dim}} $ 为计算空间维度, CPU时间取50个对流周期的结果. 通过上述结果可以看出, 在相同的网格条件下, ADCS方法能够得到比DCS方法更高的计算精度. 随着网格密度的增加, ADCS方法更易于达到理论精度, 但是也出现了ADCS方法精度略高于理论精度的情况, 这可能与时间推进方法或机器误差有关. 在相同熵$ L_2 $ 误差的要求下, ADCS方法所需的时间略少于DCS方法. 综上, 为了准确地保持流场中的涡结构, ADCS方法对网格分辨率的要求更低, 同时更易于达到设计精度. 网格 ADCS DCS $ L_2 $误差 精度 $ L_2 $误差 精度 $ 32^2 $ 5.91520$ \times 10^{-9} $ — 5.49050$ \times 10^{-9} $ — $ 48^2 $ 4.14450$ \times 10^{-9} $ 0.87 3.84780$ \times 10^{-9} $ 0.88 $ 64^2 $ 2.33030$ \times 10^{-9} $ 2.01 2.06870$ \times 10^{-9} $ 2.16 $ 96^2 $ 2.59250$ \times 10^{-10} $ 5.42 5.15010$ \times 10^{-10} $ 3.43 $ 128^2 $ 5.39380$ \times 10^{-11} $ 5.46 1.26630$\times 10^{-10}$ 4.88
表1 $ L_2 $ 误差和计算精度比较Table1. Comparison of $ L_2 $ error and accuracy of order图 2 $ L_2 $ 误差变化曲线 (a)随网格尺度$ h $ ; (b)随CPU 时间Figure2. The curve of $ L_2 $ error (a) vs . mesh scale $ h $ ; (b) vs . CPU time图3 和图4 分别给出了$ 64^2 $ 和$ 128^2 $ 网格下50个对流周期后的涡结构等值线图, 图5 给出了对应的中心线处($ x = 0.05 $ )处的水平速度型曲线. 可以看出在网格较粗的条件下, DCS方法得到的涡结构出现了较为明显的变形, 同时速度型曲线和精确解之间也存在较为明显的偏差, 但ADCS方法基本能够保持原有涡结构, 并且速度型仅在极值处与精确解间存在细微偏差. 随着网格密度增加, 两种方法均能够较好地保持原有涡结构, 但ADCS方法能够更加高效地利用现有的网格尺度, 得到更为准确的结果.图 3 $ 64^2 $ 网格下涡结构等值线图 (a) DCS; (b) ADCSFigure3. Vorticity magnitude contour of $ 64^2 $ grid: (a) DCS; (b) ADCS图 4 $ 128^2 $ 网格下涡结构等值线图 (a) DCS; (b) ADCSFigure4. Vorticity magnitude contour of $ 128^2 $ grid: (a) DCS; (b) ADCS图 5 中心线处水平速度型比较 (a) $ 64^2 $ 网格; (b) $ 128^2 $ 网格Figure5. Comparison of u velocity profile at centerline: (a) 642 ; (b) $ 128^2 $ 2.5.各向同性衰减湍流 -->2.5.各向同性衰减湍流 各向同性衰减湍流可用于分析湍流尺度特性, 标定湍流模型常数以及分析数值方法中耗散特性的影响. 各向同性湍流是一种理想化的流动, 初始流场在没有湍动能补充的情况下自然衰减. 这里基于SST-DDES模型求解流动, 模型参数已预先标定好, 仅通过此算例分析自适应耗散方法对求解小尺度湍流结构的改善效果.$ 256^3 $ 均匀网格, 计算域的特征长度需远小于湍流的积分尺度和对应风洞实验的特征尺度, 这里设置计算域边长为$ L = 0.508 $ m, 各面采用周期性边界条件, 以Commte-Bellot和Corrisin [34 ] 的实验数据作为参考结果. 在实验中, 流动以某一固定速度运动, 湍流强度随时间衰减. 实验中提供了沿流向方向3个站位的结果($ U_0 t/L = 42, 98, 171 $ ), 这里以第一个位置($ U_0 t/L = 42 $ )的数据作为初始条件, 计算得到第二、三个位置($ U_0 t/L = 98, 171 $ )的结果进行比较. 流场中水平方向的初始速度为$ U_0 = 12.7 $ m/s, 基于计算域边长的雷诺数$ Re_L = 34000 $ .$ C_{\rm {DDES}}\varDelta $ 来强制使用DDES模型中的LES部分求解. 这里采用三种方法求解并进行比较, 分别为耗散紧致格式DCS, 自适应耗散方法ADCS和强制最小耗散的自适应耗散方法ADCS$ (\alpha_{\rm {min}}) $ .$ \mu_{\rm t} = (C_{\rm S}\varDelta \sqrt{2 S_{ij}S_{ij}})^2 $ 获得涡黏性初场, 但是对于DDES模型, 由于包含了隐式时间相关项, 通常通过以下两种方式来获得初场[35 ] , 一种是采用Smagorinsky模型得到, 但是这种方法又需要标定相应的模型参数$ C_{\rm S} $ , 另一种方式是通过冻结湍流模型方程中的动量和压力计算得到, 这里采用这种方式.图6 中分别给出了采用3种方法得到的两个时刻的能量谱曲线, 并给出了相应的实验值作为对比, 其中垂直的虚线对应截断波数. 在截断波数之前, 能量谱曲线随波数增加而减少, 但由于计算方法引入的耗散, 随波数增加, 计算结果会逐渐位于参考结果下方. 从图6 可以看出, DCS方法耗散特性较为明显, 在中等波数区开始出现偏差, 而强制最小耗散的ADCS$ (\alpha_{\rm {min}}) $ 方法因趋近于中心紧致方法, 在截断波数之前基本保持无耗散特性, 满足理论分析的结果, ADCS方法的结果位于二者之间, 因为ADCS方法是通过识别涡结构来降低相应区域的耗散, 并不是一种全场低耗散的方法. 图7 和图8 中为两个时刻流场Q 准则等值面图, 从左至右分别为ADCS$ (\alpha_ {\rm {min}}) $ , ADCS和DCS得到的结果, 其中ADCS的结果采用自适应耗散方法中的耗散调节系数着色, ADCS$ (\alpha_ {\rm {min}}) $ 和DCS的结果均采用固定参数着色. 从图中可以看出, 由于DCS方法过高的耗散, 使得微小的涡结构不能充分辨识, 而ADCS$ (\alpha_{\rm {min}}) $ 方法得到了十分精细的流场结构, ADCS方法对流场辨识的精细程度略低于ADCS$ (\alpha_{\rm {min}}) $ 的结果, 但是优于DCS方法的结果. 综上ADCS方法可提高对流场中精细流动结构的辨识能力, 符合理论分析情况.图 6 不同时刻能量谱曲线 (a) $ U_0 t/L = 98 $ ; (b) $ U_0 t/L = $ 171Figure6. Comparison of energy-spectral: (a) $ U_0 t/L = 98 $ ; (b) $ U_0 t/L = 171 $ 图 7 $ U_0 t/L = 98 $ 处$ Q $ 等值面云图 (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCSFigure7. $ Q $ -criterion iso-surface at $ U_0 t/L = 98 $ : (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCS图 8 $ U_0 t/L = 171 $ 处$ Q $ 等值面云图 (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCSFigure8. $ Q $ - criterion iso-surface at $ U_0 t/L = 171 $ : (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCS2.6.平板槽道流动 -->2.6.平板槽道流动 平板槽道流动通常存在较大的梯度以及流场初始化中引入的人工扰动, 可有效验证方法求解的稳定性. 这里基于SST-DDES模型, 分别采用DCS和ADCS方法对平板槽道流动进行数值模拟. 通过对速度型的求解和流场中湍流结构的捕捉, 对比不同方法对附着湍流结构的分辨能力.$ H $ 为参考长度, 计算域沿流向方向$ L_x = 4 H $ , 展向方向$ L_z = 2 H $ , 流向和展向均采用均匀分布网格, 法向壁面第一层网格高度取为$ d_{\rm w} = 5\times10^{-4} $ , 采用固定拉伸比1.1, 得到三维网格$ 101\times111\times61 $ . 为了确保数值计算最大库朗数小于1, 无量纲时间步长设置为$ 1\times10^{-3} $ . 此外需要对速度场进行初始化, 由中心线速度、质量速度以及摩擦速度之间的关系, 结合壁面距离得到层流速度型, 通过在层流速度型中添加随机扰动对速度场进行初始化, 得到速度初场. 同时由于槽道流动流向为周期性边界条件, 需要引入压力梯度作为驱动项. 本文通过给定摩擦速度, 得到压力梯度源项为$\nabla p = {\rho u^2_{\tau}}/{h}$ . 速度初始化及压力梯度源项详细关系式可参考文献[36 ].图9 为计算得到的速度型曲线和DDES 模型中的调和函数$ f_{\rm d} $ 分布曲线, 为在同一坐标系中显示, $ f_{\rm d} $ 幅值扩大20倍. 当$ f_{\rm d} = 0 $ 时, DDES模型采用RANS模式求解, 当$ f_{\rm d} = 1 $ 时, DDES模型采用LES模式求解. 从图9 可以看出ADCS方法基本保持了DCS方法对壁面边界层的求解能力, 仅在对数率层存在细微差别. RANS模式和LES模式的过渡区位于$ y^+\approx[4, 20] $ 之间. 因为在近壁面处, ADCS方法降低了数值耗散的影响, 分辨出更多的湍流脉动, 因此基于ADCS方法的DDES模型可以略早地从RANS模式过渡到LES模式.图 9 $ Re_\tau = 180 $ 条件下$ u^+ $ 和$ 20 f_{\rm d} $ 分布曲线Figure9. $ u^+ $ and $ 20 f_{\rm d} $ curves at $ Re_\tau = 180 $ 图10 中给出了流场中$ Q $ 等值面分布, 两种方法在壁面附近均形成了大尺度的相干结构, 上下壁面之间形成了表现为朝向下游的、与壁面具有一定倾角的茎状涡结构, 也间或出现不对称的马蹄涡结构, 这些结构相互影响形成了复杂的湍流结构, 两种方法均可较好地捕捉到一定的涡结构, 但由于ADCS方法适当地降低了数值耗散的影响, 因此可得到更加复杂精细的流动结构.图 10 $ Re_\tau = 180 $ 条件下$ Q $ 等值面 (a) DCS; (b) ADCSFigure10. $ Q $ criterion iso-surface at $ Re_\tau = 180 $ : (a) DCS; (b) ADCS图11 给出了ADCS方法中自适应耗散调节参数$ \alpha $ 和DDES模型中调和函数$ f_{\rm d} $ 的三个方向截面的瞬态分布云图. $ \alpha $ 值越小, 对应的区域数值耗散越小, 当$ f_{\rm d} = 0 $ 时, 即采用DDES模型中的RANS模式求解, 当$ f_{\rm d} = 1 $ 时, 即采用DDES模型中的LES模式求解. 从图11 可以看出, 在近壁面处采用了RANS模式求解, 同时近壁面处$ \alpha = \alpha_{\rm {max}} $ , 即采用正常耗散, 保证计算的稳定性. 随着壁面距离的增加, DDES模型逐渐过渡到LES模式求解, 同时$ \alpha $ 值减小, 即该区域耗散水平降低, 微小流动结构得以更加充分地发展.图 11 $ Re_\tau = 180 $ 条件下ADCS $ f_{\rm d}$ 和$ \alpha $ 分布 (a) $ f_{\rm d} $ ; (b) $ \alpha $ Figure11. The contour of $ f_{\rm d} $ and $ \alpha $ of ADCS at $ Re_\tau = 180 $ : (a) $ f_{\rm d} $ ; (b) $ \alpha $ 图12 给出了$ y = 0.1 H $ 切面处$ y $ 方向涡量分布云图. 两种方法的结果均呈现了近壁区明显的条带结构, 以及高速条带和低速条带交替出现的现象. 在$ y = 0.1 H $ 处, DDES模型刚刚完成RANS模式和LES模式之间的过渡, 自适应调节因子也开始降低该区域的耗散水平, 因此得到的条带状结构更加丰富.图 12 $ y = 0.1 H $ 处$ y $ 方向涡量分布云图 (a) DCS; (b) ADCSFigure12. The contour of vorticity y at $ y = 0.1 H $ : (a) DCS; (b) ADCS2.7.Re =3900圆柱绕流 -->2.7.Re =3900圆柱绕流 钝头体绕流通常伴随着典型的分离流动, $ Re = 3900 $ 圆柱绕流是其中的经典算例之一. 在$ Re = 3900 $ 的亚临界条件下, 边界层在圆柱的迎风面处保持层流状态, 随后沿壁面发展为分离流动. 尽管结构简单, 但是圆柱尾流近壁面处的湍流脉动对不同的计算方法非常敏感, 并且可能导致最终结果出现较大偏差[37 ] , 因此可用来对比验证本文自适应耗散ADCS方法的求解效果.$ Re = U_{\infty}D/\nu $ , 其中$ U_{\infty} $ 是自由来流速度, $ D $ 是圆柱直径, $ \nu $ 为动力黏性系数. $ x, y, z $ 三个方向分别为流向、径向和展向, 展向采用$ \text{π} D $ 展长, $ xy $ 平面的原点位于$ z/D = 0 $ 处. 在$ xy $ 平面约有35000个结构网格单元, 三维网格共约140 万单元, 壁面第一层网格$ y^+\leqslant 1 $ , 并对尾流区网格加密. $ xy $ 方向采用远场边界条件, 展向采用周期边界条件. 时间推进采用LU-SGS双时间步法, 在整个计算过程中保证$ {\rm {CFL}}\leqslant 1 $ , 时间步长设置为$ 0.01 T $ , 其中对流时间$ T = D/U_{\infty} $ .图13 给出了圆柱绕流尾流的$ Q $ 等值面云图, 其中DCS的结果通过马赫数着色, ADCS结果通过自适应耗散调节系数$ \alpha $ 着色. 由于两种方法均采用DDES模型求解, 因此均呈现了明显的三维结构. 由ADCS的结果可以看出, 在尾流区近壁面处, $ \alpha $ 取值较小, 即该区域采用较低的耗散水平求解, 分辨出的流场结构也更加精细, 得到了流场中丰富的拟序结构. 随着壁面距离增加, 耗散调节系数$ \alpha $ 逐渐恢复到正常的耗散水平. 而DCS方法, 在尾流处过多的耗散可能会干扰涡结构的形成并且导致一些小尺度的结构不能充分发展.图 13 圆柱尾流$ Q $ 等值面云图 (a) DCS; (b) ADCSFigure13. $ Q $ criterion at the wake of circular cylinder: (a) DCS; (b) ADCS图14 给出了经时间平均和展向平均后的圆柱表面压力系数分布曲线, 其中$ \theta = 0^{\circ} $ 对应前驻点, $ \theta = 180^{\circ} $ 对应后驻点. 这里同Parnaudeau等[38 ] 的实验结果进行比较, 因为采用了DDES模型, DCS方法和ADCS方法的结果均与实验值符合较好. 在$ \theta \approx 50^{\circ} $ 时, 开始出现早期的分离流动, DCS方法得到的压力系数绝对值略小于实验值. 当压力系数达到谷底时, 对应着圆柱表面出现明显的分离点, 两种方法得到的分离点位置几乎一致, 但是ADCS得到的压力系数的绝对值略高于DCS的结果. 在ADCS的流场中, 分离区耗散水平较低, 发展了更多的湍流脉动, 更多的小尺度流动不断撞击壁面, 导致壁面压力系数略微增加. 随着$ \theta $ 继续增加直至出现大范围的分离流动, ADCS与DCS结果之间的差异更加明显. 总的来说, 两种方法得到的表面压力系数分布与实验值均符合较好, 但是ADCS方法在涡结构丰富的大范围分离区域的结果与实验值更加符合, 因而能够得到更加准确的气动力结果.图 14 圆柱表面压力系数分布曲线Figure14. $ C_{\rm p} $ around the circular cylinder图15 给出了经时间平均和展向平均后的$ y = 0 $ 处水平速度沿流向分布曲线. 水平速度在后驻点处为零, 随后在回流区内为负并达到极小值, 随流向距离增加逐步趋近某一定值. 图中ADCS方法得到的结果与实验结果几乎一致, 而DCS的结果整体略滞后于实验结果. 其中$ u\leqslant 0 $ 表示回流区的范围, 可以看出DCS得到的回流区范围明显大于ADCS的结果.图 15 $ y = 0 $ 处水平速度分布曲线Figure15. u velocity profile at $ y = 0 $ 图16 —图19 分别给出圆柱尾流近壁面处x /D = 1.06, 1.54, 2.02和远壁面处x /D = 4.0, 7.0, 10.0共6个站位的速度型和雷诺应力分布曲线. 为了在同一张图中展示曲线的发展变化, 部分站位的数据沿纵坐标平移一定距离. 在近壁区, 由于回流区的存在, 图16 中水平速度$ u $ 出现明显的负值, 并且随着壁面距离的增加, 速度型呈对称分布并逐渐由U 型过渡为V 型. 对于纵向速度$ v $ , 呈现明显的反对称分布, 并且随着壁面距离增加, 反对称幅度更加明显. 在近壁区, ADCS得到的速度型分布曲线均与实验结果符合较好, 而DCS的结果在$ x/D = 1.54 $ 和$ x/D = 2.02 $ 处与实验结果相比均出现了一定偏差, 与图15 中的水平速度分布类似, DCS的结果略滞后于ADCS.图 16 $ x/D = 1.06, 1.54, 2.02 $ 三个站位时均速度分布 (a) $ u $ ; (b) $ v $ Figure16. Mean velocity profile at $ x/D = 1.06, 1.54, 2.02 $ : (a) $ u $ ; (b) $ v $ 图 19 $ x/D = 4.0, 7.0, 10.0 $ 三个站位雷诺应力分布 (a) $ u'u' $ ; (b) $ u'v' $ ; (c) $ v'v' $ Figure19. Reynolds stress profile at $ x/D = 4.0, 7.0, 10.0 $ : (a) $ u'u' $ ; (b) $ u'v' $ ; (c) $ v'v' $ 图17 给出了近壁区雷诺应力分布曲线. 速度脉动量的量级一般小于平均速度量, 因此更容易受到不同方法引入的耗散的影响. 从$ x/D = 1.06 $ 的结果可以看出, $\left\langle {u'u' } \right\rangle $ 曲线呈对称分布并存在两个明显的峰值, 对应着尾部回流区与外流形成剪切层的位置. 随着流向距离的增加, 分离涡逐渐形成, 曲线峰值更加明显. $\left\langle {u'v' } \right\rangle $ 与速度$ v $ 类似, 呈现了反对称分布, $ \left\langle {v'v' } \right\rangle $ 呈现出中心对称分布形态并且脉动幅度逐渐增加. DCS和ADCS的结果均呈现了相似的分布趋势, 但是DCS结果的峰值略小于实验结果. 在该区域, 速度脉动发展初期易受到数值耗散的影响, 而DCS因为在该区域引入了过多的非必要的耗散, 可能导致一些微小的脉动不能充分发展, 而ADCS方法在该区域自适应的调节耗散水平, 使得湍流结构可以更加充分地发展, 从而得到了与实验值符合较好的结果.图 17 $ x/D = 1.06, 1.54, 2.02 $ 三个站位雷诺应力分布 (a) $ u'u' $ ; (b) $ u'v' $ ; (c) $ v'v' $ Figure17. Reynolds stress profile at $ x/D = 1.06, 1.54, 2.02 $ : (a) $ u'u' $ ; (b) $ u'v' $ ; (c) $ v'v' $ 图18 为远壁区$ x/D = 4.0, 7.0, 10.0 $ 三个站位平均速度分布曲线, 图19 为雷诺应力分布曲线并分别同实验结果进行比较. 图18 中水平速度V 型分布并呈现由深到浅的变化趋势, 纵向速度由反对称分布逐渐趋近于水平分布, 雷诺应力的分布曲线也呈现了类似的变化. 在圆柱尾流远壁区, 耗散调节因子逐渐增加, 但DCS和ADCS方法的结果之间还是存在较为明显的差异, ADCS 方法的结果与实验值更为符合. 但是在$ x/D = 10.0 $ 处, 由于网格过于稀疏, 不足以支持DDES模型进行高保真求解, 同时耗散调节因子也逐渐恢复到最大值, ADCS与DCS的结果与参考结果之间均存在较为明显的差异.图 18 $ x/D = 4.0, 7.0, 10.0 $ 三个站位时均速度分布 (a) $ u $ ; (b) $ v $ Figure18. Mean velocity profile at $ x/D = 4.0, 7.0, 10.0 $ : (a) $ u $ ; (b) $ v $ $ Re = 3900 $ 圆柱绕流的大范围分离流动, ADCS方法在近壁面涡结构丰富的区域可有效地降低数值耗散的影响, 同时可以与DDES模型有效地耦合求解, 分辨出更多精细的流动结构, 提高对速度型分布, 雷诺应力分布求解的准确性.3.结 论 本文针对分离流动, 在传统5阶耗散紧致DCS格式的基础上, 引入流场相关的调节因子作用于耗散项, 构造了自适应耗散ADCS方法. 通过流场中涡量、湍流黏性和当地网格尺度三者之间的关系, ADCS方法能够通过调节DCS格式中迎风偏斜模板的权重, 实现在涡结构丰富的分离流动区域降低数值耗散, 以减少耗散对精细湍流结构发展的影响, 在无旋稳态流场区域将数值耗散恢复到正常水平, 以保证数值计算的稳定性. 本文通过将ADCS方法同DDES模型耦合求解, 得到以下结论.$ Re = 3900 $ 圆柱绕流算例验证了ADCS方法对典型分离流动的求解能力, 证明了ADCS方法可有效提高对分离区近壁面处精细结构的辨识能力, 同时通过对时均速度型和雷诺应力分布曲线的比较, 证明了ADCS方法可有效提高对分离流动求解的准确性. 


































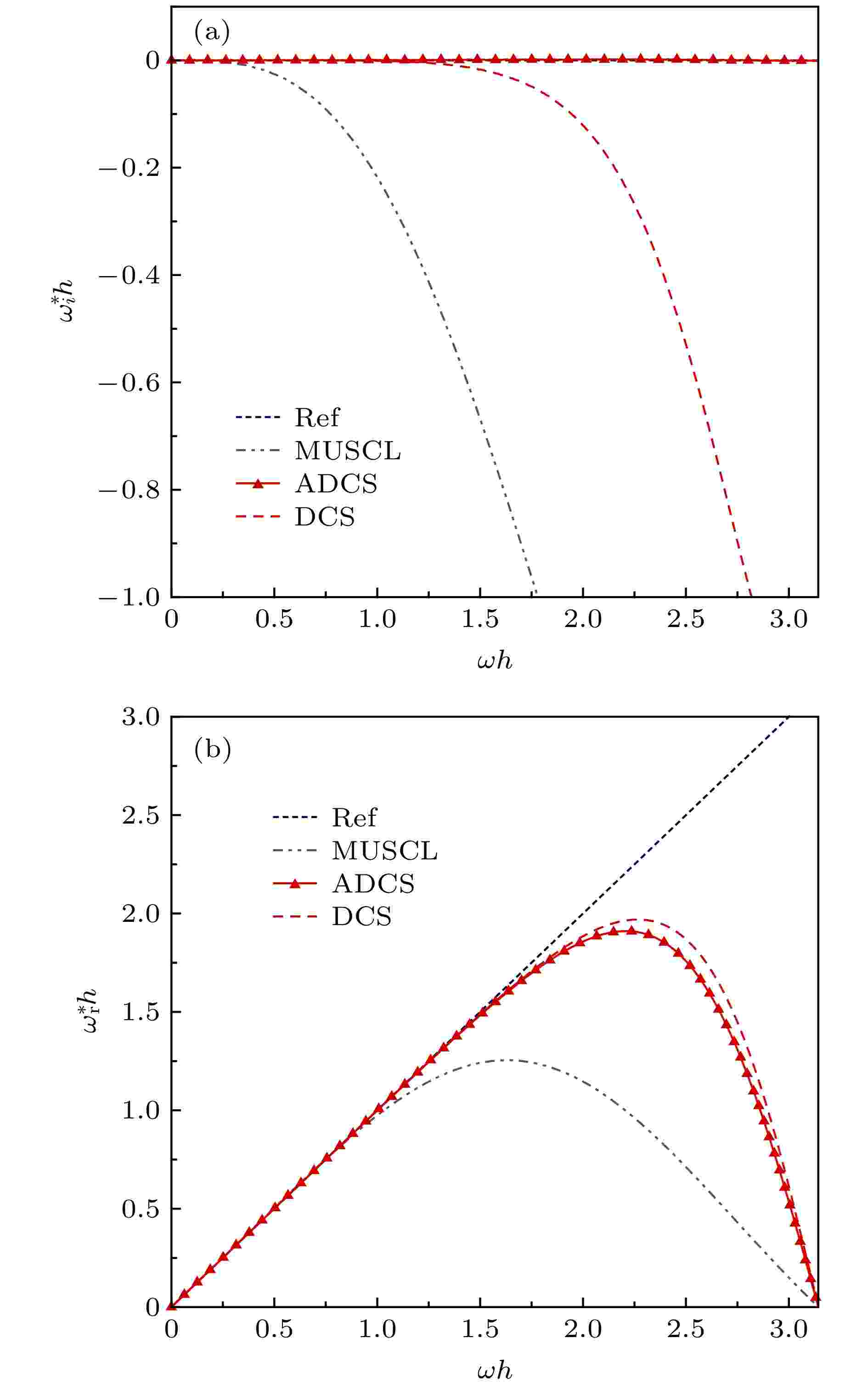 图 1 耗散色散特性分析 (a) 耗散特性; (b) 色散特性
图 1 耗散色散特性分析 (a) 耗散特性; (b) 色散特性






















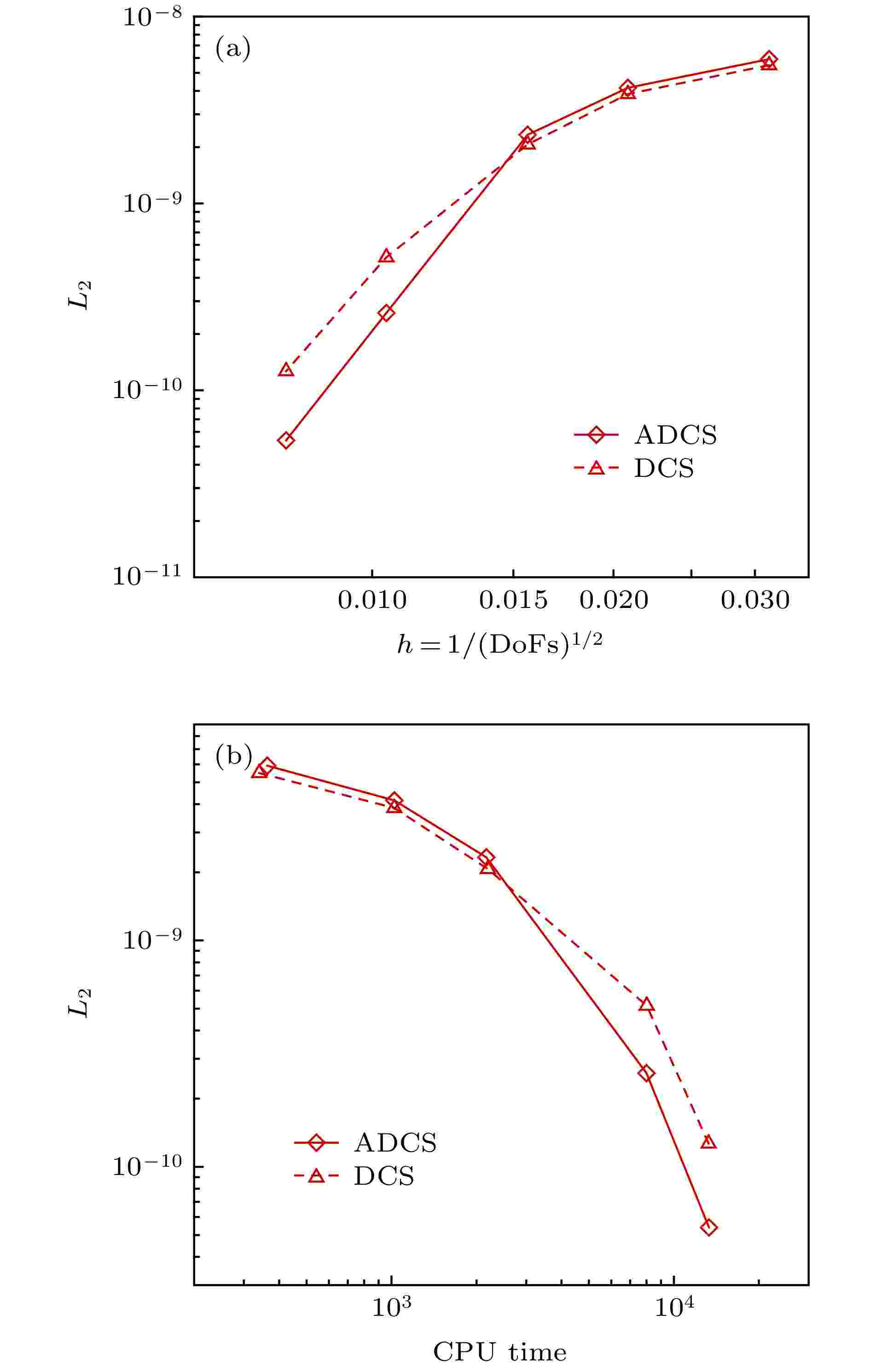 图 2
图 2 






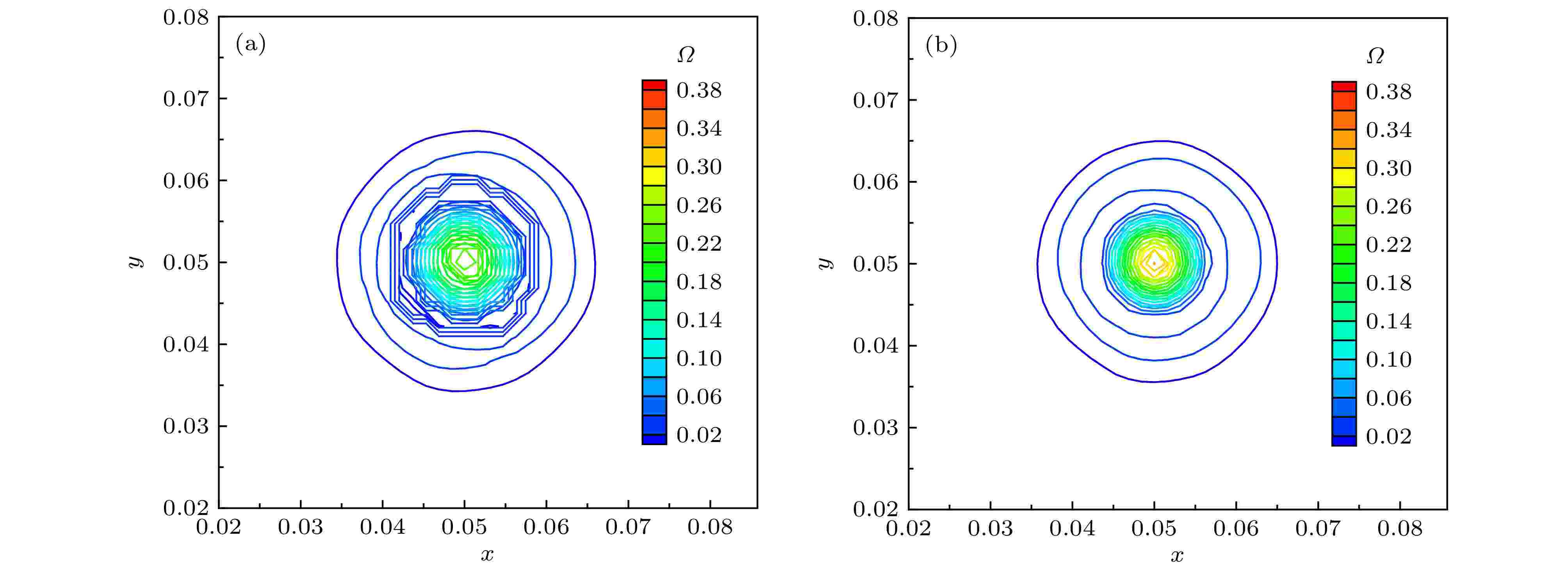 图 3
图 3 

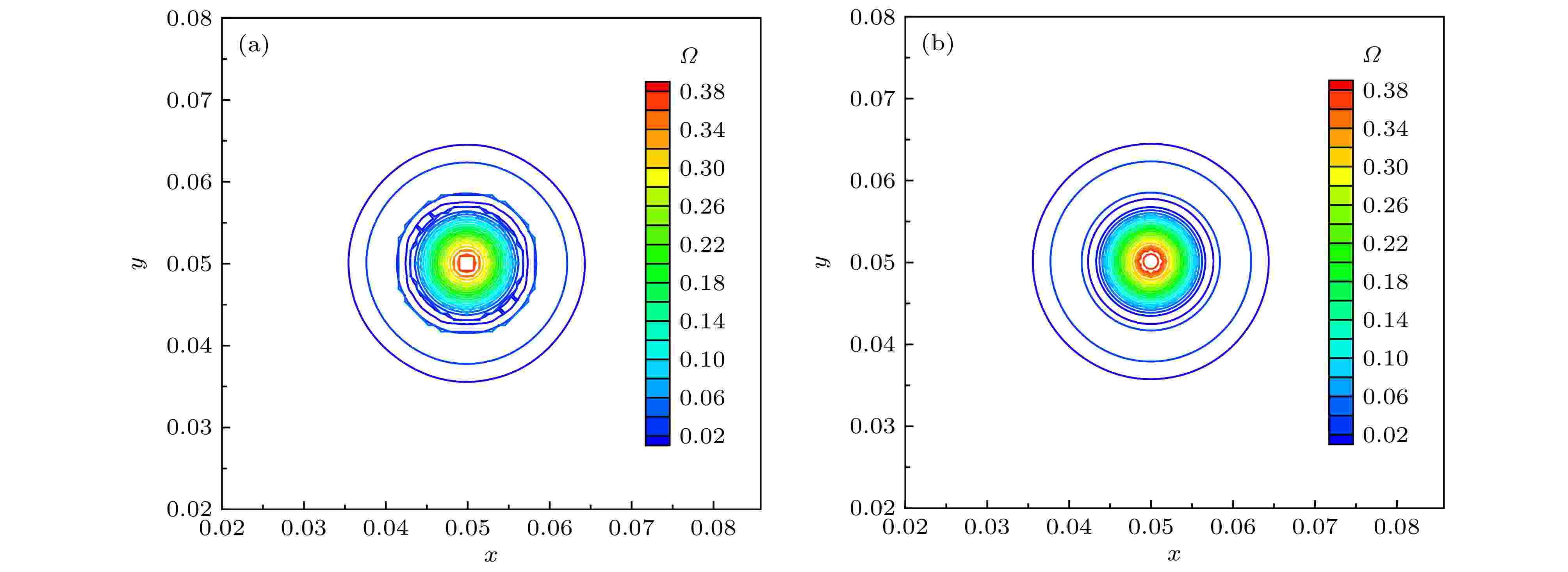 图 4
图 4 

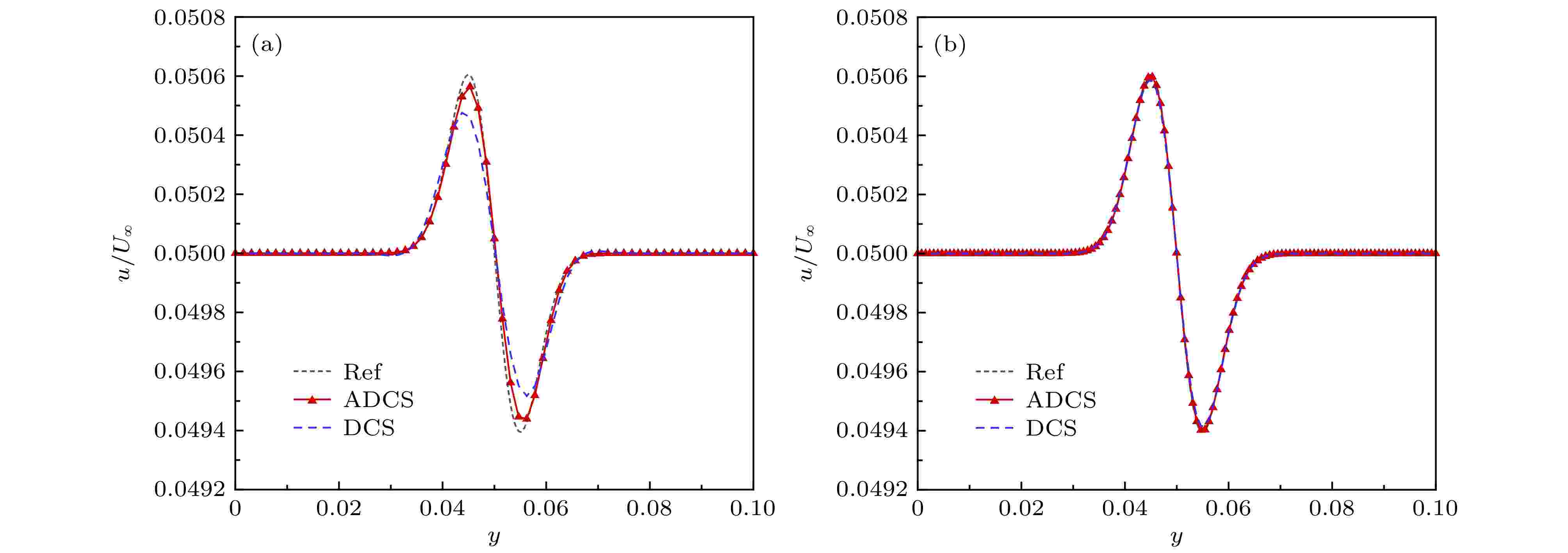 图 5 中心线处水平速度型比较 (a)
图 5 中心线处水平速度型比较 (a) 


























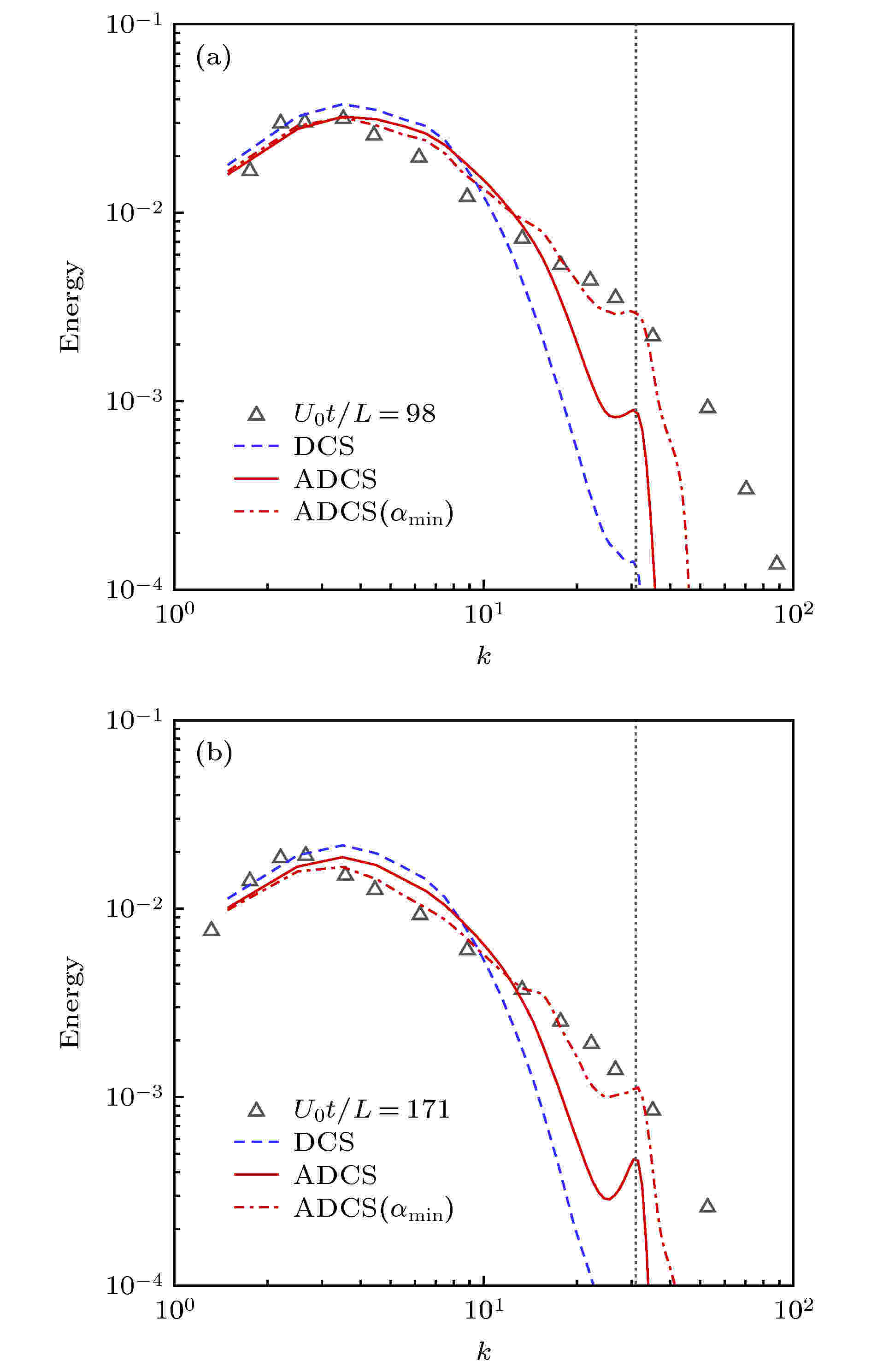 图 6 不同时刻能量谱曲线 (a)
图 6 不同时刻能量谱曲线 (a) 



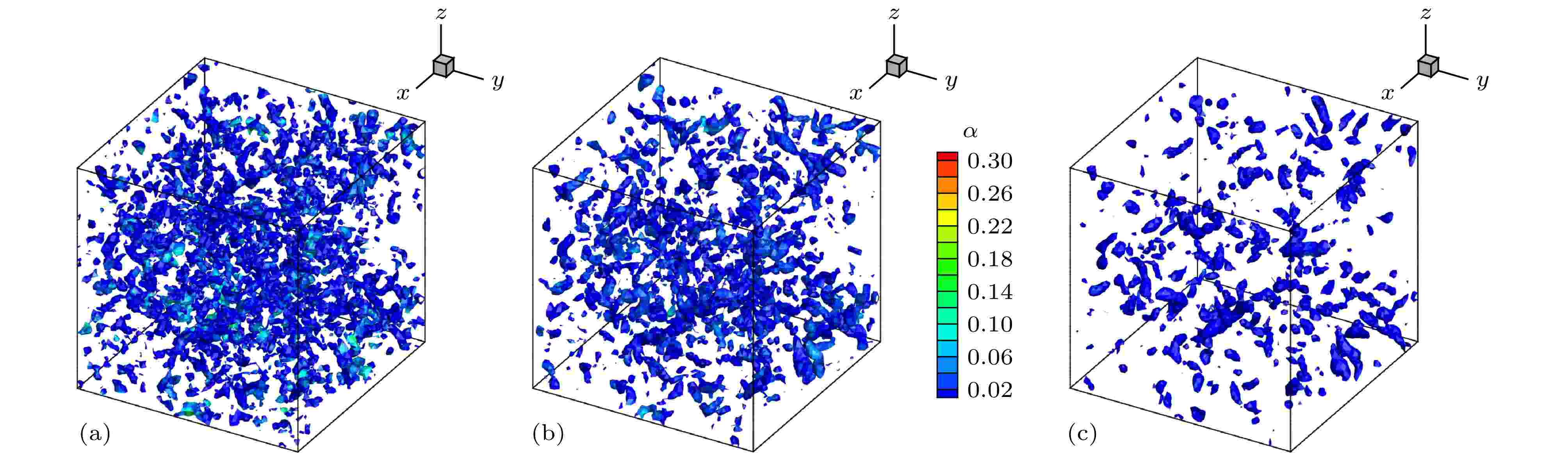 图 7
图 7 





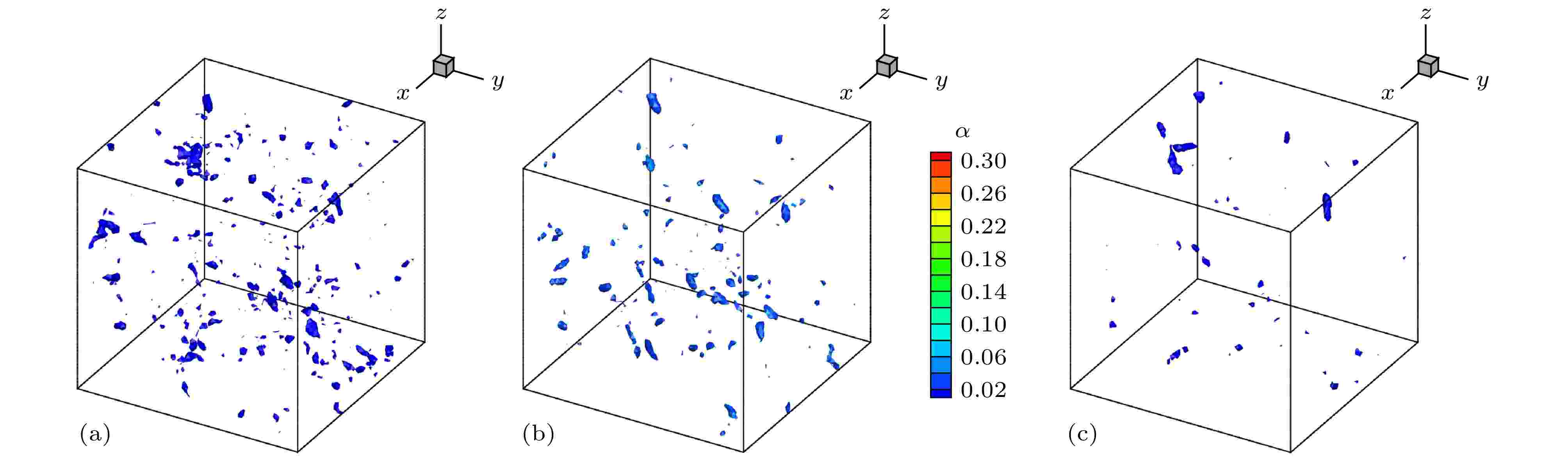 图 8
图 8 



















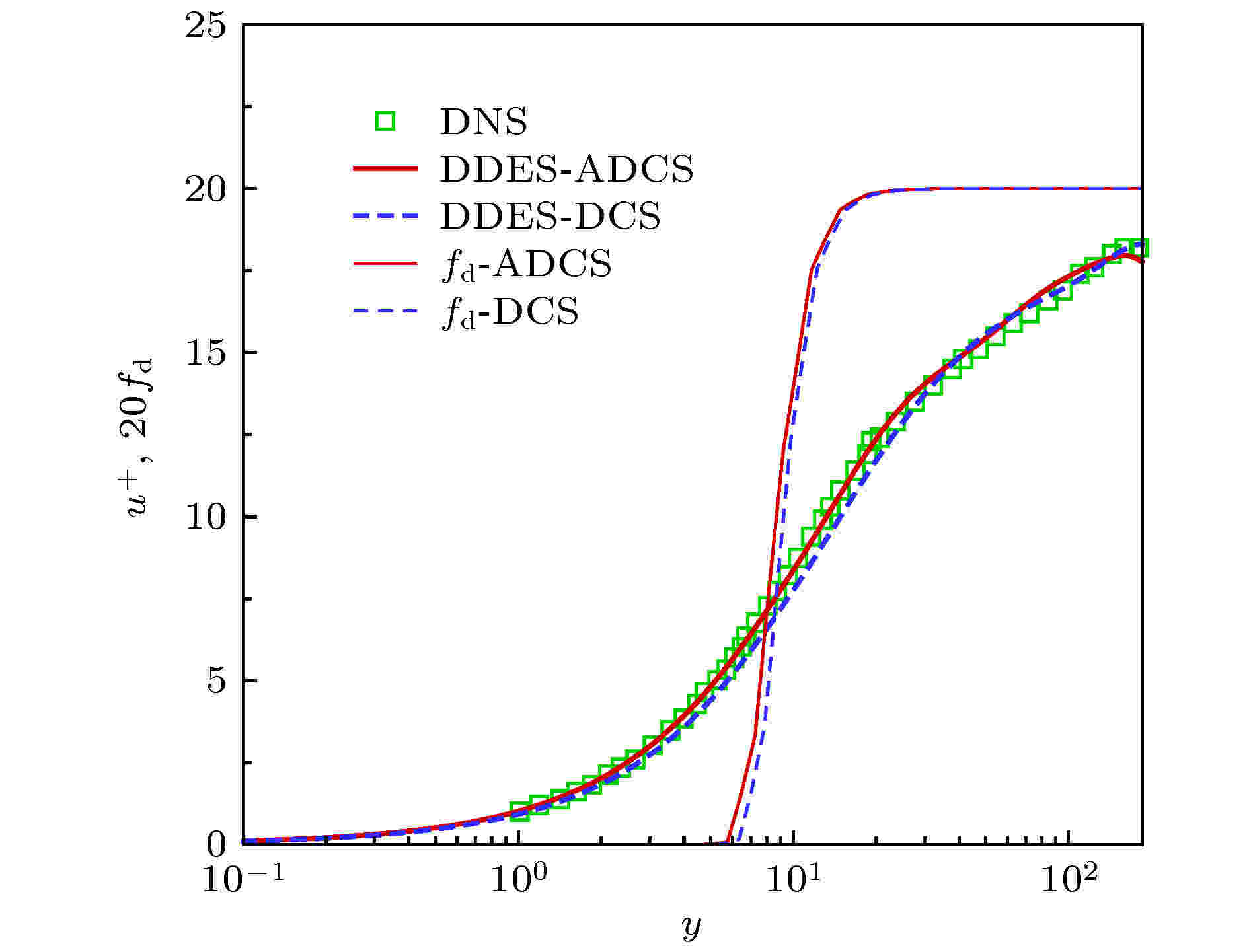 图 9
图 9 






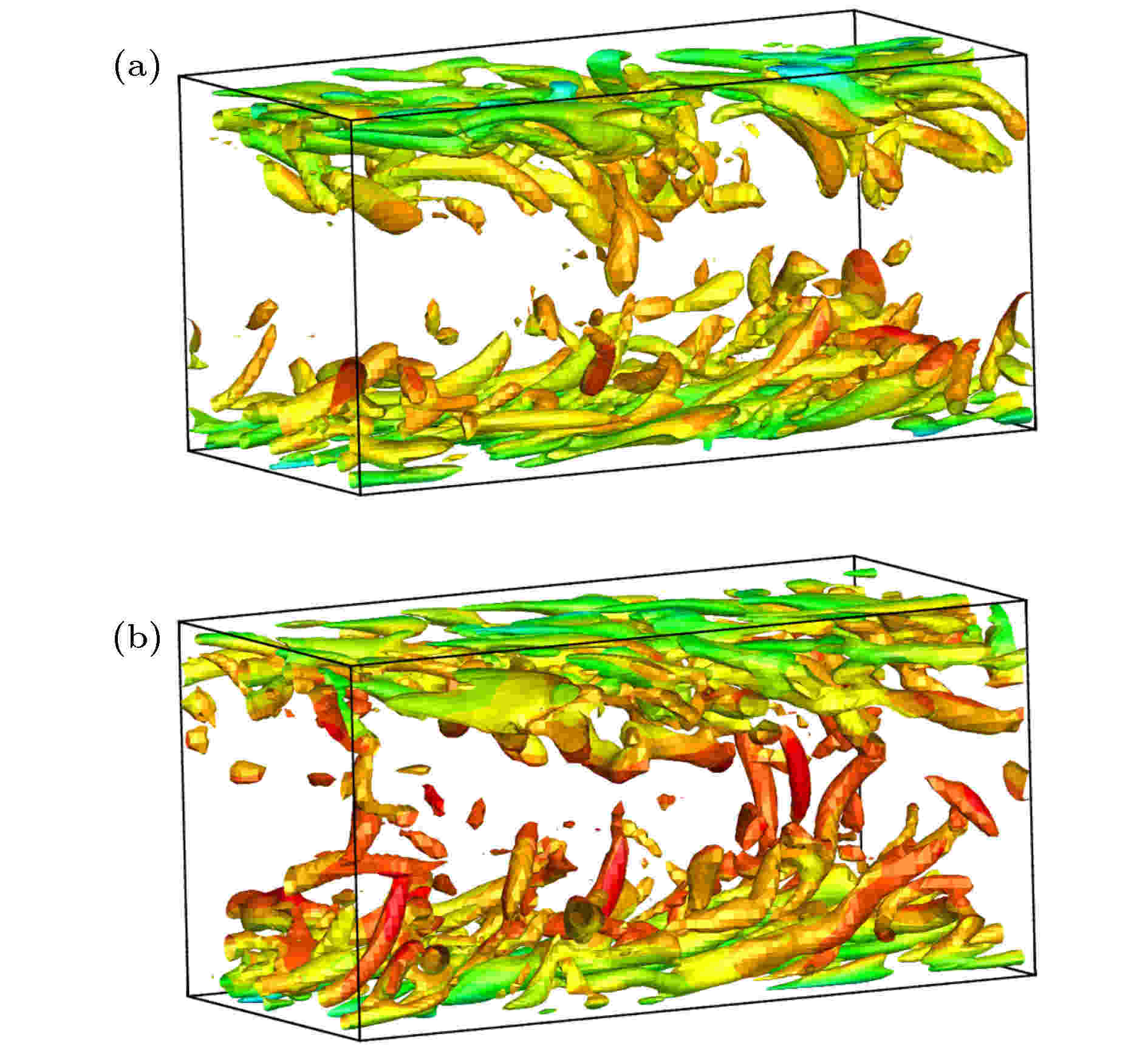 图 10
图 10 
















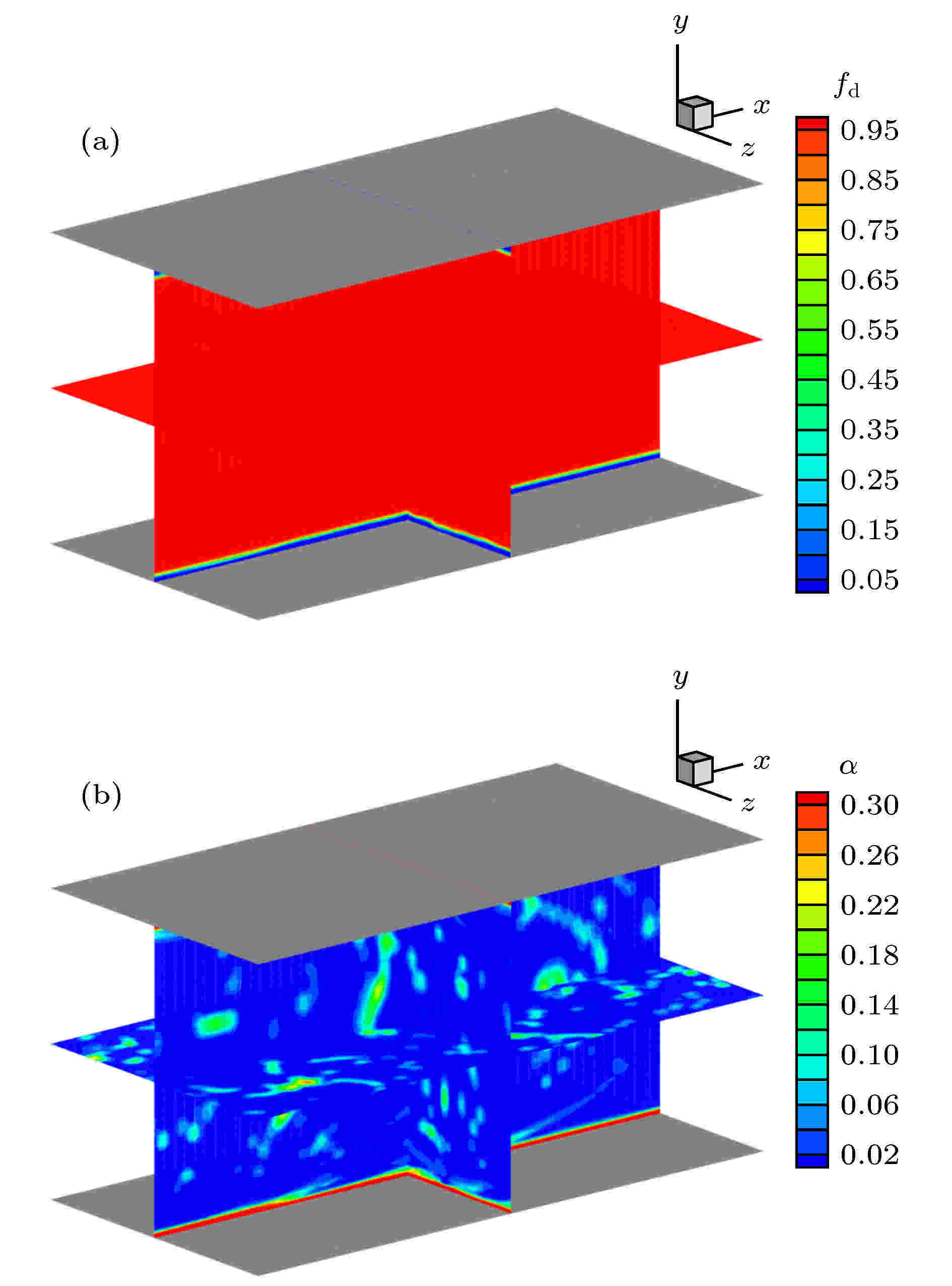 图 11
图 11 




















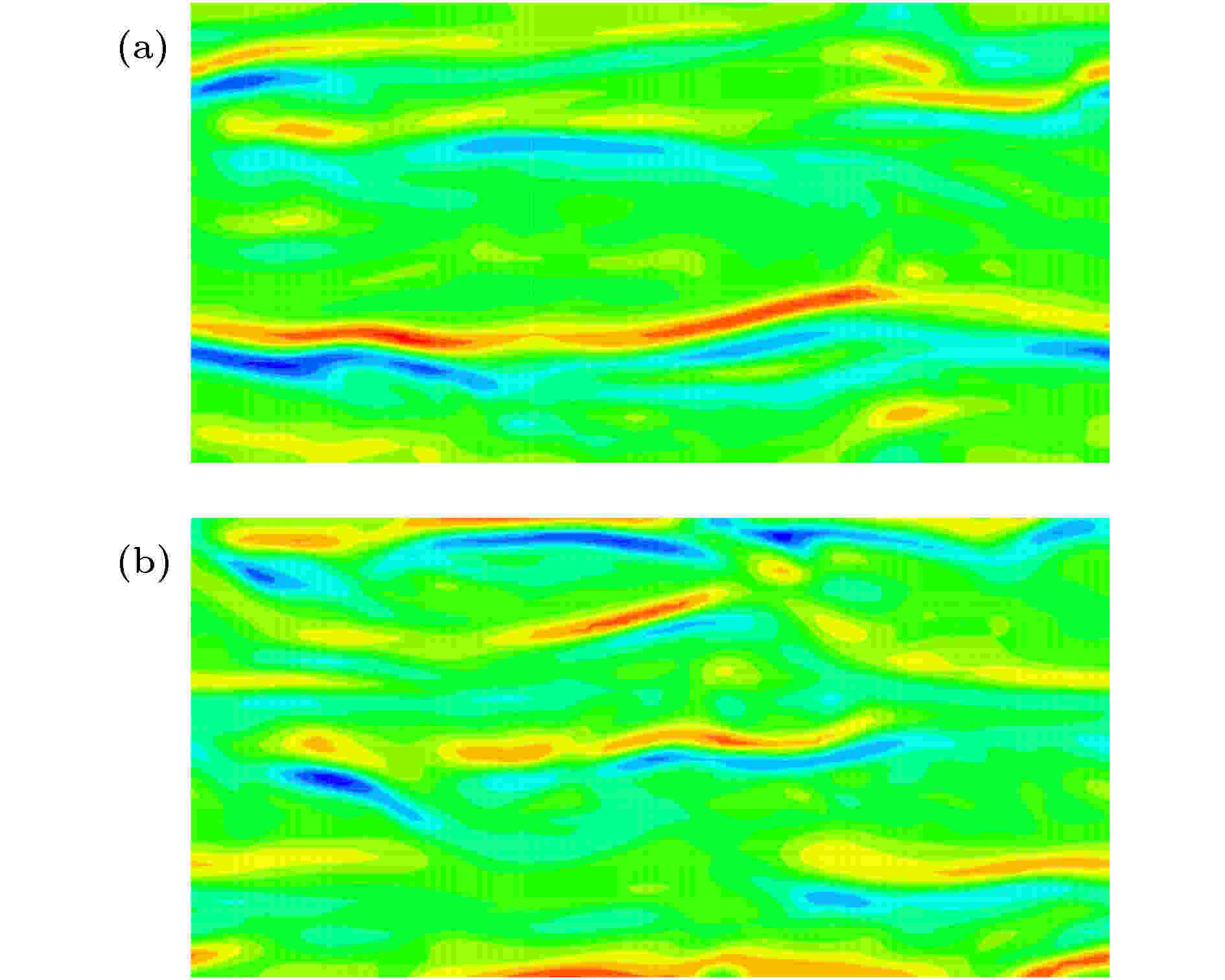 图 12
图 12 




































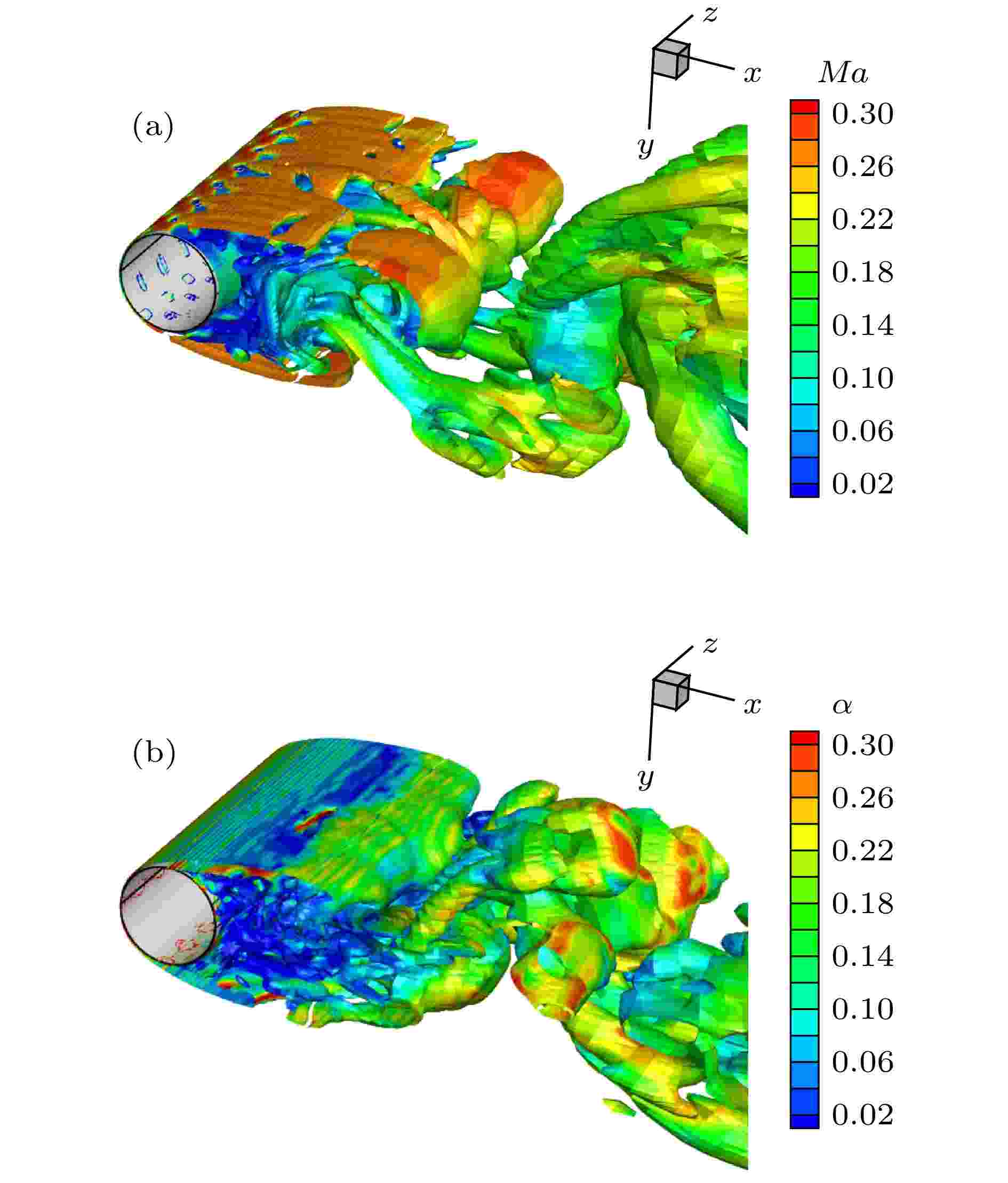 图 13 圆柱尾流
图 13 圆柱尾流





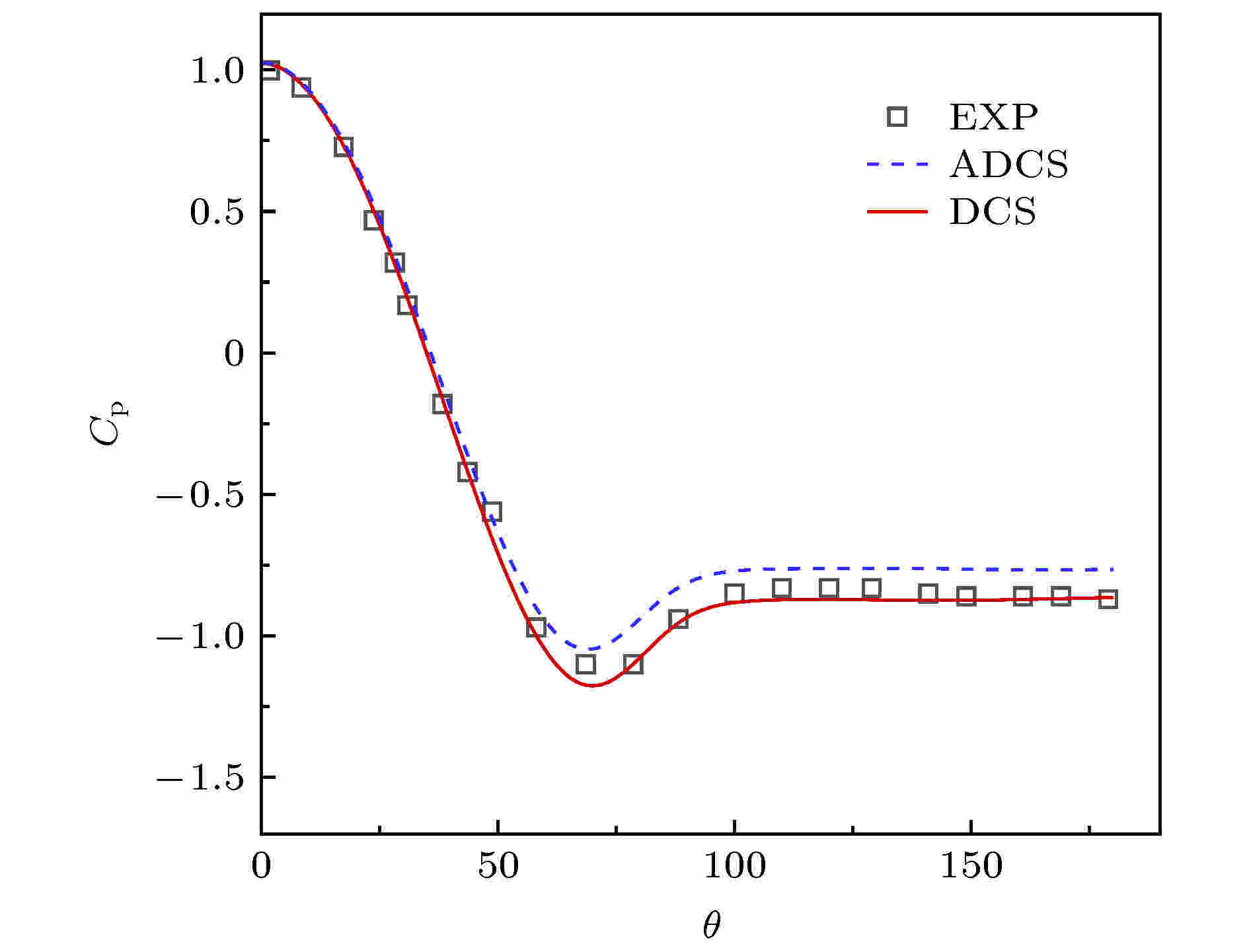 图 14 圆柱表面压力系数分布曲线
图 14 圆柱表面压力系数分布曲线


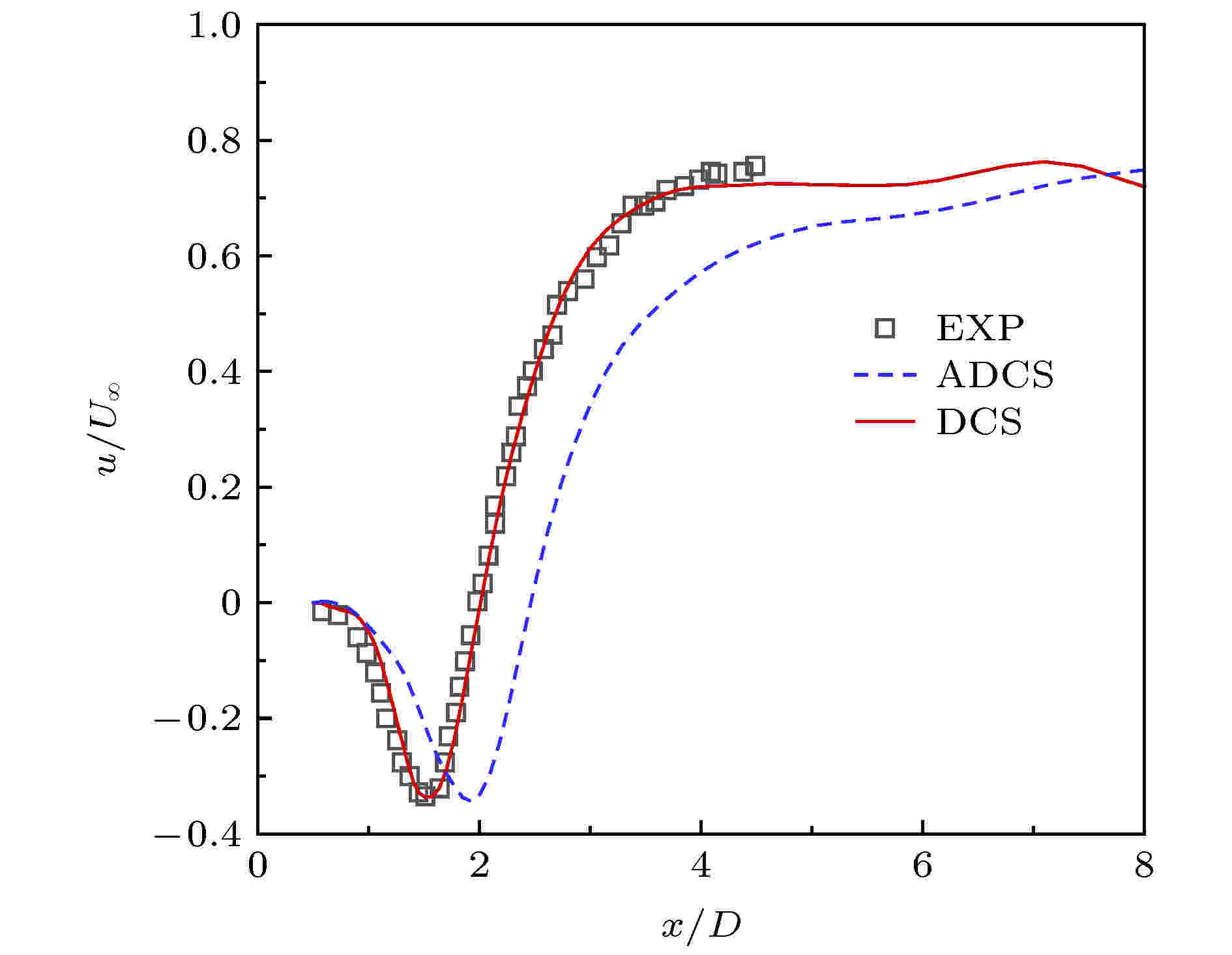 图 15
图 15 





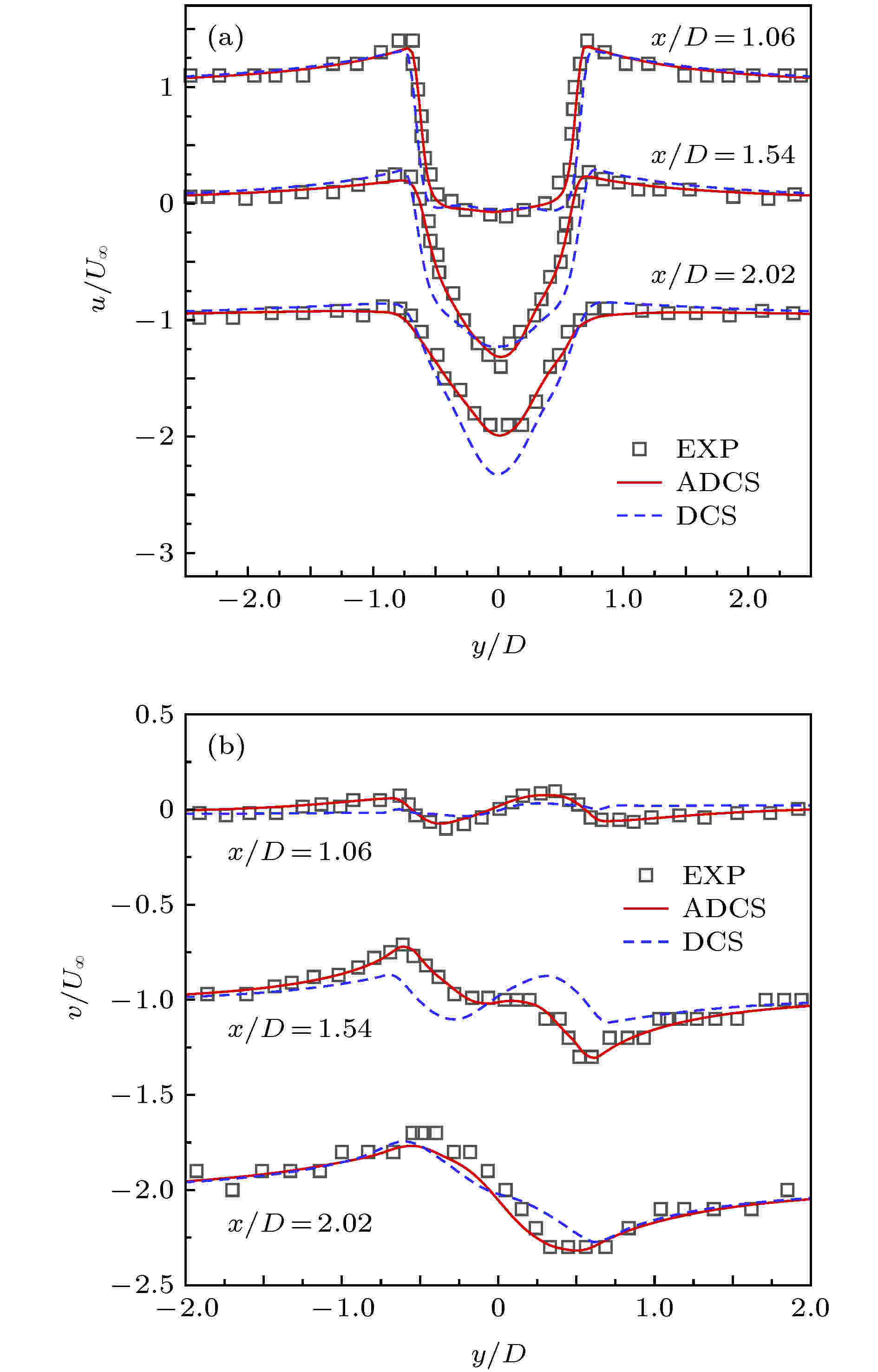 图 16
图 16 





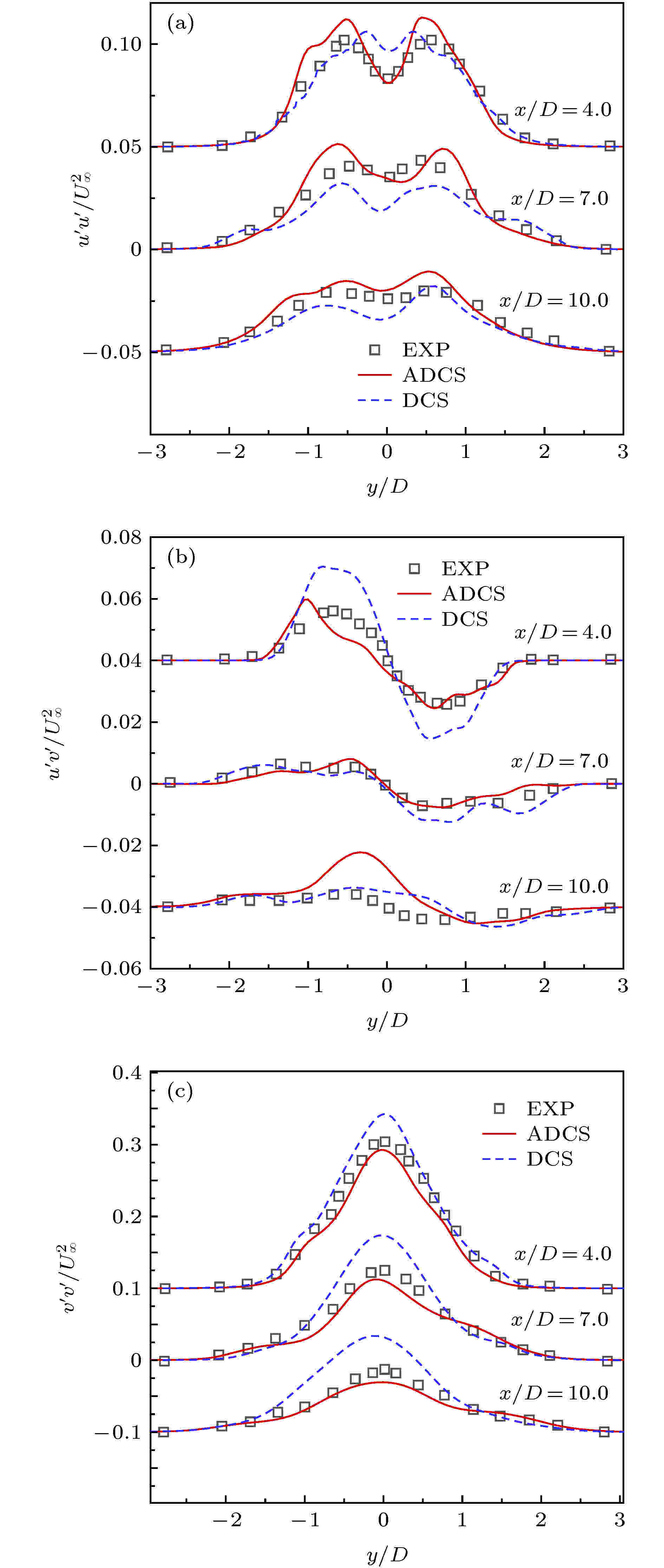 图 19
图 19 












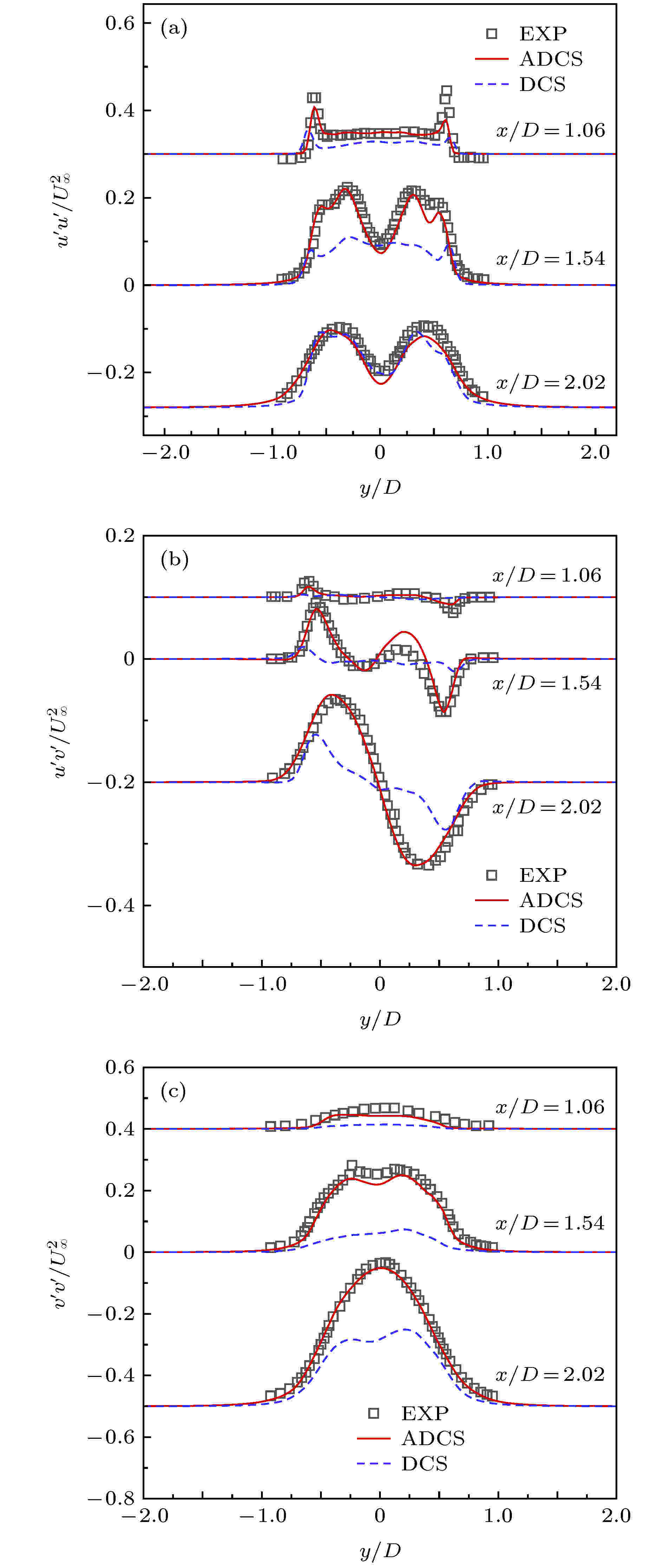 图 17
图 17 









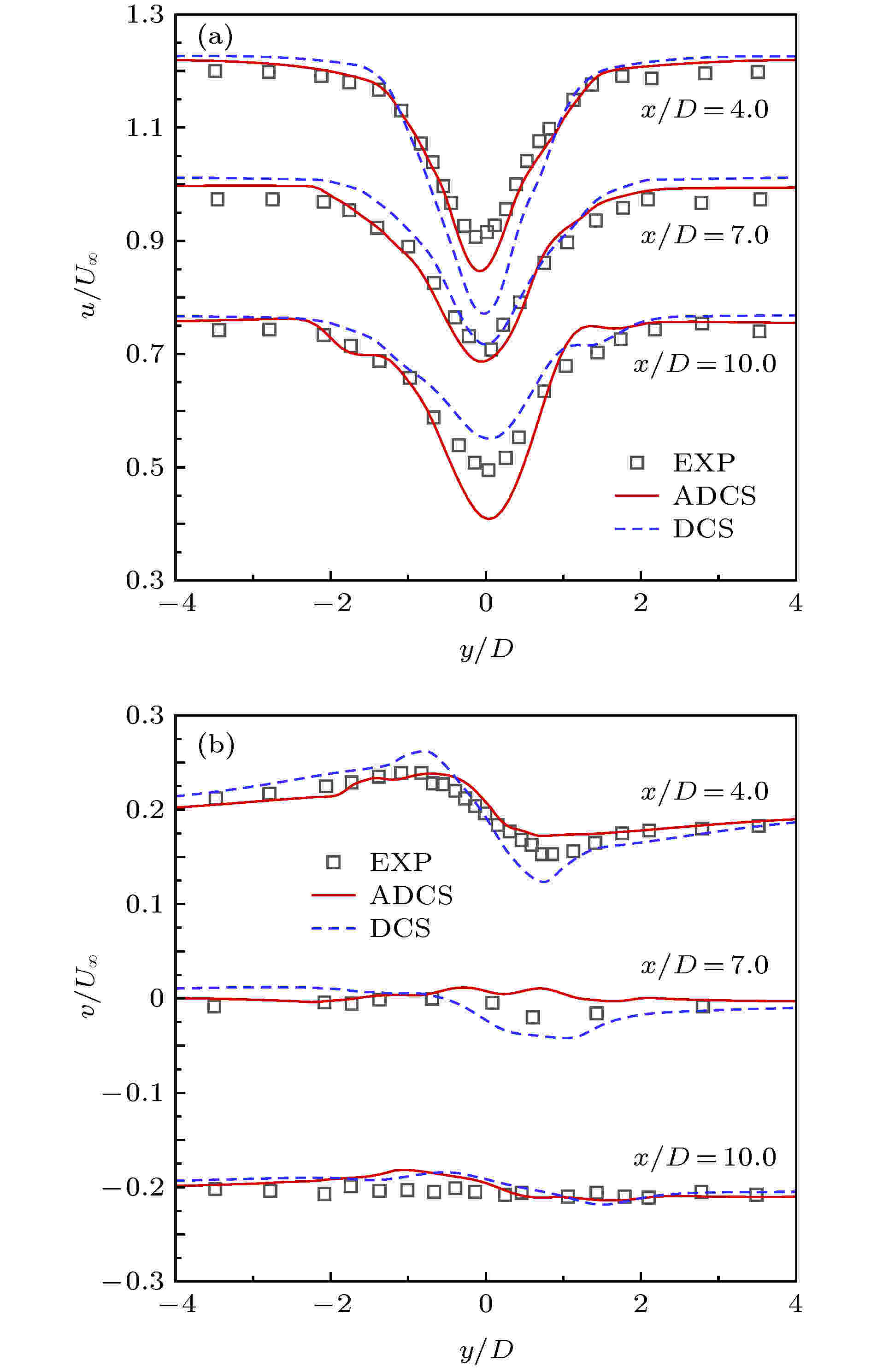 图 18
图 18 







