删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于场变换理论的大角度涡旋电磁波生成方法

本站小编 Free考研考试/2021-12-29
摘要:场变换是一种与入射角度无关的新型电磁变换方法, 可对电磁波极化和阻抗进行调控. 本文提出了一种基于场变换理论的大角度入射涡旋电磁波产生方法. 基于该方法设计了一种用于涡旋电磁波生成的人工媒质, 并通过对其仿真验证了所提出的方法. 设计的人工媒质为多层环形结构, 可以透射生成2阶涡旋电磁波, 并且具有较好的入射角度稳定性, 在60°斜入射时仍能产生涡旋电磁波.
关键词: 轨道角动量/
场变换/
大角度入射/
涡旋电磁波

English Abstract


全文HTML

--> --> -->
1.引　言
电磁波携带能量和动量, 动量可以分为线动量和角动量, 其中角动量包括由偏振决定的自旋角动量(spin angular momentum, SAM)和由光场空间分布决定的轨道角动量(orbital angular momentum, OAM)[1]. 自旋角动量与电磁波的极化有关. 轨道角动量则描述了波前围绕电磁波传播方向所在轴的旋转, 从而形成涡旋电磁波, 单光子携带的轨道角动量表示为$l\hbar $, 其中拓扑荷数l为任意整数, $\hbar $为约化普朗克常数, 不同的l代表了不同的OAM模态. l取值可以从负无穷到正无穷, 不同的OAM态相互正交[2]. 将l作为调制参数, 将不同的信息调制到不同模式的OAM涡旋波上可以实现在同一载频下拥有无穷多个相互独立的轨道角动量的信道, 这对提升通信系统的信道容量有着重大意义. 这种通信方法可应用在自由空间通信、光纤通信[2]和量子通信[3,4]中. 此外, OAM波还在超分辨率图像[5]、光镊[6], 数据存储[7]等领域有很大的潜力.
常规产生携带OAM的轨道角动量的方法有: 螺旋相位板(spiral phase plate, SPP)[8-10]、q板[11]、计算全息法[12]、天线阵列[13]等, 但有着加工难度大、尺寸较大、所生成的OAM模式单一或者转换率不高等缺点. 近年来利用超表面可以使电磁波产生相位突变的特点产生OAM波已经成为研究热点, 其中主要有基于谐振模式的超表面涡旋光束控制[14], 基于几何相位调控的涡旋光束产生[15,16]和基于传输相位的涡旋光束[17]等方法. 2016年, Yue等[18]利用几何相位的原理设计了一种理论上实现了接近100%效率的OAM反射超表面. Yang等[19]实现了平面波垂直入射和斜入射下OAM波的生成, 但其斜入射的角度较小, 为18°. 目前大多数的研究都集中在反射型生成OAM[19-21], 基本上都是垂直或者小角度入射生成OAM波, 所以在大角度入射情况下透射生成OAM波的问题亟待研究.
场变换(field transformation, FT)方法是一种调控电磁波极化和阻抗的理论方法. 它由麦克斯韦方程组和预设的边界条件推演而来, 基于无源互易材料来控制电磁波传播[22,23], 场变换方法与变换光学互补. 变换光学用于调控电磁波波前, 而场变换则用于调控电磁波极化和阻抗. 值得一提的是, 场变换能够在任意入射角度下控制每个电磁场分量阻抗和极化状态. 因此, 场变换方法被广泛用于波片[24,25]、极化器[26]和天线设计[27]等研究中.
本文利用场变换理论与等效媒质理论, 提出了一种可在大角度入射下产生涡旋电磁波的方法, 并设计了一种可以透射产生涡旋电磁波的人工媒质, 通过数值仿真验证了所提方法的有效性. 实现的人工媒质具有较好的入射波角度稳定性, 在以60°的角度斜入射仍能生成2阶OAM电磁波, 这种方法也可以实现生成任意阶次的OAM波[28].
2.理论分析与结构设计
2
2.1.场变换理论
-->

2.1.场变换理论

场变换理论示意图如图1所示. 根据场变换理论, 对于一个在$xoy$平面传播的平面波, 利用介质进行场变换的过程可以描述为[22]
$\left( {\begin{array}{*{20}{c}} {{E_z}} \\ {{\rm{i}}{H_Z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \phi }&{ - \sin \phi } \\ {\sin \phi }&{\cos \phi } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {E_z^{\left( 0 \right)}} \\ {{\rm{i}}H_z^{\left( 0 \right)}} \end{array}} \right), $
式中${E_z}$为场变换后电场的z分量, ${H_z}$为场变换后磁场的z分量, $E_z^{\left( 0 \right)}$为场变换前电场的z分量, $H_{\rm{z}}^{\left( 0 \right)}$为场变换前磁场的z分量, $\phi $为场变换参数.
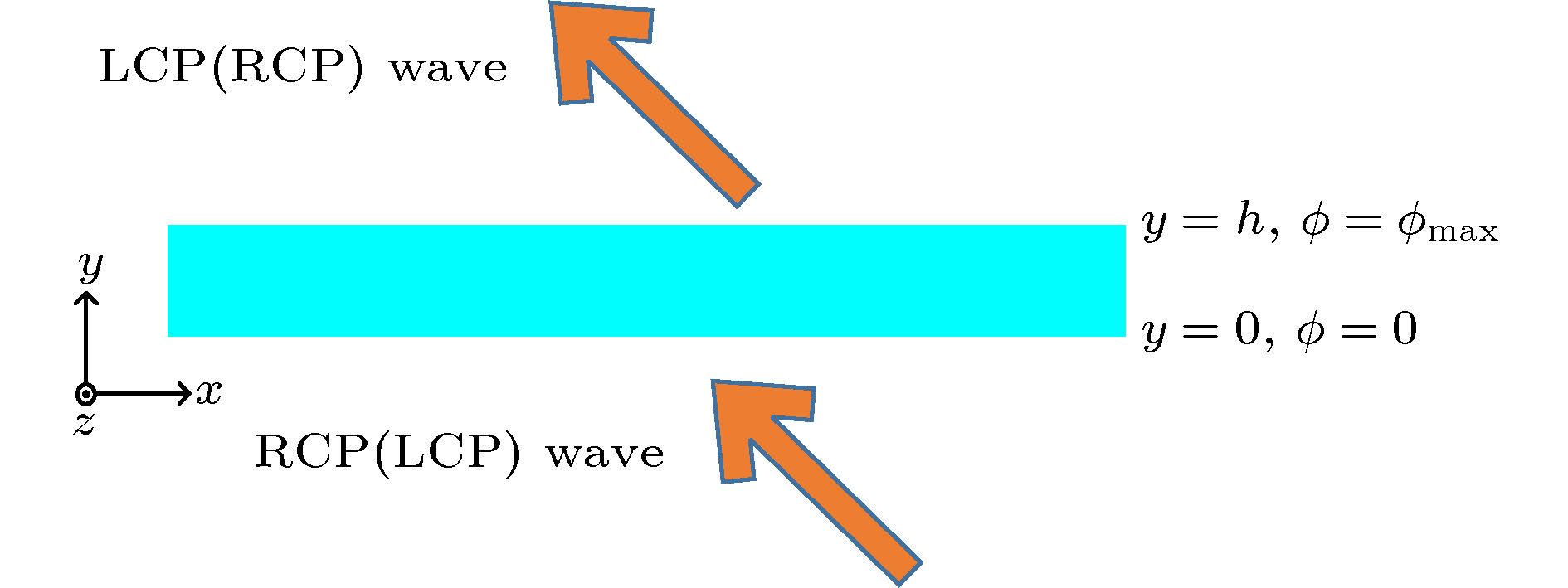图 1 场变换示意图
Figure1. Schematic diagram of the FT medium.

从(1)式可以看出, 场变换理论上与入射角度无关, 因此, 理论上可以设计出对入射角度不敏感的媒质. 当$\phi $不为零时, 通过场变换理论可以得出介质的介电常数张量和磁导率张量如下[19]:
$\overline \varepsilon \! =\! \left(\!\!{\begin{array}{*{20}{c}}n&0&{{A_y}}\\0&n&{{A_x}}\\{{A_y}}&{ - {A_x}}&n\end{array}}\!\!\right)\!,\;\overline \mu = \left(\!\!{\begin{array}{*{20}{c}}n&0&{ - {A_y}}\\0&n&{{A_x}}\\{ - {A_y}}&{{A_x}}&n\end{array}}\!\!\right),$
其中, ${A_x} = \dfrac{1}{{{k_0}}}\dfrac{{\partial \phi }}{{\partial x}}$, ${A_y} = \dfrac{1}{{{k_0}}}\dfrac{{\partial \phi }}{{\partial y}}$, ${k_0}$为电磁波在自由空间中的波数. 如图1所示, 介质中的场和介质的参数在z方向是不变的, 介质在y方向的范围为$y = 0$到$y = h$, 即h表示介质的厚度, $\phi $在此处为电磁波在介质中的相位, $\phi = 0\left( {y = 0} \right)$到$\phi = {\phi _{\max }} \left( {y = h} \right)$是线性变化的, $\phi = {{{\phi _{\max }}}/h}$与x无关的. 假设当${\phi _{\max }} = {{\text{π}}/2}\left( {y = h} \right)$时, 根据(1)式, 若此时入射波是TE(Ez0=1, iHz0=0)极化, 则经过此介质后转换为${\rm{TM}}\left( {{E_z} = 0, {\rm{i}}{H_z} = 1} \right)$极化波, 类似的入射的TM极化波可以转换为TE极化波, 此时介质可以视为半波片. 由于$\phi $仅和y相关, 则${A_x} = 0$, 而${A_y}$仅与频率相关. (2)式可化简为
$\overline \varepsilon = \left( {\begin{array}{*{20}{c}}n&0&A\\0&n&0\\A&0&n\end{array}} \right)\!,\;\overline \mu = \left( {\begin{array}{*{20}{c}}n&0&{ - A}\\0&n&0\\{ - A}&0&n\end{array}} \right),$
式中$A = {A_y}$. 但是在实际中, 想得到满足(3)式的介电常数张量和磁导率张量十分困难, 通过使用化简参数近似的方法可以将(3)式进一步化简[24,29]:
$\overline \varepsilon = \left( {\begin{array}{*{20}{c}}{{n^2}}&0&{2A}\\0&{{n^2}}&0\\{2A}&0&{{n^2}}\end{array}} \right),\overline \mu = 1,$
由$\overline \varepsilon $的对称性, (4)式中的媒质沿y轴旋转45°后可进行对角化. 此时, 经过实验近似后, 可用双折射结构来模拟这种介质. 人工双折射结构通常是将介电常数分别为${\varepsilon _1}$和${\varepsilon _2}$的两种材料以不同的厚度${t_1}$, ${t_2}$交替顺序堆叠而成的, 如图2所示. 与自然双折射材料相比, 人工双折射结构具有各向异性更强, 设计自由度高的特点. 根据双折射理论, 最终可以得到在${x'}y{z'}$坐标系中双折射媒质等效介电常数和等效磁导率为
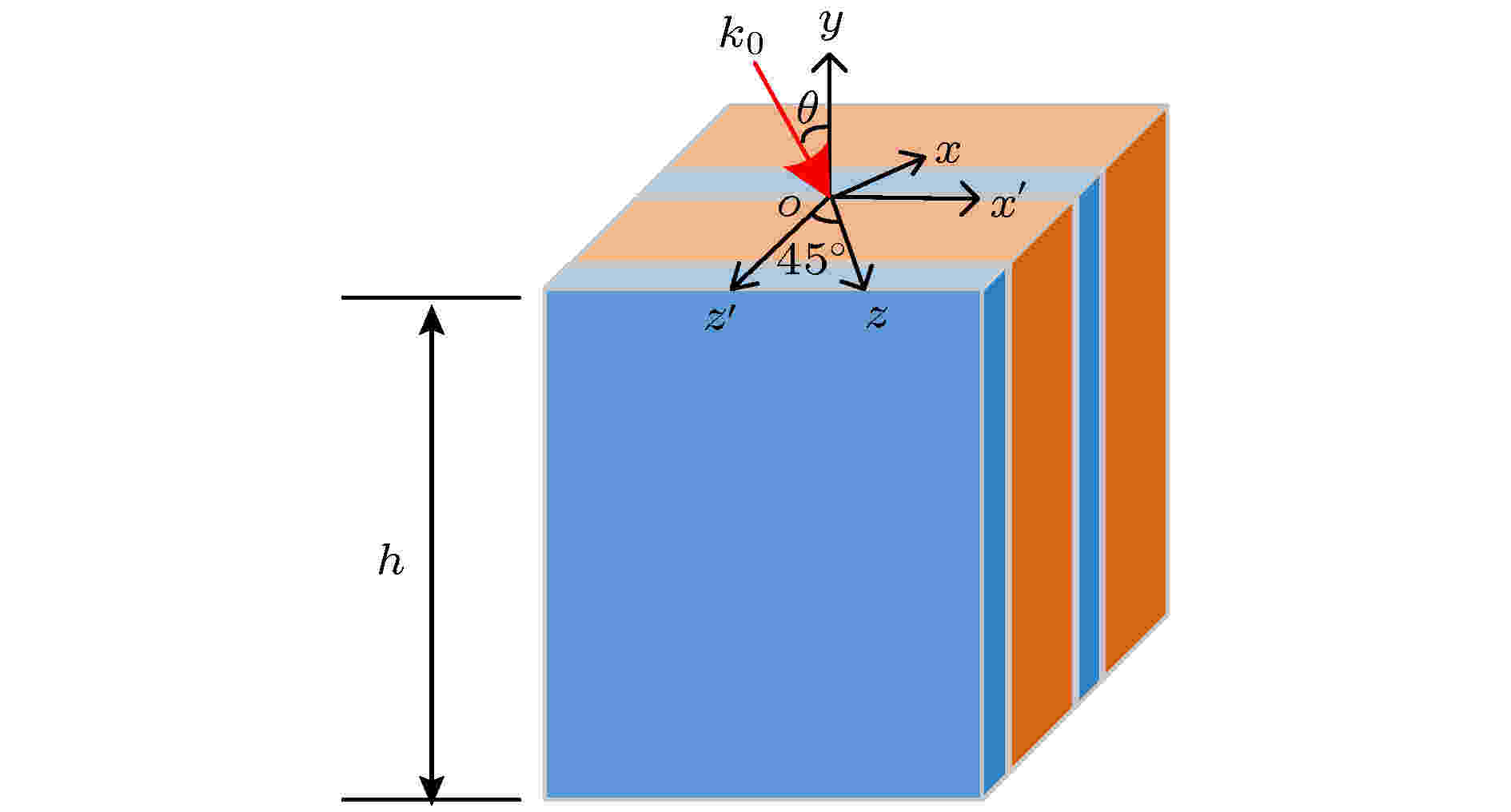图 2 人工双折射材料: $xyz$轴绕y轴旋转45°变成${x'}y{z'}$, 入射波在$xy$平面内, $\theta $为入射角, ${k_0}$是入射波的波数
Figure2. Artificial birefringence medium: The $xyz$ coordinate is twisted along the y -axis by 45° to the ${x'}y{z'}$ coordinate. The incident plane is x-y plane, $\theta $ is the incident angle, ${k_0}$ is the wave vector of the incident wave.

$\begin{split}\overline \varepsilon =\; & \left( {\begin{array}{*{20}{c}}{\dfrac{{{\varepsilon _1}{\varepsilon _2}}}{{{f_1}{\varepsilon _2} + {f_2}{\varepsilon _1}}}}&0&0\\0&{{f_1}{\varepsilon _1} + {f_2}{\varepsilon _2}}&0\\0&0&{{f_1}{\varepsilon _2} + {f_2}{\varepsilon _1}}\end{array}} \right),\\ &\overline \mu = 1,\\[-10pt]\end{split}$
其中${f_1} = \dfrac{{{t_1}}}{{{t_1} + {t_2}}}$, ${f_2} = \dfrac{{{t_2}}}{{{t_1} + {t_2}}}$[30].
利用等效介质理论计算出这两种介质叠加时的等效介电常数, 该理论要求两种材料的厚度要远小于波长, 等效介电常数为
$\begin{split} &{\varepsilon _{{x'}}} = {\varepsilon _{{y'}}} = \frac{{{\varepsilon _1} + \eta {\varepsilon _2}}}{{1 + \eta }}, \\ &\frac{1}{{{\varepsilon _{{z'}}}}} = \frac{1}{{1 + \eta }}\left( {\frac{1}{{{\varepsilon _1}}} + \frac{\eta }{{{\varepsilon _2}}}} \right),\;\eta = \frac{{{{\rm{t}}_2}}}{{{t_1}}}.\end{split}$

2
2.2.结构设计
-->

2.2.结构设计

对于透射型的人工双折射介质, 入射电磁波和透射电磁波的极化状态可以用琼斯矩阵J描述[31], 当电磁波沿着z方向入射到人工双折射介质上, 将电磁波按照圆极化分解:
${{J}^{\rm{c}}} = \left( {\begin{array}{*{20}{c}} {{J_{ + + }}}&{{J_{ + - }}} \\ {{J_{ - + }}}&{{J_{ - - }}} \end{array}} \right) = \frac{1}{2}\left( {\begin{array}{*{20}{c}} {\left( {{J_{xx}} + {J_{yy}}} \right) + {\rm{i}}\left( {{J_{xy}} - {J_{yx}}} \right)}&{\left( {{J_{xx}} - {J_{yy}}} \right) - {\rm{i}}\left( {{J_{xy}} + {J_{yx}}} \right)} \\ {\left( {{J_{xx}} - {J_{yy}}} \right) + {\rm{i}}\left( {{J_{xy}} + {J_{yx}}} \right)}&{\left( {{J_{xx}} + {J_{yy}}} \right) - {\rm{i}}\left( {{J_{xy}} - {J_{yx}}} \right)} \end{array}} \right),$
其中${{J}^{\rm{c}}}$为圆极化分解时的琼斯矩阵, ${J_{ + + }}$为右旋圆极化分量电场的同极化转化效率; ${J_{ + - }}$为右旋圆极化分量电场的交叉极化转化效率; ${J_{ - + }}$为左旋圆极化分量电场的交叉极化转化效率; ${J_{ - - }}$为左旋圆极化分量电场的同极化转化效率; ${J_{xx}}$为x方向极化分量电场的同极化转化效率; ${J_{xy}}$为x方向极化分量电场的交叉极化转化效率; ${J_{yy}}$为y方向极化分量电场的同极化转化效率; ${J_{yx}}$为y方向极化分量电场的交叉极化转化效率. 当${J_{xx}} = - {J_{yy}} = 1$且${J_{xy}} = {J_{yx}}$时, 以入射法线方向为轴将该反射体旋转α角, 此时线极化的琼斯矩阵变为
${J}\left( \alpha \right) = \left( {\begin{array}{*{20}{c}} {{J_{xx}}\cos \left( {{\rm{2}}\alpha } \right) - {J_{xy}}\sin \left( {{\rm{2}}\alpha } \right)}&{{J_{xx}}\sin \left( {{\rm{2}}\alpha } \right) + {J_{xy}}\cos \left( {{\rm{2}}\alpha } \right)} \\ {{J_{xx}}\sin \left( {{\rm{2}}\alpha } \right) + {J_{xy}}\cos \left( {{\rm{2}}\alpha } \right)}&{{J_{xy}}\sin \left( {{\rm{2}}\alpha } \right) - {J_{xx}}\cos \left( {{\rm{2}}\alpha } \right)} \end{array}} \right), $
圆极化琼斯矩阵变为
${{J}^{\rm{c}}}\left( \alpha \right) = \left( {\begin{array}{*{20}{c}} 0&{{{\rm{e}}^{ - 2{\rm{i}}\alpha }}\left( {{J_{xx}} - {\rm{i}}{J_{xy}}} \right)} \\ {{{\rm{e}}^{2{\rm{i}}\alpha }}\left( {{J_{xx}} + {\rm{i}}{J_{xy}}} \right)}&0 \end{array}} \right).$
当${J_{xy}} = {J_{yx}} = 0$时, 此时(8)式和(9)式变为
$\begin{split} &{J}\left( \alpha \right) = {J_{xx}}\left( {\begin{array}{*{20}{c}}{\cos \left( {2\alpha } \right)}&{\sin \left( {{\rm{2}}\alpha } \right)}\\{\sin \left( {{\rm{2}}\alpha } \right)}&{ - \cos \left( {2\alpha } \right)}\end{array}} \right),\\ &{{J}^{\rm{c}}}\left( \alpha \right) = {J_{xx}}\left( {\begin{array}{*{20}{c}}0&{{{\rm{e}}^{ - 2{\rm{i}}\alpha }}}\\{{{\rm{e}}^{2{\rm{i}}\alpha }}}&0\end{array}} \right),\end{split}$
此时琼斯矩阵变成对角矩阵, 可以将其等效为半波片的琼斯矩阵, 这意味着左旋圆极化(右旋圆极化)在透射后成为右旋圆极化(左旋圆极化). 同时, 引入了一个统一的相位系数${{\rm{e}}^{ \pm 2{\rm{i}}\alpha }}$, 称为Pancharatnam-Berry相位, 也被称为几何相位[32].
如图3所示, 当入射波沿着y方向入射到图2中的人工双折射材料单元上时, 将单元绕y轴旋转角度$\alpha $, 可以引起${\rm{2}}\alpha $的相位改变. 为了产生OAM, 几何相位被用于构建OAM定义要求的相位轮廓${{\rm{e}}^{{\rm{i}}l\phi }}$. 因此为实现l模式的OAM波, 单元需要被设计为有$l\phi $的相位改变, 即$\alpha = \pm l\phi /2$. 符号取决于入射圆极化波的极化状态. 当${J_{xx}} = - {J_{yy}} = \pm 1$, ${J_{xy}} = {J_{yx}} = 0$时, 可以实现OAM波的生成[31]. 根据以上的理论分析, 最终设计出的单元如图4所示.
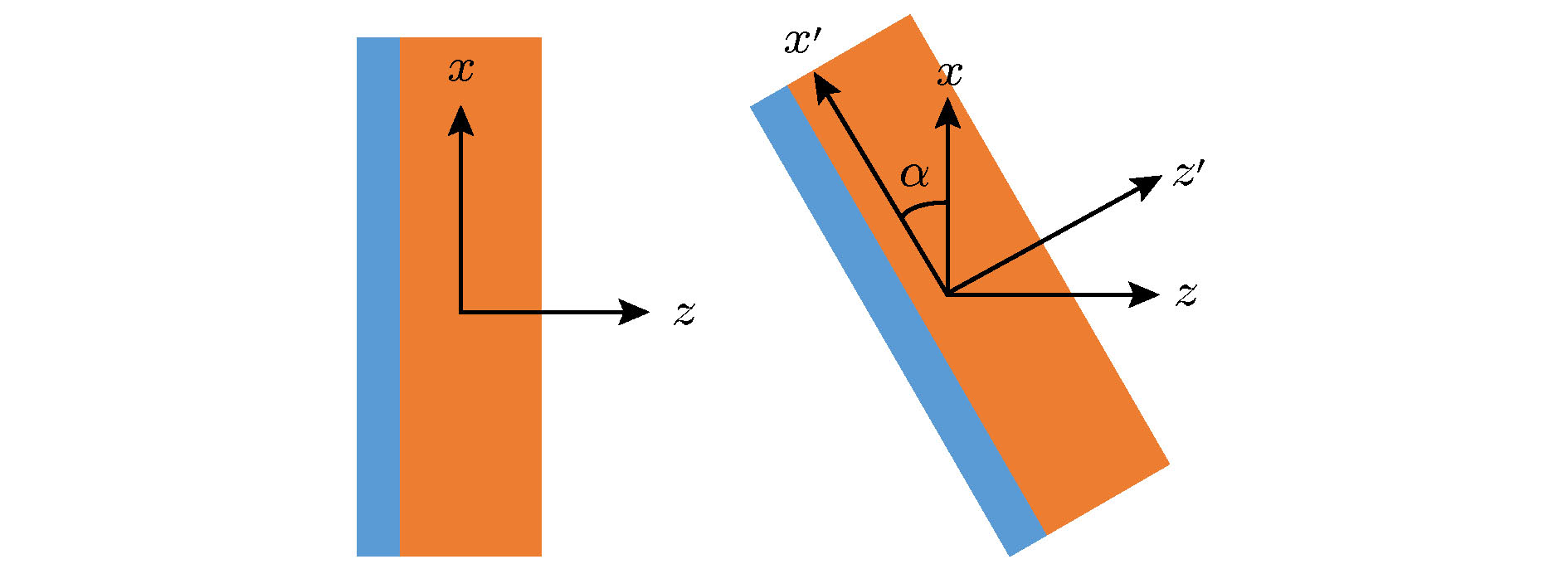图 3 Pancharatnam-Berry(几何)相位, 入射波沿y方向照射到单元上, 单元绕y轴旋转$\alpha $, 带来$2\alpha $的相位变化
Figure3. Pancharatnam-Berry phase: When the EM wave incident on the unit along y direction, and the unit rotates $\alpha $ around the y axis, the phase changed $2\alpha $.

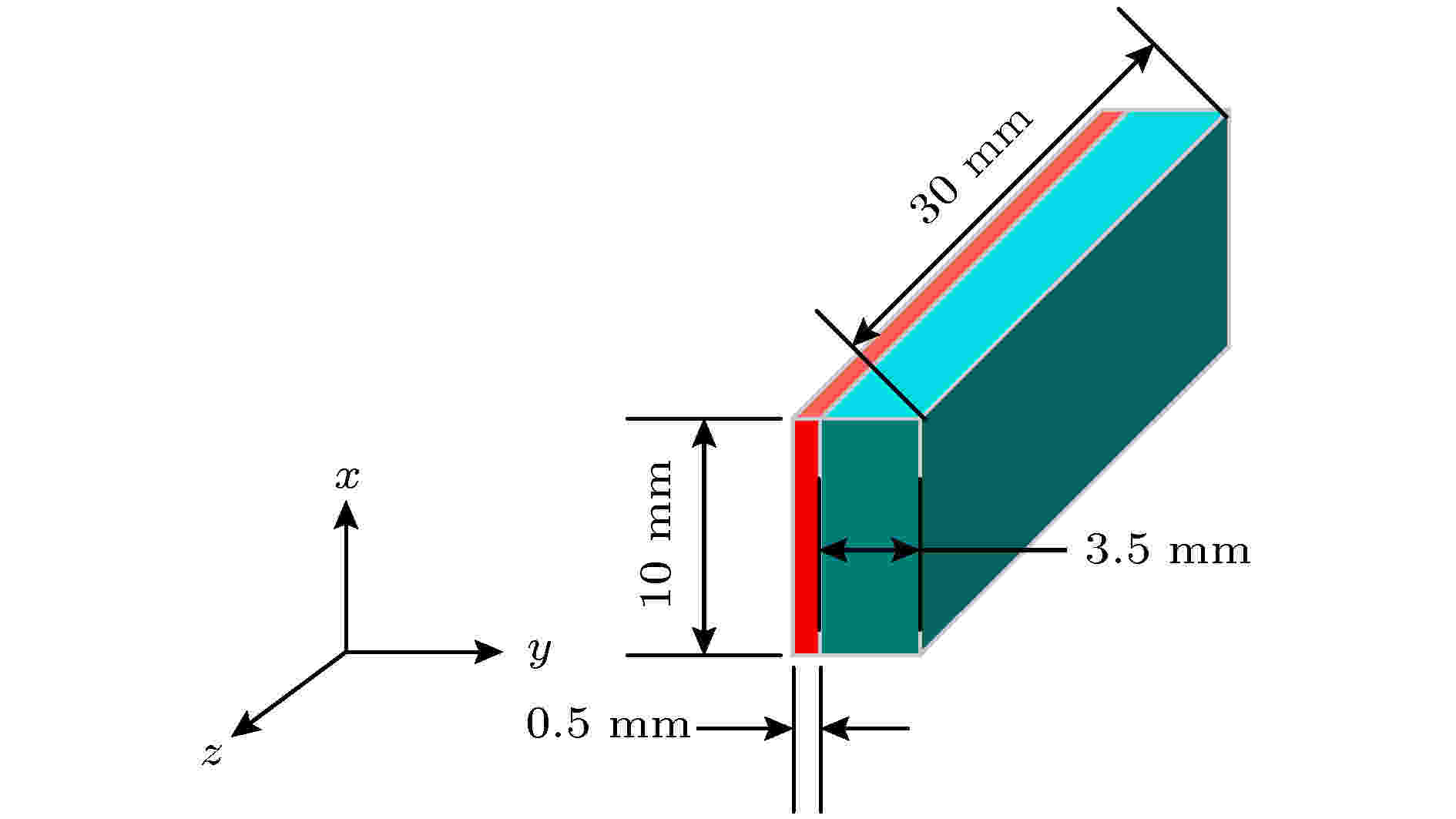图 4 单元模型
Figure4. The model of unit cell.

单元模型由两种介质组成, 红色部分介质为Arlon1000, 其介电常数为 10, 蓝色部分介质为介电常数为1.14的泡沫, 两种介质的损耗角正切分别为0.0023和0.00877, 厚度分别为0.5和3.5 mm, 在x方向的长度为10 mm, z方向的长度为30 mm. 电磁波沿着z方向入射到单元上, 经过仿真得到该单元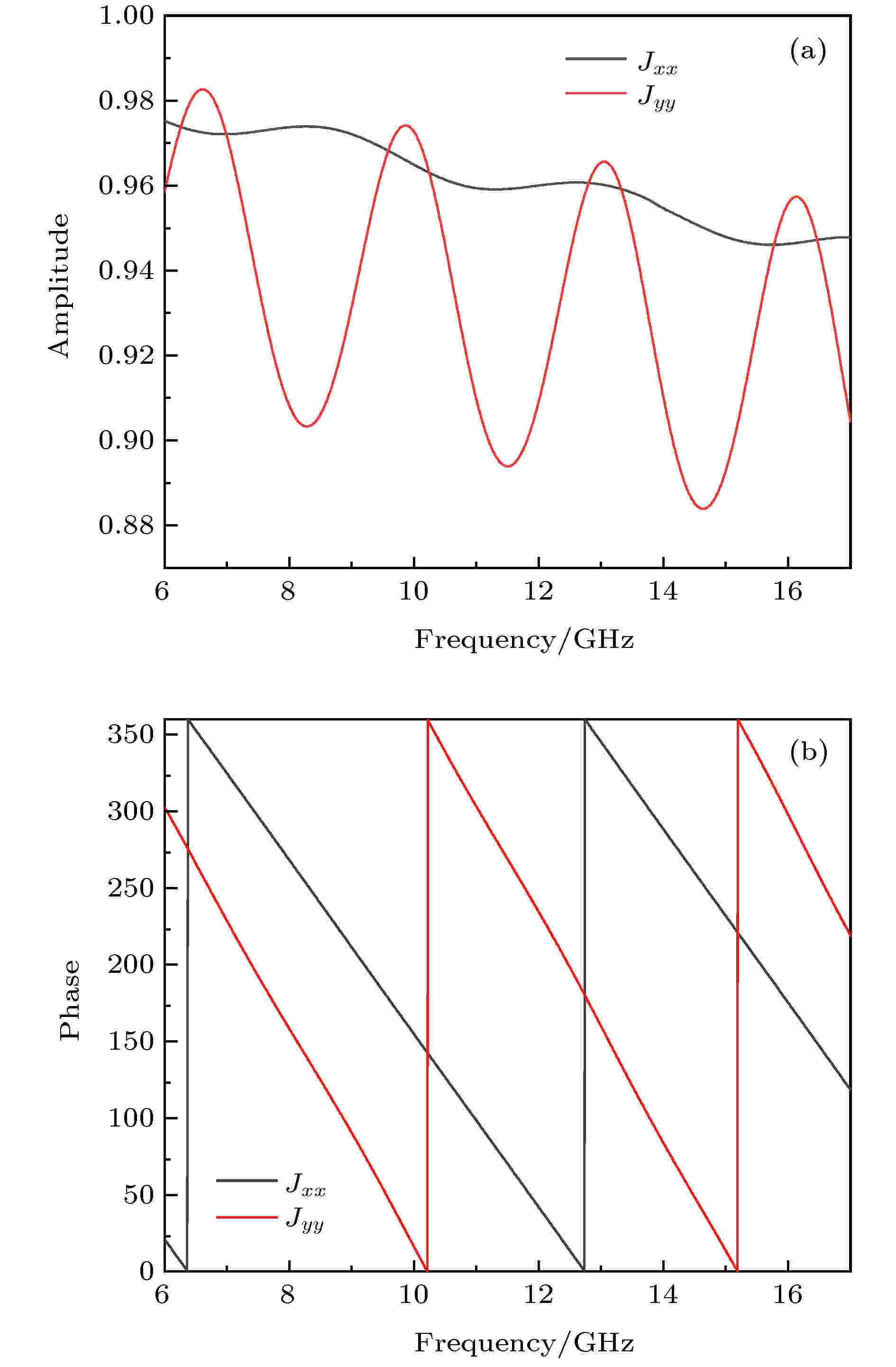${J_{xx}}$, ${J_{yy}}$的幅度如图5(a)所示, ${J_{xx}}$和${J_{yy}}$的相位如图5(b)所示, 在12.75 GHz时, ${J_{xx}}$与${J_{yy}}$的相位差为180°, 故该模型可以在12.75 GHz附近实现几何相位.
图 5 (a) ${J_{xx}}$和${J_{yy}}$的幅度 ; (b) ${J_{xx}}$和${J_{yy}}$的相位
Figure5. (a) The amplitude of ${J_{xx}}$ and ${J_{yy}}$; (b) the phase of ${J_{xx}}$ and ${J_{yy}}$.

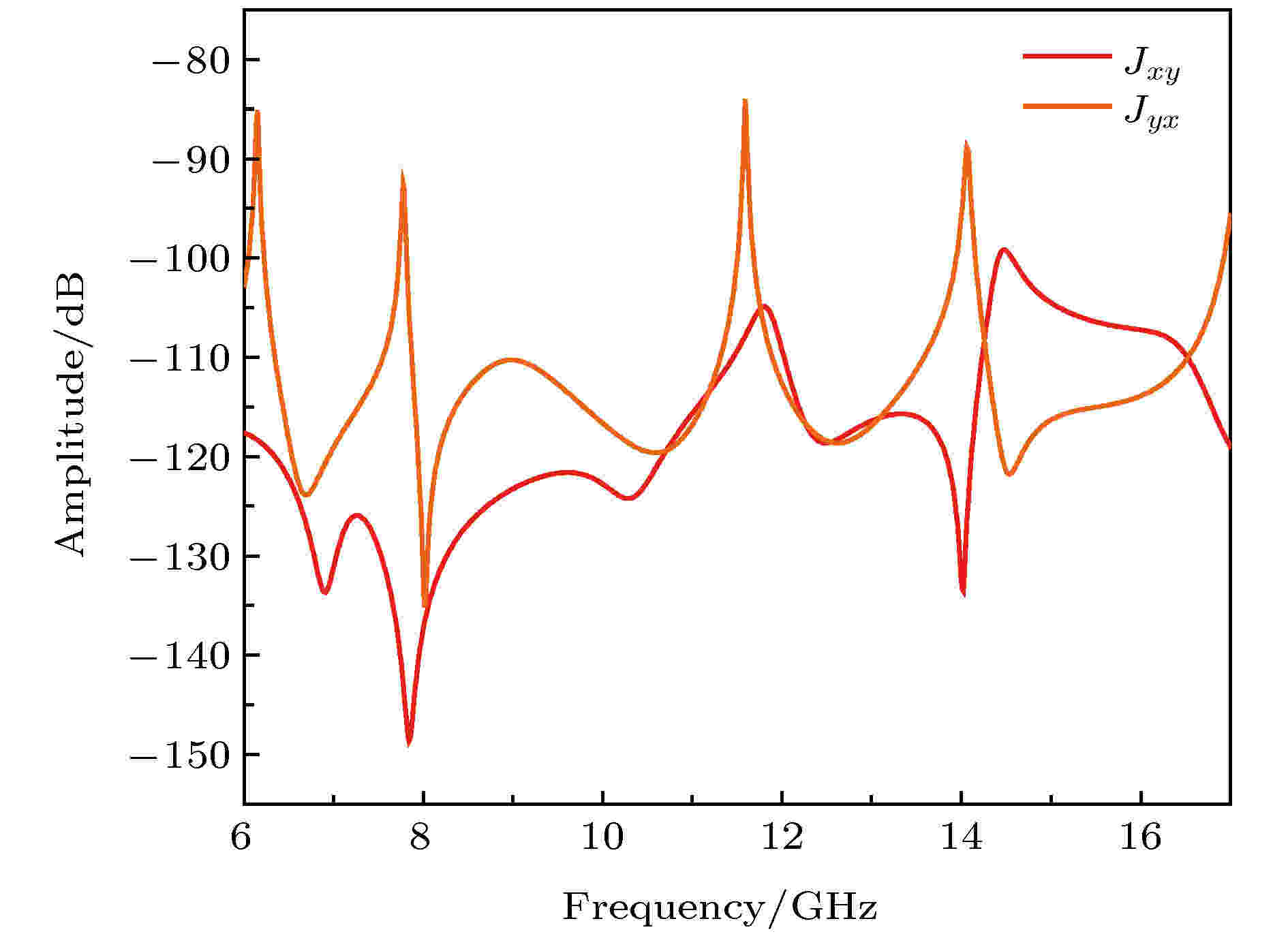${J_{xy}}$和${J_{yx}}$的幅度如图6所示. 可见${J_{xy}}$和${J_{yx}}$的幅度都低于–80 dB, 接近于0. 从以上的仿真结果可知, 单元满足${J_{xx}}$和${J_{yy}}$的幅度相等且相位相反, ${J_{xy}}$和${J_{yx}}$的幅度都接近为0.
图 6 ${J_{xy}}$和${J_{yx}}$的幅度
Figure6. The amplitude of ${J_{xy}}$ and ${J_{yx}}$.

将上述单元绕波的入射方向即z方向旋转成圆环状, 即旋转360°, 根据对几何相位的分析可知, 可以引起720° 的相位变化. 最终旋转得到的圆环如图7所示, 其半径为200 mm, 一共有100个介质圆环.
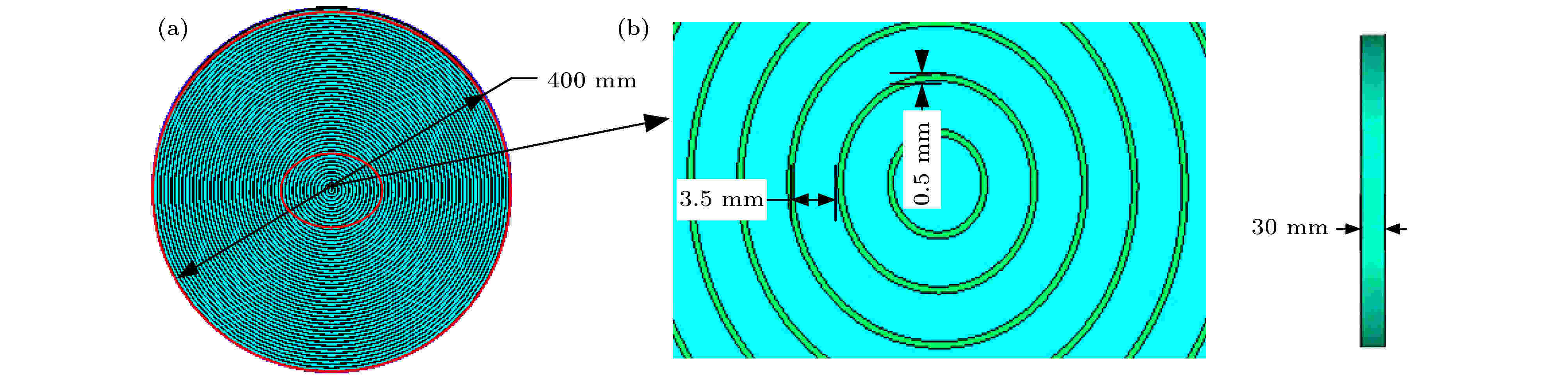图 7 (a)旋转所形成的介质圆环的主视图, 由100个圆环组成每个圆环的半径为4 mm; (b)介质圆环的侧视图
Figure7. (a) Main view of dielectric rings, it’s consists of 100 rings with radius of 4 mm and thickness of dielectric rings is 30 mm; (b) side view of dielectric rings.

3.仿真结果与分析
在仿真圆环时使用左旋圆极化的高斯波束沿着z方向入射到介质圆环的上方, 穿过圆盘后透射到介质圆环的下方. 高斯波束的束腰距离介质圆环的表面为188 mm, 束腰半径为60 mm, 当高斯波束垂直入射时, 在13 GHz时的透射波中右旋圆极化分量的电场幅度和相位如图8所示.
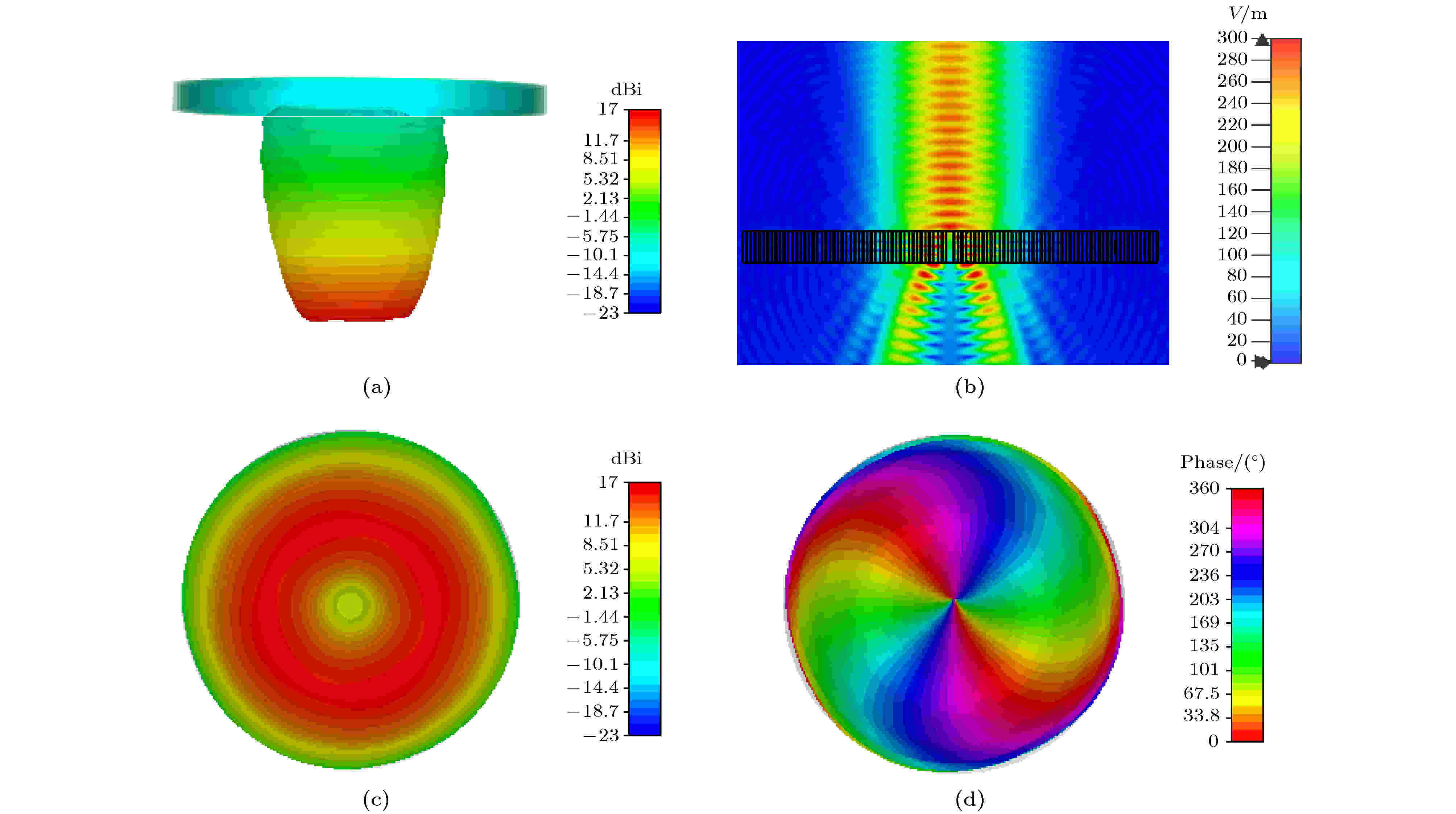图 8 (a)垂直入射的透射波; (b)介质圆环周围空间的电场分布; (c)13 GHz时右旋圆极化波的幅度; (d)13 GHz时右旋圆极化波的相位
Figure8. (a) The transmission wave while incident angle is 0°; (b) E-field distribution around dielectric rings; (c) amplitude of RCP wave at 13 GHz ; (d) phase of RCP wave at 13 GHz.

图8(b)给出了此时在介质圆环周围的电场分布. 由于相位奇点的存在, 右旋圆极化波分量的中心位置幅度非常小(如图8(c)所示), 而能量集中在圆环状区域中. 相位如图8(d)所示, 可见相位从0变化到了$4{\text{π}}$, 成涡旋状, 因此可见右旋圆极化分量作为交叉极化分量携带了2模式的OAM, 该模型的转化效率非常高. 表1列出了不同频点右旋分量的最大值. 可见该模型的带宽比较宽, 在11—15 GHz内均可较高效率地产生OAM波.
频率/GHz右旋圆极化分量最大值/dBi
1114.70
1215.80
1316.90
1417.30
1517.50


表1垂直入射时不同频点的右旋分量的最大值
Table1.Maximum values of RCP at different frequencies when normal incidence.

改变高斯波束的入射角度, 当20°斜入射时, 13 GHz时透射波的右旋圆极化分量的电场幅度和相位如图9所示. 其中介质圆环的电场如图9(b)所示, 可见在20°斜入射时有一部分高斯波束在圆环的上方被反射, 透射电磁波仍然具有明显的相位极点, 右旋圆极化波电场能量分布依然为圆环状. 右旋圆极化波的幅度分布为圆环形, 中心的相位奇点非常明显, 中心幅度非常小, 圆环处幅度比较大, 为17.2 dBi, 其转换效率仍然较高. 如图9(d)所示, 相位呈螺旋状, 从0变化到了720°, 所以透射电磁波的右旋圆极化分量仍然携带了2模式的OAM波. 表2列出了20°斜入射时不同频点右旋分量的最大值.
频率/GHz右旋圆极化分量最大值/dBi
1115.30
1216.10
1317.20
1417.70
1517.40


表220°斜入射时不同频点的右旋分量的最大值
Table2.Maximum values of RCP at different frequencies when incident angle is 20°.

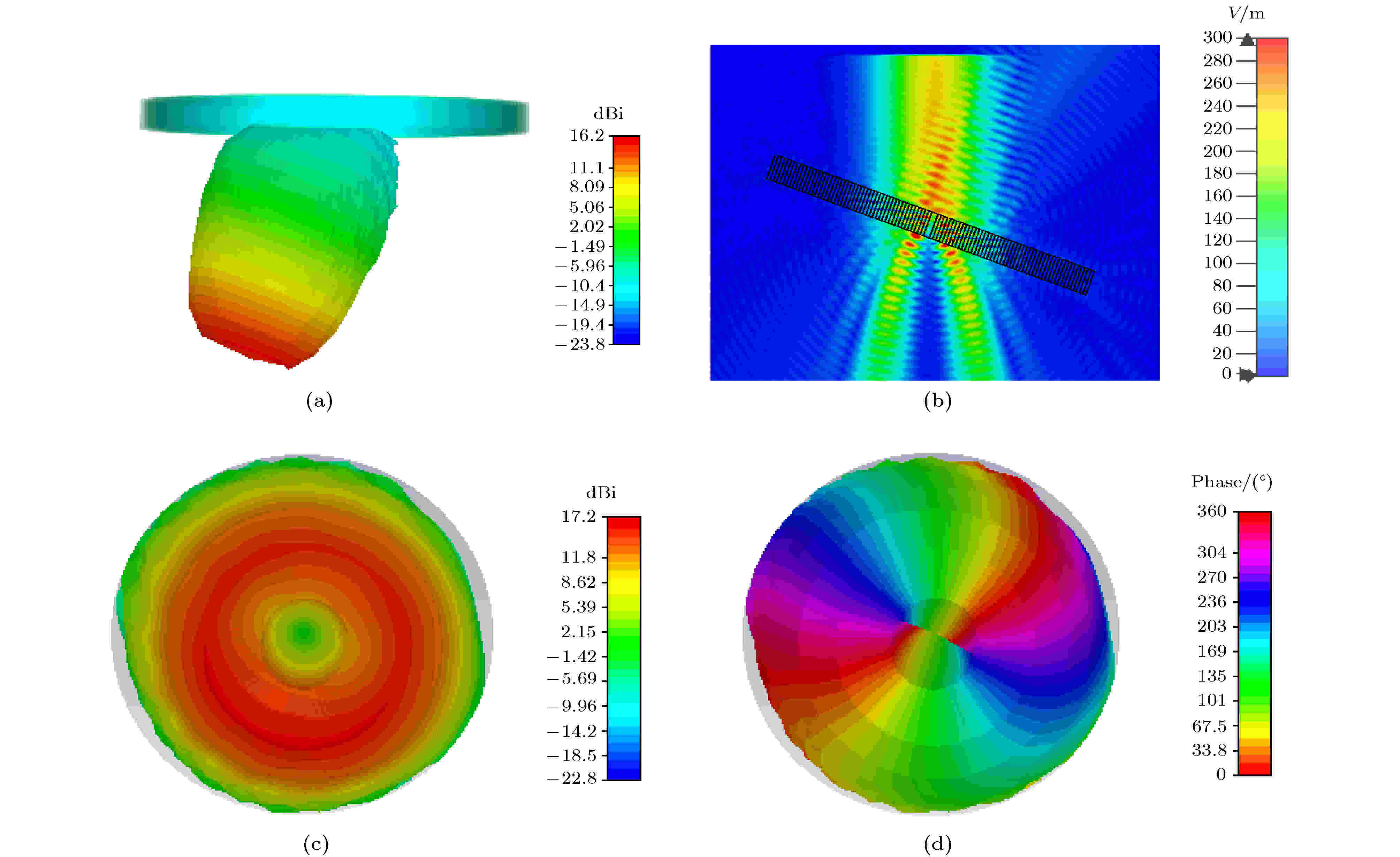图 9 (a) 20°斜入射时的透射波; (b)介质圆环周围空间的电场分布; (c) 20°斜入射时13 GHz的右旋圆极化波的幅度; (c) 20°斜入射时在13 GHz的右旋圆极化波的相位
Figure9. (a) The transmission wave while incident angle is 20°; (b) E-field distribution around dielectric rings; (c) amplitude of RCP wave at 20° oblique incidence; (d) phase of RCP wave at 20° oblique incidence.

该模型在20°斜入射时, 产生的透射电磁波的交叉极化分量中携带了2模式的OAM, 并且在13 GHz时转化效率很高, 其右旋圆极化分量为17.2 dBi, 在14 GHz时右旋圆极化分量为17.7 dBi, 14 GHz时右旋圆极化分量大于13 GHz时的右旋圆极化分量, 由此可见中心频率变为14 GHz, 带宽较宽. 相比垂直入射, 性能基本没有变化.
当入射角度为40°时, 13 GHz时透射波的右旋圆极化分量的电场幅度和相位如图10所示. 其中介质圆环周围空间的电场分布如图10(b)所示, 能明显观察到反射波束的电场; 透射电磁波的右旋圆极化分量的幅度如图10(c)所示, 有明显的相位奇点, 中心位置幅度很小, 但是最大值分布位置相比垂直入射时有变化, 最大值为17.4 dBi, 转换效率很好; 相位分布如图10(d)所示, 相位依然是从0变化到了$4{\text{π}}$, 呈螺旋状, 证明右旋圆极化分量为2模式的OAM波, 然而相比于垂直入射的情况, 分布不再均匀.
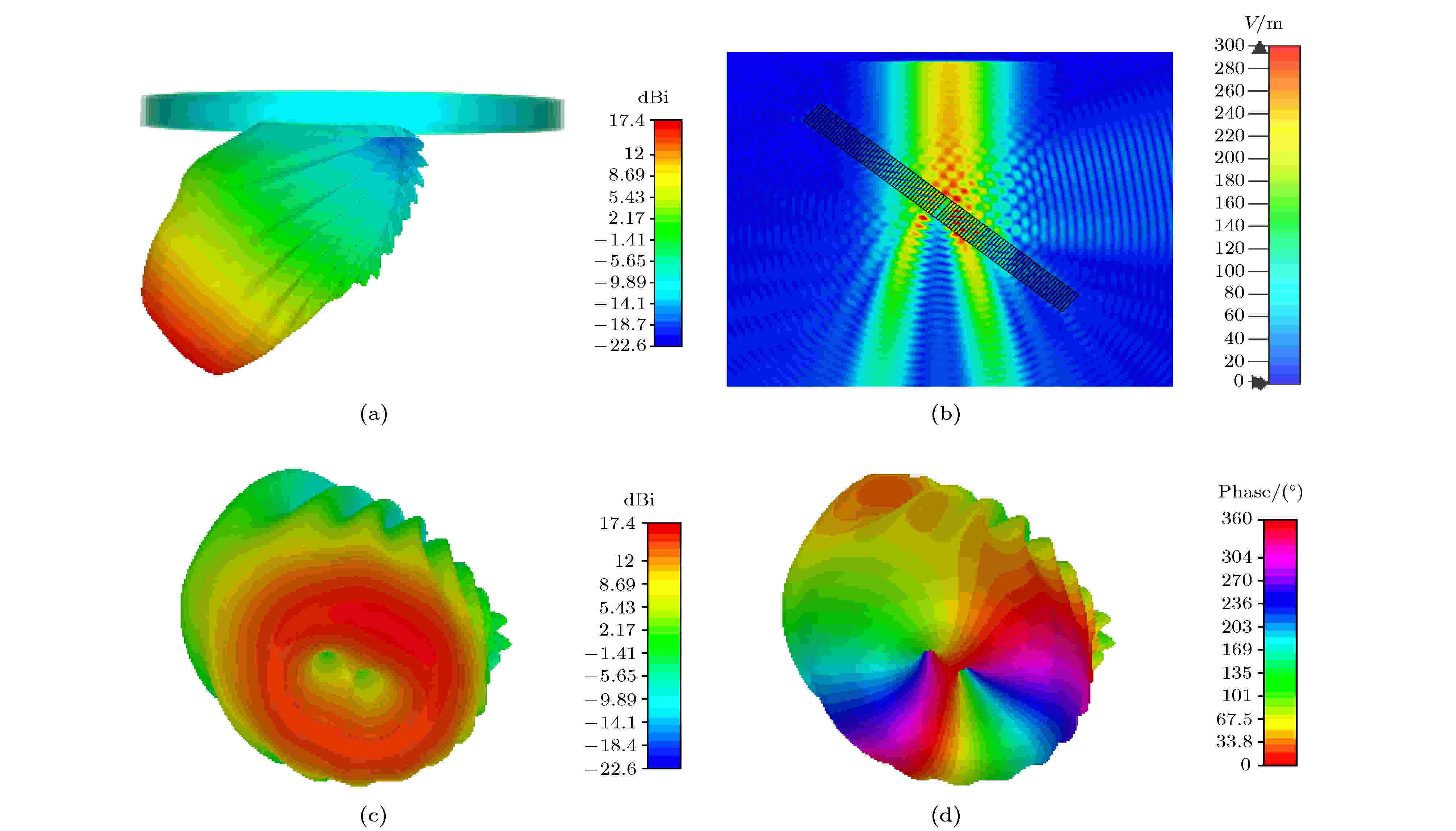图 10 (a) 40°斜入射时的透射波; (b)介质圆环周围空间的电场分布; (c) 40°斜入射时13 GHz的右旋圆极化波的幅度; (d) 40°斜入射时13 GHz的右旋圆极化波的相位
Figure10. (a) The transmission wave while incident angle is 40°; (b) E-field distribution around dielectric rings; (c) amplitude of RCP wave at 40° oblique incidence; (d) phase of RCP wave at 40° oblique incidence.

表3给出了入射角为40°时不同频点右旋分量的最大值. 入射角为40°时, 能够在13 GHz时较高效率地转化产生OAM波, 且OAM模式为2. 在13 GHz时右旋圆极化分量为17.4 dBi, 在14 GHz时右旋圆极化分量为18.6 dBi, 14 GHz时右旋圆极化波的幅度大于13 GHz时右旋圆极化波的幅度, 相比垂直入射, 中心频率也变为14 GHz, 效率有一定的下降, 转化出OAM波的效果也不如垂直入射时效果好.
频率/GHz右旋圆极化分量最大值/dBi
1116.0
1216.7
1317.4
1418.6
1518.5


表340°斜入射时不同频点右旋分量的最大值
Table3.Maximum values of RCP at different frequencies when incident angle is 40°.

当波束的入射角为50°时, 13 GHz的透射右旋圆极化分量的电场幅度和相位如图11所示. 当波束的入射角为50°时, 此时模型周围空间的电场分布如图11(b)所示, 透射电磁波的右旋圆极化分量的幅度如图11(c)所示, 可以看到携带2模式OAM波的右旋圆极化分量的幅度最大值分布在两个圆环上, 其携带的2模式OAM波不纯, 有两个相位奇点. 在13 GHz这一频率该模型的转化效率有所下降. 相位分布如图11(d)所示, 绕该透射电磁波一周相位有$4{\text{π}}$的变化, 但相位奇点非常明显地分成了两个, 且相位分别不均匀, 此时携带的2模式OAM不纯净.
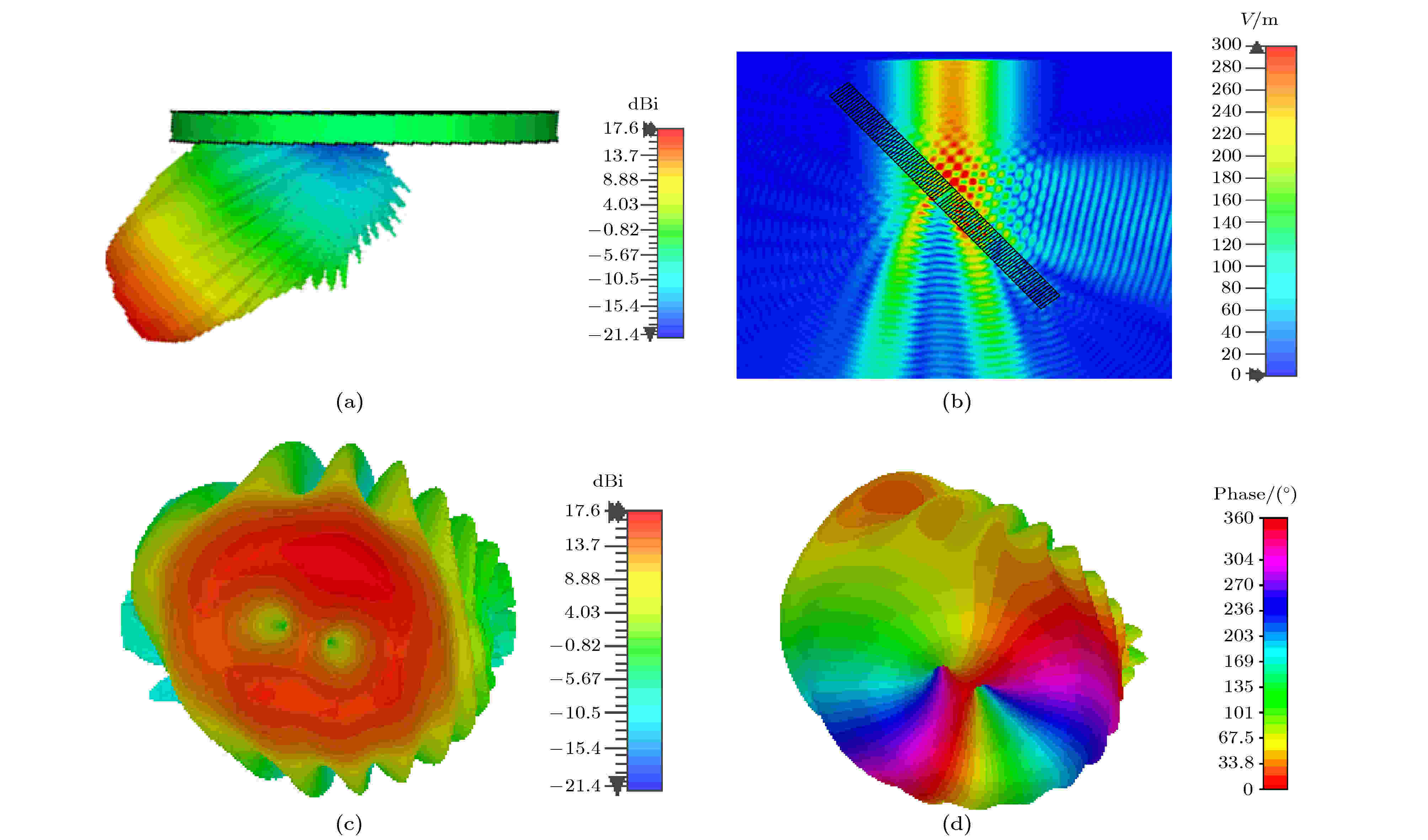图 11 (a) 50°斜入射时的透射波; (b)介质圆环周围空间的电场分布; (c) 50°斜入射时13 GHz的右旋圆极化波的幅度; (d) 50°斜入射时在13 GHz的右旋圆极化波的相位
Figure11. (a) The transmission wave while incident angle is 50°; (b) E-field distribution around dielectric rings; (c) amplitude of RCP wave at 50° oblique incidence; (d) phase of RCP wave at 50° oblique incidence.

表4列出了50°斜入射时不同频点的右旋分量的最大值. 可知50°斜入射时, 该模型可以转化入射的圆极化电磁波为交叉极化的OAM波, 但转换效率与前面的情况相比下降明显, 反射分量更大, 转化的中心频率向高频移动, 但此时仍能产生2模式的OAM波.
频率/GHz右旋圆极化分量最大值/dBi
1116.8
1217.2
1317.6
1418.6
1519.6


表450°斜入射时不同频点的左旋和右旋分量的最大值
Table4.Maximum values of RCP at different frequencies when incident angle is 50°.

当高斯波束以60°角入射时, 13 GHz时透射右旋圆极化分量的电场幅度和相位如图12所示. 其中图12(b)给出了60°入射时介质圆环周围的电场分布, 而透射电磁波的右旋圆极化分量的幅度如图12(c)所示, 可以看到携带2模式OAM波的右旋圆极化分量的幅度最大值明显地分布在两个圆环上, 证明其携带的2模式OAM波不纯, 有两个相位奇点. 在13 GHz这一频率该模型旋转60°后转化效率下降明显. 相位分布如图12(d)所示, 绕该透射电磁波一周相位有4π的变化, 但相位奇点非常明显地分成了两个, 且相位分别不均匀, 说明该分量的电磁波携带了不纯净的2模式的OAM.
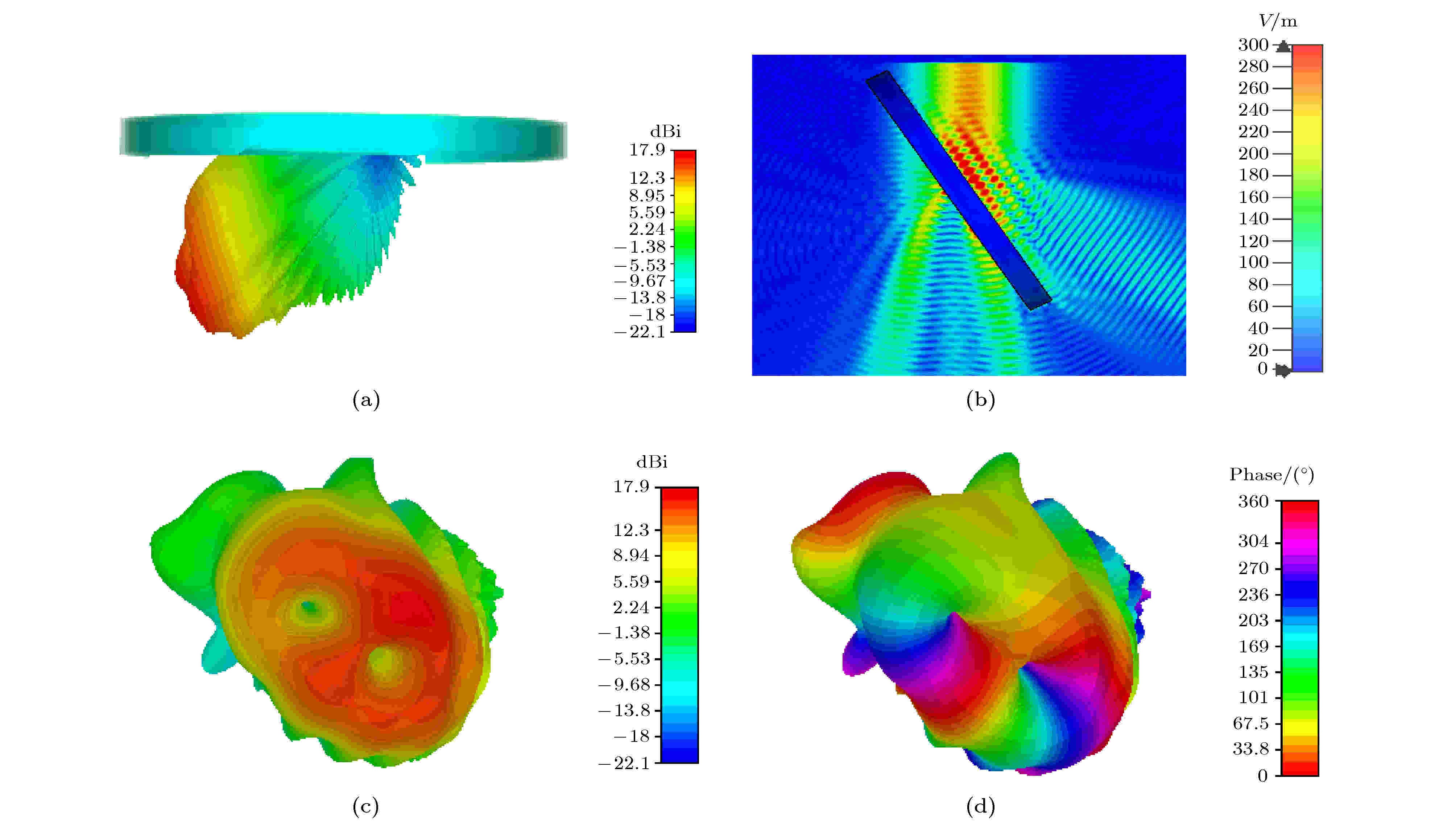图 12 (a) 60°斜入射时的透射波; (b) 60°入射时介质圆环周围的电场分布; (c) 60°斜入射时13 GHz的右旋圆极化波的幅度; (d) 60°斜入射时13 GHz的右旋圆极化波的相位
Figure12. (a) The transmission wave while incident angle is 60°; (b) E-field distribution around dielectric rings at 60° oblique incidence; (c) amplitude of RCP wave at 60° oblique incidence; (d) phase of RCP wave at 60° oblique incidence.

表5列出了60°斜入射时不同频点的右旋分量的最大值. 可见60°斜入射时, 该模型可以转化入射的圆极化电磁波为交叉极化的OAM波, 但转换效率相比垂直入射和小角度斜入射时低很多, 会产生较多的反射分量. 转化的中心频率更加明显地向高频移动, 虽然其性能有所下降, 但仍能明显观察到电磁波携带了轨道角动量.
频率/GHz右旋圆极化分量最大值/dBi
1116.1
1216.9
1317.9
1418.5
1519.6


表560°斜入射时不同频点的左旋和右旋分量的最大值
Table5.Maximum values of RCP at different frequencies when incident angle is 60°.

4.结　论
本文利用场变换理论, 提出了一种大角度涡旋电磁波产生方法. 并基于场变换理论和简化参数近似方法设计了一种大角度涡旋电磁波产生媒质, 构建出了产生2模式的OAM波的整体透射模型. 该模型有着对入射角度不敏感的特性, 在60°斜入射时仍能生成OAM波, 实现了广角入射转化产生OAM波. 此方法也可用于设计实现反射型和任意模态涡旋电磁波生成媒质.
相关话题/设计 空间 材料 相位 结构
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 电磁超材料吸波体的研究进展
    摘要:电磁吸波技术在军用和民用领域得到了广泛应用,但传统吸波技术不能满足现代吸波材料新的需求,基于超材料的吸波体具有结构简单、轻薄、吸收率高等优点,并可以实现对电磁波的灵活调控,使得电磁吸波领域获得了飞速发展.本文针对电磁超材料吸波研究进行了综述,首先介绍了电磁超材料吸波方法与机理,指出了研究中遇到 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 氧化物玻璃中的类分子结构单元
    摘要:本文引入团簇加连接原子模型来解析硅酸盐玻璃相关氧化物的结构,并给出了这些氧化物的最小结构单元——类分子结构单元.参与网络形成体的氧化物主要以三角形或者四面体的配位体形式存在,构建玻璃的三维网络状骨架.如基础的网络形成体SiO2,其类分子结构单元团簇式是为[Si-O4]Si,含有的价电子数为32 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于二维材料二硒化锡场效应晶体管的光电探测器
    摘要:以二硒化锡作为沟道材料,设计并制备基于二硒化锡场效应晶体管的光电探测器.以化学气相输运法制备的二硒化锡纯度高且结晶度良好,对二硒化锡使用机械剥离法制备出层状二硒化锡,薄膜的横向尺寸最大可达25—35μm,最薄厚度仅为1.4nm,使用图形转移法制备基于二硒化锡的场效应晶体管,表面光滑无褶皱,且表 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于机械剥离β-Ga<sub>2</sub>O<sub>3</sub>的Ni/Au垂直结构肖特基器件的温度特性
    摘要:本文制备了基于机械剥离β-Ga2O3的Ni/Au垂直结构肖特基器件,对该器件进行了温度特性I-V曲线测试.器件表现出了良好的二极管特性,随着温度从300K升高至473K,势垒高度从1.08eV上升至1.35eV,理想因子从1.32降低至1.19,二者表现出了较强的温度依赖特性,这表明器件的肖特 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 铁电材料中的电畴: 形成、结构、动性及相关性能
    摘要:铁电材料的研究有近百年的历史,而铁电畴的存在是铁电材料最基本的微观结构特征.随着材料制备和表征技术的发展,铁电畴的排列组合方式对材料性能的影响越来越凸显.而近年来的研究显示,铁电畴及畴壁甚至能够作为各种微纳电子器件的独立功能单元,在信息存储、能量转换、机电驱动、量子计算等领域有着广泛的应用潜力 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 铁电材料中的极性拓扑结构
    摘要:调控磁性材料中的自旋拓扑结构(流量闭合型、涡旋、半子(meron)、斯格明子(skyrmion)等自旋组态)可以改进材料的磁性和电磁性能,因而引起了学术界的广泛关注.最近研究表明,在尺寸效应、界面耦合及其相互作用、外延应变等作用下,铁电材料中也会出现自发的极性拓扑畴结构,同时表现出新的铁电相结 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 利用X射线衍射技术对压电材料本征与非本征起源探究的研究进展
    摘要:钙钛矿铁电压电材料具有高介电压电常数和高机电耦合系数等特点,在工业、消费电子和军事等领域具有广泛的应用,其压电性能起源的机理及与材料多尺度结构之间的关系一直是凝聚态物理和材料科学领域的研究热点.铁电材料的压电效应主要来源于本征的场致晶格畸变以及非本征的畴翻转和畴壁运动,理解并区分这两种压电效应 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 铁电材料中电场对唯象系数和电卡强度的影响
    摘要:由于电场强度能够影响铁电材料的极化强度和介电常数,因此唯象系数${a}_{0}$是电场强度的隐函数.在铁电相区域,唯象系数${a}_{0}$由铁电极化强度和介电常数倒数确定,是电场的非线性函数.在顺电相区域,唯象系数${a}_{0}$由介电常数倒数确定,也是电场的非线性函数.本文研究了铁电共聚 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 低损耗材料微波介电性能测试中识别TE<sub>01δ</sub>模式的新方法
    摘要:工作于TE01δ模式的金属谐振腔法是评价低损耗材料微波介电性能的通用方法.微波介质谐振器均为多模式谐振器,故正确识别TE01δ模式是微波介电测试的基础.TE01δ模式的识别可通过预测谐振频率及其随谐振器尺寸的变化、根据激励条件排除寄生模式等手段实现,但已有方法存在复杂、易识别错误等缺点.为此, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光子增加双模压缩真空态在马赫-曾德尔干涉仪相位测量中的应用
    摘要:量子度量学主要是利用量子效应来提高参数估计的精度,以期突破标准量子极限,甚至达到海森伯极限.本文研究了一般光子增加双模压缩真空态作为马赫-曾德尔干涉仪的探测态时,在何种情况下能够提高待测相位的测量精度.根据量子Fisher信息理论,尽管在探测态具有相同的平均光子数这一约束条件下,对称的和非对称 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.