摘要: 使用低耗散激波捕捉格式对高超声速流动问题进行数值模拟时经常会遭受不同形式的激波不稳定性. 本文基于二维无黏可压缩Euler方程, 对低耗散HLLEM格式进行激波稳定性分析. 结果表明: 激波面横向通量中切向速度的扰动增长诱发了格式的不稳定性. 通过增加耗散来治愈HLLEM格式的激波不稳定性. 为了避免引入过多的耗散进而影响剪切层的分辨率, 定义激波探测函数和亚声速区探测函数, 使得只有在计算激波层亚声速区的横向数值通量时才增加耗散, 其余地方的数值通量依然采用低耗散的HLLEM格式来计算. 稳定性分析和数值模拟的结果表明, 改进的HLLEM格式不仅保留了原格式高分辨率的优点, 还大大提高了格式的鲁棒性, 在计算强激波问题时能够有效地抑制不稳定现象的发生.
关键词: 高超声速 /
低耗散格式 /
切向耗散 /
激波不稳定性 English Abstract A modified HLLEM scheme and shock stability analysis Hu Li-Jun 1 ,Yuan Hai-Zhuan 2 ,Du Yu-Long 3 1.School of Mathematics and Statistics, Hengyang Normal University, Hengyang 421002, China Received Date: 06 December 2019Accepted Date: 12 April 2020Available Online: 09 May 2020Published Online: 05 July 2020Abstract: Reliable numerical simulations for hypersonic flows require an accurate, robust and efficient numerical scheme. The low-dissipation shock-capturing methods often suffer various forms of shock wave instabilities when used to simulate hypersonic flow problems numerically. For the two-dimensional(2D) inviscid compressible Euler equations, the stability analysis of the low-dissipation HLLEM scheme is conducted. The odd and even perturbations are added to the initial state in the streamwise direction and the transverse direction respectively, and the evolution equations of perturbations are deduced to explore the mechanism of instability inherent in the HLLEM scheme. The results of stability analysis show that the perturbations of density and shear velocity in the flux transverse to the shock wave front are undamped. Due to the symmetry, the 2D Sedov blast wave problem is computed to prove the multidimensionality of the shock instability. In the one-dimensional case which is free from the instability, the undamped property of density perturbation is also existent but no shear velocity is found. The conclusion can be drawn as follows: the shock instability of HLLEM scheme is triggered by the perturbation growth of shear velocity in the flux transverse to the shock wave front. Based on the conclusion of stability analysis, the instability of HLLEM scheme is cured by adding the shear viscosity to the transverse flux. In order to avoid affecting the resolution of the shear layer due to the introduction of too high shear viscosity, two functions to detect the shock wave and the subsonic regimes are defined, so that the shear viscosity is only added to the transverse flux in the subsonic regime of the shock layer, while the rest of numerical fluxes are still computed by the original HLLEM scheme. The results of stability analysis and some challenging numerical test problems show that the modified HLLEM scheme not only retains the merits of the original HLLEM, such as, resolving contact discontinuity and shear wave accurately, but also has greatly improved its robustness, inhibiting the unstable phenomena from occurring effectively when computing the strong shock wave problems.Keywords: hypersonic flow /low dissipation scheme /tangential dissipation /shock instability 全文HTML --> --> --> 1.引 言 尽管流体力学数值方法的研究在最近几十年取得了巨大的进步, 然而依然存在一些挑战性的问题, 涉及激波、剪切层、激波/湍流边界层干扰等现象的高超声速流动问题的数值模拟就是其中之一[1 ,2 ] . 构造精确、高效、鲁棒性好的激波捕捉格式是精确模拟高速流动问题的关键. 近似黎曼解法器是一类流行的激波捕捉方法. 一个好的黎曼解法器不仅要能够精确地分辨各种间断, 还要具有很好的鲁棒性, 能够抑制激波不稳定现象的发生. 然而, 能够精确分辨接触间断和剪切波的低耗散黎曼解法器(例如Roe, HLLC和HLLEM)在计算强激波问题时都会产生严重的不稳定现象, 从而影响数值模拟的可靠性. 因此, 分析低耗散数值格式激波不稳定性产生的根源并且在保留高分辨率优点的同时去治愈格式的激波不稳定性成为了计算流体力学数值方法研究的一个重要问题.[3 ] 指出压力和密度场的相互作用诱发了某些格式的不稳定性, 并且在强激波附近使用耗散的HLLE格式来消除Roe格式在数值模拟中的不稳定现象. Gressier和Moschetta[4 ] 利用特殊的扰动分析得出结论: 能够精确捕捉接触间断的数值格式通常都会遭受激波不稳定性的困扰. Dumbser等[5 ] 设计了一种矩阵稳定性分析方法来分析格式激波不稳定性产生的根源并且发现在计算二维稳态激波时数值格式的不稳定性与数值激波的结构密切相关. 谢文佳等[6 ] 使用奇偶失联线性方法对某些迎风格式进行稳定性分析, 结果表明: 具有充足剪切黏性的数值格式可以避免一类激波不稳定现象(“红玉”现象)的发生, 通过分析, Shen等[7 ] 也得到了同样的结论. 通过增加数值耗散来治愈格式的不稳定性已经成为了一种主流方法. 一般来说, 有以下三种方式来增加数值耗散: 将耗散格式和低耗散格式进行混合, 增加数值格式的人工黏性, 控制数值格式的耗散机制. Kim等[8 ] 构造了一种HLLC-HLLE混合格式, 通过定义开关函数将强激波附近数值通量的计算由不稳定的HLLC格式切换成稳定的HLLE格式. Wu等[9 ] 和Shen等[10 ] 构造了一种Roe-HLLE混合格式来消除Roe格式的不稳定性. 与全面混合不同的是, 他们仅仅在质量方程和切向动量方程将这两种格式进行混合. Ren[11 ] 提出了一种旋转Roe黎曼解法器, 通过自动地引入人工黏性来抑制原始Roe格式不稳定现象的发生. Rodionov[12 ] 用人工黏性系数代替分子黏性系数来治愈Godunov-型数值格式的“红玉”现象并且在文献[13 ,14 ]中分别讨论了高阶Godunov-型格式和三维情形下的激波不稳定性. Chen等[15 ] 发现Roe格式和HLLE格式在亚声速区剪切速度的差异可以解释这两种数值格式不同的激波行为, 并且在激波附近亚声速区增加Roe格式的剪切黏性来抑制不稳定现象的发生. Simon和Mandal[16 ,17 ] 使用反扩散控制和选波修正两种不同的策略来控制HLLC格式的耗散机制进而抑制格式的不稳定性, 并且使用同样的策略来构造激波稳定的HLLEM格式. Xie等[18 ] 利用相邻网格的压力比定义开关函数来控制HLLEM格式的耗散水平, 进而治愈其不稳定性. 与增加数值耗散来抑制激波不稳定性的流行方法不同的是, Fleischmann等[19 ] 通过修改Roe格式特征值的计算进而得到一种耗散更小、鲁棒性更好的Roe-M格式.2.控制方程组和HLLEM黎曼解法器 22.1.二维欧拉方程组 2.1.二维欧拉方程组 考虑二维理想气体流动的守恒律方程组${{U}}$ , 矢通量${{F}}({{U}})$ 和${{G}}({{U}})$ 的定义分别为:$\rho $ 为密度, $u$ 和$v$ 分别为全局坐标系中$x$ 方向和$y$ 方向的流体速度, $p$ 为静压力, $E$ 为总能. 使用理想气体状态方程来使守恒律系统封闭:$\gamma = 1.4$ . 求解方程组(1 )的守恒型数值方法可以表示成$\Delta t$ 为时间步长, $\Delta x$ 和$\Delta y$ 为空间步长, ${{{F}}_{i + {1 / 2}, j}}$ 和${{{G}}_{i, j + {1 / 2}}}$ 为$x$ 方向和$y$ 方向的数值通量.2.2.HLLEM黎曼解法器 -->2.2.HLLEM黎曼解法器 Einfeldt等[20 ] 在HLLE通量的基础上添加与线性退化场相对应的反扩散项, 从而得到了一种可以精确分辨接触间断和剪切波的HLLEM格式, 其通量表达式为${S_{\rm{L}}}$ 和${S_{\rm{R}}}$ 表示左、右波速, ${{{R}}_{2, 3}}$ 表示通量雅克比矩阵与线性退化场相对应的右特征向量, ${\alpha _{2, 3}}$ 为对应的波强, ${\delta _{2, 3}}$ 表示控制耗散大小的系数, 他们的计算公式分别为:$\tilde q$ 表示物理量$q$ 的Roe平均量, $\Delta q = {q_{\rm{R}}} - {q_{\rm{L}}}$ .3.HLLEM格式激波不稳定性的机理分析 23.1.线性稳定性分析 3.1.线性稳定性分析 流体介质以速度${u_0} = {M_0}{a_0}$ 沿着$x$ 正方向(纵向)运动, 沿$y$ 方向(横向)的速度${v_0} = 0$ , 其中${M_0}$ 为马赫数, ${a_0} = \sqrt {{{\gamma {p_0}} / {{\rho _0}}}} $ 为当地声速. 为了弄清楚是哪个方向的扰动增长造成了HLLEM格式的不稳定性, 考虑在初始分布上增加两类特殊的扰动.$x$ 方向上增加奇偶对称扰动, 扰动后的流场状态为:$\hat \rho $ , $\hat u$ , $\hat v$ , $\hat p$ 为各物理量的扰动量. 由于在$y$ 方向没有扰动, 因此数值通量${{{G}}_{i, j - {1 / 2}}} = {{{G}}_{i, j + {1 / 2}}} = {\rm{0}}$ . 使用HLLEM格式计算数值通量${{{F}}_{i - {1 / 2}, j}}$ 和${{{F}}_{i + {1/ 2}, j}}$ , 经过矩阵计算得到此种扰动下各个扰动量的发展方程.${M_0} > 1$ )的情况下, 扰动发展方程为:${\sigma _x} = {{\Delta t} / {\Delta x}}$ . (11 )式的特征值为:${\sigma _x} < {1/ {({u_0} + {a_0})}}$ 时, $|\lambda _i^{\sup }| < 1\;(i = 1, 2, 3, 4)$ , 此时所有扰动量都能有效衰减. 选取两组不同的初始扰动量和初值:图1 所示, 其中${\sigma _x}$ 取0.2.图 1 超声速情形下扰动量的发展曲线 (a)初始扰动量和初值(I); (b)初始扰动量和初值(II)Figure1. Evolutionary curves of perturbation under supersonic condition: (a) Initial perturbation values and initial conditions (I); (b) initial perturbation values and initial conditions (II).图1 可以看到, 当$x$ 方向存在扰动时, 在超声速情形下, 所有扰动量都会衰减到0, 此时数值格式是稳定的.$0 < {M_0} < 1$ )的情况下, 扰动发展方程为:14 )式的特征值为:${\sigma _x} < {1 / {({a_0} + {u_0})}}$ 时, $|\lambda _i^{{\rm{sub}}}| < 1\;(i = 1, 2, 3, 4)$ , 此时所有扰动量均能有效衰减. 同样选取两组不同的初始扰动量和初值:图2 所示, 其中${\sigma _x}$ 取0.4.图 2 亚声速情形下扰动量的发展曲线 (a)初始扰动量和初值(III); (b)初始扰动量和初值(IV)Figure2. Evolutionary curves of perturbation under subsonic condition: (a) Initial perturbation values and initial conditions (III); (b) initial perturbation values and initial conditions (IV).图2 可以看到, 当$x$ 方向存在扰动时, 在亚声速情形下, 所有扰动量也会衰减到0. 因此当流体沿着$x$ 方向运动时, 该方向的扰动不会诱发HLLEM格式的不稳定性.$y$ 方向增加奇偶对称扰动, $x$ 方向上流场无扰动. 此时的流场状态为$x$ 方向没有扰动, 因此数值通量${{{F}}_{i - {1 / 2}, j}} = {{{F}}_{i + {1 / 2}, j}} = {\rm{0}}$ . 使用HLLEM格式计算数值通量${{{G}}_{i, j - {1 / 2}}}$ 和${{{G}}_{i, j + {1 / 2}}}$ , 进而得到扰动量的发展方程为:18 )式的特征值为:${\sigma _y} = {{\Delta t} / {\Delta y}}$ . 当${\sigma _y} < {1 / {{a_0}}}$ 时, $\hat v$ 和$\hat p$ 是衰减的, 而密度扰动$\hat \rho $ 和切向速度扰动$\hat u$ 不会衰减. 设初值${\rho _0} = 1.4$ , ${u_0} = 1$ , ${p_0} = 1$ , 选取以下四组不同的初始扰动量来观察在该扰动下各个物理量的扰动发展趋势图3 为横向扰动下扰动量的发展曲线, 可以看到, $\hat v$ 和$\hat p$ 总是衰减的, 密度或者压力的扰动都会导致$\hat \rho $ 不会衰减, 切向速度自身的扰动$\hat u$ 也不会衰减. 我们推测: 激波面横向通量中的密度扰动$\hat \rho $ 和切向速度扰动$\hat u$ 不衰减的特性诱发了HLLEM格式的激波不稳定性.图 3 横向扰动下扰动量的发展曲线 (a)初始扰动量(V); (b)初始扰动量(VI); (c)初始扰动量(VII); (d)初始扰动量(VIII)Figure3. Evolutionary curves of perturbation in transverse direction: (a) Initial perturbation values (V); (b) initial perturbation values (VI); (c) initial perturbation values (VII); (d) initial perturbation values (VIII).3.2.激波不稳定性的多维特性 -->3.2.激波不稳定性的多维特性 关于激波不稳定性是一种一维激波的异常现象还是一种多维现象仍然是有争议的. Chauvat等[21 ] 和Kitamura等[22 ] 发现激波不稳定性与内部激波结构有关并且主张它是一种一维激波的异常现象. 然而, 纯粹的一维算例不会遭受激波不稳定现象的困扰, 并且3.1 节的线性稳定性分析的结论表明: $y$ 方向的扰动会造成$x$ 方向的激波不稳定性, 反之亦然. 因此, 本文认为它是一种多维现象.19 ]中的二维Sedov爆轰波问题来证明激波不稳定性的多维特性. 初始时, 区域$[0, \;2.4] \times [0, \;2.4]$ 中心的压力${p_{{\rm{in}}}} = 3.5 \times {10^5}$ , 其余地方的压力${p_{{\rm{out}}}} = {10^{ - 10}}$ , 整个区域的密度为1, 速度${u_0}$ 和${v_0}$ 均为0. 计算中使用$480 \times 480$ 的笛卡尔网格, 上、下、左、右都使用反射边界条件. 图4 为计算得到的二维Sedov爆轰波问题的密度等值线, 可以看到, 采用HLLEM格式进行计算时, 在激波面和坐标轴平行的位置出现了明显的“红玉”现象. 当$x$ 方向的通量采用耗散的HLLE格式计算时, $y$ 方向的“红玉”现象消失了, 反之亦然. 该数值实验的结果与线性稳定性分析的结论相一致, 从而进一步证明了激波不稳定现象的多维特性.图 4 二维Sedov爆轰波问题的密度等值线 (a) HLLEM; (b) x -HLLE+y -HLLEM (c) x -HLLEM+y -HLLEFigure4. Density contours for 2D Sedov blast wave problem: (a) HLLEM; (b) x -HLLE+y -HLLEM (c) x -HLLEM+y -HLLE.4.一种改进的HLLEM格式 激波面横向扰动的发展方程(18 )式表明: 密度和切向速度的扰动不会衰减. 由于激波不稳定性是一种多维现象, 并且一维问题存在熵波但是没有剪切波. 因此我们认为: 激波面横向通量中切向速度的扰动增长造成了HLLEM格式的激波不稳定性. 通过增加横向通量的耗散来抑制不稳定现象的发生, 其具体表达式为22 )式表明横向通量中的切向速度的扰动也会衰减.4.1.激波探测函数 4.1.激波探测函数 在实际的数值模拟中, 只需要在激波附近增加耗散就可以抑制不稳定现象的发生, 为了避免在不适当的位置增加耗散进而影响剪切层的分辨率, 利用网格界面的压力比来探测激波的位置:$h \in (0, \;1)$ , 且在激波附近压力差较大, 从而$h \to 0$ . 由前面的分析可知: 在$x$ 方向增加耗散可以抑制$y$ 方向的不稳定性, 反之亦然. 因此, 计算$x$ 方向的数值通量${{{F}}_{i + {1 / 2}, j}}$ 时, 只需检测与之相邻的$y$ 方向的网格界面. 计算$y$ 方向的数值通量${{{G}}_{i, j + {1 / 2}}}$ 时, 只需检测与之相邻的$x$ 方向的网格界面. 即15 ]中的余弦函数来定义激波探测函数:图5 画出了这三种激波探测函数的曲线图. 从中可以看到三个函数的取值都会随着激波强度的减弱而减小, 且对于固定的$h$ , 满足${g_1} > g > {g_2}$ .图 5 三种激波探测函数的函数曲线Figure5. Curves for three different shock-detecting functions.4.2.M-HLLEM格式 -->4.2.M-HLLEM格式 Xu和Li[23 ] 在分析定常激波问题时发现激波不稳定性是由激波层亚声速区的扰动增长导致的, 这一结论得到了众多研究人员的支持[6 ,15 ,19 ] . 因此定义亚声速区探测函数$M$ 表示马赫数. 在亚声速区$0 < \varphi < 1$ , 在超声速区$\varphi = 0$ .${{n}} = ({n_x}, \;{n_y})$ 为网格界面单位外法向量, $g$ 和$\varphi $ 分别为激波探测函数和亚声速区探测函数. 因此, 一种改进的HLLEM格式(M-HLLEM, Modified HLLEM)数值通量的表达式为5.数值结果和分析 本节计算一些典型的算例来检验本文构造的M-HLLEM格式的鲁棒性和精度.5.1.随机数值噪声问题 5.1.随机数值噪声问题 马赫数为6的平面激波沿着$x$ 方向运动, 初始时激波位于$x = 5$ , 右侧波前的初始条件为$({\rho _0}, {u_0}, {v_0}, {p_0}) = (1.4, \;0, \;0, \;1)$ , 左侧的波后状态可以通过激波和马赫数之间的关系式来得到. 计算区域$[0, \;1{\rm{0}}00] \times [0, \;20]$ 被划分成$1000 \times 20$ 的笛卡尔网格. 这是一个纯粹的一维激波, 为了诱发不稳定性, 在波前的初始分布上增加取值从$ - 0.5 \times {10^{ - 5}}$ 到$0.5 \times {10^{ - 5}}$ 的随机数值扰动${\alpha _k}(k = 1, \;2, \;3, \;4)$ 为$ - 0.5$ 到$0.5$ 之间的随机数.$y$ 方向速度的最大量值$\max (|v|)$ 可以用来衡量不稳定性的严重程度. 图6 展示了$t = 120$ 时, 原始的HLLEM格式以及与不同的激波探测函数结合的改进格式的密度等值线图. 图7 展示了$y$ 方向速度的最大量值随着时间变化的曲线图. 可以看到, HLLEM格式的激波结构完全被破坏, 且$y$ 方向速度的最大量值也从${10^{ - 5}}$ 量级增长到${10^0}$ 量级. 而三种改进格式都得到了清晰的激波面, 且$y$ 方向速度的最大量值也始终保持在初始时的${10^{ - 5}}$ 量级附近. 三种激波探测函数的数值结果之间几乎没有差异, 因此后面的数值算例均选用流行的余弦函数(25 )式来计算其函数值.图 6 随机数值噪声问题的密度等值线 (a) HLLEM; (b) M-HLLEM-g ; (c) M-HLLEM-g 1 ; (d) M-HLLEM-g 2 Figure6. Density contours of random numerical noise problem: (a) HLLEM; (b) M-HLLEM-g ; (c) M-HLLEM-g 1 ; (d) M-HLLEM-g 2 .图 7 随机数值噪声问题$y$ 方向速度的最大量值Figure7. Maximum magnitude of velocity in y -direction of random numerical noise problem.5.2.高超声速绕柱流问题 -->5.2.高超声速绕柱流问题 高超声速绕柱流问题经常用来检验数值格式是否会遭受一种严重的不稳定现象—“红玉”现象(carbuncle). 马赫数为20的自由来流流经半径为1的圆柱体, 整个区域流场的初始条件$({\rho _0}, {u_0}, {v_0}, {p_0}) = (1.4, \;20, \;0, \;1)$ , 具体的计算区域、网格划分和边界条件可以参考文献[24 ]. 本文采用$320 \times 40$ 的结构化贴体四边形网格来计算. 图8 画出了时间$t = 4$ 时, 使用HLLEM和M-HLLEM格式计算得到的密度等值线. 可以清晰地看到, HLLEM格式出现了严重的“红玉”现象, 而M-HLLEM格式消除了不稳定现象, 得到了具有清晰激波面的稳态弓形激波.图 8 高超声速绕柱流问题的密度等值线 (a) HLLEM; (b) M-HLLEMFigure8. Density contours of hypersonic flow over a cylinder: (a) HLLEM; (b) M-HLLEM.5.3.双马赫反射问题 -->5.3.双马赫反射问题 Woodward和Colella[25 ] 提出的双马赫反射问题是检验数值格式鲁棒性的一个著名算例. 马赫数为10的斜激波向底部壁面运动, 激波面与壁面所成角度为60°, 计算区域$[0, \;4] \times [0, \;1]$ 被划分成$480 \times 120$ 的笛卡尔网格. 详细的初始条件、边界条件可参考文献[25 ]. 图9 画出了时间$t = 0.2$ 时, HLLEM和M-HLLEM格式的计算结果. 可以看到, HLLEM格式出现了弯曲的马赫杆和一个三角点, 这是一种明显的非物理现象. 而M-HLLEM格式消除了不稳定现象, 得到了清晰的马赫杆.图 9 双马赫反射问题的密度等值线 (a) HLLEM; (b) M-HLLEMFigure9. Density contours of double Mach reflection problem: (a) HLLEM; (b) M-HLLEM.5.4.二维Sedov爆轰波问题 -->5.4.二维Sedov爆轰波问题 计算3.2 节描述的二维Sedov爆轰波问题, 由于该算例涉及高压力比的强激波问题, 因此可以用来作为检验数值格式性能的一个挑战性测试. 图10 画出了时间$t = 0.1$ 时, HLLEM和M-HLLEM格式的压力等值线. 可以清晰地看到, HLLEM格式在激波面和网格线平行的位置出现了四个明显的“红玉”现象. 而M-HLLEM格式有效地抑制了不稳定现象的发生.图 10 二维Sedov爆轰波问题的压力等值线 (a) HLLEM; (b) M-HLLEMFigure10. Pressure contours of 2D Sedov blast wave problem: (a) HLLEM; (b) M-HLLEM.5.5.二维无黏接触间断问题 -->5.5.二维无黏接触间断问题 数值格式可以用来计算黏性流的前提条件是能够精确捕捉接触间断. 该算例用来检验改进的HLLEM格式捕捉接触间断的能力. 区域$[0, \;1] \times [0, \;1]$ 被均匀划分成$10 \times 10$ 的正方形网格, 上、下两部分不同速度的两种流体的初始条件为:图11 展示了计算迭代1000步后, $x = 0.5$ 处的密度分布. 可以看到, HLLE格式得到了具有较大耗散的解, 而HLLEM和M-HLLEM格式都能准确捕捉该接触间断. 这说明M-HLLEM格式保留了原HLLEM格式精确分辨接触间断的优点.图 11 二维无黏接触间断问题的密度分布Figure11. Density distribution of 2D inviscid contact discontinuity problem.6.结 论 本文构造了一种激波稳定的HLLEM格式. 线性稳定性分析和相关的数值实验表明: 横向通量中切向速度的扰动增长诱发了HLLEM格式的激波不稳定性. 通过增加耗散来治愈格式的不稳定性, 为了防止过多的耗散影响剪切层的分辨率, 定义激波探测函数和亚声速区探测函数, 使得耗散项仅仅添加在激波层亚声速区域的横向通量上, 其余的数值通量依然采用低耗散的HLLEM格式来计算, 从而在不牺牲精度的前提下, 提高格式的鲁棒性. 数值模拟的结果表明: 改进的HLLEM格式消除了激波不稳定现象并且保留了原始HLLEM格式精确分辨接触间断的优点, 因此该格式可以广泛应用于高超声速可压缩流的数值模拟中. 采用类似的方法来改进其他的低耗散格式, 结合高阶精度重构方法并且将其推广到三维情形来计算不同的守恒律系统可以作为未来的研究工作. 













































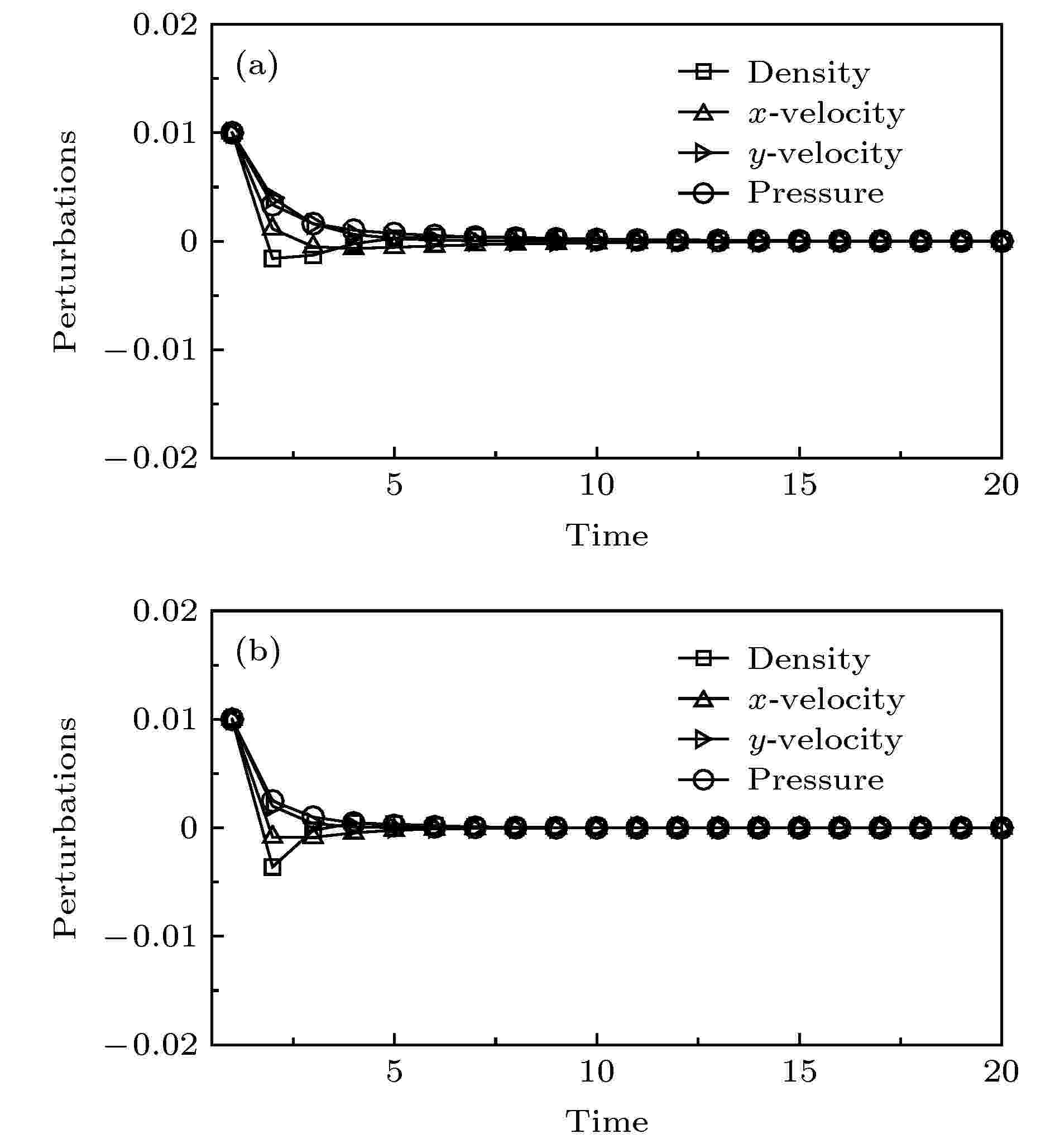 图 1 超声速情形下扰动量的发展曲线 (a)初始扰动量和初值(I); (b)初始扰动量和初值(II)
图 1 超声速情形下扰动量的发展曲线 (a)初始扰动量和初值(I); (b)初始扰动量和初值(II)




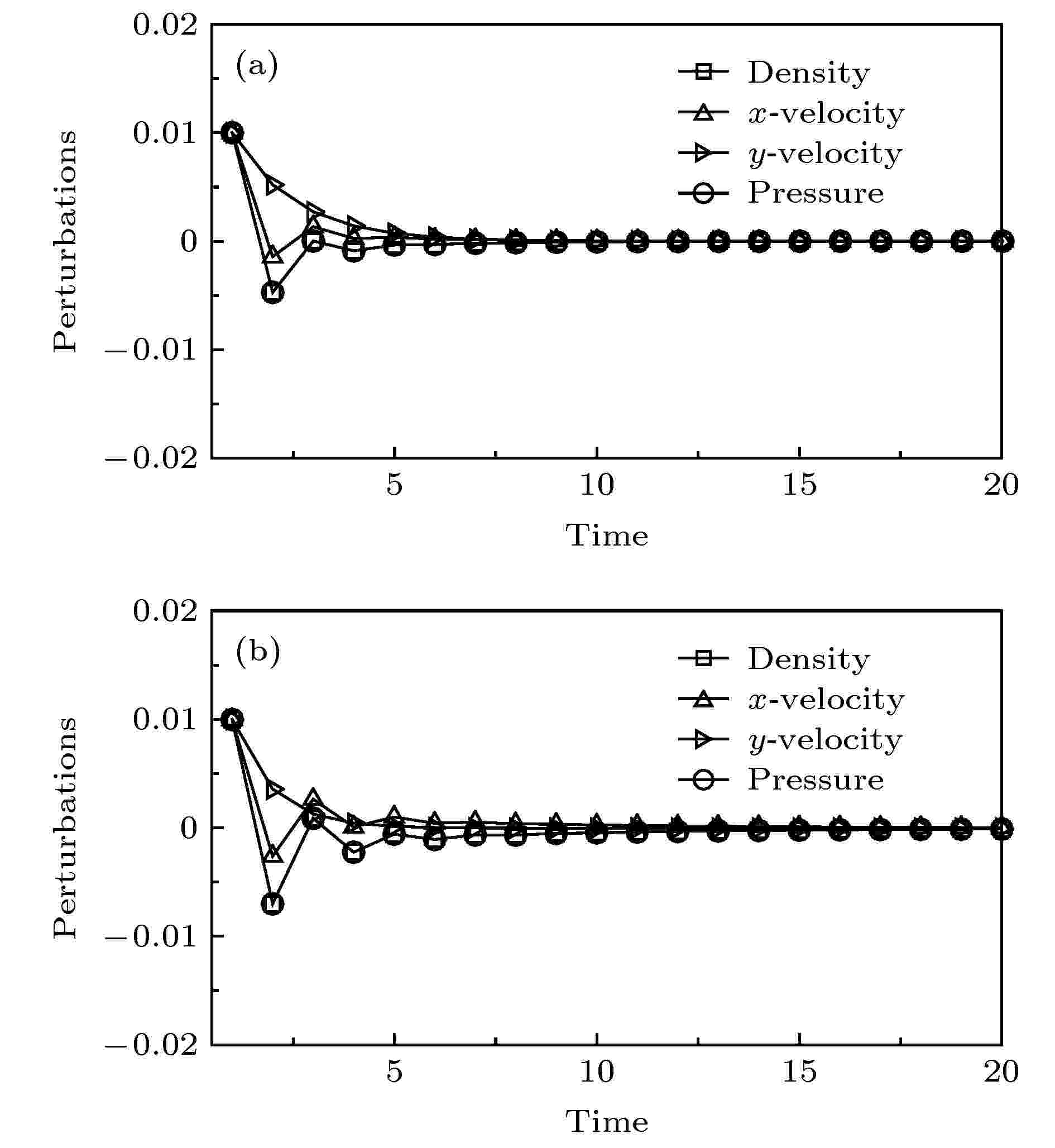 图 2 亚声速情形下扰动量的发展曲线 (a)初始扰动量和初值(III); (b)初始扰动量和初值(IV)
图 2 亚声速情形下扰动量的发展曲线 (a)初始扰动量和初值(III); (b)初始扰动量和初值(IV)




























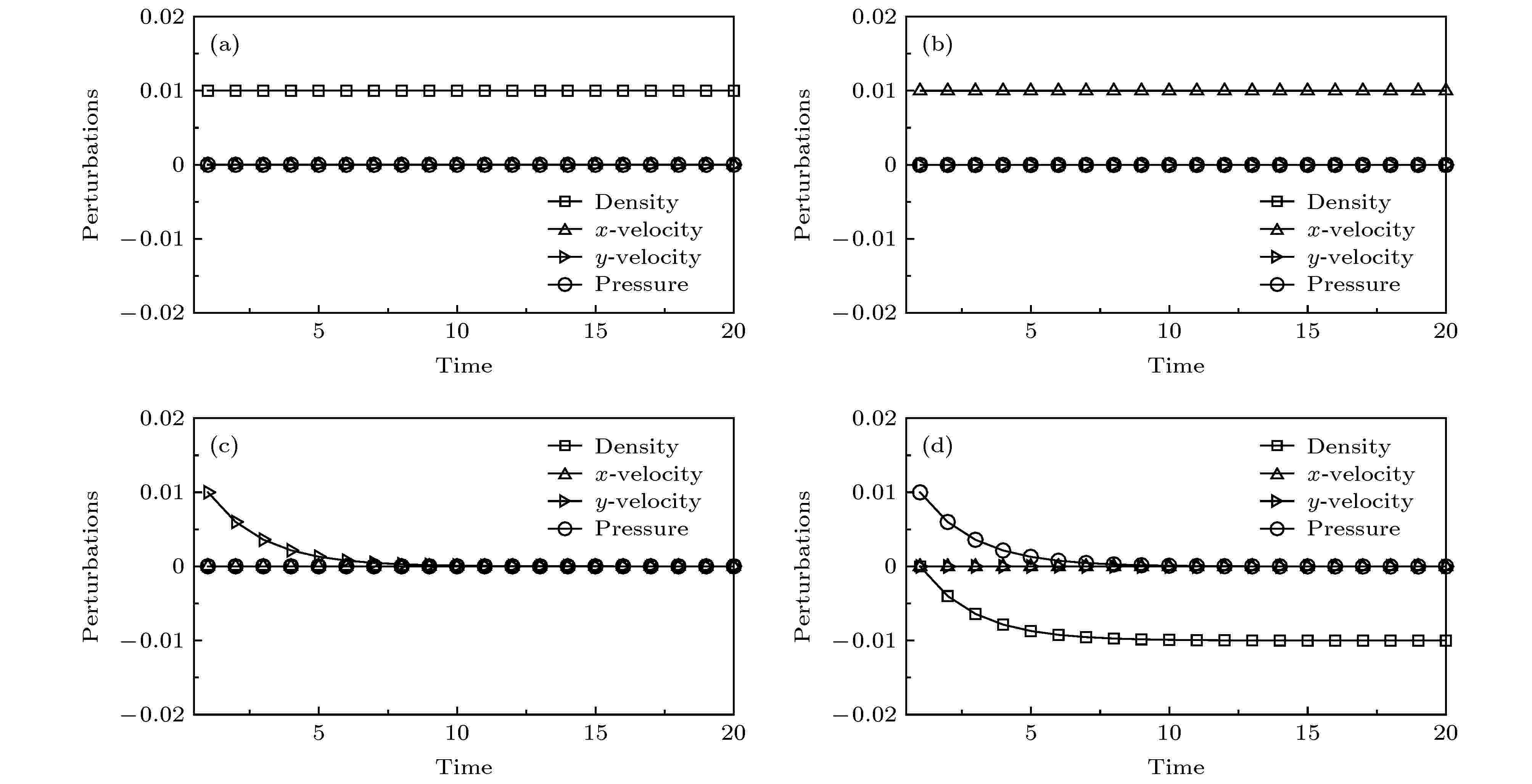 图 3 横向扰动下扰动量的发展曲线 (a)初始扰动量(V); (b)初始扰动量(VI); (c)初始扰动量(VII); (d)初始扰动量(VIII)
图 3 横向扰动下扰动量的发展曲线 (a)初始扰动量(V); (b)初始扰动量(VI); (c)初始扰动量(VII); (d)初始扰动量(VIII)









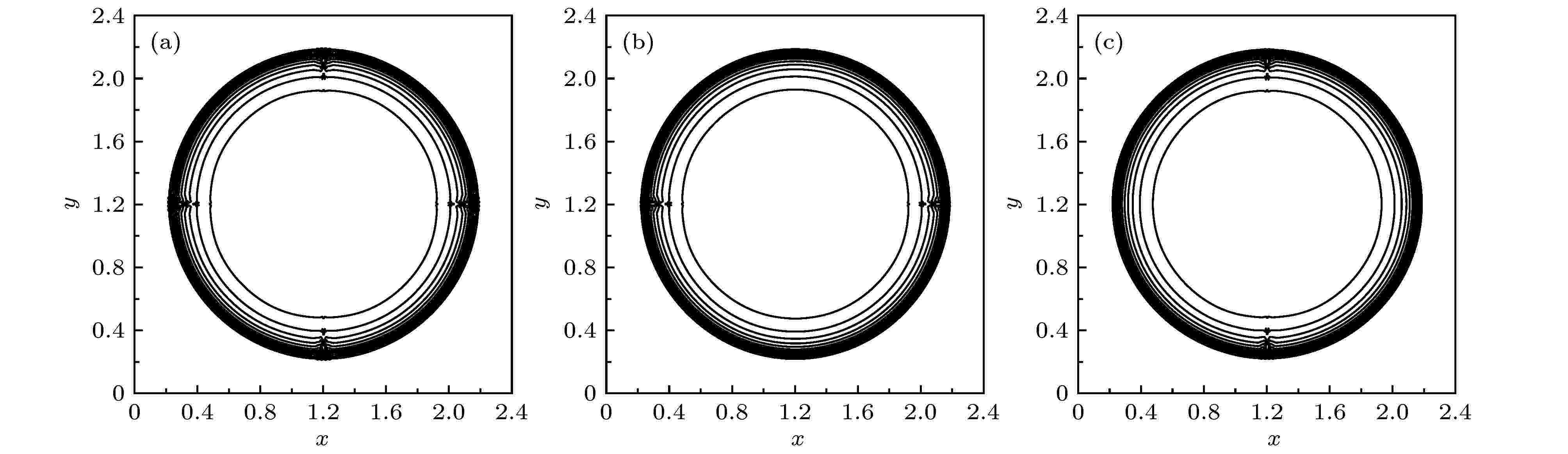 图 4 二维Sedov爆轰波问题的密度等值线 (a) HLLEM; (b) x-HLLE+y-HLLEM (c) x-HLLEM+y-HLLE
图 4 二维Sedov爆轰波问题的密度等值线 (a) HLLEM; (b) x-HLLE+y-HLLEM (c) x-HLLEM+y-HLLE























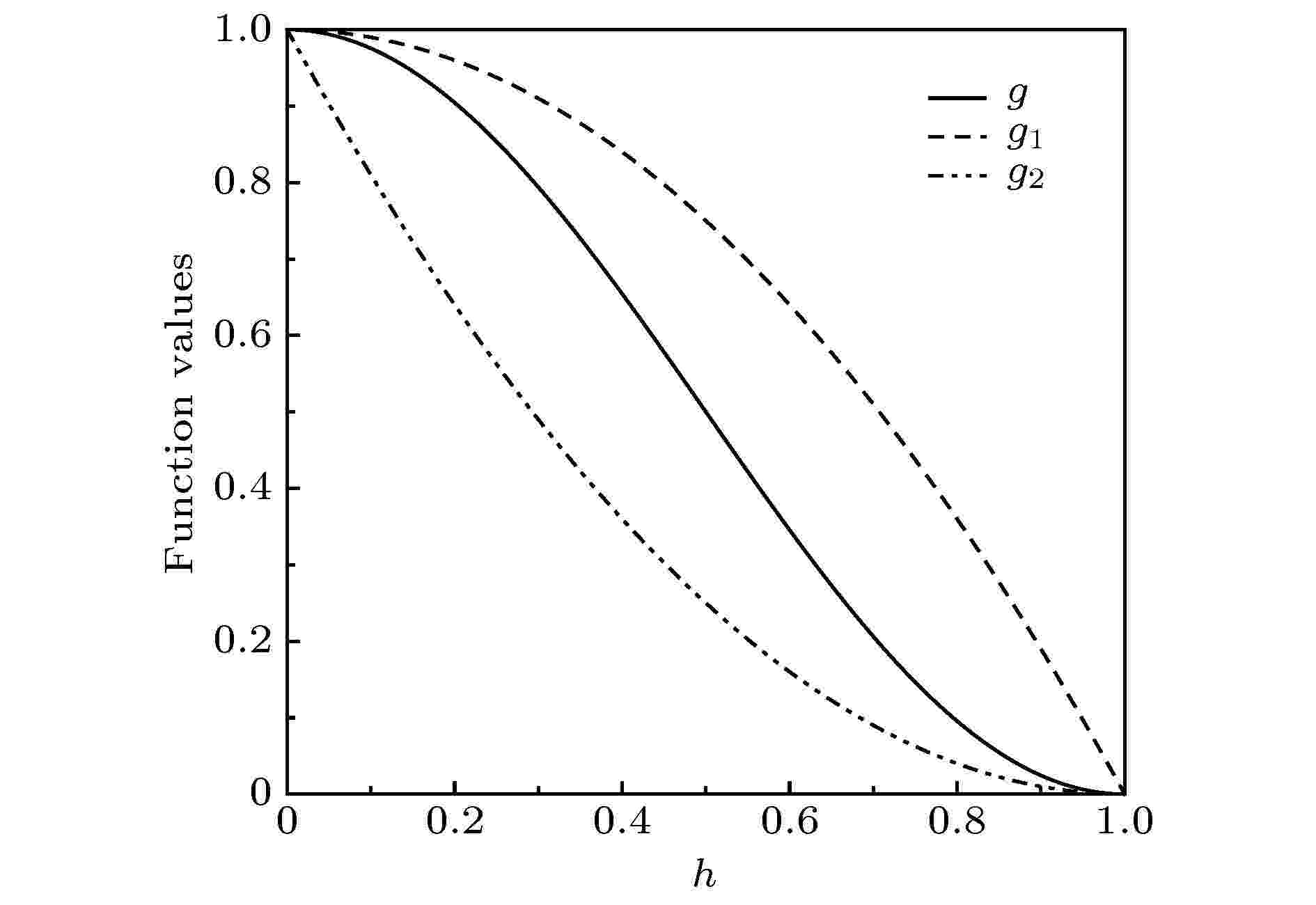 图 5 三种激波探测函数的函数曲线
图 5 三种激波探测函数的函数曲线






































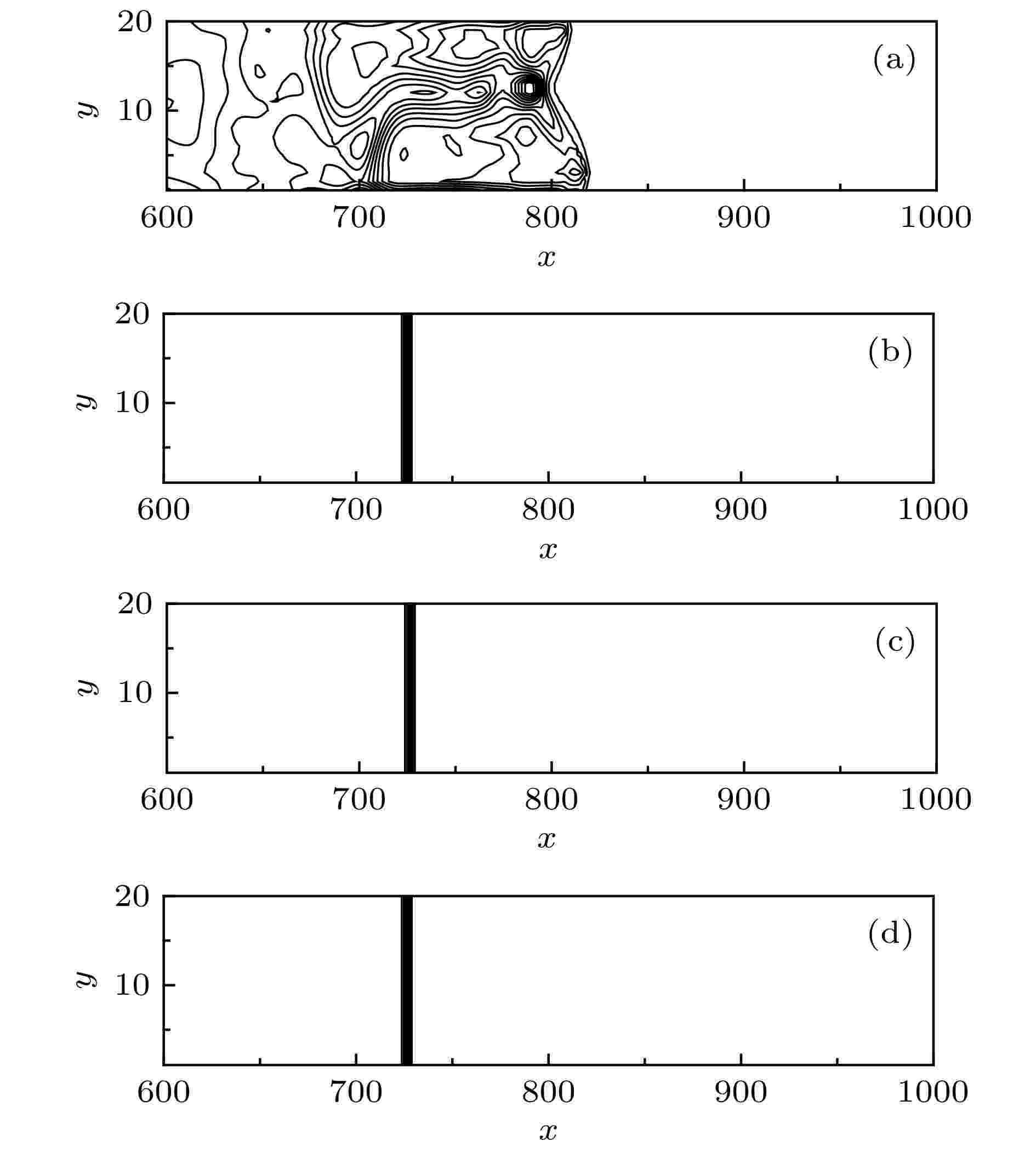 图 6 随机数值噪声问题的密度等值线 (a) HLLEM; (b) M-HLLEM-g; (c) M-HLLEM-g1; (d) M-HLLEM-g2
图 6 随机数值噪声问题的密度等值线 (a) HLLEM; (b) M-HLLEM-g; (c) M-HLLEM-g1; (d) M-HLLEM-g2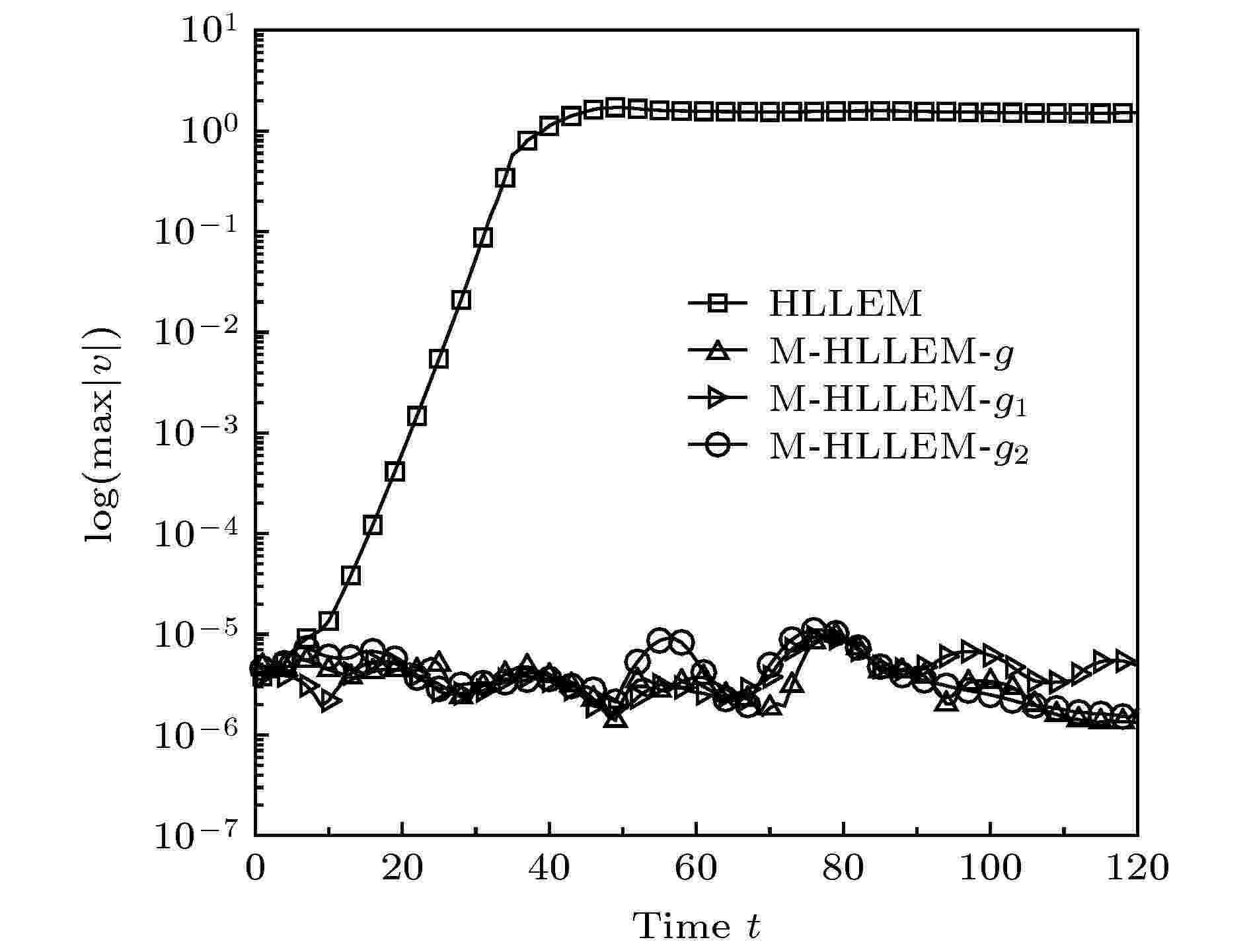 图 7 随机数值噪声问题
图 7 随机数值噪声问题



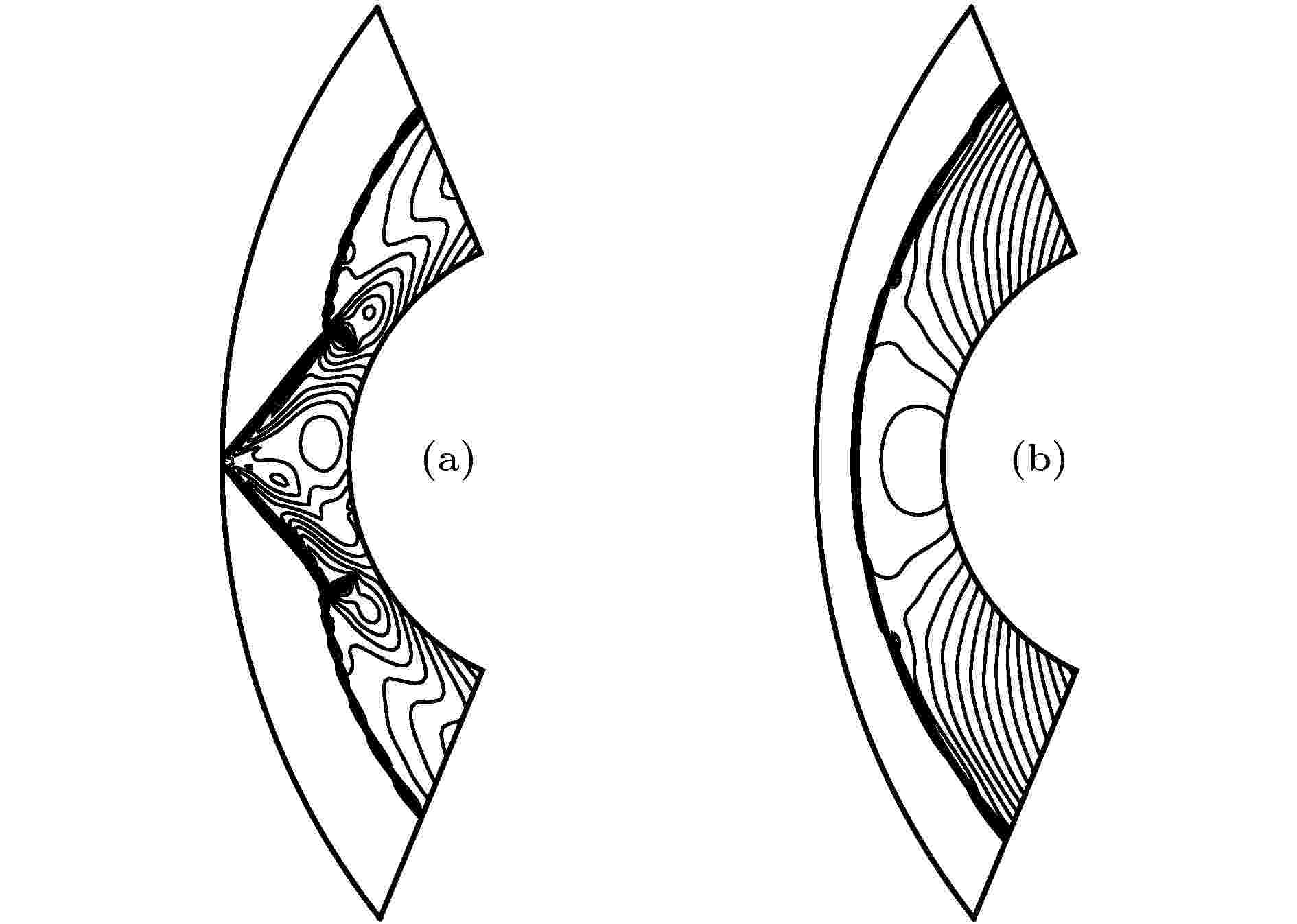 图 8 高超声速绕柱流问题的密度等值线 (a) HLLEM; (b) M-HLLEM
图 8 高超声速绕柱流问题的密度等值线 (a) HLLEM; (b) M-HLLEM


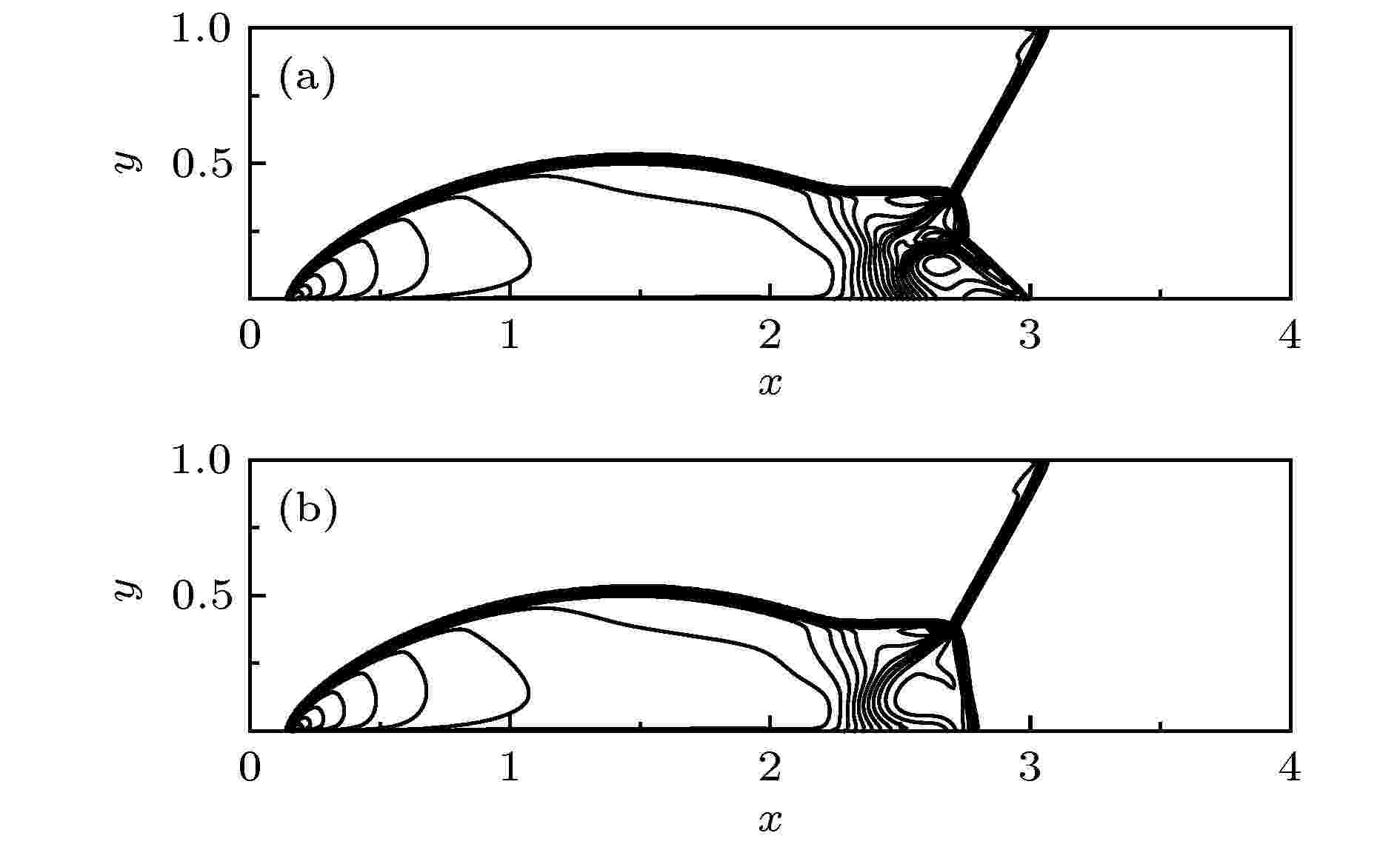 图 9 双马赫反射问题的密度等值线 (a) HLLEM; (b) M-HLLEM
图 9 双马赫反射问题的密度等值线 (a) HLLEM; (b) M-HLLEM
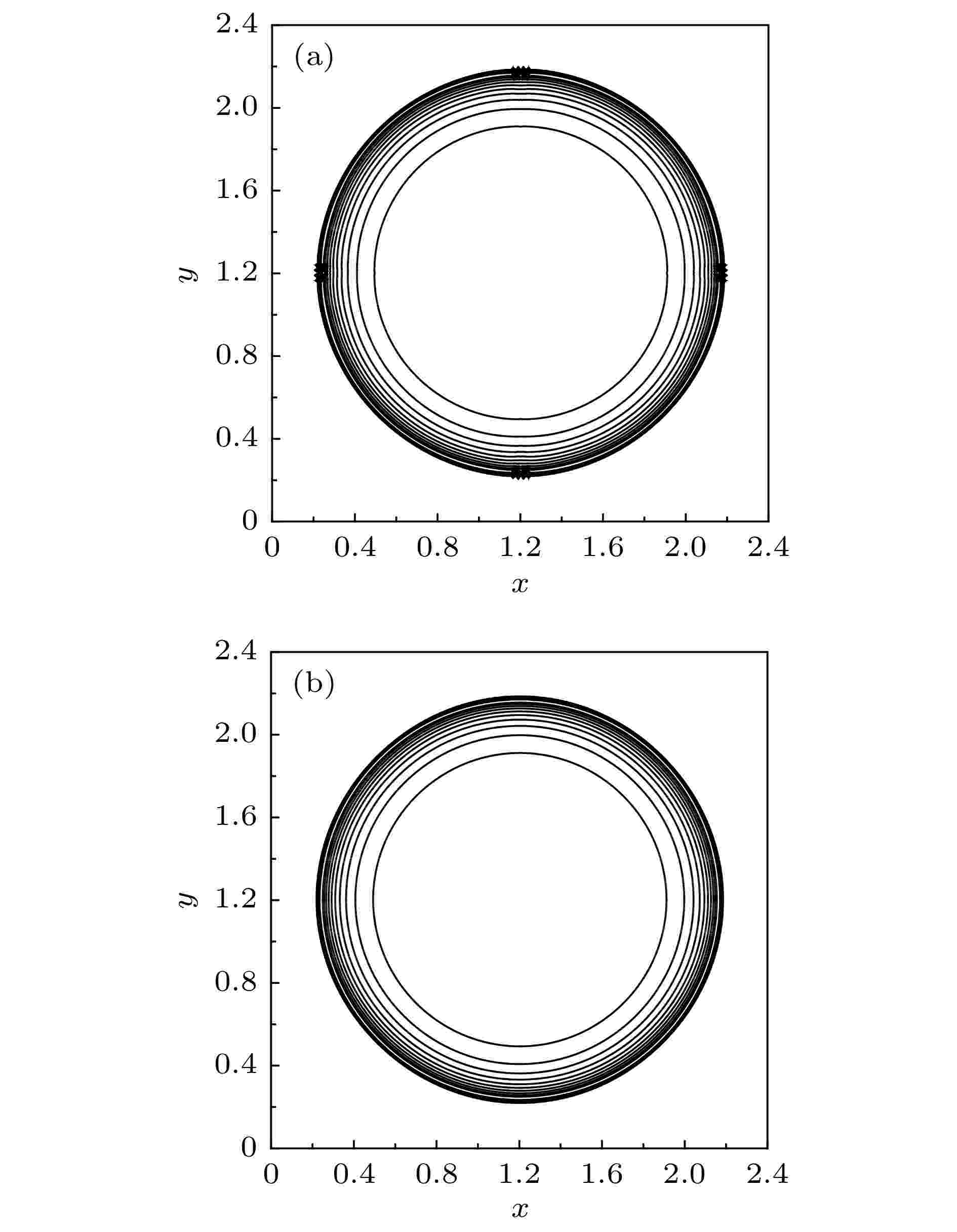 图 10 二维Sedov爆轰波问题的压力等值线 (a) HLLEM; (b) M-HLLEM
图 10 二维Sedov爆轰波问题的压力等值线 (a) HLLEM; (b) M-HLLEM


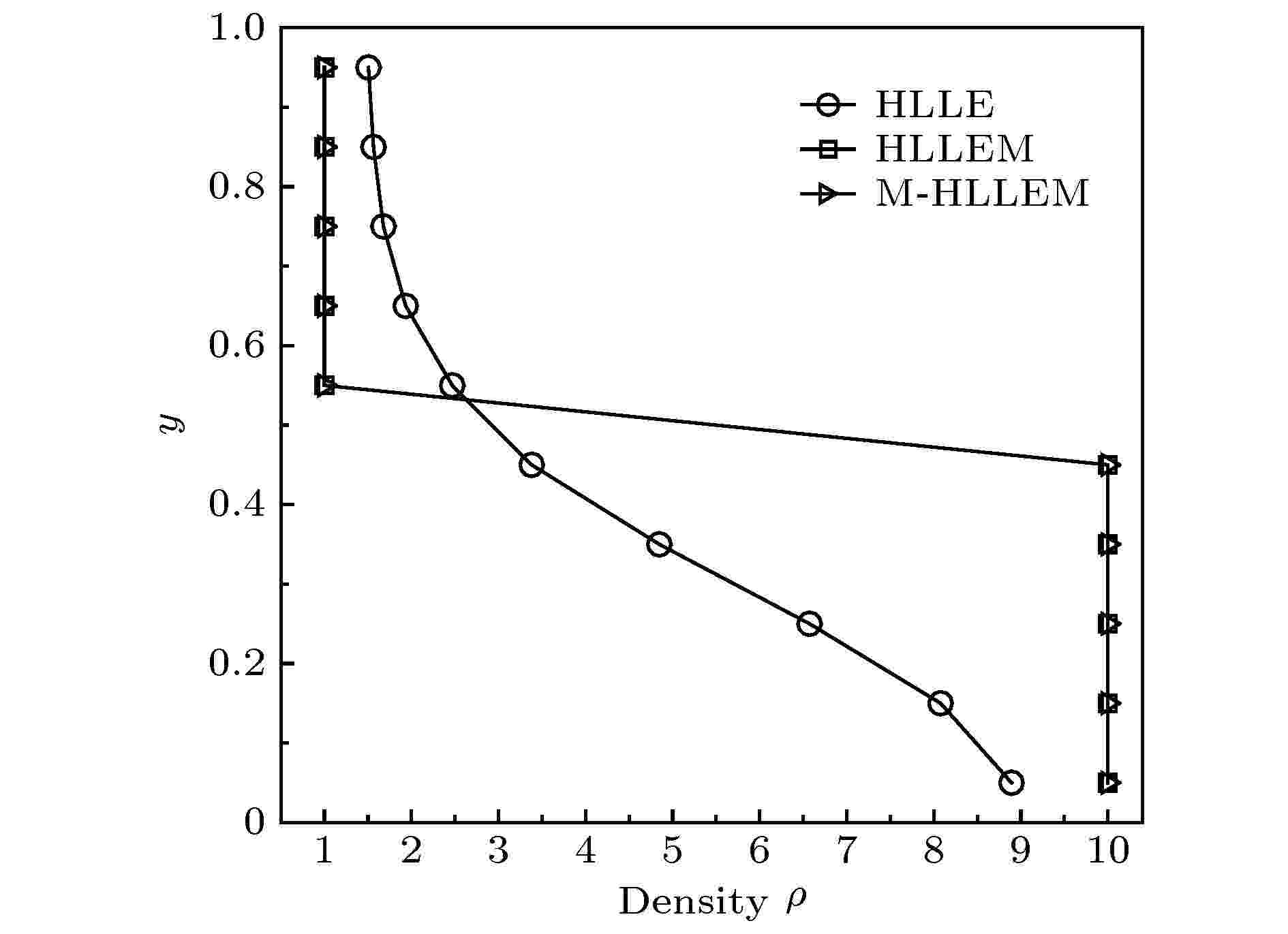 图 11 二维无黏接触间断问题的密度分布
图 11 二维无黏接触间断问题的密度分布