删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

拓扑超导Majorana束缚态的探索

本站小编 Free考研考试/2021-12-29
摘要:Majorana束缚态具有非阿贝尔量子统计特性, 是极具潜力的拓扑量子计算方案的核心. 近期有多项实验研究提供了Majorana束缚态在某些超导体系中的存在证据, 使其成为近期凝聚态物理以及量子计算领域的前沿焦点之一. 本文介绍拓扑超导的机理、Majorana束缚态的新奇物理特性、实验观测和操作的方法以及相关量子器件的设计, 最后展望该研究方向的发展前景.
关键词: Majorana束缚态/
拓扑超导/
非阿贝尔统计/
量子计算

English Abstract


全文HTML

--> --> -->
1.引　言
2016年诺贝尔物理学奖授予Thouless, Haldane和Kosterlitz, 以表彰他们关于拓扑相变和物质拓扑相的开创性理论研究. 关于物质拓扑相重要性的认识起源于von Klitzing在20世纪80年代发现的量子霍尔效应[1]. 如图1(a)所示, 在垂直强磁场下半导体界面二维电子系统出现具有线性色散关系的手征边缘状态, 其承载电流不会引起能量耗散. Thouless-Kohmoto-Nightingale-den Nijs(TKNN)理论阐明, 手征边缘态的数量正好由拓扑陈数给出[2]. Haldane[3]指出当时间反演对称性被系统的磁性所破坏时, 即使没有外部磁场也可能出现相同的手征边缘态, 这被称为量子反常霍尔效应. 2005年, 人们发现了在时间反演对称情况下由于自旋轨道耦合而产生的另一类拓扑态, 即量子自旋霍尔效应. 其特征在于螺旋边缘状态, 相反自旋的电子分别朝相反方向运动[4,5], 由Z2拓扑数描述. 经典的能带理论根据费米能处有无能隙将材料划分为金属和绝缘体, 而能带拓扑的研究指出绝缘体里面还有能带拓扑平庸和非平庸之分. 拓扑绝缘体的边缘态由于受到体能带拓扑性质的保护, 对材料缺陷或外界扰动呈现鲁棒性, 更有利于最先进的量子器件的开发. 因此, 10多年来拓扑效应引起了科学家的极大关注, 拓扑物理学和相关的材料科学也因此迎来了快速的发展.
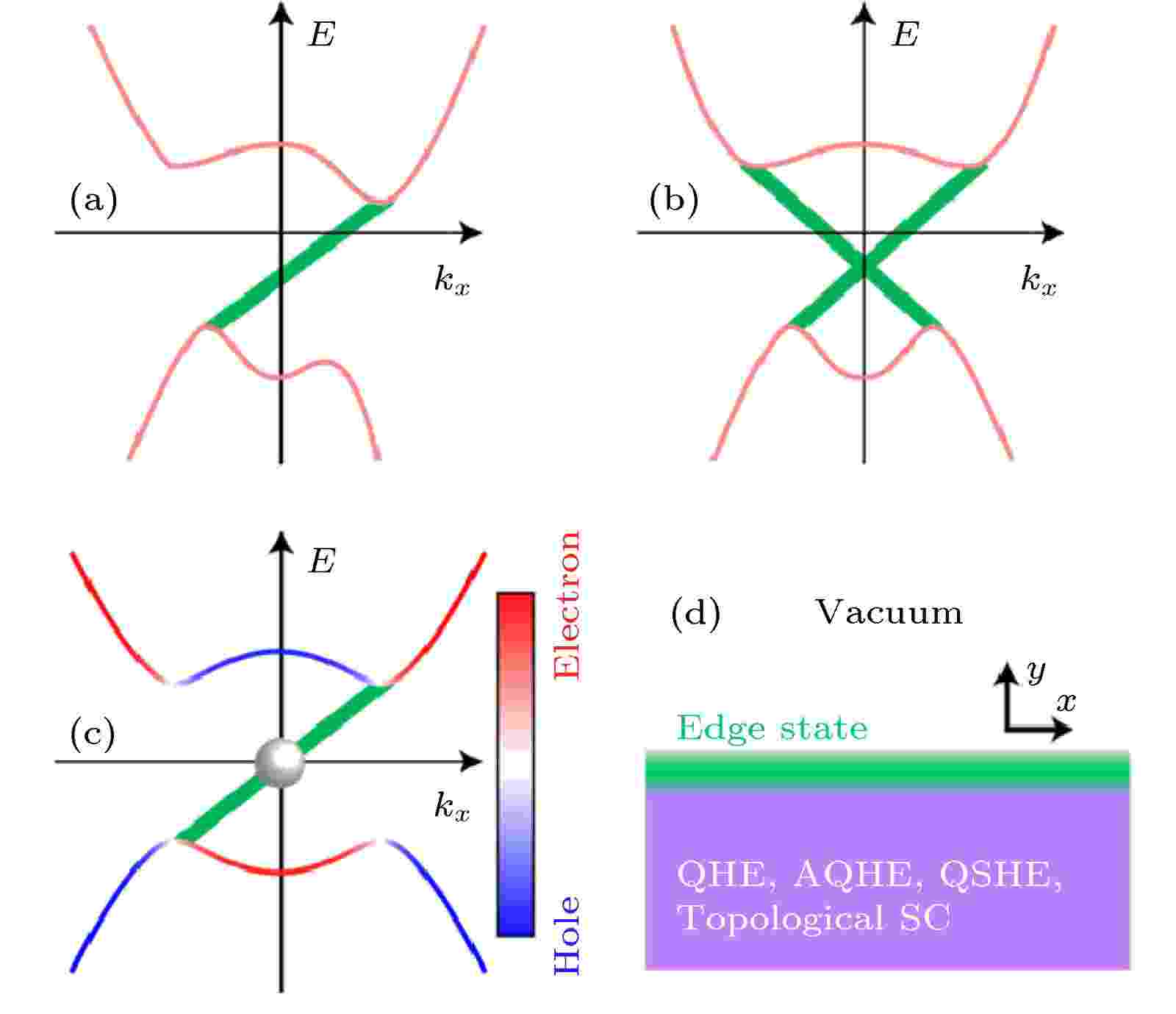图 1 (a) 量子霍尔效应及量子反常霍尔效应; (b)量子自旋霍尔效应; (c) 拓扑超导的体能带结构(红线和蓝线)和边缘态(绿色)的色散关系; (d)实空间边缘态的示意图
Figure1. Schematic energy band structures for (a) quantum Hall effect and quantum anomalous Hall effect, (b) quantum spin Hall effect, (c) a topological superconductor and (d) sche-matic diagram of topological edge/surface states in real space.

和绝缘体一样, 具有能隙的超导态也可以划分为具有非平庸拓扑特征的超导态和平庸的超导态. 因为超导具有粒子空穴对称, 拓扑超导的最显著的特征是其零能的准粒子激发[5-10]. 这些被称为零能Majorana束缚态的准粒子, 有利于稳定的拓扑量子计算的实现. 本文介绍拓扑超导的机理、Majorana束缚态的新奇物理特性、实验观测和操作的方法、量子器件的设计，并展望该研究方向的发展前景.
2.拓扑超导态
本节先从无自旋p波超导态出发, 分析其产生拓扑特性的机理. 无自旋p波超导既是拓扑超导态的最简单的例子, 作为一个模型它又可以很好地描述混合材料系统的拓扑超导性. 一般来说, 超导态的平均场哈密顿量可以由Bogoliubov-de Gennes (BdG)形式给出:
${ H_{{\rm{BdG}}}}\left( {{k}} \right) = \left[ {\begin{array}{*{20}{c}}{{{\hat h}_{{k}}}}&{{{\hat \varDelta }_{{k}}}}\\{\hat \varDelta _{{k}}^{\dagger } }&{ - \hat h_{ - {{k}}}^{\rm{T}}}\end{array}} \right],$
这里使用粒子和空穴做基底, $ {\widehat{h}}_{{k}} $是正常态的哈密顿量, ${\widehat{\varDelta}}_{{k}}$是超导序参量. 为简单起见我们考虑一个没有内部自由度的系统, 对应于自旋向上和或向下仅一个态发生超导的情况. $ {\widehat{h}}_{{k}} $和${\widehat{\varDelta}}_{{k}}$各自为简单的复数. 显然使用泡利矩阵 $ {{\sigma }}_{i}\left(i=x, y, z\right) $ 可以将BdG哈密??顿量(1)式改写成
${ H_{{\rm{BdG}}}}\left( {{k}} \right) = {{g}}\left( {{k}} \right) \cdot {{\sigma }},$
因此哈密顿量的性质归结于三维矢量$ {{g}}\left({{k}}\right) $的特性. 例如, 其绝对值$ \left|{{g}}\left({{k}}\right)\right| $给出一定动量下的超导能隙. 作为一个具体的例子我们考虑沿x轴的一维p波超导体. 因为系统没有自旋等内部自由度, 根据费米统计的要求, 超导序参量对于动量反转必须显示奇宇称, 因此我们有$ {\widehat{\varDelta}}_{{k}}={\rm{i}}\Delta{k}_{x} $. 在这里我们略去了动量的高阶贡献. 关于电子的动能, 我们假设最简单的形式$ {\widehat{h}}_{{k}}={k}_{x}^{2}/(2 m)-\mu $.
显然有$ {g}_{x}=0 $, $ {g}_{y}={\Delta }{k}_{x} $和$ {g}_{z}={k}_{x}^{2}/(2 m)-$μ. 如图2所示, 当$ \mu >0 $时矢量$ {{g}}\left({k}_{x}\right) $在动量空间中显示一种类似于Moebius环的扭曲结构. 这种扭曲结构产生非零的Berry位相, 明确显示一维p波超导态呈现拓扑特性[11,12]. 当化学势减小到$ \mu =0 $时, 在$ {k}_{x}=0 $处$ {{g}}=0 $, 能隙关闭. $ \mu <0 $时能隙再次打开, 但这种情形下扭曲结构已经不复存在, 对应于平庸的超导态. 从这个例子可以看出, 由拓扑态到非拓扑状态的转变必定伴随一次能隙关闭.
图 2 拓扑超导约化能隙$ {{g}}\left({{k}}\right)/\left|{{g}}\left({{k}}\right)\right| $的动量空间分布
Figure2. Distribution of normalized topological superconduc-tivity gap $ {{g}}\left({{k}}\right)/\left|{{g}}\left({{k}}\right)\right| $ in momentum space.

3.Majorana束缚态
作为超导的一般性质, 任何准粒子激发都可以描述为电子和空穴的叠加, 而电子型激发(图1(c)红色) 的产生与带有相反能量和动量的空穴型激发(图1(c)蓝色)的湮灭完全等价. 因此, 图1(c)中所示准粒子激发的色散关系相对于原点是对称的, 单一手征边缘态的色散关系(绿色)必定通过原点. 一维拓扑超导体的两端或者二维拓扑超导体量子涡漩所伴随的零能准粒子激发与其他准粒子激发之间保持有限的能隙, 具有非常独特的量子特性.
利用电子的产生算子$ { c}^{{\dagger }} $和湮灭算子c可以写出两个准粒子激发, ${ \gamma }_{1}={ c}+{ c}^{{\dagger }}$和${ \gamma }_{2}=({ c}-{ c}^{{\dagger }})/{\rm i}$. 显而易见这两个准粒子都满足自共轭关系[7]
${ \gamma }_{j}={ \gamma }_{j}^{{\dagger }}.$
因为这两个准粒子由粒子和空穴以完全相等的权重叠加, 其零能量为零. 1937年意大利理论物理学家Majorana[13]提出一种新奇费米型基本粒子, 其粒子与其反粒子等价. 中微子可能是Majorana粒子, 但至今尚未定论. 因为(3)式表明粒子等价于其反粒子, 人们把拓扑超导态的零能准粒子激发称为Majorana准粒子. 由于它们位于一维超导体的两端或者二维超导体量子涡漩的中心, 也被称为Majorana束缚态. 因为零能Majorana准粒子满足(3)式, 其遵循的对易关系是$ \left\{{\gamma }_{i}, {\gamma }_{j}\right\}={2\delta }_{ij} $, 与普通费米子的交换关系$ \left\{{c}_{i}, {c}_{j}\right\}=0 $不同. 换句话说, 由电子以及电子对(库珀对)形成的超导态里涌现出与费米子和玻色子满足不同量子统计的新奇准粒子激发[14]. 这种特性使得Majorana束缚态可用于拓扑量子计算.
两个Majorana束缚态可以表达一个电子态,
$ { c} = \left( {\gamma} _1 + {\rm{i}} {\gamma} _2\right)/2. $
容易验证, 这样得到的电子态服从费米统计. 然而, 很明显这里的电子数只能反映奇数和偶数的区别. 这与在宏观超导体里电子的数量不确定的特性密切相关. 两个Majorana束缚态存在于一维拓扑超导体的两端, 或者二维拓扑超导体的两个不同的量子涡漩中心. 其在空间上是分离的, 而又形成对整个宏观超导体的电子特性的一个刻画, 因此两个Majorana束缚态之间具有非局域的量子关联. 换而言之, 具有Majorana束缚态的拓扑超导态呈现一种典型的量子纠缠. 而利用Majorana束缚态来描述超导体的电子奇数态和偶数态构成拓扑量子位.
在普通的s波超导体里, 两个反向自旋的电子形成一个库珀对. 在这种情况下, 由于电子和空穴的自旋彼此相反, 由此定义出来的准粒子$ {\gamma} ={ c}_{\downarrow }^{{\dagger }}+{ c}_{\uparrow }$满足不了自共轭关系(3)式. 因此, 普通的s波超导态不能产生Majorana束缚态.
4.Majorana束缚态和非阿贝尔统计
Majorana束缚态的自共轭性(3)式使得其可能遵循与普通费米粒子不同的量子统计[14]. 我们考察伴随二维超导体量子涡旋位置交换而产生的Majorana束缚态的相位变化. 如图3所示, 每个量子涡旋都带有伴随超导能隙相位2π不连续地变化的线段. 当准粒子跨越一根线段时, 其相位增加π (超导能隙相位一半). 在图3中, 鉴于第二和第三超导量子涡旋交换位置时只有第三超导量子涡旋跨越第二超导量子涡旋所带的线段, 所以仅有第三Majorana束缚态获得相位π. 所以有$({ \gamma }_{2}, { \gamma }_{3})$$\to ({ \gamma }_{3}, {- \gamma }_{2})$. 利用自共轭性(3)式, 可以将这个变换用幺正变换来表示:
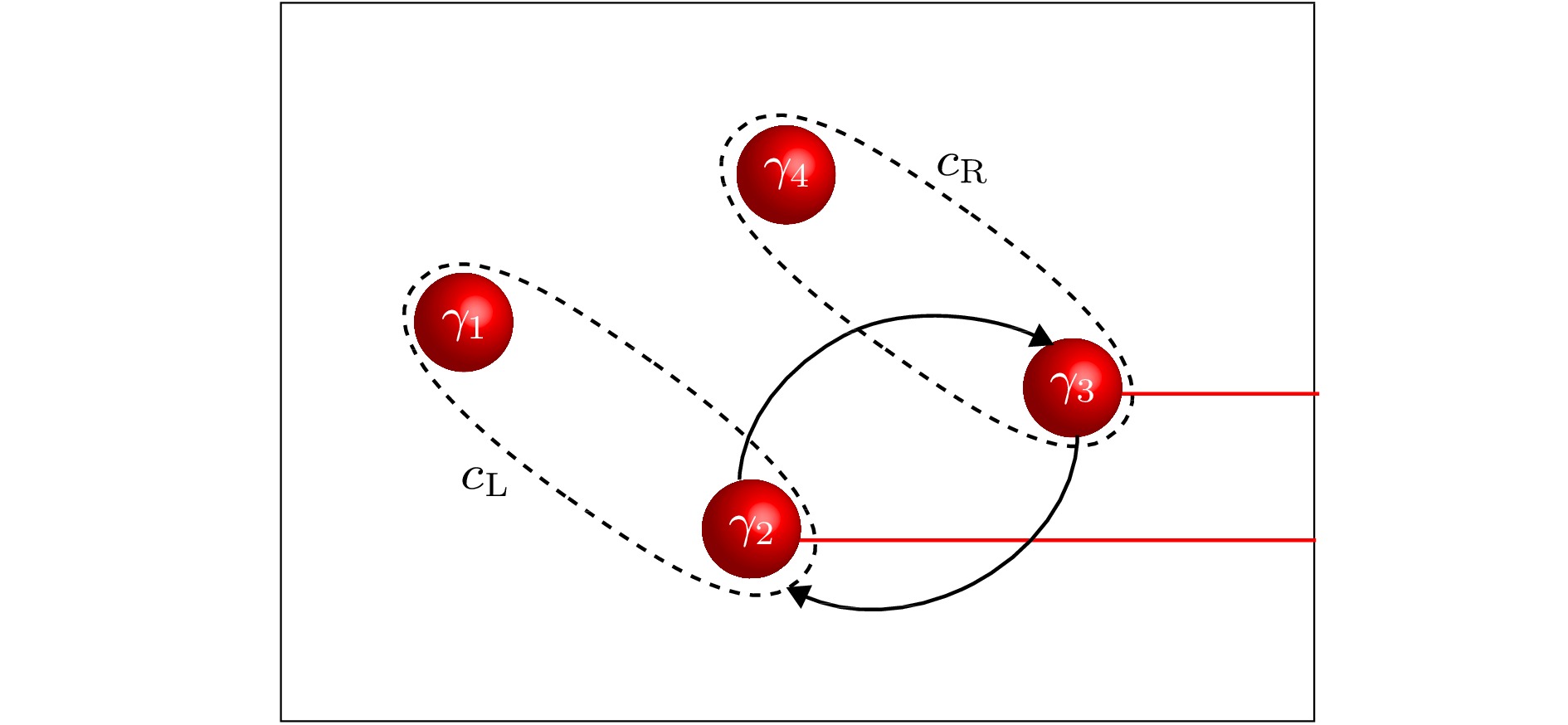图 3 利用拓扑超导量子涡旋里的Majorana束缚态实现非阿贝尔统计的示意图, 其中黑色箭号代表量子涡旋位置交换的轨迹, 当量子涡旋跨越红线时超导相位发生2π的不连续跳跃
Figure3. Schematics of realization of non-Abelian statistics using Majorana bound states in vortex cores of a topological superconductor. Black arrows denote the exchanging paths of two quantum vortices. Superconducting phase takes a 2π jump when a vortex crosses the red cuts.

$ \tau =\left(1 + { \gamma} _3{ \gamma} _2\right)/ \sqrt 2 , $
使得${ \gamma}_{j}\to \tau { \gamma}_{j}{\tau }^{-1}$. 强调一下, $ \tau $只改变${ \gamma}_{2}$的符号, 而${ \gamma}_{3}$的符号保持不变.
进一步可以考虑将(5)式用电子态湮灭算子(4)式以及对应的产生算子来表达. 如图3所示, 4个Majorana束缚态${ \gamma}_{1}, { \gamma}_{2}, { \gamma}_{3}, { \gamma}_{4}$构成两个电子态${ c}_{{\rm{L}}}=({ \gamma}_{1}+{{\rm{i}}{ \gamma} }_{2})/2$和${ c}_{{\rm{R}}}=({ \gamma}_{3}+{{\rm{i}}{ \gamma} }_{4})/2$. 在这种情况下, ${ \gamma}_{2}$和${ \gamma }_{3}$的交换(5)式可以写成
$ { \tau} ={{\left[ {1 + {\rm{i}}(c_{\rm{R}}^{\dagger } + {{ c}_{\rm{R}}})({ c}_{\rm{L}}^{\dagger } + {{ c}_{\rm{L}}})} \right]}}/{{\sqrt 2 }}. $
从表达式(6)中可以看到, Majorana束缚态的位置交换对应于电子数量改变的幺正变换. 例如, 将(6)式作用于${ c}_{{\rm{L}}}$和${ c}_{{\rm{R}}}$非占据态$ \left| 0, 0 \right\rangle $产生其本身与占据态$ \left| 1, 1 \right\rangle $的线性组合态[14]. 从量子统计角度来看, 这明显不同于玻色子和费米子的情形, 从而被称为非阿贝尔统计. 由于Majorana束缚态所描述的量子态受到拓扑保护, 许多量子系统常见的退相干问题受到抑制. 同时这些新奇的量子态满足非阿贝尔统计, 可以用于稳定的量子计算, 从而吸引了包括基础和应用各方面的广泛兴趣[7-10].
5.异质结系统中的拓扑超导
2000年的一项理论研究揭示一维无自旋p波超导态可以产生Majorana束缚态[7,15]. 近年来, 众多研究表明利用数种材料的组合形成的混合材料可以实现等效的无自旋p波超导, 例如拓扑绝缘体的表面态和s波超导的组合[16], 具有强自旋轨道耦合的半导体、铁磁交换相互作用以及s波超导的组合等[17-19]. 目前, 拓扑超导的实现以及Majorana束缚态的观测和操作的竞争在全世界范围如火如荼地展开[20-24]. 下面以我们的研究成果为中心介绍几个例子.
2
5.1.一 维量子线
-->

5.1.一 维量子线

对于二维拓扑超导体来说, 在体材料的边界处, 束缚态变成了连续的边界态. 如图1(c)所示, 这些边界态满足连续的色散关系, 因此难以实现受有限能隙保护的零能量Majorana束缚态. 另一方面, 一维的拓扑超导体, 其边界态是具有局域波函数的束缚态, 而体系具有有限能隙, 因此有利于产生具有拓扑保护的零能Majorana束缚态[15].
为了在实际体系中实现一维拓扑超导态, Lutchyn等[19]提出了一种如图4(a)所示的超导体-半导体混合系统. 在这个系统里, 半导体纳米线具有很强的自旋轨道耦合, 这样原本具有两重自旋简并的能带结构就在动量方向上发生劈裂(如图4(b)所示), 具有向外自旋的电子能带向左平移, 而具有向内自旋的电子能带则向右平移. 此时, 费米能附近主要有两类电子态: Γ点附近的线性Dirac电子, 以及两边kF费米动量附近的电子态. 如果在纳米线上施加足够大的外部磁场, 塞曼劈裂就会打破时间反演对称性带来的Kramers简并性, 使得Γ点附近的线性Dirac电子消失(图4(b)). 此时在该系统中, kF动量附近的电子具有动量-自旋锁定, 即相反动量的电子携带几乎相反的自旋. 这样, 由s波超导态带来的Cooper对可以通过近临效应在纳米线中引致超导. 同时, 由于纳米线是一维系统, 电子不会具有回旋运动, 这抑制了磁场对超导的破坏. 动量-自旋锁定的能带结构加上s波超导, 使得超导能隙仅在费米能附近的单个能带中打开, 这样就在纳米线中实现了等效的无自旋超导性. 由于泡利不相容, 无自旋超导体的超导能隙必定具有p波或者f波的空间对称性. 理论计算表明图3中的系统对应于p波超导体[17], 因此, 尽管此系统的超导Cooper对来源于正常的自旋单态s波超导体, 但通过近邻效应在自旋轨道耦合的半导体中的实现了等效的无自旋p波超导性 .
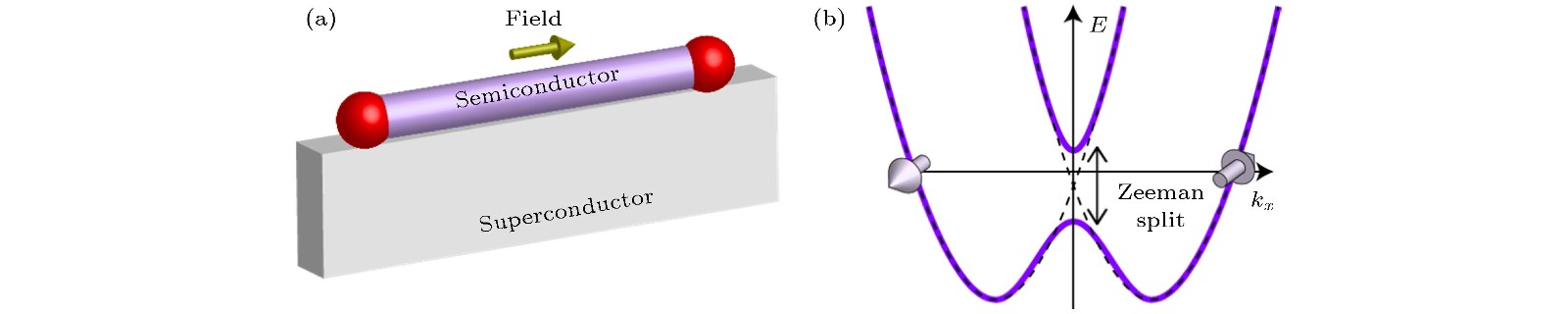图 4 (a)具有自旋轨道耦合的半导体纳米线和s波超导的混合系统的示意图; (b)半导体纳米线在有限磁场(实线)和零磁场(虚线)下的色散关系
Figure4. (a) Schematics of a heterostructure consisting of a spin-orbital coupling semiconductor nanowire and an s wave superconductor; (b) the band dispersion of the nanowire with finite magnetic field (solid lines) and zero magnetic field (dashed lines).

在最近的实验中, 哥本哈根大学的研究组实现了图4(a)所示的超导体-半导体杂化系统. 他们将超导的金属铝生长在半导体InAs纳米线的表面, 并施加合适的外部磁场, 然后进行库仑阻塞的实验测量[24]. 在传统的界观超导体中, Cooper对的两个电子必须同时隧穿, 带来分立的电导峰, 这是常见的库仑阻塞的信号. 然而在这个新的半导体-超导杂化系统中, 实验上发现了由单电子隧穿所带来的库仑阻塞的信号. 这意味着除了常规的超导基态(电子占有数的偶数状态)之外, 还存在一种电子占有数为奇数的基态. 由于超导体中电子都是以Cooper对的形式出现, 此实验就提供了一个有力的证据, 表明Majorana约束缚态状态存在于细线的两端并且带来了简并的超导基态.
2
5.2.由Majorana束缚态所带来的新奇量子隧道现象
-->

5.2.由Majorana束缚态所带来的新奇量子隧道现象

当一维拓扑超导体的末端存在如图4(a)所示的Majorana束缚态时, 在系统中会出现新的量子隧穿现象. 其中尤其有趣的一种是约瑟夫隧道效应. 我们考虑如图5(a)所示的拓扑约瑟夫森结, 两边都是一维拓扑超导体. 此时, 约瑟夫森结中的Majorana束缚态组成一个量子比特系统, 如图5(b)所示, 其有效哈密顿量为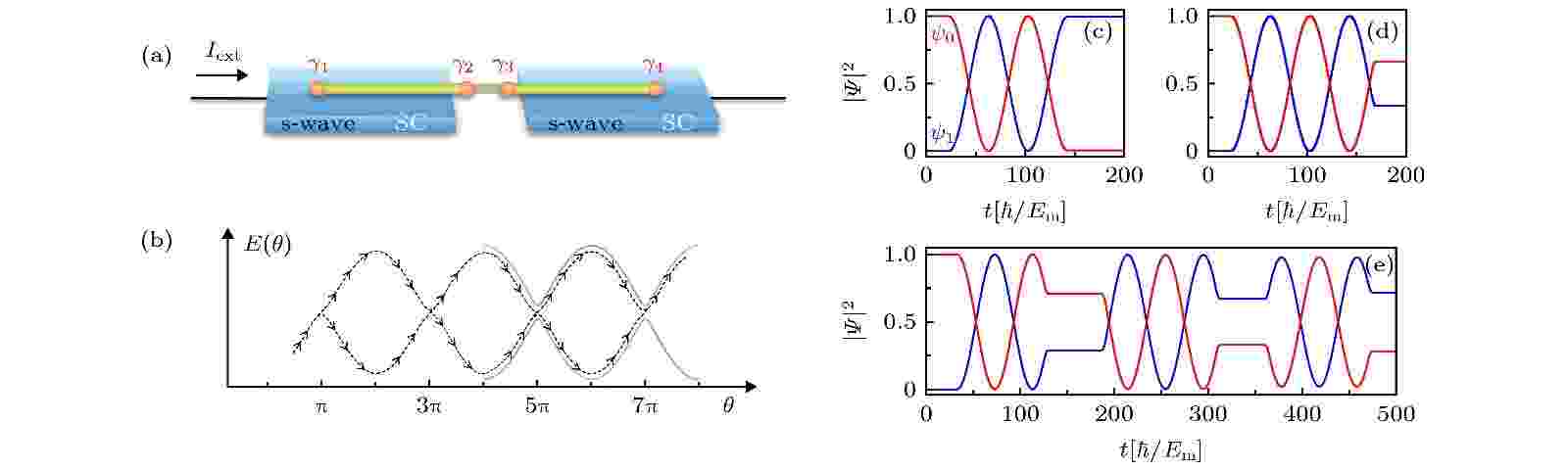
图 5 (a) 通过电压差控制Majorana量子比特的设计; (b) Majorana量子比特的两能级系统; (c)-(e) 量子比特在电流脉冲下的LZS震荡: (c)短脉冲, (d)长脉冲, (e)序列脉冲[25]
Figure5. (a) Schematic design of a universal quantum gate for Majorana qubit, where the qubit is manipulated by voltage across the Josephson-Majorana junction; (b) the two energy levels of the Majorana qubit depending on the phase difference across the junction; (c)-(e) the LZS oscillation of Majorana qubit under current pulse: (c) a short pulse, (d) a long pulse, (e) a sequence of pulses[25].

$H=-{{E}_{\rm{m}}}\cos \frac{\theta }{2}{{\tau }_{z}}+\delta {{\tau }_{x}},$
其中$ \theta $是超导体之间的相位差, $ {E}_{{\rm{m}}} $是约瑟夫森能, $ \delta $是隧道结中的Majorana束缚态与纳米线端点处Majorana束缚态的耦合能. 超导约瑟夫森电流来源于两部分的贡献. 首先是由Cooper对通过准粒子态隧穿所带来的贡献, 其次是单电子通过隧道结两侧的Majorana束缚态隧穿所带来的贡献. 前者是普通的直流约瑟夫森关系$ I={I}_{{\rm{c}}}{\rm{sin}}\theta $, 其中$ {I}_{{\rm{c}}} $为临界电流, 而后者则是$ {\rm{s}}{\rm{i}}{\rm{n}}\left(\theta /2\right) $的函数形式, 因此被称为分数约瑟夫森效应. 当约瑟夫森结两边存在电压V时, 此时超导相位差会按照交流约瑟夫森效应随时间变化 $ \dot{\theta }=2 eV/\hslash $, e为元电荷, $ \hslash $为约化普朗克常数. 超导相位差的运动会通过Landau-Zener-Stückelberg (LZS) 干涉[25], 在由Majorana束缚态所构成的量子比特上产生量子振荡${\left|{\psi }_{0}\left(t\right)\right|}^{2}=$${{\rm{cos}}}^{2}({\omega }_{{\rm{m}}}t)$, 其中LZS振荡频率为
$ {\omega }_{{\rm{m}}}=\frac{1}{\hslash }\delta {{\rm{J}}}_{0}\left(\dfrac{2{E}_{{\rm{m}}}}{eV}\right), $
其中$ {{\rm{J}}}_{0}\left(x\right) $是贝塞尔函数. 利用这种量子振荡, 可以构建出一个Majorana量子比特的通用门, 如图5(c)—(e)所示, 通过控制电流脉冲实现任意的量子操作. 这种通用型量子门有望成为拓扑量子比特的基本构件, 并与Majorana束缚态的编织操作结合, 完成拓扑量子计算中的操作. Majorana量子比特的LZS 振荡会体现在拓扑约瑟夫森结的微波辐射中[26]. 在辐射光谱中包含分数约瑟夫森效应的分量, 因此通过测量微波辐射, 就可以获得Majorana量子比特的时间演化的特征时间.
如上所述, 虽然Majorana束缚态在空间上是分离的, 但实际上一对Majorana束缚态共同描述了拓扑超导体的量子态(即电子占有数的奇偶性), 因此Majorana束缚态处于量子纠缠状态. 这个物理特性可以用来实现基于Majorana束缚态的量子传送(teleportation)[27]. 如图6(a)所示, 可以在两端带有Majorana束缚态的一维拓扑超导体的两端各自放置一个量子点, 调制一维拓扑超导体与量子点之间的量子隧穿. 由于两个远距离的Majorana束缚态之间具有长程纠缠, 而每个Majorana束缚态又分别与量子点进行局域耦合, 最后导致两个量子点的占据态之间也产生了非局域的纠缠. 如图6(b)所示, 考虑了两个量子点的电子占有率的关联函数[28]. 考虑一维拓扑超导体的库仑阻塞效应, 可以发现空间上分离的两个量子点的电子占有率之间具有非局域的量子关联, 而这种量子关联也正体现了Majorana束缚态之间的纠缠性.
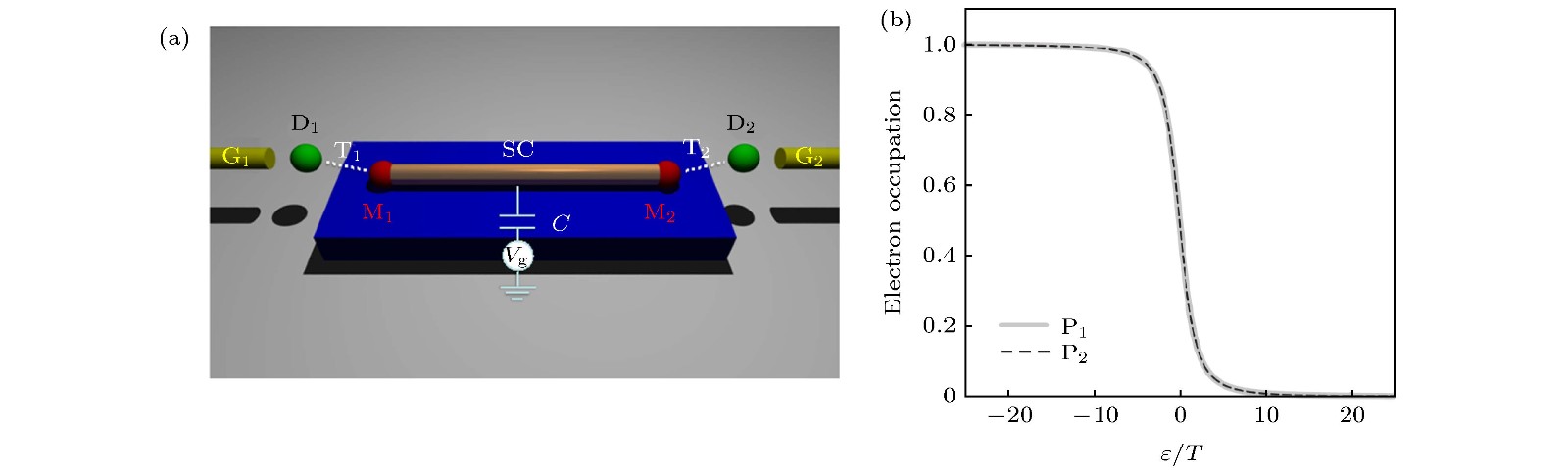图 6 (a) Majorana束缚态与量子点耦合体系; (b)两个量子点的占据态关联函数[28]
Figure6. (a) System with couplings between Majorana bound states and two quantum dots; (b) correlation between the electron occupations on the two quantum dots[28].

2
5.3.二维拓扑超导的量子涡旋和Majorana束缚态
-->

5.3.二维拓扑超导的量子涡旋和Majorana束缚态

5.2节讨论了一维拓扑超导纳米线两端的边界Majorana束缚态的物理性质, 本节讨论二维拓扑超导体的量子涡旋中的Majorana束缚态及其量子性质. 与图4(a)中具有强自旋轨道耦合的量子线相似, 三维拓扑绝缘体的表面出现自旋和动量锁定的二维Dirac表面态(如图7(a)所示). 因此该二维电子系统也可以通过类似机制实现二维无自旋的手征p波超导[16]. 由于拓扑绝缘体的上下表面在理想情况下各自仅具有一个Dirac电子态费米面, 因此实现无自旋超导无需借助Zeeman场. 根据上述理论, 上海交通大学实验组在NbSe2超导衬底上生长了三维拓扑绝缘体Bi2Te3薄膜. 通过调节拓扑绝缘体薄膜的厚度调制费米面位置使其位于拓扑绝缘体的导带和价带之间, 并利用扫描隧道显微镜/扫描隧道谱(STM/STS)观察了超导量子涡旋里的准粒子激发, 捕捉到了Majorana束缚态的信号(图7(b))[22].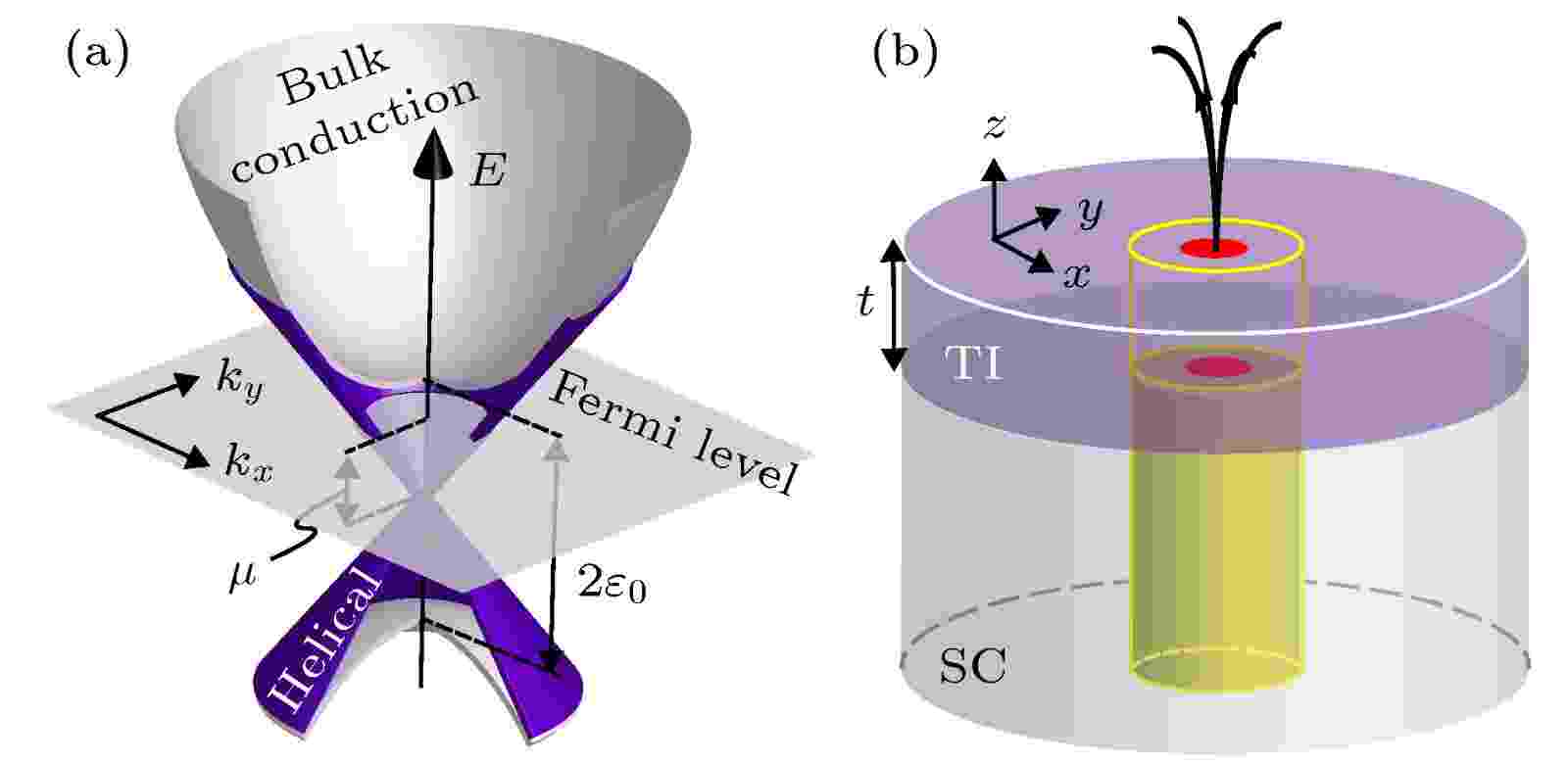
图 7 三维拓扑绝缘体(TI)色散关系(a)及TI-s波超导(SC)的异质结(b)的示意图, (b)中的红点代表Majorana束缚态[29]
Figure7. (a) Schematic of the linear dispersion of surface state of a 3D TI; (b) schematic of a TI/s-SC heterostructure, where the red points denote the Majorana bound states at the center of a quantum vortex[29].

我们再从理论上分析超导量子涡旋里的Majorana束缚态的能量和角动量. 为方便起见, 考虑单个量子涡旋. 此时, 超导准粒子激发的总角动量是一个好的量子数, 共有三项贡献:
$j=l+s/2-1/2,$
其中l为轨道角动量, $ s/2 $为自旋角动量, 由于量子涡旋引起的超导序参量的相位变化产生$ -1/2 $(符号由磁场方向决定). 因为Majorana束缚态与其反粒子空穴等价, 要求其能量和总角动量为零. 从(9)式可以看出, 总角动量归零$ j=0 $必须通过量子涡旋带来的半整数的角动量与电子自旋带来的半整数的自旋角动量的调节才能实现. 之前的研究已经从拓扑保护的角度对这一点进行了更严格的讨论[30].
Majorana束缚态的总角动量归零可以由两组不同的自旋角动量和轨道角动量的组合来实现, $ \left(s, l\right)=\left(+{1, 0}\right), (-{1, 1}) $. 如图8(a)所示, 自旋向上和自旋向下的准粒子波动函数在空间的振动满足贝塞尔函数$ {{\rm{J}}}_{l}\left({k}_{{\rm{F}}}r\right) $. 同理, 第一激发态$ j=-1 $由$ \left(s, l\right)=\left(+1, -1\right), (-{1, 0}) $的组合来实现. 从自旋向上分量和自旋向下分量之和给出的准粒子激发的态密度来看, Majorana束缚态和第一激发态并无两样, 这个特性给Majorana束缚态的推测带来了困难.
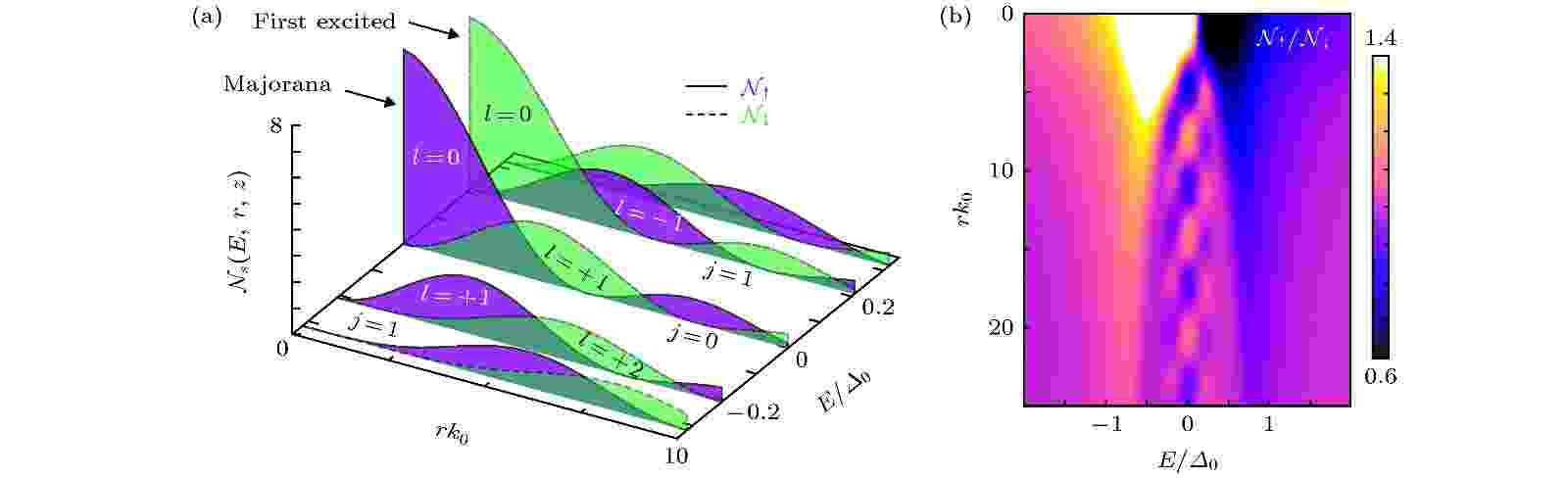图 8 (a)拓扑超导量子涡旋里的低能准粒子激发的自旋分辨波函数; (b)准粒子激发的自旋向上态密度和自旋向下态密度之比的能量-空间分布[29]
Figure8. (a) Spin-resolved wavefunctions of the low energy quasiparticle states in the vortex core of a topological superconductor; (b) spectrum of the ratio between densities of states for the spin-up and spin-down components[29].

但是, 如果区分自旋分量, 比如关注自旋向上的准粒子激发态密度, 很明显Majorana束缚态和第一激发态的波函数振荡的峰和谷正好相反. 类似的反向振荡也出现在自旋向下的准粒子激发态密度, 以及具有负能量的第一激发态中. 这个特征可以用来区分Majorana束缚态和其他的激发状态.
为了更清晰地显示Majorana束缚态和其他的激发状态的不同, 我们计算了不同能量的准粒子激发态里自旋向上和自旋向下的态密度分量的比率. 如图8(b)所示, 作为能量和实空间位置的函数, 自旋分辨态密度呈现明显的棋盘式图案. Majorana束缚态对应于棋盘中能量为零的一列, 明显区别于相邻列所对应的第一激发态. 因此, 分析显示使用自旋极化STM/STS方法可以从超导量子涡旋里准粒子激发谱利将Majorana束缚态作为单量子态分离出来. 最近实验上已经开始尝试自旋分辨STM/STS方法[31], 期待在不久的将来通过棋盘式图案的测试, 提供Majorana束缚态的精准证据.
2
5.4.实现非阿贝尔统计的纳米超导器件
-->

5.4.实现非阿贝尔统计的纳米超导器件

上面已经解释了与量子涡旋交换相关的非交换统计量, 但在技术上精确地控制和移动量子涡旋非常困难. 本节将介绍通过栅极电压操纵Majorana束缚态的理论方案[32]. 首先, 将如图9(a)中所示拓扑超导块作为方案的一个基本单元. 该单元的拓扑超导态可利用第4节所介绍的异质结机制在半导体薄膜上实现[18]. 当一个量子涡旋进入单元中心时, Majorana束缚态将出现在量子涡核心中. 由于Majorana束缚态始终成对出现, 另一伴随的Majorana束缚态将出现在块体的边缘(图9(b)).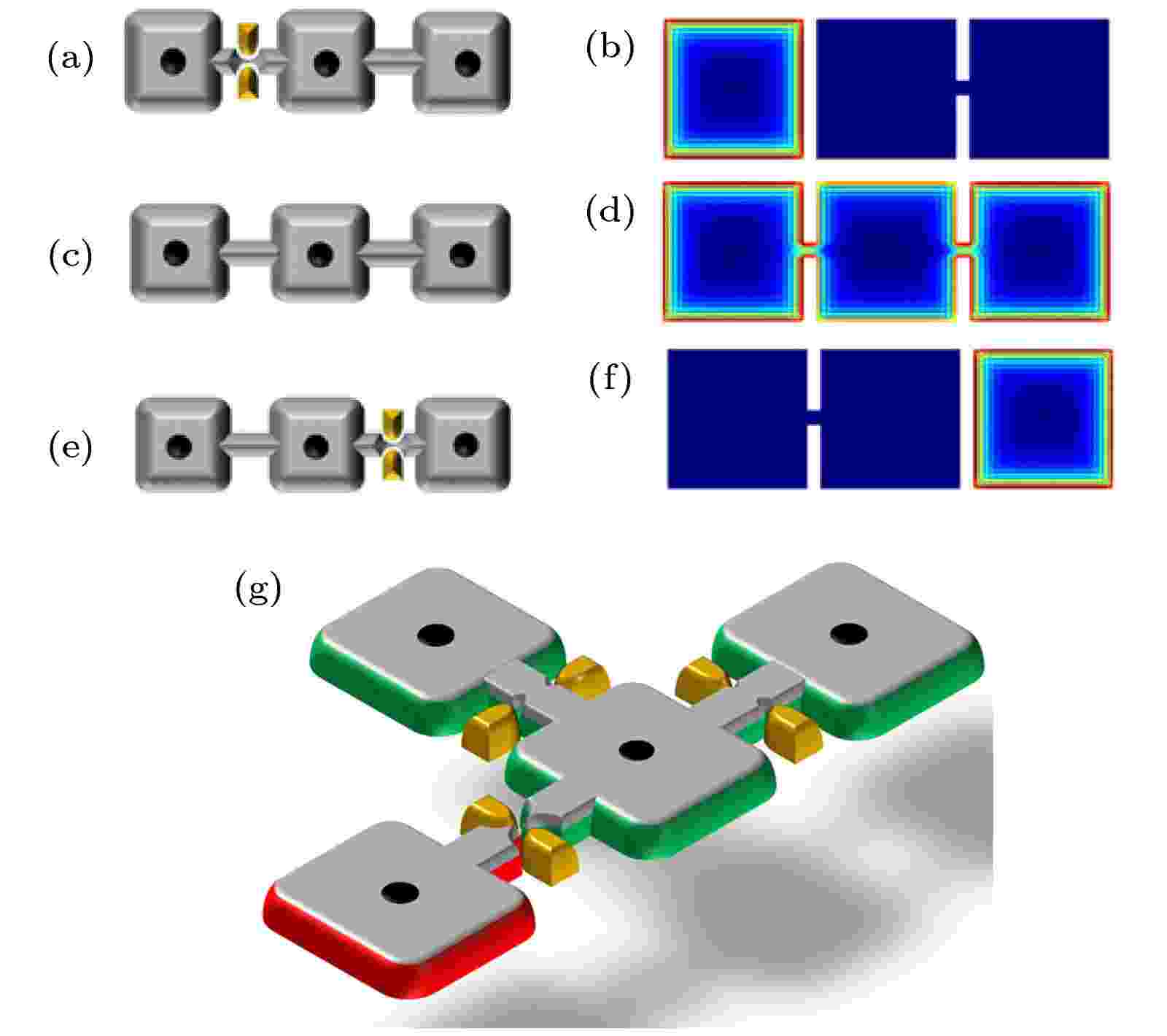
图 9 (a), (c), (e), (g)为利用栅极电压移动边界Majorana束缚态的示意图; (b), (d), (f)给出了与(a), (c), (e) 相对应的Majorana束缚态的波函数分布[32]
Figure9. (a), (c), (e), (g) Schematic of the device which transports edge Majorana states using gate voltages; (b), (d), (f) corresponding wavefunctions of the edge Majorana states in (a), (c), (e)[32].

接下来考虑三个块体的组合. 块体通过结连接起来, 结的开(on)和关(off)通过结上的栅极来控制. 在起始状态, 通过向左侧结施加栅极电压来隔离左块. 此时, 边缘的Majorana束缚态仅出现在左侧块中(图9(a),(b)). 而对于右边的处于连接状态的两个块体, 其涡流核心各有一个Majorana束缚态组成一对伴随的Majorana束缚态, 而边缘则没有Majorana束缚态. 在这里两个块体边缘的Majorana态的消失可以理解为(9)式中第三项因为两个磁通的贡献变成－1, 总角动量归零$ j=0 $条件无法满足. 随后我们降低左结栅极电压使左块的Majorana束缚态逐渐扩散到三个块体的边缘(图9(c),(d)). 接下来, 将栅极电压添加到右结并隔离右块, 处于三个块体边缘的Majorana束缚态将塌缩至右块(图9(e),(f))中. 通过该过程, Majorana束缚态从左块转移到了右块.
一个完整的编织操作(braiding)涉及两个Majorana束缚态, 需要4个超导块体来实现该操作. 考虑由如图9(g)中所示的4个块体单元组合成的器件. 在初始状态, 隔离左右块并连接中间的两个块体, 此时Majorana束缚态出现在左右块的边缘上. 参考图9(a)—(f)中的过程, 首先将左块Majorana束缚态运送到最上方的块体. 然后, 将右Majorana束缚态传送到左侧块. 之后再将已经转移到最上方块的Majorana束缚态运送到右块. 经过此过程, 器件的设置恢复至初态, 而左右块中的边界Majorana束缚态则发生了交换. 含时BdG方程的数值分析也证明经过交换后右侧Majorana束缚态获得了额外π的相位[32,33]. 以这种方式, 便实现了公式(5)中非交换统计所需的Majorana束缚态的编织操作.
2
5.5.基于Majorana量子比特的单电子泵
-->

5.5.基于Majorana量子比特的单电子泵

研究拓扑超导中的Majorana束缚态的最初动机是由于其在拓扑量子计算中的巨大应用潜力. 本节介绍利用边缘Majorana束缚态来实现Majorana量子比特的NOT操作[34]. 图10(a)和图10(b)给出了该量子器件的示意图. 图10(b)的右侧4个超导块体单元形成一个环, 环的中心固定有一个量子涡旋. 环左侧则为一个独立超导单元. 左侧超导块的边界和中心涡旋处各有一Majorana束缚态, 两者恰好构成一个量子比特. 初始状态时, 右侧4个超导块保持在图10(a)中左下角所示的状态. 随后利用5.4节介绍的Majorana束缚态转移方式, 可以驱动左边孤立块体上的边缘Majorana束缚态环绕右边4个块体组成的圆环一周, 并最终达到图10(a)中右上角所示的终态. 环绕中心涡旋一周后Majorana束缚态将获得一个π相位(图10(a)), 这相当于对左侧块体上的Majorana量子比特实施了一个NOT变换, 使其上电子数的奇偶性(parity)发生反转. 需要注意的是, 在终态时右边4个超导块体间的水平结处于导通状态而垂直结处于断开状态, 这一设置刚好与初态相反. 可以严格证明结的连接状态的转换将导致右侧超导环上的基态电子数奇偶性反转[34], 而整个系统的粒子数奇偶性仍保持不变.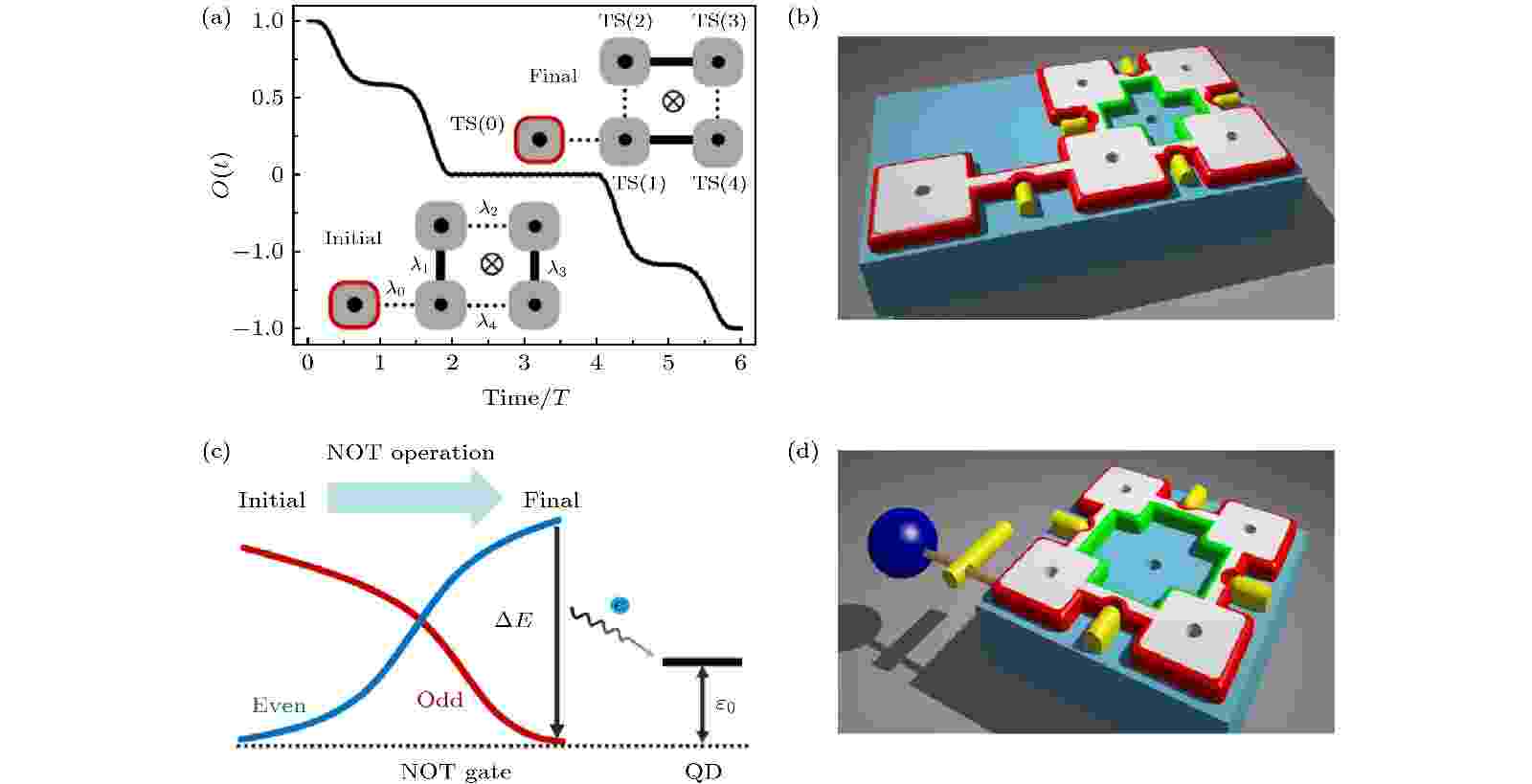
图 10 (a), (b) Majorana量子比特的NOT量子门操作; (c), (d) 基于边界Mojorana束缚态的单电子泵[34]
Figure10. (a), (b) NOT quantum gate operation of the Majorana qubit; (c), (d) a single-electron pumping based on the edge Majorana states[34].

若把图10(b)的左侧Majorana量子比特替换为常规量子点(图10(d)), 就可能实现单电子泵. 设初始时量子点处于空态, 而4个超导块之间的结处于与图10(a)中的初态. 通过对垂直结施加栅极电压而把水平结的栅压减小, 即对右侧超导块体环实行NOT操作, 超导块环的基态电子数奇偶性将发生如图10(c)所示的转变. 由于超导体环和量子点组成的体系整体电子数奇偶性守恒, 超导体因此将向量子点“排挤”出一个电子. 此时若将量子点与一个外电路连接, 就能向外逐个地输出电子, 从而实现单电子泵的功能.
6.结　论
本文着重讨论了在混合系统中实现拓扑超导性和Majorana束缚态的方法. 科学家也尝试利用单一材料实现拓扑超导态以及Majorana束缚态[35-39]. 最近铁基超导里Majorana束缚态的观测取得重大进展. 另外超流3He[40]和冷却原子气体中Majorana束缚态也有一些探索. 我们认为Majorana束缚态完美的实验验证已经近在咫尺了.
基于量子叠加态的量子计算有着广泛而重要的应用前景, 例如可以用于开发最先进的加密技术, 实现大规模量子模拟以揭示新奇物理现象和开发新型量子物质. 目前以IBM、微软和谷歌为代表的企业也开始着手量子计算机的开发, 可以说一场全球范围内的开发竞争正在如火如荼地展开. 但是, 量子系统的退相干问题依然是量子计算机开发的瓶颈, 亟待解决. 从原理上看, 使用Majorana束缚态建立拓扑量子位具有很大的优势, 期待其研究开发在不久的将来发生颠覆性进展.
尽管基于Majorana束缚态的拓扑量子计算可能提供常规量子计算方案所不具备的超强抗干扰能力, 但是它并不能够单独完成所有的量子计算操作. 因此, 研究Majorana量子比特与常规量子比特之间的耦合效应并最终实现全局量子计算, 也将会是一个重要的研究方向.
相关话题/电子 系统 计算 统计 交换
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 三模腔-原子闭环系统中可控的量子干涉和光子传输
    摘要:通过构造一个由相互垂直的两腔和一个二能级原子组成的光学腔-原子系统,研究可控的量子干涉引起的非传统光子传输现象.该系统中,两个正交腔之间通过光纤直接耦合和通过放在两腔交叉处的二能级原子间接耦合.该三模系统支持两个相互垂直的传播方向,即两探测场相互垂直.在考虑原子弛豫速率的情况下,该闭环系统中的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 受激辐射损耗超分辨显微成像系统研究的新进展
    摘要:由于受到衍射极限的影响,传统光学显微镜的分辨率被限制在半个波长左右.近二十年来出现了许多通过不同方法绕过光学衍射极限的超分辨成像技术,其中,受激辐射损耗显微(stimulatedemissiondepletionmicroscopy,STED)通过引入一束环形损耗光来抑制荧光光斑外围荧光分子的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 栅氧化层经时击穿的非平衡统计理论分析方法
    摘要:栅氧化层的经时击穿作为影响互补型金属-氧化物-半导体集成电路可靠性的一个重要因素,一直是国内外****研究的重点.为了对其进一步研究,首先从栅氧化层在电应力下经时击穿的微观机理出发,基于栅氧化层中电子陷阱密度累积达到临界值时发生击穿的原理和电子陷阱生成过程的随机性,提出了栅氧化层经时击穿的非平 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 2-甲基吡嗪分子激发态系间交叉过程的飞秒时间分辨光电子影像研究
    摘要:飞秒时间分辨光电子影像技术和飞秒时间分辨质谱技术相结合,研究了2-甲基吡嗪分子电子激发态超快非绝热弛豫动力学.用323nm光作为泵浦光,把2-甲基吡嗪分子激发到第一激发态S1,用400nm光探测激发态演化过程.通过时间分辨质谱技术测得S1态的寿命为98ps.实验中,实时观察到了单重态S1向三重 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 磁电势垒结构中光场辅助电子自旋输运特性
    摘要:基于Floquet理论和传输矩阵方法,理论研究了光场对电子隧穿两类磁电垒结构的自旋极化输运特性的影响,计算结果表明光场对两类磁电垒结构中电子的输运有显著影响:首先,原来不存在自旋过滤特性的结构应用光场后会产生低能区域明显的自旋过滤效应;其次,原来存在自旋过滤特性的结构应用光场后自旋过滤明显增强 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 双二次交换作用和各向异性对反铁磁体相变温度的影响
    摘要:本文基于双时格林函数方法,通过对不同格点和同格点的高阶格林函数分别采用Tyablikov和Callen退耦近似,系统研究了双二次型交换作用和各向异性对简单立方晶格反铁磁模型相变的影响.得到了相变温度的解析表达式,发现相变温度随着各向异性的增强而升高,但随着双二次型相互作用的增强而下降.关键词: ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 真空沟道结构GaAs光电阴极电子发射特性
    摘要:光电阴极的发射电流密度和寿命限制了其在功率器件和大科学装置中的应用.本文结合光电阴极和场发射阴极电子发射理论,设计了大电流密度的真空沟道结构光电阴极组件,并使用覆膜和刻蚀技术制备了以GaAs衬底为阴极材料的光电阴极组件.光电阴极组件电子发射特性测试结果显示,常温状态下随入射光功率增加,阴极发射 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 用于提高微波无线能量传输系统接收端能量转换效率的肖特基二极管
    摘要:转换效率是微波无线能量传输系统的关键参数,为提高该参数指标,本文提出了一种GeOI折叠空间电荷区肖特基二极管,该器件结构可以显著降低肖特基二极管的零偏置电容,利于能量转换效率的提高.通过在ADS仿真软件中使用该器件SPICE模型进行整流电路仿真,在输入能量为24.5dBm时,获得了75.4%的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于深紫外激光-光发射电子显微技术的高分辨率磁畴成像
    摘要:基于磁二色效应的光发射电子显微镜磁成像技术是研究薄膜磁畴结构的一种重要研究手段,具有空间分辨率高、可实时成像以及对表面信息敏感等优点.以全固态深紫外激光(波长为177.3nm;能量为7.0eV)为激发光源的光发射电子显微技术相比于传统的光发射电子显微镜磁成像技术(以同步辐射光源或汞灯为激发源) ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 利用正电子湮没技术研究钾掺杂钨合金中的缺陷
    摘要:钨合金中钾的掺杂会引入大量的缺陷,如尺寸几十纳米的钾泡、高密度的位错以及微米量级的晶粒带来的晶界等,这些缺陷的浓度和分布直接影响合金的服役性能.本文运用正电子湮没谱学方法研究钾掺杂钨合金中的缺陷信息,首先模拟计算了合金中各种缺陷的正电子湮没寿命,发现钾的嵌入对空位团、位错、晶界等缺陷的寿命影响 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.