摘要: 行人跟踪是计算机视觉领域中研究的热点和难点, 通过对视频资料中行人的跟踪, 可以提取出行人的运动轨迹, 进而分析个体或群体的行为规律. 本文首先对行人跟踪与行人检测问题之间的差别进行了阐述, 其次从传统跟踪算法和基于深度学习的跟踪算法两个方面分别综述了相关算法与技术, 并对经典的行人动力学模型进行了介绍, 最终对行人跟踪在智能监控、拥堵人群分析、异常行为检测等场景的应用进行了系统讲解. 在深度学习浪潮席卷计算机视觉领域的背景下, 行人跟踪领域的研究取得了飞跃式发展, 随着深度学习算法在计算机视觉领域的应用日益成熟, 利用这一工具提取和量化个体和群体的行为模式, 进而对大规模人群行为开展精确、实时的分析成为了该领域的发展趋势.
关键词: 行人跟踪 /
轨迹提取 /
计算机视觉 /
行人动力学 English Abstract Review of pedestrian tracking: Algorithms and applications Cao Zi-Qiang Sai Bin Lu Xin College of Systems Engineering, National University of Defense Technology, Changsha 410073, China Received Date: 11 November 2019Accepted Date: 18 December 2019Published Online: 20 April 2020Abstract: Pedestrian tracking is a hotspot and a difficult topic in computer vision research. Through the tracking of pedestrians in video materials, trajectories can be extracted to support the analysis of individual or collected behavior dynamics. In this review, we first discuss the difference between pedestrian tracking and pedestrian detection. Then we summarize the development of traditional tracking algorithms and deep learning-based tracking algorithms, and introduce classic pedestrian dynamic models. In the end, typical applications, including intelligent monitoring, congestion analysis, and anomaly detection are introduced systematically. With the rising use of big data and deep learning techniques in the area of computer vision, the research on pedestrian tracking has made a leap forward, which can support more accurate, timely extraction of behavior patterns and then to facilitate large-scale dynamic analysis of individual or crowd behavior.Keywords: pedestrian tracking /trajectory extraction /computer vision /human behavioral dynamics 全文HTML --> --> --> 1.引 言 近年来, 深度学习的浪潮席卷计算机视觉领域, 这不仅提高了通用物体的检测性能, 也极大地促进了行人检测的发展, 为行人跟踪领域的研究奠定了良好的基础[1 ] . 行人检测的主要任务是判断图片或者视频中是否有行人, 如果有, 则用框图把行人标记出来[2 ] , 不用考虑前后两帧中行人的匹配问题. 行人跟踪与行人检测不同, 需要利用数据关联技术关联前后两帧中相似度最大的行人, 以达到对视频中的行人持续跟踪[3 ] 的目的, 从而得到行人运动的速度、轨迹和方向等信息[4 ] , 并将其进一步应用到个人或大规模群体行为的研究领域中去[5 ,6 ] . 行人跟踪是计算机视觉应用中的一项基本任务, 虽然已有大量文献提出了各种算法, 但由于行人跟踪问题比较复杂, 不仅需要考虑拍摄的角度、光照的变化[7 -9 ] , 还需要考虑新目标出现, 旧目标消失, 以及当跟丢目标再次出现时, 如何进行再识别[10 ] 等问题, 这使得健壮的行人跟踪算法仍然是一个巨大的挑战.[11 ] . 虽然已有相关的文献综述对行人跟踪领域中的算法进行总结, 但这些综述大多不够新颖, 所提到的算法依旧是传统的目标跟踪算法, 没有将最新的深度学习算法包含进来. 为了弥补已有文献的不足, 同时使得广大科研工作者掌握行人跟踪领域的最新发展趋势, 本文首先将行人跟踪领域的算法按照传统跟踪算法和深度学习跟踪算法的分类方法进行了系统介绍, 并选取相应的指标评估性能, 然后介绍几种经典的人类行为动力学模型, 回顾人类行为动力学领域的发展历程, 最后围绕新技术条件下的视频监控、拥堵人群分析、异常行为监测等典型应用场景进行了系统地阐述.2.传统跟踪算法 22.1.卡尔曼滤波算法 2.1.卡尔曼滤波算法 1960年, Kalman[12 ] 为了解决离散数据的线性滤波问题, 提出了卡尔曼滤波算法, 该算法后来被扩展到目标跟踪领域[13 ] , 其核心思想是利用上一时刻目标状态的预测值和当前时刻目标状态的测量值得到当前时刻目标状态的最优估计, 并把当前时刻得到的最优估计作为下一时刻目标的预测值进行迭代运算, 如此循环往复, 逼近目标的真实值[14 ] . 该算法的创新点在于同时考虑了在预测过程和测量过程中的误差, 并且认为这两种误差独立存在, 不受测量数据的影响.$ \hat { x}_{k-1} $ 预测当前状态$ \hat { x}_k^- $ , 并对误差协方差矩阵$ { P}_k^- $ 进行估计; 在更新阶段, 卡尔曼滤波器用加权的测量结果来矫正预测结果[15 ] . 卡尔曼滤波的两个阶段如表1 所列,预测阶段 更新阶段 $\hat { x}_k^ - \!=\! { A}\hat { x}_{k-1}^ - \!+\! { B}{ U_{k - 1} }$ ${ { K}_k} \!=\! { P}_k^ - { { H}^{\rm T} }{({ {HP} }_k^ - { { H}^{\rm T} } \!+\! { R})^{ - 1} }$ ${ P}_k^ - \!=\! { A}{ { P}_{k - 1} }{ { A}^T} \!+\! { Q}$ ${ {\hat { x} }_k} \!=\! \hat { x}_k^ - \!+\! { { K}_k}({ { y}_k} \!-\! { H}\hat { x}_k^ - )$ ${{ P}_k} = ({ I} - {{ K}_k}{ H}){ P}$
表1 卡尔曼滤波的预测阶段和更新阶段Table1. Prediction and update process of Kalman filtering表2 所列.参数 含义 $\hat { x}_k^-$ 目标在$k$时刻的先验状态估计值, 包括目标的位置、速度等参数, 一般是$n$维向量 ${ {\hat { x}}_k}$ 目标在$k$时刻的后验状态估计值, 是对$\hat { x}_k^-$应用卡尔曼滤波更新后的值 ${{\hat { x}}_{k - 1}}$ 目标在$k-1$时刻的后验状态估计值 ${ A}$ 状态转移矩阵, 一般是$n \times n$阶的方阵 ${ B}$ 控制矩阵, 一般为0 ${ U}_{k-1}$ 外部控制量, 一般也为0 ${ P}_k^-$ $k$时刻的先验误差协方差矩阵, 需要事先给定一个初始值, 以后的值可以由卡尔曼滤波递归得到 ${ P}_k$ $k$时刻的后验误差协方差矩阵, 是对${ P}_k^-$的修正 ${ K}_k$ 卡尔曼增益 ${ y}_k$ 测量值, 一般只能测量目标的位置, 是$m$维向量 ${ Q}$ 系统噪声协方差矩阵, 是一个需要调节的参数, 一般假定它是一个固定的值, 在实验中需要通过不断 ${ R}$ 观测噪声协方差矩阵, 和测量仪器有关, 在实验中要不断尝试来确定最优的${ R}$值 ${ H}$ 观测矩阵, 是$m \times n$阶矩阵, 用于将$m$维的测量值${ y}_k$转换为与预测值${{\hat { x}}_k}$相同的$n$维向量
表2 卡尔曼滤波公式中的参数及含义Table2. Parameters and meanings in the Kalman filter formula$ \hat { x}_k^- = {[{d_x}(k), {d_y}(k), {v_x}(k), {v_y}(k)]^{\rm T}} $ , 其中$ {d_x}(k) $ , $ {d_y}(k) $ 分别表示$ k $ 时刻目标中心点的$ x $ 坐标和$ y $ 坐标, $ {v_x}(k) $ , $ {v_y}(k) $ 分别表示$ k $ 时刻目标中心点沿$ x $ 轴, $ y $ 轴的分速度[16 ] , 因为正常行人在行走过程中不会突然加速或者减速, 所以视频中相邻帧的行人之间的运动可以近似看作匀速运动, 假设相邻两帧之间的时间间隔为$ \Delta t $ , 则行人在$ k $ 时刻的运动方程为:$ \hat { x}_k^ - = [{d_x}(k), {d_y}(k), $ $ {v_x}(k), {v_y}(k)]^{\rm T} $ 代入(1 )式, 则有$ { U}_{k-1} $ 和控制矩阵$ { B} $ 均为零, 之后分别为误差协方差矩阵、系统噪声协方差矩阵赋予初始值, 一般令$ \hat { x}_k^- $ 和$ { P}_k^- $ ;$ {{ y}_k} = \left[ {{y_x}{{(k)}}, {y_y}{{(k)}}} \right] $ 表示测量的目标中心点坐标, 因为$ {{ y}_k} = { H}\times{{ x}_k} $ , 所以状态转移矩阵$ { H} = \left[ \begin{matrix} 1&0&0&0\\ 0&1&0&0 \end{matrix}\right] $ ;$ { R} = \left[ \begin{matrix} 1&0\\ 0&1 \end{matrix} \right] $ , 再结合预测阶段得到的$ \hat { x}_k^- $ 和$ { P}_k^- $ 就可以算出目标在k 时刻的后验状态估计值$ {{\hat { x}}_k} $ 和后验协方差矩阵$ { P}_k $ .[17 ] .[18 ] 用卡尔曼滤波算法原理对视频中的行人进行跟踪, 他们首先采用混合高斯模型得到运动行人的前景图像, 然后利用HSV(hue, saturation, value) 颜色空间模型和基于形态学的目标重构方法消除运动阴影, 最后用卡尔曼滤波预测行人的位置并得到了行人的运动轨迹. 石龙伟[19 ] 将卡尔曼滤波与光流法结合起来, 先用光流法对视频进行预处理, 然后根据光流法获取的目标位置等信息用卡尔曼滤波实现对行人的有效跟踪. 王宏选[20 ] 在动态行人跟踪TLD (tracking-learning-detection, 跟踪-学习-检测)算法中引入了卡尔曼滤波器预测行人下一帧可能出现的区域, 以缩小检测范围, 提高检测速度, 改善行人之间因存在遮挡而导致跟踪丢失的问题.2.2.多假设跟踪算法 -->2.2.多假设跟踪算法 1979年, Reid[21 ] 提出了多假设跟踪算法, 该算法的最初目的是解决雷达信号的自动跟踪问题, 后来Kim等[22 ,23 ] 对多假设跟踪算法进行了改进, 将其扩展到目标跟踪领域. 多假设跟踪算法本质上是基于卡尔曼滤波算法在多目标跟踪问题中的扩展, 其中假设是指聚簇内一组目标和量测的分配互联关系[24 ] . 多假设跟踪是一种延时决策算法, 在数据关联发生冲突时, 会形成多种假设, 直到获取到新的信息再做决定, 主要包括数据聚簇、假设生成、计算假设得分、假设删除四部分[25 ] , 其中假设生成和假设删除是该算法的核心, 该算法的流程如下.Step 1 数据聚簇, 将新接收的量测点迹与以前的假设进行关联.Step 2 将所有可能的航迹生成假设并保存, 生成的假设用下面的公式表示:$ { Z}(k)$ 表示$ k $ 时刻的量测集合; $ { Z}^k $ 表示$ k $ 时刻的累积量测集合; $ {{ {\varOmega}}^k} $ 表示$ k $ 时刻关联假设的集合; $ M_k $ 是可用量测个数; $ {\varOmega_i^k} $ 表示先验假设; $ Z_m (k) $ 的来源可能是原有目标的继续、新目标的量测、虚警等. 如果量测是原有目标的继续, 则它符合原有航迹的高斯分布, 否则量测是一个均匀分布的噪声; 如果是新目标的量测、虚警, 则出现当前关联的可能性可以通过泊松分布和二项分布的乘积表示.Step 3 计算假设概率:$ P_i^k $ 表示假设概率; $ c $ 表示归一化因子; $ P_{\rm D} $ 表示检测概率; $ N_{\rm {DT}} $ 表示与先前目标相关的量测数量; $ N_{\rm {FT}} $ 表示与错误目标相关的量测数量; $ N_{\rm {NT}} $ 表示与新目标相关的量测数量; $ N_{\rm {TGT}} $ 表示先前已知目标数; $ \beta_{\rm {FT}} $ 表示错误目标的密度; $ \beta_{\rm {NT}} $ 表示已检测到的先前未知目标的密度.Step 4 假设删除, 因为假设的积累会占据大量的内存, 增加运算量, 不利于实时跟踪, 所以需要对假设进行剔除. 目前有两种删除假设的方法, 分别是零扫描法和多扫描法.零扫描法 首先使用零扫描滤波器处理每个数据集, 然后仅保留概率最大的那个假设. 另外一种改进的方法是不仅选择最大似然假设, 而且增加卡尔曼滤波器中的协方差以解释误相关的可能性.多扫描法 使用多扫描算法处理数据集之后仍存在若干假设, 然后再次修剪所有不太可能的假设, 但保持所有概率高于指定的阈值的假设.[26 ] .2.3.粒子滤波算法 -->2.3.粒子滤波算法 针对卡尔曼滤波需要目标的状态变量满足高斯分布的缺点, Breitenstein等[27 ] 提出了一种基于粒子滤波框架的多行人跟踪检测算法, 该算法是卡尔曼滤波算法的一般化方法. 卡尔曼滤波建立在线性的状态空间和高斯分布的噪声上, 而粒子滤波的状态空间模型可以是非线性的, 且噪声分布可以是任何型式, 是一种通过非参数化的蒙特卡罗方法来实现递推的贝叶斯滤波, 粒子滤波的基本原理是通过先验概率和当前观测值估计后验概率[28 ] , 该算法分为两个步骤.$ s({{tr}}, d) $ 评估检测$ d $ 与跟踪器$tr$ 的每个粒子$ p $ 之间的距离, 并用为$ tr $ 训练的分类器$ctr(d)$ 对$ d $ 进行评估:$ p_N (d-p) $ 表示评估$ d $ 和$ p $ 之间距离的正态分布; $ g(tr, d) $ 是门控函数, 代表检测相对于目标的速度和运动方向的位置.$tr$ 的粒子$ p $ 的权重$ w_{({tr}, p)} $ :$ \beta $ , $ \gamma $ , $ \eta $ 是实验设定的; $ I({tr}) $ 是指示函数, 如果检测与跟踪器关联, 则返回1, 否则返回0; $ d_{\rm c} (p) $ 表示置信密度; $ p_{\rm o} ({tr}) $ 是加权函数.[29 ] . 针对现实世界中行人身体之间的遮挡问题, Xu等[30 ] 用粒子滤波跟踪行人的头部, 并用基于颜色直方图和方向梯度直方图的方法对头部外观模型进行更新, 有效地减少了由于遮挡问题而造成的行人标号变化频繁的问题. 该算法在UT-Interaction数据集的测试结果中, 行人的身份标号仅变化了4次.2.4.基于马尔科夫决策的多目标跟踪算法 -->2.4.基于马尔科夫决策的多目标跟踪算法 2015年, Xiang等[31 ] 提出了一种基于马尔可夫决策过程的在线多目标跟踪框架, 将多目标跟踪问题视作一个马尔科夫决策过程来处理. 马尔科夫决策过程由一个元组$ (S, A, T( \cdot ), R( \cdot )) $ 组成[32 ] , 其中$ S $ 表示目标所处的状态, $ A $ 表示目标可以执行的动作, $ T( \cdot ) $ 表示状态转移函数, $ R( \cdot ) $ 表示奖励方程, 行人跟踪问题的马尔科夫决策过程如图1 所示.图 1 马尔科夫决策过程流程图[31 ] Figure1. Markov decision process flow chart[31 ] Step 1 行人被检测器检测到后首先进入激活状态, 然后用一个训练好的SVM 分类器判断行人是进入跟踪状态还是停止状态, 其分类结果用一个5 维的特征向量$ {{ {\varPhi}} _{\rm {Active}}}(s) $ 表示. SVM分类器是从训练视频序列中选出训练样本, 并将行人的2 维坐标、高度、宽度以及检测得分归一化为一个5维的标准化向量训练得到的[31 ] , 其奖励函数为y (a ) = 1; 如果转移到停止状态, 则y (a) = –1; $ ({ w}_{\rm {Active}}^{{\rm T}} $ , $ {b_{\rm {active}}}) $ 用于定义SVM 的超平面.Step 2 在跟踪状态下的奖励函数:$ e_{\rm {medFB}} $ 表示预测误差的中间值, 如果预测误差$ e_{\rm {medFB}} $ 太大则跟踪失效; $ o_{\rm {mean}} $ 表示前后两帧边界框重叠区域的平均值, 只有当$ o_{\rm {mean}} $ 在阈值$ {o_0} $ 以上时才被认为正确检测到目标; 因此当且仅当$ e_{\rm {medFB}} $ 小于阈值$ e_0 $ 和 $ o_{\rm {mean}} $ 大于阈值$ {o_0} $ 才表示跟踪有效, $ y(a) $ = +1; 否则进入丢失状态, $ y(a) $ = –1.Step 3 丢失状态下的奖励函数:$ y(a) $ = +1; 如果进入停止状态, 则$ y(a) $ = –1; $ {{ w}^{\rm T}}\phi (t, {d_k}) $ 是捕捉目标和检测之间相似性的特征向量.31 ]将其在MOT Benchmark上进行了测试, 其多目标跟踪准确率可达30.3%, 多目标跟踪精度可达70.3%, 但是在行人长时间遮挡后容易发生误判.2.5.相关滤波算法 -->2.5.相关滤波算法 相关滤波最初是表示信号处理领域中两个信号之间相似度的概念, 两个信号之间的相似度越高, 它们就越相关. 2019 年, Bolme等[33 ] 首次将相关滤波算法运用到目标跟踪领域, 其核心思想是利用误差平方和最小的滤波器(minimum output sum of squared error, MOSSE)训练图像, 使得图像的平方和误差最小, 从而建立跟踪目标的外观模型. 该算法的处理流程如下:Step 1 首先训练相关滤波器, 最小化实际输出$ F_i\dot{H^*} $ 与期望输出$ G_i $ 之间的平方和误差:Step 2 然后用训练好的相关滤波器$ H^* $ 与输入图像$ F $ 做相关操作, 求其响应$ G $ :Step 3 最后用$ {\rm {PSR}} $ 作为响应$ G $ 峰值强度的度量, 只有当$ {\rm {PSR}} $ 大于某个阈值时才会跟新目标的位置, 否则执行Step 1, 一般$ {\rm {PSR}} $ 小于7 表示跟踪失败,[34 ] 提出了KCF算法, 利用$ {\rm{HOG}} $ $ ({\rm{histograms}}{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\rm{of}}{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\rm{oriented}}{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\rm{gradients}}) $ 特征代替MOSSE中使用的原像素, 增强了滤波器对目标和环境的判别能力. 此外在MOSSE线性回归模型的基础上加入了正则项$ \lambda {\left\| w \right\|^2} $ , 建立了线性岭回归模型[35 ,36 ] :$ \lambda {\left\| w \right\|^2} $ 是$ L2 $ 正则项, 用于解决过拟合问题; 对于非线性问题, 运用高斯核函数$\phi (a, b) = $ $ {\rm {exp}}\left( - \dfrac{1}{{{\sigma ^2}}}{\left\| {a - b} \right\|^2}\right) $ 将其转换为线性问题, 此时目标函数形式为:[37 ] .3.深度学习算法 深度学习是包含多级非线性变换的层级机器学习方法, 深层次神经网络是其主要形式. 神经网络中层与层之间的神经元连接模式受启发于生物神经网络[38 ] . 深度学习算法与传统算法相比, 不需要手动选择特征, 具备良好的特征提取能力. 但由于深度学习算法需要大量的数据以及高性能的计算机来训练数据, 而之前的计算机性能不能满足深度学习算法的需求, 也没有大量的数据用来训练[39 ] , 因而深度学习算法沉寂了相当长的一段时间[40 ] . 近年来, 随着大数据时代的到来、计算机性能的提升, 深度学习开始广泛应用于计算机视觉的各个领域, 深度学习算法在行人跟踪领域应用的主流思路是 tracking-by-detection[41 ] , 即首先用深度学习模型提取目标行人的特征, 检测出视频中的行人所在位置, 然后用多目标跟踪器对目标进行持续跟踪. 本文以卷积神经网络为例介绍深度学习算法在行人跟踪上的应用.3.1.卷积神经网络 3.1.卷积神经网络 卷积神经网络(convolutional neural network, CNN)是一种典型的深度学习模型. LeCun[42 ] 最早提出了CNN的概念. 2012 年, Krizhevskyd 等[43 ] 首次将深度卷积神经网络应用到图像分类领域, 其设计的AlexNet 网络模型赢得了ImageNet图像分类比赛的冠军, 成功地把深度卷积神经网络引入了计算机视觉领域. 此后ImageNet比赛的冠军均是采用深度卷积神经网络的方法完成的. CNN的基本结构包括输入层、卷积层、池化层、全连接层及输出层[44 ] , 如图2 所示.图 2 CNN基本结构图Figure2. CNN basic structure diagramt图2 中只绘制出了一个卷积层和池化层, 然而在实际的网络中经常有若干个卷积层和池化层交替连接. 在卷积层中通常使用一个大小为$ f \times f $ 的滤波器执行卷积操作来提取图像中的特征, 网络前面浅层的卷积层用来提取图像的低级特征, 后面更深层的卷积层用来提取图像的高级特征, 全连接层将提取到的图片的特征归一化为一维的特征向量, 输出层在分类问题中用来输出每个类别的概率. 在处理行人检测问题时, 卷积神经网络模型按照检测的步骤可以划分为One-stage 和Two-stage 两类. Two-stage把检测行人分为两个阶段, 首先产生行人候选区域(region proposals), 然后对候选区域进行分类, 其典型代表是RCNN, SPP-Net, Faster-RCNN等模型, 特点是准确率较高, 但检测速度慢. One-stage 可以直接生成行人的类别概率和位置坐标, 其典型代表是YOLO系列模型以及CornerNet, CenterNet等模型, 其特点是运算速度较快, 但准确率一般较低.3.2.RCNN网络模型 -->3.2.RCNN网络模型 2014年, Girshick等[45 ] 提出RCNN (regions with CNN features)模型进行目标检测, 将卷积神经网络引入目标检测领域. RCNN 就是在目标候选区内用CNN的方法来提取特征, 处理流程如图3 所示.图 3 RCNN算法流程图[45 ] Figure3. RCNN algorithm flowchart[45 ] [46 ] 在输入图片上生成2000个左右的目标候选区域, 然后对这些候选区域进行归一化操作, 并将归一化后的候选区域送到AlexNet卷积网络提取特征. 在AlexNet网络中有5个卷积层可以提取特征, 经过一轮训练后, 每个候选区域都能够得到一个4096维的特征向量, 然后将提取到的特征传入SVM分类器中进行分类, 最后使用卷积层的输出训练一个回归器(dx , dy , dw , dh ) 对候选区域进行微修, 使其接近真实标注的区域.[47 ] , 不能满足实时性要求.3.3.SPP-Net网络模型 -->3.3.SPP-Net网络模型 2014年, He等[48 ] 发现感兴趣区域(region of interest, ROI)的特征都可以与特征图上相应位置的特征一一对应, 于是提出了SPP-Net网络模型. 该模型一次检测只需一次卷积运算, 这使得检测速度得到了极大提升, 其检测速度大约是RCNN的100 倍. SPP-Net网络模型的结构如图4 所示.图 4 SPP-Net结构图[48 ] Figure4. SPP-Net structure diagramt[48 ] $ 4\times4 $ , $ 2\times2 $ , $ 1\times1 $ 的块, 然后用金字塔池化(spatial pyramid poooling, SPP)层进行池化操作, 得到维度为($ 4\times4+2\times2+1\times1 $ )$ \times256 $ 的特征向量, 最后将特征向量作为全连接层的输入, 在输出层输出. SPP-Net 网络模型的核心是在卷积层后加了空间金字塔池化层, 该层可以生成固定大小的图片, 不用对图像进行裁剪, 减少了特征的损失, 而且在整个过程中仅对图片做一次卷积特征提取, 极大地提高了通用物体的目标检测速度. 但其需要将数据分为多个训练阶段, 步骤较为复杂[49 ] .3.4.Faster-RCNN模型 -->3.4.Faster-RCNN模型 虽然RCNN网络模型和SPP-Net网络模型检测目标的准确度较高, 但是它们在检测之前均要先生成2000个左右的候选区域, 这增加了目标检测的时间. Faster-RCNN模型[47 ] 的最大贡献在于废除了选择性搜索算法, 利用区域提议网络(region proposal network, RPN)生成候选区域, 并通过共享卷积运算提取图片特征, 极大地降低了运算量[50 ] , 提高了检测速度. RPN网络模型的结构如图5 所示.图 5 RPN结构图[47 ] Figure5. RPN structure diagramt[47 ] $ n $ 维特征图的每个像素上生成$ k $ 个不同尺寸的锚框, 并给每个锚框分配一个二进制的标签(是否是目标), 若锚框与实际目标的重叠区域的面积大于0.7倍总面积则被标记为正标签, 若锚框与实际目标的的重叠区域的面积小于0.3 倍总面积则被标记为负标签. 然后用一个大小为$ s\times s $ 的滑动窗口生成一个$ n $ 维的特征, 最后连接到分类层和回归层[51 ] , 判断是否存在目标并记录目标位置.3.5.YOLO系列模型 -->3.5.YOLO系列模型 以上所介绍的目标检测算法都是先划分目标候选区域然后再预测目标类别, 而YOLO[52 ] 将目标区域候选区域的划分与类别的预测当作一个回归问题来处理, 直接在图片上输出多个目标的位置和类别, 在保证较高准确率的前提下实现目标的快速检测, 更能满足现实需求[53 ] . YOLO 总共经历了 YOLO, YOLOV2, YOLOV3三个版本, 下面分别对其进行介绍.[54 ] 模型提取图片的特征, 因为InceptionV1模型要求输入图片的尺寸大小是448 × 448, 因此首先要将输入图片的尺寸调整为448 × 448, 其次将调整过尺寸的整张图片作为卷积网络的输入, 并用大小为$ S \times S $ 的网格对原始图片划分, 此时图片中物体的中心点就会落在某个网格单元内, 则对应的网格单元就负责检测该物体. 每个网格单元预测B 个候选框和候选框内的置信度得分. 每个候选框中包含$ x $ , $ y $ , $ w $ , $ h $ 和置信度5个信息[55 ] , 其中$ (x, y) $ 表示预测边框的中心点坐标, $ (w, h) $ 表示预测边框的宽和高, 但需要注意的是中心点坐标的数值是相对于小网络边框而言的, 宽和高的数值是相对于整张图片而言的. 如果网格单元不包含物体, 则置信度为0, 否则置信度的计算公式为$ C $ 个类别的条件概率, 然后用(17 ) 式计算各个网格单元内所有类别的概率.$ S \times S \times (B \times 5 + C) $ 大小的向量中作为YOLO输出层的输出. 在预测时每个网格单元会依据类别概率生成一个候选框, 但是大物体会生成多个候选框, 作者利用非极大值抑制算法选择交并比(intersection over union, IoU)得分最高的候选框, 并去除冗余窗口, 优化检测结果. YOLO的检测速度很快, 可以达到每秒21帧, 但是精度不高, 平均精度只有0.66, 容易漏检小物体. 针对以上问题, 作者在2017年提出了YOLOV2模型[56 ] , 在YOLO模型的基础上做了5 个方面的改进. 首先在每一个卷积层后面都增加了批标准化(batch normalization, BN)操作, 对数据做归一化预处理, 加快了收敛速度. 其次将输出层的全连接层替换为卷积层, 由此可以微调图片的输入尺寸, 使网络适应不同尺寸的输入. 然后引入了Faster-RCNN中候选区域框的概念, 并采用K-均值聚类方法调整候选区域框的尺寸, 使其更好地适应目标的尺寸. 然后在模型中添加转移层, 将浅层特征图连接到深层特征图上, 有利于检测小目标. 最后 YOLOV2不再让每一个小网格预测目标类别, 而把这一任务交给候选区域框. 这5个方面的改进使得YOLOV2在PASCAL VOC数据集上的检测速度达到每秒40帧, 平均精度为0.786.[57 ] . 该模型采用具有 Darknet-53网络来做特征提取, 是YOLOV3的精度得以提升的关键因素. 为了进一步加强对小物体的检测能力, YOLOV3利用多尺度特征对目标进行检测, 在论文中作者采用了大小为$ 13\times 13 $ ,$ 26\times26 $ 和$ 52\times52 $ 三个不同尺度的特征. 最后在分类时用 Logistic回归替代YOLOV2的Softmax回归, 以便对多标签任务分类. YOLOV3 检测一张尺寸为$ 320\times320 $ 的图片所消耗的时间为22 ms, 平均精度为28.2%.3.6.CornerNet网络模型 -->3.6.CornerNet网络模型 以YOLO系列为代表的One-stage深度学习网络模型和Two-stage 深度学习网络模型均属于anchor-base模型, 需要使用不同大小、不同高宽比的 anchor作为检测目标的候选区域. anchor 的优点是将目标检测问题转化为目标与anchor 的匹配问题, 不必用目标检测算法遍历图片, 极大地缩短了检测目标的时间, 使得以YOLO 为代表的 One-stage 模型可以和Two-stage模型竞争. 但使用$ {\rm {anchor}} $ 的深度学习模型也存在着两个主要缺点, 在使用anchor时不仅需要预先生成大量的$ {\rm {anchor}} $ 以便和图片中的目标重叠, 这导致只有少量的$ {\rm {anchor}} $ 与目标重叠, 造成了正负样本不均匀的问题[58 ] , 而且这些 anchor包含很多超参数, 比如anchor的数量、尺寸等, 使得训练过程变得复杂. 针对anchor-base模型存在的缺点, Law和Deng[59 ] 提出一种新的One-stage 模型—CornerNet模型, 该模型利用一对关键点—物体边界框的左上角点和右下角点来检测物体从而取代 anchor, CornerNet网络模型的结构如图6 所示.图 6 CornerNet结构图[59 ] Figure6. CornerNet structure diagramt[59 ] $ c $ 表示类别, heatmaps的尺寸是$ H \times W $ , $ {p_{cij}} $ 为heatmaps中$ c $ 类物体在位置$ (i, j) $ 得分, $ {y_{cij}} $ 表示对应位置的groundtruth, $ N $ 是目标数量, $ \alpha, \beta $ 是超参数, 作者在实验中设置$ \alpha = 2 $ , $ \beta = 4 $ ; Embeddings的作用是匹配同一个边界框的左上角点和右下角点, 其匹配原理是, 如果左上角点和右下角点来自同一个边界框, 则它们的Embeddings之间的距离应该比较小, 反之它们的Embeddings之间的距离应该比较大. Embeddings通过两个损失函数来表示这两种距离:$ {{e_{{t_k}}}} $ 是目标$ k $ 的左上角点, $ e_{{b_k}} $ 是目标$ k $ 的右下角点, $ L_{\rm {pull}} $ 表示属于同一个边界框的左上角点和右下角点之间的距离, $ L_{\rm {push}} $ 表示属于不同边界框的左上角点和右下角点之间的距离, $ e_k $ 表示$ e_{{b_k}} $ 和$ {{e_{{t_k}}}} $ 的平均值, $ \varDelta $ 在实验中设置为1; Offset的作用是微调预测出的边界框, 因为对图片进行全卷积操作之后, 输出的图片尺寸会很小, 因此, 当将位置信息从热力图映射到输入图片时会存在精度损失, 这部分损失用$ {o_k} $ 表示:$ x_k $ , $ y_k $ )表示角点$ k $ 的($ x $ , $ y $ )坐标, 得到$ o_k $ 之后, 利用smooth L1损失函数监督学习该参数:[59 ] 提出corner pooling来确定左上角点和右下角点, corner pooling的原理是, 利用图片中的上边界和左边界的信息确定左上角点, 利用图片中的下边界和右边界确定右下角点. CornerNet 在MSCOCO数据集上测试的平均精度为42.1%, 超过了绝大部分One-stage模型 在MSCOCO数据集中的平均精度.3.7.CenterNet网络模型 -->3.7.CenterNet网络模型 虽然CornerNet网络模型利用一对边角点取代anchor提高了物体检测的精度, 由于CornerNet网络模型中的边角点不在物体内部, 因此CornerNet网络模型无法感知物体内部的信息, 这其实也是大部分One-stage模型普遍存在的问题, 而Two-stage模型可以感知物体内部的信息, 因此Two-stage模型的准确率一般比One-stage模型的准确率高. 针对CornerNet模型无法感知物体内部信息的缺点, Zhou等[60 ] 提出CenterNet网络模型, 利用关键点估计找到物体的中心点并返回目标的尺寸、$ \rm 3D $ 位置、方向、甚至姿态等其他属性, 充分利用了物体内部的信息. Zhou等[60 ] 在COCO数据集上对CenterNet网络模型的速度和精度进行了测试, CenterNet网络模型在Resnet-18网络下取得了每秒142帧的检测速度和28.1%的检测精度, 在DLA-34网络下取得了每秒52帧的检测速度和37.4% 的检测精度, 在Hourglass-104网络下取得了每秒1.4 帧的检测速度和45.1%的检测精度, 其精度可以媲美Two-stage网络, 实现了速度和精度的完美权衡. 该模型的核心思想是, 将图片输入到全卷积网络中生成一个热力图, 其中热力图的峰值对应目标的中心点, 每个峰值点的图像特征还可以预测边界框的宽和高, 返回目标的其他属性.$ ({x_1}, {x_2}, {y_1}, {y_2}) $ 表示目标边界框的坐标, 计算出真实坐标$ p $ 之后, 用下采样后的$ \widetilde p = \left\lfloor {{p}/{R}} \right\rfloor $ 替代$ p $ , 其中$ R $ 是下采样因子, 然后采用高斯核${Y_{xyc}} = $ $ \exp \left(-\dfrac{(x -{{\widetilde p}_x)}^2 + (y - {{\widetilde p}_y})^2}{{2\sigma _p^2}}\right) $ 将关键点分布到特征图上, 其中$ {\sigma _p} $ 是目标尺寸自适应标准差, 并用如下所示的损失函数使得预测的目标中心点坐标与真实值之间的距离最小:$ \alpha $ , $ \beta $ 是损失函数的超参数, 在实验中作者设$ \alpha = 2 $ , $ \beta = 4 $ ; $ N $ 是图片中关键点的数量.$ R $ 对图片进行了下采样, 把特征图重新映射到原始图片时会存在误差, 因此用local offect补偿损失, 并用L1 Loss训练偏置值$ L_{\rm {off}} $ :$ {s_k}\; = \left(x_2^{(k)} - x_1^{(k)}, y_2^{(k)} - y_1^{(k)}\right) $ 是标准边界框的大小. 最后整体的损失函数为$ L_k $ , $ L_{\rm {size}} $ 与$ L_{\rm {off}} $ 三者的和, 而且每个损失都有相应的权重.$ {\lambda _{\rm {size}}} = 0.1 $ , $ {\lambda _{\rm {off}}} = 1 $ ; 这样用一个网络就可以得到目标中心点的预测值、偏置和尺寸.[61 ] 用中心点、左上角点和右下角点三个关键点检测物体, 提高了物体的检测精度, 在MS-COCO数据集中的检测精度达到了47.0%, 但是检测速度比较慢, 检测一张图片需要340 ms[61 ] .3.8.多目标跟踪评价指标 -->3.8.多目标跟踪评价指标 由于深度学习算法的评价指标平均精度(mean average precision, mAP)属于目标检测领域的指标, 只能用于衡量检测目标的准确性, 不能用来衡量多目标算法的跟踪性能, 因此为了比较以上跟踪算法的性能, 需要选择相应的多目标跟踪评价指标对其进行衡量. 文献[62 ]最早提出了多目标跟踪准确度MOTA、多目标跟踪精度MOTP 两种评价指标, 此外在MOT Challenge[63 ] 多目标跟踪评价平台上也提供了部分评价指标, 如跟踪轨迹大致完整(大于80%) 的比率MT、虚警数FP、丢失数FN 以及轨迹误配数IDS. 其中MOTA是最重要的一个指标, 用来度量算法能否准确确定目标个数.$ {{fp}}_t $ , $ m_t $ , $ { {mme}}_t $ 分别表示在第$ t $ 帧时的误判数, 丢失数, 误配数, $ g_t $ 表示第$ t $ 帧时跟踪的目标数. MOTA的取值范围是(–∞, 1], 仅当没有错误的时候取1.$ d_t^i $ 表示目标$ i $ 的预测位置与真实位置的距离; $ g_t $ 表示第$ t $ 帧时跟踪的目标数.表3 所列.算法 MOTA↑ MOTP↑ MT↑ ML↓ IDS↓ 数据集 类别 卡尔曼滤波[64 ] 85.00% — — — — MIT Traffic video dataset 传统跟踪算法 多假设跟踪算法[21 ] 29.10% 71.70% 12.10% 53.30% 476 MOT Benchmark 传统跟踪算法 粒子滤波算法[27 ] — — 80.80% 0.70% 10 CAVIAR dateset 传统跟踪算法 基于马尔科夫决策的[31 ] 30.30% 71.30% 13.00% 38.40% 680 MOT Benchmark 传统跟踪算法 相关滤波算法[65 ] 83.40% 73.50% — — — Urban Tracker dataset 传统跟踪算法 基于Faster-RCNN的跟踪算法[66 ] 38.50% 72.60% 8.70% 37.40% 586 MOT 15 Benchmark 深度学习跟踪算法 基于YOLOV3的跟踪算法[67 ] 60.50% 79.30% 30.20% 19.60% 1129 MOT 16 Benchmark 深度学习跟踪算法
表3 不同算法之间的性能对比Table3. Performance comparison between different algorithms4.行人动力学模型 利用以上部分介绍的算法和模型, 便可以得到行人$ k $ 的边界框坐标$ ({x_{k1}}, {y_{k1}}, {x_{k2}}, {y_{k2}}) $ , 对相应的坐标求平均值便可得到行人$ k $ 的中心点坐标$ ({\overline x _k}, {\overline y _k}) $ , 然后进一步用时间间隔$ \Delta t $ 记录行人的中心点坐标, 最后用相邻两次的坐标之差与$ \Delta t $ 相除便可求得行人的速度信息. 在得到行人的运动轨迹、速度等参数之后, 便可对移动人群的运动模式进行分析, 从中挖掘出群体行为的潜在规律[68 ] . 已有大量文献建立了各种模型分析行人的动力学行为[69 ,70 ] , 本文介绍三种典型的流体动力学模型、社会力模型、启发式模型, 以及结合了多种模型的集成模型.4.1.流体动力学模型 4.1.流体动力学模型 针对人群行为分析问题, Henderson[71 -74 ] 首先将气体动力学和流体动力学模型应用到行人群体中. 他通过测量各种人群的速度频率分布发现行人在经过十字路口时大部分人为了躲避来往车辆会降低行走速度, 而少部分人会加快行走速度. 进一步的研究还表明经过十字路口时女性的速度比男性的速度要低. 因此作者用性别和遇到的车辆数量对行人群体进行划分, 对女性和男性分别用二维气体的麦克斯韦- 玻尔兹曼速度分布进行描述, 得到了很好的拟合效果, 但其存在一个动量守恒和能量守恒的假设条件.[75 ] 舍弃了动量守恒和能量守恒的假设, 用一个改进的类玻尔兹曼的气体动力学模型来描述不同的行人群体. 该模型首先将行人按照行走方向的不同划分为不同的模式 $ \mu $ , 其次给不同模式的$ \mu $ 设置三个变量 $ x $ , $ { v}_\mu ^0 $ , $ {{ v}_\mu } $ , 其中$ x $ 表示模式$ \mu $ 所处的位置, $ { v}_\mu ^0 $ 表示模式 $ \mu $ 的理想速度, $ {{ v}_\mu } $ 表示模式$ \mu $ 的实际速度, 然后利用上述三个变量建立密度方程$ {{\hat \rho }_\mu }({ x}, {{{ v}}_\mu }, { v}_\mu ^0, t) = \dfrac{{{N_\mu }(u({ x}) \times v({{{ u}}_\mu }), t)}}{{A \cdot V}} $ , 密度$ {{\hat \rho }_\mu } $ 与 行人达到理想速度${ v}_\mu ^0 $ 的趋势[76 ,77 ] 、行人间的相互作用、运动模式的改变、每单位时间内区域密度的增加或减少四个因素有关, 下面具体介绍这四个因素对密度$ {{\hat \rho }_\mu } $ 的影响.$ { v}_\mu ^0 $ 的趋势使得其密度$ {{\hat \rho }_\mu } $ 接近平衡密度$ \hat \rho _\mu ^0 $ :$ \hat \rho _\mu ^0 $ 表示理想速度为$ {{{ v}}_\mu } $ 而实际速度为$ {{ v}_\mu } $ 的行人密度, $ \delta ( \cdot ) $ 是狄拉克函数.[78 ,79 ] 建模:$ {{\hat \sigma }_{\mu v}}({ u}_\mu ^1, { u}_v^1;{ u}_\mu ^2, { u}_v^2;{ x} t) $ 表示模式$ \mu $ 和模式v 的行人将其状态从$ ({\kern 1 pt} { u}_\mu ^1, { u}_v^1{\kern 1 pt} ) $ 更改为$ ({\kern 1 pt} { u}_\mu ^2, { u}_v^2{\kern 1 pt} ) $ 的相对速度.$ \langle {{\hat \rho }_\mu }\rangle $ , 平均速度$ \langle {v_\mu }\rangle $ 和速度方差$ \langle {({\sigma _{{\mu _{u, i}}}})^2}\rangle $ 的流体动力学方程.[80 ] . 但是其忽视了人群中个体与个体之间的相互作用, 不能从微观层面刻画每个行人的行为特征, 也无法解释个体行为对群体行为的影响[81 ] .4.2.社会力模型 -->4.2.社会力模型 针对流体动力学模型无法从微观层面上描述个体行为的问题, Johansson等[82 ] 提出了社会力模型. 社会力模型中的社会力由自驱动力、排斥力和吸引力三部分组成.$ {{ v}_\alpha } $ 等于理想速度$ { v}_\alpha ^0 $ . 如果受到障碍物的干扰, 行人会调整自己的速度, 但在自驱动力的作用下会产生一个指向$ { v}_\alpha ^0 $ 的加速度, 使得实际速度$ {{ v}_\alpha } $ 向理想速度$ { v}_\alpha ^0 $ 靠近, 自驱动力的作用可以表示为${ F}_\alpha ^0 $ 表示自驱动力, $ { v}_\alpha ^0 $ 表示理想速度的大小, $ {{{ e}}_\alpha } $ 表示理想速度的方向, $ {\tau _\alpha } $ 表示从实际速度变为理想速度所需的时间.$ v_α^0 $ , 行人$ \alpha $ 在接近陌生人$ \beta $ 时, 可以用下面的方程表示:$ {V_{\alpha \beta }}[b({{ r}_{\alpha \beta }})] $ 是$ b $ 的单调递减函数, 且其椭圆形等值线指向运动方向, $ b $ 是椭圆的半短轴.$ {{ r}_{\alpha \beta }} = {{ r}_\alpha } - {{ r}_\beta } $ 是行人$ \beta $ 步距的数量级.$ {U_{\alpha \beta }}(\parallel {{ r}_{\alpha \beta }}\parallel ) $ 单调递减.$ {{ r}_i} $ 的吸引力$ {f_{\alpha i}} $ 可以用单调递增的吸引潜力$ {W_{\alpha i}}(\parallel {{ r}_{\alpha i}}\parallel, t) $ 表示:$ {f_{\alpha i}}(\parallel {{ r}_{\alpha i}}\parallel ) $ 会随着时间不断减小, 因为对行人或者障碍物的兴趣会随着时间不断降低. 同时, 这种吸引力效应是形成人群的原因.$ c $ , 0 < c < 1. 由此引入方向相关权重:4.3.行为启发式模型 -->4.3.行为启发式模型 社会力模型虽然能够解释一部分人群行为, 但是在实际的应用过程中会产生比较复杂的数学公式, 参数很难校准[83 ] . 因此Moussa?d等[84 ] 提出一种简单的行为启发式模型来捕捉人群行为中的潜在规律. 该模型认为行人行为模式的改变是通过两种简单的认知过程完成的, 并加入了行人的视觉信息[85 -87 ] . 此外还考虑了极度拥挤情况下行人之间无意的碰撞行为. 该模型主要包括视觉信息复现、认知过程、碰撞效应三部分.$ \left[ { - \varPhi, \varPhi } \right] $ 表示, 其含义是以行人行走视线$ H_i $ 所在方向为基准, 向视线$ H_i $ 左右两边最大各倾斜$ \varPhi $ 度. 视野范围内最近一个障碍物到行人$ i $ 的距离用$ f $ 表示, 如果行人i 以速度$ v_i^0 $ 在向目标方向前进的过程中不会与障碍物发生碰撞, 则令$ f $ 等于无穷大. 其次构造两个认知过程来模拟行人对视觉信息的处理, 第一个认知过程用来确定行人在遇到障碍物之后所选择的行走方向, 第二个认知过程用来确定行人遇到障碍物之后应该调整为多大的速度.[87 ] , 行人在避开障碍物的前提下并不愿意在目的路线上偏离太多. 因此, 第一个认知过程是“行人在保证不与障碍物发生碰撞的前提下, 选择一条到目的地$ O_i $ 的最短路径”, 可以表示为:$ {\alpha _{\rm {des}}} $ 表示行人遇到障碍物后所选择的最短路径方向, $ {\alpha _0} $ 表示目的地的方向.$ \tau $ 来防止与障碍物发生意外碰撞. 由此第二个启发式是“行人在所选择的行走方向上与障碍物保持一定的距离”, 可以表示为$ v_{\rm {des}} (t) $ 表示实际速度, $ v_i^0 $ 表示理想速度, $ d_{\rm h} $ 表示最近的障碍物和行人的距离, $ \tau $ 表示缓冲时间.$ {{ n}_{ij}} $ 是从行人$ i $ 指向行人$ j $ 的归一化向量; $ {d_{ij}} $ 表示行人之间的距离; $ {r_i} $ , $ {r_j} $ 分别表示行人$ i $ , $ j $ 的半径; $ kg $ 是系数; $ {f_{ij}} $ 表示行人$ i $ , $ j $ 之间的相互作用力.4.4.集成模型 -->4.4.集成模型 随着研究的深入, 人们发现单一的模型都存在一定的缺点, 很难准确描述人类行为. 比如启发式模型虽然简单高效, 但它无法像社会力模型那样描述来自其他行人或者障碍物的排斥力. 同样社会力模型中也不能运用启发式模型中的视觉信息来调节行走方向. 于是Porter等[88 ] 提出了IM模型框架, 该模型集成了社会力模型、行为启发式模型以及材料科学理论, 充分发挥了每个模型的优势.24 )式描述行人遇到障碍物后实际速度与理想速度的不同, 用(25 )式和(27 )式描述行人之间、行人与障碍物之间的排斥力. 其次用行为启发式模型确定行人在遇到障碍物时所选择的行走方向, 公式如下:$ {{ e}_\alpha }(t) $ 表示行人$ \alpha $ 的目标方向, $ {d_{\max }} $ 表示行人$ \alpha $ 视线的最远距离, $ r(e) $ 表示距离行人最近的一个障碍物的距离, $ {{ e}_0} $ 表示目的地的方向, $ { e}$ 表示视野范围内的方向.5.典型系统及应用 25.1.智能监控领域 5.1.智能监控领域 现在市场上安装的监控摄像机需要有专门的人员不断地监察影像以应付可疑事件, 但实际上这些摄像头拍摄的视频很少有人一直监察或者根本没有人监察, 导致摄像机没有起到应有的作用[89 ] . 因此, 如果计算机能自动监视它便可起到预警的作用, 帮助人们提前发现异常情况.[90 ] 建立了一种从室内场景中检测丢失物体的系统. 该系统包括目标分割、目标的识别和跟踪以及动作决策三个模块. 该系统首先将目标按照是行人还是物体、是动态还是静态划分为4 类, 然后对动态的行人和物体进行持续跟踪, 最终物体处于静止状态时则被认定为丢失, 及时发出警报, 来协助工作人员进行处理. 但该系统仅适合在室内场合使用, 并且行人之间的遮挡时间过长会导致误报, 这时就需要人工来判别.[91 ] 开发的一套集运动目标检测、目标跟踪、目标分类一体的智能监控系统, 湖南大学万琴和王耀南[92 ] 提出的一种针对固定监控场景的运动检测与目标跟踪方法. 在国外, Nikouei等[93 ] 把智能监控作为一种边缘网络服务, 提出了一种轻量级CNN算法, 拥有更高的运算速度和较少的内存使用, 提高了行人检测的实时性. Gajjar等[94 ] 用K -均值算法来跟踪监控视频中的行人, 首先在视频中记录与行人位置相关的HOG特征向量, 然后用K -均值算法聚类得到了行人的轨迹.5.2.拥堵人群分析 -->5.2.拥堵人群分析 人群踩踏是拥堵人群中最具灾难性的事件之一[95 ] . 当聚集在一个地点的人群密度过高时, 人与人之间不可避免地会发生身体接触, 此时一个行人对其周围人的作用力会像水纹一样不断向外传播, 并与其他各个方向不同大小的力相互叠加起来共同作用在人群中. 这些合力将人们在人潮中推来推去, 同时由于人群密度的增加, 人群之间的温度也随之升高. 拥挤的空间加上闷热的环境会让人产生头晕、乏力等症状. 如果此时有人不幸跌倒, 那么在多米诺骨牌效应的作用下会引发一系列连锁反应—周围的人也相继跌倒[96 ] , 从而引发大规模的踩踏伤亡事件. 拥堵人群的安全问题在应急管理、消防安全、建筑设计等领域都有着重要意义[97 ] .[98 ] 利用HUER数据集, 对6个不同的朝圣地点进行了建模, 可以实现在不同的朝圣视频场景中对仪式地点进行分类. 该系统包括预处理、分割、特征提取和位置分类四个阶段. 将视频帧作为输入输入到k 近邻(KNN)、人工神经网络(ANN) 和支持向量机(SVM)分类器中. 该系统普遍提高了六个朝觐仪式的识别准确率, 其准确率超过90%. 虽然这个系统在识别朝觐仪式上有更好的准确性, 但还不足以对踩踏事件作出预警.[99 ] 通过对拥堵人群中密度、速度、压力等参数的分析, 发现当人群中的压力是导致踩踏事件的关键因素, 一旦压力超过0.02 则踩踏事件不可避免, 由此提供了一个踩踏事件的预警机制. 在实际生活中, 踩踏事件多由突发事件引起, Zhao等[100 ] 通过对由突发事件的研究发现, 在突发事件发生之后人们会争先恐后地往出口方向逃脱, 这造成出口区域附近人员密度极高, 人与人之间的拥挤程度加深, 减缓了人们的逃离速度. 针对这一现象, Zhao等[100 ] 在出口处设置类似面板形状的障碍物引导行人分流, 降低出口区域的人群密度, 并通过实验表明该方法可以提高疏散效率, 减少人员伤亡. 因此对拥堵人群设计有效的疏散方法, 有助于减少人群中由于恐慌和从众行为所造成的经济损失和人员伤亡, 对改进应对突发事件的策略具有十分重要的意义[101 ] .5.3.异常行为分析 -->5.3.异常行为分析 在公共安全领域, 需要及时发现危险分子的异常行为, 确保人民群众的生命和财产安全. Yogameena和Nagananthini[102 ] 利用投影和骨架化方法对个体的正常和异常行为进行分类, 该系统主要包括运动检测与跟踪、行为分析,它可以检测到人类走路、跑步、打架、弯腰等异常行为, 准确率高. 但是适合稀疏人群, 在拥堵人群中效果不佳.[103 ] 认为约70%的意外摔倒是可以预防的, 并提出了一种结合个人信息(如年龄、性别、体重)的全摄像头来检测老年人是否摔倒. 摄像机的图像实时传输到一台服务器上, 对前景中感兴趣的对象进行背景减除, 然后系统使用连接组件标记来获取每个对象的面积、高度和宽度, 设置一个简单的判定跌落阈值来确定一个人是否跌落. 此外, 马里兰大学的计算机视觉实验室利用对灰度图像中的人体建模, 同时根据手、腿及头部等部位的动作的分析与跟踪, 能够实现对多个行人进行检测与跟踪[104 ] . Kocabas等[105 ] 提出了一种多人姿态估计框架, 该框架将多任务模型与残差网络相结合, 可以联合处理人体检测、关键点检测和姿态估计问题, 作者在COCO关键点数据集上测试的检测速度是23帧每秒.6.结 论 行人跟踪是计算机视觉领域中的难点和热点问题, 同时也是人类行为动力学中一个难点问题. 虽然之前的工作提出了大量再现人群行为的模型, 但由于缺乏对现有模型进行验证或校准的公开数据集, 使得这些模型之间没有一个很好的评判标准. 而且目前关于大规模人群行为的分析大都停留在统计和宏观层面上, 如基于手机数据对受地震、极端气候影响的人口迁移模式[106 -108 ] 以及对个人旅行模式的时空分布的研究[109 ,110 ] ; 基于社交网络软件对自然灾害发生前后社交网络的结构及其演化的研究[111 ] , 对男同这一特殊群体的行为研究[112 ] ; 基于传感器的应急管理救援研究等[113 ] , 但微观层面上的研究极度缺乏. 近年来, 随着深度学习技术在计算机视觉领域的兴起, 已有部分文献运用深度学习技术分析人群中的异常行为、估计行人的运动姿态, 且取得了良好的效果. 这使得人们应用开源分析平台建立大规模标准数据集成为了可能, 并为在微观和中观尺度下对大规模人群行为分析提供了一个新思路. 


























































































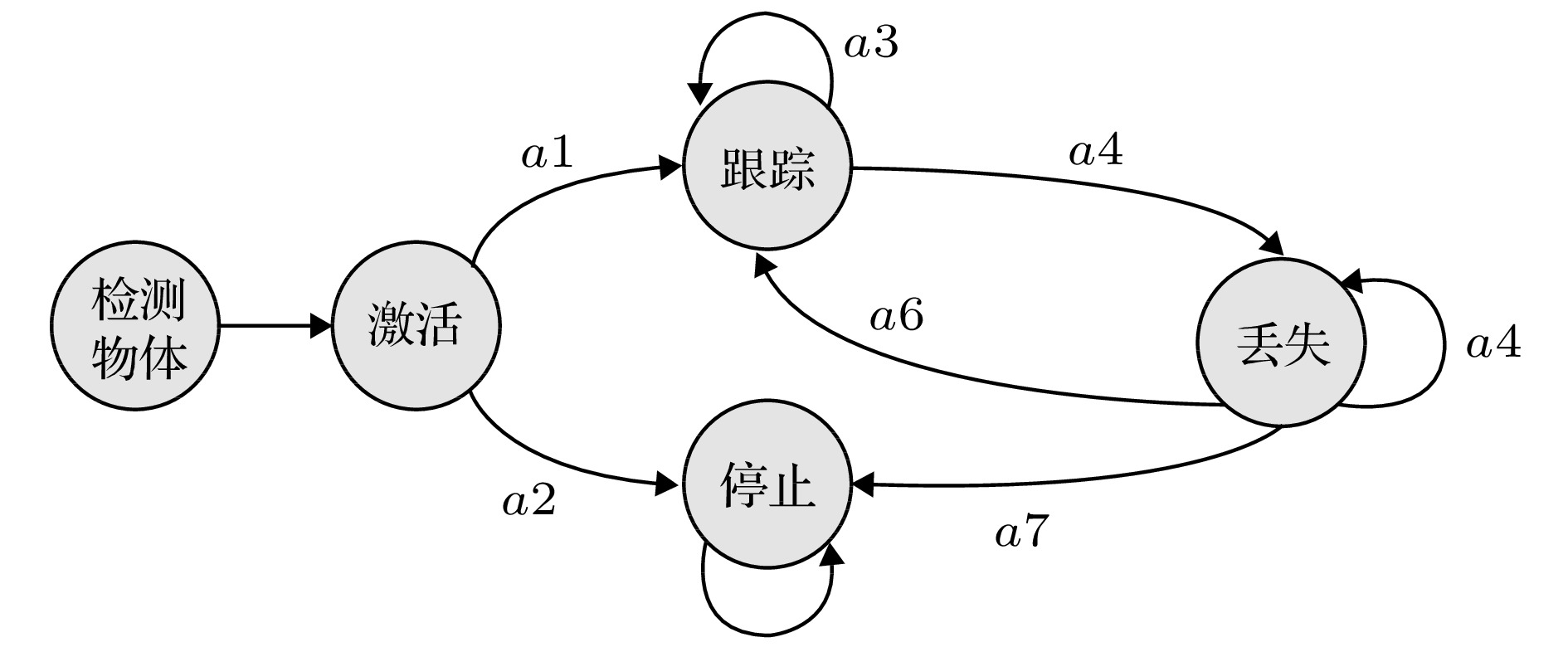 图 1 马尔科夫决策过程流程图[31]
图 1 马尔科夫决策过程流程图[31]
























































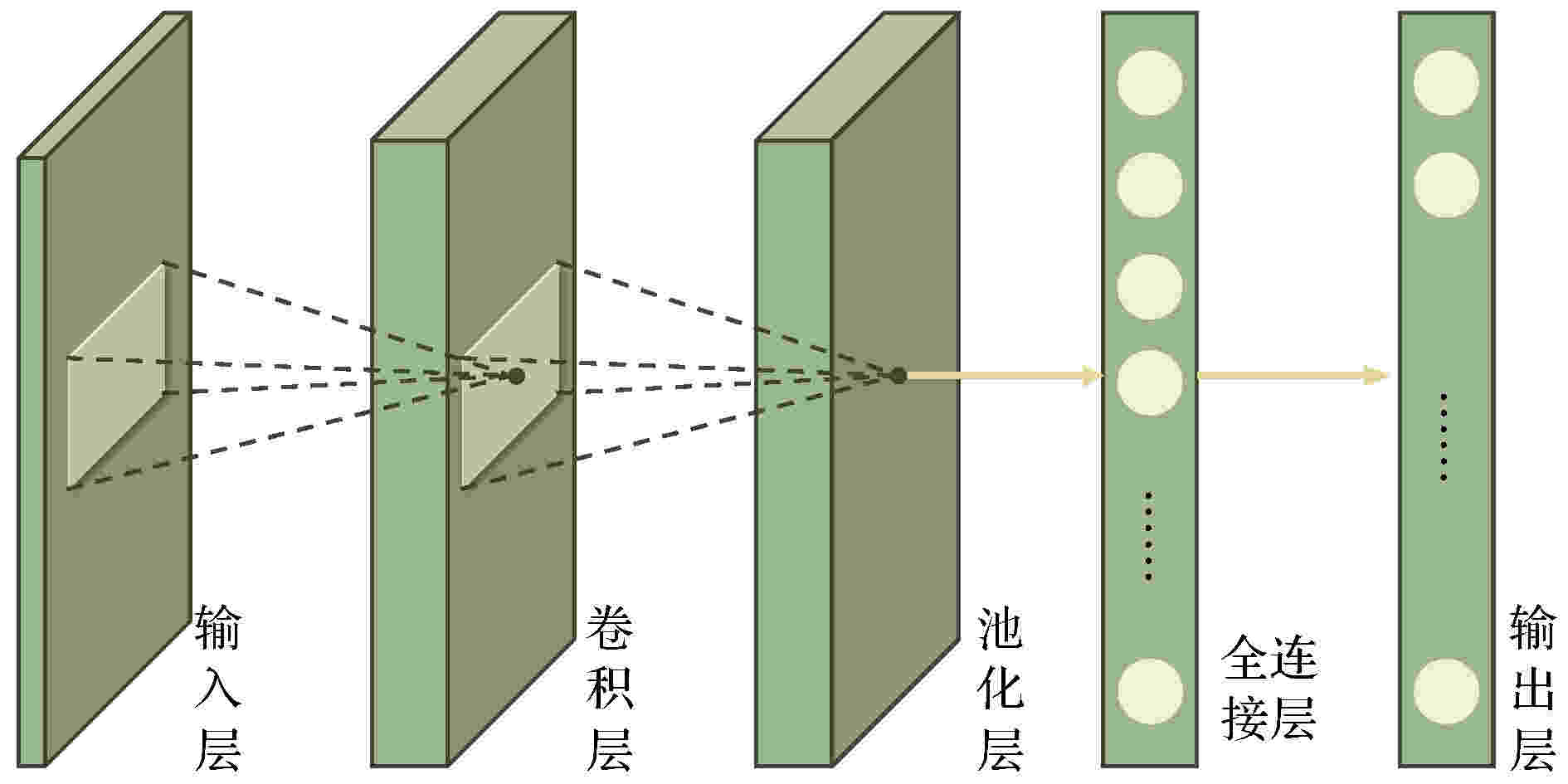 图 2 CNN基本结构图
图 2 CNN基本结构图
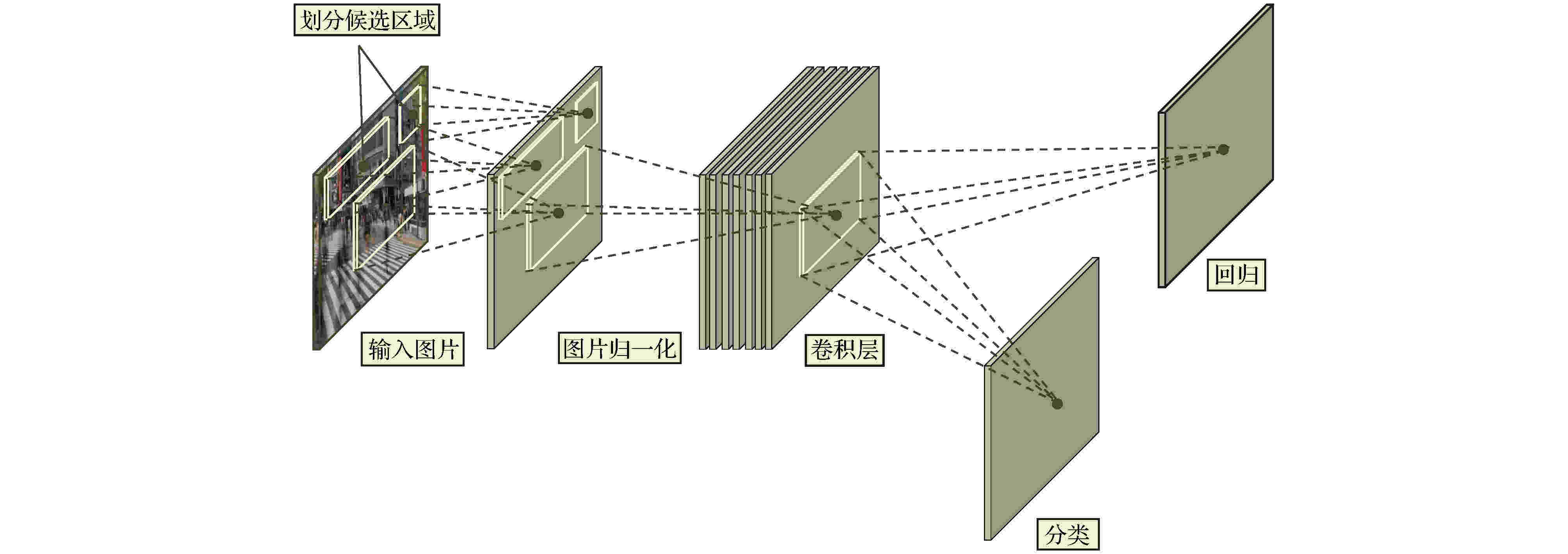 图 3 RCNN算法流程图[45]
图 3 RCNN算法流程图[45]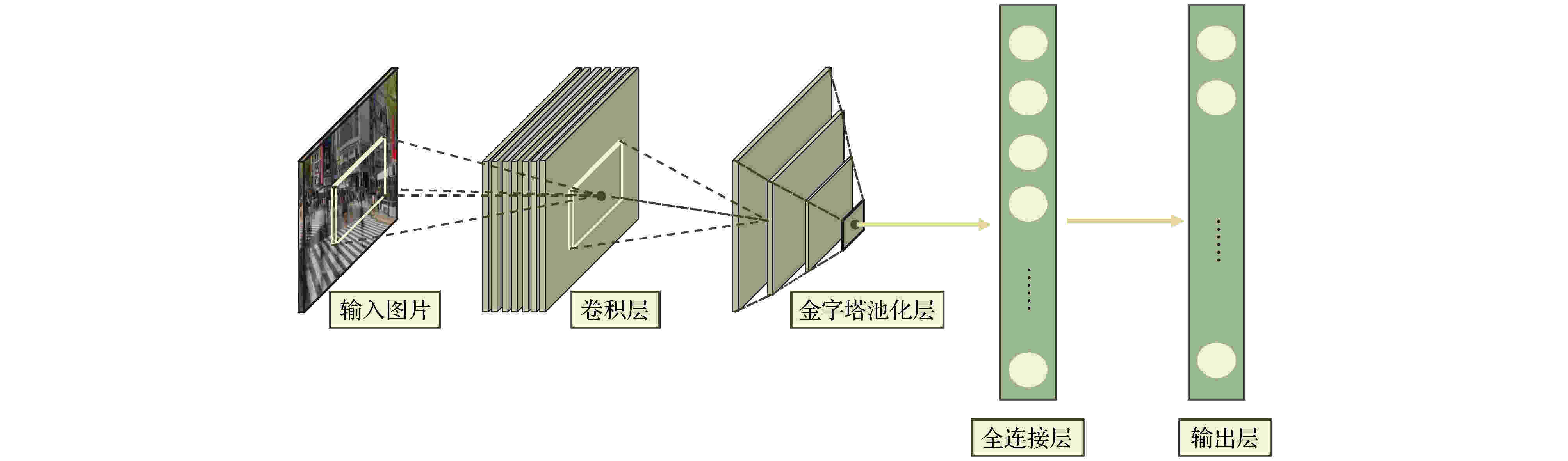 图 4 SPP-Net结构图[48]
图 4 SPP-Net结构图[48]




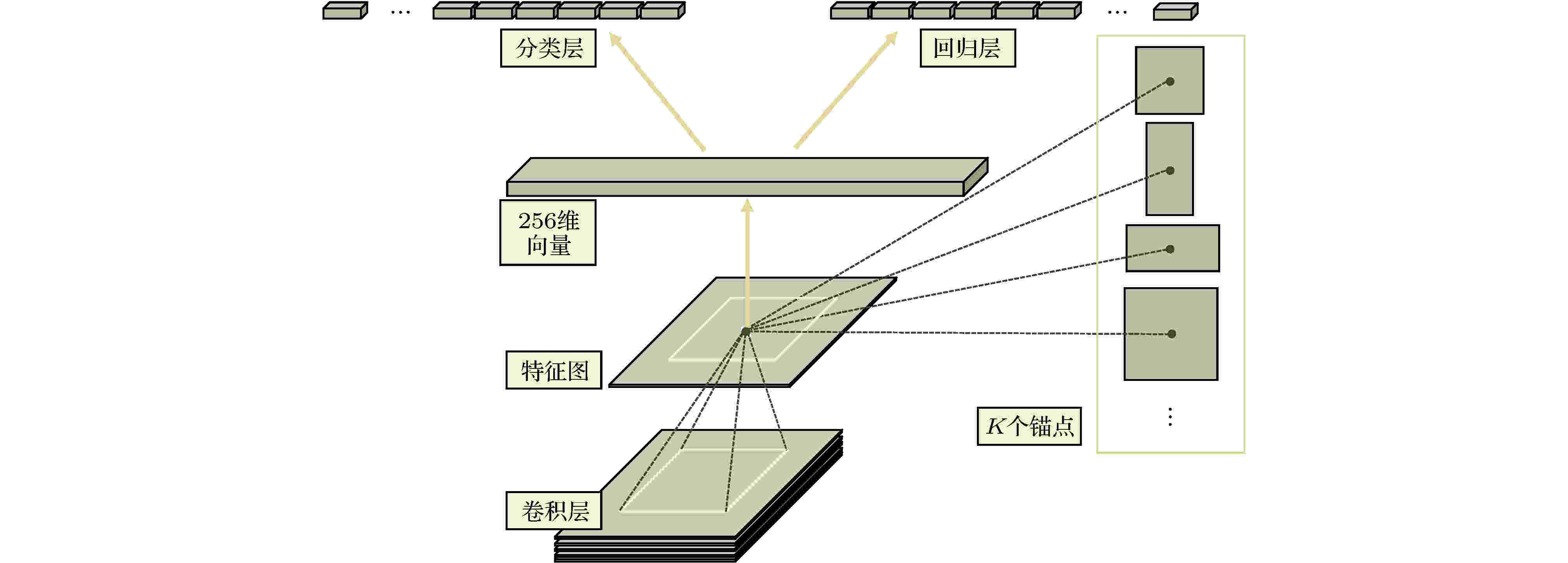 图 5 RPN结构图[47]
图 5 RPN结构图[47]



























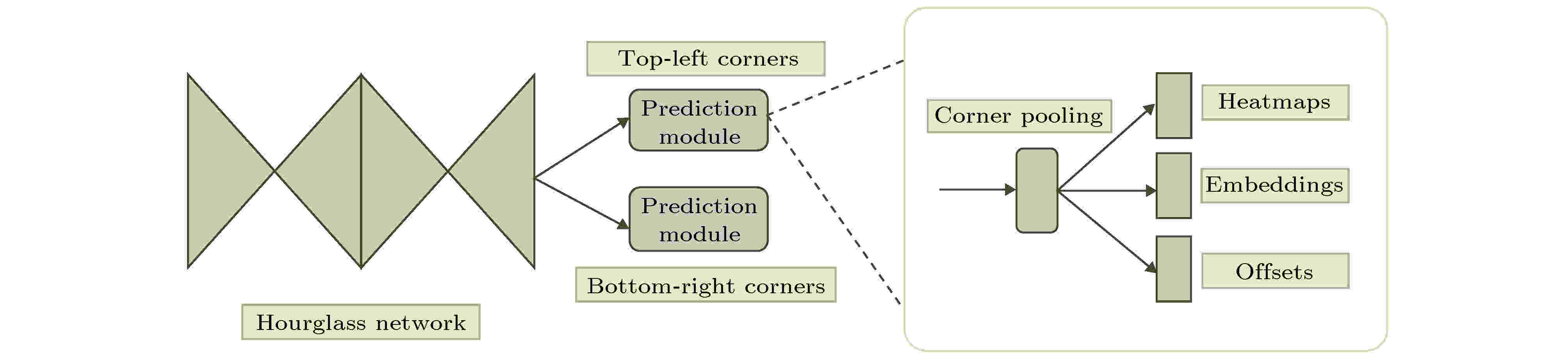 图 6 CornerNet结构图[59]
图 6 CornerNet结构图[59]































































































































































































































