摘要:Majorana准粒子是凝聚态物理版本的Majorana费米子. 由于Majorana准粒子间的交换操作服从非阿贝尔统计, 并基于此可构建更稳定的量子计算机, 近年来在凝聚态物理界引起广泛关注. 为帮助初****快速理解Majorana准粒子的形成机理, 本文回顾了在一维超导体-半导体异质纳米线系统中Majorana准粒子模型的提出和理论演化过程, 介绍Kitaev链模型并分析了模型中各要素所起的作用. 还介绍了典型Majorana器件的构成和测量方法, 并结合最新的实验进展对探测到的零能电导峰进行了分析和述评. 最后对超越一维系统的超导体-半导体异质系统的实验前景进行了展望.
关键词: 拓扑物态/
马约拉纳零模/
半导体纳米线

English Abstract

全文HTML

--> --> -->

当今人类面临的很多迫切问题, 例如预测全球气候变化、开发新型药物等, 都需要超强的计算能力来找到解决方案. 随着晶体管尺寸趋近经典物理定律极限, 传统计算机的发展面临巨大挑战. 在这种背景下, 量子计算作为新型计算技术的代表被寄予厚望. 理论预言量子计算在一些特定的算法上会优于经典计算, 量子计算的优越性(或称“量子霸权”)近日也被谷歌公司宣称实现^[1]. 然而, 可容错的量子计算机在实际工程上面临一个严峻挑战: 量子态退相干. 这是由于量子比特(量子计算的基本单元)和周围环境不可避免的相互作用所引起的对量子叠加态或纠缠态的破坏. 为了在一个量子态相干时间内进行足够多的量子门操作, 现今主流的量子计算实现方式(比如超导量子比特)一般通过捆绑多个物理比特形成一个逻辑比特进行现场冗余纠错来解决退相干问题. 但是, 在当前物理比特的错误率下, 形成一个可大规模集成的逻辑比特所需的物理比特的数量可能高达成千上万个. 这给容错量子计算机的实现设置了一个巨大的技术障碍, 目前仍然没有实现一个逻辑量子比特.
为此, 理论物理学家在21世纪初的时候提出了利用物质的拓扑性来解决量子比特退相干的问题^[2]. 这种思路是利用低维系统中遵循非阿贝尔统计的准粒子(或称非阿贝尔任意子^[3], non-Abelian anyon)来进行量子信息编码. 对这种任意子进行交换操作(braiding operation, 俗称“辫织”), 操作的结果仅与系统全局的拓扑性(也即交换的顺序)相关, 从而使其免受一般局域性环境噪声的干扰. 因此, 非阿贝尔任意子被预言为可被用于实现自容错的拓扑量子计算机^[4].
非阿贝尔任意子中被研究的最广泛的一种叫Majorana准粒子(在不同语境下又称为Majorana零模态或Majorana束缚态), 它同时也是Majorana费米子^[5]的凝聚态版本. 根据理论预测, Majorana准粒子可存在于分数霍尔效应^[6]、p波超导体^[7]、超导-拓扑绝缘体异质体系^[8]、磁性原子链^[9]或超导-半导体异质体系^[10–13]等. 其中, 超导-半导体异质结构, 特别是其一维形态, 因为对材料合成要求较低且可用门电极进行调控等原因成为当前被研究最广泛的体系之一.
在这篇综述中, 我们将聚焦超导-半导体异质纳米线体系中的Majorana准粒子. 第一部分介绍Majorana准粒子的实现机理, 第二部分概述超导-半导体异质纳米线体系中Majorana准粒子的实验探测工作进展, 最后一部分展望Majorana准粒子的应用前景、技术挑战和应对方案.

2

-->

2.1.Majorana费米子

在介绍Majorana准粒子之前有必要回顾一下Majorana粒子态(即Majorana费米子)的提出过程.
1928年Paul Dirac将薛定谔粒子波动方程${\rm{i}}\hbar \dfrac{{{\rm{d}}\psi }}{{{\rm{d}}t}} = \left( { - \dfrac{{{\hbar ^2}}}{{2 m}}{\nabla ^2} + V} \right)\psi $改写成了相对论版本的Dirac方程${\rm{i}}\hbar \dfrac{{{\rm{d}}\psi }}{{{\rm{d}}t}} = \left( { - {\rm{i}}\hbar c\vec \alpha \nabla + \beta m{c^2}} \right)\psi $. 在这个新的兼容相对论的波动方程中, 波函数ψ变成包含4个分量的向量解, 其多余的自由度刚好可以描述粒子的自旋结构. Dirac方程也预言了方程的负能解, 并最终导致反粒子概念的提出. Dirac指出所有的费米子都存在与其对应的反粒子, 具有相同的质量, 自旋和相反的电荷^[14]. 反粒子的假说很快被正电子的实验证据证实^[15].
在Dirac方程中, 系数${\vec \alpha }$和β的选择需要满足很多约束条件以及非对易关系, 1937年Ettore Majorana在考虑数学对称性的基础上找到了满足该约束条件的新的一组系数以及所对应的解. 用现代的方程表现形式可记为:

$\left( {{\rm{i}}\hbar {{\tilde {{\gamma}}}^\mu }{\partial _\mu } - mc} \right)\tilde \varPsi = 0$

其中${\tilde {{\gamma}} ^\mu }$代表四个纯虚数矩阵. 在这种形式下, Majorana方程给出了一组实数波动方程解$\tilde \varPsi $, 因此其描述的粒子的波动方程满足$\tilde \varPsi = {\tilde \varPsi ^? }$. 用二次量子化的语言描述即粒子的产生算符和湮灭算符是相同的, 或者说此粒子等同于其反粒子. 这种粒子因此被命名为Majorana粒子.
Majorana本人猜测中微子是一种Majorana粒子, 但至今尚未有定论.
2 -->

2.2.Majorana算符

在粒子物理学里, 电子的反粒子是正电子, 而在半导体中, 可将电子的反粒子看成是空穴, 也就是说, 从系统里拿走一个电子等同于创造一个空穴. 在二次量子化的表述中常用算符$c_i^?$描述产生一个电子(或者是湮灭一个空穴), 而其共轭算符c_i则描述在i态上创造一个空穴(或者是湮灭一个电子). 因为电子是费米子, 需要遵循Fermi-Dirac统计, 因此c_i^?和c_i遵循三个很关键的关系^[16].
1)不相容: ${({c_i})^2} = {(c_i^? )^2} = 0$;
2)反对易: $\{ {c_i^?, {c_j}} \} \equiv c_i^? {c_j} + {c_j}c_i^? = \left\{ {{c_i}, {c_j}} \right\} =$$\{ {c_i^?, c_j^? } \} = 0, \;\;\left( {{{i}} \ne {{j}}} \right)$;
3)完备性: $\{ {c_i^?, {c_i}} \} = 1$.
在遵循以上法则的基础上, c_i和c_i^?可以写成实部和虚部分开的形式:

$\begin{aligned}&{c_i} = \frac{1}{2}\left( {{\gamma _{i,1}} + {\rm{i}}{\gamma _{i,2}}} \right),\\& c_i^? = \frac{1}{2}\left( {{\gamma _{i,1}} - {\rm{i}}{\gamma _{i,2}}} \right).\end{aligned}$

据此, 新定义的γ_i算符可以被写成:

$\begin{aligned}&{\gamma _{i,1}} = c_i^? + {c_i}, \\& {\gamma _{i,2}} = {\rm{i}}( {c_i^? - {c_i}}).\end{aligned}$

容易证明以上三条法则也适用于γ_i. γ_i是共轭对称的: $\gamma _i^? = {\gamma _i}$, 即γ_i是Majorana算符.
2 -->

2.3.Kitaev-Chain模型

以上Majorana算符的推导只是一个数学游戏, 因为需要将一个电子c^?空间上拆分成两个Majorana粒子(γ₁和γ₂)才有物理意义. 但是Majorana算符作为一个电子的产生和湮灭算符的叠加给了理论学家们灵感, 如果把一个电子和一个空穴叠加起来即可产生一个中性的态. 例如, 超导体中的Bogoliubov准粒子便是电子和空穴的叠加态: $b = uc_{\sigma 1}^? + v{c_{\sigma 2}}$, 其中$\sigma = \uparrow, \downarrow $为自旋. 可以看出, 当不考虑自旋且u = v时, ${b^? } = uc + u{c^? } = b$, 即得到了Majorana准粒子态.
在这种想法的指导下, Alexei Kitaev提出了一个一维无自旋超导体链的玩具模型, 见图1(后来称为Kitaev链模型^[18]). 在Kitaev链模型中, 电子自旋被略去(无自旋), 其哈密顿量的离散形式可写为
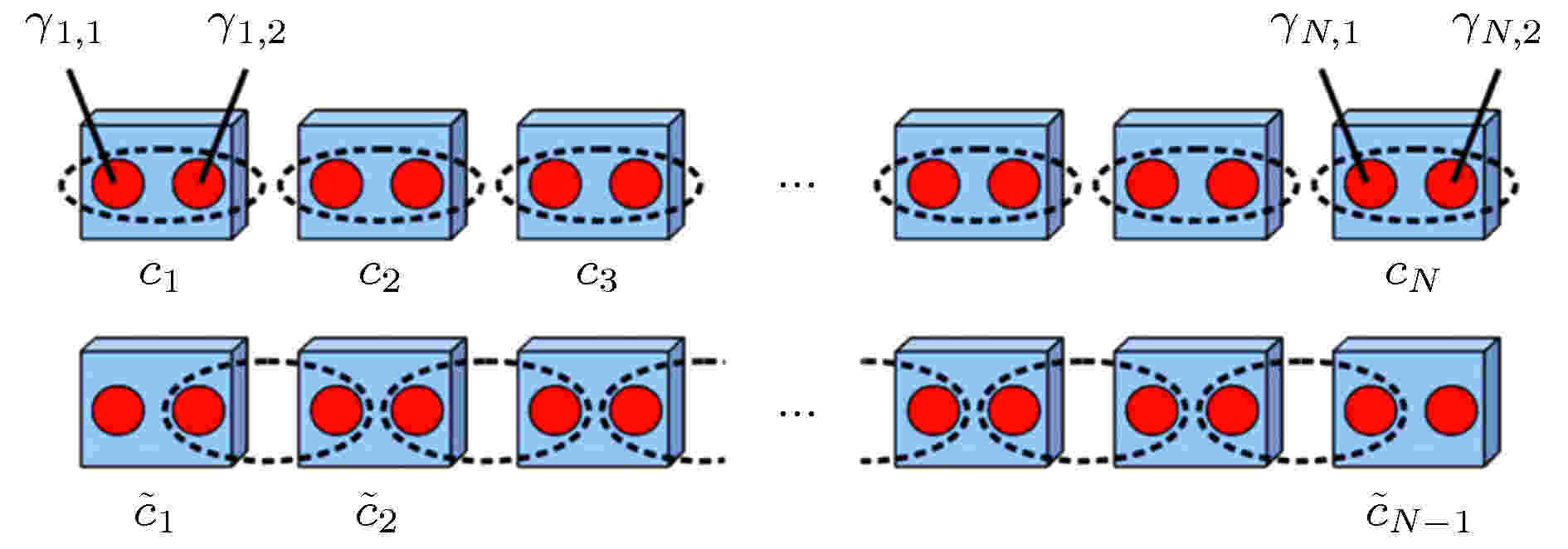图 1 Kitaev链模型示意图^[17]
Figure1. Schematic of Kitaevchain model^[17].

${H_{{\rm{chain}}}} = - \mu \sum\limits_i^N c_i^? {c_i} - \sum\limits_i^{N - 1} \left( {tc_i^? {c_{i + 1}} + \Delta {c_i}{c_{i + 1}} + {\rm{h}}.{\rm{c}}.} \right),$

其中μ是化学势, ?是p波超导配对势. 上式中的$c_i^? {c_i}$是位置i的电子数算符, 第二项是电子从i跳跃到i+1所对应的动能, 第三项是相邻位置电子的p波超导配对势. 将Majorana算符${\gamma _{i, 1}} = c_i^? +$$ {c_i}, {\gamma _{i, 2}} = {\rm{i}}\left( {c_i^? - {c_i}} \right)$代入Kitaev哈密顿量, 并记${\tilde c_i} = \left( {{\gamma _{i + 1, 1}} + {\rm{i}}{\gamma _{i, 2}}} \right)/2$, 则在μ = 0, $t = \left| \Delta \right| > 0$时(此条件仅为了使推导简便, 其余情况不改变整体图像)哈密顿量可以改写为

$H_{c{\rm{hain}}}^{\rm{\prime}} = - {\rm{i}}t\sum\limits_{i = 1}^{N - 1} {\gamma _{i,2}}{\gamma _{i + 1,1}} = 2t \sum\limits_{i = 1}^{N - 1} \tilde c_i^? {\tilde c_i}.$

新的哈密顿量包括了除γ_{i, 1}和γ_{N, 2}外所有重新配对的γ算符. 也就是说有一对未配对的Majorana算符被留在了Kitaev链的两端. γ_{i, 1}和γ_{N, 2}可以被合并为一个非局域化的费米算符${\tilde c_{\rm{M}}} =$$ \dfrac{1}{2}\left( {{\gamma _{i, 1}} + i{\gamma _{N, 2}}} \right)$. ${\tilde c_{\rm{M}}}$没有出现在哈密顿量里, 因此占据这个态所需要的能量为零. 换句话说, 这个态被占据和未被占据两种情况构成一个双重简并态, 这两个基态也就是拓扑简并态. 在理想情况下, 一个无限长Kitaev链两端的Majorana态是完全无耦合的, 因此对局域噪音是免疫的.
Kitaev链模型的本质是在相邻一维费米态中间提供了除电子(移动)之外的其他耦合项, 即p波超导配对项, 使得原本的γ_i和γ_i+1^?发生了位错配对, 从而遗留了两端未湮灭的Majorana态.
下一步便是如何在实验室里实现电子的这种无自旋超导配对.
2 -->

2.4.Kitaev链的物理实现

无自旋临近电子配对模型在实际情况下对应的是自旋极化配对(也被称为自旋三重态配对), 因为这种超导模型的对称性与原子模型中的p轨道类似, 因此又常称为p波超导体(常见的BCS超导体则对应s波超导体). 本征的p波超导体在自然界中很罕见, 有些超导体被认为有可能是自旋三重态配对超导体, 例如Sr₂RuO₄, 但目前仍处于争论中^[19].
为了得到p波超导配对, Fu和Kane^[8]设想把传统的s波超导体和拓扑绝缘体耦合成一个异质体系后, 超导的临近效应会使得拓扑绝缘体表面的自旋锁定态出现p波配对的超导表面态, 而Majorana准粒子态就会出现在超导表面态的边缘、端点或漩涡处. 受此启发, Sau等^[10]又证明了可以把上述人工结构中的拓扑绝缘体替换为实验室中更加常见的半导体而使得Majorana异质系统的实现更加容易. 他们预言的新系统为一个三明治系统: 一层具有强自旋轨道耦合(spin-orbit interaction, SOI)的半导体量子阱材料夹在一层铁磁绝缘体和一层超导体中间. 随后, Alicea^[11]又发现其实相对罕见的铁磁绝缘体也不是必须的, 可以用一个垂直于SOI场的外部磁场进行替代. 紧接着, Lutchyn等^[12]和Oreg等^[13]又证明了具有强SOI的一维纳米线也可以实现一维版本的Majorana系统, 该系统数学上和Kiteav链模型等价.
因此, 利用具有强SOI的半导体纳米线[例如砷化铟(InAs)^[20]或者锑化铟(InSb)^[21], 并将其与常见的s波超导体[例如铌(Nb)或者铝(Al)]进行耦合, 在外加磁场的帮助下, 纳米线两端便可出现Majorana准粒子态(图2). 为了清晰地分析在此模型中SOI、超导体能隙?和外加磁场B对Majorana准粒子产生的影响, 我们建立了数值模型对每个参数进行独立分析. 为此, 异质纳米线的哈密顿量可以写为
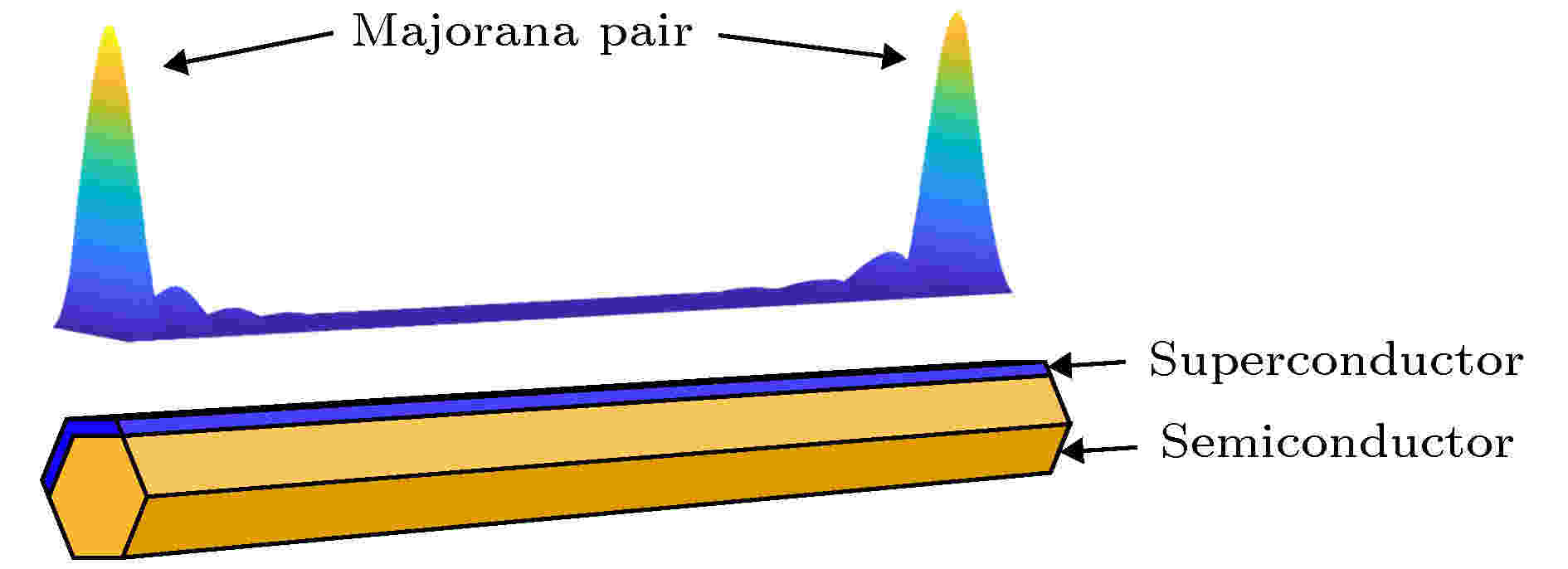图 2 一维超导体-半导体异质结构与Majorana准粒子态波函数示意图
Figure2. Schematic sketch of a nanowire-superconductor hybrid structure and the wave function of the Majorana quasiparticle.

$H = \left( {\frac{{k_x^2}}{{2m}} - \mu } \right){{{\tau}} _y} + \alpha {k_x}{{{\sigma}} _y}{{{\tau}} _y} + {E_z}{{{\sigma}} _z} + \Delta{{{\tau}} _z},$

其中第一项$\left( {\dfrac{{k_x^2}}{{2 m}} - \mu } \right){{{\tau}} _y}$是常规能量项, μ是化学势; 第二项$\alpha {k_x}{{{\sigma}} _y}{{{\tau }}_y}$是SOI项, 这里α为Rashba系数, σ_i和τ_i则分别是自旋和粒子-空穴对应的泡利矩阵; 第三项E_zσ_z描述的是系统的塞曼能, ${E_z} = \dfrac{1}{2}g{\mu _{{B}}}B$, g为Landeg-因子; 最后一项, Δτ_z描述的是超导项, Δ是由临近效应引入的有效超导能隙. 图3中给出了Δ, E_z, α三者在不同大小关系情况下的能量色散图谱. 由图可见, 当SOI和E_z都取非零值时, 纳米线在μ = 0处形成了一个螺旋能隙(helical gap), 在此能隙中的电子自旋在SOI方向上彼此反平行而在z轴方向上被外部磁场极化了. 如果在螺旋能隙内再引入超导配对, 则可形成自旋极化配对的超导环境, 再根据Kitaev模型可知, p波超导纳米线的两端将出现一对Majorana准粒子态. 这种系统的端态在量子隧穿输运测量中会以零能电导峰的形式出现在输运能谱中.
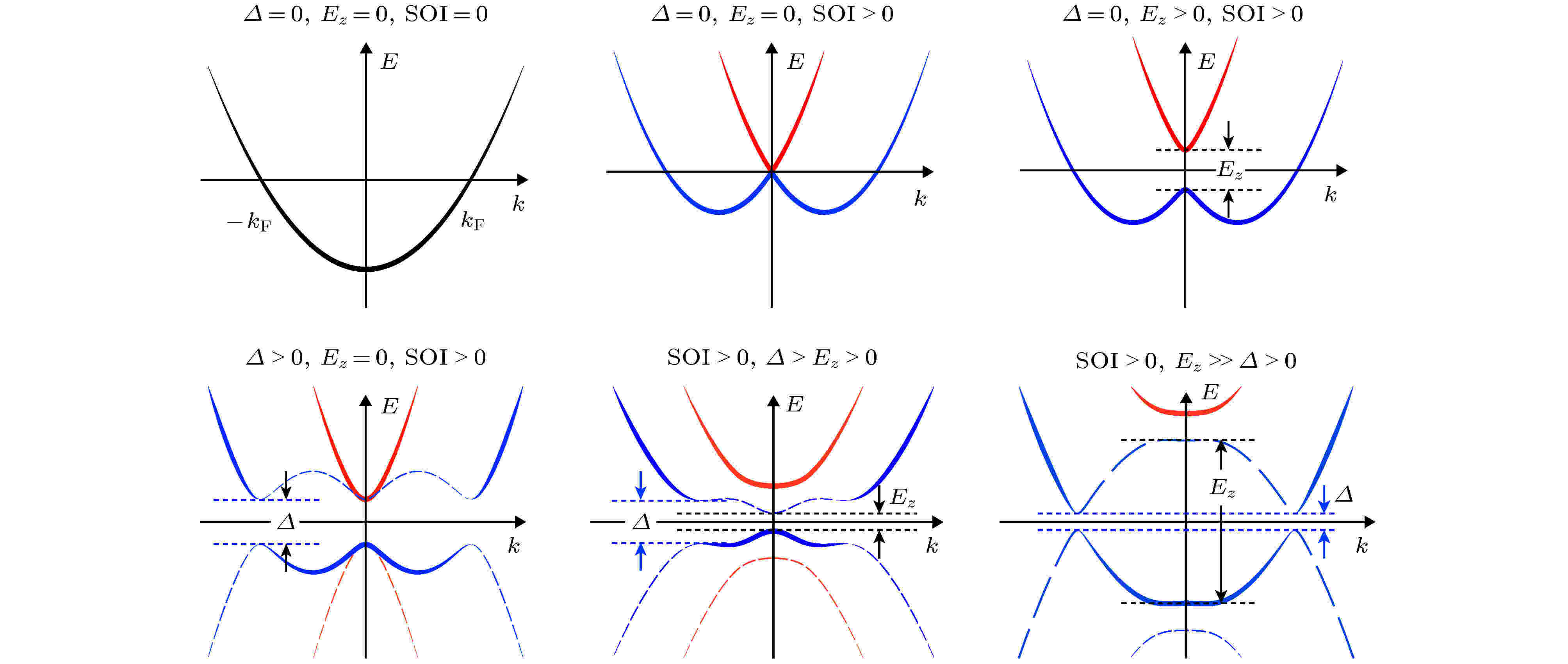图 3 超导体-半导体异质纳米线体系在不同的?-E_z-α配置下的能量色散图谱(μ = 0). 其中, 蓝线和红线分别对应两个自旋分支(SOI方向投影), 实线对应粒子项分支, 虚线对应空穴项分支
Figure3. Energy dispersion of a superconductor-semiconductor hybrid nanowire at different ?-E_z-α configurations with μ = 0. Blue and red lines correspond to the two spin branch (along SOI direction), respectively, solid lines are particle branches, while dashed line are hole branches.

在以上理论研究指导下, 实验上在超导体-半导体纳米线复合系统中寻找Majorana准粒子迅速成为过去十年凝聚态物理研究的一个热点方向. 其实在Majorana准粒子相关理论提出之前, 针对强SOI半导体纳米线就已经有了很多实验研究. 例如, 对InAs和InSb纳米线的电子输运测量表明它们是强SOI、高g-因子、高迁移率材料^[20–23], 且可与超导体形成较好的耦合^[24,25]等.
2012年荷兰Delft理工大学团队报道了在高转变磁场超导材料NbTiN与InSb纳米线的耦合系统图4(a)中观察到的零能电导峰信号作为Majorana存在的可能证据^[26], 且发现该零能电导峰与三维磁场的指向有关. 不久, Lund大学和Weizimann研究所分别利用InSb-Nb^[27]和InAs-Al^[28]等结构观察到类似的零能电导峰.
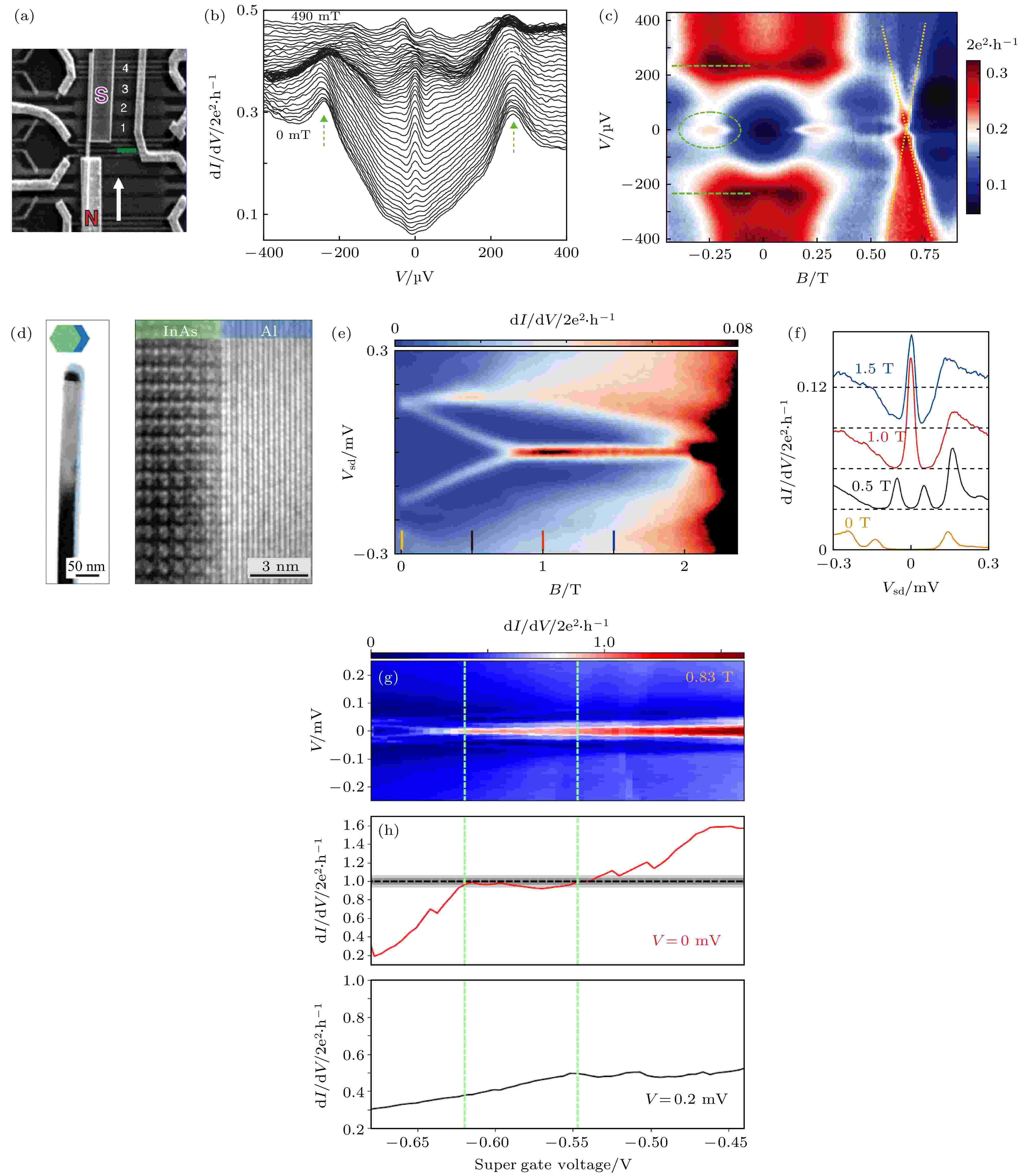图 4 超导体-半导体异质器件与探测到的零能电导峰　(a)?(c) NbTiN-InSb器件与零能电导峰^[26]; (d)?(f) 全外延Al-InAs纳米线及纯净超导能隙中的零能电导峰^[29]; (g), (h)全外延Al-InSb纳米线器件中量子化的零能电导峰^[40]
Figure4. Superconductor-semiconductor hybrid devices and the detected zero-energy conductance peaks: (a)?(c) NbTiN-InSb nanowire device and zero-energy conductance peak^[26]; (d)?(f) Fully epitaxial Al-InAs nanowire and zero-energy conductance peak in hard gap^[29]; (g), (h) Quantized zero-energy conductance peak in fully epitaxial Al-InSb nanowire devices^[40].

这些零能电导峰实验用到的典型器件结构是由普通金属(如钛/金等)作为探测端与半导体纳米线连接, 被探测端则是将超导体覆盖到半导体上形成异质结构. 探测端与被探测端有一小段裸露的半导体纳米线, 可通过门电极控制其势垒高度从而形成隧穿结. 超导体-半导体异质结构部分也有相应的门电极用于调控其电化学势. 对这样的器件再施加一个与SOI垂直的磁场, 磁场足够强时即可诱发拓扑相变从而形成Majorana准粒子态.
比较理论所预测Majorana零能电导峰^[30,31]和实验探测的零能电导峰会发现有两个显著的不同点. 一是理论预测的Majorana引起的零能电导峰是处在超导体所形成的能隙中, 而实验所得的零能信号则是伴随很多杂态;二是由于Majorana准粒子态引起的安德烈夫反射过程具有完美的粒子-空穴对称性, 其引发的电导峰应该是一个值为${{2{{\rm{e}}^2}}}/{h}$的量子电导, 而实验中观察到零能电导峰并未出现量子化行为. 为了解决这些理论与实验的不一致性, 实验上对材料和器件的制备工艺的优化成为该方向发展的瓶颈和突破口.
首先, 与零能电导峰伴随的其他杂态一般被认为是由于器件中存在大量缺陷所致. 这其中很大一部分原因要归结于超导体与半导体界面的不平整. 在实验器件制备过程中, 为了使超导体与半导体形成均匀的电接触, 需要移除纳米线外面的氧化层. 这个过程最先是通过氩离子轰击刻蚀的方式进行, 但同时会对纳米线表面造成损伤而产生大量杂质. 后来通过化学溶液有选择性地腐蚀掉氧化层并进行钝化^[32], 器件的界面质量得到了显著提高, 并在输运上表现出弹道输运的量子化电导平台^[33,34], 但能隙内部的杂态数量(特别是在高磁场情况下)仍然较多^[35].
器件质量更大的突破来自于分子束外延(MBE)超导体-半导体生长技术日趋成熟所带来的原子级平整的界面^[36], 从而直接导致无杂质态的近邻超导能隙^[37]. 利用MBE外延Al-InAs材料, 纯净能隙中的零能电导峰很快也被探测到, 实验信号的干净程度比上一代实验有了显著提高^[38]. 全外延技术很快也被成功应用到Al-InSb系统的生长上^[39]. 由于InSb本身的弹道输运特性和更小的系统耗散, 配合以遮挡法形成的天然隧穿结, Majorana理论所预言的量子化的零能电导峰在实验中也很快被探测到^[40].
自第一代实验以来, 零能电导峰虽然符合Majorana理论预言, 但同时也有很多其他可能的平庸解释. 随着材料和器件质量的不停优化以及理论模型的完善^[41–46], 每当在更干净的器件中观察到信号质量更好的零能电导峰, 一部分平庸的解释就会被排除掉, 人们对纳米线体系中Majorana存在的信心就会进一步增加. 迄今为止, 当初大部分的平庸解释已被排除, 但在极少数的条件下仍然有可能有平庸的解释. 因此零能电导峰并不能成为Majorana准粒子态存在的最终证据, 特别是有一些平庸Andreev束缚态在特定形状的势阱中仍有可能出现类似Majorana束缚态的信号^[47–54]. 该势阱通常要求电化学势在空间缓慢变化, 故宽度更窄(高度更高)的隧穿结可能成为下一步努力方向^[55]. 最终能充分证明Majorana准粒子态及其拓扑特性的实验只有通过辫织操作来验证其非阿贝尔统计性^[18,56].
除零能电导峰外, 另一个探测Majorana零模的输运手段是引入电子的充电能(charging energy). 将超导-半导体纳米线做成岛状器件结构时, 库仑相互作用导致电子只能逐个通过该岛. 而当超导能隙大于充电能时, 电子能以库珀对的形式两两通过该岛, 输运上表现为两电子周期的库仑阻塞峰. 在此基础上加磁场后在岛的两端产生两个Majorana零模时, 电子可以以‘隐形传态’的方式从岛一端的Majorana零模进去, 然后从另一端的Majorana零模隧穿出来^[57], 输运表现为单电子的库仑阻塞峰. 这种从双电子到单电子的库仑阻塞峰的演变在解决了纳米线器件中杂质(hard gap)问题后也在实验上被观察到^[58-60]. 不过该实验手段也面临着和隧穿实验类似的问题: 如何排除其他的平庸解释(比如Andreev束缚态)^[54,61,62].
该方向过去数年理论的进展大致可分为三个方面: 1)提出其他可能的平庸解释, 主要是细致研究Andreev束缚态和Majorana零模之间的相似与不同^{[46-48,50-53]}. 2)建立更精确的纳米线实验器件的理论模型. 理论模型从简单的一维扩展到三维(多个子能带)^[31]; 研究无序(电化学势、自旋轨道耦合、超导配对等)带来的变化^[48,50,63]; 用Schr?dinger-Poisson等自洽的方法研究纳米线器件中的门电极、超导半导体耦合等效应^[42,43]. 3)提出新的Majorana探测和辫织方案. 第一代辫织方案要求用门电极实现对Majorana零模在空间上的快速移动^[56]. 这一方案因超导的屏蔽效应而在实验上非常具有挑战性. 后来随着理论发展, 不需要移动Majorana零模, 只利用充电能和单电子在两个Majorana之间的隐形传态就可实现在数学上等价的辫织操作^[64,65]. 这种基于测量的辫织方案(measurement-based braiding)是当前实验努力的主流方向^[66-68]. 而基于此, 实验上也实现了各种复杂的纳米线网格结构^[39,69], 最近的突破是源自于选区外延生长技术的发展^[70-72].

除了非阿贝尔辫织操作这一长远目标, 短期内利用超导-半导体纳米线还可以做很多相对容易的实验以揭示Majorana物理的不同方面^[73]. 例如, 用来检验Majorana非局域特性的双端电导对照实验^[74], Majorana-量子点耦合实验^[75]等. 另外, 比一维纳米线更加复杂的纳米线交叉结构^[69]、纳米线网格结构^[70]和二维拓扑材料体系^[76]也被成功合成出来, 并展现出广阔的应用前景. 特别地, 多维体系对实现Majorana辫织操作^[56]和最终的拓扑量子计算有着至关重要的意义. 毫无疑问, 接连不断的技术挑战和崭新的物理发现在未来Majorana器件研究中是并存的, Majorana准粒子的研究才刚刚开始.