摘要:针对高功率激光装置中靶面辐照均匀性的高要求, 提出了一种利用束间动态干涉改善辐照均匀性的快速匀滑方法. 基本原理是利用共轭相位板阵列对存在一定波长差的多束激光附加相位调制, 从而使各子束在远场两两相干叠加以产生动态的干涉图样, 进而引起焦斑内部散斑的动态扫动, 在ps时间内抹平不均匀性. 以典型惯性约束聚变装置中的激光集束为例, 通过建立基于束间动态干涉的快速匀滑物理模型, 定量分析了相位板类型、相位调制幅度和束间波长差等因素对焦斑动态干涉图样的影响及规律, 进而对其束匀滑特性进行了讨论. 结果表明, 基于束间动态干涉的快速匀滑方法可以有效地实现多方向、多维度的焦斑内部散斑快速扫动, 且通过与传统束匀滑技术的联用, 可以在更短的时间内达到更好的焦斑均匀性.
关键词: 惯性约束聚变/
动态干涉/
束匀滑/
共轭相位板

English Abstract

全文HTML

--> --> -->

在惯性约束核聚变装置中, 实现点火对靶面的辐照均匀性提出了极高的要求^[1]. 目前, 已发展出多种空域^[2-4]与时域匀滑技术^[5-7]以改善靶面辐照均匀性. 其中, 连续相位板(continuous phase plate, CPP)作为一种纯相位元件, 能有效控制焦斑包络, 改善焦斑大尺度不均匀性. 然而, 由于激光内部子光束相互之间的干涉, 远场焦斑内部存在大量散斑, 从而会导致激光束与靶丸相互作用过程中各种非线性不稳定效应的产生, 进而降低激光束对靶丸的压缩对称性, 这对于点火的实现是极为不利的^[8], 因而需要采用时域匀滑技术抑制散斑的存在^[9,10]. 目前, 国际上主流的时域匀滑技术是光谱角色散(smoothing by spectral dispersion, SSD), 其基本原理是采用电光晶体对激光束进行相位调制, 再利用光栅使相位调制脉冲产生色散, 从而导致远场焦斑内部散斑沿光栅色散方向快速扫动, 以在较短时间内抑制辐照不均匀性^[11,12]. 然而, 受限于电光调制晶体的调制频率, SSD需要数十皮秒时间以达到较稳定的匀滑效果, 而这一时间远大于激光等离子体各种非线性不稳定效应的增长时间^[13]. 此外, 1D-SSD的焦斑存在难以避免的条纹状强度调制, 而2D-SSD也会因远场发生干涉而使得焦斑内部强度调制的匀滑不够充分^[14]. 我们曾提出一种基于光克尔效应的径向匀滑(radial smoothing, RS)方案, 通过抽运光与光克尔介质的作用对主激光束附加动态球面相位调制, 从而使焦斑内部散斑沿径向扫动, 进而改善靶面辐照均匀性. RS方案虽能实现ps量级的超快速匀滑^[15], 但其对抽运光源要求苛刻, 在工程实现上还存在困难. 文献[16]还报道了一种通过RS和螺旋相位板的联用, 实现焦斑在径向和角向方向上ps时间尺度匀滑的方案. 因此, 发展ps量级时间尺度的快速匀滑新方案对于惯性约束聚变装置的发展具有重要意义.
本文提出了一种基于束间动态干涉的快速匀滑新方案. 该方案是利用相位板阵列对高功率激光装置的激光集束进行相位调制, 并使各子束间存在一定波长差, 从而使各子束在远场两两相干叠加产生动态干涉图样, 进而引起焦斑内部散斑的动态扫动, 在一定积分时间内改善靶面辐照均匀性. 动态干涉图样的变化周期取决于子光束间的波长差, 因而通过选取合适的波长差, 可在保证子光束相干性的前提下实现皮秒时间尺度的超快速匀滑. 以典型惯性约束聚变装置中的激光集束为例, 建立了相应的物理模型. 在此基础上, 讨论了相位板类型、束间波长差、相位调制幅度等参数对动态干涉图样的影响, 并对快速匀滑新方案的束匀滑效果进行了分析.

2

-->

2.1.束间动态干涉匀滑方案

基于束间动态干涉的快速匀滑方案的基本原理(图1)是: 将每一激光集束分为两两组合的子光束对, 每一子光束对均通过相同的CPP和偏振控制板(polarization control plate, PCP)进行控制, 且使子光束的工作波长略有不同. 同时, 在CPP之后插入共轭相位板阵列, 使每一子光束对均附加相应的相位调制. 由于各子束的工作波长不同并附加了共轭的相位调制, 每一子光束对均通过干涉叠加在远场形成随时间不断变化的干涉图样, 而同一集束内部不同子光束对在远场进行非相干叠加之后, 焦斑的形态变化更加复杂. 通过共轭相位板阵列的不同设计, 可使集束焦斑内部的散斑发生多方向、多维度的快速扫动, 从而在ps积分时间内实现对靶面光强分布的匀滑化.
图 1 基于束间动态干涉的快速匀滑方案示意图
Figure1. Schematic illustration of smoothing by dynamic interference structures of beamlets.

本方案中, 束间波长差的不同决定了其相干时间的大小, 进而决定了焦斑达到稳定匀滑效果所需的时间. 例如, 当工作波长之差在0. 1—1 nm之间时, 可保证子光束之间的相干性, 并使焦斑达到稳定匀滑效果所需时间在4—0.4 ps之间, 即通过选取合适的波长差, 可在保证相干性的前提下上实现ps时间尺度的超快速匀滑.
2 -->

2.2.物理模型

以2 × 2集束为例, 建立了基于束间动态干涉的快速匀滑物理模型. 考虑到高功率激光装置中激光束难以避免存在相位畸变^[17]与振幅调制^[18], 集束中单一子束近场的光场可表示为

$\begin{split}&{{E}_{j}}\left( x,y,t \right)\\=\; & {{A}_{0}}\left[ 1+\sigma \left( x,y \right) \right] \exp\left[ -\left( \frac{{{x}^{2N}}}{{w}_{x}^{2N}}+\frac{{{y}^{2N}}}{{w}_{y}^{2N}} \right) \right]\\ & \times \exp\left( {\rm{i}}{{\varphi }_{\rm{random}}} \right)\exp\left( {\rm{i}}{{\omega }_{j}}t \right),\end{split}$

式中j = 1, 2, 3, 4, 代表集束内4个子束. 在通过PCP后, 子束1和子束3偏振方向沿x方向, 子束2和子束4偏振方向沿y方向. A₀是归一化振幅, σ(x, y)是振幅调制, w_x和w_y是近场激光束1/e束腰半径, N是激光束超高斯阶数. ${\varphi _{{\rm{random}}}}\left( {x, y} \right)$是高斯随机相位分布, 可用高斯随机相位屏模拟:

$\begin{split} &{\varphi _{{\rm{random}}}}\left( {x,y} \right) \\=&\; {\sigma _{\rm{l}}}{\rm{random}}\left( { - 1,1} \right) \otimes \exp \left[ { - \left( {\frac{{{x^2}}}{{{g_x}^2}} + \frac{{{y^2}}}{{{g_y}^2}}} \right)} \right]\\&+ {\sigma _{\rm{h}}}{\rm{random}}\left( { - 1,1} \right), \end{split}$

式中σ_l和σ_h分别是低频和高频的比例, g_x和g_y分别是x和y方向上的特征长度. ω_j是子束j的角频率, 可表示为

${\omega _j} = \frac{{2{\text{π}}c}}{{{\lambda _j}}}.$

集束在通过相位板阵列后将附加上相应的相位调制, 因而焦面光场可由Collins公式进行计算, 即:

$\begin{split} & \quad {E_{fj}}\left( {{x_f},{y_f},t} \right) = \frac{1}{{{\rm{i}}{\lambda _{3\omega j}}f}}\exp \left( {{\rm{i}}{k_{3\omega j}}2f} \right)\\& \times\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{E_j}\left( {x,y,t} \right)\exp \left[ {{\rm{i}}\left( {{\varphi _j}\left( {x,y} \right) + {\varphi _{{\rm{CPP}}}}\left( {x,y} \right)} \right)} \right]} } \\& \times\exp \left[ { - \frac{{{\rm{i}}{k_{3\omega j}}}}{f}\left( {x{x_f} + y{y_f}} \right)} \right]{\rm{d}}x{\rm{d}}y,\\[-15pt]\end{split}$

式中(x, y), (x_f, y_f)分别为近场和远场空间坐标; f为透镜焦距; φ_CPP(x, y)为CPP附加相位; φ_j(x, y)是各子束由相位板所附加的相位调制. 当附加的相位调制共轭时, φ₁(x, y) = –φ₃(x, y), φ₂(x, y) = –φ₄(x, y).
进一步令$ a_j = (1/{\rm i}\lambda_{3\omega j})\exp({\rm i} k_{3\omega j}2f) $, 由于波长差极小, 可认为a₁ = a₂ = a₃ = a₄ = a. 当不考虑CPP的作用, (4)式可写为

$\begin{split} & {E_{fj}}\left( {{x_f},{y_f}} \right) \\ =\; & a\exp \left( {{\rm{i}}{\omega _j}t} \right){\rm{FT}}\left\{ {\exp \left[ { - \left( {\frac{{{x^{2N}}}}{{w_{x}^{2N}}} + \frac{{{y^{2N}}}}{{w_y^{2N}}}} \right)} \right]} \right\} \\ &\otimes {\rm{FT}}\left[ {\exp ({\rm{i}}{\varphi _j}\left( {x,y} \right))} \right].\end{split}$

若将相位调制项的傅里叶变换写为B_j(x_f, y_f)×exp[ib_j(x_f, y_f)], 则焦面瞬时光强分布可写为

$\begin{split} &{I_i}\left( {{x_f},{y_f},t} \right) \\ =\; & {\left| {{E_{f1}} + {E_{f3}}} \right|^2} + {\left| {{E_{f2}} + {E_{f4}}} \right|^2}\\= \; &{a^2}{A_1}[B_{_1}^2 + B_3^2 + 2{B_1}{B_3}\cos \left( {\Delta \omega t + {b_3} - {b_1}} \right)]\\ & +\! {a^2}{A_2}[B_2^2 \!+\! B_4^2 \!+\! 2{B_2}{B_4}\cos \left( {\Delta \omega t \!+\! {b_4} \!-\! {b_2}} \right)],\end{split}$

式中A₁(x_f, y_f), A₂(x_f, y_f)是与振幅分布有关的项; Δω为不同波长子束的角频率之差; 以子束1为例, 不同的附加相位调制分布对应的参数B₁和b₁列于表1.

$ {\varphi }_{1}(x_{f}, y_{f}) $	$ B_{1}(x_{f}, y_{f}) $	$ b_{1}(x_{f}, y_{f}) $
x	$ {\delta }[x_{f}/({\lambda f})+1/(2\text{π} )]{\delta }[y_{f}/({\lambda f})] $	0
–x2	$ \text{π} ^{1/2}\delta [y_{f}/(\lambda f) ]$	$ \text{π} ^{2}x_{f}^{2}/({\lambda }^{2}f^{2})-3\text{π} /4 $
$ -[h_{1}{ }(x/w)^{2}+ h_{2}(y/w)^{2}] $	$ w^{2}\text{π} (h_{1}h_{2})^{-1/2} $	$ \text{π} ^{2}x_{f}^{2}/(h_{1}{\lambda }^{2}f^{2}w^{2})+\text{π} ^{2}y_{f}^{2}/(h_{2}{\lambda }^{2}f^{2}w^{2})-3\text{π} /2 $
$ \arctan(y/x) $	$ [-{\lambda f}/(2\text{π} )]\{ {\delta }[x_{f}/({\lambda f})]{\rm d}{\delta }[y_{f}/({\lambda f})]/{\rm d}y_{f }- {\rm i}{\delta }[y_{f}/({\lambda f})]{\rm d}\delta [x_{f}/({\lambda f})]/{\rm d}x_{f}\} $

表1不同相位分布的二维傅里叶变换表达式
Table1.2D-Fourier transform of different phase distribution.

从(6)式及表1可以看出, 根据所附加相位调制的不同, 不同波长子束在焦面干涉得到不同的光强分布, 且由于时空耦合项的存在, 焦斑空间分布会随时间发生变化, 其变化周期为

$T = \frac{{2{\text{π}}}}{{\Delta \omega }} = \frac{{2{\text{π}}}}{{\left( {\dfrac{{2{\text{π}}c}}{{{\lambda _3}}} - \dfrac{{2{\text{π}}c}}{{{\lambda _1}}}} \right)}} = \frac{{{\lambda _1}{\lambda _3}}}{{c\left( {{\lambda _1} - {\lambda _3}} \right)}} \approx \frac{{{\lambda ^2}}}{{c\Delta \lambda }}.$

由此可见, 当附加CPP相位时, 动态干涉将引起焦斑内部散斑在不同方向上的扫动, 从而在ps积分时间内改善靶面辐照均匀性.
于是, 焦面光强可表示为

$I = \frac{1}{{\Delta t}}\int\nolimits_0^{\Delta t} {\left( {{{\left| {{E_{f1}} + {E_{f3}}} \right|}^2} + {{\left| {{E_{f2}} + {E_{f4}}} \right|}^2}} \right){\rm{d}}t} .$

为进一步对动态干涉图样匀滑的束匀滑效果进行定量分析, 采用光通量对比度(contrast)和FOPAI (fractional power above intensity)对焦斑均匀性进行评价:

$\begin{split} & Contrast \\ =\; & \frac{{\sqrt {{{\sum\nolimits_i {\sum\nolimits_j {{{\left[ {{I_{i,j}}({x_f},{y_f}) - {I_{{\rm{mean}}}}\left( {{x_f},{y_f}} \right)} \right]}^2}} } } / {{N_x}{N_y}}}} }}{{{I_{{\rm{mean}}}}\left( {{x_f},{y_f}} \right)}},\end{split}$

$FOPAI\left( {{I_0}} \right) = \frac{{\displaystyle\int_{A~{{\rm{where}}~I\left( {x,y} \right) \succ {I_0}}} {I\left( {x,y} \right){\rm{d}}x{\rm{d}}y} }}{{\displaystyle\int\nolimits_A {I\left( {x,y} \right){\rm{d}}x{\rm{d}}y} }},$

式中I_mean(x, y)为平均强度, N_x和N_y分别是x和y方向上的采样数. 光通量对比度表征了积分时间内的激光束焦斑的均匀性, FOPAI则表征了焦斑中热斑所占的比例, FOPAI曲线左移意味着焦斑的匀滑效果越好.
利用建立的束间动态干涉快速匀滑物理模型, 可对焦斑形态进行模拟和分析. 首先, 计算分析了在不同类型相位板阵列下的束匀滑效果. 然后, 讨论了相位调制PV值和束间波长差对焦斑匀滑特性的影响. 最后, 给出了典型参数下焦斑束匀滑特性, 以及与经典束匀滑方案2D-SSD联用的效果.

主激光束的参数为: 激光集束子光束三倍频后波长为λ_3ω1 = λ_3ω2 = 351 nm, λ_3ω3 = λ_3ω4 = 351.1 nm, 光束束腰宽度w_x = w_y = 186 mm, 超高斯阶N = 6, 初始相位畸变PV值为2λ. 2D-SSD参数为: 调制深度δ = 2.4, 调制频率ν_m = 17 GHz, 总带宽约为0.3 nm, 光栅色散系数dθ/dλ = 2156.8 μrad/nm^[19]. 计算中, 积分时间Δt = 10 ps, 聚焦透镜焦距f = 7.7, 光通量对比度的积分区域取80%环围能量区域.
2

-->

3.1.相位板阵列类型

图2给出了不同相位调制方式得到的焦斑光通量对比度随时间变化曲线. 从图2可以看出, 当φ₃(x, y) = –φ₁(x, y), 即子光束对附加的相位调制共轭或互补时, 所得焦斑光通量对比度更低, 匀滑效果更为理想. 因此, 我们选择附加共轭的相位调制作为束间动态干涉匀滑的实现方法.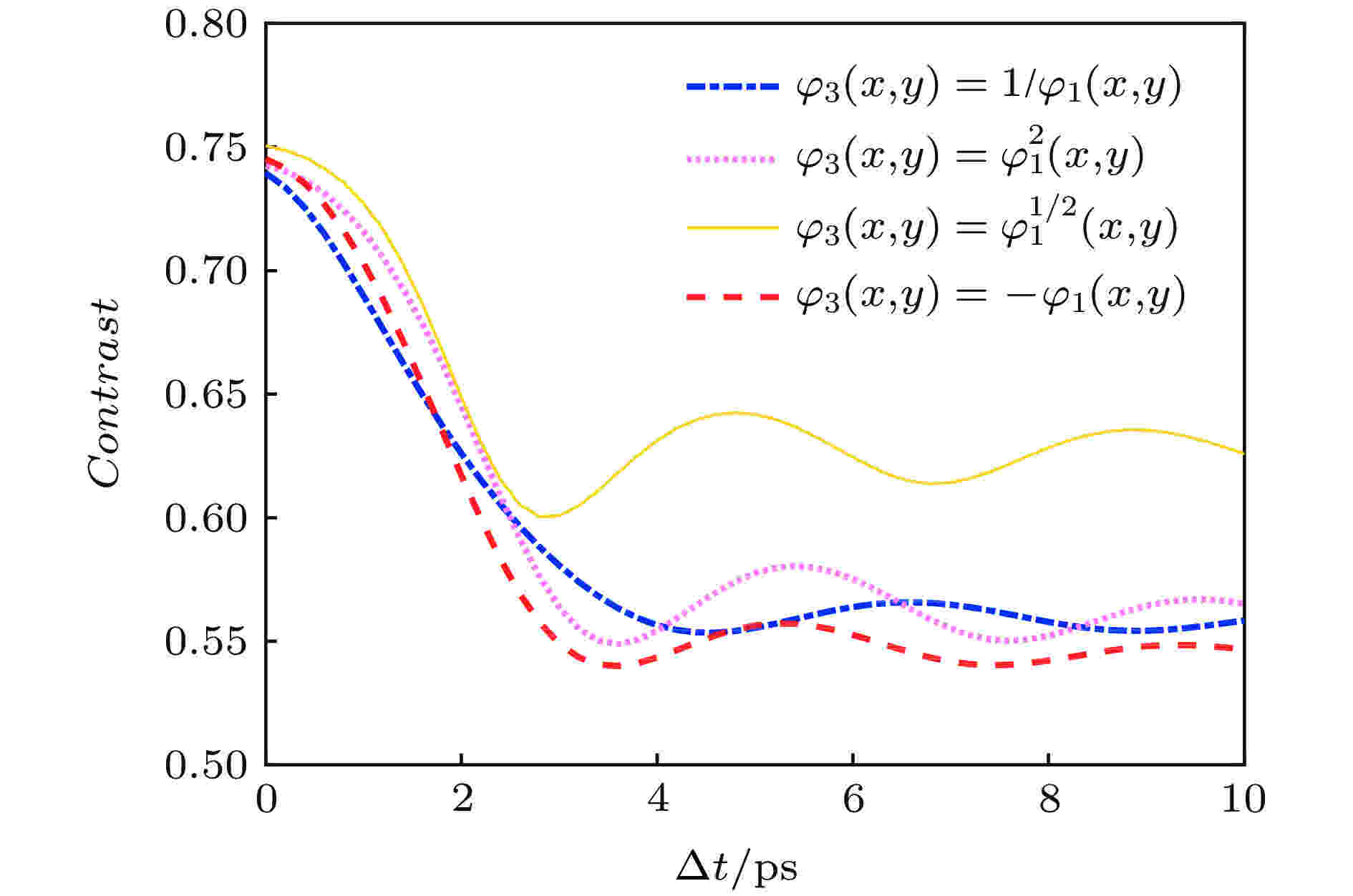
图 2 不同相位调制所得焦斑光通量对比度随时间的变化
Figure2. The contrast of focal spots with different phase modulation.

我们还进一步计算了多种类型共轭相位调制的焦斑, 并对其匀滑效果进行了对比. 图3(a)—(d)给出了相位调制分别为共轭的倾斜相位、柱面相位、椭球面相位和涡旋相位时, 4 ps积分时间内集束在焦面的动态干涉图样. 从图3可以看出, 共轭的倾斜相位和柱面相位可实现焦斑在x(y)方向的运动, 而椭球面相位和涡旋相位则可分别实现焦斑在径向和角向的运动. 由此可见, 采用不同类型相位板对集束中两子束对附加不同类型的相位调制, 可实现焦斑内部散斑在多方向、多维度的扫动, 从而更好地改善靶面辐照均匀性. 图4(a)和图4(b)分别给出了不同类型相位调制进行组合所得到的焦斑光通量对比度曲线. 其中, 倾斜相位和柱面相位的方向是指相位变化方向, 椭球相位的方向是指其长轴方向. 从图4可以看出, 相比于附加单一类型的相位调制, 由于不同类型相位调制的组合可实现焦斑内部在多方向、多维度的扫动, 焦斑光通量对比度能在更短时间内迅速下降, FOPAI曲线也发生左移, 这表明焦斑均匀性得到明显改善.
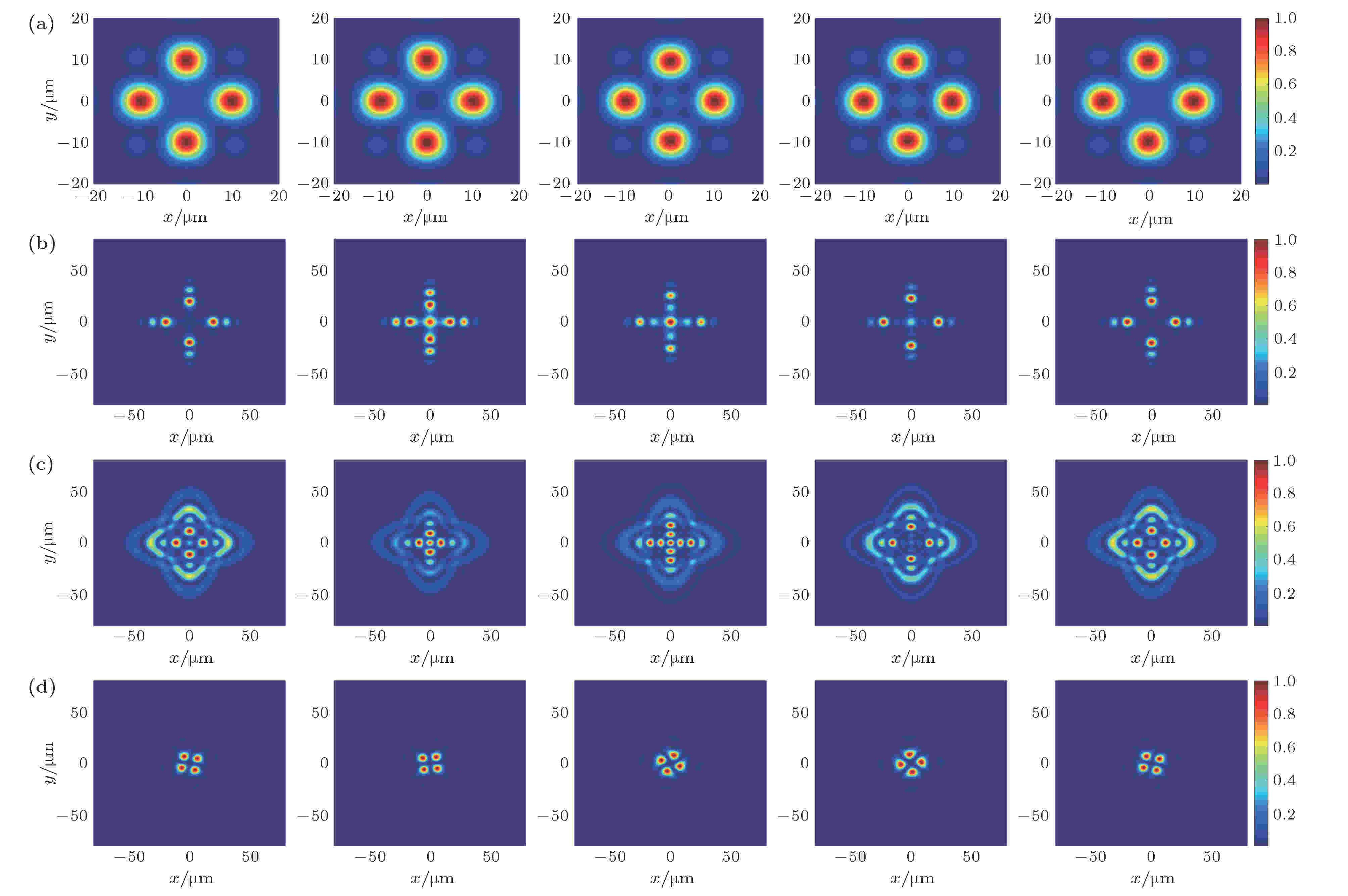图 3 不同类型共轭相位调制的动态干涉图样　(a)倾斜相位; (b)柱面相位; (c)椭球面相位; (d)涡旋相位
Figure3. Dynamic interference structures with different kinds of phase modulation: (a) Tilted phase; (b) cylinder phase; (c) ellipsoid phase; (d) spiral phase.

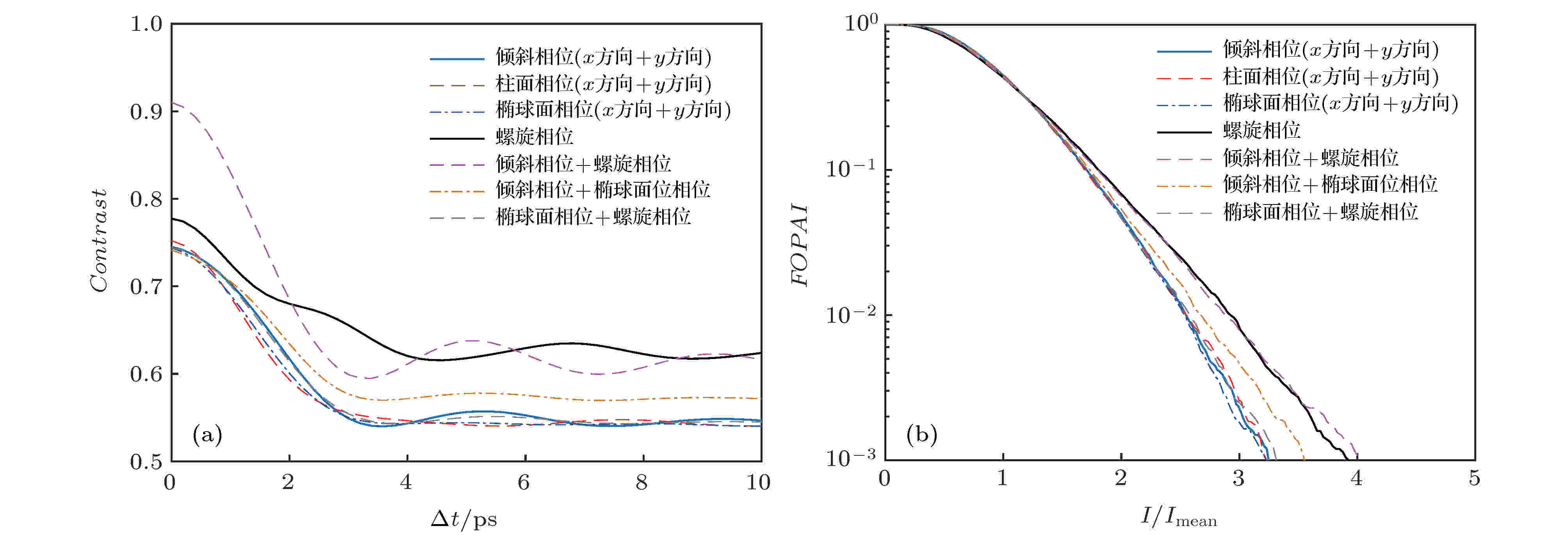图 4 不同类型相位板阵列的焦斑　(a)光通量对比度曲线和(b) FOPAI曲线
Figure4. (a) Variation of contrast with integral time and (b) FOAPI curves with different phase plate array.

基于上述结论, 我们以在x方向和y方向同时附加倾斜相位的相位板阵列为例, 进一步分析了相位调制PV值和束间波长差对靶面辐照特性的影响.
2 -->

3.2.相位调制PV值

图5给出了对集束附加不同PV值相位调制时焦斑的光通量对比度随时间变化曲线. 可以看到, 当相位调制PV值从λ增大到2λ时, 焦斑光通量对比度曲线明显下移. 然而, 随着相位调制PV值进一步增大, 焦斑光通量对比度曲线几乎没有变化. 这是由于倾斜相位PV值太小时, 子光束对在焦面相干叠加产生的动态干涉图样变化范围很小, 致使其在与CPP联用之后, 焦斑内部散斑的扫动范围过小, 不能充分抹平焦斑内部强度调制. 然而, 当相位调制PV值较大时, 焦斑内部散斑扫动范围较大, 焦斑已经得到充分匀滑, 致使相位调制PV值的进一步增大并不能明显改善焦斑均匀性. 此外, 如果相位调制PV值过大, 焦斑包络也会遭到破坏. 经综合考虑, 我们选取2λ作为动态干涉图样匀滑方法中相位调制的PV值.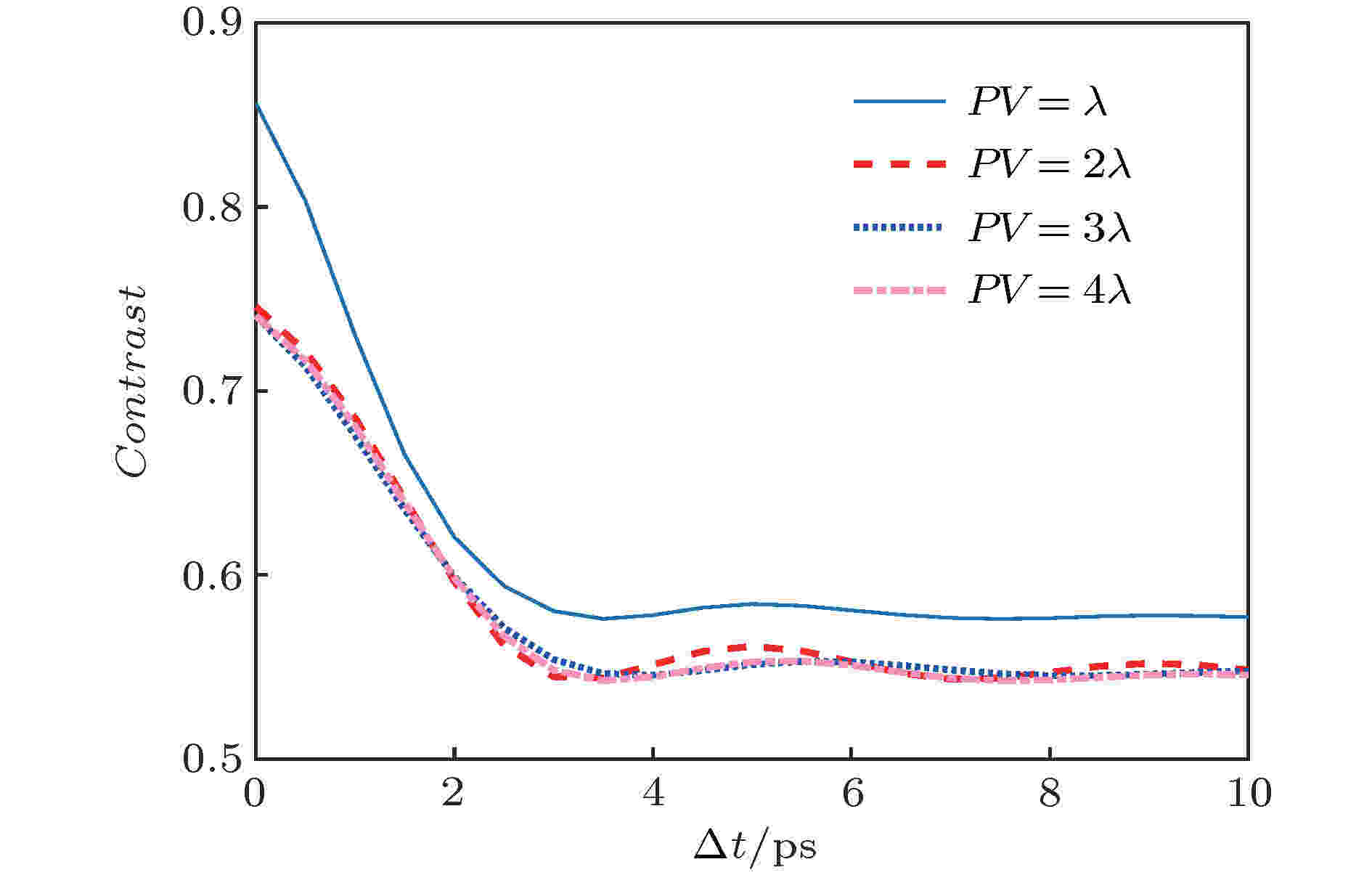
图 5 不同PV的光通量对比度曲线
Figure5. Variation of contrast with integral time with different PV.

另外, 分析图4(a)和图5可知, 采用不同类型的相位板阵列和增大相位调制PV值虽然能在一定范围内进一步改善焦斑均匀性, 但是焦斑光通量对比度的值总是只能降低到0.55左右. 这是由于基于束间动态干涉的快速匀滑方法的焦斑只有部分光强会随时间变化. 从(6)式可以看到, 此方案的焦面光强分布存在着时变项和非时变项, 即焦斑内部既存在着随时间扫动的散斑, 也存在着不随时间变化的散斑, 因此本方案所能达到的束匀滑效果有限, 可考虑与传统时域束匀滑方案进行联用.
2 -->

3.3.束间波长差

为了便于讨论, 在分析波长差的影响时, 我们假设其中一子束经三倍频后波长为λ₁ = 351 nm保持不变, 而另一子束经三倍频后的波长为λ₂ = λ₁ + Δλ. 图6给出了在不同束间波长差情况下, 相同尺寸焦斑不同区域以及不同尺寸焦斑的光通量对比度随时间的变化. 可以看出, 在三种情况下, 波长差Δλ越大, 光通量对比度随时间下降越快, 并最终获得几乎相同的匀滑效果. 这表明束间波长差越大, 焦斑达到稳定匀滑效果所需时间越短, 匀滑速度越快. 此外, 在波长差相同时, 光通量对比度达到稳定值所需时间均相等. 这是因为在本方案中, 动态干涉实现了全焦斑范围散斑的扫动, 靶面达到稳定束匀滑效果所需的时间等于动态干涉图样的变化周期, 即T ≈ λ²/(Δλ·c). 值得指出的是, 当Δλ = 0时, 两子光束经三倍频后波长均为351 nm, 它们在焦面进行干涉叠加后其光场的共轭相位将相互抵消, 不会产生动态干涉图样, 因而没有匀滑效果, 其光通量对比度不随时间变化.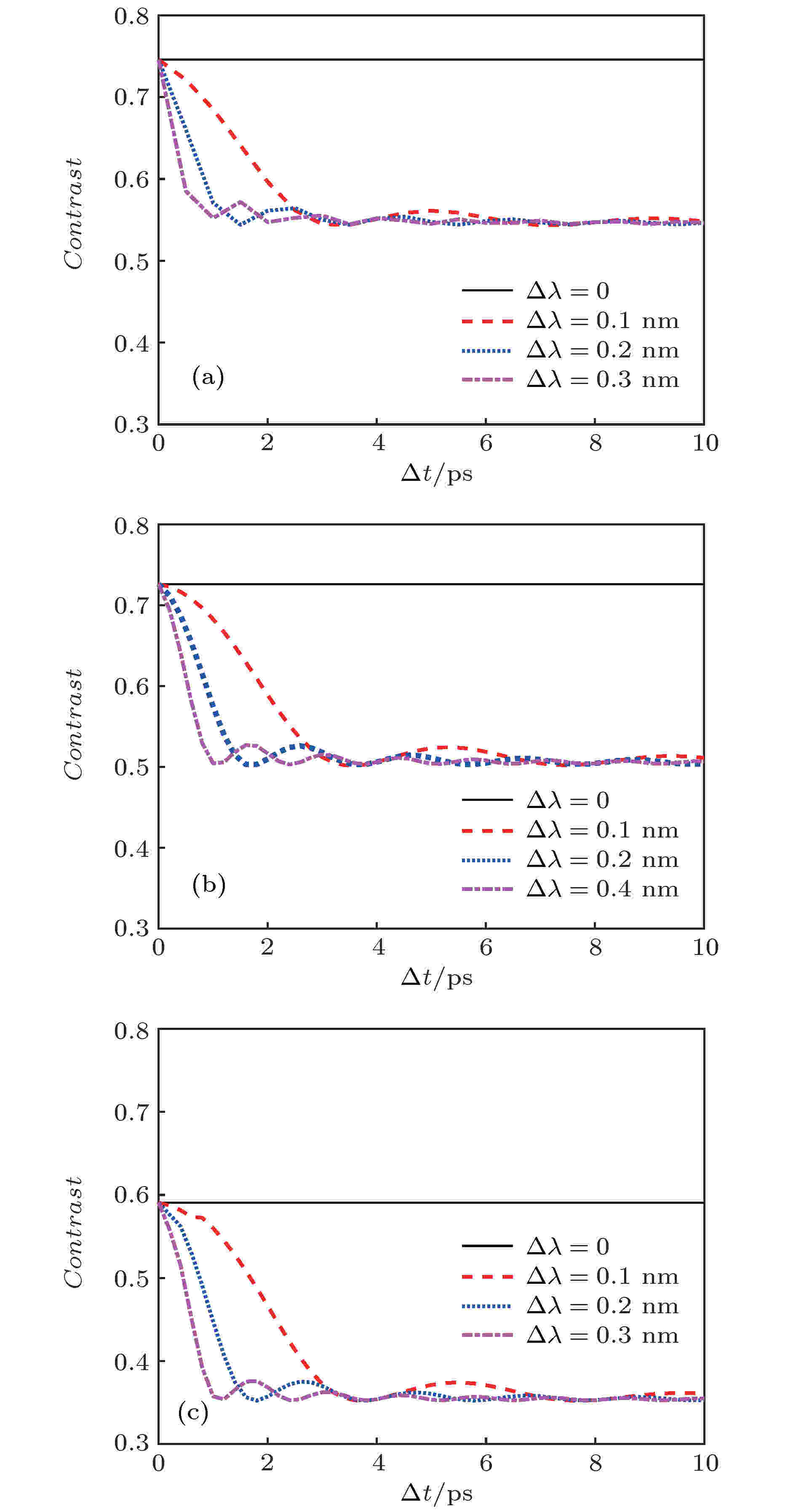
图 6 不同波长情况下, 差焦斑光通量对比度随时间的变化　(a) 600 μm × 500 μm焦斑80%环围能量; (b) 600 μm × 500 μm焦斑30%环围能量; (c) 350 μm × 350 μm焦斑80%环围能量
Figure6. Variation of contrast with integral time of different Δλ: (a) 80% energy of the 600 μm × 500 μm focal spot; (b) 30% energy of the 600 μm × 500 μm focal spot; (c) 80% energy of the 350 μm × 350 μm focal spot.

为使集束中各个子束具有1 nm左右波长差, 一种可行的技术途径是采用宽带可调谐光纤种子源作为注入, 并通过闪耀光栅选频获得具有一定波长差的相干子光束, 从而实现皮秒或亚皮秒时间尺度的快速匀滑^[20-24].
2 -->

3.4.焦斑匀滑特性分析

以x方向和y方向同时附加倾斜相位的相位板阵列为例, 计算了相位调制PV值为2λ、束间波长差Δλ为0.1 nm时基于束间动态干涉快速匀滑方案的焦斑匀滑特性, 并与典型束匀滑方案2D-SSD进行了对比.
在激光集束中, 使各子束对的SSD光栅的色散方向相互垂直, 可实现焦斑的二维匀滑^[25]. 图7给出了10 ps积分时间内仅采用CPP, 2D-SSD + CPP, 束间动态干涉匀滑方案 + CPP以及将它们联用得到的焦斑, 图8则给出了相应的光通量对比度曲线和FOPAI曲线. 从图7可以看出, 2D-SSD以及共轭的倾斜相位均使焦斑内部散斑在x, y方向上得到抹平, 并且相比于2D-SSD, 束间动态干涉匀滑的焦斑没有明显的条纹状强度调制. 同时, 动态干涉匀滑方法对于焦斑大小以及焦斑包络影响较小. 此外, 分析图7(c)可知, 两种方案的联用可使焦斑进一步得到匀滑, 均匀性得到极大改善.
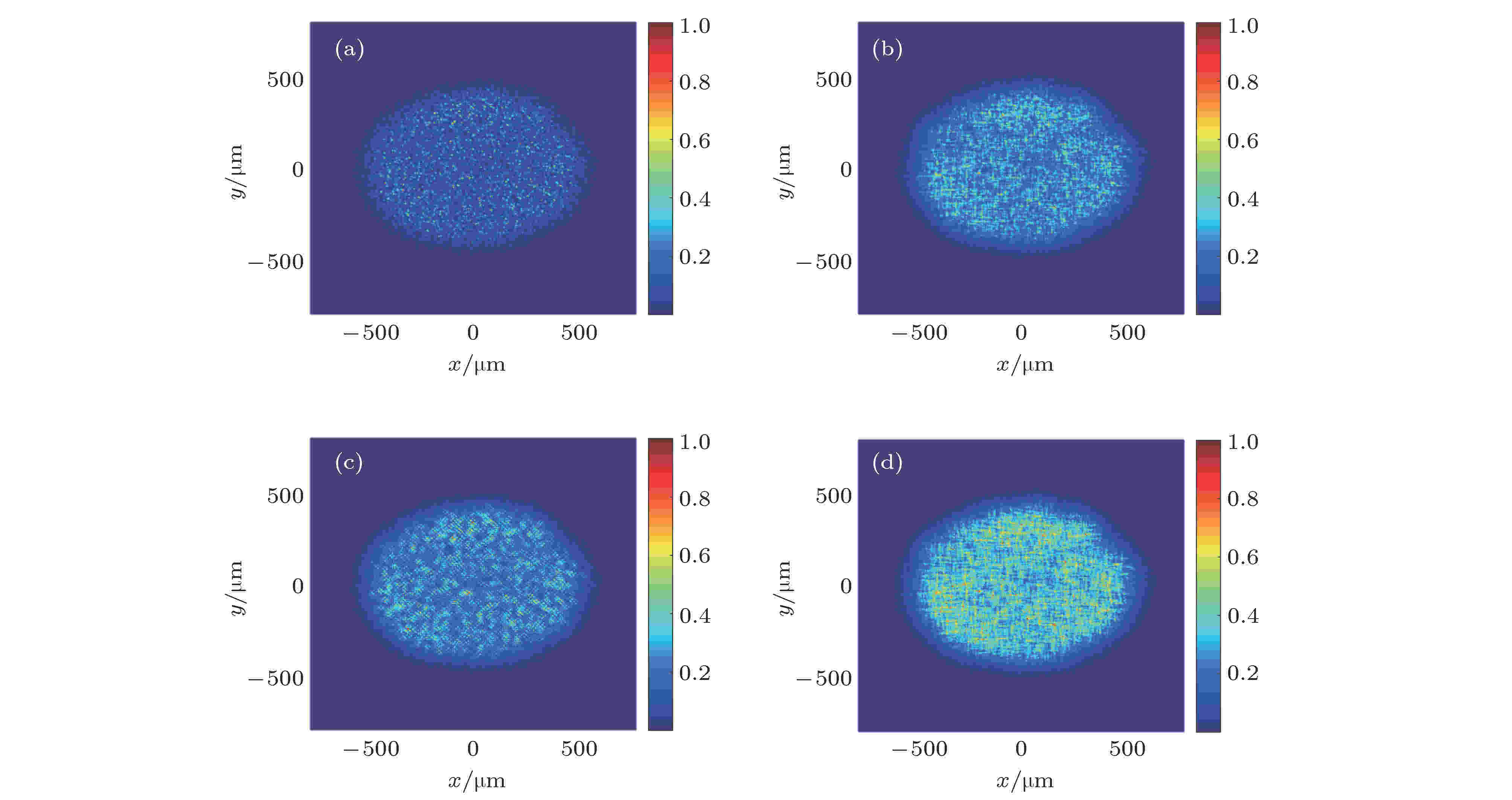图 7 不同匀滑方案的焦斑光强分布　(a)仅CPP; (b) 2D-SSD + CPP; (c)动态干涉图样匀滑方法 + CPP; (d) 2D-SSD + 动态干涉图样匀滑方法 + CPP
Figure7. Focused intensity distributions with different smoothing scheme: (a) CPP only; (b) 2D-SSD + CPP; (c) smoothing by dynamic interference structures of beamlets + CPP; (d) smoothing by dynamic interference structures of beamlets+2D-SSD + CPP.

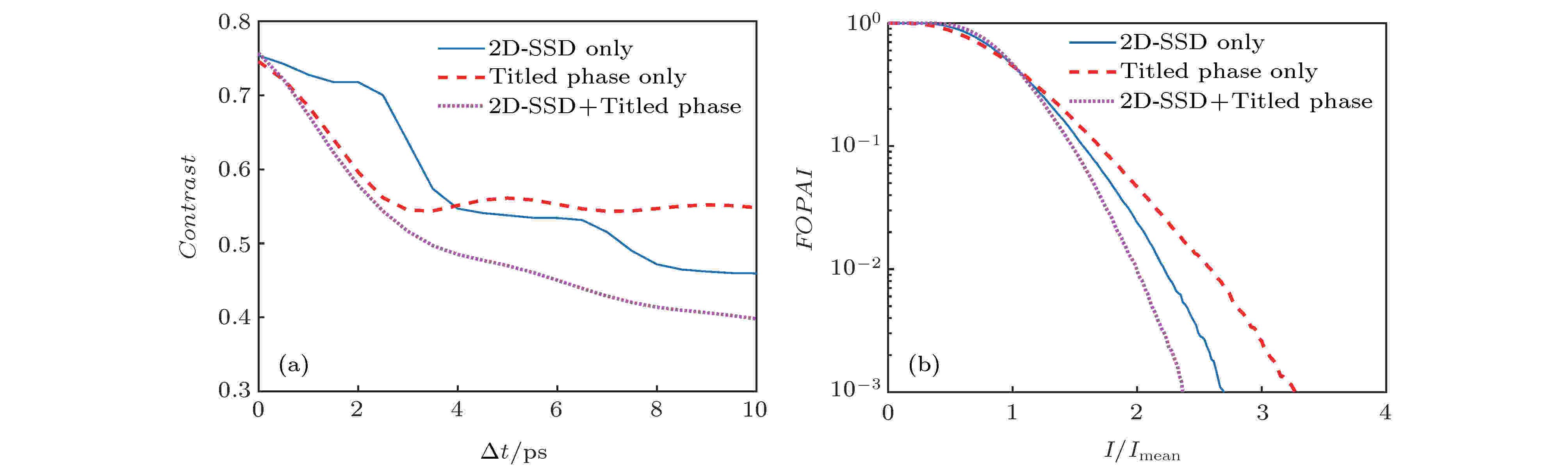图 8 不同匀滑方案下, (a)光通量对比度随时间的变化和(b) FOPAI曲线
Figure8. (a) Variation of contrast with integral time and (b) FOPAI curves with different smoothing scheme.

分析图8(a)可知, 束间动态干涉匀滑方案的焦斑光通量对比度在较短时间内迅速下降到0.55左右, 之后趋于稳定; 2D-SSD的焦斑光通量对比度则振荡下降到低于0.55的值; 二者联用的焦斑光通量对比度可在更短时间内迅速下降到更低的值. 这表明, 相比于2D-SSD, 束间动态干涉匀滑方案能在更短时间内改善焦斑均匀性, 但其匀滑速度取决于子光束间的波长差. 此外, 图8(b)中束间动态干涉匀滑与2D-SSD联用的焦斑FOPAI曲线明显左移, 表明相较于其他两种方案, 二者联用的焦斑内部热斑明显减少, 束匀滑效果得到极大改善. 由此可见, 可将束间动态干涉匀滑方案作为现有时域束匀滑技术的有效补充.

针对惯性约束核聚变装置对提高靶面辐照均匀性的高要求, 提出了一种基于束间动态干涉的快速匀滑新方法. 该方法将惯性约束核聚变装置中的激光集束分为两两组合的子光束对, 利用相位板阵列对多束激光附加共轭或互补的相位调制, 并使子光束之间存在一定波长差, 从而使各子束在远场两两相干叠加以产生动态的干涉图样, 进而通过焦斑内部散斑的动态扫动, 实时、动态地改变散斑的位置和强度, 并在ps量级积分时间内有效改善靶面辐照均匀性. 与传统的SSD匀滑方案相比, 束间动态干涉匀滑具有以下特点: 1)通过不同波长子束在远场动态干涉的方式实现焦斑在多方向的匀滑, 且束间波长差、相位板类型分别决定了匀滑速度和匀滑方向; 2)将此方案与SSD进行联用, 可在较短时间内获得均匀性较好的焦斑, 从而大幅改善靶面辐照特性, 因而该方案可作为现有束匀滑技术的有效补充. 分析结果表明, 选取合适的束间波长差、相位调制PV值, 并对相位板阵列进行合理设计, 可以利用束间动态干涉实现焦斑在多方向、多维度的皮秒时间尺度的快速匀滑, 从而改善靶面辐照均匀性.