摘要:近20年来, 大量的磁岛链现象从空间、天体物理到磁约束实验室等离子体中被观察到, 并且有关磁岛链现象的许多物理特性可以直接被计算机模拟结果所证实. 磁岛链理论在磁重联理论中的重要进展为快速磁重联的发生机制提供了更加具有说服力的解释. 本文采用二维三分量的磁流体力学模型, 数值研究了不同宽度和不同强度的垂直平面驱动流对磁重联中磁岛链不稳定性的影响, 并分析了导向场和垂直平面的驱动流对磁岛链的共同作用. 研究结果表明: 垂直平面驱动流的宽度越宽或强度越强, 越容易产生磁岛链结构. 电流片中的小磁岛个数及重联率随着垂直平面驱动流宽度及强度的增加而增加. 另外, 导向场会改变重联平面内磁岛链的对称性. 相同导向场情况下, 驱动流强度越大, 小磁岛的增长速度越快.
关键词: 磁重联/
等离子体驱动流/
磁岛链/
导向场

English Abstract

全文HTML

--> --> -->

在空间和实验室等离子体中, 有限的电导率会破坏磁冻结条件, 引起磁重联现象. 在该过程中磁力线自发或受迫地断开并重新连接, 伴随着磁能的快速释放及等离子体动能的增加, 从而引起带电粒子的加速和加热. 空间和实验室等离子体中观测到的快尺度磁流体事件, 如太阳耀斑爆发^[1-3]、地球磁层亚暴^[4,5]、聚变等离子体中的锯齿模^[6,7]等, 与磁重联现象有着紧密的联系. 因此有大量的理论模拟工作研究快尺度磁重联的物理过程, 包括经典的无碰撞磁重联^[8-10]和湍流驱动的快尺度磁重联^[11]等.
近年来, 细长电流片系统中的磁岛链不稳定性备受关注. 理论模拟研究表明: 当磁雷诺数超过临界值时, 细长的Sweet-Parker电流片就会产生二次撕裂模不稳定性, 形成磁岛的链状结构. 伴随着磁岛链的发展、聚集和喷射, 电流片最终被分解^[12-21]. Samtaney等^[22]对单电流系统中的磁岛链进行了模拟, 指出当磁雷诺数S增大时(S > 10⁴), 电流片会变得不稳定. 单X点重联会变成多X点重联, 并出现磁岛链或等离子体链(plasmoid). 而且磁雷诺数S越大, 电流片越不稳定, 越容易产生磁岛链. Samtaney等^[22]还给出了二级磁岛的增长率关于磁雷诺数S的定标率${\rm{\gamma }}{T_A} \sim {S^{1/4}}$和二级磁岛的数目关于磁雷诺数S的定标率$N \sim {S^{3/8}}$, 这与Loureiro等^[15]在2007年工作中的理论分析结果一致. Bhattacharjee等^[18]采用电阻磁流体动力学(MHD)模型数值研究了大尺度系统中的薄电流片的不稳定性. 研究表明: 当磁雷诺数超过某临界值时, 会产生超阿尔芬撕裂不稳定性(磁岛链不稳定性). 最初的Sweet-Parker重联层会破裂形成磁岛链, 而且电流片会变得更薄. 模拟研究中出现的等离子体链以及实验观测结果表明: 在细长电流片系统中, 由磁岛链引起的次级不稳定性可以实现系统的快速重联. 这有可能在地球磁层和太阳耀斑的磁重联机制中起到重要作用. 因此, 磁岛链不稳定性被认为是快速重联的主要物理机制之一.
在空间等离子体中, 经常会观测到多电流层的结构. 多层电流片系统中的撕裂模不稳定性会发生耦合, 引起所谓的双撕裂模^[23-26]、三撕裂模^[27]等多撕裂模^[28]不稳定性. Nemati等^[29]基于二维的电阻磁流体力学模型, 研究了双电流片系统中磁岛链的形成过程. 研究表明: 磁岛链的重联率随着磁雷诺数S的增大而增大. 这与普通撕裂模增长率随磁雷诺数S增大而减小的结论不同. 另外, Nemati等^[30]进一步研究了双撕裂模非线性阶段中, 电流片周期方向的长度对磁岛链的影响. 结果表明: 增加周期方向的计算区域会减弱对电阻的依赖关系.
等离子体流动普遍存在于空间和实验室等离子体中. 由于等离子体的剪切流会直接影响磁流体不稳定性的增长过程, 因此有大量的理论和模拟研究关注于剪切流对磁重联过程的影响. La Belle-Hamer等^[31]采用二维可压缩的磁流体力学模拟研究发现: 剪切流对磁重联具有抑制的作用. 剪切流越大, 重联率越低. 但相应的研究只考虑了平行于磁重联平面的剪切流. 近年来, Wang等^[32]采用二维霍尔磁流体力学模型, 数值模拟了垂直磁重联平面的剪切流对磁重联过程中磁岛结构、垂直磁重联平面的磁场结构及电流分布的影响. 发现垂直平面剪切流产生正的四极磁场结构对磁重联起到加速作用, 相应的重联率会增加; 而剪切流产生负的四极磁场时, 重联率会降低. Wang等^[33]采用二维混合模型, 研究了垂直磁重联平面的剪切流对磁重联的影响. 结果表明垂直磁重联平面的反对称“驱动流”会改变对称磁重联过程. 在该过程中会形成二级磁岛并提高重联率.
目前, 大部分的理论模拟研究主要集中在平行于磁重联平面的剪切流对磁重联的影响, 而垂直平面的剪切流对磁场重联及磁岛链影响的研究较少. 由于垂直剪切流及导向场在空间等离子体中普遍存在, 所以研究垂直平面剪切流和导向场对磁重联的影响具有一定的理论意义. Wang等^[33]曾采用混合模拟程序, 发现 “驱动型”的垂直剪切流会显著改变磁重联过程. 本文将采用二维三分量的可压缩电阻磁流体力学模型, 进一步研究垂直平面驱动流对磁重联过程中磁岛链形成的影响, 并分析垂直平面驱动流和导向场对磁岛链不稳定性的共同效应.

2

-->

2.1.理论模型

本文采用的模型方程包括质量、能量和动量的演化方程:

$\frac{{\partial \rho }}{{\partial t}} = - {u} \cdot \nabla \rho - \rho \nabla \cdot {u},$

$\frac{{\partial P}}{{\partial t}} = - {u} \cdot \nabla P - \gamma P\nabla \cdot {u},$

$\rho \frac{{\partial {u}}}{{\partial t}} = - {u} \cdot \nabla {u} + \nabla P + \frac{1}{c}{J} \times {B} + \nu {\nabla ^2}{u},$

以及电磁场方程:

$\nabla \times {E} = - \frac{1}{c}\frac{{\partial {B}}}{{\partial t}},$

${J} = \frac{c}{{4{\text{π}}}}\nabla \times {B},$

式中ρ, P和u分别是等离子体密度、压强和速度矢量; γ是绝热系数; ν是黏滞系数; B和J分别是磁场强度和电流. 电场${E} = - \dfrac{1}{c}{u} \times {B} + \eta {J}$, 其中η是电阻率.
由(3)式—(5)式整理可得:

$\frac{{\partial {u}}}{{\partial t}} = - {u} \cdot \nabla {u} - \nabla P + \frac{1}{{4{\text{π}}}}\left( {\nabla \times {B}} \right) \times {B} + \nu {\nabla ^2}{u},$

$\frac{{\partial {B}}}{{\partial t}} = \nabla \times {u} \times {B} + \eta {\nabla ^2}{B},$

在该工作中, 磁场位型取为${B} = \nabla {\psi } \times \hat{ y} + {B_y}\hat{ y}$, 其中${\psi } = {\psi }\left( {t, x, z} \right)$为磁通量函数. (x, z)为重联平面, y为垂直平面方向(导向场方向). 模拟计算中将采用如下的无量纲化参数: 密度ρ₀, 压强P₀, 长度L₀, 磁场B₀, 磁通量函数${\psi _0} = {B_0}{L_0}$, 速度${u_A} = {{{B_0}}}/{{\sqrt {4{\text{π}}{\rho _0}} }}$和时间${\tau _A} = {{{L_0}}}/{{{u_A}}}$. 并引入无量纲化参数${\nu _m} = {\nu }/({{{u_A}{L_0}{\rho _0}}})$, ${\eta _m} = {\eta }/({{{u_A}{L_0}}})$和等离子体压强与极向磁压之比$\beta = 8{\text{π}}{P_0}/B_0^2$.
2 -->

2.2.平衡条件以及算法

初始磁场选取${B_{Z0}}\left( x \right) = {B_0}\tanh \left( {x/{L_0}} \right)$, 导向场B_y为常数, 其中L₀为电流片的半宽度(L₀ = 0.05). 模拟区间为–1 ≤ x ≤ 1, –4 ≤ z ≤ 4. 边界条件为: z方向采用周期边界, x = ± 1采用开放边界条件. 空间采用二阶精度的中心差分格式, 时间上采用四阶精度的龙格库塔法的方法进行求解. 模拟中采用的参数如下: β = 0.5, ν_m = 0.2 × 10^–5, η_m = 1.0 × 10^–5. x方向和z方向的计算网格选取为[N_x = 1001, N_z = 4001], 时间步长取为Δt = 0.001. 为了研究垂直平面驱动流对磁岛链形成的影响, 我们考虑了形式为${u_{iy0}}\left( z \right) = {u_0}{\rm{exp}}\left( { - {z^2}/{L_{\rm{S}}}^2} \right)$的剪切流, 其中u₀为驱动流最大幅度, L_S为驱动流的半宽度. 该驱动流的方向垂直于重联平面, 大小沿平面内磁力线的方向变化. 驱动流剖面如图1所示.
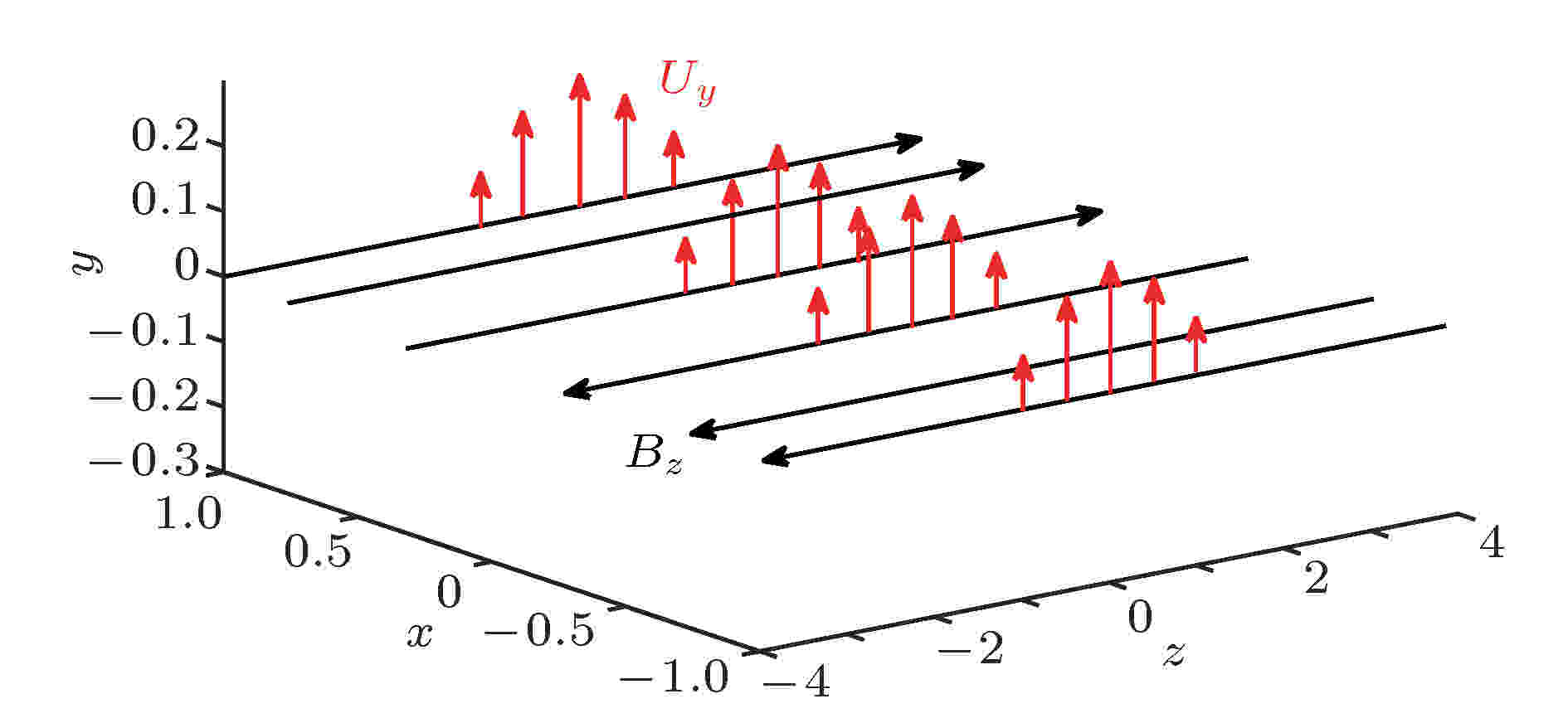图 1 垂直磁重联平面的驱动流剖面
Figure1. Profiles of the out-of-plane driving flows.

为了对比分析驱动流对磁岛链形成的影响, 首先计算了不存在驱动流的磁岛链演化情况. 图2给出了无驱动流时, t = 70, t = 74, t = 80, t = 120时刻的磁岛结构. 可以看出, 在模拟区域两侧先形成磁岛, 随后Y形的电流片变细窄, 从而引起细长电流片的磁岛链不稳定性, 在模拟区域中间形成二次磁岛.
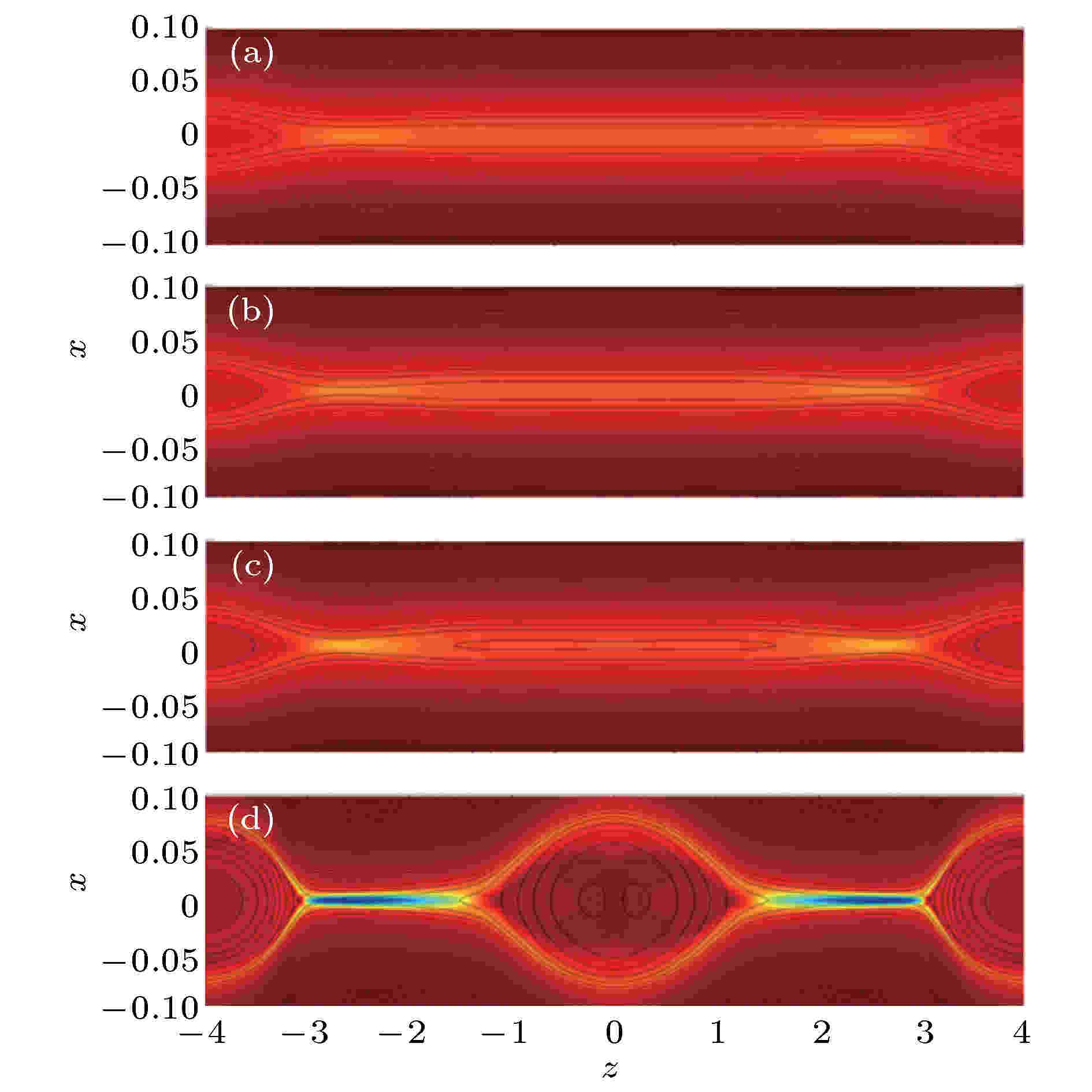图 2 无驱动流情况下的磁岛位型　(a), (b), (c), (d)分别为时间t = 70, t = 74, t = 80和t = 120的结构, 黑线和背景颜色分别为重联平面的磁力线分布和垂直平面的电流密度
Figure2. The magnetic configuration without driving flow at (a) t = 70, (b) t = 74, (c) t = 80, (d) t = 120. The black lines and background colors indicate the magnetic field line in the reconnection plane and the current density in out-of-plane direction, respectively.

2

-->

3.1.驱动流宽度对磁岛链形成的影响

图3和图4分别是加入不同宽度的驱动流情况下, 磁岛结构随时间的演化. 宽度L_S = 0.05, 强度U₀ = 0.1的数值结果如图3所示. 在该参数情况下, 磁岛的演化过程与不加入驱动流的情况类似: 模拟区域两边先形成磁岛, 随后在细长电流片中间形成X点, 并出现两个小磁岛. 之后, 两个小磁岛向中间移动, 融合成一个大磁岛, 磁岛宽度不断增加.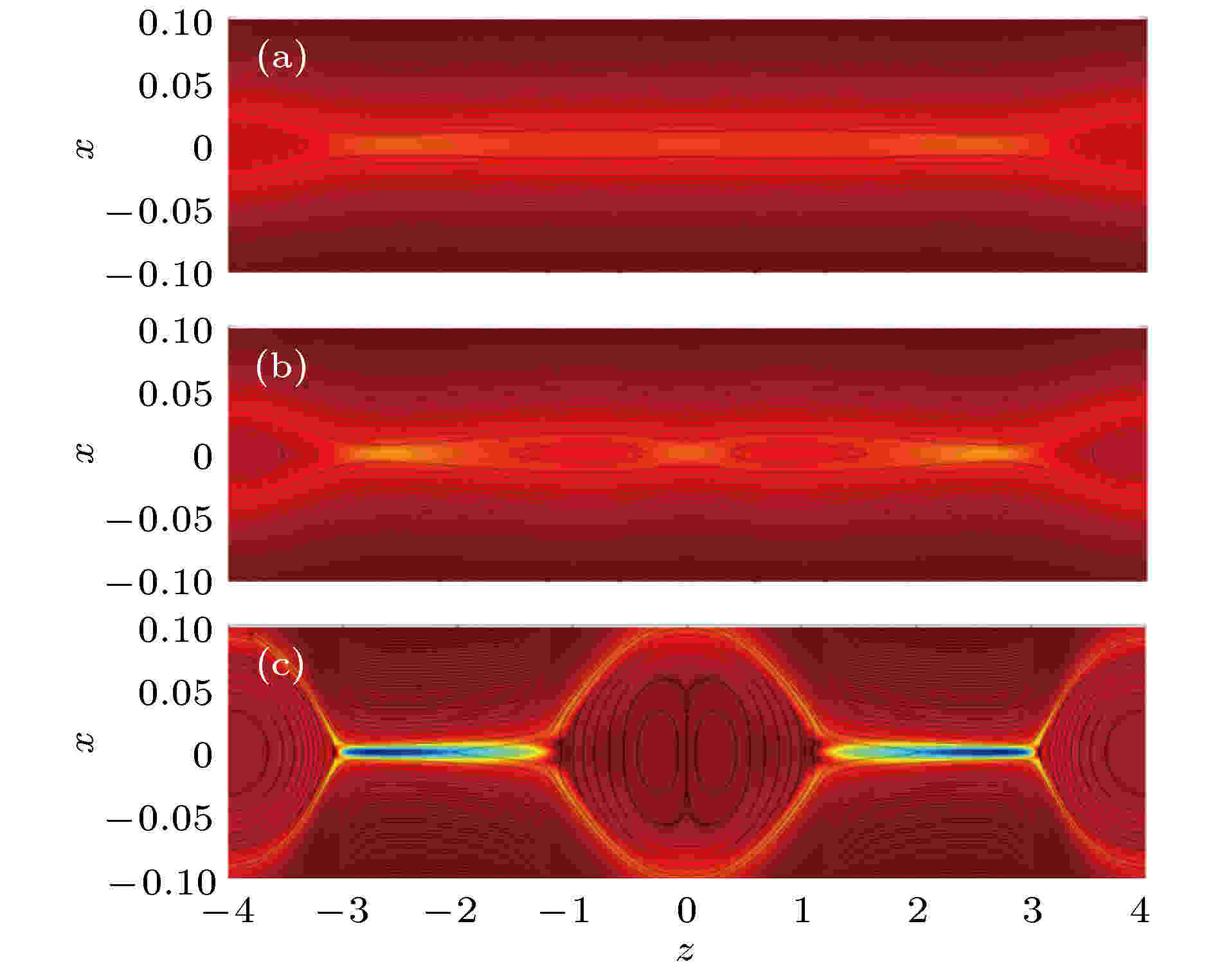
图 3 加入宽度L_S = 0.05、强度U₀ = 0.1的驱动流时, 磁岛链的演化过程　(a), (b), (c)分别为时间t = 70, t = 80和t = 110的结构, 黑线和背景颜色分别为重联平面的磁力线分布和垂直平面的电流密度
Figure3. Evolution of magnetic configuration with out-of-plane driving flow for L_S = 0.05, U₀ = 0.1 at (a) t = 70, (b) t = 80, (c) t = 110. The black lines and background colors indicate the magnetic field line in the reconnection plane and the current density in out-of-plane direction, respec-tively.

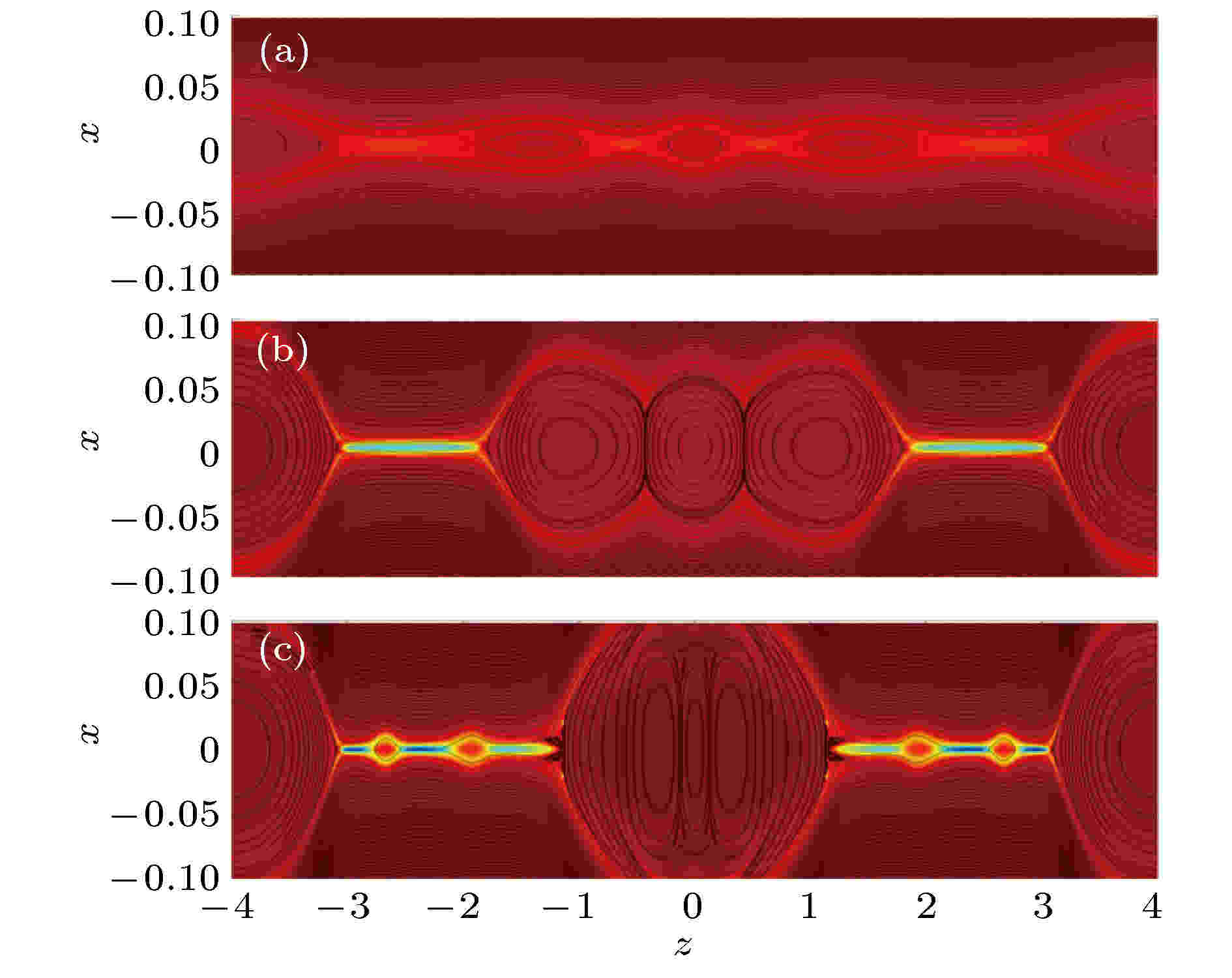图 4 加入宽度L_S = 0.3, 强度U₀ = 0.1 驱动流情况下的磁岛位型　(a), (b), (c)为时间t = 80, t = 110和t = 118的结构, 黑线和背景颜色分别为重联平面的磁力线分布和垂直平面的电流密度
Figure4. The magnetic configuration with out-of-plane dri-ving flow for L_S = 0.3, U₀ = 0.1 at (a) t = 80, (b) t = 110, (c) t = 118. The black lines and background colors indicate the magnetic field line in the reconnection plane and the current density in out-of-plane direction, respectively.

图4是在模拟平面中加入宽度L_S = 0.3, 强度U₀ = 0.1 的驱动流时, 磁岛链的演化过程. 与加入宽度L_S = 0.05 驱动流的结果不同, 在t = 80时刻, 模拟平面中间形成了2个X点, 并出现了3个小磁岛. 随后3个小磁岛向中间移动, 最后融合成一个大磁岛. 中间和两边的磁岛不断增长, 电流片不断被拉长, 最后断裂形成次级磁岛链.
对比不同宽度驱动流的数值结果可知, 小磁岛的个数随着宽度的增加而增加, 即当驱动流的宽度较大时更容易产生磁岛链结构.
2 -->

3.2.驱动流强度对磁岛链形成的影响

图5是加入相同宽度L_S = 0.3, 不同强度的垂直平面驱动流时, 重联磁通随时间的演化曲线, 其中的重联磁通定义为中性片附近磁通改变量的最大值. 可见重联速率随着驱动流强度的增加而增加, 即垂直平面的驱动流对磁岛链具有解稳的作用. 不同驱动流强度、同一时期(系统演化至非线性磁岛链不稳定性阶段出现小磁岛个数最多的时刻)的磁岛链结构见图6. 由图6可以看出, 随着驱动流强度的增大, 小磁岛个数随之增加. 并且小磁岛的运动合并过程更激烈.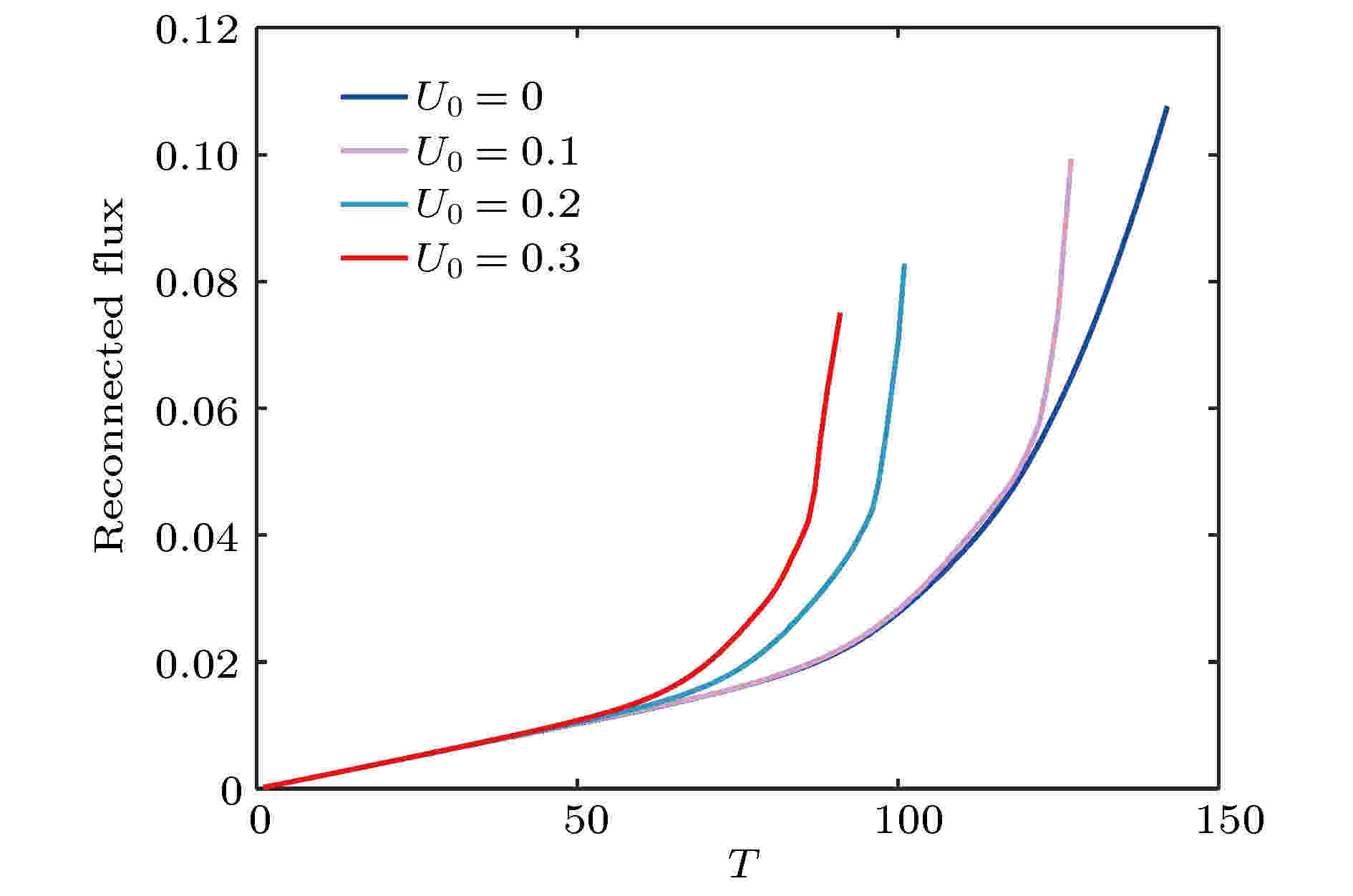
图 5 相同宽度L_S = 0.3, 不同强度的驱动流, 重联通量随时间的演化
Figure5. The evolution of reconnected flux with different driving flow strength.

图 6 加入相同宽度L_S = 0.3, 不同强度的驱动流时的典型磁岛位型, 黑线和背景颜色分别为重联平面的磁力线分布和垂直平面的电流密度　(a)无驱动流的情况t = 120的结构; (b)加入强度U₀ = 0.1的情况在t = 118的结构; (c)加入强度U₀ = 0.2的情况在t = 97的结构; (d)加入强度U₀ = 0.3的情况在t = 88的结构
Figure6. The magnetic configuration with out-of-plane dri-ving flow with different strength for L_S = 0.3 in the same phase. The black lines and background colors indicate the magnetic field line in the reconnection plane and the current density in out-of-plane direction, respectively: (a) Without driving flow at t = 120; (b) with U₀ = 0.1 at t = 118; (c) with U₀ = 0.2 at t = 97; (d) with U₀ = 0.3 at t = 88.

2 -->

3.3.垂直平面驱动流和导向场B_y对磁岛链的共同作用

图7是导向场B_y = 0.1, 垂直平面驱动流宽度L_S = 0.05, 强度U₀ = 0.1情况下, t = 100, t = 110和t = 119时刻的磁岛位型. 可以看出, 与不加导向场的结果相比, 在模拟平面形成的两个磁岛不是向中间移动, 而是向两边移动, 然后与两边的磁岛融合. 随后, 两磁岛中间的电流片变得越来越细长. 当电流片足够细长时, 电流片断裂, 产生次级磁岛链. 另外, 可以观测到, 导向场和垂直平面的驱动流可以改变磁重联位型在z 方向的对称性.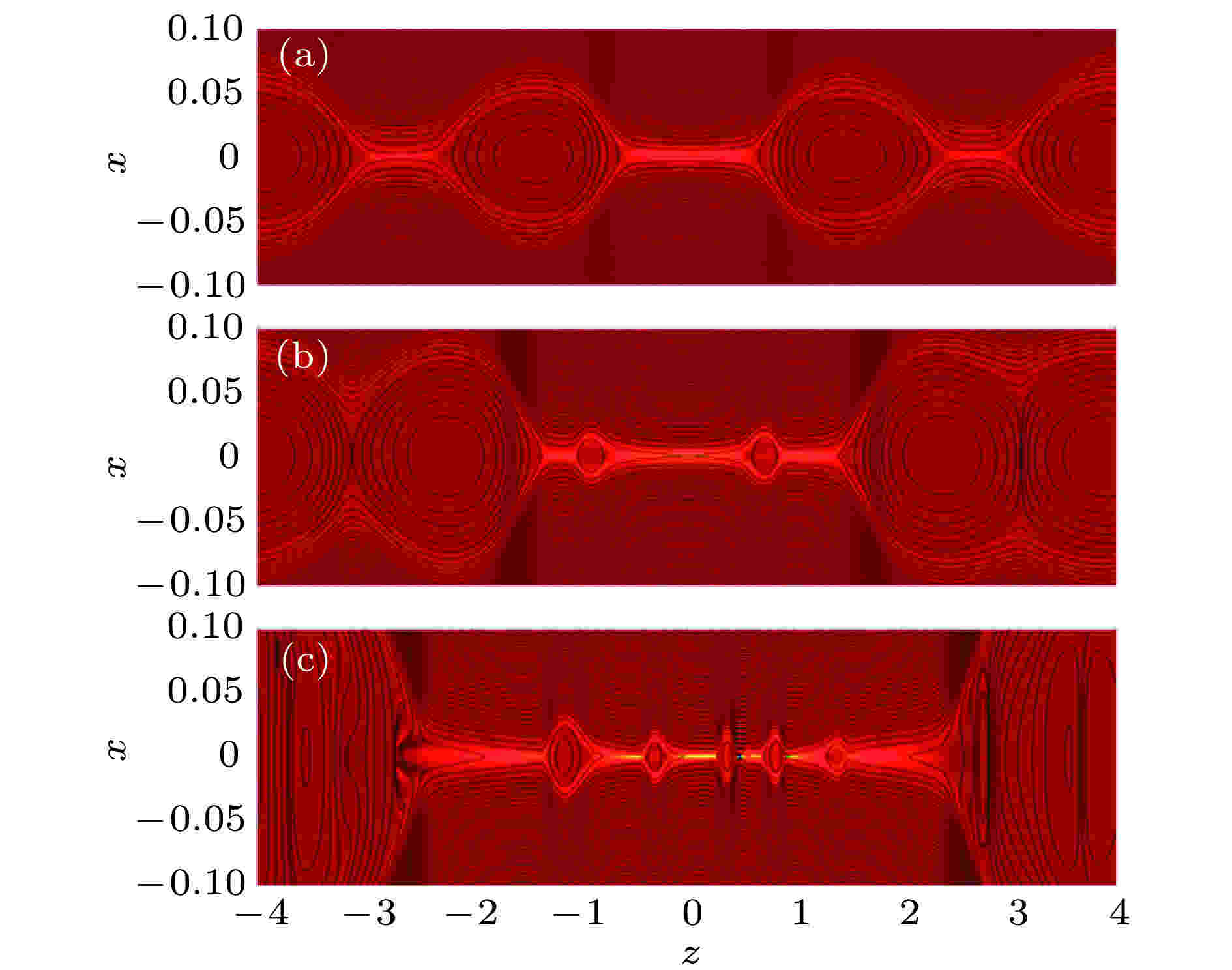
图 7 导向场B_y = 0.1, 驱动流宽度L_S = 0.05、强度U₀ = 0.1情况下的磁岛位型　(a), (b), (c)分别为时间t = 100, t = 110和t = 119的结构, 黑线和背景颜色分别为重联平面的磁力线分布和垂直平面的电流密度
Figure7. The magnetic configuration is effected by out-of-plane driving flow with L_S = 0.05, U₀ = 0.1 and guilding field B_y = 0.1 at (a) t = 100, (b) t = 110, (c) t = 119. The black lines and background colors indicate the magnetic field line in the reconnection plane and the current density in out-of-plane direction, respectively.

图8为驱动流宽度L_S = 0.3, 强度U₀ = 0.1, 导向场B_y = 0.1时的磁岛链演化情况. 与不加导向场的结果不同, 在模拟平面中间产生了四个小磁岛. 随后小磁岛分别向两边移动, 最后与模拟平面两边的磁岛融合. 磁岛个数比不存在导向场的情况多.
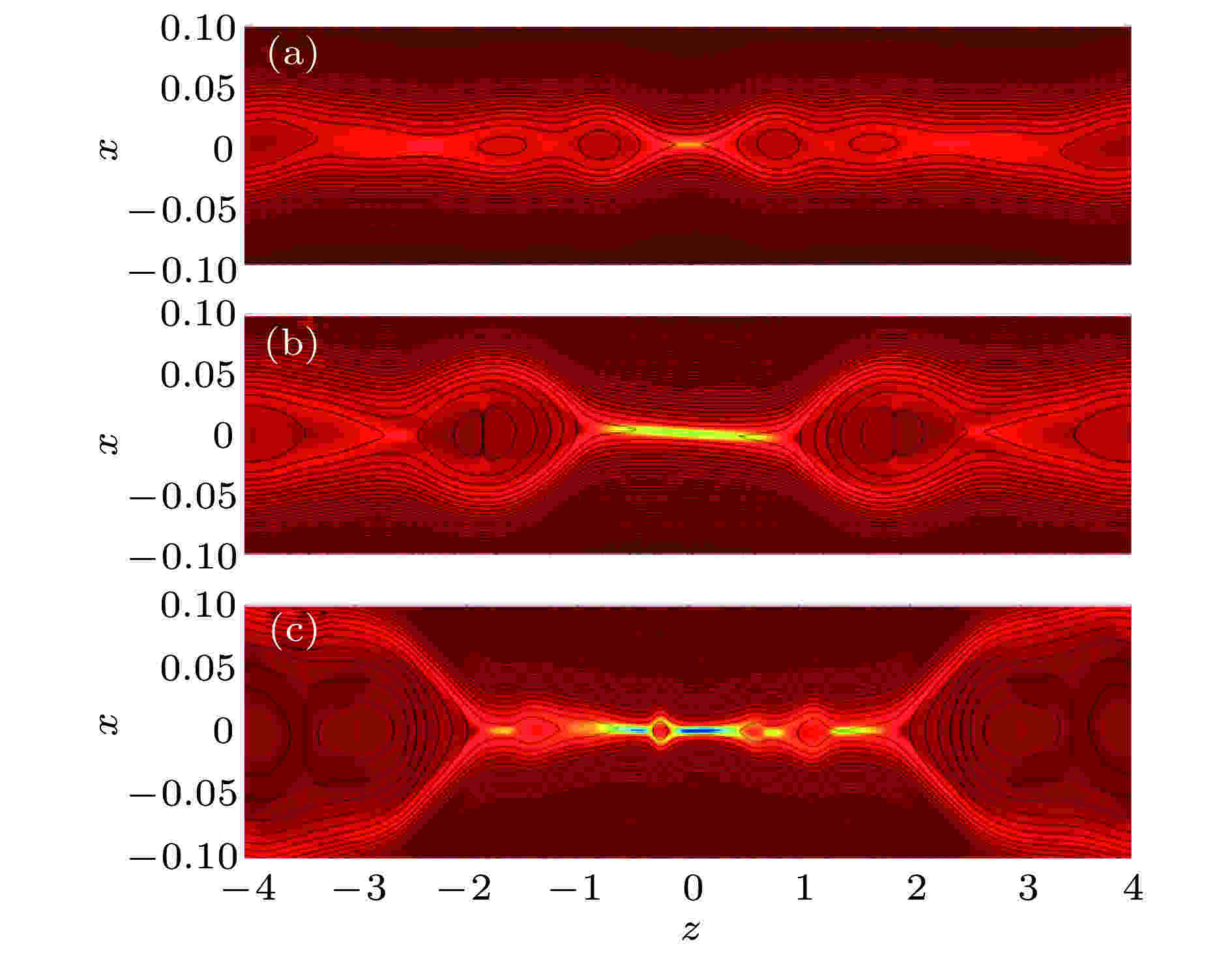图 8 驱动流宽度L_S = 0.3, 强度U₀ = 0.1, 导向场B_y = 0.1的情况下, 磁岛位形的演化　(a), (b), (c)分别为时间t = 70, t = 80和t = 88的结构, 黑线和背景颜色分别为重联平面的磁力线分布和垂直平面的电流密度
Figure8. Evolution of the magnetic configuration with out-of-plane driving flow for L_S = 0.3, U₀ = 0.1 and guilding field B_y = 0.1 at (a) t = 70; (b) t = 80; (c) t = 88. The black lines and background colors indicate the magnetic field line in the reconnection plane and the current density in out-of-plane direction, respectively.

驱动流宽度为0.05, 强度U₀ = 0.1时, 不同导向场B_y时, 重联通量随时间的演化见图9(a). 可以看出在强度相同的情况下, 导向场B_y = 0.2时, 重联速度最快, 之后随着导向场变大, 重联速度变慢. 图9(b)是导向场B_y = 0.1, 不同强度U₀时, 重联通量随时间的演化. 可以看出, 在导向场相同的情况下, 垂直驱动流强度越大, 重联速度越快. 图9(c)是导向场B_y = 0.1时, 在非线性磁岛链不稳定性阶段小磁岛宽度的增长速度$\dfrac{{\partial w}}{{\partial t}}$(w为小磁岛的半宽度)对强度U₀的依赖关系. 可见, 相同导向场情况下, 驱动流强度越大, 小磁岛的增长速度越快.
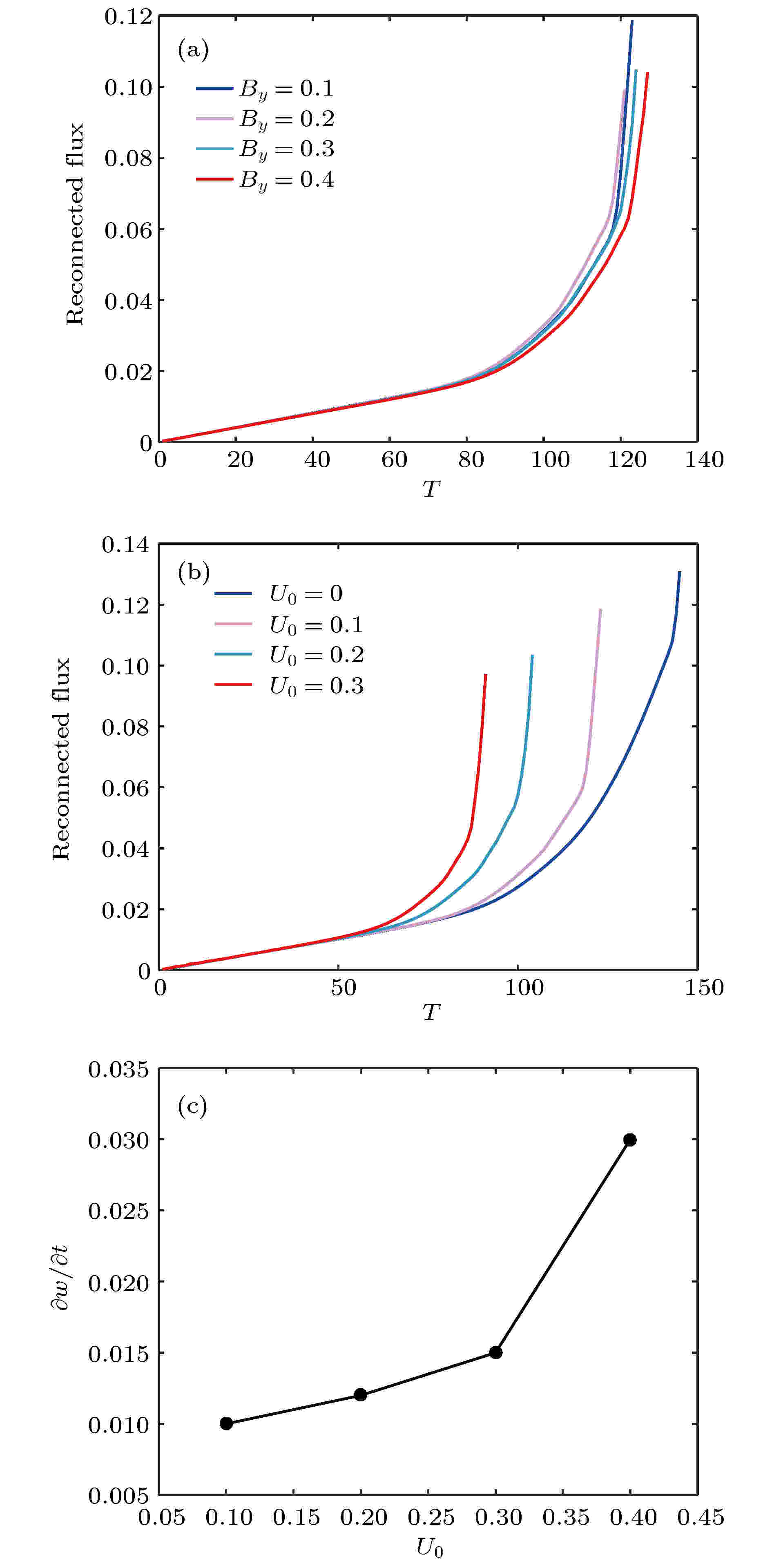图 9 (a)驱动流宽度L_S = 0.05, 强度U₀ = 0.1时, 不同导向场B_y重联通量随时间的演化; (b)导向场B_y = 0.1, 驱动流宽度L_S = 0.05时, 不同强度U₀下重联通量随时间的演化; (c)导向场B_y = 0.1, 驱动流宽度L_S = 0.05时, 小磁岛宽度的增长速度对强度U₀的依赖关系
Figure9. (a) Evolution of the reconnection flux with out-of-plane driving flow for L_S = 0.05, U₀ = 0.1 and different guilding field; (b) evolution of the reconnection flux with different driving flow strength and guilding field B_y = 0.1; (c) dependence of the growth rate of plasmoid on different driving flow strength with guilding field B_y = 0.1.

采用二维三分量的电阻磁流体力学模型, 数值研究了不同宽度的垂直平面驱动流和不同强度的垂直平面驱动流对磁重联中磁岛链的影响. 分析了垂直平面驱动流与导向场对磁岛链的共同作用. 研究结果可以总结如下:
1)垂直重联面的驱动流宽度越大, 磁岛链越不稳定, 小磁岛的个数越多;
2)垂直重联面的驱动流强度越大, 重联的速度越快, 小磁岛的个数越多;
3)导向场会改变重联平面磁岛链的对称性.
感谢哈尔滨工业大学王晓钢老师在本课题研究过程中给予的指导.