摘要:采用SST k-ω低雷诺数湍流模型对加热条件下超临界压力CO₂在内径d_i = 22.14 mm, 加热长度L_h = 2440 mm水平圆管内三维稳态流动与传热特性进行了数值计算. 通过超临界CO₂在水平圆管内的流动传热实验数据验证了数值模型的可靠性和准确性. 首先, 研究了超临界压力CO₂在水平圆管内的流动传热特点, 基于超临界CO₂在类临界温度T_pc处发生类液-类气“相变”的假设, 揭示了水平圆管顶母线和底母线区域不同的流动传热行为. 然后, 分析了热流密度q_w和质量流速G对水平圆管内超临界压力CO₂流动换热的影响, 通过获取流体域内的物性分布、速度分布和湍流分布等详细信息, 重点解释了不同热流密度q_w和质量流速G下顶母线内壁温度T_w,i分布产生差异的传热机理, 分析结果确定了类气膜厚度δ、类气膜性质、轴向速度u和湍动能k是影响顶母线壁温分布差异的主要因素. 研究结果可以为超临界压力CO₂换热装置的优化设计和安全运行提供理论指导.
关键词: 超临界CO₂/
水平流动/
传热/
数值模拟

English Abstract

全文HTML

--> --> -->

作为一种新型动力循环技术, 超临界CO₂ (supercritical carbon dioxide, S-CO₂)布雷顿循环在核能、太阳能、化石能源和地热能等领域具有广阔的应用前景^[1-4]. S-CO₂流动传热是S-CO₂布雷顿循环的关键技术之一, 充分地了解并掌握S-CO₂传热机理对于换热装置设计和安全稳定运行是至关重要的. 自20世纪50年代以来, 各国****对S-CO₂传热进行了大量的实验和数值分析, 但主要围绕S-CO₂在垂直圆管内向上和向下流动传热进行研究^[5-11]. 然而, 相对于垂直管内的流动传热, 加热条件下S-CO₂在水平管内垂直方向会受到重力和浮升力的双重作用, 发生流动分层现象, 这将引起圆管顶部和底部不同的传热行为, 使得S-CO₂在水平管内的流动传热特性更为复杂.
Adebiyi和Hall^[12]对水平圆管内S-CO₂流动传热进行了实验研究, 通过观察管壁温度变化趋势发现在圆管底部的传热能力较强, 而顶部的传热能力有所弱化, 这与Pidaparti等^[13]和Chu与Laurien^[14]的研究结果是一致的. Wang等^[15]实验研究了S-CO₂在水平圆管内的对流传热特性, 通过采用浮升力准则数$Gr/Re_{\rm{b}}^2$和流动加速准则数K_v对实验数据进行分析认为, 在高热流密度和低质量流速下, 传热恶化与浮升力效应影响有关, 而流动加速效应可以忽略不计. Tanimizu和Sadr^[16]采用Bu_C, Bu_J和Bu_P三个浮升力准则参数预测了水平圆管内浮升力效应对S-CO₂流动换热的影响, 虽然研究结果显示浮升力准则数的大小和变化趋势与传热变化关联性较小, 但Tanimizu和Sadr仍认为浮升力效应存在并且对流动传热具有重要影响. Kim等^[17]实验研究也发现浮升力准则数(Bu_C和Bu_J)的变化趋势与传热变化的关联性并不确切, 虽然Kim等同样认为浮升力效应存在, 但是由于Kim等引入了流动加速准则数q⁺并发现其与传热变化关联性较好, 认为流动加速与传热变化密切相关, 浮升力效应可能对于流动传热影响极小.
综上所述, 现有研究主要通过实验方法分析加热条件下S-CO₂在水平圆管内的流动传热特性, 而且各****对S-CO₂在水平圆管内流动传热发生变化原因的意见并不一致. 此外, 由于实验方法仅能测量表观数据, 不能获得流体域内部详细的参数分布, 因此采用数值模拟的方法, 对S-CO₂在水平圆管内流动传热机理进行进一步研究是十分必要的. 鉴于此, 本文主要包括以下研究内容. 首先, 通过S-CO₂在水平圆管内流动传热实验数据验证数值模型的可靠性和准确性, 并建立拓展计算工况, 分析水平圆管内S-CO₂在恒定热流密度加热条件下的流动传热特点. 然后, 分析热流密度q_w和质量流速G对S-CO₂在水平圆管内流动传热的影响, 通过获得流体域详细的温度分布、物性分布和流场分布等信息, 揭示不同热流密度q_w和质量流速G条件下S-CO₂在水平圆管内流动传热机理及管壁温度T_{w, i}产生差异的原因. 研究结果可以为S-CO₂布雷顿循环换热装置设计和安全稳定运行提供理论参考.

2

-->

2.1.几何模型

水平圆管的计算几何模型见图1. 计算域包括入口绝热段和加热段两部分, 入口绝热段长度L_ad = 1220 mm, 以确保加热段入口处的工质已处于充分发展状态; 加热段长度L _h = 2440 mm, 是研究S-CO₂流动传热特性的主要部分, 圆管内径d _i = 22.14 mm. 计算过程中忽略圆管壁厚, 圆管周向角度定义为φ, φ = 0°的位置定义为顶母线, φ = 180°的位置定义为底母线.
图 1 几何模型示意图
Figure1. Schematic diagram of the geometric model.

2 -->

2.2.控制方程

本文数值计算模型包括连续性方程、动量方程和能量方程, 并采用以下表示形式对上述方程进行描述.
连续性方程:

${{\partial \left( {\bar \rho {{\tilde u}_i}} \right)}/{\partial {x_i}}} = 0, $

动量方程:

${{\partial \left( {\bar \rho {{\tilde u}_i}{{\tilde u}_j}} \right)}/{\partial {x_j}}} \!=\! - {{\partial \bar p}/{\partial {x_i}}} + {{\partial \left( {{\tau _{ij}} \!-\! \overline {\rho u_i'u_j'} } \right)}\Big/{\partial {x_j}}} + \rho {g_i}, $

(2)式中, ${\tau _{ij}} = \mu \left[ {\left( {\partial {u_i}/\partial {x_j} + \partial {u_j}/\partial {x_i}} \right) - 2{\delta _{ij}}/3 \cdot \partial {u_k}/\partial {x_k}} \right]$,
能量方程:

${{\partial \left( {\bar \rho {{\tilde u}_i}\tilde h} \right)}/{\partial {x_i}}} \!=\! {{\partial \left[ {\mu \left( {\frac{1}{{\Pr }} \!+\! \frac{{{\mu _t}/\mu }}{{{{\Pr }_t}}}} \right)\frac{{\partial \tilde h}}{{\partial {x_i}}}} \right]}\bigg/{\partial {x_i}}}.$

(1)—(3)式中, u, ρ, μ和h分别表示工质的速度、密度、黏度和焓值.
选择合适的湍流模型对S-CO₂流动传热数值计算结果的准确性至关重要. 对于超临界流体流动换热计算, Wang等^[18]的计算结果显示, 采用SST k-ω低雷诺数湍流模型能够得到比其它湍流模型更准确的计算结果. 因此, 本文采用SST k-ω低雷诺数湍流模型进行数值计算. SST k-ω湍流模型简述如下.
k输运方程:

${{\partial \left( {\bar \rho {{\tilde u}_i}k} \right)}/{\partial {x_i}}} = {{\partial \left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right]}\bigg/{\partial {x_j}}} + {G_k} - {Y_k}, $

ω输运方程:

${{\partial \left( {\bar \rho {{\tilde u}_i}\omega } \right)}/{\partial {x_i}}} \!=\! {{\partial \left[ {\left( {\mu \!+\! \frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right]}\bigg/{\partial {x_j}}} + {G_\omega } - {Y_\omega } + {D_\omega }, $

(4)和(5)式中的函数项和常数项详见文献[19].
2 -->

2.3.网格划分及计算方法

计算域网格由ANSYS ICEM软件生成, 采用结构化六面体网格, 圆管横截面采用O型网格划分. 由于S-CO₂物性变化剧烈, 在圆管近壁区域流动换热情况极其复杂, 因此在流体域近壁面处对网格进行局部加密, 并始终保持第一层网格无量纲高度y⁺ < 1. 为检验计算网格独立性, 图2比较了不同网格总节点数时, 水平圆管顶母线内壁温度T_{w, i}沿圆管轴向z/d的分布情况. 由图2可以看出, 当网格总节点数大于269.7万时, 计算结果随节点总数的增加已无明显偏差. 因此, 计算网格总节点数最终确定为269.7万个.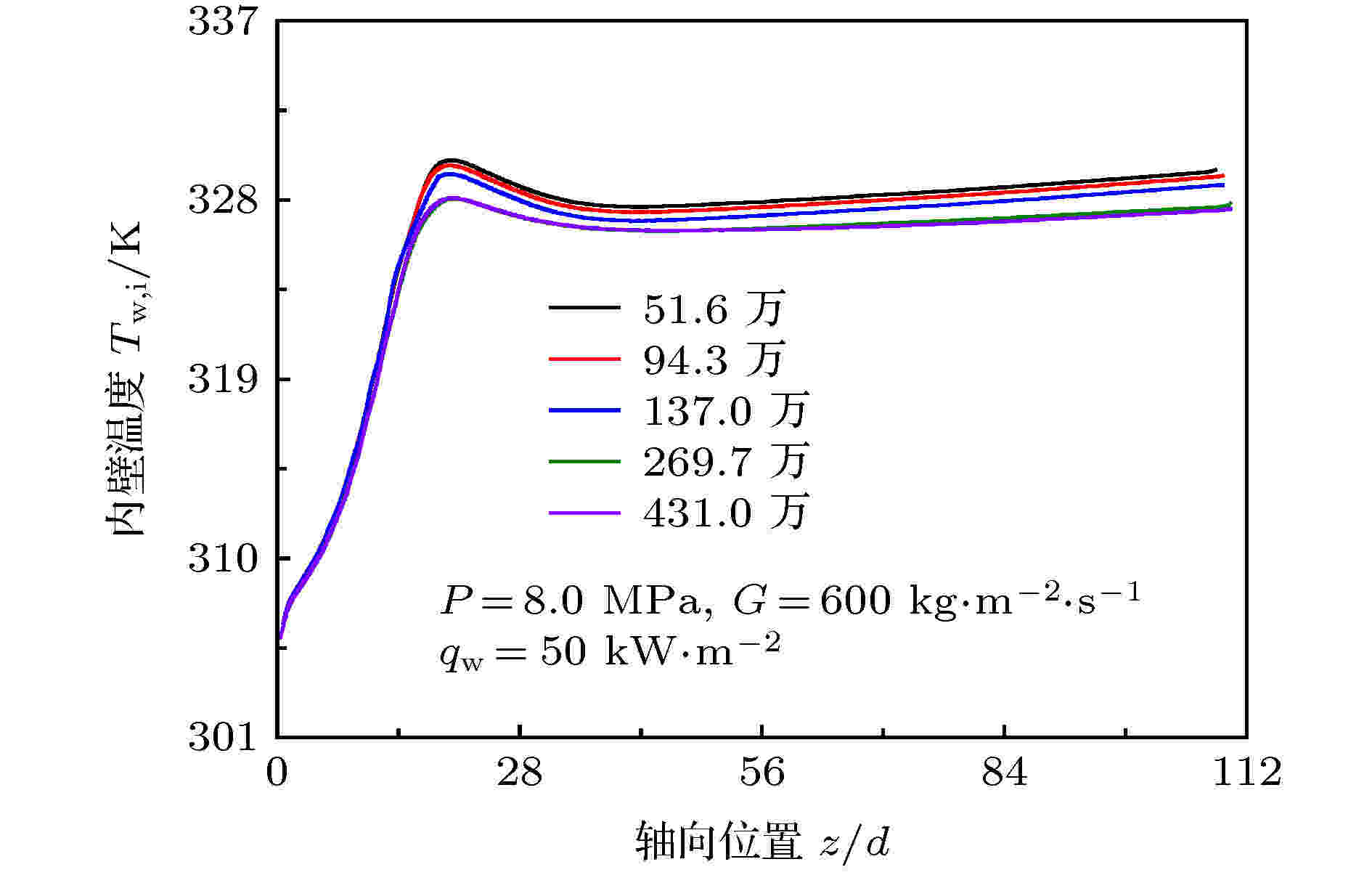
图 2 网格无关性验证
Figure2. Verification for grid independence.

采用ANSYS Fluent 15.0计算水平圆管内S-CO₂三维稳态流动传热的情况. 入口设置为质量流速入口, 出口设置为压力出口, 入口绝热段管壁设置为绝热边界, 加热段管壁设置为均匀热流密度且为无滑移剪切力边界条件. 控制方程采用有限体积法进行离散, 采用二阶迎风差分方法以提高计算精度, 压力-速度耦合方程应用SIMPLEC算法求解. 采用NIST实际气体模型以准确反映超临界流体物性变化对流动传热的影响.

2

-->

3.1.S-CO₂热物性

图3为S-CO₂在不同运行压力下物性参数(定压比热c_p、密度ρ、黏度μ和导热系数λ)随温度的变化曲线. 由图3可以看出, 不同压力下S-CO₂物性参数随温度的变化趋势是相似的, 对于给定超临界压力, c_p总是存在一个极大值, c_p极大值对应温度定义为类临界温度T_pc, 随着温度的升高, 密度、导热系数和黏度会大大降低, 特别是在类临界温度T_pc附近. Holman等^[20]对垂直加热管环内超临界R12湍流传热进行了可视化实验研究, 在近壁区域发现了类似于蒸汽的迹象, Holman等认为产生这一现象的原因可能是由于近壁区剧烈的密度梯度导致的, 即使流体在超临界状态下不存在亚临界状态时的气-液界面, 通过“类沸腾”命名这一行为也是合理的. Banuti^[21]认为, 在T_pc附近超临界流体热物性的剧烈变化相似于典型的亚临界蒸发行为, 并基于“类沸腾”的概念对超临界流体在T_pc附近的变化行为进行了详细的理论说明. 因此, 为了便于分析, 本文将温度低于T_pc的工质状态定义为类液相, 温度高于T_pc的工质状态定义为类气相, T_pc视为类气-类液的“相变”温度.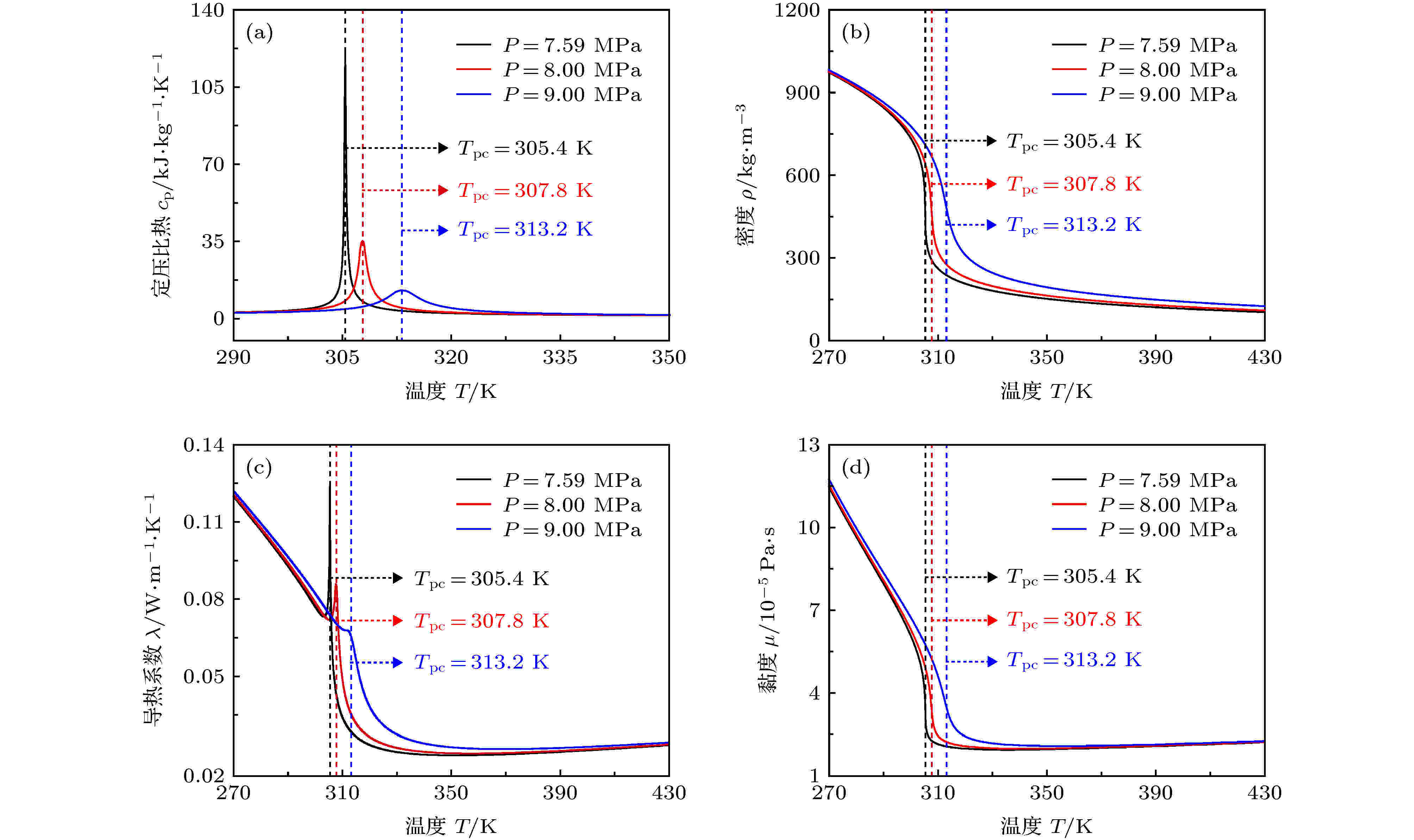
图 3 不同压力下, S-CO₂热物性曲线　(a) 定压比热c_p; (b) 密度ρ; (c) 导热系数λ; (d) 黏度μ
Figure3. Thermophysical properties of S-CO₂ under different pressures: (a) Specific heat at constant pressure c_p; (b) density ρ; (c) thermal conductivity λ; (d) viscosity μ.

需要说明的是, 与亚临界条件下相变过程以及相界面分界气-液相的现象不同, S-CO₂在T_pc附近“类相变”过程是连续的, 而且超临界状态下CO₂的表面张力σ为零^[22]. 对于传统的亚临界气-液两相流传热数值计算问题, 引入的多相流计算模型需考虑相界面的表面张力效应^[23-24]. 显然, 亚临界气-液两相流传热计算模型并不适用于S-CO₂. 因此, S-CO₂流动传热数值模拟属于单相流体流动传热的计算范畴, 引入两相流计算模型并跟踪“相界面”运动对传热的影响是难以实现的.
水平圆管内主流工质温度T_b定义:

${T_{\rm{b}}} = \int_A {\rho u{c_{\rm{p}}}T} {\rm{d}}A\Big/\int_A {\rho u{c_{\rm{p}}}{\rm{d}}A} , $

对流传热系数h定义:

$h = {q_{\rm{w}}}/\left( {{T_{{\rm{w,i}}}} - {T_{\rm{b}}}} \right), $

主流焓值i_b定义:

${i_{\rm{b}}} = \int_A {\rho ui} {\rm{d}}A\Big/\int_A {\rho u{\rm{d}}A} .$

(6)—(8)式中, ρ为当地流体密度, kg·m^–3; u为当地流体速度, m·s^–1; T为当地流体温度, K; A为水平圆管流体域横截面面积, m²; q_w为壁面热流密度, kW·m^–2; i为流体当地焓值, kJ·kg^–1.
2 -->

3.2.计算模型验证

为了验证本文所采用计算方法和湍流模型的可靠性与准确性, 本文基于Adebiyi和Hall^[12]的实验工况运行参数对水平圆管内S-CO₂流动传热进行了数值模拟. 水平管内径为22.14 mm, 均匀加热. 图4对模拟计算值与实验测量结果进行了比较, 受计算模型理想假设、几何模型简化以及实验测量误差等因素的影响, 计算值与实验值之间存在一定的偏差, 但是两者沿轴向变化趋势总体上保持一致. 图4(a)和图4(b)中计算最大偏差值分别是1.0%和0.3%, 说明计算结果与实验数据吻合良好.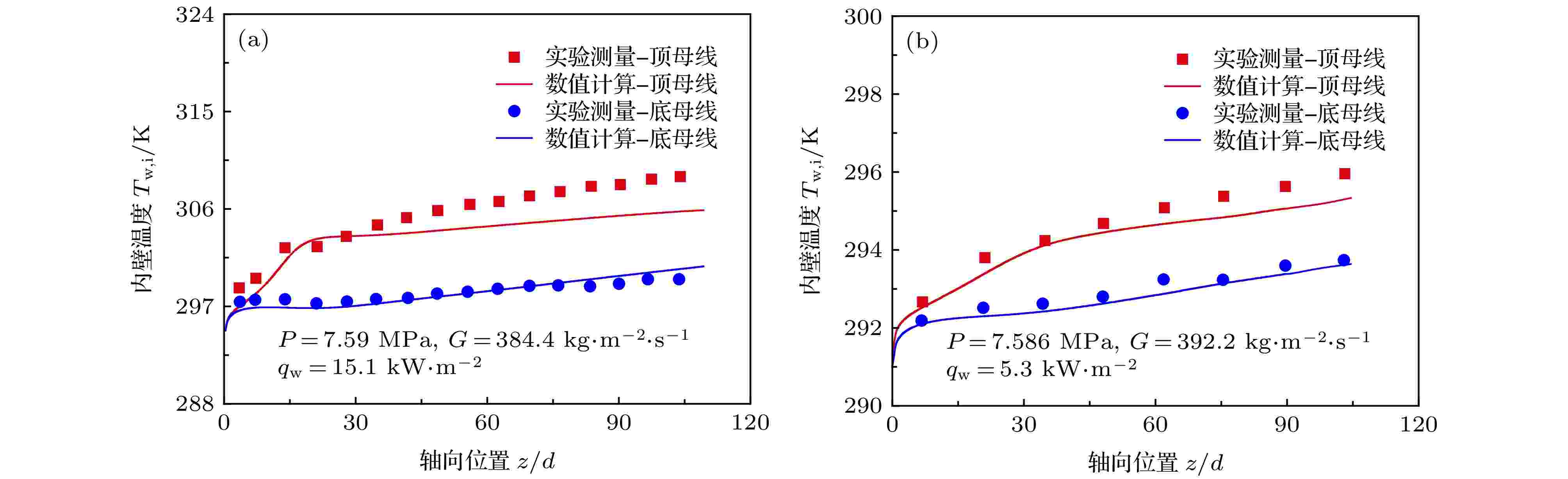
图 4 数值预测壁温与Adebiyi和Hall^[12]实验数据比较
Figure4. Comparison of wall temperature predicted by simulation against experimental data by Adebiyi and Hall^[12].

2 -->

3.3.传热特性

本节以计算工况P = 8.0 MPa, G = 600 kg·m^–2·s^–1, q_w = 40 kW·m^–2为例, 主要分析了加热条件下水平圆管内S-CO₂典型的流动传热特点. 图5给出了S-CO₂在水平圆管内流动换热过程中顶母线与底母线轴向内壁温度T_{w, i}和对流换热系数h、周向类气膜厚度δ分布的典型结果. 其中, 图5(b)中类气膜厚度δ周向分布曲线对应图5(a)中主流焓值i _b = 244.8 kJ·kg^–1处的圆管横截面. 需要说明的是, 为了便于分析, 以圆管横截面内工质当地温度T = T_pc所处位置表征稳态时类液相与类气相的“界面”, 气-液“界面”至圆管内壁的径向距离定义为类气膜厚度δ.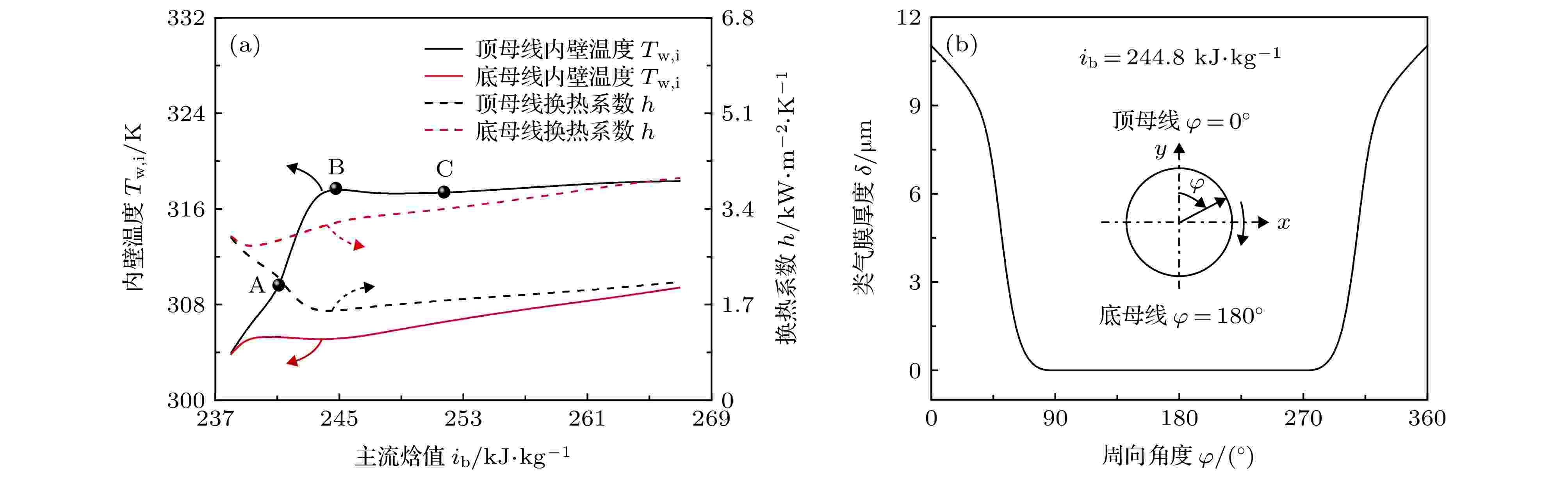
图 5 水平圆管内S-CO₂传热特性典型曲线　(a) 顶母线与底母线内壁温T_w,i和传热系数h轴向分布; (b) 类气膜厚度δ周向分布
Figure5. Typical curves of heat transfer characteristics for S-CO₂ in horizontal tube: (a) Axial distribution of inner wall temperature and heat transfer coefficient at top generatrix and bottom generatrix; (b) circumferential distribution of vapor-like film thickness.

由图5(a)可以看出, 在加热条件下, 水平圆管加热段入口区域顶母线壁温T_w,i剧烈升高, 而底母线壁温变化则比较缓和. 随着加热的不断进行, 顶母线壁温变化也逐渐趋于稳定, 但是顶母线内壁温度T_w,i明显高于底母线, 并形成较大的壁温差值. 此外, 不难发现, 顶母线与底母线换热系数h的相对大小则与壁温分布呈相反的变化趋势. 由图5(b)可以看出, 水平圆管内类气膜厚度δ沿周向是非均匀分布的, 顶母线处类气膜厚度δ最大, 底母线处类气膜厚度δ最小甚至为零.
图6和图7分别显示了水平圆管特征横截面内S-CO₂矢量速度与温度分布情况, 特征截面A, B和C的选取详见图5(a). 其中, i _b,A = 241.1 kJ·kg^–1, i _b,B = 244.8 kJ·kg^–1和i _b,C = 251.8 kJ·kg^–1. 由图6可以看出, 随着加热的不断进行, 圆管近壁区工质密度减小甚至发生类相变, 近壁区域密度低、传热能力差的工质受浮升力的影响沿管壁向顶母线区域流动, 圆管核心区域密度高、传热能力强的工质受重力影响向底母线区域流动, 横截面内由此形成二次流. 此外, 对比图6(a)—(c)可以看出, 在传热阶段A → B, 二次流速度整体有所增加, 表明近壁区类气工质将迅速汇聚至顶母线区域形成高温度、低密度、传热能力弱的类气膜, 严重抑制了顶母线区域管壁热量向主流工质的传递; 在传热阶段B → C, 二次流速度逐渐减小, 主要原因是在加热段下游区域, 近壁区工质密度与主流核心工质密度差异逐渐减小. 二次流的形成使得圆管横截面内发生流体温度和类气-类液分层现象, 而且横截面内工质的“热力学干度”沿着工质流动方向呈逐渐增加的趋势, 详见图7. 不难发现, 以上现象与亚临界条件下水平圆管内气-液两相流动出现的现象是相似的^[25].
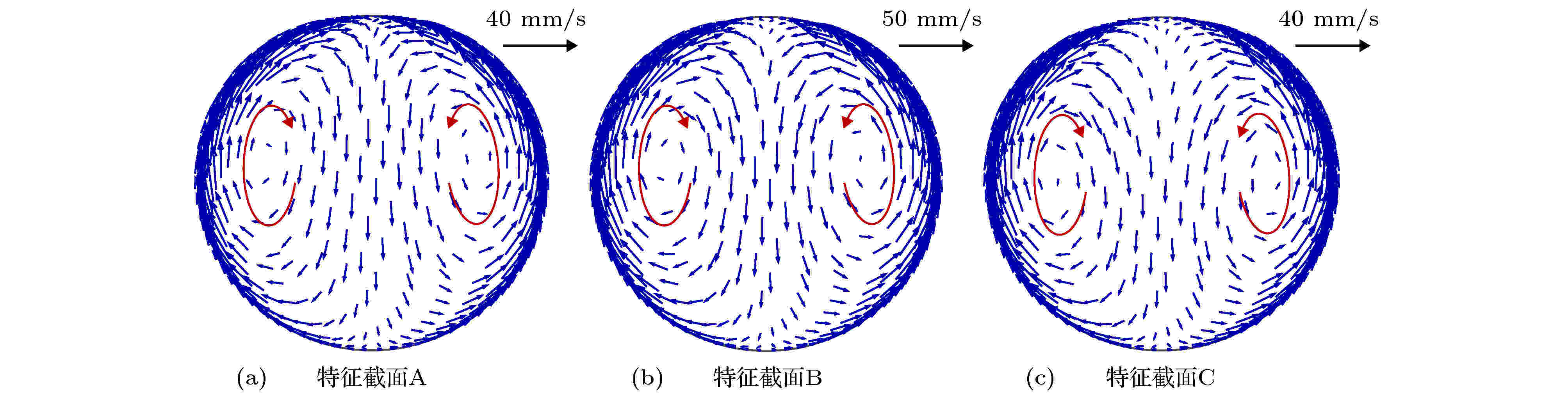图 6 特征横截面内矢量速度分布
Figure6. Vector velocity distribution in the characteristic cross-sections.

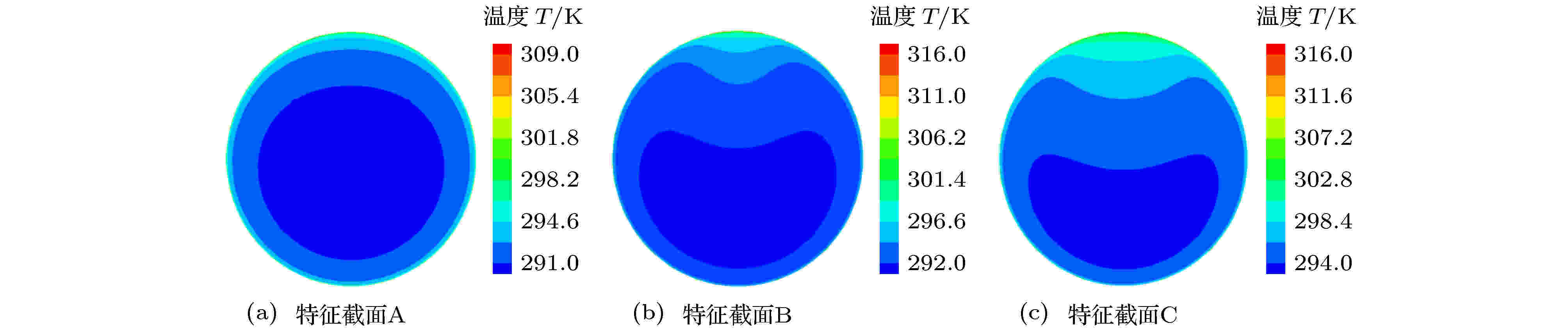图 7 特征横截面内温度分布
Figure7. Temperature distribution in the characteristic cross-sections.

图8显示了水平圆管特征截面内轴向速度u沿径向的分布情况. 由图8可以看出, S-CO₂在水平圆管内顶母线至底母线的轴向速度u相对于圆管中心呈不对称分布, 顶母线区域轴向速度u低于底母线, 因此顶母线处工质沿轴向转移来自于管壁热量的能力比底母线是更差的. 此外, 一个有趣的现象是, 随着主流焓值i_b的增加, 在发生壁温飞升的传热阶段A → B, 顶母线附近工质轴向速度u总体逐渐减小, 而在传热阶段B → C, 轴向速度u逐渐增大; 然而底母线附近工质轴向速度u则随主流焓值i _b整体总是逐渐增加的. 因此, 顶母线较厚的类气膜厚度δ和较低的轴向速度u是顶母线壁温T_w,i高于底母线的重要原因.
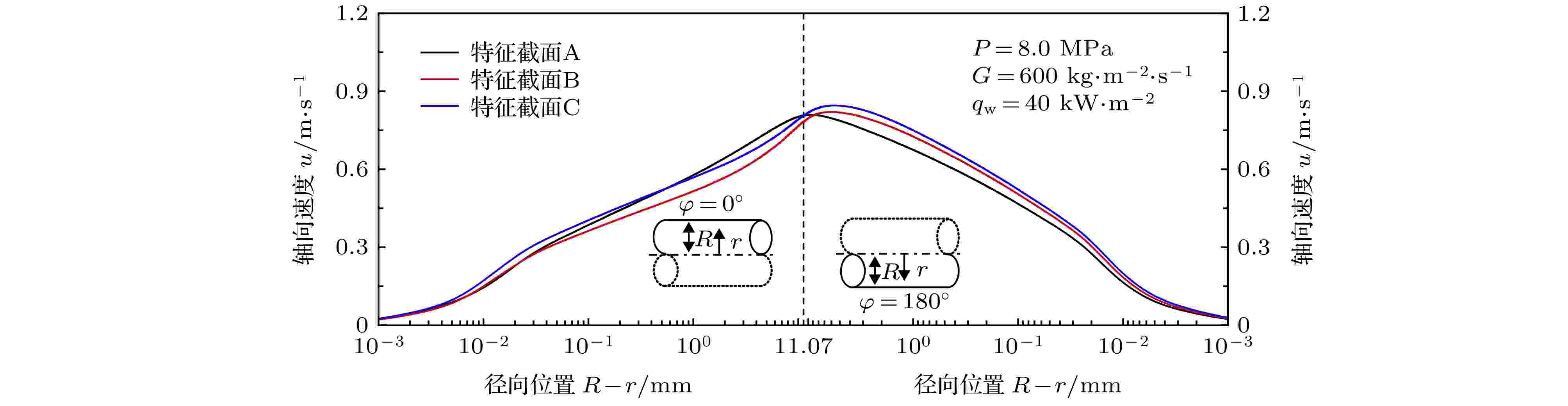图 8 水平圆管内S-CO₂轴向速度沿径向分布
Figure8. Radial distribution of axial velocity for S-CO₂ in horizontal tube.

2 -->

3.4.热流密度对传热的影响

在保持压力P = 9 MPa和质量流速G = 500 kg·m^–2·s^–1不变条件下, 分别采用q_w = 30, 50和70 kW·m^–2评价热流密度对水平圆管内S-CO₂流动换热的影响. 需要说明的是, 3.3节中的计算结果显示顶母线壁温变化特征比底母线更为显著, 因此本文主要通过分析顶母线附近的物性分布和流场分布的特点, 探究热流密度和质量流速对传热流动的影响及原因. 此外, 为了定量地说明圆管横截面内二次流对传热的影响, 本文引入二次流动能参数K_e以表征二次流强度的大小^[26-28], 其表达式为

${K_{\rm{e}}} = \frac{1}{{{A_{\rm{C}}}}}\int\nolimits_{{A_{\rm{C}}}} {\left( {{v^2} + {w^2}} \right){\rm{d}}{A_{\rm{C}}}} , $

(9)式中, v和w分别表示圆管横截面内沿x与y方向的速度分量.
图9展示了不同热流密度q_w条件下顶母线壁温T_{w, i}及二次流强度K_e随主流焓值i _b的分布曲线. 由图9(a)可以看出, 随着热流密度q_w的增加, 顶母线壁温T_w,i明显升高, 特别是加热段入口区域的壁温增加幅度逐渐剧烈, 但是在加热段下游区域, 壁温均体现出比较缓和的变化趋势. 图9(b)显示热流密度q_w越大, 二次流强度K_e总体水平越高, 说明横截面内将有更多的低密度工质沿管壁流动至顶母线附近. 而且, 不同热流密度条件下加热段入口区域K_e均先显著升高, 然后逐渐减小并呈较小幅度的变化水平. 综合图9(a)和图9(b)可以看出, 圆管横截面二次流强度K_e大小对管壁温度变化具有重要影响.
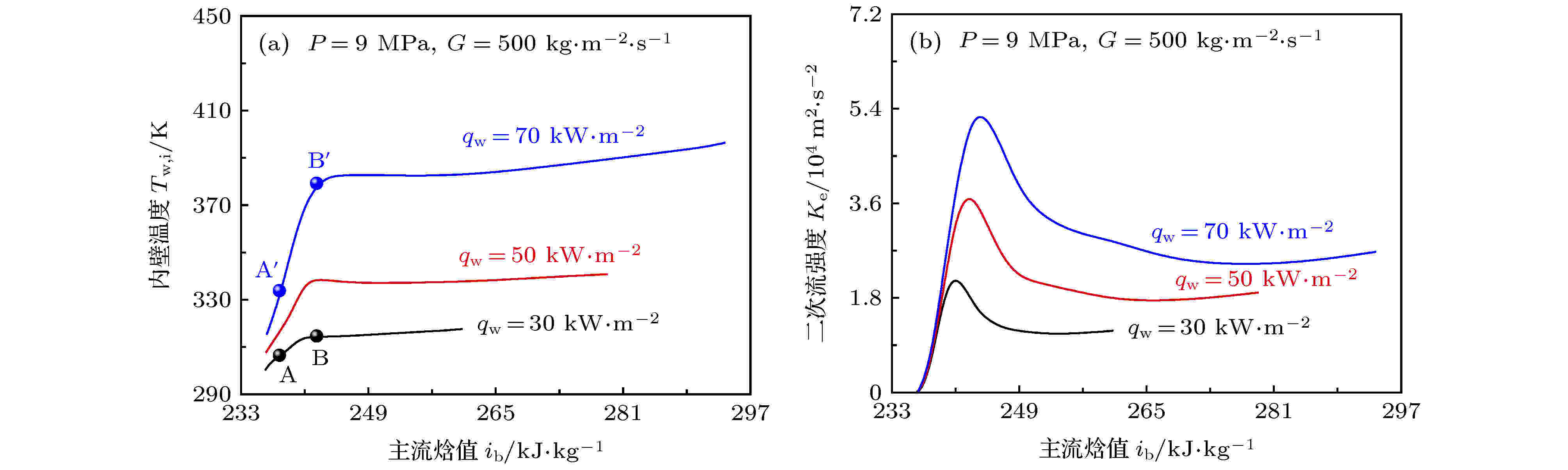图 9 热流密度q_w对壁温和二次流强度的影响
Figure9. Influences of heat flux on wall temperature and second flow intensity.

选取图9(a)中热流密度q_w = 30 kW·m^–2和q_w = 70 kW·m^–2工况下特征截面A和A' (i_b,A = i_b,A' = 236.8 kJ·kg^–1), B和B' (i_b,B = i_b,B' = 242.3 kJ·kg^–1)分析S-CO₂在不同热流密度加热条件下水平圆管内流动换热差异的原因. 图10显示了不同热流密度q_w下, 特征截面内热物性(包括定压比热c_p和导热系数λ)、轴向速度u和湍动能k沿径向分布情况. 由图10(a)和图10(b)可以看出, 热流密度(q_w = 30 kW·m^–2)较低时, 顶母线区域仍为密度较大的类液工质, 并未形成类气膜, 因此近壁区定压比热c_p和导热系数λ处于较高水平. 然而, 当q_w = 70 kW·m^–2时, 顶母线区域聚集了大量低密度类气工质并形成类气膜, 并且随着加热的进行, 类气膜逐渐增厚, 大物性变化区域逐渐远离管壁, 近壁区域表征类气膜性质的定压比热c_p和导热系数λ均较小, 弱化了近壁区类气膜的吸热能力和导热能力. 图10(c)显示在等焓特征截面处, 相对于低热流密度, 高热流密度时顶母线区域近壁工质在局部热加速效应作用下轴向速度u略大, 这有利于S-CO₂沿轴向及时输运转移来自管壁的热量. 由图10(d)可以看出, 高热流密度条件下顶母线区域类气膜内部及主流核心工质的湍动能k整体上总是较小的, 这对于管壁热量在径向向主流核心工质传递是具有抑制作用的.
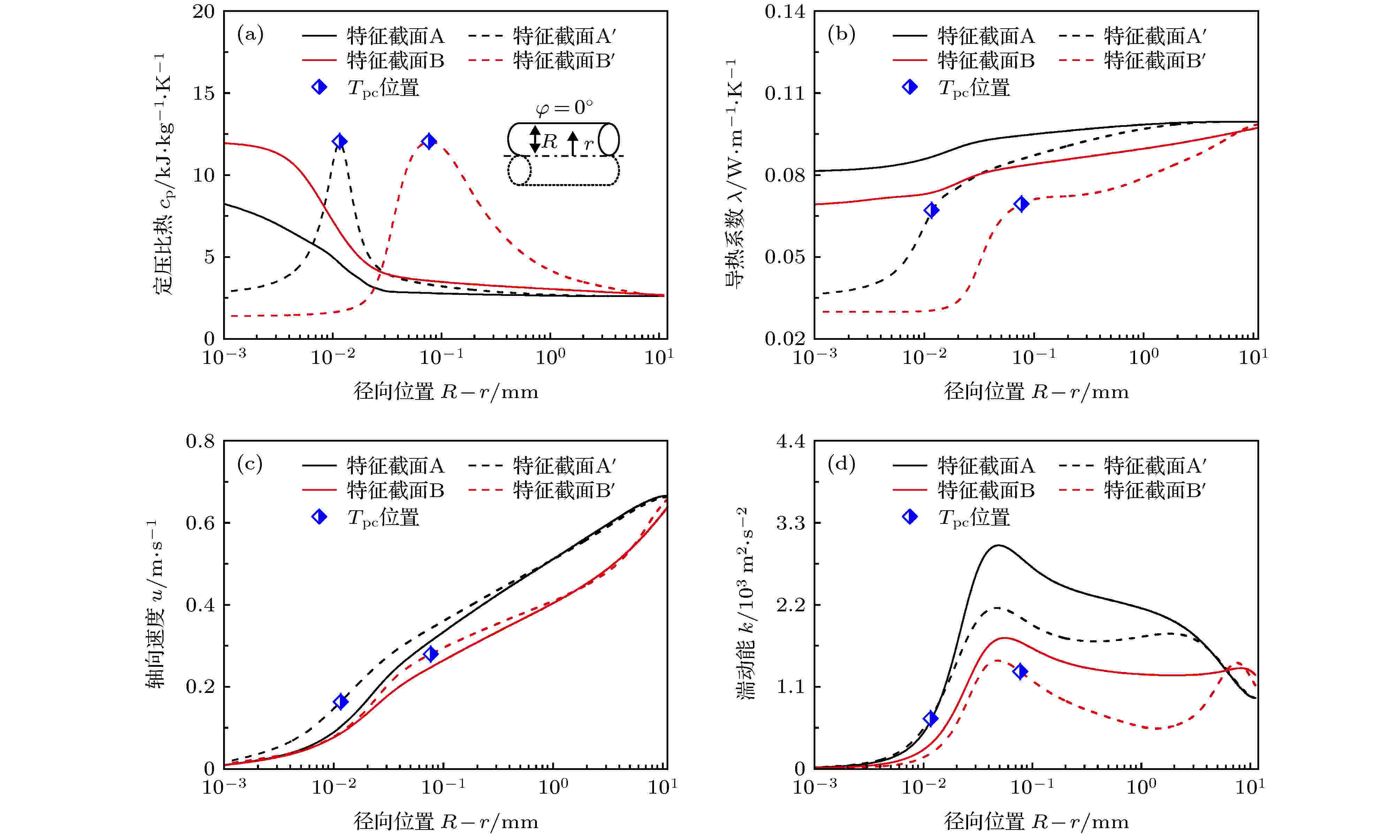图 10 不同热流密度时, 水平圆管特征截面内热物性、轴向速度和湍动能沿径向分布曲线　(a) 定压比热c_p; (b) 导热系数λ; (c) 轴向速度u; (d) 湍动能k
Figure10. Radial distribution curves of thermophyical properties in the characteristic cross-sections under different heat flux: (a) Specific heat at constant pressure c_p; (b) thermal conductivity λ; (c) axial velocity u; (d) turbulent kinetic energy k.

综上可以看出, 在高热流密度条件下, 除了施加到管壁的热量增加导致管壁温度较高这一影响因素外, 顶母线区域类气膜的形成和增厚以及类气膜内部及主流核心工质较小的湍动能k将进一步削弱圆管壁面热量向主流工质的扩散, 这是较高热流密度条件下加热段入口区域壁温增加幅度更剧烈且管壁温度总体更高的重要原因.
2 -->

3.5.质量流速对传热的影响

图11展示了不同质量流速G条件下顶母线壁温T_{w, i}及二次流强度K_e随主流焓值i_b的分布曲线. 由图11(a)可以看出, 随着质量流速G的增加, 顶母线壁温T_{w, i}显著降低, 加热段入口区域的壁温增加幅度明显减小, 说明较高的质量流速可以有效地降低壁温并抑制加热段入口处的壁温飞升. 在加热段下游区域, 壁温同样表现出比较缓和的变化趋势. 图11(b)显示质量流速G越大, 二次流强度K_e总体水平越低, 而且指定质量流速G条件下二次流强度K_e变化趋势与图9(b)相似, 同样反映出圆管横截面二次流强度K_e大小与管壁温度变化的关系.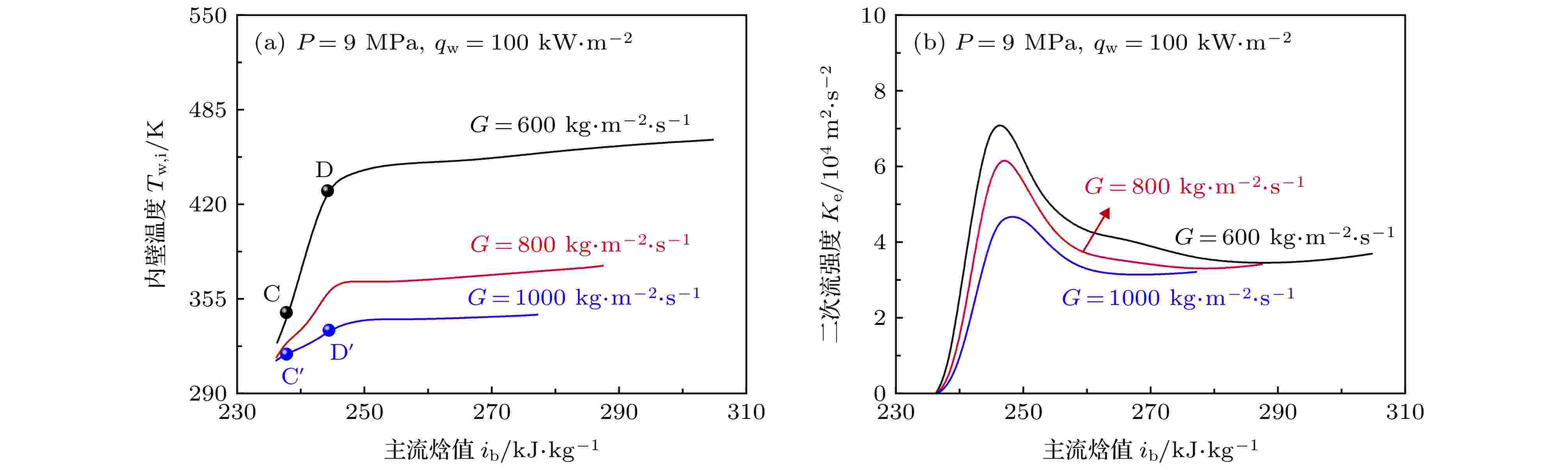
图 11 质量流速G对壁温和二次流强度的影响
Figure11. Effects of mass flux on wall temperature and second flow intensity.

选取图11(a)中质量流速G = 600 kg·m^–2·s^–1和G = 1000 kg·m^–2·s^–1工况下特征截面C和C' (i_b,C = i_b,C' = 238.4 kJ·kg^–1), D和D' (i_b,D = i_b,D' = 244.3 kJ·kg^–1)分析S-CO₂在不同质量流速G条件下水平圆管内流动换热差异的原因. 图12显示了不同质量流速下, 特征截面内热物性、轴向速度u和湍动能k沿径向分布情况. 由图12(a)和图12(b)可以看出, 相对于高质量流速(G = 1000 kg·m^–2·s^–1), 低质量流速(G = 600 kg·m^–2·s^–1)条件下, 顶母线区域更早地出现了类气工质并形成热阻较大的类气膜, 而且类气膜总是较厚的. 类气膜越厚, 大物性变化区域距离管壁越远, 近壁区类气膜性质越差. 由于类气膜不能及时有效地将管壁热量传递至主流核心区, 将导致类气温度升高, 气膜性质进一步变差. 综上可以看出, 顶母线区域类气膜的出现和增厚是低质量流速条件下壁温更高的主要原因之一.
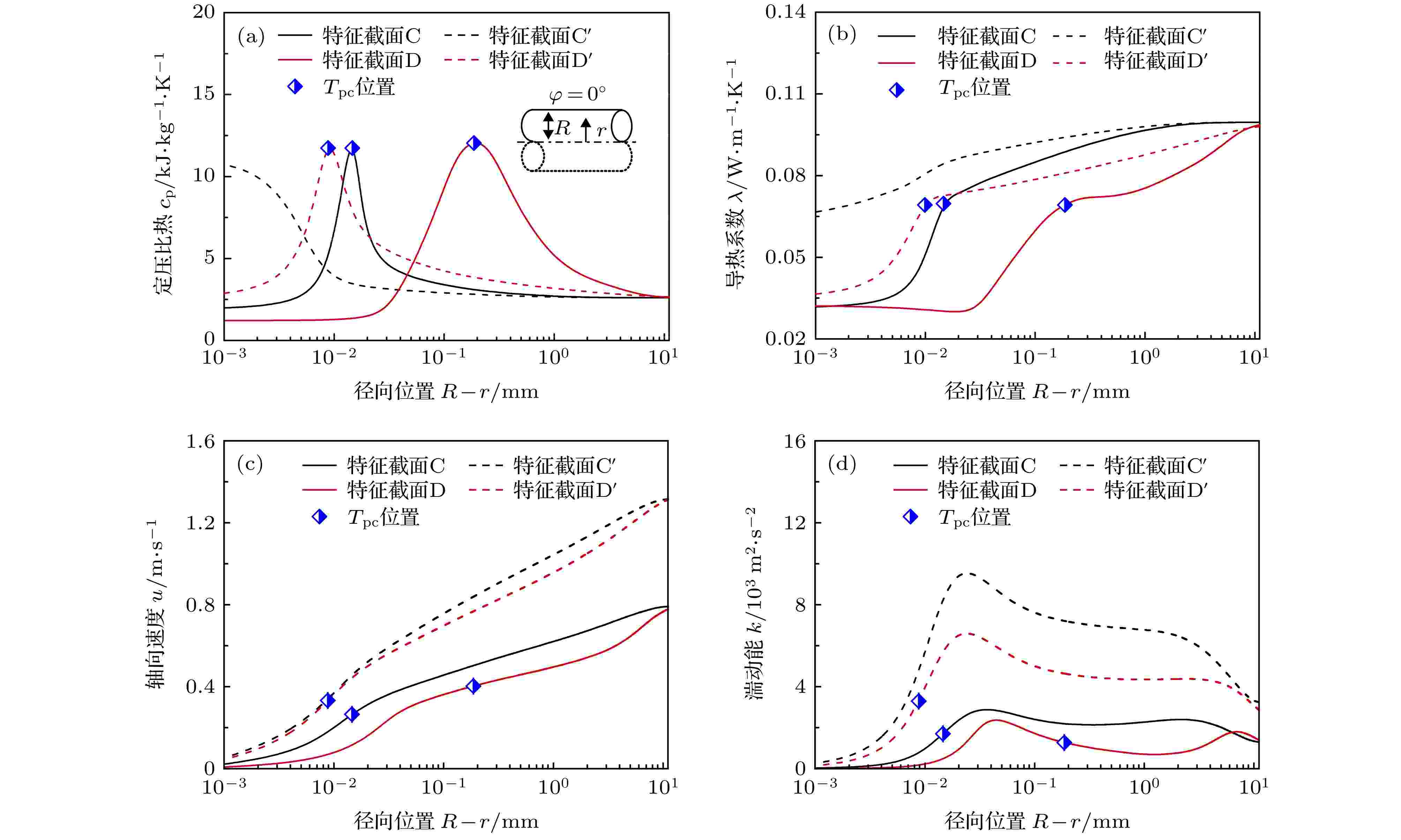图 12 不同质量流速下, 水平圆管特征截面内热物性、轴向速度和湍动能沿径向分布曲线　(a) 定压比热c_p; (b) 导热系数λ; (c) 轴向速度u; (d) 湍动能k
Figure12. Radial distribution curves of thermophyical properties in the characteristic cross-sections under different mass flux: (a) Specific heat at constant pressure c_p; (b) thermal conductivity λ; (c) axial velocity u; (d) turbulent kinetic energy k.

图12(c)显示在等焓特征截面处, 相对于高质量流速, 低质量流速时顶母线区域工质轴向速度u总是较小的, 这不利于S-CO₂沿轴向输运转移来自管壁的热量. 由图12(d)可以看出, 相对于高质量流速, 低质量流速时顶母线区域类气膜内部及主流核心工质的湍动能k整体上总是处于较低水平, 这将抑制管壁热量沿径向向主流核心工质的传递. 因此, 较低的轴向速度u和湍动能k水平是低质量流速条件下顶母线壁温更高的另一个主要原因.

1) SST k-ω低雷诺数湍流模型能够比较可靠和准确地预测S-CO₂在水平圆管内的流动换热情况.
2) 加热条件下, S-CO₂在水平圆管内的流动传热特点与亚临界压力下水平圆管内气-液两相流动传热现象是相似的. 热流密度q_w越高或质量流速G越小, 顶母线管壁温度T_{w, i}则越高, 而且加热段入口区域管壁温度飞升幅度越剧烈.
3) 高热流密度q_w或低质量流速G条件下, 圆管横截面二次流强度K_e整体总是较大的, 反映出横截面内将有更多的低密度类气工质沿管壁流动至顶母线附近, 形成热阻较大的类气膜, 同时顶母线区域工质的湍动能k处于较低水平, 两者综合效应抑制了管壁热量沿径向向主流核心工质传递, 是管壁温度较高的主要影响因素.
4) 低质量流速G条件下, 顶母线附近的轴向速度u整体总是较小的, 这将降低S-CO₂沿轴向输运转移来自顶母线管壁热量的能力, 是质量流速G较低时管壁温度较高的另一个重要影响因素.