摘要:为提升在中国原子能科学研究院的100 MeV质子回旋加速器上进行多能点质子单粒子效应实验的效率, 针对该加速器提供的100 MeV质子设计了一种二进制降能器. 降能器包括6片铝降能片, 厚度分别为0.5, 1, 2, 4, 8, 16, 32 mm, 即后一片厚度均为前一片的2倍. 提出相对厚度的概念, 此概念也可用来表示产生的质子能点的次序以及降能器的状态或操作. 降能器产生的9.69 MeV以上的61个质子能点间隔在0.84—4.09 MeV之间, 且能量岐离均在10%以下, 散射角半高宽均在45 mrad以下, 基本可满足质子单粒子效应实验的要求. 对加速器直接提供的质子的能量精度对降能器产生的质子能点的影响进行分析, 发现经降能器产生的质子能量越低, 其影响也就越大. 此外, 降能器对加速器直接能够提供的70—100 MeV能区的质子也是适用的, 且可通过增加降能片数量的方式来获得更加连续化的质子能点. 本文提出的降能器设计方法简单有效, 具有较强的借鉴价值.
关键词: 降能器/
单粒子效应/
能量岐离/
角度岐离

English Abstract

全文HTML

--> --> -->

空间辐射环境中的单个高能带电粒子入射到航天器中的微电子器件时, 会通过直接或间接的电离作用造成器件产生逻辑错误、功能异常乃至器件损毁等现象, 即发生所谓的单粒子效应(single event effect, SEE)^[1]. SEE是造成航天器发生故障乃至灾难性后果的主要因素, 严重影响空间活动的可靠性和安全性. 质子是空间辐射环境中的主要成分, 也是导致空间中微电子器件发生SEE的主要因素之一, 因此开展质子SEE的研究工作对于保障航天事业的顺利发展具有十分重要的意义^[2-4].
在质子SEE的实验研究方面, 国内起步较晚, 且已开展的实验主要集中在低能区域, 相关的加速器有北京大学的EN串列加速器^[5]、北京HI-13串列加速器^[6]和中国科学院高能物理研究所的质子直线加速器^[7]等, 这3台加速器可提供的质子的最高能量分别为10, 26, 35 MeV. 目前, 国内的中高能质子加速器较为缺乏, 已建成的仅有中国原子能科学研究院的100 MeV质子回旋加速器. 在该加速器上建设质子SEE试验装置, 不仅能够填补国内中能质子SEE试验的空白, 也能在一定程度上满足国内质子SEE考核试验的需求^[8]. 鉴于该加速器直接提供的质子的能量为70—100 MeV, 采用降能器对质子进行降能是快速获得从低到高多个能点质子束流的简单易行的方法. 质子SEE实验的主要目的是获取微电子器件的质子SEE截面的能量依赖关系, 因此降能器对提升质子SEE实验的效率具有重要意义. 本文的降能器设计主要以利用加速器提供的100 MeV质子进行SEE实验为应用背景来展开.

降能器一般由几个不同厚度的降能片组成, 每个降能片均可用计算机通过气动装置对其分别进行远程控制, 这样就能用降能片的不同组合把入射粒子降到不同的能量. 比如, 瑞士PSI (Paul Scherrer Institute)用于微电子器件SEE测试的质子辐照装置提供的最高质子能量为254 MeV, 其降能器采用8片不同厚度的铝片构成^[9].
降能器设计的核心在于降能片材料的选择, 以及降能片片数和厚度的设置. 参考PSI, 采用铝作为降能片材料. 在降能片数目方面, 考虑100 MeV比254 MeV低, 可初定为6片来进行设计. 各降能片厚度的设置是降能器设计的最关键之处. 由于每个降能片均有使用、不使用两种状态, 故理想情况下应实现2⁶ = 64种不同组合, 每种组合对应的降能片厚度之和应该不同, 这样就可将质子降到64种不同的能量, 以最大程度上满足质子SEE实验对多能点质子束流的需要. 如果能够先给出这64种质子能量, 然后去确定6片降能片的厚度, 这种情况是比较理想的. 但是, 实际上这相当于6个变量同时满足64个方程, 这个方程组一般是不可解的. 因此, 只能从相反的角度考虑, 先给出6片降能片的厚度, 然后观察相应的64种质子能量是否满足设计要求.
首先, 考虑一个数学问题. 从1, 2, 4三个数字中任选一个或多个数字取其和可得到7个数字: 1, 2, 1 + 2, 4, 1 + 4, 2 + 4, 1 + 2 + 4, 即从1到7之间的连续整数. 同理, 由1, 2, 4, 8, 16, 32六个数字可得到从1到63之间的连续整数. 因此, 若将6个降能片的厚度之比设定为1∶2∶4∶8∶16∶32, 则相应63种组合对应的降能片厚度之和构成等差数列, 其首项和步长均为第1片降能片的厚度(记为a), 算上6个降能片均不使用的情况, 共64种完全不同的组合方式, 从而最大化地实现了6个降能片的作用. 将某一种组合的降能片的厚度之和与a的比值记为t_R, 称其为相对厚度, 则t_R为0到63之间的整数. 假定质子在到达降能器之前能量为E, 其在铝中的射程为R, 则可令a = R/63, 即使用全部降能片时恰好能将质子完全阻止. 显然, 这种设计能够使该降能器产生0到E之间的64个能点的质子束流.
质子SEE实验一般要求质子束流的均匀性在70%以上, 为满足此要求, 在加速器提供的质子束流到达降能器之前利用双环双散射体法对其进行扩束及均匀化^[10], 使用的双散射靶也不可避免地产生一定的降能作用, 在降能效果上相当于1.54 mm的钽. 对于加速器直接提供的100 MeV质子而言, 质子通过双散射靶后能量会降低到90.07 MeV. 由于90.07 MeV的质子在铝中的射程为30.59 mm, 故a = 30.59/63 = 0.49 mm. 不妨取a = 0.5 mm, 从而6片降能片的厚度依次为0.5, 1.0, 2.0, 4.0, 8.0, 16.0 mm.

2

-->

3.1.降能效果

要计算穿过降能器之后质子的能量, 需要知道质子在铝中的能量-射程关系, 见图1. 能量为E、在铝中射程为R的质子, 在经过总厚度为t_i的降能片组合之后, 其剩余能量记为E_i, 则E_i对应的在铝中的射程应为$ {R-{{t_{\rm{i}}}}} $, 从而E_i可由能量-射程关系通过插值的方法得到. 据此, 可以得到90.07 MeV的质子穿过64种不同降能片组合之后的能量, 如图2所示. 本文中涉及的能量-射程关系均由SRIM程序计算, SRIM是计算离子在物质中的阻止本领(–dE/dx)和射程的常用程序, 其关于质子在物质中的阻止本领(与射程密切相关)的计算值与将近9000个实验数据点的误差总体而言在3.9%以内^[11,12], 足以保证上述能量-射程关系的准确性, 进而可保证计算的质子通过降能片之后的能量的准确性.
图 1 采用SRIM计算得到的1?100 MeV质子在铝中的阻止本领及射程
Figure1. Stopping power and range of 1?100 MeV protons in aluminum calculated by SRIM.

图 2 入射质子穿过64种不同降能片组合之后的能量
Figure2. Residual energies of the incident protons after they pass through the energy degrader with 64 kinds of combinations of 6 energy degrader plates.

由图2可知, 相对厚度t_R在0—60区间时, 可获得9.69—90.07 MeV范围内的61个质子能点, 各能点之间的间隔在0.84—4.09 MeV之间. 在该能量范围内, 阻止本领随着质子能量减小而增加, 从而使得这61个质子能点之间的间隔随着t_R的增大而增大. t_R = 61时, 出射质子能量为3.21 MeV, 此时降能器引起的能量岐离、角度岐离以及加速器直接引出的质子能量的精度误差均较大, 参见后面的讨论. t_R = 62, 63时, 降能器可将90.07 MeV的质子全部阻止. 进行质子SEE实验时, 质子与降能材料发生核反应产生的中子本底是不可避免的, 而此时产生的中子本底应该是最多的, 故可在此保守情况下估计中子本底对质子SEE实验产生的影响, 这也是设计降能器时使a值稍大的一个目的.
相对厚度t_R除了能够表示使用的降能片的总厚度之外, 还能够表示使用降能器产生的质子能点的次序以及降能器的状态或操作. 以t_R = 41为例, 降能片的总厚度为41 × 0.5 = 20.5 mm. 按图2中所示的质子能点由高到低排列, 以不使用降能器时产生的90.07 MeV为第0个能点, 以仅使用第一片降能片时产生的89.23 MeV为第1个能点, 依次类推, 则t_R = 41时产生的质子能点48.26 MeV在上述一系列能点中为第41个. 41 = 1 + 8 + 32, 即使用的是第1, 4, 6片降能片. 41的二进制写法为101001, 若以1代表使用, 以0代表不使用, 最低位到最高位依次代表第1片到第6片, 则101001正好可以代表6片降能片的状态, 也就是降能器的相应操作, 这样就方便了我们对降能器的远程控制.
2 -->

3.2.能量岐离

带电粒子在物质中与靶核及其核外电子发生多次碰撞而损失能量, 由于其经受的碰撞次数、每次碰撞所转移的能量都是随机变化的, 这种碰撞过程的统计涨落引起粒子在穿过靶物质后产生能量岐离现象. 对本文所涉及的在快速能区的质子而言, 能量岐离主要是由于质子与靶原子的核外电子相互作用而产生. 根据Bohr理论, 这种能量岐离可用高斯分布来描述, 相应的均方差参数为

$\sigma = 2z{e^2}{\left( {{\text{π}}ZNt} \right)^{\frac{1}{2}}},$

其中, z为入射粒子原子序数, Z为靶物质原子序数, e为电子电荷, N为单位体积内的靶核数, t为靶物质厚度^[13-15]. 由(1)式可看出, 对于特定的入射粒子和靶物质, 表征能量岐离的均方差参数σ与入射粒子的能量无关, 与靶厚t的平方根成正比.
以${{S = \sigma } / {{E_{\rm{i}}}}}$来表示能量岐离的程度, 将质子穿过双散射靶产生的能量岐离也计算在内时, 经降能器产生的不同能点质子的能量岐离程度如图3所示. 质子经过降能片组合的总厚度越大, 出射质子的能量E_i就越低, 均方差参数σ就越大, 因而能量岐离程度S也就越大. 由图3可见, 质子能量E_i从90.07 MeV降低到3.21 MeV时, 能量岐离程度S从0.45%升高到27.53%. 由于均方差参数σ与靶厚的平方根成正比, 故其随靶厚增加地越来越缓慢, t_R从1增加到62时, σ仅从0.41 MeV增加到0.90 MeV. 而出射质子能量随着靶厚增加而降低地越来越快, 因此S随E_i的降低而增加地越来越快. 这也决定了在出射质子能量E_i的低能端, S的升高主要是由E_i的降低来决定的. 比如, E_i从9.69 MeV降低到3.21 MeV时, S从9.06%升高到27.53%.
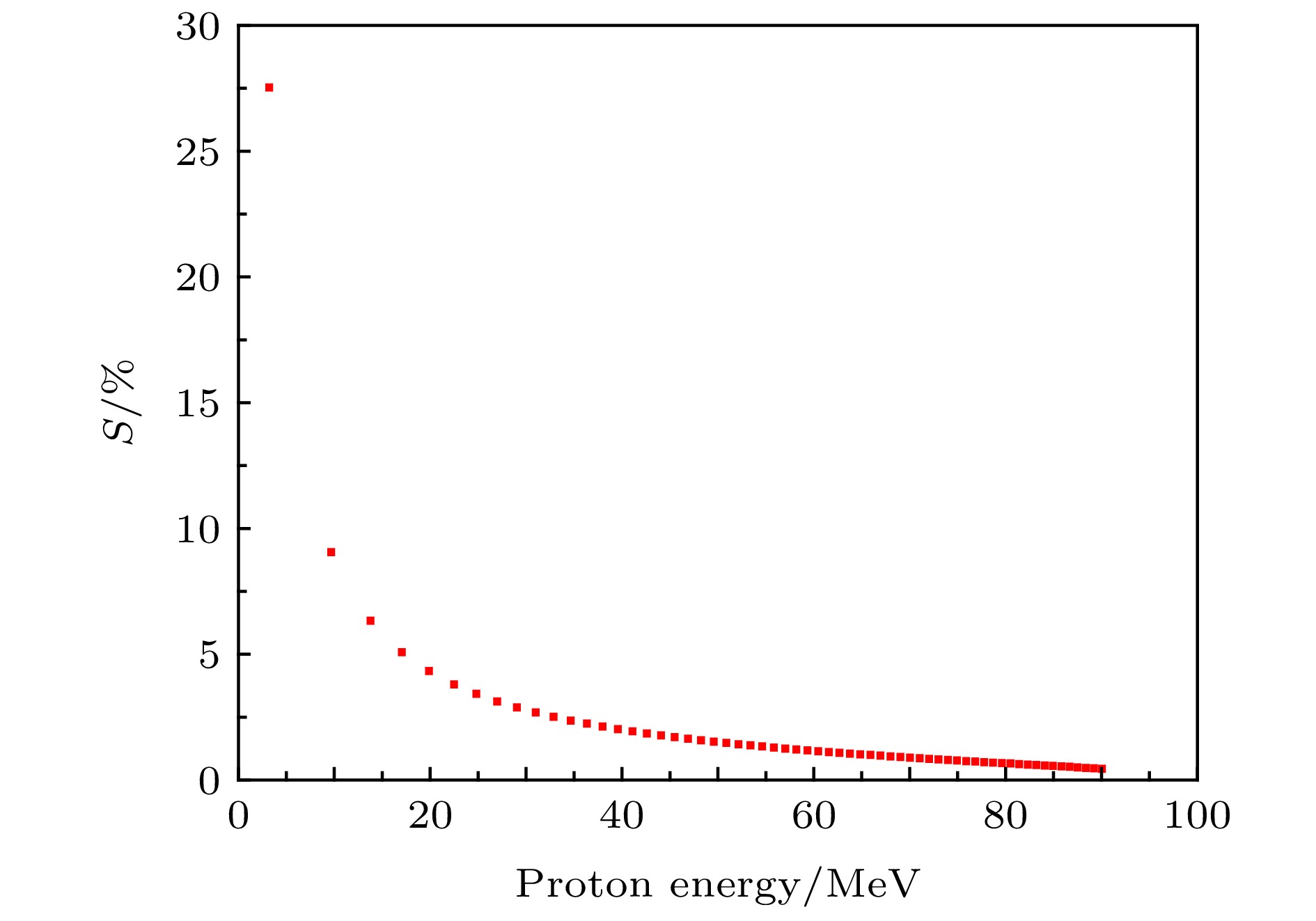图 3 质子经过降能器产生的各能点质子的能量岐离程度
Figure3. Energy straggling degree of the resulting protons at each energy point produced by the energy degrader.

2 -->

3.3.角度岐离

单个入射粒子在靶物质中与靶核碰撞会产生小角度偏转, 而与靶原子的核外电子碰撞引起的偏转可以忽略, 经多次碰撞之后, 粒子会偏离原来的运动方向. 一束具有相同入射方向的带电粒子, 在靶物质中穿过厚度t之后, 粒子偏转角度在小散射角内满足高斯分布, 该高斯分布的半高宽${\theta _{{\rm{FWHM}}}}$可用Highland公式来进行计算^[16,17], 即

${\theta _{{\rm{FWHM}}}} = \frac{{{E_{\rm{s}}}}}{{p\beta }}\sqrt {\frac{t}{{{L_{\rm{R}}}}}} \left[ {1 +\varepsilon \lg \left( {\frac{t}{{{L_{\rm{R}}}}}} \right)} \right],$

其中, ${E_{\rm{s}}} = $14.1 MeV; $\varepsilon ={1}/{9}$; p为入射粒子的动量; β为入射粒子速度与光速之比; ${L_{\rm{R}}}$为靶物质的辐射长度, ${L_{\rm{R}}}$的计算可参考文献[18]. 理想细小束流经靶物质散射后, 在与靶物质距离为L的测量平面内, 束流分布密度函数也可用高斯分布来描述^[10,19,20], 即

$f\left( r \right) = \frac{1}{{{\text{π}}{R^2}}}\exp \left( { - \frac{{{r^2}}}{{{R^2}}}} \right),$

其中, $R = \sqrt 2 L{\theta _{{\rm{FWHM}}}}$, r为测量平面上任一位置到束流中心的距离. 由(3)式可见, 束流在经靶物质散射后, 除了产生角度岐离外, 还在横向方向上产生一定的扩展, 也使得粒子注量率产生一定程度的降低.
要详细了解进行质子SEE实验时DUT (device under test)位置处的束流横向分布情况, 需对质子SEE实验装置中的双散射靶、降能器、DUT以及所涉及的空间几何关系进行全面考虑. 为方便起见, 本文仅考虑降能器的影响, 且忽略各降能片之间实际存在的间隙, 在此情况下对质子束流在降能器中产生的角度岐离进行粗略的估计, 图4给出了通过(2)式计算得到的经降能器产生的各能点质子的角度歧离情况. 当t_R = 61时, 质子剩余能量为3.21 MeV, 此时质子角度岐离最大, ${\theta _{{\rm{FWHM}}}}$为45.20 mrad. 降能器与DUT距离L约为0.25 m, 相应的$R = \sqrt 2 L{\theta _{{\rm{FWHM}}}} = 1.60$ cm, 即在DUT位置距离束流中心1.60 cm处质子注量率是束流中心处的$1 / {{\rm{e}}} \approx 36.79\% $. 在实际情况中, 各降能片之间的间隙及降能器前后存在的空气会使得角度歧离略微增大; 双散射靶也会导致质子束流产生角度歧离, 其位置距离DUT较远, 主要作用是对质子束流进行横向扩展, 使其均匀化^[10].
图 4 经过降能器产生的各能点质子的散射角半高宽
Figure4. Full width at half maximum of the scattering angle of the resulting protons at each energy point produced by the energy degrader.

2 -->

3.4.初始质子能量精度的影响

加速器直接引出的初始质子能量可能存在一定偏差, 假定引出100 MeV质子时偏差为0.1%, 探讨此时质子经降能器不同状态后剩余能量E_i的变化, 结果见图5. 可见, 质子经过降能器后的能量越低其偏差就越大. 以加速器引出100.1 MeV质子为例, 与引出100 MeV质子情况相比, 当t_R = 1时, 经过降能器之后质子能量E_i由89.22 MeV提高0.11 MeV, 即0.12%; 当t_R= 61时, E_i由3.21 MeV提高1.23 MeV, 即38.35%. 造成这种结果的原因是质子的阻止本领随着能量的降低而增高(见图1), 因此对同样厚度的铝而言, 质子能量越低, 在其中所损失的能量就越大. 如100 MeV质子在64.5 μm厚的铝内损失能量约为0.1 MeV, 而2.62 MeV的质子恰好在其中损失全部能量. 也正是由于同样的原因, 99.9 MeV情况造成的质子能量偏差要稍大于100.1 MeV情况. 类似地, 可以推测, E_i的能量越低, 铝片的加工精度、SRIM计算结果的精度给其带来的误差也就越大.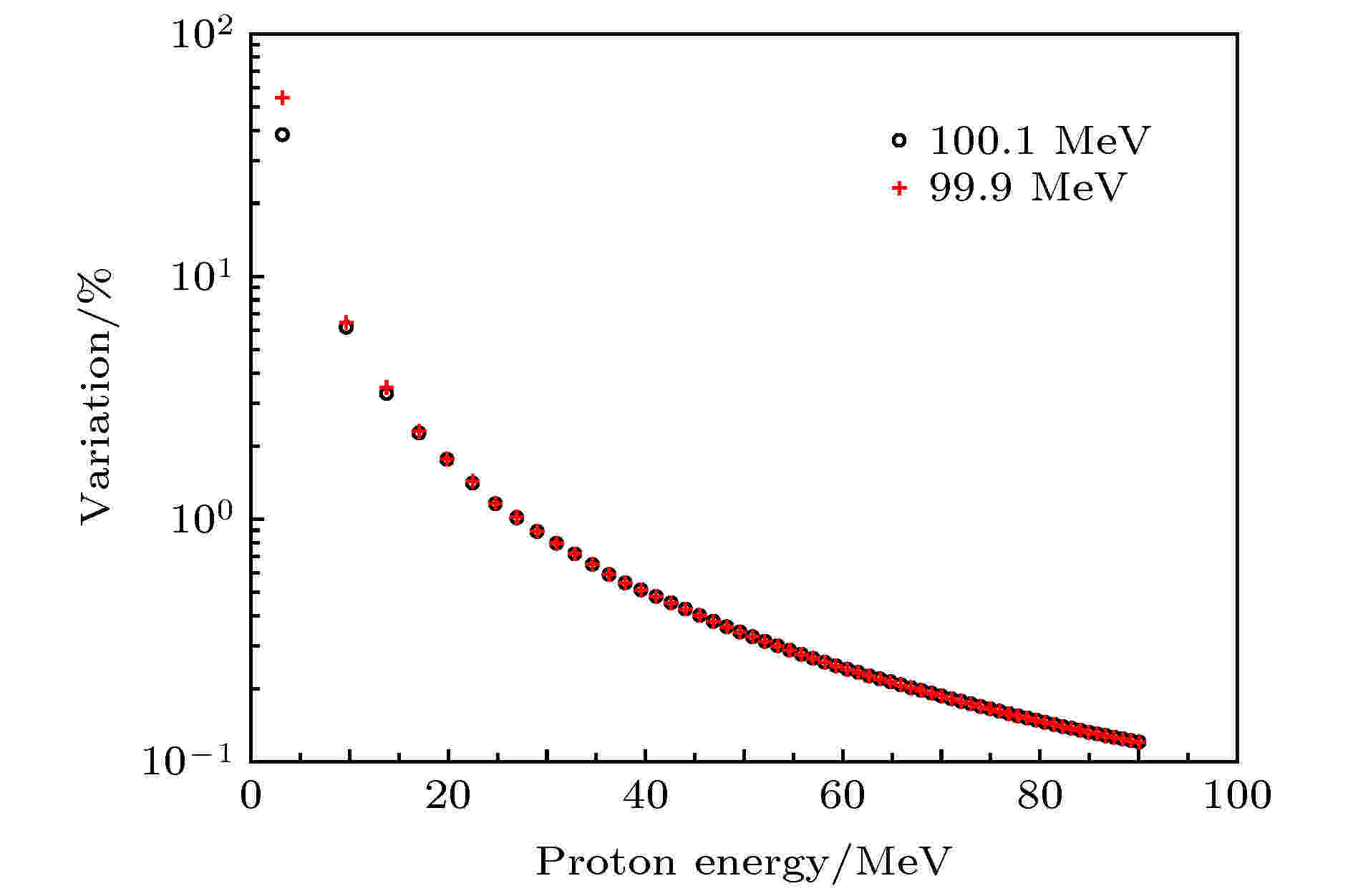
图 5 加速器直接提供的质子能量偏差0.1 MeV时造成质子经过降能器后剩余能量的偏差情况
Figure5. Variation of the residual energy after the protons with the energy deviation of 0.1 MeV directly provided by the accelerator pass through the energy degrader.

2 -->

3.5.对70—100 MeV质子的适用性

加速器可直接提供70—100 MeV的质子, 故对所设计的降能器对其提供100, 90, 80, 70 MeV四种能量质子情况下的降能效果进行了考察. 双散射靶的存在使得四种情况下的质子能量分别降为90.07, 79.12, 68.15, 56.70 MeV, 使用降能器可提供的质子的最低能量分别为3.21, 6.75, 4.59, 8.29 MeV, 提供的各质子能点的最大间隔分别为6.48, 4.92, 5.78, 4.44 MeV, 在降能器状态t_R分别为62, 49, 38, 27时即可将质子全部阻止, 如图6所示. 可见, 该降能器不仅适用于100 MeV质子, 对于加速器直接提供的70—100 MeV范围内的质子也都是基本适用的. 另外, 使用能量低的质子比使用能量高的质子经降能器降到同样的能量时所使用的降能片的总厚度小, 显然产生的能量岐离和角度岐离也小. 如100 MeV质子在t_R = 40时能量降为49.58 MeV, 表征能量岐离的均方差参数σ为0.75 MeV, 散射角半高全宽${\theta _{{\rm{FWHM}}}}$为35.82 mrad; 而70 MeV质子在t_R = 6时即降为49.21 MeV, 相应的σ仅为0.47 MeV, ${\theta _{{\rm{FWHM}}}}$仅为19.55 mrad.
图 6 降能器对加速器直接提供的100, 90, 80, 70 MeV 四种能量质子的降能效果
Figure6. Effects of the energy degrader for the protons at 100, 90, 80 and 70 MeV directly provided by the accelerator.

若想通过降能器获得更多的质子能点, 使这些能点更加连续化, 显然增加降能片的数目是一种可行的方法. 下面分别对使用7片和8片降能片的情况进行讨论. 按前述设计方法, 对7片降能片情况, 可将其厚度之比设定为1∶2∶4∶8∶16∶32∶64, t_R取值从0到127, 第1片厚度a = 30.59/127 = 0.24 mm, 不妨取a值为0.25 mm. 对8片降能片情况, 可将其厚度之比设定为1∶2∶4∶8∶16∶32∶64∶128, t_R取值从0到255, 第1片厚度a = 30.59/255 = 0.12 mm, 不妨取a值为0.122 mm, 然后8片降能片厚度按上述比例与a的乘积保留两位小数进行取值, 即8片降能片的厚度取值依次为0.12, 0.24, 0.49, 0.98, 1.95, 3.90, 7.81, 15.62 mm. 图7为使用6, 7, 8片降能片三种情况下降能器对于加速器提供的100 MeV质子所实现的降能效果. 在三种情况下, 降能器可提供的各质子能点数目分别为62, 126和251, 各能点的间隔分别在0.84—6.48, 0.40—3.81, 0.20—2.11 MeV之间. 可见, 每增加1片降能片, 所获得的质子能点数目约增加1倍, 各能点的间隔更小, 更加能够实现质子能量准连续可调的目的. 在8片降能片情况下, 降能器所实现的能点已经相当密集: 在54.81—90.07 MeV以内的148个能点的间隔在0.2—0.3 MeV之间, 在25.57—54.49 MeV以内的76个能点的间隔在0.3—0.5 MeV之间, 在12.73—25.04 MeV以内的20个能点的间隔在0.5—1.0 MeV之间, 在3.21—11.71 MeV以内的7个能点的间隔在1.0—2.11 MeV之间.
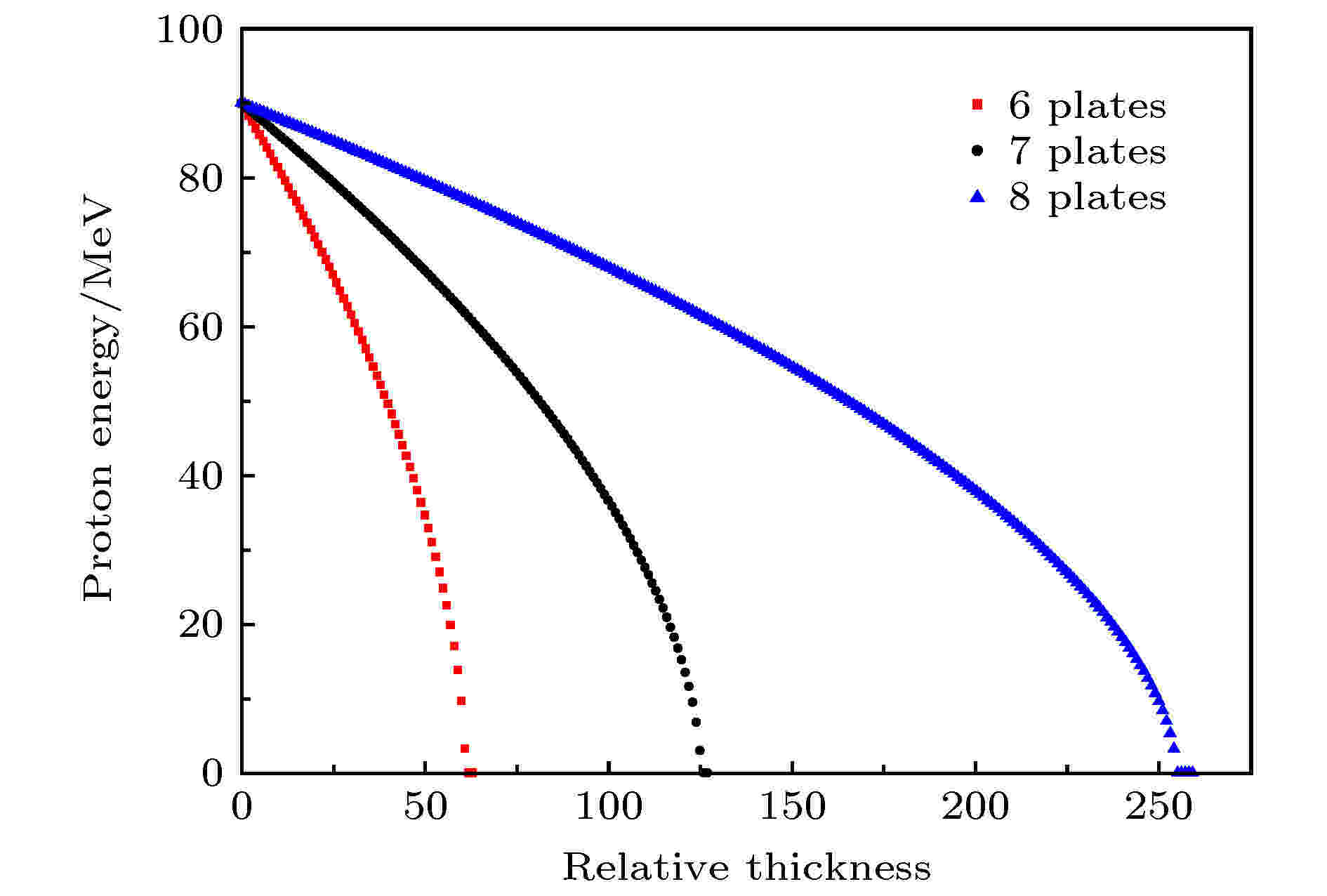图 7 降能器使用6, 7, 8片降能片时的降能效果
Figure7. Effects of the energy degrader using 6, 7 and 8 aluminum plates, respectively.

为在原子能院的100 MeV质子回旋加速器上快速进行多能点的质子SEE实验, 针对其直接提供的100 MeV质子设计了一种二进制降能器. 该降能器由6片铝降能片组成, 最薄一片厚度为0.5 mm, 其余每片厚度均为前一片的2倍. 基于降能器设计的特殊性, 提出相对厚度t_R的概念, t_R也可表示产生的质子能点的次序以及降能器的状态或操作. 本文对该降能器的降能效果、产生的质子能点的能量岐离和角度岐离、加速器直接引出的质子能量精度对产生的质子能点的影响进行分析与讨论, 并对加速器能够直接提供的70—100 MeV能区质子的适用性以及改进降能器以获得更加连续化的质子能点的方法进行了分析与讨论.
考虑降能器之前的双散射靶, 该降能器能够产生9.69—90.07 MeV范围内的61个质子能点, 这些能点之间的间隔在0.84—4.09 MeV之间, 且能量岐离均在9.06%以下, 角度岐离在44.79 mrad (2.57°)以下, 基本可满足质子SEE实验的要求. 降能器产生的质子能量越低, 其带来的能量岐离和角度岐离也就越大, 对加速器直接引出的质子能量精度的影响也就越大. 降能器产生的角度岐离将使得质子束流在横向上产生一定的扩展, 从而使质子注量率有所降低. 该降能器产生的质子最低能量为3.21 MeV, 其能散约为28%, 且加速器提供的初始质子能量的微小变动对其影响很大, 100 MeV质子能量上下变动0.1%使其产生的变化分别约为38%和55%. 由于3 MeV左右对很多微电子器件而言是质子SEE截面刚出现或快速上升的区域, 故当其应用于质子SEE实验时应对其能散及可能的误差有明确的认识. 经计算, 该降能器不仅适用于100 MeV质子, 对加速器直接提供的70— 100 MeV能区的质子也是适用的. 若要通过降能器获得更加连续化的质子能点, 可按该设计方法增加降能片的片数来实现, 另外, 本文对7片、8片降能片情况进行了讨论. 最后, 本文提出的二进制降能器设计方法简单有效, 对于实现多能点快速降能的降能器的设计具有较强的借鉴价值.