摘要: 环状暗孤子最早是在非线性光学系统中理论预言并实验实现的一种二维孤子类型. 跟通常的二维孤子(如条纹孤子)相比, 环状暗孤子具有更好的稳定性和更加丰富的动力学行为. 玻色-爱因斯坦凝聚由于其高度可调控性为研究环状暗孤子提供了一个全新的平台. 本文结合玻色-爱因斯坦凝聚和孤子研究的现状, 综述玻色-爱因斯坦凝聚中环状暗孤子的解析解、稳定性调控及其衰变动力学等方面的研究进展. 首先介绍了一套变换方法将均匀系统中非线性系数不随时间变化的环状暗孤子解析解推广到谐振子外势下非线性系数随时间变化的环状暗孤子解析解; 然后讨论在形变扰动下环状暗孤子的稳定性相图, 并介绍了如何利用周期调制的非线性来增强环状暗孤子的稳定性; 此外, 还重点讨论了环状暗孤子衰变导致的涡旋极子动力学以及斑图形成.
关键词: 玻色-爱因斯坦凝聚 /
环状暗孤子 /
涡旋极子 /
斑图 English Abstract Dynamics of ring dark solitons in Bose-Einstein condensates Guo Hui 1,2 ,Wang Ya-Jun 1,2 ,Wang Lin-Xue 3 ,Zhang Xiao-Fei 1,2 1.Key Laboratory of Time and Frequency Primary Standards, National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11775253, 11704383) and the Natural Science Basic Research Plan in Shaanxi Province of China (Grant No. 2019JQ-058)Received Date: 18 September 2019Accepted Date: 29 October 2019Available Online: 05 December 2019Published Online: 05 January 2020Abstract: Soliton is an exotic topological excitation, and it widely exists in various nonlinear systems, such as nonlinear optics, Bose-Einstein condensates, classical and quantum fluids, plasma, magnetic materials, etc. A stable soliton can propagate with constant amplitude and velocity, and maintain its shape. Two-dimensional and three-dimensional solitons are usually hard to stabilize, and how to realize stable two-dimensional or three-dimensional solitons has aroused the great interest of the researchers. Ring dark soliton is a kind of two-dimensional soliton, which was first theoretically predicted and experimentally realized in nonlinear optical systems. Compared with the usual two-dimensional solitons, ring dark solitons have good stability and rich dynamical behaviors. Owing to their highly controllable capability, Bose-Einstein condensates provide a new platform for studying the ring dark solitons. Based on the recent progress in Bose-Einstein condensates and solitons, this paper reviews the research on the analytic solutions, stability, as well as the decay dynamics of ring dark solitons in Bose-Einstein condensates. A transform method is introduced, which generalizes the analytic solutions of ring dark solitons from a homogeneous system with time-independent nonlinearity to a harmonically trapped inhomogeneous system with time-dependent nonlinearity. The stability phase diagram of the ring dark soliton under deformation perturbations is discussed by numerically solving the Gross-Pitaevskii equations in the mean-field theory. A method of enhancing the stability of ring dark solitons by periodically modulating the nonlinear coefficients is introduced. It is also shown that the periodically modulated nonlinear coefficient can be experimentally realized by the Feshbach resonance technology. In addition, we discuss the dynamics of the decay of ring dark solitons. It is found that the ring dark soliton can decay into various vortex clusters composed of vortices and antivortices. This opens a new avenue to the investigation of vortex dynamics and quantum turbulence. It is also found that the ring dark solitons combined with periodic modulated nonlinearity can give rise to the pattern formation, which is an interesting nonlinear phenomenon widely explored in all the fields of nature. Finally, some possible research subjects about ring dark solitons in future research are also discussed.Keywords: Bose-Einstein condensation /ring dark soliton /vortex dipole /pattern formation 全文HTML --> --> --> 1.引 言 孤子是一种存在于非线性系统中的奇异拓扑激发. 孤子的概念最早是在1965年由Zabusky和Kruskal[1 ] 在研究Korteweg-de Vries方程时提出的. 稳定的孤子在传播过程中可以保持形状、幅度和速度不变. 孤子广泛存在于经典和量子流体、非线性光学、等离子体等各种非线性系统中[2 ,3 ] , 引起了不同领域科学家的广泛关注[4 -10 ] . 自从1995年超冷原子玻色-爱因斯坦凝聚(BEC)在实验上实现[11 -14 ] 以来, BEC中的孤子性质及其动力学成为冷原子物理领域的重要课题. 跟其他非线性系统(如经典流体等)相比, BEC具有高度可操控性, 可以通过光场、磁场、电场跟冷原子耦合来改变BEC的几何结构、维度、外势以及相互作用等[15 -21 ] , 从而为孤子的理论和实验提供了优越的平台, 并为孤子研究注入了新的活力[2 ,22 -25 ] .[26 ] . 1999年Denschlag等[27 ] 和Sanpera等[28 ] 利用相位刻印技术(phase imprinting technique)在超冷23 Na和87 Rb原子的BEC中观察到暗孤子, 标志着孤子这一非线性现象在BEC系统中的首次实验实现. 两个研究组分别用了不同的原子种类, 即23 Na和87 Rb. 由于这两种原子之间的相互作用都是排斥相互作用, 因而亮孤子一般是不稳定的. 但当排斥相互作用和孤子的相位梯度达到某种平衡时, 系统中允许存在稳定的暗孤子. 随着Feshbach共振技术在超冷原子BEC中的广泛应用[19 ,29 ,30 ] , 2002年Strecker等[31 ] 和Khaykovich等[32 ] 科学家利用Feshbach共振技术调节原子间的相互作用从排斥到吸引, 首次在7 Li原子BEC系统中实验观察到亮孤子. 之后?Cornish等[33 ] 同样利用Feshbach共振技术, 在超冷85 Rb原子BEC系统中实验观察到亮孤子.[27 ,28 ,31 ,32 ] , BEC中高维孤子的产生、稳定性及其衰变动力学成为当前科学家关注的热点和难点问题[34 ] . 以暗孤子为例, 在BEC中产生物质波暗孤子需要具备如下几个特点: 首先在原子背景上具有局部的密度最小值, 而且在局部密度最小值处波函数的相位有一个突变, 与此同时局域密度最小值的幅度和形状不发生改变[28 ,35 ] . 研究发现暗孤子两侧的相位对暗孤子的速度和深度起了决定性作用[36 ] . 特别地, 当暗孤子两侧的相位差为$ \text{π}$ 时, 暗孤子的深度为$ 100\% $ , 即孤子中心处没有粒子, 我们称之为全暗孤子或黑孤子. 此时孤子的速度为零. 暗孤子的这一特点以及BEC中原子分布的不均匀性, 使得在二维BEC系统中, 条纹暗孤子很不稳定, 极易受到横向扰动的影响, 表现出蛇形(snake)不稳定性[37 ,38 ] , 最终衰变为涡旋对[39 ] . ?Dutton等[40 ] 利用慢光技术(slow light technique)在BEC中引入密度缺陷, 在密度缺陷的衰变过程中产生了条纹暗孤子. 他们进一步观察到条纹暗孤子的蛇形不稳定性, 以及从条纹暗孤子衰变成涡旋的动力学过程. 在三维BEC系统中, Anderson等[41 ] 发现条纹暗孤子更加不稳定, 会很快衰变成各种涡旋环结构.[42 ] , 人们逐渐认识到在二维非线性均匀系统中, 条纹暗孤子的不稳定性区域是由最大扰动波数$ Q_{\rm max} $ 表征的[43 ] . 当条纹暗孤子的长度$ L < 2{\text{π}}/Q_{\rm max} $ 时, 条纹暗孤子的不稳定性会被抑制[44 ] . 此时直的条纹暗孤子会发生弯曲, 进而闭合成可以长时间稳定存在的环状暗孤子. 环状暗孤子最早是在非线性光学系统中理论预言[45 ,46 ] 和实验实现的[47 ,48 ] . 在非线性光学系统中, 环状暗孤子可以用于全光控制、光学开关以及块体介质中光学信息传输通道的多路复用与分解[47 ] . 由于环状暗孤子比一般的孤子如条纹暗孤子、块状(lump)暗孤子等具有更好的稳定性和更丰富的动力学性质, 因而引起了冷原子物理学家的关注[24 ,44 ,49 -51 ] . Theocharis等[44 ] 最早在BEC中引入了环暗孤子的概念, 并讨论了BEC中环状暗孤子的解析解、稳定性以及动力学性质. 他们发现由于环状暗孤子特殊的对称性质, 使得即使在谐振子外势下, 密度不均匀的BEC系统中, 环状暗孤子在某些条件下仍然可以较长时间稳定存在. 环状暗孤子可用于产生量子湍流, 进而理解量子湍流的统计性质及其内在的物理机理[52 -54 ] . 利用环状暗孤子衰变可以产生各种类型的涡旋结构和斑图, 从而为深入研究涡旋动力学和斑图动力学等各类非线性现象提供新的技术手段和思路. 在负质量流体[55 ] 、人造规范系统[21 ,56 ] 、SU(3)自旋轨道耦合[57 ] 等特殊量子体系中研究环状暗孤子的性质, 还有望发现新的量子流体动力学规律, 为设计各种新的拓扑功能材料提供理论依据. 因此, 在量子流体系统中研究环状暗孤子的基本性质和动力学行为具有非常重要的意义.2.相互作用可调的BEC中环状暗孤子的解析解 一般来说, BEC系统中的相互作用是不随时间和空间变化的. 但随着Feshbach共振技术的发展, 科学家已经可以对BEC系统中的相互作用强度甚至正负进行调节. 目前为止, 科学家已经相继发现了磁Feshbach共振[29 ,30 ] 、光Feshbach共振[58 ,59 ] 、束缚诱导的共振[60 ,61 ] 以及轨道Feshbach共振[62 ,63 ] 等. 这些类型的Feshbach共振技术为调节BEC中的相互作用提供了有力工具. 利用Feshbach共振相关技术, 科学家已经理论预言和实验实现了各种随时间[31 ,64 -66 ] 和空间[67 ,68 ] 变化的原子间相互作用. 因而, 在BEC系统中研究相互作用随时间变化的孤子解具有重要的现实意义.[51 ] $ \varOmega = 0 $ 时, 根据环状暗孤子的对称性, 系统可以表示为如下形式:2 )可以变换到著名的CKdV方程[45 ,46 ] . 利用CKdV方程的解析解[69 -74 ] , 可以间接得出方程(2 )的环状暗孤子解析解. 当存在谐振子外势即$ \varOmega\neq 0 $ 时, Theocharis等[44 ] 讨论了相互作用为常数时, 系统可能存在的环状暗孤子解.[51 ] . 首先, 将方程(1 )做如下变换:$ R(r, t) $ ,$ T(t) $ ,$ \alpha(r, t) $ 和$ \beta(t) $ 为实函数, 并且满足$ C_0 $ 为常数. 该变换成立的条件是2 )的所有解析解都可以转化为方程(1 )的解析解. 这就在非线性光学均匀系统和非均匀BEC系统之间建立了一个桥梁. 利用这一变换关系, 在其中一个系统中得到的相关结果, 都可以在另一个系统中找到对应, 从而为研究非线性光学和BEC动力学提供新的思路.[51 ] $ g(t)\propto D(t) $ . 对于BEC系统来说, 因为$ D(t) $ 为常数, 所以此时相互作用也必须为常数. 因而方程(9 )转化为谐振子外势束缚强度随时间变化的情形10 ), 可以求解谐振子束缚强度随时间变化的BEC系统的环状暗孤子解析解.1 ).3.BEC中环状暗孤子的稳定性 23.1.环状暗孤子在形变扰动下的稳定性相图 3.1.环状暗孤子在形变扰动下的稳定性相图 环状暗孤子的稳定性首先受到横向扰动的影响, 表现出蛇形不稳定. Theocharis等[44 ] 率先研究了横向扰动对BEC中环状暗孤子稳定性的影响, 指出浅的环状暗孤子可以不受蛇形不稳定影响而长时间稳定存在, 而深的环状暗孤子将遭受蛇形不稳定而衰变成环状分布的涡旋阵列. 考虑到真实的实验情况, 除了横向扰动之外, 环状暗孤子还有可能受到包括径向扰动在内的更为复杂形式的外部扰动. 下面重点讨论形变扰动对环状暗孤子稳定性的影响.1 )来进行分析[51 ] . 首先选择如下形式的环状暗孤子解$ Z(r_1) \!=\! (r_1\!-\!R_0)\cos{\phi(0)} $ , $ r_1 \!= \!\sqrt{(1\!-\!e_{\rm c}^2)x^2\!+\!y^2} $ , $ e_{\rm c} $ 表示环状暗孤子发生形变的偏心率, $ \cos{\phi(0)} $ 刻画了环状暗孤子的初始深度, $ R_0 $ 为发生形变之前环状暗孤子的初始半径, 对应于发生椭圆形变后短半轴的长度. 特别地, 固定$ g(t) = 1 $ ,$ \varOmega = 0.028 $ ,$ R_0 = 28.9 $ , 通过调节环状暗孤子的深度和形变程度观察环状暗孤子的稳定性. 数值模拟计算结果表明环状暗孤子的稳定性明显受到形变扰动的影响. 对于相同深度的浅的环状暗孤子, 当偏心率$ e_{\rm c} $ 超过某一临界值$ e_{\rm max} $ 时, 环状暗孤子会由稳定而变得不稳定, 进而衰变成涡旋对(后面将详细讨论环状暗孤子的衰变动力学). 图1 给出了环状暗孤子关于深度和最大偏心率的稳定性相图. 从图中可以看出, 当环状暗孤子很浅时, 环状暗孤子即使在很大的偏心率下也可以稳定存在; 当环状暗孤子较深时, 很小的偏心率就会导致环状暗孤子失稳. 特别地, 当深度$ \cos{\phi(0) > 0.67} $ 时, 即使在零形变下环状暗孤子也变得不稳定.图 1 形变扰动下环状暗孤子的稳定性相图[51 ] Figure1. Stability phase diagram of ring dark solitons under deformation perturbation.3.2.基于Feshbach共振的环状暗孤子稳定性操控 -->3.2.基于Feshbach共振的环状暗孤子稳定性操控 Feshbach共振技术在BEC孤子研究中扮演了重要的角色. 实验上利用Feshbach技术不但可以产生孤子[31 -33 ] , 而且还可以用来调控孤子的稳定性[75 ] . 最近, 利用Feshbach共振随时间周期性改变原子间的相互作用引起了理论和实验学家的极大兴趣[65 ,76 -80 ] . Saito和Ueda[78 ] 以及Abdullaev等[79 ] 发现利用Feshbach共振调节原子间相互作用在吸引和排斥之间的快速振荡, 可以在二维空间维持稳定的物质波亮孤子. Liang等[80 ] 进一步研究了在周期调控的原子间相互作用下, 物质波亮孤子跟背景之间的原子数目交换规律. 本节将从理论上讨论如何利用Feshbach共振技术增强环状暗孤子的稳定性.12 )表明原子间的排斥相互作用强度在$ 0-2 $ 之间周期性振荡. 计算结果表明[51 ] 在某一振荡频率附近, 环状暗孤子的稳定性明显增强. 即使对于较深的暗孤子, 在相互作用处于该振荡频率下, 仍然可以具有很长的寿命. 以环状暗孤子深度$ \cos{\phi(0)} = $ 0.76为例, 通过上一节的讨论, 我们知道环状暗孤子在此深度下是极不稳定的. 通过数值模拟计算, 得到了环暗孤子寿命随相互作用振荡频率的变化情况, 如表1 所列. 可以发现, 当相互作用振荡频率在谐振子固有频率$ \varOmega $ 附近时, 环暗孤子的寿命急剧增长; 当相互作用的振荡频率远离该固有频率时, 环状暗孤子的寿命迅速减小. 这说明环状暗孤子寿命的增长是由于相互作用的振荡频率跟谐振子的振荡频率发生共振引起的. 相互作用振荡频率$\omega$/$\varOmega$ 环状暗孤子寿命t /ms $ < 0.5$ $ < 15$ 0.6 17 0.8 43 1.0 45 1.5 16 $ > 1.7$ $ < 15$ 注1: 原子间相互作用$g(t) = 1-\sin{\omega t}$, 环状暗孤子深度$\cos{\phi(0)} = 0.76$.
表1 环状暗孤子寿命随相互作用振荡频率的变化[51 ] Table1. Life of the ring dark soliton as a function of the interaction oscillation frequency.$ \cos{\phi(0)} = 0.6 $ , 形变引起的偏心率$ e_{\rm c} = 0.4 $ 时环状暗孤子的寿命. 计算结果表明, 当相互作用为常数即$ g = 1 $ 时, 环状暗孤子的寿命小于$ 10\ {\rm ms} $ . 而当相互作用以频率$ \varOmega $ 在$ g = 1 $ 附近振荡, 即$ g = 1-\sin{\varOmega t} $ 时, 环状暗孤子的寿命可以长达$ 50\ {\rm ms} $ .4.环状暗孤子衰变动力学 当环状暗孤子处于不稳定区域时, 通常会在遭遇蛇形不稳定下发生衰变[39 ,44 ] , 导致各种类型和数目的涡旋极子或者不同样式的斑图. 从而建立了BEC中孤子和涡旋以及斑图[81 ] 等非线性现象之间的密切联系. 研究BEC中环状暗孤子衰变引起的各种涡旋动力学和斑图形成有助于理解量子湍流[52 ,82 ,83 ] 和各类相关非线性现象的物理机理.4.1.环状暗孤子衰变与涡旋动力学 4.1.环状暗孤子衰变与涡旋动力学 34.1.1.单分量BEC中的环状暗孤子衰变与涡旋动力学 -->4.1.1.单分量BEC中的环状暗孤子衰变与涡旋动力学 Theocharis等[44 ] 最早研究了单分量BEC中环状暗孤子的衰变动力学. 他们发现较深的环状暗孤子在横向扰动下将衰变为由涡旋-反涡旋对构成的环形分布的涡旋链. 越深的环状暗孤子将衰变出更多的涡旋. 涡旋-反涡旋对的数目满足某种规律, 即总是4的倍数, 并且长时间演化后部分涡旋湮灭, 最后只剩下4个涡旋-反涡旋对可以长时间稳定存在. 与此同时, 环暗孤子在BEC中衰变产生的涡旋团簇不是固定不动的, 而是以某种规律做周期性运动. 运动的形式依赖于涡旋的个数和系统的对称性质.11 )式作为初始态代入方程(1 )进行演化. 特别地, 假设环状暗孤子的深度为$ \cos{\phi(0)} = 0.6 $ , 相互作用强度和谐振子束缚频率固定在$ g = 1 $ ,$ \varOmega = 0.028 $ , 发生形变的偏心率为$ e_{\rm c} = 0.4 $ . 前边的结果已经表明当不发生形变时, 深度为$ 0.6 $ 的环状暗孤子是相对稳定的, 因而接下来观察到的孤子衰变主要是由形变引起的. 数值模拟计算指出[51 ] , 在环状暗孤子发生形变时的衰变行为跟不发生形变时的衰变行为具有明显的不同. 在椭圆形变影响下, 环状暗孤子衰变产生的涡旋-反涡旋对的数目不再是4的倍数, 或2的偶数倍, 而是2的奇数倍, 如图2 所示. 这可以从椭圆形变扰动打破了系统的旋转对称性来理解. 涡旋个数的不同引起了不同的涡旋运动规律. 对于图2 所示的两个涡旋对的情况, 可以看到每个涡旋分别在$ 1/4 $ 圆周的扇形轨迹上做周期性运动. 而对于四个涡旋对的情况, 每个涡旋分别在$ 1/8 $ 圆周的扇形轨迹上做周期性运动[44 ] .图 2 单分量BEC中形变扰动下环状暗孤子的衰变行为[51 ] Figure2. Decay of the ring dark soliton under deformation perturbation in a single-component BEC.[51 ] : 首先环状暗孤子沿着径向收缩到一个最小半径$ R_{\rm min} $ , 然后在蛇形不稳定性作用下迅速衰变为两个暗块孤子; 这两个暗块孤子随后沿着相反的方向远离BEC中心移动, 并随着背景原子数密度的减小而劈裂为两个涡旋极子, 涡旋极子继续向前运动; 当涡旋极子到达凝聚体边界时, 正负涡旋分开并以相反的方向沿着凝聚体边界做近似圆周运动; 当旋转90°角后, 来自不同涡旋极子的涡旋相遇, 并重新组合成新的涡旋极子, 然后朝着BEC中心运动. 随着背景原子数密度的增大, 涡旋极子中的涡旋间距逐渐减小, 重新融合成暗块孤子, 并试图恢复原来的环状暗孤子状态; 当到达$ R_{\rm min} $ 附近时, 两个暗块速度降为0, 然后按照原来的路径返回, 并周期性地沿着四个扇形边界做往复运动. 值得注意的是, 在返回途中由于运动方向相反, 暗块分裂成的涡旋极子中的两个涡旋的旋转方向也同时发生了反转. 此外, 环状暗孤子衰变形成的两个涡旋极子的运动跟涡旋四极子在BEC中的运动规律有些类似[84 ] .4.1.2.两分量BEC中的环状暗孤子衰变与涡旋动力学 -->4.1.2.两分量BEC中的环状暗孤子衰变与涡旋动力学 当BEC中的原子处于两个超精细能级时, 系统是由两个非线性薛定谔方程耦合的方程组来描述的, 一般具有如下形式:[2 ] . 由于不同分量原子之间的相互碰撞, 使得处于不同分量的孤子可以相互耦合, 表现为更为丰富的非线性动力学性质[85 ] .$ Z_i(\!r_1\!) \!=\! (\!r_1\!-\!R_{i0}\!)\cos{\phi_i(0)} $ , $ r_1\!= \!\!\sqrt{\!(1\!- \!e_{\rm c}^2)x^2\! +\!y^2} $ . 类似于前边单分量的情况, 固定环状暗孤子偏心率$ e_{\rm c} = 0.4 $ , 谐振子束缚频率$ \varOmega = 0.028 $ , 相互作用强度$ g_{11} = g_{12} = g_{21} = g_{21} = 1 $ . 假设两个环状暗孤子具有不同的初始半径, 分别为$ R_{10} = 27.9 $ 和$ R_{20} = 28.9 $ . 与此同时, 假设两个分量的环状暗孤子处于相同的背景深度. 当两分量的环状暗孤子具有相同的深度$ \cos{\phi_{1}(0)} = \cos{\phi_{2}(0)} = 0.6 $ 时, 数值模拟计算结果表明, 两分量BEC的环暗孤子衰变动力学跟前边提到的单分量BEC的环状暗孤子衰变动力学非常相似[86 ] .$ \cos{\phi_{1}(0)} = $ $\cos{\phi_{2}(0)} = 0.75 $ 时, 系统表现出完全不同的环状暗孤子衰变动力学[86 ] , 如图3 和图4 所示. 首先, 由于深度的增加, 环状暗孤子衰变生成了更多数目的涡旋极子. 由图3(b) 可以看到共产生了6对涡旋极子, 这跟前边单分量系统中提到的椭圆形变下, 环状暗孤子衰变成涡旋极子的个数总是2的奇数倍的结论一致. 这些涡旋极子产生后, 分为两组(每组三对)分别沿着相反的方向朝BEC边界上运动; 在运动的同时同一组的涡旋极子之间逐渐散开, 形成一种三角结构, 如图3(c) 所示; 之后靠近边缘的两对涡旋极子分别贡献一个涡旋而重组成一个新的涡旋极子; 新组的涡旋极子沿着BEC中心运动, 当到达最小半径$ R_{\rm min} $ 处后原路返回, 并在到达BEC边界后很快湮灭. 剩下的4对涡旋极子可以在BEC中保持非常的寿命, 并以某种规律做周期性运动, 如图4 所示.图 3 两分量BEC中相同深度环状暗孤子的衰变行为[86 ] Figure3. Decay of the ring dark solitons with the same depth in two-component BECs.图 4 四组涡旋极子在两分量BEC中的动力学演化[86 ] Figure4. Evolution of four vortex dipoles in two-component BECs.[44 ] . 当存在形变扰动时, 环状暗孤子衰变最终生成的4对涡旋极子, 表现出跟没有形变扰动时完全不同的运动规律. 当没有形变扰动时, 四对涡旋极子的运动是同步的, 四组涡旋极子会在同一时刻发生重组, 并且每个涡旋都沿着$ 1/8 $ 的扇形边界做周期性往复运动[44 ] . 当存在形变扰动时, 四对涡旋极子分为运动不同步的两组, 当其中一组发生重组时, 另外一组尚未发生重组, 两组涡旋极子中的涡旋以相同的规律分别沿着$ 1/4 $ 圆的扇形边界做周期性往复运动, 如图4 所示.$ \cos{\phi_{1}(0)} = 0.6 $ , $ \cos{\phi_{2}(0)} = $ 0.75, 根据经验我们期待较深的环状暗孤子将衰变出更多数目的涡旋. 事实上, 在环状暗孤子发生衰变的初期确实观察到了两个组分中环状暗孤子不同的衰变行为, 如图5(b) 所示. 但由于两个组分之间的耦合作用, 较深的环状暗孤子衰变成涡旋的数目被抑制, 最终导致衰变产生的涡旋数目跟$ \cos{\phi_{1}(0)} = \cos{\phi_{2}(0)} = 0.6 $ 时相同, 如图5(c) 所示. 由于初始衰变行为的不同, 本来两个分量的涡旋运动应该是不同步的, 但数值模拟结果显示, 两个分量的涡旋会在产生后很短的时间内趋于同步, 如图5(c) —图5(g) 所示, 这可以理解为两分量之间原子相互碰撞耦合的结果.图 5 两分量BEC中不同深度环状暗孤子的衰变行为[86 ] Figure5. Decay of the ring dark solitons with different depths in two-component BECs.[86 ,87 ] . 这是由于来自两个分量的涡旋一般是不相互重合的, 一个分量的涡旋核总是被另一个分量的原子填充, 形成所谓的半量子化涡旋[20 ,88 ] . 由于在同一位置附近, 来自两个分量的涡旋具有相同的旋转方向, 在分量间原子的碰撞耦合作用下, 它们将绕着两个涡旋的中间位置(即质心处)沿涡旋自转的同一方向作进动.4.2.环状暗孤子衰变与斑图形成 -->4.2.环状暗孤子衰变与斑图形成 斑图(pattern)是指空间上具有某种规律性的非均匀分布. 在自然界中, 虽然不同系统所显示的斑图结构无论从时空尺度还是从形成机制等方面都各不相同, 但他们在形态上都有一定的相似性. 斑图动力学就是研究自然界中千变万化的斑图结构的生长与形成、竞争与选择、渐变与突变等的共性规律. 斑图动力学作为非线性科学的一个重要研究方向[81 ] , 目前已经深入到非常广泛的研究领域, 例如光学[89 ] 、流体力学[90 ] 、等离子体物理[91 ] 以及材料科学[92 ] 等. BEC作为一种非线性多体系统, 为研究斑图动力学提供了高度可控的优越平台[93 ] .13 )式和(14 )式中的非线性系数可表示为g 11 = g 22 = 1, g 12 = g 21 = $1-\sin{\omega t} $ . 考虑方程(15 )式和(16 )式描述的环状暗孤子, 并假设偏心率$ e_{\rm c} = 0 $ . 当谐振子频率$ \varOmega = 0.028 $ , 相互作用的周期调制频率跟谐振子发生共振, 即$ \omega = \varOmega $ , 初始时刻环状暗孤子深度$ \cos{\phi_{1}(0)} = $ $\cos{\phi_{2}(0)} = 1 $ , 半径为$ R_{10} = 27.9 $ 和$ R_{20} = 28.9 $ 时, 环状暗孤子的衰变行为如图6 和图7 所示[94 ] .图 6 周期调制相互作用系统中环状暗孤子衰变引起的斑图形成[94 ] Figure6. Pattern formation induced by the decay of ring dark solitons in a system with periodically modulated interactions.图 7 斑图在周期调制相互作用系统中的演化[94 ] Figure7. Evolution of the pattern in a system with periodically modulated interactions.图6(d) 所示. 这种环状暗孤子的不稳定性逐渐从BEC边缘进入到BEC内部, 最终在整个BEC中形成了随时间不断变化的斑图结构, 如图6(e) 、图6(f) 和图7 所示.[95 -98 ] . 对于不随时间变化的原子间相互作用, 当$ g^2_{12} < $ g 11 g 22 时, 系统表现为相混合, 此时两分量中的原子密度分布在空间上是相互重叠的; 当$ g^2_{12} > g_{11}g_{22} $ 时, 系统表现为相分离, 此时两分量中的原子密度分布在空间上是相互填充的. 当前考虑的系统相互作用$ g_{12} $ 是在0—2之间随时间周期性变化的, 既不满足$ g^2_{12} > g_{11}g_{22} $ 又不满足$ g^2_{12} < g_{11}g_{22} $ . 数值模拟结果表明: 在该条件下系统倾向于相分离, 两个分量的原子相互在对方的低密度区域填充, 如图6(d) —图6(f) 和图7 所示.图6 和图7 中斑图的形成依赖于环状暗孤子的自发旋转对称性破缺. 但是单纯依靠环状暗孤子的自发破缺只能得到有限数目的涡旋极子, 并不能得到斑图结构. 周期调制的非线性在斑图形成过程中同样扮演了重要角色. 此外, 由于BEC具有多参数、高度可控的特点, 利用环状暗孤子的自发对称性破缺性质, 结合对BEC其他相关参数的调控, 模拟量子体系中各种样式的斑图形成是一个非常有益的工作.5.总结与展望 环状暗孤子作为一种非线性激发跟涡旋、斑图等非线性现象具有密切的联系, 环状暗孤子衰变过程中导致的各类涡旋极子动力学以及斑图形成等正在引起非线性科学研究的广泛关注. 玻色-爱因斯坦凝聚作为一种高度可调控的非线性系统, 为研究环状暗孤子及其相关动力学提供了优越平台. 最近, 超冷原子玻色-爱因斯坦凝聚领域取得了一些新的理论和实验进展, 其中包括人造规范势[56 ] 、自旋轨道耦合[99 ] 、量子液体[100 ] 等. 这些进展也正在促进孤子研究的突破[101 ] , 例如理论上已经预言自旋轨道耦合可以用于稳定高维孤子[102 ,103 ] . 人造规范势尤其是非阿贝尔规范势在超冷原子气体中的实验实现[21 ] , 为研究和发现新的量子流体动力学开辟了道路. 在不同规范势作用下, 环状暗孤子可能表现出各种新奇的动力学行为. 与此同时, 通过设计合适的规范势来增强环状暗孤子的稳定性也是一个非常有益的工作. 本文讨论了环状暗孤子衰变导致的涡旋及其运动规律, 最近的研究表明自旋轨道耦合也可以在超冷原子系统中诱导出各种丰富的涡旋结构[57 ,93 ,104 -109 ] . 因而在自旋轨道耦合作用下, 环状暗孤子的衰变行为将发生明显变化, 可能产生新的涡旋结构和非传统的涡旋运动规律. 量子液体跟量子气体相比, 一个明显的不同是原子数密度发生了急剧增大[100 ] . 急剧增大的原子数密度可能对环状暗孤子的稳定性以及衰变动力学产生重要影响. 在这些全新的非线性量子多体系统中、借助新的实验技术研究环状暗孤子的运动规律、稳定性以及相关的衰变动力学将是一个重要的研究课题. 

























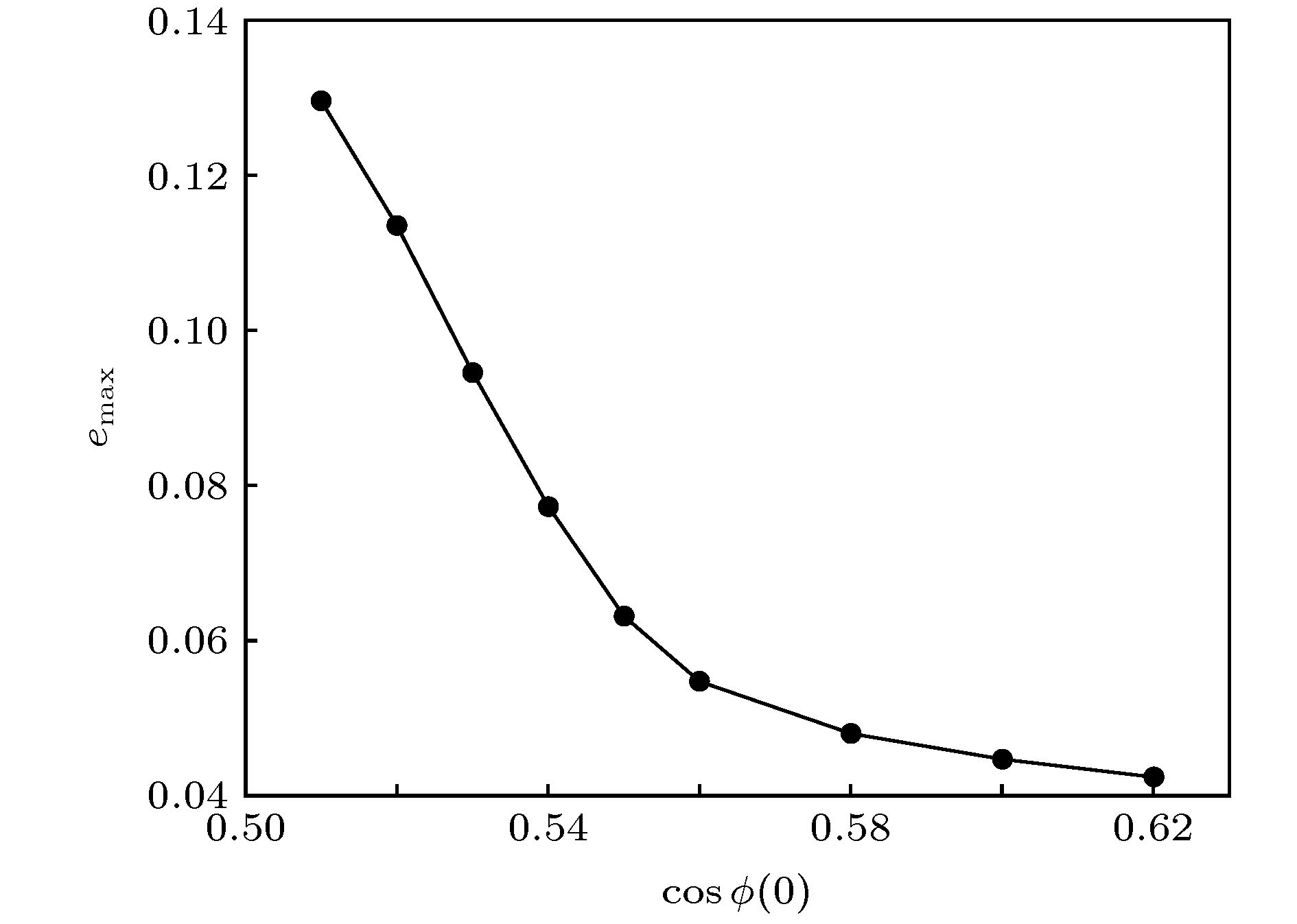 图 1 形变扰动下环状暗孤子的稳定性相图[51]
图 1 形变扰动下环状暗孤子的稳定性相图[51]



















 图 2 单分量BEC中形变扰动下环状暗孤子的衰变行为[51]
图 2 单分量BEC中形变扰动下环状暗孤子的衰变行为[51]














 图 3 两分量BEC中相同深度环状暗孤子的衰变行为[86]
图 3 两分量BEC中相同深度环状暗孤子的衰变行为[86] 图 4 四组涡旋极子在两分量BEC中的动力学演化[86]
图 4 四组涡旋极子在两分量BEC中的动力学演化[86]




 图 5 两分量BEC中不同深度环状暗孤子的衰变行为[86]
图 5 两分量BEC中不同深度环状暗孤子的衰变行为[86]







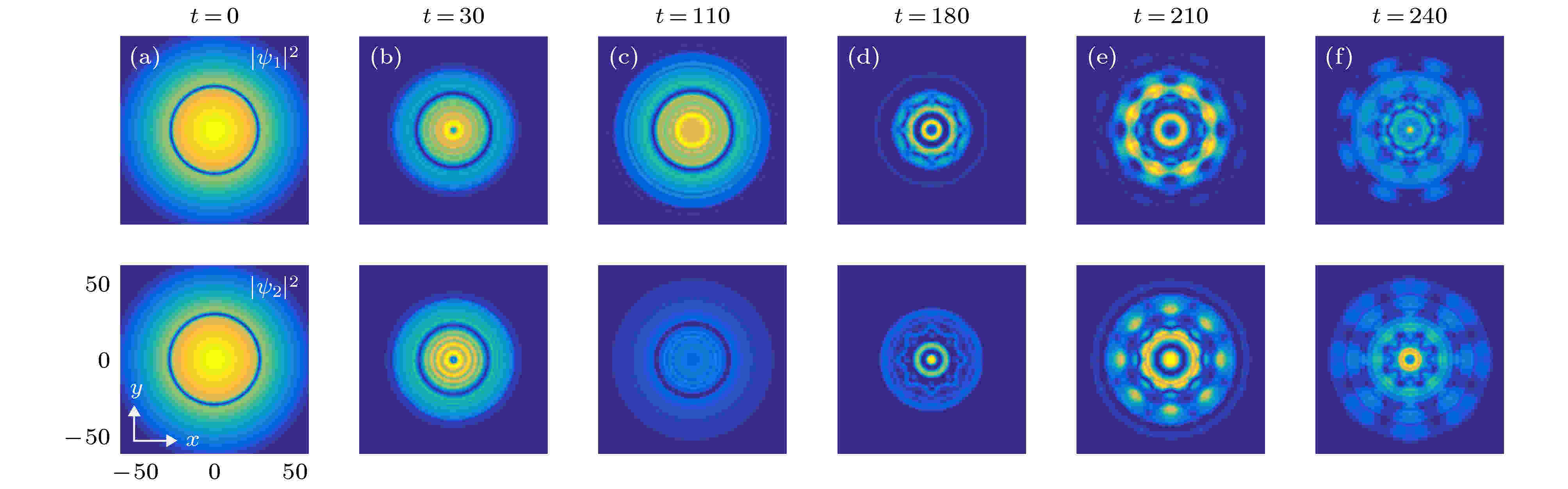 图 6 周期调制相互作用系统中环状暗孤子衰变引起的斑图形成[94]
图 6 周期调制相互作用系统中环状暗孤子衰变引起的斑图形成[94] 图 7 斑图在周期调制相互作用系统中的演化[94]
图 7 斑图在周期调制相互作用系统中的演化[94]






