摘要: 从声散射基本理论出发, 考虑弹性粒子与空化泡之间耦合作用, 结合边界条件, 推导了弹性粒子外部声流分布, 得到了声微流的
n = 0和
n = 1模式近似表达式和粒子表面应力分布函数. 数值分析结果表明: 气泡和弹性粒子之间的耦合作用增加了粒子周围的微流分布与剪应力场分布, 特别是微流速度的切向分量. 随着两者间距与相对位置的距离增大, 粒子与气泡之间相互作用减弱, 粒子周围微流幅值减小; 当气泡处于共振状态时, 粒子周围的微流分布显著增强. 粒子表面剪应力场受粒子半径与声场频率影响, 当粒子半径与声场频率越大, 外部散射声强越强, 粒子表面剪应力幅值越大.
关键词: 弹性粒子 /
空化泡 /
微流 /
声散射 English Abstract Effect of micro-bubble in ultrasonic field on microstreaming of elastic particle Feng Kang-Yi Wang Cheng-Hui Shaanxi Key Laboratory of Ultrasonics, Shaanxi Normal University, Xi’an 710119, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11474191, 11474192)Received Date: 19 August 2019Accepted Date: 11 October 2019Available Online: 27 November 2019Published Online: 01 December 2019Abstract: In this paper, the interaction between elastic particle and cavitation bubble is considered, the expression of microstreaming velocity and shear stress around the elastic particle are derived by using the theory of acoustic scattering. Taking into account the two predominant modes of elastic particle: n = 0 mode and n = 1 mode, the effects of the distance and the ratio of the radius and the relative position on microstreaming distribution, and the effects of the particle radius and the driving frequency on shear stress distribution are investigated. It is demonstrated that the interaction can increase the amplitude of microstreaming velocity, especially the tangential component of microstreaming velocity, and the shear stress. As the distance between elastic particle and cavitation bubble increases, the interaction weakens and the amplitude of the microstreaming velocity around the elastic particle decreases. When the bubble is in resonance, the microstreaming velocity around the elastic particle is significantly enhanced. The shear stress of the particle is affected by the particle radius and the frequency of sound field. As the particle radius and the frequency of sound field are larger, the external scattering sound becomes stronger and the amplitude of shear stress on the surface of particles turns larger.Keywords: elastic particle /cavitation bubble /microstreaming /acoustic scattering 全文HTML --> --> --> 1.引 言 在声场下单泡、双泡以及多泡体系已进行了广泛的理论和实验研究, 使人们对超声清洗、超声波碎石和靶向药物传递以及超声聚焦治疗癌症等已有一定的了解[1 -4 ] , 都与超声作用下液体内部微小空化核的非线性振荡、急速变化的微射流场、化学效应、生物效应等密不可分. 在实际应用过程中液体内往往分布有大量气泡, 气泡之间的相互作用可以显著增强动力学响应. 当驱动声波压力相对较弱时, 气泡做弱非线性振动, 伴随着稳态空化发生. 同时, 气泡在声场中作为声散射体存在, 其散射声波和非线性振动的相互作用可能改变气泡或者液体中粒子周围的声微流分布状态. 声微流分布可改变粒子或者气泡周围液体黏性层应力场分布, 进而影响内外物质交换, 形成与声动力学相关的效应.[5 -14 ] . Doinikov和Ayache[15 ] 的研究表明, 当有壁面存在时, 可以改变气泡振荡的振幅和相位. Tho等[16 ] 的研究表明, 可采用粒子图像测速仪器和条纹摄影技术等实验探究固定界面上单泡和双泡以特定模式振动时其周围的微流场分布. Wang等[17 ] 考虑壳层的弹性和黏度以及非线性流变效应的微泡动力学模型, 数值分析了细胞膜附近振荡气泡产生的微流场和剪切应力, 表明气泡位于细胞膜的紧邻处时, 具有较软且黏性较低的外壳材料的微气泡可以实现更有效的声波穿透效果. 文献[18 -20 ]基于声散射理论分别发展了声场中双泡、悬浮颗粒为刚性体时与气泡体系周围的微流场分布, 发现两者之间的耦合作用显著影响气泡内外和悬浮粒子表面微流大小与方向, 特别是声流速度的切向分量.[21 ] 测量了对处于无界非黏性液体中钢球与黄铜球等所受的声辐射力, 实验结果表明钢球与黄铜球的弹性对声辐射力有明显的影响. Lin和Wen[22 ] 研究了黏性液体中钢质材料的弹性柱与弹性粒子的声散射、声辐射力、声衰减等影响因素. 液体中微粒所受声辐射力是声操控技术的理论依据, 此外, 声场作用下的粒子周围声微流对超声清洗等应用的理论解释具有重要的现实意义. 尽管在一定程度上可将悬浮粒子粒当作刚性粒子对待, 但为了更好地描述具有一定弹性的粒子在声场中受到的空化影响, 有必要进一步发展气泡-弹性粒子体系声空化理论. 本文基于声场中微粒和气泡的声散射理论, 引入黏性边界层, 分析弱声场中气泡与粒子相互作用相关的微流响应.2.理论分析 22.1.一阶流速 2.1.一阶流速 为简化分析, 本文考虑声波作用下单个弹性粒子和气泡间的相互影响, 如图1 所示. 弹性粒子与气泡中心分别为${O_1}$ , ${O_2}$ , 两者中心间距为D , 以各自中心为始点建立坐标$(({r_j}, {\theta _j}\; (j = 1, 2))$ . 由薄黏性边界层理论知[8 ] , 弹性粒子与气泡的外部以及气泡内部的边界层厚度分别为$\beta _{\rm{o}}^{ - 1}$ 和$\beta _{\rm{i}}^{ - {\rm{1}}}$ , 其中${\beta _{\rm{o}}} \!=\! \sqrt {{{2\omega } / {{\nu _{\rm{o}}}}}} $ 和${\beta _{\rm{i}}} \!=\! \sqrt {{{2\omega } / {{\nu _{\rm{i}}}}}} $ , ${\nu _{\rm{i}}} \!=\! {{{\mu _{\rm{i}}}} / {{\rho _{\rm{i}}}}}$ , ${\nu _{\rm{o}}} \!=\! {{{\mu _{\rm{o}}}} / {{\rho _{\rm{o}}}}}$ , ${\mu _{\rm{i}}}$ 和${\mu _{\rm{o}}}$ 分别是内部和外部的切向黏度系数, ${\rho _{\rm{i}}}$ 和${\rho _{\rm{o}}}$ 分别是气泡内部气体与液体的密度, ω 是声波角频率.图 1 简化模型Figure1. Geometry of the model.${{{u}}_{\rm{1}}}={{{u}}_{\rm{a}}}+{{{u}}_{\rm{b}}}$ , ${{{u}}_{\rm{a}}}, {{{u}}_{\rm{b}}}$ 分别是与散射和Helmholtz方程有关的部分, 且${{{u}}_{\rm{a}}} = - \nabla {\varphi _{\rm{a}}}$ , 其中${\varphi _{\rm{a}}}$ 是液体中的速度势. 略去声波时间相${{\rm{e}}^{{\rm{i}}\omega t}}$ , 则球坐标下与弹性粒子和气泡有关的入射波速度势$\varphi _{\rm{I}}^{\left( j \right)}$ 可表示为${\varphi _0} = {{{u_0}} / k}$ , ${u_0}$ 是声源辐射面振动速度幅值, k 是入射波的波数, $k = {\omega / c}$ , c 为液体中的声速; ${{\rm{J}}_n}( \cdot )$ 是第一类球贝塞尔函数. 弹性粒子和气泡的外部散射波速度势为${\rm{H}}_n^{\left( 2 \right)}( \cdot )$ 为第二类球汉克函数.[21 ] ${k_{\rm{p}}}$ 与${k_{\rm{s}}}$ , ${c_{\rm{p}}}$ 与${c_{\rm{s}}}$ 分别为纵波与横波的波数和波速, 且有${k_{\rm{p}}} = {\omega / {{c_{\rm{p}}}}}$ 和${k_{\rm{s}}} = {\omega / {{c_{\rm{s}}}}}$ .$\phi _{\rm{a}}^{\left( j \right)} = {\phi _{\rm{I}}} + \phi _{\rm{s}}^{\left( 1 \right)} + \phi _{\rm{s}}^{\left( 2 \right)}$ 可近似表示为$j = 1 \to 3 - j = 2$ , $Q_{nm}^{\left( j \right)}$ 的具体表达式可参考文献[18 ].[21 ] ${p_{\rm{a}}} = {\rm{i}}\omega {\rho _1}\varphi _{\rm{a}}^{(1)}, \;u_{{{\rm{a}}r}}^{\left( 1 \right)} = \dfrac{{\rm{i}}}{\omega }\dfrac{{\partial \varphi _{\rm{a}}^{\left( 1 \right)}}}{{\partial r}},\;\sigma _{rr}^{\left( 1 \right)} = \lambda \varDelta +$ $ 2{\mu _0}\left( {\dfrac{{\partial {u_r}}}{{\partial r}}} \right), \sigma _{r\theta }^{\left( 1 \right)} = {\mu _0}\left( {\dfrac{{\partial {u_\theta }}}{{\partial r}} - \dfrac{{{u_\theta }}}{r} + \dfrac{1}{r}\dfrac{{\partial {u_r}}}{{\partial \theta }}} \right) $ , 其中${p_{\rm{a}}}$ 与$u_{{{\rm{a}}r}}^{\left( 1 \right)}$ 分别为外部液体的总声压和径向速度分量, $\varDelta = k_{\rm{p}}^2\displaystyle\sum\nolimits_{n = 0}^\infty {b_{_n}^{\left( 1 \right)}} {{\rm{J}}_n}\left( {{k_p}r} \right){P_n}\left( {\cos {\theta _1}} \right)$ , $\sigma _{rr}^{(1)}$ 与$\sigma _{{r\theta }}^{(1)}$ 分别为粒子剪应力的径向和切向分量, 可得到系数$a_n^{(1)}, b_n^{(1)}, c_n^{(1)}$ 的表达式详见附录A .${\partial \phi _{\rm{b}}^{(2)}} / \partial r\big|_{R_2}= $ ${\partial \phi _{\rm{a}}^{(2)}} / {\partial r}\big|_{R_2}, ~{\rho _{\rm{i}}}\phi _{\rm{b}}^{(2)}\big|_{{R_2}} = {\rho _{\rm{o}}}\phi _{\rm{a}}^{(2)}\big|_{{R_2}}$ , 且有$\bar \rho = {{{\rho _{\rm{i}}}} / {{\rho _{\rm{o}}}}}$ 和$\overline k = {k / {{k_{\rm{i}}}}}$ , 则系数$a_n^{\left( 2 \right)}$ 与$d_n^{\left( 2 \right)}$ 化简的具体形式参加附录A .$\left( {R_j, j = 1, 2} \right)$ 远小于声波波长$\lambda = {{2{\text{π}}} / k}$ , 则当$k{R_j} \ll 1$ 时, 综合考虑声散射影响以及矢量的黏性和非黏性分量的贡献, 总速度矢量${{ u}_{\rm{a}}}$ 在r 和θ 方向分量可近似表示为${h_{\rm{i}}} = \left( {1 + {\rm{i}}} \right){\beta _{\rm{i}}}, {h_{\rm{o}}} = \left( {1 + {\rm{i}}} \right){\beta _{\rm{o}}}$ , 在${r_j} = {R_j}$ 时, 切向速度与剪应力在弹性粒子和气泡表面处连续, 即$\upsilon _{1\theta {\rm{o}}}^{\left( j \right)} = \upsilon _{1\theta {\rm{i}}}^{\left( j \right)}, \sigma _{1\theta {\rm{o}}}^{\left( j \right)} = \sigma _{1\theta {\rm{i}}}^{\left( j \right)}$ , 得$ \bar \mu ={{{\mu _{\rm{i}}}} / {{\mu _{\rm{o}}}}}.$ r 与θ 分量可分别表示为6 )式可得弹性粒子表面剪应力表达式近似为2.2.声 流 -->2.2.声 流 弹性粒子外部的声流速度满足下式[8 ] :$ f_{\theta {\rm{o}}}^{\left( 1 \right)}\left( {{r_1}, {\theta _1}} \right) = f_{\theta {\rm{o}}0}^{\left( 1 \right)}\left( {{r_1}, {\theta _1}} \right) + f_{\theta {\rm{o}}1}^{\left( 1 \right)}\left( {{r_1}, {\theta _1}} \right).$ 17 )式, 可得$n = 0$ 模式,$n = 1$ 模式. 参数${a_{{\rm{o}}0}}$ —${a_{{\rm{o3}}}}$ 其具体表达参见附录B .${r_1} = {R_1}$ 时, 在弹性粒子表面与声微流相关的切向分量和剪应力连续, 可确定积分常数${c_{{\rm{o}}\theta 0}}$ —${c_{{\rm{o}}\theta 1}}$ 表达式, 即19 )—(20 )代入(21 )式得到积分常数${c_{{\rm{o}}\theta 0}}$ —${c_{{\rm{o}}\theta 1}}$ 的表达式, 其具体表达式参见附录B .$u_{{2 r{\rm{o}}}}^{\left( 1 \right)}$ 满足$\nabla \cdot {u_2} = 0$ , 且在$ {r_1} = {R_1} $ 时满足$ u_{2 r{\rm{i}}}^{\left(1\right)} = u_{2 r{\rm{o}}}^{\left( 1\right)} = 0 $ , 故有$n = 0$ 模式,$n = 1$ 模式, 且${b_{{\rm{o}}0}}$ —${b_{{\rm{o}}3}}$ 的具体表达式参见附录B .3.数值计算 根据(15 )和(16 )式, (19 )和(20 )式以及(23 )和(24 )式, 利用Matlab软件对平面波声场中弹性粒子外部声流速度和剪应力分布做数值计算. 假定声强为100 W/m2 , 驱动频率为100 kHz, 气泡半径为20 μm, 弹性粒子半径与密度分别为30 μm和7900 kg/m3 , 弹性粒子与气泡之间距离D = R 1 + R 2 , 弹性粒子纵波与横波声速分别为${c_{\rm{p}}} = 5240\;$ m/s和${c_{\rm{s}}} = 2978\;$ m/s, 其他的数值参考文献[8 ]. 在数值计算的过程中, 图2 —图5 中实线均表示切向分量, 短划线均对应径向分量, 考虑弹性粒子外部流速场时, 相对位置均取${{{r_1}} /{{R_1}}} = 1 + 2{\left( {{\beta _{\rm{o}}}{R_1}} \right)^{ - 1}}$ .图 2 ${\theta _1}$ 对弹性粒子壁面流速场分布影响 (a) $n = 0$ 模式; (b) $n = 1$ 模式Figure2. Streaming as a function of ${\theta _1}$ : (a) $n = 0$ mode; (b) $n = 1$ mode.图 5 弹性粒子壁面的剪应力分布 (a)与(b)初始半径分别为7.5, 15, 30 μm; (c)与(d)驱动频率分别为80, 100, 120 kHzFigure5. Shear stresses versus ${\theta _1}$ : (a) and (b) The radius is equal to 7.5, 15, 30 μm; (c) and (d) the driving frequency is equal to 80, 100, 120 kHz.图2 给出了在$n = 0$ 和$n = 1$ 模式弹性粒子外部声流的切向与径向分量随θ 变化的规律. 当θ 从0增加到π时, 对$n = 0$ 模式的声流速度的切向分量从零先增加后减小, $\theta = {{\text{π}} / 2}$ 时达到最大值, 径向分量先减小后增加, $\theta = {{\text{π}} / 2}$ 时等于零; 对$n = 1$ 模式声流速度, 切向分量在θ 处于0到${{\text{π}} / 2}$ 之间先增加后减小, $\theta = {{\text{π}} / 4}$ 时达到最大值, θ 处于${{\text{π}} / 2}$ 到π时先增加后减小, $\theta = {{3{\text{π}}} / 4}$ 时达到最大值; 径向分量在θ 处于0到${{\text{π}} / 2}$ 之间先减小后增加, $\theta = {{\text{π}} / 4}$ 时等于零, θ 处于${{\text{π}} / 2}$ 到π时先减小后增加, $\theta = {{3{\text{π}}} /4}$ 时等于零. 通过将粒子的$n = 0$ 与$n = 1$ 模式对微流场分布的影响进行对比, 发现$n = 0$ 模式对微流分布的贡献起主要作用. 同时, 与Wu等[20 ] 的研究结论相比较, 考虑粒子的弹性影响后, 其周围声流强度增加, 且大于刚性粒子周围声流分布.图3 分别分析了相对位置以及两者间距对粒子外部微流的影响. 结果表明: 1)在弹性粒子外部, 随着到粒子表面距离的增加, 微流速度减小并逐渐趋近于0, 如图3(a) 与图3(b) 所示, 微流分布在粒子周围有限的范围之内, 符合薄黏性边界层理论假设; 2)随着弹性粒子与气泡之间的距离增加, 两者之间的相互作用减弱, 弹性粒子周围声流速度的径向与切向分量幅值均减小, 逐渐接近单个弹性粒子存在时的微流分布. Li等[23 ] 通过实验与理论研究了气泡与悬浮粒子之间的非线性相互作用, 结果表明: 随着两者间隙的增加, 粒子速度呈线性减小, 进一步说明了粒子与气泡之间相互作用越弱, 粒子周围声流强度越小.图 3 ${{{r_1}} / {{R_1}}}\;\left( {\theta = {{\text{π}} / 4}} \right)$ 和${{D'} / {{R_1}}}\;(D' = D - {R_1} - {R_2}, {\theta _1} = {{\text{π}} / 4})$ 对弹性粒子壁面微流分布影响 (a)与(c)$n = 0$ 模式; (b)与(d) $n = 1$ 模式Figure3. Streaming as a function of ${{{r_1}} / {{R_1}}}$ $\left( {\theta = {{\text{π}} / 4}} \right)$ and ${{D'} / {{R_1}}}\;(D' = D - {R_1} - {R_2}, {\theta _1} = {{\text{π}} / 4})$ : (a) and (c) $n = 0$ mode; (b) and (d) $n = 1$ mode.图4 给出了随气泡初始半径变化时弹性粒子周围微流分布, 结果表明: 弹性粒子周围$n = 0$ 与$n = 1$ 模式声流速度幅值变化存在共振峰值, 峰值位置对应的粒子和气泡半径比值约为1.2, 在计算过程中粒子半径为30 μm, 因此, 峰值处对应的气泡半径约为36 μm, 其共振频率和驱动声波频率100 kHz可相比拟, 即微流速度峰值分布区内气泡处于共振状态. 因此, 声场中气泡的共振响应可增加其对粒子的微流影响, 且对切向分量幅值变化影响更为显著.图 4 ${{{R_2}} / {{R_1}}}\;({\theta _1} = {{\text{π}} / 4})$ 对弹性粒子壁面微流分布影响 (a)$n = 0$ 模式; (b)$n = 1$ 模式Figure4. Streaming as a function of ${{{R_2}} / {{R_1}}}\;({\theta _1} = {{\text{π}} / 4}):$ (a)$n = 0$ mode; (b)$n = 1$ mode.图5 所示. 对比粒子半径分别为7.5, 15, 30 μm时应力分布情况可以看出, 粒子半径在一定范围内, 随着半径的增加, 粒子表面应力增大; 极角${\theta _1}$ 变化对径向应力分量影响不大, ${\theta _1}$ 从0 增加到π, 切向应力分量从零先增加后减小, 在${{\text{π}} / 2}$ 达到极大值, 如图5(a) 与图5(b) 所示. 弹性粒子半径越大, 其声散射截面积越大, 声散射越强, 故微流场越强, 由(14 )式可知, 剪应力分布与微流分布正相关, 因而粒子表面剪应力幅值越大. 对比声波频率分别为80, 100, 120 kHz时应力分布情况可看出, 对半径为30 μm弹性粒子而言, 声波频率在一定范围内, 声波频率增加, 应力值增大, 极角对应力分布的影响也越显著, 如图5(c) 与图5(d) 所示. Shi等[24 ] 的研究表明, 包膜泡的散射截面积与声波频率呈正相关, 同时, 散射截面积越大时, 表面剪应力幅值越大. 因此, 当外部声场频率越大, 微粒引起的声散射越强, 粒子表面剪应力幅值越大. 与Doinikov和Bouakaz[10 ] 与Liu和Wu[9 ] 的研究结果相比较, 由于粒子和气泡之间的耦合作用, 一定程度增加了粒子周围的剪应力分布, 进一步增强周围流体介质的声动力学响应.图6 所示, ${\theta _1}\;=\;0{^{\circ }}$ 与$180{^{\circ }}$ 处粒子声流速度趋于0, 在弹性粒子表面附近, 可观察到较为明显的径向与切向微流, 从粒子表面向外, 随着距离的增加, 微流径向分量越来越小, 到一定距离后, 几乎可以忽略不计, 此时, 声微流只剩下切向分量. Liu和Wu[9 ] 对单个包膜泡周围微流分布的研究结果表明随着到包膜泡表面距离的增加, 声流速度减小, 与本文研究结果一致. 此外, 考虑了空化泡与粒子之间的相互作用之后, 可以看到粒子表面产生更为显著的切向微流, 进而影响液体中切应力分布, 可增强对液体中其他界面的切向影响.图 6 声流速度的矢量分布图Figure6. Distribution of streaming velocity vector.4.结 论 本文基于声散射理论, 研究无界黏性液体内的平面波场中弹性粒子与气泡体系的声微流分布, 考虑了二者间相互作用的影响, 得到了$n = 0$ 和$n = 1$ 模式声流表达式以及弹性粒子表面黏性层内剪应力分布式. 以钢质微球为例数值分析了其周围微流分布以及表面应力分布, 考虑了气泡半径、气泡到微球距离、微球半径、微球-气泡间半径比以及驱动声波频率的影响. 结果表明: $n = 0$ 模式对微流场贡献较大; 气泡的存在能够显著增强微流场整体分布, 特别是其切向分量; 粒子周围声流速度随气泡到微球距离的增加而减小; 当气泡处于共振状态时, 粒子周围声流速度幅值更大, 说明气泡的共振声响应能够有效增强声波对粒子的微流效应. 驱动声波压力幅值一定时, 随着粒子半径和声波频率的增大, 粒子表面剪应力分布增强.$\small a_n^{(1)}, b_n^{(1)}, c_n^{(1)},a_n^{(2)}, d_n^{(2)}$ 的表达式$a_n^{(1)}, b_n^{(1)}, c_n^{(1)}$ 系数的具体表达式:$\chi = {1 / {\sqrt {{\varOmega ^2}{\sigma ^2} + \left( {1 - {\varOmega ^2}} \right)} }}$ , 其中$\varOmega = {\omega / {{\omega _{\rm{r}}}}}$ , ${\omega _{\rm{r}}}$ 为气泡本征频率,k 为外部液体的波数; ${\rho _1}$ 为粒子的密度, 且有${\bar \rho _1} = $ ${{{\rho _{\rm{o}}}} / {{\rho _1}}}, {\bar k_1} = {k / {{k_{\rm{p}}}}}, {\bar k_2} = {k / {{k_{\rm{s}}}}}, {\bar k_3} = {{{k_{\rm{s}}}} / {{k_{\rm{p}}}}}.$ $a_n^{(2)}, d_n^{(2)}$ 化简的具体形式:${a_{{\rm{o0}}}}$ —${a_{{\rm{o3}}}}$ , ${c_{{\rm{o}}\theta }}$ —${c_{{\rm{o}}\theta 1}}$ , ${b_{{\rm{o}}0}}$ —${b_{{\rm{o}}12}}$ 具体 表达式${a_{{\rm{o0}}}}\text{—}{a_{{\rm{o3}}}}$ 具体表达式:${c_{{\rm{o}}\theta }}\text{—}{c_{{\rm{o}}\theta 1}}$ 的具体表达式:${b_{{\rm{o}}0}}\text{—}{b_{{\rm{o}}12}}$ 的具体表达式: 












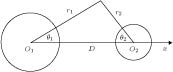 图 1 简化模型
图 1 简化模型






























































 图 2
图 2 





 图 5 弹性粒子壁面的剪应力分布 (a)与(b)初始半径分别为7.5, 15, 30 μm; (c)与(d)驱动频率分别为80, 100, 120 kHz
图 5 弹性粒子壁面的剪应力分布 (a)与(b)初始半径分别为7.5, 15, 30 μm; (c)与(d)驱动频率分别为80, 100, 120 kHz



















































 图 3
图 3 










 图 4
图 4 












 图 6 声流速度的矢量分布图
图 6 声流速度的矢量分布图






















