全文HTML
--> --> -->Andreev反射, 是指在正常金属/超导体异质结中, 当正常金属中的电子的能量低于超导能隙时, 能够找到自旋和动量相反的电子配对, 透过界面进入超导体形成库珀对, 并对结电导形成增强效应[8]. 在铁磁体/超导体界面, 铁磁体中不同自旋方向电子数目的不平衡将导致Andreev反射被压制. 通过对Andreev反射谱进行修正的Blonder-Tinkham-Klapwijk (BTK)理论拟合, 能够得到载流子的自旋极化率[9-14].
Andreev反射谱方法进行自旋极化率测量所使用的器件结构主要有两种: 点接触模式和平面结构[15-18]. 点接触模式一般采用超导针尖按压待测材料的方式形成欧姆接触, 其优势在于快速、灵活, 对薄膜和块材都适用. 点接触模式的缺点主要是在存在较高界面势垒的情况下(例如表面氧化物), 高自旋极化材料的Andreev反射谱和隧道谱非常类似, 这导致测量结果不可靠. 此外, 在点接触模式下由于界面电阻不均匀往往会存在一些较大的电流热点(hot spot), 导致实际测量温度远高于标称温度, 从而给自旋极化率的分析带来困难[19,20]. 相对而言, 平面Andreev结构采用实际的电子器件结构, 能够可控性的制备更干净的界面, 并且其可靠性已在CrO2, HgCr2Se4等高自旋极化率的材料上被验证[18,21,22]. 但是, 平面Andreev结构的界面上有时会存在超导元素的扩散或与待测材料发生化学反应, 导致自旋极化率偏离真实值. 因此, 如何避免界面反应、制备界面干净的超导异质结, 对于准确获得待测材料的载流子自旋极化率具有重要的意义.
FexTaS2体材料是一种典型的磁性层状过渡族金属硫化物, 母体材料TaS2为层状结构, 层与层之间靠范德瓦耳斯力连接, Fe原子以插层的形式存在于TaS2之间, 原则上可以通过机械剥离的方法将FexTaS2减薄至纳米尺度[23-26]. 在较高Fe含量范围(0.20 ≤ x ≤ 0.40)内, FexTaS2依然具有长程铁磁性并能保有序的晶体结构, 居里温度最高为160 K (x = 0.25), 接近最近报道的二维铁磁体Fe3GeTe2[27]. 理论计算表明FexTaS2费米能级附近具有较高的自旋极化率并且不受铁的无序分布的影响[28,29], 但Arai等[30]采用机械剥离方法将其减薄至100 nm左右, 在Fe0.25TaS2隧道结中仅观察到了约7%的隧穿磁电阻, 远低于根据电子自旋极化率估计出的理论预期值, 这可能是因为隧穿层氧化不足而导致过多的界面缺陷散射. 然而到目前为止, 还没有直接测量Fe0.25TaS2自旋极化率的实验报道.
本文聚焦于Fe0.26TaS2单晶, 进行了材料的磁性、电子输运和自旋极化率研究. 通过Fe0.26TaS2/Pb, Fe0.26TaS2/Al/Pb, Fe0.26TaS2/NbSe2等磁性/超导异质结的Andreev反射谱的测量, 发现只有干法转移方法能够制备足够干净的界面, 并首次提取出这种层状铁磁体的自旋极化率. 本文工作为进一步研究该体系的二维铁磁性和自旋调控打下了基础.
3.1.Fe0.26TaS2单晶样品的磁性和输运性质
图1为Fe0.26TaS2单晶样品的磁性测量结果. 不同方向的零场冷(zero-field cooling, ZFC)和场冷(field cooling, FC)磁化率在居里温度以下迅速上升, 面外磁矩远大于面内磁矩(图1(a)和图1(b)). 对高温段磁化率进行居里-外斯定律拟合显示不同方向的居里-外斯温度存在较大的差别(H⊥ab时约为121 K; H//ab时约为66 K), 这起源于单晶样品的强磁各向异性[23, 32]. 等温磁化率测量结果也证明了这一点(图1(c)和图1(d)). H⊥ab方向的等温磁化曲线在转变温度以下存在明显的磁滞回线行为, 最大饱和磁矩约为3.85 μB/Fe, 表明样品为铁磁性. 在H//ab方向, 磁化曲线随磁场线性变化, 高场下也没有达到饱和(65 K左右的弱磁滞回线来源于磁场与ab面不完全平行).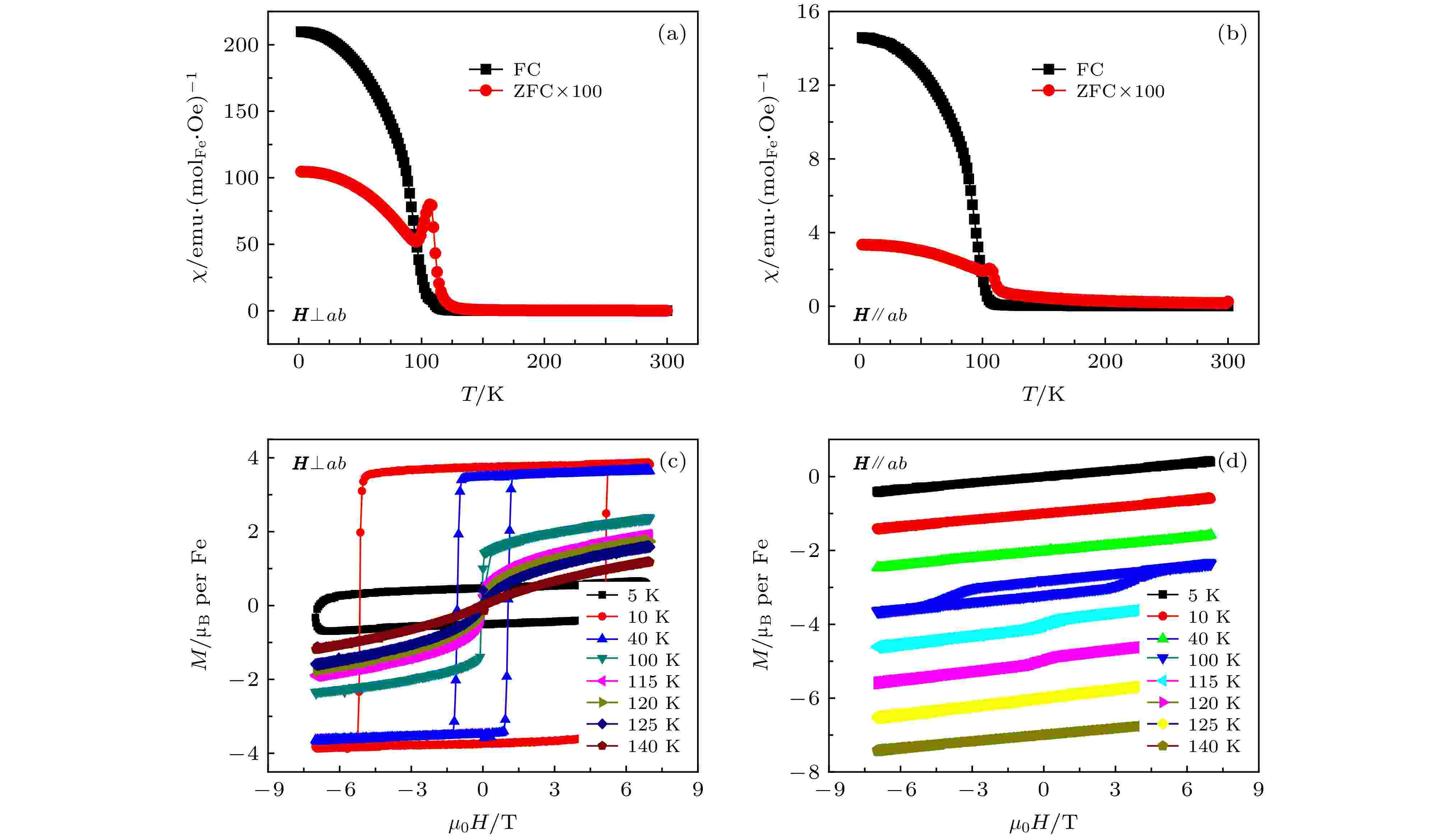
图 1 Fe0.26TaS2单晶样品的磁性测量结果 (a) 外加磁场垂直于ab面(H⊥ab)时的FC和ZFC磁化曲线, 测量磁场为100 Oe (1 Oe = 103/(4π) A/m); (b)外加磁场平行于ab面时 (H//ab)的FC和ZFC磁化曲线, 测量磁场为100 Oe; (c) H⊥ab的等温磁化曲线随外加磁场的变化; (d) H//ab的等温磁化曲线随外加磁场的变化(为清楚起见, 在垂直方向做了等间距平移)Figure1. Magnetization measurement results of Fe0.26TaS2: (a) Magnetization measurement with ZFC and FC process while H⊥ab, the measurement field is 100 Oe; (b) magnetization measurement with ZFC and FC process while H//ab, the measurement field is 100 Oe; (c) isothermal magnetization measurements for H⊥ab; (d) isothermal magnetization measurements for H//ab. For clarify, the data is shift equally in Fig. 1(d).
为了确定样品的居里温度, 对H⊥ab方向的等温磁化曲线使用Arrott图方法处理(图2(a)), 获得样品的居里温度为115 K. 磁性测量结果表明, Fe0.26TaS2单晶是铁磁性材料, 磁化方向平行于样品c轴, 具有强磁各向异性. 这些性质与Morosan等[23]和Checkelsky等[32]关于Fe0.25TaS2单晶样品的实验结果基本一致.
图 2 Fe0.26TaS2等温磁化曲线和电阻-温度曲线(1 emu = 10–3 A·m2) (a) H⊥ab方向Fe0.26TaS2等温磁化曲线的Arrott图, 居里温度为115 K; (b) Fe0.26TaS2的电阻-温度曲线Figure2. Isothermal magnetization and temperature dependence of resistance of Fe0.26TaS2: (a) Arrot plot for isothermal magnetization in H⊥ab; (b) temperature dependence of resistance.
图2(b)为Fe0.26TaS2样品电阻随温度的变化. 在居里温度(115 K)以下, 由于磁有序转变, 磁矩指向逐渐一致, 对载流子自旋依赖的散射减小, 电阻随温度降低而迅速下降, 与其他FexTaS2单晶的电阻-温度行为一致[33].
图3为Fe0.26TaS2单晶不同方向的磁电阻和霍尔效应, 磁电阻定义为
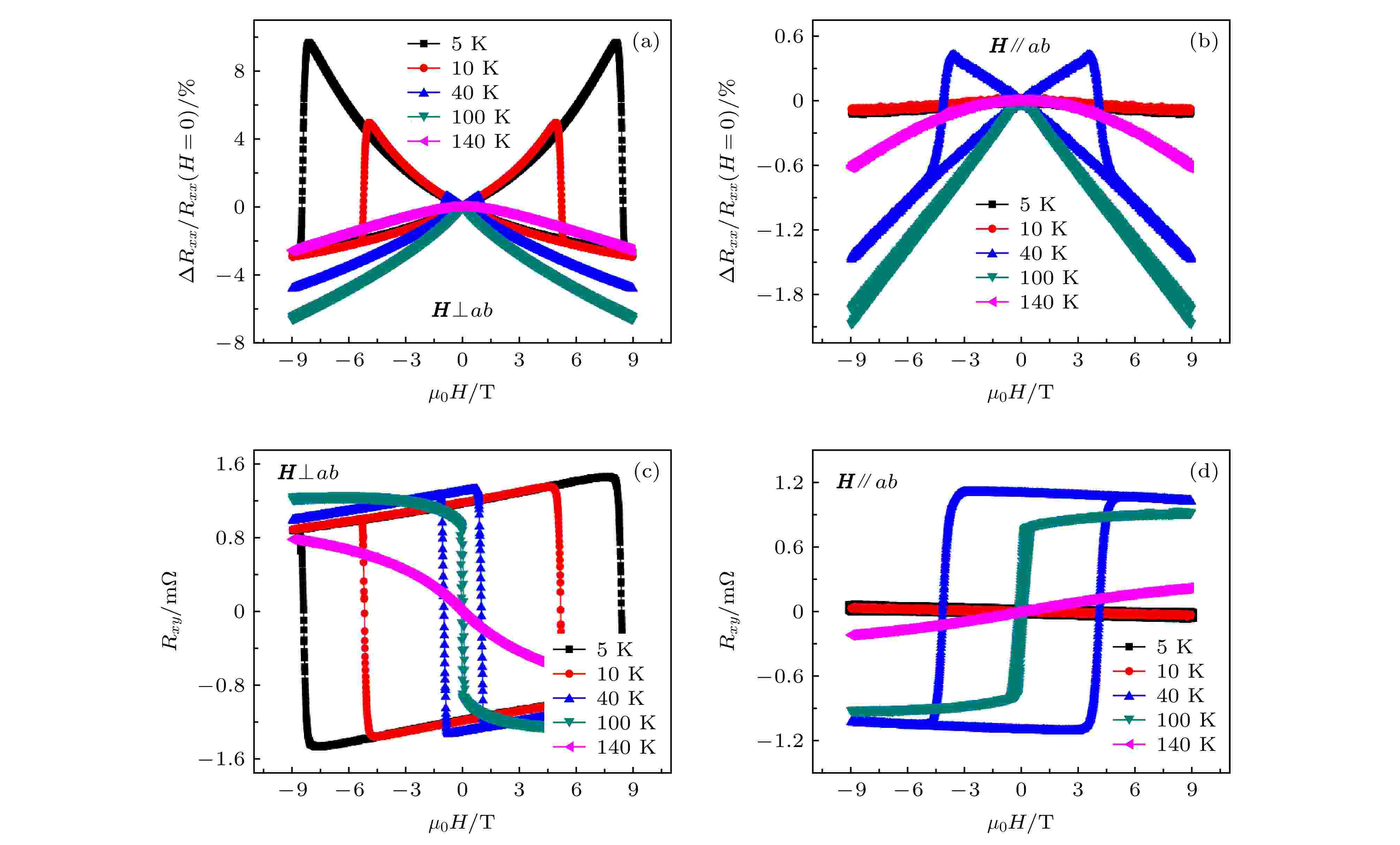图 3 磁电阻和霍尔电阻随外加磁场的变化 (a) H⊥ab时, 磁电阻随外加磁场的变化; (b) H//ab时, 磁电阻随外加磁场的变化; (c) H⊥ab时, 霍尔电阻随外加磁场的变化; (d) H//ab时, 霍尔电阻随外加磁场的变化Figure3. Magnetic field dependence of magnetoresistance and Hall effect: (a) Magnetic field dependence of magnetoresistance, H⊥ab; (b) magnetic field dependence of magnetoresistance, H//ab; (c) magnetic field dependence of Hall effect, H⊥ab; (d) magnetic field dependence of Hall effect, H//ab.
2
3.2.Fe0.26TaS2的自旋极化率测量
准确测量自旋极化率是自旋电子学领域的基础问题, 对铁磁材料的应用具有重要意义. 为了可靠地提取Fe0.26TaS2的自旋极化率, 采用不同的超导电极Pb, Al, NbSe2, 制备了三种超导异质结并测量了Andreev反射谱.首先制备了Fe0.26TaS2/Pb Andreev结, 在Pb的临界温度以下测量了微分电导谱. 图4(a)为不同温度下Fe0.26TaS2/Pb的归一化微分电导谱, 可以看到零偏压电导被轻微压制, 表明Fe0.26TaS2存在一定自旋极化的电子. 图4(b)—(d)为修正的BTK理论对实验数据的拟合结果, 表明Fe0.26TaS2的自旋极化率P最高为23%, 低于理论计算结果[28]. 拟合得到的超导能隙Δ = 0.35 meV, 远低于体态铅的超导能隙(～1.2 meV). 考虑到在异质结制备过程中, 热蒸发的Pb极易扩散进入Fe0.26TaS2并与其发生硫化反应, 形成新的超导化合物(PbS)1.13TaS2 (TC = 3.08 K, Δ～0.42 meV)[35], 这和拟合所获得的超导带隙基本一致. 因此, 测量的自旋极化率很可能由于界面铅扩散的影响而并不准确.
图 4 Fe0.26TaS2/Pb的Andreev反射谱 (a)不同温度下Andreev结的归一化微分电导谱; (b) T = 1.6 K, 修正的BTK理论对微分电导谱的拟合结果; (c) T = 2 K, 修正的BTK理论对微分电导谱的拟合结果; (d) T = 4 K, 修正的BTK理论对微分电导谱的拟合结果. 黑色点为实验数据, 红色线为理论计算结果Figure4. Andreev reflection spectroscopy of Fe0.26TaS2/Pb: (a) Normalization of Andreev reflection spectroscopy from T = 2 K to 8 K; (b) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 1.6 K; (c) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 2 K; (d) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 4 K. The black dot is experimental data and red line is fitting.
为阻止铅扩散对异质结界面的污染, 在Fe0.26TaS2/Pb之间插入50 nm的铝, 制备了Fe0.26TaS2/Al/Pb结. 图5(a)为低温下归一化微分电导谱的测量结果. 在铝超导温度(～1.2 K)以下, 电导谱表现出明显的超导隧穿行为; 在铝超导温度之上时则类似于Andreev反射谱行为. 修正的BTK理论拟合表明界面存在较大的势垒强度(图5(b)—(d)). 以温度在0.36 K的数据(图5(b))为例, 首先由修正的BTK理论拟合, 提取了Fe0.26TaS2自旋极化率在40%, 势垒散射因子Z在2.4左右. 从拟合参数可以看出, Fe0.26TaS2/Al/Pb异质结的界面存在较大的散射势垒, 透过率较差, 导电机制可能以隧穿为主. 造成这一情况的原因是Fe0.26TaS2/Al/Pb异质结中Al膜和Pb膜是在不同镀膜机沉积的, 在转移过程中, Al膜短暂暴露于空气中, 氧化形成了AlOx势垒, 最终结构变成了Fe0.26TaS2/Al/AlOx/Pb. 在高界面散射强度的情况下, 高自旋极化率的Andreev反射谱和超导隧道谱很难区分[18,20]. 如图6所示, 使用较高的势垒强度Z同样能够很好地拟合不同温度下的实验数据. 因此, 使用这一方法仍然不能得到可靠的电子自旋极化率. 类似的现象在CrO2/I/Pb异质结中也曾被观测到[18].
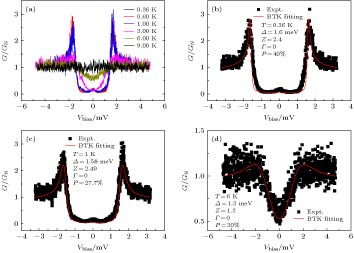图 5 Fe0.26TaS2/Al/Pb异质结的Andreev反射谱 (a)不同温度下的归一化微分电导谱; (b) T = 0.36 K, 修正的BTK理论对微分电导谱的拟合结果; (c) T = 1 K, 修正的BTK理论对微分电导谱的拟合结果; (d) T = 6 K, 修正的BTK理论对微分电导谱的拟合结果; 黑色点为实验数据, 红色线为理论计算结果, 自旋极化率P ≠ 0Figure5. Andreev reflection spectroscopy of Fe0.26TaS2/Al/Pb: (a) Normalization of Andreev reflection reflection spectroscopy from T = 0.36 K to 9 K; (b) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 0.36 K; (c) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 1 K; (d) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 6 K. The black dot is experimental data and red line is fitting. Spin polarization is fixed to none-zero (P ≠ 0).
图 6 修正的BTK理论对不同温度下微分电导谱的拟合结果 (a) T = 0.36 K; (b) T = 1 K; (c) T = 3 K; (d) T = 6 K; 黑色点为实验数据, 红色线为理论计算结果; 自旋极化率固定为零(P = 0)Figure6. Modified BTK fitting for normalized Andreev reflection spectroscopy of Fe0.26TaS2/Al/Pb: (a) T = 0.36 K; (b) T = 1 K; (c) T = 3 K; (d) T = 6 K. The black dot is experimental data and the red line is fitting. Spin polarization is fixed to zero (P = 0).
界面的自旋依赖散射如自旋轨道耦合、无序引入的自旋激活散射等都将直接影响载流子自旋极化率和自旋器件的性能. 如何避免界面扩散、污染, 始终是实验过程中需要耗费很大精力去解决的问题. Fe0.26TaS2作为层状铁磁体, 其优势在于可以用机械解理的方法将其减薄至数十纳米厚度, 甚至制备出二维铁磁材料. 为了获得干净的超导异质结界面, 最终选择干法转移工艺, 在保护性气氛下将Fe0.26TaS2解理至60 nm, 并与层状超导体NbSe2结合, 制备了Fe0.26TaS2/NbSe2 Andreev结[25].
低温下Fe0.26TaS2/NbSe2的归一化微分电导谱和拟合如图7(a)所示, 在NbSe2超导温度以下, 带隙内微分电导被抑制, 明显低于带隙外电导, 表明存在较高的载流子自旋极化率. 以温度为4 K的归一化电导谱为例(图7(b)), 使用修正的BTK理论可以非常好地拟合实验曲线, Fe0.26TaS2的自旋极化率P为54%, 并且界面势垒强度Z和非弹性散射因子Γ值很小. 而且, 对比磁性隧道结, 使用Andreev反射谱获得了更高的自旋极化率[30]. 这些都表明干法转移技术能够避免可能的界面污染和氧化层生成, 获得非常干净的异质结界面, 从而可靠的提取材料的自旋极化率. 测量了多个器件, 拟合所得的自旋极化率分布在40%—54%之间. 根据理论计算, FexTaS2费米面上自旋极化电子主要来自于Fe的3d电子, 少部分来自于Ta的5d电子, 而且即使Fe原子的分布存在无序, 并不会对费米面上自旋极化电子的态密度分布或者载流子自旋极化率产生很大影响[28,29]. FexTaS2单晶材料, Fe作为插层原子, 在TaS2层间形成超晶格结构, Fe的分布并不是绝对均匀的, 会偏离名义上浓度, 也可能会形成一些Fe团簇, 这些都是实验测量的自旋极化率在一定区间内分布的原因[23,24].
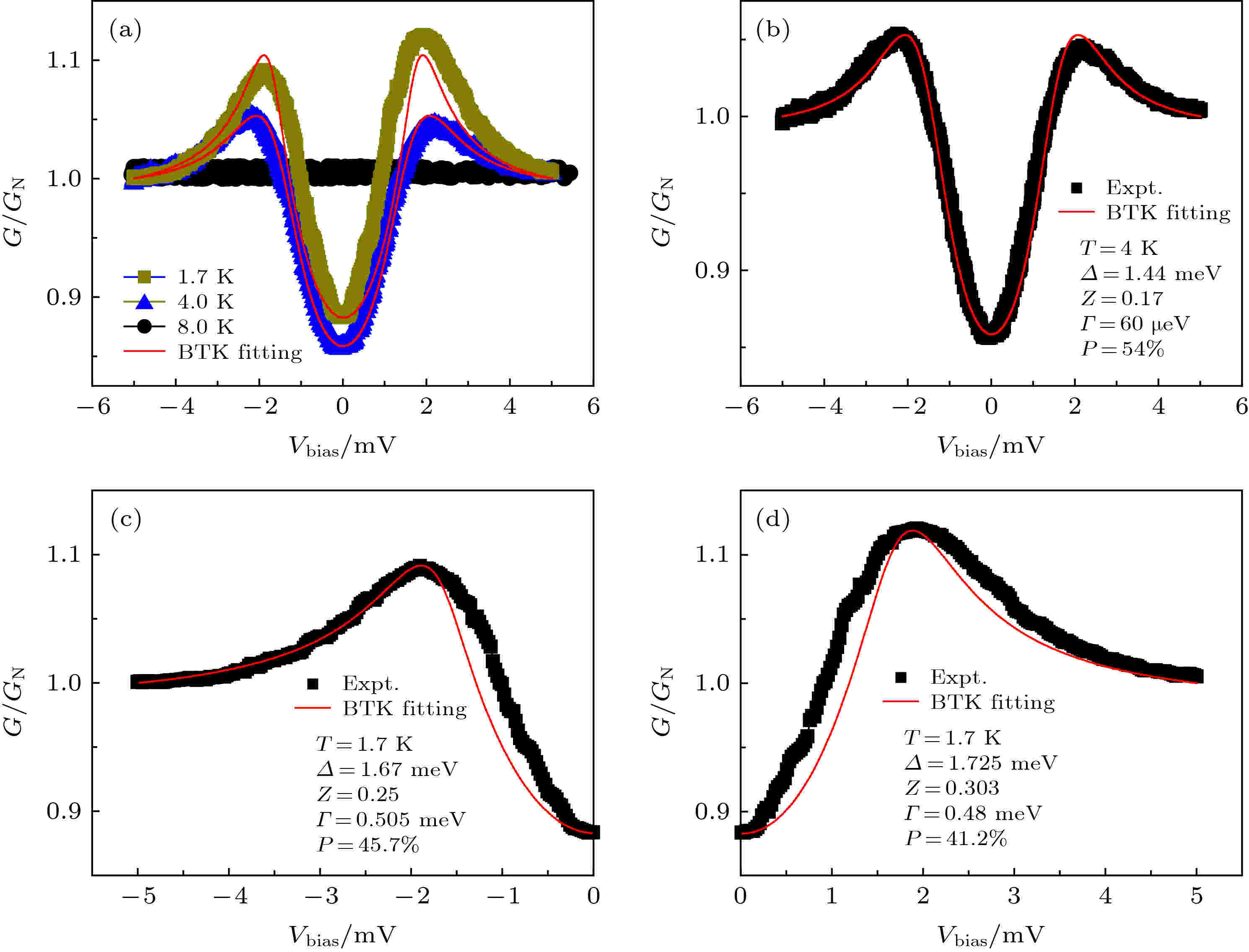图 7 Fe0.26TaS2/NbSe2的Andreev反射谱 (a)不同温度下的归一化微分电导谱和修正的BTK拟合; (b) T = 4 K的微分电导谱和修正的BTK拟合; (c) T = 1.7 K下, 负偏压的归一化微分电导谱及修正的BTK拟合; (d) T = 1.7 K下, 正偏压的归一化微分电导谱及修正的BTK拟合; 黑色点为实验数据, 红色线为理论计算结果Figure7. Andreev reflection spectroscopy of Fe0.26TaS2//NbSe2: (a) Normalization of Andreev reflection spectroscopy from T = 1.7 K to 8 K; (b) modified BTK fitting for normalized Andreev reflection spectroscopy at T = 4 K; (c) modified BTK fitting for normalized Andreev reflection spectroscopy at T = 1.7 K; (d) modified BTK fitting respectively for negative bias or positive bias Andreev reflection spectroscopy at T = 1.7 K. The black dot is experimental data and red line is fitting.
值得注意的是, Fe0.26TaS2/NbSe2 Andreev结在更低的温度下(T = 1.7 K), 超导带隙两侧的微分电导谱分布不对称, 两侧相干峰的高度不一致, 而且带隙内电导偏离了修正的BTK理论. 这种正负偏压区电导谱不对称的现象在铁磁半金属EuB6[36]、HgCr2Se4[22], 以及电子强关联化合物CeCoIn5、UBe13[37]、URu2Si2[38]等材料的Andreev结中也有报道, 但不对称的物理机制是否与电子关联性目前并没有明确的证据. 为了分析电导谱不对称对自旋极化率提取的影响, 将T = 1.7 K的微分电导谱分成正负偏压两部分分别进行拟合, 如图7(c)和图7(d)所示. 最好的拟合结果表明, 二者所提取的自旋极化率相差在4%左右, 这进一步说明干法转移所制备的Fe0.26TaS2/NbSe2异质结能够可靠地提取材料的自旋极化率.
