摘要: 二硫化钼(MoS
2 )作为一种层状过渡金属硫族化合物, 是未来光子学与光电子学领域的重要组成材料. 本文设计实现了MoS
2 与谐振腔耦合系统, 将蝴蝶结型等离子体谐振腔的谐振模式与单层MoS
2 光致发光(PL)谱相耦合, 得到该条件下最佳PL强度增强效果. 通过理论模型与实验数据的分析, 利用珀塞尔效应对自发辐射速率进行控制, 得到了峰值为9.5倍、带宽为100 nm的宽带增强谱. 同时, 增强的PL强度随激发光和探测光的偏振角度满足余弦函数规律的依赖特性, 证明了谐振模式来自谐振腔中的电场偶极子. 该研究提供了在单层MoS
2 与等离子体谐振腔耦合结构中研究光与物质相互作用增强的可行性, 为今后基于MoS
2 光子学器件的发射与探测效率提升开辟出一条新途径.
关键词: 二硫化钼 /
光致发光 /
等离子体谐振腔 /
珀塞尔效应 English Abstract Fluorescence enhancement of monolayer MoS2 in plasmonic resonator Meng Fan 1 ,Hu Jin-Hua 2 ,Wang Hui 1 ,Zou Ge-Yin 3 ,Cui Jian-Gong 4 ,Zhao Yue 5 1.School of Information Science and Technology, Shijiazhuang Tiedao University, Shijiazhuang 050043, China Fund Project: Project supported by the Science Foundation for the Excellent Youth Scholars of Hebei Province, China (Grant No. F2018210100), the Top Young Talents in Hebei Colleges and Universities, China (Grant No. BJ2018003), the Natural Science Foundation of Hebei Province, China (Grant No. F2017402068), and the Natural Science Foundation of Shanxi Province, China (Grant No. 201801D221198)Received Date: 21 July 2019Accepted Date: 18 September 2019Available Online: 27 November 2019Published Online: 05 December 2019Abstract: Molybdenum disulfide (MoS2 ), as a layered transition metal chalcogenide, plays an important role in fields of photonics and photoelectronics. Here, a coupled system consisting of monlayer MoS2 and nano-resonator is designed and implemented. The photoluminescence (PL) spectrum of the MoS2 is coupled with the resonant mode of plasmonic bowtie resonator, thus achieving an optimal PL enhancement condition. Based on the analysis of theoretical model and experimental data, the spontaneous emission rate can be controlled by the Purcell effect, and the broadband enhanced spectrum is obtained in which its peak value increases 9.5 times and bandwidth is 100 nm . Meanwhile, the enhanced PL intensity also satisfies the cosine function relation between the polarization angle of the exciting light and that of the detecting light, which proves that the resonance mode comes from the electric field dipole in the resonator. This study provides the feasibility of studying the enhancement of light-matter interaction in an MoS2 -plasmonic resonator coupled structure, which opens up a new route to improving the emission and detection efficiency of MoS2 -based photonic devices in future.Keywords: MoS2 /photoluminescence /plasmonic resonator /Purcell effect 全文HTML --> --> --> 1.引 言 作为层状过渡金属硫化物的典型代表, 二硫化钼(MoS2 )具有非常优异的电学和光学特性, 近年来一直得到人们的重点关注[1 -7 ] . MoS2 材料的能带结构会随着其层数的变化而改变, 当层数从多层减少到单层时, MoS2 将由间接带隙半导体变成禁带宽度为1.8 eV的直接带隙半导体[8 ] . 与块状MoS2 晶体材料相比, 单层MoS2 的光致发光(PL)效率提升了104 倍[9 ,10 ] , 这为二维材料在光子器件和光电子器件应用方面开辟了新的天地. 截至目前, 已有不少关于MoS2 的开拓性研究报道, 如基于MoS2 的光电探测器可实现880 A/W的超高光电响应度[11 ] , 利用单层MoS2 直接跃迁的电致发光器件[12 ] 以及MoS2 纳米薄片中超快非线性饱和吸收效应[13 ] 等. 虽然单层MoS2 的量子产量已有较大提升, 但由于其PL效率由非辐射复合速率1/τ nr (远大于自发辐射速率, τ nr ≈ 100 ps)所主导, 使得整体效率仅为10–2 量级[9 ] . 在光与微纳结构谐振腔相互作用的研究中, 后者能够克服光衍射带来的探测极限, 通过其谐振效应对光场进行高效限制并控制其中多项参数[14 ] , 从增强光场密度角度来看极大地增强了光与物质的相互作用. 甘雪涛等[15 ] 通过将单层MoS2 与高品质因数(Q ~320)的光子晶体谐振腔(PPC)耦合, 利用珀塞尔效应得到了峰值为5.3倍的PL增强结果, 但增益带宽仅为2—3 nm. 吴三丰等[16 ] 将单层二硒化钨与PPC进行耦合, 除了得到珀塞尔因数为60的窄带PL增强效果外, 还通过PPC结构参数的设计实现了对发射光子极性和方位角的重新分配. 在PL宽谱增强方面, Moerner研究组[17 ] 利用溶于聚甲基丙烯酸甲酯中的发光具有光致漂白效应的荧光分子(TPQDI)覆盖在蝴蝶结型等离子体谐振腔上, 得到了高达1340倍的PL增强效果.2 与基于银薄膜的蝴蝶结型纳米谐振腔相互集成, 前者的辐射荧光通过倏逝波效应与后者谐振模式进行耦合, 光场以超过衍射极限的程度被压缩时其局部态密度也会随之改变[18 ,19 ] . 通过对单层MoS2 中激子自发辐射速率的有效控制, 该珀塞尔效应能够实现峰值为9.5倍的PL增强效果. 随着激发光(探测光)的偏振方向与谐振腔长轴方向夹角的变化, 各点PL强度值具有清晰而强烈的偏振依赖性, 场强的空间分布与不同激发条件下的谐振腔模式分别对应, 证明了该增强结果来源于谐振腔中电场偶极子发射效应.2.光与物质耦合系统模型 22.1.理论模型 2.1.理论模型 为了定量分析单层MoS2 自发辐射速率的增强效果, 我们建立了MoS2 与谐振腔耦合的荧光增强系统(PES)模型. 假设MoS2 是大量激射偶极子发射体的集合, 且激子复合速率为辐射复合速率与非辐射复合速率之和, 即$\varGamma = {\varGamma _{{\rm{nr}}}} + {\varGamma _{\rm{r}}}$ . 在实验测量中, 由于谐振模式的PL强度与激发光功率呈线性关系, 说明自发辐射速率还未达到MoS2 的饱和程度. MoS2 的辐射功率P 与$P{}_{{\rm{in}}}A{\varGamma _{\rm{r}}}/\left( {{\varGamma _{{\rm{nr}}}} + {\varGamma _{\rm{r}}}} \right)$ 成正比, 这里P in 为激发光功率, A 为MoS2 在激发光波长处的吸收率. 由于${\varGamma _{{\rm{nr}}}} \gg {\varGamma _{\rm{r}}}$ 且光学探测角度有限, 在PES中可近似有$P \propto \eta {\varGamma _{\rm{r}}}/{\varGamma _{{\rm{nr}}}}$ , $\eta $ 为PL辐射的探测效率. 将激子视为衬底上MoS2 中的大量发射体, 本征自发辐射速率${\varGamma _0}\left( \lambda \right){\rm{d}}\lambda $ 对应到光谱$\lambda $ 到$\lambda + {\rm{d}}\lambda $ 后, 修正的自发辐射分布$\varGamma \left( \lambda \right){\rm{d}}\lambda $ 为$L\left( \lambda \right) = 1\bigg/\left[ {1 + 4{Q^2}{{\left( {\dfrac{\lambda }{{{\lambda _{{\rm{re}}}}}} - 1} \right)}^2}} \right]$ 为谐振模式的洛伦兹拟合谱线, Q 为谐振模式的品质因数, λ re 为中心谐振波长, $\psi = E \cdot \mu /(\left| {{E_{\max }}} \right|\left| \mu \right|)$ 为偶极子发射体μ 与谐振光场E 的空间角度重叠因子, F n ${F_{{\rm{re}}}} = \dfrac{3}{{4{{\text{π}} ^2}}}\dfrac{Q}{{{V_{\, od \, }}}}{\left( {\dfrac{{{\lambda _{{\rm{re}}}}}}{n}} \right)^3}$ 为最大自发辐射增强(珀塞尔)系数, V mod 为有效模式体积, n 为银材料的折射率.${I_{{\rm{re}}}}(\lambda )$ 在不同偏振角度$\varPhi $ 的变化规律, 可以由同时考虑修正的自发辐射速率、谐振模式探测效率以及泄露模式效率的PES进行分析. 通过将(1 )式在空间上和平面内发射体分布密度$\rho (r, \lambda , \mu )$ 进行积分可得到${\eta _{{\rm{re}}}}$ 和${\eta _n}$ 分别是谐振模式和非谐振模式的辐射PL与探测装置的耦合效率. 由于等离子体谐振腔的模式具有偏振依赖性, 不同激发角度下PL谱的增强倍数为2.2.实 验 -->2.2.实 验 单层MoS2 与谐振腔耦合系统(图1(a) 所示)采用CMOS工艺流程制作. 金属银层由电子束蒸镀过程沉积到石英衬底上表面, 通过聚焦离子束(FIB)技术刻蚀成蝴蝶结型等离子体谐振腔阵列即基于银层的刻蚀图案. 随后, 利用原子层沉积法在银层上表面生长一层3 nm厚度的二氧化硅隔离层, 用于防止单层MoS2 中光生载流子转移到下面的银层抵消荧光增强效果. MoS2 材料通过CVD法在隔离层上表面生长, 再经过拉曼光谱法和激射荧光光谱法验证为单层后转移到隔离层表面. 为得到最佳结构参数, 制备的谐振腔长度分别从L = 180, 220, 260, 300, 340, 380和420 nm等梯度变化, 如图1(b) 所示为研究对象的扫描电子显微图像, 长宽比约为2∶1. 通过电子倍增电荷耦合器件(EMCCD)预实验扫描, 选取与单层MoS2 荧光峰重叠效果最好的进行实验测量, 谐振腔尺寸约为340 nm × 180 nm. MoS2 在制备过程中的不均匀性导致出现了一些裂纹(条形纹理), 如图1(c) 所示.图 1 MoS2 与谐振腔耦合系统(样品)的(a)结构示意图, (b)扫描电子显微镜(SEM)图像和(c)光学图像Figure1. The MoS2 -cavity coupled system’s (a) structural diagram, (b) scanning electron microscope image, and (c) optical image.3.实验系统及测量 为了研究金属等离子体谐振腔对MoS2 的PL增强效应, 采用如图2(a) 所示的共焦显微系统进行测量. 波长为532 nm的单色激发光通过激发端的线偏振器和半波片组合, 使其能够以任意角度对MoS2 进行激发. 双色镜(反射波长范围在596 nm以上的光而透射596 nm以下的光)对激发光透射并通过100 × 的显微物镜(NA = 0.9)聚焦到样品上, 入射功率值为150 μW、光斑直径约为400 nm. 样品受激发后, 中心波长在670 nm附近的宽谱增强PL和小部分激发光将原路返回. 由于PL强度较微弱, 残留的激发光不能忽略, 双色镜使混合光通过532 nm的陷波滤光片后几乎只剩下PL, 最终通过探测端的半波片和线偏振器组合选择不同角度的PL进行探测. 本系统采用了三种探测装置: 1)商用光谱仪测量单层MoS2 材料激射前后的PL谱; 2) EMCCD用来扫描谐振腔阵列并寻找其中最优结构参数的谐振腔; 3)雪崩光电二极管(APD)测量PL增强前后的光子数. 图2(b) 所示为EMCCD扫描(空间步长为30 nm)谐振腔阵列得到的PL强度分布图: 叉形区域是没有分布MoS2 的区域, 光子数为背景噪声; 蓝色均匀区域为连续的单层MoS2 区域, 光子数为PL增强前的强度; 在中央区域可以看到明显的谐振腔阵列增强效果(也为蝴蝶结型), 光子数为连续MoS2 区域的7—9倍. 由于结构参数的梯度分布和制作工艺的不完美性, 每个金属等离子体谐振腔增强效果都不一致, 选择PL增强效果最好的谐振腔进行研究.图 2 (a)研究单层MoS2 PL增强效应的共焦显微系统装置图; (b) EMCCD得到的样品远场PL强度扫描图Figure2. (a) The con-focal microscope setup of measuring PL enhancement of monolayer MoS2 ; (b) the sample's far-field PL intensity image of EMCCD.4.讨 论 已有报道对蝴蝶结型等离子体谐振腔的谐振模式进行了仿真, 采用时域有限差分法(FDTD)得到不同激发条件下的电磁场分布[20 ] . 我们在实验中也得到了一致的规律: 当MoS2 辐射光(波长处于谐振腔传输谱内)的偏振方向与谐振腔长轴平行(如图3(a) 所示, Φ = 0°)时, 绝大部分光场能量(PL)位于几十纳米量级的间隙区域(中央区域), 而两侧区域只有很少部分, 为谐振模式1; 当辐射光偏振方向与长轴方向垂直(如图3(b) 所示, Φ = 90°)时, 会在两侧区域产生相对均匀分布的光场能量(PL), 而位于中央区域的能量非常少, 为谐振模式2. 由图3 可知, 模式2中更多激子(谐振区域面积大)产生自发辐射, APD的空间积分具有更多光子数. 虽然模式1中光子数较少, 但大多数光子都集中在更小的有效模式体积V mod (≈ 0.69(λ /n )3 )中, 因而具有更高密度的局部场, PL增强效果更加明显. 由于单层MoS2 与谐振腔的耦合作用, 后者平面内的辐射通道被非谐振模式所抑制, 垂直方向的自发辐射通道被谐振模式重新分布后由测量装置所接收. 在这两种情况下, 谐振模式将面内激子的辐射速率进行抑制, 有效提升垂直方向的自发辐射速率, 进而增强了单层MoS2 的PL强度.图 3 MoS2 辐射光偏振与谐振腔长轴方向在不同夹角 (a) Φ = 0° 和(b) Φ = 90°下得到的PL增强扫描图Figure3. The APD scanning images of MoS2 PL enhancement when the angles between the excitation light and resonator’s long-axis are (a) Φ = 0° and (b) Φ = 90°.图4(a) 和图4(b) 所示的光子数变化规律(散点所示), 这些曲线能够通过a cos2 θ + b 公式(虚线所示)很好地拟合.图 4 不同激发光(探测光)偏振角度下, 探测光(激发光)的光子数变化规律曲线 (a) Φ ex(co) = 0°; (b) Φ ex(co) = 90°Figure4. The photon counts of APD at different angle combinations of the excitation and detection lights: (a) Φ ex(co) = 0°; (b) Φ ex(co) = 90°.2 辐射PL最佳的增强条件. 图5(a) 所示为三种不同情形下利用光谱仪得到的PL谱线: 本征谱(单层MoS2 的PL谱, 蓝色实线), Φ ex = Φ co = 0°(模式1的PL增强谱, 绿色实线)和Φ ex = Φ co = 90°(模式2的PL增强谱, 红色实线). 由于模式1有效模式体积较小, 其对单层MoS2 PL强度的增强效果远大于模式2, 增强倍数的峰值达到9.5. 通过对比三条谱线, 谐振腔的中心谐振波长(~670 nm)比MoS2 PL中心波长(~680 nm)略短, 同时MoS2 PL增强谱线的整体上移说明谐振模式具有很宽的FWHM (~100 nm). 为标定谐振腔的模式1, 搭建了传输谱测量系统, 利用超连续谱光源(NKT SuperK Extreme)通过线偏振器和半波片组合、100 × 显微物镜(NA = 0.9)将光信号聚焦到谐振腔中央区域; 在样品背面还有一个60 × 油浸物镜(Olympus, Japan)与前方物镜准直在一条线上, 两者焦点相互重合. 在系统中, 样品表面的反射光沿入射光路返回, 探测物镜可收集其数值孔径内、散射在4π立体角中的近场谐振信号, 这样光谱仪得到的传输谱具有很高的信噪比(如图5(b) 所示, 内置图为样品测试局部图). 谐振模式的中心波长${\lambda _{{\rm{re}}}}$ 为667 nm, 品质因数Q 仅为6.7, 得到相应的珀塞尔因数为0.74. 根据图5(a) 中的PL谱线, 可以计算该谐振腔最大PL增强倍数曲线, 如图5(c) 所示. 在PES模型中, 通过谐振腔模式中谐振和失谐的偶极子远场辐射在物镜数值孔径内的积分, 得到该共焦显微系统中模式1的耦合效率${\eta _{{\rm{re}}}}/{\eta _n}$ 约为80%; 在模式激发区域, 仿真求得${(\left| E \right|\left| \mu \right|/\left| {{E_{\max }}} \right|\left| \mu \right|)^2}$ 的空间积分为0.8—0.9. 另外, 由于偶极子发射体在单层MoS2 中的指向随机分布, 与谐振腔场强的角度积分为0.5. 取Φ ex/co = 0°情况下峰值增强倍数为9.5时, 得到${F_n}$ 约为0.03. 如图5(c) 所示, PL增强的理论曲线(虚线所示)与实验数据(散点所示)达到了很好的拟合结果. 两者的差异主要来自以下原因: 1)采用洛伦兹型曲线拟合谐振模式的误差; 2)样品工艺制作时引入的不完美性; 3)建立理论模型时假设的近似条件等. 与图5(a) 中的PL增强谱相比, 谐振腔对二硫化钼中激子自发辐射速率和方向的进行了人为修正, 使得PL谱线形状得到重塑.图 5 (a)单层MoS2 在不同情形下的PL谱线; (b)等离子体谐振腔的传输谱; (c)实验中得到的最大PL增强倍数曲线Figure5. (a) The PL spectra of monolayer MoS2 in different cases; (b) the transmission spectrum of the plasmonic resonator; (c) the PL enhancement of the MoS2-cavity coupled system.2 的PL增强因数η 等于激发光增强因数η 1 与辐射PL增强因数η 2 的乘积. 第一, η 1 是由于激发光频率处于谐振腔谐振模式内, 可以提高光场密度激发更多的激子; 第二, η 2 是由于辐射的激子频率处于谐振模式内, 有更多的相同频率的激子被激发出来, 两种因素的综合效果实现了对自发辐射速率的调控. 受到客观条件限制, 实验中的激发光波长并没有位于谐振腔的传输谱中, 因而PL增强因数没有达到最佳结果. 以往报道中类似的蝴蝶结型等离子谐振腔虽然能够达到η = 1340倍的总体增强效果[17 ] , 但其η 2 仅为9.32, 比我们的值略低. 如果采用波长范围在600—630 nm之间的激发光源(与谐振中心波长接近, 同时光子能量大于单层MoS2 的能级差), 将得到更高的激发光增强因数η 1 , 使得光与物质相互作用增强的效果极大提升.5.结 论 证实了通过将单层MoS2 与等离子体谐振腔耦合, 谐振时可以较大程度地增强其内部量子跃迁效率. 实验测量和理论计算揭示了MoS2 自发辐射速率最大增强倍数为9.5、FWHM为100 nm的宽带增强谱线, 并实现了两者理想的吻合结果. 增强的PL强度还满足a cos2 θ + b 规律的偏振特性, 证明了谐振模式来自谐振腔中的电场偶极子和理论假设的合理性. 如果进一步优化激发光波长和谐振腔结构参数, 预计可以达到更高倍数的增强效果. 单层MoS2 中谐振腔增强的光与物质耦合作用将固态腔体电动力学扩展到原子层厚度二维材料中, 对非线性基础研究和光子学器件应用都具有重要价值. 
















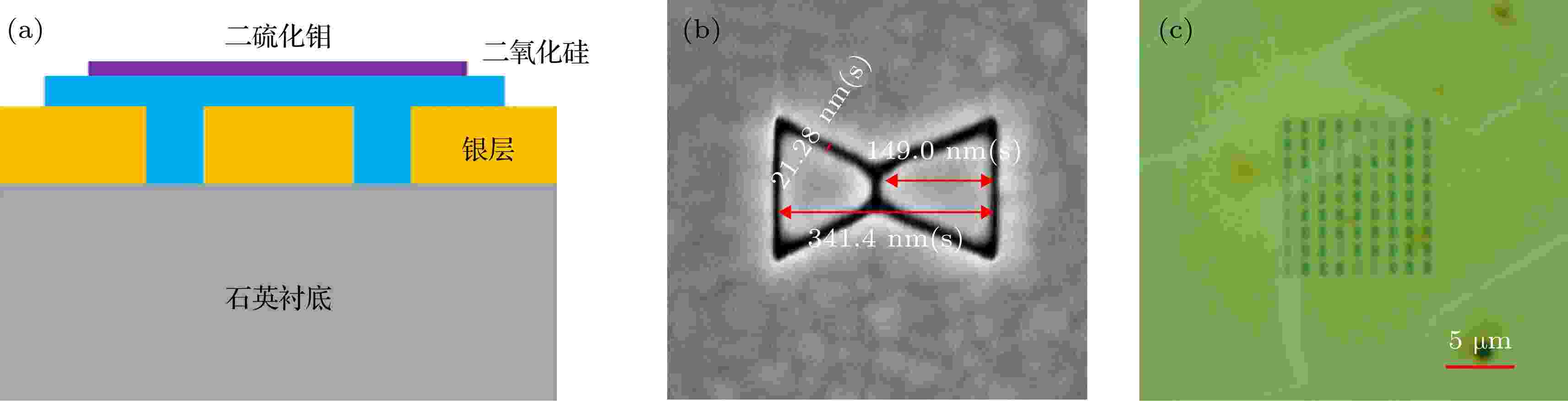 图 1 MoS2与谐振腔耦合系统(样品)的(a)结构示意图, (b)扫描电子显微镜(SEM)图像和(c)光学图像
图 1 MoS2与谐振腔耦合系统(样品)的(a)结构示意图, (b)扫描电子显微镜(SEM)图像和(c)光学图像 图 2 (a)研究单层MoS2 PL增强效应的共焦显微系统装置图; (b) EMCCD得到的样品远场PL强度扫描图
图 2 (a)研究单层MoS2 PL增强效应的共焦显微系统装置图; (b) EMCCD得到的样品远场PL强度扫描图 图 3 MoS2辐射光偏振与谐振腔长轴方向在不同夹角 (a) Φ = 0° 和(b) Φ = 90°下得到的PL增强扫描图
图 3 MoS2辐射光偏振与谐振腔长轴方向在不同夹角 (a) Φ = 0° 和(b) Φ = 90°下得到的PL增强扫描图 图 4 不同激发光(探测光)偏振角度下, 探测光(激发光)的光子数变化规律曲线 (a) Φex(co) = 0°; (b) Φex(co) = 90°
图 4 不同激发光(探测光)偏振角度下, 探测光(激发光)的光子数变化规律曲线 (a) Φex(co) = 0°; (b) Φex(co) = 90°



 图 5 (a)单层MoS2在不同情形下的PL谱线; (b)等离子体谐振腔的传输谱; (c)实验中得到的最大PL增强倍数曲线
图 5 (a)单层MoS2在不同情形下的PL谱线; (b)等离子体谐振腔的传输谱; (c)实验中得到的最大PL增强倍数曲线