拓扑光子学研究进展

全文HTML

--> --> -->

3.二维拓扑光子体系

3.1.基于二维拓扑光学系统的整数量子霍尔效应

-->

3.1.基于二维拓扑光学系统的整数量子霍尔效应

如前文所述, 光的整数量子霍尔效应的提出充分借鉴了凝聚态电子气体系的经验. Haldane和Raghu在提出光学体系量子霍尔效应时便是基于凝聚态物理中无质量的Dirac方程^[1]. 以类石墨烯体系为例, 它的能带在倒易空间的K与K′处形成具有线性色散关系的Dirac点, 这种高对称点附近的准粒子特性可以通过哈密顿量H_D来描述:

${H_{\rm{D}}}\left( {{k}} \right) = {v_x}{\sigma _x}{k_x} + {v_y}{\sigma _y}{k_y} + {\varDelta _m}{\sigma _z},$

这里的v_{x, y}为光的有效群速度, k = (k_Δ, k_y)为二维系统的倒易空间矢量, Δ_m为系统的有效质量. 当Δ_m = 0时, 描述为无质量的Dirac准粒子, 对应的贝利相位(Berry Phase)为 ± π. 而当Δ_m ≠ 0时, 描述为有质量的Dirac准粒子, 产生相应的带隙. 物理上, 可以通过对无质量体系引入旋磁材料来打破时间反演对称性, 原有的Dirac点所在的两个能带之间会形成一个与外加磁场相关的带隙, 从而产生光的量子霍尔效应. 它的拓扑不变量可以通过陈数来描述. 值得注意的是, 我们把一个2n维度系统所具有的陈数叫做第n陈数, 通常情况下所说的陈数为第一陈数, 描述的是二维动量空间的情况, 它的形式可以写为^[26]

${C_n} = \frac{1}{{2{\text{π}}}}\int_{{\rm{BZ}}} {{{\rm{d}}^2}{{k}}{\varOmega _n}\left( {{k}} \right)} ,$

其中${\varOmega _n}\left( {{k}} \right) = {\nabla _{{k}}} \times {{\cal A}_n}\left( {{k}} \right)$

为贝利曲率(Berry curvature), 而${{\cal A}_n}\left( {{k}} \right) = {\rm{i}}\left\langle {{\varphi _{n, {{k}}}}} \right|{\nabla _{{k}}}\left| {{\varphi _{n, {{k}}}}} \right\rangle $

为贝利联络(Berry connection), 根据斯托克斯公式不难发现陈数的值可以为0或其他整数值.
2008年, Wang等^[2]意识到构造线性色散Dirac点并非产生量子霍尔效应的必然条件, 他们利用忆铁石榴石铁氧体(YIG)的旋磁特性(即磁张量的非对角项μ_ij在外加磁场下不为零), 在具有四方点阵结构的光子晶体中构造出了陈数不为零的拓扑绝缘体, 并于2009年在实验上观测到背散射抑制的拓扑边界态^[3], 如图 3(a)和图3(b). 随后, Skirlo等^[4]利用铁磁光子晶体在高能带上设计并观测到了大陈数的拓扑绝缘体, 其相邻两条能带的陈数差大于1, 即: C_gap > 1, 对应于更多条数的边界态, 如图 3(c)和图3(d)所示. 这种效应在诸如光学耦合腔^[93,94]、光子晶体板^[95]、动态调制谐振器^[96]等不同的耦合平台上也被先后实现.

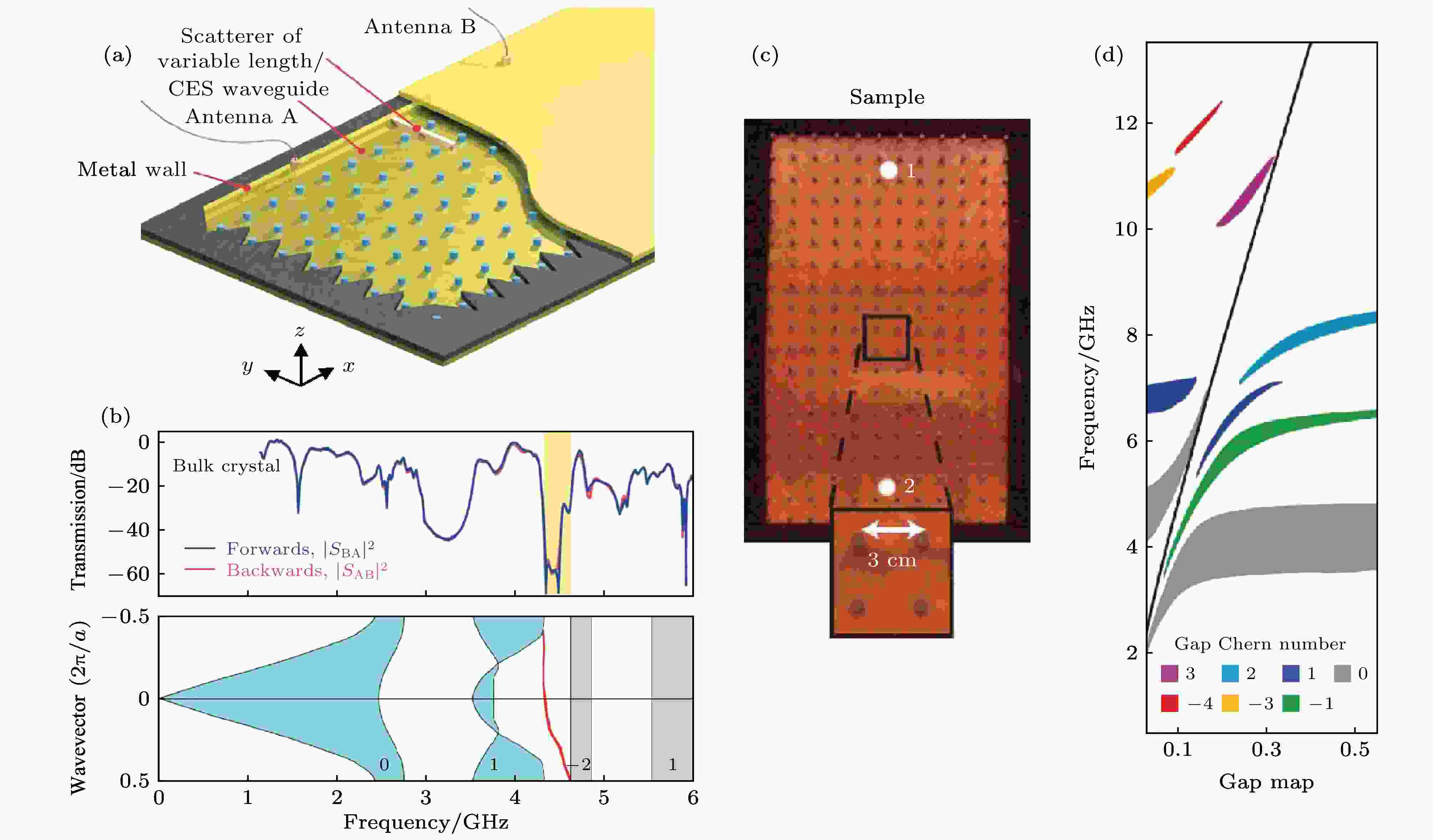图 3 (a) 旋磁光子晶体的示意图; (b) 向前向后的传输谱以及具有手性边界态的投影能带; (c) 大陈数光子晶体结构图; (d) 能带的带隙及其陈数
Figure3. (a) Schematic of the gyromagnetic photonic crystal; (b) forward and backward spectra, and projected band structures with chiral edge states; (c) the diagram of large Chern number photonic crystals; (d) the band gap map and their Chern number.

2

3.2.二维光量子自旋霍尔效应

-->

3.2.二维光量子自旋霍尔效应

拓扑光子学中的另一大类就是保持时间反演(或赝时间反演)对称性的量子自旋霍尔效应系统. 对电子系统来说, 由于电子本身具有 ± 自旋, 因此对于每一个自旋s都可以利用(5)式单独地指定一个陈数C_{↑, ↓}, 来表示有相应自旋的能带. 因此拓扑不变量可以用两种量表征, 一种是传统的陈数C, 另一种则是自旋陈数C_s.

$C = {C_ \uparrow } + {C_ \downarrow },$

${C_s} = \left( {{C_ \uparrow } - {C_ \downarrow }} \right)/2.$

由于广泛意义上系统仍然具有时间反演对称性, 所以陈数C = 0, 而自旋陈数C_s为整数值, 这种自旋陈数可以用来刻画量子自旋霍尔效应. 值得注意的是, 在仅有时间反演对称性的情况下, 自旋陈数不再存在明确的定义, 这时可以用$\mathbb{Z}_2$

拓扑不变量代替.
光子系统的自旋与电子的内禀自旋还是有很大不同的, 目前主要有三种方案来实现光子的自旋霍尔效应. 第一种方案是利用光子的偏振自由度. 2013年, 德克萨斯大学奥斯汀分校的Khanikaev等^[9]利用光的TE与TM偏振自由度, 构造了两种赝自旋态TE+TM与TE-TM. 通过控制偏振的耦合, 系统实现了自旋轨道的耦合并产生量子自旋霍尔效应. 然而这一工作没有说明时间反演对称性与此现象的关系. 2016年, 南京大学He等^[97]提出了一种基于压电(PE)—压磁(PM)超晶格的光子晶体模型, 并以左旋(LCP)和右旋(RCP)光为赝自旋态, 如图4(a)所示. 模型采用了四方晶格构型, 并保证了时间反演破缺, 而仅保存了电磁耦合与时间反演联合的对称性(赝时间反演对称性), 从而证实时间反演对称性本身也只是针对于固有的电场磁场系统, 即使时间反演对称性破缺, 光量子自旋霍尔效应仍然可以发生, 如图4(b)所示. (赝)自旋态的选取发生改变, 相应的(赝)时间反演对称性算符也可能发生改变, 这对理解时间反演对称性在光量子自旋霍尔效应中的角色起到了很大作用. 2014年, Chen等^[20] 利用微波超构材料在实验上观测到了以TE+TM和TE-TM为赝自旋态的量子自旋霍尔效应.

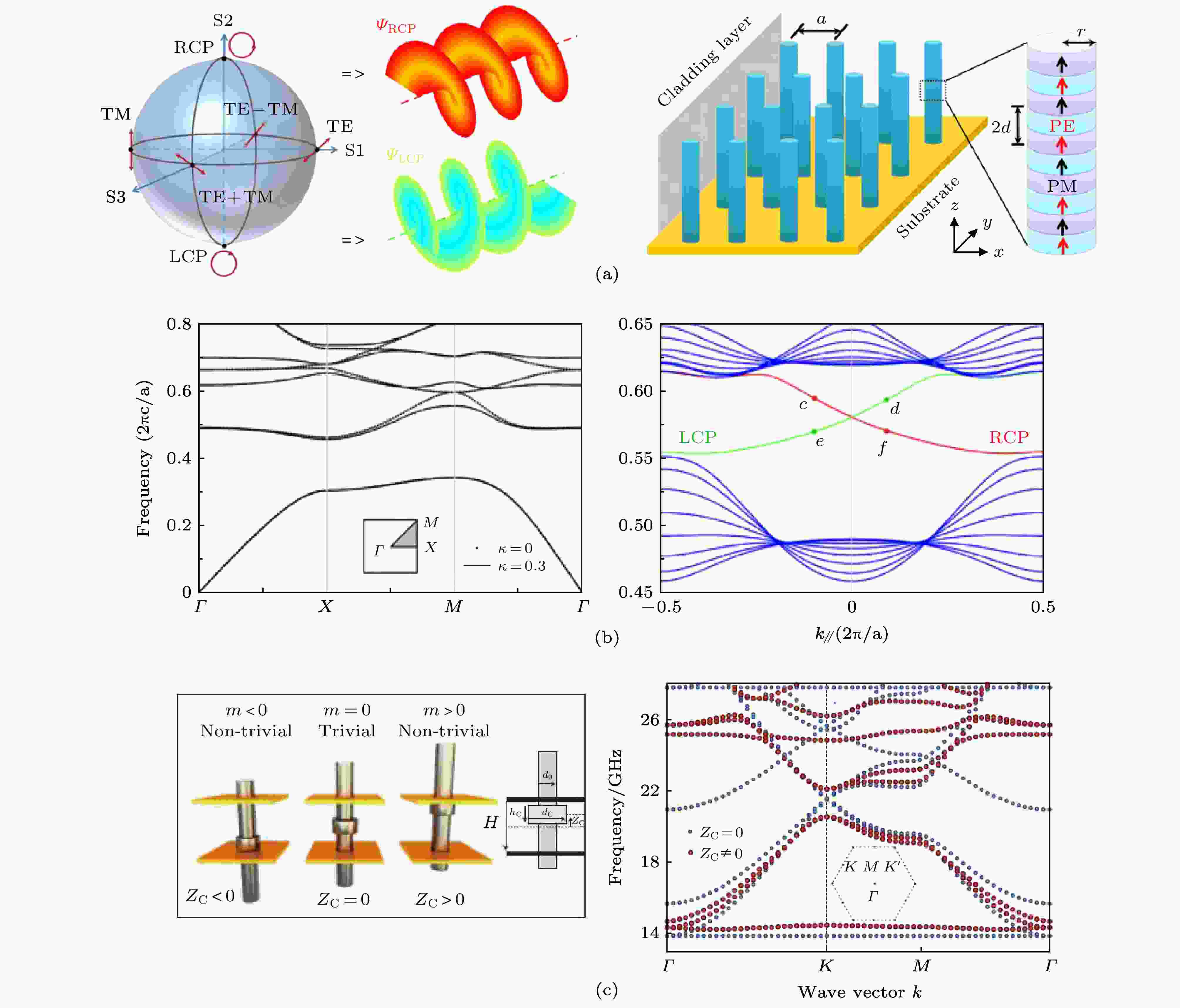图 4 (a) Poincaré球上的LCP和RCP, 以及由PE和PM材料构成的光子晶体; (b) 没有赝自旋耦合以及具有赝自旋耦合的能带以及后者的投影能带; (c) 通过调节金属柱子实现赝自旋的耦合
Figure4. (a) The polarization of LCP and RCP on the Poincaré sphere, and the photonic crystal consisting of PE and PM superlattices; (b) band structures without coupling between dseudospin states and with their coupling, and the projected band structures for the latter case; (c) photonic crystals consisting of metallic rods and collars at different positions, and their band strucutres.

第二种产生光量子自旋霍尔效应的方案是通过晶格对称性来实现, 这种方案最早由Wu和Hu^[6]在2015年提出. 如图 5所示, 对于同一类偏振态而言, 利用蜂窝结构的位于K和K'的狄拉克点以及能带折叠概念, 当柱子距中心距离为高对称的石墨烯参数时, 系统在Γ点实现四重简并的Dirac点. 而当结构距离参数发生改变时, Γ点双Dirac点发生去简并, 出现两两简并的p_x, p_y和d_xy, $d_{{x^2}-{y^2}} $

对称性模式. 利用对称和反对称模式, 他们构造了两种赝自旋态p_±和d_±, 并以此为基础构造出电磁波的拓扑绝缘体^[8]. 然而需要指出的是, 由于构成边界态波导的两侧布洛赫态并不完全一致, 因此本质上边界态的投影能带并不是严格无带隙的. 这一简单的设计构想先后在微波平台、光子晶体板以及超构表面等实验体系上得到了大量推广, 同时, 全介质的系统在应用上也具有很大的潜力.

图 5 (a) 全介质光子晶体结构; (b) 收缩、高对称以及扩张晶格所对应的能带; (c) 赝自旋依赖的边界态的实验观测
Figure5. (a) Schematic of all-dielectric photonic crystals; (b) band structures of shrinking and expanding lattices; (c) visualization of pseudospin-dependent edge states.

第三种方案是利用光在环形谐振腔体系的耦合来实现的. 通过控制光沿着谐振腔顺时针和逆时针传播的路径, 使得系统具有类比于电子自旋的自由度, 由于这样的系统天然保持了时间反演对称性, 因此可以类比于量子自旋霍尔效应. 如图6所示, Hafezi等^[22,33,98]利用耦合环将两个环形谐振腔相连并以此为单元构成周期耦合阵列, 提出并在实验上实现了具有自旋量子霍尔效应的光学腔传输边界态, 在单一自旋下具有单向传输且缺陷免疫的特性.

图 6 (a) 谐振腔耦合单元; (b) 周期排布形成的耦合阵列
Figure6. (a) Two coupled resonators in one unit cell; (b) a periodic array arranged by unit cells.

2

3.3.光Floquet拓扑绝缘体

-->

3.3.光Floquet拓扑绝缘体

通过在哈密顿量中引入时间调制或等效于时间的调制, 也可以使得材料产生新奇的拓扑特性, 通常这一类拓扑绝缘体被称为Floquet拓扑绝缘体. 2012年, Fang等^[16]将这一思想引入光子晶体体系, 从而实现了光学的Floquet拓扑绝缘体. 如图7(a)所示, 通过在光学谐振腔耦合阵列中引入耦合相关的动态调制${\rm{V}}\left( t \right) = {V_0}{\rm{cos}}\left( {\varOmega t + {\phi _{ij}}} \right)$

, 其中Ω为调制频率, ?_ij为两个格点间的调制相位, 原有的哈密顿量中周期调制的耦合系数则等效为一个有效磁场B_eff

图 7 (a) 光学谐振腔阵列的动态调制; (b) 激光直写波导系统的拓扑绝缘体构型; (c) 四种耦合组成的周期构型
Figure7. (a) The resonator lattice with dynamic modulation; (b) floquet topological insulators using the femtosecond laser writing method; (c) four different bonds with different coupling.

${B_{{\rm{eff}}}} = \frac{1}{{{a^2}}}\mathop \oint \nolimits^ {A_{{\rm{eff}}}}{\rm{d}}l = \frac{\phi }{{{a^2}}},$

这里a为晶格常数, A_eff为由于时间调制而引入的有效规范势, 且满足${\phi _{ij}} =\displaystyle\int_i^j {{A_{{\rm{eff}}}}{\rm{d}}l} $

. Fang等的设计依赖于电路的控制, 事实上, 在除了微波以外的系统中, 这种动态调控过程的实现还是有一定难度的. 2013年, Rechtsman等^[15]提出, 通过激光直写技术在耦合波导阵列中同样能够实现等效磁场, 从而构造出了光Floquet拓扑绝缘体. 如图7(b)所示, 傍轴传输的光波导系统在传输方向具有丰富的调控维度. 通过引入螺旋传输调节, 傍轴传输方程可以写为

$\begin{split}{\rm{i}}{\partial _Z}\psi ' =\, & - \frac{1}{{2{k_0}}}{\left( {\nabla ' + {\rm{i}}{{A}}\left( Z \right)} \right)^2}\psi '\\ &- \frac{{{k_0}{R^2}{\varOmega ^2}}}{2}\psi ' - \frac{{{k_0}\Delta n\left( {X,Y} \right)}}{{{n_0}}}\psi ',\end{split}$

其中X = x + Rcos(Ωz), Y = y + Rsin(Ωz), Z = z. ${{A}}\left( Z \right) = {k_0}R\varOmega \left[ {\sin \left( {\varOmega Z} \right), - \cos \left( {\varOmega Z} \right), 0} \right]$

为等效的规范势. 此时的本征值(或准能量)对应于传输方向的传播常数. 当R = 0时, 系统形成类似于石墨烯的Dirac点, 而当R > 0时, 能带简并被打开, 在波导阵列的边界处形成拓扑保护的边界态. 由于激光直写波导系统加工更为简单, 因此利用这一技术实现光学Floquet拓扑的方案更具现实意义. 2017年, Mukherjee等^[14]在一个传播周期内引入四种耦合方式同样构造出了具有手性边界态的Floquet拓扑绝缘体, 如图7(c)所示. 除此之外, 准晶构型^[34]以及网络模型的Floquet构型^[99]也不断被设计出.

4.三维拓扑光子体系

4.1.外尔(Weyl)点和节线(nodal-line)

-->

4.1.外尔(Weyl)点和节线(nodal-line)

类比于二维体系的Dirac点, 在三维系统中可以找到与之对应的点, 即外尔(Weyl)点, 它对应于在三维动量空间都具有线性色散的简并点. Weyl点附近的色散关系可以通过哈密顿量H_W表示

${H_{\rm{W}}}\left( {{k}} \right) = {v_x}{k_x}{\sigma _x} + {v_y}{k_y}{\sigma _y} + {v_z}{k_z}{\sigma _z},$

这里v_{x, y, z}为三个方向的群速度, k = (k_x, k_y, k_z)为三维的动量空间位置. 通过对包含Weyl点的二维平面进行贝利曲率的积分, 会发现在时间反演对称性和空间反演对称性都存在时, Weyl点对应的陈数为 ± 1. 如果空间反演对称性被破坏, 能带系统将至少存在4个Weyl点; 而当时间反演对称性被破坏, 系统则至少存在2个Weyl点. 当Weyl点附近的线性色散斜率足够大, 两个交叉的能带具有相同符号的群速度, 此时对应于第二类Weyl点. 2013年, Lu等^[100]通过打破时间反演对称性或空间反演对称性最先在双螺旋光子晶体体系中提出了Weyl点的设计, 如图8(a)所示, 然后2015年首次在微波波段观察到了这种现象^[101], Yang等^[102]于2018年利用微波超材料实现了更丰富的Weyl平台, 如图8(b)所示. 另外, 在光学晶格体系^[103,104]、磁化等离子体^[105]以及手性超构材料^[106]等体系中, Weyl点也不断地被构造出来研究三维光子晶体的体拓扑性质以及表面态(对应于Fermi弧等)输运性质.

图 8 (a) 能够产生Weyl点以及节线的双螺旋光子晶体; (b) 具有Weyl点的金属夹杂的光子晶体
Figure8. (a) Photonic crystals with two gyroid structures in one unit cell, and their band structures with Weyl points or nodal-line; (b) schematic of photonic crystals with the saddle-shaped metallic inclusion, and their Weyl points.

在三维体系中, 还存在一类奇特的简并点, 其能带沿着三维布里渊区的一条线简并形成所谓的节线(nodal-line). 这种节线在一定对称性保护下可以具备拓扑稳定性, 并且每个节线具有π的贝利相位. 例如, 一个简化的双能级的节线模型的哈密顿量可以表示为

${H_{\rm{N}}} = \left[ {k_0^2 - \left( {k_x^2 + k_y^2 + k_z^2} \right){\sigma _z}} \right] + {k_z}{\sigma _y}.$

此系统同时具有空间反演对称性(对应于操作算符${\sigma _z}$

)以及时间反演对称性(对应于复共轭算符$\hat \kappa $

), (11)式刻画了${k_z} = 0$

时, 在${k_x} - {k_y}$

平面存在闭合节线的系统, 这种系统的哈密顿量对应的贝利相位±π与二维Dirac点对应性质一致. 光子体系节线的设想同样是Lu等^[100]于2013年提出的, 之后Lin等^[107]研究发现节线同样可以存在于二维光子晶体系统中. 节线系统的表面态受螺旋旋转和时间反演对称性的保护, 并且具有非零的陈数. 除此之外, 节点链^[108,109]、节点连接^[110]、节点结^[111]概念等也在不断的探索与研究之中.
2

4.2.三维光学拓扑绝缘体

-->

4.2.三维光学拓扑绝缘体

在三维光子晶体体系中, 拓扑绝缘体产生的关键在于利用拓扑简并点(例如Weyl点和Dirac点)得到三维k空间中的非平庸能带带隙, 从而支持各种拓扑界面态. 截至目前, 已提出的三维光学拓扑绝缘体机制主要有三维光整数量子霍尔效应、三维光量子自旋霍尔效应等. 三维光整数量子霍尔效应可以通过三个第一陈数刻画, 即${C^{(1)}} = \big( {C_x^{\left( 1 \right)}, C_y^{\left( 1 \right)}, C_z^{\left( 1 \right)}} \big) $

, 其对应于单向传输且缺陷免疫的无能隙界面态. 2018年, Lu等^[112]提出在Weyl双螺旋光子晶体中, 通过引入超元胞的能带折叠机制将一对Weyl点折叠成一个三维Dirac点, 再利用外加磁场作用于构成光子晶体的磁性材料, 从而产生了由于Dirac点退简并导致的拓扑带隙, 形成三维Chern拓扑绝缘体, 相应的陈数可表示为(0, 0, 1). 值得注意的是, 由于要保证第一陈数的存在, 这种系统中时间反演对称性的破缺是必要的.
三维光量子自旋霍尔效应则是通过直接构造Dirac点来实现, 这种方案最早由Slobozhanyuk等^[113,114]于2016年提出, 他们将双各向异性超构材料组合成新的光子晶体, 利用电场和磁场之间的交错耦合, 构造出了新的赝自旋自由度, 如图9(a)所示. 通过控制三维结构的空间分布, 高对称点处的Dirac点被打开, 实现了拓扑保护的界面态, 如图9(b)所示. 2019年, Yang等^[115]在三维光子超材料中, 利用金属劈裂环谐振腔(SRRS)操纵Dirac点的打开, 也实现了微波频段的三维拓扑绝缘体. 在三维光量子自旋霍尔效应的设计中, 还存在一种由旋磁材料光子晶体构造Dirac点的情况, 其拓扑带隙的打开需要引入外加磁场, 如图9(c)所示. 然而由于光频段材料对磁场的响应十分有限, 因此这种设计在实验上存在一定难度并且在应用上也存在很大限制^[116].

图 9 (a) 三维全介质与双各向异性光子晶体; (b) 两种构型的光子晶体对应的能带; (c) 通过引入磁场破缺Dirac点的光子晶体构型
Figure9. (a) 3 D all-dielectric and bianisotropic metacrystals; (b) band structures corresponding to two structures in (a); (c) photonic crystals with opened Dirac points when magnetization is applied on rods.

事实上, 通过操纵三维晶格对称性, 光子晶体有可能实现Z₂拓扑绝缘体所具有的特点, 这种拓扑晶体绝缘体最早由Fu^[117]于2011年提出. 2017年, Ochiai^[118]利用三维立方光子晶体, 提出了偶然简并导致的无能隙的界面态. 至此, 产生三维拓扑绝缘体的各种机制的探索、相应拓扑保护的界面态传输特性的研究变得越来越清晰.

5.光子学领域的新拓扑效应

5.1.非厄米拓扑光子效应

-->

5.1.非厄米拓扑光子效应

在光子系统中引入增益与损耗相比在电子体系中具有更大优势, 例如增益材料在光能量补偿及光场放大中发挥着重要作用, 而所有光学器件都不可避免地具有光子的损耗. 通过在光学系统中引入增益和损耗, 传统光学系统可以从非厄米性的视角进行分析与设计, 将会为系统带来更为丰富的物理性质. 目前, 非厄米体系的研究主要基于两点, 其一是拓扑相以及体边对应关系的探索, 另一方面是非厄米体系对称性的研究, 主要为宇称时间反演对称性(PT symmetry). 为了便于讨论, 这里从简单的阶梯模型出发^{[35, 119]}. 如图10(a)所示, 当考虑非厄米的引入时, 系统的哈密顿量可以写作

图 10 (a) 动量空间中的奇异点以及具有增益损耗的紧束缚模型; (b) 具有增益损耗的波导阵列; (c) 具有奇异环的光子晶体板结构
Figure10. (a) Exceptional points in momentum space, and the tight-binding model with gain and loss for α_i and β_i; (b) the waveguide array with gain and loss; (c) photonic crystal slabs with the ring of exceptional points.

${H_{\rm{N}}}\left( k \right) = {h_x}\left( k \right){\sigma _x} + \left( {{h_z}\left( k \right) + {\rm{i}}\gamma /2} \right){\sigma _z},$

这里的γ为实参数, 控制着哈密顿量非厄米的自由度, ${h_x}\left( k \right) = v + r{\rm{cos}}\left( k \right)$

, ${h_z}\left( k \right) = r{\rm{sin}}\left( k \right)$

, 其中v和r也都为实数, 不难发现在$\left( {{h_x}, {h_z}} \right) = \left( { \pm \gamma /2, 0} \right)$

处出现了奇异点(Exceptional Point, 也称为EP点), 即能带实部虚部完全简并的点. 这种构型可以通过在紧束缚模型的单个元胞中引入增益和损耗实现, 如图10(a)所示.
(12)式中的哈密顿量与PT算符对易. 如果所有哈密顿量的本征值也是PT算符的本征值, 此时的本征值将为实数. 值得注意的是, 此模型具有一个只存在于系统一端的零能边界态, 这与厄米系统中的体边对应关系(分数绕数)有所不同, 是非厄米矩阵出现缺陷的结果. 2015年, Zhen等^[120]将光子晶体板的辐射损耗视为材料损耗, 在此体系中观察到了由奇异点构成的环. 此工作展示了非厄米的引入在能带和群速度调控中的重要作用, 如图10(c)所示. 2017年, Weimann等^[121]利用一维激光直写波导阵列实现了非厄米体系的拓扑保护的边界态, 如图10(b)所示, 展示了非厄米性在具有增益(或损耗)的边界态传输上的应用前景. 直至最近, 宾夕法尼亚大学Zhao等^[122]提出, 利用耦合环形谐振腔阵列, 在同一种拓扑相结构的内部, 当边界两侧引入的增益损耗之差超过奇异点时, 边界上可以实现可重构的单向手性拓扑边界态, 这展示了非厄米的引入对拓扑边界态调控的巨大影响.
在这些新奇的物理效应不断被发现之际, 相应的拓扑分类与体边对应关系也变成研究者非常关心的问题. 目前提出的非厄米体系拓扑分类方式主要有以下两种. 一种方式是2018年由Shen等^[48]提出的, 将能带分为可分离的(即对于所有m ≠ n和k, 本征值都满足${E_n}\left( k \right) \ne {E_m}\left( k \right)$

)、孤立的(即对于所有m ≠ n和k(k′), 本征值都满足${E_n}\left( k \right) \ne {E_m}\left( {k'} \right)$

)和不可分离的(即在某些动量空间上两条能带的复数本征值发生简并)几种构型分别对应于可以产生带隙, 全带隙以及无带隙能带的哈密顿量系统. 在此情况下, Shen等提出了推广的二维系统中的陈数概念, 并对一维情况进行了新的分类. 有趣的是关于后者, 系统的拓扑不变量取决于哈密顿量的本征值而不是本征态. 另一种拓扑分类方式是对所有非厄米系统做一个统一的分类, 这种分类是基于两个重要的假设^[123], 第一是非厄米体系的拓扑相可以理解为与本征值的虚部相关的动力学相位; 第二是非厄米体系带隙概念的推广, 即广义的带隙可以理解为能带的实部与虚部都无简并. 然而由其得到的一个主要结论就是二维系统中不存在非厄米拓扑相, 这与其他的工作结论较为不同^[48]. 由此可见, 目前提出的这些分类方式仍然具有诸多挑战, 可以总结为三点: 其一是如何定义一个复数能带的全带隙, 虽然以上给出一些方案, 但由于复数没有大小之分, 目前仍然缺乏统一的标准; 其二是边界条件对边界态的影响极为敏感, 单纯从能带出发定义整个体系仍然具有较大挑战; 其三是在一个有序的非厄米体系中, 或许存在所有的态都异常的局域在边界上的状况^[119,124], 诸多类似的异常现象缺乏深层次的统一的物理图像. 即使遇到以上问题, 但由于非厄米光子体系更高自由度的调控特性与潜在的应用前景, 目前在非厄米光学结构的设计与实验^{[41,42,45-47,49,125,126]}以及相关理论上的探索^[40,43,127]方面仍然不断有新的工作出现.
2

5.2.非线性拓扑光子效应

-->

5.2.非线性拓扑光子效应

非线性光学是近代光学的重要分支, 对光谱技术、成像技术以及光学信息处理技术的发展具有重要的意义. 半经典的非线性过程可以通过在麦克斯韦方程中引入非线性项实现, 是电极化矢量对电场的非线性响应的结果, 可以表示为^[128,129]

${{P}} \!=\! {\varepsilon _0}\left( {{\chi ^{\left( 1 \right)}} \cdot E + {\chi ^{\left( 2 \right)}}:EE + {\chi ^{\left( 3 \right)}} \vdots EEE + \cdots } \right),$

其中χ⁽¹⁾为传统的线性响应, 表现为折射率特性. χ⁽²⁾为二阶磁化率, 是诸多二阶非线性的源头, 例如二次谐波、参量下转换等. χ⁽³⁾为三阶磁化率, 产生的效应有四波混频、三次谐波、非线性折射率等. 目前大部分光子晶体非线性效应的引入都是基于χ⁽²⁾与χ⁽³⁾项. 最近将光学非线性和拓扑物理相结合, 从而实现更丰富的光学效应越来越引起人们的研究兴趣^{[13,17,51,54,57-60,130]}. 以引入类克尔非线性的SSH模型为例^[60], 如图11(a)所示, 这种非线性薛定谔方程可以描述为

图 11 (a) 非线性SSH模型; (b) 与光强度相关的环绕数(贝利相位); (c) 将量子比特与它们的耦合器铺成二维格子的示意图; (d) 包含三个超导量子比特的超导回路
Figure11. (a) The nonlinear SSH model; (b) the winding number (Berry phase) changed by intensity; (c) schematic diagram of qubits and their couplers in 2 D lattice; (d) the superconducting circuit including three qubits.

${\rm{i}}\frac{{{\rm{d}}{\psi _n}}}{{{\rm{d}}t}} = \varOmega {\psi _n} + {{{K}}_m}\left( n \right){\psi _{n - 1}} + {{{K}}_p}\left( n \right){\psi _{n + 1}},$

其中${\psi _n} = {\left[ {{a_{1, n}}, {a_{2, n}}} \right]^{\rm{T}}}$

, $\varOmega = \left[ {{\omega _0}, v;v, {\omega _0}} \right]$

, ω₀和v分别描述了单位元胞中谐振腔的本征频率与元胞内两个格点间的耦合系数. 元胞之间的耦合表示为矩阵${{{K}}_m}\left( n \right) = \big[ {0, {\kappa _0} + \alpha \big( {{{\left| {{a_{1, n}}} \right|}^2} + {{\left| {{a_{2, n - 1}}} \right|}^2}} \big);0, 0} \big]$

和${{{K}}_p}\left( n \right) = \big[ {0, 0;{\kappa _0} + \alpha \big( {{{\left| {{a_{1, n + 1}}} \right|}^2} + {{\left| {{a_{2, n}}} \right|}^2}} \big), 0} \big]$

, 其中κ₀ > 0为线性耦合项, α ≥ 0为类克尔非线性系数. 如图11(b)所示, 当光场强度增强, 此模型经历了从拓扑平庸系统到无能隙系统再到拓扑非平庸系统的转变. 这种弱非线性效应在Floquet^[17]、非厄米^[130]以及光隔离系统^[58]也有一系列的重要成果.
当非线性效应很强时, 系统会展现出光子的离散特征, 需要用量子的手段描述. 在强非线性光子拓扑效应中, Rydberg-EIT(电磁感应透明)配置的包含一致性原子气体的非平面腔^[131]以及强非线性作用的超导QED回路^[132]是两个的重要平台. 例如, 2011年Reinhard等^[133]利用片上集成的QED腔, 展示了基于量子强非线性效应的光子阻塞效应, 即在单模非线性谐振腔中, 满足空腔共振模式的入射光束, 当第一个光子自由地进入腔体后, 对第二个光子来说有效谐振频率将会发生偏移, 使得只有第一个光子离开后第二个才能进入. 将光子阻塞效应与人工合成势场相结合, 就产生了丰富的强非线性拓扑光子效应. 2016年, Roushan等^[132]利用超导量子比特与耦合器(超导QED回路)构造出有效的晶格结构, 实现了合成磁场与粒子间的强相互作用. 通过正弦调制比特间的耦合来引入人工磁场, 可以在三个比特构成的回路中观测到打破时间反演对称性的光子定向流动, 这种设计为强相互作用的量子相位调控构造了一个有效的平台. 2018年, Jia等^[131]将Rydberg EIT与光学谐振腔相结合, 前者提供了针对单光子非线性的原子传感器, 而后者则加强了光与物质的相互作用, 由此证实了第一个强相互作用的极化子量子点, 为拓扑多光子态的制备提供了思路. 由于光子的寿命相对较长, 实验中只需在起始时制备单光子和双光子的Fork态^[132,134], 之后在没有泵浦的情况下测量光子的演化即可, 相关的实验与理论还在不断的发展与完备之中.
2

5.3.高阶拓扑光子效应

-->

5.3.高阶拓扑光子效应

通常认为, 一个N维的拓扑光子体系其拓扑边界态为N-1维, 这使得我们在局域场维度上的调控十分有限. 最近研究表明, 一些拓扑绝缘体具有$ N-1,?N-2,?\cdots,?N-m-1 $

维的有能隙边界态, 直到最后一个维度N-m的边界态, 我们把这种拓扑绝缘体叫做m阶拓扑绝缘体. 这种设想在凝聚态物理中由紧束缚模型构造出^[65], 2018年Peterson等^[74]提出了微波体系中的高阶拓扑绝缘体, 然而这种设计需要引入负耦合机制, 在光学系统中很难广泛推广. 同年, 南京大学Xie等^[75]首次提出了能够在传统全介质光子晶体结构中实现的二阶拓扑绝缘体, 这种设计结构简单, 能够在二维光子晶体中实现一维边界态和零维拐角态. 如图12(a)所示, 其能带可以用2D的SSH模型描述

图 12 (a) 介质柱构成的二维SSH模型的光子晶体; (b) 收缩、高对称与扩张晶格构型的能带结构; (c) 由收缩区域包围扩张区域构成的整体结构, 解的序号与本征频率的关系; (d) 实验中放于一个角的源激发的拐角态
Figure12. (a) Photonic crystals of the 2D SSH model consisting of dielectric pillars; (b) band structures of shrinking, high symmetry and expending structures; (c) shrinking supercells contain expanding supercells, and the relationship between solution numbers and eigenfrequencies; (d) experimentally measured corner states when the source is placed at the corner.

$H\left({{k}} \right) = \left(\!\!\!\begin{array}{*{20}{c}}0&{{h_{12}}}&{{h_{13}}}&0\\{h_{12}^*}&0&0&{{h_{24}}}\\{h_{13}^*}&0&0&{h_{24}^*}\\0&{{h_{34}}}&{h_{34}^*}&0\end{array}\!\!\!\right),$

这里${h_{12}} = {h_{34}} = {t_1} + {t_2}{\rm{exp}}\left( {{\rm{i}}{k_x}a} \right)$

, ${h_{13}} = {h_{24}} = {t_1} + $

${t_2}{\rm{exp}}\left( { - {\rm{i}}{k_y}a} \right) $

, 而${{k}} = \left( {{k_x}, {k_y}} \right)$

. 其中t₁, t₂为元胞内部和元胞与元胞之间的耦合强度. 当晶格格点位于高对称点处时, 其能带发生简并, 而当结构发生收缩或扩张时, 能带发生打开并分别构成拓扑平庸与拓扑非平庸的能带结构, 如图12(b)所示. 这种二维体系拓扑不变量是通过2D的Zak相位刻画的:

${P_i} = - \frac{1}{{{{\left( {2{\text{π}}} \right)}^2}}}\int_{{\rm{BZ}}} {{{\rm{d}}^2}k{\rm{Tr}}\left[ {{{\hat {\cal A}}_i}} \right]} ,\;i = x,y,$

其中${\left( {{{\hat {\cal A}}_i}} \right)_{mn}}\left( k \right) = {\rm{i}}\left\langle {{\varphi _m}\left( k \right)} \right|{\partial _{{k_i}}}\left| {{\varphi _n}\left( k \right)} \right\rangle $

, 由此构造了二分量的2D的Zak相位P = (P_x, P_y). 拓扑平庸的能带对应于P = (0, 0)的拓扑不变量, 而拓扑非平庸的能带对应于P_x或P_y为1/2. 利用拓扑平庸构型将方形区域的非平庸构型(P = (1/2, 1/2))包裹, 由此可以得到具有关联的拐角态. 在这种设想提出的同年, 南京大学Xie等^[76]利用微波波段光子晶体在实验上观测到了能够同时在四个拐角激发的拐角态, 如图12(c)和图12(d)所示. 相关理论提出不久, 便在不同的体系引起了广泛的兴趣, 随后在光子晶体板^[135], 光子晶体微腔^[136]等体系不断地有新的工作出现. 高阶拓扑绝缘体为实现具有拓扑保护的光学局域态调控提供了新的研究思路.

6.总结与展望

拓扑光子学的发展与传统光子学研究与凝聚态物理中物质拓扑相的研究息息相关. 本文简要地介绍了拓扑光子学领域的若干基本概念以及主要研究进展, 从拓扑光子体系的维度出发介绍了一维体系中SSH模型的拓扑描述方法和应用, 二维体系的光整数量子霍尔效应、光量子自旋霍尔效应以及Floquet拓扑绝缘体, 三维无能隙系统的Weyl点和节线以及三维拓扑绝缘体. 另外, 针对当前拓扑光子学领域的发展趋势, 对非厄米拓扑光子学、非线性拓扑光子学以及高阶拓扑绝缘体进行了简要的介绍与探讨.
光子体系与凝聚态物理中的电子等体系相比, 无论从结构设计, 还是调控方式, 均具有更高的自由度, 在某些方面能够构造出与其他自然材料体系相比更为完美的物理模型以及测量到更加丰富的物理量. 因此, 拓扑光子学已经成为研究拓扑物理机制的重要平台. 并且, 从光场操控角度而言, 具有拓扑保护的、背向散射抑制的边界态以及高阶拓扑态, 在光学输运、场维度调控以及量子的光学传输等方面都有巨大的基础研究和应用前景.
当然, 目前拓扑光子学领域也面临一些挑战, 其中很重要的一方面是集成化拓扑光子器件的挑战, 通信波段的光子器件与现有的硅基半导体工艺相结合将在光通信、光计算方向具有较大前景, 然而中红外甚至更短波长的应用波段使得拓扑光子器件需要做得更小, 这受制于微纳加工工艺以及拓扑结构设计; 另一方面是可调谐性的挑战, 可调谐拓扑光子体系的构建受制于光学材料的特性, 通常光学材料可以通过热光、电光、声光以及磁光等方式调控, 然而它们在调制速率、调制幅度等方面都具有各种局限性; 此外是理论与设计上的挑战, 例如在非厄米系统体边对应关系、三维(或更高维度)光子拓扑绝缘体和高阶拓扑绝缘体等方面仍有许多亟待研究的问题.

本站小编 Free考研考试/2021-12-29

English Abstract

Research progress of topological photonics

Corresponding author:Lu Ming-Hui, luminghui@nju.edu.cn

全文HTML

3.1.基于二维拓扑光学系统的整数量子霍尔效应

3.2.二维光量子自旋霍尔效应

3.3.光Floquet拓扑绝缘体

4.1.外尔(Weyl)点和节线(nodal-line)

4.2.三维光学拓扑绝缘体

5.1.非厄米拓扑光子效应

5.2.非线性拓扑光子效应

5.3.高阶拓扑光子效应

相关话题/光子 系统 光学 材料 结构

领限时大额优惠券,享本站正版考研考试资料!

拓扑半金属材料角分辨光电子能谱研究进展

拓扑材料等离激元谱学研究

光子驱动量子点制冷机

双凹型谐振腔结构的金属半导体纳米激光器的数值仿真

微光学元件宽带光源照明下无色散边界条件探讨

半导体激光器储备池计算系统的工作点选取方法

氮化物子带跃迁探测器材料结构对器件效率的影响

基于正交偏振场的双光学控制方案获得孤立阿秒脉冲产生

薄膜与Helmholtz腔耦合结构低频带隙

塑料类高分子聚合物材料水中目标声学参数反演