删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

淬火动力学中的拓扑不变量

本站小编 Free考研考试/2021-12-29
摘要:本文主要介绍了近期关于一维拓扑能带系统中淬火动力学的研究. 从两能带模型入手介绍了动力学陈数, 并给出它与初末态拓扑不变量之间的关系. 进而通过将一维含时波函数看作为1 + 1维母哈密顿量的基态, 给出了Altland-Zirnbauer分类对应的动力学拓扑分类, 并简要介绍了动力学的体边对应以及空间无序和能带色散对纠缠谱交叉的影响. 最后还介绍了利用超导量子比特模拟观测到动力学陈数.
关键词: 拓扑相变/
淬火动力学

English Abstract


全文HTML

--> --> -->
1.引　言
1980年整数量子霍尔效应的发现开启了拓扑量子物态研究的大门[1,2]. 不同于传统的量子物态, 拓扑物态不存在局域的序参量, 而是由波函数的几何或拓扑性质决定, 且可以用拓扑不变量来描述. 在有能隙的系统中, 人们对于拓扑能带系统的分类和性质的研究已经有了系统的方法和深刻的认识[3,4,5]. 然而目前关于拓扑物态的研究大都集中在研究系统基态波函数的性质, 对于远离平衡态过程的拓扑性质的认识还非常不足. 近年来, 由于冷原子技术的迅速发展, 已经能够模拟许多重要的拓扑模型, 如一维Su-Schrieffer-Heeger(SSH)模型[6—11], 这为进一步探索它们的非平衡性质提供了有力的工具.
一类典型的远离平衡态的过程就是淬火动力学. 在$ t\leqslant 0 $时系统的波函数$ |\varPsi_{\rm i}\rangle $处于哈密顿量$ H^{\rm i} $的基态, 在$ t = 0 $时刻突然改变哈密顿量的某些参数, 即淬火, 这样初态波函数按照新哈密顿量$ H^{\rm f} $做幺正演化. 这里有两点需要特别指出: 首先, 淬火过程分为局域的淬火和全局的淬火, 对局域的淬火, 系统参数的改变局限在有限的尺度内, 而对全局的淬火, 哈密顿量的参数在整个系统内都发生了改变, 本文中仅研究全局淬火; 其次, 淬火前后哈密顿量的性质原则上没有任何约束, 作为一种最简单的特例, 我们要求初末态哈密顿量具有相同的对称性. 在这些限制下, 我们关心在波函数$ |\varPsi(t)\rangle $中是否有拓扑性质的体现.
对波函数$ |\varPsi(t)\rangle $拓扑性质的研究仍然有三种不同的方法. 第一种直观的思路是研究在每一个固定时刻t波函数本身的拓扑性质. 这也是到目前为止最常用的方法. 例如, 在陈绝缘体中, 系统的陈数在淬火后会保持不变, 这也被称为NO-GO定理[12,13]. 从一个平庸的态出发, 可以制备出的量子态能多接近于拓扑非平庸的态[14,15]. 最近Cooper等还证明了在淬火动力学过程中只有幺正对称性会被保持, 反幺正的对称性会在含时演化中被破坏, 这被称作动力学诱导的对称性破缺[16]. 进一步, 当只考虑幺正对称性时, 我们可以研究系统在每个时刻t的拓扑性质并可以给出拓扑分类[16,17]. 第二种方法是将时间和空间放在一起研究$ (D+1) $维波函数的拓扑性质. 在研究二维陈绝缘体中的淬火动力学时, 翟荟研究组首先注意到这个动力学过程可以看作$ (k_x, k_y, t) $到Bloch球上的映射, 它可以由Hopf不变量或连环数描述, 并且若初态为拓扑平庸态, Hopf不变量就等于演化哈密顿量$ H^{\rm f} $的陈数[18,19], 紧接着Weitenberg等通过在实验中观测到了动力学涡旋与静态涡旋的连环数[20]. 我们研究组系统地研究了一维拓扑系统的淬火动力学, 定义了动力学陈数, 并指出动力学陈数与初末态哈密顿量拓扑不变量之间的关系[21], 随后同实验组合作在超导量子比特模拟实验中观测到了动力学陈数和动力学量子相变的特征[22]. 另外, Ueda研究组利用K理论也给出了$ (1+1) $维系统的拓扑分类和动力学实现. 并且指出当初态为拓扑平庸态时, 这个动力学拓扑不变量意味着纠缠谱的演化在某些时刻会有交叉, 这可以看作动力学的体边对应[23]. 第三种方法是研究布里渊区中的能带反转面(BIS), 通常它为$ (D-1) $维, 刘雄军研究组注意到初态为拓扑平庸态时, 演化哈密顿量$ H^{\rm f} $的拓扑性质由在能带反转面上定义的缠绕数得到[24—26], 并在冷原子实验中被观测到[27].
这三种方法从不同的角度给出了初态波函数$ |\varPsi_{\rm i}\rangle $在含时演化时的性质, 尽管它们之间存在一些关联, 但它们并不等价. 另外需要指出, 在研究系统拓扑性质时需要要求哈密顿量是局域的, 但在时间演化过程中, 系统的关联不断传播, 等效哈密顿量将不再局域, 因此我们要求时间尺度小于$ L/v_{\rm LR} $, 其中$ v_{\rm LR} $是Lieb-Robinson速度[28,29]. 在这篇综述中, 我们主要利用第二种方法讨论$ (1+1) $维系统的拓扑性质.
本文首先从两能带模型入手, 介绍淬火动力学过程中动量时间流形的结构, 定义了动力学陈数, 并指出动力学陈数与初末态拓扑数之间的关系. 接着给出更普遍情况下$ (1+1) $维系统的动力学拓扑分类和体边对应, 即纠缠谱演化过程中出现的交叉, 接着简要分析纠缠谱交叉受空间无序和能带色散的影响. 最后介绍利用单量子比特模拟淬火动力过程, 直观看到动力学陈数的几何意义.
2.一维二能带系统中的动力学拓扑不变量
我们首先以一维二能带系统为例, 讨论它的动力学拓扑不变量. 动量空间中的哈密顿量可写为
$ h(k) = d_0(k){ I}+{ d}(k)\cdot{{\sigma}}, $
其中泡利矩阵$ {\sigma} $作用在(赝)自旋$ 1/2 $的空间, 其本征值为$ E_{\pm}(k) = d_0(k)\pm|{ d}(k)| $, 对应的本征态记为$ |\psi_{\pm}(k)\rangle $, 因此密度矩阵可表示为
$ \hat{\rho}_{\pm}(k) = |\psi_{\pm}(k)\rangle\langle\psi_{\pm}(k)| = \frac{1}{2}[1\pm\hat{{ d}}(k)\cdot{ \sigma}], $
其中$ \hat{{ d}}(k) = {{ d}(k)}/{|{ d}(k)|} $是归一化的Bloch矢量. 尽管一维有能隙的系统的基态一定是拓扑平庸的, 但当对称性存在时, 系统可以有对称性保护的拓扑态. 对无相互作用费米子, 在由时间反演对称性, 粒子空穴对称性和手征对称性组成的Altland-Zirnbauer分类拓扑分类表中, 系统的拓扑不变量有$ {\mathbb Z} $和$ {\mathbb Z}_2 $两类[30,31,32], 它们均可由Bloch矢量$ \hat{{ d}}(k) $求出. 将系统制备成初态哈密顿量$ h^{\rm i} $的基态, 即$ \rho^{\rm i}(k) = [1-\hat{{ d}}^{\rm i}(k) \cdot{\sigma}] /2$, 在$ t = 0 $时刻开始用淬火的哈密顿量$ h^{\rm f} $进行演化, t时刻系统的密度矩阵为
$ \rho(k,t) = {\rm e}^{-{\rm i} h^{\rm f}(k)t}\rho(k,0){\rm e}^{{\rm i} h^{\rm f}(k)t}. $
如果将t时刻的密度矩阵写为
$ \rho(k,t) = \frac{1}{2}[1-\hat{{ d}}(k,t)\cdot{ \sigma}], $
直接计算可以得到Bloch矢量$ \hat{{ d}}(k, t) $为[21]
$\begin{split}\hat{{ d}}(k,t) =\, & \hat{{ d}}^{\rm i}\cos(2|{ d}^{\rm f}| t) + 2\hat{{ d}}^{\rm f}(\hat{{ d}}^{\rm i}\cdot\hat{{ d}}^{\rm f})\\& \times \sin^2(|{ d}^{\rm f}| t) + \hat{{ d}}^{\rm i}\times{\hat{{ d}}}^{\rm f}\sin(2|{ d}^{\rm f}| t),\end{split}$
其中$ \hat{{ d}}^{\rm i}(k) $和$ \hat{{ d}}^{\rm f}(k) $分别是初态和末态哈密顿量的Bloch矢量.
对于平带化的哈密顿量, 不同的动量模式具有相同的周期$ {{\text{π}} }/{|{ d}^{\rm f}|} $, 动量时间流形为$ T^2 = S^1\times S^1 $, 如图1(a)所示. 更进一步, 如果动量空间中存在一些不动点满足$ { d}^{\rm i}(k_{\rm c}) $和$ { d}^{\rm f}(k_{\rm c}) $共线, 对于这些$ k_{\rm c} $, Bloch矢量除了一个整体的相位将不会演化, 因此将这些$ k_{\rm c} $称为不动点. 如图1(b)所示的$ k_1 $和$ k_2 $. 在这些不动点上, 时间轴可以连续的收缩为一点, 将动量时间流形约化为了一系列的球面$ S^2 $. 如果布里渊区内有N个不动点, 则动量时间流形将约化为N个球面. 在每一个球面上, 密度矩阵可以看作从动量空间子流形$ S^2 $到Bloch球的映射, 因此我们可以定义动力学陈数
图 1 (a) 每个截面对应固定动量, 截面内的极角对应于时间. 橘黄色的环代表$k=0$和$2{\text{π}} $, 它们粘合起来组成了$T^2$; (b) 如果动量空间中存在一些不动点$k_1$, $k_2$, 截面的时间可连续收缩为一个点, 动量时间流形约化成一系列球面[21]
Figure1. (a) For any fixed momentum k, the cross section can be viewed as a circle $S^1$ where the azimuthal angle represents the time t. After gluing $k=0$ and $k = 2{\text{π}} $ (saffron circles), the topology of the momentum-time manifold becomes $T^2$; (b) if there are two fixed points $k=k_1$ and $k_2$, the corresponding circle contracts to a point, then the momentum-time manifold reduces to a series of spheres $S^2$[21].

$ C_{\rm dyn}^{m} = \frac{1}{4{\text{π}} }\int_{k_m}^{k_{m+1}}{\rm d} k\int_{0}^{\textstyle\frac{{\text{π}} }{|{ d}^{\rm f}|}}{\rm d}t^{\prime} (\hat{{ d}}\times\partial_{t^{\prime}} \hat{{ d}})\cdot\partial_k, \hat{{ d}} ,$
其中$ k_{m} $表示第m个不动点而$ m = 1, 2, \cdots, N $, 直接计算得到
$ C_{\rm dyn}^{m} = \frac{1}{2}(\cos\theta_{k = k_{m}}-\cos\theta_{k = k_{m+1}}). $
其中$ \theta(k) $为$ \hat{{ d}}^{\rm i}(k) $和$ \hat{{ d}}^{\rm f}(k) $的夹角. 从(7)式可以看出如果初态制备成$ h^{\rm f} $的基态, 用$ h^{\rm i} $做幺正演化, 系统具有相同的动力学陈数.
根据Altland-Zirnbauer分类, 一维二能带系统拓扑非平庸类有BDI, AIII和D. 其中BDI和AIII类具有手征对称性, 对于BDI和AIII类, 不动点的个数存在下限$ 2 |n^{\rm i}-n^{\rm f}| $, 相应的非平庸陈数的个数M也存在下限$ 2 |n^{\rm i}-n^{\rm f}| $, 其中$ n^{\rm i} $和$ n^{\rm f} $分别是初末态哈密顿量$ h^{\rm i} $和$ h^{\rm f} $的缠绕数, 由于静态哈密顿量的拓扑分类为$ {\mathbb Z} $, 因此由$ 2 |n^{\rm i}-n^{\rm f}| $决定的动力学拓扑分类也是$ {\mathbb Z} $. 而D类的具有粒子空穴对称性系统的不动点为$ k = 0 $和$ k = {\text{π}} $[33], 因此对称性保护的不动点个数为$ 2 |n^{\rm i}-n^{\rm f}| $, 此时$ n^{\rm i} $, $ n^{\rm f}\in\{0, 1\} $是系统的$ {\mathbb Z}_2 $不变量, 因此由$ 2 |n^{\rm i}-n^{\rm f}| $决定的动力学拓扑分类也是$ {\mathbb Z}_2 $. 特别的, 由于系统所有动力学陈数之和为0, 我们仅需考虑子流形$ (k, t)\in $$(0, {\text{π}} )\times(0, {{\text{π}} }/{|{ d}^{\rm f}|}) $对应的动力学陈数$ C_{\rm dyn}^{1} $. 则可以证明若$ h^{\rm i} $和$ h^{\rm f} $位于同一个相, 动力学陈数$ C_{\rm dyn}^{1} = 0 $; 若$ h^{\rm i} $和$ h^{\rm f} $位于不同的相, 动力学陈数$ C_{\rm dyn}^{1} = \pm 1 $. 综上所述, 对BDI、AIII和D类, 非平庸动力学陈数的个数均只依赖于初末态哈密顿量拓扑数之差.
现在, 我们以两个例子展示动力学陈数. 首先我们考虑SSH模型[34], $ d_x = (1+\delta)+(1-\delta)\cos k $, $ d_y = (1-\delta)\sin k $, 其中$ \delta < 0 $时系统的基态是拓扑非平庸的, 而$ \delta > 0 $时基态是拓扑平庸的. 哈密顿量具有时间反演对称性$ Kh(k)K = h(-k) $和手征对称性$ \sigma_z h(k)\sigma = -h(k) $, 属于BDI类. 容易看出对于任意的初末态$ \delta^{\rm i} $和$ \delta^{\rm f} $, 系统只有两个不动点$ k = 0 $和$ k = {\text{π}} $. 布里渊区被分为$ k\in(0, {\text{π}} ) $和$ k\in({\text{π}}, 2{\text{π}} ) $. 若$ \delta^{\rm i} $和$ \delta^{\rm f} $同号, Bloch矢量满足$ \hat{{ d}}^{\rm i}(0) = \hat{{ d}}^{\rm f}(0) $和$ \hat{{ d}}^{\rm i}({\text{π}} ) = \hat{{ d}}^{\rm f}({\text{π}} ) $. 跟据(7)式有动力学Chern数为$ C_{\rm dyn}^1 = C_{\rm dyn}^2 = 0 $, 非平庸的Chern数个数为$ 0 = $$2 |n^{\rm i}-n^{\rm f}|$. 另一方面, 若$ \delta^{\rm i} $和$ \delta^{\rm f} $异号, Bloch矢量满足$ \hat{{ d}}^{\rm i}(0) = \hat{{ d}}^{\rm f}(0) $和$ \hat{{ d}}^{\rm i}({\text{π}} ) = -\hat{{ d}}^{\rm f}({\text{π}} ) $, 动力学Chern数为$ C_{\rm dyn}^1 = -1 $和$ C_{\rm dyn}^2 = 1 $, 非平庸Chern数的个数为$ 2 = 2 |n^{\rm i}-n^{\rm f}| $. 我们在考虑推广的p波超导模型[33,35], $ d_x = \varDelta_2\sin\phi\sin 2 k $, $ d_y = \varDelta_1\sin k+\varDelta_2\cos\phi\sin 2 k $, $ d_z = -t_1\cos k\!- \!t_2\cos 2 k\!+\!\mu $, 此处$ t_1(t_2) $和$ \varDelta_1(\varDelta_2 {\rm e}^{{\rm i}\phi}) $分别是最(次)近邻格点的跃迁强度和p波配对强度, $ \mu $是化学势, 次近邻跃迁带有的相位破坏了系统的时间反演对称性. 为了方便我们取$ \varDelta_1 $ = t1 = 0.5, $ \varDelta_2 = t_2\equiv \varDelta $, $ \phi = {{\text{π}} }/{2} $以及$ \mu = 1 $. 此时若$ 0.5 < \varDelta < 1.5 $时, 基态是拓扑超导态; 若$ \varDelta < 0.5 $或$ \varDelta > 1.5 $时, 基态是普通超导态. 容易看出Bloch矢量在不动点满足$ \hat{{ d}}(k = 0) = (0, 0, {\rm sgn}(0.5-\Delta)) $和$ \hat{{ d}}(k = {\text{π}} ) = (0, 0, {\rm sgn}(1.5-\varDelta)) $. 利用(7)式容易验证当初末态在同一个相时$ C_{\rm dyn}^{1} = \pm 0 $, 而初末态处在不同相时$ C_{\rm dyn}^{1} = \pm 1 $.
3.(1 + 1)维系统的动力学拓扑分类
在第2节中我们直观的讨论了一维二能带系统的动力学拓扑不变量, 这一节中, 我们用更一般的方法计算$ (1+1) $维系统的动力学拓扑分类. 我们记初末态平带化的哈密顿量为$ \tilde{h}^{\rm i}(k) $和$ \tilde{h}^{\rm f}(k) $满足$ h^{\rm i2}(k) = h^{\rm f2}(k) = 1 $, 于是可以定义母哈密顿量
$ \tilde{h}(k,t) = {\rm e}^{-{\rm i}\tilde{h}^{\rm f}(k)t}\tilde{h}(k)^{\rm i }{\rm e}^{{\rm i}\tilde{h}^{\rm f}(k)t}, $
系统的波函数$ |\psi(k, t)\rangle $是母哈密顿量的瞬时本征态, 化学势位于$ \mu = 0 $. 由矩阵指数公式直接计算得到[23]
$\begin{split} \tilde{h}(k,t) =\, & \frac{1}{2}\bigg\{\tilde{h}^{\rm i}(k)+\tilde{h}^{\rm f}(k)\tilde{h}^{\rm i}(k)\tilde{h}^{\rm f}(k)\\ &+ \bigg[\tilde{h}^{\rm i}(k)-\tilde{h}^{\rm f}(k)\tilde{h}^{\rm i}(k)\tilde{h}^{\rm f}(k)\bigg]\\& \times\cos(2t)+ {\rm i} [\tilde{h}^{\rm i}(k),\tilde{h}^{f}(k)]\sin(2t)\bigg\}, \end{split}$
可以看出平带化的母哈密顿量满足$ \tilde{h}(k, t+{\text{π}} ) = $$ \tilde{h}(k, t) $. 特别的, 对二能带系统, 母哈密顿量为$ \tilde{h}(k, t) = -\hat{{ d}}(k, t)\cdot{ \sigma} $, 而$ \hat{{ d}}(k, t) $即(5)式.
进一步利用(9)式, 我们从平衡态哈密顿量的对称性得到$ (1+1) $维母哈密顿量的对称性
$ \begin{split} & T \tilde{h}^{\rm i(f)}(k) T^{-1} = \tilde{h}^{\rm i(f)}(-k),\\ & T \tilde{h}(k,t) T^{-1} = \tilde{h}(-k,-t), \\ &C \tilde{h}^{\rm i(f)}(k) C^{-1} = -\tilde{h}^{\rm i(f)}(-k),\\ & C \tilde{h}(k,t) C^{-1} = -\tilde{h}(-k,t), \\ &\varGamma \tilde{h}^{\rm i(f)}(k) \varGamma^{-1} = -\tilde{h}^{\rm i(f)}(k),\\ & \varGamma \tilde{h}(k,t) \varGamma^{-1} = -\tilde{h}(k,-t). \end{split} $
这里我们直接将对称性算符记号T, C和$ \varGamma $用在了母哈密顿量中, 而将时间看作额外维度的准动量, 然而它们并不是真正的时间反演对称性, 粒子空穴对称性和手征对称性的. 根据文献[16]中可知只有粒子空穴对称性在含时演化中会保持, 时间反演对称性和手征对称性都将被破坏. 根据文献[36,37,23]中的方法, 母哈密顿量的拓扑分类可利用K群$ K_{\rm C}^{\rm U/A}(K_{\rm R}^{\rm U/A}) $得到, 如表1所示. 可以看出A、AI和AII类中母哈密顿量的对称性与AZ分类相同, 具有相同的拓扑不变量.
AZ class TRS PHS CS $(s, t, d, d_{//}, \text{original~class,} P)$ $K_{\rm C}^{\rm U/A}(K_{\rm R}^{\rm U/A})$ Dynamical realization Stable against dispersion
A 0 0 0 $(\sim, \sim, 2, \sim, A, \sim)$ ${\mathbb Z}$ 0 0
AIII 0 0 1 $(0, 1, 2, 1, A, \bar{U})$ ${\mathbb Z}\bigoplus{\mathbb Z}$ ${\mathbb Z}$ 0
AI 1 0 0 $(\sim, \sim, 2, \sim, AI, \sim)$ 0 0 0
BDI 1 1 1 $(0, 3, 2, 1, AI, \bar{A}_{+}^{+})$ ${\mathbb Z}$ ${\mathbb Z}$ ${\mathbb Z}_2$
D 0 1 0 $(2, \sim, 2, 1, A, \bar{A}^{+})$ ${\mathbb Z}_2$ ${\mathbb Z}_2$ ${\mathbb Z}_2$
DIII –1 1 1 $(4, 1, 2, 1, AII, \bar{A}_{+}^{+})$ ${\mathbb Z}_2\bigoplus{\mathbb Z}_2$ ${\mathbb Z}_2$ 0
AII –1 0 0 $(\sim, \sim, 2, \sim, AII, \sim)$ ${\mathbb Z}_2$ 0 0
CII –1 –1 1 $(4, 3, 2, 1, AII, \bar{A}_{+}^{-})$ ${\mathbb Z}$ ${\mathbb Z}$ 0
C 0 –1 0 $(6, \sim, 2, 1, A, \bar{A}^{-})$ 0 0 0
CI 1 –1 1 $(0, 1, 2, \sim, AI, \bar{A}_{+}^{-})$ 0 0 0


表1母哈密顿量$\tilde{h}(k, t)$的拓扑分类. TRS、PHS、CS分别是时间反演对称性, 粒子空穴对称性和手征对称性. s, t, d, $d_{//}$, 额外对称性P参见文献[37]; original class是没有额外对称性时系统的拓扑分类. $K_{\rm C}^{\rm U/A}(K_{\rm R}^{\rm U/A})$是系统的K群. Dynamical realization表示在淬火动力学中存在的拓扑分类. Stable against dispersion指能带存在色散时纠缠谱交叉能够稳定存在的拓扑分类
Table1.Topological classification of parent Hamiltonian. TRS, PHS and CS represent the time reversal symmetry, particle hole symmetry and chorial symmetry, respectively. The definition of s, t, d, $d_{//}$ and additional symmetry P can be found in Ref.[37]. Original class represents the topological classification without additional symmetry. $K_{\rm C}^{\rm U/A}(K_{\rm R}^{\rm U/A})$ is the K group. Dynamical realization means the topological classes which can be realized in quench dynamics. Stable against dispersion means entanglement spectrum crossing which is stable against band dispersion.

尽管我们得到了母哈密顿量的拓扑分类, 但对于淬火动力学过程, 只有部分拓扑等价类能够实现. 对于A类, 系统的拓扑不变量为陈数, 利用(9)式可得系统的陈数为$ 0 $, 因此动力学分类为$ {\mathbb Z}\rightarrow 0 $. 对于AIII类, 系统在高对称点$ t_{\rm s} = 0, {\text{π}} $满足$ \{\tilde{h}(k, t_{\rm s}), \varGamma\} = 0 $, 因此可以定义缠绕数n = $ \dfrac{1}{4{\text{π}} {\rm i}}\displaystyle\int {\rm d} k\; {\rm Tr}[\varGamma \tilde{h}(k, t_{\rm s})d\tilde{h}(k, t_{\rm s})] $. 根据文献[38], 系统的拓扑不变量分别为陈数和高对称点处缠绕数之差, 因此动力学分类为$ {\mathbb Z}\bigoplus{\mathbb Z}\rightarrow {\mathbb Z} $. 利用(9)式可得
$ n = 2(n^{\rm i}-n^{\rm f}), $
其中$ n^{\rm i} $和$ n^{\rm f} $是初末态哈密顿量的缠绕数. 特别的, 若系统只有两个能带, 这里的两个独立的拓扑数分别分别对应上一节中的动力学陈数之和与非平庸动力学陈数个数的下限. 类似的, 对于BDI和CII类, 时间反演对称性保证系统陈数为0[23], 动力学分类即K群$ {\mathbb Z}\rightarrow{\mathbb Z} $, 系统的拓扑不变量为高对称点处缠绕数之差, 即(11)式. 对于AII类, 系统拓扑不变量为Fu-Kane不变量[39], Moore和Balents提出它等价于三部分陈数之和$ C_{\rm Tot} = C_{\rm L}+C_{BZ^{\frac{1}{2}}}+C_{\rm R} $[40], 其中$ C_{BZ^{\frac{1}{2}}} $是半布里渊区$ BZ^{\textstyle\frac{1}{2}} = (k, t)\in(0, {\text{π}} )\times(0, {\text{π}} ) $上的陈数, 而$ C_{\rm L} $和$ C_{\rm R} $分别是将$ BZ^{\textstyle\frac{1}{2}} $的两个边界收缩为一点时补上的陈数. 利用(9)式可直接求得系统总的动力学陈数是拓扑平庸的, 即动力学分类为$ {\mathbb Z}_2\rightarrow 0 $. 类似地, 对于D类可以得到总的陈数
$ C_{\rm Tot}({\rm mod}\,2) = \frac{1}{2}|N^{\rm f}-N^{\rm i}|, $
其中$ N^{\rm i(f)} = \dfrac{1}{2}|{\rm sgn}\, {\rm Pf}[{\rm i} h^{\rm i(f)}({\text{π}} )]- {\rm sgn}\, {\rm Pf}[{\rm i}h^{\rm i(f)}(0)]| $, 系统的动力学分类为$ {\mathbb Z}_2\rightarrow{\mathbb Z}_2 $. 特别地, 如果系统只有两个能带时, 在$ k = 0 $和$ k = {\text{π}} $点是不动点, 动量时间流形自然的收缩为一点, 不需要额外的收缩过程, 因此拓扑不变量(12)式等价于上一小节中D类的动力学陈数$ C_{\rm dyn}^{1} $. 最后, 由AIII类和AII类可以得到DIII类动力学拓扑分类为$ {\mathbb Z}_2\bigoplus {\mathbb Z}_2\rightarrow {\mathbb Z}_2 $, 拓扑不变量也为(12)式.
4.动力学体边对应与无序
平衡态哈密顿量存在体边对应, 体态的拓扑性质在开边界下等于边界态的个数[41]. 对于平带化的哈密顿量, 开边界下系统的能谱也是基态的单粒子纠缠谱[42], 因此我们通过系统纠缠谱的演化来研究动力学体边对应. 对于费米子二次型 H = $ \displaystyle\sum\nolimits_{ij}h_{ij}\hat{c}_{i}^\dagger \hat{c}_{j} $, 其中$ i, j $是格点指标, 系统的基态记为$ |\varPsi\rangle $. 我们将系统分为子系统A和环境B, 则子系统的约化密度矩阵为$ \rho_{\rm A} = {\rm Tr}_{\rm B} (|\varPsi\rangle\langle\varPsi|) = \dfrac{1}{Z_{\rm A}}{\rm e}^{-H_{\rm A}} $, 其中纠缠哈密顿量$ H_{\rm A} $仍为费米子二次型, 它的本征值记作$ \varepsilon_n $. 此外我们将子系统关联矩阵$ C_{ij} = \langle\varPsi|c_{i}^{\dagger}c_{j}|\varPsi\rangle $的本征值$ \xi_n $定义为单粒子纠缠谱, 则有$ \xi_n = {1}/({e^{\varepsilon_n}+1})$[43,44].
在淬火动力学演化的过程中, 系统波函数仍然是高斯态, 因此瞬时波函数的单粒子纠缠谱可以写为:
$ \xi_n(t) = \frac{1}{{\rm e}^{\varepsilon_n(t)}+1}, $
其中纠缠谱$ \xi_n(t) $是瞬时关联矩阵$ C_{ij}(t) = $$\langle\varPsi(t)|c_{i}^{\dagger}c_{j}|\varPsi(t)\rangle $的本征值, $ \varepsilon_n(t) $是瞬时纠缠哈密顿量的本征值. 容易看出纠缠哈密顿量若存在零模$ \varepsilon_n(t) = 0 $, 则纠缠谱存在模$ \xi_n(t) = {1}/{2} $. 有了单粒子纠缠谱进而可以得到多体纠缠谱为[42]
$ \lambda_{\{s_n\}} = \prod_n \Big[\frac{1}{2}+s_n \Big(\xi_n-\frac{1}{2}\Big)\Big],\; \; \; \; s_n = \pm 1, $
从此式可以看出纠缠哈密顿量的零模意味着多体纠缠谱的简并.
下面我们以SSH模型为例, 初态$ \delta^{\rm i} = 1 $为拓扑平庸的, $ \delta^{\rm f} $取不同值时纠缠谱的演化见图2(a). 从图中看出, 若末态也是拓扑平庸的, 纠缠谱在含时演化过程中能隙始终打开, 然而若末态哈密顿量是拓扑非平庸的, 则纠缠谱会在某时刻发生交叉, 此时在系统虚拟的边界会存在纠缠哈密顿量的边界态. 对于拓扑超导系统, 纠缠谱的交叉意味着子系统宇称发生了改变, 整个周期内有奇数个电子从子系统流向外部[45,46]. 为了确定系统的动力学拓扑分类, 我们可以考虑多条链的耦合. 我们用平带化的末态哈密顿量进行时间演化, 对于$ {\mathbb Z} $类系统, 纠缠谱交叉时刻的简并度正比于链数, 而对于$ {\mathbb Z}_2 $类系统, 纠缠谱是否会出现交叉仅仅依赖与链数目的奇偶性[23].
图 2 (a) SSH模型, 初态$\delta^{\rm i}=1$为拓扑平庸的, 末态$\delta^{\rm f}$取不同的值. 仅当末态为拓扑非平庸时, 纠缠谱在$1/2$处有交叉; (b)扩展的SSH模型, 次次次近邻跃迁具有相位, 系统属于AIII类. 蓝色的线代表用平带化的哈密顿量进行动力学演化, 红色的线代表由真实末态哈密顿量进行演化. 可以看出能带的色散打开了纠缠谱的能隙
Figure2. (a) In SSH model, the initial state of $\delta^{\rm i}=1$ is topologically trivial, evolution of entanglement spectrum for different post-quenched $\delta^{\rm f}{\rm{s}}$ are shown with different colors. If and only if the post-quenched Hamiltonian is topologically nontrivial, the entanglement spectrum can cross at $1/2$; (b) in Extended SSH model, the third-nearest-neighbor hopping carries a phase factor, and the Hamiltonian belongs to class AIII. The blue curve shows the dynamics of entanglement spectrum evolved by flattened Hamiltonian, and the red curve shows the dynamics evolved by entanglement spectrum of real Hamiltonian. It can be seen that the band dispersion opens the gap of entanglement spectrum.

我们知道对于平衡态拓扑系统, 若在实空间中加入弱的无序时, 只要不破坏系统的对称性则其边缘模依旧存在. 在淬火动力学中, 无序既可以出现在实空间, 也可以出现在频率空间, 末态哈密顿量的色散即可看成一种频率空间的无序[23]. 特别地, 如果系统的能带具有色散, 对称性关系(10)式不再成立, 根据文献[16], 只有反幺正对称性才能在含时演化中继续存在, 幺正对称性在含时演化中将被破坏, 这也被称作动力学诱导的对称性破缺, 因此只有粒子空穴对称性在含时演化中能够保持. 进一步由于我们考虑的是纠缠的边界态, 能带色散使得时间反演对称性和手征对称性在边界处无法保持对称性, 系统的动力学对称性被破坏. 这类似于空间群对称性保护的拓扑态中体边对应的破缺[5,47,48]. 于是AIII类和CII类的动力学拓扑性质不能在能带有色散时稳定存在; D类的拓扑性质不受能带色散影响; 对于BDI类, 能谱的色散使得高对称线$ t = 0 $和$ t = {\text{π}} $变得动量依赖, 两条高对称线可以连续形变, 这使得高对称线上缠绕数之差允许模2改变, 从而系统稳定的动力学分类为$ {\mathbb Z} \rightarrow {\mathbb Z}_2 $; 最后DIII类通过数值验证能带色散会导致纠缠谱能隙打开, 稳定的动力学分类为$ {\mathbb Z}_2\rightarrow 0 $. 最后我们以AIII类为例展示了能带色散对纠缠谱能隙的影响. 我们将SSH模型加上次次近邻跃迁[46], 哈密顿量为$ d_x = (t_0+\delta)+(t_0-\delta)\cos k+J\cos(2 k+\phi) $, $ d_y = (t_0-\delta)\sin k+J\sin(2 k+\phi) $. 为了方便我们固定$ t_0 = 0.75 $, $ J = 0.2 $和$ \phi = 0.5{\text{π}} $, 初态取为$ \delta^{\rm i} = 0.25 $, 基态是拓扑平庸的, 末态取$ \delta^{\rm f} = -0.25 $, 基态是拓扑非平庸的. 纠缠谱的演化如图2(b)所示, 可以看出能带的色散打开了纠缠谱的能隙, 动力学拓扑性质不再存在.
5.实验测量
超导Xmon量子比特是研究量子模拟和量子计算的一个非常有前景的实验平台[49—51], 这一小节简要介绍由单量子比特模拟淬火动力学的过程[22]. 对于每个固定的动量k, 通过外加脉冲制备出初态哈密顿量的基态, 在时间t改变外加脉冲实现淬火过程, 如图3(a)所示, 通过态层析测量可以得到Bloch矢量的演化[52]. 实验中布里渊区取了$ 30 $个点, 相当于系统尺寸$ L = 30 $, 一个时间周期内有$ 70 $离散的步长, 每个步长为15 ns, 因此整个周期的演化时间为$ 1.05$ μs, 每一次态层析测量是$ 5000 $次测量的平均. 系统能量的弛豫时间为T1 = 8.3 μs, 失相时间为$ T_{2*} = 6.8$ μs, spin echo的失相时间为$ T_{\rm 2 se} = 11.7$ μs.
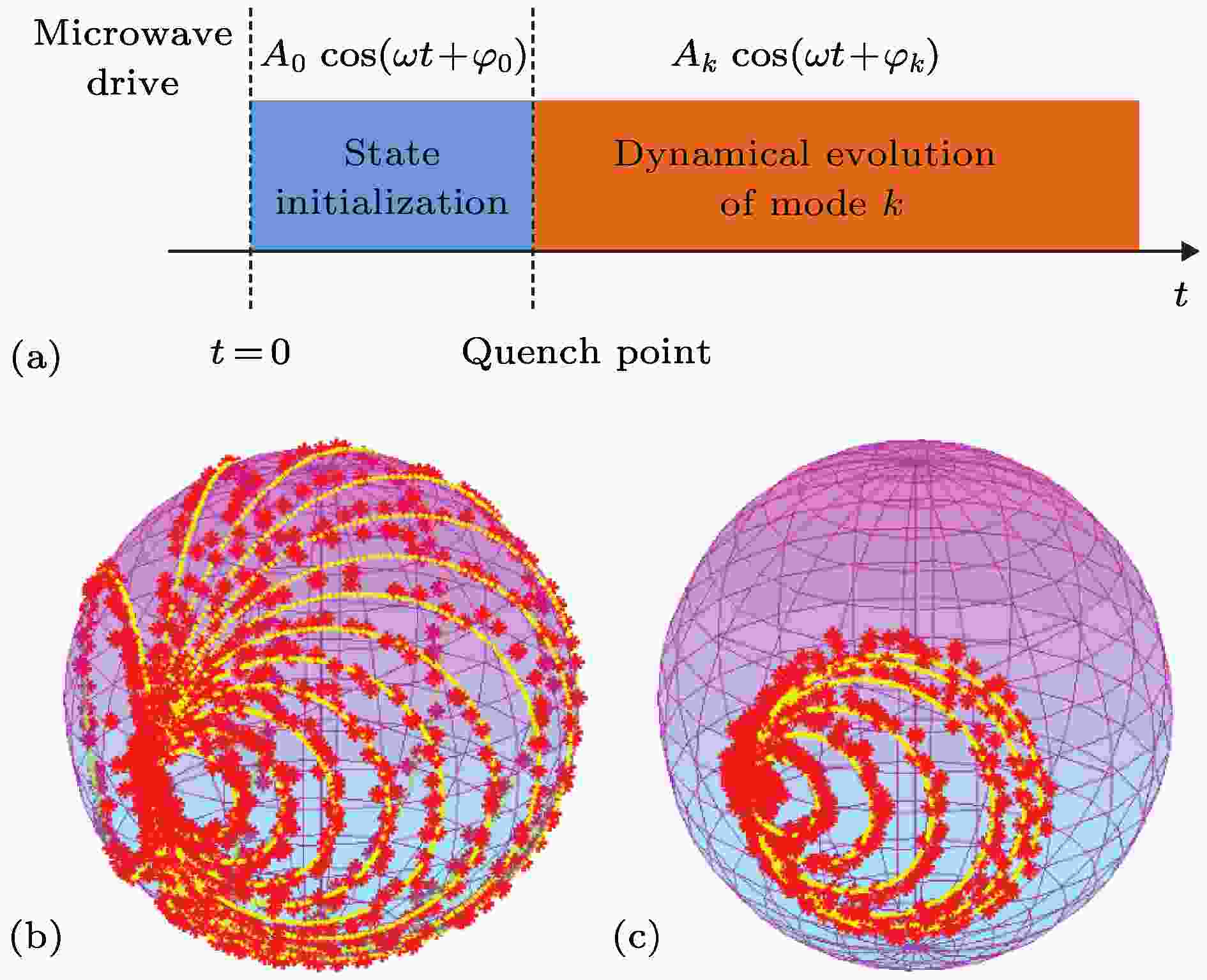图 3 (a)实验过程序列示意图. 对每一个动量k, 初始时刻通过脉冲$A_0\cos(\omega t+\phi_0)$ 制备初态, 而后通过改变外加的脉冲的$A_k$和$\phi_k$ 实现淬火动力学. (b), (c) 不同动量k对应的Bloch矢量的演化. 红色的星为实验的数据, 黄色的环为数值计算的数据. (b)初态$h^{\rm i}=0.2$, 末态$h^{\rm f}=1.5$. (c) 初态$h^{\rm i}=0.2$, 末态$h^{\rm f}=0.5$[22]
Figure3. The scheme of experiment control sequence. The initial state is prepared at the state-initialization period by control quantity $A_0\cos(\omega t+\phi_0)$ for a fixed momentum k. Then for a quantum quench, by controlling $A_k$ and $\phi_k$, we adjust the direction of the rotation axis. (b), (c) the evolution of Bloch vectors for different momenta. The red points and yellow rings are experimental and numerical datas. (b) pre-quenched parameter $h^{\rm i}=0.2$, post-quench parameter $h^{\rm f}=1.5$. (c) pre-quenched parameter $h^{\rm i}=0.2$, post-quench parameter $h^{\rm f}=0.5$.

实验模拟的为横场伊辛模型, 通过Jordan-Wigner变换后它等效于Kitaev提出的p波超导链, 哈密顿量为$ d_x \!=\! 0 $, $ d_y = \sin k $, $ d_z \!=\! J_z \!-\! \cos k $[53], 其中若$ J_z < 1 $基态为铁磁相或拓扑超导相, 若$ J_z > 1 $基态为顺磁相或普通超导相. 通过Jordan-Wigner变换, 我们将伊辛模型映射为一系列二能级系统, 而对于每个由动量k标记的二能级系统我们可以利用单量子比特模拟其动力学演化. 容易看出系统的不动点为$ k = 0 $和$ k = {\text{π}} $. 我们始终取初态$ J_z^{\rm i} = 0.5 $, 图3(b)和图3(c)分别展示了在半布里渊区中Bloch矢量的演化. 可以看出当初末态哈密顿量在同一个相时, Bloch球被完整覆盖, 动力学陈数$ |C_{\rm dyn}^{1}| = 1 $; 而初末态哈密顿量在同一个相时, Bloch球上的轨迹互相抵消, 动力学陈数$ |C_{\rm dyn}^{1}| = 0 $.
6.总结与展望
本文主要介绍了一维对称性保护的拓扑态的淬火动力学. 首先以两带系统为例, 从直观上定义了动力学陈数, 并给出了动力学陈数与初末态哈密顿量拓扑数之间的关系. 然后通过分析$ (1+1) $-维母哈密顿量的拓扑性质给出了一般情况下系统的动力学拓扑分类和拓扑不变量. 此外利用纠缠谱的动力学演化介绍了动力学的体边对应, 并分析了实空间和频率空间无序对纠缠谱交叉的影响. 最后介绍了利用了单量子比特模拟系统的动力学演化, 通过测量Bloch矢量的演化直观的展示了平庸和非平庸的动力学陈数.
此外, 除了在一维系统, 淬火动力学中的拓扑不变量在二维和高维系统[18,19,54,55], 非厄米系统[56—58]等也有许多研究, 但尚没有完整成熟的理论. 并且, 如何在相互作用系统中定义动力学的拓扑不变量也尚未可知. 在相互作用系统中单粒子关联矩阵和纠缠哈密顿量并没有这简单的关系, 只能直接求解系统的多体纠缠谱的演化. 得益于冷原子, 原子模拟, 超导量子比特模拟等技术的迅速发展, 淬火动力学的研究有了更好的实验平台, 使得我们能更加深刻的理解拓扑系统的动力学性质.
相关话题/系统 空间 过程 介绍 实验
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于紧束缚模型的拓扑物理微波实验验证平台的开发
    摘要:拓扑光子学、拓扑物理与光学的结合,为凝聚态理论的验证以及新型光学器件的构建提供了新的视角.紧束缚模型是凝聚态物理的重要研究手段.我们发现,将传统光子晶体的背景材料由通常的空气改为有效介电常数为负数的材料之后,这样的光子晶体和紧束缚模型有一一对应的关系,可以用于相关理论的验证.通过数值仿真实验, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 半导体激光器储备池计算系统的工作点选取方法
    摘要:半导体激光器储备池计算系统的性能受很多因素的影响,如虚节点间隔、激光器的偏置电流和反馈强度等.对于光注入信号方式,注入强度和频率失谐的大小也会影响系统的性能,使得工作点更难确定.为此,本文以10阶非线性自回归移动平均任务为基础,提出一种选取半导体激光器储备池计算系统的最佳反馈强度与注入强度的方 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 忆容器多谐振荡器及其实验
    摘要:忆容器是一种具有记忆性的非线性电容,为研究忆容器的电路特性,提出了一种压控型忆容器的二次曲线模型,利用电流反馈型运放等器件构建了能够动态模拟忆容器q-v特性的仿真器.通过仿真和实验观测到忆容器的滞回曲线,以及随外加激励频率增加而收缩的特性.分析了周期性激励信号的参数对忆容值取值范围的影响,并对 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 人工磁导体对无线能量传输空间场的调控
    摘要:为了提高无线能量传输系统的传输效率,将正六边形人工磁导体结构引入非共振双线圈无线能量传输系统中,展开对空间场调控的研究.研究结果发现,在人工磁导体介入非共振双线圈无线能量传输系统后,在发射线圈和接收线圈之间的电磁场发生了变化,这是由于近磁场激发了人工磁导体的多个谐振模式,同时人工磁导体屏蔽了磁 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 利用海洋环境噪声空间特性估计浅海海底分层结构及地声参数
    摘要:海洋环境噪声场中包含了海洋中的诸多信息,海底地声参数是影响海洋环境噪声场空间分布的主要因素之一.对于不同的海底分层结构,海底反射损失会根据沉积层厚度和各层声速呈现出不同的临界角和干涉条纹结构.本文利用Harrison能流理论,从理想反射系数出发,分别考虑了声速、密度、衰减系数、沉积层厚度等几种 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 全固态磁制冷系统物理模型的研究进展
    摘要:磁制冷是一种节能环保的制冷技术,具有广阔的应用前景.目前,基于主动磁回热循环的磁制冷系统被广泛研究并诞生了多个原型制冷机.然而,这些系统主要采用流体换热,导致系统存在工作频率低、回热损失大、子部件设计复杂等问题,使得制冷机成本升高和效率降低.针对上述问题和难点,引入固态传热增强机制和全固态磁制 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 氩气空心阴极放电复杂动力学过程的模拟研究
    摘要:利用流体模型模拟研究了氩气空心阴极放电的动力学过程.数值模型考虑了直接基态电离、基态激发、分步电离、潘宁电离、解激发、两体碰撞、三体碰撞、辐射跃迁、弹性碰撞和复合反应等31个反应过程.计算得到了电子密度,Ar+密度,激发态氩原子Ar4s、Ar4p、Ar3d能级的密度,电势和电场强度等的分布特性 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于基频放大的紫外皮秒355 nm输出效率提升系统
    摘要:在腔外和频获得紫外355nm皮秒激光输出的过程中,和频晶体的长度是影响转换效率的重要因素.和频过程的激光输入参数和晶体吸收系数都会影响和频晶体的最适长度选取.目前缺乏对于腔外和频产生紫外355nm激光过程中输入激光光子数配比以及晶体吸收对于和频晶体最适长度影响的研究.本文基于三波耦合方程进行了 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种基于压缩感知和多维混沌系统的多过程图像加密方案
    摘要:随着计算机科学的快速发展,信息的存储和传播常常在各类计算机硬件以及多种网络之间进行,传统的信息加密方案已逐渐不再适用.因此,基于计算机的信息加密算法近年来逐步成为研究热点.通过结合小波包变换、压缩感知、混沌系统等理论,一种基于压缩感知和多维混沌系统的多过程图像加密方案被提出.该加密方案实现了针 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 螺旋波等离子体原型实验装置中天线的优化设计与功率沉积
    摘要:近年来,螺旋波等离子体源在核聚变条件下等离子体与材料的相互作用方面具有十分重要的研究意义.本文对高密度螺旋波等离子体原型实验装置(heliconphysicsprototypeexperiment,HPPX)中的螺旋波系统发射天线进行了优化设计,利用HELIC程序,对螺旋波的耦合和功率沉积与天 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.