拓扑节线与节面金属的研究进展

全文HTML

--> --> -->

2.节线金属

2.1.节线的概念

-->

2.1.节线的概念

我们对节线可以有一个很直观的理解. 如图2(a)所示, 当固体中的两个能带相交的时候, 就在布里渊区中形成了一个一维的节线. 对单粒子系统, 这个线总是闭合的, 因此很多研究也把它称为一个节环(nodal loop). 通常碰到的节线都是由两个能带线性交叉而形成的. 在线上的任意一点P的附近, 可以给出一个低能有效模型^[61]: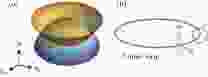

图 2 节线的示意图　(a)由两条能带交叉所形成的节线; (b)绿色的环代表节线, $\ell $

是环绕节线一个路径, 沿着$\ell $

走一圈的贝利相为π^[61]
Figure2. Schematic figure of a nodal loop: (a) Nodal loop formed by two crossing bands; (b) the Berry phase of a closed path $\ell $

circling the nodal loop (green circle) is π^[61].

${\cal H}\left( {{q}} \right) = {v_1}{q_1}{{{\sigma }}_x} + {v_2}{q_2}{{{\sigma }}_y} + {{w}} \cdot {{q}},$

这里q是从P出发的波矢, ${q_i}\left( {i = 1, 2} \right)$

是其在(过P点)垂直于节线的平面中的两个分量, v_i是相应的费米速度, 泡利矩阵σ_i代表了相交的两个能带的自由度(这个模型展开到q的一阶项, 沿着线的切线方向的色散至少是二阶, 因此没有包括在内). 由这个模型, 可以得到节线附近的色散关系. 对应于两个本征态${u_ \pm }\left( q \right)$

的能量本征值是:

${E_ \pm } = {{w}} \cdot {{q}} \pm \sqrt {v_1^2q_1^2 + v_2^2q_2^2}.$

如果考虑图2(b)中在q₁–q₂平面里的一个闭合路径$\ell $

(它上面处处有局部的能隙, 可以被看作是一个一维的绝缘体), 当$\ell $

足够靠近节线的时候, 沿着它走一圈的贝利相位为π, 即:

$\oint_{\ell }{{\cal A}\left( { q} \right)\cdot {\rm d}{ q}={\text{π}} ,}$

这里${\cal A}\left( q \right) = \left\langle {{u_ - }|{\rm{i}}{\nabla _q}{u_ - }} \right\rangle $

是价带的贝利联络. 这一点也很容易理解, 可以看到当沿着$\ell $

走一圈时, 赝自旋σ是怎么旋转的. 这里需要注意的是(3)式中的相等是近似的. 当包括了高阶项时, 这个值一般会偏离π. 不过当体系具有一些特殊的对称性时, 这个等式是严格的. 比如当体系同时具有时间反演和空间反演对称性, 并且没有SOC(即具有自旋的旋转对称性)时, 沿着任一闭合路径的贝利相位都要求是π的整数倍. 在这种情况下, (3)式也就要求这个节线不能打开能隙; 因为一旦打开能隙, 贝利相就会偏离π而违反量子化的条件.
模型(1)给出了节线的一个局部描述. 这里再给出一个简单的、可以整体描述一个节线的模型. 当然, 与模型(1)不同, 这个模型不具有普适性, 但是它可以增进我们对节线概念的理解, 也可以作为计算节线物理性质的一个出发点. 我们考虑一个在${k_x}\text- {k_y}$

平面上的一个圆形的节环(如图2(b)), 从而给出下面这个模型^[61]:

$H = \frac{1}{{2m}}k_\rho ^2 + \frac{1}{{2\eta }}\left( {k_\rho ^2 - k_0^2} \right){\sigma _x} + {v_z}{k_z}{\sigma _y},$

这里${k_\rho } = \sqrt {k_x^2 + k_y^2} $

, k₀代表这个环的半径; m, η, 和v_z是模型的参数. 可以看到当在环上某一点展开的时候, 这个模型可以化简为模型(1).
2

2.2.节线的对称性保护

-->

2.2.节线的对称性保护

前面已经提到, 除了外尔点可以有一个很强的拓扑保护, 其他的能带简并都需要一些额外的对称性保护. 下面讨论可以保护节线的几种对称性. 它们也代表了形成节线的几种机制.
1)手征对称性(chiral symmetry). 手征对称性指的是存在一个与系统哈密顿量反对易的幺正(unitary)对称操作. 用Π代表这个对称操作, 那么

$\varPi H\left( {{k}} \right){\varPi ^{ - 1}} = - H\left( {{k}} \right).$

这个对称性在系统能谱上的反映特别明显: 能谱是上下对称的样子. 对于固体系统, 这个对称性通常在两种情况下可以遇到: 一个是在超导系统中, 在利用Nambu表象描述超导准粒子激发谱时, 由于人为地引入了空穴自由度(当时间反演对称性被保持时), 对应的BdG模型自然的会有一个手征对称性; 另一种情况是系统的晶格是一种二分的(bipartite)类型, 即可以分成两套子晶格(sublattice), 每一个子晶格中的轨道只与另一个子晶格中的轨道有耦合, 对于这种情况, 手征对称性也被称为子晶格对称性(sublattice symmetry); 就具体材料而言, 这种对称性一般在单质材料中出现; 并且一般对轻元素, 比如碳, 硼等所组成的结构, 会保持的比较好^[56,62,63].
当系统具有手征对称性时, 对于大多数情况我们都可以在一个动量空间的一维的闭合路径上定义一个拓扑绕数(winding number)(见文献[16]中的具体讨论). 类似于图2(b)中的情况, 一个节线可以被绕着它的路径$\ell $

上的非平庸(即不为零的)拓扑绕数所刻画和保护. 只要系统的对称性不被破坏, 这个节线就不会被任何微扰打开能隙.
2014年, 我们在反常超导的准粒子激发谱中讨论了这类节线的拓扑性质^[51]. 该项研究预言了一种叫作狄拉克超导的拓扑相(可能存在于Cu掺杂的Bi₂Se₃, 或者UPt₃之中). 当体系的一种中心反演对称性被破坏时, 原本激发谱中四重简并的狄拉克点就会演化成一个手征对称所保护的节环(见图3(a)). 研究在体系的表面上, 这个体能带中的节环投影为表面布里渊区中的一个环, 在环内会出现鼓膜状的表面态(drumhead surface state)能带^[51]. 值得注意的是, 由于存在手征对称性, 这里的节环和鼓膜表面态都被限制于零能. 在这个例子中, 体系具有强SOC. 需要指出的是手征对称所保护的节线也可以存在于没有SOC的系统中^[56].

图 3 在狄拉克超导体中出现的由手征对称性保护的节线　(a)当空间反演或者时间反演破坏时, 一个狄拉克点会变为一个节环或两个外尔点; (b)?(d)刻画了(a)中几种简并点的拓扑保护机制, 其中节环是由拓扑绕数所保护^[51]
Figure3. Chiral symmetry protected nodal line in a Dirac superconductor: (a) A Dirac node can evolve into a nodal ring or two Weyl nodes under different symmetry breaking; (b)?(d) illustrate the different topological protection for the degeneracies in (a). Here, the nodal ring is protected by the winding number^[51].

2)时空反演(PT)对称性. 当一个系统具有空间反演(P)和时间反演(T)的联合操作的对称性, 并且SOC可以忽略时, 布里渊区中的任何一条闭合路径上贝利相位都必须是量子化的(π的整数倍, 这个整数就是一个拓扑绕数). 如图2所示, 路径$\ell $

上的非平庸的(π)贝利相位为节线提供了一个保护.
因为这里的对称性要求没有SOC, 所以这种节线一般是在SOC比较弱的轻元素材料中出现. 2015年, 几个研究组分别在不同的碳的同素异形体中发现了这种节线(见图4)^[52,53,56]. 在一些例子中, 节线还同时受到手征对称性的双重保护^[56]. 在早期的研究中, Yu等^[54]和Kim等^[]^55]也发现反钙钛矿材料Cu₃PdN中当不考虑SOC时也会有这种类型的节环; 当考虑SOC时, 节环被破坏而只留下一对狄拉克型的简并点. 之后找到的不少节线材料是属于这一类的, 比如Ca₂As^[64], CaP₃家族^[65], Ca₃P₂材料^[66], CaTe材料^[67], BaSn₂^[68], CuTeO₃^[69]和碱土金属单质^[70].

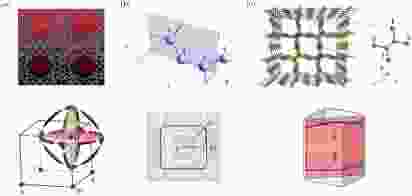图 4 在三种碳材料中发现的节线　(a) Mackay-Terrones结构的三维碳和节线在动量空间的表示^[52]; (b) hyperhoneycomb结构的三维碳和节线在动量空间的表示^[53]; (c)三维的石墨烯网络结构和节线在动量空间的表示^[56]
Figure4. Nodal lines found in three carbon allotropes: (a) 3D carbon with Mackay-Terrones crystal structur^[52]; (b) 3D hyperhoneycomb carbon^[53]; (c) 3D graphene network structure^[56].

3)镜面对称性. 这种情况是最容易理解的. 假定系统具有一个镜面对称性M_z, 即垂直于z轴的一个镜面, 那么布里渊区中的k_z = 0和k_z = π平面便是在这个对称操作下的不变子空间: 在这两个面上每个k点的能量本征态同时也是(当存在简并时, 总可以选为)镜面的本征态. 如果两个能带在其中一个平面上的镜面本征值相反, 那么它们在这个面上的交点就被镜面对称所保护. 而在一个二维平面, 两个能带一般都会交出一个一维的节线. 需要注意的是, 镜面保护的节线既可以出现在没有SOC的系统, 也可以出现在有SOC的系统, 并且与系统存在的其他对称性(比如P和T)有关^[71].
4)滑移镜面(glide mirror)对称性. 滑移镜面是一种非简单的(nonsymmorphic)晶格对称性. 它也是一种镜面操作, 但要额外加上一个分数晶格矢量的平移. 这里我们对滑移镜面单独进行分析, 因为它所导致的节线有其独特的性质. 我们考虑一个具有时间反演对称但没有空间反演对称的三维系统. 在布里渊区中, 存在八个时间反演不动点(time reversal invariant momenta, TRIM), 即满足$k=-k+G$

的点, 这里G是某个倒格矢. 在这些TRIM点上, 能带要满足Kramers双重简并. 如果晶格具有一个包含平移半个晶格矢量的滑移镜面, 那么可以发现这个对称操作的本征值在TRIM点可以是以下两种类型: 在四个TRIM点是 ± 1, 在另外四个TRIM点是 ± i. 由于时间反演操作要取复共轭, 所以在 ± 1的TRIM点, Kramers双重简并的配对是$(+1, +1)$

和$ (-1, -1)$

; 而在 ± i的TRIM点, 配对必须是$\left( { + {\rm{i}}, - {\rm{i}}} \right)$

. 这两种配对类型的不同, 导致从一类TRIM点到另一类TRIM点的路径上, 随着k值得变化, 能带本征值也跟着变化, 在中间过程中, 能带必然发生了交换, 从而导致一种沙漏状的色散(如图5(b)). 沙漏脖子处的交点是一个二重简并点, 为滑移镜面所保护. 由于这里连接两个TRIM点的路径可以是保持滑移镜面对称的平面上的任何一条路径, 所以不同路径上的二重简并点会最终形成一个外尔型的节环, 见图5(a).

图 5 滑移镜面所保护的节线　(a) O和X是滑移镜面上对应两个不同配对类型的TRIM点; (b)展示了沿着连接O和X的一条路径L上的能带特征, 这里每四条能带都会形成一种沙漏形的结构; 沙漏脖子处的交叉点P在滑移镜面上会形成一条节线
Figure5. Nodal line protected by the glide mirror symmetry: (a) Shows the glide-mirror-invariant plane in Brillouin zone, O and X are two TRIM points with different glide mirror eigenvalues; (b) shows the band structure along a path L connecting O and X (as in (a)); it displays an hourglass shaped spectrum. The degeneracy point P in the hourglass traces out a nodal loop in the glide mirror plane.

上面的讨论中假定了空间反演是破缺的. 当系统同时还具有空间反演时, 图5(b)中的每条能带都因为PT对称而有一个额外的二度简并. 一般来说, 由于引入了额外的简并度, 沙漏脖子处的交点会被破坏. 但是当空间反演和滑移镜面满足某种特定的代数关系时(见文献[72]中的讨论), 这个交点也有可能仍然被保持, 而成为一个四度简并的狄拉克点. 这样的话, 在保持滑移镜面不变的面上就会出现一个狄拉克型的节环^[73,74].
就材料而言, Bzdusek等^[75]提出滑移镜面保护的外尔型节环有可能在IrF₄的高温顺磁相中实现. Wang等^[73]和Li等^[74]提出上面讨论的狄拉克型节环可能在真实材料ReO₂和X₃SiTe₆(X = Ta, Nb)中实现, 见图6. 最近, 几个研究组的ARPES实验和输运实验都给出了Ta₃SiTe₆和Nb₃SiTe₆具有拓扑性质的证据^[76,77].

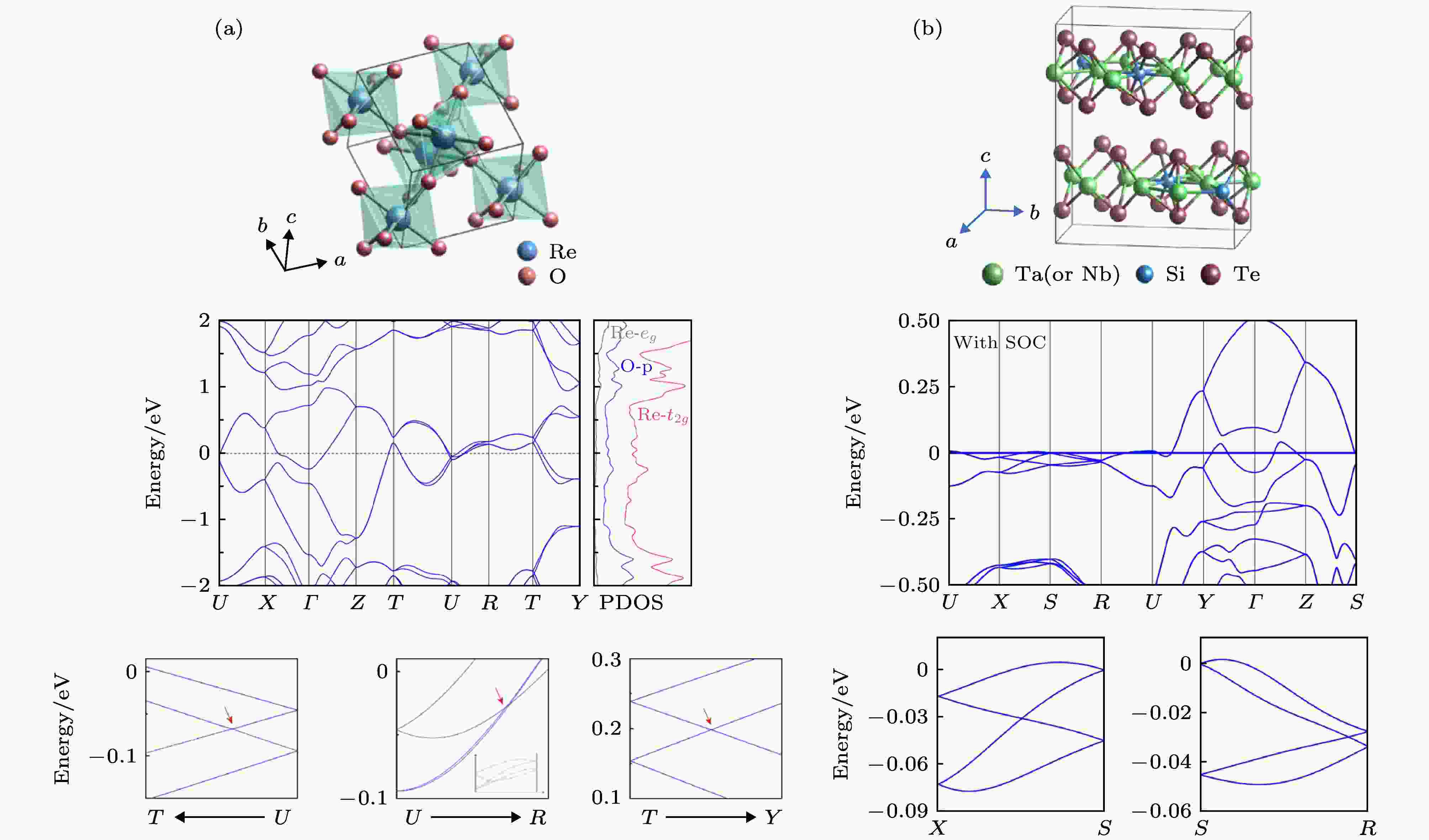图 6 具有滑移镜面所保护的节线的例子　(a) ReO₂的晶体结构和能带结构, 可以看到高对称线上的沙漏型色散^[73]; (b) X₃SiTe₆(X = Ta, Nb)的晶体结构和能带结构, 以及在高对称线上的沙漏型能量色散^[74]
Figure6. Material examples with glide-mirror-protected nodal rings: (a) ReO₂^[73]; (b) X₃SiTe₆(X = Ta, Nb)^[74], the hourglass dispersions can be observed in their band structures.

2

2.3.节线的特征和分类

-->

2.3.节线的特征和分类

一个概念可以按照它的特征来进行分类. 对于节线来说, 它的主要特征包括以下几个方面: 简并度、色散和形状. 对节线的分类也正是从这几个方面展开.
1)按照简并度分类: 外尔型和狄拉克型节线. 在对节点的定义中, 外尔点指的是满足外尔模型的二度简并点; 狄拉克点指的是满足狄拉克模型的四度简并点. 对节线来说, 虽然没有可以直接对应的基本粒子模型, 大家仍简单沿用了外尔和狄拉克这两个名词来说明节线的简并度, 即二度简并的节线被称为外尔节线(Weyl nodal line), 四度简并的节线被称为狄拉克节线(Dirac nodal line).
狄拉克型节线一般出现在具有PT对称性、考虑了SOC的体系中. 对于SOC可以忽略的(SOC-free)材料, 一些文献把两个能带相交得到的节线也称为狄拉克型节线, 这可能是考虑到每个态都有一个自旋自由度, 所以简并度要乘以二(对非磁性材料). 但是, 对于这种情况, 自旋是一个不起作用的自由度, 低能的电子为一个两带模型所描述, 所以将其称为外尔型是更加合适的.
2)按照色散的类型分类: type-I, type-II, 和hybrid节线. 在对外尔点的研究中, 依据节点附近色散的不同, 把节点分成type-I和type-II两类^[78,79]. type-I类型的色散就是通常见到的立着的锥状色散. 而对于type-II色散, 这个锥是倒下来的. 也就是说在动量空间的某个方向上, 两条相交能带的斜率有相同的符号(一些研究工作中还定义了所谓type-III的色散, 意指在某个方向上, 其中一条能带的色散是完全平的; 但是, 这个态对应的是type-I和type-II两个相区之间的边界, 其本身并不是一个稳定存在的相).
2017年, Li等^[61]将这种分类推广到节线, 提出了type-II和hybrid节线的概念. 考虑节线上某个点P附近的色散, 前面的(2)式刻画了相交的两条能带在过P点垂直于节线的${q_1} \text- {q_2}$

平面里的色散. 如果这两个能带的斜率反号, 定义点P是type-I的; 如果这两个能带的斜率同号, 则定义点P是type-II的. 节线由这些点组成. 如果组成节线的点都是type-I的, 这个节线就被定义为type-I节线. 类似地, 可以定义type-II节线. 还有第三种情况, 即节线既包括type-I点也包括type-II点, 这被称为hybrid节线. 这三种类型可以比较直观地在图7中反映出来. type-I节线可以看作是由一个电子型能带和一个空穴型能带相交产生; type-II节线可以看作是由两个电子型(或两个空穴型)能带相交产生; 而一个hybrid节线可以由一个电子型(或空穴型)能带和一个马鞍型能带相交产生(图7中给出的是几个典型例子, 当然还存在别的情况).

图 7 三种不同色散类型的节线　(a) type-I节线; (b) type-II节线; (c) hybird节线; (d)?(f)三种节线的等能面^[64]
Figure7. Three types of nodal lines classified by the energy dispersion: (a) Type-I nodal line; (b) type-II nodal lines; (c) hybrid nodal lines; (d)?(f) show the typical shapes of the constant energy surface for the three types^[64].

上面这种分类的意义在于不同类型的节线会有不同的费米面结构, 进而可以导致一系列物理性质的不同. 图7(d)—(f)给出了三种类型节线对应的等能面, 可以看出它们之间有非常大的差别. 基于这个认识, 文献[61]中讨论了type-II节线在磁振荡、磁响应、光响应和输运性质上的特征, 指出相比于type-I节线, type-II节线会使得光吸收受到抑制, 同时会使材料有更高的迁移率(图8(a)). 之后, Zhang等^[64]从理论上研究了hybrid节线的磁响应性质, 发现它会具有一个零场的磁坍塌(zero-field magnetic breakdown)效应以及磁共振中显著的各向异性(图8(b)).

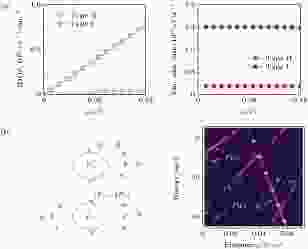图 8 Type-II节线和hybrid节线的特殊物理性质　(a) Type-II节线和type-I节线的光学性质的比较^[61]; (b) hybrid节线导致的磁坍塌效应和磁振荡中的各向异性^[64]
Figure8. Unique properties of type-II and hybrid nodal lines: (a) Comparison between type-I and type-II nodal lines in terms of JDOS and optical absorption rate^[61]; (b) the magnetic breakdown and its feature in anisotropic magnetic oscillation for a hybrid nodal loop^[64].

就材料而言, 大多数被报道的节线材料属于type-I类型. 具有type-II节线的材料包括K₄P₃^[61], Mg₃Bi₂^[80,81]. 具有hybrid节线的材料包括Ca₂As^[64]和Be₂Si^[82].
3)按照色散的次数分类: 线性、二次(quadratic)和三次(cubic)节线. 材料中发现的节线绝大多数都具有线性的色散, 即它们是由两条能带线性交叉所产生. (1)式反映的就是这种情况. 那么有没有可能存在具有高次色散的节线呢? 2019年, Yu等^[83]回答了这一问题. 通过对晶体空间群对称性的分析, 他们得到了下面的结果: 1)在所有高次色散节线中, 只有二次和三次节线(quadratic/cubic nodal line, QNL/CNL)能够被对称性所保护(图9(a)), 这里需要指出的是我们总可以写出一个有高次色散的节线模型, 关键是这个节线有没有对称性保护; 如果没有保护, 那么任何微扰都会破坏这个线, 这个线就不能够稳定存在; 2)高次的节线的简并度只能是二重的; 3)所有的高次节线都分布在布里渊区的主旋转轴上.

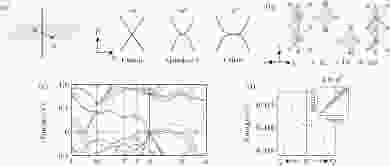图 9 (a)按照节线的色散次数进行分类的示意图; (b)?(d)展示了一个具有二次节线的材料ZrPtGa, (c)是ZrPtGa的能带结构, 蓝色实线标记了二次节线, (d)是这个节线在垂直于Γ-A的平面上的色散, 可以清楚地看到是二次色散^[83]
Figure9. (a) Schematic figure for the higher order nodal lines; (b)?(d) show the quadratic nodal line in ZrPtGa: (c) the band structure of ZrPtGa, the blue solid curve indicates the quadratic nodal line; (d) shows the band dispersion in the plane perpendicular to Γ-A, which clearly demonstrates a quadratic dispersion^[83].

文献[83]中给出了二次和三次节线附近的低能有效模型. 类似(1)式, 对二次节线,

${{\cal H}_{{\rm{QNL}}}}\left( {{q}} \right) = \alpha q_ - ^2{\sigma _ + } + {\rm{H}}.{\rm{c}}.,$

这里α是一个取复数值的模型参数, ${q_ \pm } = {q_x} \pm {\rm{i}}{q_y}$

, ${\sigma _ \pm } = {\sigma _x} \pm {\rm{i}}{\sigma _y}$

. 三次节线的模型则有下面的形式:

${{\cal H}_{{\rm{CNL}}}}\left( {{q}} \right) = {\rm{i}}(\alpha q_ - ^3 + \beta q_ + ^3){\sigma _ + } + {\rm{H}}.{\rm{c}}.,$

这里的α和β是取实数值的模型参数. 色散次数的不同自然的带来物理性质的巨大差异. 文献[83]具体的讨论了二次和三次节线在磁振荡行为、朗道能级的结构和光学响应方面的特征.
就材料而言, 具有二次节线的材料包括WC族的一类材料, ZrPtGa(图9(b)—(d)), V₁₂P₇, 和ZrRuAs^[83]. 具有三次节线的材料包括CaAgBi (这也是一个具有多种狄拉克点的材料^[36]). 目前找到的材料在费米面附近的能带都不理想. 因此通过材料搜索和设计来得到具有高次节线的材料仍是将来的一个重要研究课题.
4)按照形态的拓扑分类. 图10中展示了两个真实材料中的二类节线的例子. 图10(a)中的是一个三维的碳结构中出现的节线, 在布里渊区的一个镜面上有两条时间反演操作所联系的节线, 每一条都从左到右穿越了整个布里渊区^[56]. 图10(b)中展示的是材料CuTeO₃中的节线^[69], 这个节线是围绕着布里渊区的中心Γ点的一个圈. 从图中可以直观地感觉到这两个节线是不一样的: 一个穿越了布里渊区, 而另一个则局域在布里渊区中的某个点附近. 那么怎样刻画这种不同呢? 2017年, Li等^[61]指出这里的区别反映的是一条节线缠绕布里渊区的拓扑结构的不同. 我们知道, 因为布里渊区有周期性的结构, 它等价于一个三维的环面(3D torus). 一条在布里渊区里的节线的拓扑可以由它的基本同伦群(fundamental homotopy group)来刻画, 对应着三个整数, 分别代表节线在三个方向上穿越布里渊区的次数. 比如图10(b)中的节线没有穿越布里渊区, 所以它对应的类就是(0, 0, 0), 而图10(a)中的节线在一个方向(定义为x方向)上穿越了一次, 所以它对应着(1, 0, 0). 这个拓扑性质在物理上的一个直接影响是: 在不破坏系统对称性的前提下, 图10(b)中的节线可以(通过调节系统参数, 如施加应变等)连续的变成一个点然后消失; 而图10(a)中的节线不可以. 图10(a)中的节线必须要和另一条相配对, 才可以一起湮灭掉.

图 10 具有不同形态的节线　(a)穿越布里渊区的一对节线^[56]; (b)局域在布里渊区某个点周围的节线^[69]
Figure10. Nodal lines with different kinds of distribution in Brillouin zone: (a) Nodal lines in a carbon allotrope, which traverse the Brillouin zone^[56]; (b) nodal line in CuTeO₃, which is located around a point in Brillouin zone^[69].

以上的讨论是对于三维系统进行的, 对二维系统也可以做类似讨论. 此时一条单独的节线可以由它沿着两个方向穿越布里渊区的次数来刻画. 这方面的讨论可以参考近期关于氧化硼烯(B₂O)^[84]和单层MnN中的节线的工作^[85].
以上的分类都是对单个节线进行的. 在一些材料中会存在多个节线, 并且它们还会互相连接形成复杂的结构. 对这些情况很难有一个系统的分类. 下面我们主要讨论一些典型的例子.
1)环绕布里渊区中同一个高对称点的几个节环可以互相交叉, 形成一个笼子状的结构, 或者称为crossed nodal rings. 比如图11(a)中所示, 在LiOsO₃的铁电相中, 环绕布里渊区中T点的三个节环在高对称轴上相交, 每一个环都处在一个镜面里^[38]. 类似的其他例子还包括Cu₃PdN^[54,55], LaN系列材料^[86], YH₃^[87], 以及一类层状的BN和SiC结构^[88]. 这里需要指出的是, 在LiOsO₃中讨论的节线结构是在考虑SOC下稳定存在的^[38]. 而在后面的几个例子中的节线是在没有考虑SOC时才会有; 当加入SOC后, 这些节线会被完全打开能隙或只留下某些节点.

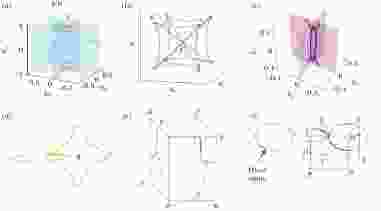图 11 节环可以形成的一些复杂结构　(a)笼子状的结构^[38]; (b)骨架状的结构^[89];(c)三能带形成的结状节线^[90]; (d) Hopf链环^[91]; (e)外尔链; (f)狄拉克链^[73]
Figure11. Different structures formed by nodal lines: (a) Crossed nodal rings^[38]; (b) nodal box^[89]; (c) inter-connected nodal loops^[90]; (d) nodal Hopf link^[91]; (e) weyl chain; (f) dirac chain^[73].

2)由几个能带互相交叉所产生的节线也可能形成一个骨架状的结构. 比如在CuAgSe中, Sheng等^[89]发现四个低能能带间的相交会在一个镜面上形成蝴蝶形状的节线. 体系存在多个互相联系的镜面, 因此这些节线会组成图11(b)中所显示的结构, 被作者们称为一个nodal box.
3)两个节环还可以扣在一起, 形成一个结. 例如图11(c)所示在三维的五边形碳(pentagon carbon)材料中由三条能带交叉形成的节线结构^[90]. 图11(d)展示的是在Co₂MnGa中存在的Hopf链环(Hopf link)类型的节线结构^[91].
4)几个节环可以接在一起, 形成在动量空间延展的一条链. Bzdusek等^[75]的工作中提出了在空间反演对称性破缺的系统中存在的外尔链(Weyl chain). 如图11(e)中所示, 这个链由两个在不同的滑移镜面上的外尔节环相接而成, 并且沿着一个方向延展(注意到布里渊区的周期性). 这里每一个节环的形成对应着图5中所讨论的机制. 之后, Wang等^[73]提出了狄拉克链(Dirac chain)的概念, 指出当空间反演保持并且与滑移镜面满足某种特定的代数关系时, 四重简并的节环所组成的链(见图11(f))就有可能在某些空间群实现. 该研究还预言了一个真实材料ReO₂是含有这种狄拉克链的材料.
2

2.4.二维材料中的节线

-->

2.4.二维材料中的节线

上面的讨论都是关于三维非磁性材料的. 近期对节线的研究开始拓展到两个新的方向: 一是二维材料中的节线, 二是磁性材料中的节线. 在这一节中, 我们先讨论二维材料中的节线.
二维材料指的是由有一层或几层原子组成的可单独稳定存在的材料. 二维材料是伴随着2004年石墨烯的实现而发展起来的^[7], 如今已成为一个跨学科的庞大研究领域. 相比于传统的三维材料, 二维材料具有以下优势: 首先由于其厚度很薄, 它们的性质可以很容易地在大范围内进行调控, 比如二维材料中的载流子浓度可以有效地用栅极控制; 第二, 二维材料大多具有优异的力学性质, 比如石墨烯可以承受超过10%的应变, 而施加的应变也可以有效的调控材料的性质^[92,93]; 第三, 二维材料具有极大的表体比(surface-to-volume ratio), 这对于催化和储能等应用都非常有利; 第四, 二维材料本身提供了具有原子级别平整的界面, 由二维材料构建出的异质结可以有效地解决传统三维材料异质结中界面上无序所带来的问题. 因此, 假如可以在二维材料中实现拓扑态, 我们可以预期这将带来很多基础研究和应用上的突破.
在实际的二维材料中实现拓扑态也面临着几方面的挑战. 首先, 由于维度的降低, 在三维体系中稳定的能带拓扑结构往往到了二维变得不再稳定. 比如一个单独的外尔点在三维具有陈数保护的拓扑稳定性, 而到了二维则失去了这种拓扑保护, 因此实现二维材料中的外尔点需要找到额外的对称性保护(关于二维材料中外尔点的实现, 可以参考近期对单层GaTeI^[94]和PtCl₃^[95]的两个工作). 第二, 维度的降低也带来了对称性的减少. 一个直观的反映就是对应于三维非磁性材料的空间群有230个, 而对应于二维非磁性材料的空间群(也称为layer group)则减少到了80个. 因此, 要在二维材料中实现受对称性保护的能带简并就变得更为困难, 特别是当材料中的SOC不可忽略的时候. 例如三维系统中的狄拉克点可以由多种对称性来保护(例如BiO₂^[27]和Na₃Bi中的狄拉克点^[44]), 但是在二维系统中要得到(SOC作用下)稳定的狄拉克点变得非常困难(注意石墨烯和很多二维材料中所讨论的狄拉克点在有SOC时都是不稳定的). Young和Kane^[72]指出二维中的狄拉克点需要有特殊的非简单对称操作, 如二度螺旋轴或滑移镜面, 才可以被保护. Guan等^[96]在单层的HfGeTe族材料中找到了这种在SOC作用下仍然稳定的狄拉克点. 第三, 在近年来的研究中, 虽然新的二维材料不断被发现, 但相比于三维材料, 二维材料的数目特别是其晶格的种类还是有限的. 这也加大了在真实材料中找到合适的能带拓扑结构的难度. 在这个方面, 我们不仅要利用实验的进展, 也可以利用结构搜索和高通量计算等理论方法构建满足对称性要求的新二维材料来实现想要的拓扑相.
具体到节线的情况, 在早期的研究工作中零星报道过一些在忽略SOC时具有节线的二维材料. 例如Jin等^[97]预言的PdS一族有褶皱的二维节线材料, Li等^[74]在X₃SiTe₆(X = Ta, Nb)的单层中发现的处于布里渊区边界的节线, 以及Zhou等^[98]和Zhong等^[84]分别在单层B₂C和B₂O中预言的节线. 在实验上, 单层Cu₂Si和CuSe中存在的节线也为ARPES方法所观测到^[99,100].
在上面这些例子中, 节线只有在忽略SOC时可以稳定存在. 加上SOC后, 这些节线或者完全打开能隙, 或者部分打开能隙, 只留下几个孤立的节点. 那么在二维是否可以存在SOC作用下仍然稳定存在的节线呢? 近期文献[85, 94]给出了肯定的答案. 首先是Wu等^[94]分析了一类在二维系统由滑移镜面所保护的节线, 给出了所需要的对称性条件. 这种节线的形成机制类似于文献[75]在三维中所讨论的情况(见图5(a)). 滑移镜面和时间反演对称导致了在连接两个TRIM点的路径上能带会出现沙漏型的色散. 这个沙漏脖子处的二度简并点在布里渊区里形成了一条节线, 见图12(a)—(c). 由于这个分析的出发点就包含了SOC, 因此得到的节线本征的具有在SOC下的稳定性. 该工作进一步在GaTeI一族的单层材料中找到了这种节线^[94]. 与此同时, Wang等^[85]在单层MnN中发现了由镜面对称性保护的节线, 见图12(d)—(f). 尤其值得注意的是这里的系统基态具有铁磁序, 形成一个半金属态(half metal), 即费米面附近只存在属于一个自旋的能带. 因为基态的磁化方向垂直于材料所在的平面, 因此水平镜面在形成铁磁序之后仍然得以保持, 进而保护了能带在费米面附近形成的两个节环(见图12(f)). 在这里, SOC的作用并不影响相交能带具有相反的镜面本征值, 因此两个节环在考虑SOC时仍然是稳定的.

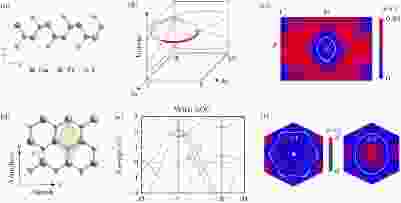图 12 二维材料中在SOC作用下仍然稳定的节线　(a)?(c)二维GaTeI中的节线^[94]; (d)?(f)单层MnN中的节线, 单层MnN是一个铁磁材料, 在费米面处只存在一个自旋通道, 因此这里的节线是完全自旋极化的^[85]
Figure12. Stable nodal lines under SOC in 2D: (a)?(c) GaTeI family materials^[94]; (d)?(f) MnN monolayer, here MnN is a half metal, so the nodal loops are fully spin^[85].

2

2.5.磁性材料中的节线

-->

2.5.磁性材料中的节线

拓扑材料的另一个发展方向是将拓扑能带结构和其他的长程序(如铁电序, 铁磁序等)相结合. 这样一方面可以通过调节长程序来达到控制能带拓扑的目的, 另一方面低能的电子(作为拓扑演生费米子, 如外尔费米子)也可以具有如自旋极化等特殊性质. 将拓扑金属态与铁电序结合不是很容易, 因为铁电序通常是在绝缘体中实现. 但是也存在特例. 比如Li等^[101]预言了HgPbO₃是一种铁电金属, 并且在铁电相具有外尔点. 这种铁电金属相是伴随着晶格从非极化结构到极化结构的一个相变而产生, 最先在LiOsO₃中为实验证实^[102]. 之后, Yu等^[38]通过理论分析和计算发现其实LiOsO₃的铁电相和非铁电相都具有拓扑能带结构: 它的非铁电相(即高温相)具有三次狄拉克点(即在面内的色散是三次的四重简并点); 而在铁电相(即低温相), 这个三次狄拉克点则变化为三个相交的节环.
相比较而言, 将拓扑金属态与磁性结合会容易一些. 在之前的工作中, 已经找到了几种具有节线的磁性材料. 例如铁磁材料Co₂TiX (X = Si, Ge, or Sn)^[103], MnF₃^[104], 具有立方晶格的氧化物磁性材料(如Fe₃O₄和CrO₂)^[105], 和Li₃(FeO₃)₂^[106]. 值得注意的是Wang等^[105]指出在Fe₃O₄和CrO₂中的节线受到镜面对称性保护, 是可以在SOC作用下仍然稳定存在的. 另外, 节线也可以在反铁磁材料中存在. Wang^[107]从理论上对(考虑SOC的)反铁磁节线的形成机制进行了探讨, 提出了两类不同的节线: 一类是由于能带反转所导致, 可以被称为accidental nodal line; 另一类是由某些磁性空间群所完全决定的, 因此被称为essential nodal line. 在实验上, 最近的报道了在反铁磁材料GdSbTe中利用ARPES观测到的节线的证据^[108].
以上的讨论都是关于三维的磁性材料. 关于二维, 2.4节提到了在单层铁磁半金属MnN中存在完全自旋极化的在SOC下也稳定的节环(见图12(d)—(f))^[85]. Zhou等^[109]在单层的CsS一族材料中也找到了类似的节环, 但是这个节环不是出现在基态, 而是需要将磁化方向转到垂直于易磁化平面的方向. Feng等^[110]在铁磁单原子层GdAg₂中观察到了自旋极化的外尔节线, 该节线受镜面对称性保护, 不同的磁化方向可以调节节线.
2

2.6.节线对应的拓扑表面态

-->

2.6.节线对应的拓扑表面态

体态的拓扑能带结构往往对应着系统边界上存在的拓扑表面态. 例如在三维强拓扑绝缘体(strong topological insulator)的表面上存在外尔锥形式的无能隙表面能带^[111]. 又如在三维外尔半金属的表面上存在费米弧(Fermi arc)形式的拓扑表面态^[22]. 这里, 表面态的“拓扑”指的是任何局域的满足体系对称性要求的微扰都不能破坏无能隙表面态的存在.
节线也对应着其特有的表面态, 即所谓鼓膜状表面态. 我们在2014年的工作中指出了这种表面态的存在(图13(a))^[51]. 在二维的表面布里渊区内, 这些表面态分布于(体里的)外尔节线在该表面的投影区域内(也可能在外部, 取决于边界条件). 对于超导的准粒子谱, 由于粒子空穴对称性的存在, 这些态的能量严格为零, 形成一个没有色散、完全平的表面能带. 对于金属材料来说则没有这个对称性的限制, 表面能带一般会具有色散, 导致这个鼓膜在能量上不是平的. 这种节线金属中的鼓膜状表面态已经在很多例子中被证实(如图13(b)^[52]).

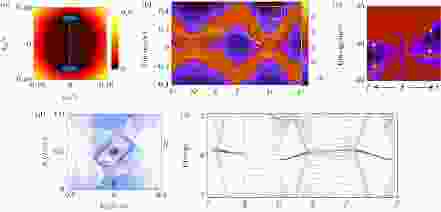图 13 节线对应的拓扑表面态　(a)狄拉克超导体中节线导致的鼓膜态^[51]; (b)碳的同素异形体中的鼓膜态^[52]; (c), (d) ReO₂^[73]和Ta₃SiTe₆^[74]中的双鼓膜态; (e)对应着三次节线的遍布布里渊区的环面表面态^[83]
Figure13. Surface states of nodal line metals: (a) Drumhead surface states for nodal rings in superconductors^[51]; (b) drumhead surface states in a 3D carbon allotrope^[52]; (c), (d) show the double drumhead surface states in ReO₂^[73]and Ta₃SiTe₆^[74]; (e) surface states of cubic nodal line, which spreads over the whole BZ^[83].

当节线是四度简并的狄拉克型节线时, 对应的鼓膜状表面态往往也会翻倍, 被称为双鼓膜表面态(double drumhead surface state)^[73]. 图13(c)和图13(d)展示了两个这样的例子. ReO₂^[73]和Ta₃SiTe₆^[74]是含有狄拉克型节线的材料, 在它们的表面能谱中都可以发现存在着两个鼓膜状表面能带.
在2.3节第3)部分的讨论中, 我们提到除了线性色散的节线, 还存在二次和三次色散的节线. 对应这些特别种类节线的表面态也是大不相同的. 余智明等^[83]指出二次节线一般不对应着受保护的表面态, 而三次节线则对应着一种非常奇特的表面能带. 如图13(e)所示, 与之前的鼓膜状表面态不同, 这个表面能带覆盖了整个的表面布里渊区. 由于表面布里渊区是一个二维的环面(或者叫轮胎面), 这种表面态也可以被称为是环面表面态(torus surface state).
在实验上, 这些拓扑表面态可以用ARPES或者STS来进行探测. Li等^[70]的工作指出早先在碱土金属Be单质中ARPES观测到的表面能谱对应着体内节线产生的拓扑鼓膜状表面态. 他们还进一步指出之前实验中观察到的Be(0001)表面上的巨大的Friedel振荡也是源自这个表面能带. 如果这个表面能带色散比较小(这也要求体内的节线在能量上比较平)并且接近费米面的话, 它会在费米能处引起一个表面态密度(surface density of states)的尖峰. 在考虑相互作用的影响后, 这有可能会导致一个相变, 产生表面超导或者表面磁性^[111,112].

3.节面金属

3.1.节面的概念

-->

3.1.节面的概念

对于一个三维的系统, 它的能带简并点原则上也可以形成一个二维曲面. 2016年, 这种节面的存在首先在两个理论工作中被提出. Zhong等^[59]预言了一类稳定的三维碳材料, 其中每一个都在费米面附近有一对由两条能带线性交叉形成的节面, 如图14(a)所示. Liang等^[60]在六角结构的BaMX₃(M = V, Nb, Ta; X = S or Se)材料中发现存在于布里渊区边界k_z = π面上的一个节面, 如图14(b)所示. 值得注意的是, 在最早的这两个例子中, 节面的稳定存在都要求SOC是可忽略的. 比如对于BaTaS₃, 在考虑SOC后, 节面上的简并会被打开, 只留下一些沿着高对称线的节线^[60]. 在2016年后, 对节面有一些利用理论模型的研究工作. 例如Bzdusek和Sigrist^[113]讨论了在具有中心反演对称的体系中实现节面的可能性. Xiao和Fan^[114]提出了一个具有拓扑电荷的节面的模型, 并设计了一种用声学超材料来实现的方案.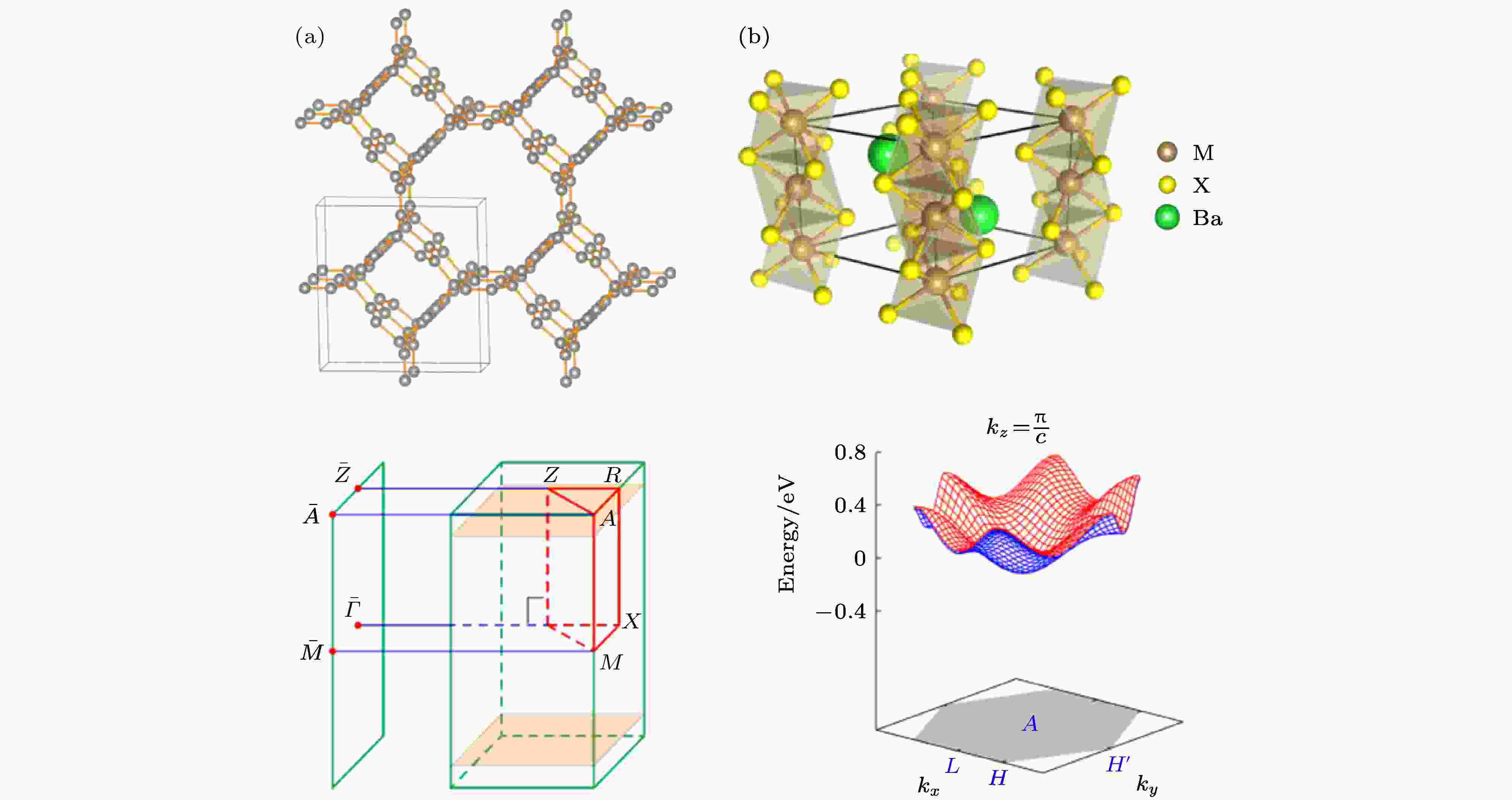

图 14 两种不同的节面　(a)三维碳材料中的节面^[63]; (b) BaMX₃中的节面^[60]
Figure14. Two kinds of nodal surfaces: (a) Nodal surfaces in a 3D carbon allotrope^[63]; (b) nodal surface in BaMX₃^[60].

2018年, Wu等^[63]对节面进行了系统的研究, 揭示了之前发现的节面的拓扑性质, 并将它们归入两种不同的类型. 他们还进一步将节面推广到具有SOC的系统以及具有磁性的系统, 扩展了可能出现节面的材料体系. 基于理论分析得到的对称性条件, 在这个工作以及后续的工作中, 又有不少具有节面的真实材料被发现, 例如K₆YO₄, Ta₃TeI₇, CsCrI₃, 和Ti₃Al等^[63,115].
2

3.2.节面的分类

-->

3.2.节面的分类

图14(a)和图14(b)中的节面是很不相同的: 图14(a)中的节面出现在布里渊区的内部, 而图14(b)中的节面则固定在布里渊区边界的平面上. 文献[63]提出了两种类型的节面, 分别对应着图14中的两种情况(注意: 这里的两个节面都要求没有SOC, 因此在这一小节的讨论考虑没有SOC的情况).
3

3.2.1.第一类(class-I)节面和Z₂拓扑电荷

-->

3.2.1.第一类(class-I)节面和Z₂拓扑电荷

第一类节面对应着三维碳材料(图14(a))中的节面. 这个体系具有时间反演和中心反演对称性, 因此也就有PT对称性. 同时, 这里还有一个非常重要的对称性, 即2.2节中提到过的子晶格对称性. 对图14(a)中的具体例子来说, 这表示可以把晶格分成两组, 每一组中的原子都只和另一组中的有耦合. 在能谱上, 这个对称性表现为能带结构是上下对称的. 当然, 在真实体系中, 这个子晶格对称性不可能是严格的: 总是多少存在次近邻原子轨道之间的跃迁, 材料的能谱也不可能是严格上下对称的. 但是在不少材料中, 这个对称性在低能(即费米能附近)是一个很好的近似. 特别在很多单质轻元素材料中, 例如图14(a)对应的碳材料中, 子晶格对称性可以保持得非常好.
当存在子晶格对称性时, 系统的哈密顿量总可以化为如下的块矩阵形式:

${\cal H}\left( {{k}} \right) = \left[ {\begin{array}{*{20}{c}}{}&{Q\left( {{k}} \right)}\\{{Q^\dagger }\left( {{k}} \right)}&{}\end{array}} \right].$

因为又存在PT对称性(并且无SOC), Q总可以通过幺正变换化为一个实矩阵. 在拓扑上, 对应着一个k点的哈密顿量可以分为两类, 由Q的行列式的符号${\rm{sgn}}\left[ {{\rm{Det}}\;Q\left( {{k}} \right)} \right]$

所决定(这里考虑的是存在能隙, 即不在节面上的k点; 在节面上时, Q的行列式为零). 因此, 布里渊区内存在能隙的k点可以分为两类, 对应着两种区域, 而这两种区域之间的边界(畴壁)则对应着节面. 基于这一理解, 我们可以对第一类节面定义一个Z₂的拓扑电荷:

$\nu = \left( {{\rm{sgn}}\left[ {{\rm{Det}}\;Q\left( {{{{k}}_1}} \right)} \right] - {\rm{sgn}}\left[ {{\rm{Det}}\;Q\left( {{{{k}}_2}} \right)} \right]} \right)\;{\rm{mod}}\;2,$

这里k₁和k₂是节面两边的两个点. 对图14(a)中碳材料的模型计算验证了图14(a)中节面具有的非平庸拓扑电荷.
3

3.2.2.第二类(class-II)节面

-->

3.2.2.第二类(class-II)节面

第二类节面是由体系非简单对称性所要求的一种必要的(essential)能带结构. 图14(b)对应的材料具有一个二度的螺旋轴(screw axis)${S_{2 z}}:\left( {x, y, z} \right) \to \left( { - x, - y, z + {1}/{2}} \right)$

, 同时还有时间反演对称性. 这两者的联合对称操作满足

${\left( {T{S_{2z}}} \right)^2} = {{\rm{e}}^{ - {\rm{i}}{k_z}}}.$

在布里渊区的边界k_z = π平面的每一个k点上, 都有${\left( {T{S_{2 z}}} \right)^2} = - 1$

, 因而就会产生一个Kramers二度简并. 所有这些简并点就组成了一个节面. Zhao等^[116]指出这种非简单对称性导致的简并对应着一种莫比乌斯带形式的能带拓扑结构, 可以与用对称性算符相联系的一个绕数来刻画.
这里对两类节面做一个比较. 由于子晶格对称性, 第一类节面在能量上是平的, 并且固定在费米面处. 而它们在布里渊区中的位置则不固定. 图14(a)中的情况有一对由时间反演(或空间反演)操作联系的节面. 通过调节系统参数, 这两个节面的位置和形状都可以变化, 也可能合并成一个单独的球状节面. 对于第二类节面, 它们的能量不固定, 节面上的点一般都会有能量的起伏(而且也不一定在费米面附近), 然而它们在布里渊区中的位置是固定的, 总是出现在边界的平面上. 前面提到第二类节面是一种必要的能带简并, 是完全由对称性所决定的. 在这个意义上, 第一类节面就是一种偶然的能带简并, 它的产生需要在布里渊区的某些区域中出现能带反转. 由于这个原因, 也由于子晶格对称性在真实材料中比较难得, 第一类节面比较少见, 而第二类节面的材料则比较容易寻找(如文献[63]中讨论的K₆YO₄和TlMo₃Te₃, 见图15).

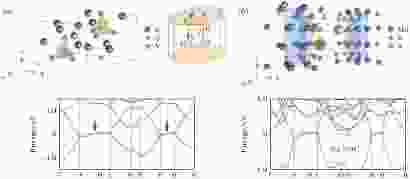图 15 具有第二类节面的材料　(a) K₆YO₄; (b) TlMo₃Te₃^[63]
Figure15. Materials with Class-II nodal surfaces: (a) K₆YO₄; (b) TlMo₃Te₃^[63].

2

3.3.自旋轨道耦合作用下稳定的节面

-->

3.3.自旋轨道耦合作用下稳定的节面

上面讨论的那些例子都是在没有SOC的系统中才可以稳定存在的. 当加入SOC后, 这些节面会全部或者部分地打开能隙. 比如对图15中的TlMo₃Te₃, 加上SOC后, 节面上的大部分点都会解除简并. 对第一类节面, 如图14(a)中那个碳材料的节面, 也有类似的结果. 只是由于碳本身的SOC非常小, 在节面处打开的能隙通常可以忽略不计.
那么在SOC作用下是否仍然存在稳定的节面呢? Wu等^[63]给出肯定的答案, 指出当体系具有第二类节面的TS_2z对称性, 同时PT对称性破缺的时候, 就可以存在SOC下稳定存在的节面. 这里, PT对称性破缺是一个必要条件, 因为如果具有PT对称性, 那么每个能带都至少是二重简并的, 于是节面就必须是四重简并, 但是没有对称性可以保证在一个面上的每一点都有四重简并, 所以节面的稳定存在就必须要求PT被破坏. 图16(a)和图16(b)中展示了在半导体材料Ta₃TeI₇中的这种节面.

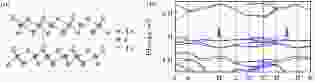图 16 SOC作用下稳定的节面　(a)展示了Ta₃TeI₇晶体结构; (b)是Ta₃TeI₇在考虑SOC时的能带结构; 能带在考虑SOC时没有打开能隙^[63]
Figure16. Nodal surface robust against SOC: (a) Crystal structure of Ta₃TeI₇; (b) is the band structure of Ta₃TeI₇ in the presence of SOC with no gap opening^[63].

2

3.4.磁性材料中的节面

-->

3.4.磁性材料中的节面

注意到对第二类节面(3.2节)的讨论中, 真正重要的是TS_2z这个联合对称性, 而并不要求单独的T或S_2z被保持. 而且TS_2z本身就属于一种磁性空间群的对称操作. 因此第二类节面的概念可以很自然地推广到磁性材料中.
文献[63]中分别讨论了体系没有SOC和有SOC的情况下存在节面的一组充分条件. 当体系没有SOC(或SOC可以忽略)时, 那么S_2z螺旋轴的存在就可以保证在k_z = π平面上出现的节面. 当体系具有SOC时, 这个条件变为: TS_2z对称性被保持, 同时PT对称性必须破缺. 图17给出了一个铁磁节面金属CsCrI₃的例子. 它的晶格具有S_2z对称性. 在不考虑SOC时, 它的能带在k_z = π平面上出现节面. 考虑SOC后, 依赖于磁化方向, 当TS_2z对称性被保持时, 节面就被保持(图17(c)); 当TS_2z被破坏时, 节面也就被破坏(图17(d)). 在以上这些情况中, PT对称性总是破缺的.

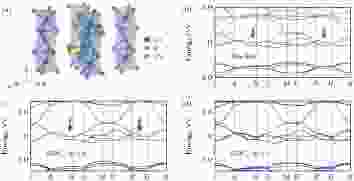图 17 磁性材料中的节面　(a) CsCrI₃晶体结构; (b)不考虑SOC时的能带结构; (c), (d)考虑SOC时, 磁矩分别沿面内和面外时的能带结构^[63]
Figure17. Nodal surface in magnetic materials: (a) The crystal structure of CsCrI₃; (b) the band structure of CsCrI₃ without SOC; (c) and (d) band structures with magnetic moment along x and z directions respectively^[63].

2

3.5.多节面金属和不可行定理

-->

3.5.多节面金属和不可行定理

在上面的讨论中看到, 在很多情况下, TS_2z对称性都保证了在k_z = π平面上的节面. 那么假如同时具有两个或三个TS_2i对称性$(i=x, y, z)$

, 系统就会在布里渊区的多个边界上存在节面. 图18显示了这样的具有多个节面的例子.

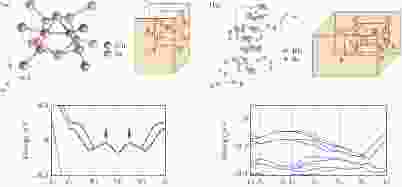图 18 存在多个节面的材料　(a) Cu₃Se₂; (b) Rb₂Se₅; 布里渊区中的节面分布用橙色标记^[63]
Figure18. Materials with multiple nodal surfaces: (a) Cu₃Se₂; (b) Rb₂Se₅. The location of the nodal surfaces is indicated by the orange color^[63].

这种多节面金属会带来什么样的特殊性质呢? 在近期工作中^[117], Yu等^[118,119]给出了一个有趣的结果: 它可以用来绕过Nielson-Ninomiya不可行定理(no-go theorem). 对于这个定理, 大多数文献中的表述是: 无相互作用的格子模型(lattice model)的能带中的外尔点必须要成对出现, 也就是说不可能存在单独的外尔点. 这个定理的一个直接后果就是在系统表面上会存在连接外尔点的投影的费米弧. 这些要求在迄今为止所有具有外尔点的材料中都得到了验证. 而余智明等发现, 在一个所有布里渊区的边界都是节面的多节面金属中, 布里渊区内部允许存在单独的外尔点(如图19所示). 并且在表面上, 也可以不存在任何从这个外尔点发出的费米弧(图19(c)和图19(d)). 文献[117]中给出了具体的格子模型, 分别在有SOC和没有SOC的情况下验证了这两点结论.

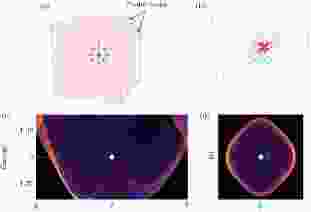图 19 绕过Nielson-Ninomiya不可行定理的方法　(a)一个单独外尔点的示意图; (b)贝利曲率分布; (c), (d)显示了在表面上不存在连接单外尔点的费米弧表面, 白色点标记了体内外尔点在表面的投影^[117]
Figure19. A method to circumvent the Nielson-Ninomiya no-go theorem: (a) Schematic figure showing the single Weyl point; (b) Berry curvature distribution; (c), (d) show that there is no surface Fermi arc emitted from the Weyl point, the white dot labels the surface projection of the Weyl point^[117].

需要指出的是, 上面的结果并不代表Nielson-Ninomiya不可行定理被违反了. 这个定理其实有一个隐含的前提条件, 即体系无能隙激发必须只包含外尔点. 在文献[117]的例子中, 由于节面的存在, 费米面处除了外尔点, 必定要包含其他穿过费米面的能带, 因此不满足这个隐含的前提. 在大部分文献的讨论中, 这个前提条件都没有得到重视, 可能是因为现有的外尔半金属材料中能带本身就很复杂(因而不满足这个前提). 这里的多节面金属的例子无疑加深了我们对这个基本定理的理解.

本站小编 Free考研考试/2021-12-29

English Abstract

Progress on topological nodal line and nodal surface

1.School of Physics, Southeast University, Nanjing 211189, China
2.Research Laboratory for Quantum Materials, Singapore University of Technology and Design, Singapore 487372, Singapore

Corresponding author:Wang Shan-Shan, 101012564@seu.edu.cn

全文HTML

2.1.节线的概念

2.2.节线的对称性保护

2.3.节线的特征和分类

2.4.二维材料中的节线

2.5.磁性材料中的节线

2.6.节线对应的拓扑表面态

3.1.节面的概念

3.2.节面的分类

3.2.1.第一类(class-I)节面和Z₂拓扑电荷

3.2.2.第二类(class-II)节面

3.3.自旋轨道耦合作用下稳定的节面

3.4.磁性材料中的节面

3.5.多节面金属和不可行定理

相关话题/材料 结构 系统 金属 空间

领限时大额优惠券,享本站正版考研考试资料!

拓扑半金属材料角分辨光电子能谱研究进展

拓扑半金属ZrSiSe器件中面内霍尔效应的观测

拓扑材料等离激元谱学研究

拓扑半金属的红外光谱研究

双凹型谐振腔结构的金属半导体纳米激光器的数值仿真

半导体激光器储备池计算系统的工作点选取方法

氮化物子带跃迁探测器材料结构对器件效率的影响

人工磁导体对无线能量传输空间场的调控

金属开口环谐振器超构分子中二次谐波偏振态的调控

薄膜与Helmholtz腔耦合结构低频带隙