摘要:孪晶界是单层过渡金属二硫族化物材料中的一种重要结构缺陷. 本文通过分子动力学模拟结合Stillinger-Weber势函数研究单轴拉伸过程中孪晶界对单层MoS₂力学行为的影响. 结果表明: 1)孪晶界能够诱发裂纹在孪晶界附近形核, 并促使裂纹沿界面扩展, 从而降低晶体的断裂应变; 2)温度的升高能够加剧孪晶界附近的裂纹形核过程, 从而进一步减弱单层MoS₂的断裂强度和断裂应变; 3)孔洞能够造成应力集中, 从而进一步触发断裂过程, 但孪晶界能够阻碍孔洞应力场的扩散, 从而延缓单层MoS₂材料的断裂过程; 4)孪晶片层间距对单层MoS₂断裂应变具有重要影响, 特别是对于含孔洞的单层MoS₂材料, 材料断裂应变能够随着片层间距的减小而显著提高.
关键词: 单层二硫化钼/
孪晶界/
力学性能/
分子动力学

English Abstract

全文HTML

--> --> -->

石墨烯的出现带来了二维材料的蓬勃发展^[1,2]. 近年来, 与石墨烯结构相似的单层过渡金属二硫族化物(transition metal dichalcogenide crystals, TMDCs)由于其独特的物理性能展示出广阔的应用前景, 从而引起了材料科学和物理学界的极大关注^[3-6], 相应地其结构和力学性能亦成为研究的焦点. 一方面, 良好的结构稳定性能够提高单层TMDCs器件的使用寿命, 是器件发挥物理功效的基础; 另一方面, 单层MoS₂的能带结构^[7]和磁通量^[8]的应变调控研究结果表明单层TMDCs结构和力学性能的研究能够促进柔性电子器件的发展. 在此背景下, 国内外若干研究单位相继开展了关于单层TMDCs材料结构和力学性能的研究工作. 例如, Dang等^[9]研究了晶界和点缺陷对单层MoS₂拉伸行为的影响; Casillas等^[10]研究了单层至少数几层的MoS₂弹性变形过程; 李明林等^[11]研究了单层MoS₂力学性能随温度的变化趋势以及手性的影响; Wang等^[12]研究了单层MoS₂结构相变导致的晶体塑性问题; Wu等^[13]研究了晶粒尺寸对单层多晶MoS₂拉伸强度的影响. 由于单层TMDCs样品仅几个原子层厚, 在制备和测试过程中存在诸多困难和挑战^[14-16], 因此以第一性原理计算和分子动力学模拟为代表的纳米尺度计算模拟方法成为分析单层TMDCs材料结构和力学性能的重要手段^[17,18].
过去几年来, 人们对单层TMDCs的结构缺陷进行了大量计算模拟研究工作^[19,20]. 晶界是单层TMDCs材料的重要结构缺陷之一, 几乎不可避免地存在于一些广为使用的制备方法(如化学气相沉积法)所制备出的实验样品之中, 因而日益引起人们的关注^[21,22]. 其中, 孪晶界是一种具有低应变能的特殊晶界, 界面两侧晶体呈镜像对称结构, 在2013年van der Zande等^[23]的电镜实验中被观察到, 并根据Barja等^[24]的研究展示出独特的电学性能. 然而, 孪晶界对单层TMDCs力学行为的影响机制却缺乏深入系统的研究^[25]. 本文以单层二硫化钼为模型材料, 利用分子动力学拉伸模拟为上述问题的解答提供了有益参考.

如图1(a)所示, 类石墨烯的单层MoS₂具有“夹心三明治”形貌的层状结构, 中间的红色Mo原子层被夹在上下两层蓝色S原子中间, 模型沿x轴镜像对称, 其中D表示界面单侧的晶体尺寸. 模型沿x, y, z三个方向采用周期性边界条件, 为了在z方向上避免薄膜周期镜像彼此之间的影响, 保证薄膜的单层属性, 设置毗邻镜像之间的真空层厚度L_z = 4 nm. 为了对比孪晶界的影响, 本文还实施了理想单晶模型的拉伸模拟, 晶体构型如图1(b)所示. L_x和L_y的具体参数列于表1中. 单层MoS₂原子间相互作用过程由Jiang等^[26]开发的Stillinger-Weber (SW)势函数^[27]描述. 拉伸过程通过Lammps软件^[28]完成, 模拟结果通过OVITO软件^[29]输出原子构型. 模型以每皮秒0.1%的应变率对单层MoS₂沿x轴施加应变, 通过NPT系综获得较为合理的弛豫构型. 分子动力学模拟的时间步长设为0.5 fs, 拉伸过程最大持续800000步, 相应最大应变不超过40%. 系统温度设为1 K, 温度和压强均采用Nose-Hoover方法调控.
图 1 单层MoS₂的分子动力学模型　(a)含孪晶界; (b)不含孪晶界
Figure1. Molecular dynamics model of mono-layer MoS₂: (a) With twin boundaries; (b) without twin boundary.

	Lx/nm	Ly/nm
含孪晶模型	25.96	5.70
不含孪晶模型	13.16	5.70

表1模型平面内初始尺寸
Table1.Initial in-plane size of model.

根据Virial应力原理计算整个试样的拉伸应力^[30]

$\sigma = - \bigg[ {\sum\limits_{k = 1}^N {{m_k}{v_k}_x{v_k}_x + \sum\limits_{k = 1}^{N'} {r{}_{kx}{f_{kx}}} } } \bigg]/({L_x}{L_y}{L_z}),$

其中, N表示系统原子总数; m为原子质量; v和f分别为原子的速度和所受的力; 下标k表示第k个原子序数; L_x, L_y和L_z分别为模型拉伸过程中的即时构型尺寸.

图2给出了单层MoS₂在拉伸过程中的应变能和应力曲线. 开始阶段, 理想模型和含孪晶界模型的应变能、应力曲线均单调上升, 表示材料处于弹性变形过程, 当应变约为18%时, 两曲线出现第一次突降, 这是由于少数局部原子的位置在拉伸过程中出现了微小变化, 从而造成了应变能和应力的释放. 与含孪晶界的模型相比, 理想模型尺寸较小, 原子数量相对也较少, 所以释放的应变能在总能量中的比重更大, 因此图2(a)中的曲线突降更显著. 两模型的应变能和应力曲线经过A点后迅速下降, 这意味着材料发生了脆性断裂过程, 因此A点对应的应力和应变标记为晶体的断裂强度和断裂应变. 对于不含孪晶界的理想晶体, 断裂应变约为29%, 与Xiong等^[30]的研究结论(断裂应变约为32%、应力曲线首次突降发生于应变17%处)相当一致, 表明了当前模型参数选择的可靠性. 单层TMDCs材料在拉伸过程中的脆性断裂行为最近已经被实验和模拟所证实^[16]. 与理想晶体相比, 含孪晶界晶体的断裂强度和断裂应变均略有下降, 表明两者断裂过程的微观机制可能存在差异.
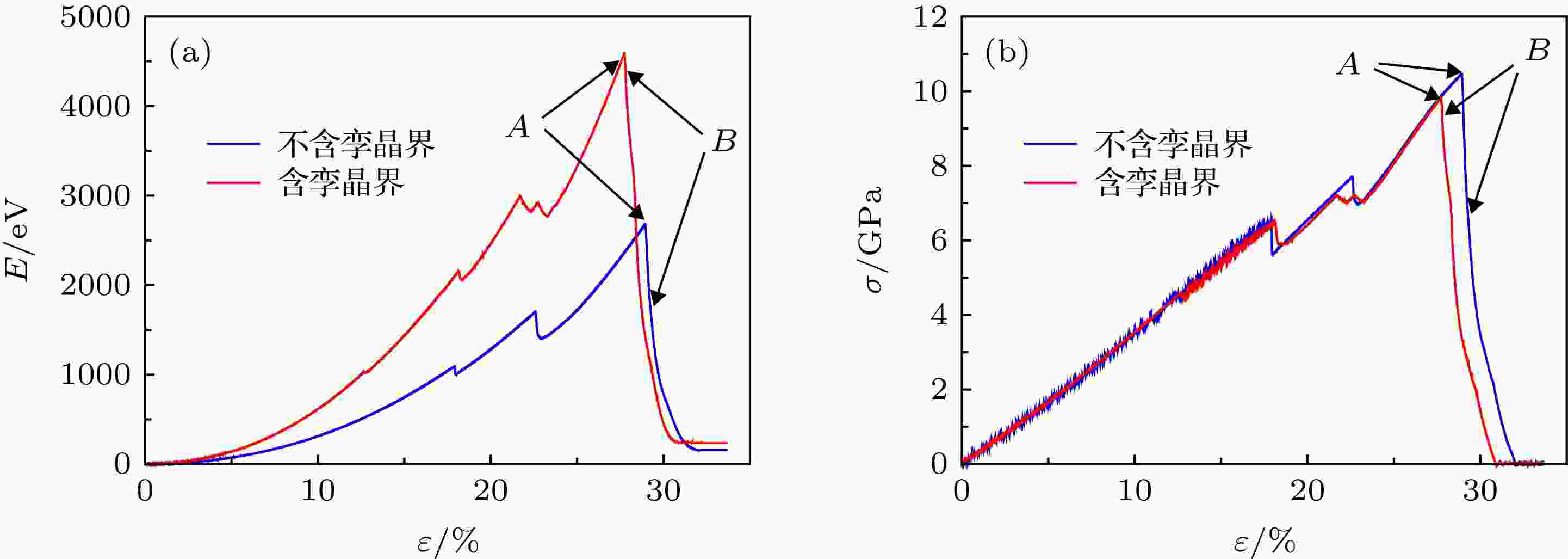图 2 (a)应变能E; (b)应力σ, 其中ε表示应变
Figure2. (a) Strain energy E and (b) stress σ, where ε denotes strain.

图3给出了断裂应变前后的模型原子结构. 从图3可以看出, 两模型的微观断裂机制确实存在差别. 对于含孪晶界的模型, 裂纹沿孪晶界形成, 并迅速扩展; 对于不含孪晶界的理想材料, 模拟结果与前人研究报道一致^[11], 裂纹的形成形核于微观孔洞, 并在周围基体中激发新的微观孔洞.
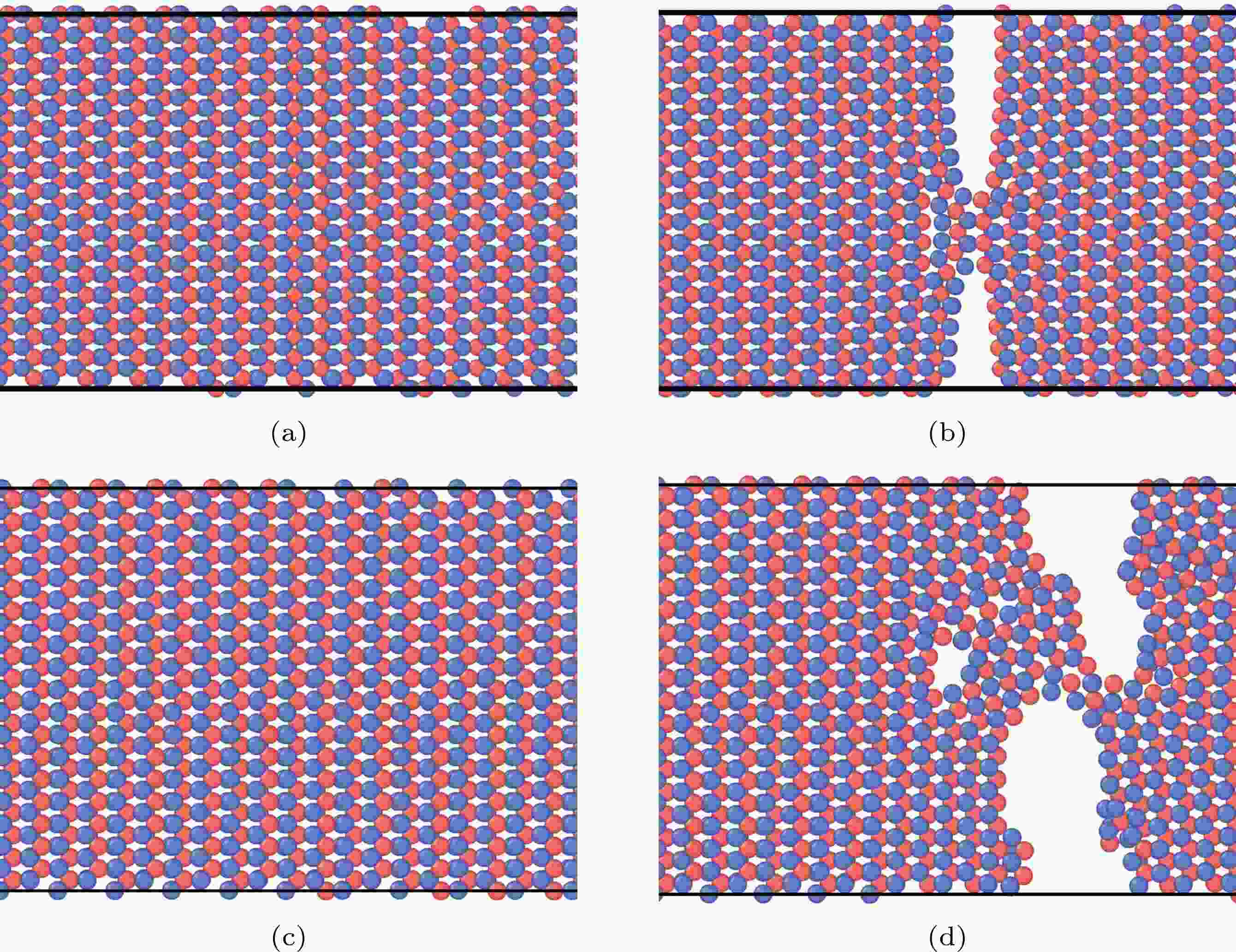图 3 与拉伸曲线相对应的原子结构　(a)孪晶界, A点, ε = 27.74%; (b)孪晶界, B点, ε = 27.79%; (c)不含孪晶界, A点, ε = 28.94%; (d)不含孪晶界, B点, ε = 29.24%
Figure3. Atomic structures corresponding to the tensile curves: (a) With twin boundary, point A, ε = 27.74%; (b) with twin boundary, point B, ε = 27.79%; (c) without twin boundary, point A, ε = 28.94%; (d) without twin boundary, point B, ε = 29.24%.

2

-->

4.1.温度和孪晶片层间距的影响

上面模拟结果显示了孪晶界在1 K条件下对脆性断裂的影响. 过去一些研究工作表明温度是单层TMDCs材料结构、物理性能的重要影响因素^[11,31]. 受此启发, 本文针对25.96 nm × 5.70 nm尺寸模型分别调整系统温度为300和600 K, 获得不同温度下的应变能和应力曲线, 结果见图4. 从图4可知, 随温度的升高, 材料仍表现出脆性断裂行为, 但断裂强度和断裂应变显著下降, 同时曲线变得光滑, 表明局部原子位置扰动造成应变能释放的影响随着温度升高而减弱. 此外, 对于纳米金属晶体, 孪晶界能够显著提升材料强度^[32]. 本文在系统温度保持为1 K的条件下, 改变模型x方向的尺寸L_x, 观察孪晶片层间距D (= L_x/2)的影响, 结果见图4(c)和图4(d), 可见, 随着孪晶片层间距的减小, 断裂应变有所增加.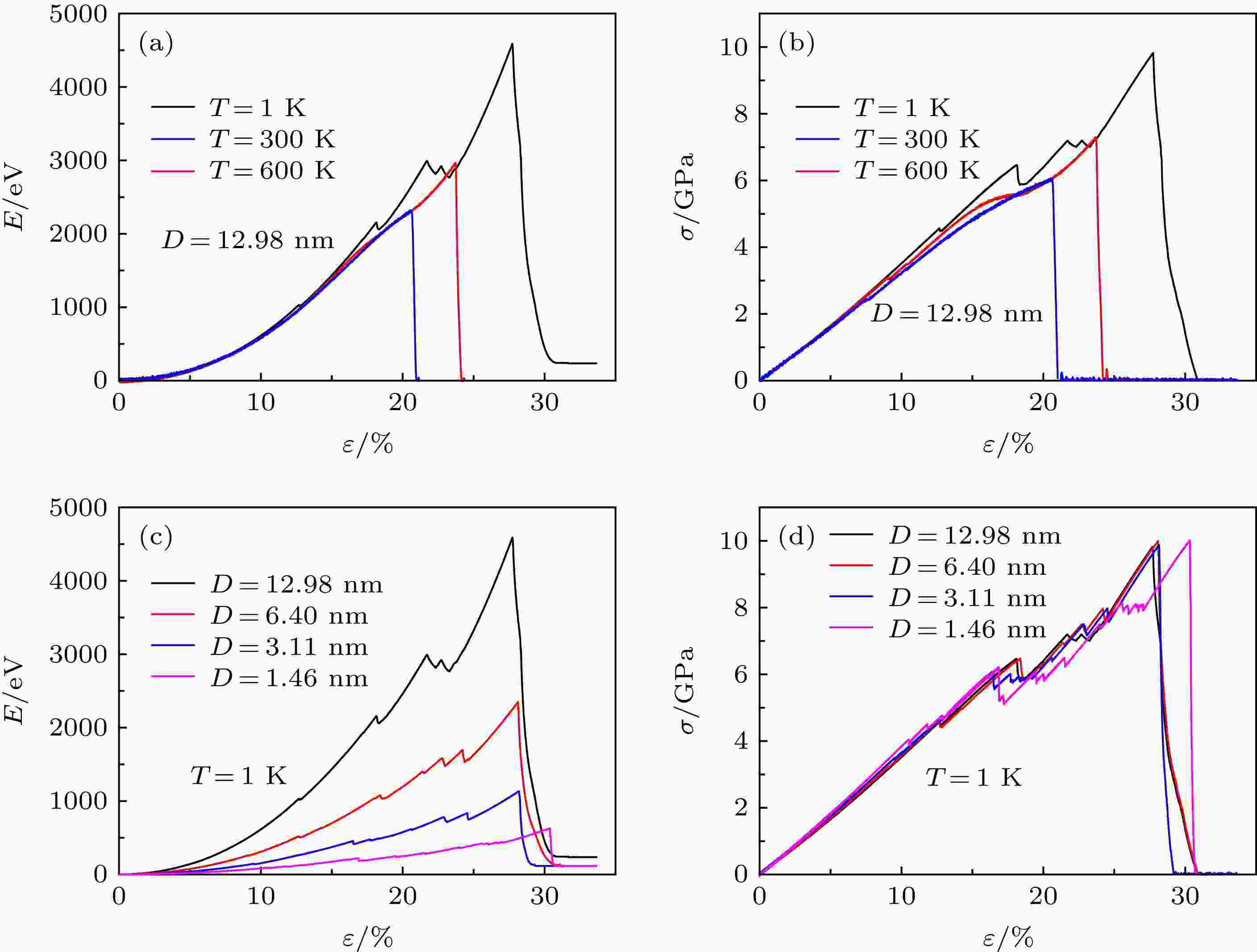
图 4 温度和孪晶界面间距的影响　(a)不同温度下的应变能; (b)不同温度下的应力; (c)不同孪晶片层间距下的应变能; (d)不同孪晶片层间距下的应力
Figure4. Effects of temperature and the twin lamellar spacing: (a) Effect of temperature on strain energy; (b) effect of temperature on stress; (c) effect of twin lamellar spacing effect on strain energy; (d) effect of twin lamellar spacing effect on stress.

2 -->

4.2.微观孔洞的影响

孔洞是晶体中常见的缺陷, 通常会显著改变材料的力学性能^[9,33]. 为了观察孔洞对含孪晶界晶体拉伸行为的影响, 本文在基体中引入一个Mo₃S₂型空洞, 即在理想晶体中去掉上下2个S原子以及与其形成价键的3个Mo原子, 再按照前述方式进行拉伸, 系统温度设为1 K. 整个试样的拉伸应力曲线见图5, 其中, 显示了图2(b)所示应力曲线, 以便于比较. 对比可见, 虽然孔洞较小, 在模型中体积占比不足1%, 但由于孔洞的存在, 含/不含孔孪晶界的两个晶体断裂强度降幅均超过35%, 断裂应变降幅超过22%. Peron-Luhrs等^[34]发现孔洞相对于整个样品的体积占比与金属晶界临界切应力的衰减呈线性关系^[34], 然而对于单层MoS₂, 孔洞体积占比对晶界弹性行为的影响规律仍有待进一步研究.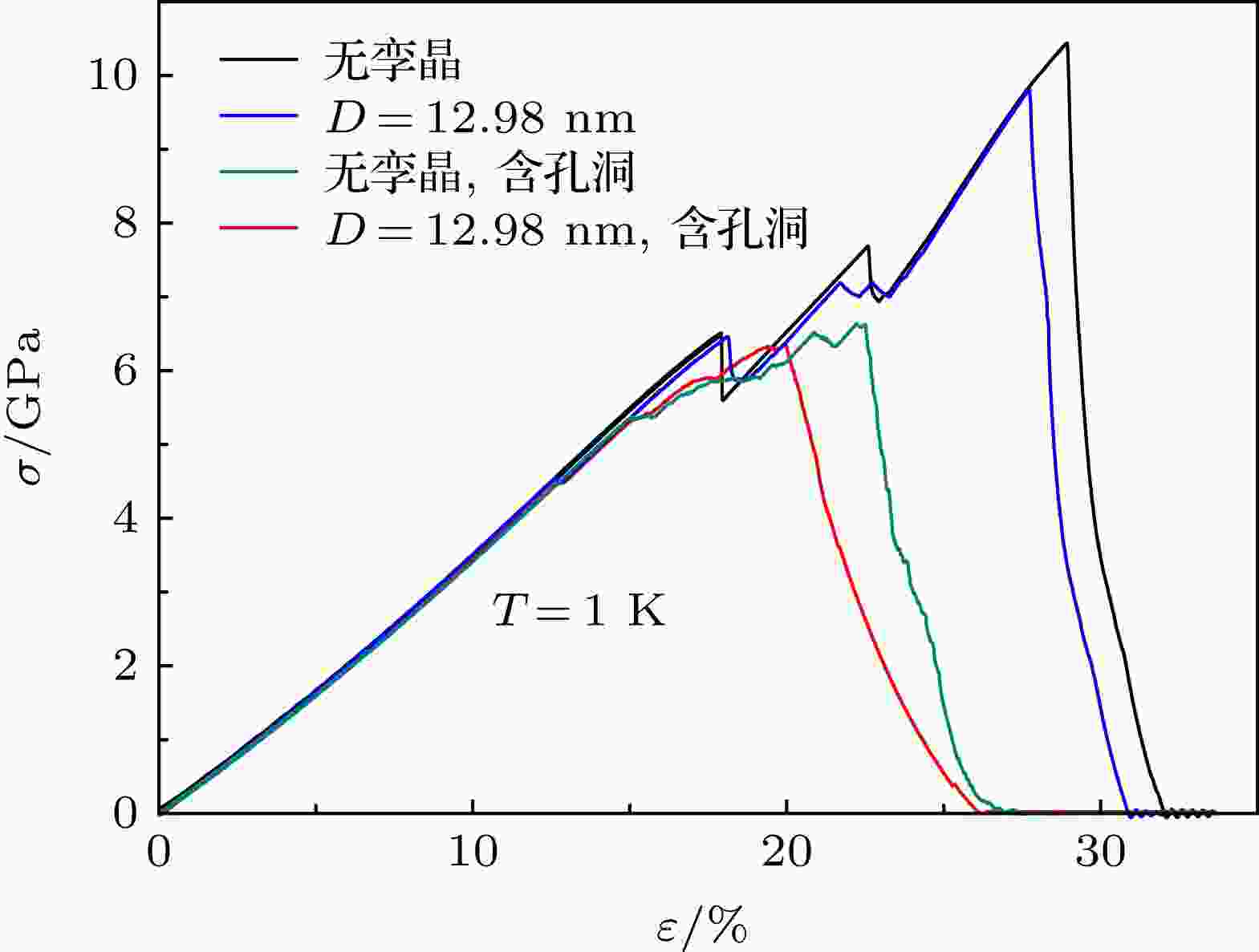
图 5 孔洞对拉伸应力的影响
Figure5. Effect of a Mo₃S₂ void on the tensile stress of specimen

图6、图7和图8依次给出了材料断裂前后的原子结构和应力分布状态, 其中, 应力分布状态通过(1)式去掉求和符号并将试样体积代之以原子体积而求得. 可以看到, 即使存在孪晶界, 孔洞的存在仍会造成应力集中, 并率先引起局部相变^[35], 当局部相变不足以释放积累的应变能时, 诱发裂纹在其附近萌生, 催发脆性断裂过程. 值得注意的是, 红色曲线断裂阶段的斜率要明显小于蓝色曲线断裂阶段的斜率, 说明D = 12.98 nm的含孪晶界模型的断裂过程明显受到了延滞, 图8显示这是由于孪晶界对孔洞的应力场传播起到了明显的阻碍作用, 孪晶片层间距越小, 这种阻碍作用越明显.
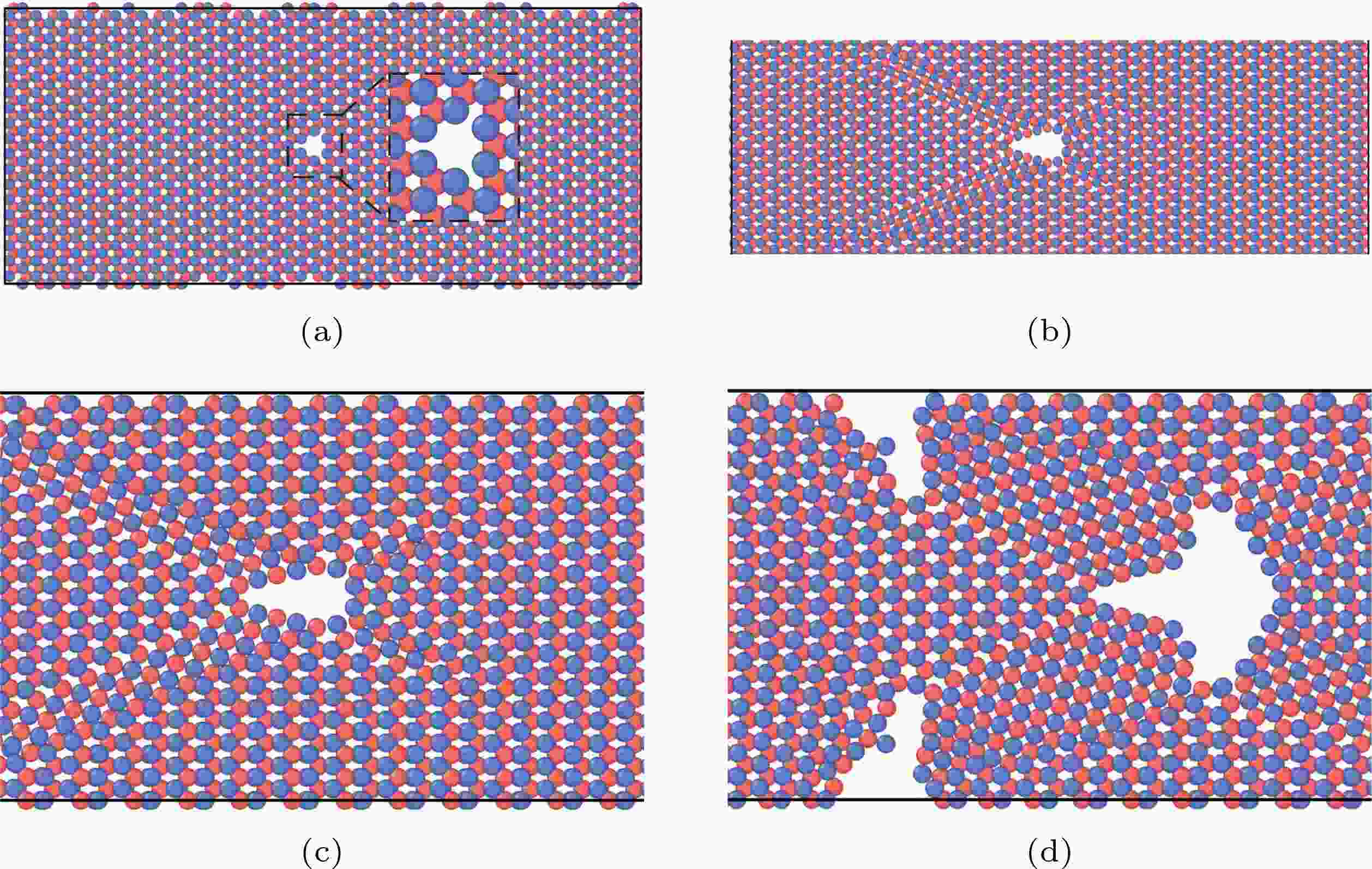图 6 不含孪晶界的带孔洞的单层MoS₂　(a) ε = 0; (b) ε = 22.514%; (c) ε = 22.514%, 放大视图; (d) ε = 23.345%, 放大视图
Figure6. Voided mono-layer MoS₂ without twin boundary: (a) ε = 0; (b) ε = 22.514%; (c) ε = 22.514%, enlarged view; (d) ε = 23.345%, enlarged view.

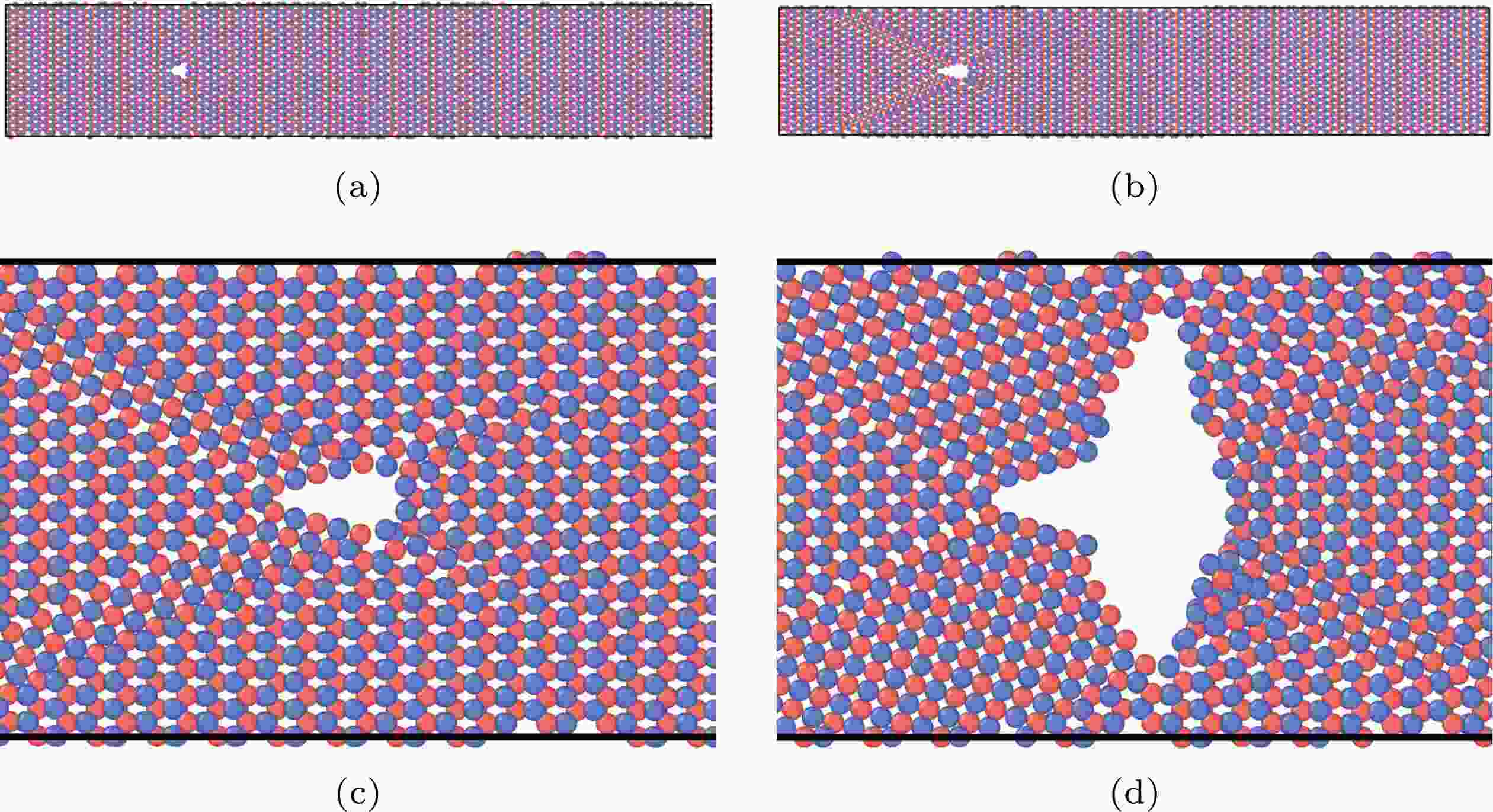图 7 含孪晶界的带孔洞的单层MoS₂　(a) ε = 0; (b) ε = 19.971%; (c) ε = 19.971%, 放大视图; (d) ε = 20.779%, 放大视图
Figure7. Voided mono-layer MoS₂ with twin boundaries: (a) ε = 0; (b) ε = 19.971%; (c) ε = 19.971%, enlarged view; (d) ε = 20.779%, enlarged view.

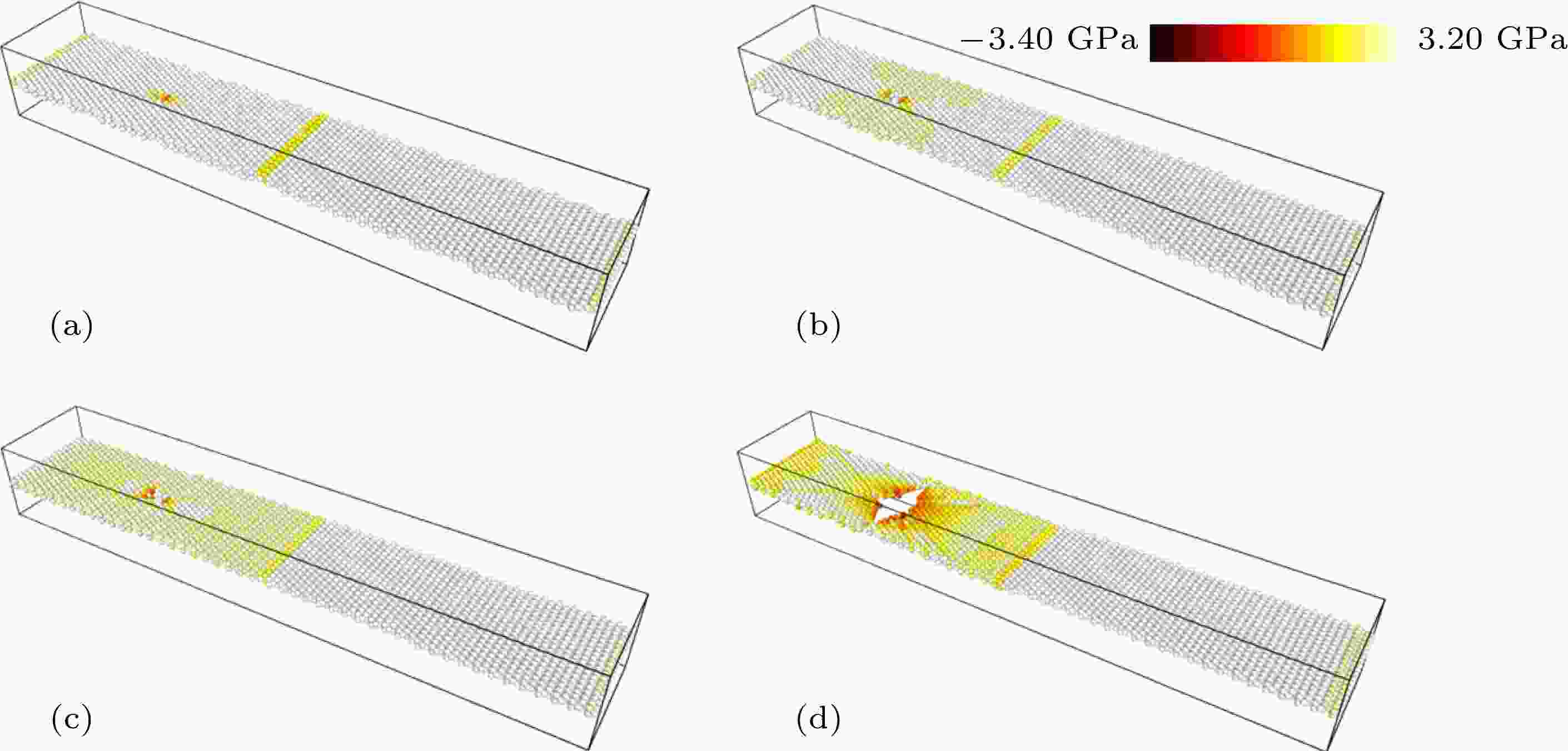图 8 带孔洞的含孪晶界模型断裂前后应力分布状态　(a) ε = 14.34%; (b) ε = 16.92%; (c) ε = 18.25%; (d) ε = 20.87%
Figure8. Distribution of tensile stress in the voided mono-layer MoS₂ sheet with twin boundaries: (a) ε = 14.34%; (b) ε = 16.92%; (c) ε = 18.25%; (d) ε = 20.87%.

2 -->

4.3.断裂应变与孪晶片层间距之间的关系

对于块体纳米孪晶金属来说, 由于孪晶界对位错、层错等缺陷的运动具有强烈的阻碍作用, 因此可以显著提高材料屈服强度, 并且在孪晶片层间距不小于15 nm时^[36], 屈服强度σ_y与孪晶片层间距λ存在如下关系:

${\sigma _y} \propto {\lambda ^{ - 1/2}}.$

具有准二维结构的单层MoS₂材料, 也可以尝试寻找类似的关联, 如图9所示, 断裂应变 ε_A可以看作孪晶片层间距 D 的函数, 即 ε_A = ε_A(D^–1). 图4(d)的应力曲线已经表明, 几个不同孪晶片层间距的样品具有几乎相同的断裂强度. 这意味着样品的断裂过程均沿着孪晶界发生, 且均需达到孪晶界裂纹形核的临界应力. 尽管当应变超过18%时, 应力与应变不再呈理想的线性关系, 但仍然可以做近似线性分析: 假设孪晶界裂纹形核的临界应力为σ_A, 且$ \sigma_A = \mu \varepsilon_A $, $ \mu $为有效弹性模量, 由于样品内部渐次发生局部结构转变, 造成应力释放, 有效弹性模量$ \mu $会低于理想晶体杨氏模量$ \mu_0 $, D^–1 越大, 则单位体积内的孪晶界越多, 局部结构转变越容易发生, 应力释放越频繁, 有效弹性模量$ \mu $越小, 达到σ_A 需要的 ε_A 越大. 然而根据图9, 这种片层间距对断裂应变的影响仅在D很小时比较明显, 更加值得注意的是由于孪晶界与孔洞存在相互作用, 孪晶界密度的增加能够显著提高含Mo₃S₂孔洞晶体的断裂应变.
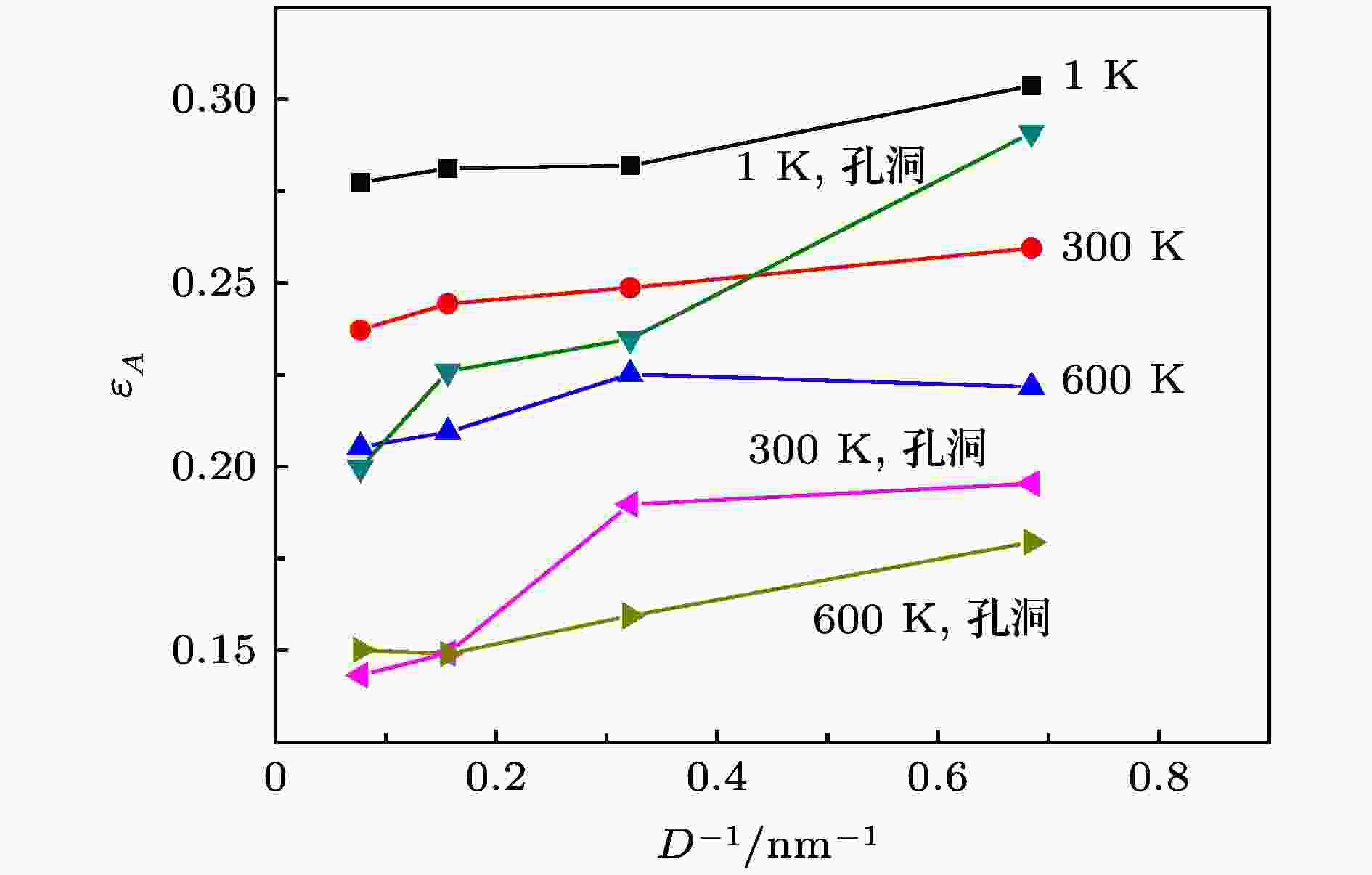图 9 断裂应变ε_A与孪晶片层间距D的关联
Figure9. Correlation of the fracture strain ε_A and the twin lamellar spacing D.

本文通过分子动力学模拟方法结合SW势函数研究了单轴拉伸过程中孪晶界对单层MoS₂力学行为的影响, 主要得出以下结论.
1)与理想晶体相比, 孪晶界能够诱发裂纹在孪晶界附近形核, 并促使裂纹沿界面扩展, 从而降低晶体的断裂强度和断裂应变; 温度的升高能够加剧孪晶界附近的裂纹形核过程, 从而进一步显著减弱单层MoS₂的断裂强度和断裂应变.
2)少量原子缺失造成的孔洞能够造成应力集中, 从而进一步触发脆性断裂过程, 降低含孪晶界单层MoS₂的断裂强度和断裂应变, 但是对于孪晶界包围的孔洞, 孪晶界能够有效阻碍孔洞应力场的传播, 进而延缓脆性断裂过程.
3)孪晶片层间距对单层MoS₂断裂应变具有重要影响, 特别是对于含孔洞的单层MoS₂材料, 材料断裂应变能够随着片层间距的减小显著提高.
需要指出的是, 真实的单层MoS₂孪晶界可能存在其他类型或其他晶体取向, 还有可能处于表面皱褶或临近杂质原子的环境中, 晶体甚至可能存在片层交叠, 这些结构变化均可能对材料拉伸行为造成影响. 如何考虑这些影响是本文后续工作拟研究解决的问题.