摘要:声波在含流体孔隙介质内传播的过程当中, 会产生耦合电磁波, 根据这一现象前人提出了声电效应测井的方法. 本文探究了井外为柱状双层孔隙地层声电效应测井耦合声电场的产生机理和传播规律. 通过计算电场支点的垂直割线积分, 得到以地层电磁波速度传播的界面转换电磁波. 对比不同夹层孔隙介质层厚的界面转换电磁波时域波形, 可以发现每一次地层纵、横波传播至界面发生折反射时, 都会产生界面转换电磁波, 这些成分构成了界面转换电磁波的总响应. 考察了孔隙介质流体矿化度对界面转换电磁波的影响, 发现当介质分界面两侧孔隙介质流体矿化度差异越大时, 界面转换电磁波的幅度越大, 且两个界面所产生的电磁波互不影响. 同时考察了仅存在矿化度界面的情况, 发现声波传播至矿化度界面处也会产生界面转换电磁波, 可以利用这一特性来探测井外介质电化学界面的位置. 研究界面转换电磁波对于认识柱状双层孔隙地层声电效应测井的界面响应规律具有重要意义.
关键词: 声电效应/
孔隙地层/
割线积分/
界面转换电磁波

English Abstract

全文HTML

--> --> -->

石油、天然气和水的储层主要为含流体的孔隙介质, 由于孔隙介质中双电层结构的存在, 声波在含液孔隙介质中传播时会产生耦合电磁波^[1,2]. 利用这一现象, 前人提出了声电效应测井的办法^[3,4], 即在井内流体放置声源, 在距离声源一定位置上放置接收器用来接收声波以及电磁波, 进而通过波的传播规律来分析地层信息. 近年来有关声电效应的研究备受关注^[5-7], 其在地震预报、油气储层勘探等领域有很大的应用潜力^[8,9]. 目前关于声电效应的理论公式推导、波场模拟等工作已广泛开展^[10], 声电耦合现象也能够在现场和实验室观测到^[8,11-13].
Pride^[1]在Biot^[14,15]孔隙介质理论的基础上推导了完整的声电耦合波控制方程, 为后续的工作奠定理论基础. 胡恒山和王克协^[3]推导了井轴上点声源激发的井内外声场和转换电磁场的计算公式, 并在后续的工作中^[4]给出了数值算例, 说明了转换电场的基本特性以及部分介质参数对声波以及转换电场的影响, 并且首次提出以电磁波波速传播的“电磁首波”的概念. 胡恒山等^[16]针对声电效应测井问题, 提出了一种简化算法, 该方法忽略转换电场对声场的影响, 对Pride声电控制方程组进行简化, 为声、电场求解提出了新的思路. Guan等^[17]则给出了利用似稳法计算声电效应测井井内声电场的合理性证明以及适用条件. Gao等^[18]利用似稳法和耦合法给出流体中多孔弹性空心圆柱内声电耦合波的传播规律, 考查了主要介质参数对声电耦合波的影响. Guan和Hu^[19]以及关威等^[20]是国际上最早开展采取有限差分方法模拟声电效应和电声效应测井声、电场相关工作的. 在单极点声源声电效应理论的基础上, 崔志文^[21]对多极源以及偏心源声电效应随钻测井的响应进行了理论求解、数值计算与分析. 丁浩然等^[22]将声电效应测井应用于随钻测井方法, 提出采用双声源后能够有效抑制钻铤波, 并且提高地层波信噪比. 对于井外为复杂结构孔隙介质的情况, Ding等^[23]模拟了井外为矿化度不连续地层的声电效应测井声电场. 赵永吉等^[24]对柱状分层孔隙介质的声场、电场进行了数值模拟, 并且在电场全波当中也发现了“电磁首波”的存在, 不过对于其产生机理以及传播规律并没有进行详尽的解释. 麻省理工学院最早展开声电测井的观测实验^[12,13]. Wang等^[25]通过实验证明, 可以利用声电测井方法评价地层渗透率, 并在后续的实验中^[26]给出了实验条件下声电信号的真实幅度, 给声电测井仪器的精度等参数提出了参照依据. Peng等^[27]通过对砂岩的实验探究了声电效应界面响应规律, 同时得到了可以通过声电效应反演渗透率的结论. Liu等^[7]在实验室中观测了垂直震电剖面的震电信号. Lu等^[28]则自行设计仪器现场探测, 发现了与预期一致声场和电场信号, 这为声电效应在现场探测的应用提供了很好的参考依据.
上述理论与模拟都仅限于对声电效应测井中声、电场的全波分析, 进行分波分析能够对某一种类的波进行详细分析, 可以深入探究其应用价值. 胡恒山^[29]分析了孔隙地层井壁上声波首波诱导电磁场的原因, 指出伴随声波首波的电场主要是由慢纵波势引起的. Hu等^[30]采用割线积分的办法计算了声电测井的电磁首波, 并证明它是以地层电磁波速度在井壁传播并返回井内的. 王治等^[31]采取围道积分的办法对井外为无限大均匀地层声电效应测井声场、电场进行了较为全面的分波分析, 计算并讨论了各个侧面波和模式波的电声激发比及其影响因素. Guan等^[32,33]以此为依据提出了基于声电效应测井的渗透率和弯曲度的反演方法. 但是目前针对井外为柱状分层结构孔隙介质的声电效应测井的分波分析以及对耦合声电场在柱状分层结构孔隙介质中的产生机理、传播和界面响应等规律认识较少. 本文在前人工作的基础上, 采用计算支点的垂直割线积分的方法, 计算了柱状双层孔隙介质声电效应测井的界面转换电磁波. 利用界面转换电磁波, 不仅能够清楚地接收到井壁以及井外地层分界面处的界面响应, 而且能够反映声波在介质内的折反射规律并用来探测井外介质厚度和介质电化学界面位置. 对于进一步认识井外为复杂分层结构孔隙介质的声电耦合波产生机理和传播规律有重要意义.

2

-->

2.1.Pride声电耦合方程组

由于孔隙介质中双电层结构的存在, 声波在孔隙介质中传播的过程中会产生耦合电磁波. 在均匀孔隙地层当中, Pride声电耦合波控制方程组的表达形式为^[1,34]:

$\nabla \times {{E}} = {\rm{i}}\omega {{B}},$

$\nabla \times {{H}} = - {\rm{i}}\omega {{D}} + {{J}},$

$\nabla \cdot \tau = - {\omega ^{{2}}}(\rho {{u}} + {\rho _{\rm{f}}}{{w}}),$

${{J}} = \sigma E + L( - \nabla P + {\omega ^2}{\rho _{\rm{f}}}{{u}}),$

$ - {\rm{i}}\omega {{w}} = L{{E}} + ( - \nabla P + {\omega ^2}{\rho _{\rm{f}}}{{u}})\kappa /\eta,$

$\tau = (H - 2G)(\nabla \cdot {{u}}){{I}} + C(\nabla \cdot {{w}}){{I}} + G(\nabla {{u}} + \nabla {{{u}}^{\rm T}}),$

$ - p = C\nabla \cdot {{u}} + M\nabla \cdot {{w}},$

${{B}} = \mu {{H}},$

${{D}} = \varepsilon {{E}},$

其中E为电场强度, D为电位移矢量, B为磁感应强度, H为磁场强度; 渗流位移w可以用流相平均位移${{{u}}_{\rm{f}}}$和固相平均位移u表示: ${{w }} =\phi \left( {{{{u}}_{\rm{f}}}{{ - u}}} \right)$, 其中?为地层孔隙度; p为孔隙流体压强, ${{\tau }}$为应力张量, I为二阶单位张量, η为孔隙中流体黏滞系数, ${\rho _{\rm{f}}}$为孔隙流体密度, ρ是地层密度, G是地层骨架剪切模量; H, C, M分别是四个独立的孔隙介质弹性模量; σ为电导率, ${\mu _0}$是真空磁导率, ε是真空电容率, L为动电耦合系数, 体现了声电耦合强弱, 含有L的(4)式和(5)式两式体现了声场弹性波与电磁波的耦合. 当L = 0时, 声场与电场解耦, Pride声电耦合方程组就退化为Biot孔隙介质弹性动力学方程组和Maxwell电磁方程组.
2 -->

2.2.径向分层地层声电效应测井波场数学表达式

本文研究的模型是井外为径向分层孔隙地层的声电效应测井问题, 模型示意图如图1所示. a为井孔半径, 井外介质由两层孔隙介质构成, 声源与电磁波接收器都位于井轴z. 孔隙介质1为有限厚度孔隙地层, 孔隙介质2为无限大孔隙地层, 界面I为井壁, 界面II为两层孔隙介质之间的界面.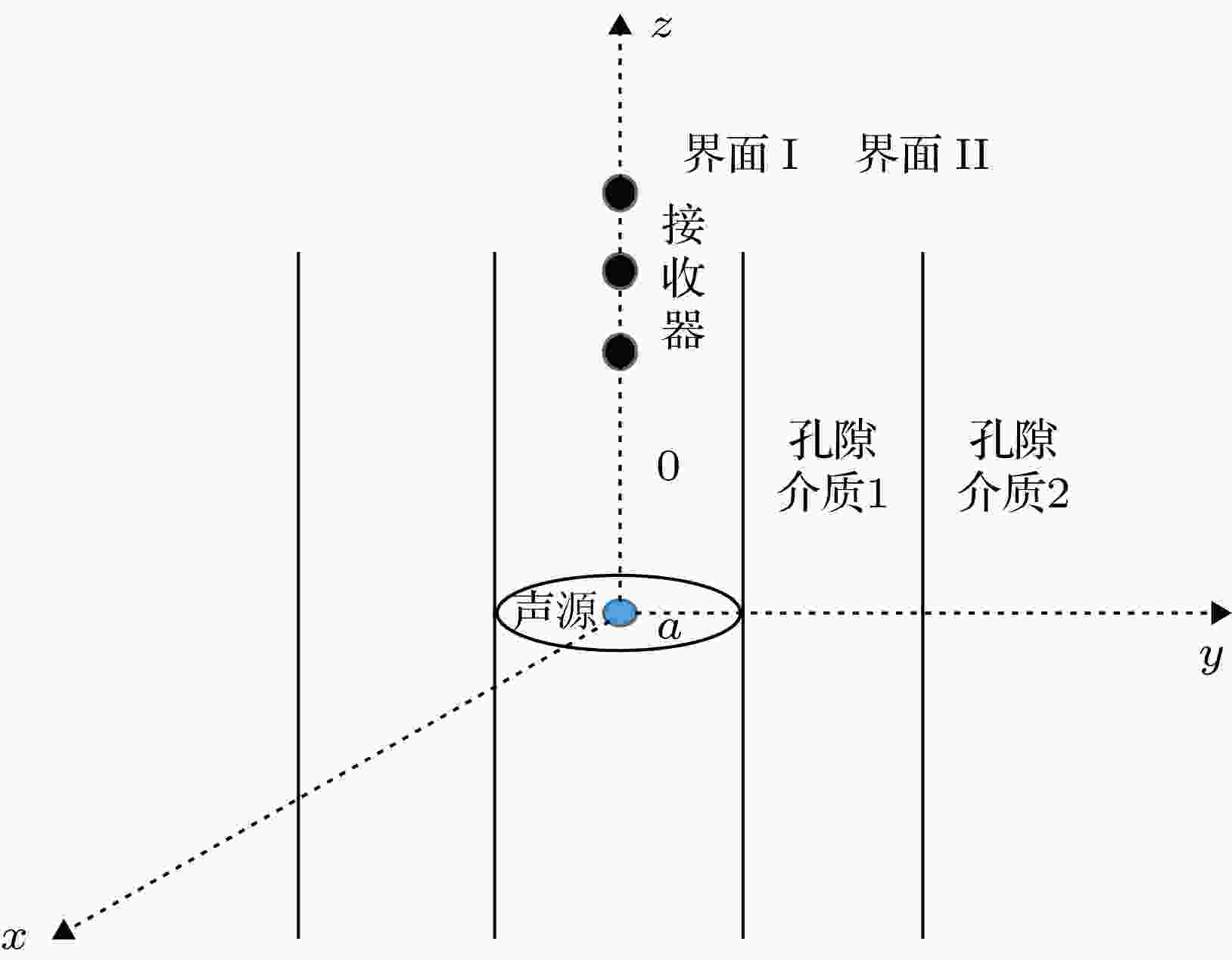
图 1 柱状双层孔隙介质声电效应测井模型
Figure1. Double-cylindrical-layer porous medium electrokinetic effect logging model.

通过对位移矢量和电矢量进行亥姆霍兹分解, 把Pride方程组转化为关于势函数的波动方程组, 得到夹层孔隙介质1内的声压和轴向电场的表达式为^[23]

$\begin{split} p ={}& \int\nolimits_{ - \infty }^\infty {\sum\limits_{j = {\rm{pf_1,ps_1}}} {(C + {\alpha _j}M)l_j^2 [{A_j}} } {K_0}\left( {{\eta _j}r} \right) \!+\! {B_j}{I_0}\left( {{\eta _j}r} \right)] \\ & \times {{\rm{e}}^{{\rm{i}}kz}}{\rm{d}}k, \\[-15pt] \end{split} $

$ \begin{split}{E_z} =\; & \int\nolimits_{ - \infty }^\infty \bigg\{{\rm{i}}k\sum\limits_{j = {\rm{p}}{{\rm{f}}_1},{\rm{p}}{{\rm{s}}_1}} {{\beta _j}\left[ {{A_j}{K_0}\left( {{\eta _j}r} \right) + {B_j}{I_0}\left( {{\eta _j}r} \right)} \right]} \\ & + \sum\limits_{j = {\rm{s}}{{\rm{v}}_{{\rm{1,}}}}{\rm{e}}{{\rm{m}}_1}} {{\beta _j}\left[ { - {A_j}{\eta _j}{K_0}\left( {{\eta _j}r} \right) + {B_j}{\eta _j}{I_0}\left( {{\eta _j}r} \right)} \right]} \bigg\}\\& \times{{\rm{e}}^{{\rm{i}}kz}}{\rm{d}}k, \\[-15pt] \end{split}$

最外层无限大地层中声压和轴向电场表达式为

$p = \int\nolimits_{ - \infty }^\infty {\sum\limits_{j = {\rm{p}}{{\rm{f}}_2},{\rm{p}}{{\rm{s}}_2}} {\left( {C + {\alpha _j}M} \right)} } l_j^2{A_j}{K_0}\left( {{\eta _j}r} \right){{\rm{e}}^{{\rm{i}}kz}}{\rm{d}}k, $

$\begin{split}{E_z} = \; &\int\nolimits_{ - \infty }^\infty \bigg[{\rm{i}}k\sum\limits_{j = {\rm{p}}{{\rm{f}}_2},{\rm{p}}{{\rm{s}}_2}} {\beta _j}{A_j}{K_0}\left( {{\eta _j}r} \right) \\ & - \sum\limits_{j = {\rm{s}}{{\rm{v}}_2},{\rm{e}}{{\rm{m}}_2}} {{\beta _j}{A_j}{\eta _j}{K_0}\left( {{\eta _j}r} \right)} \bigg] {{\rm{e}}^{{\rm{i}}kz}}{\rm{d}}k, \end{split}$

其中p为声压, E_z为轴向电场强度, ${A_j},{B_j}$为与波数和频率相关的透射系数; ${\eta _j} = \sqrt {{k^2} - l_j^2} $, $\left( {j = {\rm{p}}{{\rm{f}}_1},{\rm{p}}{{\rm{s}}_1},{\rm{s}}{{\rm{v}}_1},{\rm{e}}{{\rm{m}}_1},{\rm{p}}{{\rm{f}}_2},{\rm{p}}{{\rm{s}}_2},{\rm{s}}{{\rm{v}}_2},{\rm{e}}{{\rm{m}}_2}} \right)$为径向波数, ${\rm{p}}{{\rm{f}}_1},{\rm{p}}{{\rm{s}}_1},{\rm{s}}{{\rm{v}}_1},{\rm{e}}{{\rm{m}}_1}$分别对应内层孔隙介质1地层快纵波、慢纵波、横波和电磁波参量; ${\rm{p}}{{\rm{f}}_2},{\rm{p}}{{\rm{s}}_2},{\rm{s}}{{\rm{v}}_2},{\rm{e}}{{\rm{m}}_2}$分别对应最外层无限大孔隙介质2快纵波、慢纵波、横波和电磁波参量. 将声场和电场的表达式代入边界条件当中, 即可解得所有反射和透射系数, 进而得到井内声、电场的解析表达式.
2 -->

2.3.垂直割线积分理论

计算界面波应当采取计算支点割线积分的办法. Pride和Harrtsen^[34]提出孔隙地层中一共有四种体波, 分别为快纵波、慢纵波、横波和电磁波. 图2给出了地层当中所有体波的可能支点分布. 其中与内层介质相对应的支点分别为$ \pm {k_{{\rm{pf}}1}}, \pm {k_{{\rm{ps}}1}}, $ $\pm {k_{{\rm{sh1}}}}, \pm {k_{{\rm{em1}}}}$与外层介质相对应的支点分别为$ \pm {k_{{\rm{pf2}}}}, \pm {k_{{\rm{ps2}}}}, \pm {k_{{\rm{sh2}}}}, \pm {k_{{\rm{em2}}}}$. 井内流体有声波和电磁波两种体波, 与其对应的支点分别为$ \pm {k_{\rm{m}}}, \pm {k_{\rm{e}}}$. Kurkjian^[35]提出井内流体声波支点$ \pm {k_{\rm{m}}}$不是井内声场的实质性支点, 同理可知$ \pm {k_{\rm{m}}}$也不是井内电场的实质性支点. 王治等^[31]数学证明了$ \pm {k_{\rm{e}}}$也不是井内声场和电场的实质性支点. Chew^[36]证明了柱状分层介质$k_z$复平面上的唯一实质性支点是与最外层无限大介质相对应的支点. 李清亮和潘威炎^[37]利用数学归纳法, 证明了只有沿与最外层无限大介质对应支点的支割线两岸积分不为0, 其余均为0. 所以与井内流体体波相对应的支点$ \pm {k_{\rm{m}}}, \pm {k_{\rm{e}}}$和与内层介质相对应的体波支点$\pm {k_{{\rm{pf}}1}}, \pm {k_{{\rm{ps}}1}}, \pm {k_{{\rm{sh}}1}},$ $ \pm {k_{{\rm{em1}}}}$对割线积分的贡献为0. 在本文的算例中, 轴向电场的界面波是由与最外层无限大地层相对应的电场支点$ \pm {k_{{\rm{em2}}}}$的垂直割线积分计算得到.
图 2 垂直割线积分支点分布示意图
Figure2. Branch point distribution of the vertical secant integral.

通过计算电场支点${k_{{\rm{em2}}}}$的垂直割线积分, 可以得到界面转换电磁波的时域波形. 本文采取的地层参数由表1给出, 声源中心频率为6 kHz. 本文所给参数下孔隙介质1中的理论快纵波、慢纵波、横波波速分别为3936.96, 547.75和2534.5 m/s. 如图3所示是孔隙介质1厚度为5 m时, 随着接收器与声源距离增加, 不同接收器的界面转换电磁波归一化波形. a, b, c, d是井壁处或孔隙介质分界面处产生的界面转换电磁波. 不同接收器的界面转换电磁波到时并没有随着源距的增大而增加, 而是几乎同时接收到电场响应. 这说明与模式波的伴随电场以声波波速传播不同, 界面转换电磁波在孔隙介质中是以地层电磁波速度传播并返回接收器的.

参数	孔隙 介质1	孔隙 介质2	井内 流体
孔隙度$\phi $	0.2	0.2	—
渗透率κ0/μm2	1.0	1.0	—
弯曲度${\alpha _\infty }$	3.0	3.0	—
骨架压缩模量${K_{\rm{b} } }/10^9{\rm{Pa} }$	14.39	2.61	—
介质剪切模量${G_{\rm{b} } }/10^9{\rm{Pa} }$	13.99	2.83	—
介质密度$\rho /{\rm{kg} } \cdot { {\rm{m} }^3}$	2650	2650	1000
基质体积弹性模量${K_{\rm{s} } }/10^9{\rm{Pa} }$	35.79	33.40	—
流体体积弹性模量${K_{\rm{f} } }/10^9{\rm{Pa} }$	2.25	2.25	2.25
矿化度$C/{\rm{mol} } \cdot { {\rm{L} }^{ - 1} }$	0.01	0.01	0.01
流体介电常数${\varepsilon _{\rm{f}}}/{{\rm{\varepsilon}} _0}$	80	80	80

表1孔隙介质和井内流体参数
Table1.Porous medium and borehole fluid parameters.

图 3 柱状双层介质界面转换电磁波归一化波形
Figure3. Normalized interface converted electromagnetic waveform of double-cylindrical-layer medium.

为了说明波包成分a的产生机理并验证本文算法的正确性, 井外为分层孔隙介质的界面转换电磁波时域波形与井孔外为单层无限大地层的界面转换电磁波时域波形作对比, 结果如图4所示. 如图4(a)所示, 当孔隙介质1的参数与单层无限大介质参数一致时, 第一组波包a与井外为单层无限大地层界面转换电磁波时域波形完全重合. 这说明第一组波包a是在I界面处(即井壁处)产生的转换电磁波. 除了第一组波包a外, 后面的成分都是由于孔隙介质分界面的存在而产生的. 将双层孔隙介质退化成单层无限大孔隙介质, 并与井外为单层无限大孔隙介质的界面转换电磁波模拟波形对比如图4(b)所示, 可以发现二者时域波形完全一致, 说明了本文算法的正确性.
图 4 双层介质与单层无限大介质声电测井界面转换电磁波波形对比　(a)孔隙介质1与单层无限大介质参数一致时的界面转换电磁波; (b)双层介质退化为单层介质时的界面转换电磁波(实线对应单层无限大介质, 虚线对应双层介质)
Figure4. Comparison of electrokinetic logging interface converted electromagnetic wave waveforms between two-layer medium and single-layer infinite medium: (a) Interface converted electromagnetic waveform when porous medium 1 parameters are consistent with single layer infinite medium; (b) interface converted electromagnetic wave when double-layer medium degenerates into single-layer medium (the solid line corresponds to the single-layer infinite medium, the dashed line corresponds to the double-layer medium).

为了进一步说明每组成分的产生机理, 对比了不同孔隙介质1层厚的界面转换电磁波波形. 图5为当孔隙介质1厚度分别为5和7 m时, 界面转换电磁波的波形对比, 其中${r_2}$为孔隙介质1的厚度. 图6(a)—图6(c)分别为两种情况下成分b, c, d到时差对比示意图.
图 5 不同夹层介质层厚的界面转换电磁波(实线和虚线分别对应夹层介质层厚5 m和7 m)
Figure5. Interface converted electromagnetic wave waveforms of different interlayer medium thickness (the solid and dashed lines correspond to the interlayer dielectric layer thickness of 5 m and 7 m, respectively).

图 6 界面转换电磁波不同成分到时差　(a)成分b; (b)成分c; (c)成分d (实线和虚线分别对应夹层介质层厚5和7 m)
Figure6. Arrival time difference of different components of the interface converted electromagnetic wave: (a) Component b; (b) component c; (c) component d (the solid and dashed lines correspond to the interlayer medium thickness of 5 m and 7 m, respectively).

通过对比, 发现夹层孔隙介质1厚度的改变并没有影响第一组波包的到时和幅度, 这进一步说明了第一组波包a是由井内声波传播至井壁(界面I)产生的声电转换电磁波. 当夹层孔隙介质1的厚度增大时, 界面转换电磁波时域波形除了波包a以外的成分到时有明显增加. 如图6(a)所示, 当夹层孔隙介质厚度增大2 m时, 第二组波包b的到时之差为0.508 ms, 计算波速为3937.0 m/s, 这与孔隙度为0.2的地层快纵波理论波速一致, 所以第二组波包b为地层快纵波传播至界面II而产生的转换电磁波.
如图6(b)所示, 当孔隙介质1的厚度改变2 m时, 第三组波包c到时之差为0.789 ms, 计算得到波速为2534.9 m/s, 与理论地层横波波速一致, 所以第三组波包c为地层横波传播至界面II时产生的转换电磁波. 图6(c)显示了第四组波包d到时之差为1.016 ms, 与地层快纵波传播4 m的距离时长一致. 所以第四组波包为地层快纵波在夹层内传播至界面II并经过一次反射后传播回到界面I时产生的转换电磁波. 以此类推, 地层纵、横波在井外为分层的孔隙地层传播的过程当中, 每一次在界面处发生折反射时, 都会产生以地层电磁波速度传播的界面转换电磁波.
接下来考察孔隙介质流体矿化度对界面电磁波的影响. 图7是不同孔隙介质流体矿化度下的界面转换电磁波波形, 其中C, C₁, C₂分别为井内流体矿化度, 孔隙介质1流体矿化度和孔隙介质2流体矿化度.
图 7 不同孔隙介质流体矿化度下的界面转换电磁波波形(a)不同夹层孔隙介质流体矿化度的界面转换电磁波波形(实线, 虚线, 点划线分别对应夹层孔隙介质流体矿化度C₁ = 0.01, 0.005, 0.0025 mol/L); (b)不同最外层孔隙介质流体矿化度的界面转换电磁波波形(实线, 虚线, 点划线分别对应最外层孔隙介质流体矿化度C₂ = 0.01, 0.005, 0.0025 mol/L)
Figure7. Interface converted electromagnetic wave waveforms under different porous medium fluid salinity: (a) Interface converted electromagnetic wave waveforms of different interlayer porous medium fluid salinity (solid line, dashed line, dash-dotted line corresponding to interlayer porous medium fluid salinity C₁ = 0.01, 0.005, 0.0025 mol/L respectively); (b) interface converted electromagnetic wave waveforms of different outermost porous medium fluid salinity (solid line, dashed line, dash-dotted line corresponding to outermost porous medium fluid salinity C₂ = 0.01, 0.005, 0.0025 mol/Lrespectively).

图7(a)所示是井内流体矿化度与最外层孔隙介质流体矿化度不变, 仅孔隙介质1的流体矿化度发生变化时界面转换电磁波的时域波形对比. 夹层孔隙介质流体矿化度的改变对I, II两个界面的界面转换电磁波幅度都有影响. 这是因为界面转换电磁波是由声波传播到界面时产生的, 而孔隙介质1与界面I, II都有交接, 所以孔隙介质1流体矿化度的改变会影响界面转换电磁波所有成分的幅度. 但是介质矿化度的改变对于界面转换电磁波的到时没有影响, 这是因为电场由声波在界面处转化而来, 而孔隙介质流体矿化度的改变不影响声波的传播速度. 当井内流体与内层孔隙介质流体矿化度不变, 仅最外层无限大孔隙介质(孔隙介质2)的流体矿化度发生变化时的波形对比如图7(b)所示. 孔隙介质2的流体矿化度改变对第I界面的转换电场幅度与到时都没有影响, 仅对第II界面的转换电场幅度有影响, 并且孔隙介质流体矿化度之间的差异越大, 界面转换电磁波的幅度越大.
当井外孔隙介质存在液体侵入带时, 侵入液体导致孔隙介质流体矿化度之间不匹配, 进而形成了矿化度界面. 针对这种情况, 对井外孔隙介质仅存在矿化度界面的情况进行考察. 不同矿化度界面位置的界面转换电磁波时域波形与不存在矿化度界面的情况对比如图8所示, ${r_3}$为矿化度界面与井壁的距离.
图 8 不同矿化度界面位置的界面转换电磁波波形对比(实线对应不存在矿化度界面时的界面转换电磁波, 虚线和点划线分别对应矿化度界面距离井壁5 m和6 m时的界面转换电磁波)
Figure8. Waveform comparison of interface converted electromagnetic wave waveforms of different salinity interface position (the solid line corresponds to the interface converted electromagnetic wave when there is no salinity interface, the dashed line and the dash-dotted line respectively correspond to the interface converted electromagnetic waves when the salinity interface is 5 m and 6 m away from the well wall).

界面转换电磁波共有两组波包, 通过对比可知第一组波包为声波传播至井壁处所产生的转换电磁波. 当矿化度界面位置远离井壁1 m时, 第二组波包的到时差为0.25 ms, 与地层声波传播1 m所需时间一致. 所以第二组波包为声波传播至矿化度界面所产生的转换电磁波. 由于孔隙介质不存在物理界面, 声波不会在孔隙介质中发生多次折反射, 所以除了井壁处和矿化度界面处的转换电磁波, 并无其他响应产生. 同时考察了矿化度对界面转换电磁波的影响. 图9显示了矿化度界面两侧孔隙介质流体矿化度差异对界面转换电磁波的影响, 其中${\text{δ}} C$为界面外侧孔隙流体矿化度与界面和井壁之间的孔隙流体矿化度之差.
图 9 矿化度差异对界面转换电磁波的影响(实线, 虚线和点划线分别对应矿化度差异为${\text{δ}} C =$0.0005, 0.0015, 0.0025 mol/L)
Figure9. Effect of salinity difference on interface converted electromagnetic waves (the solid line, the dashed line and the dash-dotted line respectively correspond to the salinity difference of ${\text{δ}} C=$0.0005, 0.0015, 0.0025 mol/L).

当矿化度界面两侧孔隙流体矿化度差异越大时, 界面转换电磁波的幅度越大. 而矿化度界面两侧孔隙流体矿化度差异对于井壁处产生的界面转换电磁波没有影响. 将${\text{δ}} C$定义为矿化度界面和井壁之间的孔隙流体矿化度与界面外侧孔隙流体矿化度之差时, 其规律不变, 在此不再赘述.

本文应用计算电磁波支点的垂直割线积分的方法计算了井外为柱状双层孔隙介质声电效应测井的界面转换电磁波. 并且对每一组波包成分的产生机理和传播规律进行解释, 而且考查了当内、外层孔隙介质流体矿化度发生改变时对界面转换电磁波的影响. 同时考察了当仅存在矿化度界面的界面转换电磁波产生机理. 通过对比双层孔隙介质与单层孔隙介质声电效应测井的界面转换电磁波波形, 发现夹层的存在导致界面转换电磁波成分变得复杂. 将井外为分层介质模型退化为无限大地层并与井外为无限大地层的界面转换电磁波模拟结果做对比, 发现二者完全一致, 说明了本文算法的正确性. 通过计算夹层孔隙介质厚度不同时每组波包的到时差, 计算波速后与理论波速作对比, 可以证明界面转换电磁波的第一组波包成分为井内声场传播至界面I时产生的转换电场, 第二组波包成分为地层快纵波传播至II界面时产生的转换电场, 第三组波包成分为地层横波传播至II界面时产生的转换电场, 第四组波包成分为地层快纵波传播至II界面发生反射, 传播回到I界面时产生的转换电场. 以此类推, 介质内声波体波即纵、横波每次在介质界面处发生折反射时都会有转换电场产生, 这些响应叠加, 构成了柱状双层声电效应测井界面转换电磁波的时域波形. 在对孔隙介质流体矿化度的考察中, 当仅改变内层孔隙介质1流体矿化度时, 对两个界面的界面转换电磁波幅度都有影响. 而仅改变最外层孔隙介质矿化度时, 只对第二界面的转换电场幅度有影响. 这是因为夹层孔隙介质与两个界面都有交接, 而最外层孔隙介质只与第二界面有交接, 而界面转换电磁波是声波传播至界面产生的, 所以其性质只与界面两侧介质的性质有关. 并且介质流体矿化度差异越大, 界面转换电磁波的幅度越大. 同时针对孔隙介质有流体侵入带的情况, 考查了当井外介质仅存在矿化度界面时界面转换电磁波波形, 发现此时界面转换电磁波时域波形仅剩两组波包, 分别为井壁处产生的转换电场和矿化度界面处产生的转换电场. 这是由于井外孔隙介质之间不存在物理界面, 所以声波不会发生多次折反射, 所以不会多次产生界面转换电磁波. 在对这种情况下矿化度的考察中, 得到了与井外为分层孔隙介质时相同的结论.
研究柱状双层孔隙介质界面转换电磁波的产生机制和传播规律对于声电效应声波测井中地层含有侵入带以及液体侵入地层等问题具有重要意义. 由于声波每次传播至介质界面时都会产生转换电场, 而界面转换电磁波是以地层电磁波波速传播的, 所以每当声波传播至介质界面时, 接收器都会几乎同时接收到转换电场的响应, 能够直观反映声波传播至界面的到时. 这不仅有助于分析井外为复杂介质情况的界面响应, 而且能够反映地层声波在地层当中的折反射规律. 考察对比了当内外层孔隙介质流体矿化度改变时的波形, 由模拟结果来看, 井中流体、孔隙介质流体矿化度相对关系的改变对界面转换电磁波的幅度影响较大, 但是对到时没有影响. 可以通过观察界面转换电磁波波形的改变来判断孔隙介质流体矿化度的相对关系, 进而初步判断井外孔隙介质流体种类. 当井外仅存在矿化度界面时, 界面转换电磁波的成分变得简单, 可以直接利用界面转换电磁波估测矿化度界面两侧孔隙流体矿化度的关系并探测矿化度界面的位置. 此外, 地层水污染不改变地层弹性性质, 也可以视作地层仅存在矿化度界面的情况, 所以利用孔隙地层声电耦合物理效应的另一个潜在应用是监测地下水污染的情况.