摘要:非约束环境下采集的人脸图像复杂多变, 将其直接作为字典原子用于稀疏表示分类(sparse representation based classification, SRC), 识别效果不理想. 针对该问题, 本文提出一种基于旋转主方向梯度直方图特征的判别稀疏图映射(discriminative sparse graph embedding based on histogram of rotated principal orientation gradients, DSGE-HRPOG)算法, 用于构建类内紧凑、类间分离的低维判别特征字典, 提高稀疏表示分类准确性. 首先, 采用旋转主方向梯度直方图(histogram of rotated principal orientation gradients, HRPOG)特征算子提取非约束人脸图像的多尺度多方向梯度特征, 有效去除外界干扰和像素间冗余信息, 构建稳定、鉴别的HRPOG特征字典; 其次, 引入判别稀疏图映射(discriminative sparse graph embedding, DSGE)算法, 以类内重构散度最小、类间重构散度最大为目标计算特征字典的最佳低维投影矩阵, 进一步增强低维特征字典的判别性、紧致性; 最后, 提出投影矩阵和稀疏重构关系交替迭代优化算法, 将维数约简过程伴随在稀疏图构建过程中, 使分类效果更理想. 在AR, Extended Yale B, LFW和PubFig这4个数据库上进行大量实验, 验证了本文算法在实验环境数据库和真实环境数据库上的有效性.
关键词: 非约束人脸识别/
流形学习/
稀疏保持投影/
方向梯度直方图

English Abstract

全文HTML

--> --> -->

随着互联网技术和人工智能技术的飞速发展, 实时采集人脸图像进行身份认证、安全监控和信息提取已成为机器视觉领域最热门的研究课题之一^[1,2]. 然而, 非控环境中采集的人脸图像受光照、姿态、表情、遮挡、年龄等多种因素影响, 导致人脸图像复杂多变, 严重抑制了非约束人脸识别的准确性.
2009年, Wright等^[3]受生物视觉稀疏性启发, 首次提出稀疏表示分类模型(sparse representation based classification, SRC), 并将其成功应用于非约束人脸识别中, 很好地解决了人脸图像中光照、遮挡、噪声等因素的影响. 分析其原因, 关键在于稀疏表示分类中并不需要精确的特征表达, 只需遵循“简约性”原则, 从字典中选择“有限”原子对待测样本进行线性表示, 并期望达到所选“原子”仅与待测样本同类. 由此可见, 构建学习紧致、判别的字典在稀疏表示分类中具有极其重要的作用. Yang等^[4]提出Fisher判别字典学习(fisher discrimination dictionary learning, FDDL)方法, 将Fisher判别准则引入结构字典学习中, 使得同类字典原子具有相似性而异类字典原子具有差异性. Vu等^[5]在此基础上引入低秩共享字典(low-rank shared dictionary, LRSD)用于表示人脸本质特征, 与表示人脸差异性的类特定字典(class-specific dictionary, CSD)相结合, 进一步提高了字典空间的判别性. 为使学习得到的字典具有更丰富的语义信息, Babaee等^[6]摒弃了二值标签信息而采用相对属性信息, 提出相对属性引导字典学习(relative attribute guided dictionary learning, RAGDL)算法. 同时, 文献[7-10]在字典学习方面也进行了深入研究.
分析发现, 字典学习(dictionary learning, DL)方法虽然在构建学习紧致、判别字典空间上取得一定效果, 但仍受2个方面限制: 1)稀疏表示分类^[3]要求字典原子的维度远远小于字典原子个数, 从而保证解空间存在最优稀疏解, 然而, 以M×N像素大小的样本图像作为字典原子构建字典空间, 其维度远大于样本个数, 容易导致出现“小样本”问题; 2)字典学习方法通过增加各种约束条件优化字典满足类内紧凑和类间分离, 然而, 由于原始样本图像的高维性、复杂性和冗余性, 使得优化效果大打折扣, 严重抑制了待测样本稀疏表示分类的准确性.
鉴于此, 大量****提出采用降维(dimensionality reduction, DR)方法克服上述不足, 一方面通过降低字典空间维度可以避免“小样本”问题, 减少稀疏编码计算复杂度, 加速搜寻最优解; 另一方面增加投影约束条件, 使高维样本字典在低维子空间更具紧致性、判别性, 稀疏表示更准确, 这已成为稀疏表示分类中必不可少的步骤.
以主成分分析(principle components analysis, PCA)^[11]、线性鉴别分析(linear discriminant analysis, LDA)^[12]为代表的经典降维方法被首先用于稀疏表示分类模型中^[3,4,13], 但受数据全局线性分布条件的限制, 当处理复杂扭曲的非线性分布的真实数据时, 这类方法效果不佳. 鉴于此, 广大****提出采用基于核的方法^[7,14-16]和流形学习方法^[17-21]进行数据非线性降维. 核方法的本质是利用核函数映射样本到高维空间进行线性划分, 但起关键作用的核函数的选择机制和意义并不明确. 因此, 以等距映射(isometric mapping, ISOMAP)^[17]、局部线性嵌入(locally lineare mbedding, LLE)^[18]、拉普拉斯特征映射(Laplacian eigenmaps, LE)^[19]、平行向量场嵌入(parallel vector field embedding, PFE)^[20]、测地线距离学习(geodesic distance function learning, GDL)^[21]等为代表的非线性流形学习方法更受青睐. 这类方法符合人眼视觉感知机制, 可以有效挖掘出隐藏在错综复杂的高维数据中的低维流形本质结构. He等^[22,23]针对LE和LLE的隐式映射问题进行改进, 在不改变原有目标函数的基础上增加线性约束, 提出具有显式映射函数的局部保持投影(locality preserving projections, LPP)和近邻保持嵌入(neighborhood preserving embedding, NPE)算法, 有效克服了样本外扩展问题(out-of-sample extension problem)^[24], 使得流形学习方法在图像、视频、文本等高维、海量、真实数据中的应用成为可能. 随后, 大量改进算法被陆续提出, 例如, 指数判别局部保持投影(exponential discriminant locality preserving projection, EDLPP)^[25]、二维判别局部保持投影(two-dimensional discriminant LPP, 2DDLPP)^[26]、双向二维近邻保持判别嵌入(bilateral two-dimensional neighborhood preserving discriminant embedding, B2DNPDE)^[27]、快速正交局部保持投影(fast and orthogonal LPP, FOLPP)^[28]、监督近邻保持嵌入(supervised NPE, SNPE)^[29]等.
Yan等^[30]对LPP, NPE及改进算法的实现原理进行分析, 将它们归纳到图映射框架(graph embedding framework, GEF)中. 分析发现, GEF的核心思想是通过构建高维样本近邻分布图, 寻找使低维子空间数据仍保持高维样本分布特性的最优投影矩阵. 因此, 在GEF中如何构建一个准确的高维样本近邻分布图是这类方法的关键. 近邻图的构建包含2个关键步骤: 图顶点选择和图边权分配. 传统方法多采用k-nearest^[31]或ε-ball^[23]方法搜索样本近邻点, 并用热核函数^[31]或逆欧式距离^[32]计算近邻点之间的权值. 然而, 实际应用中真实数据的分布是未知的、复杂的, 选择合适的近邻点非常困难, 并且样本之间距离测度的可区分性也会随着样本维数的增加而减弱, 这在一定程度上抑制了基于GEF的降维方法的广泛应用.
2010年, Qiao等^[33]受信号稀疏表示(sparse representation, SR)^[3-5]的启发, 首次将稀疏技术引入图映射框架中, 提出稀疏保持投影(sparsity preserving projections, SPP)算法. 这是一种不以距离测度为区分, 而以保持样本间稀疏重构关系为目标的全新降维方法. 它通过优化求解每一个样本在全局超完备字典下的线性稀疏表示, 自适应得到与该样本近邻的少量重构样本以及样本之间的重构权值, 有效克服了传统图映射方法中预定义近邻图的弊端. 这种以SPP为代表的自适应稀疏图映射(sparse graph embedding, SGE)方法极大提高了真实复杂数据低维投影的准确性, 受到广大****们的高度关注.
Lai等^[34]将稀疏表示技术引入LLE框架中, 提出稀疏线性映射(sparse linear embedding, SLE)算法, 并扩展到核空间, 在3个人脸库和2个目标库上验证了其降维有效性, 尤其是在小样本情况下表现更突出. Yin等^[35]将稀疏表示与LPP相结合, 提出局部稀疏保持投影(local sparsity preserving projection, LSPP)算法, 并成功应用于生物大数据的降维与识别中. Zhang等^[36]结合近邻图和稀疏图优点, 提出稀疏邻域保持投影(sparsity and neighborhood preserving projections, SNPP)算法. 分析发现, 基于全局样本的稀疏关系约束会破坏样本局部结构, 导致样本间的近邻关系描述并不准确. Lu等^[37]在SPP基础上引入类别标签, 提出鉴别稀疏邻域保持嵌入(discriminant sparsity neighborhood preserving embedding, DSNPE)算法, 分别考虑待测样本与同类样本的重构关系, 以及异类样本对待测样本的重构影响, 有效提高了待测样本稀疏近邻图的准确性, 相比SPP算法识别性能大大提升. 同样地, Wei等^[38]提出加权判别稀疏保持映射(weighted discriminative sparsity preserving embedding, WDSPE)算法, Lou等^[39]则将稀疏表示技术引入LPP框架中, 提出正则图稀疏判别分析(graph regularized sparsity discriminant analysis, GRSDA)算法. 鉴于传统方法中多将降维和分类作为2个独立步骤分别建模, 存在降维效果与分类器不匹配的问题, Yang等^[40]提出稀疏表示分类引导判别投影(sparse representation classifier steered discriminative projection, SRC-DP)算法, 以同类重构残差最小、异类重构残差最大为目标, 联合优化投影矩阵以及稀疏表示分类系数, 使SRC分类器在投影子空间获得最佳性能. 类似地, Zheng等^[41]提出特征加权组稀疏判别投影(feature weighted group sparse classification steered discriminative projection, FWGSDP)算法, 并采用迭代重约束稀疏编码优化方法对该模型进行高效求解. Gao等^[42]基于Fisher判别准则引导数据降维和分类. Zhang等^[43]将SRC-DP进一步扩展到核空间, 从多个不同角度验证算法有效性. 可见, 由于稀疏表示技术的引入, 以SPP为代表的稀疏图映射方法具有非常好的图自适应性和噪声鲁棒性, 将其与SRC分类器相结合, 用于构建低维、紧致、判别字典可以显著提高分类器的精度和速度, 是近年来值得研究和探索的热点方向之一.
受基于统计局部特征的鲁棒核表示(robust kernel representation with statistical local features, RKR-SLF)^[44]以及基于Gabor特征的鲁棒表示分类^[45](gabor feature based robust representation and classification, RRC-GF)等算法的启发, 我们发现, 采用LBP, Gabor等鉴别力和鲁棒性较强的局部特征代替传统的冗余数据样本构建特征字典, 可以显著提高稀疏表示分类的准确性. 因此, 本文考虑将局部特征算子与降维方法相结合, 提出一种基于旋转主方向梯度直方图特征的判别稀疏图映射(discriminative sparse graph embedding based on histogram of rotated principal orientation gradients, DSGE-HRPOG)算法, 实现流程如图1所示. 首先, 从特征描述角度设计一种旋转主方向梯度直方图(histogram of rotated principal orientation gradients, HRPOG)特征算子, 相比传统方向梯度直方图(histogram of oriented gradients, HOG)特征算子, 它从多个尺度、多个方向捕捉人脸纹理的梯度变化信息, 可以更准确提取出人脸本质特征, 显著提高了特征字典的鉴别性和鲁棒性. 其次, 从降维角度提出判别稀疏图映射(discriminative sparse graph embedding, DSGE)算法, 在DSNPE算法^[37]的基础上, 通过引入类内、类间紧凑度约束, 有效增强了待测样本与同类非近邻样本的重构关系, 并削弱了异类伪近邻样本的重构影响; 同时, 在低维投影阶段又增加了全局约束因子, 利用样本全局分布中隐含的鉴别信息使HRPOG特征字典在低维子空间更判别、更紧致. 最后, 受SRC-DP^[40]的启发, 提出一种投影矩阵和稀疏重构关系交替的迭代优化算法, 将维数约简过程伴随在稀疏图构建过程中, 使分类效果更理想. 经实验环境下采集的人脸数据库(AR和Extended Yale B)和真实环境下采集的人脸数据库(LFW和PubFig)验证, DSGE-HRPOG算法可以有效提取这些高度扭曲的人脸数据的低维流形本质结构, 大大增强特征字典的紧致性、判别性和鲁棒性, 使SRC分类性能更突出.
图 1 本文算法的实现流程
Figure1. Flow chart of the proposed algorithm.

2

-->

2.1.方向梯度直方图(histogram of oriented gradients, HOG)

2005年, Dalal和Triggs^[46]提出方向梯度直方图(histogram of oriented gradients, HOG)用于行人检测, 其基本原理是统计图像中各个像素点的梯度幅值和梯度方向, 用于表征目标形态、轮廓变化等信息. 相比LBP, Gabor等局部纹理特征算子, HOG算子提取的方向梯度变化信息更符合人眼视觉感知特性, 受光照、旋转、噪声等外界干扰影响更小, 提取目标特征效果更佳、更鲁棒^[47,48]. 实现步骤如下:
1)将图像$f(x,y)$划分成大小相同的无重叠单元格(cell);
2)将$0\text{—}{180^ \circ }$分为9个区间, 平均每${20^ \circ }$为一个区间, 统计每个单元格中所有像素的梯度幅值和梯度方向, 将属于同一梯度方向区间的像素点的梯度幅值按照权重累加, 组成该单元格的9维方向梯度直方图;
3)将4个相邻的无重叠的单元格组合成一个块(block), 级联块中单元格的方向梯度直方图构成该块的方向梯度直方图特征;
4)级联所有块的方向梯度直方图, 得到整幅图像的HOG特征.
2 -->

2.2.HRPOG特征算子

分析发现, 在HOG算子实现过程中, 图像$f(x,y)$中任意像素的梯度$\overrightarrow {\nabla f} (x,y)$是一个具有大小和方向的矢量, 由$\dfrac{{\partial f}}{{\partial x}}$和$\dfrac{{\partial f}}{{\partial y}}$顺序表示:

$\overrightarrow {\nabla f} (x,y) = {\left[ {\dfrac{{\partial f}}{{\partial x}},\dfrac{{\partial f}}{{\partial y}}} \right]^{\rm{T}}}.$

可见, $\dfrac{{\partial f}}{{\partial x}}$和$\dfrac{{\partial f}}{{\partial y}}$计算是否准确直接决定了HOG特征的表征能力. 在传统HOG算子中, $\dfrac{{\partial f}}{{\partial x}}$和$\dfrac{{\partial f}}{{\partial y}}$计算公式如下:

$\left\{ \begin{aligned}& \dfrac{{\partial f}}{{\partial x}} = {h_x}*f(x,y) = f(x + 1,y) - f(x - 1,y), \\ & \dfrac{{\partial f}}{{\partial y}} = {h_y}*f(x,y) = f(x,y + 1) - f(x,y - 1),\end{aligned} \right.$

这里, ${h_x}$和${h_y}$为梯度卷积模板, 记为${h_x} =\left[{ - 1}\quad 0\quad 1\right]$, ${h_y} =\left[ { - 1} \quad 0 \quad 1 \right]^{\rm{T}}$.
可以看出, 依据(2)式计算图像梯度受2个方面限制: 1) $\dfrac{{\partial f}}{{\partial x}}$和$\dfrac{{\partial f}}{{\partial y}}$仅考虑了中心像素点周围2个像素点的灰度变化情况, 提取的图像标量场的微观信息并不丰富, 也不准确; 2) $\dfrac{{\partial f}}{{\partial x}}$和$\dfrac{{\partial f}}{{\partial y}}$仅描述了图像在水平方向和垂直方向上的灰度变化程度, 其他方向上的灰度变化并未考虑. 鉴于此, 本文提出一种HRPOG特征算子, 一方面, 增加梯度卷积模板${h_x}$和${h_y}$的计算范围, 充分考虑中心像素点周围邻域像素点的灰度变化情况; 另一方面, 旋转模板${h_x}$和${h_y}$, 使HRPOG算子可以提取图像在不同方向上的梯度特征, 具有旋转不变性. 具体设计细节如下:
首先, 将梯度卷积模板${h_x}$和${h_y}$设计为3×3大小(图2). 模板中, 主方向(箭头指向)上的卷积权值设为3, 其余卷积权值设为1或–1, 使模板中所有卷积权值的和为零. 可以看出, 相比传统HOG算子, HRPOG算子的梯度卷积模板既充分考虑了中心像素点周围邻域像素点的灰度变化情况, 同时, 卷积权值设置也可以有效增强图像在主方向(箭头指向)上的梯度变化信息. 这里, 为了区分HRPOG算子中设置不同尺度的梯度卷积模板的情况, 定义3 × 3尺度下的HRPOG算子为3-HRPOG. 依据图2得到3-HRPOG算子的梯度矢量${\left( {\overrightarrow {\nabla f} } \right)_{3 - {\rm{HRPOG}}}}$计算公式如下:
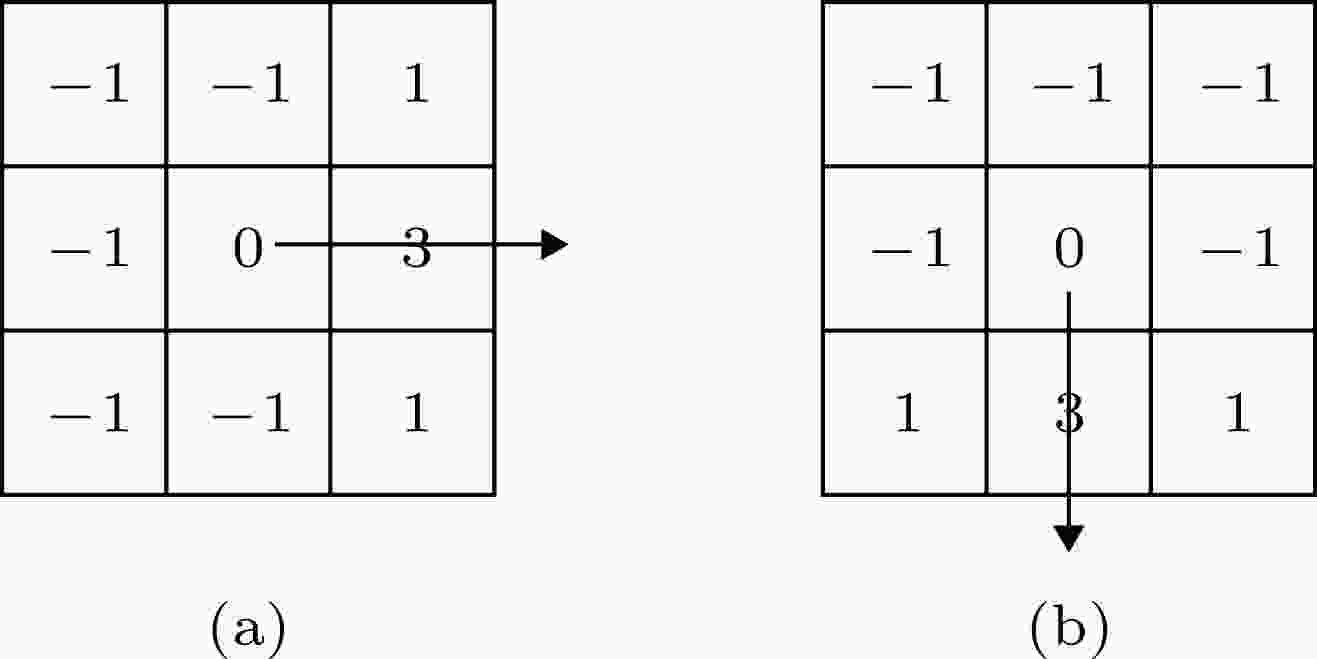图 2 3-HRPOG算子的梯度卷积模板示意图　(a) ${h_x}$模板; (b) ${h_y}$模板
Figure2. Gradient convolution masks of 3-HRPOG feature descriptor: (a) ${h_x}$ mask; (b) ${h_y}$ mask.

${\left( {\overrightarrow {\nabla f} } \right)_{3 - {\rm{HRPOG}}}} = \left[ \begin{array}{l} {\left( {\dfrac{{\partial f}}{{\partial x}}} \right)_{3 - {\rm{HRPOG}}}} \\ {\left( {\dfrac{{\partial f}}{{\partial y}}} \right)_{3 - {\rm{HRPOG}}}}\end{array} \right],$

其中,

$\left\{ \begin{aligned}{\left( {\dfrac{{\partial f}}{{\partial x}}} \right)_{3 - {\rm{HRPOG}}}} = \; & {h_x}*f(x,y) = f(x - 1,y + 1) \\ & + 3f(x,y + 1) + f(x + 1,y + 1) \\ & - f(x - 1,y - 1) - f(x - 1,y) \\ & - f(x,y - 1) - f(x + 1,y - 1) \\ & - f(x + 1,y) \\ {\left( {\dfrac{{\partial f}}{{\partial y}}} \right)_{3 - {\rm{HRPOG}}}} =\; & {h_y}*f(x,y) = f(x + 1,y - 1) \\ & + 3f(x + 1,y) + f(x + 1,y + 1) \\& - f(x,y - 1) - f(x - 1,y - 1) \\ &- f(x - 1,y) - f(x - 1,y + 1) \\ &- f(x,y + 1)\end{aligned} \right..$

其次, 在图2的基础上, 依据梯度卷积模板的主方向(箭头指向), 将${h_x}$和${h_y}$分别沿逆时针以${45^ \circ }$为间隔旋转一周, 依次得到8组旋转梯度卷积模板, 记为$3 - {\rm{Group}}(i)$($i = 1,2,...8$), 如图3所示. 采用(5)式分别计算图像在每组旋转梯度卷积模板主方向上的梯度矢量, 统计得到对应的主方向梯度直方图. 将8组主方向梯度直方图依次累加, 得到最终的3-HRPOG特征向量.
图 3 3-HRPOG算子的旋转梯度卷积模板
Figure3. Rotated gradient convolution masks of 3-HRPOG feature descriptor.

$\left\{ \begin{aligned}& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {0^ \circ }}} \right. = {[{h_{x1}}*f(x,y),\; {h_{y1}}*f(x,y)]^{\rm{T}}} \\& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {{45}^ \circ }}} \right. = {[{h_{x2}}*f(x,y),\; {h_{y2}}*f(x,y)]^{\rm{T}}} \\& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {{90}^ \circ }}} \right. = {[{h_{x3}}*f(x,y),\; {h_{y3}}*f(x,y)]^{\rm{T}}} \\& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {{135}^ \circ }}} \right. = {[{h_{x4}}*f(x,y),\; {h_{y4}}*f(x,y)]^{\rm{T}}} \\& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {{180}^ \circ }}} \right. = {[{h_{x5}}*f(x,y),\; {h_{y5}}*f(x,y)]^{\rm{T}}} \\& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {{225}^ \circ }}} \right. = {[{h_{x6}}*f(x,y),\; {h_{y6}}*f(x,y)]^{\rm{T}}} \\& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {{270}^ \circ }}} \right. = {[{h_{x7}}*f(x,y),\; {h_{y7}}*f(x,y)]^{\rm{T}}} \\& {\overrightarrow {\nabla f} _{3 - {\rm{HRPOG}}}}\left| {_{\theta = {{315}^ \circ }}} \right. = {[{h_{x8}}*f(x,y),\; {h_{y8}}*f(x,y)]^{\rm{T}}}.\end{aligned} \right.$

图4进一步说明了3-HRPOG算子的旋转不变性. 图4(a)是一幅二值图像(紫色表示0, 绿色表示1), 将其沿逆时针方向旋转${45^ \circ }$, 得到图4(b), 分别采用传统HOG算子以及3-HRPOG算子计算2种情况下的梯度矢量. 分析发现, 传统HOG算子受图像旋转影响, 梯度矢量由${[1,0]^{\rm{T}}}$变为${[1, - 1]^{\rm{T}}}$, 而3-HRPOG算子的8组梯度矢量值不变, 仅出现顺序发生变化, 可见, 3-HRPOG算子可以提取图像在各个不同方向上的梯度变化信息, 不受图像旋转影响.
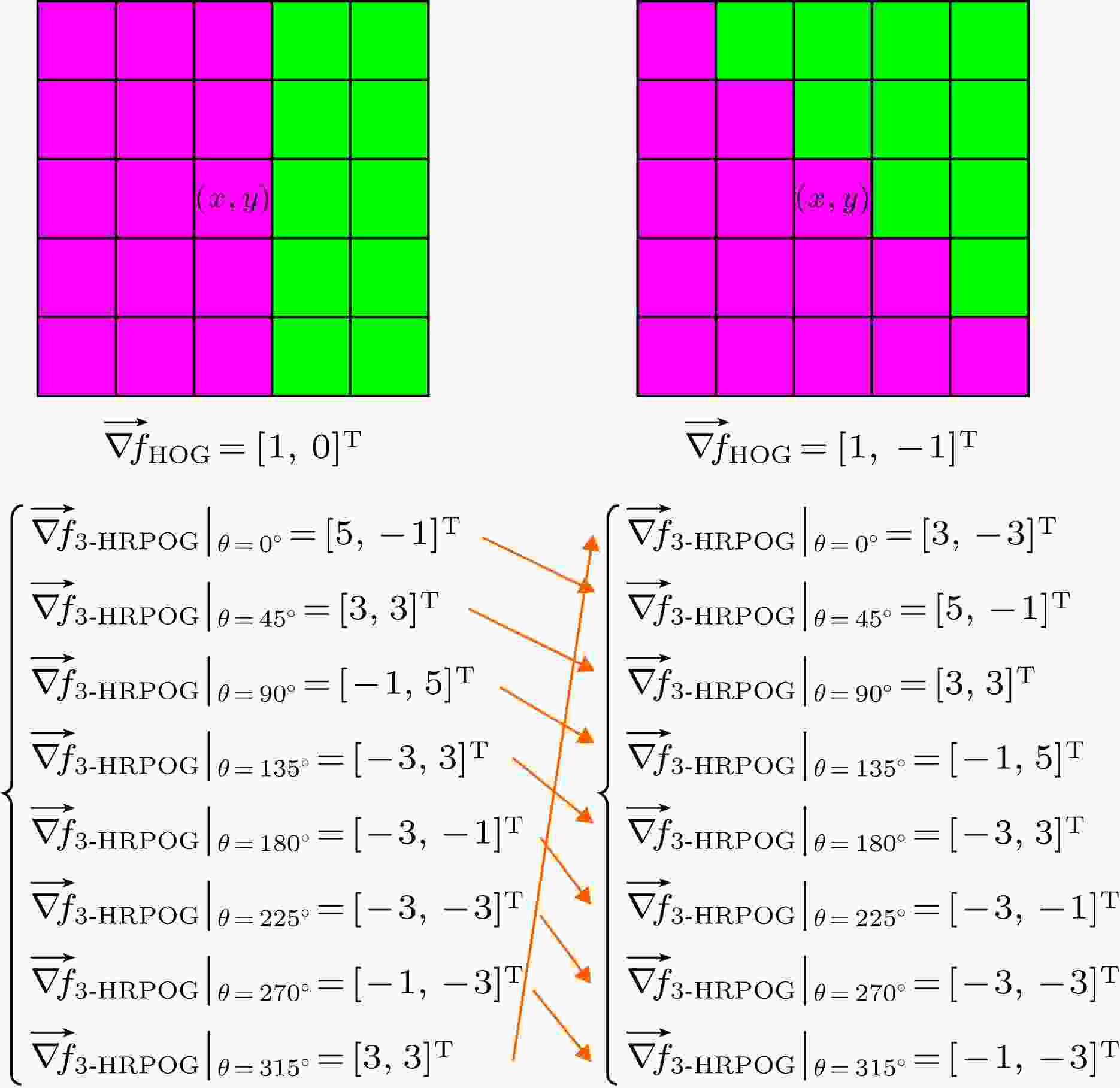图 4 旋转不变性分析　(a) 原图及HOG和3-HRPOG的梯度矢量值; (b) 旋转${45^ \circ }$图像及HOG和3-HRPOG的梯度矢量值
Figure4. Rotation invariance analysis: (a) Original binary image and gradient vectors of HOG and 3-HRPOG; (b) rotated ${45^ \circ }$ binary image and gradient vectors of HOG and 3-HRPOG.

2 -->

2.3.多尺度旋转主方向梯度直方图(multi-scale histogram of rotated principal orientation gradients, Ms-HRPOG)特征算子

研究表明, 人眼视觉系统具有多尺度分析能力, 通过调节视网膜细胞感受野范围可以提取不同尺度下的目标信息, 从而更加全面准确地“认识”目标^[49,50]. 受此启发, 本文在2.2节3×3尺度的3-HRPOG算子基础上(图3), 将卷积模板尺寸扩展为5×5大小, 且卷积权值设置方法不变, 进一步设计出5×5尺度的5-HRPOG算子(图5), 并将2种算子相互结合, 提出一种Ms-HRPOG特征算子, 特征提取流程如图6所示, 其中, 5-HRPOG特征提取步骤与3-HRPOG特征提取一致, 将二者级联得到最终的Ms-HRPOG特征向量.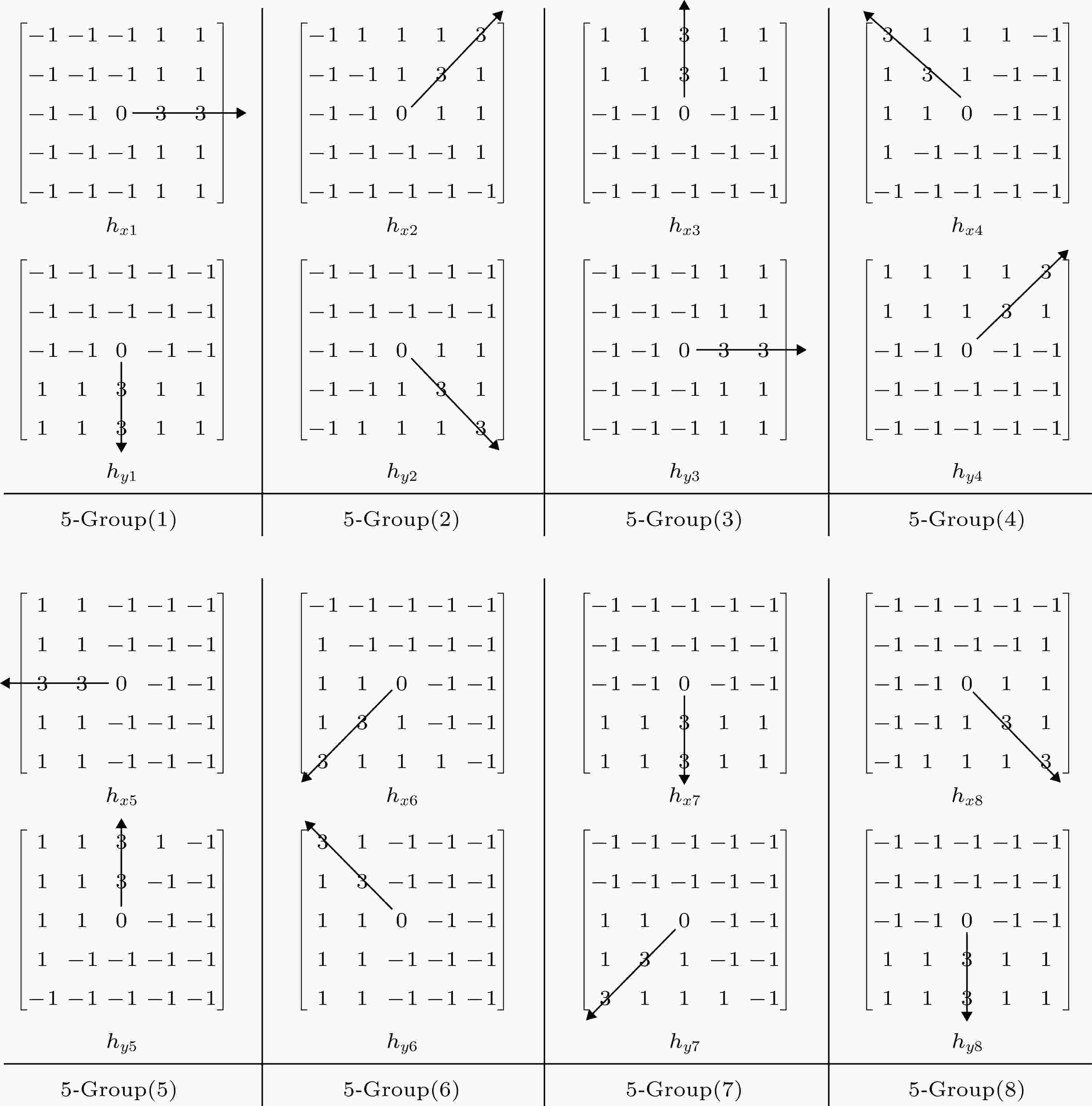
图 5 5-HRPOG算子的旋转主方向梯度模板
Figure5. Rotated dominant direction gradient masks of 5-HRPOG feature descriptor.

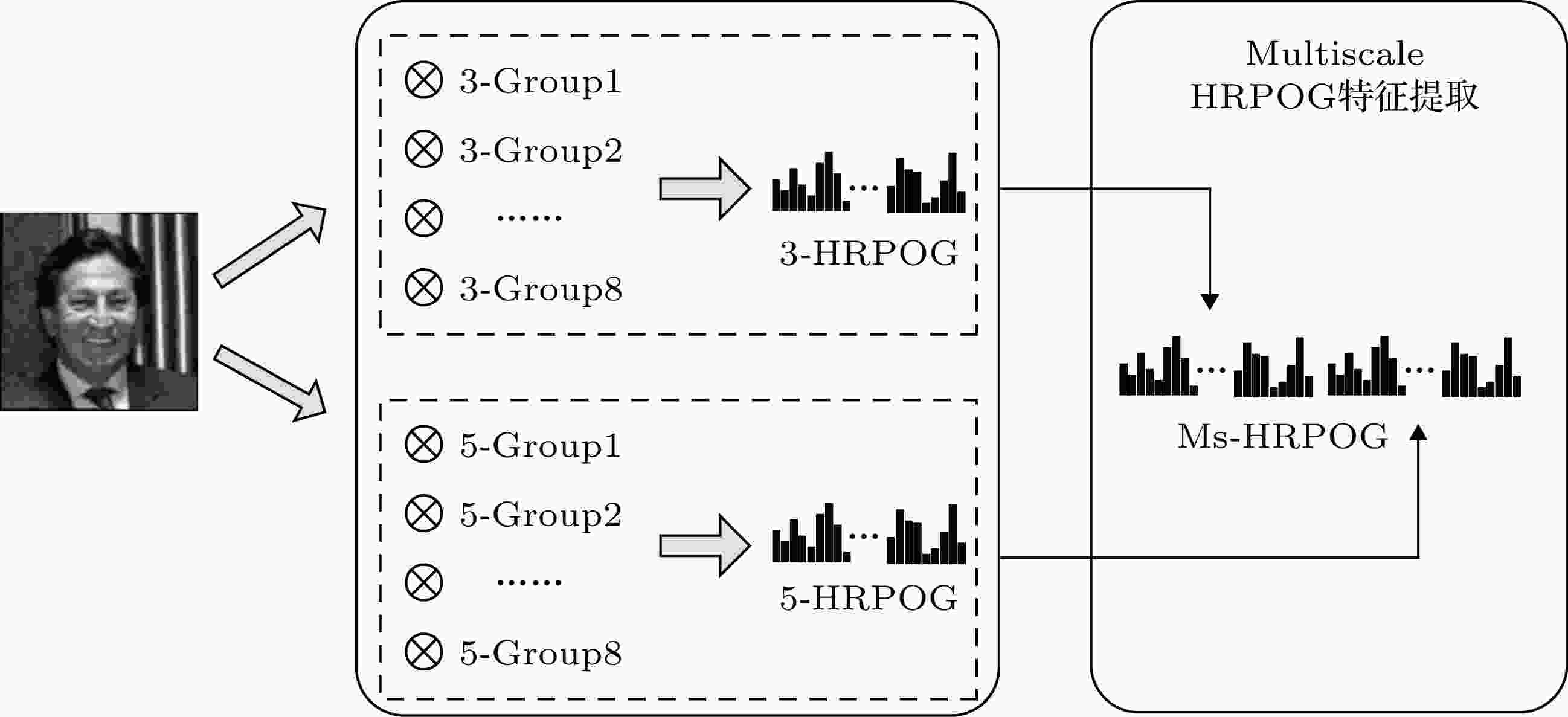图 6 Ms-HRPOG特征提取示意图
Figure6. The sketch of Ms-HRPOG feature descriptor.

稀疏表示(sparse representation, SR)^[3]是继小波变换、多尺度几何分析后, 又一新的信号表示方法, 基本思想是用超完备字典$D$中少量(稀疏)原子线性组合来近似表示待测样本$y$:

$\mathop {\min }\limits_\alpha \left\| {y - D\alpha } \right\|_2^2 + {\left\| \alpha \right\|_1},$

这里采用${l_1}$范数${\left\| \bullet \right\|_1}$约束向量$\alpha $中非零编码个数, 使其最少(最稀疏). 乔立山等^[33]受SR启发, 提出了稀疏保持投影(sparsity preserving projections, SPP)算法, 通过在低维子空间保持高维样本之间的稀疏重构关系, 寻找最佳低维投影, 目标函数如下:

$\left\{ \begin{aligned}& \mathop {\min }\limits_{{s_i}} \; {\left\| {{s_i}} \right\|_1} \\ & {\rm{s}}{\rm{.t}}.\; \; \; \left\| {{x_i} - {X_i}{s_i}} \right\|_2 < \varepsilon \\ & \quad\quad {{{1}}^{\rm{T}}}{s_i} = 1\end{aligned} \right.,$

$\left\{ \begin{aligned}& \mathop {\min }\limits_P {\rm{ }}\sum\limits_{i = 1}^N {{\rm{ }}\left\| {{{{P}}^{\rm{T}}}{x_i} - {{{P}}^{\rm{T}}}X{s_i}} \right\|_2^2} \\& {\rm{s}}{\rm{.t}}.\; \; \; \; {{{P}}^{\rm{T}}}X{X^{\rm{T}}}{{P}} = I\end{aligned} \right.,$

其中, ${X_i} = \left[ {{x_1}, \ldots,{x_{i - 1}},0,{x_{i + 1}}, \ldots,{x_N}} \right] \in {R^{mn \times N}}$是样本集$X$中去除样本${x_i}$的超完备字典, 约束式$ \left\| {{x_i} - {X_i}{s_i}} \right\|_2 < \varepsilon $松弛了重构条件, ${{{1}}^{\rm{T}}}{s_i} = 1$使样本${x_i}$的稀疏重构权值${s_i}$归一化, 这里${{1}} = {[1,1,...,1]^{\rm{T}}} \in $${R^{N \times 1}} $. 可见, SPP中${s_i}$描述了高维空间中样本${x_i}$与剩余样本的稀疏重构关系, 通过在低维空间中约束保持该局部属性, 由(8)式优化得到最佳低维投影矩阵${{P}} \in {R^{mn \times d}}$.
以LFW数据库为例, 图7给出了根据(7)式计算得到的某一样本图像的稀疏重构权值. 图中, 前10个为同类样本的重构权值, 后90个为异类样本的重构权值. 由图7可以看出, 图中仅同类的第4个样本和第8个样本参与了重构(有权值), 而剩余的同类样本均未参与重构(权值为0); 相反, 某些异类样本在重构中具有较大权值, 如第29, 39, 48, 65个样本等. 造成这种结果的原因是, 真实采集的人脸图像复杂多变, 同类样本受光照、遮挡、表情、年龄、姿态等影响, 彼此之间存在差异, 导致部分同类非近邻样本重构权值为0, 而不同类样本间又具有人脸结构相似特征, 造成部分异类伪近邻样本参与重构. 可见, SPP算法在非约束人脸识别中仍有局限性, 不能准确描述样本的近邻重构关系.
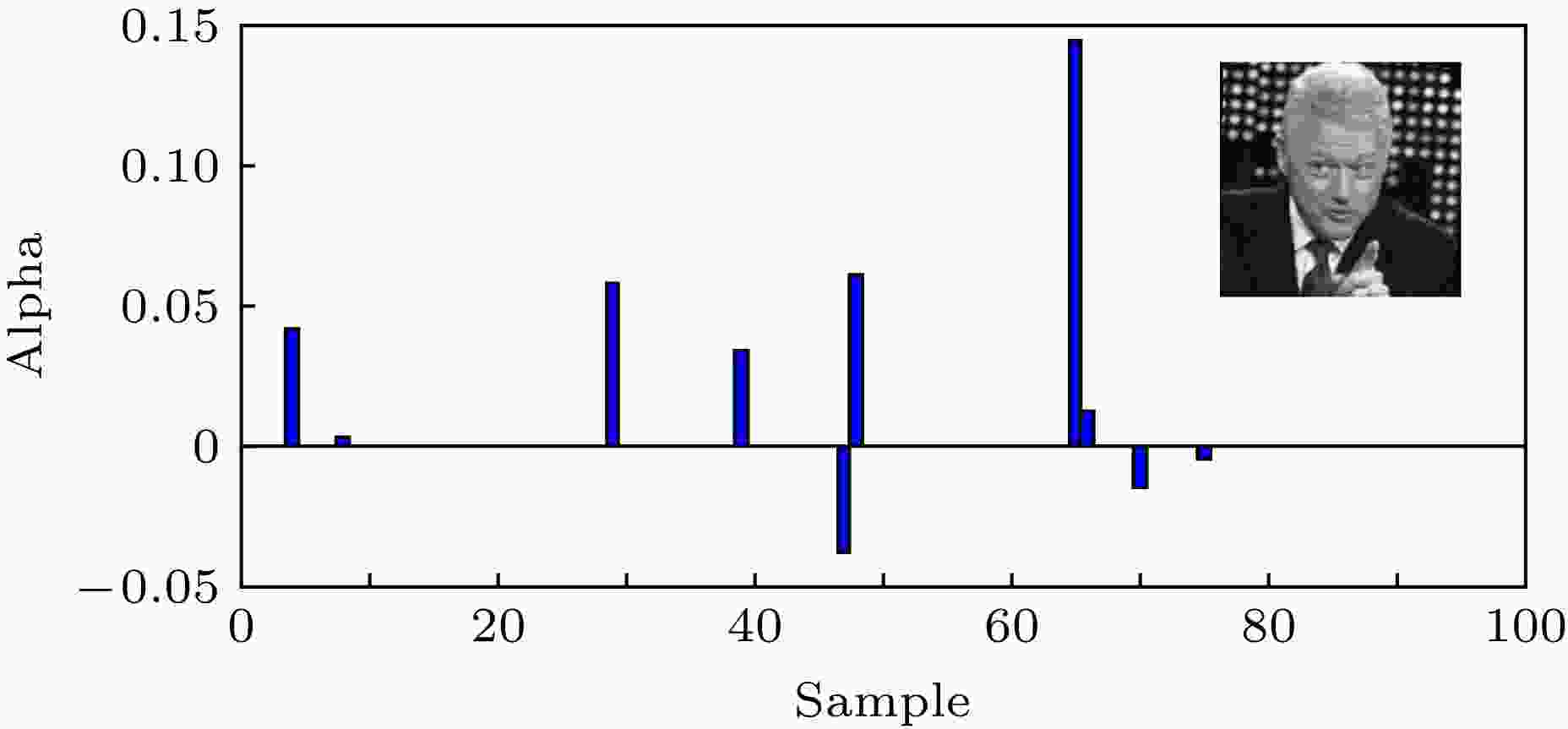图 7 LFW数据库中某一图像的SPP稀疏重构权值
Figure7. Sparsity reconstruction weights of one sample with SPP algorithm on the LFW database.

鉴于SPP的局限性, 本文提出DSGE算法, 从2个方面进行改进. 一方面, 在稀疏图构建阶段, 利用类别标签分别构建类内、类间重构关系矩阵, 并且引入类内、类间紧凑度约束因子, 用以增强待测样本与同类非近邻样本的重构关系, 以及削弱异类伪近邻样本的重构影响; 另一方面, 在低维投影阶段, 增加全局约束因子, 利用样本全局分布中隐含的鉴别信息, 以类间重构散度最大、类内重构散度最小为目标计算最佳投影矩阵, 使低维子空间更紧致、更判别.
2

-->

4.1.类内、类间重构关系矩阵

首先, 分析待测样本与同类样本之间的重构关系. 设训练样本集$X$由$C$类样本子集${X_1},{X_2}, \ldots,{X_C}$组成, 表示为

$ \begin{split}X & = \left[ {{X_1},{X_2}, \ldots,{X_c}} \right]\\ & = \left[ {\underbrace {{x_{11}},{x_{12}}, \ldots,{x_{1{n_1}}}}_{{n_1}},...,\underbrace {{x_{c1}},{x_{c2}},...,{x_{c{n_c}}}}_{{n_c}}} \right] \\ & \in {R^{mn \times N}}, \end{split}$

其中, ${n_k}$表示为第$k$类样本子集个数, 满足$\sum\limits_{k = 1}^C {{n_k} = N} $. 引入类别标签, 优化求解待测样本${x_{ij}}$的类内稀疏重构权值$\theta _{ij}^w$, 目标函数如下:

$\left\{ \begin{split}& \mathop {\min }\limits_{\theta _{ij}^w} {\rm{ }}\left\| {{x_{ij}} - {X_{^{l({x_{ij}})}}}\theta _{ij}^w} \right\|_2 + {\rm{ }}{\lambda _1}{\left\| {\theta _{ij}^w} \right\|_1}\\ & \quad\quad +{\lambda _2}{\left\| {\theta _{ij}^w - {\Gamma _{^{l({x_{ij}})}}}} \right\|_1} \\& {\rm{s}}{\rm{.t}}.\; \; \; \; {{{1}}^{\rm{T}}}\theta _{ij}^w = 1,\end{split} \right.$

这里, $l({x_{ij}})$表示待测样本${x_{ij}}$的类别, 取$l({x_{ij}}) = i$, 定义类内超完备字典

${X_{l({x_{ij}})}} = [{x_{i{\kern 1pt} 1}},...,{x_{i{\kern 1pt} j - 1}},0,{x_{i{\kern 1pt} j + 1}},...,{x_{i{\kern 1pt} {n_i}}}] \in {R^{mn \times {n_{_i}}}},$

表示为除${x_{ij}}$外的剩余同类样本子集. 定义${\varGamma _{^{_{l({x_{ij}})}}}}$为类内紧凑度约束因子, 记为与${x_{ij}}$同类的所有样本的类内稀疏重构权值的平均向量, 最小化${\left\| {\theta _{ij}^w - {\varGamma _{^{{\rm{label}}({x_{ij}})}}}} \right\|_1}$可以使同类样本的稀疏重构权值接近中心值, 增强待测样本与同类非近邻样本的重构关系.
依据(10)式分别计算样本子集${X_i}$$(i = 1,2,...C)$中同类样本的类内稀疏重构权值${{\theta }}_{ij}^w \in {R^{{n_i} \times 1}}$, 从而得到样本子集${X_i}$的类内重构权值矩阵$\varTheta _i^w = $$ \left[ {\theta _{i1}^w,\theta _{i2}^w, \ldots ,\theta _{i{n_i}}^w} \right] \in {R^{{n_i} \times {n_i}}}$, 由此构建样本集$X$的类内重构关系矩阵${{{\varLambda }}^w} \in {R^{N \times N}}$:

${{{\varLambda }}^w} = {\rm{diag}}\left( {{{\varTheta }}_1^w,{{\varTheta }}_2^w,...,{{\varTheta }}_C^w} \right).$

分析发现, (11)式保证了待测样本与同类样本的重构关系, 然而大量研究表明, 异类样本在样本集中的空间分布对低维投影的准确性也有很大影响, 因此, 有必要进一步考虑待测样本与异类样本的重构关系. 定义目标函数如下:

$\left\{ \begin{aligned}& \mathop {\min }\limits_{\theta _{ij}^b} \left\| {{x_{ij}} - {X_{\overline {l({x_{ij}})} }}\theta _{ij}^b} \right\|_2 + {\rm{ }}{\lambda _3}\left\| {\theta _{ij}^b} \right\|_1 \\ & \quad+ {\lambda _4}\left\| {\theta _{ij}^b - \varGamma _{\overline {l({x_{ij}})} }} \right\|_1 \\& {\rm{s}}{\rm{.t}}. {{{1}}^{\rm{T}}}\theta _{ij}^b = 1,\end{aligned} \right.$

其中, ${X_{\overline {l({x_{ij}})} }}$为类间超完备字典, 由与${x_{ij}}$不同类别的训练样本组成. 设${x_{ij}}$属于第$k$类样本子集, 则${X_{\overline {l({x_{ij}})} }}\! =\! [{X_1},{X_2},...,{X_{k - 1}},{X_{k + 1}},...,{X_c}] \!\in \!{R^{mn \times (N - {n_k})}}$, 根据(12)式优化得到待测样本${x_{ij}}$的类间稀疏重构权值${\theta }_{ij}^b$. 定义$\varGamma _{\overline {l({x_{ij}})} }$为类间紧凑度约束因子, 记为与${x_{ij}}$同类样本的类间稀疏重构权值的平均向量, 最小化$\left\| {\theta _{ij}^b - \varGamma _{\overline {l({x_{ij}})} }} \right\|_1$可以进一步削弱异类伪近邻样本对待测样本的重构影响.
为了便于描述样本集$X$的类间重构关系, 将${\theta }_{ij}^b$扩展为$N$维列向量, 即

$\begin{split} {\bf{\theta }}_{ij}^{b - {\rm{extended}}} = & \left[{\beta _{i1}},{\beta _{i2}},...,{\beta _{i({n_1} + ... + {n_{i - 1}})}},\underbrace {0......0,}_{{n_i}{\text{个}}0}\right.\\ & \Bigggl.{24} {\beta _{i({n_1} + ... + {n_i} + 1)}},...,{\beta _{iN}}\Bigggr]{24}^{\rm T} \in {R^{N \times 1}}, \end{split}$

则样本子集${X_i}$的类间重构权值矩阵表示为

$ \begin{split} & \varTheta _i^{b - {\rm{extended}}} = \left[ {\theta _{i1}^{b - {\rm{extended}}},\theta _{i2}^{b - {\rm{extended}}},...,\theta _{i{n_i}}^{b - {\rm{extended}}}} \right]\\ \in & {R^{N \times {n_i}}},\end{split}$

由此得到样本集$X$的类间重构关系矩阵${{{{B}}}^b} \in {R^{N \times N}}$:

${{{{B}}}^b} = \left[ {{{\Theta }}_1^{b - {\rm{extended}}},{{\Theta }}_2^{b - {\rm{extended}}},...,{{\Theta }}_c^{b - {\rm{extended}}}} \right].$

2 -->

4.2.DSGE低维投影

首先, 为了使低维子空间中同类样本尽可能聚合, 在最小化类内重构误差基础下, 增加全局类内约束条件, 使得低维子空间数据既保留了样本间局部类内稀疏重构关系, 又考虑了同类样本子集的全局紧凑度分布特性. 最小化类内重构散度目标函数如下:

$\mathop {\min }\limits_{{P}} \; \; {\kern 1pt} \sum\limits_{i = 1}^N {\left( {\left\| {{{{P}}^{\rm{T}}}{x_i} - \sum\limits_{j = 1}^N {{{{P}}^{\rm{T}}}\alpha _{ji}^w} {x_j}} \right\|_F^2} \right)} + \left\| {{{{P}}^{\rm{T}}}{X_w}} \right\|_F^2.$

这里为了描述方便, 不考虑样本类别, 定义${x_i}$为样本集$X$中的第$i$个样本, ${x_j}$为第$j$个样本, $\alpha _{ji}^w$对应类内重构关系矩阵${{{\varLambda }}^w}$中相应元素, 描述了样本${x_i}$与${x_j}$的类内重构关系. 定义全局类内约束因子${X_w} = \left[ {{X_1} - \overline {{X_1}}, \ldots,{X_i} - \overline {{X_i}}, \ldots,{X_c} - \overline {{X_c}} } \right]$, ${X_i}$是第$i$类样本子集, $\overline {{X_i}} $则是第$i$类样本子集的均值矩阵, 约束$\left\| {{P^{\rm{T}}}{X_w}} \right\|_F^2$最小, 可以使得各类样本子集类内更紧凑. 推导目标函数(14)得到

$\begin{split} & \sum\limits_{i = 1}^n {\left( {\left\| {{{{P}}^{\rm{T}}}{x_i} - \sum\limits_{j = 1}^n {{{{P}}^{\rm{T}}}} \alpha _{ji}^w{x_j}} \right\|_F^2} \right)} + \left\| {{{{P}}^{\rm{T}}}{X_w}} \right\|_F^2 \\ =\; & \sum\limits_{i = 1}^n {\left( {\left\| {{{{P}}^{\rm{T}}}{x_i} - {{{P}}^{\rm{T}}}X{{\varLambda }}_i^w} \right\|_F^2} \right)} +\left\| {{{{P}}^{\rm{T}}}{X_w}} \right\|_F^2\\ =\; & \sum\limits_{i = 1}^n {\left[ {{\rm{tr}}\left( {{{{P}}^{\rm{T}}}\left( {x{}_i - X{{\varLambda }}_i^w} \right){{\left( {{x_i} - X{{\varLambda }}_i^w} \right)}^{\rm{T}}}{{P}}} \right)} \right]} \\ & +{\rm{tr}}\left( {{{{P}}^{\rm{T}}}{X_w}{X_w}^{\rm{T}}{{P}}} \right)\\ = \;& {\rm{tr}}\left[ {{{{P}}^{\rm{T}}}\left( {\sum\limits_{i = 1}^n {\left( {x{}_i - X{{\varLambda }}_i^w} \right){{\left( {{x_i} - X{{\varLambda }}_i^w} \right)}^{\rm{T}}}} } \right){{P}}} \right] \\ & + {\rm{tr}}\left( {{{{P}}^{\rm{T}}}{X_w}{X_w}^{\rm{T}}{{P}}} \right) \\ =\; &{\rm{tr}}\left[ {{{{P}}^{\rm{T}}}X\left( {I - {{{\varLambda }}^w} - {{\left( {{{{\varLambda }}^w}} \right)}^{\rm{T}}} + {{\left( {{{{\varLambda }}^w}} \right)}^{\rm{T}}}{{{\varLambda }}^w}} \right){X^{\rm{T}}}{{P}}} \right] \\ & + {\rm{ tr}}\left( {{{{P}}^{\rm{T}}}{X_w}{X_w}^{\rm{T}}{{P}}} \right). \end{split}$

取${L^w} = I - {{{\varLambda }}^w} - {\left( {{{{\varLambda }}^w}} \right)^{\rm{T}}} + {\left( {{{{\varLambda }}^w}} \right)^{\rm{T}}}{{{\varLambda }}^w}$, 则目标函数(14)转换为

$\mathop {\min }\limits_{{P}} \; \; \; \; {\kern 1pt} {\rm{tr}}\; {\kern 1pt} \left[ {{{{P}}^{\rm{T}}}\left( {X{L^w}{X^{\rm{T}}} + {X_w}{X_w}^{\rm{T}}} \right){{P}}} \right].$

同理, 为了使低维子空间中异类样本尽可能分离, 在最大化类间重构误差基础下, 又增加全局类间约束条件, 得到最大化类间重构散度目标函数如下:

$\mathop {\max }\limits_{{P}} \; \; \; \sum\limits_{i = 1}^N {\left( {\left\| {{{{P}}^{\rm{T}}}{x_i} - \sum\limits_{j = 1}^N {{{{P}}^{\rm{T}}}\beta _{ji}^b} {x_j}} \right\|_F^2} \right)} +\left\| {{{{P}}^{\rm{T}}}{X_b}} \right\|_F^2,$

其中, $\beta _{ji}^b$为类间重构关系矩阵${{{{ B}}}^b}$中相应元素, 描述了样本${x_i}$与${x_j}$的类间重构关系. 定义全局类间约束因子${X_b} = \left[ {\overline {{X_1}} - \overline X, \ldots,\overline {{X_i}} - \overline X, \ldots,\overline {{X_c}} - \overline X } \right]$, 取$\overline X $为所有样本的均值矩阵, 约束$\left\| {{{{P}}^{\rm{T}}}{X_b}} \right\|_F^2$最大, 可以使得各类样本子集尽可能分离, 低维子空间数据更具有判别性. 依据目标函数(14)推导过程, 目标函数(17)也可转换(18)式, 其中, ${L^b} = I - {{{B}}^b} - $${\left( {{{{B}}^b}} \right)^{\rm{T}}} + {\left( {{{{B}}^b}} \right)^{\rm{T}}}{{{B}}^b} $.

$\mathop {\max }\limits_{{P}} \; \; \; {\rm{tr}}\left[ {{{{P}}^{\rm{T}}}\left( {X{L^b}{X^{\rm{T}}} + {X_b}{X_b}^{\rm{T}}} \right){{P}}} \right].$

结合(16)式和(18)式, 基于最大边界准则(maximum margin criterion, MMC)得到DSGE低维投影目标函数:

$ \begin{split}\mathop {\max }\limits_{{P}} J\left( {{P}} \right) =\; & {\rm{tr}}\left[ {{{{P}}^{\rm{T}}}\left( {X{L^b}{X^{\rm{T}}} + {X_b}{X_b}^{\rm{T}}} \right){{P}}} \right]\\ & - {\rm{tr}}\left[ {{{{P}}^{\rm{T}}}\left( {X{L^w}{X^{\rm{T}}} + {X_w}{X_w}^{\rm{T}}} \right){{P}}} \right] \end{split}$

由拉格朗日乘子法, 在${{{P}}^{\rm{T}}}{{P}} = {{I}}$约束条件下, (19)式转换为如下特征方程:

$\left[ {X{L^b}{X^{\rm{T}}} + {X_b}X_b^{\rm{T}} - X{L^w}{X^{\rm{T}}} - {X_w}X_w^{\rm{T}}} \right]p = \lambda p.$

求取前$d$个最大特征值对应的特征向量, 构成最佳低维映射矩阵${{{P}}^*} = \left[ {{p_1},{p_2} \ldots,{p_d}} \right] \in {R^{mn \times d}}$.

综上所述, 稀疏表示可以理解为函数逼近问题, 选择一个好的基函数对SRC分类器非常重要, 因此, 本文将HRPOG和DSGE相结合, 提出一种DSGE-HPROG算法, 用以增强低维特征字典的鉴别性、紧致性和稳定性, 使SRC分类效果更理想. 同时, 考虑DSGE算法中稀疏重构关系与SRC分类器的稀疏表示系数具有相同物理意义, 本文又借鉴SRC-DP^[40]思想, 将低维投影和稀疏图构建联合优化, 使SRC分类器在低维投影子空间获得最佳识别效果, 具体实现步骤如算法1所示.
算法1 DSGE-HRPOG算法
输入: 训练样本${{X}}\! =\! \left[ {{{{X}}_1},{{{X}}_2}, \cdots,{{{X}}_c}} \right]\! \in \!{\mathbb{R}^{mn \times N}}$, 参数${\lambda _{ 1}}$、${\lambda _{ 2}}$、$\lambda { _3}$、$\lambda { _4}$、${k_{\max }}$和PCA Ratio.
输出: 最佳投影矩阵${{{P}}^*}$.
步骤1. 采用HRPOG算子(单尺度或多尺度)提取训练样本X的特征, 并采用PCA对HRPOG特征向量进行预处理降维, 构建特征字典${D_{{\rm{HRPOG}}}}$
步骤2. 初始化投影矩阵${{{P}}_0}$, 取迭代次数$k = 1$;
步骤3. 将特征字典${D_{{\rm{HRPOG}}}}$投影到变换空间$Z = P_{k - 1}^{\rm{T}}{D_{{\rm{HRPOG}}}}$;
步骤4. 依据(10-13)式计算变换空间$Z = [{Z_1},{Z_2},...{Z_c}]$中任一样本${z_{ij}}$与同类样本的重构关系矩阵${{{\varLambda }}^w}$, 以及与异类样本的重构关系矩阵${{{B}}^b}$;
步骤5. 计算${L^w} = I - {{{\varLambda }}^w} - {\left( {{{{\varLambda }}^w}} \right)^{\rm{T}}} + {\left( {{{{\varLambda }}^w}} \right)^{\rm{T}}}{{{\varLambda }}^w}$和${L^b} = I - {{{B}}^b} - {\left( {{{{B}}^b}} \right)^{\rm{T}}} + {\left( {{{{B}}^b}} \right)^{\rm{T}}}{{{B}}^b}$, 代入特征方程(20)中, 取前$d$个最大特征值对应的特征向量构成投影矩阵${{{P}}_k}$;
步骤6. 取$k = k + 1$, 计算收敛条件$\left| {J({{{P}}_k}) - J({{{P}}_{k - 1}})} \right|/\left| {J({{{P}}_k})} \right|$;
步骤7. 若$\dfrac{{\left| {J({{{P}}_k}) - J({{{P}}_{k - 1}})} \right|}}{{\left| {J({{{P}}_k})} \right|}} < \varepsilon $或迭代次数$k$大于设定值${k_{\max }}$, 则最佳投影矩阵${{{P}}^*} = {{{P}}_k}$, 反之, 重复步骤3—步骤7.

为了验证DSGE-HRPOG算法的有效性, 分别在AR, Extended Yale B, LFW和PubFig这4个人脸数据库上进行实验仿真. 实验主要参数设置为${\lambda _1} = {\lambda _3} = 0.5$, ${\lambda _2} = {\lambda _4} = 1$, ${k_{\max }} = 20$. 所有实验均采用PCA进行数据预处理(取PCA Ratio = 0.98), 在Win10 64位操作系统、8 GB内存和MATLAB R2017a仿真环境下完成.
2

-->

6.1.AR数据库

AR数据库是在严格控制实验环境条件下采集的具有不同面部表情、照明条件和遮挡(包括太阳镜和围巾)的人脸正视图, 图像尺寸为50×40像素大小. 本文选取120类人(65男55女)在2个阶段拍摄的图像, 其中每人每个阶段包含7张无遮挡图像(包含表情、光照影响)和6张遮挡图像(3张墨镜遮挡, 3张围脖遮挡), 样本如图8所示. HRPOG算子的参数设置为1个cell = 2×2 pixels, 1个block = 2×2 cells, bin = 9.
图 8 AR数据库部分样本图像
Figure8. Samples of one person in the AR database.

3 -->

6.1.1.表情、光照、时间的影响

本实验主要分析表情、光照、时间等非遮挡因素对人脸识别的影响. 取AR数据库中每类人在Session1中7张无遮挡图像作为训练样本, Session2中7张无遮挡图像作为测试样本进行实验仿真(表1). 由表1可以看出, 在本文提出的DSGE-HRPOG算法框架下, 无论采用单尺度特征算子(3-HRPOG和5-HRPOG), 还是多尺度特征算子(Ms-HRPOG)构建特征字典, DSGE-HRPOG的识别率均高于其他算法, 与DSNPE^[37], DP-NFL^[51]和SRC-DP^[40]相比, 识别率最大提升了12.74%, 17.01%和13.61%. 这说明, 本文提出的DSGE-HRPOG算法在降低人脸识别中表情、光照、时间等非遮挡影响时, 具有绝对的优势. 同时, 本实验又基于原始图像构建样本字典, 并采用DSGE算法进行字典降维, 得到DSGE-pixels的识别率为76.79%, 相比SPP^[33], DSNPE^[37], DP-NFL^[51]和SRC-DP^[40], 识别率分别提升了8.58%, 0.72%, 4.99%和1.59%. 这也从另一个角度说明, 摒弃特征字典的作用, 本文提出的DSGE算法在去除数据冗余、构建低维判别字典方面也具有一定优势, 但将DSGE与HRPOG特征字典相结合, 识别效果更佳, 如表1中所示, DSGE-HRPOG算法的识别率比DSGE-pixels最大提升了12.02%.

Method	LPP[22]	NPE[23]	SPP[33]	DSNPE[37]	DP-NFL[51]	SRC-DP[40]	DSGE-pixels	DSGE-HRPOG
								3-HRPOG	5-HRPOG	Ms-HRPOG
Recognition Rate/%	67.14	68.69	68.21	76.07	71.8	75.2	76.79	88.45	88.21	88.81
Dimension	115	311	220	140	63	63	322	777	754	774

表1AR数据库在表情、光照和时间干扰因素下的实验结果
Table1.Experimental results on the AR database with the interference factors of expression, illumination and time.

3 -->

6.1.2.遮挡的影响

本实验主要分析遮挡因素对人脸识别的影响, 包括眼镜遮挡、围巾遮挡以及混合遮挡3个方面. 下面有针对性地设计3个实验, 依次进行实验仿真(表2).

	Experiment 1/%	Experiment 2/%	Experiment 3/%
LPP[22]	71.39	68.68	69.46
NPE[23]	72.64	71.81	71.08
SPP[33]	75.90	72.92	74.07
DSNPE[37]	80.28	78.26	78.14
SRC-DP[40]	78.35	76.50	77.80
SRC-FDC[42]	80.90	79.90	80.30
DSGE-pixels	79.03	78.75	82.65
DSGE-HRPOG (3-HRPOG)	88.54	89.51	90.53
DSGE-HRPOG (5-HRPOG)	89.31	89.58	90.98
DSGE-HRPOG (Ms-HRPOG)	89.31	90.00	91.06

表2AR数据库在遮挡干扰因素下的实验结果
Table2.Experimental results of AR database with the occlusion interference.

实验1: 取AR数据库中每类人在Session1中7张无遮挡图像和任意1张眼镜遮挡图像作为训练样本, 而Session2中7张无遮挡图像和3张眼镜遮挡图像, 以及Session1中剩余的2眼镜遮挡图像作为测试样本.
实验2: 取AR数据库中每类人在Session1中7张无遮挡图像和任意1张围巾遮挡图像作为训练样本, 而Session2中7张无遮挡图像和3张围巾遮挡图像, 以及Session1中剩余的2围巾遮挡图像作为测试样本.
实验3: 取AR数据库中每类人在Session1中7张无遮挡图像和任意1张眼镜遮挡图像以及任意1张围巾遮挡图像作为训练样本, 而Session2中7张无遮挡图像、3张眼镜遮挡图像、3张围巾遮挡, 以及Session1中剩余的眼镜和围巾遮挡图像作为测试样本.
分析表2中3个实验结果, 可以看出, 本文提出的DSGE-HRPOG算法在眼镜遮挡、围巾遮挡以及混合遮挡3种真实遮挡情况下, 均具有最佳识别效果, 其中, 基于Ms-HRPOG特征字典的识别率最高, 分别为89.31%, 90.00%和91.06%, 比次优算法SRC-FDC^{[42, 52]}高8.41%, 10.1%和10.76%. 这说明, DSGE-HRPOG算法通过结合HRPOG特征字典以及DSGE低维投影的优势, 可以有效消除人脸识别中各种遮挡因素的影响, 具有较强的遮挡鲁棒性. 同时, 从表2中也可以看出, 基于多尺度特征字典(Ms-HRPOG)的DSGE-HRPOG的识别率均高于基于单尺度特征字典(3-HRPOG和5-HRPOG)的情况, 这也说明, 采用多尺度特征融合策略有助于进一步提升特征字典的鉴别能力, 增强系统的稳定性.
3 -->

6.1.3.混合影响

前2个实验分别分析了遮挡因素以及非遮挡因素对人脸识别的影响, 本实验将遮挡因素和非遮挡因素综合考虑, 分析混合因素(遮挡、表情、光照、时间)对人脸识别的影响. 随机取每类人26张(2个Session)图像中的13张图像作为训练样本, 剩余图像作为测试样本进行实验仿真, 交叉验证10次(表3). 分析发现, 当样本中随机包含各种不同干扰因素时, 本文提出的DSGE-HRPOG算法在消除人脸识别中遮挡、表情、光照、时间等混合影响时, 仍具有一定优势. 相比文献[53]和[54]中提出的2个先进算法, 基于Ms-HRPOG特征字典的DSGE-HRPOG算法的平均识别率提升最多, 分别提升了0.96%和1.7%. 同时, 文献[53]和[54]算法的标准差分别为0.53和0.93, 而DSGE-HRPOG的标准差最大为0.17, 远远小于文献值, 这也进一步说明了本文提出的DSGE-HRPOG算法不受样本选择和干扰因素变化的影响, 具有分类稳定性.

	Mean/%	Std/%	Dimension
LPP[22]	95.90	0.38	141
NPE[23]	95.87	0.55	311
SPP[33]	90.39	0.90	151
DSNPE[37]	98.02	0.33	200
Wang[54]	97.85	0.93	—
Gao[53]	98.59	0.53	—
DSGE-pixels	98.45	0.27	202
DSGE-HRPOG (3-HRPOG)	99.45	0.17	1350
DSGE-HRPOG (5-HRPOG)	99.37	0.12	1297
DSGE-HRPOG (Ms-HRPOG)	99.55	0.13	1385

表3AR数据库在混合干扰因素下的实验结果
Table3.Experimental results on the AR database with the mix interference factors.

2 -->

6.2.Extended Yale B数据库

Extended Yale B数据库包含38类人在不同光照条件下拍摄的人脸正视图, 每类人约64张图像, 共2414张, 图像尺寸为32×32像素大小, 部分样本图像如图9所示. 这里, HRPOG算子的参数设置与AR数据库一致.
图 9 Extended Yale B数据库部分样本图像
Figure9. Samples of one person in the Extended Yale B database

在Extended Yale B数据库上, 首先分析不同强度光照对人脸识别的影响. 随机选取每类人的10张图像作为训练样本, 剩余图像作为测试样本进行实验仿真(表4). 由表4可以看出, 在多尺度特征字典情况下(Ms-HRPOG), DSGE-HRPOG算法可以达到92.48%的识别率, 相比近年来提出的先进算法GRSDA^[39]和RCDA^[52], 分别提升了9.78%和0.48%, 识别效果最佳. 而在单尺度特征字典(3-HRPOG和5-HRPOG)情况下, DSGE-HRPOG的识别率分别为91.35%和89.77%, 略低于RCDA^[52]. 可见, 在少量训练样本条件下, 多尺度特征更有助于消除人脸识别中不同强度的光照影响.

Method	LPP[22]	NPE[23]	SPP[33]	DSNPE[37]	GRSDA[39]	RCDA[52]	DSGE-pixels	DSGE-HRPOG
								3-HRPOG	5-HRPOG	Ms-HRPOG
Recognition Rate/%	87.86	89.31	85.79	85.74	82.7	92	86.03	91.35	89.77	92.48
Dimension	65	160	95	85	266	—	83	355	345	351

表4Extended Yale B数据库在光照干扰因素下的实验结果
Table4.Experimental results of Extended Yale B database with the illumination interference.

其次, 进一步验证DSGE-HRPOG算法在Extended Yale B数据库上的遮挡鲁棒性. 本文又随机选取每类人14张图像, 在上面分别添加大小随机、位置随机的黑白点噪声块, 得到部分遮挡样本图像(图10). 这里, 噪声块大小与图像大小比例在0.05—0.15任意取值.
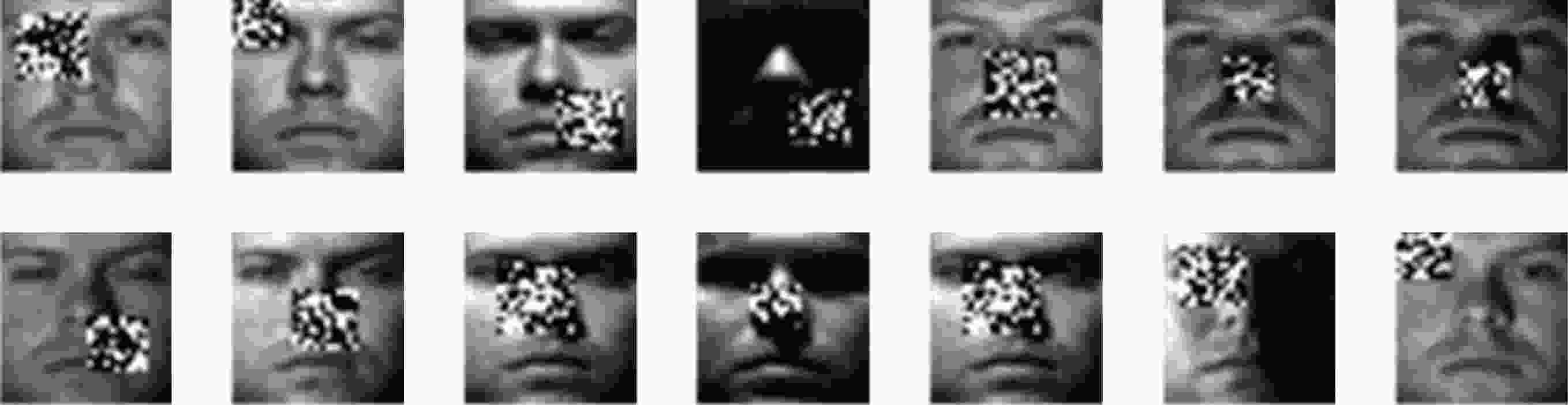图 10 Extended Yale B数据库部分遮挡样本图像
Figure10. Occlusion samples of one person in the Extended Yale B database.

下面设计2个实验, 用以讨论遮挡样本数量不同时, DSGE-HRPOG算法的性能. 实验1: 随机选取每类人32张图像作为训练样本, 其中包含14张遮挡图像, 剩余图像作为测试样本, 交叉验证10次; 实验2: 随机选取每类人32张图像作为训练样本, 其中包含7张遮挡图像, 剩余图像作为测试样本, 交叉验证10次, 实验仿真结果如表5所示. 从表5中可看出, 在光照和遮挡混合干扰情况下, DSGE-HRPOG算法仍具有最佳性能. 当遮挡样本数为7张时, 基于Ms-HRPOG特征字典的平均识别率为98.10%, 当遮挡样本数增大到14张时, 识别率仍有97.98%, 二者仅相差0.12%. 同样地, 基于3-HRPOG和5-HRPOG特征字典的平均识别率也高于其他算法, 并且在不同遮挡样本数量条件下, 实验结果仅相差0.43%和0.08%, 而其余算法则有近1%左右的差值. 这充分说明, 无论是基于单尺度特征字典还是多尺度特征字典, DSGE-HRPOG算法不受遮挡样本数量和质量的影响, 系统性能稳定.

	Experiment 1/%	Experiment 2/%
LPP[22]	95.51 ± 0.40	96.78 ± 0.72
NPE[23]	96.43 ± 0.23	97.85 ± 0.31
SPP[33]	92.57 ± 0.84	93.05 ± 0.77
DSNPE[37]	94.18 ± 0.48	95.29 ± 0.54
Gao[53]	86.91 ± 1.07	88.23 ± 0.91
DSGE-pixels	95.83 ± 0.66	96.21 ± 0.21
DSGE-HRPOG(3-HRPOG)	97.30 ± 0.20	97.73 ± 0.35
DSGE-HRPOG (5-HRPOG)	96.85 ± 0.38	96.93 ± 0.60
DSGE-HRPOG G(Ms-HRPOG)	97.98 ± 0.50	98.10 ± 0.31

表5Extended Yale B数据库在遮挡干扰因素下的实验结果
Table5.Experimental results of Extended Yale B database with the occlusion interference.

2 -->

6.3.LFW和PubFig数据库

前面讨论是基于实验环境下采集的人脸数据库(AR和Extended Yale B)进行实验仿真和分析的, 实验结果具有一定的局限性, 本节将进一步对真实环境中采集的LFW和PubFig数据库上进行实验仿真, 使实验结果更具有说服力.
LFW(labeled faces in the Wild database)数据库^[55-57]是从Internet上采集的真实人脸数据库, 共有13233张5749类人脸图像, 包含了光照、表情、姿态、遮挡、年龄、种族等多种混合干扰, 对于人脸识别来说非常具有挑战性. 部分样本如图11(a)所示, 图像尺寸为128×128 pixels. 本文从中选取包含10张以上图像的人进行辨识, 得到158类人, 共4324张图像, 随机选取每类人的5张图像作为训练样本, 5张图像作为测试样本进行实验(表6). HRPOG特征算子的参数设置为一个cell = 4×4 pixels, 一个block = 2×2 cells, bin = 9.
图 11 部分样本图像　(a) LFW数据库部分样本; (b) PubFig数据库部分样本
Figure11. Samples of one person: (a) LFW database; (b) PubFig database.

	LFW/%	PubFig/%
LPP[22]	35.32	24.00
NPE[23]	35.19	25.00
SPP[33]	31.52	29.00
DSNPE[37]	44.05	30.90
WGSC[58]	47.60	37.50
RSRC[3]	42.80	47.00
RRC[57]	53.20	42.20
IRGSC[41]	56.30	48.50
DSGE-pixels	51.52	38.60
DSGE-HOG	69.62	49.00
DSGE-HRPOG(3-HRPOG)	76.71	54.20
DSGE-HRPOG (5-HRPOG)	76.58	53.30
DSGE-HRPOG (Ms-HRPOG)	73.80	53.70

表6LFW和PubFig数据库的实验结果
Table6.Experimental results on the LFW database and PubFig database.

PubFig(public figures face database)数据库^[56]与LFW数据库类似, 包括从互联网上采集到的200类知名人物的58797张图像. 数据库中的人脸都是真实环境下拍摄的, 包含部分遮挡(眼镜、帽子等饰物)、极端光照、较大的姿势变换(> 45°)、不同种族、年龄等干扰因素. 部分样本如图11(b)所示, 图像尺寸为100×100 pixels. 本文从PubFig数据库中随机选取100类人, 每类人20张图像进行实验仿真, 其中每类人的10张图像作为训练样本, 剩余图像作为测试样本(表6). HRPOG特征算子的参数设置为一个cell = 10×10 pixels, 一个block = 2×2 cells, bin = 9.
从表6中可以看出, DSGE-HRPOG算法在LFW和PubFig这2个数据库上的识别率均高于其他算法, 其中, 基于3-HRPOG特征字典的识别率最高, 达到76.71%和54.20%, 比文献[41]提出的IRGSC算法提升了20.41%和5.7%, 比文献[57]提出的RRC算法提升了23.51%和12%, 比其他算法则提升更多. 然而, 表中DSGE-pixels的识别效果并不理想, 在LFW数据库上识别率仅为51.52%, 低于IRGSC^[41]和RRC^[57], 在PubFig数据库上识别率为38.6%, 低于IRGSC^[41], RRC^[57]和RSRC^[3]. 可见, 在LFW和PubFig这2个具有挑战性的非约束人脸数据库上, DSGE算法容易受样本影响, 近邻图构建不准确, 而DSGE-HRPOG算法通过结合HRPOG特征字典以及DSGE低维投影两方面的优势, 能够更准确挖掘出嵌入在真实复杂数据中的低维流形本质结构, 显著提高了系统的判别能力.
值得注意的是, 本文也采用传统HOG特征算子构建特征字典, 再与DSGE算法相结合, 得到DSGE-HOG的识别率为69.62%和49.00%, 分类效果仅次于DSGE-HRPOG算法, 并优于其他非特征字典算法. 这进一步说明了, 在稀疏表示分类中, 首先采用特征算子提取图像特征用以构建特征字典, 对准确区分受不同因素干扰的真实环境采集的非约束人脸图像十分有效. 同时, 这也从另一角度验证了, 相比传统HOG特征算子, 本文提出的HRPOG特征算子从多个尺度、多个方向捕捉人脸纹理的梯度变化信息, 可以更准确提取出人脸本质特征, 从而显著提高特征字典的鉴别性和鲁棒性.
2 -->

6.4.参数性能分析

本节主要讨论DSGE-HRPOG算法中最优参数选择, 包括初始投影矩阵${{{P}}_0}$的选择、最大迭代次数${k_{\max }}$的选择, 以及有联合优化和无联合优化条件下的分类结果比较. 以PubFig数据库为例, 图12为${P_0}$取随机矩阵、单位矩阵以及LDA投影矩阵作为初始值时, 在不同特征字典条件下的识别结果. 从图12中可以看出, 无论采用单尺度特征字典(3-HRPOG或5-HRPOG), 还是多尺度特征字典(Ms-HRPOG), 取初始投影矩阵${{{P}}_0}$为随机矩阵时, 联合优化得到的${{{P}}^*}$最佳, 分类效果最好.
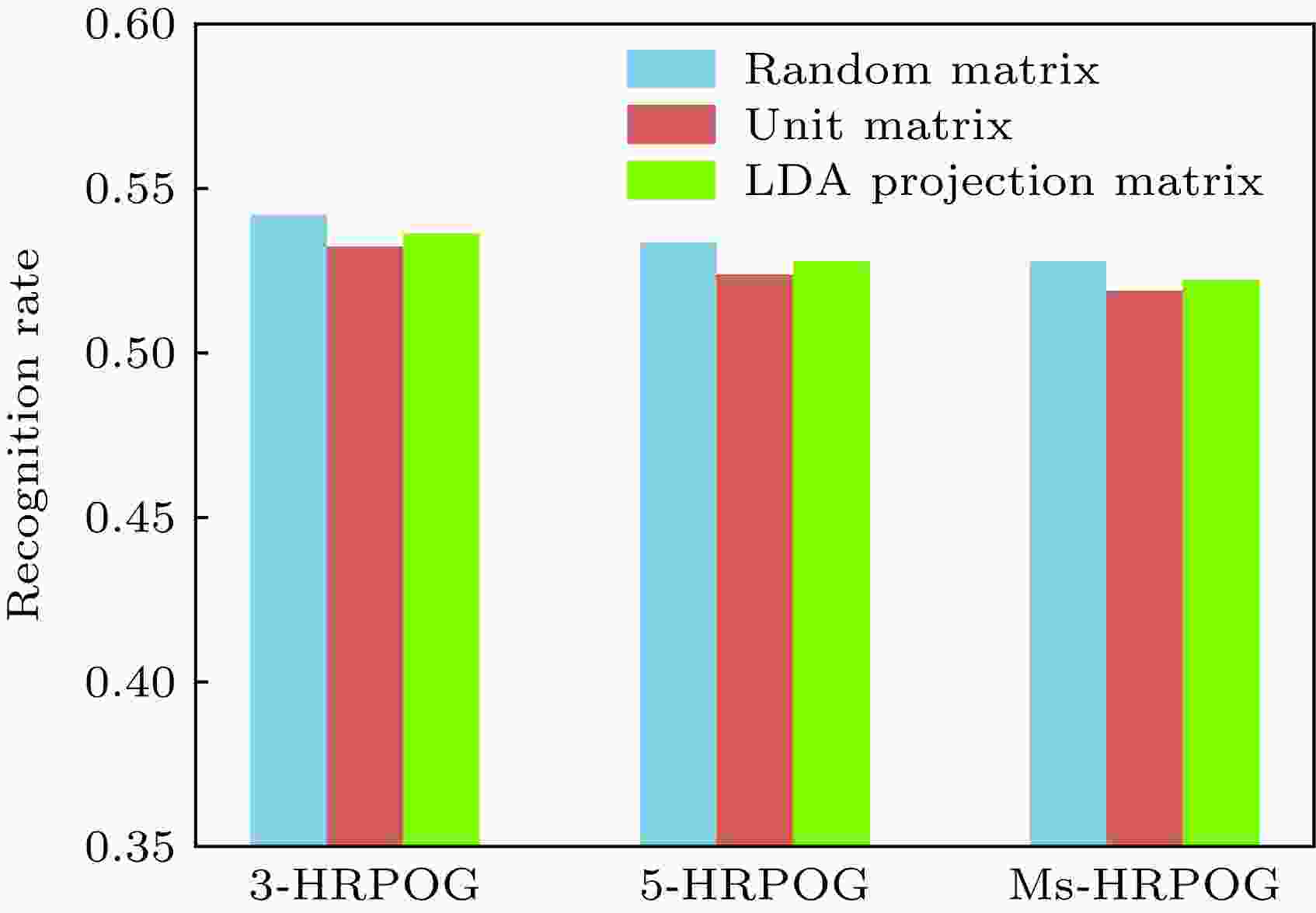图 12 不同初始投影矩阵${{{P}}_0}$的识别率
Figure12. Recognition rates based on different initial matrix${{{P}}_0}$.

图13为迭代次数与目标函数差值的曲线图, 从图13中可以看出, 随着迭代次数$k$的增加, 目标函数$J({{{P}}_k})$与$J({{{P}}_{k - 1}})$的差值越来与小, 当$k \geqslant 20$后, 逐渐趋于稳定, 目标函数收敛. 因此, 本文选取最大迭代次数${k_{\max }} = 20$作为算法1的截止条件之一.
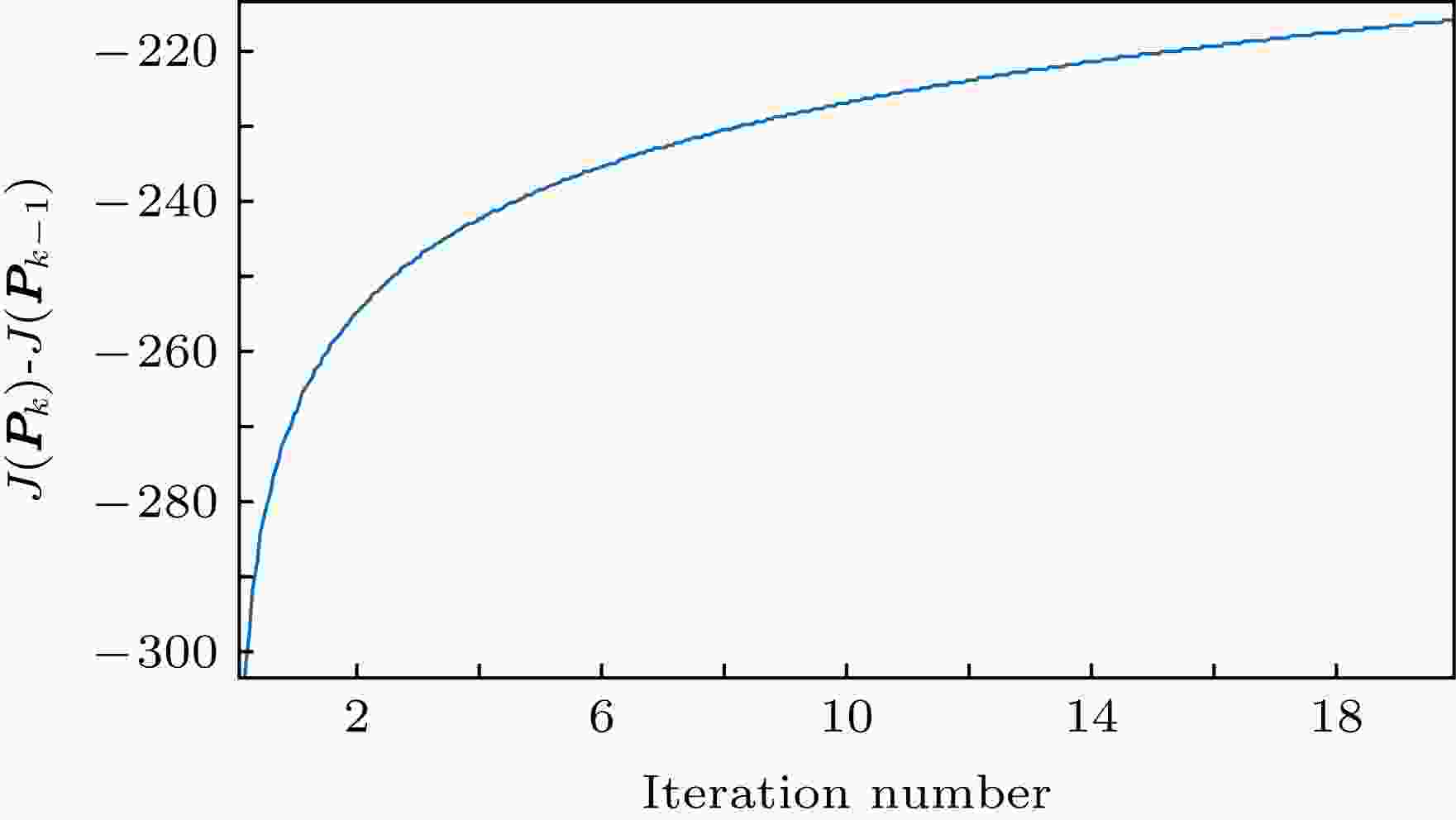图 13 目标函数收敛曲线
Figure13. Convergence curve of the objective function.

最后, 表7给出有联合优化和无联合优化条件下, DSGE-HRPOG算法在PubFig数据库上的识别结果及对应最佳投影维度. 这里取初始投影矩阵${{{P}}_0}$为随机矩阵, 最大迭代次数${k_{\max }} = 20$. 从表7中可以看出, 将维数约简过程伴随在稀疏图构建过程中, 可以使低维子空间数据逐渐逼近最佳判别分布, DSGE-HRPOG分类效果更理想.

	DSGE-HRPOG
	3-HRPOG	5-HRPOG	Ms-HRPOG
with joint optimization	54.20 (630)	53.30 (473)	53.70 (514)
without joint optimization	53.50 (514)	50.90 (423)	53.20 (514)

表7PubFig数据库上有联合优化和无联合优化的实验结果
Table7.Experimental results with joint optimization and without joint optimization on the PubFig database.

鉴于SRC分类器的局限性, 本文从字典构建、低维投影以及联合优化3个方面进行改进, 提出一种基于DSGE-HRPOG的算法. 首先, 利用鉴别力和鲁棒性更强的HRPOG特征算子提取样本本质特征, 去除非约束人脸图像中包含的各种干扰因素, 增强同类字典原子间的相关性和异类原子间的差异性; 然后, 再与DSGE算法相结合, 进一步提升了特征字典的紧致性、判别性和稳定性; 最后, 将稀疏图构建与低维投影联合优化, 在AR, Extended Yale B, LFW以及PubFig这4个人脸数据库上进行实验仿真, 实验结果均表明, DSGE-HRPOG算法相比传统流形学习算法以及现有先进算法, 均表现出卓越性能. 需要强调的是, DSGE-HRPOG算法提供了一种稀疏图映射与局部特征提取相结合的研究思路, 为非约束人脸识别的实用化提供了有效解决方案.
近年来, 有许多****^[59,60]将图像、视频等数据组织为张量形式进行稀疏图映射降维, 避免了将多维数据强制表示为向量形式而引发的一系列问题. 下一步, 我们将研究基于张量特征字典的稀疏重构技巧及优化算法, 对流形学习与字典学习进行改进和推广, 力争进一步提高非约束人脸识别准确率.