摘要:针对传统相对论返波管振荡器低磁场工作束波转换效率较低的问题, 本文提出并研究了一种带中间调制腔链及TM₀₂模式提取腔的相对论返波管模型: 中间调制腔链用于进一步群聚电子束, 提高电子束的基波调制深度; TM₀₂模式的提取腔用于提高返波管的Q值, 增强提取腔中的驻波电场; 漂移段用于调节电子束在调制腔链中的群聚相位和提取腔中的换能相位. 在此基础上, 设计了一个S波段高效率相对论返波管振荡器, 器件输出微波功率4.2 GW, 频率2.38 GHz, 束波转换效率达到50%, 引导磁场强度0.7 T.
关键词: 相对论返波管振荡器/
低磁场/
调制电子束/
调制腔

English Abstract

全文HTML

--> --> -->

随着高功率微波研究从关键技术研究向实用化方向过渡和发展, 对高功率微波源系统的功耗、重量和体积等参数提出了越来越高的要求^[1—3]. 在现有的高功率微波源中, 为维持较高的束波转换效率, 一般需要较强的引导磁场, 特别是当微波源运行在重复频率状态时, 需要一个体积庞大的、高耗能的螺线管磁体系统或维护麻烦的超导磁体系统^[4—7], 这无疑增加了系统的体积、重量、功耗及操作难度. 降低高功率微波器件的工作磁场, 提高器件在低磁场工作条件下的束波转换效率, 一直是高功率微波器件研究领域的热点问题之一.
过模相对论返波管振荡器, 作为一种代表性的高功率微波器件, 在较高的引导磁场下已经证明其具有较高的束波转换效率^[8—11]: 一方面, 采用谐振反射腔替代截止颈反射返向微波, 高频互作用区横向尺寸大大增加, 降低了电子束的空间电荷密度^[12,13]; 另一方面, 谐振反射腔对阴极发射的强流电子束进行预调制, 调制电子束在慢波结构中换能输出, 电子束群聚过程和换能过程实现了部分分离^[14,15]. 但随着磁场强度的降低, 电子束品质变差, 导致调制电子束的群聚效率和换能效率均降低, 影响了振荡器的束波转换效率, 目前低磁场返波管振荡器的效率普遍不超过40%. 针对传统相对论返波管振荡器低磁场工作束波转换效率较低的问题, 本文提出并研究了一种带中间调制腔链及TM₀₂模式提取腔的相对论返波管模型, 从提高电子束群聚深度、增强提取腔驻波电场及优化群聚电子束换能相位三方面着手, 对相对论返波管结构各部分进行了相对独立的理论分析和模拟设计. 通过粒子模拟, 验证了中间调制腔链及电子束群聚相位对提高电子束群聚深度的作用^[16—18], 验证了TM₀₂模式的提取腔及电子束换能相位对提高电子束换能效率的作用^[19,20]. 在此基础上, 设计了一个S波段高效率相对论返波管振荡器, 在电子束参数电压650 kV、电流13 kA条件下, 器件输出微波功率4.2 GW, 频率2.38 GHz, 束波转换效率达到50%, 引导磁场强度仅0.7 T.

2

-->

2.1.设计考虑

考虑调制电子束与提取腔中换能电场的互作用, 忽略电子束在提取腔内的群聚, 则器件的输出微波功率可写为

${P_{{\rm{out}}}} = \frac{1}{2}(M{I_1}) \cdot {V_1}{\rm{cos}}\delta,$

其中M为电子束与提取腔的耦合系数, ${I_1}$为进入提取腔的基波调制电流, ${V_1}$为提取腔的间隙电压, δ为调制电子束与提取腔换能电场的相对相差. 要提高器件的束波转换效率, 就需要提高进入到提取腔中的基波调制电流${I_1}$, 增强提取腔中的换能电场${V_1}$, 优化群聚电子束的换能相位δ.
基于以上思路, 借助粒子模拟软件MAGIC, 我们建立了S波段低磁场高效率HPM振荡器的整管模拟模型如图1所示. MAGIC软件仿真采用时域有限差分方法, 计算中包含了强流电子束与高频结构束波互作用的全部物理过程, 其计算结果的有效性已经得到了其他仿真软件及实验的验证, 是相对论微波器件设计行业内使用最广泛的粒子模拟软件之一. 器件采用轻度过模结构(D/λ ≈ 1.2)的O型振荡器, 一方面过模结构有利于反馈过程的建立和功率容量的提升, 另一方面轻度过模又避免了低频段器件横向尺寸过大. 器件结构上包括环形阴极、阳极、反射腔、调制腔链和换能腔等部分. 为提高低磁场条件下电子束的流通效率, 阴极与漂移管壁的距离扩大到6 mm, 以避免电子包络扰动过大而轰击管壁. 一方面, 电子束与管壁距离的增加导致电子束传输路径上的电场减弱, 互作用阻抗降低; 另一方面, 距离增加也导致空间电荷势能增加, 可提取的动能减少. 两方面都将导致电子束的群聚效率及换能效率降低. 为提高群聚效率, 器件采用谐振反射腔 + 中间调制腔链的两级调制结构, 谐振反射腔用于对二极管产生强流电子束的预调制, 中间调制腔链用于对预调制电子束的进一步群聚, 通过优化调制电子束的群聚相位, 可以有效提高电子束的基波调制深度. 为改善换能效率, 采用TM₀₂模式的提取结构, 利用TM₀₂模提取腔对出射微波的反射, 增强提取腔中的驻波电场, 通过优化群聚电子束的换能相位, 可以有效提高换能结构中的束波转换效率.
图 1 S波段低磁场高效率HPM振荡器模拟模型
Figure1. Model of the S-band high efficiency HPM oscillator with low magnetic field.

2 -->

2.2.提高电子束群聚深度

低磁场条件下, 谐振反射腔的调制效率将大大降低, 这势必严重影响振荡器的束波转换效率. 为提高进入到提取腔中的基波调制电流深度, 考虑增加中间腔以进一步增强电子束的群聚^[8]. 文献[17]中推导出了电子束通过调制腔(在返波管中即谐振反射腔)和中间腔两级调制后的调制电流演化规律,

${I_1} = 2{I_0}{J_1}({X_2}) + {i_1}{I_0}{J_0}({X_2}){{\rm{e}}^{ - {\rm{j}}\varDelta }} + {i_1}{I_0}{J_2}({X_2}){{\rm{e}}^{{\rm{j}}\varDelta }},$

式中, ${i_1} = 2{I_0}{J_1}({X_1})$, 表示经调制腔调制后到达中间腔的基波调制电流深度; Δ表示到达中间腔的基波调制电流与中间腔间隙电场的相对相差; ${X_{1,2}}$为调制腔群聚参数. 求解该式, 可以给出不同相位Δ的调制电子束经过中间腔调制后的演化规律如图2所示.
从图2可以看到, 调制电子束的演化规律对电子束进入中间腔的相位Δ非常敏感: 当$\varDelta = 0$时, 中间腔可以对调制腔产生的调制电子束进一步群聚, 调制深度进一步提升; 但当$\varDelta = \pi $时, 调制电子束离开中间腔后调制深度反而降低. 因此, 通过引入中间调制腔, 并优化调制电子束在高频场中的群聚相位, 可以有效提高电子束的基波调制电流. 由此可以建立包含多个中间腔的调制腔链结构(其作用类似于直线加速器中的聚束段), 有望解决低磁场条件下电子束群聚效率低的问题. 由于相位Δ与谐振反射腔和中间腔之间的直流渡越角有关, 在粒子模拟中, 需要合理选择谐振反射腔和中间腔之间的漂移段长度.
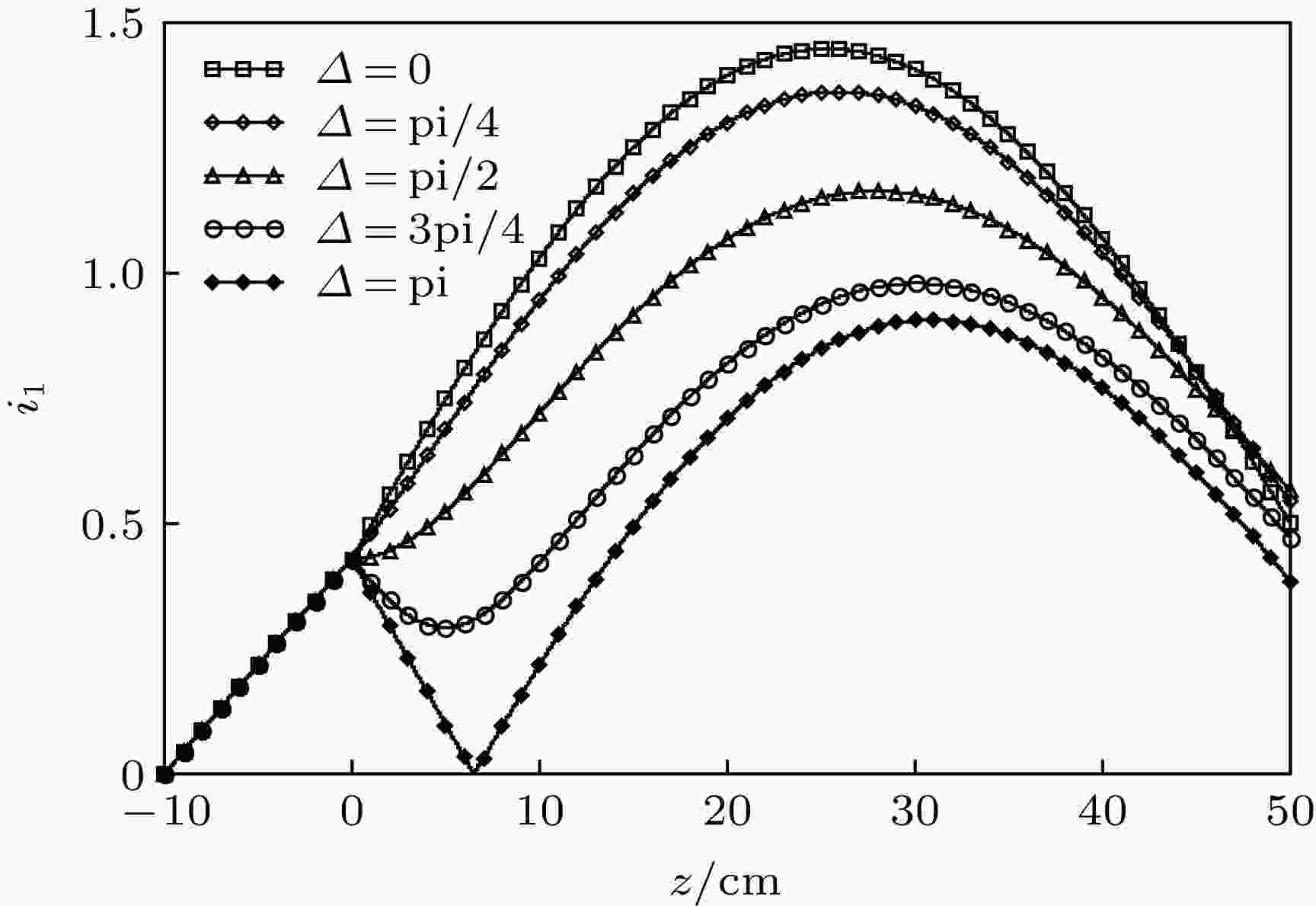图 2 不同相位Δ的调制电子束经中间腔调制后的演化规律
Figure2. The fundamental harmonic current distribution after the idler cavity with different phase.

图3给出了优化设计后的调制腔链中的电流和纵向电场随时间的变化, 可以看到进入到调制腔链中的群聚电子束处于最佳群聚相位, 可以实现高效的电子束群聚.
图 3 调制腔链中电流和纵向电场随时间的变化
Figure3. The temporal plots of the current and the longitudinal electric field in the cavity-chain modulator.

图4对比了反射腔调制、反射腔 + 中间腔调制以及反射腔 + 中间腔链调制三种情况下, 基波调制电流的演化规律, 电子束参数为650 kV, 13 kA. 可以看到, 仅采用谐振反射腔对电子束进行预调制, 基波调制电流最大值约11.5 kA, 对应调制深度为88.5%. 若引入一个中间调制腔, 基波调制电流可以提高到12.8 kA, 相应的调制深度为98.5%. 若采用中间调制腔链, 基波调制电流可以大大提高, 最大值为18.9 kA, 调制深度可以达到145.4%.
对于反射腔 + 中间腔链的调制结构中, 器件换能区与调制结构间的耦合较弱, 反射腔与中间腔链中的电场较低, 电子束与调制结构的互作用以及电子束的群聚是分布完成的, 同时可以通过合理选择中间腔链的纵向模式使得电子束始终处在最佳群聚相位, 因此群聚深度较高. 但对于仅反射腔以及一个中间腔的结构, 随着器件的起振, 换能区的微波场反馈到调制结构中, 使得调制区的电场过强而发生电子束的过群聚, 导致进入换能区的电子束调制深度降低.
图 4 调制电子束基波调制电流的演化规律
Figure4. The fundamental harmonic current distributions in three types of modulation structures.

2 -->

2.3.提高换能腔驻波电场

通过谐振反射腔和中间调制腔链的群聚, 可以达到提高基波调制电流深度的目的, 为提高器件的束波转换效率, 需要进一步提高提取腔中的驻波电场. 提取腔内的驻波电场可以写为

${V_1} = \sqrt {2{P_{{\rm{out}}}} \cdot \rho {Q_{{\rm{ext}}}}}, $

其中, ρ为工作模式的特性阻抗, ${Q_{{\rm{ext}}}}$为工作模式的外观品质因子. 在输出功率一定的条件下, 提高外观品质因子${Q_{{\rm{ext}}}}$, 可以增强提取腔中的换能电场.
为此, 我们采用TM₀₂模式工作的提取腔, 通过增强换能腔中的微波反射, 提高换能腔的外观品质因子, 从而提高换能腔中的驻波电场, 提高振荡器的束波转换效率^[10]. 图5对比了TM₀₁和TM₀₂提取腔的传输特性, 由于输出波导输出的是TM₀₁模式(波导半径6 cm对TM₀₂模式截止), 相比于工作在TM₀₁模式的提取腔, TM₀₂模式提取腔耦合到输出波导TM₀₁模式的效率较低, 反射较大.
图 5 TM₀₁和TM₀₂提取腔的传输特性
Figure5. The transmission characteristics of the TM₀₁ and TM₀₂ extractor.

图6给出了采用TM₀₁和TM₀₂提取腔结构下器件的频率响应, 可以看到由于TM₀₂提取腔对出射微波的反射, 导致器件工作点的${Q_{{\rm{ext}}}}$显著提高.
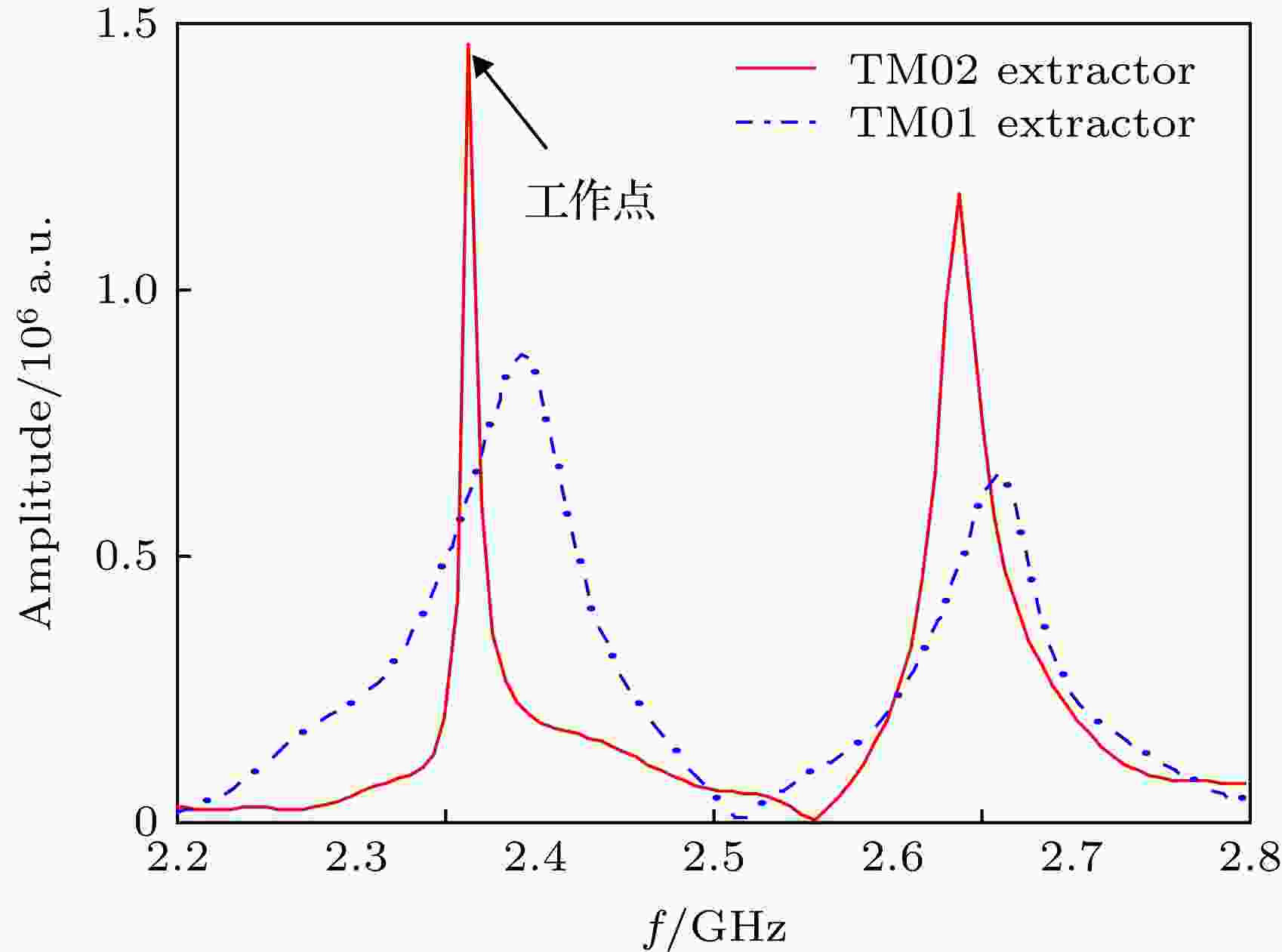图 6 采用TM₀₁和TM₀₂提取腔器件的频率响应
Figure6. The resonant characteristics of the device with TM₀₁ and TM₀₂ extractor.

图7对比了采用TM₀₁提取腔和TM₀₂提取腔两种情况下, 纵向电场幅值的差异. 可以看到, 采用TM₀₁模式的提取腔, 提取腔中的电场最大值约34 MV/m, 而采用TM₀₂模式的提取腔, 最大电场达到了44 MV/m. 若能控制调制电子束进入提取腔的相位, 有望提高器件的效率.
图 7 采用TM₀₁和TM₀₂提取腔器件的纵向电场分布
Figure7. The longitudinal electric field distributions in the device with TM₀₁ and TM₀₂ extractor.

图8是器件提取腔内的纵向电场幅值沿径向的分布, 可以看到提取腔中的电场分布具有典型的TM₀₂模式的特征.
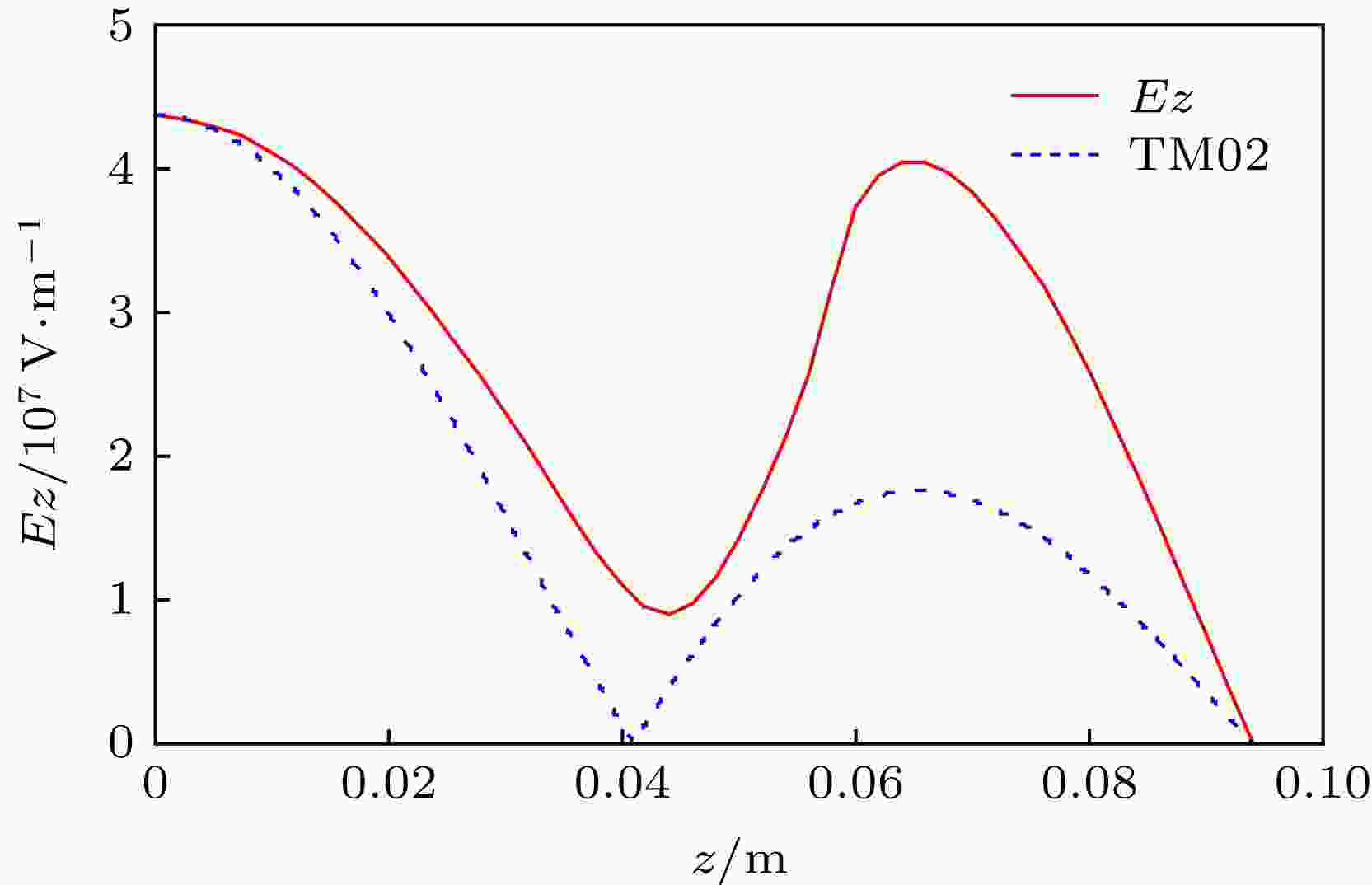图 8 器件提取腔内的纵向电场幅值沿r向的分布
Figure8. The longitudinal electric field distribution along radial direction in the extractor.

图9给出了器件内的纵向电场幅值以及基波调制电流沿z向的分布, 可以看到基波调制电流和纵向电场均是在提取腔中达到最大. 从(1)式可以看出, 只要保证合适的换能相位δ, 如此高的调制电流和纵向电场, 一定可以实现高效的束波转换.
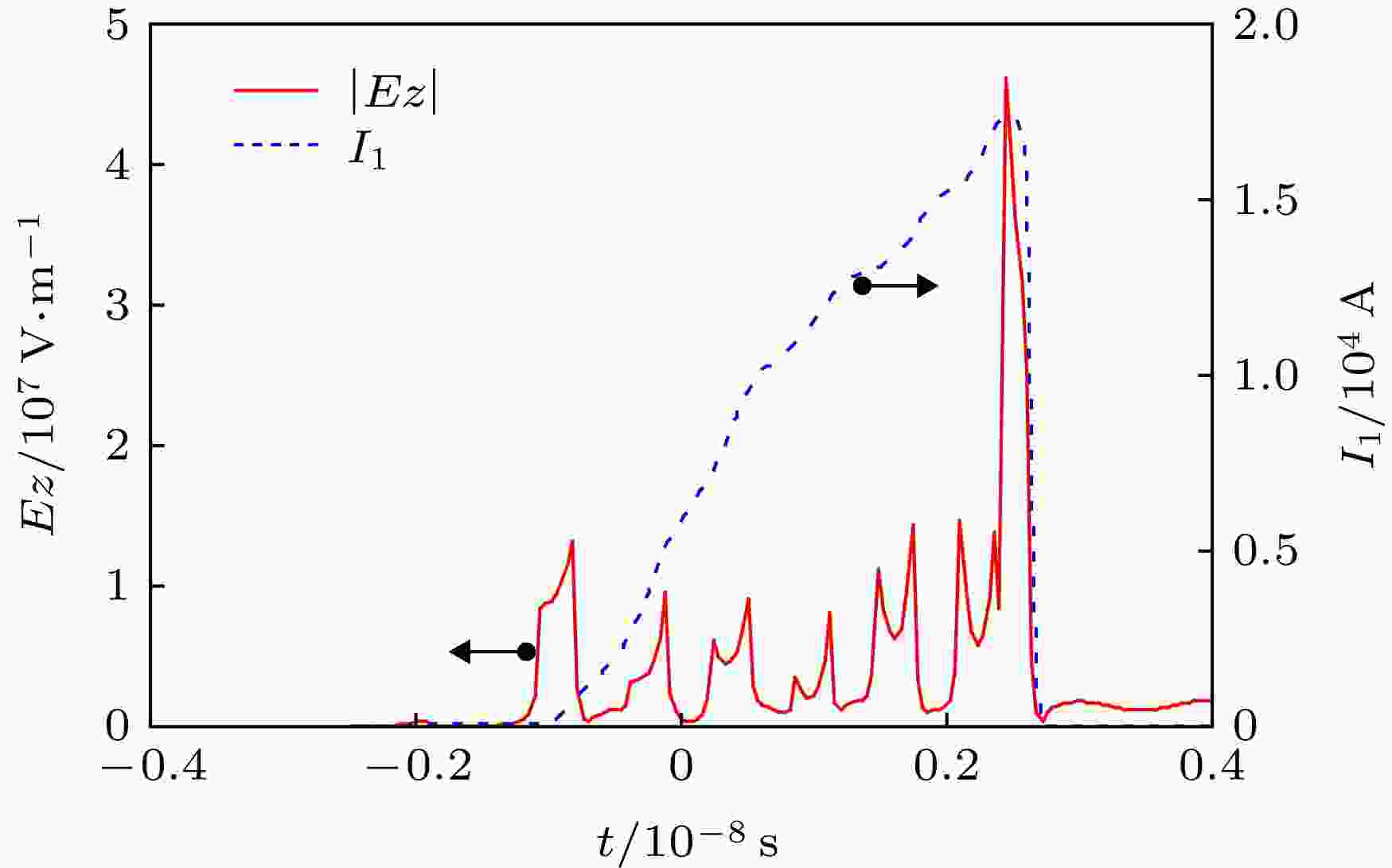图 9 器件内的纵向电场幅值及基波调制电流的分布
Figure9. The distributions of the amplitude of the longitudinal electric field and the fundamental harmonic current in the device.

2 -->

2.4.优化群聚电子束的换能相位

从(1)式可以看出, 器件的输出微波功率对调制电子束与换能腔间隙场的相对相差δ非常敏感, 若能优化群聚电子束的相位使得δ = 0, 将大大提高器件的束波转换效率. 图10给出了提取腔中的电流和纵向电场随时间的变化, 可以看出进入到提取腔中的群聚电子束其群聚中心刚好处于换能相位, 同时相比于调制腔中的群聚电流(如图3), 其电子束的群聚更强烈, 调制深度更高.
图 10 提取腔中电流和纵向电场随时间的变化
Figure10. The temporal plots of the current and the longitudinal electric field in the extractor.

从上面的分析可以看到, 相位、调制电流和换能电场三者在提取腔中都达到了最佳状态, 由此器件可以实现高效的束波转换. 图11为器件内的净功率流沿z向的分布, 可以看到在器件的谐振反射腔和调制腔链中, 电子束与微波场的净功率交换较少, 但在提取腔中, 净功率交换显著增强, 提取腔的提取功率大于4 GW.
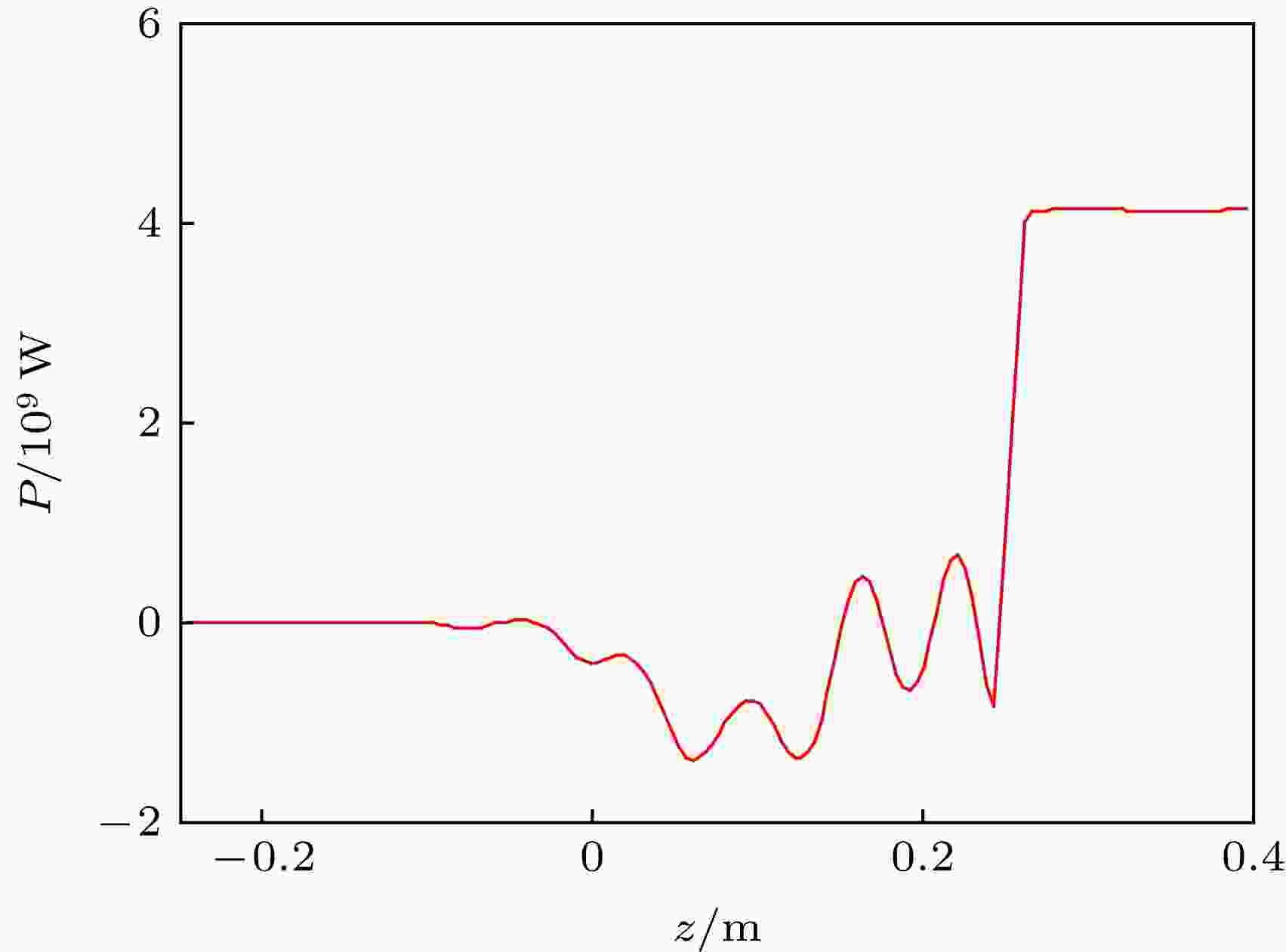图 11 器件内的净功率流沿z向的分布
Figure11. The net power flux distribution in the device along axial direction.

图12是器件输出微波功率与提取腔半径的关系, 可以看到存在最佳的提取腔半径使得器件的提取效率最高. 当提取腔半径低于8.8 cm时, 由于在提取腔中激励起TM₀₁模式, 相比于工作模式TM₀₂, 相位刚好相差π, 使得群聚电子束处于吸能相位, 而无法起振.
图 12 器件输出微波功率与提取腔半径的关系
Figure12. The relation between the output power and the radius of the extractor.

2 -->

2.5.粒子模拟结果

据此开展了S波段高效低磁场HPM振荡器的整管粒子模拟, 在二极管电压约650 kV、束流约13 kA(输入电子束功率8.45 GW)情况下, 振荡器输出微波功率约4.2 GW, 束波转换效率约为50%, 输出微波中心频率为2.38 GHz, 引导磁场强度仅0.7 T. 图13是器件输入电功率、收集极收集功率和输出微波功率随时间的变化, 也可以看到随着器件的起振至饱和, 收集极收集功率逐渐减小, 约有一半的输入电功率转换为射频能量输出.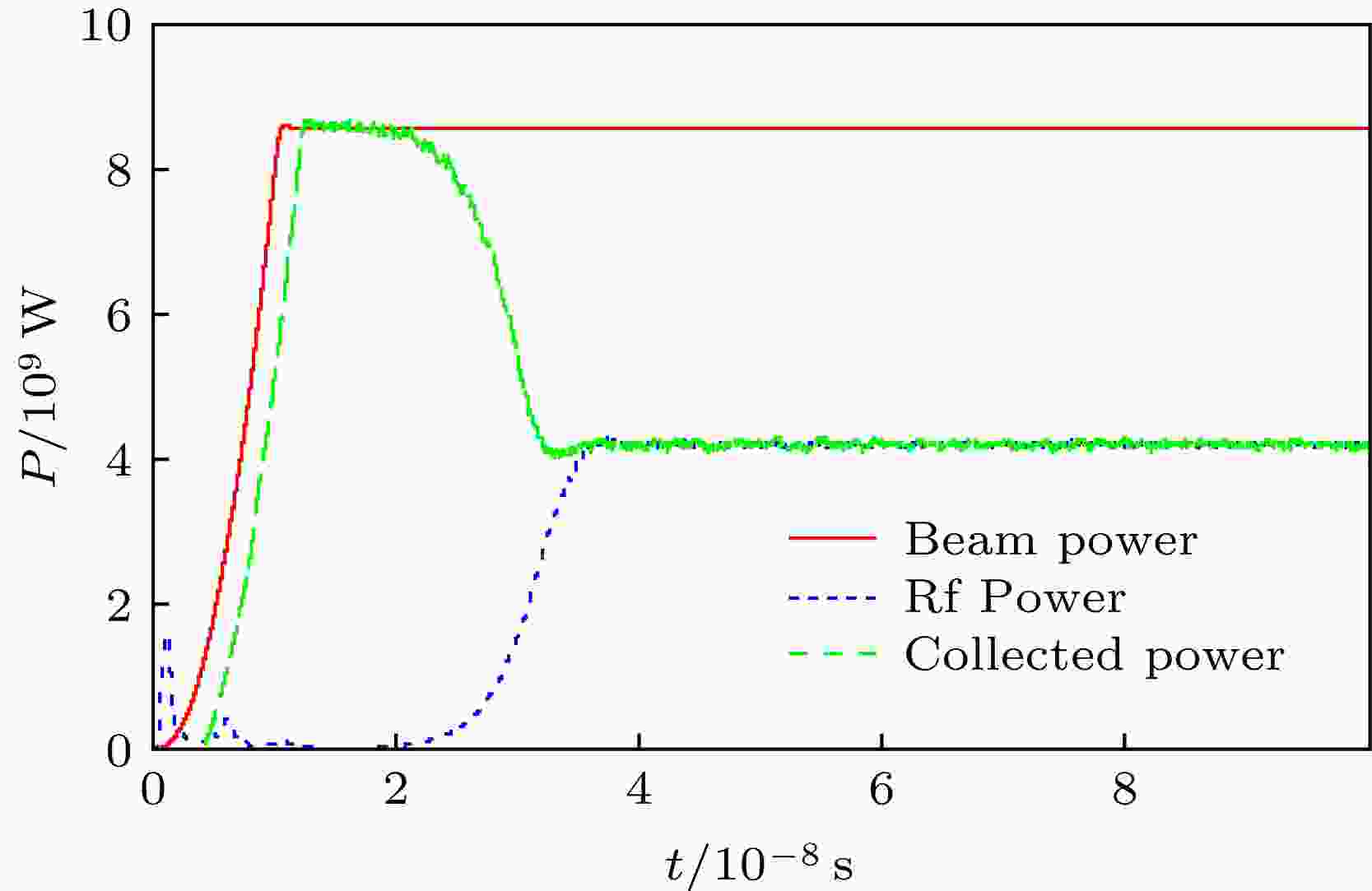
图 13 电功率、微波功率和收集极功率随时间的变化
Figure13. The temporal plots of the beam power, RF power and the dumped power.

器件输出微波功率、电子束损失动能以及图11所示器件输出波导中的净功率流三者结果吻合. 此外, 在粒子模拟中还分别采用了PORT边界和吸收边界两种算法对器件输出功率进行了对比, 其结果也接近一致. 上述结果验证了粒子模拟结果的正确性.
图14是固定电子束电流13 kA, 改变电子束电压, 器件的输出功率及效率随电压的变化. 可以看到, 器件在约150 kV的电压范围内(580—730 kV)均能保持较高的束波转换效率(η > 40%), 当电压低于550 kV时, 器件将因同步关系无法满足而无法起振.
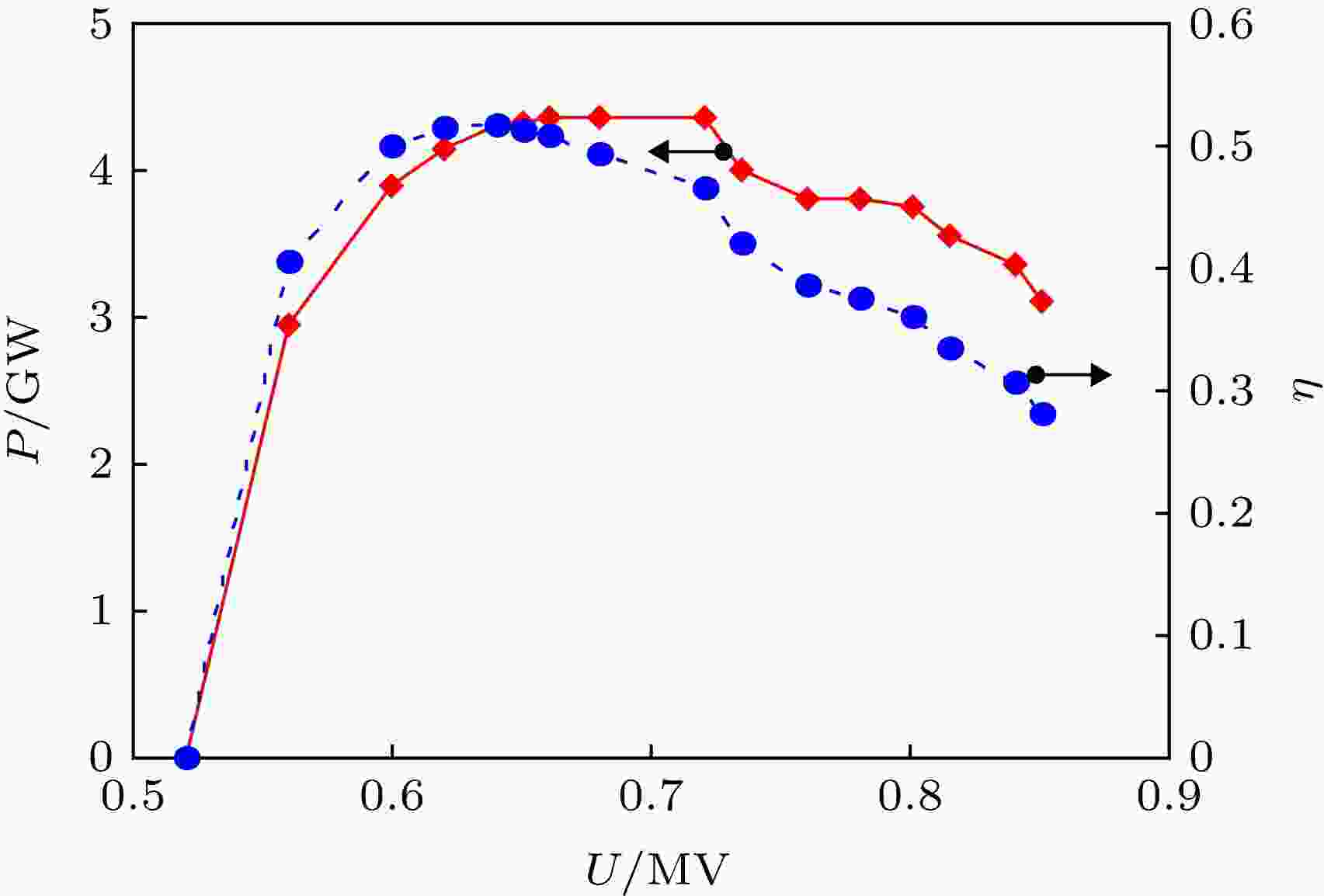图 14 器件输出功率及效率与二极管电压的关系
Figure14. The relations of the output power and efficiency to the diode voltage.

针对传统相对论返波管振荡器低磁场工作束波转换效率较低的问题, 本文提出并研究了一种带中间调制腔链及TM₀₂模式提取腔的相对论返波管模型. 研究表明: 通过在振荡器设计中引入中间调制腔链, 并优化电子束的群聚相位, 可以大大提高调制电子束的群聚深度, 最大群聚深度可以达到145.4%; 通过引入TM₀₂模式的提取腔, 可以提高提取腔中的换能电场, 最大纵向电场达到了44 MV/m; 并且, 基波调制电流和纵向电场均是在提取腔中达到最大, 基波调制电流处于合适的换能相位. 由此, 器件实现了较高的束波转换效率, 在电子束参数电压650 kV、电流13 kA条件下, 器件输出微波功率4.2 GW, 频率2.38 GHz, 束波转换效率达到50%, 引导磁场强度仅0.7 T.