摘要:仿真模拟是开展航天器内带电风险评估的重要方法之一. 基于电荷守恒定律, 建立了内带电电位和电场三维计算模型, 给出了模型的一维稳态和瞬态求解算法及二维和三维求解方案, 设计了迭代算法来解耦电导率与电场强度, 并分析了该迭代算法的收敛性; 运用有限元算法和局部网格细化, 该模型具有方便考察关键点处电场畸变的优势; 与现有的辐射诱导电导率模型对比分析, 新模型更适合内带电三维数值计算; 与实验数据对比, 验证了内带电三维计算模型的正确性. 为解决航天器内介质带电评估问题提供了手段.
关键词: 内带电/
航天器/
电场畸变/
辐射诱导电导率模型

English Abstract

全文HTML

--> --> -->

航天器在轨充电事件和地面模拟试验均表明内带电致静电放电是导致航天器故障或损毁的重要原因^[1,2]. 发生严重内带电的区域位于地球中高轨道空间. 许多大型通信卫星位于高轨(如地球同步轨道), 而我国北斗导航系统的绝大多数卫星都位于中轨. 经过多年发展, 虽然已经制定了内带电防护参考手册, 但是从近几年出现的航天器事故来看^[3,4], 内带电仍对航天器的安全运行构成重大威胁.
建模仿真是航天器带电研究的重要途径和方法, 航天器带电研究的每个阶段都经历了建模仿真与在轨测试的过程. 特别是对于航天器内带电来讲, 建模仿真的意义尤其重大. 一方面由于高能电子辐射环境不易实现, 导致内带电的地面模拟试验比表面充电更难开展; 另一方面内带电建模研究起步较表面充电晚且涉及的充电机理复杂, 在仿真方面远没有达到表面充电能够采用的成熟软件的水平. 于是研究者通常采用计算机仿真与地面模拟实验相结合的方法, 侧重研究内带电建模仿真与得到贴近实际的仿真结果. 最早的内带电仿真工具是著名**** Jun等^[5]给出的NUMIT(NUMerical InTegration, NUMIT), 另一款较出名的仿真工具为欧空局的DICTAT(dielectric internal charge threat analysis tool, DICTAT)^[6], 但二者都是针对平板或圆柱等简单几何结构, 且涉及到电荷输运模拟部分均采用经验拟合公式^[7-9]. 文献[10-13]在内带电仿真评估方面做出了许多有意义的探索. 黄建国和陈东^[14,15]给出平板和圆柱结构的内带电一维模型, 分析了介质厚度和接地方式对充电的最大电场强度的影响. 乌江等^[16]尝试对介质材料进行掺杂改性以得到非线性电导率, 当内电场高于某个阈值后, 电导率非线性增大有利于及时泄放电荷, 从而避免严重的内带电事件.
在表面充电中, 利用三维仿真可以探讨太阳帆板处电位势垒空间分布对充电的影响, 对于内带电评估, 三维仿真同样具有不可替代的作用. 尽管多年来已经进行了不少模拟实验和计算机仿真研究^[11,15], 但远没有实现内带电的准确评估和预测, 这是因为地面模拟和仿真计算并不能充分考虑空间多因素的作用, 如空间温度作用和部件本身三维结构对放电的影响等. 在1970年前后, 研究者基于NASCAP (NASA charging analyzer program, NASCAP)构建了一种三维仿真模型, 用来动态仿真涂覆介质薄层的导体结构的充电过程, 但仅是介质薄层结构. 真正的内带电二维或三维仿真, 只是在近几年才出现的, 得益于电荷输运模拟软件Geant4在航天器内带电中的应用^[17,18]. 国外研究者尝试用SPIS (spacecraft plasma interaction software, SPIS)进行内带电三维仿真^[19], 但缺乏技术方案和结果分析; 王松等^[19]利用有限差分算法开发出一个三维计算工具, 用来仿真暴露在木星辐射带的电路板及其未接地金属走线的充电情况, 结果表明, 三维仿真得到的充电电位要显著大于一维情况的电位. 秦晓刚^[20]提出了用于介质内带电数值模拟的Geant4-RIC (radiation induced conductivity, RIC)仿真方案, 其采用的RIC模型的控制方程是三元偏微分方程组, 但RIC模型并不便于三维计算和工程应用; 中国科学院空间中心报道了关于介质内带电的二维仿真结果^[21], 但是由于更多关注的是电位分布结果, 并没有针对电场分布特征进行深入研究. 王松等^[22]基于Geant4开发出实用工具ATICS (assessment tool of internal charging for satellite, ATICS), 来分析三维介质结构的电荷输运问题. 总之, 一维仿真终究只是得到内带电一般规律, 比如不同屏蔽厚度或者接地方式(正面接地、背面接地或者双面接地)对充电结果的影响^[23], 却不能考虑复杂的几何结构, 从而容易忽视非规则接地条件下充电最严重的关键点; 而已有的三维仿真没能合理评估局部特殊结构的充电水平, 缺乏对局部电场畸变特征的探索研究. 鉴于上述问题, 本文基于电荷守恒定律建立了内带电三维计算模型—CCL模型(charge conservation law, CCL), 该模型实现了内带电的三维数值仿真, 能够更加准确地考虑局部电场畸变特征, 并且比原有的RIC模型计算效率更高.

2

-->

2.1.CCL模型的控制方程与边界条件

由内带电机理分析可知, 内部电荷沉积率Q_j是电流源, 充电过程满足电荷守恒定律. 得到的CCL模型的控制方程为

$\nabla \cdot \left( {{{J}} + {{{J}}_{\rm{e}}}} \right) = 0,$

式中J_e是高能电子入射导致的电流密度, 满足$\nabla \cdot {{{J}}_{\rm{e}}} = - {Q_j}$, J为介质的传导电流密度和位移电流密度之和, $\nabla $是Hamilton算子, ${{J}} \!=\! \left( {\sigma \!+\! \varepsilon \dfrac{\partial }{{\partial t}}} \right){{E}}$, σ和ε分别是介质的电导率和介电常数, E是电场强度, Q_j为介质内单位体积电荷沉积率(单位: A/m³), 可写成关于空间位置的表达式Q_j(x), x代表空间位置坐标. 利用电场强度E是电位U的负梯度(即${{E}} = - \nabla U$), 控制方程(1)式实际上是关于未知变量U的单变量方程, 表达式为

$\nabla \cdot \left( {\left( {\sigma + \varepsilon \frac{\partial }{{\partial t}}} \right)\nabla U} \right) = - {Q_j},$

(2)式是内带电电位计算的时域三维表达式, 式中, 电导率σ受温度、辐射剂量率和电场强度三个参数的影响, 又因为这三个参数都是空间位置的表达式, 因此可以将σ写成关于位置x和时间t的形式σ(x, t). 一维简化模型的控制方程为

$\begin{split} & \varepsilon \frac{\partial }{{\partial t}}\frac{{{\partial ^2}U\left( {x,t} \right)}}{{\partial {x^2}}} + \sigma \left( {x,t} \right)\frac{{{\partial ^2}U\left( {x,t} \right)}}{{\partial {x^2}}} \\ \; & + \sigma {\rm{'}}\left( {x,t} \right)\frac{{\partial U\left( {x,t} \right)}}{{\partial x}} = - {Q_j}\left( {x,t} \right),\end{split}$

式中σ'(x, t)是σ(x, t)关于x的一阶导数.
已知控制方程, 还需结合特定的边界条件来得到定解. 对于航天器内带电, 通常只考虑绝缘边界和接地边界条件, 其表达式为

$\left\{\begin{aligned} &{{{n}} \cdot {{J}}{|_{{{{S}}_{{\rm{ins}}}}}} = 0,}\\ &{U{|_{{{{S}}_{{\rm{grd}}}}}} = {U_0},}\end{aligned} \right.$

式中S_ins和S_grd分别代表绝缘边界和接地边界. 此处接地代表航天器结构电位U₀. 由于U₀仅是参考电位, 不影响电场强度的计算结果, 而且内带电主要考察电场强度来判断是否发生介质击穿放电, 所以通常设置U₀ = 0. 对于U₀≠0的情况, 只需要在得到的充电电位基础上叠加U₀, 而电场强度并不发生改变. 边界条件(4)式对应的一维形式为

$\left\{\begin{aligned}&{E\left( {{x_{{\rm{ins}}}}} \right) = 0,}\\& U\left( {{x_{{\rm{grd}}}}} \right) = {U_0},\end{aligned} \right.$

其中x_ins为绝缘边界点和x_grd接地边界点.
综上, CCL模型是关于电位的一元偏微分方程, 适用于求解一维到三维的时域或稳态充电问题. 总结内带电三维仿真方案, 如图1所示, 图中箭头代表前因后果的关系. 介质的三维结构对电荷输运和电场计算都产生影响. 该图仅代表固定温度下的仿真方案. 进一步考虑温度对介质电导率的影响, 可以分析不同温度下和存在非均匀温度分布情况下的充电规律.
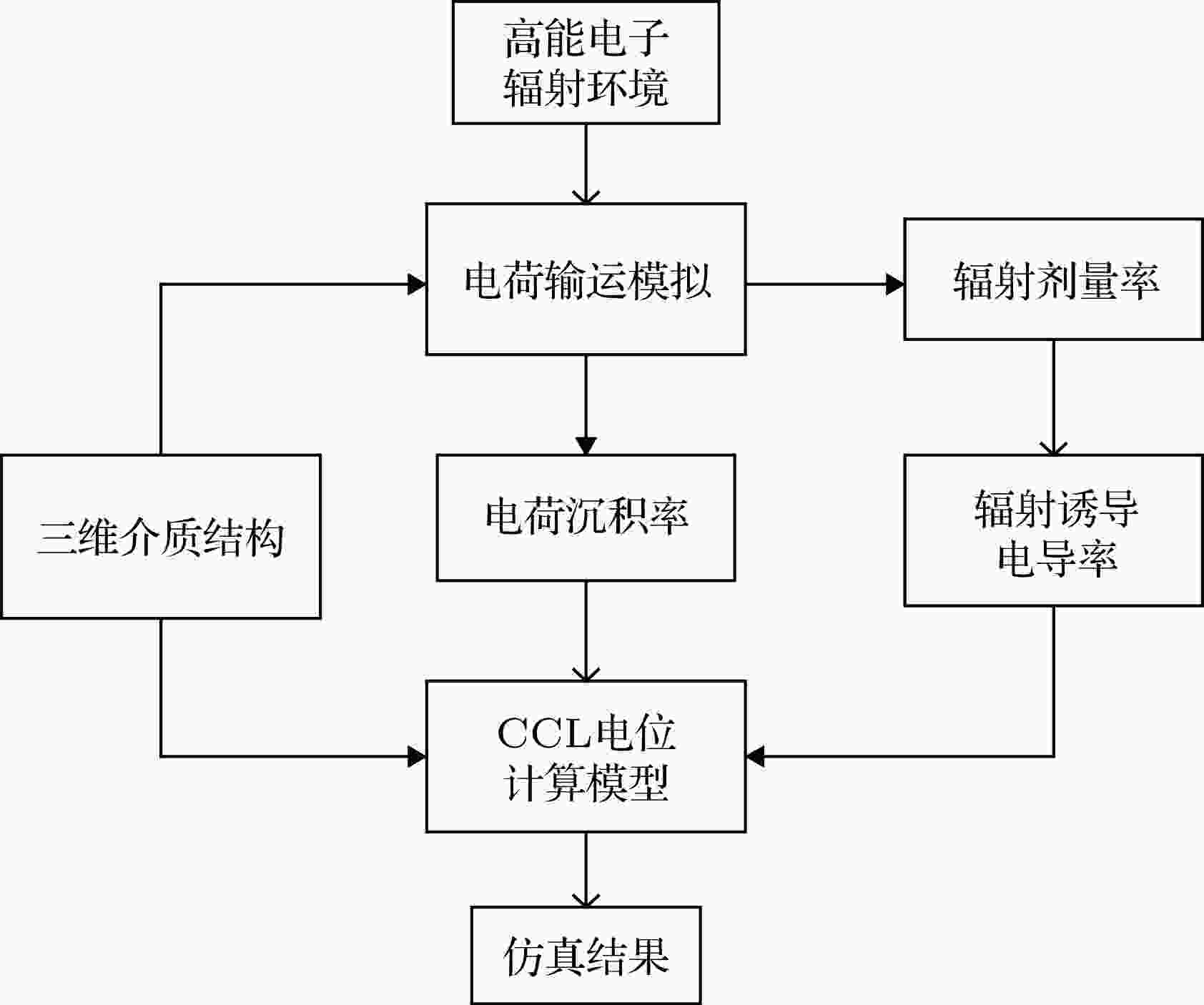图 1 内带电三维仿真方案
Figure1. 3-D simulation scheme for internal charging.

2 -->

2.2.CCL模型的一维数值解法

求解CCL模型的难点在于σ不仅是温度和辐射剂量率的函数, 还会随场强增大而增大, 而电导率的增大会增强电荷泄放, 从而限制场强的进一步增大, 也就是电导率与电场强度存在耦合. 首先得到电导率分布为定值情况下的稳态与瞬态解法, 然后提出迭代算法, 解耦电场强度与电导率, 从而得到完整解.
3 -->

2.2.1.一维稳态求解

充电平衡时, 控制方程为

$\sigma \left( {x,t} \right)\frac{{{\partial ^2}U}}{{\partial {x^2}}} + \sigma {\rm{'}}\left( {x,t} \right)\frac{{\partial U}}{{\partial x}} = - {Q_j},$

对(6)式积分得到

$ \begin{split}E\left( x \right) = \; & - \frac{{\partial U}}{{\partial x}} = - \exp \left( {\mathop \int \nolimits_0^x p\left( x \right){\rm{d}}x} \right)\\ & \times\left[ {\mathop \int \nolimits_0^x \!\!q\left( x \right)\exp \left(\!\!{ - \!\!\mathop \int \nolimits_0^x \!\!p\left( x \right){\rm{d}}x} \!\!\right){\rm{d}}x \!+\! {c_1}}\! \right],\end{split}$

于是

$U\left( x \right) = - \mathop \int \nolimits_0^x E\left( s \right){\rm{d}}s + {c_0},$

式中$p\left( x \right) = - \sigma '\left( x \right)/\sigma \left( x \right)$, $q\left( x \right) = - {Q_j}\left( x \right)/\sigma \left( x \right),$ 待定系数c₀, c₁ 由边界条件得出.
以背面接地的平板模型为例, 结构如图2所示.
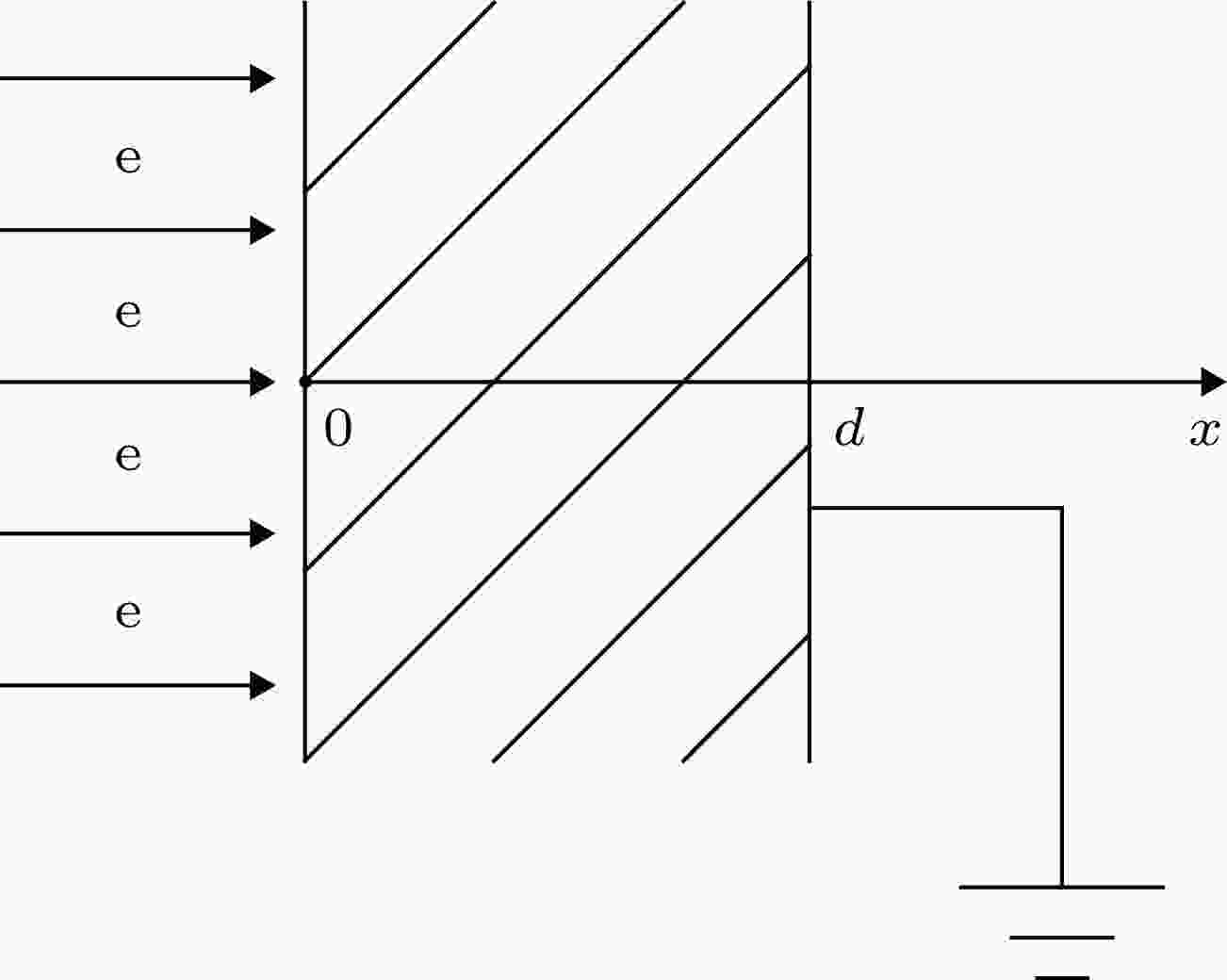图 2 背面接地的平板内带电模型
Figure2. Internal charging model of back grounded planar board.

得到的边界条件为

$\left\{ {\begin{aligned}& {U\left( d \right) = 0,}\\& {\frac{{{\rm{d}}U}}{{{\rm{d}}x}}{\Big|_{x = 0}} = 0.}\end{aligned}} \right.$

对应得到

${c_1} = 0,\;{c_0} = \mathop \int \nolimits_0^d E\left( x \right){\rm{d}}x,$

从而得到模型的定解, 式中d为平板厚度.
3 -->

2.2.2.一维瞬态求解—时域有限差分算法

CCL模型的一维瞬态控制方程为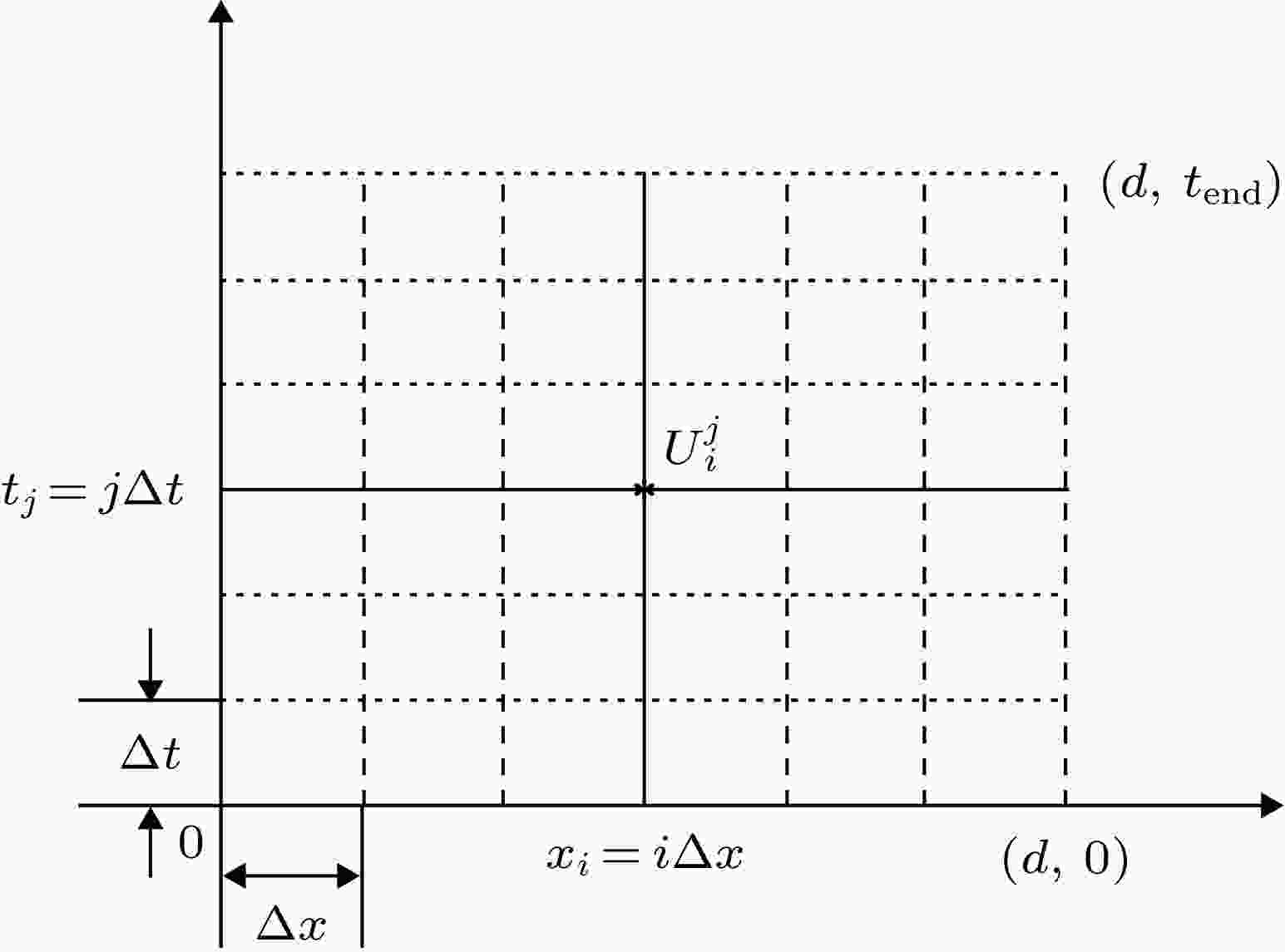

$\varepsilon \frac{\partial }{{\partial t}}\frac{{{\partial ^2}U}}{{\partial {x^2}}} + \sigma \left( x \right)\frac{{{\partial ^2}U}}{{\partial {x^2}}} + \sigma {\rm{'}}\left( x \right)\frac{{\partial U}}{{\partial x}} = - {Q_j}\left( x \right),$

初始条件U(x, 0) = 0, 边界条件为

$\left\{ {\begin{split}& {U{|_{x = 0}} = 0,}\\& {\frac{{{\rm{d}}U}}{{{\rm{d}}x}}{\Big|_{x = 0}} = 0.}\end{split}} \right.$

与稳态解不同, (11)式难以得到解析解, 于是采用时域有限差分算法进行求解. 将求解区域在空间和时间上分别离散, 得到

$\left\{\begin{aligned}& x = {x_i} = i\Delta x,\left( {i = 0,1,2,3, \cdots ,n,n\Delta x = d} \right),\\& t = {t_j} = j\Delta t,\left( {j = 0,1,2,3, \cdots ,m,m\Delta t = {t_{{\rm{end}}}}} \right).\end{aligned} \right.$

以横坐标为空间, 纵坐标为时间, 离散效果见图3.
图 3 时域有限差分计算过程的空间与时间离散
Figure3. Mesh on space and time domain in the finite difference time domain method.

记$U\left( {i\Delta x,j\Delta t} \right) = U_i^j$, $\sigma \left( {i\Delta x} \right) = {\sigma _i}$, $\sigma '\left( {i\Delta x} \right) = $${\sigma '_i} $, 采用前向差分和二次中心差分分别逼近未知变量U关于x和t的一阶和二阶导数, 即

$ \begin{split}&\frac{{\partial U}}{{\partial x}} = \frac{{U_{i + 1}^j - U_i^j}}{{\Delta x}},\frac{{{\partial ^2}U}}{{\partial {x^2}}} = \frac{{U_{i + 1}^j + U_{i - 1}^j - 2U_i^j}}{{\Delta {x^2}}},\\ &\frac{{\partial U}}{{\partial t}} = \frac{{U_i^{j + 1} - U_i^j}}{{\Delta t}},\end{split}$

得到

$ \begin{split}\frac{\partial }{{\partial {\rm{t}}}}\frac{{{\partial ^2}U}}{{\partial {x^2}}} =\; &\dfrac1{\Delta t}\left( \frac{{U_{i + 1}^{j + 1} + U_{i - 1}^{j + 1} - 2U_i^{j + 1}}}{{\Delta {x^2}}}\right. \\ & - \left.\frac{{U_{i + 1}^j + U_{i - 1}^j - 2U_i^j}}{{\Delta {x^2}}} \right),\end{split}$

代入到控制方程(11)并适当化简得到

$U_{i + 1}^{j + 1} + U_{i - 1}^{j + 1} - 2U_i^{j + 1} = b_i^j,i = 1,2, \cdots\!,n - 1,$

$ \begin{split}b_i^j =\; & - \frac{{\Delta {x^2}\Delta t}}{\varepsilon }{Q_j}\left( {i\Delta x} \right) + \left( {1 - \frac{{{\sigma _i}\Delta t}}{\varepsilon }} \right)\\ & \times\left( {U_{i + 1}^j + U_{i - 1}^j - 2U_i^j} \right) \\ &- \frac{{\Delta x\Delta t{{\sigma '}_i}}}{\varepsilon }\left( {U_{i + 1}^j + U_i^j} \right).\end{split}$

以上是控制方程的差分格式, 在此基础上结合边界条件的离散结果

$\left\{ {\begin{aligned}& {{U_1} - {U_0} = 0,}\\& {{U_n} = 0.}\end{aligned}} \right.$

就得到一维瞬态求解方程, 将其写成矩阵形式为

${{A}}{{{U}}^{j + 1}} = f\left( {{{{U}}^j}} \right) = {{{b}}^j},$

式中

$ \begin{split} & A = \begin{bmatrix}\; 1 & 1 & \cdots & \cdots & \cdots & \;\\\; 1& - 2& 1 & \cdots & \cdots & \;\\\; 0 & 1& - 2 & 1 & \cdots & \;\\\; \vdots & & \ddots & & \vdots & \;\\\; 0& 0 & \cdots & 0& 1 & \;\end{bmatrix} ,\\ & f({U^j}) = {b^j} = \left[ \begin{gathered} 0 \\ \vdots \\ b_i^j \\ \vdots \\ 0 \end{gathered} \right],~~\left\{\begin{array}{lll} i = 1,2,\cdots,n - 1, \\ A_{n,n} = 0, \\ j = 0,1,2,\cdots,m.\end{array} \right.\end{split}$

利用(19)式, 根据初始值U_i⁰ = 0, i = 1,2,···,n得到下一个时间步的电位值U¹_i = 0, i = 1,2,···,n, 以新得到的电位更新初始值继续往下迭代求解, 直到达到预期的求解时间t_end.
3 -->

2.2.3.解耦电场强度与电导率－提出迭代收敛算法

当电场强度超过10⁷ V/m时, 电导率会出现显著增大, Adamec 和Calderwood^[24]通过考虑外加电场对载流子浓度和迁移率的影响, 理论推导出强电场作用下电导率公式, 根据此公式得到了电场强度对电导率的增大系数, 如图4所示, 其中纵坐标代表增大倍数, σ_ET(E, T)为电场强度E和温度T影响下的电导率. 从充电过程考虑, 电场强度增大使电导率增大, 而根据欧姆定律, 在一定的入射电流密度下, 电导率增大会使得电场强度降低. 利用这种反馈机理, 提出一种迭代算法^[25], 如图5所示. 图示参数是迭代求解的关键参数, 对于其余参量如介质厚度和介电常数等, 在迭代过程中是不变的.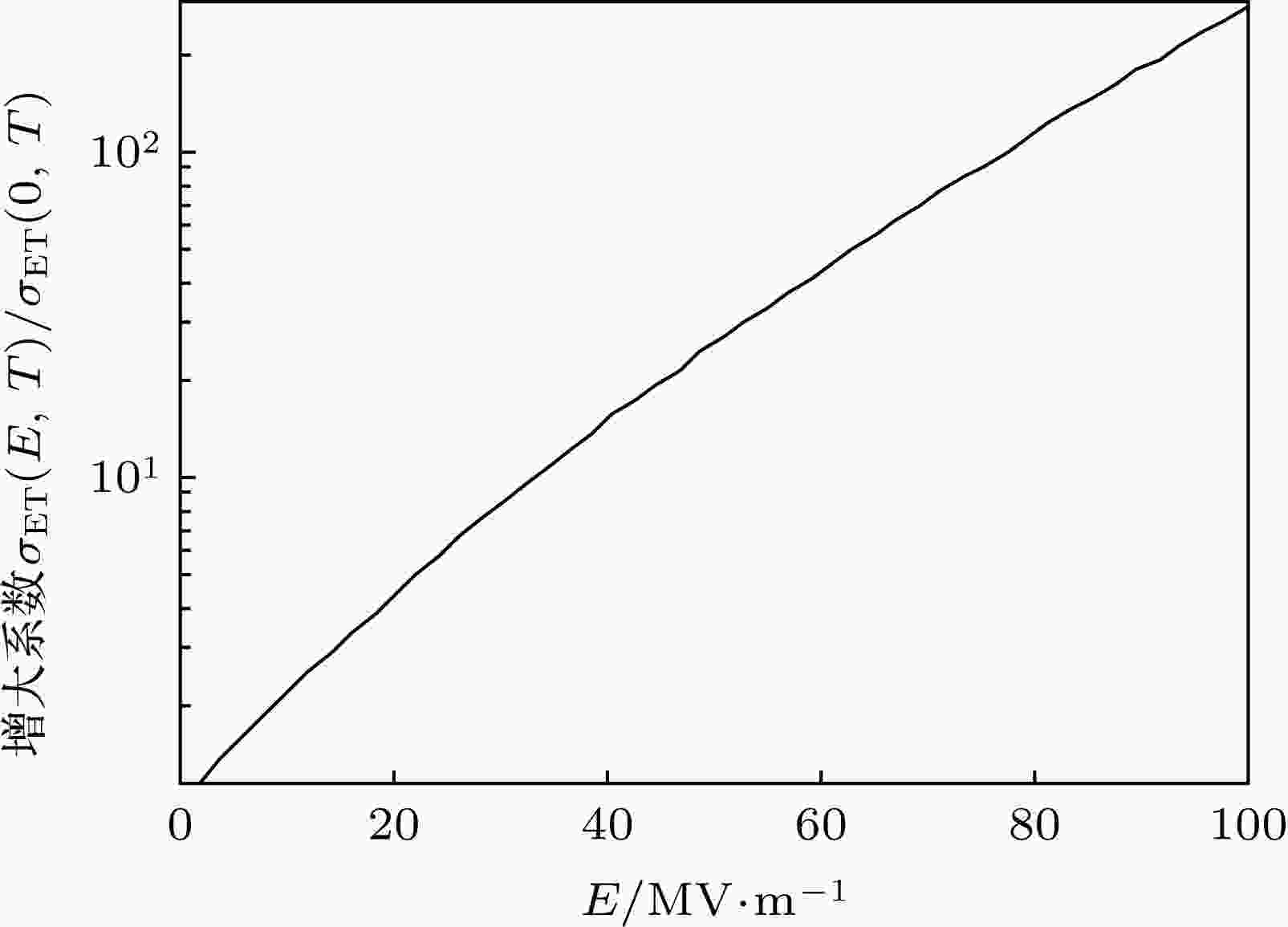
图 4 电导率的强电场效应图示(T = 293 K)
Figure4. Schema of conductivity enhance due to intense electric field (T = 293 K).

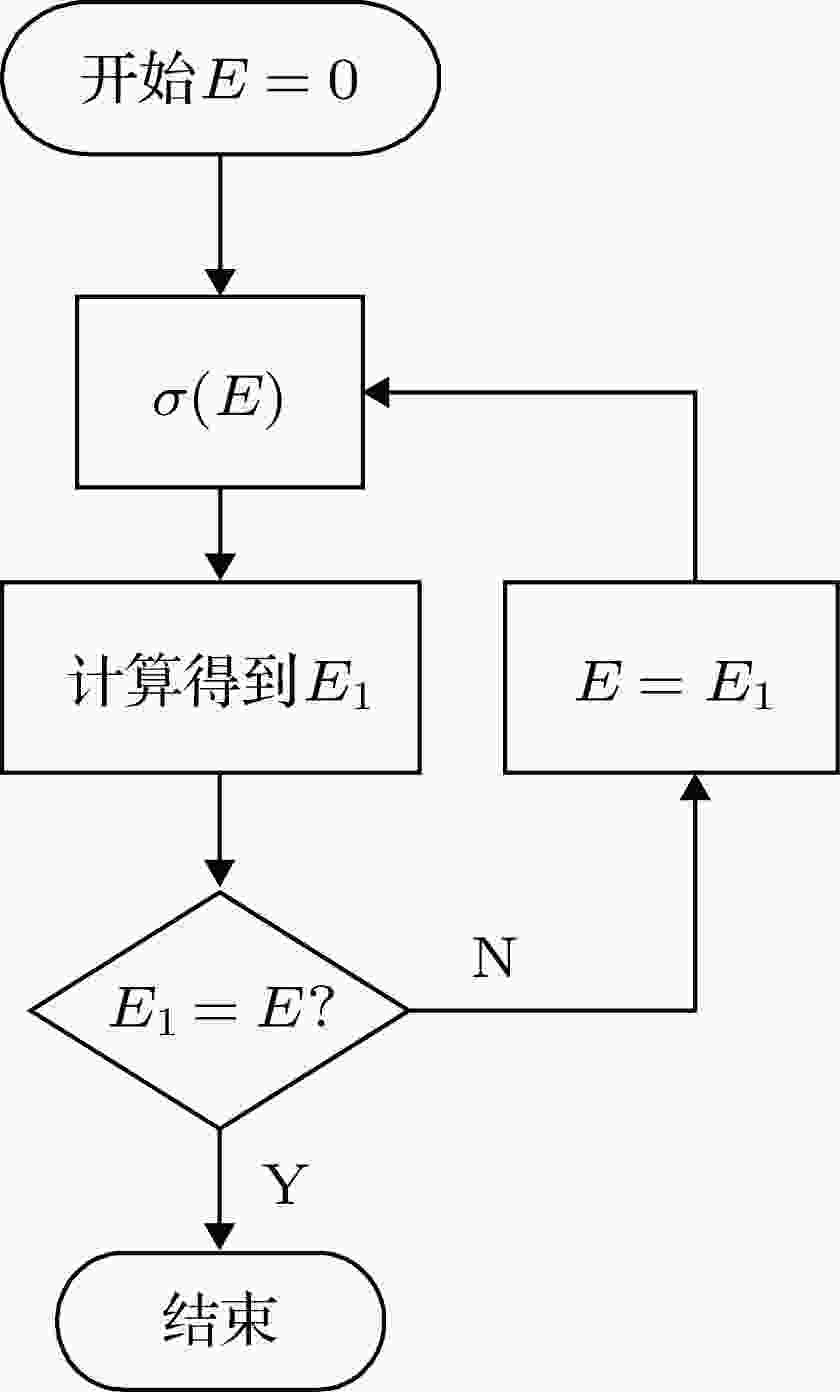图 5 迭代算法流程图
Figure5. Flowchart for the iterative algorithm.

假设在已知电导率分布σ(x)情况下得到了CCL模型的解, 即上述稳态或瞬态解法. 起始状态令电场强度E = 0, 得到固定的电导率分布σ(x), 根据CCL模型进行求解得到对应的电场强度, 然后用新得到的电场强度更新电导率, 并再次求解. 终止条件判据并不一定是严格相等, 而是利用二者的相对误差(2范数意义上)进行合理判定. 对于一维模型, 终止条件设置为‖E₁–E‖/‖E‖ < 0.001, 即前后两次迭代计算对应的电场强度以向量2-范数为度量的相对变化 < 0.001. 因为电导率与电场强度正相关, 而且电导率增大会限制电场强度的进一步增大, 所以该迭代算法是收敛的, 从而解决了电场强度与电导率的耦合计算问题.
2 -->

2.3.CCL模型的二维和三维求解方案

对于二维和三维的CCL模型, 本文采用Comsol Multiphysics软件进行求解. Comsol采用有限元方法进行求解, 在选中软件网格剖分功能后, 可根据求解对象的结构来合理设置网格尺寸. 合理的网格剖分不仅有助于提高计算效率, 而且是得到可靠结果的必要条件. 从发表的文献来看, 目前实现内带电三维仿真的相关报道极少. 国外****提到三维仿真的重要性^[19], 但没有给出完整的仿真方案; 由于电场强度是判断是否发生介质击穿放电的重要参数, 而且场强峰值一般出现在介质结构的接地边角的地方, 所以对于二维或三维模型, 需要特别注意峰值场强附近的网格剖分. 图6给出了SADM (solar array drive mechanism, SADM)介质盘环局部结构的仿真结果. 由图可得电场强度峰值出现在介质结构与导体接触的边界点上, 该点处在接地面的边缘, 是内部沉积电荷最近的泄放点, 由于介质和导体连接处局部电荷泄放路径的不规则性, 使得该处存在电流密度汇集的“漏斗”效应, 容易导致电场畸变放大. 利用这种网格加密处理, 使得本文的内带电三维仿真具有更加准确考察特殊边界对充电结果影响的优势.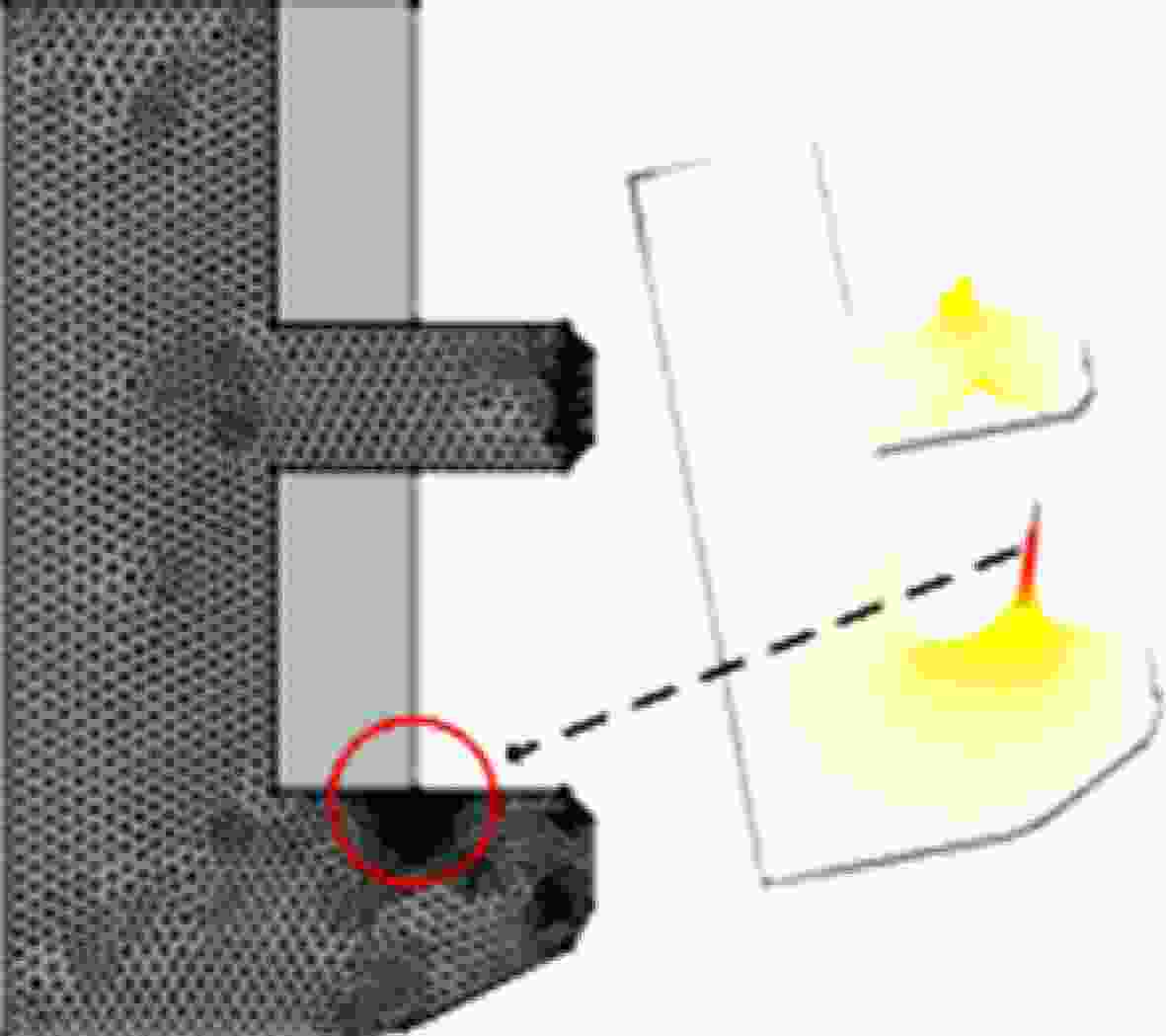
图 6 关键点处的网格加密和对应的电场分布
Figure6. Mesh refinement and the corresponding enlarged electric field.

根据控制方程(1)式和边界条件(4)式, 利用Comsol的AC/DC模块中的电流物理场(electric current interface), 得到的计算设置界面如图7所示. 在全局定义里利用插值函数(interpolation), 可以将电荷沉积率和辐射剂量率等电荷输运模拟结果代入, 分别为电流源和辐射诱导电导率提供必要输入.
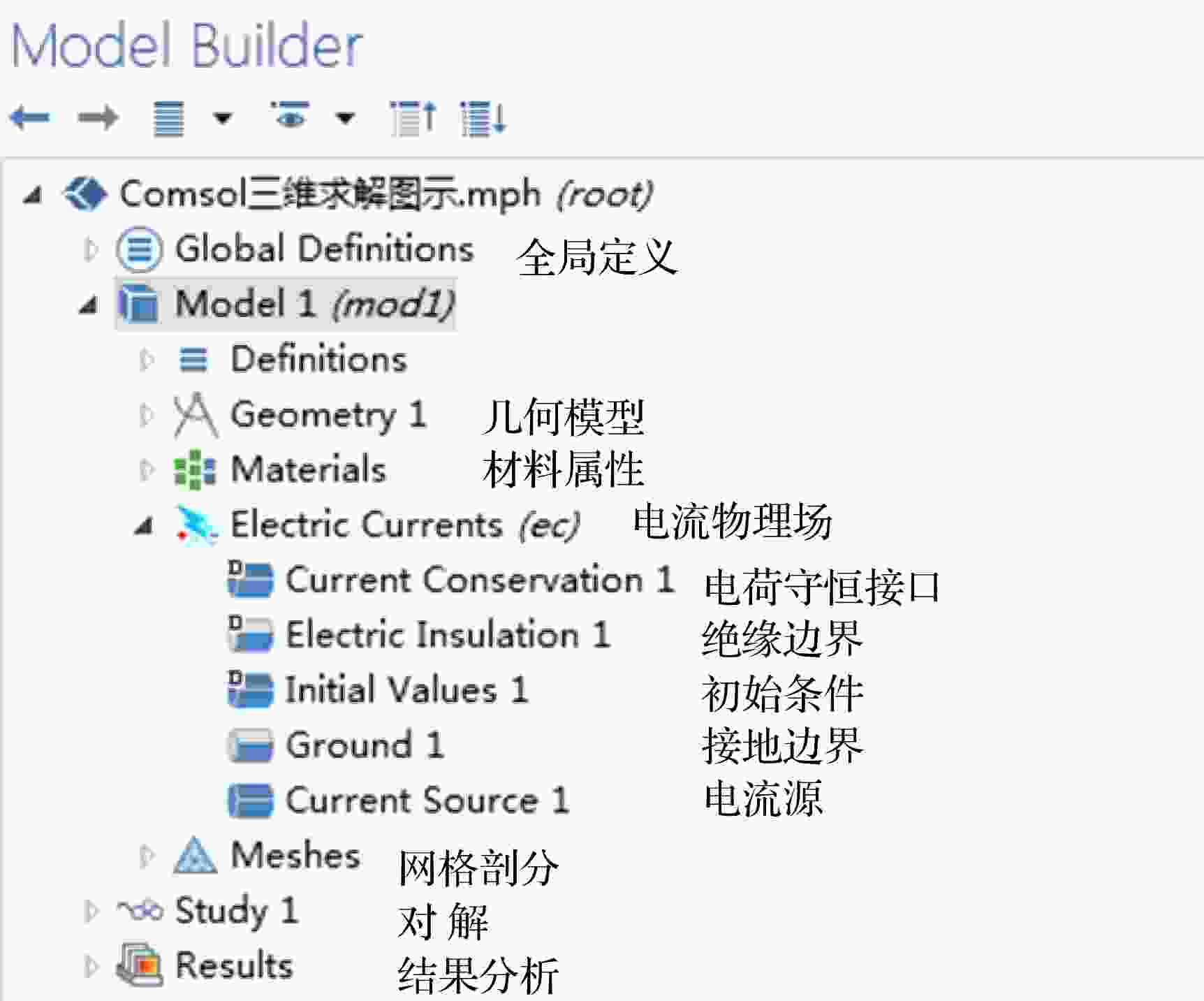图 7 基于Comsol平台的内带电三维求解图示
Figure7. 3-D computation of internal charging on the Comsol platform.

利用Comsol中的插值函数将电荷沉积率Q_j代入, 如图8所示, 并作为内带电电流源进行计算; 同理可以代入辐射剂量率. 计算过程涉及的环境温度和材料参数可以通过全局变量进行合理设置.
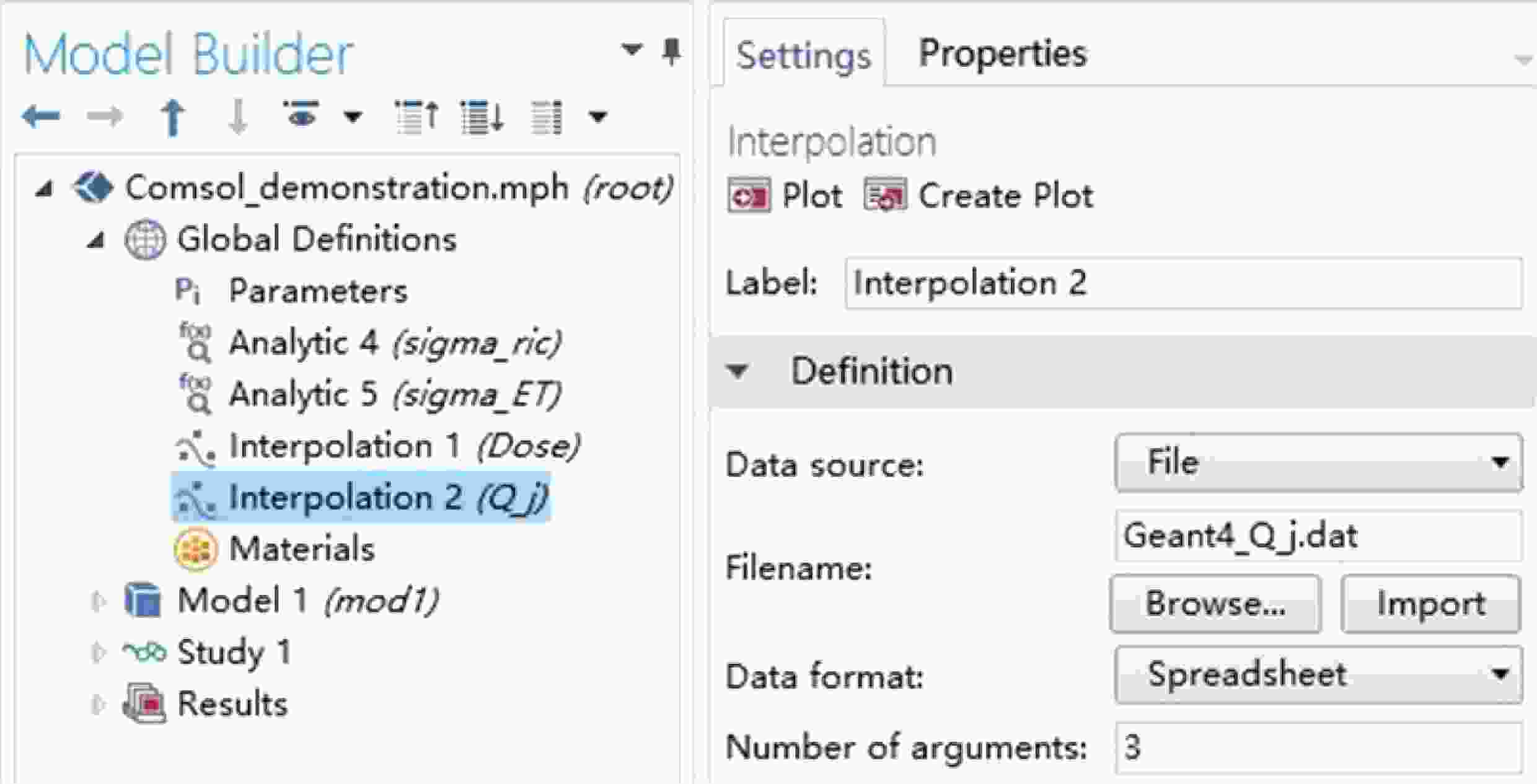图 8 利用插值函数导入Geant4的计算结果Q_j
Figure8. Importing Q_j of Geant4 into computation by interpolation function in Comsol.

虽然内带电计算中通常仅考虑两类边界条件, 但是不同几何模型的边界存在较大差异. 以SADM介质盘环的局部结构为例, 其充电源与边界设置如图9所示, 源Q_j作用到整个介质区域, 而介质与金属板接触的边界才是接地边界, 其余为绝缘边界. 在设置好输入条件和边界条件后, 进行求解. 图中所示 “study” 为求解模块, 可选择瞬态或稳态求解方式. 稳态解对应于充电平衡下的结果, 而瞬态解可考察充电过程.
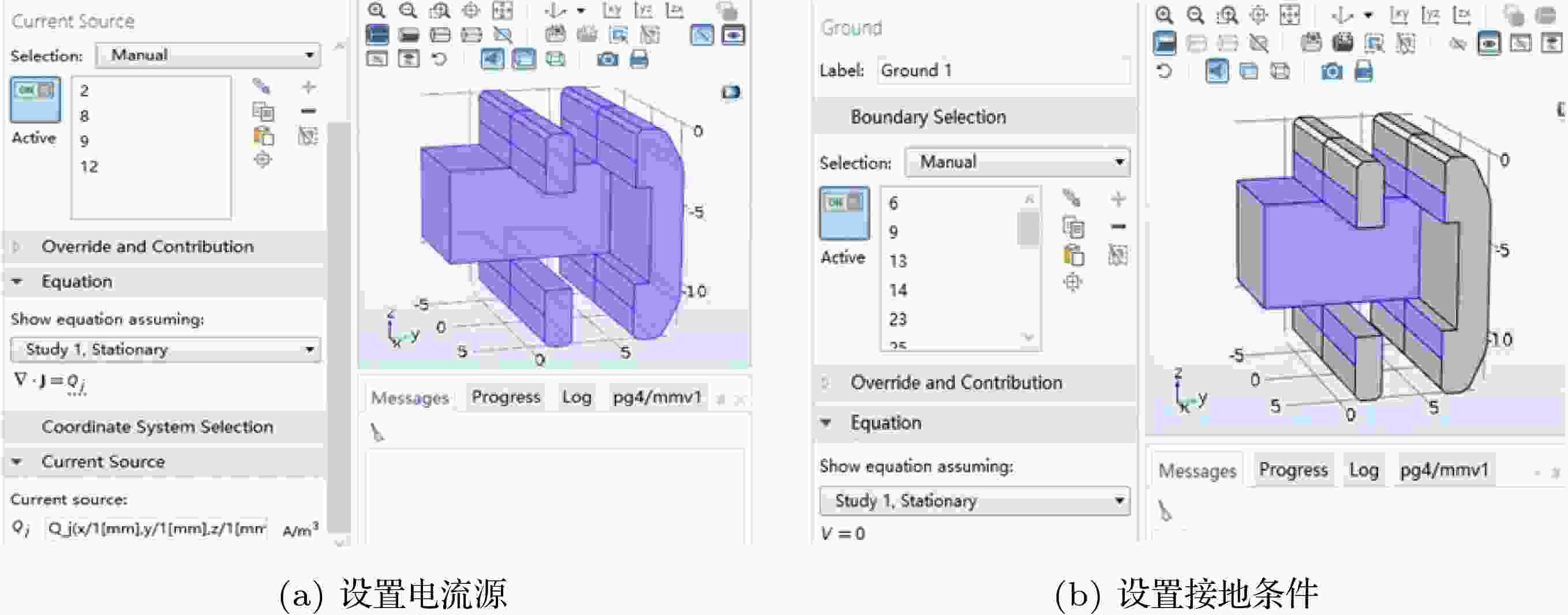图 9 内带电数值计算设置
Figure9. Configurations of internal charging numerical simulation.

GR(generation and recombination, GR)模型与RIC模型曾被用来研究介质内电现象^[20], 二者的对比分析结果表明RIC模型是GR模型的合理近似^[26]. 本文将RIC模型与CCL模型进行对比分析. 为不失一般性, 选择一维充电情况, 首先在理论和数学表达式方面将CCL模型与RIC模型进行对比分析, 然后分别采用这两类模型进行实例仿真分析.
RIC模型的一维时域模型为

$\left\{ {\begin{aligned}& {\varepsilon \frac{{\partial E}}{{\partial x}} = - {\rho _{\rm{f}}} - {\rho _{\rm{t}}},}\\& {\frac{{\partial \left( {{\rho _{\rm{f}}} + {\rho _{\rm{t}}}} \right)}}{{\partial t}} = \frac{{\partial {J_{\rm{e}}}\left( x \right)}}{{\partial x}} + \frac{{\partial \left( {\mu {\rho _{\rm{f}}}E} \right)}}{{\partial x}} + \frac{{\partial \left( {{\sigma _{{\rm{ric}}}}E} \right)}}{{\partial x}},}\\&{\frac{{\partial {\rho _{\rm{t}}}}}{{\partial t}} = \frac{{{\rho _{\rm{f}}}}}{\tau }\left( {1 - \frac{{{\rho _{\rm{t}}}}}{{{\rho _{\rm{m}}}}}} \right).}\end{aligned}} \right.$

式中函数J_e(x)为高能电子入射导致的介质内部电流密度, 其余各参数为介电常数ε、电荷迁移率μ、电荷俘获时间τ和陷阱密度ρ_m. RIC模型由泊松方程、电荷守恒定律和陷阱电荷俘获方程组成, 是自由电荷密度ρ_f(x, t)、俘获电荷密度ρ_t(x, t)和电位U(利用变换$E = - \nabla U$)关于空间x与时间t的非线性偏微分方程组. 初始条件为U = ρ_f = ρ_t = 0, 参考(4)式可设置电位U的边界条件, 例如背面接地情况下有$U(d) = 0,~\dfrac{\partial U}{\partial x}\Big|_{x = 0}= 0$; 考虑到与介质接触的金属或真空中电荷密度均为0, 故ρ_f和ρ_t的左右边界都为0. 值得注意的是: 虽然RIC模型是对GR模型在一定程度上的近似, 但仍保留了诸如τ和ρ_m等微观参量.
CCL模型的一维形式为:
引入空间电荷密度ρ, 由高斯定理得

$\varepsilon \frac{{\partial E}}{{\partial t}} = \rho ,$

替换${{J}} = \left( {\sigma + \varepsilon \dfrac{\partial }{{\partial t}}} \right){{E}}$中的位移电流项, 并代入(1)式中得到

$ - \frac{{\partial \rho }}{{\partial t}} = \frac{{\partial {J_{\rm{e}}}}}{{\partial x}} + \frac{{\partial \left( {\sigma E} \right)}}{{\partial x}}.$

与RIC模型对比可知, 当–ρ = ρ_f + ρ_t, σ = μρ_f + σ_ric时, (23)式与(21)式中第2式是等价的. 利用$E = - \nabla U$, 得到关于U的单变量方程

$\frac{{\partial {J_{\rm{e}}}}}{{\partial x}}= - \frac{{\partial \left( {\sigma \partial U/\partial t} \right)}}{{\partial x}} - \varepsilon \frac{\partial }{{\partial t}}\left( {\frac{{{\partial ^2}U}}{{\partial {x^2}}}} \right) = 0.$

同样地, 电位U初始值为0, 参考(5)式可得到模型的边界条件.
RIC模型的控制方程((21)式)包含三个待求解变量, 而CCL模型的控制方程((1)式)只有U, 其余变量如电场强度和空间电荷密度是U的关联变量. 在μ = 0, σ = σ_ric且充电平衡条件下(导数项为0), (21)式的第2式与(23)式是相同的; 对于瞬态充电方程, 假设-ρ = ρ_f + ρ_t, 那么得到的方程亦是相同的. μ ≠ 0代表本征电导率不为0, 于是在CCL模型中增加本征电导率对σ的贡献, 即σ = σ_ric + σ_ET. 对于航天器内带电计算, 一方面介质材料对应的电荷俘获时间τ(秒量级)远小于内带电充电时间(小时量级), 另一方面介质内陷阱密度ρ_m远大于充电平衡后介质中的电荷密度, 因此ρ_f会迅速转化为ρ_t, 也就是没必要考虑RIC模型中的电荷俘获机制, 此时满足假设“–(ρ_f + ρ_t)与ρ对应”, 且μρ_f→0. 可见, 在二者考虑相同电导率且充电时间远大于电荷俘获时间情况下, CCL模型与RIC模型可得到相同的内带电结果; 对于内带电三维仿真, 采用CCL模型更容易实现三维数值求解.
考虑地球同步轨道恶劣电子辐射环境(利用Flumic3模型^[27]评估航天器内带电的恶劣充电环境), 对比CCL模型与RIC模型的内带电计算结果. 一方面, 边界条件设置为背面接地, 正面绝缘. 综合考虑辐射诱导电导率和本征电导率的影响. 取σ_T = 3.73 × 10^–15, 并在RIC模型中考察取值分别为μ = 0和μ = 10^–11, 其余参数τ = 1s, ρ_m = 4.0 × 10³ C/m^3[28], 得到介质背面电位随时间变化结果如图10所示. 该结果表明μ的取值从0直到10^–11都对结果不产生明显影响, 两种模型得到的结果是非常一致的; 另一方面, 针对正面接地和介质双面接地情况做出对比. 令RIC模型中μ = 0且二者取相同的σ, 再次得到了一致的电位分布结果, 如图11所示. 比较来看, 背面接地是充电最严重的情况, 这与前人得到的规律是一致的^[20].
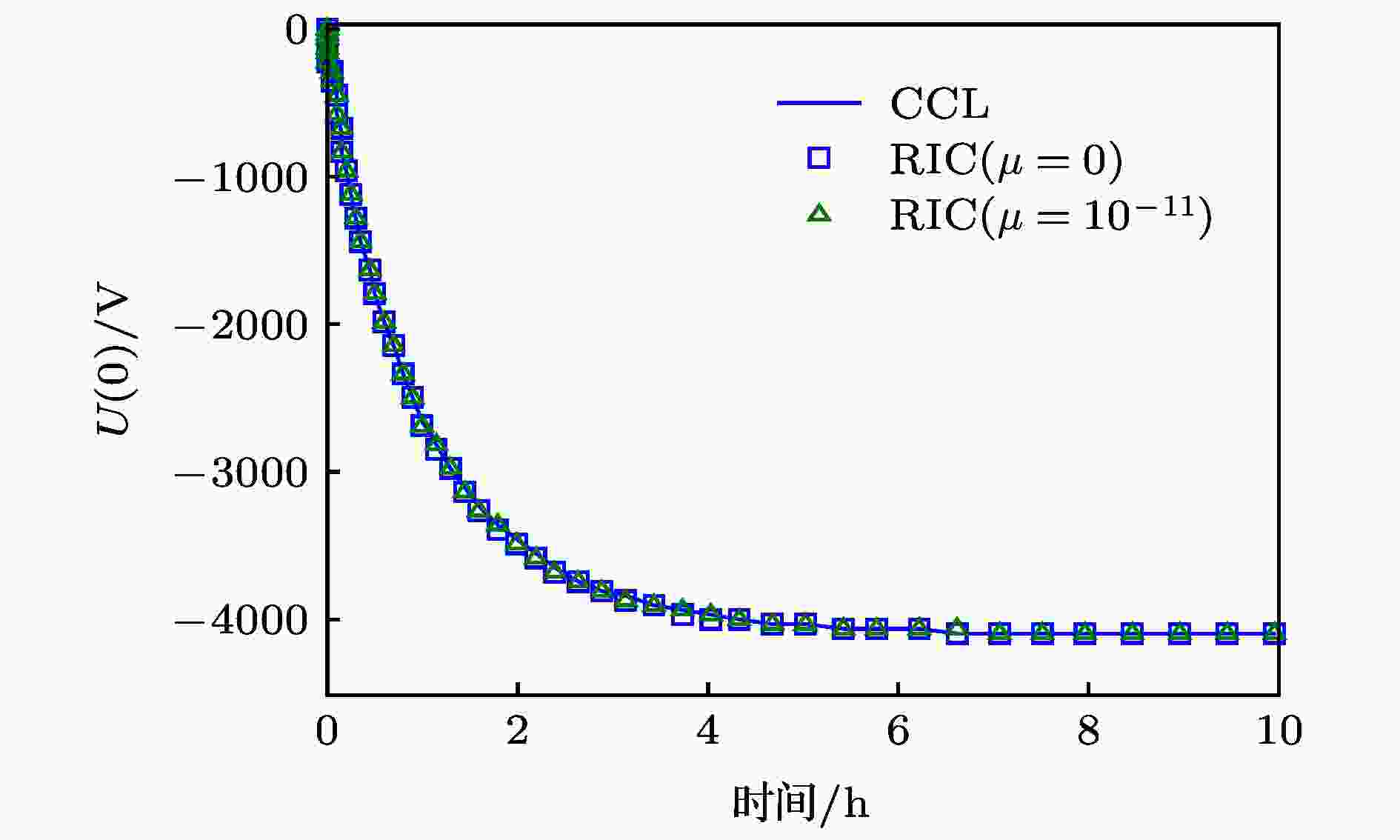图 10 时域充电电位对比(背面接地)
Figure10. Comparison of the charging potential in time domain.

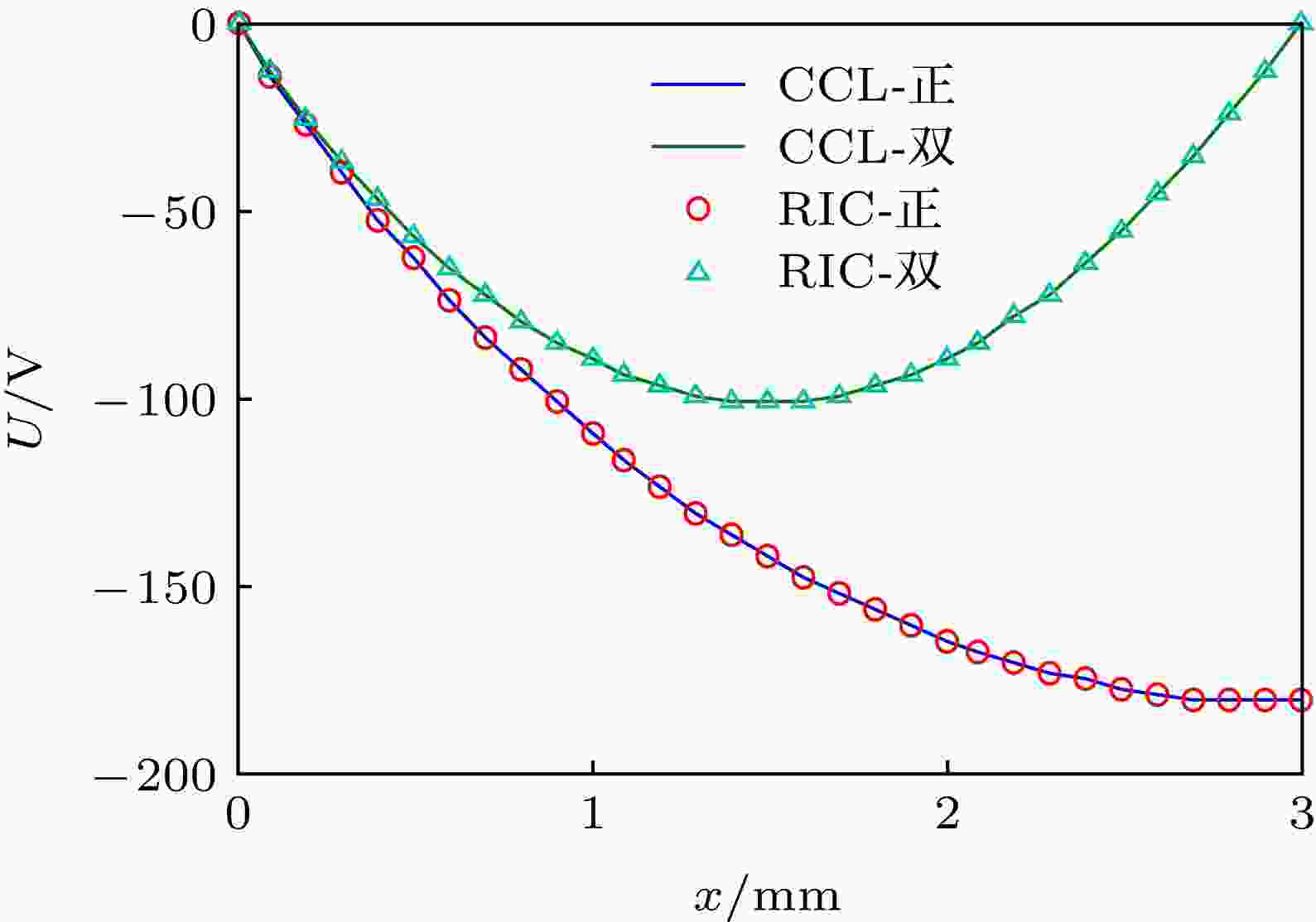图 11 正面与双面接地情况下的电位对比
Figure11. Comparisons in cases of front &both surfaces grounding.

CCL模型与RIC模型的对比分析结果如表1所示. 因为RIC模型额外考虑了电荷俘获机理, 涉及到介质中电荷输运的多个微观机制相关参数, 导致RIC模型比CCL模型数学表达式更加复杂. 又因为内带电评估只关心电位和电场强度, 当采用相同的介质总电导率, 在充电时间远大于电荷俘获时间条件下, CCL模型与RIC模型得到的结果是一致的, 所以本文构建的内带电三维仿真方案具有计算效率更高的优势.

类别	充电机理	数学表达式	边界条件	是否便于三维计算	内带电计算效果
CCL	电荷守恒	一元偏微分方程	清晰	是	一定条件下充电结果相同
RIC	电荷守恒与电荷俘获机制	三元偏微分方程组	较难设定	否

表1CCL模型与RIC模型对比分析
Table1.Comparison of CCL model and RIC model.

采用航天器内带电的典型介质结构-电路板作为研究对象, 当考虑沿深度方向的充电结果时, 可以将其近似为一维充电模型. 为便于测量介质内部电位或电场, 采用多层电路板试样以得到深度方向的电位和电场分布.
2

-->

4.1.实验布局

多层电路板试样如图12所示, 该试样是覆铜层与FR-4(环氧玻璃布层压板)的叠合结构, 总厚度为3 mm, 包含8个厚度为9 μm的覆铜层. 第1层和第8层分别位于电路板的上、下表面, 其余沿厚度方向等间距分布. 所有覆铜层均为圆形, 从而尽量避免尖端放电. 对各覆铜层引出电极, 以便测试每层的充电电位.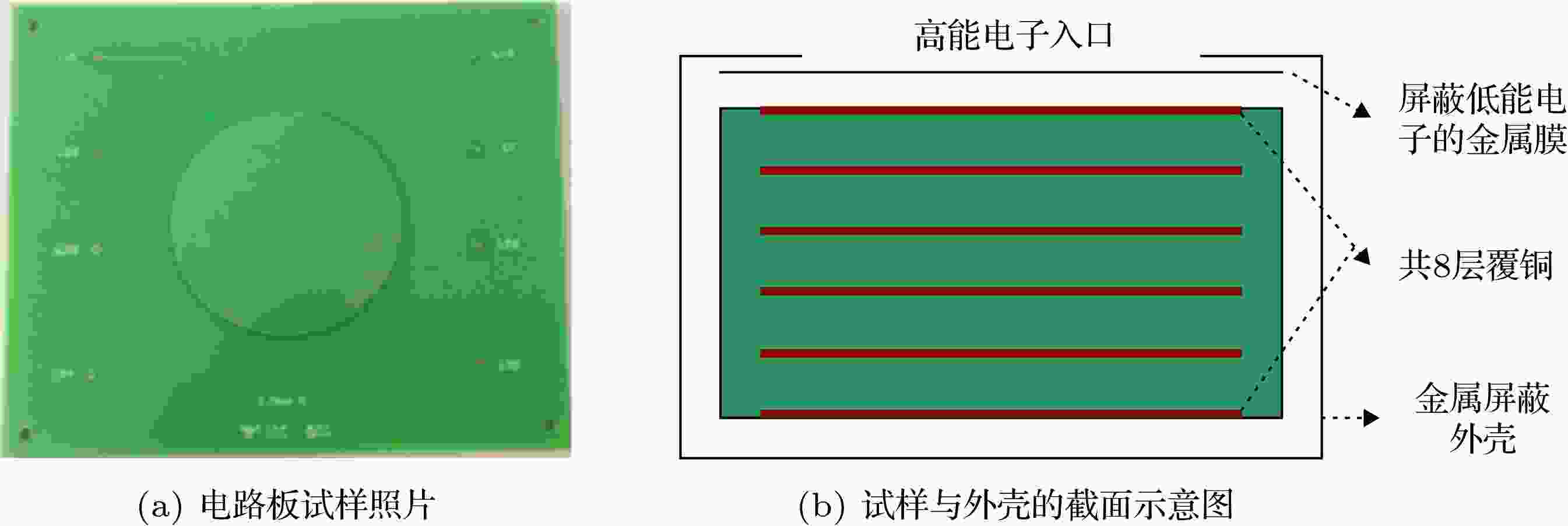
图 12 电路板试样与外壳结构示意图
Figure12. Structure diagram of PCB sample and its crust.

电路板内带电实验系统示意图如图13所示. 电子加速器可产生能量0.1 — 2.0 MeV、束流密度0.1 —100 pA/cm²的电子束, 真空室为圆形(直径150 cm, 高度200 cm, 真空度优于1.0 × 10^–4 Pa), 内部放置样品台, 通过引出电极, 采用非接触式表面电位计(Trek 341B, 量程0— ± 20 kV)测量电路板中各个金属薄层的充电电位. 实验时, 高能电子束垂直入射电路板试样. 为准确限定电子对电路板的入射范围, 将试样放置在单面开口的金属壳体中, 即图12(b)所示, 壳体材料选用航天器常用的铝合金材料, 不会造成次级辐射效应.
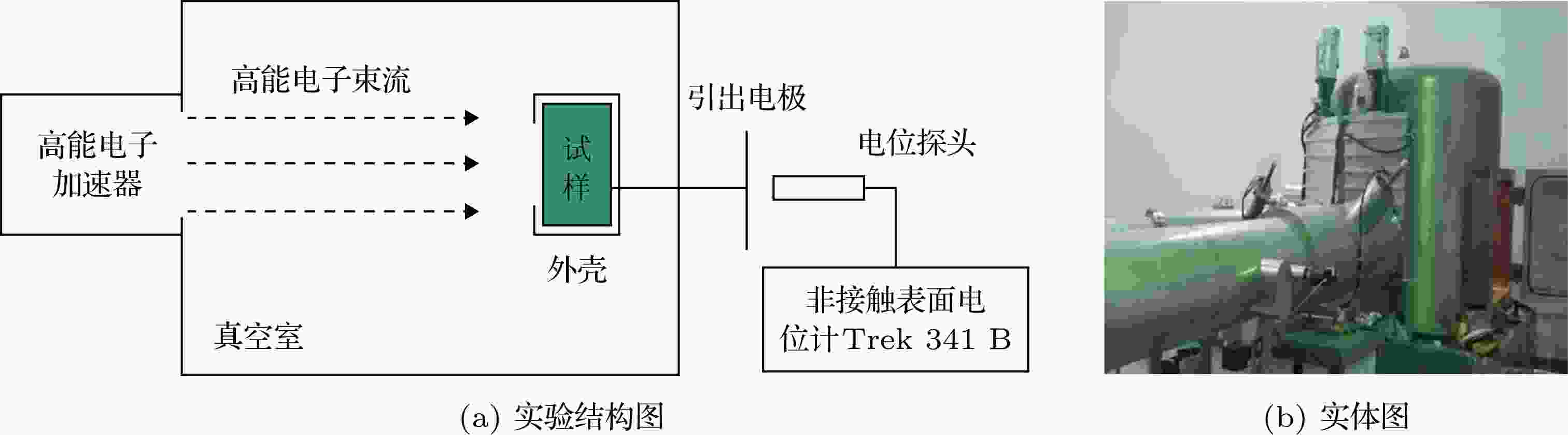图 13 电路板内带电实验系统示意图
Figure13. Diagram of the experiment system for PCB internal charging.

2 -->

4.2.仿真与实验结果的对比分析

沿深度方向取仿真结果与实验数据进行对比, 结果如图14所示. 从图14(a)可知, 介质正面(x = 0)保持0电位, 满足正面接地的边界条件. 随着深度增大, 充电电位(幅值)逐步增大, 到介质背面达到电位峰值; 最大电位偏差出现在介质背面, 即仿真峰值的–578 V和实验的–737 V, 考虑到材料电导率测试和束流密度监测存在的误差以及试样制备精度等不确定因素, 该偏差在可接受范围内.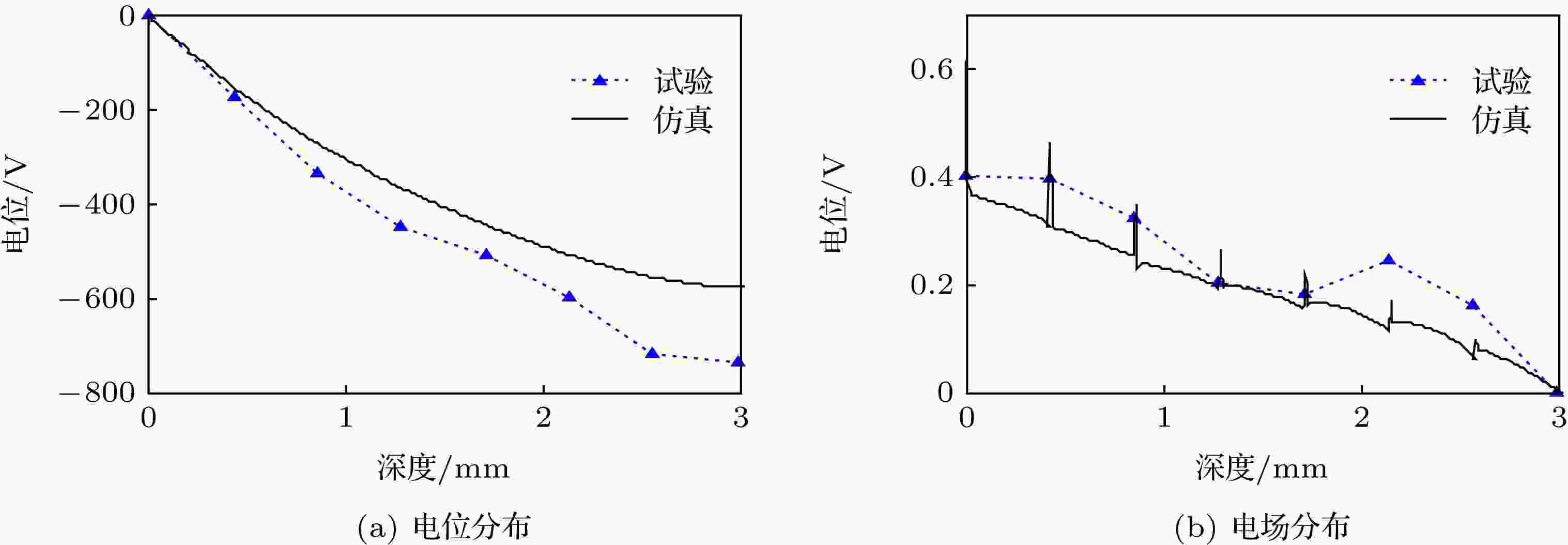
图 14 实验与仿真结果的对比
Figure14. Comparison of charging results from experiment and numerical simulation.

虽然电位较好的一致性决定了电场强度不会发生太大的偏差, 但是仅对比电位分布仍然是不充分的. 这不仅是因为内带电更关注电场强度的大小以判断是否发生介质击穿放电, 而且从电场分布可以更加清楚地看出内部覆铜层对充电的影响. 产生的局部电场畸变如图14(b)所示, 由于覆铜层导致电荷输运结果的局部波动, 最终形成局部电场畸变. 除去畸变值, 场强峰值出现在接地边界, 这与先前的研究结果是一致的. 总体来讲, 实验与仿真的充电规律是相同的, 得到的电位和电场结果是十分接近的, 这验证了仿真模型的正确性.

本文基于电荷守恒定律建立了内带电三维计算模型(CCL模型), 给出了该模型的一维稳态和瞬态求解算法及二维和三维求解方案, 将它与先前的RIC模型进行了对比分析, 并从实验上验证了仿真结果的正确性.
由于内带电时间常数远大于电荷俘获时间且介质内陷阱密度远大于充电平衡后的电荷密度, 导致自由电荷会迅速转化为被俘获电荷, 从而没必要考虑RIC模型中的电荷俘获机制; 采用CCL模型可以实现内带电评估, 且具有更高的计算效率. 利用具体算例证实了该结论. 此外, 借助有限元局部网格加密处理, CCL模型具有更加准确刻画局部场强畸变的优势.