摘要:硼烯作为一种性能优异的二维材料, 其界面动力学行为值得探讨. 本文采用解析法研究了石墨烯与六方氮化硼(h-BN)以及一种硼烯之间的相互作用. 结果表明, 石墨烯在六方氮化硼上滑动时, C原子和B原子之间的相互作用弱于C原子和N原子之间的相互作用. 石墨烯与硼烯界面间的势能起伏明显小于石墨烯和六方氮化硼之间的势能起伏, 表明其界面摩擦力可能更小. 此外, 石墨烯从硼烯上滑出时拉出力较小, 其边界效应更弱, 因此硼烯有望成为一种摩擦性能优异的二维材料.
关键词: 硼烯/
石墨烯/
势能起伏/
摩擦

English Abstract

全文HTML

--> --> -->

石墨烯^[1]因具有优异的力学、电学和热学等性能^[2-5]而受到了研究者的广泛关注, 有望应用于高性能纳电子器件和微纳机电系统中^[6]. 在石墨烯的应用中, 界面摩擦、黏着行为是亟待解决的重要问题. 目前研究者对石墨烯的摩擦行为已经开展了较为充分的研究, 如Zheng等^[7]发现通过摩尔纹超晶格适配可实现石墨烯的超低摩擦. Guo等^[8]模拟了层间距对石墨烯摩擦的影响, 指出随着层间距的减小摩擦力增大. 层数^[9]、褶皱^[10]对石墨烯摩擦的影响已被充分讨论. 氢化^[11]、氟化^[12]、羟基^[13,14]对石墨烯运动和摩擦的影响也得到了研究. 此外, Berman等^[15]还采用石墨烯与纳米粒子的组合实现了宏观尺度界面间的超低摩擦.
石墨烯与其他二维材料之间由于晶格失配, 具有不公度接触构型^[16-18], 对减小摩擦具有积极作用, 因此以石墨烯为代表的二维异质结构的摩擦行为也受到了研究者的关注, 如石墨烯与h-BN之间的超低摩擦行为得到了研究者的确认. Leven等^[19]研究了方向性、厚度和滑动约束对石墨烯和h-BN之间层间滑动的影响. Wang等^[20]研究了氟化石墨烯和MoS₂之间的超低摩擦行为. Spear等^[21]综述了二维材料应用于控制表面和界面摩擦性能的最新进展.
在目前制备的多种二维材料中, 二维硼烯(Borophene)^{[22, 23]}表现出独特的力学、电学和化学性能^[24], 具有良好的应用前景. 程鹏等^[25]制备出了单层硼烯, 并指出一些硼烯结构可在大气环境下稳定存在. 但目前对硼烯的摩擦特性以及其与其他二维材料间相互作用的研究较为欠缺. Crisafulli等^[26]的研究表明采用解析法研究石墨烯层间滑动的动力学行为具有可行性, 因此本文采用解析法研究了石墨烯和一种稳定的二维平面结构的硼烯之间的层间相互作用, 并与石墨烯和h-BN之间的相互作用相比较, 讨论了硼烯在摩擦学领域应用的可能性.

本文建立了两种模型, 包括石墨烯在h-BN基底上滑动以及石墨烯在硼烯基底上滑动的模型. 其中为了简化计算, h-BN和硼烯基底均固定, 滑动的石墨烯片为刚性, 并在滑动过程中保持匀速. 模型示意图如图1所示, 其中模型a, b分别为石墨烯/h-BN和石墨烯/硼烯组成的模型. 考虑到石墨烯和h-BN均为六角形蜂巢结构, 为了方便计算模型的尺寸, 可定义两个参数a₀ = 0.142 nm和a₁ = 0.246 nm, 如图1(a)中所示. 对于模型a, 固定h-BN的尺寸为: L_x = 3.37 nm, L_y = 2.18 nm, N = 256; 模型b中固定硼烯的尺寸为: L_x = 3.33 nm, L_y = 2.00 nm, N = 272. 其中L_x, L_y分别指两组模型中固定基底(硼烯和h-BN)在x, y方向上的长度; N为原子个数. 值得注意的是, 由于模型的简化, 该模型的建立仅适用于二维平面、无褶皱的结构, 若应用于二维结构中存在较大褶皱的情况时则会存在构型不准确的问题. 两组模型中滑动石墨烯片尺寸的计算公式如下:
图 1 石墨烯在固定基底上滑动的模型　(a) 石墨烯在h-BN上, 模型a; (b) 石墨烯在硼烯上, 模型b
Figure1. Graphene slides on substrates: (a) On h-BN, model a; (b) on borophene, model b.

${L_x} = {a_0} \times {h_x} + 2{a_0} \times \left( {{h_x} - 1} \right),$

${L_y} = {a_1} \times {h_y},$

$N = 2{h_x} \times \left[ {3 + 2 \times \left( {{h_y} - 1} \right)} \right],$

其中(h_x, h_y)指在x, y方向分别有h_x和h_y个正六边形.
基于固定基底假设以及石墨烯为刚性的假设, 模型中需要考虑的作用力仅为固定基底和滑动石墨烯之间的范德瓦耳斯力^[26-28]. 范德瓦耳斯力采用Lennard-Jones势函数^[29]描述:

${U_{{\rm{LJ}}}}\left( {{r_{ij}}} \right) = 4{\varepsilon _{ij}}\left[ {{{\left( {{{{\sigma _{ij}}} / {{r_{ij}}}}} \right)}^{{1 / 2}}} - {{\left( {{{{\sigma _{ij}}} / {{r_{ij}}}}} \right)}^6}} \right],$

相应的作用力函数是

${F_{{\rm{LJ}}}}\left( {{r_{ij}}} \right) = 4{\varepsilon _{ij}}{{\left[ {12{{\left( {{{{\sigma _{ij}}} / {{r_{ij}}}}} \right)}^{{1 / 2}}} - 6{{\left( {{{{\sigma _{ij}}} / {{r_{ij}}}}} \right)}^6}} \right]} / {{r_{ij}}}},$

其中, r_ij指固定基底上的原子与石墨烯滑动片上的原子之间的距离, ε_ij为势能阱的深度, σ_ij为相互作用势能为零时的两体距离. 计算中ε_ij与σ_ij的取值如表1所列^[27].

模型	原子	σ/nm	ε/kJ·mol–1
Graphene/h-BN	C—B	0.343	0.329
	C—N	0.338	0.407
Graphene/Borophene	C—B	0.343	0.329

表1Lennard-Jones势函数参数表
Table1.Parameters for Lennard-Jones potential.

2

-->

3.1.石墨烯与h-BN之间的相互作用

由于h-BN在结构上是由B原子和N原子交替连接而成的多个正六边形, 因此分析石墨烯在h-BN上的滑动能够比较由于原子类型的不同而导致的界面间势能起伏的差异. 在h-BN上滑动的石墨烯片由28个原子组成, 其中h_x = 2, h_y = 3, 在x, y方向上的长度分别为0.57, 0.74 nm. 本文对石墨烯与h-BN之间法向载荷F_z为25, 50, 75, 86, 100, 125和150 nN的情况进行了计算. 由于不同载荷下界面间的作用力和势能曲线具有相似性, 这里选择载荷为86 nN的情况进行讨论.
石墨烯中C原子与h-BN中B, N原子间的相互作用以及石墨烯与h-BN间的总作用力和势能如图2所示. 图2(a)显示了滑动过程的三个阶段. 阶段I, 石墨烯从开始进入至刚好完全进入h-BN的过程; 阶段II, 石墨烯在h-BN上滑动的过程; 阶段III 石墨烯从即将开始滑离h-BN至完全滑出h-BN的过程. P_s为阶段I最后时刻所对应的势能数值, P_b为阶段II中势能最大值与最小值的差值, 即界面间势能起伏的幅值. 界面间的最大作用力产生在石墨烯片完全进入h-BN以及石墨烯片即将开始滑离h-BN的时刻, 可将其命为拉出力, 意为滑动片滑离h-BN时需克服的层间作用力, 记作F_exit, 如图2(b)所示.
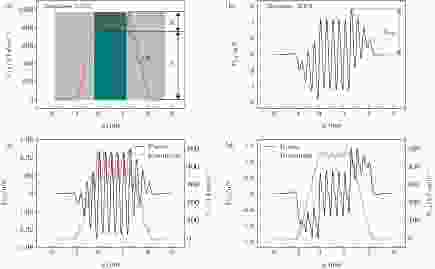图 2 石墨烯与h-BN在相对滑动过程中的层间作用力F_LJ与势能V_LJ　(a) 石墨烯与h-BN之间的势能; (b) 石墨烯与h-BN之间的作用力; (c) 石墨烯中的C与N原子的相互作用; (d) C与B原子的相互作用
Figure2. Force and interface potential between graphene and h-BN during the sliding process: (a) The interface potential from phase I to phase III; (b) the force between graphene and h-BN; (c) the interaction between C and N atoms; (d) the interaction between C and B atoms.

图2(c)和图2(d)为石墨烯中的C原子和h-BN中的N, B原子之间的范德瓦耳斯力和势能图. 可知整个滑动过程C, B原子之间的最大层间作用力小于C, N原子之间的作用力. 并且当石墨烯完全在h-BN上滑动时(阶段II), C, B之间的作用力比C, N之间小, C, B之间的P_b值也明显小于C, N之间. 研究者的结果表明^[30], 在纳米尺度界面间势能的起伏与摩擦相关. 鉴于此, 石墨烯和硼烯之间的相互作用值得进行探讨.
2 -->

3.2.石墨烯与硼烯之间的相互作用

在石墨烯与硼烯组成的模型中, 基本设定与前一模型类似. 石墨烯依然由28个原子组成, 其中h_x = 2, h_y = 3, 在x, y方向上的长度分别为0.57, 0.74 nm. 法向载荷F_z也选择25, 50, 75, 86, 100, 125和150 nN进行计算. 图3显示了当界面法向载荷为86 nN时石墨烯与硼烯之间的范德瓦耳斯力和势能图, 曲线形式与石墨烯和h-BN之间的相互作用类似. 图4(a)和图4(b)分别为不同的载荷下, 石墨烯与硼烯和h-BN之间的势能起伏P_b和拉出力F_exit. 可以看出载荷在25—150 nN之间时, 在相同的载荷下, 石墨烯和硼烯之间的势能起伏更小. 由于界面间作用力与势能之间为偏导关系(见(5)式), 势能起伏小意味着界面间相互作用力弱, 摩擦力更小. 此外, 由图4(b)可以看出, 在相同的载荷下石墨烯与硼烯之间的拉出力也更小. 这一结果表明石墨烯与硼烯之间的摩擦可能更小, 并且边界效应更不明显.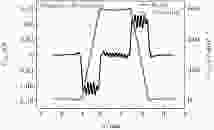
图 3 石墨烯与硼烯相对滑动过程中界面间的相互作用力和势能
Figure3. Force and interface potential between graphene and borophene during the sliding process.

图 4 不同载荷下石墨烯与h-BN和硼烯之间势能起伏和拉出力　(a) 势能起伏P_b; (b) 拉出力F_exit
Figure4. Corrugation and pull out force between graphene and h-BN, borophene under different load:　(a) P_b; (b) F_exit.

图5显示了在不同的载荷25, 50, 75, 100, 125和150 nN下, (2, 3), (4, 3), (4, 5)和(6, 5)四种不同尺寸的石墨烯相对硼烯滑动时的P_b值, 其中(2, 3), (4, 3), (4, 5)和(6, 5)尺寸石墨烯的L_x和L_y可以根据(1)和(2)式计算, 其数值分别为0.57, 0.74, 1.42, 0.74 nm和1.42, 1.23, 2.27, 1.23 nm. 可以看出石墨烯片的尺寸与P_b数值的大小为正相关, 原因是原子数的增加增大了界面间的相互作用. 载荷越大P_b的数值越大, 这与文献[26]结果一致.
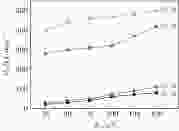图 5 在不同的载荷下, 不同尺寸的石墨烯相对硼烯滑动时界面间的势能起伏
Figure5. Influence of graphene size on P_b under different load

本文采用解析法分别研究了石墨烯在h-BN、硼烯上滑动时界面间相互作用的动力学过程. 结果表明, 石墨烯的运动可分为进入、稳定滑动和滑出三个阶段. 在稳定滑动阶段, 当基底为h-BN时, C, B原子之间的势能起伏弱于C, N原子之间. 滑出阶段C, B原子作用导致的拉出力也比C, N原子作用小. 石墨烯与硼烯界面间的势能起伏以及拉出力均比石墨烯与h-BN之间小, 表明界面间的摩擦力可能更小, 因此硼烯有望成为一种性能优异的润滑材料.