摘要: 基于改进的移动最小二乘插值法, 提出了黏弹性问题的插值型无单元Galerkin方法. 采用改进的移动最小二乘插值法建立形函数, 根据黏弹性问题的Galerkin弱形式建立离散方程, 推导了相应的计算公式. 与无单元Galerkin方法相比, 本文提出的黏弹性问题的插值型无单元Galerkin方法具有直接施加本质边界条件的优点. 通过数值算例讨论了影响域、节点数对计算精确性的影响, 说明了该方法具有较好的收敛性; 将计算结果与无单元Galerkin方法和有限元方法或解析解比较, 说明了该方法具有提高计算效率的优点.
关键词: 无网格方法 /
改进的移动最小二乘插值法 /
插值型无单元Galerkin方法 /
黏弹性问题 English Abstract Interpolating element-free Galerkin method for viscoelasticity problems Zhang Peng-Xuan Peng Miao-Juan Department of Civil Engineering, Shanghai University, Shanghai 200444, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11571223)Received Date: 09 July 2019Accepted Date: 31 July 2019Available Online: 01 September 2019Published Online: 05 September 2019Abstract: In this paper, based on the improved interpolating moving least-square (IMLS) approximation, the interpolating element-free Galerkin (IEFG) method for two-dimensional viscoelasticity problems is presented. The shape function constructed by the IMLS approximation can overcome the shortcomings that the shape function of the moving least-squares (MLS) can-not satisfy the property of Kronecker function, so the essential boundary conditions can be directly applied to the IEFG method. Under a similar computational precision, compared with the meshless method based on the MLS approximation, the meshless method using the IMLS approximation has a high computational efficiency. Using the IMLS approximation to form the shape function and adopting the Galerkin weak form of the two-dimensional viscoelasticity problem to obtain the final discretized equation, the formulae for two-dimensional viscoelasticity problem are derived by the IEFG method. The IEFG method has some advantages over the conventional element-free Galerkin (EFG) method, such as the concise formulae and direct application of the essential boundary conditions, For the IEFG method of two-dimensional viscoelasticity problems proposed in this paper, three numerical examples and one engineering example are given. The convergence of the method is analyzed by considering the effects of the scale parameters of influence domains and the node distribution on the computational precision of the solutions. It is shown that when d max = 1.01?2.00, the method in this paper has a good convergence. The numerical results from the IEFG method are compared with those from the EFG method and from the finite element method or analytical solution. We can see that the IEFG method in this paper is effective. The results of the examples show that the IEFG method has the advantage in improving the computational efficiency of the EFG method under a similar computational accuracy. And the engineering example shows that the IEFG method can not only has higher computational precision, but also improve the computational efficiency.Keywords: meshless method /improved interpolating moving least-squares approxiamtion /interpolating element-free Galerkin method /viscoelasticity problem 全文HTML --> --> --> 1.引 言 无网格方法作为一种新的数值方法, 因其只需要节点信息, 从而可以避免网格的划分以及重构[1 ] , 因此具有前处理简单、计算精度高等特点, 已经成为科学和工程计算发展的重要趋势之一. 当前已经发展的无网格方法有无单元Galerkin方法(element-free Galerkin method, EFG)[1 -3 ] 、重构核粒子方法(reproducing kernel particle method, RKPM)[4 -6 ] 、有限点方法(finite point method, FPM)[7 ] 、无网格局部Petrov-Galerkin方法(meshless local Petrov-Galerkin method, MLPG)[8 ] 、单位分解法[9 ,10 ] 、复变量无网格方法[11 -15 ] 、维数分裂无网格方法[16 -19 ] 和无网格的边界积分方程方法[20 -26 ] 等.[20 ] 以及Cheng和Peng[21 ] 提出了改进的移动最小二乘法. 该方法选取正交函数作为基函数, 从而致使法方程既不病态也不会奇异, 同时也不需要求解矩阵的逆, 可以直接得到方程组的解, 降低了计算量. Zhang等[27 -29 ] 采用改进的移动最小二乘法建立形函数, 提出了瞬态热传导、波动方程和弹性动力学等问题改进的无单元Galerkin方法. Cheng和Liew[30 ] 以及Cheng和Wei[31 ] 利用改进的无单元Galerkin方法求解波动方程和广义Camassa-Holm方程. 文献[32 -35 ]建立了三维黏弹性、三维弹塑性和弹塑性大变形等问题改进的无单元Galerkin方法, 并将改进的无单元Galerkin方法用于机场复合道面的断裂力学分析. Wu等[36 ] 建立了弹性力学拓扑优化问题改进的无单元Galerkin方法. Meng等[37 -39 ] 将维数分裂法与改进的无单元Galerkin方法相结合, 提出了三维势问题、瞬态热传导问题和波动方程的杂交无单元Galerkin方法.$\delta $ 函数性质, 使得基于其形成的无网格方法不能直接施加本质边界条件. Lancaster和Salkauskas[40 ] 提出了移动最小二乘插值法, 该方法得到的逼近函数满足Kronecker $\delta $ 函数性质, 从而可以直接施加本质边界条件.[41 ,42 ] 提出了改进的移动最小二乘插值法, 该方法证明了Lancaster的形函数公式中的一些内积可以为零, 可得到更为简单的形函数计算公式, 从而减少了方程个数以及未知量个数, 提高了计算效率. Ren和Cheng [41 ,42 ] 基于改进的移动最小二乘插值法, 建立了势问题和弹性力学的插值型无单元Galerkin方法(interpolating element-free Galerkin method, IEFG). Cheng等[43 ,44 ] 建立了弹塑性和非线性大变形等问题的插值型无单元Galerkin方法. Deng等[45 ] 建立温度场问题的插值型复变量无单元Galerkin方法.[46 ] 和Sun等[47 ,48 ] 提出了基于非奇异权函数改进的移动最小二乘插值法, 建立了势问题、弹性问题和弹塑性问题改进的插值型无单元Galerkin方法. 该方法形函数的待定系数比传统的移动最小二乘法少一个, 求逆矩阵的阶数比移动最小二乘法少一阶, 提高了计算效率和计算精度. 基于非奇异权函数改进的移动最小二乘插值法, Wang等[49 ,50 ] 研究了两点边值问题改进的插值型无单元Galerkin方法的误差估计和插值型移动最小二乘法的误差估计. Sun等[51 ] 分析了在n 维空间的插值型移动最小二乘法的误差估计. Liu等[52 -54 ] 建立了弹性大变形、弹塑性大变形和凝胶非均匀溶胀大变形等问题改进的插值型无单元Galerkin方法.[55 ] 把无单元Galerkin方法和时域精细算法结合, 用于求解黏弹性问题. Canelas和Sensale[56 ] 运用无网格边界节点法分析了弹性和黏弹性材料中的简谐波问题. 彭妙娟和程玉民等建立了改进的无单元Galerkin方法[32 ] 、黏弹性问题复变量无单元Galerkin方法[57 ] 和改进的复变量无单元Galerkin方法[58 ] .2.改进的移动最小二乘插值法 对于改进的移动最小二乘插值法[41 ,42 ] , 定义奇异权函数$\alpha $ 是正整数, ${\rho _I}$ 是影响域${{{x}}_I}$ 的影响半径.$f({{x}})$ 和$g({{x}})$ 的内积为$\bar \varOmega = \varOmega \cup \partial \varOmega $ , ${C^0}(\bar \varOmega )$ 是$\bar \varOmega $ 域中所有连续函数的集合, $n$ 是影响域覆盖场点$x$ 的节点数. 这样可得${p_i}({{x}})$ 做标准化处理. 在空间${\rm{span}} ({p_1},{p_2}, \ldots,{p_m})$ 中, 在${{x}}$ 点将基函数${p_1}({{x}}) \equiv 1$ 单位化,${p_2}({{x}}),{p_3}({{x}}), \ldots,{p_m}({{x}})$ 与${q_1}({{x}})$ 正交化, 可得${q_i}({{x}})$ 应用于移动最小二乘法可得10 )式代入(6 )式可得16 )式可以写成$\delta $ 函数性质, 因此在建立离散方程时, 可以直接施加本质边界条件, 从而减少了计算时间, 提高了计算效率.3.黏弹性问题的基本方程 黏弹性问题的应力-应变关系与时间相关, 其材料参数是时间的函数. 假定${{\sigma }}(t)$ 在整个加载过程中恒定, 然而${{\varepsilon}} ({{t}})$ 和位移${{u}} ({{t}})$ 随着时间变化. 如果给定求解域$\varOmega $ 内的体力${{b}}$ , 应力边界${\varGamma _t}$ 上的面力${\bar {{t}}}$ 及位移边界${\varGamma _u}$ 上的位移${\bar {{u}}}$ (边界条件与时间无关), 下面给出二维黏弹性问题的基本方程和边界条件.${{L}}$ 是微分算子矩阵${{\sigma}} $ 是域内任意一点的应力${{b}}$ 是域内任意一点的体力${{\varepsilon}} $ 和${{u}}$ 分别为域内任意点的应变和位移,$J(t)$ 为不同流变模型的蠕变柔量, 对Maxwell模型,$G$ , ${G_{\rm{1}}}$ 和${G_{\rm{2}}}$ 分别是各模型中弹簧的剪切弹性模量, $\eta $ 是各模型中黏壶的黏性系数, $K$ 为体积弹性模量.${n_{\rm{1}}}$ 和${n_{\rm{2}}}$ 是边界点的外法线方向余弦.4.黏弹性问题的插值型无单元Galerkin方法 设问题求解域$\varOmega $ 内配有$M$ 个节点, 节点的影响域${\varOmega _I}$ ($I = 1, 2, \cdots, M$ )的并集覆盖了整个域$\varOmega $ . 由改进的移动最小二乘插值法, 位移向量36 )式可以写为${\sigma _{33}} = 0$ , 可得${\beta _1}$ 和${\beta _2}$ 是常数,53 )式可写为${\varepsilon _{{\rm{33}}}} = {\rm{0}}$ , 可得49 )式和(50 )式代入(48 )式得到44 )式和(61 )式代入(35 )式得到$\delta {{{U}}^{\rm{T}}}$ 的任意性, 得到最后的离散系统方程为63 )式中, 对于平面应力问题,5.数值算例 为了验证上述理论的准确性, 以下通过该方法对4个算例进行了计算, 并将计算结果与无单元Galerkin方法以及有限元方法的计算结果或解析解进行对比. 在算例中, 构造移动最小二乘插值法的形函数采用线性基函数和奇异权函数. 在每个积分单元, 采用$4 \times 4$ 的Gauss积分.${L^2}$ 范数定义为$u_k^I$ 为第$I$ 种节点分布时变量$u$ 在节点${x_k}$ 处的数值解, $\bar u_k^{IJ}$ 为第$I$ 种和$J$ 种节点分布时变量$u$ 在节点${x_k}$ 处数值解的平均值.算例1 受均布荷载的悬臂梁图1 所示的受均布荷载作用的悬臂梁, 梁长$L = {\rm{8\;}}{\rm{m}}$ , 梁高$D = {\rm{2\;}}{\rm{m}}$ , 取单位厚度, 按平面应力计算. 材料体积变化是弹性的, $E = 1.0 \times 1{0^8}\; {\rm{Pa}}$ , $v = 0.25$ , 剪切变形流变性质满足Kelvin黏弹性模型, 其参数为$G = 2.0 \times 1{0^8} \;{\rm{Pa}}$ , $\eta = 6.0 \times 1{0^8} \;{\rm{Pa}} \cdot {\rm{s}}$ , 均布荷载为$p = 3.0 \times 1{0^4} \;{\rm{Pa}}$ , 不计自重.图 1 受均布荷载的悬臂梁Figure1. A cantilever beam subjected to a distributed loading$17 \times 9$ , $21 \times $ 11, $29 \times 11$ , $33 \times 11$ , $33 \times 13$ , $37 \times 17$ , 图2 给出了不同节点分布下有限元法解的方差. 从图2 可以看出, 节点分布越密方差越小, 说明有限元法得到的解是收敛的. 在此选用$33 \times 13$ 的节点布置.图 2 不同节点分布下有限元法解的方差Figure2. The variances of the solutions of FEM under different node distributions.$9 \times 3$ , $11 \times 4$ , $13 \times 5$ , $15 \times 6$ , $17 \times 7$ 和$19 \times 8$ 的情况下, 利用本文提出的插值型无单元Galerkin方法计算, 图3 给出了不同节点分布下数值解的相对误差. 从图3 可以看出, 节点分布越密相对误差越小, 即插值型无单元Galerkin方法具有较好的收敛性. 在考虑计算效率的情况下, 采用图4 所示的$17 \times 7$ 节点布置, 背景积分网格选取$16 \times 6$ .图 3 不同节点分布下的相对误差Figure3. The relative error under different node distributions.图 4 节点布置Figure4. Node distribution.图5 所示, 当${d_{{\rm{max}}}} = $ 1.7—1.9时, 该方法数值解的精度较高. 本算例选用${d_{{\rm{max}}}} = 1.7$ .图 5 不同影响域比例参数下的相对误差Figure5. The relative error for different scale parameters of influence domains.$17 \times 7$ , 背景积分网格选取$16 \times 6$ , ${d_{{\rm{max}}}} = 1.7$ , 此时中轴线各点挠度和右端中点挠度随时间变化的总相对误差为$1.29\% $ , 计算时间为31.19 s.$17 \times 7$ , 背景积分网格选取$16 \times 6$ , ${d_{{\rm{max}}}} = 3.0$ , $\alpha = 2.3 \times 1{0^{10}}$ , 从而可以得到与插值型无单元Galerkin方法相近的计算精度, 计算时间为34.67 s.图6 和图7 所示, 可以看出, 两种方法得到的数值解与有限元法的数值解较为符合, 但插值型无单元Galerkin方法能够提高计算效率.图 6 $t = 20 \;{\rm{s}}$ 时悬臂梁中轴线上各点的挠度Figure6. Vertical displacements of nodes on the neutral axis of the beam when $t = 20 \;{\rm{s}}$ .图 7 梁右端中点的挠度随时间的变化Figure7. Time history of vertical displacement of midpoint in the right end of the beam.算例2 受纯弯曲的梁图8 为受纯弯曲的梁, 几何参数为$L = 5\;{\rm{m}}$ , $H = 2\;{\rm{m}}$ , 单位厚度. 材料体积变化是弹性的, $E = 1.0 \times 1{0^6}\; {\rm{Pa}}$ , $\nu = 0.3$ , 剪切变形的流变性质满足三参数模型, 其参数为${G_1} = 5.0 \times 1{0^5}\; {\rm{Pa}}$ , G 2 = $ 1.0 \times 1{0^6} \;{\rm{Pa}}$ 和$\eta = 2.0 \times 1{0^6} \;{\rm{Pa}} \cdot {\rm{s}}$ . 其所受三角形分布荷载大小如图8 所示, 不计体力, 按平面应力问题计算.图 8 纯弯曲的梁Figure8. A beam subjected to simple bending${x_{\rm{1}}}$ 轴和${x_{\rm{2}}}$ 轴上, 位移${u_{\rm{1}}}$ 均为0, 为了消除结构在${x_{\rm{2}}}$ 方向上刚体位移, 可令原点处${u_{\rm{2}}}$ 为0. 有限元法采用四边形4节点单元, 节点布置为$21 \times 13$ . 无单元Galerkin方法和插值型无单元Galerkin方法均采用图9 所示的$15 \times 7$ 的节点布置, 背景积分网格选取$14 \times 6$ .图 9 节点分布Figure9. Node distribution.${d_{{\rm{max}}}} = 2.0$ , 此时中轴线各点挠度和右端中点挠度随时间变化的总相对误差为$0.30\% $ , 计算时间为21.88 s.${d_{{\rm{max}}}} = 3.0$ , $\alpha = 1.5 \times 1{0^8}$ , 从而可以得到与插值型无单元Galerkin方法相近的计算精度, 计算时间为28.76 s.图10 和图11 所示. 可以看出, 插值型无单元Galerkin方法和无单元Galerkin方法都可以达到较高的精度, 但插值型无单元Galerkin方法能够提高计算效率.图 10 $t = 30 \;{\rm{s}}$ 时梁中轴线上的节点挠度Figure10. Vertical displacements of nodes on the neutral axis of the beam when $t = 30 \;{\rm{s}}$ .图 11 梁右端中点的挠度随时间$t$ 的变化Figure11. Time history of vertical displacement of midpoint in the right end of the beam.算例3 受均布内压的圆环图12 所示, 其内表面承受均匀分布的压力$p = 30 \;{\rm{kPa}}$ . 几何参数为$a = 1\;{\rm{m}}$ , $b = 5\;{\rm{m}}$ . 材料体积变化是弹性的, $E = 1.0 \times 1{0^7}\; {\rm{Pa}}$ , $\nu = 0.25$ , 剪切变形的流变性质采用Kelvin模型. 其参数为$G = 5.0 \times 1{0^5}\; {\rm{Pa}}$ , $\eta = 2.0 \times 1{0^6} \;{\rm{Pa}} \cdot {\rm{s}}$ . 不计体力, 按平面应变问题计算.图 12 受均布内压的厚壁圆筒Figure12. Circular ring under a distributed inner pressure70 )式表明Kelvin模型加载瞬时位移为零, 当时间足够长, 位移将趋于稳定.图13 , 由于对称性, 只取1/4区域为研究对象. 无单元Galerkin方法和插值型无单元Galerkin方法均选用如图14 所示的${\rm{1}}7 \times 12$ 的节点布置, 背景积分网格选取$16 \times 11$ .图 13 受均布内压1/4圆筒Figure13. A quarter of the circular ring under a distributed inner pressure图 14 1/4圆筒的节点分布Figure14. Node distribution of a quarter of the circular ring.${d_{{\rm{max}}}} = 1.01$ , 此时$t = 30 \;{\rm{s}}$ 时沿${x_2} = {\rm{0}}$ 线上节点的位移和点$(2,0)$ 的径向位移随时间变化的总相对误差为$1.10\% $ , 计算时间为23.38 s.${d_{{\rm{max}}}} = 1.5$ , $\alpha = 8.0 \times 1{0^7}$ , 此时可得到与上述插值型无单元Galerkin方法相近的相对误差, 计算时间为28.66 s.图15 和图16 所示. 从以上分析和图15 和图16 的对比可看出, 插值型无单元Galerkin方法和无单元Galerkin方法的数值解均与解析解符合得较好, 但插值型无单元Galerkin方法能够提高计算效率.图 15 $t = 30 \;{\rm{s}}$ 时沿${x_2} = {\rm{0}}$ 线上节点的位移Figure15. Radial displacements at${x_2} = {\rm{0}}$ when $t = 30 \;{\rm{s}}$ .图 16 点$(2,0)$ 的径向位移随时间$t$ 的变化Figure16. Time history of radial displacement at point $(2,0)$ .算例4 工程算例: 受静水压力的混凝土水坝图17 所示. 坝高100 m, 上游水位90 m, 下游无水. 坝底部完全固定, 仅考虑坝体受到的上游水荷载. 坝体材料为混凝土, 所以需要考虑建造完工后期混凝土的流变效应. 假定混凝土材料体积变化是弹性的, $E = 2.0 \times 1{0^{10}}\; {\rm{Pa}}$ , $\nu = 0.2$ , 混凝土的早期流变性质满足三参数模型, 其参数为${G_1} = 8.33 \times 1{0^9}\; {\rm{Pa}}$ , ${G_2} = 4.0 \times 1{0^{10}}\; {\rm{Pa}}$ 和$\eta = 8.0 \times $ $ 10^{16} \;{\rm{Pa}} \cdot {\rm{s}}$ . 不计体力, 按平面应变问题计算.图 17 受静水压力的混凝土水坝Figure17. A concrete dam under hydrostatic pressure.图18 所示的255个节点, 背景积分网格选取231个.图 18 混凝土水坝的节点分布Figure18. Node distribution of a concrete dam.${d_{{\rm{max}}}} = 1.2$ , $t = 500$ d时沿${x_1} = 15$ 方向上节点的水平位移和点$(15, 50)$ 的水平位移与时间关系的总相对误差为$0.27\% $ , 计算时间为50.42 s.${d_{{\rm{max}}}} = 3.0$ , $\alpha = 2.0 \times 1{0^{12}}$ , 其总相对误差为$1.36\% $ , 计算时间为94.44 s.图19 和图20 所示. 从以上分析和图19 和图20 的对比可以看出, 与无单元Galerkin方法相比, 插值型无单元Galerkin方法具有更高的精度和效率, 说明该方法在解决复杂工程问题时能够提高计算精度和计算效率.图 19 $t = 500$ d时沿${x_1} = 15$ 方向上节点的水平位移Figure19. Horizontal displacements at ${x_1} = 15$ when $t = 500\; {\rm d}$ .图 20 混凝土坝上点$(15, 50)$ 的水平位移与时间的关系Figure20. Time history of horizontal displacement of the point $(15, 50)$ .6.结 论 本文基于改进的移动最小二乘插值法构造形函数, 建立了黏弹性问题的插值型无单元Galerkin方法. 由于改进的移动最小二乘插值法的形函数满足Kronecker$\delta $ 函数性质, 避免了传统无单元Galerkin方法要利用Lagrange乘子法或者罚函数法来施加本质边界条件, 大大减少了计算量, 从而有效地提高了在求解黏弹性问题时的计算效率. 通过数值算例讨论了影响域大小、节点数对计算精确性的影响, 说明了该方法具有较好的收敛性; 将计算结果和有限元解或解析解进行对比, 说明了插值型无单元Galerkin方法较无单元Galerkin方法在求解黏弹性问题上具有提高计算效率的优点. 















































































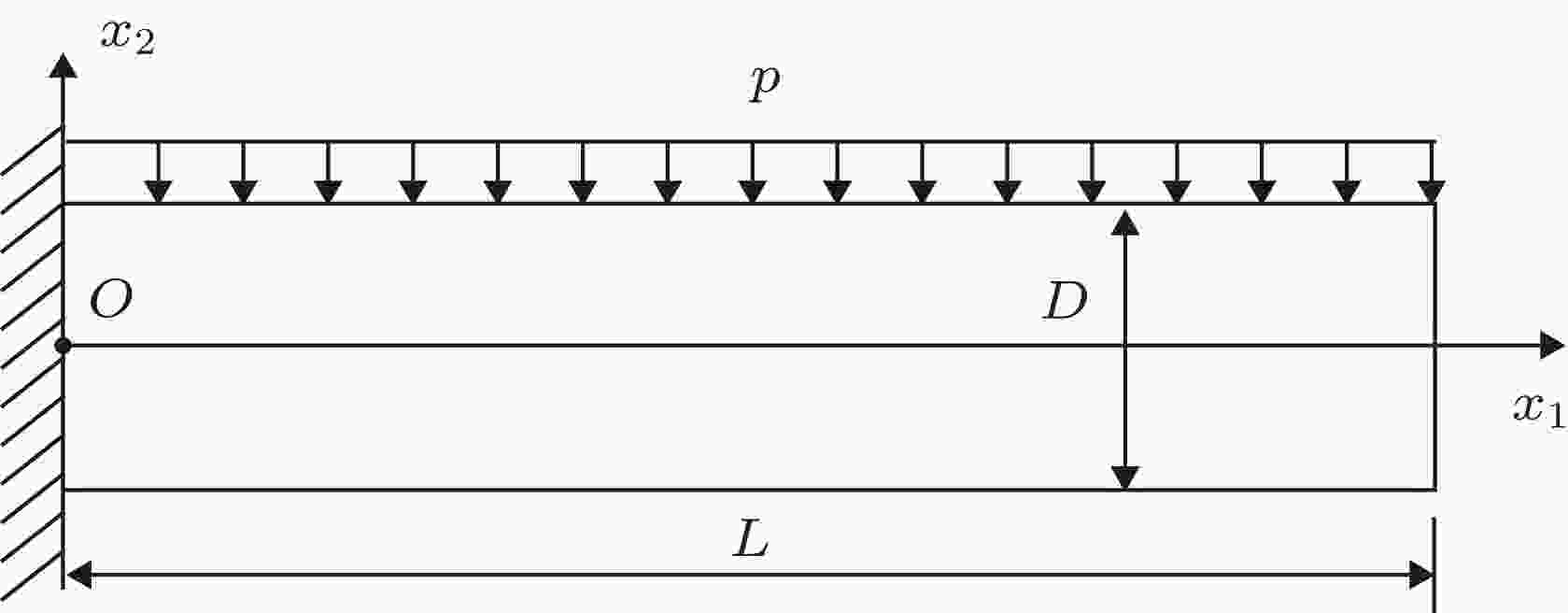 图 1 受均布荷载的悬臂梁
图 1 受均布荷载的悬臂梁








 图 2 不同节点分布下有限元法解的方差
图 2 不同节点分布下有限元法解的方差









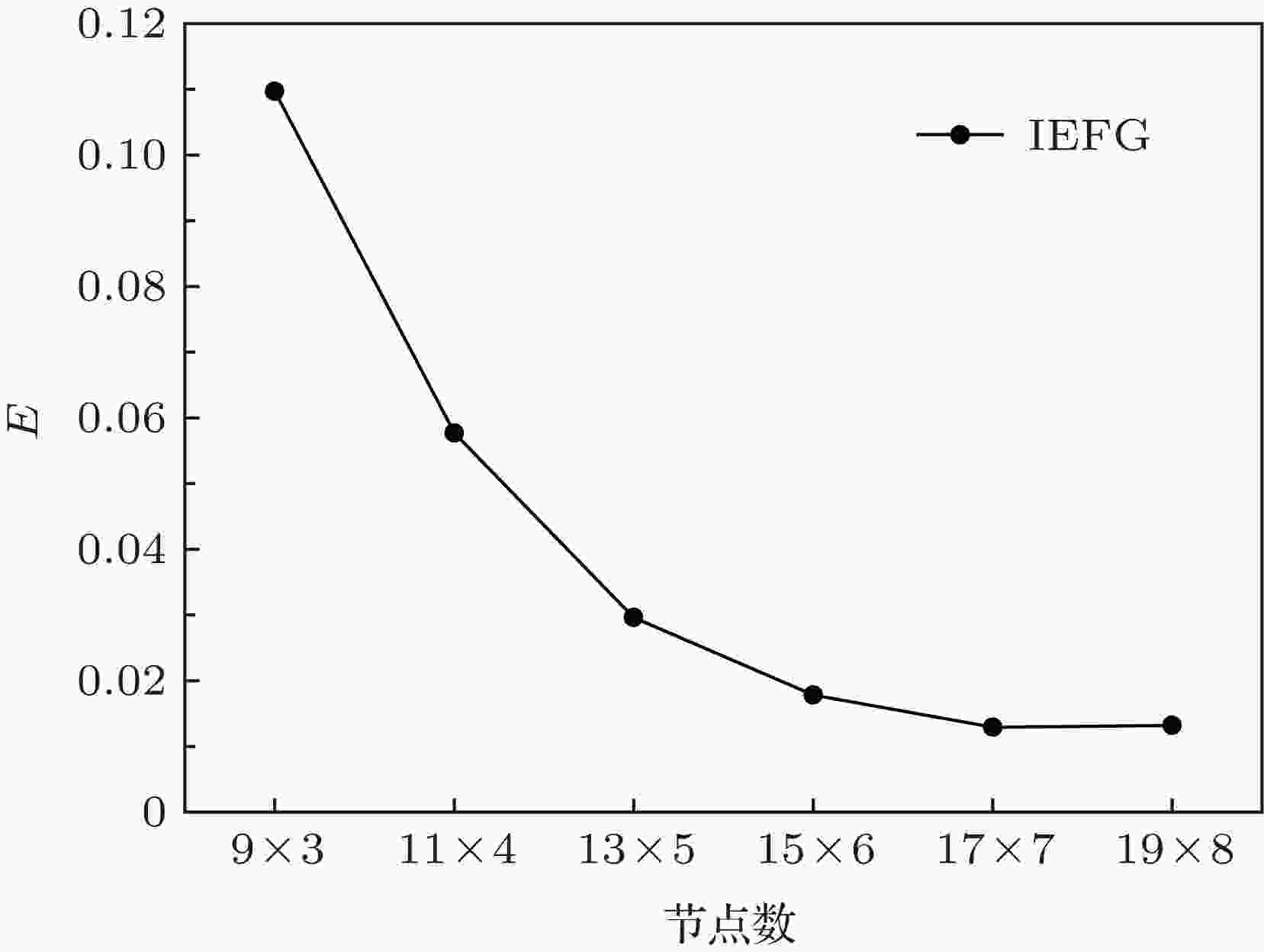 图 3 不同节点分布下的相对误差
图 3 不同节点分布下的相对误差 图 4 节点布置
图 4 节点布置

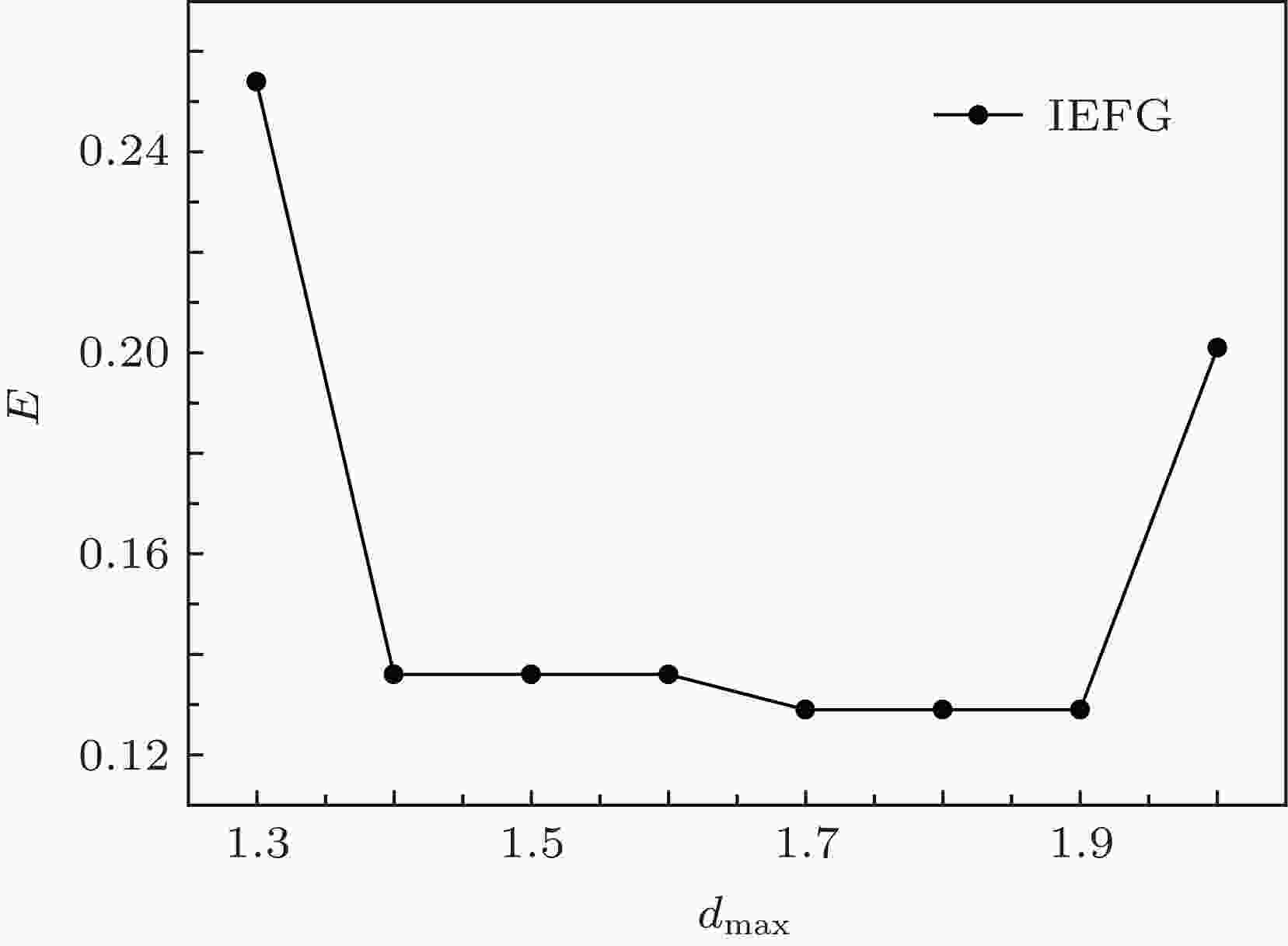 图 5 不同影响域比例参数下的相对误差
图 5 不同影响域比例参数下的相对误差







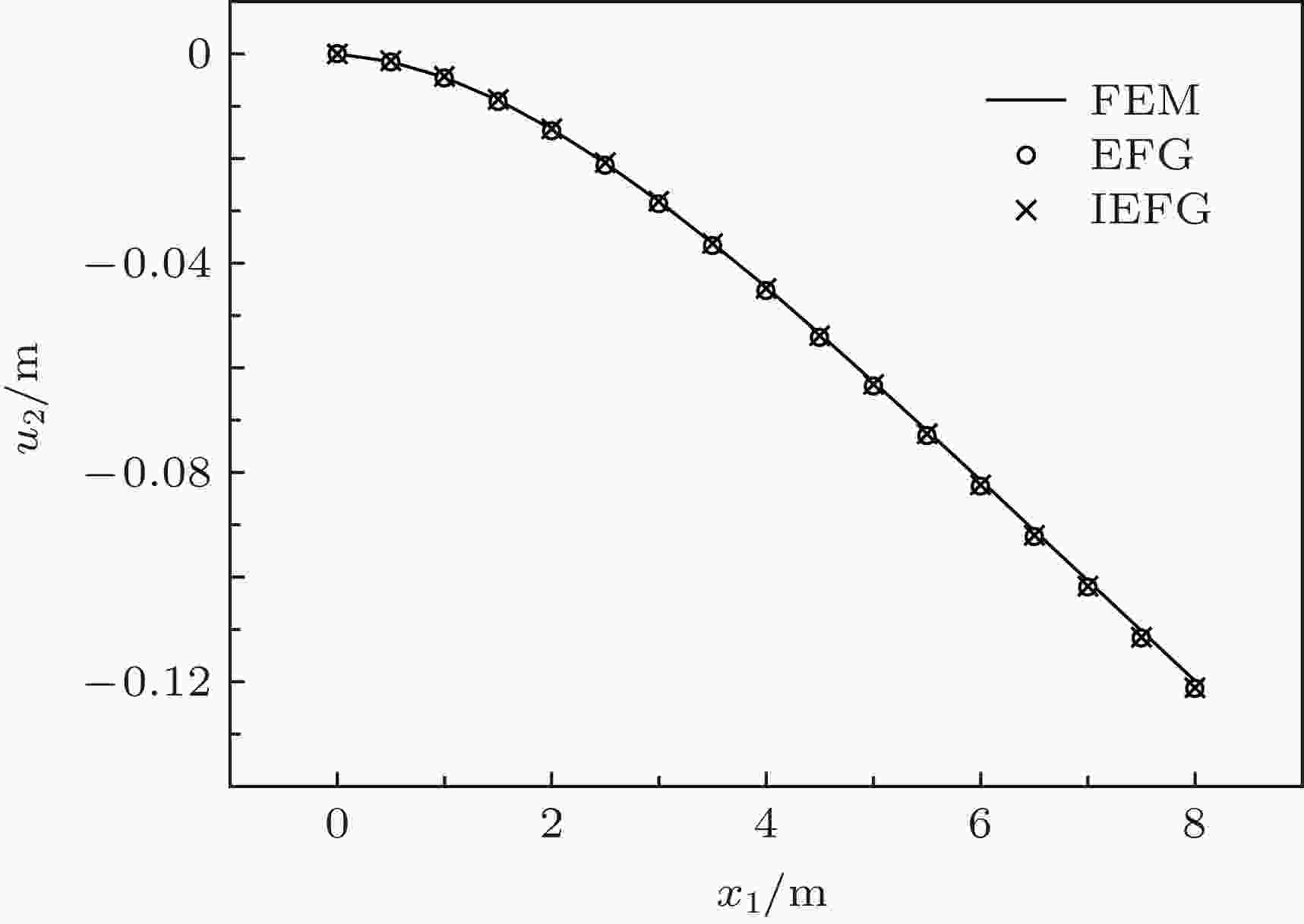 图 6
图 6 

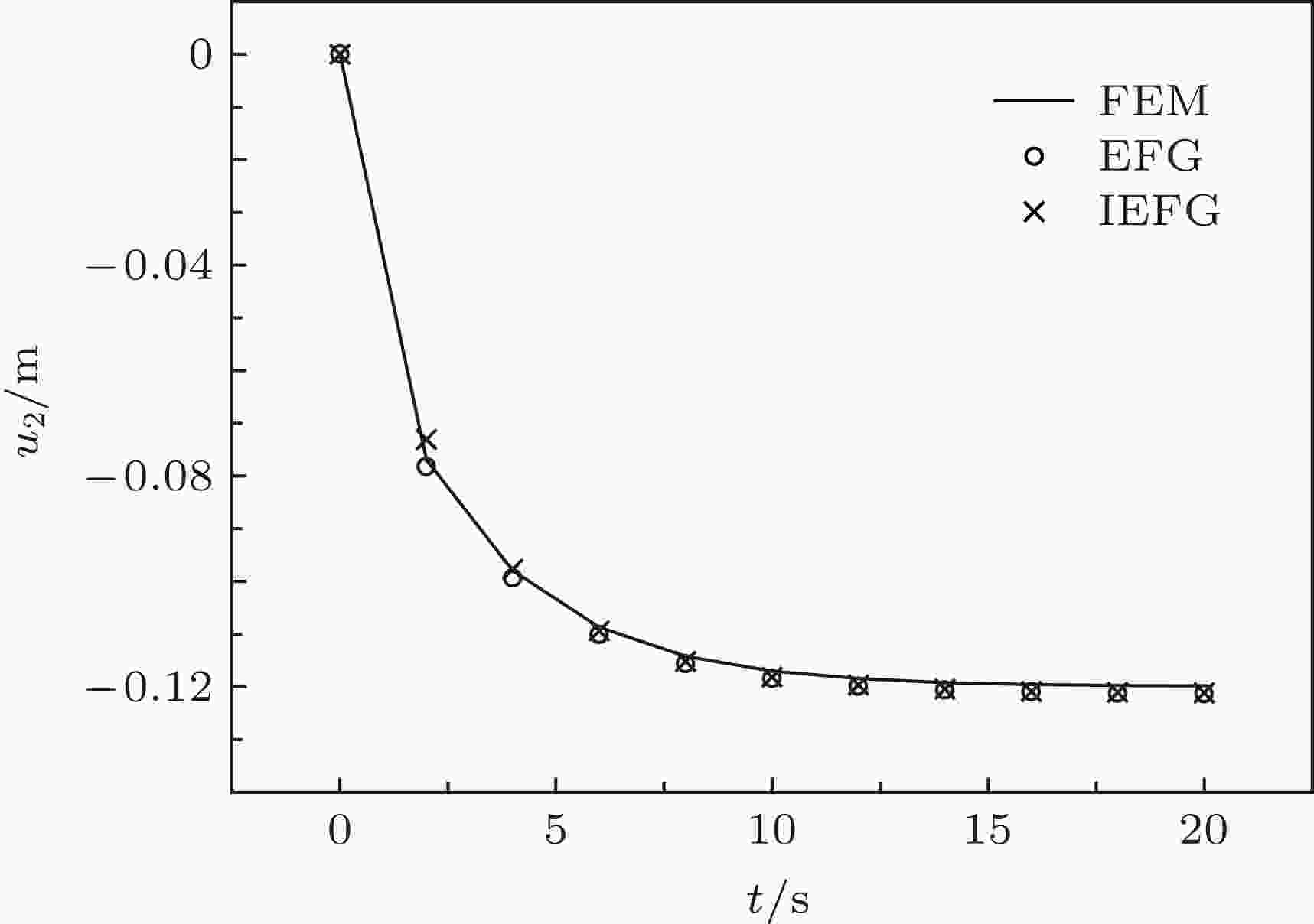 图 7 梁右端中点的挠度随时间的变化
图 7 梁右端中点的挠度随时间的变化






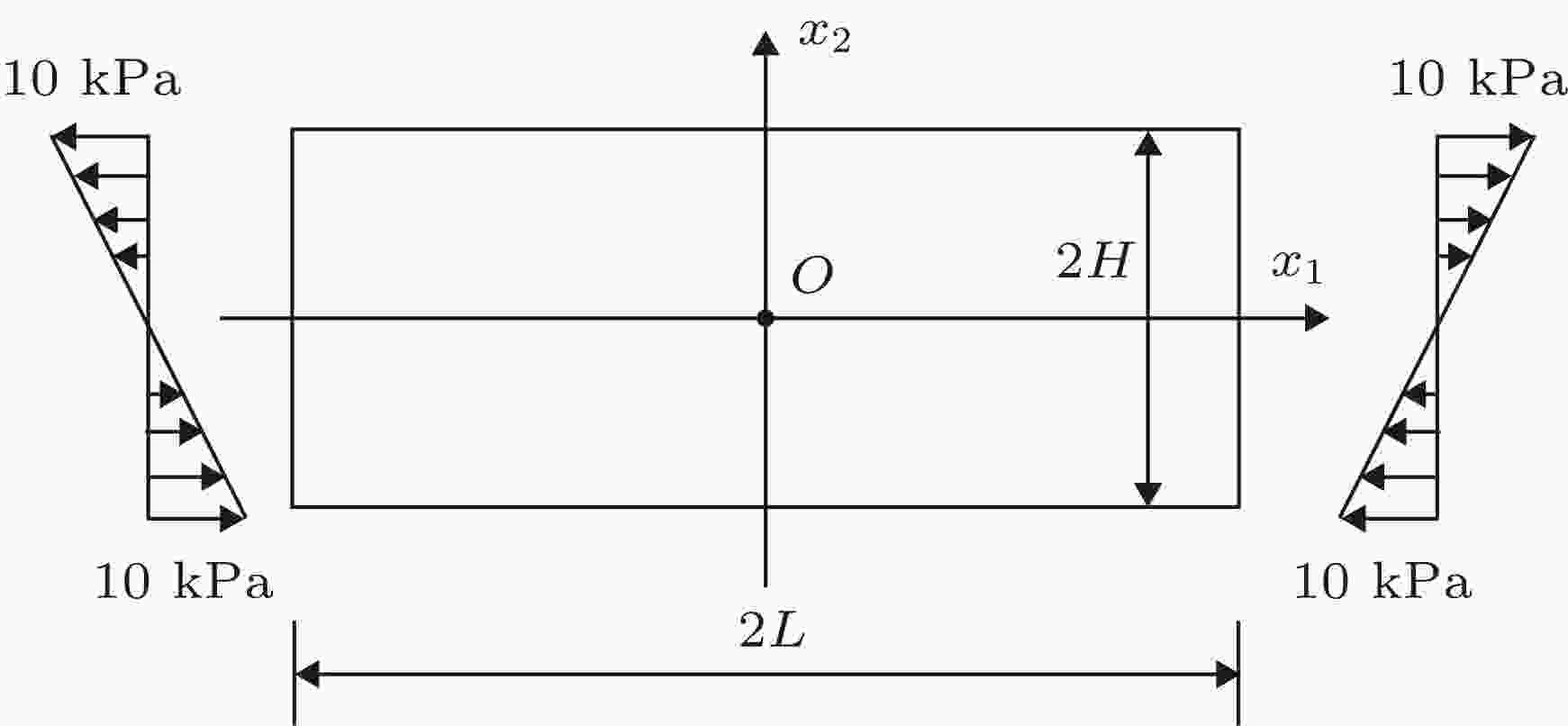 图 8 纯弯曲的梁
图 8 纯弯曲的梁









 图 9 节点分布
图 9 节点分布



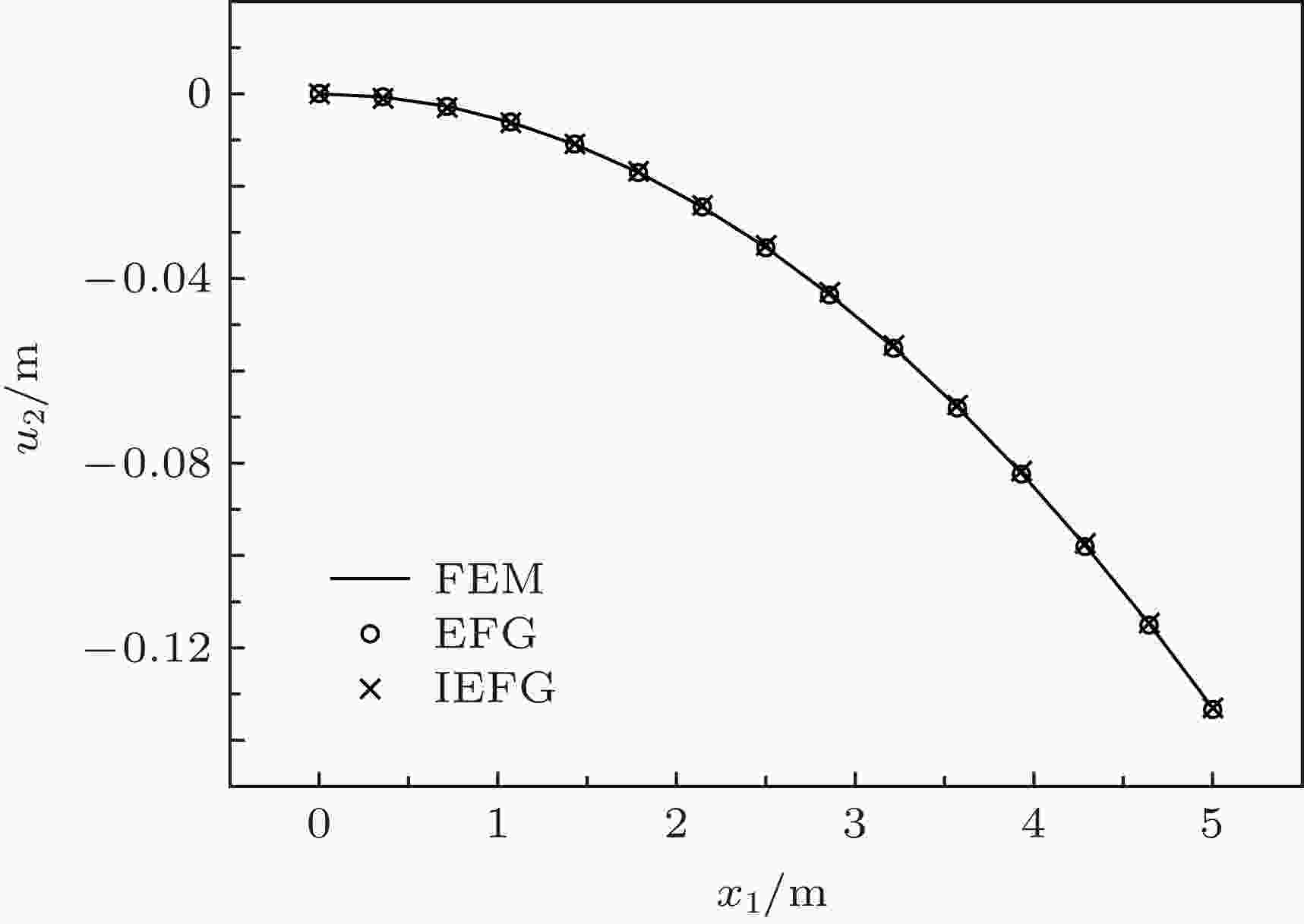 图 10
图 10 

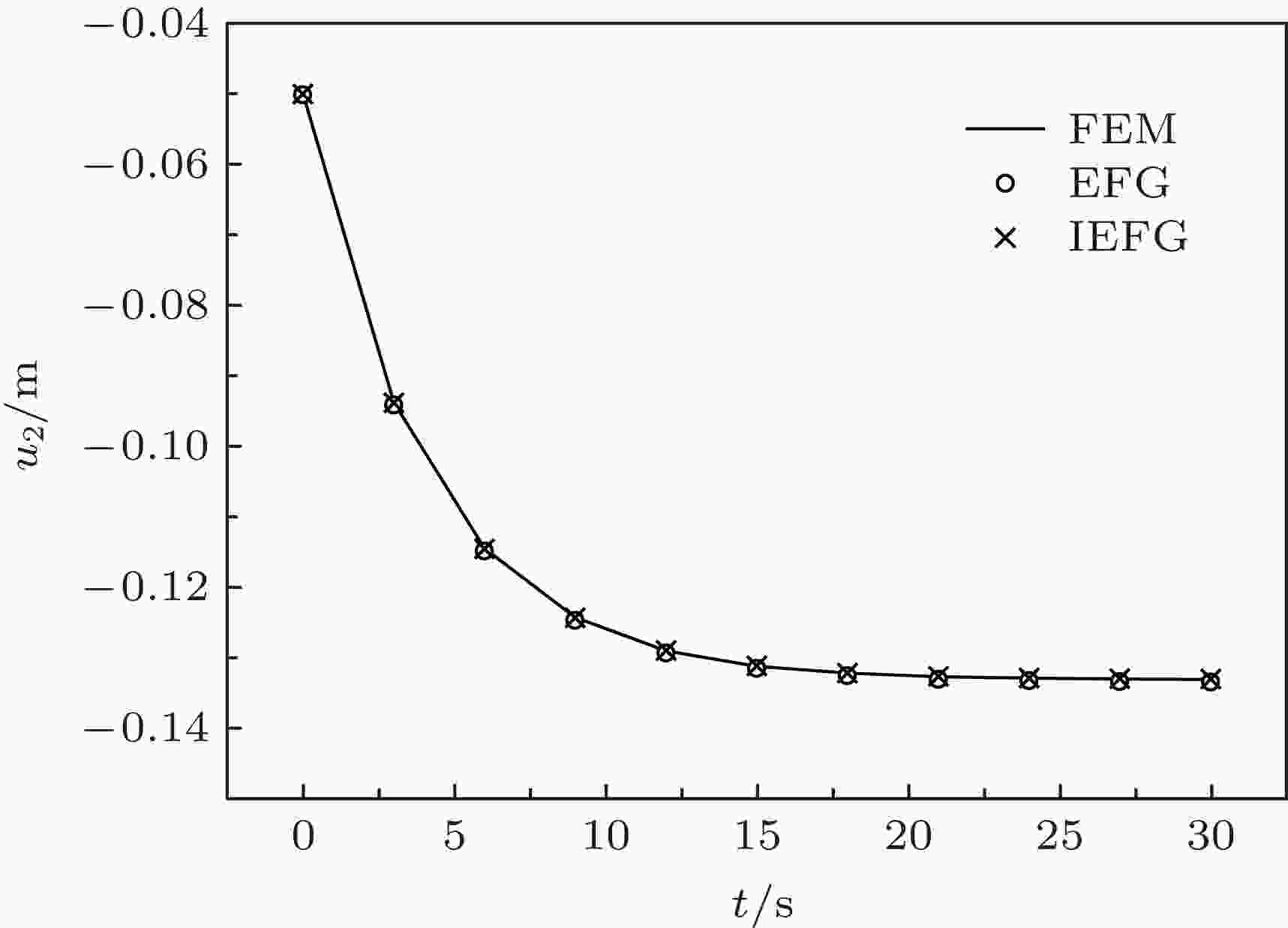 图 11 梁右端中点的挠度随时间
图 11 梁右端中点的挠度随时间







 图 12 受均布内压的厚壁圆筒
图 12 受均布内压的厚壁圆筒

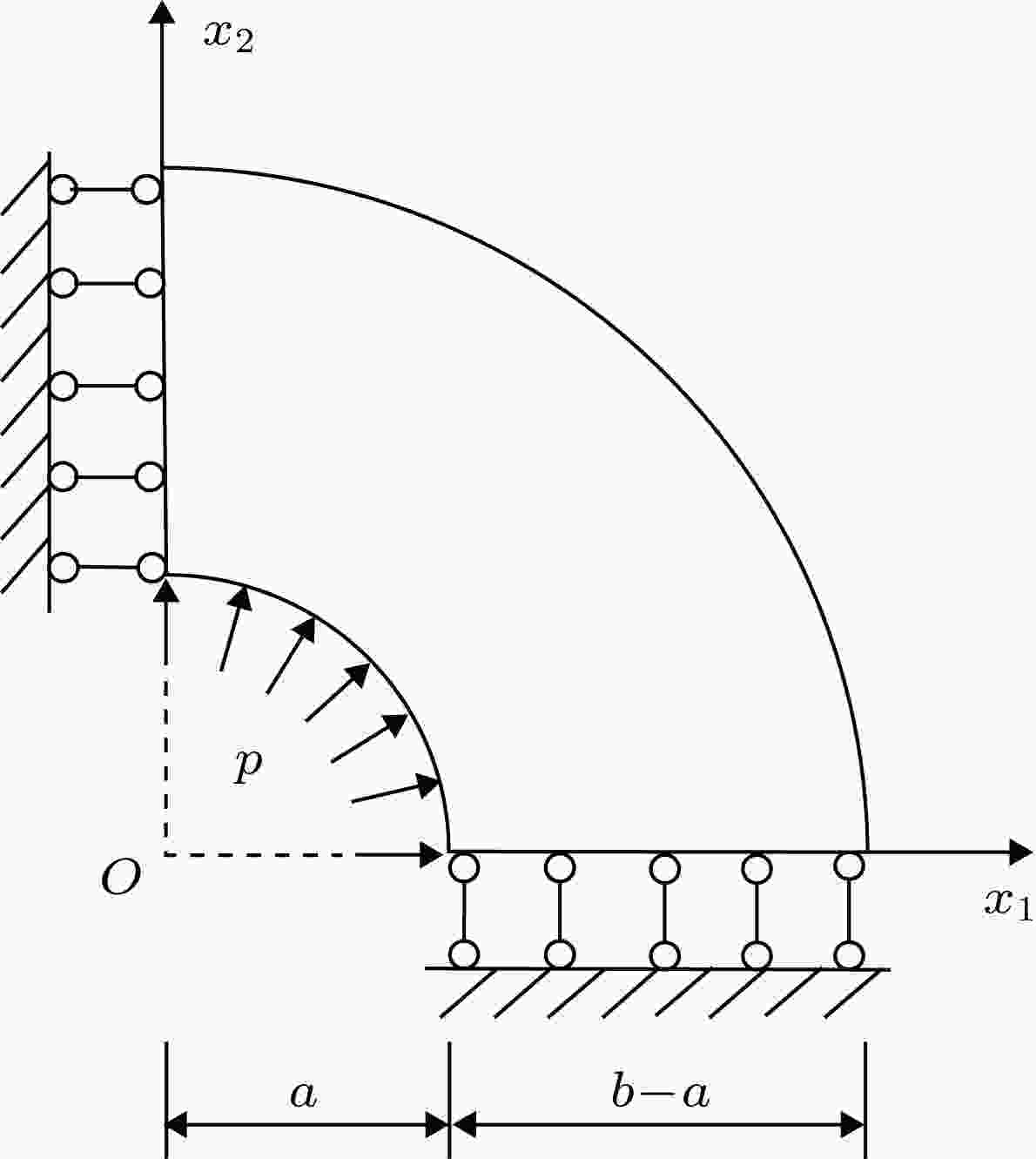 图 13 受均布内压1/4圆筒
图 13 受均布内压1/4圆筒 图 14 1/4圆筒的节点分布
图 14 1/4圆筒的节点分布






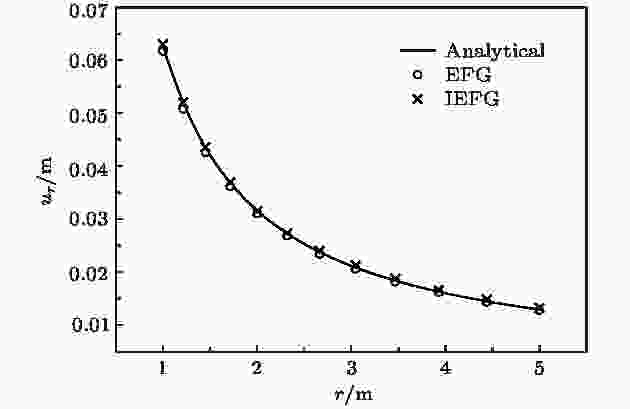 图 15
图 15 



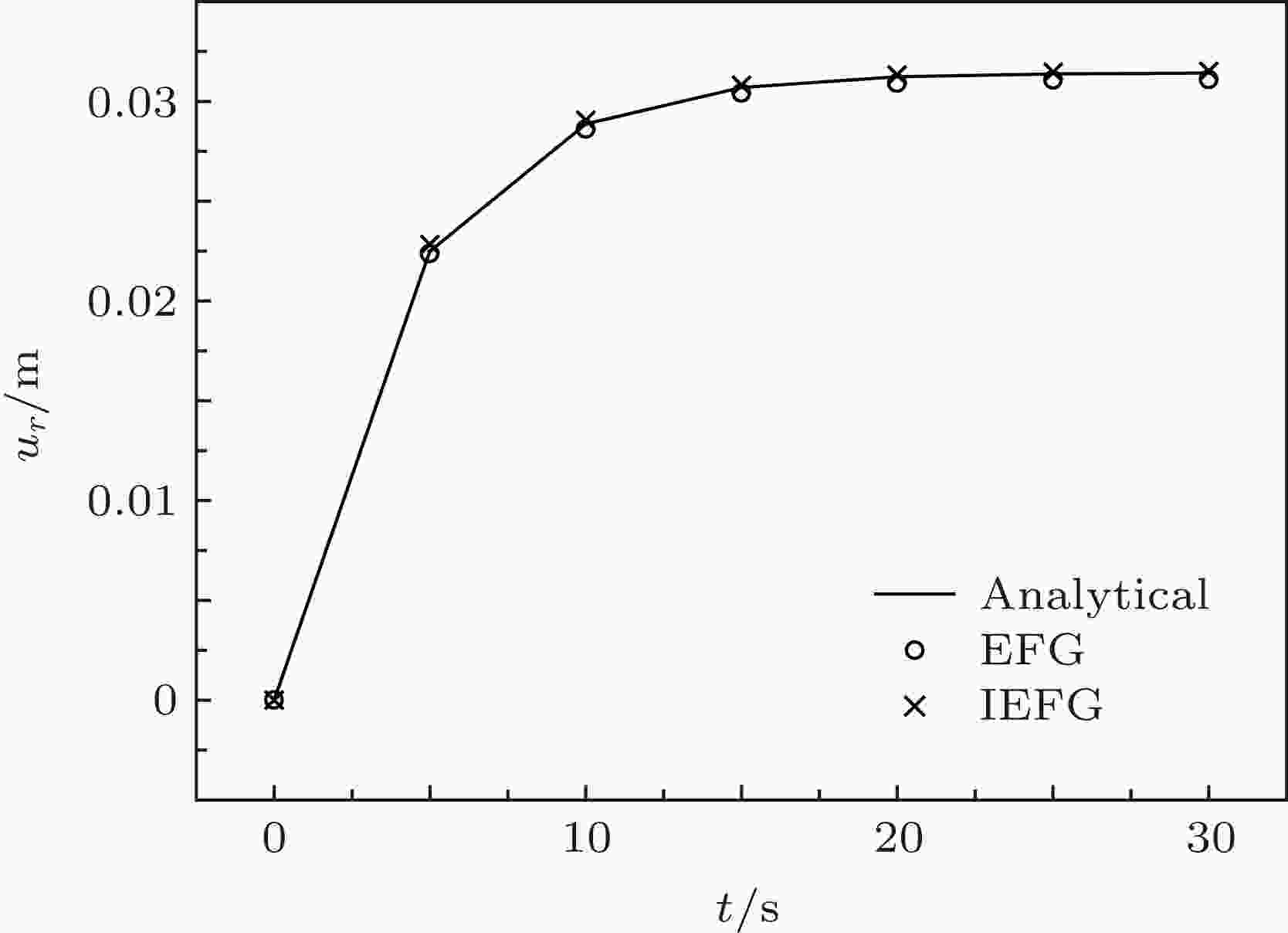 图 16 点
图 16 点








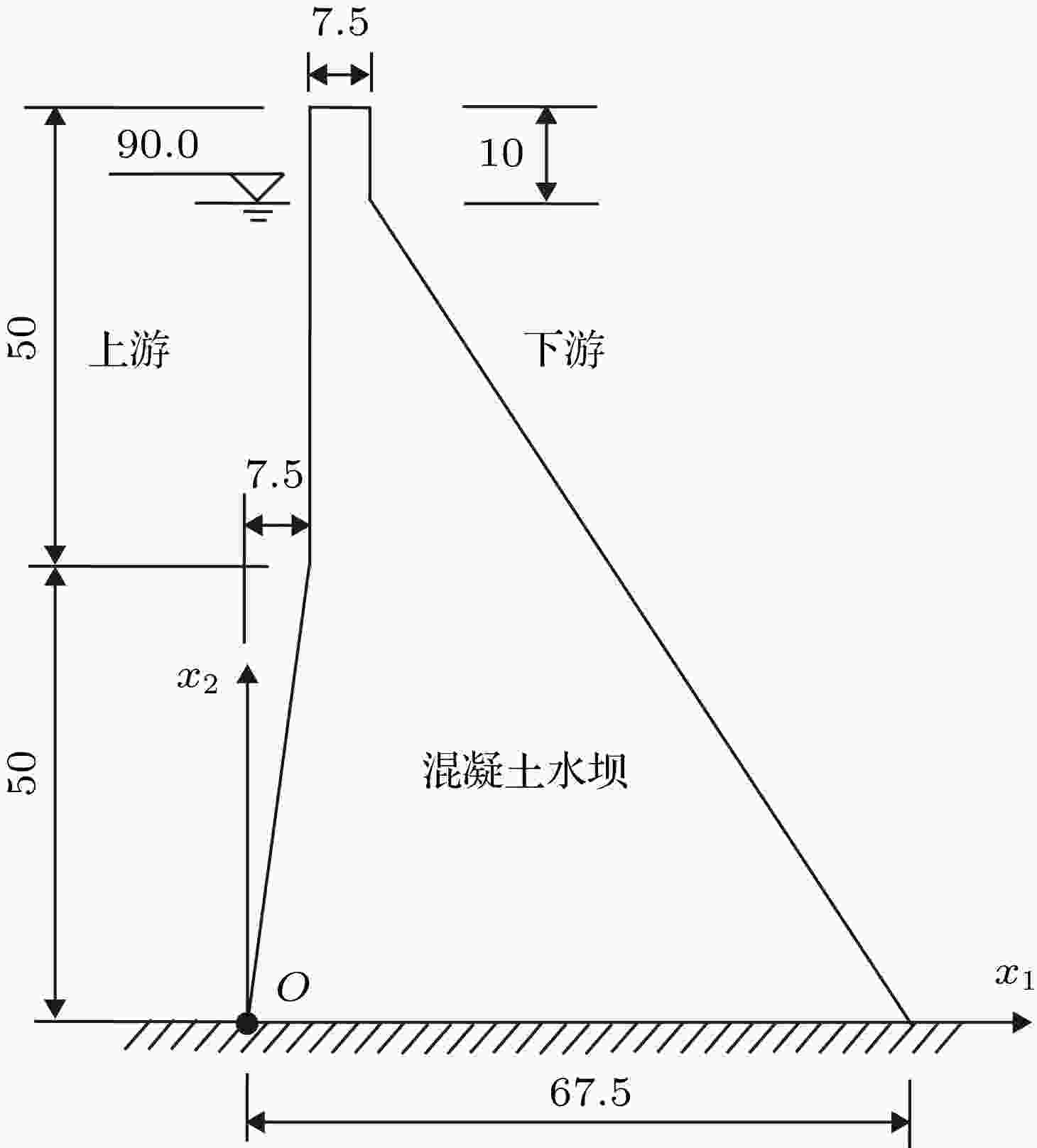 图 17 受静水压力的混凝土水坝
图 17 受静水压力的混凝土水坝 图 18 混凝土水坝的节点分布
图 18 混凝土水坝的节点分布







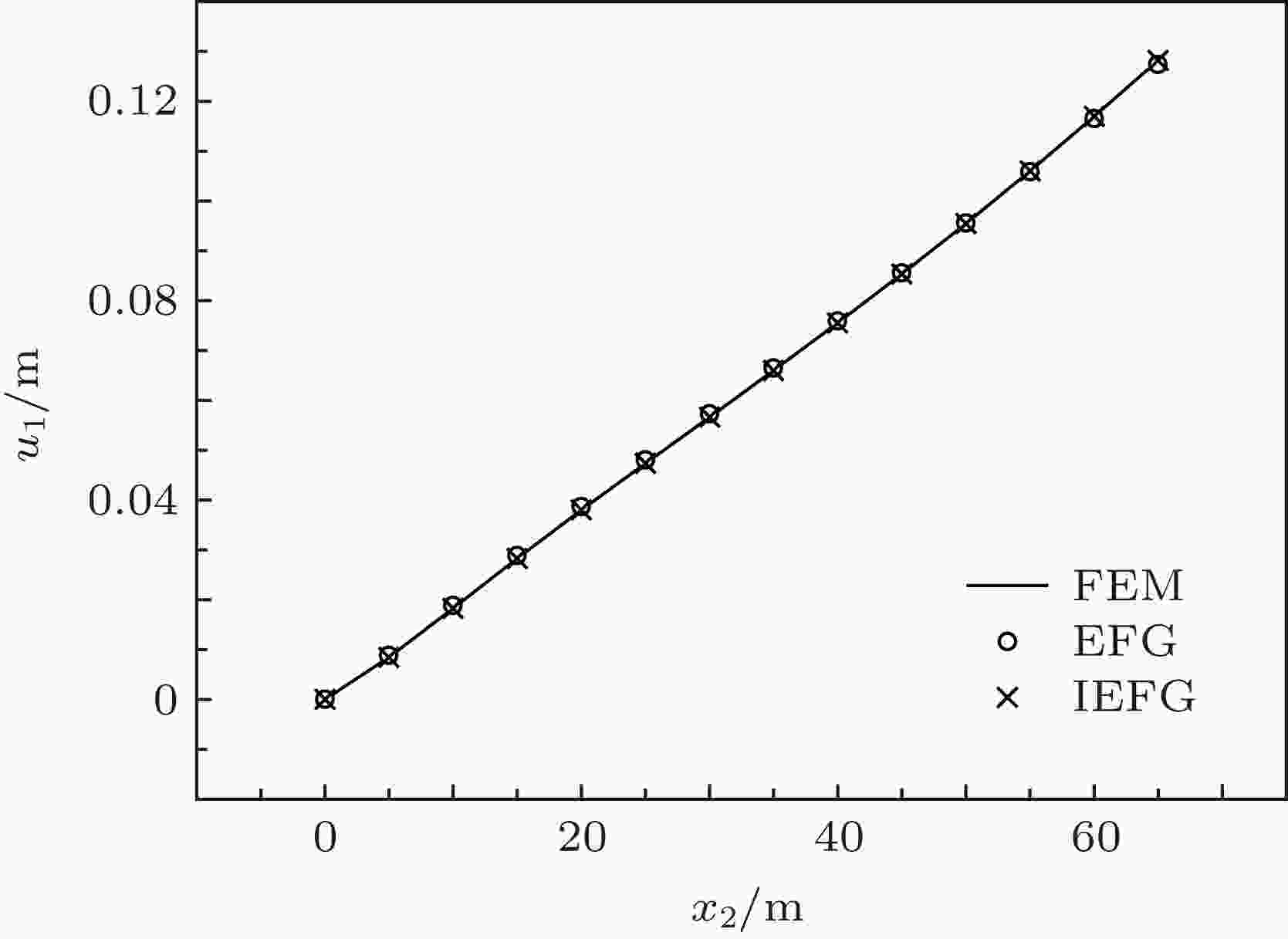 图 19
图 19 



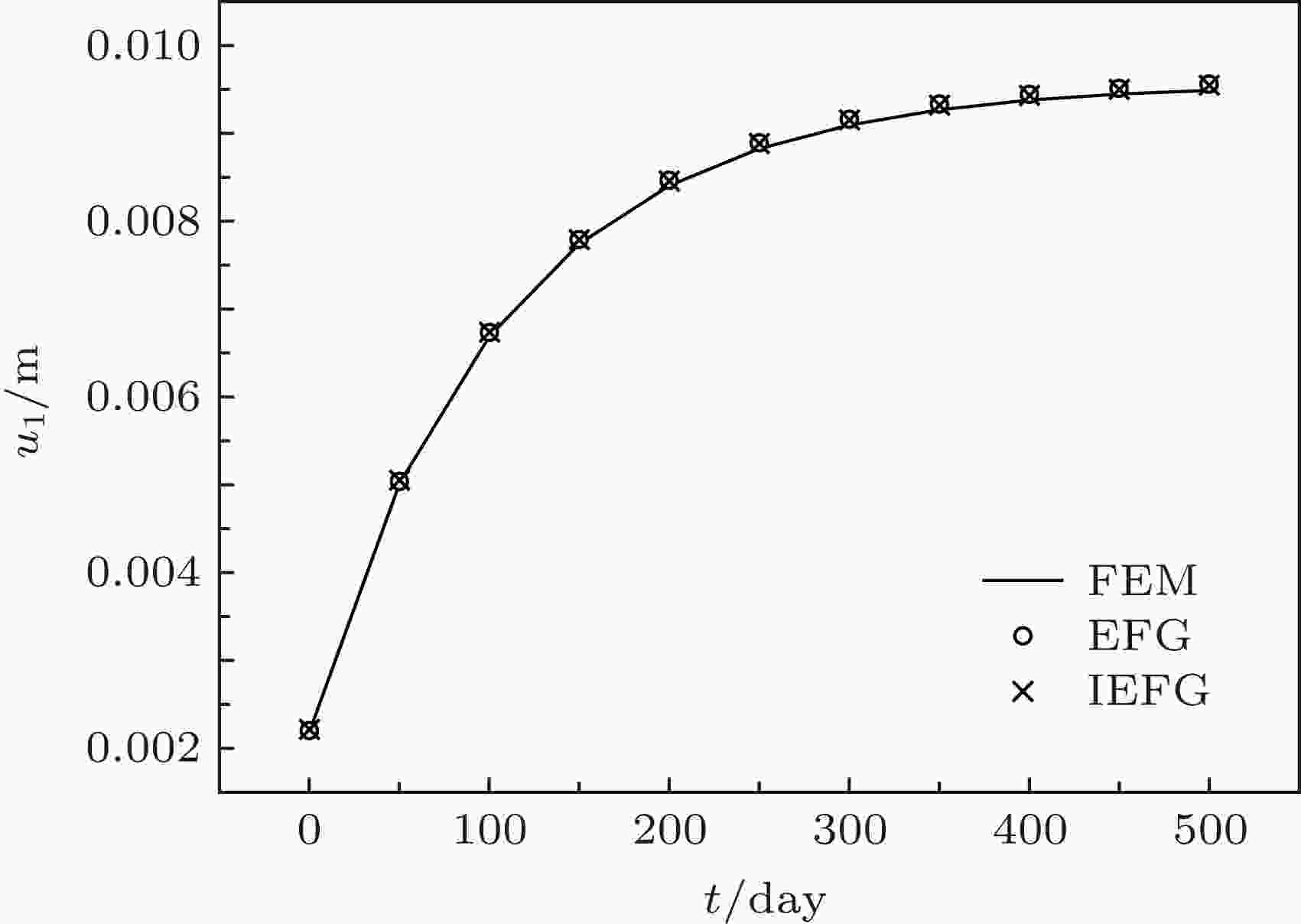 图 20 混凝土坝上点
图 20 混凝土坝上点


