全文HTML
--> --> -->随着计算机技术的不断发展和数值计算理论的逐步完善, 数值模拟已经被越来越多地应用于科学研究与工程领域. 对于电弧等离子体的数值模拟, 国内外****在基于局域热平衡的基础上, 报道了众多研究成果[9-20]. 进一步地, 研究人员考虑了电弧的非平衡过程, 建立了双温度模型[21-23], 甚至包括了化学非平衡的影响和电极鞘层区[24-28]. 这些模型避免了平衡态假设, 更加接近物理实际, 得出了许多重要的新结论, 使人们对电弧等离子体的认识更加深入. Zhang等[29]和Li等[30]针对众多双温度等离子体模型存在较大差异的问题, 提出了一种自洽的数值计算模型, 但并不增加其复杂性, 同时也包括了输运系数的计算. 值得注意的是, 由于电弧等离子体的高温使得阴极或者阳极材料蒸发, 产生的蒸汽进入电弧会对电弧行为产生影响, 这种混合的等离子体特性受到越来越多的关注[31-35]. 而对于混合气体电弧, 研究人员一般将其简化为均匀混合的等离子体, 并得到了有意义的结果. Savas和Ceyhun[36]在假设Ar-H2气体混合均匀的基础上, 研究了混合气体的电弧特性; Wang等[37]研究了保护气体中CO2浓度对熔化极气体保护焊电弧行为的影响, 同样没有考虑混合气体电弧中CO2组分的分布; 类似地, Murphy等[1]研究了Ar-H2, Ar-He, Ar-N2等多种混合气体电弧的特性, Rao等[38]研究了不同混合浓度的Ar-He熔化极气体电弧的特性.
尽管这些研究已经得到了比较精确的结果, 但是, 假设混合气体电弧各组分均匀分布, 这些研究就不能反映混合气体电弧发生的实际的物理过程, 从而也不能揭示混合气体改变阴极和阳极行为更本质的原因. Murphy[39]的研究表明, 混合气体组分在电弧中分布并不均匀, 出现明显的分层, Murphy和合作者[40,41]考虑了多种混合气体电弧由于浓度梯度、温度梯度、电场强度等因素导致的组分之间的扩散行为, 对混合气体电弧特性进行了深入研究, 获得了一系列重要的结果. Bitharas等[42]考虑了熔化极气体保护焊时空气环境对电弧的影响, 发现氧在电弧及其周围区域也呈现非均匀分布的特征. 黄勇等[43]研究了氧在电弧气氛中的分布, 探讨了O2流量对气体熔池耦合活性钨极惰性气体(tungsten inert gas, TIG)电弧行为的影响, 但是忽略了氧浓度随温度变化而造成的氧扩散过程. Chen等[44]对Ar/O2电感耦合等离子体的特性进行了模拟研究, 杨郁等[45]对甚高频的Ar/O2容性耦合等离子体的电负特性进行了研究. 但是, 电感耦合等离子体和容性耦合等离子体放电形式与电弧不同; Murphy[39,40]的研究中电流都为200 A, 也没有在模型中包括阴极, 有关不同电流下的研究结果还未见报道, 由于电流对电弧温度场和流场会产生明显的影响, 进而可能改变混合组分在电弧气氛中的分布. 而混合组分在电弧气氛中的分布与其在阴极和阳极的分布密切相关, 最终影响焊接稳定性、焊缝成形和接头质量[2-9]. 因此, 对混合气体电弧的行为做进一步的研究, 不仅有助于理解混合气体电弧的物理本质, 也有助于深入认识混合气体组分对阴极和阳极的作用机制, 为更有效地利用混合气体电弧和实现高效焊接提供理论基础和技术借鉴.
本文针对Ar-O2混合气体电弧, 采用磁流体动力学方程组描述混合气体电弧, 采用组分输运方程描述氧的传质过程, 建立了Ar-O2混合气体电弧的稳态轴对称二维数学模型, 求解得到了不同电流条件下混合气体电弧的温度场、流场和氧组分的分布等结果, 并研究了氧对电弧温度场和流场等电弧特性的影响. 数值计算结果与已有的研究结果吻合良好.
2.1.方程描述
由于Ar-O2混合气体电弧中存在两种组分的阳离子(Ar+, Ar++, Ar+++, O+, O2+, O++, O+++)、原子(Ar, O)、分子(O3, O2,)、负离子(O2–, O–)和电子等众多等离子体成分, 对其单独采用守恒方程描述将会使模型极其复杂, 这种复杂性一方面体现在物性参数的计算, 尤其是扩散系数的计算[39-41,46-47], 另一方面还体现在对多组分多离子系统采用自洽的守恒方程进行准确的描述[29,30,39-41,46-47]. 为简化描述混合气体电弧, 本文采用Murphy提出的方法[40,46], 即假定等电弧离子体仍然满足局域热平衡状态(local thermodynamic equilibrium, LTE), 将多种等离子体成分简化处理为二元组分混合物. 本模型中, 一种为氩组分, 另一种为氧组分, 两种组分之间的扩散通过组合扩散系数方法描述, 从而可以采用磁流体动力学方程组描述混合气体电弧. 除假设混合气体等离子满足LTE之外, 还假设等离子流动状态为层流且满足光学薄性质[10]; 作为初步的研究, 模型未包括阳极并忽略阳极金属蒸汽的影响; 忽略黏性效应导致的热损失和重力影响[10]. 描述电弧等离子体的磁流体动力学方程组包括连续性方程、动量守恒方程、能量守恒方程电磁学方程[1,10-20].连续性方程
本模型所用的电磁学方程如下:
电流连续性方程
此外, 两种组分之间的扩散用一个组分输运方程描述[39-41,46,47], 这里氧组分以A表示, 氩组分以B表示, 则氧组分的输运方程为










2
2.2.热力学参数和输运系数
包括上述的



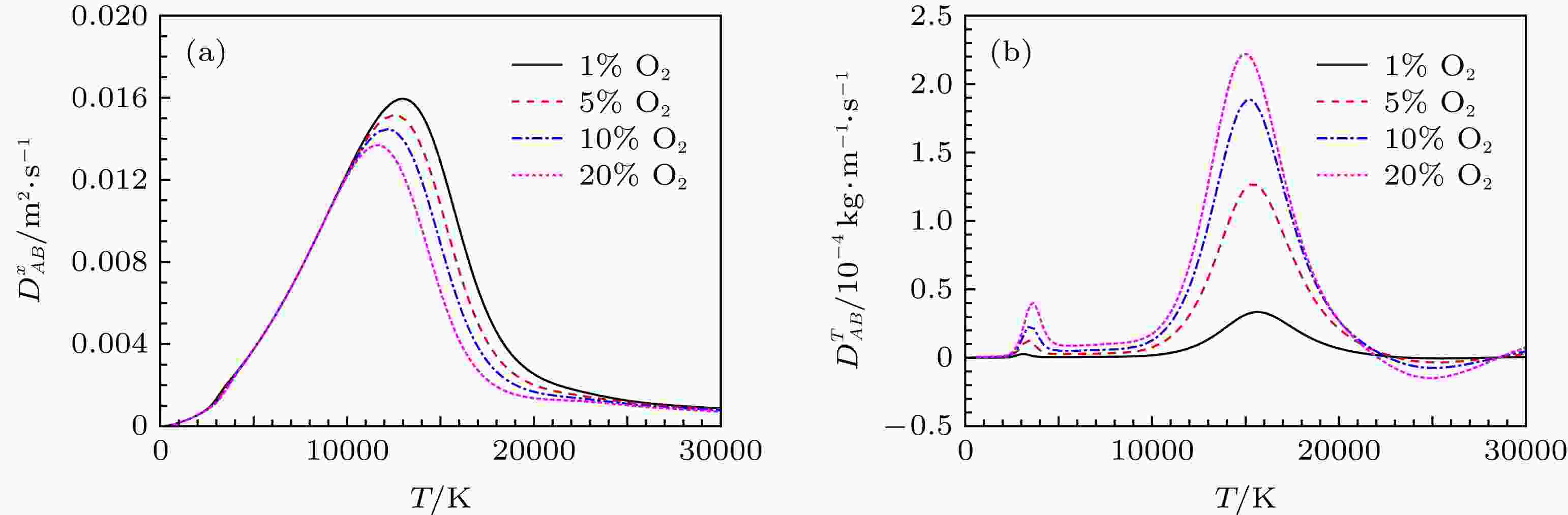 图 1 扩散系数 (a) 组合普通扩散系数
图 1 扩散系数 (a) 组合普通扩散系数

Figure1. Diffusion coefficients: (a) Combined ordinary diffusion coefficient


2
2.3.求解域和边界条件
求解域如图2所示, 灰色部分为钨极区域, 其余为电弧区域. AB为钨极截面, BC为气体进口, 气流量为10 L/min, CD为出口, DE为阳极表面, ABHGF为钨极区域. 求解域尺寸为10 mm × 10 mm, 钨极尖端距离阳极为5 mm, 钨极直径为3.2 mm, 尖端角度为60°, 尖端平台直径为0.2 mm.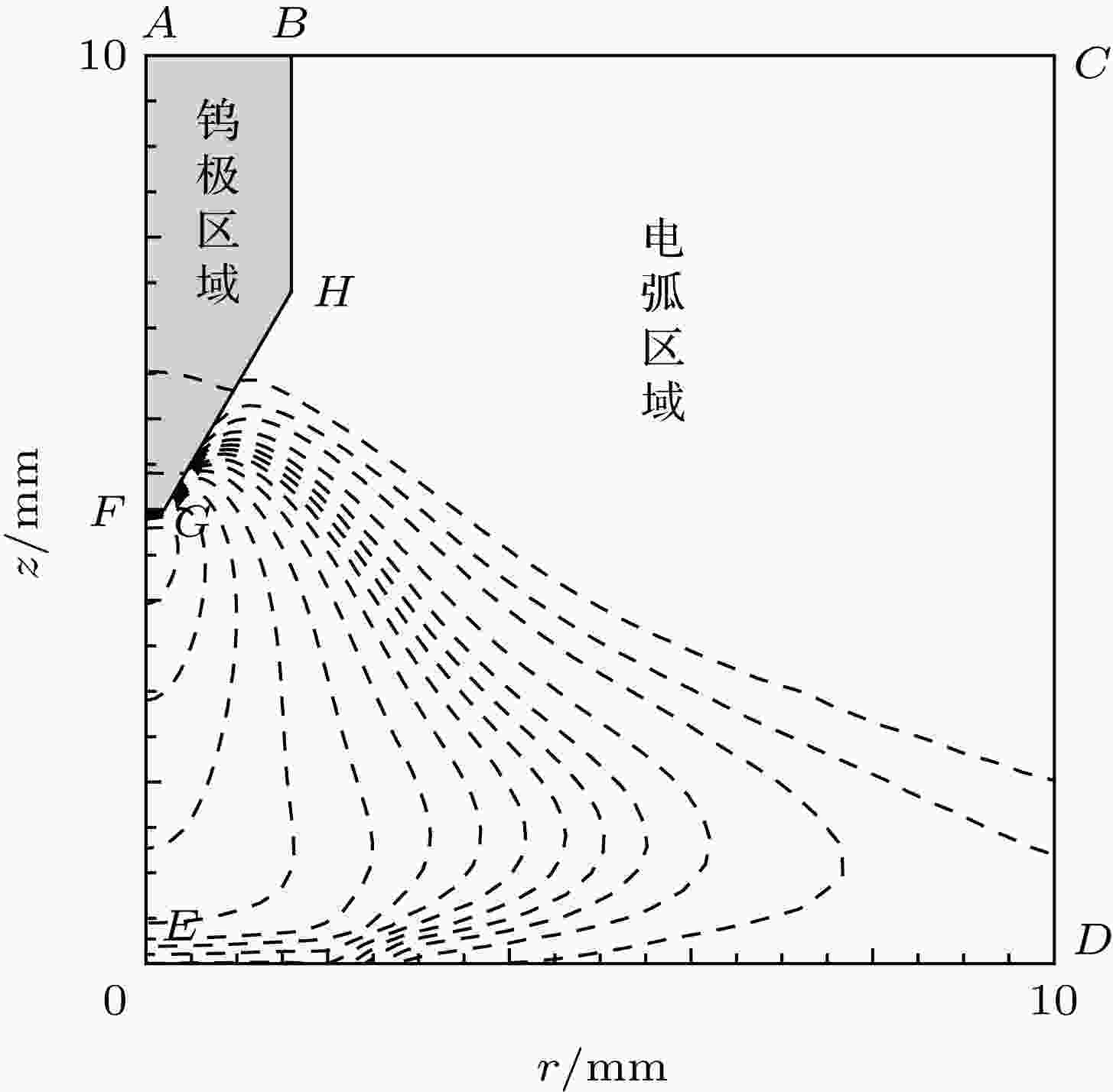 图 2 求解域示意图
图 2 求解域示意图Figure2. Schematic of the computation domain.
对于外部边界条件, AB为钨极横截面, 给定温度和电流密度, BC为气体入口; 给定气体流速, CD为出口, DE为阳极表面, 设定温度为2000 K, 电势为0, 采用无滑移条件, EA为对称边界. 对于磁矢势A的边界条件, 理论上, 在出口为无限远处时趋于0, 对于有限大的边界, 可设定更加精确的边界条件[53], 但为了计算简化, 一般在出口处设定为0, 得到的结果与解析解和单独用磁通密度描述的结果吻合得很好[53], 且为众多的计算模型所采用[1,9,19,20,24,25,33-35].
在求解域内部, 由于阴极区已经严重偏离LTE, 对于阴极表面FGHB区域, 忽略阴极和电弧之间的复杂作用过程, 这里考虑电弧和阴极之间的热作用, 电势和磁矢势采用耦合条件[9,19,20], 以保证其在整个求解域上连续, 电弧对阴极的热作用由下式给出[1]:
对于氧质量分数YA, 边界条件的设定与Murphy的模型[40]类似, 进口给定混合气体中的质量分数, 本文中设定质量分数为5%, 即相当于气体的摩尔分数或者气流量比近似为6%, 出口处也可认为趋于进口处的浓度; 在阴极和阳极附近表面, 由于局域热平衡假设不再适用, 相应的边界条件很难被确定. 这里进行简化处理, 即阳极表面设定其梯度为0, 而在阴极表面给定质量分数分布. 结果表明, 这种简化处理是合理的. 具体边界条件见表1.
| 边界 | v/m·s–1 | T/K | Φ/V | A/Wb·m–1 | YA | |
| AB | — | 1000 | jz | $\partial$A/$\partial$n=0 | — | |
| BC | vgiv | 500 | $\partial$Φ/$\partial$n=0 | $\partial$A/$\partial$n=0 | 0.05 | |
| CD | $\partial$v/$\partial$n=0 | 500 | $\partial$Φ/$\partial$n=0 | A=0 | 0.05 | |
| DE | — | 2000 | 0 | $\partial$A/$\partial$n=0 | $\partial$YA/$\partial$n=0 | |
| EA | $\partial$v/$\partial$n=0 | $\partial$T/$\partial$n=0 | $\partial$Φ/$\partial$n=0 | $\partial$A/$\partial$n=0 | $\partial$YA/$\partial$n=0 | |
| BF | Non-slip | (12)式 | Coupled | Coupled | YAgiv | |
表1边界条件
Table1.Boundary conditions.
2
2.4.求解方法
求解域离散化为非结构化四边形网格, 钨极尖端附近局部加密; 模型采用FLUENT求解, 能量守恒方程和电磁学方程在整个区域求解, 动量守恒方程、连续性方程和组分输运方程在等离子体区域求解; 采用SIMPLE 算法, 方程用二阶迎风格式进行离散, 能量方程收敛标准为10–6, 其余方程为10–3.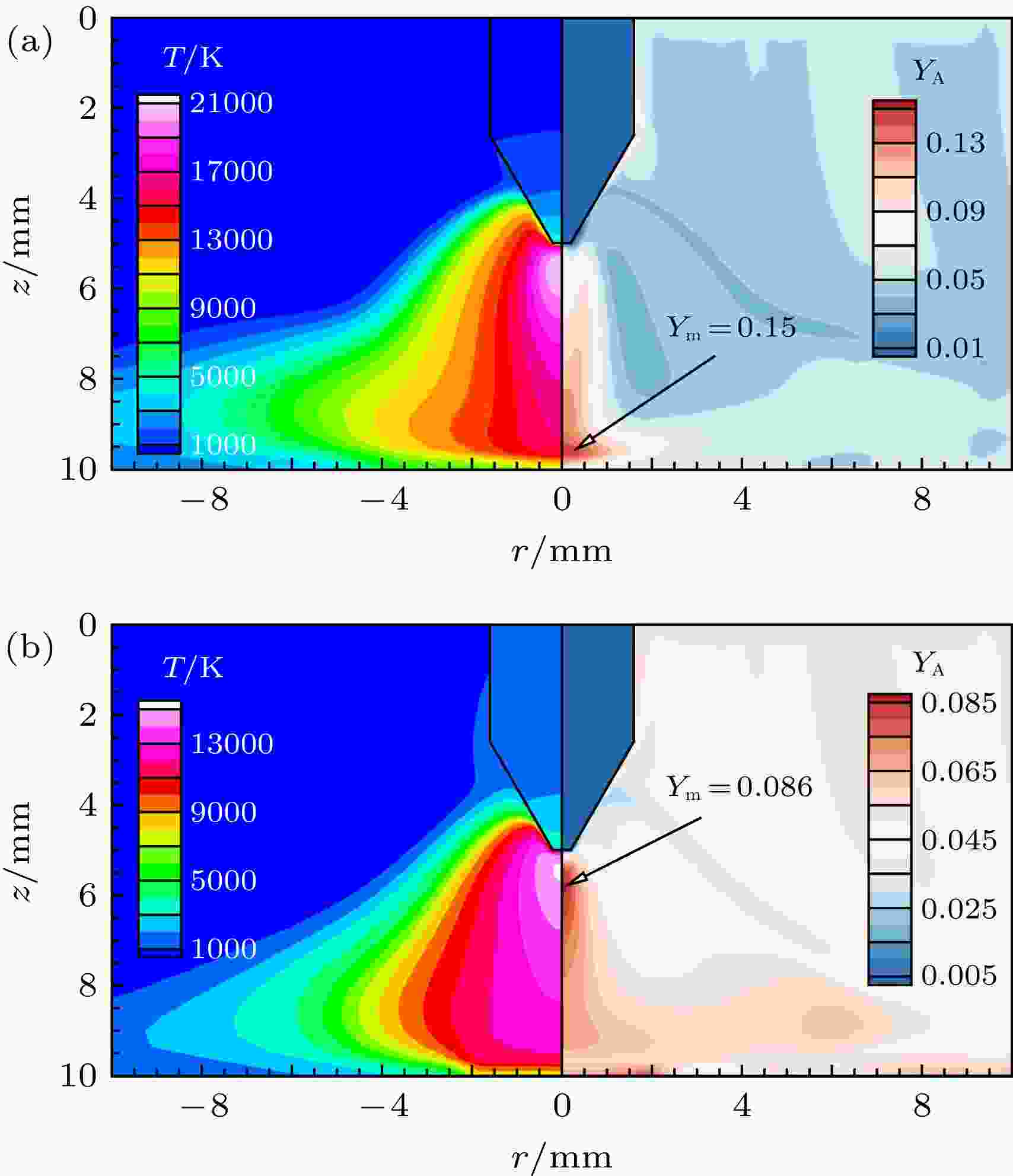 图 3 混合气体电弧的温度场和氧组分质量分数分布 (a) 200 A; (b) 80 A
图 3 混合气体电弧的温度场和氧组分质量分数分布 (a) 200 A; (b) 80 AFigure3. Temperature field and oxygen mass fraction of Ar-O2 mixture gas arc for different current: (a) 200 A; (b) 80 A
氧的这种不均匀分布在图4可以更加明显的看到. 如图4(a)所示, 在电流为200 A时, 在钨极下方4 mm处, 随着径向距离增加, 氧质量分数迅速下降, 且当r > 2 mm时, 出现一定的波动, 峰值出现在钨极正下方, 达到12.5%. 在钨极下方其它位置, 随着径向距离的增加, 氧质量分数先略有上升, 然后迅速下降到5%以下, 即低于氧在混合气体中的质量分数, 并出现明显的波动; 而且, 峰值偏离中轴线, 且距离钨极越远, 峰值越大; 如图4(b)所示, 与200 A的情形类似, 当电流为80 A时, 随着径向距离的增加, 氧质量分数逐渐下降, 并出现明显波动, 不同的是, 随着到钨极尖端距离的增加, 氧质量分数峰值逐渐下降, 且峰值总是出现在钨极正下方.
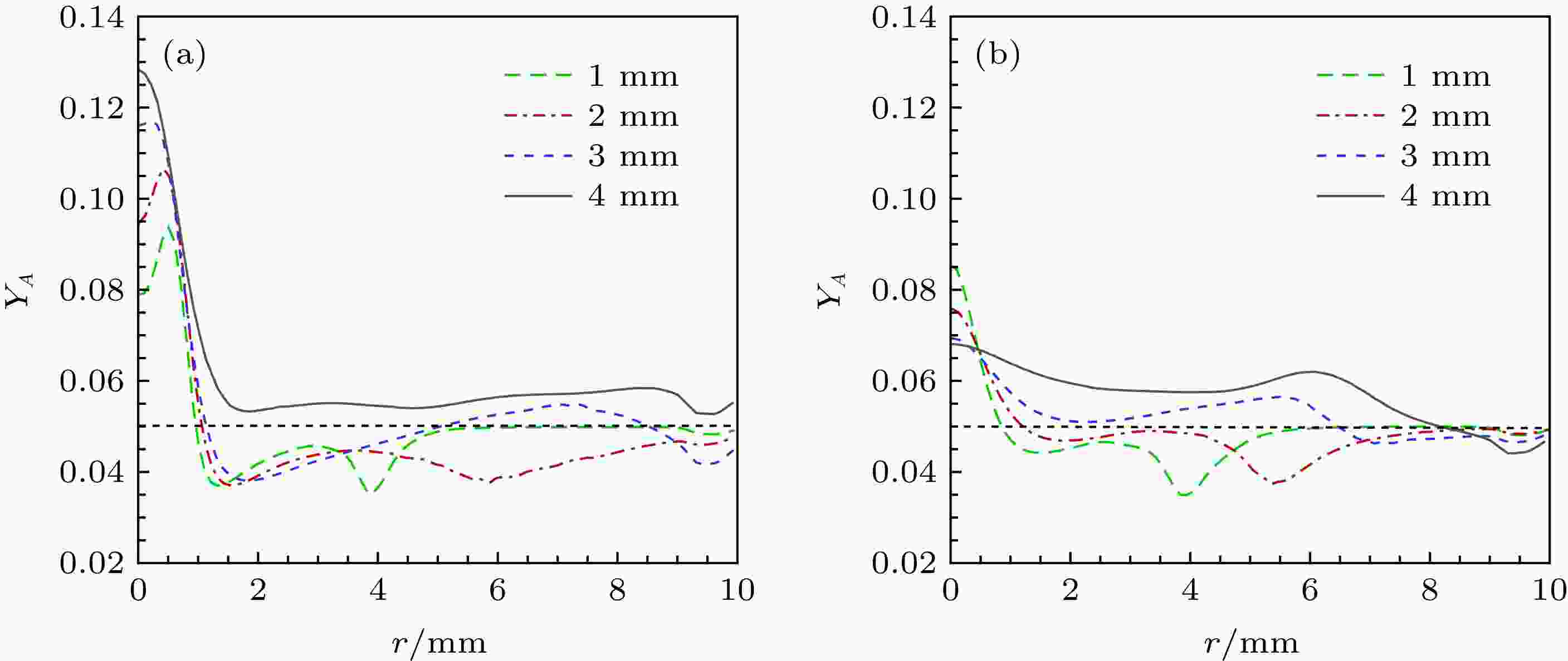 图 4 距离钨极尖端不同位置氧组分质量分数的径向分布 (a) 200 A; (b) 80 A
图 4 距离钨极尖端不同位置氧组分质量分数的径向分布 (a) 200 A; (b) 80 AFigure4. Radial distributions of the mass fraction of oxygen at different distances below the cathode: (a) 200 A; (b) 80 A.
从(10)式和(11)式可以看到, 氧的这种不均匀分布受到等离子体流动、普通扩散和温度梯度导致的扩散三者的影响. 普通扩散即由于浓度梯度引起, 是一种很普遍的扩散现象, 而对于温度梯度导致的扩散, 这里用组合温度扩散系数来描述. 由浓度梯度引起的扩散导致氧的分布趋于均匀, 而由温度梯度导致的扩散受温度分布的影响, 两者的作用往往并不一致[48]. 根据Murphy的研究[39,40], 由温度梯度导致的扩散主导氧扩散过程, 最后决定其分布. 由于在阴极和阳极附近存在很大的温度梯度, 因此, 在靠近阴极和阳极的区域, 氧的浓度明显升高; 但是对于两种不同的电流, 氧的峰值浓度出现的位置不同, 这是由于由等离子体流动引起的对流传质的强弱不同所致. 如图5(a)所示, 在200 A 时, 中心轴线附近的等离子流速明显超过100 m/s, 在钨极下方约2 mm处达到峰值, 约366 m/s, 如此之大的等离子流使得氧的分布明显向阳极集中, 在阳极附近, 等离子流速迅速下降, 最后导致了图3(a)中氧在阳极附近聚集的现象. 与之相比, 80 A时的等离子体流速度明显减小, 峰值仅有95 m/s, 对流传质的作用明显减弱, 远远不及200 A时强, 如图5(b)所示; 另外值得注意的是, 由图1(b)可以看到, 组合温度扩散系数随氧质量分数的增加而增加, 且在15000 K附近出现峰值, 而80 A时阴极尖端附近的温度非常接近15000 K, 这意味着此时氧在温度梯度作用下的扩散更加明显. 因此, 氧也会使得氧向阴极附近集中. 由此可知, 氧的分布受到等离子体流动的影响比较显著, 不同的电流条件下, 由于产生的等离子体流动强弱不同, 导致氧的分布也会不同, 电流和其他参数如电弧长度和混合气体浓度等的影响将在后续的研究中进行.
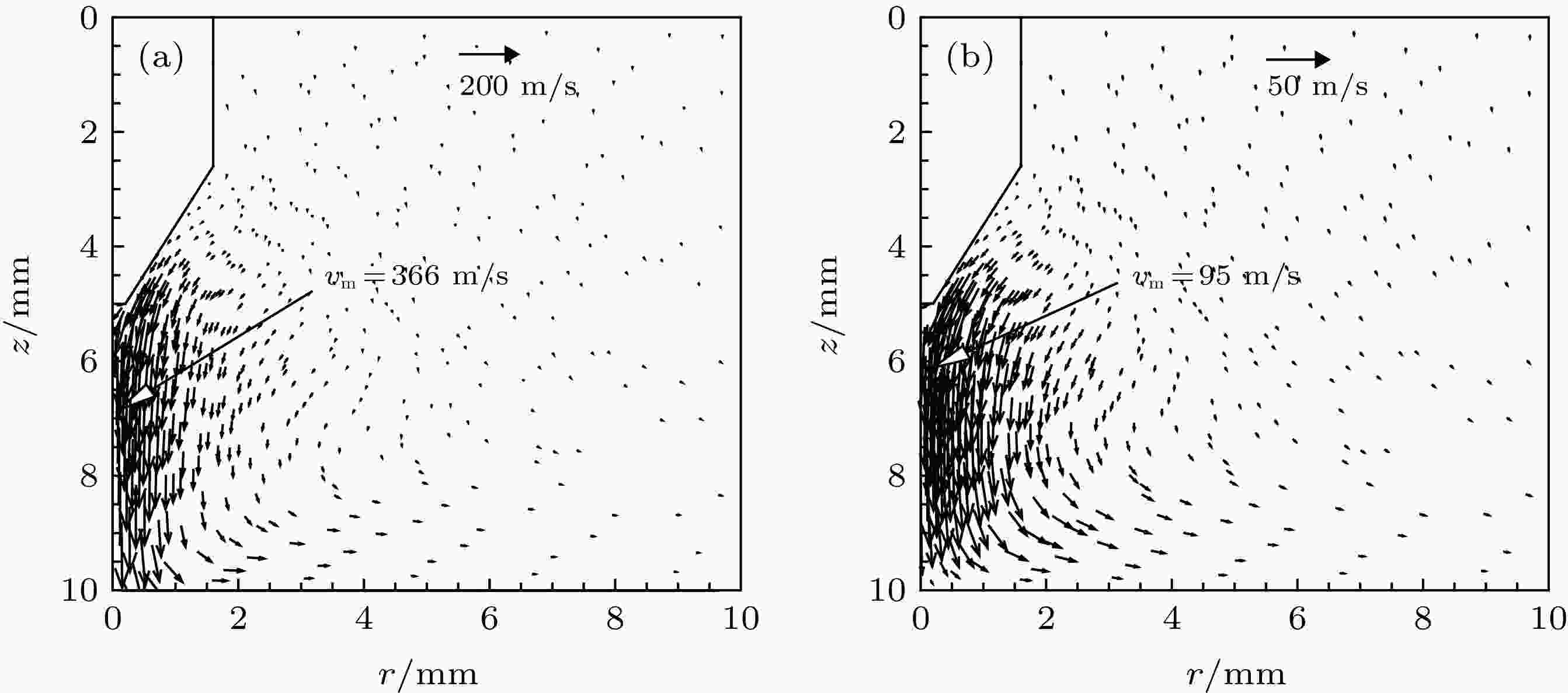 图 5 混合气体电弧的流场 (a) 200 A; (b) 80 A
图 5 混合气体电弧的流场 (a) 200 A; (b) 80 AFigure5. Flow fiels of mixture gas arc:(a) 200 A; (b) 80 A.
需要指出的是, 在电弧温度接近环境温度的周围较冷区域, 会明显偏离LTE假设, 因此计算得到的氧分布与实际的可能有所不同, 但是整体上, 在电弧高温区域, 由于高温和较大的温度梯度, 氧的分布仍然受到温度梯度导致的扩散主导, 因而其结果当与实际的接近. 一般地, 气体保护焊接的熔池尺度在毫米量级[1,3,5,6,8], 处于高温区域的覆盖之下, 因此, 对于探究混合气体电弧中氧对熔池的作用, 这些结果仍然具有重要的参考价值.
图6为距离阳极表面0.1 mm处氧组分的径向分布, 0.1 mm的尺度大约相当于阳极区的宽度. 可以看到, 在两种电流条件下, 氧的分布出现明显的波动. 相比之下, 200 A时的波动更加强烈, 而且明显地集中于中心区域, 峰值接近11.5%. 此外, 氧组分浓度在大部分区域高于其在混合气体中的浓度. 电流为80 A时, 大约在1.6 mm < r < 4 mm的范围, 氧组分浓度略低于混合浓度; 电流为200 A时, 大约在3.2 mm < r < 7 mm的范围, 氧组分浓度略低于混合浓度. 可以推测, 这个位置的氧的不均匀分布必然会使得熔池表面的氧分布呈现不均匀的特性. 作为一种能决定熔池Marangoni对流的活性元素, 氧的这种不均匀的分布会对熔池的流动和焊缝成形产生非常显著的影响[4,55,56]. 然而, 由于阳极区偏离了LTE状态, 而且存在明显的电场强度的影响[25], 阳极的蒸发作用[34,35,41]也会进一步影响氧的传质过程, 氧在阳极区的传质行为将更加复杂. 尽管如此, 氧在阳极附近的分布将直接决定氧在熔池表面的分布, 因而是值得进一步研究的方面.
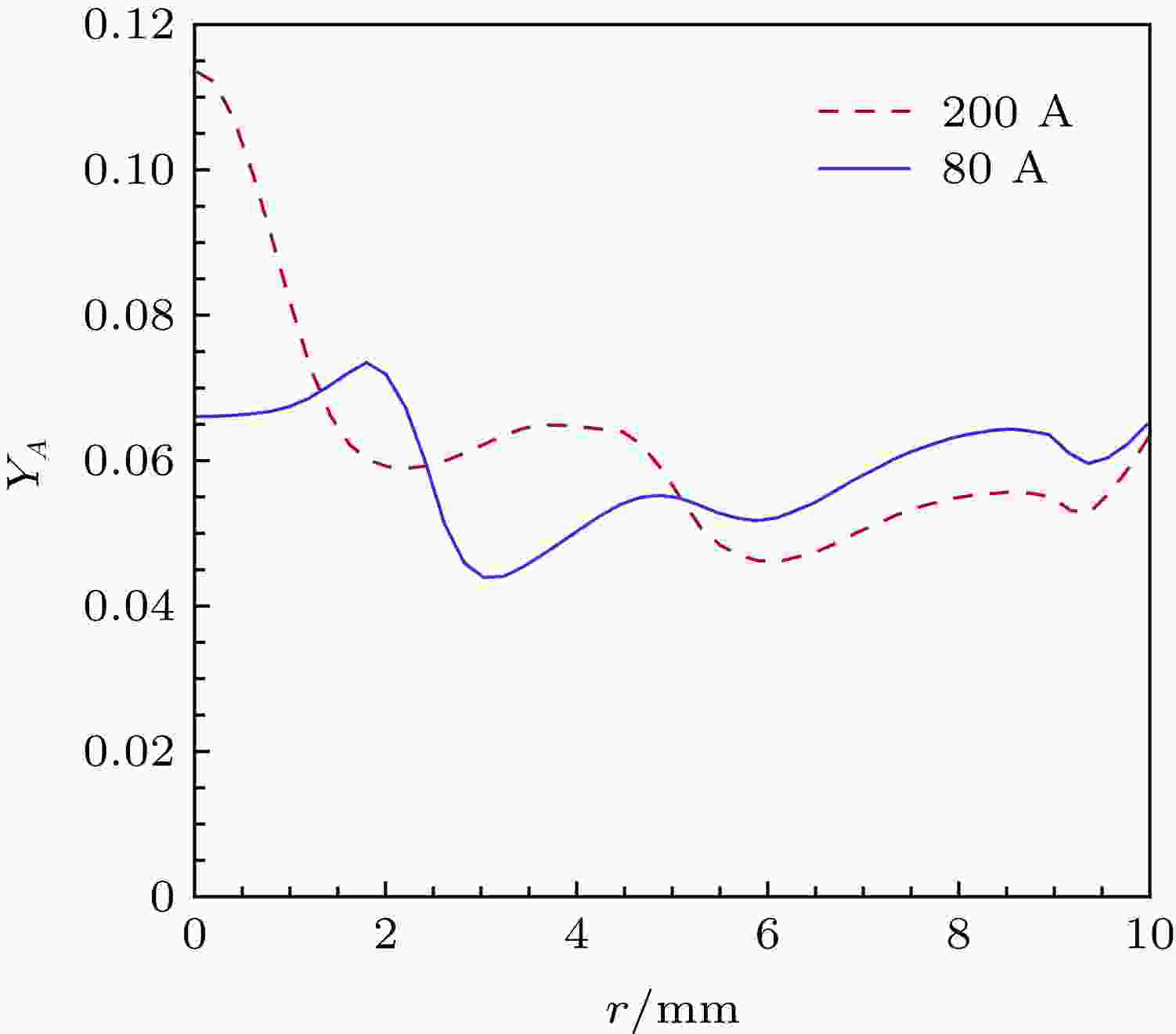 图 6 混合气体电弧阳极表面0.1 mm处氧组分的分布
图 6 混合气体电弧阳极表面0.1 mm处氧组分的分布Figure6. Oxygen mass fraction of mixture gas arc 0.1 mm above the anode.
氧的不均匀分布对电弧温度场的影响如图7所示, 可以看到, 在两种电流条件下, 氧的存在使电弧外围靠近阳极的区域出现明显收缩, 而使电弧外围靠近阴极的区域和中心区域温度场出现轻微的扩张, 总体上表现为电弧的收缩, 这种收缩实质上导致了电弧温度的升高. 如图7(a)所示, 在80 A电流时, 最高温度从14871 K上升到15133 K, 而由图7(b)可知, 电流为200 A时, 最高温度从20658 K增大到20968 K. 由于O2在电弧高温气氛中会发生解离和电离, 这需要额外消耗电弧的一部分能量, 为了维持其自身能量损失最小, 电弧出现收缩, 同时电弧导电通道集中, 电流密度增加, 产生的焦耳热增加, 温度上升. 这一结论与Murphy[40]的研究结果一致, 黄勇等[57]对气体熔池耦合活性TIG电弧的光谱测量也得到了类似的结论. 在靠近阳极区域外围电弧收缩明显, 这是由于这一区域氧的浓度更高, 因此其收缩作用更加显著. 靠近阴极区域出现的电弧外围温度场扩张, 可以认为是电弧收缩后产生的焦耳热增加, 而氧的存在对电弧能量的辐射损失影响极小[51]; 同时, 如图5所示, 这一区域等离子体流速明显下降, 热对流的作用已不显著, 因此, 在热扩散的作用下, 更多热量向低温区域传递, 导致等温线扩展.
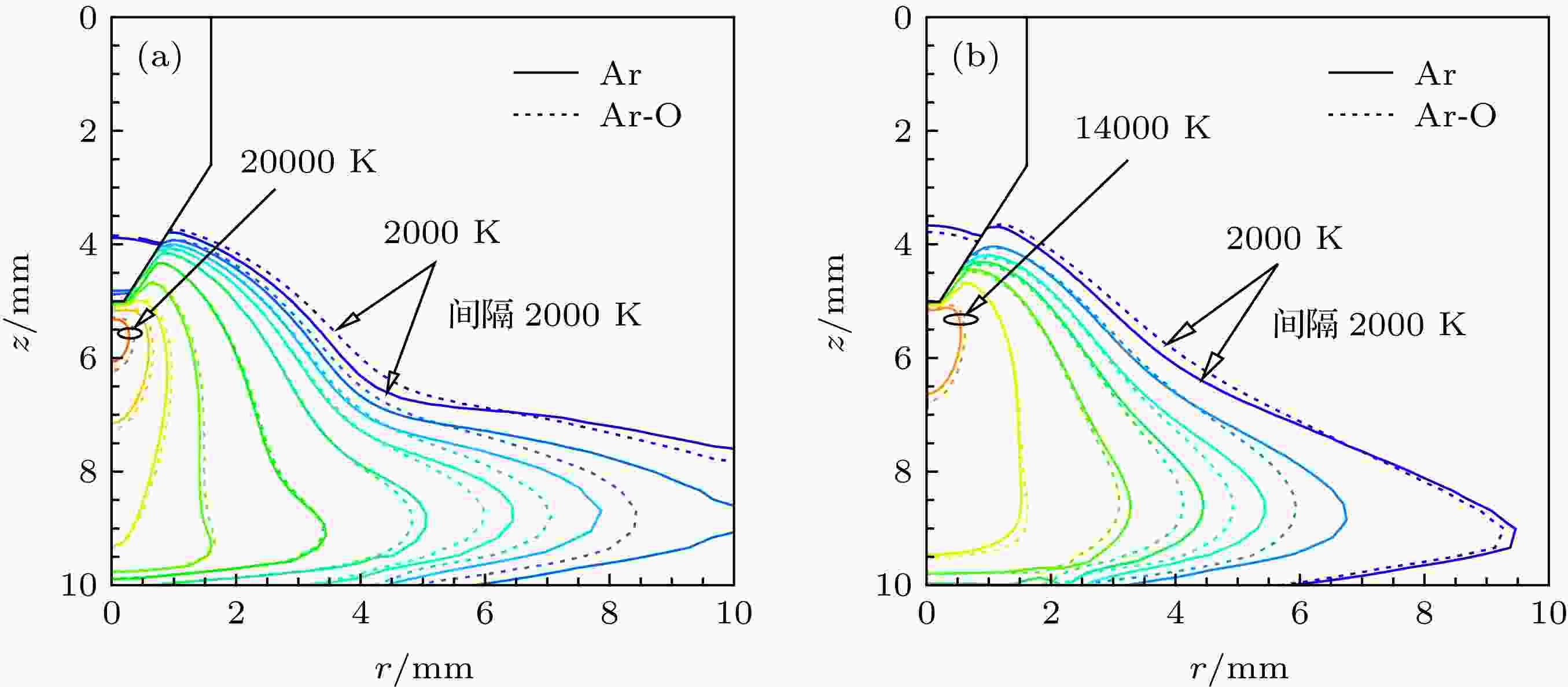 图 7 氧组分对电弧温度场的影响 (a) 200 A; (b) 80 A
图 7 氧组分对电弧温度场的影响 (a) 200 A; (b) 80 AFigure7. Effect of oxygen on the arc temperature field: (a) 200 A; (b) 80 A.
氧的存在对电弧等离子体流场的影响如图8所示, 可以看到, 在两种电流条件下, 氧的存在使电弧外围等离子体流速下降, 而在电弧中心区域等离子体流速增加, 80 A时最大流速从86 m/s增加到95 m/s, 200 A时最大流速从341 m/s 增加到366 m/s, 等速线明显扩展, 这种变化趋势与温度场的变化类似. 实质上, 这也是电弧收缩的一种表现. 温度的收缩引起导电通道的收缩, 导致电弧外围驱动等离子流动的电磁力减弱, 流速下降. 而在中心区域, 由于温度明显超过10000 K, 黏度随着温度升高而迅速减小[51], 加之电弧收缩导致的电磁力增加, 使得等离子体流速显著增强, 流速等值线明显扩展.
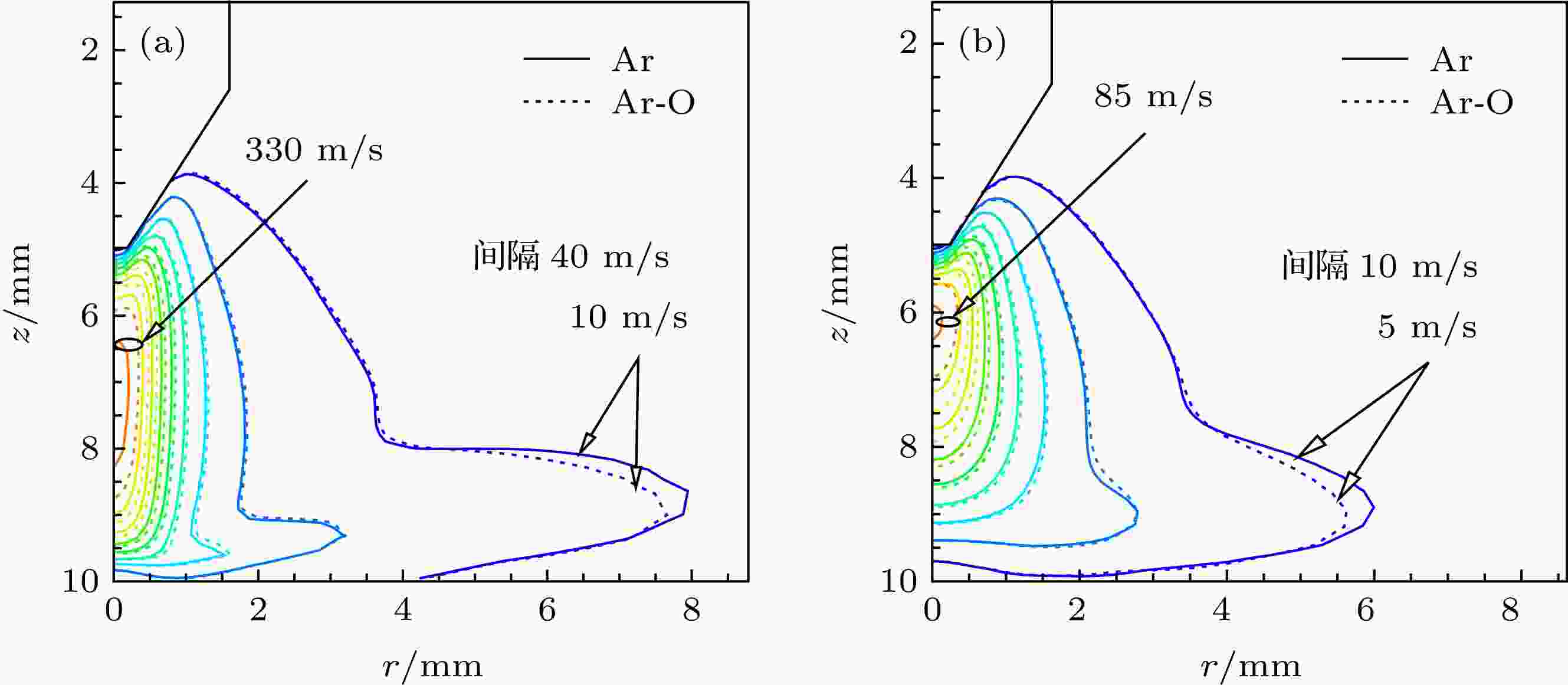 图 8 氧组分对电弧流场的影响 (a) 200 A; (b) 80 A
图 8 氧组分对电弧流场的影响 (a) 200 A; (b) 80 AFigure8. Effect of oxygen on the arc flow field: (a) 200 A; (b) 80 A.
图9为200 A的纯Ar保护TIG电弧温度场的计算结果对比, 左半部分为Lowke等[12]的结果, 右边为本文模型的计算结果. Lowke的研究考虑了电子扩散对阴极鞘层区的作用, 结果与实验吻合得很好; 本文采用了简化处理, 可以看到两者的结果很接近, 而在阴极附近温度分布出现一定程度的差异, 本模型得到的最高温度超过20500 K, 而Lowke的结果超过23000 K. 可能的原因是本模型没有考虑阴极附近的非LTE状态, 从而使得电弧热的计算偏低. 总体上, 本文的单组分气体电弧模型可靠, 具有较高的计算精度, 从而表明了在此基础上建立的混合气体电弧模型的可靠性.
 图 9 200 A电流TIG电弧的温度场对比
图 9 200 A电流TIG电弧的温度场对比Figure9. Comparison of the calculated temperature fiels of TIG arc for 200 A current.
图10为本文模型的模拟结果和Murphy研究结果[40]的对比, 电流为200 A, 阴极距离阳极5 mm. 图10(a)为Murphy的结果, 图10(b)为本文的结果. 可以看到两者吻合良好, 不同的是本文的计算结果峰值相对较高; 在钨极尖端下方4 mm处, Murphy得到的氧质量分数峰值约为0.11, 本文则为0.127. 其余位置的峰值也有类似的差异, 而且氧质量分数的分布也有一定程度的差别, 其原因可能是由于所采用的边界条件不能完全一致, 而且本文所用的热力学参数和输运系数线性差值的间隔更小所致. 但两者都表明了氧在电弧气氛中的不均匀分布, 以及其更加聚集于阳极附近的分布规律.
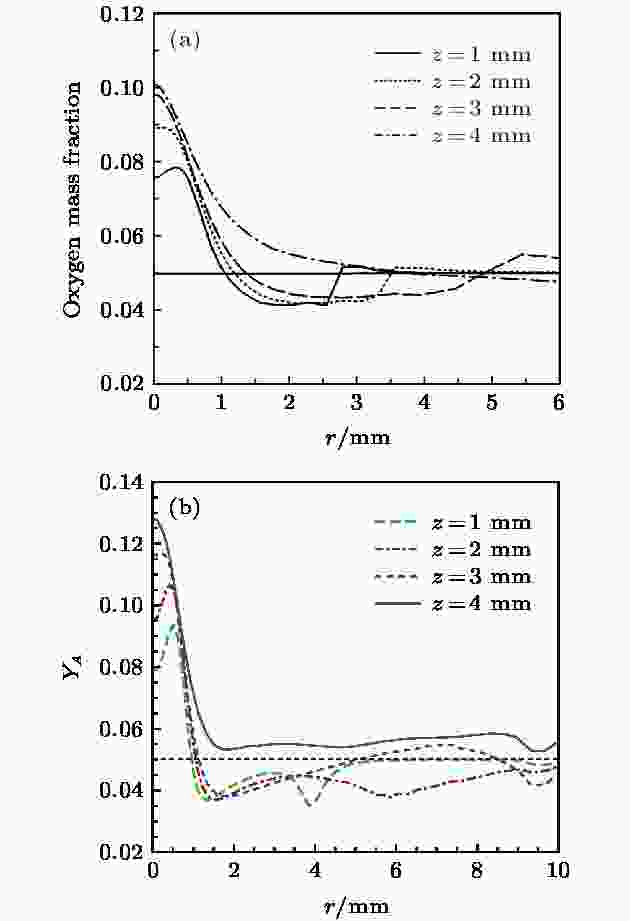 图 10 距离阴极尖端不同位置氧组分径向分布的计算结果对比 (a) Murphy的结果[40]; (b) 本文的结果
图 10 距离阴极尖端不同位置氧组分径向分布的计算结果对比 (a) Murphy的结果[40]; (b) 本文的结果Figure10. Comparison of radial distribution of oxygen calculated at different distances below the cathode: (a) Murphy’s results[40]; (b) the present model’s results.
1)氧在Ar-O2混合气体电弧中呈现明显的不均匀分布, 在电弧中心轴线和两极附近浓度较高, 超过其在混合气体中的浓度, 而在其他区域低于混合气体中的浓度;
2)不同电流下的等离子体流速大小对氧分布有较明显的影响, 在大电流条件下, 氧更集中地分布于阳极附近, 而在小电流条件下, 氧更集中地分布于阴极附近;
3)在两种电流条件下, 氧在阳极附近0.1 mm处沿径向分布并不均匀, 预示着作用于阳极表面氧的不均匀分布;
4)与纯氩气保护相比, 混入5%的氧气使电弧出现一定程度的收缩, 电弧温度和等离子体流速有所增加.
感谢澳大利亚CSIRO Manufacturing的A. B. Murphy博士提供的Ar-O2混合气体电弧的热力学参数和输运系数以及与他的有益讨论.
