摘要:建立了基于有限元法(FEM)的三维心磁正问题计算框架, 以研究人体心脏电生理活动产生的磁场问题. 首先对被试的心脏和躯干磁共振影像数据源进行三维个性化建模, 获得心脏-躯干几何模型. 其次结合心脏三维模型与修正的FitzHugh-Nagumo (FHN)方程研究由跨膜电位 (TMP)产生的电兴奋在心脏内部的传导. 随后利用躯干三维模型与准静态麦克斯韦方程, 研究心脏电兴奋产生的生物电磁场在体内的传播过程, 进而获得体表外的心脏磁场分布. 心磁计算框架仿真结果显示, 使用FEM的模型可以较好地模拟体表外磁场分布. 一维FHN方程和直导线的简化模型数值结果分别与解析解呈现出较好的一致性, 验证了该计算框架的可行性. 综上, 该框架成功地仿真了TMP在心脏内部的传播过程及其在体表外投影的磁场分布, 这将有助于未来心磁逆问题求解的研究.
关键词: 心磁/
FitzHugh-Nagumo方程/
有限元法/
跨膜电位

English Abstract

全文HTML

--> --> -->

心磁正问题是通过构建心脏电生理和体表磁场模型, 描述心脏电兴奋起搏点激发的心脏电生理活动, 并在体表投影磁场的研究过程. 这是深入理解心脏体表磁场形成机制的重要手段, 使得心磁信号的生成过程有了理论指导. 心磁图(magnetocardiography, MCG)作为一种新型无创检测技术, 通过记录心脏电生理活动产生体表外的磁场分布变化, 来反映心动周期的过程. 由于人体组织磁导率接近真空磁导率的特性, MCG不受组织和空间的影响, 相比传统多导联心电图(ECG)可捕获更微弱的生物信息, 对冠心病及心律失常表现出更高的敏感度和准确度^[1,2]. 而ECG受组织电导率等物理因素制约, 抑制了一些不正常的电信号在体表的表现^[3]. 因此我们认为研究心脏电生理活动产生的体表外磁场分布的心磁正问题是必要的. 另一方面, 可以在完成心磁正问题的前提下, 从实测MCG出发, 反演重建心脏等效电源或跨膜电位(transmembrane potential, TMP)分布, 研究心脏电生理活动过程的心磁逆问题. 这或许可以为定位心脏异常信号源头提供帮助^[4]. 然而心磁信号极为微弱, 准确测量心磁信号比较困难. 传统基于超导量子干涉器件(superconducting quantum interference device, SQUID)的磁力仪制造成本和维护费用高昂, 不适于MCG临床推广. 但是, 近年来原子磁力仪技术发展迅速, 在测量极弱磁场方面展现了优异的性能^[5], 并且原子磁力仪价格大约只有SQUID磁力仪的1/10. 何祥等^[6]于2017年报道了一种基于非线性磁光旋转效应的脉冲泵浦式铷原子磁力仪, 并在常温下清晰地测得了心脏磁场信号, 这是国内首次用原子磁力仪实现对心脏磁场信号的探测. 随着基于原子磁力仪技术的心磁图仪的发展和实用化, MCG将有希望成为临床上与ECG互为补充的心脏电生理活动检测技术. 心磁正问题的研究可以更好地利用原子磁力仪测得的体表外心磁信号, 描述心脏的电生理活动, 并为后续心磁逆问题提供验证. 这也为我们研究心磁正问题提供了动力.
在过去几十年里, 随着生物医学知识和计算机技术的发展, 研究者从细胞离子通道到组织层面的不同尺度研究并开发了多种心脏模型. 这些模型不仅可以用于更加深入地了解心律失常等疾病的机理, 还可以用于设计新的治疗方法来治疗心脏疾病等. 1952年, Hodgkin和Huxley^[7]对鱿鱼轴突的刺激反应进行了研究, 得出了有关动作电位的复杂关系式, 这为之后的心脏电生理学模型的研究奠定了基础^[8-10]. 最早的三维心脏模型由奥克兰大学Nielsen等^[11]在1991年基于解剖犬心脏, 通过组织学分析建立, 这为后续研究者创建心脏计算模型提供了三维几何基础. 之后, 各国发起“可视人计划”^[12], 通过人体解剖切片获得高精度的人体组织数据. Xia等^[13]在可视人数据基础上, 从心脏细胞模型出发建立了代表国际先进水平的Cardiome-CN虚拟心脏电生理数学模型, 并将其应用于各类心脏疾病的研究. 李心雅等^[14]基于波面型仿真算法完成了全心的电生理建模和体表电位标测图(body surface potential mapping, BSPM)仿真, 降低了仿真所需的计算量. 而医学断层成像技术的普及, 为研究人员无创获取个性化的人体心脏几何数据提供了一种便捷的方式. Wang等^[4]使用磁共振影像(MRI)数据, 结合心电正问题和逆问题, 构建了个性化的三维心肌梗死电生理学模型. 随着计算机技术的不断发展, 越来越精细的心脏电生理学模型开始建立并用于正常心脏状态以及各类心脏疾病的仿真.
本研究将建立一个基于三维个性化几何的心磁正问题计算框架, 加深对心脏电生理活动演变, 以及在躯干表面形成生物磁场的物理过程的理解. 本文将对被试的MRI进行图像分割, 分离出心脏各腔室与躯干表面, 之后对处理好的图片进行三维重建, 建立一个个性化的人体心脏和躯干三维几何模型. 在该三维几何模型的基础上, 用修正后的FitzHugh-Nagumo (FHN)方程建立心脏电生理扩散模型, 以求得TMP变化和电兴奋在心脏内的传播过程. 之后, 以准静态麦克斯韦方程组为基础建立体表外心脏磁场模型, 模拟由TMP演变产生的心脏磁场在身体内和空气中的传播过程, 求得体表外磁场投影分布. 本研究的计算过程将基于伽辽金法(Galerkin method)的有限元分析(finite element analysis, FEA). 最后, 将通过简化模型, 对其解析解与数值解做误差分析, 验证心磁计算框架的可行性.

2

-->

2.1.心脏躯干三维几何模型的构建

本研究使用MRI影像数据, 通过图像分割与三维重建, 建立一个个性化心脏躯干三维几何模型. 传统三维心脏数据源来自犬等解剖模型, 与真实人体几何存在较大差异. 另一方面, 侵入式的数据采集方法不利于获取人体心脏数据, 因而存在较大局限性. 而人体医学断层影像(如CT, MRI等)技术可以无创便捷地从被试者获取医学影像. 通过对医学影像进行图像分割与三维重建, 即可获得研究所需的三维模型. 该模型可以在更贴近真实生理状态的情况下, 模拟心脏TMP传播以及由此产生的磁场体表外的分布. 本研究根据医学图像中的灰度值范围, 通过将二值化后的心脏和躯干MRI影像进行阈值分割, 得到目标的基本轮廓, 最后将处理好的图像进行三维图像重建^[15,16]. 在不影响心脏和躯干结构的前提下, 对重建完成的三维几何进行适当平滑处理, 消除图像分割过程中由于偏差等造成的表面不平滑的状况.
本研究使用一位26岁健康女性志愿者的平扫MRI数据, 构建三维几何模型. 其中, 心脏图像由18张像素为$256 \times {\rm{256}}$, 分辨率为1 mm × 1 mm断层分辨率为10 mm的MRI切片构成; 躯干数据由60张像素为$768 \times {\rm{504}}$, 分辨率为1 mm × 1 mm, 断层分辨率为4 mm的MRI切片构成. 使用最大类间方差法^[17]对心脏和躯干图像切片依次进行图像分割, 结合手绘处理的方式, 分离出心脏中心室和心房的内外轮廓和躯干表面轮廓, 如图1所示.
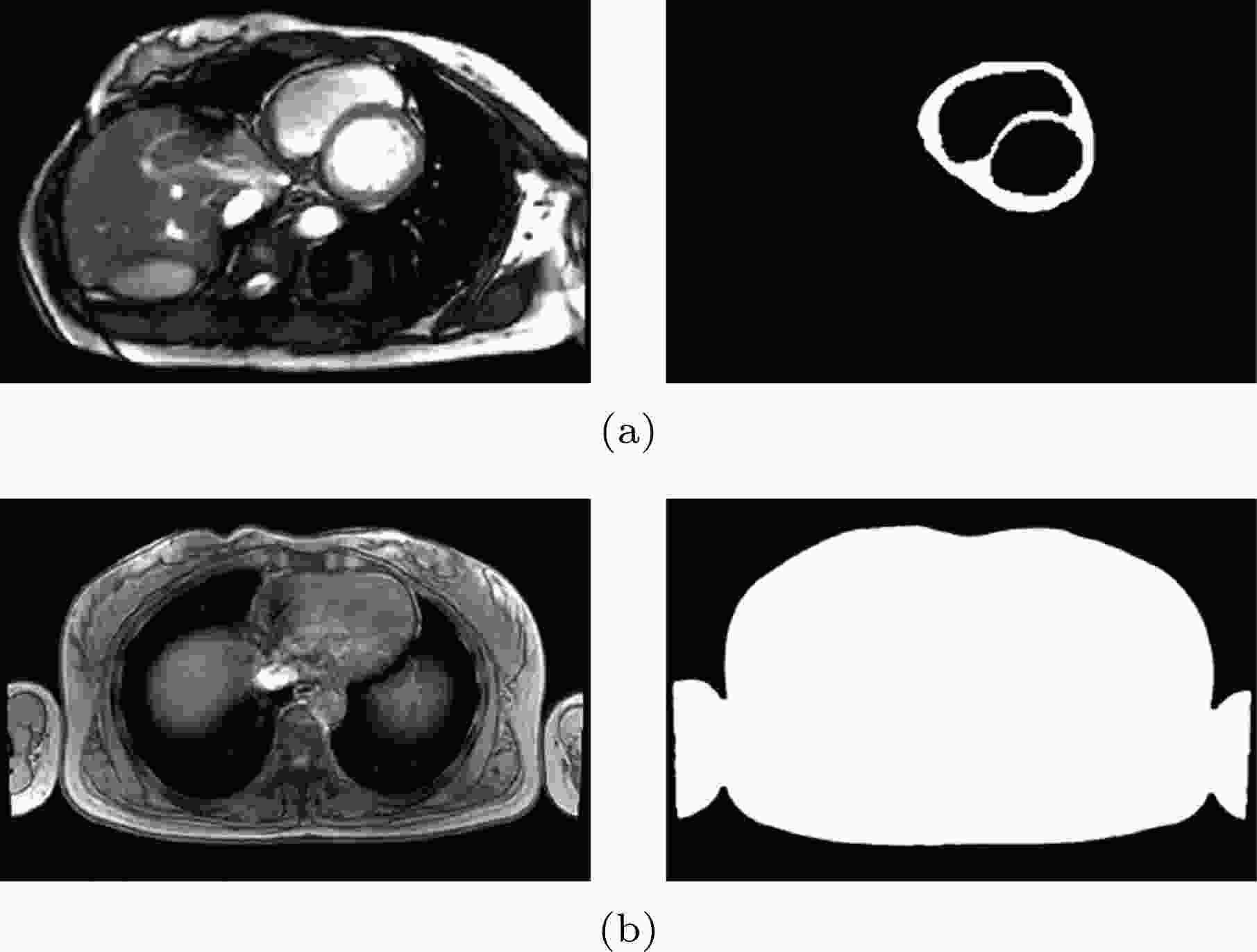图 1 MRI切片的图像分割　(a) 心脏; (b) 躯干
Figure1. Image segmentation of MRI slices: (a) Heart; (b) torso

对分割完成的图像进行体绘制三维重建^[15]并利用移动平均滤波器进行平滑处理^[12], 可以最终得到个性化的心脏和躯干三维结构. 重建完成后的心脏结构包括左右心房以及左右心室共四个腔室. 与仿真体表处心脏电势分布不同的是, 心磁的计算需要考虑体外区域的磁场分布. 本文构建了一个半径为2 m的球形区域将心脏-躯干模型包裹, 以模拟人体周围的空气, 如图2所示. 构建完成后的几何模型将被应用到心脏电生理活动和体表外心脏磁场分布的仿真计算.
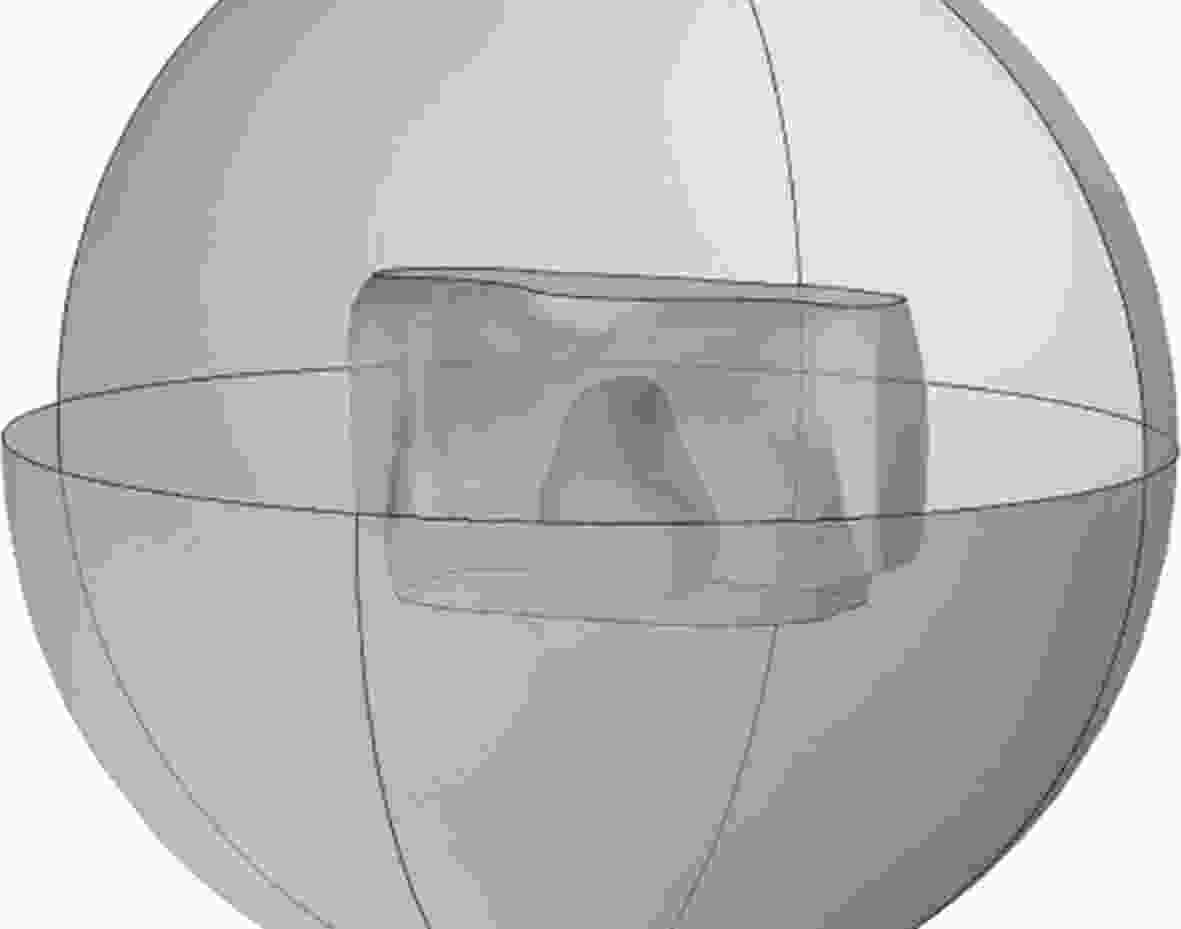图 2 个性化心脏-躯干三维几何模型
Figure2. Personalized three-dimensional heart-torso model.

2 -->

2.2.心脏电生理扩散模型

根据心脏TMP演变的特点, 构建能较好模拟兴奋传导且计算代价较小的电生理扩散模型. 心脏去极化和复极化过程中, 心肌细胞膜内外离子发生转移, TMP发生变化. 不同位置的细胞TMP变化整体上表现为宏观层面的心脏电兴奋传导. FHN模型^[18]是一种定性研究心脏电生理学活动的反应扩散系统经典模型, 最早由Hodgkin和Huxley^[7]通过简化多变量的Hodgkin-Huxley细胞模型得到. 与元胞自动机模型模拟电兴奋类似, FHN模型并不直接模拟单个细胞的兴奋特性和细胞之间的偶联关系. 由于不必大规模计算心脏细胞兴奋特性, 因此可用较小的计算代价仿真心脏电生理活动的TMP动态特性. 而基于简单规则的元胞自动机模型对解释电兴奋传导的物理过程不利^[19]. FHN模型包含描述动作电位产生的细胞模型和心肌兴奋传导的扩散模型, 较符合实际的电兴奋传导特征. FHN模型是由两个未知变量的非线性偏微分方程组成的反应扩散系统:

$\begin{split}& \left\{ {\begin{aligned}& {\dfrac{{\partial u}}{{\partial t}} = \nabla \cdot \left( {{{D}}\nabla u} \right) + {f_1}\left( {u,v} \right),}\\& {\dfrac{{\partial v}}{{\partial t}} = {f_2}\left( {u,v} \right),}\end{aligned}} \right.\\& {f_1}\left( {u,v} \right) = u\left( {u - a} \right)\left( {1 - u} \right) - v,\\& {f_2}\left( {u,v} \right) = b\left( {u - dv} \right),\end{split}$

其中$u$表示激发变量, 变化范围从0到1, $\nu $表示恢复变量, $\nabla \cdot \left( {{{D}}\nabla u} \right)$表示扩散项, ${{D}}$表示扩散张量, 而${f_1}\left( {u,v} \right)$和${f_2}\left( {u,v} \right)$则定义了动作电位的形状.
FHN模型存在较多变式, 为了更为准确地表示真实心脏TMP变化(如去除原始FHN模型中实际不存在的过极化现象), 本研究采用了Aliev等^[20]修正的FHN模型

$\left\{ {\begin{aligned}& {\dfrac{{\partial u}}{{\partial t}} \!=\! \nabla \cdot \left( {{{D}}\nabla u} \right) + ku\left( {u - a} \right)\left( {1 - u} \right) \!- \!uv,}\\& {\dfrac{{\partial v}}{{\partial t}} = - e\left[ {v + ku\left( {u - a - 1} \right)} \right],}\end{aligned}} \right.$

其中参数$a = 0.15$, $e = 0.01$, $k = 8$^[21], 研究初期忽略心肌纤维的各向异性, 即假设扩散张量${{D}}$为单位矩阵. 实际的心脏TMP(${V_{\rm{m}}}$)范围是–80—20 mV, 可以表示为

${V_{\rm{m}}}\left[ {{\rm{mV}}} \right] = 100u - 80.$

通常认为心脏作为一个孤立的连续体, 即没有有功电流流入或流出心脏表面, 所以存在纽曼边界条件$\partial u/\partial {{n}} = 0$, 其中${{n}}$表示心脏边界的法向量.
2 -->

2.3.体表外心脏磁场模型

根据电磁学理论, 计算心脏电兴奋产生磁场在体内的传播过程. 人体心脏电磁场频率大约在1—100 Hz之间, 对这种频率的低频电磁场通常使用准静态电磁学的知识处理^[22].
在宏观表现为兴奋传导的TMP变化以电流密度的形式, 生成磁场在躯干以及体外传播. 心磁信号就是心脏磁场在体外的投影积分. 心脏中外电流密度${{{J}}^{\rm{i}}}$与TMP之间满足方程:

${{{J}}^{\rm{i}}} = {\sigma _{\rm{H}}}\nabla {V_{\rm{m}}},$

其中${\sigma _{\rm{H}}}$表示心脏组织的电导率(下标H是heart的缩写, 下同). 由于心脏和躯干被视为容积导体, 模型中的全电流密度${{J}}$为外电流密度${{{J}}^{\rm{i}}}$与无源容积电流密度之和:

${{J}} = - \sigma \nabla \varphi + {{{J}}^{\rm{i}}},$

其中$\sigma $表示电导率, $\varphi $表示电势. 电流密度${{J}}$满足电流守恒定律^[8]

$\nabla \cdot {{J}} = 0.$

心脏TMP转化为电流密度的变量${{{J}}^{\rm{i}}}$后, 将其应用到准静态麦克斯韦方程. 由于心磁问题满足磁准静态场, 位移电流${{{J}}_D}$远小于传导电流, 即忽略电场变化率引起的磁场变化$\dfrac{{\partial {{D}}}}{{\partial t}} \approx 0$. 磁感应强度${{B}}$满足

$\nabla \times {{B}} = \mu \left( { - \sigma \nabla \varphi + {{{J}}^{\rm{i}}}} \right),$

其中$\mu $是磁导率. 由于人体组织的无磁性, 即相对磁导率${\mu _{\rm{r}}} = 1$, $\mu = {\mu _0}{\mu _{\rm{r}}} = {\mu _0}$. 矢量磁位${{A}}$满足$ {{B}} =$$ \nabla \times {{A}}$, 并满足库仑规范, 得到

${\nabla ^2}{{A}} = - {\mu _0}{{J}}.$

由此可得, 心脏区域${\varOmega _{\rm{H}}}$和躯干区域${\varOmega _{\rm{T}}}$矢量磁位分别满足:

${\nabla ^2}{{A}} = - {\mu _0}\left( {-{\sigma _{\rm{H}}}\nabla \varphi + {{{J}}^{\rm{i}}}} \right),$

${\nabla ^2}{{A}} = - {\mu _0}\left( {-{\sigma _{\rm{T}}}\nabla \varphi } \right),$

其中${\sigma _{\rm{T}}}$表示躯干电导率. 由于体外空气域${\varOmega _{\rm{A}}}$的电导率非常小, 忽略体外电流, 体表外区域矢量磁位满足

${\nabla ^2}{{A}} = 0.$

根据电磁学理论可知, 磁场传播在心脏表面${\varGamma _{\rm{H}}}$和体表${\varGamma _{\rm{T}}}$的边界条件都分别满足, 磁感应强度法向量方向相同${{{B}}_{1{\rm{n}}}} = {{{B}}_{2{\rm{n}}}}$, 磁场切线方向相同${{{H}}_{1{\rm{t}}}} = {{{H}}_{2{\rm{t}}}}$.
2 -->

2.4.模型的有限元仿真计算

分别对心脏电生理扩散模型和体表外心脏磁场模型进行数值计算, 最终合成完整的心磁正问题计算框架. 求解复杂边界下的偏微分方程和物理场问题的数值解通常包括边界元法(boundary element method, BEM)^[23]、有限元法(finite element method, FEM)^[24]、无网格法(meshfree method)^[25]等. 本研究采用了FEM对心磁正问题进行计算. 由于使用等效积分弱形式的方式相对于变分法使用范围更广泛, 能较好地应对偏微分方程和电磁学问题. 另外, 伽辽金法在加权余数法中拥有更加优异的精度^[26], 因此本研究采用了伽辽金法对心脏电生理扩散模型和体表外心脏磁场模型进行数值计算.
本文采用二阶10节点的四面体单元, 对心脏、躯干以及体外空气域进行离散化处理, 以便进行有限元计算, 如图3所示. 为准确仿真心脏电生理活动和体表外磁场分布, 并考虑计算成本, 采取相对密集的心脏四面体网格与相对稀疏的躯干四面体网格, 如图4所示. 心脏部分包括9723个四面体单元, 躯干部分包括11698个四面体单元, 而空气域部分包括10762个四面体单元(图中未显示空气域).
图 3 二阶10节点四面体单元
Figure3. The second-order tetrahedral element with 10 nodes.

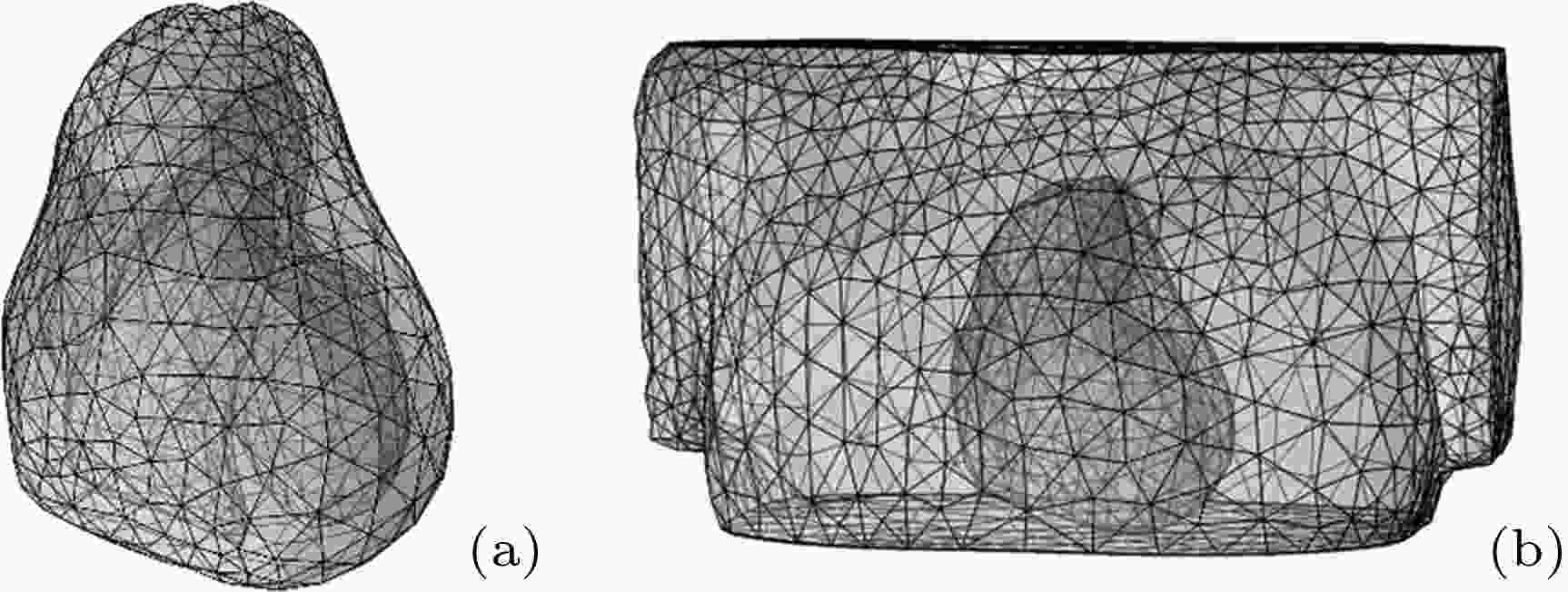图 4 离散的心脏-躯干三维模型　(a) 心脏三维模型; (b) 心脏-躯干模型组合
Figure4. Discretized three-dimensional heart-torso model: (a) 3D cardiac model; (b) heart-torso model.

本研究采用的单元形函数类型为二阶拉格朗日单元^[27]. 这种单元类型可以更好模拟弯曲的边界, 对拥有不规则几何的心脏和躯干模型具有较好的计算精度. 伽辽金法的特点是选取形函数作为权函数, 最终获得含待定系数的有限元方程, 通过计算有限元方程求得相应数值解.
本研究首先求得心脏电生理模型中不同坐标和时间的TMP分布. 之后将TMP转化为电流密度参数, 应用到体表外心脏磁场模型, 最终求得在体表外磁场的分布情况.
2 -->

2.5.心磁计算框架的解析解验证

本研究分别设计了一维状态的反应扩散模型和三维简化几何的磁场模型, 通过求解上述简化模型的精确解, 并与相应FEM数值解进行误差分析, 最终验证心磁正问题计算框架数值解的可信度.
本研究对FHN模型的有限元数值解的准确性进行验证, 以保证心脏电生理扩散模型的准确性. 为了能简便求得FHN模型解析解, 本研究考虑一维条件下的FHN方程, 并与对应条件下的伽辽金有限元数值解进行对比. 由于FHN方程由两个相互耦合的非线性偏微分方程构成, 因此对方程组的求解具有困难. 本文考虑适当简化FHN方程组, 再对方程进行求解.
以原始FHN方程(1)为例, 由于在心脏电生理模型中, 参数$b$满足$0 < b < < 1$, 因此可以认为因变量$v$对时间$t$的偏导为0, 即$v$为常数, 进一步假设$v$为0. FHN方程组可以简化为一个非线性反应扩散方程

$\frac{{\partial u}}{{\partial t}} = D\frac{{{\partial ^2}u}}{{\partial {x^2}}} + u\left( {u - a} \right)\left( {1 - u} \right).$

较多文献对反应扩散方程(12)式有研究, 如通过李群法^[28]、Tanh法^[29]、变系数Bernoulli辅助法^[30]等求得反应扩散方程的多个解析解.
本文参考Tanh法^[29], 对反应扩散方程进行精确解计算. 假设方程(12)存在行波解, 并设$u\left( {x,t} \right) = u\left( \xi \right)$, 其中$\xi = k\left( {x - ct} \right)$, 将方程转化为$u$关于$\xi $的常微分方程. 可以通过构造$Y = {\tanh ^2}\xi $, 变换$\dfrac{{{\rm{d}}u}}{{{\rm{d}}\xi }} = 1 - {Y^2}$, 根据齐次平衡原则得到关于$Y$的齐次方程. 根据方程系数都为0的特性, 可以求得若干行波解, 具体过程本文不再详述. 可以将精确解与对应数值解进行误差分析, 验证简化的心脏电生理学模型的精确性.
另一方面, 为了验证体表外磁场数值解的精确性, 本研究建立了一个简易几何的测试模型, 并在测试模型下求解基于麦克斯韦方程组的磁场解析解.
在BSPM的仿真中, Fischer等^[24]采用了同心球模型进行解析验证. 即用同心内球的电势分布表示心脏TMP分布情况, 通过求解外球电势模拟躯干表面的电势分布. 本文首先假定内球中存在均匀并垂直向上的电流密度${{{J}}^{\rm{i}}}$. 模型内各点磁感应强度已由Geselowitz给出^[31]:

${{B}} = \frac{{{\mu _0}}}{{4{\text{π}}}}\left[ {\int {\frac{{{{{J}}^{\rm{i}}} \times {{R}}}}{{{R^3}}}{\rm{d}}v - \sum {{\sigma _{\rm{i}}}\nabla V} } \times \nabla \left( {\frac{1}{{{R}}}} \right){\rm{d}}v} \right],$

其中${{R}}$为场点到源点的向量, ${\sigma _{\rm{i}}}$表示各区域的电导率. 直接求解内球电流产生磁场的分布情况存在困难. 由于对称性, 柱坐标系下内球电流所产生的磁场不存在$r$和$z$方向的磁场分量, 即磁场方向为方位角$\varphi $方向. 这与有限长直导线产生的磁场方向一致.
假设长度$L$, 电流为$I$的直导线等价贡献了内球电流产生的磁场. 并假设外球导电率${\sigma _{\rm{T}}}$远小于1, 即忽略(13)式等号右边的第二项, 求解磁场在半径为$R$的外球中的分布. 简化后的直导线模型产生的磁感应强度${{B}}$为

${{B}} = \dfrac{{{\mu _0}}}{{4{\text{π}}}}\int_L {\frac{{I{\rm{d}}{{l}} \times {{R}}}}{{{R^3}}}} ,$

其中${{R}}$为场点${{r}} = \left( {r,\varphi,z} \right)$到源点${{r}}' = \left( {0,0,z'} \right)$的向量${{R}} = {{r}} - {{r'}} = r{{{e}}_r} + \left( {z - z'} \right){{{e}}_z}$. 将(14)式在柱坐标系下进行积分计算:

$B = \frac{{{\mu _0}}}{{4{\text{π}}}}\int_{ - \frac{L}{2}}^{\frac{L}{2}} {\frac{{{\rm{d}}z' \cdot {{{e}}_z} \times \left[ {r{{{e}}_r} + \left( {z - z'{{{e}}_z}} \right)} \right]}}{{{{\left[ {{r^2} + {{\left( {z - z'} \right)}^2}} \right]}^{\frac{3}{2}}}}}},$

简化(15)式, 可以求得

${{B}} = {{{e}}_\varphi }\frac{{{\mu _{\rm{0}}}I}}{{4{\text{π}}r}}\left. {\frac{{z - z'}}{{{{\left[ {{r^2} + {{\left( {z - z'} \right)}^2}} \right]}^{1/2}}}}} \right|_{z' = L/2}^{z' = - L/2}.$

(16)式表示有限长直导线模型在大球内的磁场分布的解析解, 之后将与对应数值解进行误差分析.

2

-->

3.1.心脏电生理扩散模型的验证和结果

通过Tanh法, 求得了一维条件下简化的FHN方程的15个行波解, 本文以其中一个解为例

$u\left( {x,t} \right) = \frac{1}{2} - \frac{1}{2}\tanh \left( {\frac{x}{{2\sqrt {2D} }} + \frac{1}{4}\left( {2a - 1} \right)t} \right).$

将t = 0时(17)式求得的$u\left( {x,0} \right)$作为(12)式的初值条件, 求解在一维条件下的有限元数值解. 分别求得t = 20, 40, 60三个时刻$x$在0—40范围内各134个数据点的数值解. 通过与相同时刻、坐标下的解析解进行对比, 验证简化后的FHN方程在一维条件下用伽辽金法求解的精确性. 定义相对均方根误差(relative root mean squared error, RRMSE)

${\rm{RRMSE}} = \sqrt {\frac{{{{\sum\limits_N {\left( {{b_n} - {a_n}} \right)} }^2}}}{{\sum\limits_N {a_n^{\rm{2}}} }}} \times 100\% ,$

其中${a_n}$为模型解析解, ${b_n}$为模型数值解, $N$为数值解的所有时间步长或计算节点.
图5显示了FHN方程的解析解与数值解的激发电位曲线图. 求得在$t = 20,\;40,\;60$时, 简化的FHN方程解析解与对应数值解之间的${\rm{RRMSE}}$分别为0.39%, 0.53%和0.79%, 如表1所列. 结果显示, 在一维条件下用伽辽金法求得简化后的FHN方程的数值解与Tanh法求得的解析解的误差较小, 展现了较好的准确性. 可以相信本研究通过伽辽金法求解的心脏电生理扩散模型的结果是有保障的.
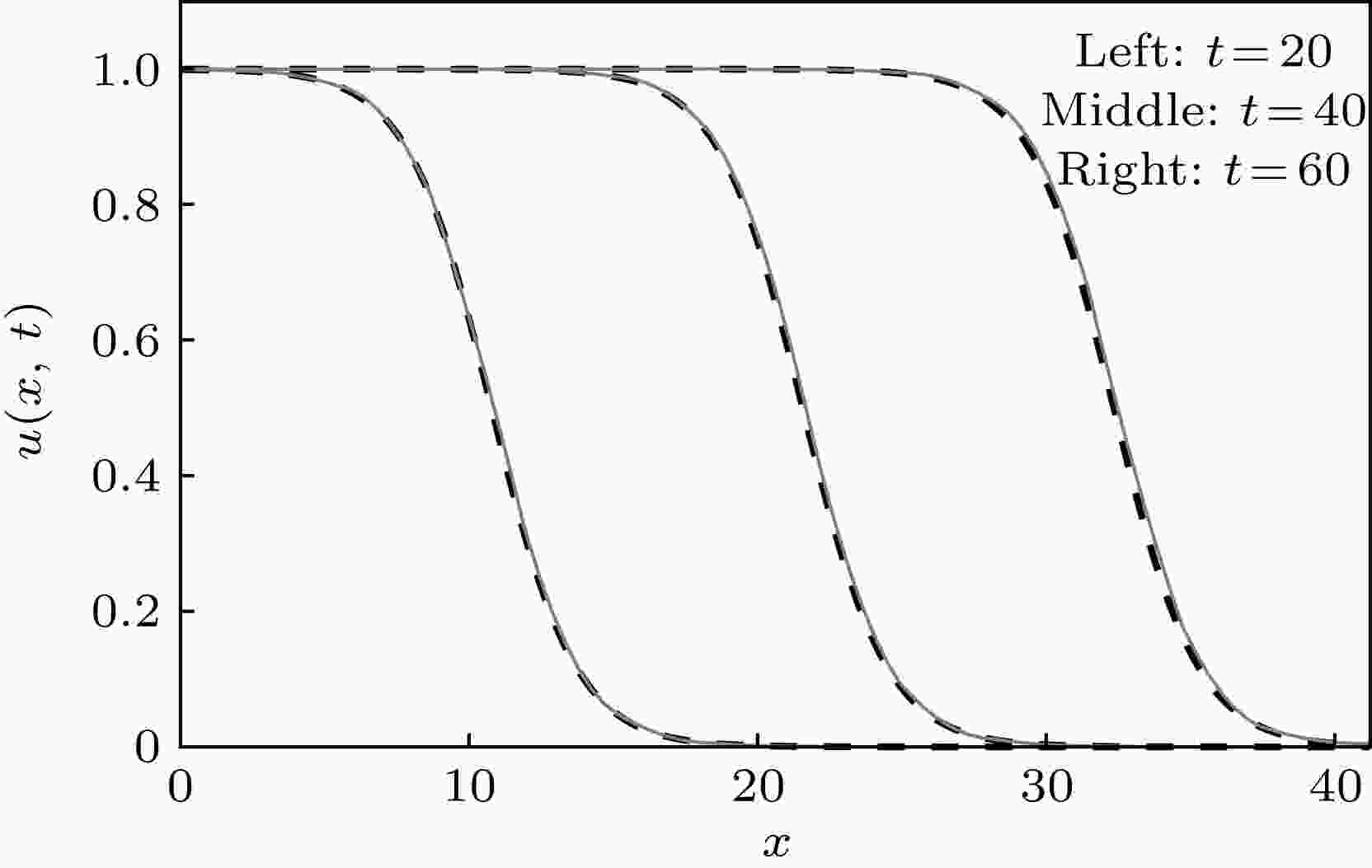图 5 t = 20, 40, 60时, 激发电位u的变化　实线: FHN方程数值解; 虚线: FHN方程行波解
Figure5. Evolution of excitation potential u at t = 20, 40, 60. Solid line: numerical solution of FHN equation. Dotted line: analytical solution of FHN equation.

时间	t = 20	t = 40	t = 60
RRMSE	0.39%	0.53%	0.79%

表1FHN方程相对均方根误差RRMSE
Table1.Relative root mean squared error of FHN equation.

在求解心脏电生理扩散模型前, 需要假定修改的FHN方程初值条件. 由于正常功能的心脏是窦性心律的, 即窦房结作为心脏正常起搏点, 产生激发电位, 并形成TMP的传播. 因此可以设定在窦房结位置导入一个$u = 1$的激发电位, 作为FHN方程的初值条件模拟TMP兴奋的激发. 之后通过有限元法计算, 可得到心脏TMP随时间$t$变化的动态分布.
图6所示为在一个完整的心动周期中, 心室的TMP分布的演变情况. 其中图6(a)—图6(c)表示心室去极化过程, 对应时刻分别为t = 30, 60, 90. 而图6(d)—图6(f)表示心室复极化过程, 对应时刻分别为t = 120, 150, 180. 分别取左右心室的心外膜上一点, 观察TMP随时间的变化, 如图7所示. 其中实线表示右心室心外膜上一点的TMP变化, 虚线表示左心室心外膜上一点的TMP变化. 这与文献中正常心率的心室跨膜电位波形一致^[32], 表明了以修正的FHN方程为基础的心脏电生理扩散模型是符合真实心脏电生理活动特性的.
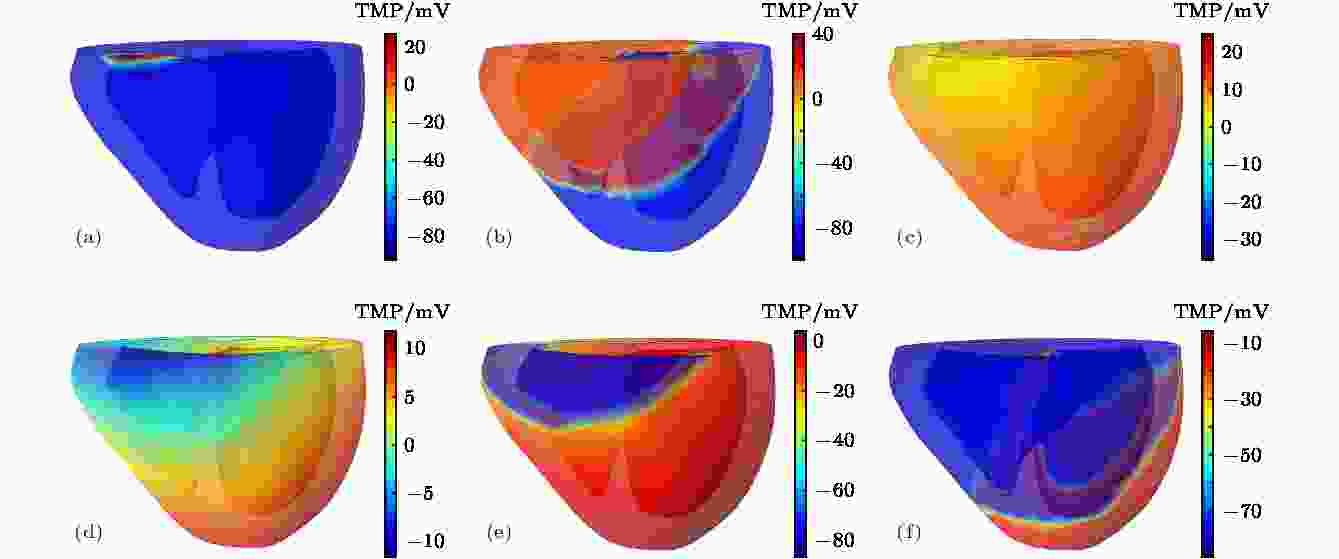图 6 一个心动周期的TMP分布图　(a), (b), (c) 为去极化过程 (t = 30, 60, 90); (d), (e), (f)为复极化过程(t = 120, 150, 180)
Figure6. TMP distribution of a cardiac cycle: (a), (b), (c) Depolarization process (t = 30, 60, 90); (d), (e), (f) repolarization process (t = 120, 150, 180).

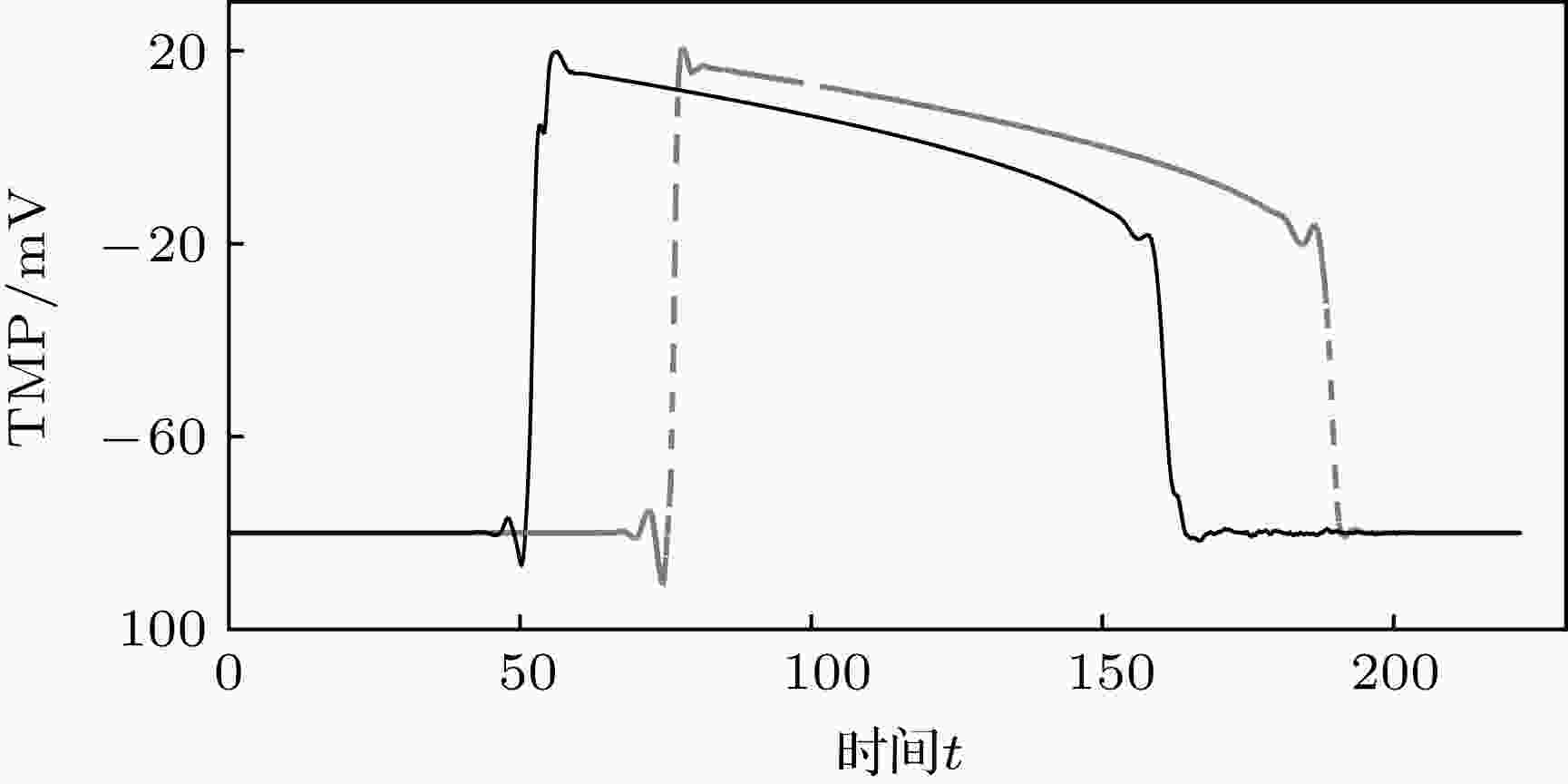图 7 TMP随时间变化曲线　实线: 右心室TMP变化; 虚线: 左心室TMP变化
Figure7. TMP time evolution curve, solid line: right ventricular TMP; dashed line: left ventricular TMP.

2 -->

3.2.体表外磁场的验证和仿真结果

如图8(a)显示的是在直导线模型中, 中轴面上$\varphi $方向磁感应强度${{{B}}_\varphi }$的分布情况. 图8(b)显示了${{{B}}_\varphi }$的数值解与解析解的曲线图, 其中仿真过程中直导线的线径$r = 0.1\;\operatorname{m} $无法忽略. 使用相对误差(relative error, RE)求解中轴面上各坐标点的磁场数值解与解析解之间的误差
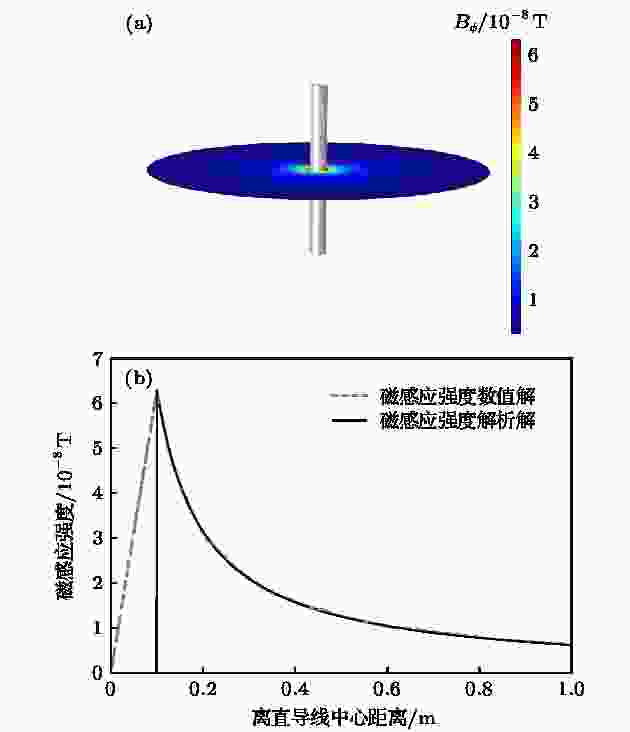图 8 (a) 直导线模型; (b)中轴面磁感应强度的分布, 实线: 解析解; 虚线: 数值解
Figure8. (a) Straight wire model; (b) distribution of magnetic field on the axial plane. Solid line: analytical solution; dotted line: numerical solution.

${\rm{RE}} = {{\left| {{b_n} - {a_n}} \right|}}/{{{a_n}}} \times 100\%,$

其中${a_n}$为模型解析解, ${b_n}$为模型数值解. 图9显示了中轴面上磁感应强度${{{B}}_\varphi }$解的相对误差RE分布. 其中散点表示中轴面上离导线中心各距离所对应的误差分布. 而RE曲线由基于最小二乘法的二次多项式拟合得到. 从图9中可以看出, 随着离直导线中心距离的增加, RE也随之变大. $0.1 \leqslant r \leqslant 1.0\; {\rm{m}}$时, ${\rm{RE}}$最大为2.85%. 对比心脏到体表处的距离, 我们认为这个误差是可以接受的. 经过直导线模型的计算验证, 说明构建的伽辽金法求解体表外心脏磁场模型是可行的.
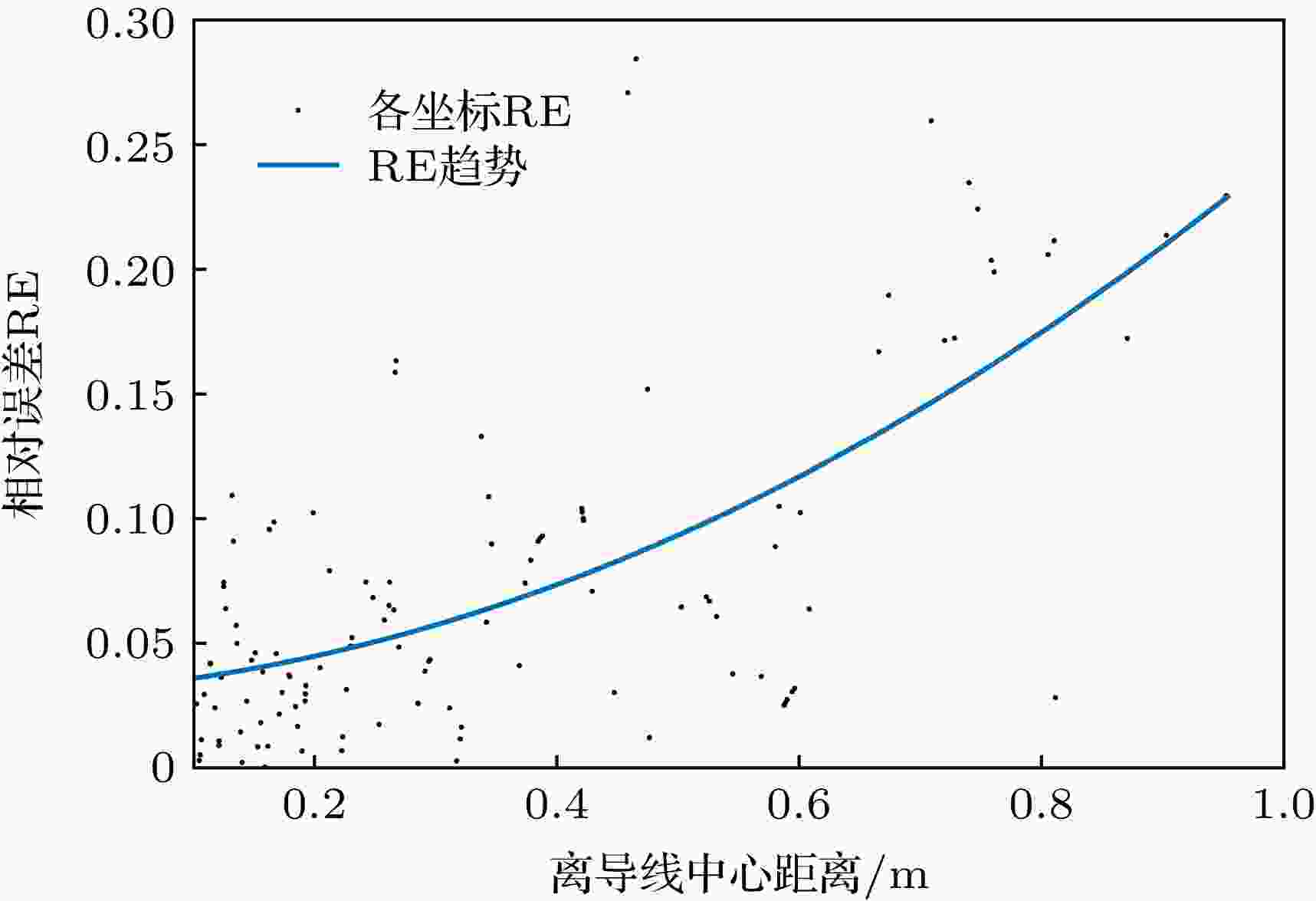图 9 磁场的相对误差分布
Figure9. Relative error distribution of magnetic field.

在心脏电磁场正问题中, 为较好地模拟心脏产生的磁场在体表外的分布, 通常需要设置各向异性的心脏电导率, 而由于躯干电导率对心磁传播影响较小, 通常设置为各向同性的躯干电导率. 但由于被试的MRI数据不包含心肌纤维取向, 因此本研究建立的个性化三维心脏-躯干几何模型前期并未考虑心肌细胞的纤维取向, 并设定心脏电导率${\sigma _{\rm{H}}} = 0.48$ S/m, 躯干电导率${\sigma _{\rm{T}}} = 0.2$ S/m^[21].
本研究在胸腔前方约5 mm处模拟设置一个探测传感器, 仿真计算在该平面的磁场分布情况, 即求解体外该平面处的磁场数值解. 通过将心脏电生理扩散模型随时间变化的结果应用到静态的体表外心脏磁场模型, 即可求得该探测平面的不同时刻的磁感应强度分布状况.
图10(a)—图10(h), 显示了本研究仿真的垂直于探测平面体表外磁感应强度${{{B}}_z}$在一个心动周期内的分布状况. 从图中可以看出, 仿真的心脏磁场在垂直于探测面方向存在两极对称的形态. 在同一个心动周期中, 随着心脏从去极化向复极化过程的演变, 磁场两极相对位置发生了变化. 而图10(i)是用9通道心磁图仪采集人体心磁信号, 并通过线性插值得到的健康人体表心磁图^[33]. 该心磁地图与心脏功能异常的心磁图在进行了对比, 显示正常心磁地图在形态上拥有规则的两极形态特征.
图 10 体表外磁感应强度${{{B}}_z}$分布　(a)?(h) 模拟的心磁分布图(t = 40, 60, 80, 100, 120, 140, 160, 180)；(i) 文献中的实测心磁图分布图^[26]
Figure10. Extracorporeal magnetic field distribution: (a)?(h) Simulated cardiac magnetic distribution (t = 40, 60, 80, 100, 120, 140, 160, 180); (i) measured human MCG in the literature.

对比图10(a)—图10(h)与图10(i), 看到本研究仿真模拟得到的心磁图与实测心磁图在形态上是类似的, 因此可以定性地表明本研究建立的计算框架是可行的.

本研究构建的几何模型数据来自被试的MRI切片数据. 由于MRI切片数据的高精度性以及需求的可定制性, 为更好地用于分割重建真实并且各种分辨率的三维心脏-躯干几何模型提供了基础. 并且为后续定制化仿真被试的心磁分布与实测心磁图的对比提供了良好的条件.
本研究采用修正的FHN方程组作为心脏电生理扩散模型的基础, 模拟的心脏跨膜电位传播过程符合心脏电生理实际状况, 对深入理解心脏电生理活动过程较为有利. 另一方面, 反应扩散模型以较小的计算代价仿真心脏电生理活动过程, 展现了一定的优势.
本研究对心磁正问题计算框架进行了解析解验证. 首先, 在一维条件下求解简化的FHN方程解析解, 与相同情况方程伽辽金有限元法数值解对比. 其次, 简化体表外心脏磁场模型为直导线模型, 求解模型磁感应强度解析解与有限元解对比. 通过对上述解的误差分析, 证明了该计算框架计算心脏电生理活动和体表磁场的可行性.
该计算框架有较好的扩展能力. 通过替换所需的心脏-躯干几何模型, 可以个性化仿真不同被试者的心脏电生理活动和体表心磁信号. 另一方面, 可以通过修改FHN方程组参数, 甚至修改FHN方程组形式, 模拟不同状态或者心律失常等疾病状况下心脏跨膜电位不同或异常波形产生的异常磁场分布, 并加以总结和分析. 此外, 通过设置不同位置的激发电位模拟心脏异常起搏点位置, 模拟非窦性心律情况的心磁分布状况. 也可以通过抑制心脏中某些位置的兴奋传导, 模拟左束支传导阻滞(left bundle branch block, LBBB)或右束支传导阻滞(right bundle branch block, RBBB)等异常传导状态下心脏电生理活动和和心磁信号特征. 该计算框架在这些情况都保留了优异的扩展能力.
但是, 本研究仍然存在一些不足. 首先, 研究前期的三维心脏几何模型较为简陋, 虽然采用了人体真实三维心脏作为模型对象, 但是未准确分割出包括窦房结具体形态在内的各部分结构细节, 只是在窦房结对应位置设置了兴奋激发的位置. 其次, 忽略了重要的心脏内外膜与心肌细胞的纤维取向扩散张量, 但实际情况中TMP传播过程受心脏各向异性结构的影响较大, 使得心脏电生理模型与实际情况存在较大差异. 传统的心脏纤维取向的设定依靠人为定义, 这种方式与心脏实际的心肌旋向存在差异. 而扩散张量磁共振成像(DTMRI)等技术可以映射心脏几何模型的真实纤维结构^[34], 使得心脏电兴奋传播过程能受到纤维各向异性的电导率张量影响. 为了心脏三维几何模型更贴近实际情况, 后期应该将心脏纤维数据加入模型, 以提高心磁正问题计算框架的精确性. 另外, 本研究只考虑了静止空间状态下的心磁正问题, 并未讨论心脏收缩和舒张对心脏电生理活动和体表磁场带来的影响. 因此, 本文只定性地将求得的心磁分布图与实际的心磁图进行比较, 用以验证本研究计算框架的可行性. 但是该心磁计算框架较好的扩展能力为进一步优化心脏几何结构等提供了基础.
由于MCG的优势, 以及开始在临床用于互补心电图的前景, 本研究构建了一个心磁正向问题计算框架. 该框架包括建立一个个性化三维心脏躯干几何, 在该几何模型的基础上, 通过构建心脏电生理扩散模型和体表外心脏磁场模型, 研究心脏电生理活动的演变以及由此产生的体表磁场的分布. 通过该框架, 可以仿真基于真实心脏-躯干模型的心脏TMP传播和体表外磁场分布状况. 最后使用简化的一维FHN方程和直导线模型验证了心磁正问题计算框架的可行性. 这为后续心磁逆问题打下坚实基础.